伴随着交通监测设备的广泛使用，智能交通系统可以广泛采集城市路网及高速公路上的交通流量。在这一背景下，交通流预测的目标是根据交通网络上的历史信息，对未来一段时间内交通流量进行预测。准确有效的交通流预测可以帮助交管部门更合理地引导车辆，提升路网的运营服务能力和效率，同时有助于减少拥堵，避免事故，节约人们的外出时限和成本费用^[1]。

交通流预测的本质是时空流数据的学习和预测，其模式往往伴随时间和空间的变化。现有研究中，已经有一些工作着眼于捕捉交通流的时空变化^[2]，然而依然面临以下挑战。(1) 交通流的变化模式同时依赖于时空2个维度上的历史信息。各个网络区域相互之间的流量密度会改变，相应地，附近相邻的网络区域各个时间的历史流量也会给与其有关联的区域未来时间的流量带来影响。(2) 时间本身具有的多粒度特性。某个区域各个时间的历史流量会对该区域未来时间的流量产生影响，并且时间往往不是单一的一天或者一个小时，每个时间的流量都不同^[3]。所以，要从此类复杂且高度非线性的时空数据中发掘出时间与空间的模式，同时能够与实际问题相结合，就需要空间信息的整合和对时间多粒度特性的思考，从而进行更加精准的预测。

为解决上述问题，本文提出一种多粒度时空深度回归模型(Spatial-temporal Deep Regression Model for Multi-granularity，MGSTDR)，通过建模和捕获数据的时空特性，有效处理和学习路网上交通流量的模式变化。具体而言：(1) 针对交通流量的模式变化受到时间和空间影响的特性，设计了多粒度时间和空间邻域信息的融合学习模块，通过神经网络组件将两个维度的历史信息进行融合并输出。(2) 针对时间多粒度特性，采用平均池化和多层感知机技术分别捕获中心及相邻区域不同粒度下的自身历史信息和邻居信息，将时间划分为小时周期、时段周期和日周期3个粒度。最后通过引入多粒度时空信息相关的损失函数，引导模型的训练过程。本文的主要贡献概括如下。

(1) 针对多粒度交通流预测这一独特而实际的问题，提出了一类能够建模和捕捉不同时间粒度模式的学习方法，实现了多粒度的时序交通流预测。

(2) 改进了时间序列领域中的ARIMA(Autoregressive Integrated Moving Average)模型，提出了一类可以同时捕捉时间和空间双维度依赖关系的神经网络化的ARIMA学习方法(MGSTDR)，可以为当前时间序列模型的深度化提供一种新的思路。

(3) 本文提出的模型在实际的城市道路数据集上的实验结果表明，其预测效果优于当前其他的预测方法。

1 相关工作

交通流量预测的研究已有几十年的历史，经过不断的钻研和实践，取得了大量的成果。

1.1 基于时序模式的交通流预测

目前基于时序模式的交通流预测算法已走向成熟，例如历史均值法、整合移动平均自回归模型ARIMA^[4]等经典的研究方法。历史均值法是以某一变量历史数据的平均值为根据，从而对其未来进行预测。ARIMA模型^[5]是通过寻找历史数据之间的自相关性，描述当前值与历史值之间的关系，来预测未来(假设未来将重复历史的走势)，要求序列必须是平稳的。然而现实中往往都是复杂非线性、非平稳的数据，由于它们通常很难满足上述的前提假设，因此这类方法的数据处理能力不足。交通预测根据想要预测时间的不同又可以分为不同的区间(短期、中期、长期)，大多数目前流行的方法都能在短期预测内表现良好，但在长期的时间序列预测中表现欠佳。Yang等^[6]使用具有特征增强的长短期记忆(Long Short-Term Memory, LSTM)进行交通流预测，将非常长的序列时间步长的高影响值连接到当前时间步长，并使用注意力机制捕获这些高影响流量值，同时，对一些超出正常范围的数据进行平滑处理。Zhang等^[7]提出了图注意−卷积−注意网络(Graph Attention-Convolution-Attention Networks, GACAN)模型，用图注意力层捕获时间特征，整合了4种不同时间粒度的时间序列：原始时间序列，以及每小时、每日和每周时间序列。

1.2 基于时空相关性的交通流预测

随着更深入的研究，学者们发现交通数据并不仅仅只是与时间相关，更与空间紧密联系。近年来基于时空相关性的交通流预测方法也日渐成熟，Wu等^[8]在充分考虑交通流数据的情况下，数据的空间特性和短期变化、周期性分别通过一维的卷积神经网络(Convolution Neural Network，CNN) 和2个LSTM来捕获和挖掘，期望将特征融合，实现短期预测的目标。Ma等^[9]为实现对大规模、全网络的流量速度进行高精度预测的目标，选择用图像来表示流量的学习。交通流时空关系的图像由二维时空矩阵将时空交通动态数据转换而成。由此提出了一种采用CNN的方法。CNN将抽象交通特征提取和网络范围的交通速度预测这2个连续的步骤应用于图像。Zhang等^[10]考虑到时空数据的动态特性，设计了由时空和全局2个部分组成的基于深度学习的预测模型(Deep Learning-based Prediction Model，DeepST)。时空模块主要捕捉空间近距和远距之间的依赖关系，还有时间的紧密度、周期性以及趋势。全局模块主要用于捕捉时间具体代表周末或者工作日这类全局因素。Zheng等^[11]发掘人群流量的特征与交通流量的特征相似，因此，他们使用残差神经网络框架来拟合人群流量数据的时间邻近程度、周期性以及趋势属性，提出了一种可以同时预测城市各个区域的人群流入流出，以深度学习为基础的端到端的方法，称为ST-ResNet。Cheng等^[12]利用循环神经网络(Recurrent Neural Network ，RNN) 和CNN来捕获时空流量，传递拓扑网络中的信息，另外，加入了用注意机制将空间和时间信息对齐的名为DeepTransport的端到端框架。

但是上文中所提到的这些模型方法均在不同的问题上存在不足，因此，本文针对非平稳且存在图结构的交通流量数据提出基于多粒度时序的深度学习模型，同时捕获空间与时间上的信息，有效地解决交通流预测问题。

2 问题定义

定义1 　本文将空间道路网络定义为无向图G=(V，E)，如图1(a)所示。其中，V为节点集，|V|=N为节点个数；E 为边集，代表节点间的连通性。节点V是从图1(b)的经纬度网格中筛选的含有一阶邻居的中心节点。

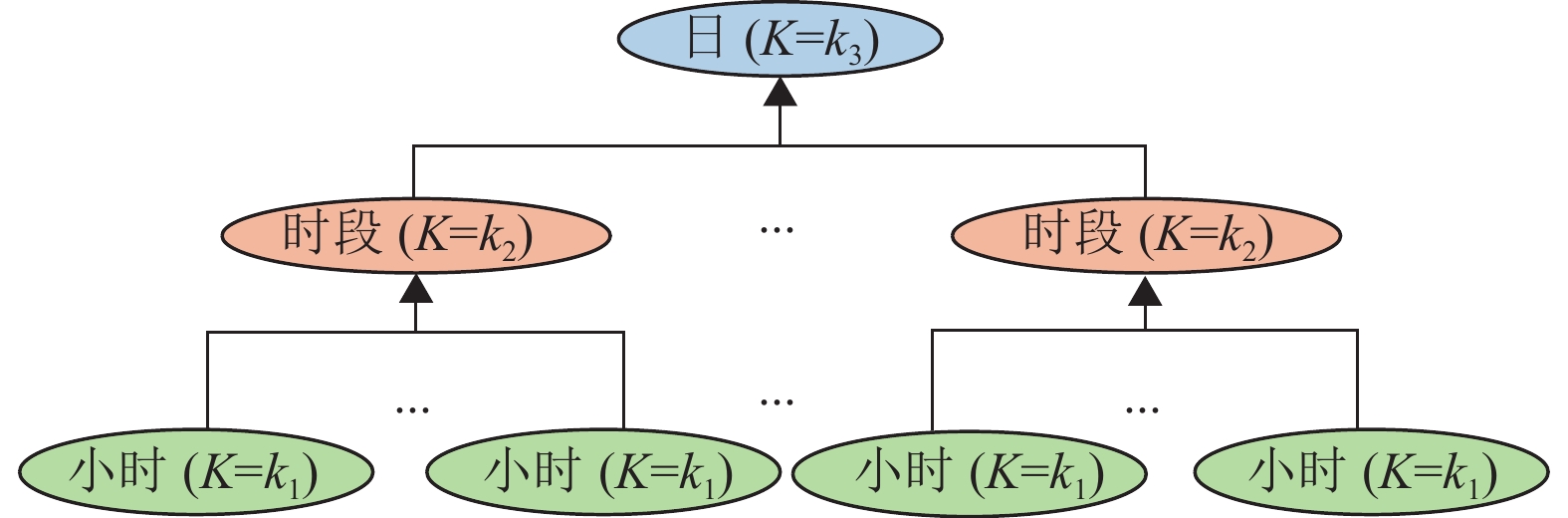
时间是一类实数值顺序变量，可以按照不同粒度划分不同的单元。记K为从细到粗的不同粒度层次，图2展示了一个3层粒度的时间划分。其中K=k₁, k₂, k₃分别表示小时、时段、日各粒度所在的时间层次。

设空间路网G中某一节点的第 $ s \in \left( {1, \cdots ,S} \right) $ 个时间序列为流量序列，预测未来某个时期内此节点不同时间粒度的流量是本文的目标。形式化定义如下。

定义2(多粒度交通流预测) 　用 $ x_{t - 1,c}^K\left( i \right) \in {\bf{R}} $ 表示中心节点的第t−1天中第K层粒度第i个时刻的车流量， $ x_{t - 1,d}^K\left( i \right) \in {\bf{R}} $ 表示第 $ d \in \left( {1, \cdots ,8} \right) $ 个邻居节点的第t−1天中第K层粒度第i个时刻的车流量，其中，d是c的一阶邻居。已知c节点和所有邻居节点历史的流量序列，预测t天c节点的不同时间粒度(例如 $ K = {k_1}, {k_2},{k_3} $ 的流量值)，具体如式(1)所示。

$ y_{t,c}^K = \left\langle {\begin{array}{*{20}{c}} {y_{t,c}^K\left( i \right), }& \cdots &,{y_{t,c}^K\left( {n - 1} \right) } \end{array}} \right\rangle $

(1)

下面以时段为例。

中心节点c在t−1天凌晨、上午、下午、晚上这4个时段的流量序列为

$ \left\langle {\begin{array}{*{20}{c}} {x_{t - 1,c}^2\left( 0 \right) ,}& {x_{t - 1,c}^2\left( 1 \right) ,}& {x_{t - 1,c}^2\left( 2 \right) ,}& {x_{t - 1,c}^2\left( 3 \right) } \end{array}} \right\rangle $

(2)

邻居节点d在t−1天凌晨、上午、下午、晚上这4个时段的流量序列为

$ \left\langle {\begin{array}{*{20}{c}} {x_{t - 1,1}^2\left( 0 \right) ,}& {x_{t - 1,2}^2\left( 0 \right) ,}&{ \cdots }&,{x_{t - 1,8}^2\left( 0 \right) } \end{array}} \right\rangle $

(3)

$ \left\langle {\begin{array}{*{20}{c}} {x_{t - 1,1}^2\left( 1 \right) ,}& {x_{t - 1,2}^2\left( 1 \right) ,}&{ \cdots }&,{x_{t - 1,8}^2\left( 1 \right) } \end{array}} \right\rangle $

(4)

$ \left\langle {\begin{array}{*{20}{c}} {x_{t - 1,1}^2\left( 2 \right) ,}& {x_{t - 1,2}^2\left( 2 \right) ,}&{ \cdots }&,{x_{t - 1,8}^2\left( 2 \right) } \end{array}} \right\rangle $

(5)

$ \left\langle {\begin{array}{*{20}{c}} {x_{t - 1,1}^2\left( 3 \right) ,}& {x_{t - 1,2}^2\left( 3 \right) ,}&{ \cdots }&,{x_{t - 1,8}^2\left( 3 \right) } \end{array}} \right\rangle $

(6)

运用中心节点第t−1天的4个时段的流量序列式(2) 和邻居节点0这个时段的流量序列式(3) 来预测中心节点第t天0这个时段的流量值 $ y_{t,c}^2\left( 0 \right) $ ，另外3个时段如上述示例一样。表1列出了本文的符号约定。

3 面向多粒度交通流预测的时空深度回归模型

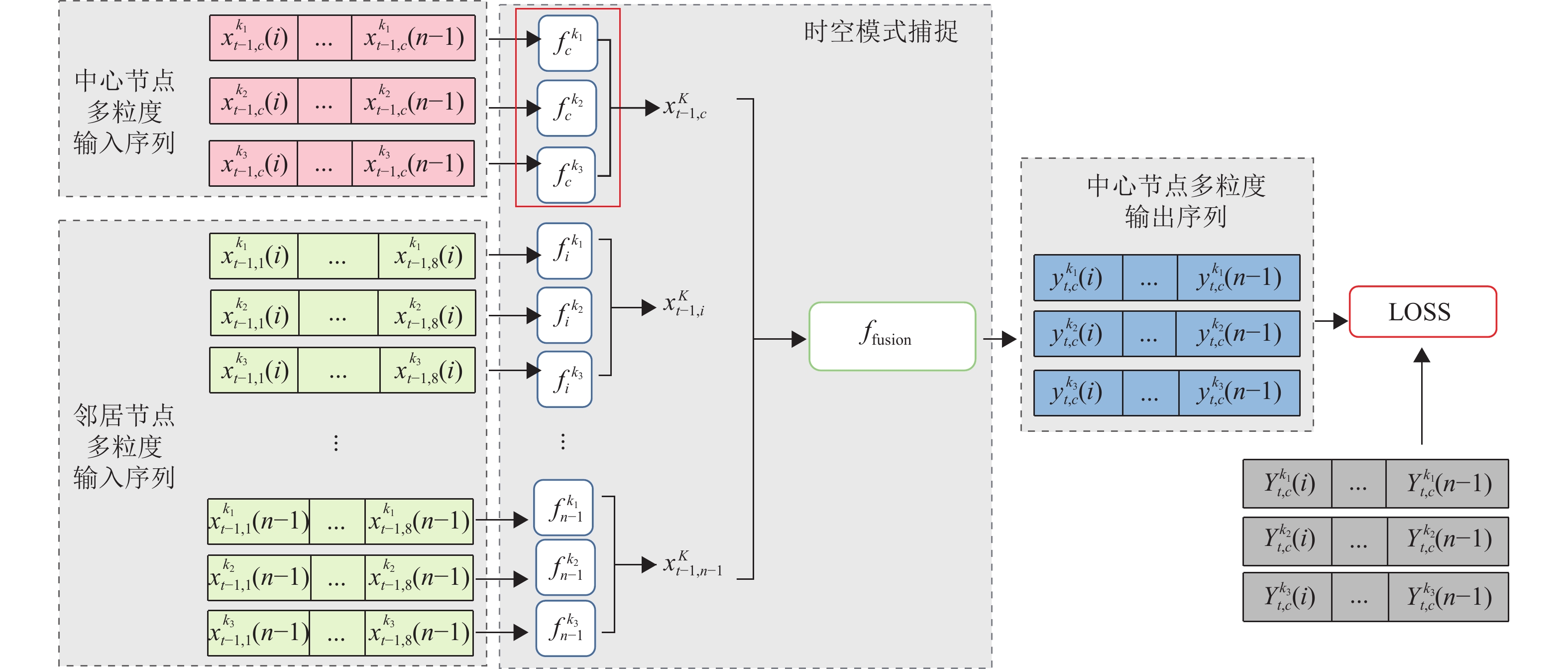
图3展示了本文提出的MGSTDR的总体结构,它由3个主要部分构成，分别用来建模中心节点及其周围邻居节点前一天的小时周期、时段周期和日周期的输入流量值，以及学习各个周期邻居节点的权重。例如，对某一个区域当天上午这个时间段的车流量进行预测，那么该区域前一天的所有时间段及其周围邻居区域前一天上午这个时间段的道路交通数据都会对该预测问题提供可用有效信息，而当天上午之前也就是凌晨这个时间段的道路交通情况与本文的预测目标关系不大。另外2个时间粒度的流量预测也采用上述同样的方法。为确保获取到足够多的节点信息，这里设计了2个组件分别用来描述中心节点区域和其周围邻居节点区域的3个时间粒度序列值。

3.1 输入序列

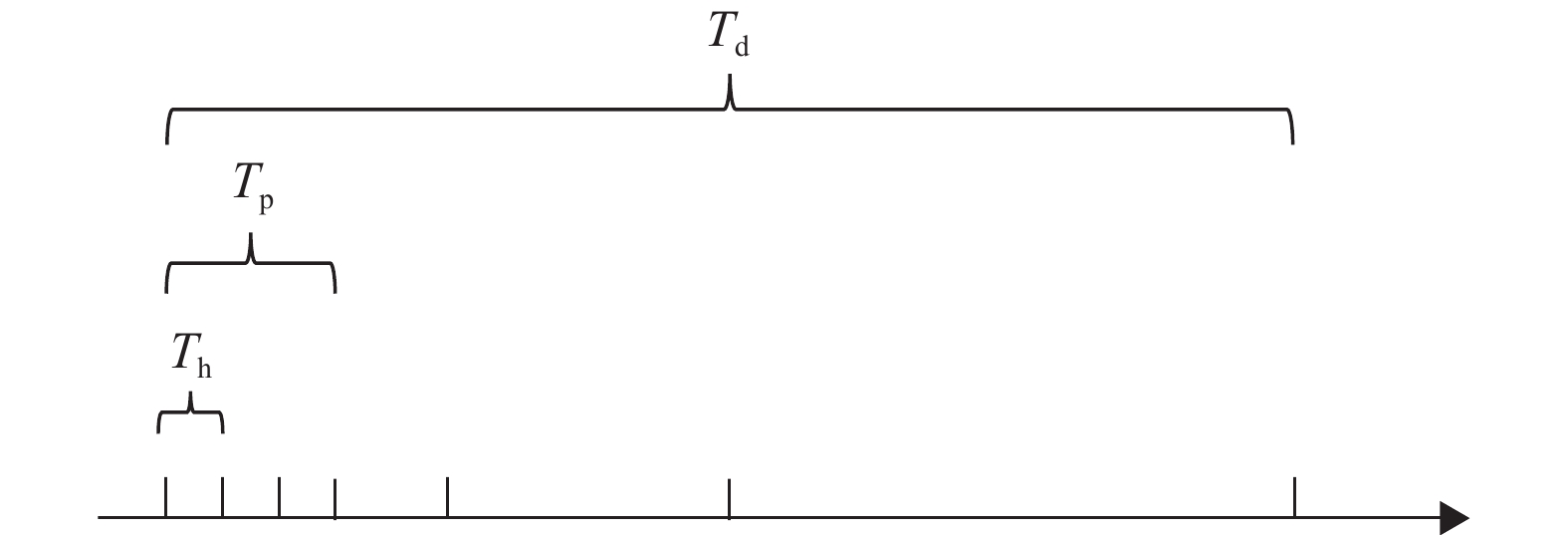
输入模块分为3个粒度：小时、时段和日。中心节点与其邻居节点流量序列值处理方式一样。具体来说，以10 min为间隔，将全天划分为144个时间片。假设当前时刻为t，待预测的时间窗口T_f,h，T_f,p，T_f,d沿时间轴依次截取长度为T_h，T_p和T_d的3个时间序列片段作为模型中的小时、时段、日周期的输入，如图4所示。

小时周期片段： ${x_{{\rm{h}} }} = ( {x_{t - {T_{\rm{h}}} + 1}},{x_{t - {T_{\rm{h}}} + 2}}, \cdots ,{x_t} )$ ，如图4中T_h部分所示；时段周期片段： ${x_{{\rm{p}} }} = ( {x_{t - {T_{\rm{p}}} + 1}},{x_{t - {T_{\rm{p}}} + 2}}, \cdots, {x_t})$ ，如图4中T_p部分所示；日周期片段： ${x_{{\rm{d}} }}= ( {x_{t - {T_{\rm{d}}} + 1}}, {x_{t - {T_{\rm{d}}} + 2}},\cdots ,{x_t} )$ ，如图4中T_d部分所示。它们是与要预测的时间序列直接相对应的不同粒度的历史时间序列片段。

3个时间粒度预测共用一个网络结构，由时间组件 $ ( {f_c^K,} {f_i^K,} {f_{i + n - 1}^K} ) $ ,其中 $ K = {k_1},{k_2},{k_3} $ ，与时空融合组件 $ \left( {{f_{{\rm{fusion}}}}} \right) $ 组成，如图3所示。多层感知机MLP对中心节点产生的序列数据进行处理(见图3的红色框部分)，同时学习权重为α，meanpooling对周围邻居节点的序列数据进行处理，取其平均值。最后，模型对中心节点与邻居节点的数据进行加权求和，得到最终的预测值，再与真实值计算损失。

3.2 时空模式捕捉组件

时空组件模块中，本文对中心节点和邻居节点采用了不同的操作方式，分别对应的是图3中的 $ f_c^K $ 和 $ ( {f_i^K,} {f_{i + n - 1}^K} ) $ ，其中 $ K = {k_1},{k_2},{k_3} $ 。针对中心节点，选用了MLP，隐藏层、神经元之间的连接强度由权重α表示，经过偏置，保证输入算出的输出值后不能随便激活。选择ReLU函数作为激活函数，进行非线性变换，得到最终的值；针对邻居节点，采用meanpooling操作，得到8个邻居在不同粒度下的均值，从而保留主要特征，同时减少参数与计算量，每个粒度的邻居运用一个meanpooling。如图5所示。

空间组件这个模块本文采用了加权求和，将中心节点各粒度的流量值与其权重相乘再加上邻居节点对应粒度的流量值与剩余权重相乘，具体公式为

$ x_{t - 1,c}^K \times {\alpha _d} + x_{t - 1,d}^K \times \left( {1 - {\alpha _d}} \right) $

(7)

式中： $ K = {k_1},{k_2},{k_3} $ 分别表示小时、时段、日3个粒度下的时间层次。

3.3 本文模型与ARIMA模型的相关性

本文模型是ARIMA模型在时间和空间2个方向上的拓展，借助深度学习技术实现其学习过程。如式(8) 所示，经典的ARIMA模型主要针对时间序列，即假设目标变量伴随时间而改变^[13]，并通过捕捉时间方向上的模式实现预测。而本文提出的MGSTDR模型则进一步考虑了空间信息，即通过同时捕捉时间和空间方向^[14]上的模式，结合两者的特征进行预测。中心节点与邻居节点历史信息的捕捉方法如式(9) 、式(10) 所示，可以视为本文所提出的MGSTDR在时间方向和空间方向上所对应的预测函数(其中 $ \beta ,\rho ,\sigma ,\omega ,\gamma ,\theta $ 均为参数)，中心节点最终的预测函数如式(11) 所示。

$ {X_t} = \begin{array}{*{20}{c}} {{\alpha _1}{X_{t - 1}} + {\alpha _2}{X_{t - 2}} + }& \cdots &{ + {\alpha _{{p}}}{X_{t - p}}} \end{array} + {\mu _t} $

(8)

式中：p为个数，表示第p个。

中心节点：

$ \begin{gathered} \left[ {\begin{array}{*{20}{c}} {{\beta _{11}}}&{{\beta _{12}}}&{{\beta _{13}}}&{{\beta _{14}}} \\ {{\beta _{21}}}&{{\beta _{22}}}&{{\beta _{23}}}&{{\beta _{24}}} \\ {{\beta _{31}}}&{{\beta _{32}}}&{{\beta _{33}}}&{{\beta _{34}}} \\ {{\beta _{41}}}&{{\beta _{42}}}&{{\beta _{43}}}&{{\beta _{44}}} \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {x_{t - 1,c}^0} \\ {x_{t - 1,c}^1} \\ {x_{t - 1,c}^2} \\ {x_{t - 1,c}^3} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\hat x_{t,c}^0} \\ {\hat x_{t,c}^1} \\ {\hat x_{t,c}^2} \\ {\hat x_{t,c}^3} \end{array}} \right] \\ \left[ {\begin{array}{*{20}{c}} {{\sigma _1}}&{{\sigma _2}}&{{\sigma _3}}&{{\sigma _4}} \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {\hat x_{t,c}^0} \\ {\hat x_{t,c}^1} \\ {\hat x_{t,c}^2} \\ {\hat x_{t,c}^3} \end{array}} \right] = X_{t - 1}^c \\ \end{gathered} $

(9)

邻居节点：

$ \begin{gathered} \left[ {\begin{array}{*{20}{c}} {{\omega _1}} & \cdots & {{\omega _8}} \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {x_{t - 1,1}^0} \\ \vdots \\ {x_{t - 1,8}^0} \end{array}} \right] = X_{t - 1}^0 \\ \left[ {\begin{array}{*{20}{c}} {{\gamma _1}} & \cdots & {{\gamma _8}} \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {x_{t - 1,1}^1} \\ \vdots \\ {x_{t - 1,8}^1} \end{array}} \right] = X_{t - 1}^1 \\ \left[ {\begin{array}{*{20}{c}} {{\theta _1}} & \cdots & {{\theta _8}} \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {x_{t - 1,1}^2} \\ \vdots \\ {x_{t - 1,8}^2} \end{array}} \right] = X_{t - 1}^2 \\ \left[ {\begin{array}{*{20}{c}} {{\rho _1}} & \cdots & {{\rho _8}} \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {x_{t - 1,1}^3} \\ \vdots \\ {x_{t - 1,8}^3} \end{array}} \right] = X_{t - 1}^3 \\ \end{gathered} $

(10)

中心节点预测：

$ X_{t - 1}^c \times \left[ {\begin{array}{*{20}{c}} {X_{t - 1}^0} \\ {X_{t - 1}^1} \\ {X_{t - 1}^2} \\ {X_{t - 1}^3} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {y_{t,c}^0} \\ {y_{t,c}^1} \\ {y_{t,c}^2} \\ {y_{t,c}^3} \end{array}} \right] $

(11)

4 实验与结果分析 4.1 数据集

本文分别使用了巴西里约热内卢公交车数据集BX_bus、kaggle竞赛里纽约出租车数据集KNYC_taxi，以及美国旧金山出租车数据集San_taxi来验证此模型。BX_bus是在里约热内卢运输公司联合会网站上获得的交通管制员的运行数据，实时位置数据每分钟更新1次。KNYC_taxi是Google Cloud Platform上的Big Query 提供的2016年纽约黄色出租车旅行记录数据。San_taxi包含美国旧金山出租车的轨迹点，每辆出租车都配备了GPS接收器，并向中央服务器发送位置更新(时间戳、标识符、地理坐标)，2次连续位置更新之间的平均时间间隔小于10 s。3个数据集均包含了带时间戳的车流量值以及这些车辆实时的地理位置信息。

(1) BX_bus：巴西里约热内卢公交车数据集，其包含了12000多辆公交车的日期、时间(24小时格式)、公交ID、公交线路、经纬度以及车速等信息。日期是从2014-10-01到2014-10-30，一共30 d。选取前24 d作为训练集，后6 d作为测试集。

(2) KNYC_taxi：纽约市出租车数据集，其包含了每次行程的唯一标识符id、乘客上下车时的日期与时间、乘客上下车时的经纬度，以及旅行的持续时间。日期是从2016-01-01到2016-06-30，一共181 d。选取前145 d作为训练集，后36 d作为测试集。

(3) San_taxi：美国旧金山出租车数据集，其包含旧金山湾区大约500辆出租车的移动时间、GPS坐标。日期是从2008-05-17到2008-06-10，一共25 d。选取前20 d作为训练集，后5 d作为测试集。

4.2 数据预处理

本文对3个数据集都采用了相同的处理方式。首先，筛选掉其中重复、格式错误的数据；其次，基于各个地区的经纬度范围对其划分为32×32的网格^[11]；最后，对时间进行处理，以10为时间间隔形成一个时间片，从而得到一个三维的张量矩阵，再将其转换为空间与时间的二维矩阵，从而进行车流量数据的统计。

4.3 实验参数设置

本文基于Pytorch框架实现了该模型，将空间地理位置固定为1024个，将时间分为3个粒度，分别是小时(hour)、时段(period)、天(day)，数据输入长度分别设置为L_hour=24，L_period=4，L_day=6。均方误差是反映估计量与被估计量之间差异程度的一种度量，因此，本文采用该度量指标作为损失函数。

4.4 基准方法

将本文提出的模型与以下4种己有的时间序列预测方法进行比较。

ARIMA^[4]：2003年Williams等提出的差分整合移动平均自我回归法，是时间序列预测分析中的一种经典方法。

分层门控网络(Hierarchical Gating Networks，HGN)^[15]：2019年Ma等提出的分层门控网络模型，由1个特征门控模块、1个实例门控模块和1个item-item产品模块组成，用于捕捉长期和短期用户的兴趣。

循环独立机(Recurrent Independent Mechanisms，RIM)^[16]：2021年Goyal等提出循环独立机制神经网络，该模型是由多组循环神经元组成的循环结构，每组神经元可以独立地转换动态。

双向长短时记忆方法(LSTM_BILSTM Method，LSTM_BILSTM)^[17]：2022年Ma等提出了基于LSTM和双向LSTM网络的改进LSTM模型。结合时序数据的优点以及正向LSTM和反向LSTM的长期依赖性，将双向长期记忆网络集成到预测模型中，提高短期交通流预测的准确性。

选用均方误差(Root Mean Square Error，RMSE)作为本文的评价指标，具体的计算公式为

$ {\text{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{x_i} - {{\hat x}_i}} \right) }^2}} } $

(12)

4.5 实验结果及分析

将本文模型在数据集BX_bus、KNYC_taxi和San_taxi上与前3种基准方法进行了比较，表2展示了对未来1小时、1时段、1天的流量进行预测的结果。

从表2可以看出，本文的方法在3个真实数据集上性能优于现有的算法。为了证明模型预测性能的最优性，本文计算了MGSTDR在3个数据集上RMSE指标在不同时间粒度下与基线中最优的预测结果相比提升的百分比(见表2)。

从计算的百分比可以看出，随着预测粒度的变大，预测难度也越来越大，模型预测结果的提升百分比变得缓慢。本文提出的MGSTDR模型在小时的预测中取得了较优的预测结果，这表明了时间与空间特性的结合策略能充分挖掘交通数据的有效特征。

综上所述，得出以下结论^[18]：

(1) 对比MGSTDR和ARIMA模型，发现MGSTDR模型能够取得较为全面且更加准确的预测结果。这是因为经典的ARIMA模型对于一些非线性数据不能进行很好的线性拟合，并且在多变量的时序预测场景下，它也往往不能充分考虑到变量之间的相关性。

(2) 对比MGSTDR、RIM、HGN以及LSTM_BILSTM模型，发现MGSTDR在预测性能、预测误差，以及其与真实数据的拟合效果方面优于目前采用神经网络方法的相关模型。这是由于RIM与HGN模型都是只获取单一的时序模式，并且基于节点本身的历史数据进行预测，没有多方位地选取其他有效辅助信息，LSTM_BILSTM模型是对单一粒度的短期时序数据进行预测，没有考虑到多粒度下的时序模式。

4.6 消融实验

为验证MGSTDR模型设计的效果和合理程度，本文采用真实的交通数据集完成消融实验。一次删除模型的一个变量，并与MGSTDR模型进行对比，将删除不同变量的模型加以命名作为实验分类。

MGSTDR-1：数据处理中不同时刻的影响因子α一致；MGSTDR-2：数据处理中删除邻居这一变量。

表3展示了消融实验在不同真实数据集上的预测结果。

从表3可以看出，数据处理的2种变化都会影响最终的预测结果。由于现实生活中某个路口的车流量因时刻的变化和相邻路口的影响会造成它在未来时刻的流量值有所不同，所以在新的设置下，预测结果相比原来的变差。由此可知，加入时间与空间2个变量对提高MGSTDR模型的性能有一定作用。

5 结语

本文提出一种多粒度时序的MGSTDR，它将经典的ARIMA模型与深度学习结合，在交通数据中捕获时空特征进行交通预测。使用3个时间序列作为不同时间粒度的输入：小时数据、时段数据和每日数据，充分考虑了时间的多粒度特性和空间依赖性。在现实生活中的道路交通车流量数据集上的实验结果表明，本文提出的模型的预测效果较其他现有交通流预测方法表现更好,证明了该模型在进一步探索时空特征方面仍存在巨大潜力。多个时间序列的预测是一种有趣的技术，并且还有很多信息可以考虑以提高预测的准确性，例如天气状况、事故、紧急情况等。MGSTDR提供了一个通用框架，未来的研究方向是应用其他影响因素的数据，提高预测的准确性和适应性。