横向磁通永磁电机(Transverse Flux Permanent Magnet Motor, TFPM) 因自身磁路和电路在空间上解耦，有效解决了定子齿和线圈两者在空间上相互制约的问题，易被设计成多极电机，具有转矩密度大、低速性能好等特征，这恰好与低速大转矩电机的应用需求相契合^[1]。但其轴向长度较长、漏感大、功率因数低。因此，如何改善TFPM的轴向长度和功率因数引起了研究者的关注注^[2]。与永磁同步电机相比，盘式电机整体构造更紧凑，转矩密度更高、轴向长度更短^[3]，但电机外径大，定子铁心卷绕难度大。

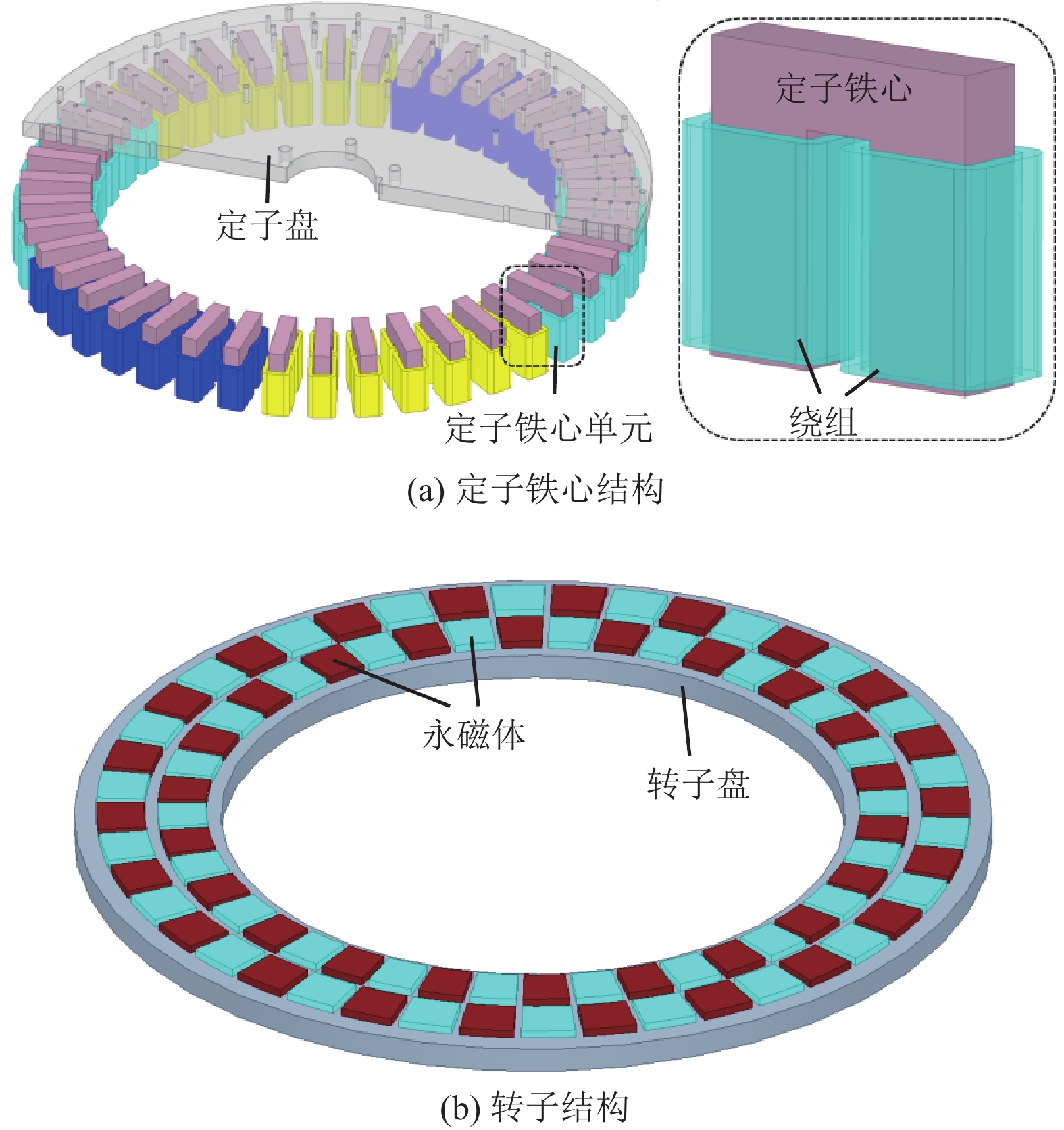
为了使TFPM得到更好的应用，Patterson等^[4]提出了C型定子的盘式横向磁通电机(Disk Transverse Flux Motor, DTFM)。DTFM融合了轴向磁通电机和TFPM的优点，不仅转矩密度高、轴向长度短，而且低速性能好。但C型定子加工复杂，电机装配难度高，结构稳定性差，且槽满率较低。在C型定子基础上，国内徐衍亮教授团队提出了U型定子的DTFM^[5-6]。然而，并未将DTFM中U型定子槽内侧充分利用起来，电机的转矩密度未得到有效提升。为改善U型定子DTFM槽满率，提升DTFM转矩密度，本文提出了4层绕组盘式横向磁通电机(Four-winding Disk Transverse Flux Motor, FWDTFM) ，如图1所示。

另外，DTFM磁路呈三维圆柱型分布，运用三维有限元法(3D Finite Element Method，3D FEM) 计算其气隙漏磁和空载电动势存在耗时长、计算量大等问题，不利于DTFM的初步设计。等效磁网络法是电机初步设计中最常用的方法，它能在保证一定精度的同时，快速计算出气隙磁通。因此，在电机的初始设计中得到了广泛应用^[7]。文献[8]采用精确子域模型法对永磁电机气隙磁密进行求解，计算精度高，但计算量较大。文献[9-11]分别对双定子单相、单定子单相、C型定子的DTFM进行了二维等效磁网络分析，其分析模型简单，忽略了DTFM三维磁通中的周向漏磁通，因此计算出的主磁通比有限元分析、实验测试数据更大。文献[12]将三维等效磁网络运用于E型定子的DTFM，由于相邻定子磁通方向相同，极间漏磁较小，故最终等效的二维模型误差小，精度高。徐衍亮等^[13]将变网络等效磁路模型应用在C型定子的DTFM中，验证了分析模型的有效性，但该模型计算量大，计算参数多，与电机初步设计快速的要求相悖。伍小杰教授团队建立了圆筒型直线TFPM的三维线性等效模型，在考虑铁芯轴向漏磁和磁饱和的情况下，证明了分析模型准确有效^[14]。

本文首先介绍了FWDTFM的结构和原理。其次，以输出转矩和空载反电动势为目标，建立了FWDTFM的三维等效磁网络模型，在考虑复杂空间漏磁的情况下，对模型进行了解析，确定了主磁通、电机主要尺寸、空载反电动势和输出转矩之间的关系。然后，对比提出样机和双层绕组DTFM的齿槽转矩和转矩密度，突出新结构的优越性。最后搭建FWDTFM样机平台进行空载反电动势测试，通过解析模型与实验测试、3D FEM进行结果对比，验证了解析模型的有效性和正确性。

1 FWDTFM的拓扑结构和工作原理 1.1 拓扑结构

FWDTFM的电磁结构主要包含定子和转子。其中，定子部分由42个沿周向均匀布设的定子铁心单元组成，定子铁心单元相互独立，且由非导磁性材料制作的定子盘进行固定。定子铁心单元导磁部分为U型模块化定子，且采用周向平行齿结构，定子铁心两端齿部由两个匝数相当的绕组反向串联而成，沿周向每槽含4层集中式绕组，如图1(a)所示，定子铁心尺寸小，形状规则、简单，有利于生产加工和线圈绕组的自动化绕制。

转子部分由永磁体和具有导磁性能的圆盘构成，如图1(b)所示。永磁体形状规则，极弧系数相同，厚度相等。若将径向相邻两永磁体称为一组永磁体，则一共有44组沿周向均匀布设的永磁体组，径向和周向相邻永磁体极性均相反。

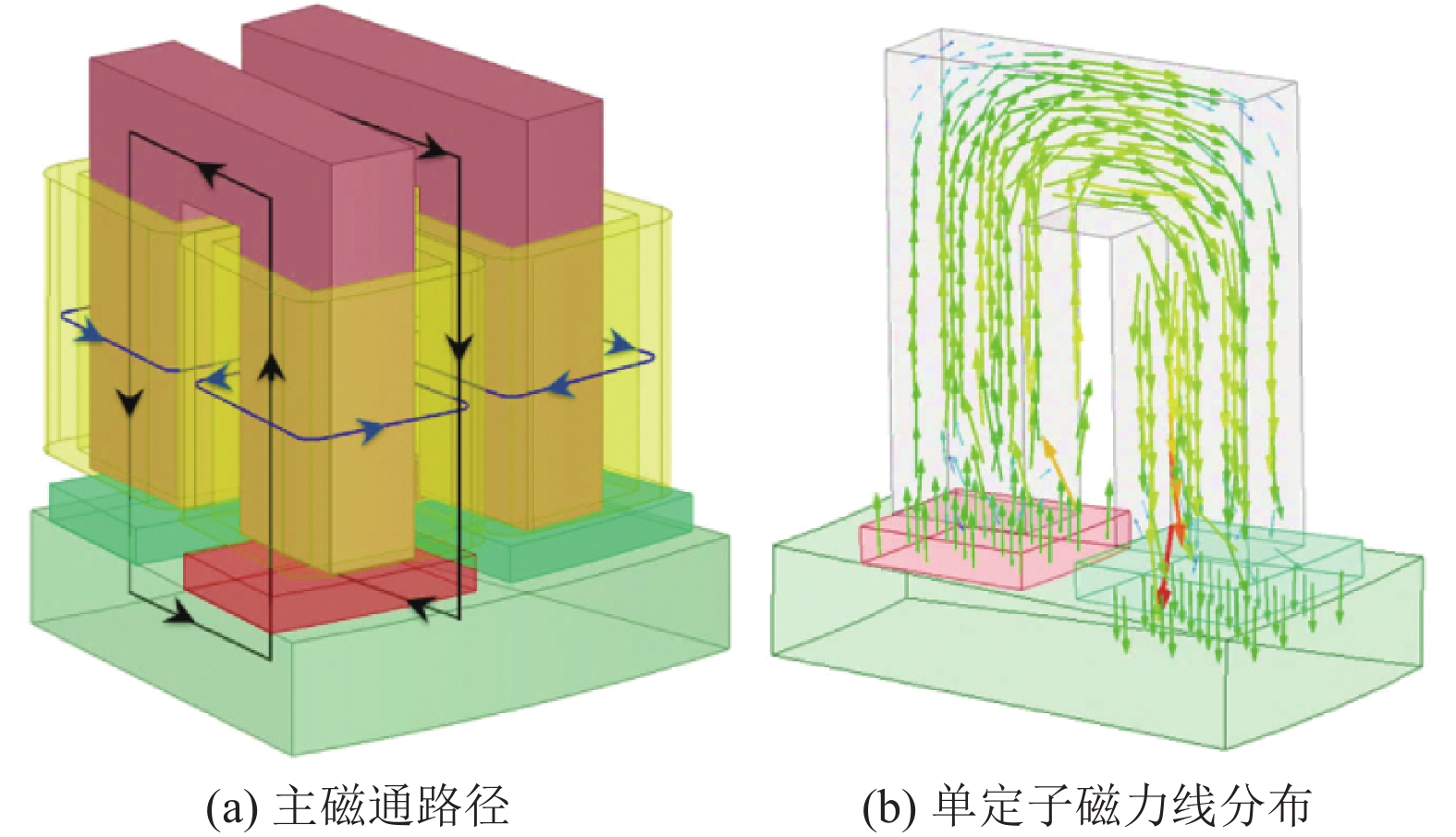
1.2 工作原理

FWDTFM的主磁通路径沿径向闭合，路径为：永磁体N极→气隙→U型定子→气隙→永磁体S极→转子盘→永磁体N极，同相相邻两定子铁心内磁通方向相反；水平闭合路径为电枢绕组中激励电流方向，如图2(a)所示。电机转子沿周向运动，与主磁通路径相互垂直。当转子以转速n旋转时，定子中的磁通周期性交变，从而在定子线圈中产生感应电动势，当在线圈中通以同频率的电流时，通过电磁耦合，将电能转化为机械能，带动转子同步旋转。电机单定子磁力线分布如图2(b)所示，由图可知，每个定子磁通路径相互独立。

2 空载反电动势及磁阻计算 2.1 空载电动势计算

FWDTFM由于内外侧气隙有效面积不同，径向极间漏磁受径向永磁体极间气隙影响，无法准确估计，造成内外侧定子齿所产生的输出转矩并不相等，从而对FWDTFM的快速准确设计造成困难。本文以输出转矩和空载反电动势为基础，对FWDTFM进行建模分析。输出转矩P_N为

$ \left\{ \begin{array}{l} P_{{\rm{N}}}=m \eta_{{\rm{N}}} E I \cos \varphi_{{\rm{N}}} / K_{{\rm{u}}} \\ T_{{\rm{N}}}=9 \;550 P_{{\rm{N}}} / n \end{array} \right. $

(1)

式中： $ m $ 为相数， $ \eta_{{\rm{N}}} $ 为电机额定工况时的效率， $ \cos \varphi_{{\rm{N}}} $ 为功率因数， $ E $ 为空载反电动势有效值， $ I $ 为相电流有效值， $ K_{{\rm{u}}} $ 为电压系数， $ T_{{\rm{N}}} $ 为额定转矩， $ {n} $ 为额定转速， $ P_{{\rm{N}}} $ 为额定功率。

将式(1) 进行整理，得到空载反电动势有效值为

$ E=\frac{T_{{\rm{N}}} n K_{{{\rm{u}}}}}{9 \; 550 m \eta_{{\rm{N}}} I \cos \varphi_{{\rm{N}}}} $

(2)

由式(2)可知，输出转矩与空载反电动势有效值、额定电流成正比，与转速成反比，即对于低速大转矩电机而言，可通过提升空载反电动势有效值或降低转速来获得更大输出转矩。

在FWDTFM空载运行过程中，当A相定子齿和永磁体中轴线正对时，空载主磁通达到最大值，则A相初始位置对应定子的主磁通为

$ \varPhi_{{\rm{A}}}=\varPhi_{{\rm{m}}} K_{\varPhi} \cos (\omega t) $

(3)

式中： $ \varPhi_{{\rm{m}}} $ 为定子齿中的主磁通； $ \omega $ 为转子旋转的电角速度； $ {K}_{\varPhi} $ 为主磁通的波形系数， $ K_{\varPhi}=8 /\left({\text{π}}^{2} \alpha_{{\rm{i}}}\right) \sin \left(\alpha_{{\rm{i}}} {\text{π}}/ 2\right) $ ； $ \alpha_{{\rm{i}}} $ 为计算极弧系数；t为时间。

设每相共有i个定子，每个线圈有N匝导线，则一共有2i个线圈，导线匝数为2Ni匝，每个定子铁心两端为1对永磁体， $ \varPhi_{{\rm{m}}}=\varPhi_{{\rm{m}} 1}+\varPhi_{{\rm{m}} 2} $ ，A相绕组的空载磁链为

$ \psi_{{\rm{A}}}=N i \varPhi_{{\rm{m}}} K_{\varPhi} \cos (\omega t) $

(4)

A相的空载反电动势e为

$ {{e}}=-\frac{\mathrm{d}\left(\psi_{{\rm{A}}}\right) }{\mathrm{d} t}=\omega N i \varPhi_{{\rm{m}}} K_{\varPhi} \sin (\omega t) $

(5)

根据式(5) 可以看出，通过增绕线圈能有效提升空载反电动势，同时，磁通总量 $ {\varPhi}_{{\rm{m}}} $ 的计算对FWDTFM空载反电动势的解析至关重要。

2.2 三维等效磁网络

盘式电机在运行过程中各向漏磁通变化不大，在初始设计时，为快速估算主磁通，多采用二维解析模型分析其漏磁，选取定子齿与永磁体中轴线正对位置的磁路进行计算^[11]，FWDTFM运行原理与盘式电机类似，气隙漏磁组成和大小与盘式电机基本相同，仅在径向永磁体间多了径向极间漏磁。为更准确快速计算FWDTFM漏磁通并减少永磁体工作点的校核，本文采用三维等效磁网络模型对FWDTFM主磁通进行计算。

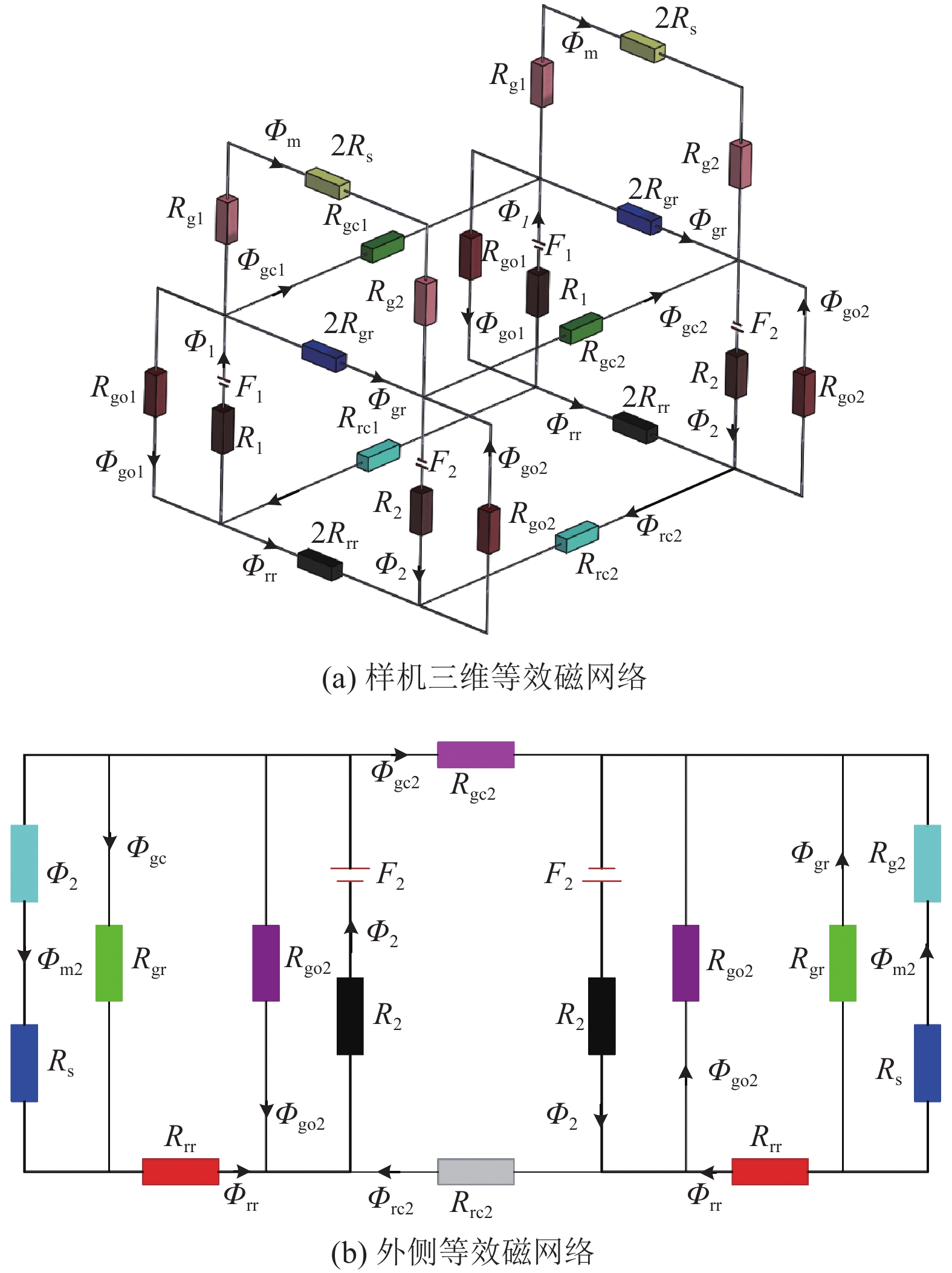
等效磁路计算可先采用空间磁场转化为空间磁路的方法对模型进行简化，再将各向上实际存在的不均匀分布的磁场用三维空间磁路进行等效，如图3(a)所示。

假设主磁路为线性，定子铁心和转子盘未达到磁饱和状态，将等效磁网络沿径向两永磁体的气隙中轴线进行拆分。内外侧永磁体的周向磁阻、外侧永磁体外侧漏磁、内侧永磁体内侧漏磁由于相互独立，可直接进行拆分；对于径向的定子铁心内磁阻 $ 2 R_{{\rm{s}}} $ 、径向极间气隙漏磁阻 $ 2 R_{{\rm{g r}}} $ 和转子盘径向极间磁阻 $ 2 R_{{\rm{r r}}} $ 则采用对半拆分方式，主磁通 $ \varPhi_{{\rm{m}}} $ 拆分成 $ \varPhi_{{\rm{m}} 1} $ 和 $ \varPhi_{{\rm{m}} 2} $ 。将外圆周方向等效磁路图提取出来，如图3(b)所示。将复杂的三维等效磁网络模型拆分成二维等效磁网络模型进行计算，从而确定每个拆分模型的磁通量，最后通过叠加法确定模型主磁路磁通和漏磁通的大小。

在图3(b)中，主磁路依然沿径向分布，根据磁回路列出磁路方程组如下。

$ \left\{ \begin{array}{l} \varPhi_{2}=\varPhi_{{\rm{m}} 2}+\varPhi_{{\rm{g c}} 2}+\varPhi_{{\rm{g r}}} \\ \varPhi_{2}=\varPhi_{{\rm{rr}}}+\varPhi_{{\rm{r c}} 2} \\ F_{{\rm{m}} 2}=\varPhi_{2} R_{{\rm{x}}}++\varPhi_{{\rm{m}} 2}\left(R_{{\rm{g}} 2}+R_{{\rm{s}}}\right) +\varPhi_{{\rm{r r}}} R_{{\rm{r r}}} \\ F_{{\rm{m}} 2}=\varPhi_{2} R_{{\rm{x}}}+\varPhi_{{\rm{g c }}2} R_{{\rm{g c}} 2}+\varPhi_{{\rm{r c}} 2} R_{{\rm{r c}} 2} \\ F_{{\rm{m}} 2}=\varPhi_{2} R_{{\rm{x}}}+R_{{\rm{r r}}} \varPhi_{{\rm{r r}}}+R_{{\rm{g r}}} \varPhi_{{\rm{g r}}} \\ \varPhi_{{\rm{g r}}} R_{{\rm{g r}}}-\varPhi_{{\rm{g c}} 2} R_{{\rm{g c}} 2}=0 \\ \varPhi_{{\rm{r r}}} R_{{\rm{r r}}}-\varPhi_{{\rm{r c }}2} R_{{\rm{r c}} 2}=0 \end{array} \right. $

(6)

式中： $ \varPhi_{2} $ 为永磁体总磁通， $ \varPhi_{{\rm{m}} 2} $ 为定子磁路总磁通， $ \varPhi_{{\rm{rr}}} $ 为转子盘内径向磁路总磁通，其余磁通对应各条漏磁路， $R_2 $ 与 $R_{{\rm{g o}} 2}$ 并联，令 $ R_{{\rm{x}}}=R_{2} // R_{{\rm{g o}} 2} $ 。考虑到导磁材料的磁阻远小于气隙磁阻，因此将定子和转子盘的磁阻 $ R_{{\rm{s}}} $ 和 $ {R}_{{\rm{r r}}} $ 均忽略掉后，对式(6) 中的定子主磁通 $ \varPhi_{{\rm{m}} 2} $ 求解可得方程式

$ \varPhi_{{\rm{m}} 2}=\frac{F_{{\rm{m}} 2}}{R_{{\rm{x}}}+R_{{\rm{g}} 2}+\frac{R_{{\rm{x}}} R_{{\rm{g}} 2}}{R_{{\rm{g c }}2} / / R_{{\rm{g r}}}}} $

(7)

那么，气隙平均磁密 $ B_{2 {\rm{r}}, {\rm{ave}}} $ 为

$ B_{2 {\rm{r}},{ {\rm{ave}}}}=\varPhi_{{\rm{m}} 2} / A_{{\rm{g}}} $

(8)

式中： $ A_{{\rm{g}}} $ 为每极气隙有效面积。

2.3 各项漏磁阻参数的确定 2.3.1 永磁体等效内磁阻 $ {R}_{2} $ 与气隙磁阻 $ R_{{\rm{g}} 2} $

永磁体等效内磁阻R₂与气隙磁阻R_g2计算如下：

$ {R}_{2}=\frac{h_{{\rm{m}}}}{\mu_{{\rm{r}}} \mu_{0} A_{{\rm{m}}}} $

(9)

式中： $ h_{{\rm{m}}} $ 为永磁体厚度， $ \mu_{{\rm{r}}} $ 为永磁体的相对磁导率， $ \mu_{0} $ 为空气磁导率， $ A_{{\rm{m}}} $ 为永磁有效截面积。

$ R_{{\rm{g}} 2}=\frac{g^{\prime}}{\mu_{0} A_{\mathrm{eff}}} $

(10)

式中： $ A_{\text {eff }} $ 为考虑边缘效应时每极气隙的有效面积， $ g^{\prime} $ 为考虑开槽效应的气隙长度。

由于电机在运转时，沿运动方向的气隙长度会出现周期性变化，文献[11]引入了卡特系数 $ k_{{\rm{c}}} $ 对气隙长度进行修正，修正表达式为

$ \begin{split} &g^{\prime}=k_{{\rm{c}}} g \\ &k_{{\rm{c}}}=\left[1-\frac{w_{{\rm{s}}}}{\tau_{{\rm{s}}}}+\frac{4\left(h_{{\rm{m}}}+g\right) }{{\text{π}} \tau_{{\rm{s}}}} \ln \left(1+\frac{{\text{π}} \tau_{{\rm{s}}}}{4\left(h_{{\rm{m}}}+g\right) }\right) \right]^{-1} \end{split}$

(11)

式中： $ \omega _{{\rm{s}}} $ 为定子齿宽； $ \tau _{{\rm{s}}} $ 为齿距，此处取平均值；g为气隙长度。

2.3.2 周向漏磁阻 $ {R}_{ {{\rm{gc}} } 2} $ 和外周边漏磁阻 $ R_{{\rm{g o}} 2} $

图3(b)中等效磁网络与盘式电机漏磁路的差异在于径向极间漏磁阻 $ {R}_{{\rm{g r}}} $ 的差异，因此周向漏磁阻 $ {R}_{{{\rm{gc}} } 2} $ 和外周边漏磁阻 $ R_{{\rm{g o}} 2} $ 计算可参考文献[15]。

外侧永磁体的外周边漏磁导 $ \lambda_{ {{\rm{go}} } 2} $ 为

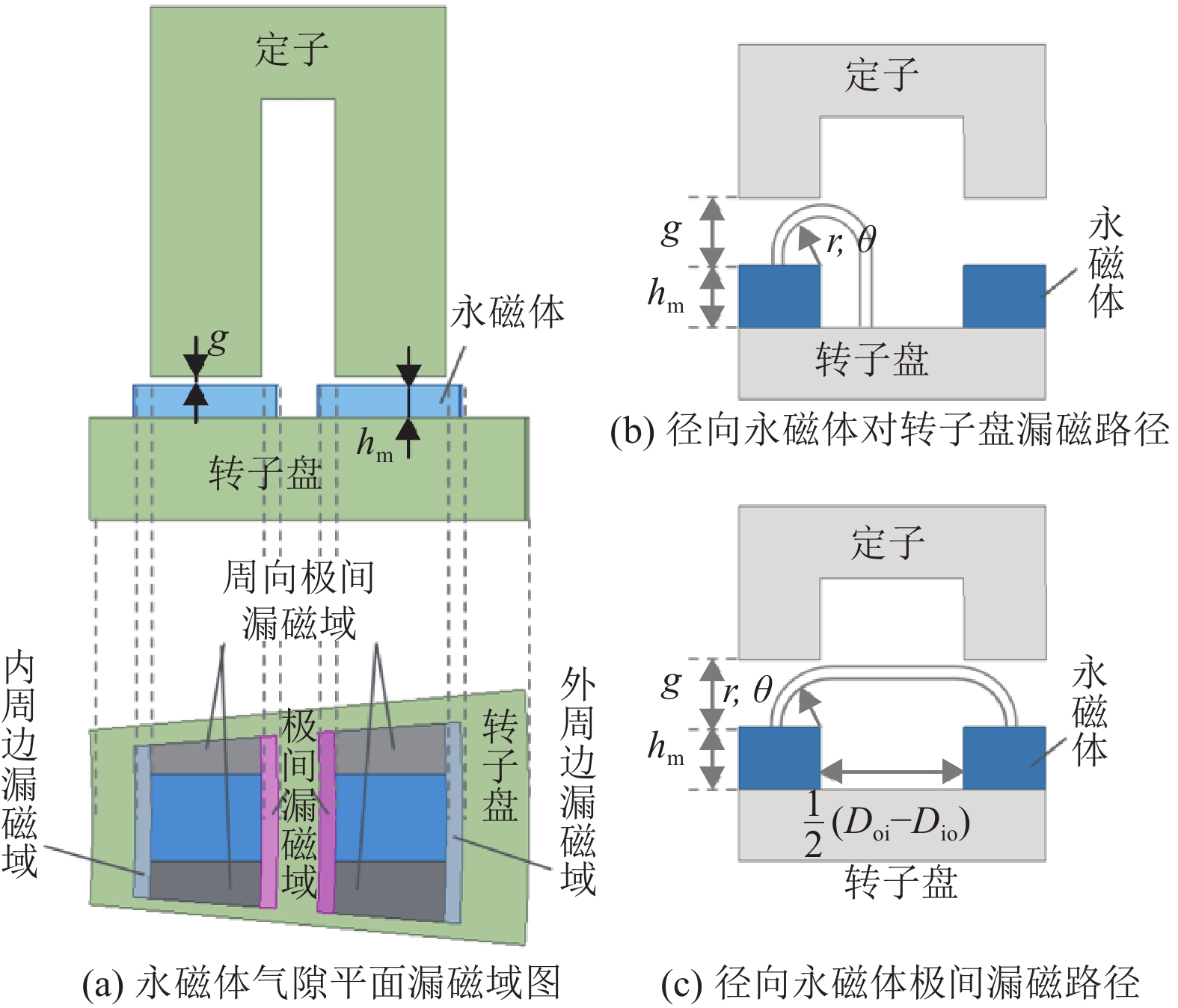
$ \lambda_{{\rm{g o}} 2}=\int_{\tfrac{1}{2} D_{{\rm{o o}}}-g}^{\tfrac{1}{2} D_{{\rm{oo}}}} \int_{0}^{\tfrac{ {\text{π}} }{p} \alpha_{{\rm{p}}}} \frac{\mu_{0} r {\rm{d}} r {\rm{d}} \theta}{ {\text{π}} \left(\dfrac{1}{2} D_{{\rm{o o}}}-r\right) +h_{{\rm{m}}}} $

(12)

式中：D_oo为外侧永磁体的外径，p为DTFM的周向极对数；α_p为永磁体极弧系数， $ r $ 为漏磁半径，可参照图4(b)。

周向永磁体与转子盘形成的漏磁导 $ \lambda_{{\rm{c}}1} $ 为

$ \lambda_{{\rm{c}} 1}=\int_{\tfrac{1}{2} D_{{\rm{o i}}}+g}^{\tfrac{1}{2} D_{{\rm{oo}}}-g} \int_{0}^{\tfrac{g}{r} } \frac{\mu_{0} r {\rm{d}} r {\rm{d}} \theta}{{\text{π}} r\theta +h_{{\rm{m}}}} $

(13)

式中：D_oi为外侧永磁体的内径。

周向永磁体极间漏磁导 $ \lambda_{\mathrm{c}} $ 为

$ \lambda_{{\rm{c}} 2}=\int_{\tfrac{1}{2} D_{{\rm{o i}}}+g}^{\tfrac{1}{2} D_{{\rm{o o}}}-g} \int_{0}^{\tfrac{g}{r}} \frac{\mu_{0} r {\rm{d}} r {\rm{d}} \theta}{ {\text{π}} r \theta+r \dfrac{{\text{π}}}{p}\left(1-\alpha_{{\rm{p}}}\right) } $

(14)

式(13) 和(14) 求和可得到周向漏磁导 $ \lambda_{{\rm{gc2}}} $ 。

2.3.3 永磁体径向漏磁阻 $ 2 R_{{{\rm{gr}}}} $

永磁体沿气隙平面的漏磁域如图4(a)所示，此前已对图中外周边漏磁阻 $ {R}_{{\rm{g o}} 2} $ 、圆周方向永磁体漏磁阻 $ {R}_{ {{\rm{gc}} } 2} $ 进行了计算。将径向永磁体漏磁阻拆分为永磁体对转子盘漏磁 $ R_{{\rm{r}}1} $ 和永磁体极间漏磁阻 $ R_{{\rm{r}} 2} $ ，其漏磁路径分别对应图4(b)和图4(c)。

永磁体的内周边对转子盘的漏磁导 $ \lambda_{{\rm{r}}1} $ 为

$ \lambda_{{\rm{r}} 1}=2 \int_{\tfrac{1}{2} D_{{\rm{o i}}}-g}^{\tfrac{1}{2} D_{{\rm{o i}}}} \int_{0}^{\tfrac{g}{r}} \frac{\mu_{0} r \mathrm{d} r \mathrm{d} \theta}{ {\text{π}} r \theta+h_{{\rm{m}}}} $

(15)

永磁体的径向极间漏磁导 $ \lambda_{{\rm{r}}2} $ 为

$ \lambda_{{\rm{r}}2}=\int_{\tfrac{1}{4}\left(D_{{\rm{o i}}}+D_{{\rm{i o}}}\right) -g }^{\tfrac{1}{4}\left(D_{{\rm{o i}}}+D_{{\rm{i o}}}\right) +g} \int_{0}^{\tfrac{g}{r}} \frac{\mu_{0} r \mathrm{d} r \mathrm{d} \theta}{ {\text{π}} r \theta+\dfrac{1}{2}\left(D_{{\rm{o i}}}-D_{{\rm{i o}}}\right) } $

(16)

式中： $ D_{ {{\rm{io}} }} $ 为内侧永磁体的外径。将式(15) 、(16) 相加求倒数即可得到 $ 2 R_{{\rm{g r}}} $ 。

根据以上公式得到的各项磁阻，代入到式(7) ，计算得到外侧永磁体的主磁通，根据式(8) 求出外侧气隙磁通密度。内侧永磁体的磁阻、主磁通等参数均可参照以上公式进行求取。叠加内侧永磁体和外侧永磁体分别产生的主磁通 $ {\varPhi}_{{\rm{m}} 1} $ 和 $ {\varPhi}_{{\rm{m}} 2} $ ，得到定子齿中的磁通总量 $ \varPhi_{{\rm{m}}} $ 。根据式(5) 求出空载反电动势大小，从而实现对FWDTFM的快速准确计算。

3 3D FEM分析与验证 3.1 磁场分析

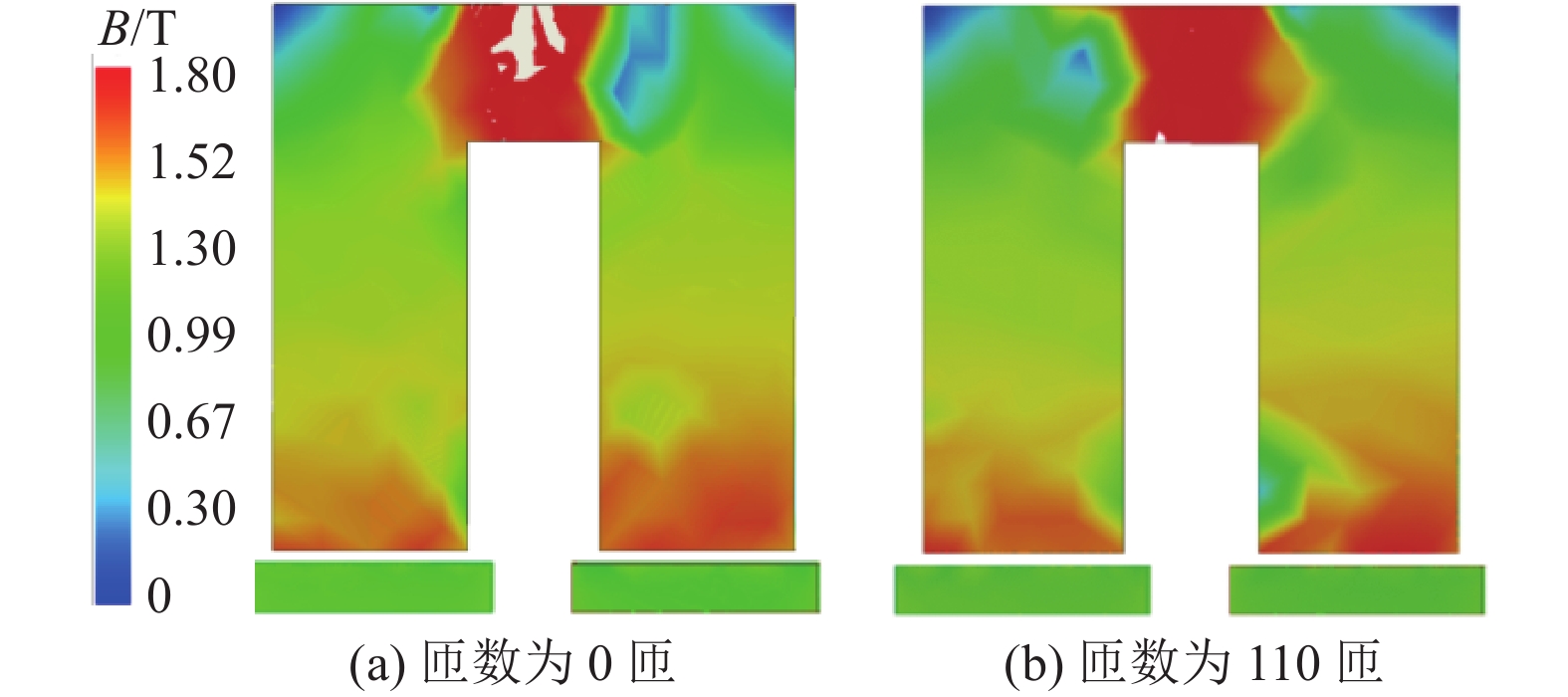
FWDTFM的3D FEM磁场分布情况如图5所示，由图可知，通过增加线圈匝数并不能提升电机定子铁芯中的主磁通，与式(7) 结论相同。

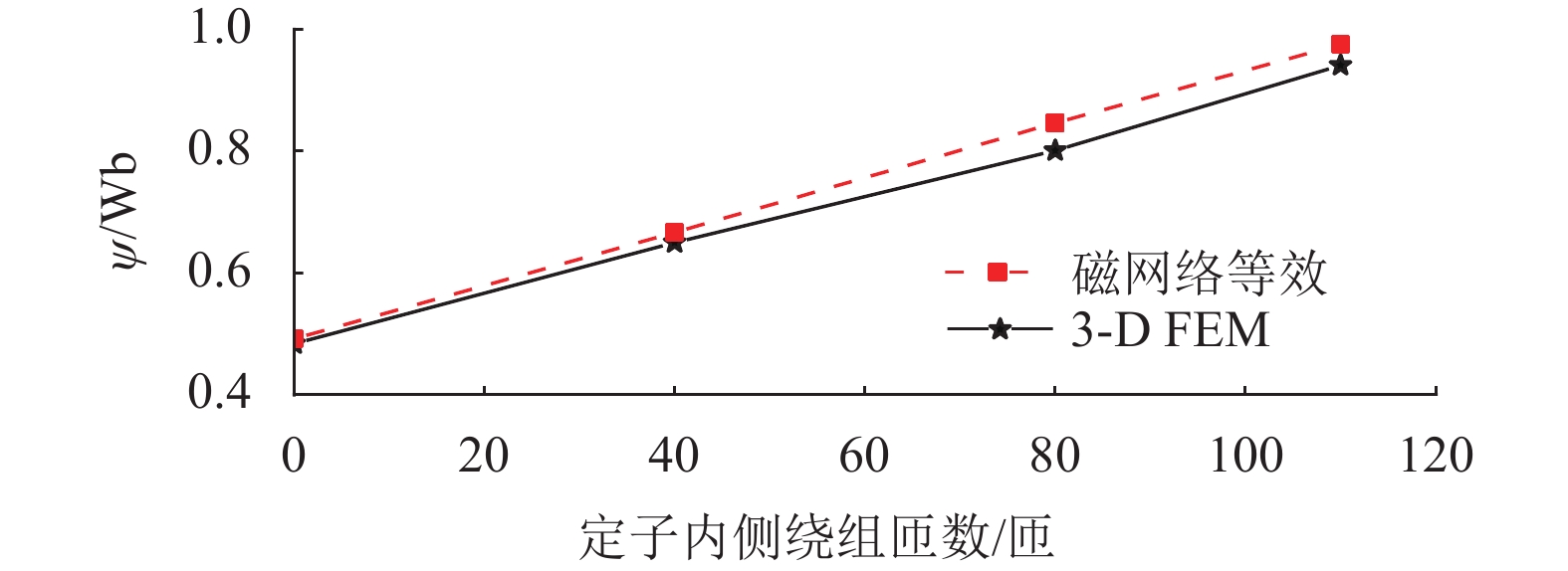
三相FWDTFM的3D FEM仿真磁链和解析模型磁链对比如图6所示，解析模型计算空间漏磁时，并未考虑定子铁心的饱和程度和局部漏磁，因此，解析结果略大于3D FEM，同时，解析模型和3D FEM误差较小，证明解析模型较为准确，可以应用于电机初步设计。

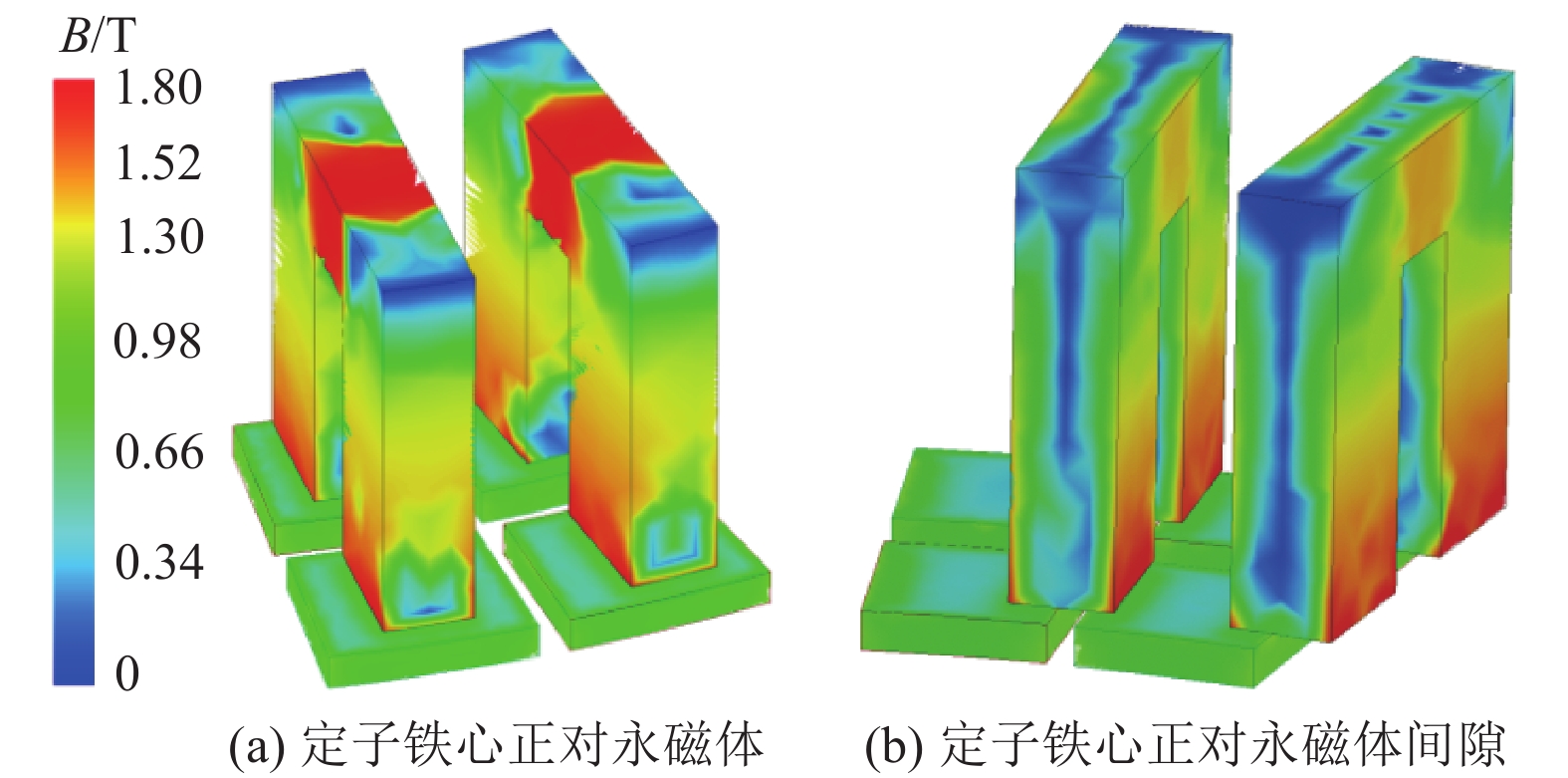
电机定子铁心与永磁体中轴线对齐时的磁密云图、定子铁心中轴线与永磁体极间轴线对齐时的磁密云图如图7所示，由图可见，定子轭部由于截面积小，磁通密度在1.8 T左右，较为饱和，需改善定子轭部厚度。而定子齿部磁通密度在1.5 T左右，尺寸合理。

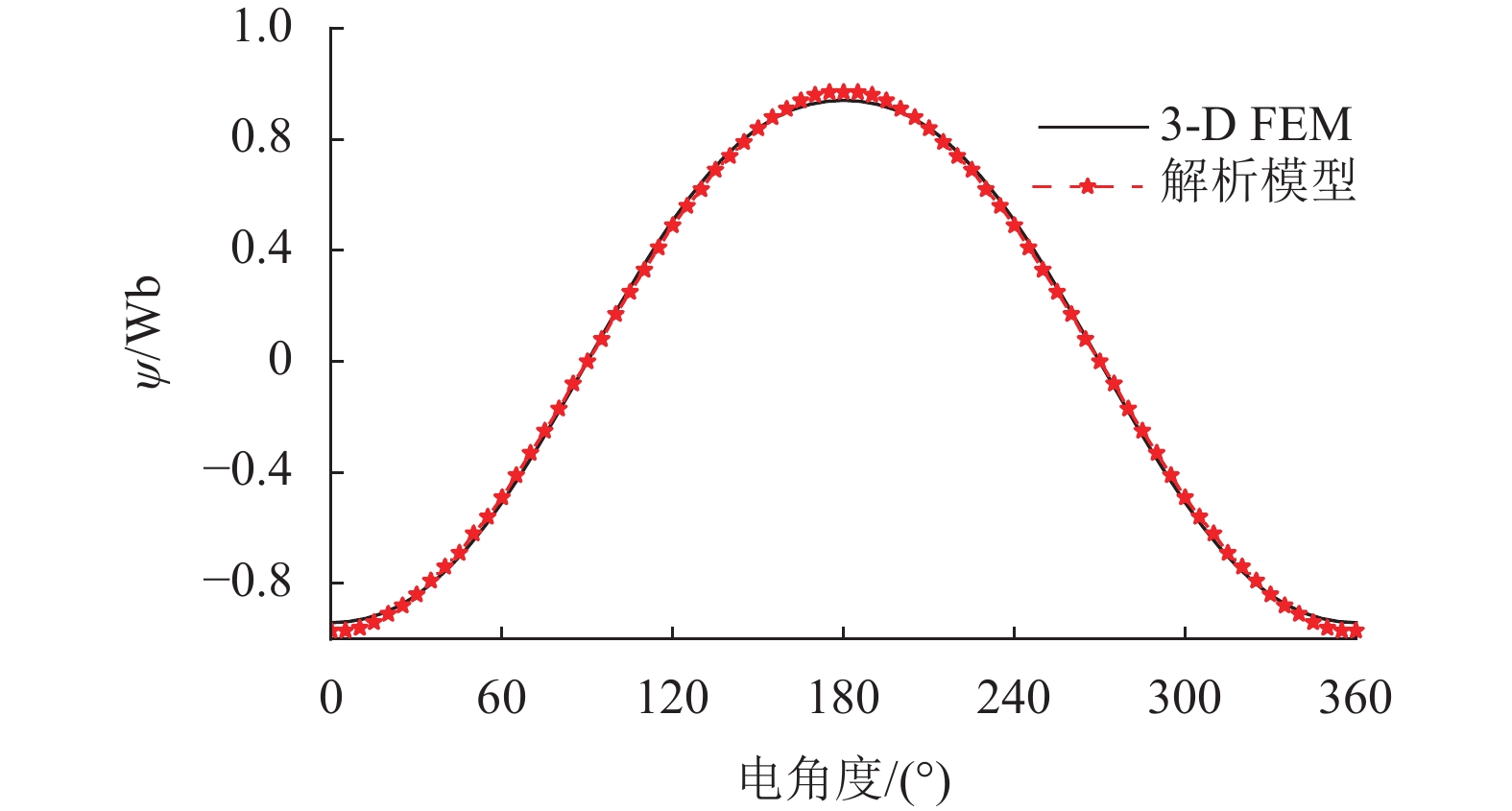
FWDTFM额定转速时，线圈磁链的3D FEM仿真和解析磁链波形图如图8所示。仿真曲线呈正弦波，在初始位置磁链达到最大值，与式(4) 吻合。其中，3D FEM磁链峰值约为0.94 Wb，等效磁网络解析模型峰值约为0.97 Wb，两者误差为3.1%，具有较好的一致性。

3.2 性能对比分析

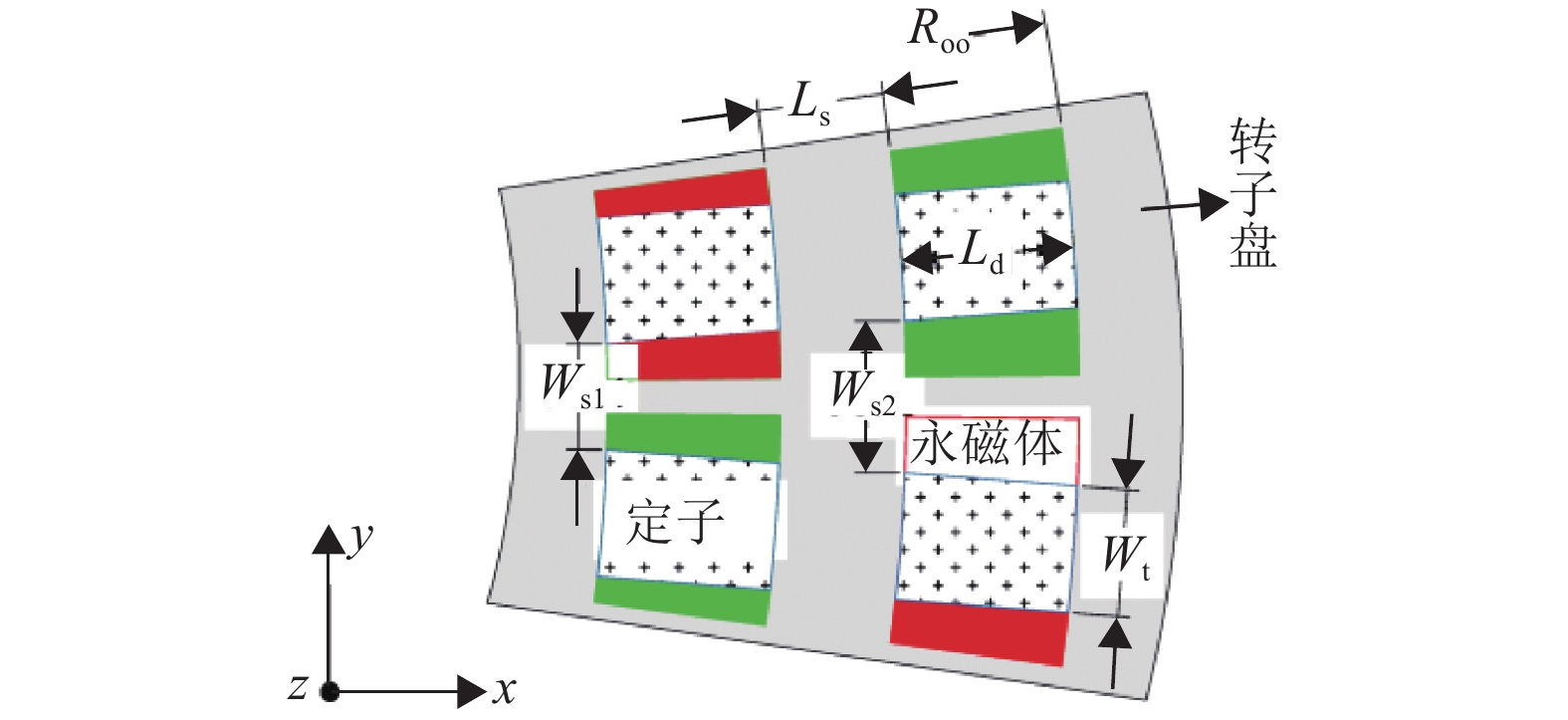
DTFM的局部俯视图如图9所示，在保证径向槽L_s中槽满率相同的情况下，所提FWDTFM和文献[6]中的双层绕组DTFM尺寸对比如表1所示。运用3D FEM仿真对两者进行性能对比分析。

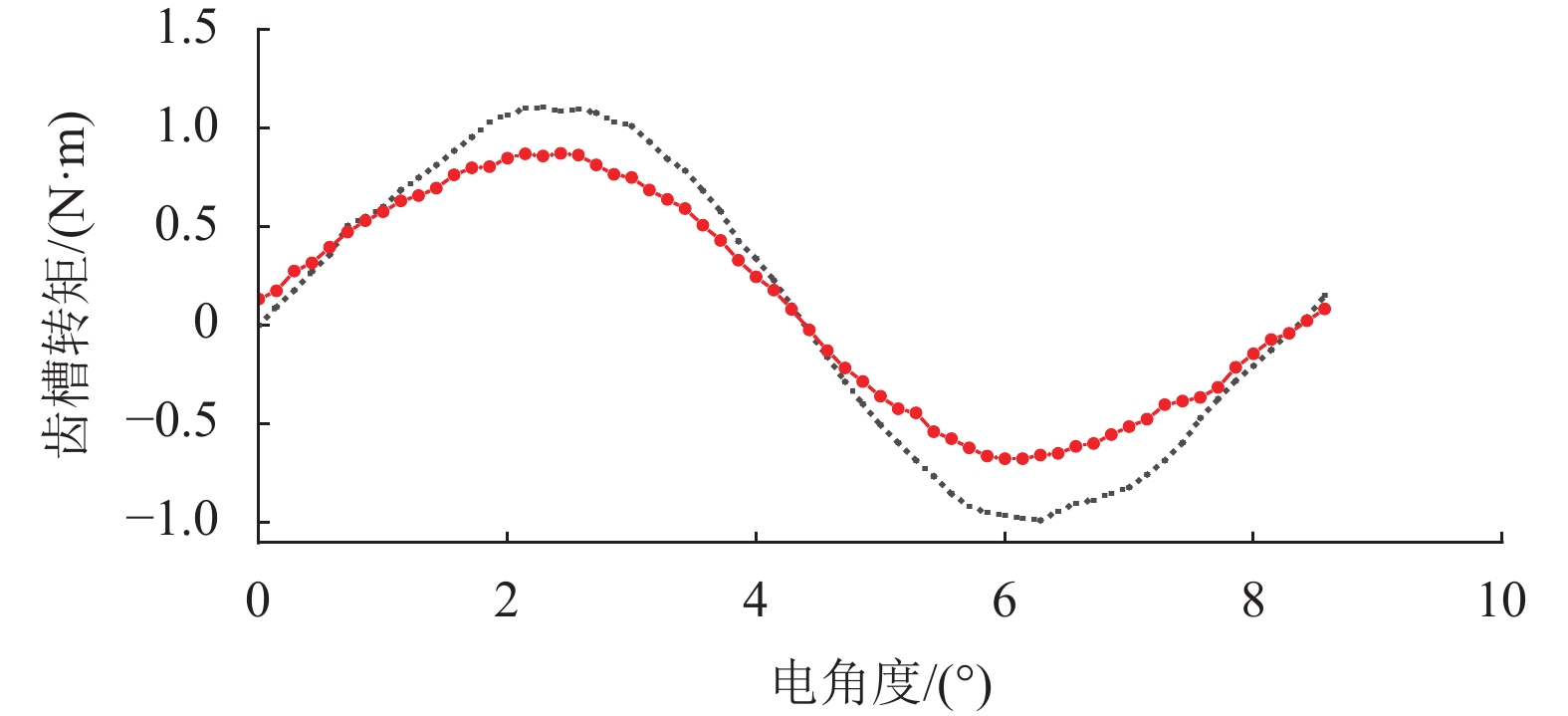
由图10可见，FWDTFM和双层绕组DTFM的齿槽转矩峰峰值分别为1.55 N·m和2.09 N·m，两种DTFM的外侧电磁结构相同，双层绕组DTFM内侧周向槽间距更大，使得齿槽转矩也更大。本文DTFM均采用周向开口槽和平行齿，周向等效槽口较大，但电机旋转一周共有924个齿槽周期，可以较好地削弱齿槽转矩。

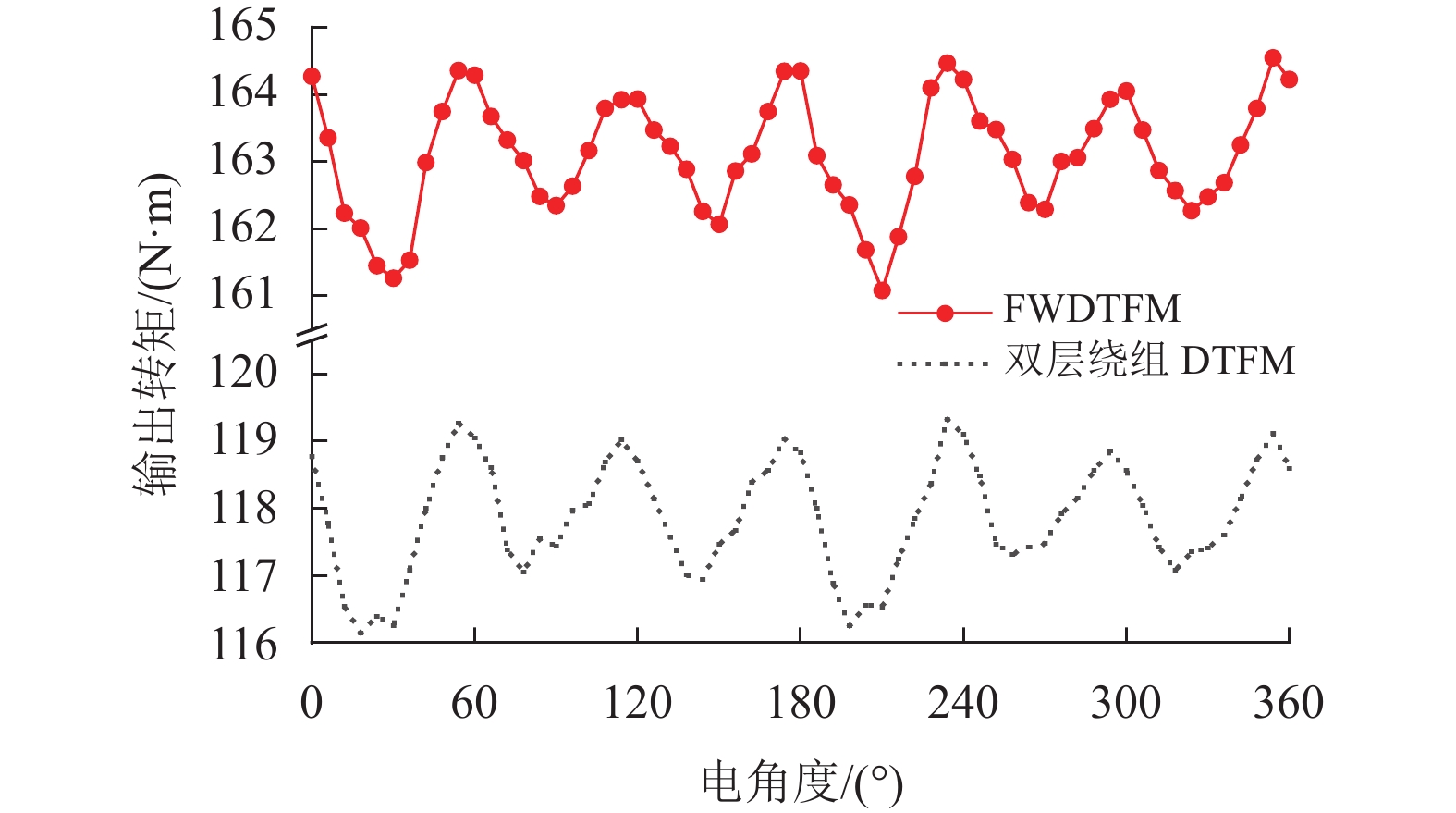
运用i_d=0电流控制方法，给两款电机通入幅值为5.23 A的激励电流时，输出转矩如图11所示。FWDTFM和双层绕组DTFM的平均输出转矩分别为163.08 N·m和117.86 N·m，转矩脉动分别为2.12%和2.69%，以平均输出转矩与永磁体体积的比值为转矩密度，则FWDTFM与双层绕组DTFM的转矩密度分别为2.764×10⁴和2.203×10⁴ N·m/m³，与式(2)和式(5)中转矩与线圈匝数成正比的结论基本相符，出现差异的原因主要是负载时，随着绕组匝数增多，定子铁心磁路逐渐饱和及铁心局部漏磁的增加。转矩脉动由齿槽转矩和纹波转矩组成。当绕组匝数下降时，漏磁系数基本不变，根据式(5)，空载反电动势谐波同比下降，而齿槽转矩恒定，因此双层绕组DTFM的转矩脉动占比升高，可通过优化电机拓扑结构对齿槽转矩进行优化。

i_d=0时，DTFM的功率因数表达式为

$ \cos \varphi_{\mathrm{N}}=\frac{E+I R}{\sqrt{(E+I R) ^{2}+\left(X_{{\rm{q}}} I\right) ^{2}}} $

(17)

式中：X_q为交轴同步电抗值。

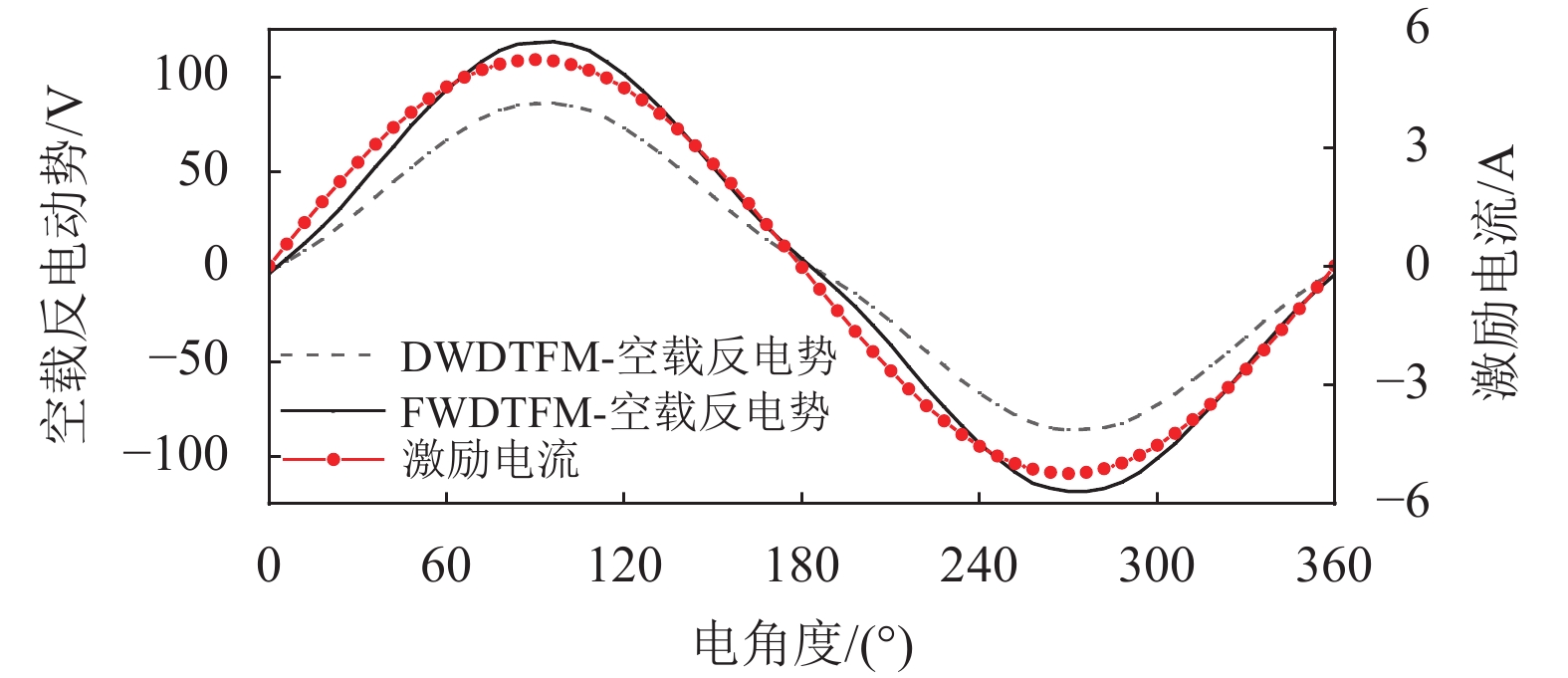
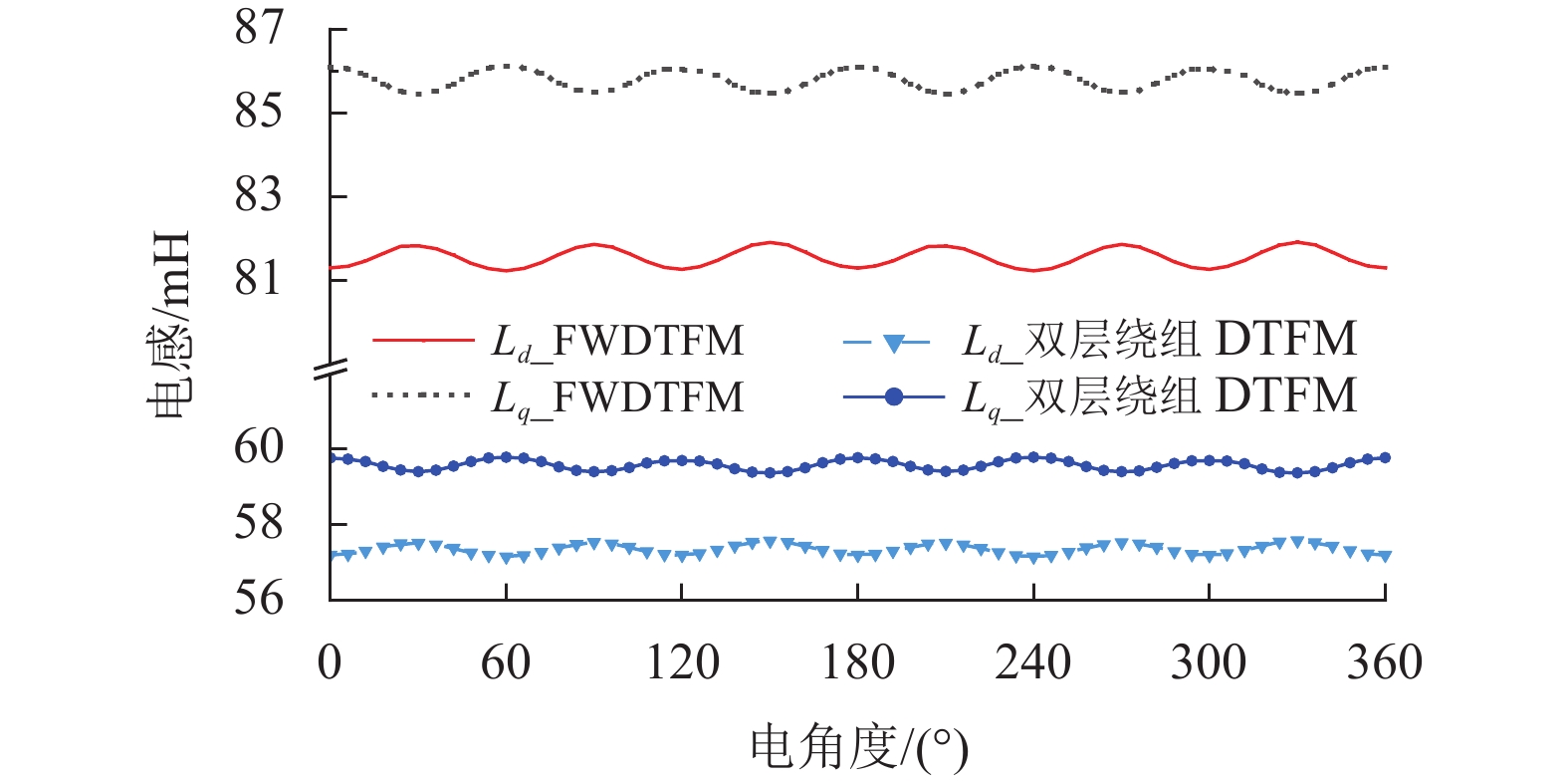
额定转速时，FWDTFM和双层绕组DTFM的空载反电动势幅值分别为118.6 V和86.22 V，如，如图12所示。交轴同步电抗的均值分别为85.8 mH和59.57 mH，直轴同步电抗的均值分别为81.56 mH和57.48 mH，可近似认为L_d=L_q，如图13所示。线圈直径1.08 mm，其他参数见表1，代入式(17) 可得，双层绕组DTFM和FWDTFM的功率因数分别为0.943和0.937，可见，DTFM有效克服了TFPM功率因数低、相邻永磁体极间漏磁严重等问题。

4 FWDTFM的实验验证 4.1 样机模型参数

根据图1的电机结构图，以及表2所示的样机主要结构参数，加工制造出了一款FWDTFM电机，样机实物模型和定子硅钢片如图14所示。

4.2 样机空载反电动势测试

搭建的FWDTFM样机实验平台如图15所示。实验时，原动机以16 r/min的转速旋转，通过传动杆带动FWDTFM转动，从而测出样机的线电动势。

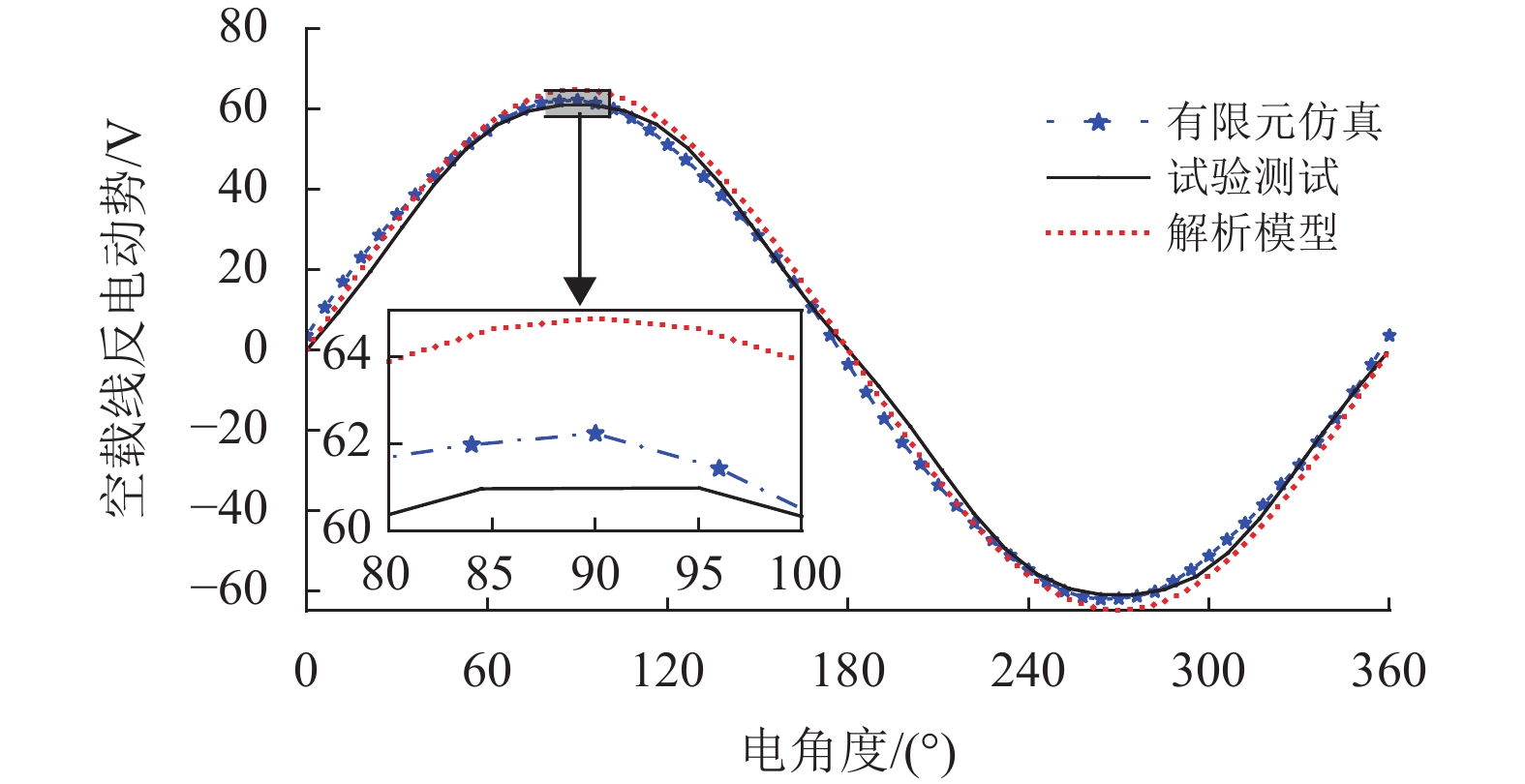
三维等效磁网络模型、3D FEM仿真、样机测试的空载反电动势波形对比如图16所示。可以看出等效磁网络分析得到的空载反电动势最大，为37.46 V，3D FEM为35.93 V，两者结果相差4.26%，与磁链误差3.10%不同，主要是由于空载反电动势中存在一些谐波分量，对空载反电动势产生一定影响。实验测试空载反电动势幅值约为35.22 V，与3D FEM十分接近。存在误差主要是由于电机加工制造过程中产生的工艺性误差，且转子盘采用了Q235钢板，周向相邻永磁体间通过转子盘同样存在漏磁路，增加了转子盘的子盘的铁耗。

经过三者结果对比，可以发现等效磁网络模型与实验测试空载反电动势误差为6.36%，差异较小。验证了本文所提出的数学模型的有效性。

5 结论

本文提出了一种FWDTFM拓扑，以输出转矩和空载反电动势为基础，建立了该电机的等效磁网络模型，通过与双层绕组DTFM的3D FEM仿真对比，并制作样机进行实验测试，得到结论如下。

(1) 在槽满率相同的情况下，FWDTFM通过在定子齿内周向增加总线圈匝数，可以有效提升DTFM的空载反电动势，使DTFM拥有更高的转矩密度和更好的转矩性能。

(2) U型定子设计灵活，有利于生产加工，线圈绕制方便，比C型定子拥有更高的空间利用率。

(3) DTFM解析结构分析与3D FEM、样机测试结果具有较高的吻合度，验证了解析模型的可行性和准确性。

(4) 解析所运用的数学模型将复杂的三维漏磁路简化为二维漏磁路，解析简洁明了，在保证一定准确度的同时，也大大降低了计算难度，可用于DTFM的初步设计。