2. 南华大学 机械工程学院,湖南 衡阳 421000
2. College of Mechanical Engineering, University of South China, Hengyang 421000, China
能源互联网是各种能源网络深度融合和相互渗透的复杂能源生态系统,其以电力系统为核心,连接天然气网、热网等能源节点[1-2]。能源互联网的出现为不同网络之间的能量双向流动提供了通道[3-4]。因此,可以通过能源互联网实现一种能源网络中的富余资源支持另一种能源网络中的紧急供需平衡,从而提高了整体能源的利用效率。
针对需求响应资源的利用问题,电网本身就具有一个比较成熟的调用机制——需求侧响应[5-6]。该调用机制主要是利用电网里面本身的富余电力资源来参与电网的安全稳定运行。本文试图将这一概念扩展到基于能源互联网下的电网和天然气网。也就是说,本文旨在探索一种潜在的利用电网需求响应资源跨网参与气网供需平衡的方案。该方案主要需要考虑以下3点。
(1) 电网需求响应资源到达气网的物理传输通道。
(2) 考虑到分布式的电网需求响应资源,提出该资源加入气网供需平衡的数量限制。
(3) 考虑电网需求响应资源跨网参与天然气市场竞争的电力报价建设。
第一点是现在能源互联网研究人员关注的焦点之一。大多数研究主要集中于电转气跨网络能量流动物理通路的实现,例如传统的电转气技术(Power-to-Gas,P2G)[7],冷热电三网联合的热电联产技术(Combined Heat and Power,CHP) [8],交通网络与电网络之间的V2G(Vehicle-to-Grid) 技术[9]。此外,其他的研究大多数关注了基于能源互联网下,在不同能源网络之间的跨电网运行。文献[10]以电−气综合能源系统为例,建立了一个考虑综合需求响应不确定性的电气一体化优化调度模型,有效分析了综合需求响应不确定性对电力系统安全稳定运行带来的影响。文献[11]构建了含电转气的热电耦合优化调度模型,提高了区域综合能源系统中多能级耦合的利用效率。文献[12]设计了一个能源枢纽的综合需求响应方案,实现了电力、天然气和热力系统的最优调度。
本文在基于能源互联网的基础上,研究了从电网到天然气网的跨电网需求响应问题,提出了一个电网需求响应资源通过燃气轮机参与天然气网运行的框架。该框架不仅考虑了跨网能量的物理传输路径,还考虑了参与跨网需求响应资源的传输量和报价结构。提出了一个整合了所有利益相关者的实体运营和经济行为的市场框架。该框架从物理方案和经济方案两方面对电网需求响应资源支持天然气网络运行进行了尝试和建议。在这个市场框架下,界定了每个利益相关者的功能和利益实现。在这个框架下,富余的电网需求响应资源可以跨网支持气网运行。该框架与现有的天然气市场投标结构相兼容。
1 电气跨网需求侧响应框架 1.1 电网到气网的跨网需求侧响应市场框架供需平衡是每个市场都必须要考虑的问题。当供给量大于需求量时就会产生富余资源。电网的富余需求响应资源主要来源于3部分,一部分是基于市场上报或计划上报机制中的估计偏差将导致电网需求响应资源的广泛存在[13],一部分是“分布式发电技术”的应用可产生电网的需求响应资源[14],一部分是电力期货交易市场可形成电网的需求响应资源[15]。这些富余的电力资源除了可以满足电网的需求外,还可以跨网支持天然气网的运行。
为了支持天然气网络的安全运行,需要将燃气轮机作为电−气能量转换点。与传统的P2G技术不同,本文将该能量转换点视为一个等效的用户负荷,通过电网需求侧响应机制,等效地抵消掉转换点机组的部分出力,降低了转换点的天然气需求,相当于进行了“电−气”的转换产生了天然气资源。图1为电网需求响应资源参与天然气市场的框架。

|
图 1 电网需求资源参与天然气市场框架 Figure 1 The framework of power demand response resources participation in the natural gas market |
如图1所示,该框架有5个参与主体,分别是:虚拟电厂、电−气转换点、电网络管理方、其他富余天然气气源、天然气网络管理方。
(1) 虚拟电厂:虚拟电厂指代所有愿意贡献富余电力资源的资源拥有方。它不仅包括拥有实际电力供应的发电厂,也包括那些希望减少消耗量以建立同等电力供应的电力消费者。每个虚拟电厂会向电网络管理方提交其富余电力资源的最大容量及其期望进行交易的价格来参与对气网的跨网运行支持。
(2) 电−气转换点:在定义上,电−气转换点是能够将电力转化为天然气并参与天然气市场销售所产生等效天然气的实体。一个典型的电−气转换点是燃气轮机所有者,如燃气热电厂或带有燃气轮机的微电网。本文采取了一种等效替代的方式进行了“电−气”转换,通过降低燃气轮机的机组出力来降低机组的天然气需求,在气网侧相当于增加了一部分天然气资源。在这个提出的框架中,这部分天然气资源可以参与气网的运行。此外,整个电网被划分为多个区域。假设每个区域只有一个电−气转换点,该区域内的富余电力资源只能传输到同一区域的转换点形成需求响应。区域内的富余电力资源只能传输到同一区域的转换点形成需求响应。
(3) 电网络管理方:电网络管理方拥有电网的全部信息和参数。在收到虚拟电厂提交的信息后,会估算出该区域转换点的最大可减少机组出力。
(4) 其他富余天然气资源方:与电网需求响应资源转换的等效天然气量的竞争者。典型的富余天然气资源方包括燃气供应商的备用余量、“分布式发电+P2G”产生的富余气网资源等。
(5) 气网络管理方:当气网出现负荷临时变动或者预测误差时,气网络管理方可以通过下一级天然气市场交易或者气网运行调度解决该问题。因此,通过电网需求响应资源得到的等效天然气量可以参与下一级的天然气市场交易,与其他富余天然气资源方进行竞价。
如图1所示,该框架包含了3个流程。
流程1:如何得到电−气转换点所能提供的最大等效富余天然气量?
本文采取了一种等效转换的方式完成了电力与天然气之间的转换。电−气转换点的最大等效富余天然气量,在电网侧相当于转换点燃气机组的实际最大出力可减少量。流程1显示了求取该实际最大出力可减少量所需的2个步骤(图1中的步骤1和步骤2)。步骤1是虚拟电厂向电网络管理方提交其富余电力资源的供应能力(最大供应量)及其单位成本报价。步骤2是转换点燃气轮机实际最大出力可减少量估计。该步骤模型在2.1节的电−气转换点最大出力可减少量等效模型详细介绍,具体表现为式(1)~(5)。这一步的优化结果为优化问题2提供了约束边界。
流程2:电网需求响应资源转换的等效富余天然气量如何参与天然气市场的竞争?
与发电商参与电力市场竞价的方式相似,每个天然气供气商通过提交其成本容量函数或成本容量曲线的方式,参与天然气市场的竞争。成本容量函数体现了天然气供气商不同容量下的供气成本。在本文中,电网需求响应资源转换的等效富余天然气量通过电−气转换点将跨网需求响应成本容量函数提交给天然气市场,参与天然气市场的竞争,具体表现为流程2。流程2中的步骤3通过求取不同容量下的电−气跨网需求响应成本,构建跨网需求响应成本容量函数。该步骤模型在2.2.2节跨网需求侧响应成本估算模型详细介绍,具体表现为式(3) 和式(6)~(9)。这一步优化结果为优化问题3提供了约束边界。
流程3:等效富余天然气量如何在天然气市场与其他富余天然气资源进行竞争?
通过提交跨网需求响应成本容量函数,等效富余天然气量可以加入天然气市场,与其他富余天然气资源方共同竞争。在此过程中,本文构建了考虑价格成本的最优气网模型,该模型考虑了所有供气商的投标(包括等效富余天然气量和其他富余天然气资源方)、气网运行参数、气网负荷的最新变化、燃气市场的日前预定交易结果。该流程的模型在2.3节电网需求响应资源转换的等效天然气量参与天然气市场竞价模型详细介绍,具体表现为式(10)~(16)。该流程最后输出每个供气商的中标量(包括等效富余天然气量和其他富余天然气资源方的中标量),以及中标等效富余天然气量对应所需电网需求响应资源的最优分配情况。
1.2 电网需求响应资源参与跨网需求侧响应的时间天然气市场与电力市场的结构相似,它的用户需求预测和调度通常发生在气负荷发生前的某一时刻。随着时间越接近负荷发生,市场管理者获得的信息越多,获得新的负荷变化的可能性越大。电网需求响应资源的跨网需求响应就是用于满足调度之后不可预测的负荷变化。
考虑到用户负荷变化和电力需求响应资源进行跨网需求响应在短时间内的不可到达性,图2揭示了需求响应从虚拟电厂向天然气市场跨电网支持的时间发生情况。

|
图 2 需求响应从虚拟电厂向天然气市场跨电网支持的时间发生情况 Figure 2 The timing of cross−grid support for demand response from virtual power plants to the natural gas market |
如图2所示,跨网需求侧响应机制,其执行时间存在以下3个特点:一是在机制中电网部分启动发生的时间应该在完成某一时间级电力市场交易或者电网络调度之后,以确定电力富余资源容量;二是在机制中电网部分启动发生的时间应该在某一时间级天然气市场交易或者天然气网络调度之前,以保证由电力富余资源形成的富余等效天然气量可以参与该时间级的市场交易或者气网运行调度;三是电力富余资源与虚拟电厂的数量存在着时间相反性。第一点和第二点给出了该机制执行时间的限度,在该限度内,执行时间越靠近上一时间级电力市场交易或者电网络调度的完成时间,虚拟电厂所估算的电力富余资源越少(富余电量越靠近使用时间越明确) ,可以参与跨网支持气网运行的虚拟电厂反而越多(电力网络输电需要一定的时间,时间越长,囊括的范围越广,可以参与的虚拟电厂越多) 。相反,在该限度内,执行时间越靠近下一时间级电力市场交易或者电网络调度的完成时间,虚拟电厂所估算的电力富余资源越多,可以参与跨网支持气网运行的虚拟电厂越少。
2 电网需求响应资源参与跨网需求侧响应等效模型 2.1 电−气转换点最大出力可减少量等效模型电网需求响应资源并非都可以通过电−气转换点参与气网的运行,其主要受到以下几个方面的影响。
虚拟电厂出力限制:所有的跨网资源都来自拥有富余资源的电网用户或发电厂,其所能参与跨网支持的资源刚好小于或等于电网用户或发电厂的所能提供的最大富余资源。
电力传输限制:从电力到天然气的转换需要电力从虚拟电厂传输到转换点,传输的限制存在两个问题。一是电网的输送约束,如各线路的输送能力限制,二是电力传输时间限制,它应该小于转换商中交易和发生的时间间隔。
转换点最大出力可减少量限制:虚拟电厂支持转换点需要考虑转换点出力减少量限制,其所能支持的电力资源小于等于转换点最大出力可减少量。
由于转换点的燃气轮机需要从富余电力中获得机组最大出力可减少量,即相当于转换点的最大天然气可供给量以供天然气市场报价,因此最初需要获得转换点的最大出力可降低幅度。它可以通过求解式(1)~(5) 中的一个优化问题(简称优化1) 得到。
| $ \mathrm{m}\mathrm{a}\mathrm{x}:\mathrm{O}\mathrm{b}\mathrm{j}\_1({P}^{\mathrm{v}},{P}^{\mathrm{g}\mathrm{r}}) =\mathrm{\Delta }{P}^{\mathrm{g}\mathrm{r}} $ | (1) |
式(1) 为优化1的目标函数,表示转换点机组最大出力可减少量。
| $ {P}^{\mathrm{g}\mathrm{r}}+\sum {P}^{\mathrm{d}\mathrm{r}}+\sum {P}^{\mathrm{v}}=\sum D $ | (2) |
式(2) 为负荷平衡约束。
| $ 0\leqslant {P}^{\mathrm{v}}\leqslant {P}^{\mathrm{v},\mathrm{m}\mathrm{a}\mathrm{x}} $ | (3) |
式(3) 为虚拟电厂出力约束。
| $ \left\{\begin{split} &\Delta {P}^{\mathrm{g}\mathrm{r}}={P}^{\mathrm{g}\mathrm{r},\mathrm{a}\mathrm{f}}-{P}^{\mathrm{g}\mathrm{r}}\\ &0\leqslant \Delta {P}^{\mathrm{g}\mathrm{r}}\leqslant \Delta {P}^{\mathrm{g}\mathrm{r},\mathrm{m}\mathrm{a}\mathrm{x}}\end{split}\right. $ | (4) |
式(4) 为转换点燃气轮机出力降低量的约束。
| $ \left\{\begin{split} &{\boldsymbol{J}}={\boldsymbol{H}}\otimes ({\boldsymbol{R}}\otimes {\boldsymbol{P}}-{\boldsymbol{U}}\otimes D) \\ &\left|\boldsymbol{J}\right|\leqslant {\boldsymbol{J}}^{{\rm{re,max}}}\\ &{J}_{n}={J}_{n,\mathrm{a}\mathrm{f}}\end{split}\right. $ | (5) |
式(5) 为线路潮流约束。
优化1显示了转换点机组的最大出力可减少量,相当于获得了跨网需求响应支持气网运行的最大等效天然气量。此最大容量反映了跨网需求响应对气网的最大支持。但是,容量的使用量取决于天然气网络的运行要求,气网也会购买不同的容量。因此,对于转换商中的投标建设,需要估算不同容量水平下的电网需求响应资源进行跨网需求响应的成本。
图3揭示了电网需求响应资源参与气网运行的物理通路。如图3所示,将富余电力资源从来源方传输到气网的需求端,影响跨网需求响应成本的因素主要有两个。一是虚拟电厂提交的报价;二是电网络管理方收取的调度费用,它起到了一个类似高速公路收费站的作用。

|
图 3 电网需求资源参与气网运行的物理通路示意图 Figure 3 Schematic diagram of physical path of power demand response resources participation in gas network operation |
通过式 (3)、(6)~(9) 对不同容量水平下电网需求响应资源进行跨网需求响应的成本(简称优化2) 进行建模求解。
| $ \mathrm{m}\mathrm{i}\mathrm{n}:\mathrm{O}\mathrm{b}\mathrm{j}\_2\left(\mathrm{\Delta }{P}^{\mathrm{g}\mathrm{r},x}\right) =(1+\varepsilon ) {\sum }_{k=1}^{K}({\xi }_{k}\cdot {P}_{k}^{\mathrm{v}}) $ | (6) |
式(6) 为优化2目标函数,表示跨网需求响应成本最低。
| $ \left\{\begin{split} &{P}^{\mathrm{g}\mathrm{r},x}={P}^{\mathrm{g}\mathrm{r},\mathrm{a}\mathrm{f}}-\Delta {P}^{\mathrm{g}\mathrm{r},x}\\ &0\leqslant \Delta {P}^{\mathrm{g}\mathrm{r},x}\leqslant \Delta {P}^{\mathrm{g}\mathrm{r}}\end{split}\right. $ | (7) |
通过式(7) ,当不同容量下的
| $ {P}^{\mathrm{g}\mathrm{r},x}+\sum {P}^{\mathrm{d}\mathrm{r}}+\sum {P}^{\mathrm{v}}=\sum D $ | (8) |
式(8) 为负荷平衡约束。
| $ \left\{\begin{split} &{\boldsymbol{J}}={\boldsymbol{H}}\otimes ({\boldsymbol{R}}\otimes {\boldsymbol{P}}+{\boldsymbol{O}}\otimes {P}^{\mathrm{v}}-{\boldsymbol{U}}\otimes D) \\ &\left|\boldsymbol{J}\right|\leqslant {\boldsymbol{J}}^{\mathrm{r}\mathrm{e},\mathrm{m}\mathrm{a}\mathrm{x}}\\ &{J}_{n}={J}_{n,\mathrm{a}\mathrm{f}}\end{split}\right. $ | (9) |
式(9) 为线路潮流约束条件。
通过优化2得到了电网需求响应资源参与跨网需求响应的成本与此时转换点燃气轮机的实际出力
| $ \left\{\begin{split} &{G}^{\mathrm{g}\mathrm{r},x}=\alpha \cdot ({P}^{\mathrm{g}\mathrm{r},x}\cdot {P}^{\mathrm{g}\mathrm{r},x}) +\beta \cdot {P}^{\mathrm{g}\mathrm{r},x}+\gamma \\ &\Delta {G}^{\mathrm{g}\mathrm{r},x}={G}^{\mathrm{g}\mathrm{r},\mathrm{a}\mathrm{f}}-{G}^{\mathrm{g}\mathrm{r},x}\end{split}\right. $ | (10) |
式中
得到不同容量水平下电网需求响应资源转换的等效天然气量和对应成本后,选取作为转换点的燃气轮机作为该需求响应资源参与天然气市场竞争点。通过公式(11)~(16) 构建等效天然气量参与天然气市场竞价模型,得到等效天然气量在市场中的中标量(简称优化3) 。
| $ \mathrm{m}\mathrm{i}\mathrm{n}:\mathrm{O}\mathrm{b}\mathrm{j}\_3(W,{\rm{Gr}}) ={\sum }_{i=1}^{I}({\omega }_{i}\cdot {W}_{i}) +\mathrm{Cos}\mathrm{t}\left({\rm{Gr}}\right) $ | (11) |
式(11) 为优化3目标函数,表示气网最优调度。
| $ {\boldsymbol{T}}^{{{\rm{W}}}}\otimes W-{\boldsymbol{T}}^{{{\rm{l}}}}\otimes \boldsymbol{L}+{\boldsymbol{T}}^{{{\rm{gr}}}}\otimes Gr={\boldsymbol{T}}^{{{\rm{f}}}}\otimes \boldsymbol{F} $ | (12) |
式(12) 为天然气系统气量平衡方程。式中,T W为节点−气源关联矩阵,T l为节点−负荷关联矩阵,T gr为气网节点−转换点关联矩阵,T f为节点−管道关联矩阵。L和F分别为气网负荷矩阵与管道潮流矩阵。
| $ \sum W+{\rm{Gr}}=\sum \boldsymbol{L} $ | (13) |
式(13) 为气网负荷平衡方程。
| $ \left|\boldsymbol{F}\right|\leqslant {\boldsymbol{F}}^{{\rm{re,max}}} $ | (14) |
式(14) 为管道潮流约束条件。F re,max为管道满足日前市场后的剩余容量最大值矩阵。
| $ 0\leqslant W \leqslant {\boldsymbol{W}}^{{\rm{re,max}}} $ | (15) |
式(15) 为其他富余天然气资源方的供气量约束边界条件。Wre,max为天然气气源日前市场后的剩余容量最大值矩阵。
| $ 0\leqslant {\rm{Gr}}\leqslant \mathrm{\Delta }{\rm{G}}{{\rm{r}}}^{\mathrm{g}\mathrm{r},x} $ | (16) |
式(16) 为等效天然气量的边界约束条件。
3 优化模型求解本文根据所构建模型的不同特点,分别采用了不同的优化算法进行了求解。对于优化1,选用了Matlab作为仿真平台,并采用了Gurobi作为优化工具箱进行求解。
3.1 优化2模型求解对于优化2,由于转换点需要转换的等效天然气量取决于气网络管理方的需求,这意味着转换点对于每个不同的供气能力都需要对Obj_2进行独立的优化以得到最优成本。然而,处理无限优化问题是不可能的。于是,本文采用了文献[16]提出的一种直接求解法,将整个优化问题整合为一个函数,只需要输入此时转换点燃气轮机机组出力的减少量即可得到对应最优成本与转换中标等效天然气量所需电网需求响应资源的最优分配。具体解法如下:
步骤1:建立约束方程组
| $ \left\{\begin{split} {\boldsymbol{C}}\left({P}^{\mathrm{v}}\right) ={\boldsymbol{0}}\\ {\boldsymbol{S}}\left({P}^{\mathrm{v}}\right) ={\boldsymbol{0}}\end{split}\right. $ | (17) |
式中:
| $ \boldsymbol{C}\left({P}^{{{\rm{v}}}}\right) =\left[{\boldsymbol{C}}_{{{1}}}\left({P}^{\rm{v}}\right) ;{\boldsymbol{C}}_{{{2}}}\left({P}^{\rm{v}}\right) ;{\boldsymbol{C}}_{{{3}}}\left({P}^{\rm{v}}\right) ;{\boldsymbol{C}}_{{{4}}}\left({P}^{\rm{v}}\right) \right] $ | (18) |
步骤2:引入变量转换点燃气轮机机组出力的减少量
| $ {\boldsymbol{P}}^{{x}}=[{P}^{\mathrm{g}\mathrm{r},x};{P}^{\mathrm{d}\mathrm{r}}] $ | (19) |
步骤3:将4个不等约束转变成等式约束。
线路潮流上限约束:
| $ {\boldsymbol{C}}_{{{1}}}\left({P}^{\mathrm{v}}\right) =\boldsymbol{H}\otimes \left(\boldsymbol{R}\otimes {{\boldsymbol{P}}}^{x}+\boldsymbol{O}\otimes {P}^{\mathrm{v}}-\boldsymbol{U}\otimes D\right) -{\boldsymbol{J}}^{\mathrm{r}\mathrm{e},\mathrm{m}\mathrm{a}\mathrm{x}} $ | (20) |
将该约束转换为
| $ \left\{\begin{split} &{\boldsymbol{A}}_{1}={\boldsymbol{H}}\otimes {\boldsymbol{O}}\\ &{\boldsymbol{B}}_{1}={\boldsymbol{H}}\otimes ({\boldsymbol{U}}\otimes D-{\boldsymbol{R}}\otimes {{\boldsymbol{P}}}^{x}) +{\boldsymbol{J}}^{\rm{re,max}}\end{split}\right. $ | (21) |
式(21) 为线路潮流上限约束转换的等效等式约束。同理,求出另外3个不等式约束的等效等式约束。约束等式
步骤4:提取等式方程。
优化2目标函数有
| $ {\boldsymbol{E}} = \left\{ {\left. {{e_{j \times l}}} \right\}} \right.;j = C_{2 \cdot ({\rm{NL}} + K)}^{K - 1} - KN,l = 2 (N + K) $ | (22) |
如式(22) 所示,E为
步骤5:求解方程组。
提取方程组:
| $ \left\{\begin{split} {\boldsymbol{C}}\left({P}_{q}^{\mathrm{v}}\right) ={\boldsymbol{0}}\\ {\boldsymbol{S}}\left({P}^{\mathrm{v}}\right) ={\boldsymbol{0}}\end{split}\right. $ | (23) |
式中:
| $ \left\{\begin{split} {\boldsymbol{E}}\_{\boldsymbol{A}}_{{{1}},{q}}={ O}({\boldsymbol{E}}_{{q}}^{\rm{T}}\odot {\boldsymbol{A}}) \\ {\boldsymbol{E}}\_{\boldsymbol{B}}_{{{1}},{q}}={ O}({\boldsymbol{E}}_{{q}}^{\rm{T}}\odot {\boldsymbol{B}}) \end{split}\right. $ | (24) |
式中:
| $ \left\{\begin{split} &{\boldsymbol{E}}\_{\boldsymbol{A}}_{{{2}},\boldsymbol{q}}={{{\rm{ones}}({\boldsymbol{1}},{{K}})}} \\ &{{{\boldsymbol{E}}}}\_{{{{\boldsymbol{B}}}}}_{{{2}},{\boldsymbol{q}}}=\sum D-\sum {P}^{\mathrm{d}\mathrm{r}}-{P}^{\mathrm{g}\mathrm{r},x}\end{split}\right. $ | (25) |
| $ \left\{\begin{split}{\boldsymbol{E}}\_{\boldsymbol{A}}_{{q}}=\left[\boldsymbol{E}\_{\boldsymbol{A}}_{{{1}},{q}}\text{;}\boldsymbol{E}\_{\boldsymbol{A}}_{{{2}},{q}}\right]\\ {\boldsymbol{E}}\_{\boldsymbol{B}}_{{q}}=\left[\boldsymbol{E}\_{\boldsymbol{B}}_{{{1}},{q}}\text{;}{\boldsymbol{E}}\_{{\boldsymbol{B}}}_{{{2}},{{q}}}\right]\end{split}\right. $ | (26) |
如式(26) 所示,联立方程求出虚拟电厂供电量
| $ {P}_{q}^{\mathrm{v}}=\boldsymbol{E}\_{\boldsymbol{A}}_{{q}}^{{{-1}}}\otimes \boldsymbol{E}\_{\boldsymbol{B}}_{{q}} $ | (27) |
依次计算所有
步骤6:从得到的对应方程组的解集中选择最优解。
| $ \mathrm{m}\mathrm{i}\mathrm{n}:\mathrm{O}\mathrm{b}\mathrm{j}\_2=(1+\varepsilon ) {\sum }_{k=1}^{K}({\xi }_{k}\cdot {P}_{k}^{\mathrm{v}}) $ | (28) |
令
| $ \mathrm{m}\mathrm{i}\mathrm{n}:\mathrm{O}\mathrm{b}\mathrm{j}\_2=\frac{{\displaystyle\sum }_{q=1}^{q}\left[\Biggr(\dfrac{\dfrac{1}{\mathrm{O}\mathrm{b}\mathrm{j}\_{2}_{z}}}{{\displaystyle\sum }_{q=1}^{q}\dfrac{1}{{\rm{Obj}}\_{2}_{z}}}\Biggr) ^\varLambda\odot \mathrm{O}\mathrm{b}\mathrm{j}\_{2}_{z}\right]}{{\displaystyle\sum }_{q=1}^{q}\Biggr(\dfrac{\dfrac{1}{\mathrm{O}\mathrm{b}\mathrm{j}\_{2}_{z}}}{{\displaystyle\sum }_{q=1}^{q}\dfrac{1}{\mathrm{O}\mathrm{b}\mathrm{j}\_{2}_{z}}}\Biggr) ^\varLambda}-{t} $ | (29) |
对于优化3,本文引入了辅助惩罚函数
| $ f(x)=\left\{\begin{array}{l} {\rm{e}}^{a (-x+x^{{\rm{bor}}})} \\ {\rm{e}}^{a (x-x^{{\rm{bor}}} )} \end{array}\right. $ | (30) |
| $ g\left(x\right) ={\mathrm{e}}^{{u} (x{) }^{\mathrm{b}}}$ | (31) |
如式(30)、(31)所示,
采用了如图4所示的9节点电力系统[17]与6节点气网系统[18]进行案例分析。

|
图 4 9节点电力系统和6节点气网系统 Figure 4 The 9−bus power system and 6−node gas system |
如图4所示,在电力系统中划分了一个区域,区域1包含了Bus1和Bus3。TAP表示电−气转换点,它位于电力系统的Bus1,与气网节点5相连接。在区域1中存在两个虚拟电厂,一个位于Bus1(V1) ,一个位于Bus3(V2) 。此外,发电厂G2、G3和G4仅参加日前市场,不加入需求响应市场。表1和表2提供了用于仿真的关键参数。
| 表 1 虚拟电厂的最大出力和报价 Table 1 Maximum output and quotation of virtual power plants |
| 表 2 转换点燃气轮机机组参数 Table 2 Gas turbine unit parameters at the transition point |
优化1的目标是求出转换点燃气轮机的最大出力可减少量,相当于天然气市场中转换点所能提供的最大等效天然气量。图5展示了Obj_1的优化结果,图中有3条曲线,分别代表转换点机组最大出力可减少量,区域1虚拟电厂最大出力总和以及转换点机组实际最大出力减少结果。如图所示,从1:00~14:00,转换点机组实际最大出力减少结果维持在11 MW,这相当于虚拟电厂V1和V2的最大出力之和。这意味着,在这个时间段内,虚拟电厂所有的出力都能被等效的转换为天然气。在15:00以后,转换点机组最大出力可减少量减少。由于受到最大出力可减少量的限制,转换点机组的实际最大出力减少结果开始下降。
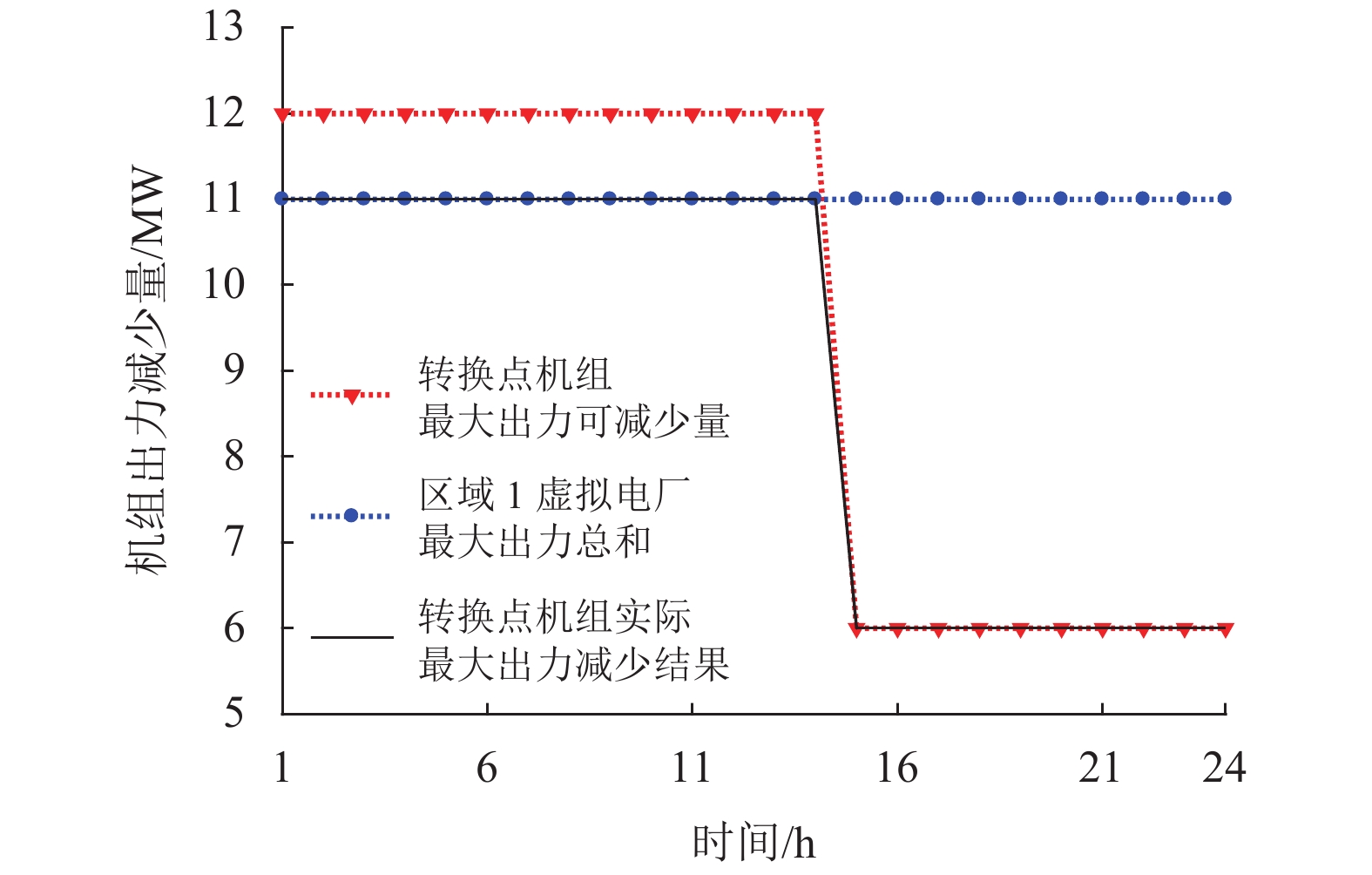
|
图 5 优化目标1结果 Figure 5 Result of Obj_1 |
优化2解决了在转换点燃气轮机用气减少量确定时,跨网需求响应成本最小的问题。图6展示了凌晨4点Obj_2的部分优化结果,图中有两条曲线,分别为“成本−等效天然气量曲线”以及“成本−虚拟电厂出力曲线”。从图中可以看出,曲线存在转折点,这是由于虚拟电厂之间存在价格差异产生的。当天然气市场的用气需求下降时,转换点将先降低V2的出力,因为V2的价格昂贵。考虑到电力系统传输限制,只有在清除所有V2的出力后,才会减少来自V1的出力。因此,在转折点的右侧,到达的虚拟电厂出力大于转折点,曲线下降速度与V2的价格有关。在转折点的左侧,曲线下降速度与V1的价格有关。并且转折点位于这样一种情况,即来自V2的所有出力都被清除了,只提供了来自V1的所有出力。从图中可以明显看出,在转折点所能提供的等效天然气量为84.92 m3,这是V1的最大出力所能转换的等效天然气量。
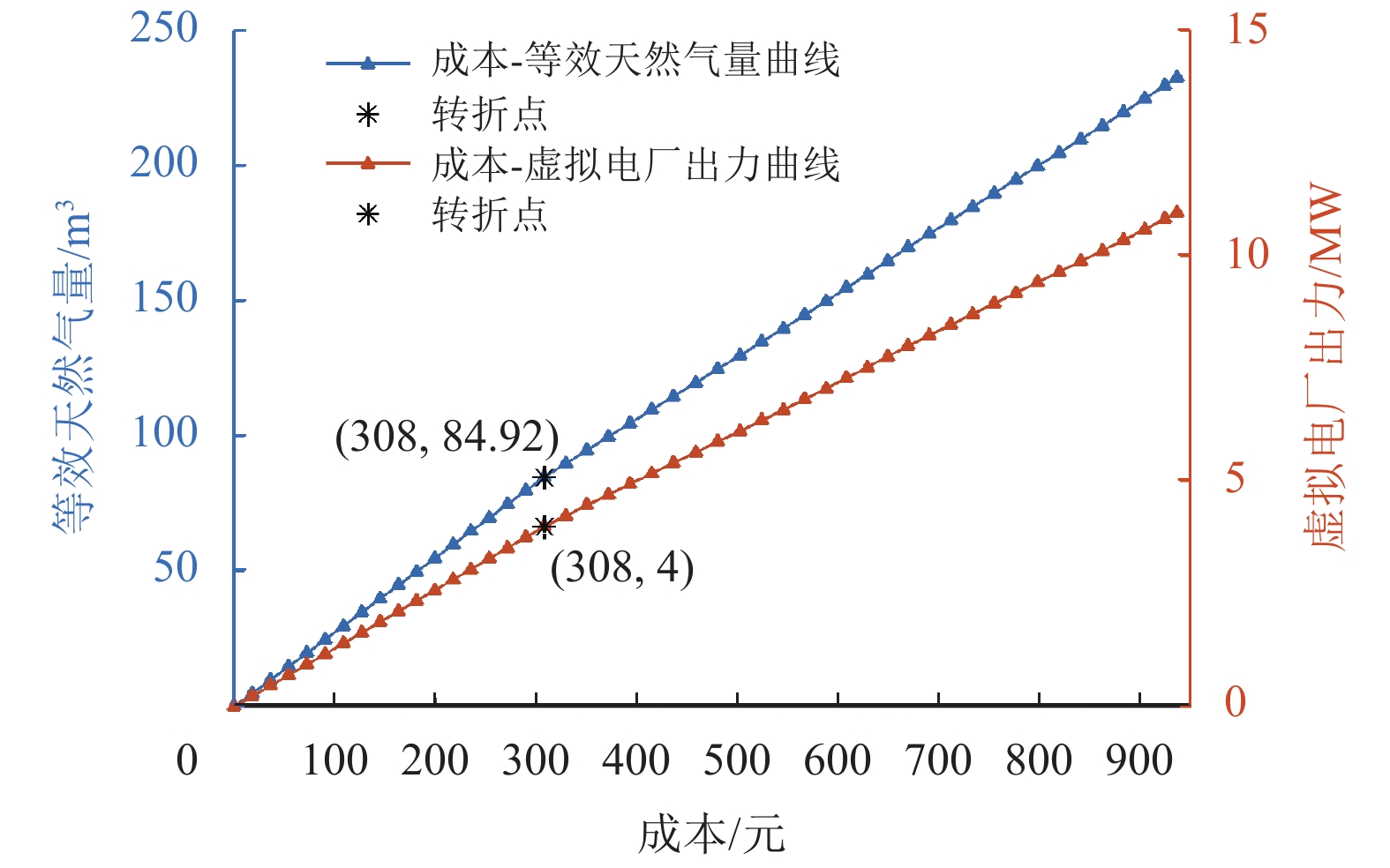
|
图 6 优化目标2结果 Figure 6 Result of Obj_2 |
优化3解决了电网需求响应资源转换的等效天然气量参与天然气市场竞价的问题,得到了该等效天然气量在市场中的竞争结果。图7为优化3目标函数收敛曲线图,由图可知,其收敛速度较快,在迭代次数将近100次前便已收敛,停止迭代。

|
图 7 LM法目标函数收敛图 Figure 7 The convergence graph of the objective function of LM method |
图8和图9展示了Obj_3的优化结果。从两图中可以看出等效天然气量在天然气市场中的中标量以及对应中标天然气量所需的虚拟电厂出力与虚拟电厂出力在电网需求响应资源中的最优分配。如图8所示,转换点的所有等效天然气量都赢得了天然气市场的竞争,其相应的气量由气网络管理方购买。这是由于其报价相对于其他富余天然气气源更加便宜。如图9所示,对于虚拟电厂的最优分配,由于V1的价格比V2便宜,因此优先选择由V1提供。例如,从图9中可以看出,从1:00~14:00,中标等效天然气量的所需虚拟电厂出力等于V1和V2的出力总和。而在14:00后,中标等效天然气量下降,所需虚拟电厂出力降低,由于V1出力成本较低,此时转换点会选择降低V2的出力,而保持V1的出力。
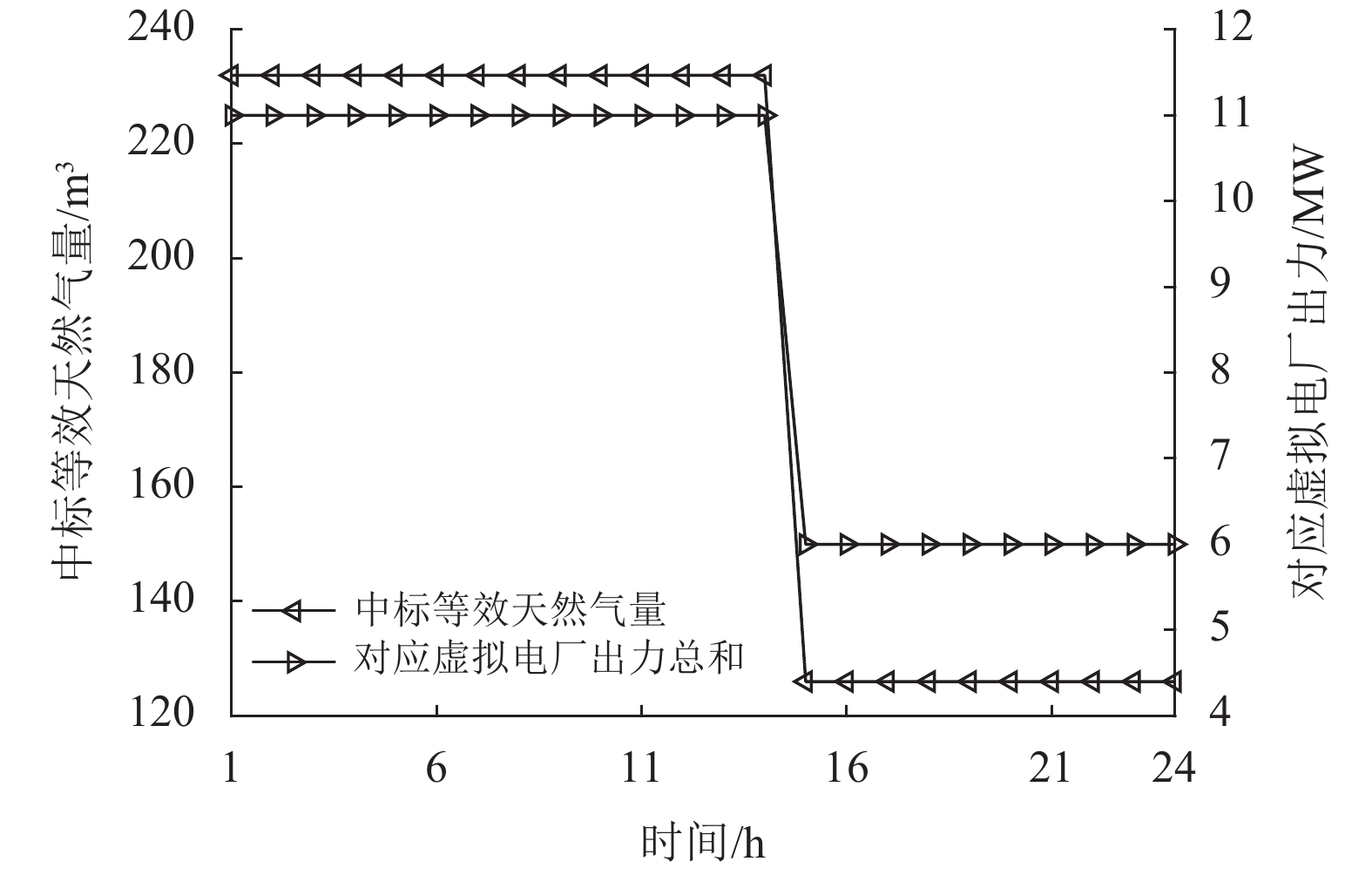
|
图 8 等效天然气量中标结果 Figure 8 Bidding results of equivalent natural gas volume |
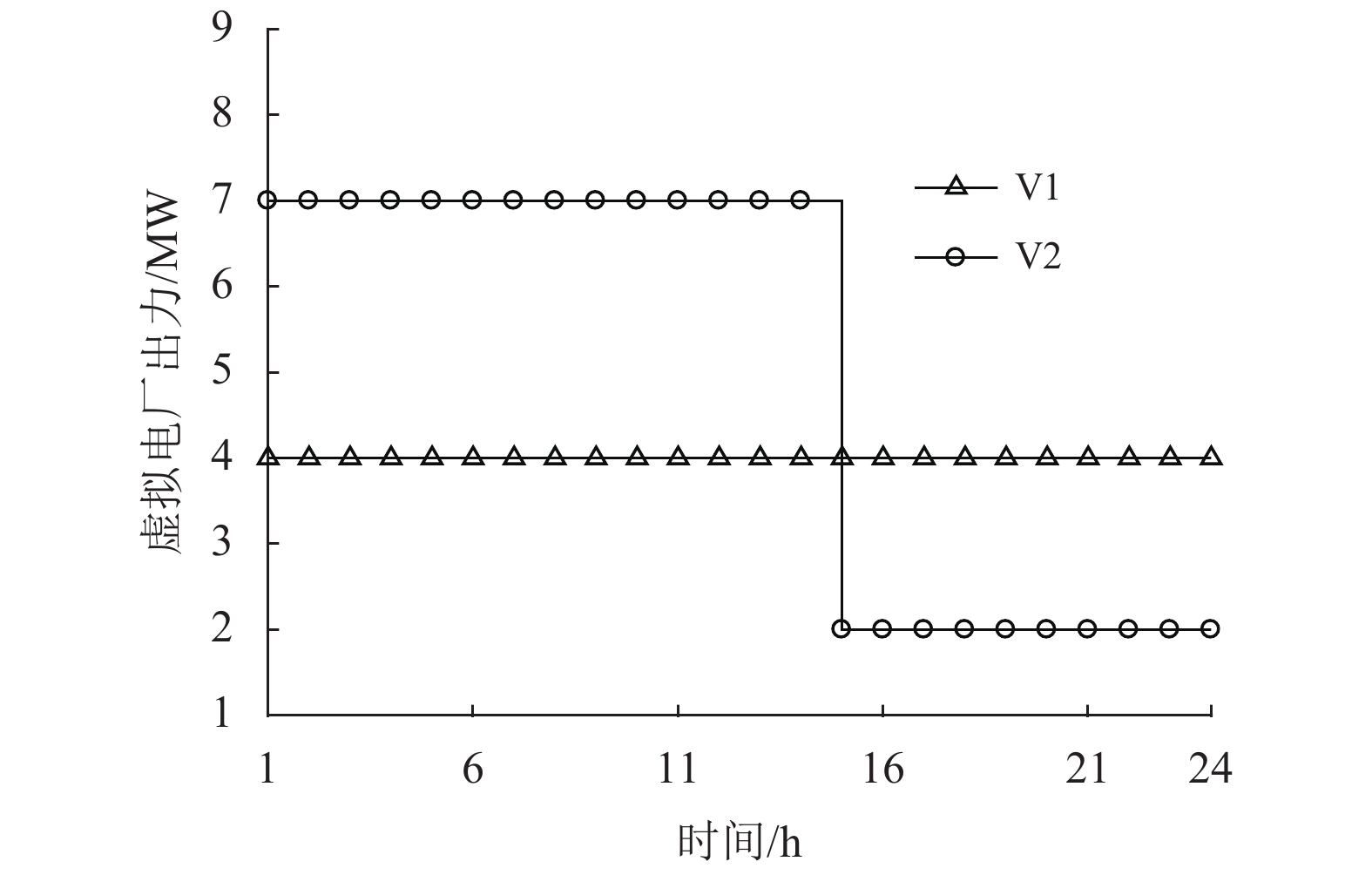
|
图 9 虚拟电厂最优分配结果 Figure 9 Optimal allocation results of virtual power plants |
本文采用了一种模拟的方法,通过尝试不同的虚拟电厂报价和电网络管理方调度费用展示了虚拟电厂报价价格和电网络调度费用的敏感性效应。本次分析选取了凌晨4点模拟的情况,如表3所示。通过表3可知,报价和调度费用的变动会影响天然气市场竞争的结果。随着虚拟电厂报价价格和电网调度费用价格的上涨,电网需求响应资源转换等效天然气量的成本随之增加。因此,等效天然气量正在丧失其在天然气市场上的竞争优势。当两者价格足够高到某个阈值时,气网络管理方将取消等效天然气量的交易优先级,转而使用其他富余气网资源。这就是表3的最后几个案例中,中标等效天然气量从最大等效天然气量233 m3逐渐降到0的原因。
| 表 3 虚拟电厂报价和电网络调度费用敏感性分析结果 Table 3 Sensitivity analysis results of quotation of virtual power plant and dispatch cost of power system |
本文提出了一个从电网到气网的跨网需求响应市场框架。在提出的框架中,电−气转换点是电网向天然气市场输送电网需求响应资源的切入点。本文利用3个优化模型(优化1、优化2、优化3)将富余的电网需求响应资源等效地转换为富余天然气资源,使得转换点能以富余天然气气源拥有方的形式加入天然气市场与其他富余气源拥有方竞价。并在天然气市场竞争后,将转换中标等效天然气量所需的虚拟电厂出力以成本最优的方式分配给同区域的虚拟电厂。
本文旨在使人们意识到,一种能源的富余资源可以通过能源市场来实现另一种能源网络的供需平衡。本文试图通过天然气市场将电力系统需求侧响应应用于天然气网络平衡。
同时,针对虚拟电厂分布在电网多个不同节点的情况,本文提出的逻辑和模型是在天然气市场中寻找一个可以作为代理的能源转换实体(电−气转换点)。考虑到虚拟电厂出力限制、电力传输限制以及转换点机组最大出力可减少量限制,所有的参与跨网需求响应的富余电力资源在该代理集成。集成富余电力资源(转换点机组实际出力减少量)的最大到达量和成本容量函数可以用两个优化(优化1和优化2)实现。优化1是估算转换点机组实际最大出力可减少量,优化2是估算每一次跨网需求响应所需总成本。
同时,对于电网需求响应资源转换的等效富余天然气资源,本文构建了以价格成本最低为目标的气网最优调度模型(优化3),实现了等效富余天然气资源与其他富余天然气资源的竞价。
| [1] |
杨晚生, 郭开华. 分布式供能系统的定义及其内涵[J].
广东工业大学学报, 2010, 27(3): 76-82.
YANG W S, GUO K H. Definition and connotation for distributed energy system[J]. Journal of Guangdong University of Technology, 2010, 27(3): 76-82. DOI: 10.3969/j.issn.1007-7162.2010.03.019. |
| [2] |
赵军, 王妍, 王丹, 等. 能源互联网研究进展: 定义、指标与研究方法[J].
电力系统及其自动化学报, 2018, 30(10): 1-14.
ZHAO J, WANG Y, WANG D, et al. Research progress in energy internet: definition, indicator and research method[J]. Proceedings of the CSU-EPSA, 2018, 30(10): 1-14. DOI: 10.3969/j.issn.1003-8930.2018.10.001. |
| [3] |
王毅, 张宁, 康重庆. 能源互联网中能量枢纽的优化规划与运行研究综述及展望[J].
中国电机工程学报, 2015, 35(22): 5669-5681.
WANG Y, ZHANG N, KANG C Q. Review and prospect of optimal planning and operation of energy hub in energy internet[J]. Proceedings of the CSEE, 2015, 35(22): 5669-5681. DOI: 10.13334/j.0258-8013.pcsee.2015.22.001. |
| [4] |
SALDARRIAGA C A, HINCAPIÉ R A, SALAZAR H. A holistic approach for planning natural gas and electricity distribution networks[J].
IEEE Transactions on Power Systems, 2013, 28(4): 4052-4063.
DOI: 10.1109/TPWRS.2013.2268859. |
| [5] |
CHEN Y B, ZHANG L X, PENG X, et al. Electricity demand response schemes in China: pilot study and future outlook[J]. Energy, 2021, 224: 120042.
|
| [6] |
PALENSKY P, DIETRICH D. Demand side management: demand response, intelligent energy systems, and smart loads[J].
IEEE Transactions on Industrial Informatics, 2011, 7(3): 381-388.
DOI: 10.1109/TII.2011.2158841. |
| [7] |
张磊, 秦光宇, 刘亚玲. 含电转气的多能源中心协调优化运行策略[J].
中国电力, 2020, 53(10): 113-122.
ZHANG L, QIN G Y, LIU Y L. Coordinated optimization operation strategy for multi-energy center with power-to-gas devices[J]. Electric Power, 2020, 53(10): 113-122. |
| [8] |
卢志刚, 乞胜静, 蔡瑶, 等. 基于改进MOBCC算法的热电联合系统经济环境调度[J].
中国电力, 2021, 54(2): 164-174.
LU Z G, QI S J, CAI Y, et al. Economic and environmental dispatch of combined heat and power system based on improved MOBCC algorithm[J]. Electric Power, 2021, 54(2): 164-174. |
| [9] |
陈凯炎, 牛玉刚. 基于V2G技术的电动汽车实时调度策略[J].
电力系统保护与控制, 2019, 47(14): 1-9.
CHEN K Y, NIU Y G. Real-time scheduling strategy of electric vehicle based on vehicle-to-grid application[J]. Power System Protection and Control, 2019, 47(14): 1-9. DOI: 10.7667/PSPC20191401. |
| [10] |
罗金满, 赵善龙, 封祐钧, 等. 考虑综合需求响应不确定性的电−气综合能源系统优化运行[J].
中国电力, 2020, 53(12): 119-126.
LUO J M, ZHAO S L, FENG Y J, et al. Optimal operation of integrated electricity-gas system considering uncertainty of integrated demand response[J]. Electric Power, 2020, 53(12): 119-126. |
| [11] |
崔杨, 闫石, 仲悟之, 等. 含电转气的区域综合能源系统热电优化调度[J].
电网技术, 2020, 44(11): 4254-4264.
CUI Y, YAN S, ZHONG W Z, et al. Optimal thermoelectric dispatching of regional integrated energy system with power-to-gas[J]. Power System Technology, 2020, 44(11): 4254-4264. DOI: 10.13335/j.1000-3673.pst.2019.2468. |
| [12] |
NI L N, LIU W J, WEN F S, et al. Optimal operation of electricity, natural gas and heat systems considering integrated demand responses and diversified storage devices[J].
Journal of Modern Power Systems and Clean Energy, 2018, 6(3): 423-437.
DOI: 10.1007/s40565-017-0360-6. |
| [13] |
陈冠廷, 张利, 刘宁宁, 等. 基于区块链的面向居民用户需求响应交易机制[J].
电力自动化设备, 2020, 40(8): 9-17.
CHEN G T, ZHANG L, LIU N N, et al. Blockchain-based transaction mechanism for residential users demand response[J]. Electric Power Automation Equipment, 2020, 40(8): 9-17. DOI: 10.16081/j.epae.202008024. |
| [14] |
高赐威, 李倩玉, 李慧星, 等. 基于负荷聚合商业务的需求响应资源整合方法与运营机制[J].
电力系统自动化, 2013, 37(17): 78-86.
GAO C W, LI Q Y, LI H X, et al. Methodology and operation mechanism of demand response resources integration based on load aggregation[J]. Automation of Electric Power Systems, 2013, 37(17): 78-86. DOI: 10.7500/AEPS201211091. |
| [15] |
杜江, 董超, 邸鹏宇, 等. 电力市场期货交易的分析与应用[J].
机电信息, 2018(30): 114-115+117.
DOI: 10.3969/j.issn.1671-0797.2018.30.065. |
| [16] |
XU F Y, TANG R X, XU S B, et al. Neural network-based photovoltaic generation capacity prediction system with benefit-oriented modification[J]. Energy, 2021, 223: 119748.
|
| [17] |
LI D S, GAO C W, SHI X M. Study on coupled planning of power grid and gas network considering P2G device [C]// 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2) , Beijing: IEEE, 2017.
|
| [18] |
ZHANG Y C, HUANG Z H, ZHENG F, et al. Interval optimization based coordination scheduling of gas–electricity coupled system considering wind power uncertainty, dynamic process of natural gas flow and demand response management[J]. Energy Reports, 2020, 6: 216-227.
|
 2023, Vol. 40
2023, Vol. 40