2. 南京大学 新型软件技术国家重点实验室,江苏 南京 210093
2. State Key Lab for NoveI Software Technology, Nanjing University, Nanjing 210093, China
近年来,随着各种成像技术的飞速发展,高光谱图像受到了越来越多的关注,并且广泛应用于食品安全[1]、环境监测[2]、公共安全[3]等诸多领域。高光谱图像聚类是高光谱图像处理技术的重要方向,迄今,已经有多种聚类算法应用于高光谱图像分割,其中包括基于质心的聚类方法[4-5]、基于核的聚类方法[6]、基于图的聚类方法[7]和支持向量机的聚类方法。基于质心的聚类方法有K均值聚类(K-means)[4]和模糊C均值聚类(Fuzzy C-means, FCM)[5]。基于质心的聚类方法主要是根据距离或相似度测量将数据点分配到最近的质心,然后通过更新迭代求解最终的簇。但是高维数据的结构复杂性和相似度计算的不准确性都会导致聚类性能下降。事实上,许多高维数据可能在低维子空间中表现出可分性。因此,许多学者在进行聚类分析之前,通常会通过主成分分析等一些降维技术将高维数据投影到低维子空间上,如对高维数据进行降维迭代的K均值聚类[8]。但是当高维数据结构非凸时,这类算法的聚类性能会下降,因此学者们探索了新的算法−谱聚类(Spectral Clustering, SC)[9]。谱聚类是一种基于图论的聚类方法,它可以对任意形状的样本空间进行聚类,得到全局最优解。SC更适合流形数据,在一个低维数据流形的高密度区域中,相邻的两个数据点具有相同的簇标签。然而,对于高维稀疏数据,最近邻实际上可能仍然相距甚远。此外,谱聚类是一种基于相似度矩阵的聚类方法,因此有很多算法旨在探索更精确的相似度矩阵,如文献[10]提出了基于Nyström扩展和基于锚的图的有效逼近技术来构建相似度矩阵。另外稀疏子空间算法(Sparse Subspace Clustering, SSC)[11]旨在揭示高维数据子空间结构,进而得到更准确的相似度矩阵。然而稀疏子空间聚类应用于高维数据如高光谱图像时,会存在一定的信息冗余,文献[12]提出了一种基于信息熵的加权块稀疏子空间聚类算法,通过正向干预稀疏表示进而降低冗余。SSC算法在稀疏表示过程中并没有考虑像素点的空间分布,为了充分利用高光谱图像的空间信息,文献[13]提出了一种相似矩阵构建方法——余弦欧氏动态加权相似矩阵(Cosine-Euclidean Dynamic Weighting Similarity Matrix, CEDW)。
对于高维数据来说,用欧几里德距离来度量高维稀疏样本的相似度并不是最好的选择,因为当高光谱图像的维数增加时,算法将陷入维数灾难。
因此,本文提出了一种基于Fréchet距离的高光谱图像聚类算法。相似度矩阵构建过程如图1所示。高光谱图像矩阵
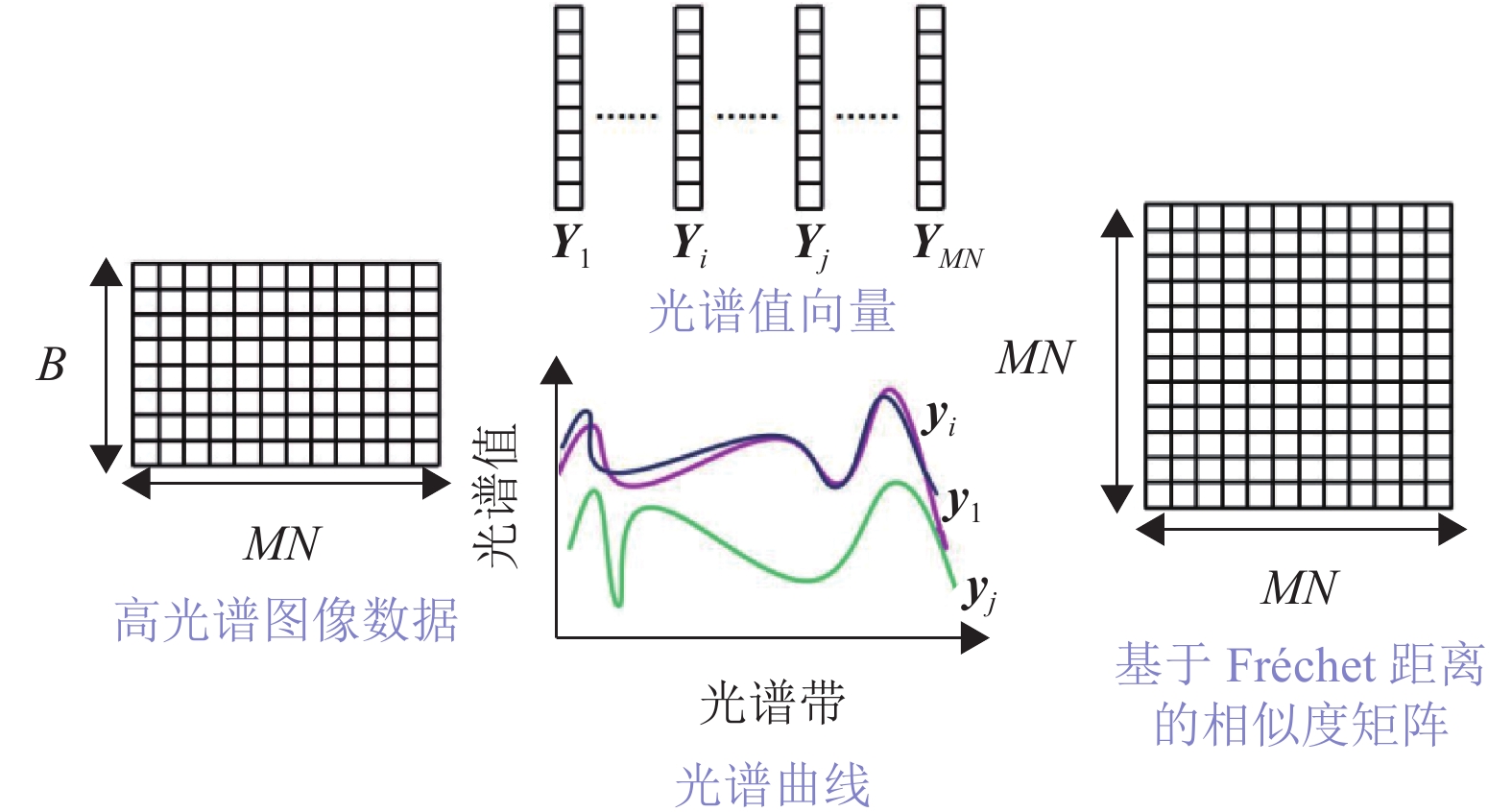
|
图 1 Fréchet距离构建相似度矩阵的过程 Figure 1 Construction the similarity matrix by Fréchet distance |
首先将簇数为K的高光谱图像展开为二维矩阵
| $ {w_{ij}} = \sum\nolimits_{i = 1,j = 1}^{MN} {\exp \frac{{ - {{\left\| {{{\boldsymbol{Y}}_i} - {{\boldsymbol{Y}}_j}} \right\|}^2}}}{{2{\sigma ^2}}}} $ | (1) |
式中:
| $ {\boldsymbol{L}} = {\boldsymbol{D}} - {\boldsymbol{W}} $ | (2) |
式中:
Fréchet距离是由法国著名数学家Maurice René Fréchet 提出的,已经广泛应用于计算机图形和地理应用程序[14-15]等。Fréchet距离的定义如下。
设
| $ F({\boldsymbol{A,B}}) = \mathop {\inf }\limits_{\alpha ,\beta } \mathop {\max }\limits_{t \in [0,1]} \{ d({\boldsymbol{A}}({\boldsymbol{\alpha}} (t)),{\boldsymbol{B}}({\boldsymbol{\beta}} (t)))\} $ | (3) |
式中:
由于高光谱图像的高分辨率、多波段的特征,可以得到几乎连续的地物光谱特征曲线。图2展示了Indian pines的4种地物的光谱曲线,相似像素点之间的相似度较大,反之则较小。Fréchet距离可以准确地衡量空间曲线的相似度,因此把像素光谱向量映射到曲线上,然后通过Fréchet距离计算光谱曲线的相似度,最后重建相似矩阵。
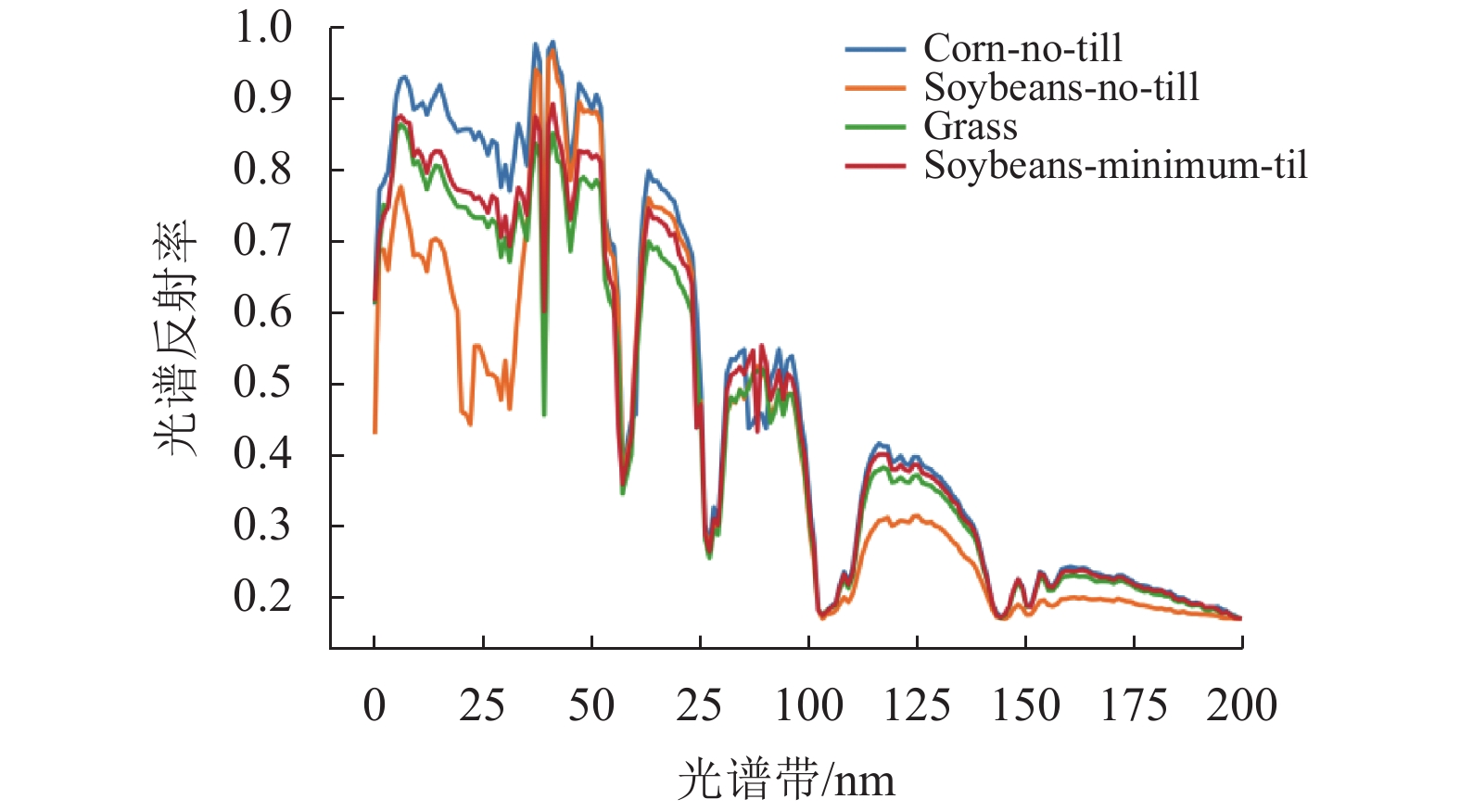
|
图 2 Indian pines数据集的4种类别的光谱曲线 Figure 2 Four spectral curves of the Indian pines |
在离散化的Fréchet距离下,对于高光谱图像矩阵
| $ {{\boldsymbol{F}}_{ij}} = \inf \mathop {\max }\limits_{t \in [0,1]} \{ d({{\boldsymbol{y}}_i}(t),{{\boldsymbol{y}}_j}(t))\} $ | (4) |
式中:
| $ {{\boldsymbol{F}}}_{ij}=\frac{{{\boldsymbol{F}}}_{ij}}{{{\boldsymbol{F}}}_{i.}}\text{,}i=1,2,\cdots ,MN $ | (5) |
式中:
构造相似矩阵通常有
| $ {w_{ij}} = \left\{ \begin{gathered} 0,\;\;\;\;\;{\text{if}}\;\;{}_{}{{\boldsymbol{y}}_i} \notin {\rm{knn}}{({{\boldsymbol{y}}_j})_{}}\;\;{\text{and}}\;\;{{\boldsymbol{y}}_j} \notin {\rm{knn}}({{\boldsymbol{y}}_i}) \\ {{\boldsymbol{F}}_i}_j,\;\;{\text{if}}\;\;{}_{}{{\boldsymbol{y}}_i} \in {\rm{knn}}{({{\boldsymbol{y}}_j})_{}}\;\;{\rm{or}}{_{}}\;\;{{\boldsymbol{y}}_j} \in {\rm{knn}}({{\boldsymbol{y}}_i}) \\ \end{gathered} \right. $ | (6) |
为保持图的全连通性,由式(7)重建相似矩阵。
| $ {\boldsymbol{W}} = ( {\left| {\boldsymbol{W}} \right| + | {{{\boldsymbol{W}}^{\rm{T}}}} |} )/2 $ | (7) |
最后,将相似矩阵
算法1 高光谱图像的FSC算法
输入:高光谱图像
输出:聚类结果
1: 利用
2:
3: 由式(4)计算矩阵
4: 由式(5)对
5: 由式(6)和(7)求解相似矩阵
6: 将谱聚类应用于相似矩阵
返回 聚类结果
为评估FSC算法的有效性,使用Indian pines、Salinas-A和KSC三个高光谱遥感图像进行实验,并以K均值(K-means) [4]、模糊C均值(FCM) [5]、谱聚类(SC) [9]、稀疏子空间聚类(SSC) [11]和余弦欧几里得动态加权 (CEDW)[13]作为基准。
3.1 实验数据集Indian pines数据集的大小为145×145,包含200 个光谱特征,考虑到计算效率,本文切割了一个大小为 85×70 的子图像来进行实验,其中包括4个主要的土地覆盖类别:Corn_no_till、Grass、Soybeans_no_till 和 Soybeans_minimum_till。其地面实况如图3(a)所示。

|
图 3 高光谱图像地面实况图 Figure 3 Ground truth of hyperspectral images |
Salinas数据集是在美国加利福尼亚州萨利纳斯谷获取,其覆盖的区域为512×217。本文使用图像的典型子图像Salinas-A作为测试区域,大小为86×83,其地面实况图见图3(b)。它主要包含6种覆盖类别:Brocoli_green_weeds_1、Corn_senesced_green_weeds、Lettuce_romaine_4wk、Lettuce_romaine_5wk、Lettuce_romaine_6wk、Lettuce_romaine_7wk。
KSC数据集的大小为512×614,包含176 个波段。由于某些植被类型的光谱特征表现较为相似,对该图像的土地覆盖精确划分是一项艰难的任务。地面实况图如图3(c)所示,该图像包含了13个类别:Scrub, Willow swamp, CP hammock, Slash pine, Oak, Hardwood, Swamp, Graminoid marsh, Spartina marsh, Cattail marsh, Salt marsh, Mud flats, Water。
3.2 评价指标本文通过用户精度(UA)[12]、总体精度(OA)和卡帕系数(Kappa)来评估算法的聚类性能。
3.3 实验结果与分析 3.3.1 Indian pines数据集的实验结果与分析表1展示了Indian pines数据集在不同算法下的聚类精度对比,可以看出,本文所提算法FSC的OA分别比SSC和CEDW提高了11.88%和11.86%,Kappa系数提高到了0.5906。其中Corn_no_till、Grass、Soybeans_no_till 和 Soybeans_minimum_till的分类准确率得到了显著提升,Grass的聚类准确率达到了99.86%。为了直观地观察聚类结果,图4展示了Indian pines数据集在不同聚类方法下的聚类图,与图4对比可以看出FSC的聚类图更接近Ground Truth。
| 表 1 Indian pines在不同算法下的聚类精度 Table 1 The clustering accuracy of Indian pines under different algorithms |
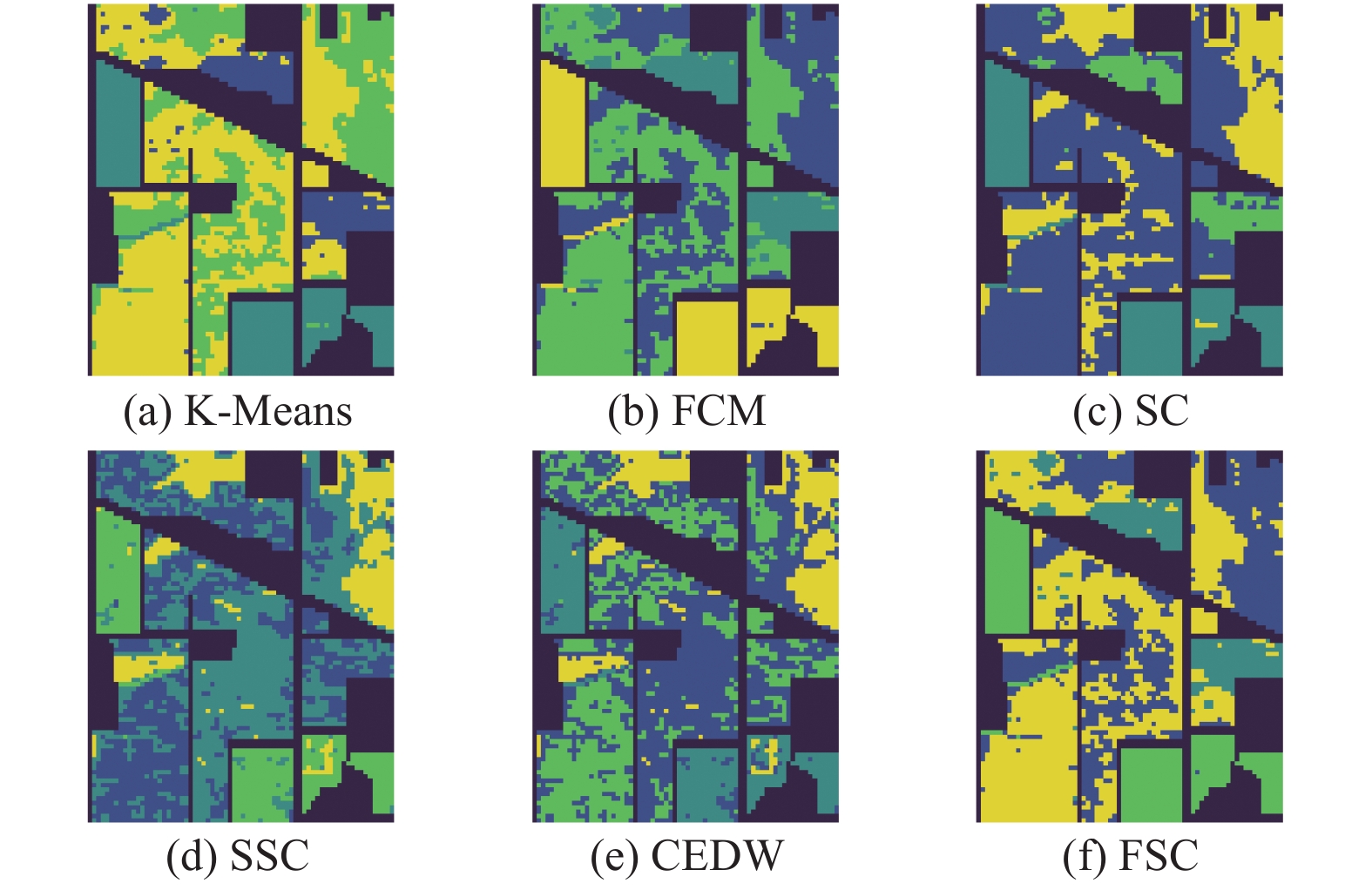
|
图 4 Indian pines在不同算法下的聚类结果 Figure 4 The clustering results of Indian pines under different algorithms |
表2比较了不同聚类算法下Salinas-A的聚类精度。从表中可以看出,所提出算法FSC的总体准确率分别比SC、SSC和CEDW分别提高了11.56%、13.39%和2.96%。与 CEDW 相比,Kappa 系数提高了0.1388。其中Brocoli_green_weeds_1、Lettuce_romaine_5wk和Lettuce_romaine_7wk的聚类准确率保持在95%以上。为了直观地观察聚类结果,图5可视化了Salinas-A在不同聚类算法下的聚类结果。很容易看出FSC的聚类图更接近Ground Truth。
| 表 2 Salinas-A在不同算法下的聚类精度 Table 2 The clustering accuracy of Salinas-A under different algorithms |

|
图 5 Salinas-A在不同算法下的聚类结果 Figure 5 The clustering results of Salinas-A under different algorithms |
表3比较了KSC数据集在不同算法的聚类精度,从表3中可以看出,与SSC和CEDW相比,所提算法FSC的OA分别提高了6.95%和8.89%,Kappa系数提高到了0.4883,其中Scrub、Oak、Swamp和Graminoid marsh的准确性均优于其他算法。图6可视化了KSC在不同聚类方法下的分割结果,可以看出FSC的聚类图更接近Ground Truth。注意同一类的颜色在不同的类映射中可能不同,因为标签值可能通过不同的聚类方法排列。
| 表 3 KSC在不同算法下的聚类精度 Table 3 The clustering accuracy of KSC under different algorithms |

|
图 6 KSC在不同算法下的聚类结果 Figure 6 The clustering results of KSC under different algorithms |
设样本数据矩阵
本文提出了一种新的高光谱图像聚类算法−FSC。FSC的关键是使用Fréchet距离来重构光谱曲线之间的相似度,这很大程度上提高了现有算法对高光谱图像空间和光谱信息的利用率。在3个高光谱图像上的实验结果表明,FSC的聚类性能明显优于许多现有的聚类算法。然而,FSC 算法也有一定的局限性,为更加充分地融合空谱信息,将Fréchet距离矩阵作为空谱信息约束到稀疏子空间算法中是未来的一个研究方向。
| [1] |
ZHU M, HUANG D, HU X J, et al. Application of hyperspectral technology in detection of agricultural products and food: a review[J].
Food Science & Nutrition, 2020, 8(10): 5206-5214.
|
| [2] |
马少鹏, 梁路, 滕少华. 一种轻量级的高光谱遥感图像分类方法[J].
广东工业大学学报, 2021, 38(3): 29-35.
MA S P, LIANG L, TENG S H. A lightweight hyperspectral remote sensing image classification method[J]. Journal of Guangdong University of Technology, 2021, 38(3): 29-35. DOI: 10.12052/gdutxb.200153. |
| [3] |
ALSAMHI S H, MA O. Collaboration of drone and internet of public safety things in smart cities: an overview of QoS and network performance optimization[J].
Drones, 2019, 3(1): 13.
DOI: 10.3390/drones3010013. |
| [4] |
KUMAR V S, SIVAPRAKASAM S A, NAGANATHAN R, et al. Fast K-means technique for hyper-spectral image segmentation by multiband reduction[J].
Pollack Periodica, 2019, 14(3): 201-212.
DOI: 10.1556/606.2019.14.3.19. |
| [5] |
SALEM R B, ETTABAA K S, HAMDI M A. Fuzzy C-mean for unsupervised spectral-spatial SVM classification of hyperspectral images[C]//2017 IEEE/ACS 14th International Conference on Computer Systems and Applications (AICCSA). Piscataway, NJ: IEEE, 2017: 759-765.
|
| [6] |
SHAHID K T, MALHOTRA A, SCHIZAS I D, et al. Unsupervised kernel correlations based hyperspectral clustering with missing pixels[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(6): 1799-1810.
DOI: 10.1109/JSTARS.2018.2797052. |
| [7] |
WANG R, NIE F, YU W. Fast spectral clustering with anchor graph for large hyperspectral images[J].
IEEE Geoscience and Remote Sensing Letters, 2017, 14(11): 2003-2007.
DOI: 10.1109/LGRS.2017.2746625. |
| [8] |
YE J, ZHAO Z, LIU H. Adaptive distance metric learning for clustering[C]//2007 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2007: 1-7.
|
| [9] |
SUN W, PENG J, YANG G, et al. Correntropy-based sparse spectral clustering for hyperspectral band selection[J].
IEEE Geoscience and Remote Sensing Letters, 2019, 17(3): 484-488.
|
| [10] |
ZHAO Y, YUAN Y, WANG Q. Fast spectral clustering for unsupervised hyperspectral image classification[J].
Remote Sensing, 2019, 11(4): 399.
DOI: 10.3390/rs11040399. |
| [11] |
ZHAI H, ZHANG H, ZHANG L, et al. A new sparse subspace clustering algorithm for hyperspectral remote sensing imagery[J].
IEEE Geoscience and Remote Sensing Letters, 2016, 14(1): 43-47.
|
| [12] |
龙咏红, 邓秀勤, 王卓薇. 基于信息熵的加权块稀疏子空间聚类算法[J].
数据采集与处理, 2021, 36(3): 544-555.
LONG Y H, DENG X Q, WANG Z W. Weighted block sparse subspace clustering algorithm based on information entropy[J]. Journal of Data Acquisition and Processing, 2021, 36(3): 544-555. |
| [13] |
YAN Q, DING Y, ZHANG J J, et al. A discriminated similarity matrix construction based on sparse subspace clustering algorithm for hyperspectral imagery[J].
Cognitive Systems Research, 2019, 53: 98-110.
|
| [14] |
WENG H, WANG S, WAN Y, et al. Discrete Fréchet distance algorithm based criterion of transformer differential protection with the immunity to saturation of current transformer[J].
International Journal of Electrical Power & Energy Systems, 2020, 115: 105449.
|
| [15] |
BANG Y, KIM J, YU K. An improved map-matching technique based on the Fréchet distance approach for pedestrian navigation services[J].
Sensors, 2016, 16(10): 1768.
DOI: 10.3390/s16101768. |
| [16] |
FRÉCHET M M. Sur quelques points du calcul fonctionnel[J].
Rendiconti del Circolo Matematico di Palermo (1884-1940), 1906, 22(1): 1-72.
|
| [17] |
张文昊. 弗雷歇距离判断曲线相似度的嵌入式模块[J].
单片机与嵌入式系统应用, 2020, 20(9): 17-20.
ZHANG W H. Embedded module of curve similarity judging based on Fréchet distance[J]. Microcontrollers Embedded Systems, 2020, 20(9): 17-20. |
 2023, Vol. 40
2023, Vol. 40

