图的支配问题[1]是图论的重要内容,在实际应用和其他学科中都有非常广泛的应用。随着人们对支配问题研究的深入,根据不同的实际问题背景,衍生出了很多种支配类型,例如双罗马支配、意大利支配等。图的意大利支配是一种新兴的支配类型,也称为罗马{2}支配[2]。确定图的意大利支配数是NP困难的。
可拓学[3]是由我国学者蔡文创立的一门数学、哲学与工程学交叉的新兴学科。分合链方法是一种可拓创新方法[4],是可拓学应用于实际的桥梁。可拓创新方法已被应用于物流网络[5]、企业管理[6]、产品设计[7-9]、建筑设计[10]等领域。
本文利用分合链方法证明了图的意大利支配数下界等于上界,从而确定出图的意大利支配数。通过将图中顶点表示为物元,利用分合链方法能非常形象地表述组合的思想。该方法的可移植性较好,可用于确定多种图形不同类型的支配数。在图的支配数教学中,使用该方法可以使学生既快又好地理解和掌握并能举一反三。
1 意大利支配意大利支配的直观描述是在某个地区(可以将该地区看作一个图,用
若用
在确定图的意大利支配数时,通常是先找出意大利支配数的上界,然后证明意大利支配数的下界与上界相等。假设已知图G的意大利支配数
| $ {\gamma _I}(G) {\text{ = }}\sum\nolimits_{i = 1}^m {w({M_i}) } \geqslant a 。$ |
分合链方法是一种可拓创新方法,是根据可扩规则,利用领域知识判断基元组合、分解或扩缩的可能性,以寻找创新或解决矛盾问题的途径的方法。组合、分解和扩缩都是创新或解决矛盾问题的有效手段。
基元是可拓学的逻辑细胞,分为物元、事元和关系元。本文研究的是图,使用的基本表达是物元。
可扩原则在本文中是指可组合原则,即给定物元
若
| $ M{ = {M_1} \oplus {M_2}} = ({O_1},{c_1} \oplus {c_2},{v_1} \oplus {v_2})= \left[ {\begin{array}{*{20}{l}} {{O_1},}&{{c_1},}&{{v_1}} \\ {}&{{c_2},}&{{v_2}} \end{array}} \right] \\ $ |
若
| $ M{ = {M_1} \oplus {M_2}} { = ({O_1} \oplus {O_2},{c_1},{v_1} \oplus {v_2}) } $ |
若
| $ M{ = {M_1} \oplus {M_2}} \\ {}{ = \left[ {\begin{array}{*{20}{l}} {{O_1} \oplus {O_2},}&{{c_1},}&{{v_1} \oplus {c_1}({O_2}) } \\ {}&{{c_2},}&{{c_2}({O_1}) \oplus {v_2}} \end{array}} \right]} $ |
本文中物元
分合链方法的基本步骤为:(1) 将所要分析的对象用物元
确定图
本节以确定广义彼得森图
广义彼得森图是图论中一类非常重要的图,用符号
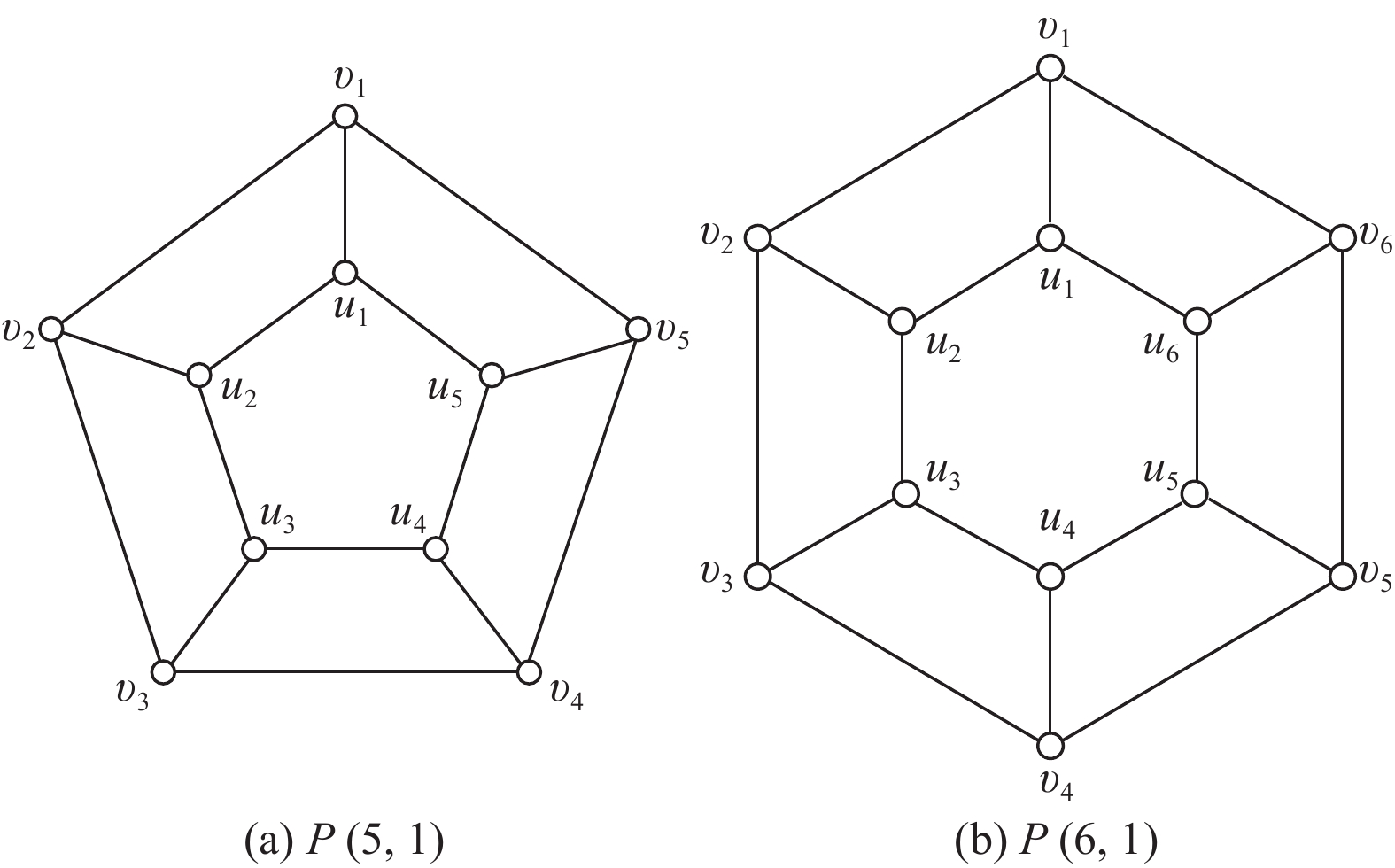
|
图 1 广义彼得森图 Figure 1 Generalized Petersen graph |
设
当
当
按照上述方式构造的意大利支配函数
| $ {\gamma _I}(P(n,1) ) \leqslant n $ | (1) |
图2所示的是
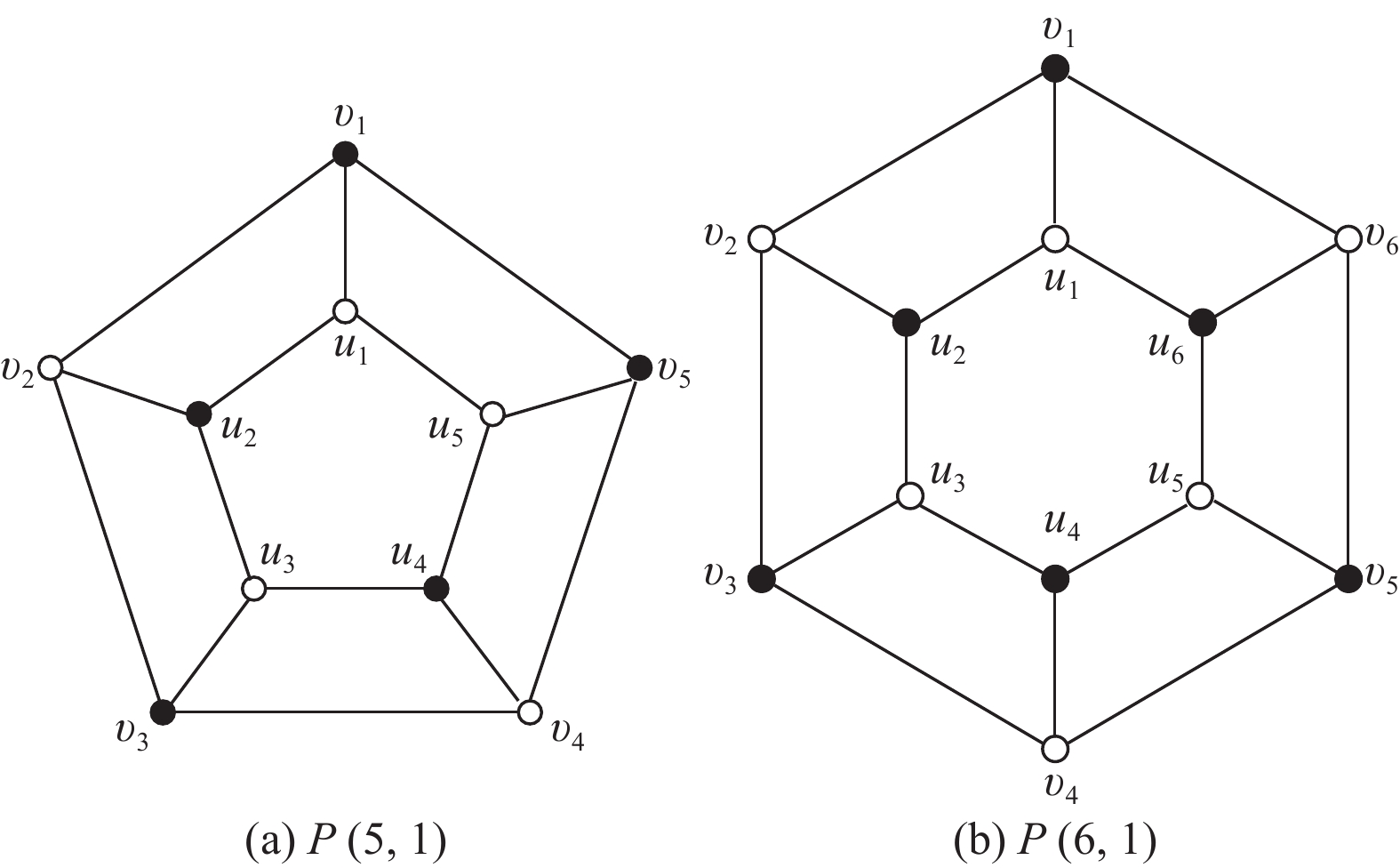
|
图 2 |
将
| $ {M}_{i}=\left[\begin{array}{lll}{O}_{i}\text{,} & 权重\text{,} & w({M}_{i}) \\ & 可组合性\text{,} & D({M}_{i}) \\ & 组合数\text{,} & N({M}_{i}) \\ & 平均权重\text{,} & \overline{w}({M}_{i}) \end{array}\right] $ |
式中:
欲证明
为了解决上述问题,考察聚合物元。为了区分物元和聚合物元,以下用
| $B ={M}_{1}\oplus {M}_{2}\oplus \cdots \oplus {M}_{k} =\left[\begin{array}{lll}O, & 权重\text{,} & w(B) \\ & 可组合性\text{,} & D(B) \\ & 组合数\text{,} & N(B) \\ & 平均权重\text{,} & \overline{w}(B) \end{array}\right] $ |
式中:
下面证明
设
| $ w({M_i}) = 0 \Rightarrow w({M_{i - 1}}) {\text{ + }}w({M_{i + 1}}) \geqslant 4 $ | (2) |
其中脚标对
定理
| $ {\gamma _I}(P(n,1) ) \geqslant n $ | (3) |
证明:(1) 将
| $ {M}_{i}=\left[\begin{array}{lll}{O}_{i},& 权重,& w({M}_{i}) \\ & 可组合性,& D({M}_{i}) \\ & 组合数,& 1 \\ & 平均权重,& \overline{w}({M}_{i}) \end{array}\right] $ |
设
(2) 假设当前处理的物元为
(3) 通过下面的步骤选取
首先对参数初始化,令
第一步:选择权重特征值大于等于3的物元作为
从
| $ m = m + 1 。$ |
由物元
如果拓展出的物元
如果
如果
如果是其他情况,则
此时,
| $ {B}_{m}=\left[\begin{array}{lll}{O}_{m}, & 权重\text{,} & w({B}_{m}) \\ & 可组合性\text{,} & D({B}_{m}) \\ & 组合数\text{,} & N({B}_{m}) \\ & 平均权重\text{,} & \overline{w}({B}_{m}) \end{array}\right] $ |
式中:
第二步:选择权重特征值等于2的物元作为
从
| $ m = m + 1 。$ |
根据式(2),如果与
因此,当
此时,
| $ {B}_{m}=\left[\begin{array}{lll}{O}_{m}, & 权重\text{,} & w({B}_{m}) \text=2 \\ & 可组合性\text{,} & D({B}_{m}) \\ & 组合数\text{,} & N({B}_{m}) \leqslant 2 \\ & 平均权重\text{,} & \overline{w}({B}_{m}) \geqslant 1 \end{array}\right] $ |
经过前两步处理以后,所有满足可组合性特征值为0的物元其权值特征值均为1。
第三步:选择权重特征值等于1的物元作为
从
| $ m = m + 1 \text{,} {B_m} = {M_i} \text{,} D({M_i}) {\text{ = }}1 。$ |
此时,
| $ {B}_{m}=\left[\begin{array}{lll}{O}_{m}, & 权重\text{,} & w({B}_{m}) \text=1 \\ & 可组合性\text{,} & D({B}_{m}) \\ & 组合数\text{,} & N({B}_{m}) \text=1 \\ & 平均权重\text{,} & \overline{w}({B}_{m}) \text=1 \end{array}\right] $ |
由第一步到第三步可知,
| $ \sum\nolimits_{t = 1}^m {w({B_m}) } \geqslant n $ |
因此,
| $ w(f) = \sum\nolimits_{i = 1}^n {w({M_i}) } = \sum\nolimits_{i = 1}^m {w({B_i}) } \geqslant n $ |
即
| $ {\gamma _I}(P(n,1) ) \geqslant n $ |
由式(1)和(3)知,
本文利用可拓学中分合链方法证明了图的意大利支配数下界与上界相等,从而确定了图的意大利控制数。以广义彼得森图
该方法的可移植性好,可用于确定多种图形的不同支配数。在图的支配数教学中使用该方法,可以使学生既快又好地理解和掌握。学生利用这种证明方法还可以得到其他图形(如梯形图、格图等)的多种支配数(双罗马支配数、彩虹支配数等)。
| [1] |
韦斯特. 图论导引 [M]. 李建中, 骆吉洲, 译. 2版. 北京: 机械工业出版社, 2020: 88-92.
|
| [2] |
CHELLALI M, HAYNES T W, HEDETNIEMI S T, et al. Roman {2}-domination[J].
Discrete Applied Mathematics, 2016, 204(5): 22-28.
|
| [3] |
杨春燕, 蔡文. 可拓学[M]. 北京: 科学出版社, 2014: 1-2.
|
| [4] |
杨春燕. 可拓创新方法[M]. 北京: 科学出版社, 2017: 1-2.
|
| [5] |
马航通. 基于可拓创新方法的J公司物流设施网络研究[D]. 广州: 广东工业大学, 2018: 29-56.
|
| [6] |
刘昱麟. 基于可拓创新方法的U企业退货物流流程优化研究[D]. 广州: 广东工业大学, 2019: 11-19.
|
| [7] |
楼炯炯. 基于可拓学与TRIZ理论的创新方法研究及其在裁床设计中的应用[D]. 杭州: 浙江工业大学, 2017: 77-88.
|
| [8] |
李仔浩, 杨春燕, 李文军. 可拓创新方法在发电机创新设计中的应用[J].
广东工业大学学报, 2020, 37(1): 1-6.
LI Z H, YANG C Y, LI W J. An application of extension innovation method in generator innovation design[J]. Journal of Guangdong University of Technology, 2020, 37(1): 1-6. |
| [9] |
张文林. 基于可拓学与TRIZ的专利产品创新设计方法[D]. 广州: 广东工业大学, 2019: 20-27
|
| [10] |
胡啸. 建筑设计中的可拓思维模式及创新方法分析[J].
建筑设计, 2018, 45(2): 18-19.
HU X. Analysis of extension thinking mode and innovation method in architectural design[J]. Architectural Design, 2018, 45(2): 18-19. |
| [11] |
HENNING M A, KLOSTERMEYER W F. Italian domination in trees[J].
Discrete Applied Mathematics, 2017, 217(1): 557-564.
|
 2023, Vol. 40
2023, Vol. 40
