非线性负载的大量应用,给电网带来了严重的谐波问题。为保证电网电能质量,许多谐波治理方案被提出,其中最具可行性方案之一是并联有源电力滤波器。随着电力电子器件成本的不断降低以及电力电子技术的发展[1-2],针对不同应用场景的有源电力滤波器拓扑结构不断被提出。
在并联有源滤波器发展和应用过程中,适于不同使用环境的电路拓扑不断涌现[3-8],文献[5-6]提出了一种两桥臂VSI与双谐振支路组合的混合有源滤波器(Hybrid Active Power Filter, HAPF),减少了开关器件的数量,降低系统成本。文献[7]提出了一种单谐振LC无源滤波器与VSI组合结构,需通过补偿算法提高补偿效果。
针对这些拓扑结构,研究者也提出了诸多控制策略。文献[7]采用了全补偿算法,并针对5次谐波进行了特定次补偿,提高补偿效果;文献[8]给出了一种在每相增加一路晶闸管控制的LC谐振环节的拓扑结构,提出了一种基于晶闸管导通角控制策略;文献[9-12]提出了相应的特定次谐波补偿算法;文献[13-14]针对负载不平衡基波电流,在特定次补偿的基础上,提出了双序dq控制策略,消除负序基波电流分量;文献[15]针对分流、串联和更复杂的有源滤波器网络,利用了波形整形解决方案之间的对称性,提出了电压−电流整形控制。这些控制策略都是针对三相对称的APF拓扑结构提出的。
受器件参数和环境的影响,有源电力滤波器的拓扑结构难以保证三相对称。针对有源电力滤波器拓扑结构三相不对称存在的问题,本文提出了加入虚拟电容控制策略,解决不对称对有源滤波器性能的影响,最后通过仿真实验验证了该方法的可行性。
1 APF不对称拓扑结构基于不对称双谐振型有源电力滤波器的主电路拓扑结构如图1所示。
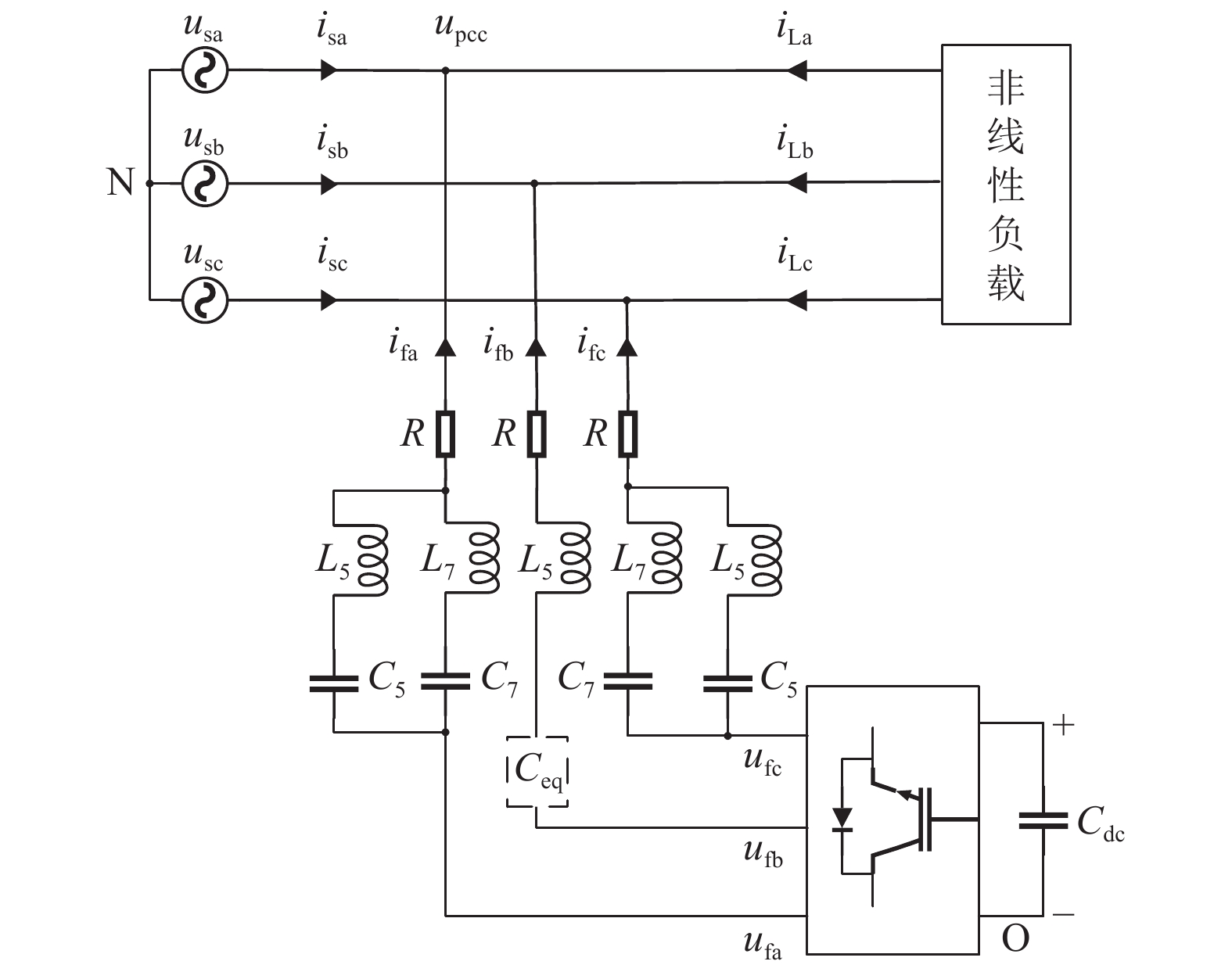
|
图 1 不对称APF拓扑 Figure 1 The asymmetric topological structure diagram of the new APF |
图1中,Cdc为直流侧电容,C5、C7为5、7次谐振支路电容值,L5、L7为5、7次谐振支路电感值,L5与C5组成五次谐振支路,L7与C7组成七次谐振支路,R为器件及导线等效电阻,O、N分别为直流侧电容负极和三相电网中点,upcc为APF与电网的公共接入点电压,isx、iLx、ifx分别为网侧、负载侧和APF侧电流,usx为电网三相电压,ufx为变流器三相输出电压(x=a,b,c) ,Ceq为虚拟电容。
2 稳定性分析 2.1 主电路数学模型分析根据基尔霍夫电压定律(KVL) 和电流定律(KCL) ,由图1可得特定次谐振支路电流电压关系:
| $ \left\{ {\begin{array}{*{20}{l}} {{u_{{\rm{fa}}n}} = L\dfrac{{{\text{d}}{i_{{\rm{f}}m{\rm{a}}n}}}}{{{\rm{d}}t}} + {u_{{\rm{ca}}m}} + R{i_{{\rm{fa}}n}} + {u_{{\rm{sa}}n}}} \\ {{u_{{\rm{fb}}n}} = L\dfrac{{{\text{d}}{i_{{\rm{f}}m{\rm{b}}n}}}}{{{\rm{d}}t}} + R{i_{{\rm{fb}}n}} + {u_{{\rm{sb}}n}}} \\ {{u_{{\rm{fc}}n}} = L\dfrac{{{\text{d}}{i_{{\rm{f}}m{\rm{c}}n}}}}{{{\rm{d}}t}} + {u_{{\rm{cc}}m}} + R{i_{{\rm{fc}}n}} + {u_{{\rm{sc}}n}}} \end{array}} \right. $ | (1) |
式中:ufan、ufbn、ufcn为APF三相输出电压;usan、usbn、uscn为电网三相电压;ifan、ifbn、ifcn为APF侧总输出电流;ifman、ifmbn、ifmcn为APF侧流过某一LC谐振支路电流;ucam、uccm为A、C相某一LC谐振支路电容电压;n为谐波次数(n=1、6k−1、6k+1, k=1,2,3,···) ;m为5次或7次LC谐振支路(m=5,7);L为5或7次谐振支路电感。
由式(1) 可知,APF输出电压、电流和拓扑阻抗均不对称。
2.2 加入虚拟电容的补偿控制法为解决滤波电路拓扑结构不对称带来的电压电流不对称问题,本文控制策略的基本思路是:在控制系统中,采用了虚拟缺相电容电压作为APF输出电压补偿的方法,来保证整个APF系统的输出电流对称,实现对低次谐波的有效补偿。
根据此控制策略,等同在B相加入一个虚拟电容Ceq,位置如图1所示。针对特定次谐波补偿,如对5、7次谐波进行补偿时,虚拟电容值分别与5、7次支路电容值相等。在此条件下,当补偿的谐波电流为5次和7次谐波时,APF输出拓扑是对称的。
由图2和图3可得,5次谐波下电流环生成的APF输出电压中,A、C相输出电压为A、C相LC谐振支路及阻尼电阻总电压,B相输出电压中的电容补偿电压与电路中虚拟电容电压抵消;同理可得7次谐波电流控制算法。下面以5次谐波为例介绍具体的控制方案。
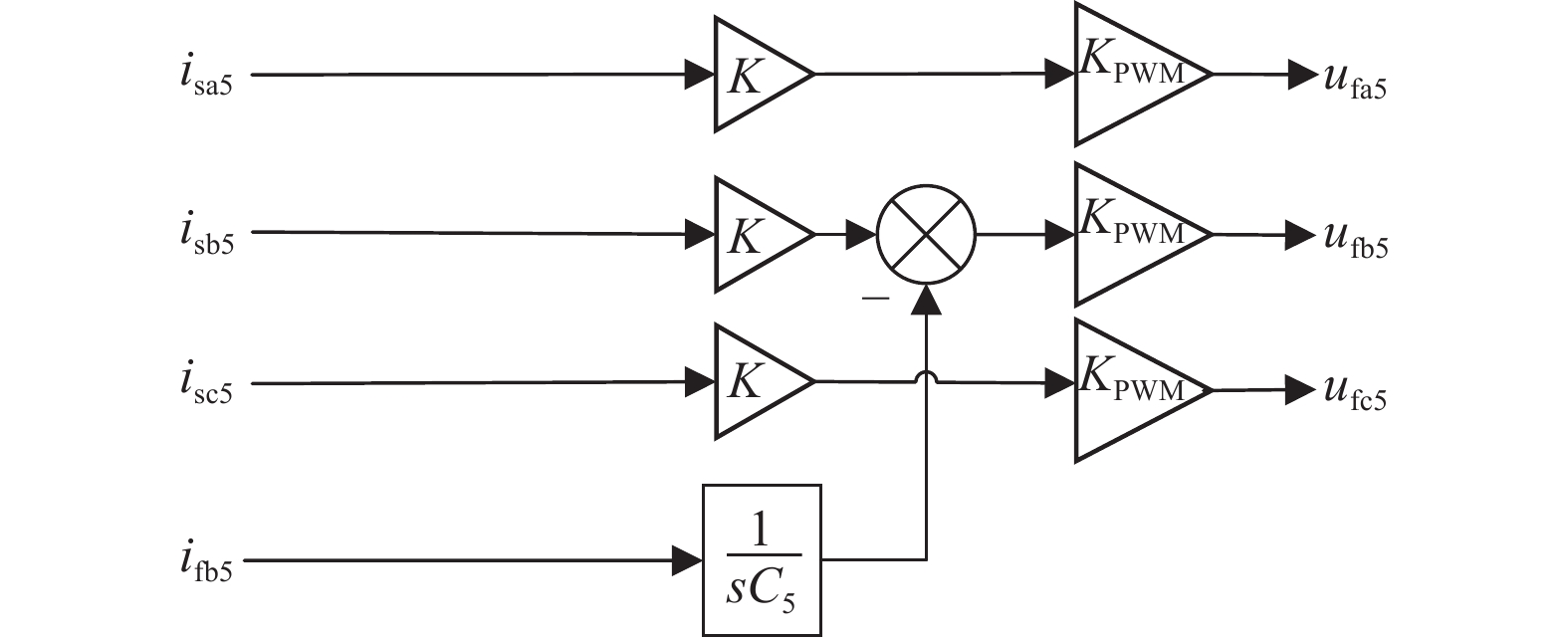
|
图 2 五次谐波电流控制原理图 Figure 2 Fifth harmonic current control schematic diagram |
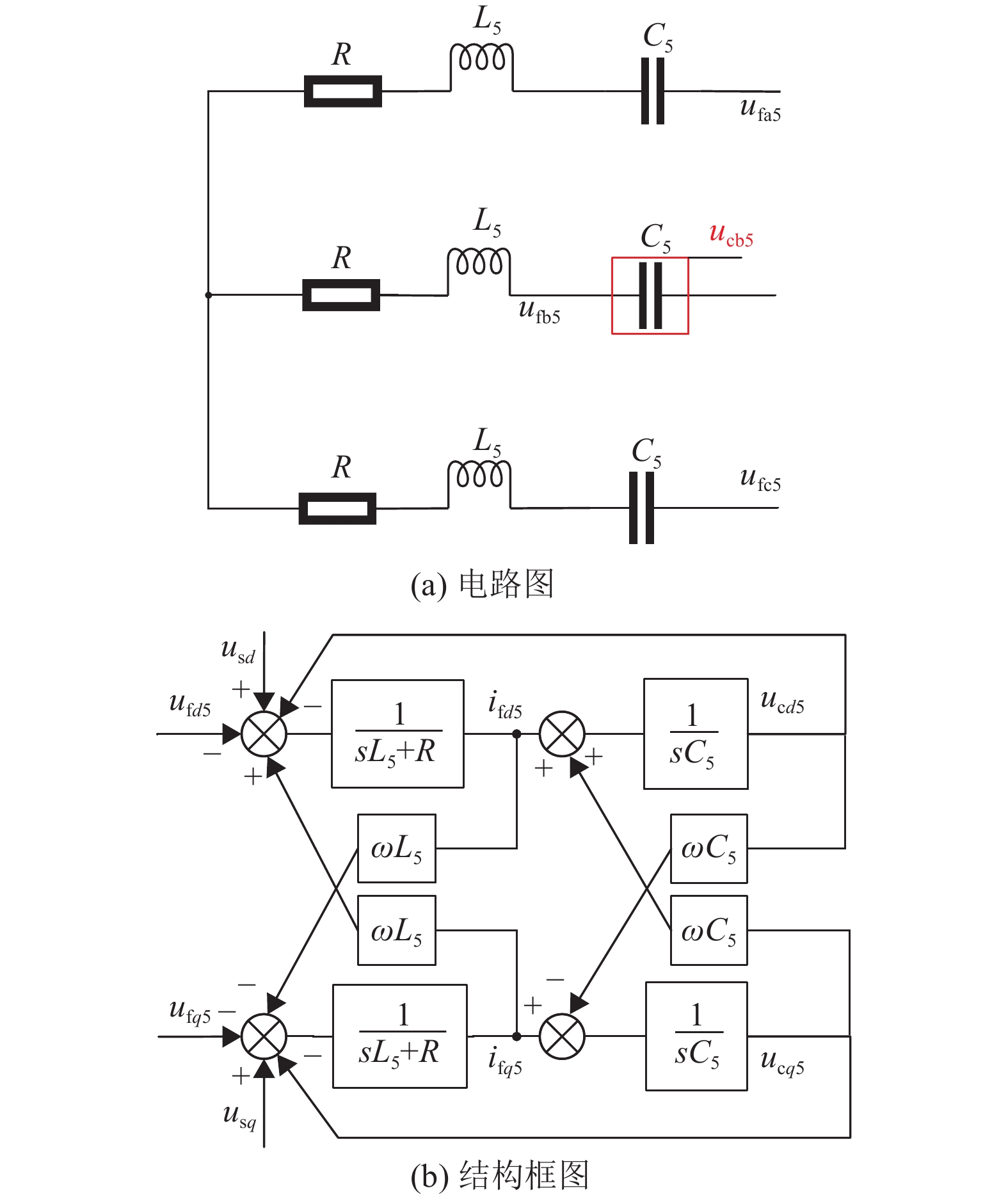
|
图 3 五次谐波电流下系统原理图 Figure 3 System schematic diagram of fifth harmonic current |
图2中,ufa5、ufb5、ufc5为针对不对称数学模型的控制电压,isa5、isb5、isc5分别为网侧5次谐波参考电流,ifb5为APF侧B相5次谐波电流,K为全补偿放大系数,KPWM为控制系统标幺化系数,s为微分算子。
图3(a)中,ucb5为加入LC滤波电路的虚拟电容电压;图3(b)为引入虚拟电容的等效结构框图,ω为dq坐标系旋转角速度。
5次谐振支路和7次谐振支路电容、电感参数值关系如式(2)所示。
| $ \left\{ {\begin{array}{*{20}{l}} {L = {L_5} = {L_7}} \\ {C = {C_5} = 2{C_7}} \end{array}} \right. $ | (2) |
基波及谐波系统等效电抗为
| $\begin{split}& {X_{{\text{eq}}}} = {X_n} - {X_{{\text{BL}}}} = \frac{1}{2}sL + \frac{{3{s^2}LC + 1}}{{4{s^2}L{C^2} + 6sC}} - s{L_{\rm{B}}} = \\& \frac{{ - {s^4}{L^2}{C^2} + 2}}{{2{s^2}L{C^2} + 3sC}} \end{split}$ | (3) |
| $ {X_{{\text{eq}}}} = \frac{1}{{s{C_{{\text{eq}}}}}} = \frac{{ - {s^4}{L^2}{C^2} + 2}}{{2{s^3}L{C^2} + 3sC}} $ | (4) |
式中:Xn为5、7次谐振支路总电抗;Xeq为B相等效补偿容抗;XBL为B相感抗,LB为B相电感。
5、7次谐波等效容抗为
| $ {X_{{\text{eq5}}}} = \frac{1}{{s{C_5}}} = \frac{1}{{sC}} $ | (5) |
| $ {X_{{\text{eq7}}}} = \frac{1}{{s{C_7}}} = \frac{2}{{sC}} $ | (6) |
式(5~6)中:Xeq5为5次谐波下等效容抗;Xeq7为7次谐波下等效容抗。
由式(4)可知,等效容抗表达式为4阶;由式(5~6)可知,特定次谐波下等效容抗表达式为1阶。补偿电容电压在特定次下更易于工程实现。由式(3~6)可知,基波及其他次谐波电流控制算法与5、7次谐波算法相同。
表1为 5、7次谐振支路各器件电抗(5、7次支路电感2 mH,电容为200 μF、100 μF)、三相不控整流电路纯电阻负载基波及谐波含量。
| 表 1 5、7次谐振支路各器件电抗及负载电流各谐波含量 Table 1 The component reactance of 5 and 7 resonant circuit and harmonic content of load current |
APF在理想情况下运行(可忽略APF基波电流),故表2将5次谐波电流含量作为基准值,统计了11、13次谐波下补偿电容电压对总支路电压的影响。
| 表 2 特定次电容补偿电压影响分析 Table 2 Analysis of influence of capacitor compensation voltage by the selective harmonic control |
由表1、2计算分析可知,不对11、13次补偿电容进行电压补偿,其对输出谐波总电压的影响比例约4.3%。
2.3 单相等效电路稳定性分析由图4可得系统开环传递函数为
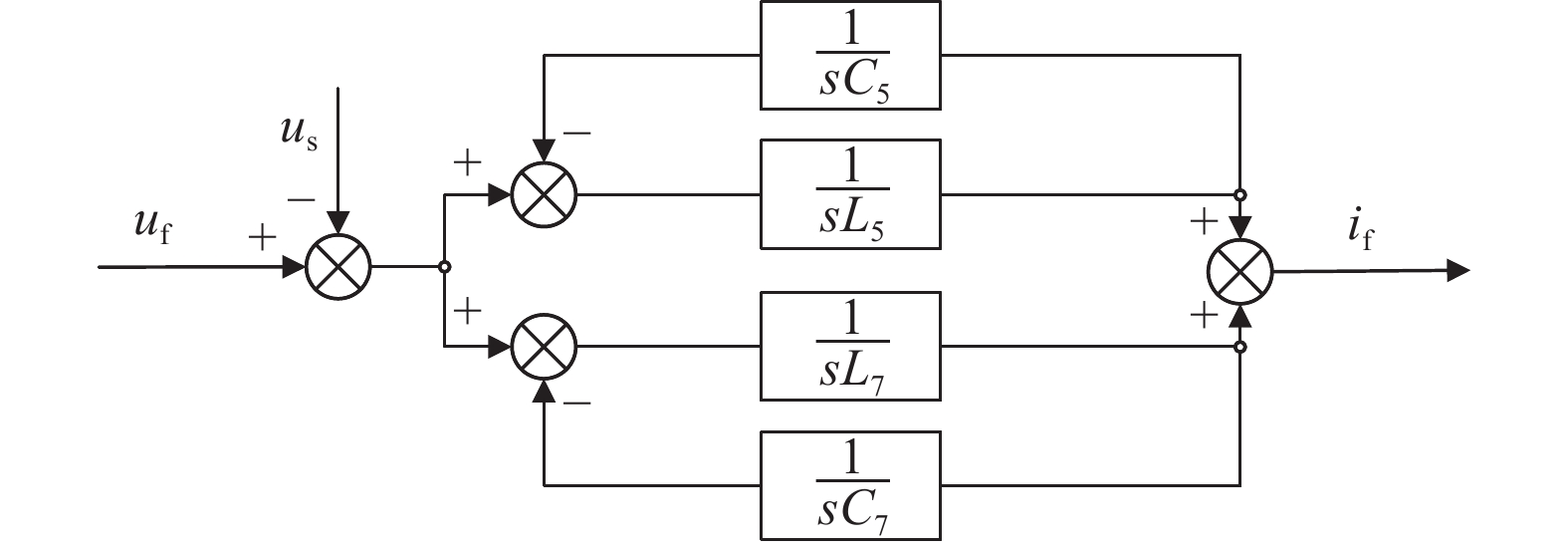
|
图 4 系统结构框图 Figure 4 System structure block diagram |
| $ {G_{{\rm{open}}}}(s) = \frac{{{i_{\rm{f}}}(s) }}{{{u_{\rm{f}}}(s) }} = \frac{{s{C_5}}}{{{s^2}{L_5}{C_5} + 1}} + \frac{{s{C_7}}}{{{s^2}{L_7}{C_7} + 1}} $ | (7) |
式中:Gopen(s)为系统开环传递函数;if(s) 为系统输出电流;uf(s)为系统输入电压。
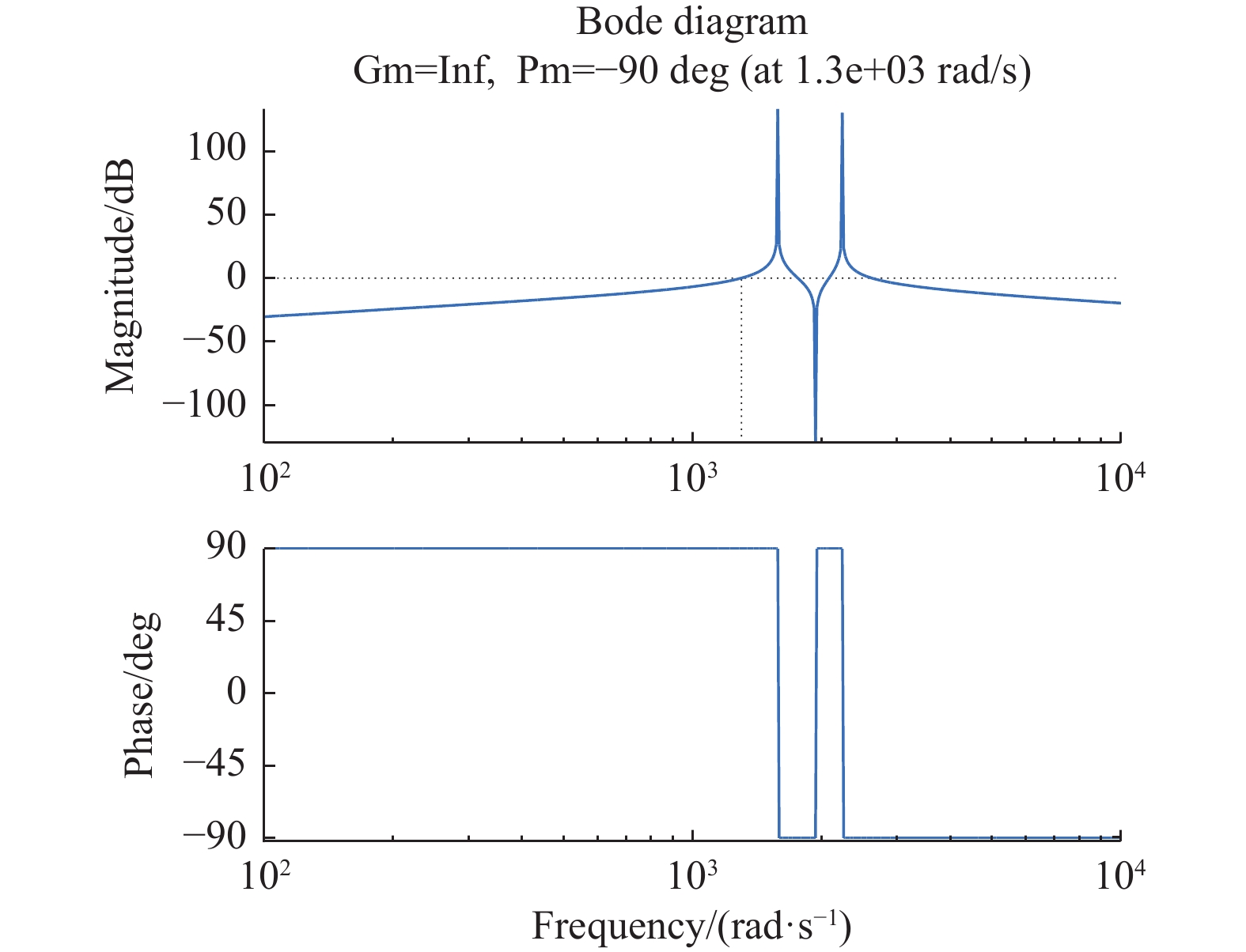
取L5=2 mH,C5 =200 μF,L7 =2 mH,C7 =100 μF绘制该传递函数的Bode图,如图5所示。从图5中可以看出,LC支路谐振频率分别为252 Hz和358 Hz,该滤波电路在这两个频率点存在谐振。
|
图 5 滤波电路传递函数的 Bode 图 Figure 5 Bode diagram of filter circuit transfer function |
由式(7)可知,该开环传递函数缺少阻尼项,谐振尖峰的两个谐振角频率点分别为
| $ {\omega _5} = \frac{1}{{\sqrt {{L_5}{C_5}} }} $ | (8) |
| $ {\omega _7} = \frac{1}{{\sqrt {{L_7}{C_7}} }} $ | (9) |
由上节分析可知,基波及各次谐波电流控制算法与5次谐波电流控制算法原理相同。在此,仿真验证分析以5次谐波为例。
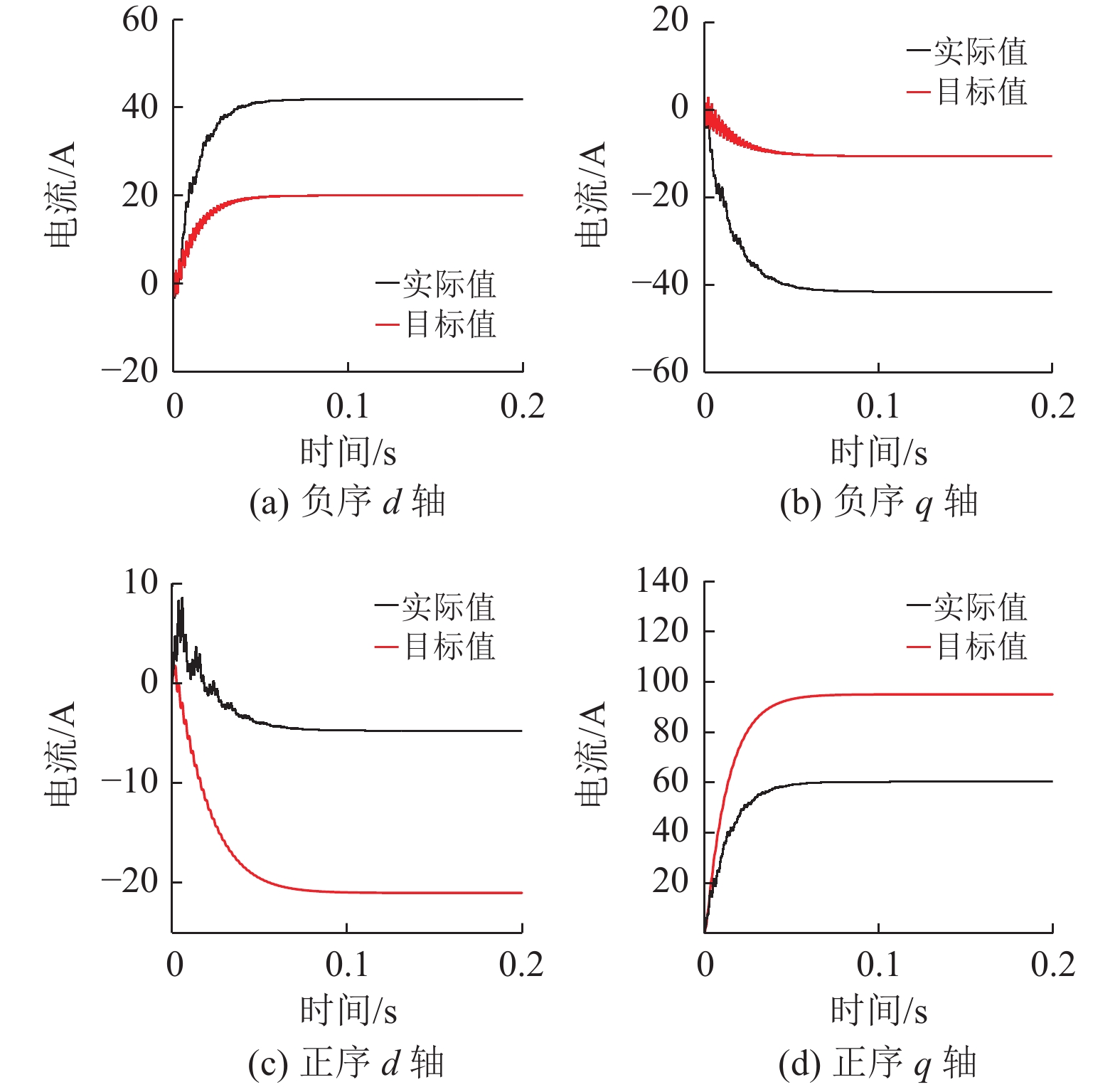
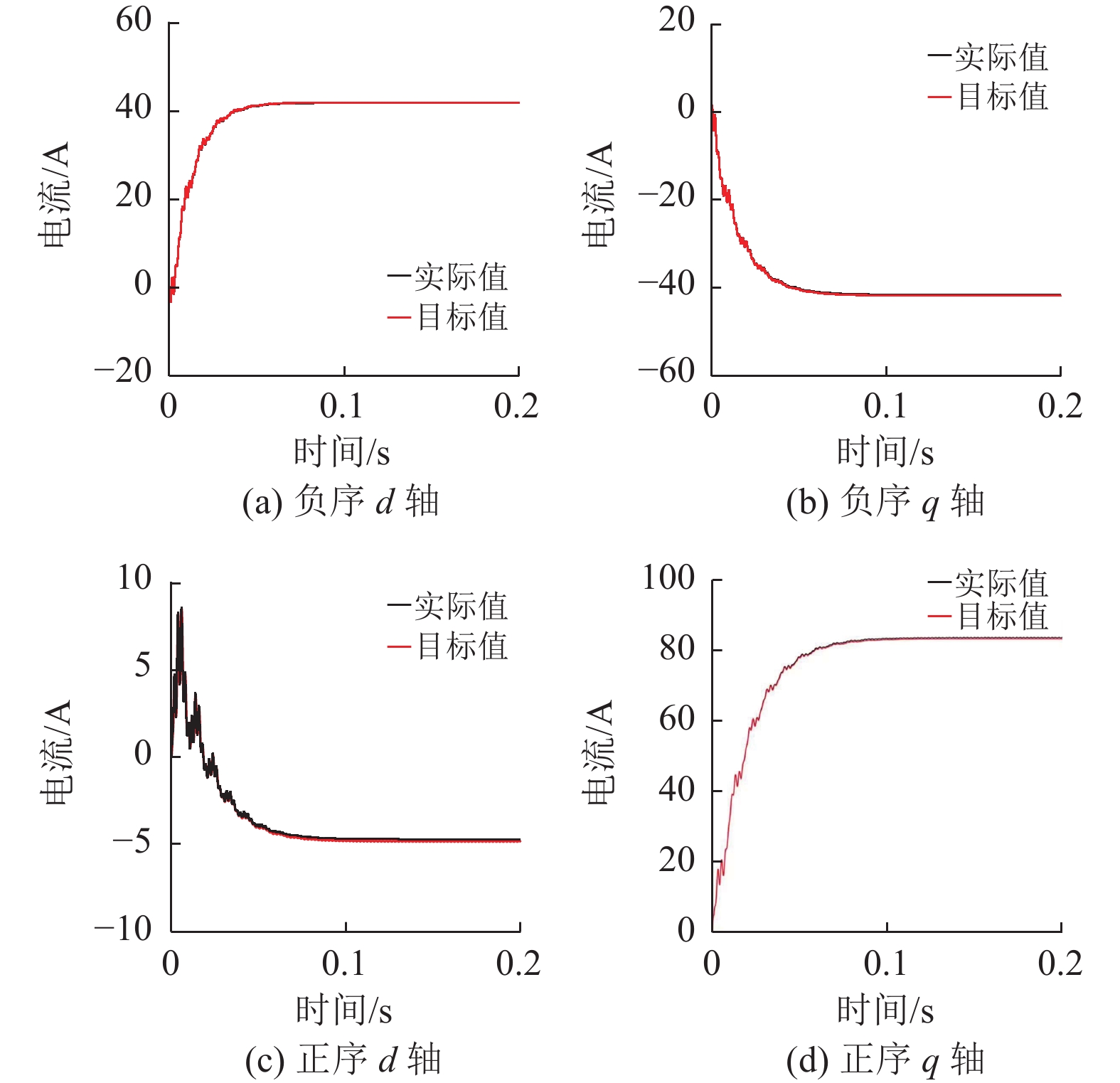
为验证上述方案的可行性,在此,利用Matlab搭建上述系统等效模型与基于拓扑电路构建的对象进行对比。输入为三相5次谐波电压源,通过对APF输出电流正负序分离,由输出滤波器LC无源滤波器的APF的数学模型得到d、q轴电流;同时将电路拓扑工作电流也进行正负序分离,得到其d、q轴上电流。补偿前5次谐波电流如图6所示。补偿后5次谐波电流如图7所示。其中,图6和图7中的目标值和实际值分别为电路拓扑和数学模型中的电流值。
|
图 6 补偿前正负序的d、q轴电流 Figure 6 The d and q axis current of the positive and negative sequence before the compensation |
|
图 7 补偿后正负序的d、q轴电流 Figure 7 The d and q axis current of the positive and negative sequence after the compensation |
对比图6、7可知,在加入虚拟电容电压补偿后,正负序5次谐波电流d、q轴输出均能进行有效跟随。
2.4.2 算法模型验证在理想情况下,5或7次谐波电流仅流过5或7次谐振支路,基波及除5、7次之外的其他特定次谐波电流在5、7次谐振支路均有电流流过。下面以5次谐波和基波为例,Matlab仿真验证模型包含:三相220 V基波或5次谐波受控电压源,输出滤波器A、C相为5、7次谐振结构,B相为与5、7次谐振支路相同参数的电感元件,以及电容电压补偿算法模块。
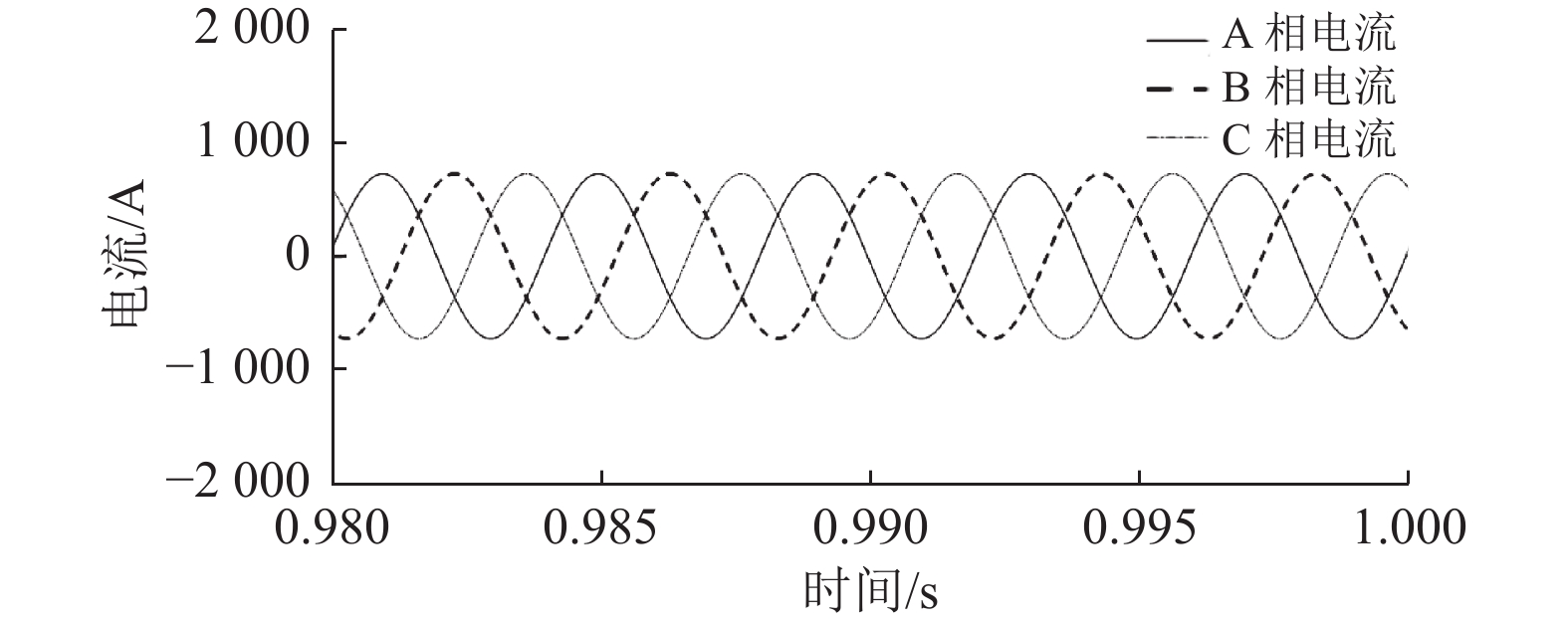
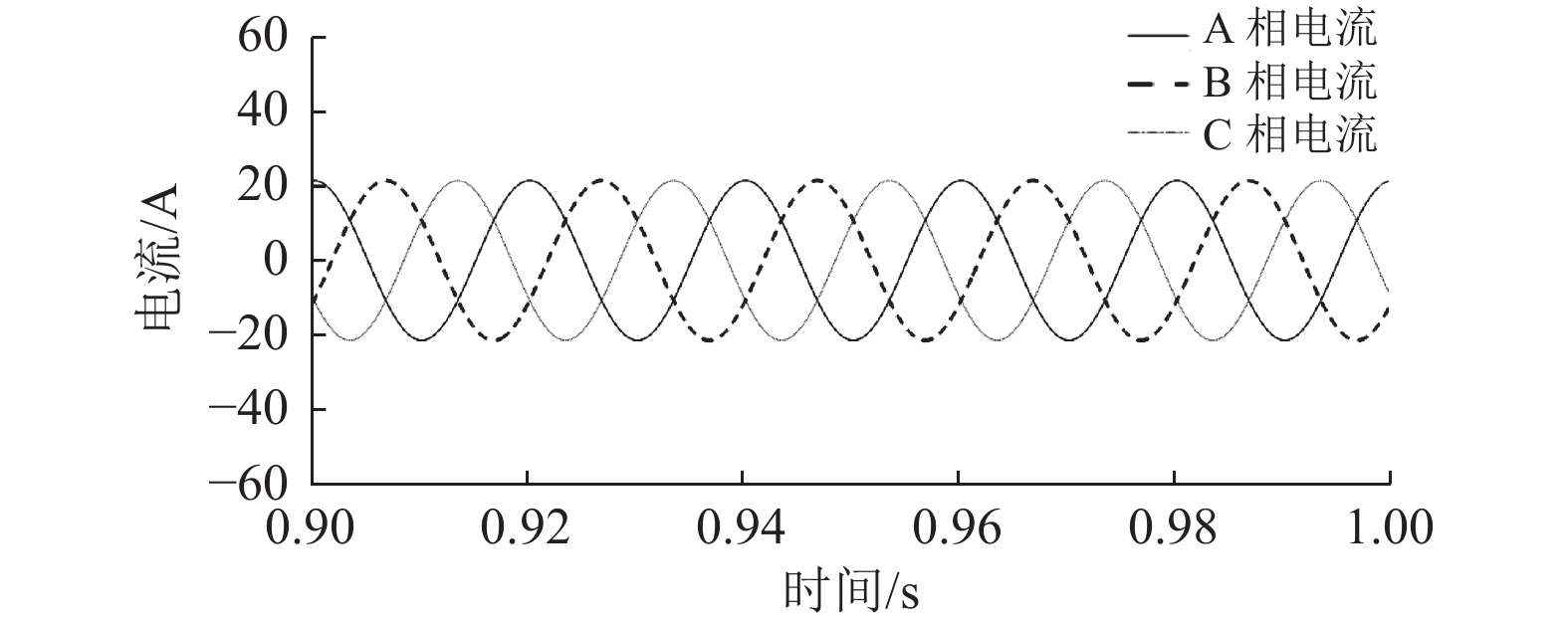
5次谐波及基波电容电压算法等效电路模型验证结果如图8和图9所示。由图可知5次谐波电流及基波电流均三相对称。
|
图 8 5次谐波电流仿真图 Figure 8 The simulation diagram of fifth harmonic current |
|
图 9 基波电流仿真图 Figure 9 The simulation diagram of fundamental current |
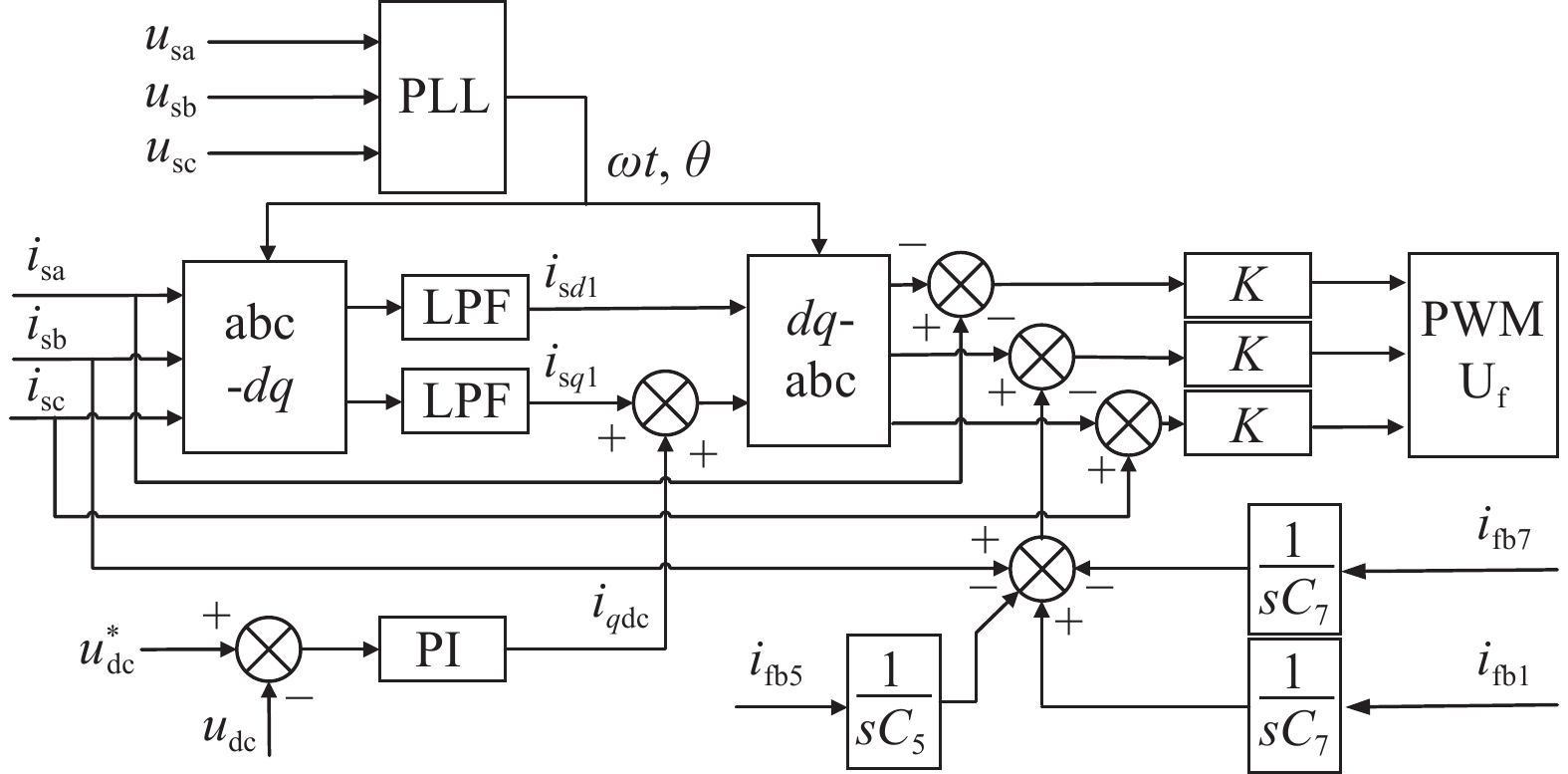
APF系统控制框图如图10所示,该控制结构框图包括主要基波电流提取、直流电压控制、虚拟电容补偿及PLL模块。
|
图 10 系统控制结构框图 Figure 10 Block diagram of the system control |
通过控制电网提供的有功功率,可以控制直流侧电压,即通过控制基波有功电流iqdc可达到控制直流侧电压的目的;对于谐波补偿电流的控制,检测网侧电流经低通滤波器提取基波电流,将网侧电流与基波电流作差提取谐波电流,与B相虚拟电容补偿电压之和放大K倍,计算得到调制电压。
将计算所得结果进行脉宽调制,控制变流器的输出电压,获得相应的基波有功电流和各次谐波注入电流,达到直流侧电压稳压、补偿电网谐波的目的。
4 仿真及实验结果分析为了更清晰地展示系统不同负载下的动态和稳态特性,本文搭建了Matlab仿真模型。仿真模型参数如下:L5=2 mH,C5 =200 μF,L7 =2 mH,C7=100 μF;网侧线电压为 380 V;非线性负载为三相不控整流器20 Ω纯电阻负载;变流器开关频率fs为20 kHz;直流侧电容容量Cdc为4700 μF;直流侧电压参考值为500 V。
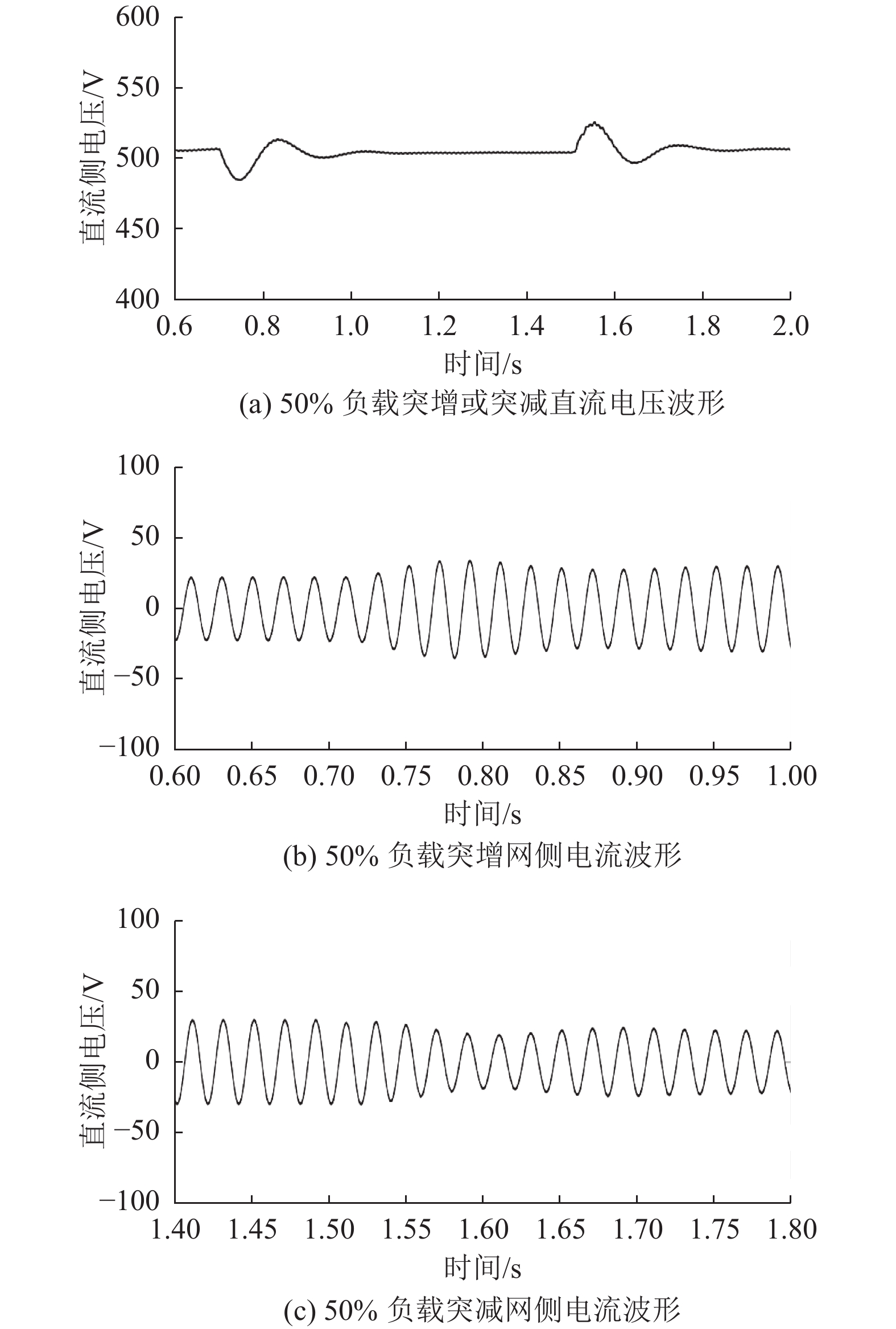
动态实验仿真结果如图11所示,当非线性负载突增或突减50%负载时,直流侧电压跌落或增大幅度均小于5%,并在0.3 s左右恢复稳定,未出现长时间振荡、大幅度上升或跌落。在非线性负载变化瞬间,电网电流波形未见明显畸变。
|
图 11 动态实验仿真图 Figure 11 Dynamic experimental simulation waveform |
为了进一步验证本文提出的理论方案可行性,搭建了实验平台进行实验验证。实验平台采用 TMS320F28335 芯片为主控制器,该芯片自带FPU浮点运算单元。实验平台拓扑电路参数如下:L5=1.96 mH,C5=200 μF,L7 =1.91 mH,C7 =100 μF,网侧线电压有效值为 110 V,非线性负载为三相不控整流器带10 Ω电阻,变流器开关频率fs=20 kHz,直流侧电容容量为 2200 μF,APF对谐波补偿方式为全补偿,直流侧电容电压控制在150 V。
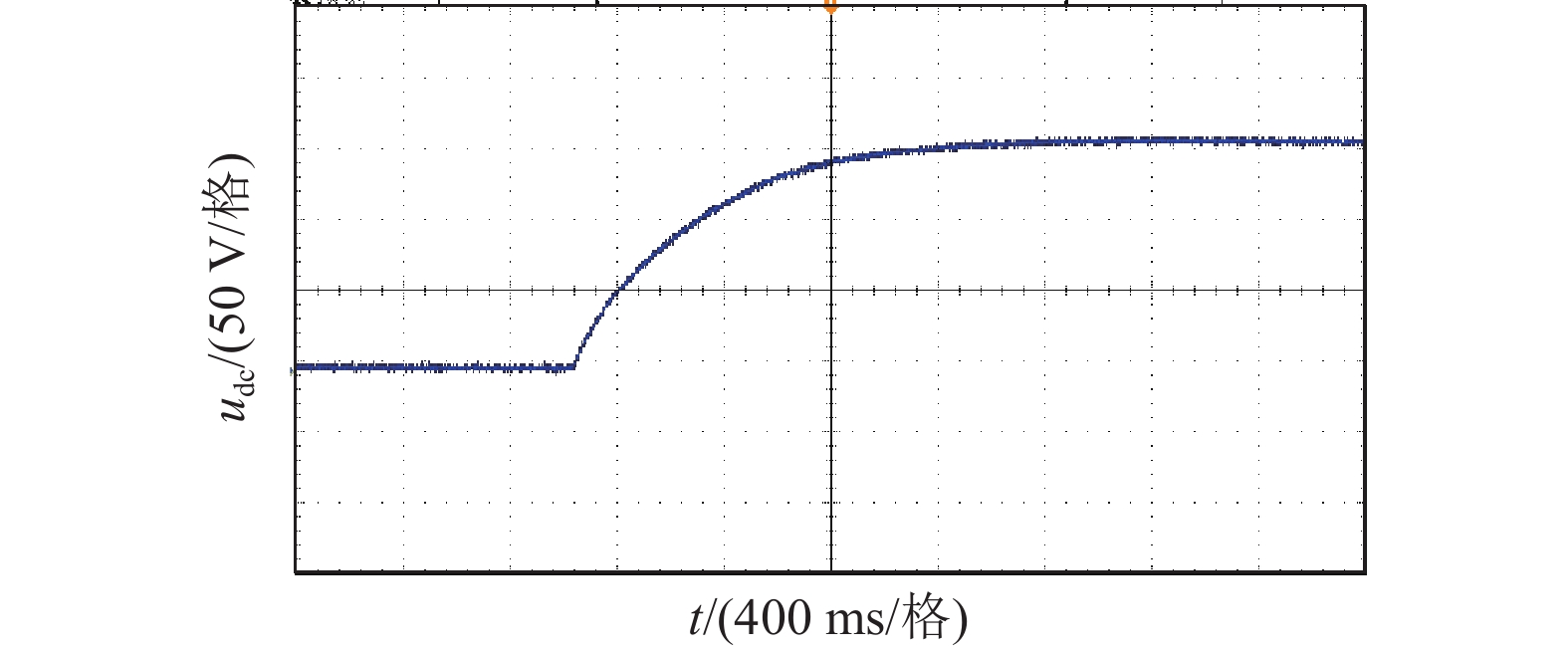
变流器直流侧电压波形均如图12所示。由实验结果可以看出,启动过程中,直流侧电压上升较为稳定,无超调振荡,能够稳定控制在预设值附近,稳态直流侧电压波动率小于5%,满足设计要求。
|
图 12 直流侧电压波形 Figure 12 Voltage waveform of DC side |
在未投入有源滤波器前,三相电网电流波形产生严重畸变,电流总谐波畸变率约为25.4%。
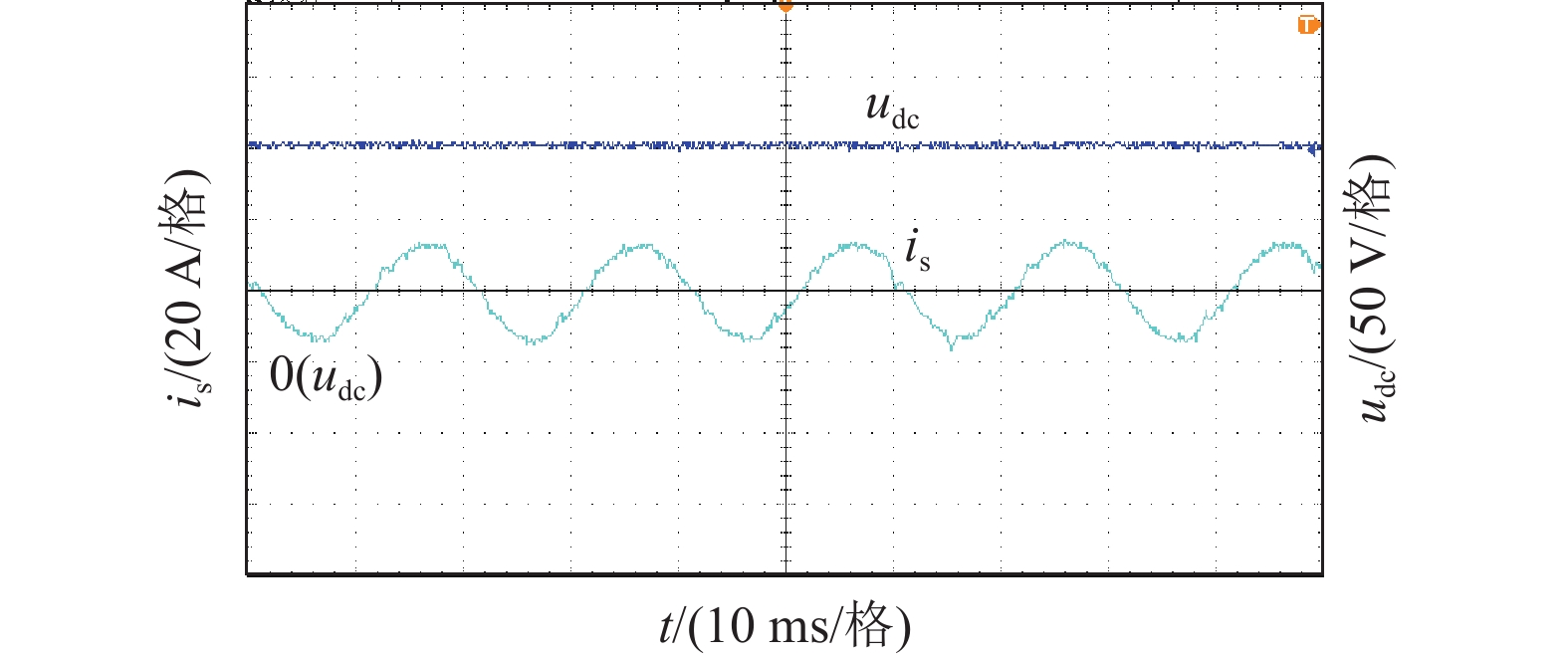
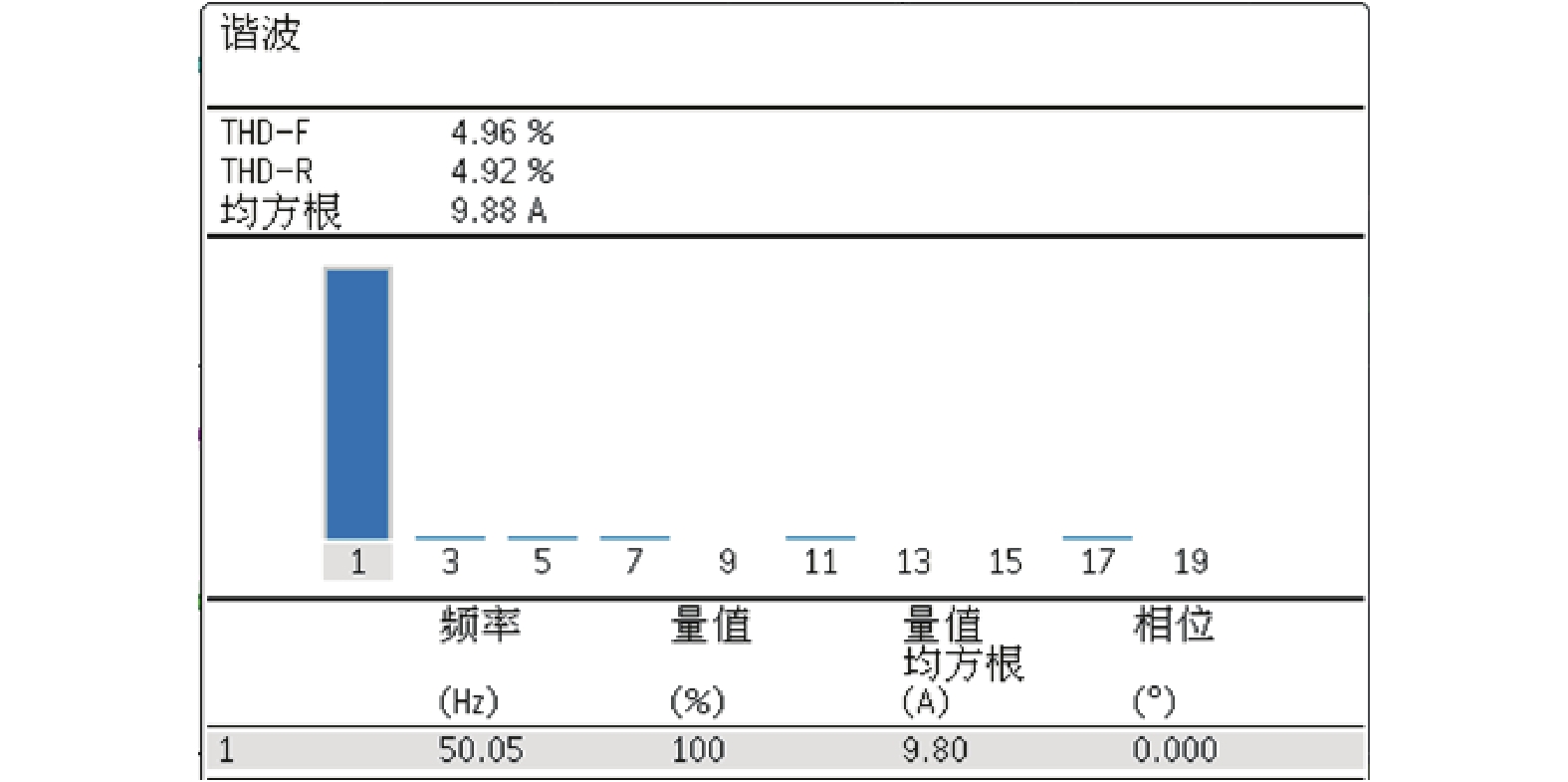
在对称拓扑下,投入新型有源电力滤波器进行全补偿后,电网侧电流波形、电流畸变率如图13和图14所示。由实验结果可以看出,直流侧电压较为平稳,能够稳定控制在预设值。投入新型有源电力滤波器后,电网侧电流谐波被有效滤除,网侧电流波形接近正弦波,总谐波畸变率为 4.96%。
|
图 13 对称拓扑下网侧电流波形 Figure 13 The current waveform of grid side in the symmetric topology |
|
图 14 对称拓扑下网侧电流畸变率 Figure 14 The current THD of grid side in the symmetric topology |
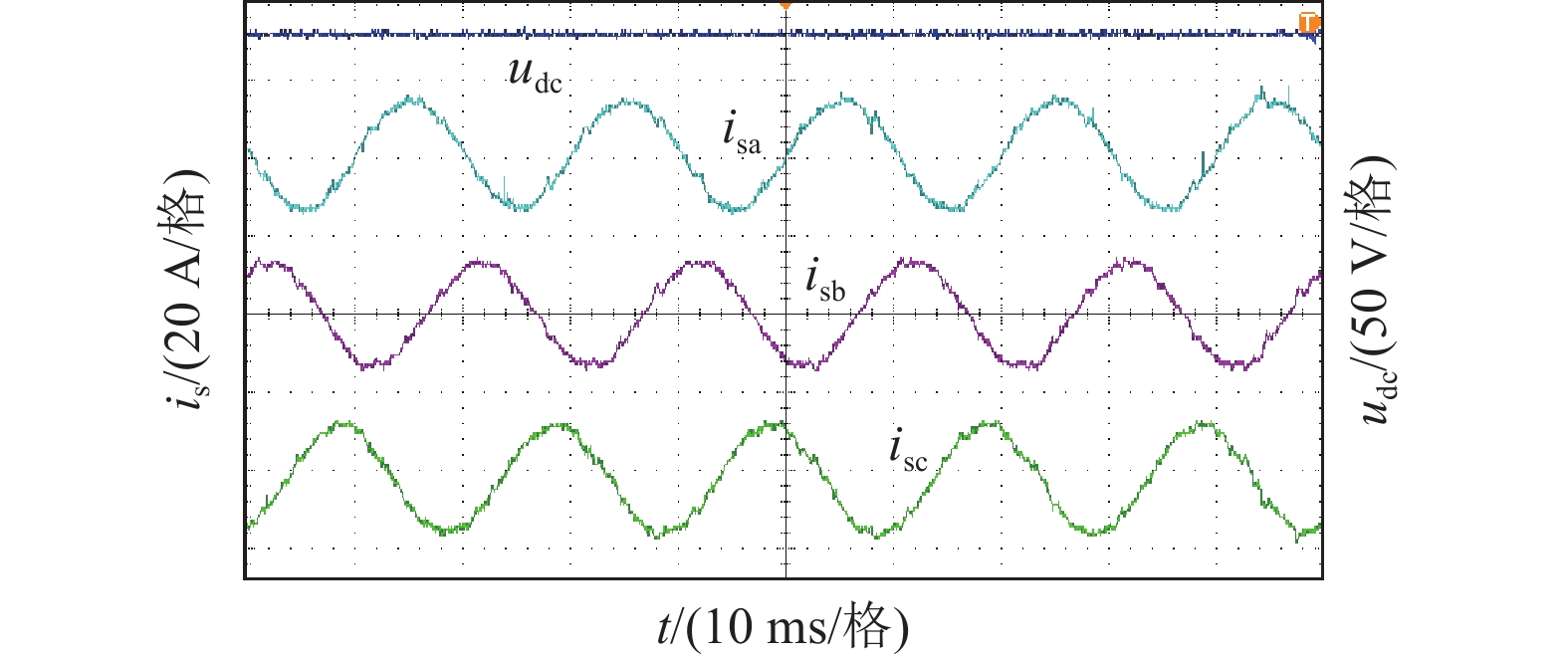
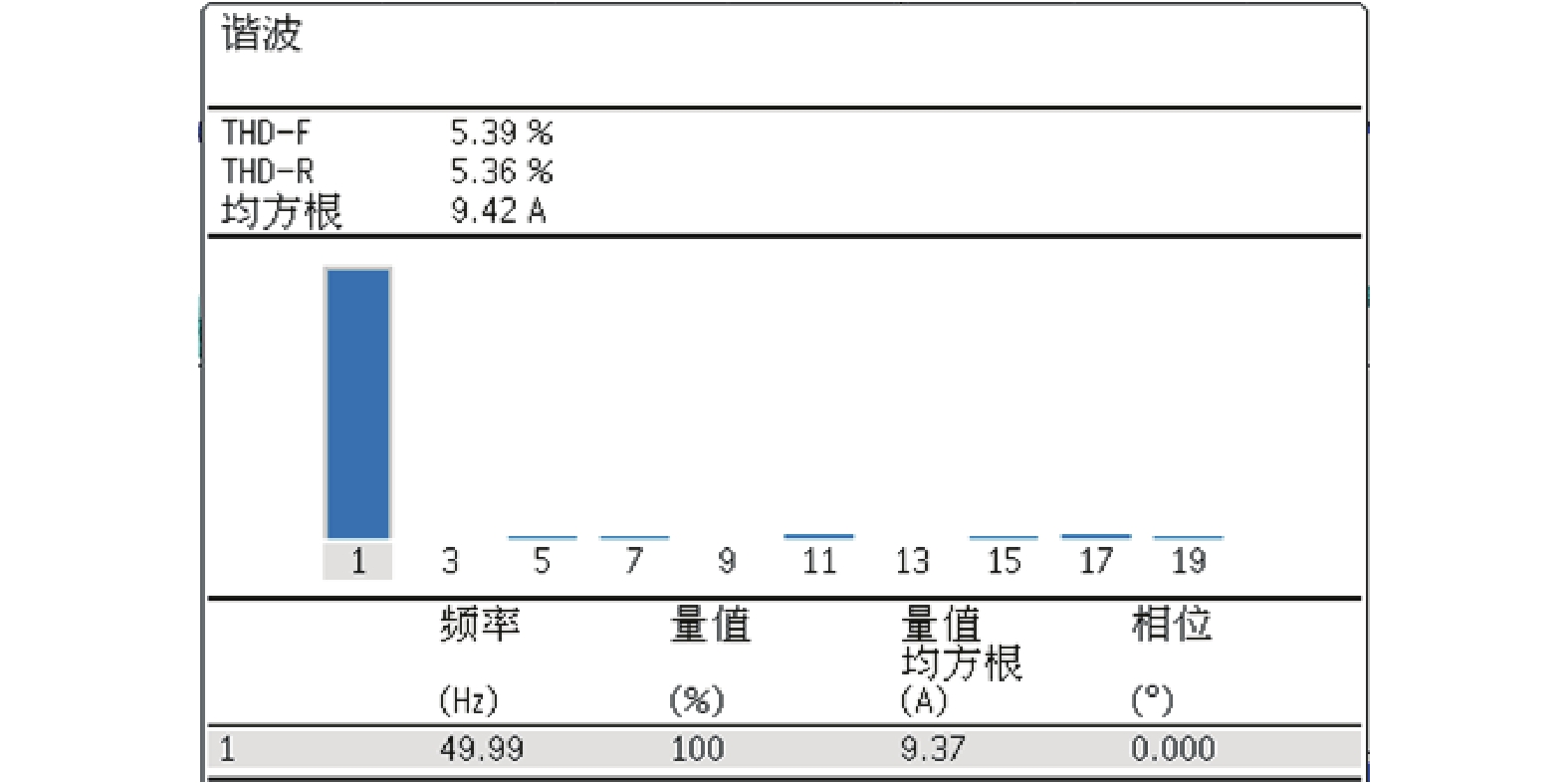
在不对称拓扑下,投入新型有源电力滤波器进行全补偿后,电网侧电流波形、电流畸变率、变流器侧电流波形如图15~图17所示,图17中的箭头可辅助观察APF侧电流波形三相对称。由实验结果可以看出,直流侧电压较为平稳,能够稳定控制在预设值。投入新型有源电力滤波器后,网侧、APF侧电流均基本三相对称,电网电流谐波被有效滤除,波形接近正弦波,总谐波畸变率为 5.39%,可以达到预期目标。
|
图 15 不对称拓扑下网侧三相电流波形 Figure 15 The current waveform of grid side in the asymmetric topology |
|
图 16 不对称拓扑下网侧电流畸变率 Figure 16 The current THD of grid side in the asymmetric topology |
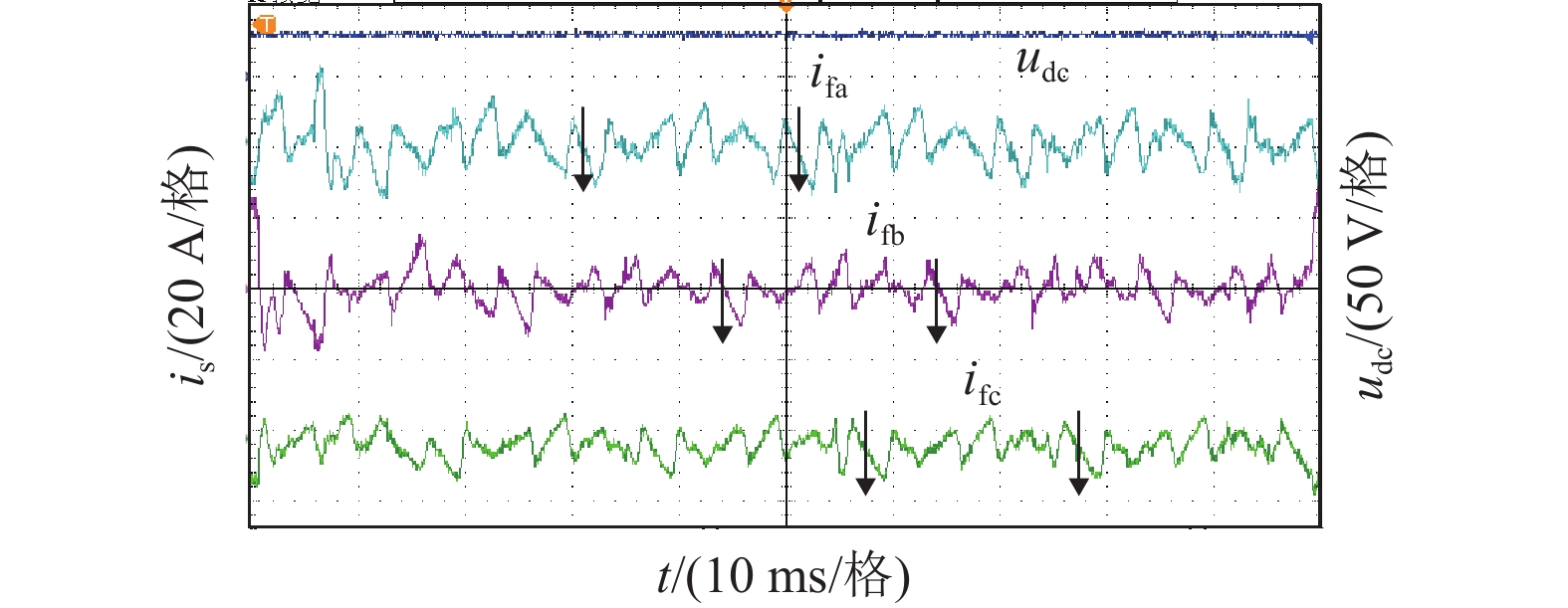
|
图 17 不对称拓扑下APF侧电流波形 Figure 17 APF-side current waveform in the asymmetric topology |
本文提出了一种新型的混合有源电力滤波器不对称拓扑。与对称拓扑相比,本文拓扑减少了一相谐振支路,滤波电路体积成本减小了近1/3;同时提高滤波电路参数一致性。提出的特定次虚拟电容补偿控制策略,易于适应不同类型负载和工程实现的同时,也易于配合传统对称拓扑控制策略使用,使不对称拓扑补偿电流三相对称,实现预期补偿目标;尽管该控制策略对控制芯片提出了更高要求,但目前数字处理器的运算速度已经可以满足该控制策略的需求,因此该控制策略仍有广阔的应用前景。
| [1] |
王兆安. 谐波抑制和无功功率补偿[M]. 北京: 机械工业出社, 2015.
|
| [2] |
张兴, 张崇巍. PWM整流器及其控制[M]. 北京: 机械工业出版社, 2012.
|
| [3] |
肖琦, 唐芬, 辛振, 等. 低开关频率下LCL型并网变流器复矢量分析及改进解耦控制[J].
电网技术, 2018, 42(9): 2821-2829.
XIAO Q, TANG F, XIN Z, et al. Complex vector analysis and improved decoupling control for LCL-filtered grid-connected converters with Low switching frequency[J]. Power System Technology, 2018, 42(9): 2821-2829. DOI: 10.13335/j.1000-3673.pst.2018.1000. |
| [4] |
LEE T L, WANG Y C, LI J C, et al. Hybrid active filter with variable conductance for harmonic resonance suppression in industrial power systems[J].
IEEE Transactions on Industrial Electronics, 2015, 62(2): 746-757.
DOI: 10.1109/TIE.2014.2347008. |
| [5] |
TAREEN W K, MEKHILEF S. Three-phase transformer- less shunt active power filter with reduced switch count for harmonic compensation in grid-connected applications[J].
IEEE Transactions on Power Electronics, 2018, 33(2): 4868-4881.
|
| [6] |
郭亚男, 孟庆达, 刘培忠, 等. 三相四开关并联型有源电力滤波器选择性谐波补偿方法[J].
电力电容器与无功补偿, 2018, 39(3): 5-10.
GUO Y N, MENG Q D, LIU P Z, et al. Selective harmonic compensation method for three- phase four-switch SAPF[J]. Power Capac React Power Compens, 2018, 39(3): 5-10. |
| [7] |
时晓洁, 张军明, 钱照明, 等. 并联混合有源电力滤波器的关键技术研究[J].
电力电子技术, 2010, 44(6): 82-84.
SHI X J, ZHANG J M, QIAN Z M, et al. Research on the key technologies of hybrid active power filters[J]. Power Electronics, 2010, 44(6): 82-84. DOI: 10.3969/j.issn.1000-100X.2010.06.032. |
| [8] |
WANG L, LAM C, WONG M. Unbalanced control strategy for a thyristor-controlled LC-coupling hybrid active power filter in three-phase three-wire systems[J].
IEEE Transactions on Power Electronics, 2017, 32(2): 1056-1069.
DOI: 10.1109/TPEL.2016.2555330. |
| [9] |
周京华, 张 荣, 章小卫, 等. APF改进型指定次谐波电流补偿控制策略[J].
电力电子技术, 2017, 51(11): 105-107.
ZHOU J H, ZHANG R, ZHANG X W, et al. Selective harmonic current control strategy based on shunt active power filter[J]. Power Electronics, 2017, 51(11): 105-107. |
| [10] |
赵鑫涛, 裘智峰, 于晶荣, 等. 并联型有源滤波器精细化补偿方案[J].
电网技术, 2018, 42(4): 1290-1299.
ZHANG X T, QIU Z F, YU J R, et al. Research of refined compensation method on shunt active power filter[J]. Power System Technology, 2018, 42(4): 1290-1299. DOI: 10.13335/j.1000-3673.pst.2017.1971. |
| [11] |
张树全, 戴珂, 谢斌, 等. 多同步旋转坐标系下指定次谐波电流控制[J].
中国电机工程学报, 2010, 30(3): 55-62.
ZHANG S Q, DAI K, XIE B, et al. Selective harmonic current control based on multiple synchronous rotating coordinates[J]. Proceedings of the Chinese Society for Electrical Engineering, 2010, 30(3): 55-62. |
| [12] |
王大波, 王逸超, 洪海彬, 等. 一种改进的有源滤波器分频闭环控制策略[J].
电力电子技术, 2019, 53(1): 134-137.
WANG D B, WANG Y C, HONG H B, et al. An improved frequency dividing control strategy in active filter[J]. Power Electronics, 2019, 53(1): 134-137. |
| [13] |
DIAN R J, XU W, MU X C. Improved negative sequence current detection and control strategy for H-bridge three-level active power Filter[J].
IEEE Transactions on Apply Superconductivity, 2016, 26(7): 1051-1056.
|
| [14] |
张松, 陈燕东, 伍文华, 等. 不对称负载下离网逆变器的双序控制方法[J].
电源学报, 2020, 18(2): 15-23.
ZHANG S, CHEN Y D, WU W H, et al. Dual-sequence control method for off-grid inverter under asymmetric load[J]. Journal of Power Supply, 2020, 18(2): 15-23. |
| [15] |
KETZER M B, JACOBINA C B, LIMA A M N. Shaping control strategies for active power filters[J].
IET Power Electronics, 2017, 11(1): 175-181.
|
 2023, Vol. 40
2023, Vol. 40

