目前,我国船舶设备的维修主要采用定期维修和事后维修,对于一些容易监测状态的关键部件同时辅以状态维修的检修模式[1]。固定周期的维修虽然为设备的正常运行做出了较大贡献,但也容易造成过维修问题。事后维修虽然能避免过维修,但非预期的故障会给船舶运营造成意想不到的损失。状态维修也存在着检测不完全、检测策略和维修方案不合理的现象。针对船舶现行检修模式的不足,不少学者对船舶关键部件的性能退化建模方法进行了广泛研究。Giorgio等[2]用非齐次泊松过程建立了船舶柴油机缸套磨损过程的累积损伤模型,并用极大似然估计法估计了模型参数。Hermann等[3]分析了颗粒对磨损过程的影响,建立了船舶柴油机缸套磨损过程的随机差分模型,并给出了贝叶斯推理。杨立乾等[4]构建了船舶关键部件的Gamma退化过程模型,制定了船舶关键部件的状态维修策略,该策略能显著降低船舶维修费用。孙林凯等[5]研究了维修次数对维修周期的影响,建立了周期可变的船舶设备预防性维修模型,并用MATLAB分析了维修周期的变化规律。文献[6]基于威布尔比例风险模型,建立了船舶关键部件的状态机会维修策略,使船舶关键部件单位时间维修成本降至最低。上述研究使用不同方法分别对船舶关键部件的维修进行了优化,但多数只考虑了单个部件的退化及其维修策略,并未考虑多部件的联合维修优化问题。
设备或部件的故障往往不是瞬间发生的,在发生功能故障前往往先发生了一些缺陷,如疲劳裂纹、磨损颗粒、腐蚀过度等,如果提前通过检测发现缺陷并采取维修活动,可以避免故障的发生。基于这一思想,Christer等[7]提出了时间延迟模型,并被广泛应用于维修建模中。Kerres等[8]以可用度和维修费用为优化目标,建立了基于时间延迟模型的风电机组维修策略,并对比了多种维修策略,得出延迟时间模型在风电机组的维修策略中具有明显优势。Wang等[9]建立了基于时间延迟理论的多部件系统成组维修模型。Jones等[10-11]以碳粉生产车间设备为例,对缺陷发生率进行深入剖析,研究了设备故障率的变化规律,并应用贝叶斯网络对维修周期进行优化。吕文元等[12]基于时间延迟理论, 建立了维修类型优化组合模型, 优化了多种维修类型的检测周期和设备的维修计划。胡海军等[13]根据比例役龄递减模型的假设,提出一种包含非完美维修的时间延迟模型,并用数值仿真的方法获得了检测周期与费用的关系。刘葛辉等[14]建立了部件的不完全检测和不完全维修模型,证实了在检出率较高时,检测维修策略比非检测维修策略具有更低的费用率。Wang[15]对近30年来延迟时间模型的研究进行了综述。以上学者在不同的维修领域对时间延迟理论展开了研究,并取得相应的成果,但在船舶关键部件上的研究则很少见。
本文尝试将时间延迟模型应用到船舶关键部件的预防性检测维修上来。根据部件的故障和寿命的不同特点以及检修要求,将不同部件的维修策略分为检测维修和检测延迟维修。为减少停机损失和固定维修费用,在时间延迟阶段以其他部件的检测维修、故障维修或预防维修为机会,建立了基于时间延迟理论的船舶关键部件状态机会维修模型。根据船舶维修的实际数据,利用极大似然估计法进行模型的参数估计。最后以部件检测间隔和延迟时间为决策变量,以长期使用下总平均维修费用率最低为优化目标对模型进行求解,并对模型进行仿真分析,为船舶关键部件的维修提供理论支持和决策参考。
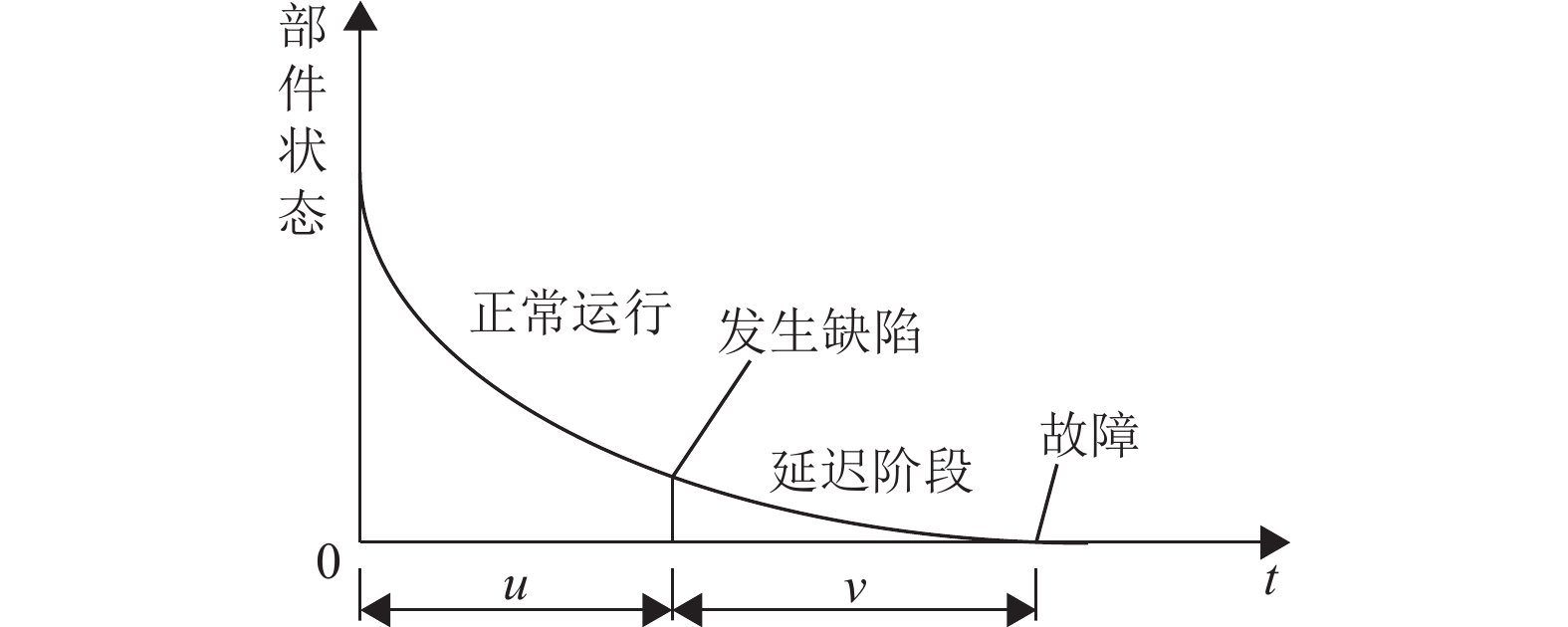
1 问题描述根据时间延迟理论,部件的状态分为正常阶段、延迟阶段和故障,如图1所示。部件发生缺陷前为正常运行阶段,时间为u,发生缺陷后到发生功能故障之前这段时间为时间延迟阶段,时间为v,部件总寿命为u+v。u和v分别独立服从某种分布,其概率密度函数分别为f(u) 和g(v) 。如果在部件发生缺陷后能及时检测发现,并安排恰当的维修活动,就能减少部件故障。因此,如何安排检测间隔和维修活动,是部件维修决策的重要内容。
|
图 1 延迟时间模型 Figure 1 Delay time model |
由于船舶关键部件维修的复杂性,为了方便维修建模,故做如下假设:
(1) 检测能准确检出部件所发生的缺陷,即检测是完全的。
(2) 部件的初始状态为全新,维修效果完全,即修复如新,维修后部件概率属性不变,维修结束后开始新一轮检测周期。
(3) 各部件正常阶段和延迟阶段的分布函数相互独立,且遵循威布尔分布。
(4) 部件在缺陷发生后仍能正常运行,延迟维修部件在检测发现缺陷后推迟维修,延迟维修阶段不再进行检测。
(5) 维修只考虑经济相关性。
2 船舶关键部件的机会维修模型 2.1 船舶关键部件概率密度函数机械设备的缺陷和故障多是由磨损、腐蚀、疲劳等导致的,威布尔分布被广泛应用于描述这类故障。因此,在两阶段模型中,应用威布尔分布分别对正常阶段和延迟阶段进行建模[13-14,16-17]。则有
| $ f\left( u \right) = \frac{{{m_1}}}{{{\mu _1}}}{\left( {\frac{u}{{{\mu _1}}}} \right) ^{{m_1} - 1}}{\text{exp}}\left[ { - {{\left( {\frac{u}{{{\mu _1}}}} \right) }^{{m_1}}}} \right] $ | (1) |
| $ g\left( v \right) = \frac{{{m_2}}}{{{\mu _2}}}{\left( {\frac{v}{{{\mu _2}}}} \right) ^{{m_2} - 1}}{\text{exp}}\left[ { - {{\left( {\frac{v}{{{\mu _2}}}} \right) }^{{m_2}}}} \right] $ | (2) |
式中:f(u) 、g(v) 分别为部件正常阶段和延迟阶段的概率密度函数,m1、m2分别为部件正常阶段和延迟阶段的形状参数,μ1、μ2分别为部件正常阶段和延迟阶段的特征寿命参数。
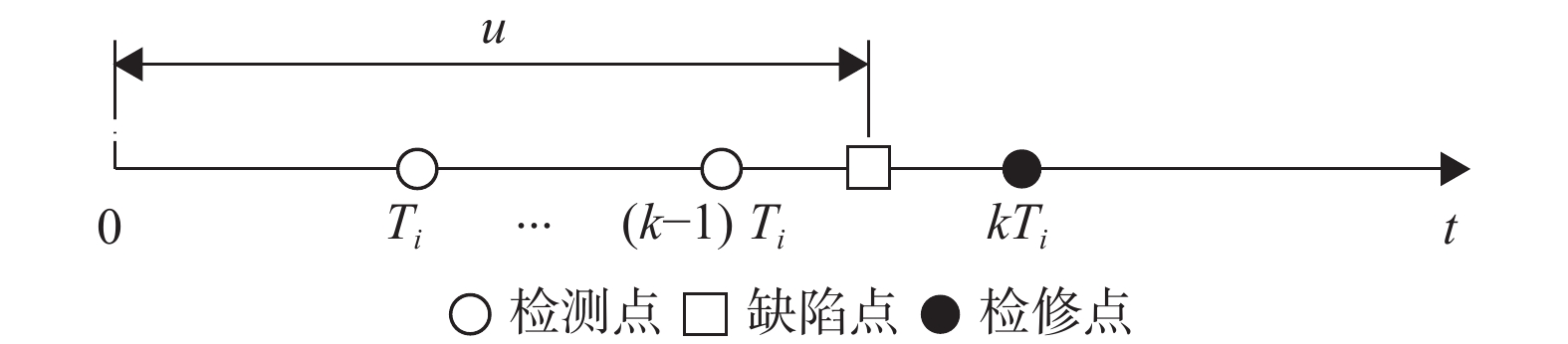
2.2 船舶关键部件的机会维修 2.2.1 检测维修策略在检测维修策略下,部件在检测到缺陷或发生故障时进行维修。假设以周期Ti对部件i进行检测,当部件在检测周期[(k − 1) Ti,kTi]内产生缺陷,并在第k次检测时刻kTi前未发生功能故障,则在第k次检测时对部件进行检测维修,如图2所示。部件在kTi时刻进行检测维修的概率为
| $ {P_{\rm{d}}}\left( {k,{T_i}} \right) = {\mathop \int \nolimits_{\left( {k - 1} \right) {T_i}}^{k{T_i}}} f\left( u \right) \mathop \int \nolimits_{k{T_i} - u}^\infty g\left( v \right) {\text{d}}v{\text{d}}u $ | (3) |
|
图 2 部件检测维修 Figure 2 Component inspection and maintenance |
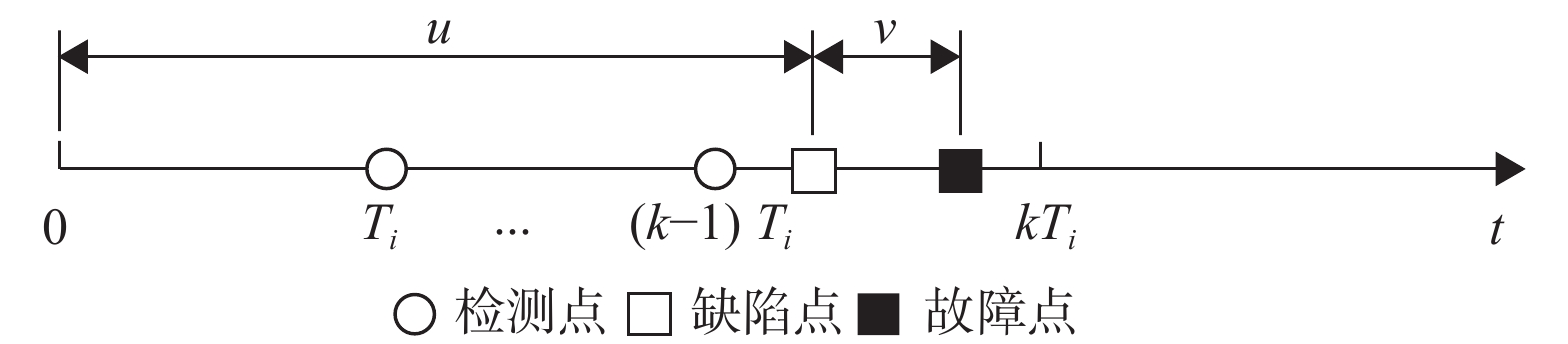
当部件在检测周期[(k − 1) Ti,kTi]内产生缺陷,并在第k次检测前发生功能故障,则在发生故障后对部件进行故障维修,如图3所示。部件在[(k − 1) Ti,kTi]时段内进行故障维修的概率为
| $ {P_{\rm{f}}}\left( {k,{T_i}} \right) = \mathop \int \nolimits_{\left( {k - 1} \right) {T_i}}^{k{T_i}} f\left( u \right) \mathop \int \nolimits_0^{k{T_i} - u} g\left( v \right) {{\rm{d}}} v{{\rm{d}}} u $ | (4) |
|
图 3 部件故障维修 Figure 3 Component failure and maintenance |
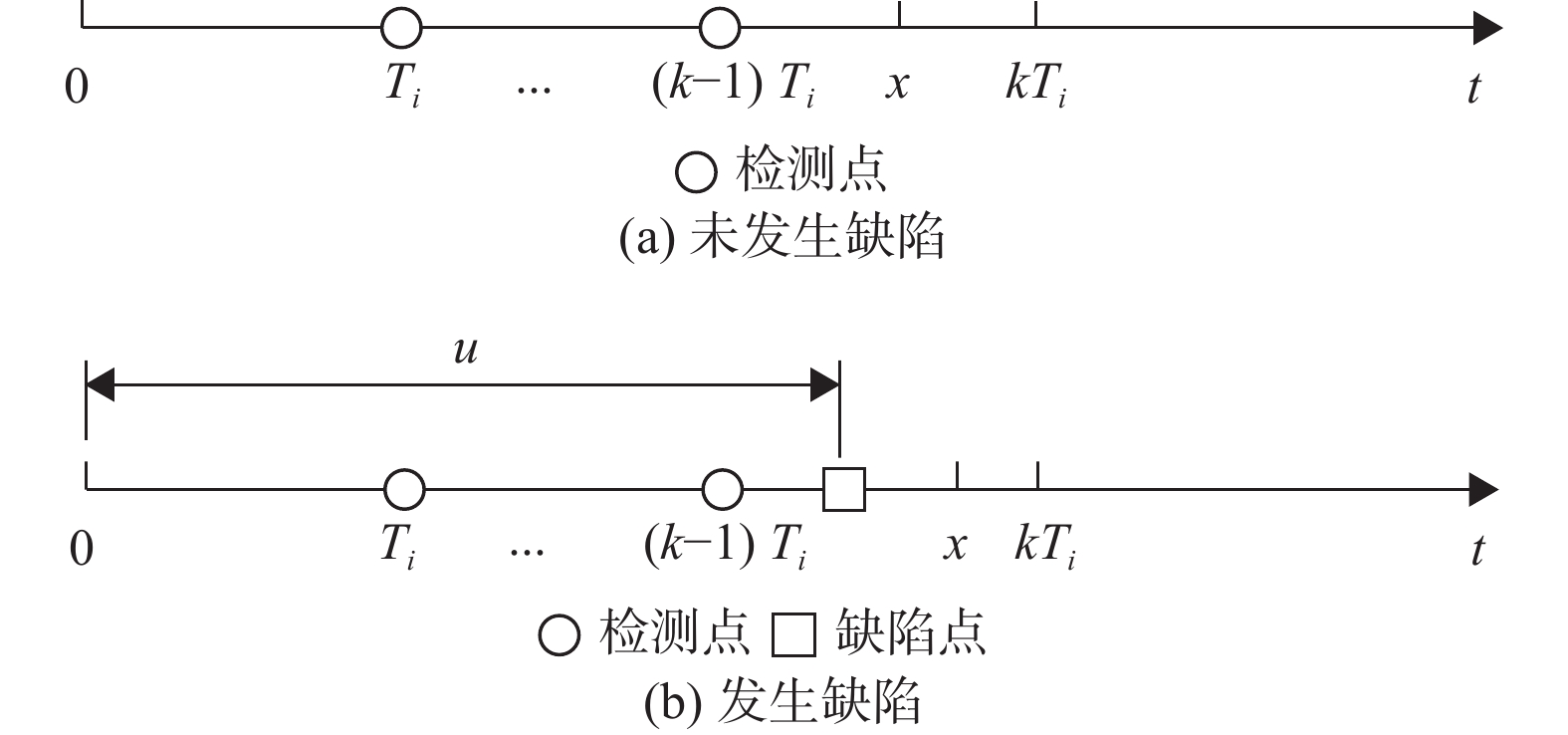
若部件在x时刻((k − 1) Ti<x<kTi) 未发生故障,则说明部件在x时刻可靠。分为两种情况,一是部件未发生缺陷,二是在((k − 1) Ti,x) 期间产生缺陷,至x时刻未发生故障,分别如图4中(a) 、(b) 所示,其概率为
| $ R\left( {x{\text{|}}\left( {k - 1} \right) {T_i}} \right) = \mathop \int \nolimits_x^\infty f\left( u \right) {{\rm{d}}} u + \mathop \int\nolimits_{\left( {k - 1} \right) {T_i}}^x f\left( u \right) \mathop \int \nolimits_{x - u}^\infty g\left( v \right) {{\rm{d}}} v{{\rm{d}}} u $ | (5) |
|
图 4 部件未发生故障 Figure 4 The component not failing |
当某部件的机会维修由其他部件的停机维修提供时,则需要先求出这些部件的更新率。根据更新过程理论可知,当一个部件经过一定的更新周期或更换次数后,其更换率会接近一常数,为其期望更新周期的倒数[18-19]。在长期使用下,部件i的期望更新周期为
| $\begin{split} {{\rm{E}}} \left( {{T_i}} \right) =& {\sum }_{k = 1}^\infty \Big[ k{T_i}{P_{\rm{d}}}\left( {k,{T_i}} \right) +\Big. \\& \Big.\mathop \int \nolimits_{\left( {k - 1} \right) {T_i}}^{k{T_i}} f\left( u \right) \mathop \int \nolimits_0^{k{T_i} - u} \left( {u + v} \right) g\left( v \right) {{\rm{d}}} v{{\rm{d}}} u \Big] \end{split}$ | (6) |
则部件i的更新率为
图5为部件延迟维修原理图,由于部件状态的演化都有一定的规律,当在kTi处检测到缺陷后,停止检测并将维修延迟到kTi +τi处,若在延迟时间段内有其他部件进行停机维修,为减少固定维修费用和停机损失,则连同该部件一起维修。
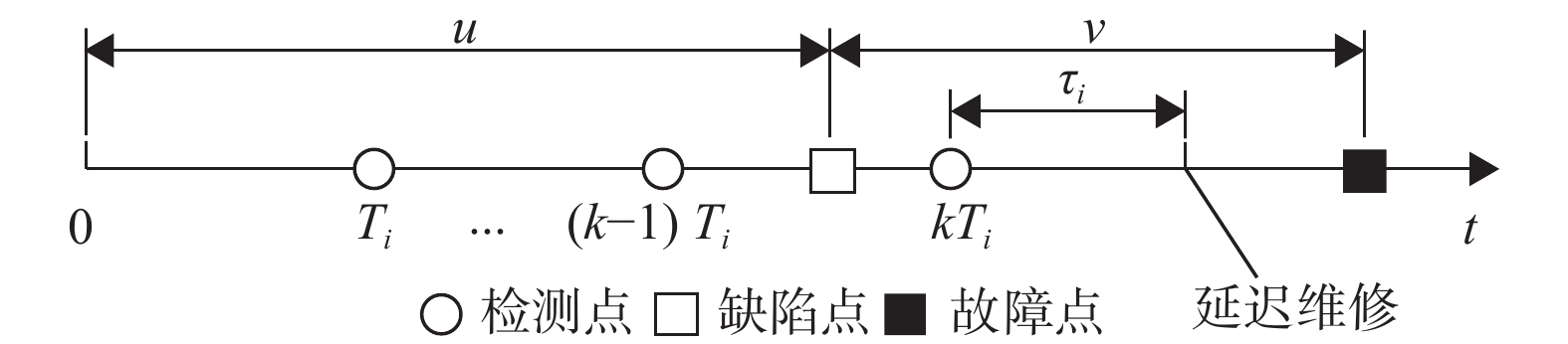
|
图 5 部件延迟维修 Figure 5 The component delaying maintenance |
对于采取延迟机会维修的部件,机会维修是由采取检测维修部件的检测维修和故障维修时机,以及其他采取延迟机会维修部件的故障维修和预防维修时机提供的,可以近似将机会维修概率密度函数看成如式(7)所示的指数分布函数[18-19]。
| $ {p_i}\left( {t,k{T_i}} \right) = {\theta _i}{\rm{exp}}\left[ { - {\theta _i}\left( {t - k{T_i}} \right) } \right] $ | (7) |
式中:
| $ {\lambda _i} = 1/{L_{{\rm{E}}} }({T_i}) = {\lambda _{{\rm{f}}} }(k,{T_i}) + {\lambda _{{\rm{f}}} }({\tau _i},k{T_i}) + {\lambda _{\rm{o}}}({\tau _i},k{T_i}) + {\lambda _{\rm{p}}}({\tau _i},k{T_i}) $ | (8) |
式中:LE(Ti) 为部件i的期望寿命;λf(k,Ti) =Pf(k,Ti)
由于维修机会只能由其他部件的检测维修、故障维修和预防维修提供,所以,对于采取延迟机会维修的部件
当部件采取延迟维修策略时,在下面4种情况下对其进行维修:
(1) 在检测到缺陷前发生故障。由于部件从产生缺陷到发生故障之间的时间过短,未等检测到缺陷即发生故障,假设缺陷和故障都发生在[(k − 1) Ti,kTi]时间段内,其概率计算同式(4) 。
(2) 在延迟维修阶段进行故障维修。当在kTi时刻检测到部件缺陷后进入延迟阶段,如果延迟时间过长,且等不到其他部件提供的维修机会即已发生故障,这时需立即采取故障维修,其概率为
| $ {P_{\rm{f}}}\left( {{\tau _i},k{T_i}} \right) = \mathop \int \nolimits_{\left( {k - 1} \right) {T_i}}^{k{T_i}} f\left( u \right) \mathop \int \nolimits_{k{T_i} - u}^{k{T_i} + {\tau _i} - u} g\left( v \right) \mathop \int \nolimits_{u + v}^\infty {p_i}\left( {t,k{T_i}} \right) {{\rm{d}}} t{{\rm{d}}} v{{\rm{d}}} u $ | (9) |
(3) 在延迟维修阶段进行机会维修。在第k次检测进入延迟维修阶段后,若有其他部件进行检测维修或故障维修提供机会,则对部件进行机会维修,其概率为
| $ {P_{\rm{o}}}\left( {{\tau _i},k{T_i}} \right) = \mathop \int \nolimits_{\left( {k - 1} \right) {T_i}}^{k{T_i}} f\left( u \right) \mathop \int \nolimits_{k{T_i}}^{k{T_i} + {\tau _i}} {p_i}\left( {t,k{T_i}} \right) \mathop \int \nolimits_{t - u}^\infty g\left( v \right) {{\rm{d}}} v{{\rm{d}}} t{{\rm{d}}} u $ | (10) |
(4) 在延迟维修阶段结束时进行预防维修。当在第k次检测进入延迟维修阶段后,部件不发生故障,也没有其他部件需要维修时,在延迟阶段结束,即
| $ \begin{split} {P_{{\rm{p}}} }\left( {{\tau _i},k{T_i}} \right) =& \mathop \int \nolimits_{\left( {k - 1} \right) {T_i}}^{k{T_i}} f\left( u \right) \mathop \int \nolimits_{k{T_i} + {\tau _i}}^\infty {p_i}\left( {t,k{T_i}} \right) \times \\& \mathop \int \nolimits_{k{T_i} + {\tau _i} - u}^\infty g\left( v \right) {{\rm{d}}} v{{\rm{d}}} t{{\rm{d}}} u \end{split}$ | (11) |
若部件在检测期间的x时刻((k − 1) Ti<x<kTi) 未发生故障,其可靠度计算同式(5) 。如图6所示,若部件在[(k − 1) Ti,kTi]期间发生缺陷,在kTi发现缺陷后停止检测的延迟阶段x时刻幸存,其概率为
| $ \begin{split}R\left( {x|\left( {k - 1} \right) {T_i};{P_{\rm{d}}}} \right)=&\mathop \int \nolimits_{\left( {k - 1} \right) {T_i}}^{k{T_i}} f\left( u \right) \mathop \int \nolimits_x^\infty {p_i}\left( {t,k{T_i}} \right) \times \\& \mathop \int \nolimits_{x - u}^\infty g\left( v \right) {{\rm{d}}} v{{\rm{d}}} t{{\rm{d}}} u \end{split}$ | (12) |
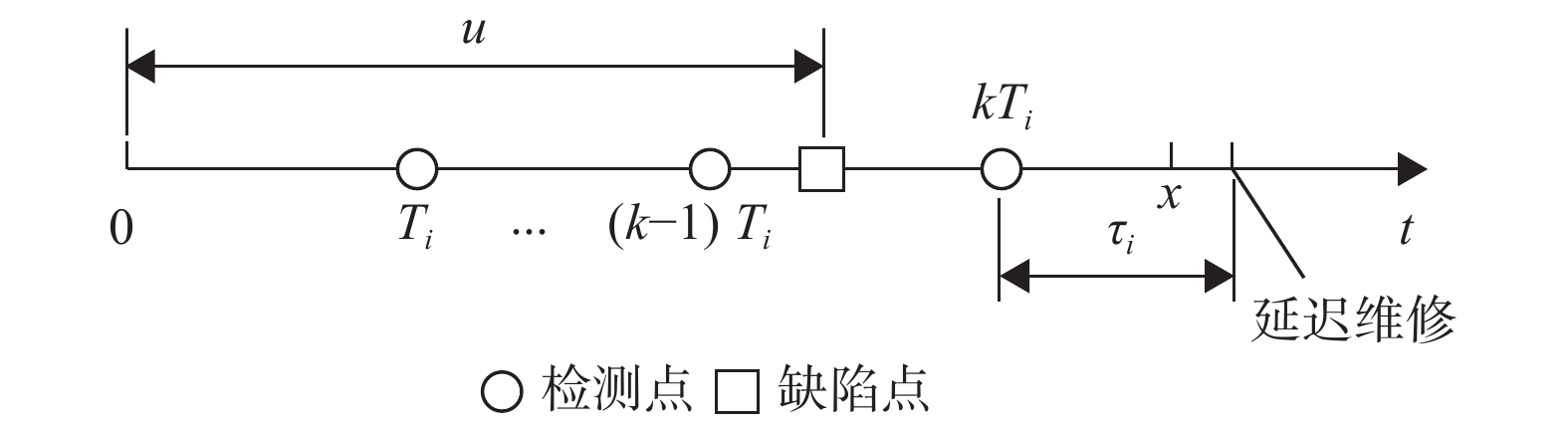
|
图 6 部件延迟时间未发生故障 Figure 6 The component not failing in the delay time |
在长期使用下,更新周期的期望长度为
| $ \begin{split}{L_{{\rm{E}}} }\left( {{T_i}} \right) =& \sum\nolimits_{k = 1}^\infty \left\{ \int_{(k - 1) }^{k{T_i}} f(u) \int_0^{k{T_i} - u} (u + v) g(v) {{\rm{d}}} v{{\rm{d}}} u +\right.\\ &\left.\int_{(k - 1) {T_i}}^{k{T_i}} f(u) \int_{k{T_i} - u}^{k{T_i} + {\tau _i} - u} (u + v) g(v) \times \right.\\ & \left. \int_{u + v}^\infty {{p_i}(t,k{T_i}) {{\rm{d}}} t{{\rm{d}}} v{{\rm{d}}} u +} \right. \\& \left. \int_{(k - 1) {T_i}}^{k{T_i}} f(u) \int_{k{T_i}}^{k{T_i} +\tau _i} t{p_i}(t,k{T_i}) \times \right.\\ &\left.\int_{t - u}^\infty {g(v) {{\rm{d}}} v{{\rm{d}}} t{{\rm{d}}} u + (k{T_i} + {\tau _i}) {P_{{\rm{p}}} }({\tau _i},k{T_i}) } \right\} \\[-8pt] \end{split} $ | (13) |
在已知各部件的寿命分布规律和给定各部件的检测间隔和延迟时间的条件下,由式(7) 可知,计算部件i的机会更新率θi需要先根据式(6) 、(8) 、(13) 求出各检测维修部件和其他机会维修部件的更新率,而要得到其他机会维修部件的更新率需要通过式(4) 、(9) 、(11) 计算Pf(k,Ti) 、Pf(τi,kTi) 、Pp(τi,kTi) 。而要计算Pf(k,Ti) 、Pf(τi,kTi) 、Pp(τi,kTi) ,又需要知道各部件的机会更新率θi。这是一种互为因果的关系,可以通过设定各部件的机会更新率初始值
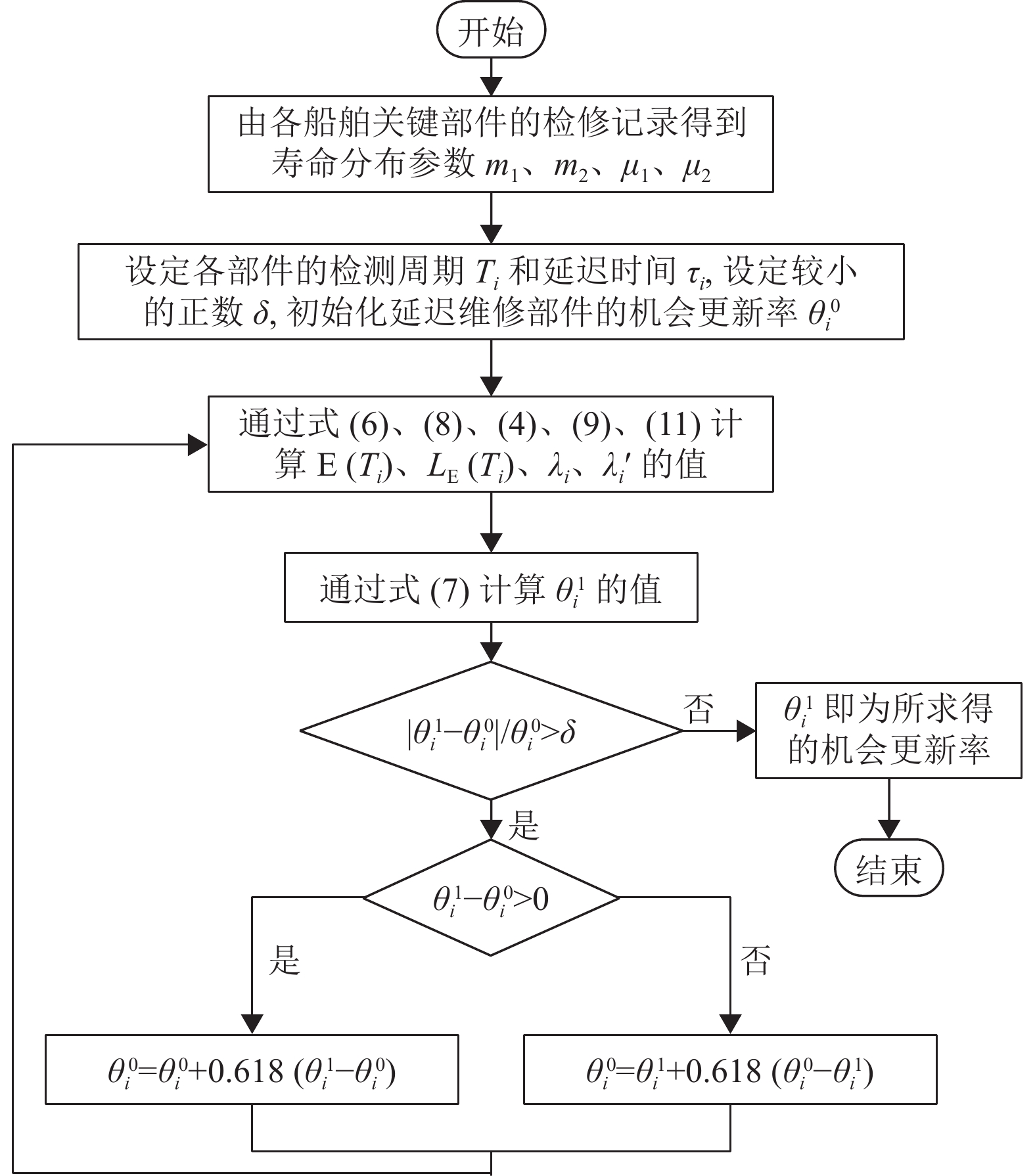
|
图 7 机会更新率求解流程图 Figure 7 Opportunity renewal rate solution flow chart |
在延迟时间的机会维修模型中,需要估计各部件的缺陷分布参数和故障分布参数,基于文献[20]提出检测维修部件和机会维修部件的极大似然参数估计方法。极大似然估计的基本思想是认为已发生的事件概率最大。
2.3.1 检测维修部件分布参数估计对于采用检测维修策略的部件,其维修发生在检测出缺陷或发生故障时。在实际检测中,存在维修和不维修两种情况。根据前面的假设,缺陷和故障的发生是两个相互独立的事件,且部件每一次维修后进入新一轮寿命周期。对相同型号系列部件的实际检修数据进行统计分析,构建似然函数。记录到部件i在kTi时刻进行检测维修的次数为m(k) ,在第k个检测间隔[(k − 1) Ti,kTi]内发生故障的次数为p(k) 。在观测截止时刻,未发生故障的部件中,处于第k个检测间隔[(k − 1) Ti,kTi]的部件数为u(k) 。似然函数就是在各检测时刻发生维修事件的概率、各检测间隔发生故障维修事件的概率和观测截止时刻未发生故障事件概率的乘积。则维修序列的对数似然函数为
| $\begin{split} \text{ln}{L_1} =& \mathop \sum \limits_{k = 1}^n \left[ {m\left( k \right) {\text{ln}}{P_{{\rm{d}}} }\left( {k,{T_i}} \right) } \right] + \mathop \sum \limits_{k = 1}^q \left[ {p\left( k \right) {\text{ln}}{P_{{\rm{f}}} }\left( {k,{T_i}} \right) } \right] +\\& \sum\limits_{k = 1}^s {\sum\limits_{j = 1}^{u(k) } {{\text{ln}}R\left( {{x_{k - 1,j}}|\left( {k - 1} \right) {T_i}} \right) } } \end{split} $ | (14) |
式中:n为检测维修前的最大检测次数;q为发生故障维修的最大检测周期序号;s为观测截止时刻,统计到的正常运行部件所属的最大检测周期;R(xk − 1, j|(k − 1) Ti) 为检测间隔[(k − 1) Ti,kTi]内正常运行的第j个部件可靠度。求取似然函数
对于采用延迟维修策略的部件,其在4种情况下进行维修,即检测期间发生故障维修、延迟期间发生故障维修、延迟期间进行机会维修和延迟时间结束进行预防性维修。对相同型号系列部件的实际检修数据进行统计分析,构建似然函数。记录到部件i在第k次检测间隔[(k − 1) Ti,kTi]内发生故障的次数为b(k) ,在第k次检测后延迟时间段内发生故障维修的次数为c(k) ,在第k次检测后延迟时间段内发生机会维修的次数为d(k) ,在第k次检测后延迟时间结束进行预防性维修的次数为e(k) 。在观测截止时刻,处于检测阶段[(k − 1) Ti,kTi]内的部件数为l(k) 。处于第k次检测后延迟阶段的部件数为y(k) 。似然函数就是以上各事件概率的乘积。则维修序列的对数似然函数为
| $ \begin{split} {\text{ln}}{L_2} =& {\sum }_{k = 1}^r \left[ {b(k) {\text{ln}}{P_{{\rm{f}}} }\left( {k,{T_i}} \right) } \right] + {\sum }_{k = 1}^h \left[ {c\left( k \right) {\text{ln}}{P_{{\rm{f}}} }\left( {{\tau _i},k{T_i}} \right) } \right] +\\& {\sum }_{k = 1}^z \left[ {d\left( k \right) {\text{ln}}{P_{\rm{o}}}\left( {{\tau _i},k{T_i}} \right) } \right] + {\sum }_{k = 1}^w \left[ {e\left( k \right) {\text{ln}}{P_{{\rm{p}}} }\left( {{\tau _i},k{T_i}} \right) } \right] +\\& \sum\nolimits_{k = 1}^t {\sum\nolimits_{j = 1}^{l(k) } {{\text{ln}}R\left( {{x_{k - 1,j}}|\left( {k - 1} \right) {T_i}} \right) } } + \\&\sum\nolimits_{k = 1}^g {\sum\nolimits_{j = 1}^{y(k) } {{\text{ln}}R\left( {{x_{k - 1,j}}|\left( {k - 1} \right) {T_i};{P_{\rm{d}}}} \right) } } \\[-18pt] \end{split} $ | (15) |
式中:r为故障维修的最大检测周期序号;h为发生延迟故障维修前的最大检测次数;z为发生延迟机会维修前的最大检测次数;w为进行延迟预防性维修前的最大检测次数;t为观测截止时刻,属于检测阶段的最大检测周期序号;g为观测截止时刻、延迟阶段前的最大检测次数。最大化似然函数
(1) 检测维修部件费用。部件在检测到缺陷和发生故障后都会进行维修,且假设维修是完全的,即每一次维修结束都开始新一轮检测周期。如果检测维修发生在第k次检测时,则检修费用为
| $ {C_{{\rm{d}}} }\left( {k,{T_i}} \right) = k{C_i} + {C_{\rm{p}}} + {C_{\rm{o}}} $ | (16) |
式中:
如果在检测间隔[(k − 1) Ti,kTi]内发生故障维修,则检修费用为
| $ {C_{{\rm{f}}} }\left( {k,{T_i}} \right) = \left( {k - 1} \right) {C_i} + {C_{{\rm{f}}} } $ | (17) |
式中:Cf为故障维修费用。部件长期使用下更新周期费用期望为
| $ {C_{{\rm{E}}} }\left( {{T_i}} \right) = {\sum }_{k = 1}^\infty \left[ {{P_{{\rm{d}}} }\left( {k,{T_i}} \right) {C_{\rm{d}}}\left( {k,{T_i}} \right) + {P_{{\rm{f}}} }\left( {k,{T_i}} \right) {C_{{\rm{f}}} }\left( {k,{T_i}} \right) } \right] $ | (18) |
(2) 延迟维修部件费用。如前所述,延迟维修部件在4种情况下进行维修活动,维修结束当前更新周期。如果在检测阶段发生故障维修,记故障发生的检测间隔为[(k − 1) Ti,kTi],则其检修费用计算公式同式(17) 。如在第k次检测后延迟阶段内发生故障维修,则检修费用为
| $ {C_{{\rm{f}}} }\left( {{\tau _i},k{T_i}} \right) = k{C_i} + {C_{{\rm{f}}} } $ | (19) |
如在延迟时间内进行机会维修,则检修费用为
| $ {C_{\rm{o}}}\left( {{\tau _i},k{T_i}} \right) = k{C_i} + {C_{{\rm{p}}} } $ | (20) |
如在延迟阶段结束进行预防性维修,则检修费用为
| $ {C_{\rm{p}}}\left( {{\tau _i},k{T_i}} \right) = k{C_i} + {C_{\rm{o}}} + {C_{{\rm{p}}} } $ | (21) |
部件长期使用下更新周期费用期望为
| $ \begin{split}{C_{\rm{E}}}\left( {{\tau _i},k{T_i}} \right) = &{\sum }_{k = 1}^\infty \left[ {{P_{\rm{f}}}\left( {k,{T_i}} \right){C_{\rm{f}}}\left( {k,{T_i}} \right) + } \right.\\&\left. {{P_{\rm{f}}}\left( {{\tau _i},k{T_i}} \right){C_{\rm{f}}}\left( {{\tau _i},k{T_i}} \right) + } \right.\\&\left. {{P_{\rm{o}}}\left( {{\tau _i},k{T_i}} \right){C_{\rm{o}}}\left( {{\tau _i},k{T_i}} \right){\rm{ + }}} \right.\\&\left. {{P_{\rm{p}}}\left( {{\tau _i},k{T_i}} \right){C_{\rm{p}}}\left( {{\tau _i},k{T_i}} \right)} \right] \end{split}$ | (22) |
(3) 检修费用率优化模型。定义示性变量θ,当部件i采用检测维修部件时θ = 1,当部件i采用检测延迟维修部件时θ = 0。由以上分析,建立长期使用下船舶关键部件费用率优化模型
| $ {\text{min}}\overline C\left( {{\tau _i},{T_i}} \right) = {\sum }_{i = 1}^N \left[ {\theta \frac{{{C_{{\rm{E}}} }\left( {{T_i}} \right) }}{{{{\rm{E}}} \left( {{T_i}} \right) }} + \left( {1 - \theta } \right) \frac{{{C_{{\rm{E}}} }\left( {{\tau _i},k{T_i}} \right) }}{{{L_{{\rm{E}}} }\left( {{T_i}} \right) }}} \right] $ | (23) |
| ${\rm{s}}.{\rm{t}}. \;\left\{ \begin{gathered} 0 < {T_i} < {{\rm{E}}} \left( {u + v} \right) ,\theta = 1 \\ 0 < {T_i} < {{\rm{E}}} \left( u \right) ,\theta = 0 \\ \end{gathered} \right. $ | (24) |
| $ 0 \leqslant {\tau _i} \leqslant {{\rm{E}}} \left( v \right) $ | (25) |
式中:
本文所建立的模型需要分两步求解,首先需要由实际检修序列通过式(14)~(15) 求解得到检测维修和延迟维修部件的分布参数,再通过式(23) 优化部件检测间隔和延迟时间。求解对象是多变量、非线性、多约束问题,很难通过求导得到一阶导数和Hessian矩阵,无法用牛顿法迭代求解。遗传算法在解这类问题时具有较强的全局寻优能力[21],因此本文采用遗传算法进行模型的求解。
首先需要由部件检修记录求出分布参数,接着根据各部件寿命分布和维修实际,决定检测间隔和延迟时间范围,采用二进制编码。由于目标值为求最小值,以进化到当代的最大目标值减去个体目标值之差作为个体适应度。采用轮盘赌法进行选择,根据其原理,适应值越大即目标值越小的个体被选中的机会越大。采用均匀交叉算子,相邻两个体的各基因位以一定概率进行交叉操作产生新个体,该算子以较快速度发现较优基因,从而快速收敛到最优解。采用均匀变异进行变异操作,在一定概率下,对随机选中的码位进行取反,从而得到新的变异个体。当迭代次数达到设定值时停止遗传,反复多次试验取其中最优值作为目标值。算法流程图如图8所示。
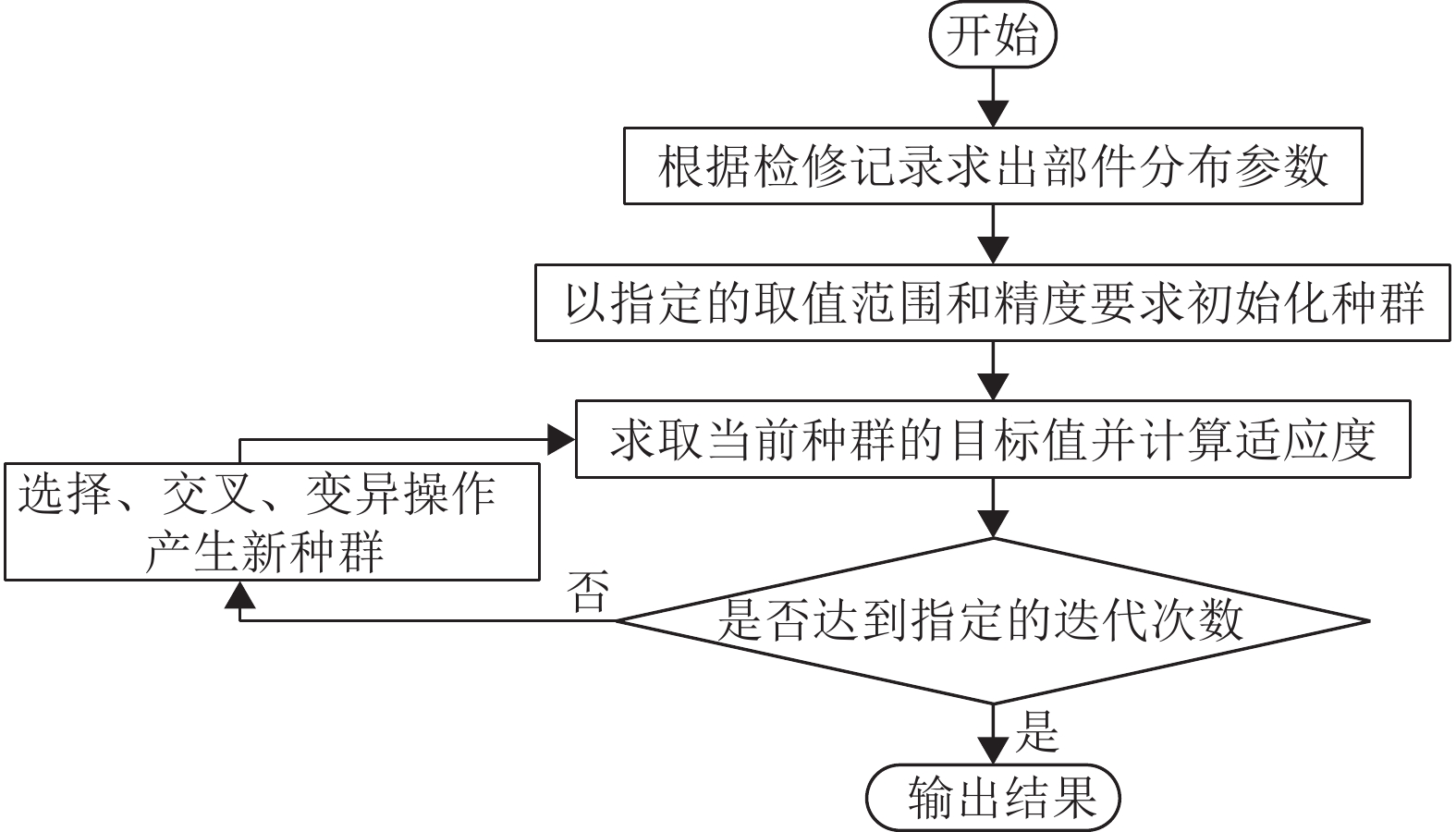
|
图 8 遗传算法求解最优值流程图 Figure 8 Flow chart of genetic algorithm to solve the optimal value |
以船舶主传动系统关键部件齿轮箱、尾轴前轴承和后轴承的检测维修为例。齿轮箱平时故障率低、故障停机时间长、维修成本高[16],采用检测延迟维修策略。如在检测间隔发生非预期故障则进行故障维修,在延迟维修时间段内,如发生故障就进行故障维修,若有其他部件进行预防性维修或故障维修,为减少固定维修费用和停机损失,则将齿轮箱一起进行机会维修,否则等到延迟维修时间结束采取预防性维修。尾轴前轴承和后轴承则采用检测维修策略,即在检测中发现缺陷则安排预防性维修,如检测前发生非预期故障则立即采取故障维修。
以某船舶修造公司的船舶维修作为研究对象,对某型货船主传动系统的齿轮箱、尾轴前轴承和后轴承 3 个关键部件的维修数据进行整理分析,分别编号为1、2、3,用2.3节介绍的方法进行参数估计,结果如表1所示,所有参数均通过
| 表 1 部件寿命参数估计结果 Table 1 The results of component life parameter estimation |
| 表 2 船舶关键部件维修费用 Table 2 Maintenance costs of ship’s key components |
用遗传算法对船舶关键部件维修间隔和延迟维修时间进行优化,设定种群规模为50,二进制编码长度为41位,根据精度要求,检测和延迟时间精确到天即可,其中部件1的检测时间间隔为11位,部件2和部件3检测时间间隔均为10位,延迟时间为10位。交叉率0.5,变异率0.1,迭代次数100,经过5次运算,选取其中最优值作为目标函数值,优化结果如表3所示。
| 表 3 检测延迟机会维修优化结果 Table 3 Optimization result of inspection delay opportunity maintenance |
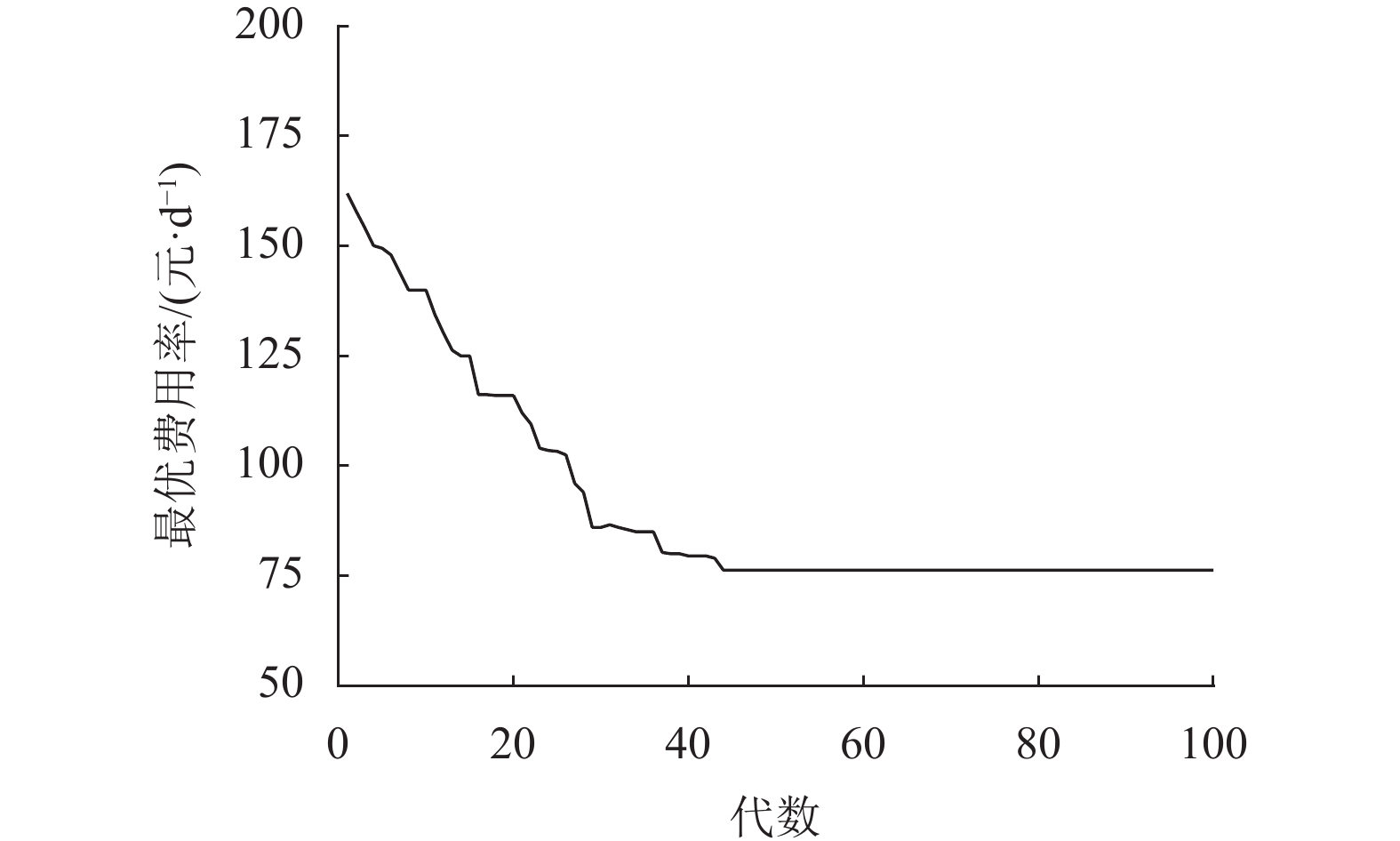
如图9所示为优化过程中船舶关键部件每一代最优费用率变化曲线。算法在44代时取得最优值,此时总最小维修费用率为76.25元/d。
4.3 船舶关键部件预防性维修优化结果对比为比较各种维修策略的优劣,对比本文模型和传统预防性维修策略、检测维修策略。船舶的传统维修策略以定期维修为主,其维修费用包括预防性维修费用、故障维修费用和固定维修费用。而检测维修策略则是对每个部件采取检测维修策略。船舶关键部件采用不同维修策略结果如表4所示。
|
图 9 最优费用率变化曲线 Figure 9 Curve of optimal cost ratio |
| 表 4 传统预防性维修和检测维修优化结果 Table 4 Traditional preventive maintenance and test maintenance optimization results |
对比表3、表4的数据可知,检测维修策略比传统定周期预防性维修策略节省费用18.87%,而检测延迟机会维修策略比检测维修策略节省费用9.18%。在3种维修策略中,检测维修策略优于传统预防性维修策略,因为检测可以及时发现部件缺陷并及时安排预防性维修,减少了部件发展到故障而进行的非预期故障维修,而故障造成的损失通常都比较大,并且检测费用与维修费用相比较低。而检测延迟机会维修策略中,齿轮箱可以利用延迟时间进行机会预防性维修,在延迟时间段内若有其他部件进行预防性或故障维修提供维修机会,则一起进行维修,从而节约固定维修成本和停机损失。而单纯的检测维修策略不考虑部件间的经济相关性,对各部件进行的每次维修都会产生固定维修费用,而在检测维修中考虑机会维修可以节省固定维修费用,所以采用检测延迟机会维修策略更科学。
5 结论本文基于延迟时间理论,建立了船舶关键部件的检测延迟机会维修优化模型,并根据部件实际维修数据利用极大似然估计法对模型参数进行了估计。运用遗传算法优化各部件总维修费用率,确定各部件的最优检测间隔和延迟维修时间。结果表明,相对于传统预防性维修和不考虑部件经济相关性的检测预防性维修,检测延迟机会维修模型能有效降低各部件总维修费用率,减小固定维修支出和总停机次数。本文研究为部件间的联合检测维修策略提供参考,在实际维修中并不是每次维修都能完全修复,因此在后续的研究工作中,考虑将不完全维修等不同维修方式加入到模型中来,以提高该模型在实际维修计划中的适应性。
| [1] |
王子睿. 基于状态的船舶动力系统维修时机决策研究[D]. 武汉: 武汉理工大学, 2016.
|
| [2] |
GIORGIO M, GUIDA M, PULCINI G. A wear model for assessing the reliability of cylinder liners in marine diesel engines[J].
IEEE Transactions on Reliability, 2007, 56(1): 158-166.
DOI: 10.1109/TR.2006.890901. |
| [3] |
HERMANN S, RUGGERI F. Modeling wear in cylinder liners[J].
Quality and Reliability Engineering International, 2017, 33(4): 839-851.
DOI: 10.1002/qre.2061. |
| [4] |
杨立乾, 赵金楼, 李根. 基于性能退化的船舶关键部件视情维修策略[J].
哈尔滨工程大学学报, 2020, 41(4): 613-618.
YANG L Q, ZHAO J L, LI G. Condition-based maintenance strategy for critical components of ships based on performance degradation[J]. Journal of Harbin Engineering University, 2020, 41(4): 613-618. DOI: 10.11990/jheu.201905015. |
| [5] |
孙林凯, 耿俊豹, 金家善, 等. 基于可变周期的船舶预防性维修策略[J].
船海工程, 2009, 38(1): 97-100.
SUN L K, GENG J B, JIN J S, et al. Preventive maintenance strategy of ship based on variable period[J]. Ship & Ocean Engineering, 2009, 38(1): 97-100. DOI: 10.3963/j.issn.1671-7953.2009.01.029. |
| [6] |
李冀晖, 黄锦敬, 韦发清. 基于比例风险模型的船舶状态机会维修策略[J].
广东海洋大学学报, 2021, 41(5): 122-129.
LI J H, HUANG J J, WEI F Q. Ship state opportunity maintenance strategy based on proportional hazard model[J]. Journal of Guangdong Ocean University, 2021, 41(5): 122-129. DOI: 10.3969/j.issn.1673-9159.2021.05.016. |
| [7] |
CHRISTER A H, WALLER W M. Delay time models of industrial inspection maintenance problems[J].
Journal of The Operational Research Society, 1984, 35(5): 401-406.
DOI: 10.1057/jors.1984.80. |
| [8] |
KERRES B, FISCHER K, MADLENER R. Economic evaluation of maintenance strategies for wind turbines: a stochastic analysis[J].
IET Renewable Power Generation, 2015, 9(7): 766-774.
DOI: 10.1049/iet-rpg.2014.0260. |
| [9] |
WANG W, CHRISTER A H. Solution algorithms for a nonhomogeneous multi-component inspection model[J].
Computers & Operations Research, 2003, 30(1): 19-34.
|
| [10] |
JONES B, JENKINSON I, WANG J. Methodology of using delay-time analysis for a manufacturing industry[J].
Reliability Engineering and System Safety, 2009, 94(1): 111-124.
DOI: 10.1016/j.ress.2007.12.005. |
| [11] |
JONES B, JENKINSON I, YANG Z, et al. The use of Bayesian network modeling for maintenance planning in a manufacturing industry[J].
Reliability Engineering and System Safety, 2010(95): 267-277.
|
| [12] |
吕文元, 郑睿. 基于时间延迟的维修类型优化组合模型及案例分析[J].
系统工程理论与实践, 2013, 33(7): 1654-1660.
LYU W Y, ZHENG R. Delay-time-based model of optimization grouping maintenance type and case study[J]. Systems Engineering-Theory & Practice, 2013, 33(7): 1654-1660. DOI: 10.3969/j.issn.1000-6788.2013.07.004. |
| [13] |
胡海军, 程光旭, 段权, 等. 一种包含非理想维修的延迟时间模型[J].
西安交通大学学报, 2009, 43(6): 103-107.
HU H J, CHENG G X, DUAN Q, et al. Delay time model based on imperfect maintenance[J]. Journal of Xi’an Jiaotong University, 2009, 43(6): 103-107. DOI: 10.3321/j.issn:0253-987X.2009.06.022. |
| [14] |
刘葛辉, 陈绍宽, 金华, 等. 基于延迟时间模型的不完全检修计划优化模型[J].
浙江大学学报(工学版), 2020, 54(7): 1298-1307.
LIU G H, CHEN S K, JIN H, et al. Optimum imperfect inspection and maintenance scheduling model considering delay time theory[J]. Journal of Zhejiang University (Engineering Science), 2020, 54(7): 1298-1307. DOI: 10.3785/j.issn.1008-973X.2020.07.007. |
| [15] |
WANG W. An overview of the recent advances in delay-time-based maintenancemodeling[J].
Reliability Engineering & System Safety, 2012, 106(5): 165-178.
|
| [16] |
李想, 朱才朝, 李垚, 等. 基于延迟时间模型的风电机组维修策略[J].
重庆大学学报, 2020, 43(10): 20-28.
LI X, ZHU C C, LI Y, et al. Maintenance strategy of wind turbine based on the delay time model[J]. Journal of Chongqing University, 2020, 43(10): 20-28. DOI: 10.11835/j.issn.1000-582X.2020.10.003. |
| [17] |
柏文华, 左洪福, 吕德峰, 等. 基于延迟时间模型的民机部件维修优化方法[J].
南京航空航天大学学报, 2015, 47(6): 890-896.
BAI W H, ZUO H F, LYU D F, et al. Maintenance optimization method of civil aircraft based on delay time mode[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(6): 890-896. |
| [18] |
赵洪山, 鄢盛腾, 刘景青. 基于机会维修模型的风电机组优化维修[J].
电网与清洁能源, 2012, 28(7): 1-5.
ZHAO H S, YAN S T, LIU J Q. Optimization maintenance of wind turbines based on opportunistic maintenance model[J]. Power System and Clean Energy, 2012, 28(7): 1-5. DOI: 10.3969/j.issn.1674-3814.2012.07.001. |
| [19] |
贺德强, 罗安, 邓建新, 等. 列车转向架关键部件预防性维修决策优化模型[J].
计算机集成制造系统, 2018, 24(5): 1155-1161.
HE D Q, LUO A, DENG J X, et al. Optimization model of preventive maintenance decision-making for train bogie key components[J]. Computer Integrated Manufacturing Systems, 2018, 24(5): 1155-1161. |
| [20] |
WANG L, HU H, WANG Y, et al. The availability model and parameters estimation method for the delay time model with imperfect maintenance at inspection[J].
Applied Mathematical Modelling, 2011, 35(6): 2855-2863.
DOI: 10.1016/j.apm.2010.11.070. |
| [21] |
温正, 孙华克. MATLAB智能算法[M]. 北京: 清华大学出版社, 2017: 145-196.
|
 2023, Vol. 40
2023, Vol. 40
