2. 华南理工大学 工商管理学院,广东 广州 510640
2. School of Business Administration, South China University of Technology, Guangzhou 510640, China
围棋作为一项启迪人类智慧的运动,受到了广泛青睐。人们通常会选择在电脑或手机上练习围棋以提高自己的围棋水平,但是这种方式脱离了真实的对弈环境,使对弈体验与学习效果都大打折扣。研究人员将围棋与机器人技术相结合,利用工业机械臂构建围棋机器人,虽然定位精度较好,但体积庞大、成本高,难以很好地满足市场需求[1-3]。本文在对围棋对弈过程中的图像处理、运动控制及其位置误差补偿进行深入研究的基础上,设计了一套能够实时辅助对弈的围棋落子指引装置,使围棋的学习过程变得更加真实生动,从而激发棋手对围棋的学习兴趣,提升学习效果。
针对围棋的图像处理,一般先对棋盘进行定位,然后对棋子进行识别。在处理围棋棋盘时,主要采用霍夫变换、角点检测等方法。文献[4]利用霍夫直线检测对棋盘进行分割并获取棋盘交叉点坐标。文献[5]通过霍夫变换定位棋盘的4个顶点像素坐标并结合几何计算,确定棋盘交叉点坐标。但是当背景环境比较嘈杂时,该方法的鲁棒性会降低。针对棋子的识别,文献[6]选择不同视角的黑白棋子组成8个模板用于棋子的检测。文献[7]通过帧间图像差分获取变化的棋子的位置,再通过形态学处理与图像掩膜操作来避免光照的影响,该方法图像之间的运算过多,会导致单张图片处理时间偏长,不利于执行装置进行快速响应。
运动控制中的位置误差补偿可以用于提高运动末端的绝对定位精度,方法大致分为两种:离线误差补偿和在线误差补偿[8-9],本文主要对离线补偿的方法进行研究,即在机器人开始作业前,对机器人的定位精度进行补偿[10],计算末端执行器在目标位置的定位误差,之后对其进行逆补偿进而提高机器人的绝对定位精度。文献[11]用BP神经网络的多因素非线性映射构建误差补偿模型。文献[12]通过测量运动末端运行轨迹上各个特定点的位置误差并为轨迹上的所有点建立一个广义误差模型,进而建立一个反向模型,用于计算修正后的标准坐标,从而实现末端执行器的精确定位。
为进一步提高棋子识别准确率和效率,本文将从以下两个方面开展研究:(1) 标准棋盘图像提取;(2) 棋子识别。针对标准棋盘的提取,本文设计了特殊的定位标识用于定位棋盘角点位置,以减小嘈杂环境对棋盘定位的干扰,并在多尺度空间下检测棋盘,可以在不同视角下准确定位棋盘,进一步提高检测的鲁棒性。在棋子识别部分通过自适应阈值处理,找到最佳分割阈值完成棋子的分割,同时,通过形态学处理找到棋盘中存在的反光区域,利用机器学习的方法对此区域中的棋子进行单独的检测,节省处理过程中的运算时间。
在完成棋子识别之后,棋子的位置信息将会被传送至服务端的围棋AI引擎,引擎返回决策位置信号,控制执行机构末端运动到棋盘中指定位置,完成指引动作。为求解舵机的运动控制参数,本文首先根据围棋落子指引装置的实际物理结构,建立了运动学模型,并进行仿真计算,得到了舵机运动到棋盘指定位置时对应的角度值,应用此角度值控制指引装置末端运动时,末端实际位置与目标位置之间存在偏差,因此构建了基于透视变换的误差补偿模型,对运动末端位置进行精准修正。
1 围棋图像处理 1.1 标准棋盘图像提取首先在棋盘的4个顶点设置定位标识,用于确定棋盘顶点的像素坐标,如图1(a)所示;然后分别在3个不同的尺度空间中对图像的轮廓进行检测,如图1(b)所示。检测结果中可能存在其他干扰轮廓,因此根据定位标识中轮廓层级关系对检测到的轮廓进行筛选,接着提取上述结果的中像素点并将其变换至原始尺度,得到原尺度下的一个像素点集合,对点集进行聚类并结合对应的数量关系,得到棋盘4个顶点的像素坐标,如图1(c)所示。最后,利用透视变换进行视角修正,得到分辨率统一的标准棋盘图像。

|
图 1 标准棋盘图像提取过程 Figure 1 Standard chessboard image extraction process |
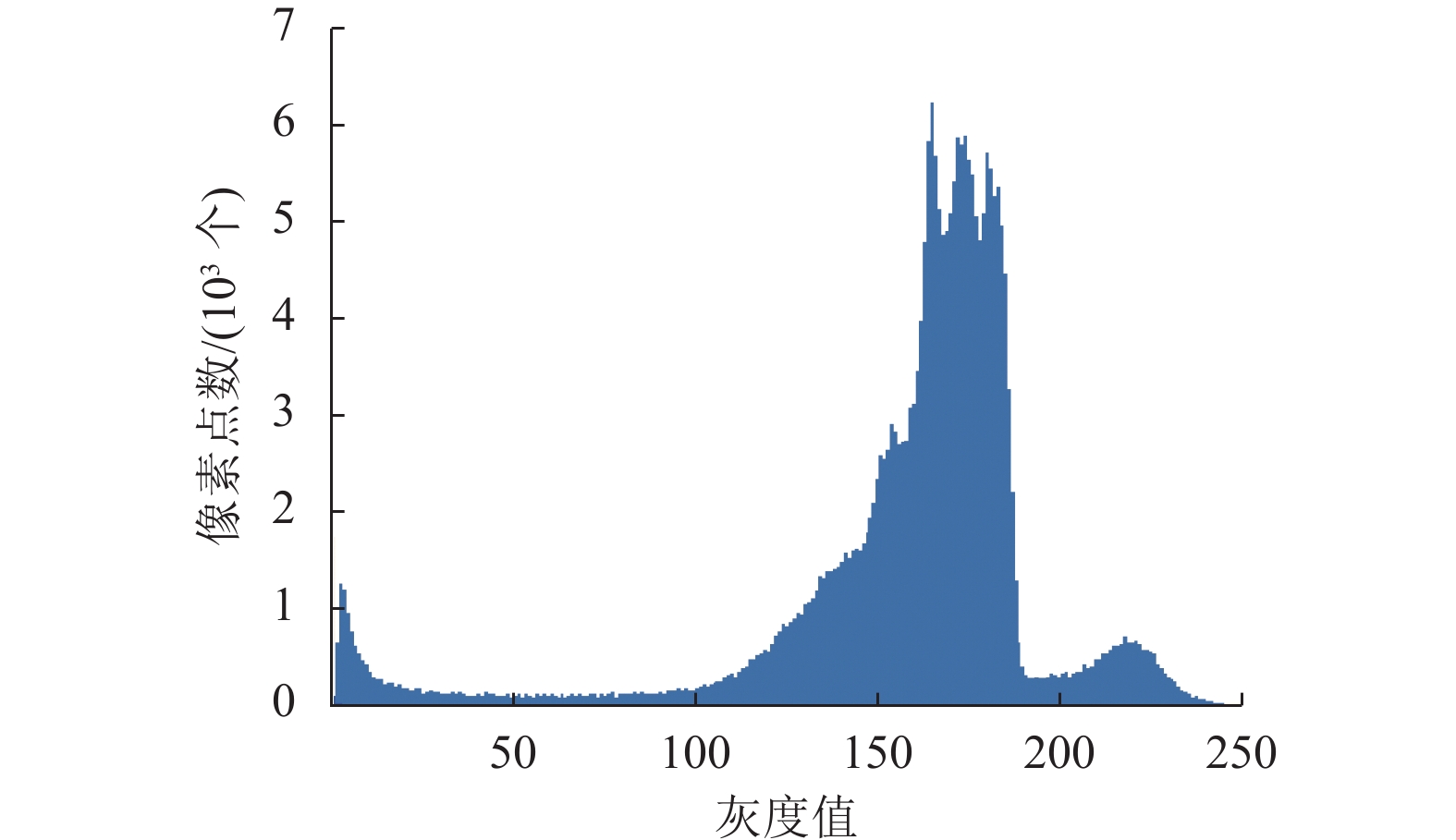
对棋子进行识别之前需要先将棋盘中的棋子与棋盘背景进行分割,但固定阈值的分割方法对光照变化比较敏感。为减少不同环境光对阈值选择造成的影响,采用针对围棋棋盘的自适应阈值分割方法进行处理。通过曲线拟合图像灰度直方图的像素变化,将两类主要像素之间的波谷作为最佳阈值分割点,如图2所示。应用此阈值进行阈值分割并获取棋子中心点的像素坐标,同时结合Shi-Tomasi角点检测法[13]获取的标准棋盘图像中交叉点的像素坐标,确定棋子在棋盘中的位置。
|
图 2 灰度直方图 Figure 2 Gray histogram |
考虑到在光照不均匀的情况下,棋盘中会出现反光区域,如图3(a)所示。对于该区域的棋子,很难找到合适的阈值进行阈值分割,因此需要对反光区域的棋子进行单独的检测。首先将棋盘中的反光区域作为ROI (Region Of Interest) 进行提取,对图像进行形态学处理得到反光区域的封闭区域,然后通过边缘检测得到ROI的轮廓,如图3(b)所示,并用矩形拟合目标区域,如图3(c)所示。最后利用支持向量机作为分类器、方向梯度直方图作为特征描述子训练棋子检测器,对反光区域中的棋盘交叉点上的目标进行检测,最终检测效果如图3(d)所示。训练样本源为反光区域中以棋盘线交叉点为中心截取的20×20像素区域,分为3类:无棋子、黑棋、白棋,共计1 200个样本。

|
图 3 光照区域棋子识别 Figure 3 Chess recognition in illumination region |
围棋机器人落子指引装置的运动执行机构由两个高精度数字舵机和激光指引器组成。为了控制激光光点运动到棋盘中的指定位置,根据运动装置的实际物理结构建立对应的机械臂模型,共有3个自由度,包括由两个数字舵机所组成的旋转关节和由激光指引器光路所模拟的伸缩关节。考虑到运动末端为一光点,在本模型中只考虑末端的位置变化,不考虑末端姿态的变化。由各连杆的结构参数和各关节的运动参数得到模型的D-H参数表如表1所示,每一组参数确定了两个关节坐标系之间的变换关系,θ表示绕z轴转动的角度,d表示沿z轴方向平移的距离,a表示沿x轴方向平移的距离,α表示绕x轴转动的角度。关节变量θ2、θ3分别表示绕关节2与关节3的坐标系z轴旋转的角度,d4则表示沿关节4坐标系z轴平移的距离,即本文模型中光路的长度。
| 表 1 D-H参数 Table 1 D-H parameter |
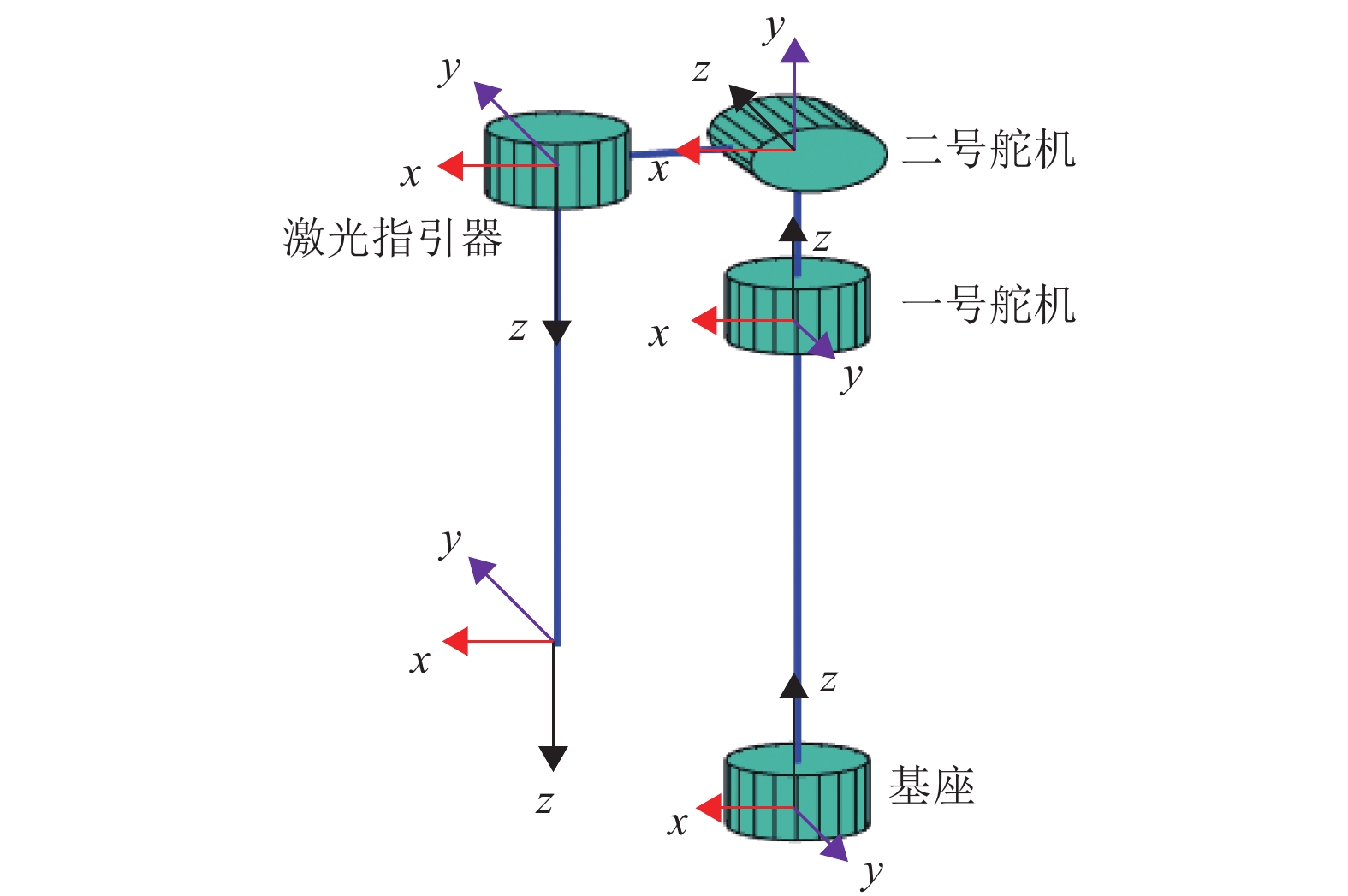
基于表1所示的D-H参数,并以基座中心作为固定坐标系原点,构建机械臂的模型如图4所示。
|
图 4 模型连杆坐标系 Figure 4 Model linkage coordinate system |
|
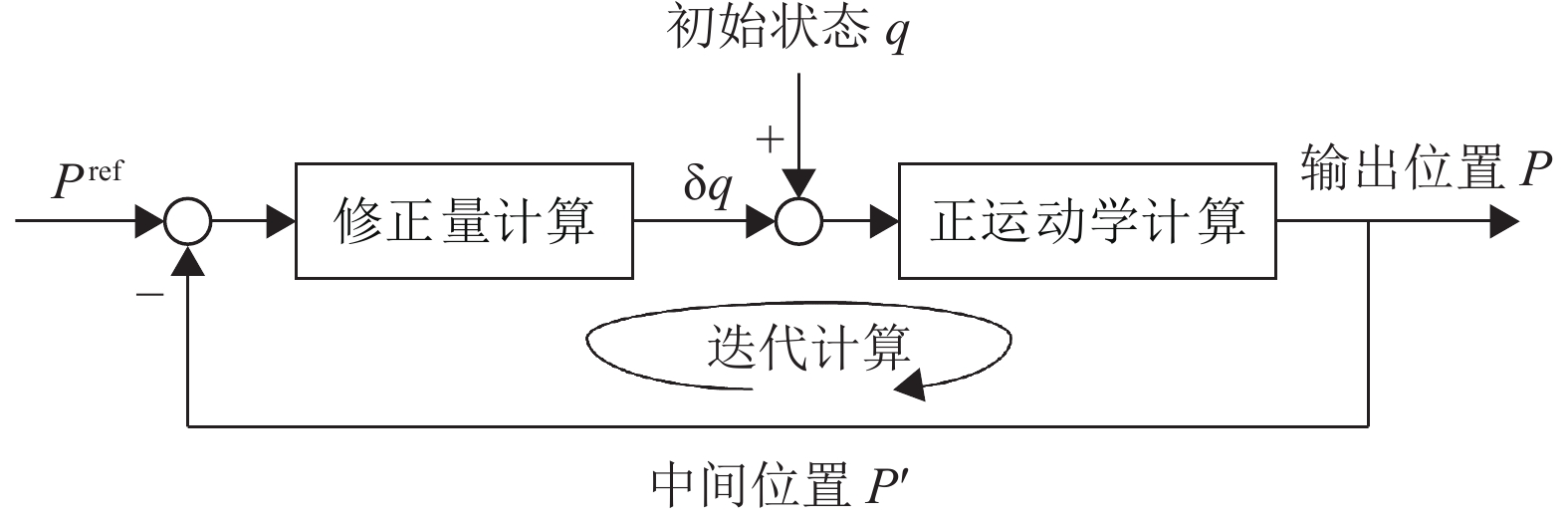
图 5 数值解计算过程 Figure 5 Calculation process of numerical solution |
关节变量θ2、θ3与d4之间的几何关系如式(1)所示,其中光源高度为h。因此只需计算两个旋转关节的角度修正量,即可确定某时刻下运动末端相对于固定坐标系的位置坐标。
| $ d_{4} = {{h}} \times \sqrt {{{\left( {\frac{{{\rm{sin}}\;{\theta _3}}}{{{\rm{sin}}\;{\theta _{\rm{2}}} \times {\rm{cos}}\;{\theta _{\rm{3}}}}}} \right) }^{\rm{2}}}{\rm{ + 1}}} $ | (1) |
δq的计算如式(2)所示,式中J为雅克比矩阵,反映运动末端速度和各个关节速度之间的关系,δp、δω分别表示运动末端微小位移量与微小转动量。
| $ \text{δ} {{q = }}\lambda {{\boldsymbol{J}}^{{\rm{ - 1}}}}\left[ {\begin{array}{*{20}{c}} {\text{δ} {{p}}}\\ {\text{δ}{{w}}} \end{array}} \right]{\rm{(}}\lambda \in ({\rm{0}},{\rm{1}}]) $ | (2) |
由表1可求得各关节间的齐次变换矩阵:1T2,2T3,3T4,4T5。根据正运动学可将坐标系原点到模型末端的齐次变换矩阵表示为
| $ \begin{split} {}^1{\boldsymbol{T}}_5=&{}^1{\boldsymbol{T}}_2 \times {}^2{\boldsymbol{T}}_3 \times {}^3{\boldsymbol{T}}_4 \times {}^4{\boldsymbol{T}}_5 =\\& \left[\begin{array}{cccc} C \theta_2 C \theta_3 & 0 & C \theta_2 S \theta_3 & d C \theta_2 S \theta_3+2 C \theta_2 C \theta_3 \\ S \theta_2 C \theta_3 & -1 & -S \theta_2 S \theta_3 & -2 d S \theta_2 C \theta_3 \\ S \theta_3 & 0 & -1 & 48-d+2 S \theta_3 \\ 0 & 0 & 0 & 1 \end{array}\right] \end{split} $ | (3) |
式中:Sθn=sin θn, Cθn=cos θn。
计算修正之后的关节变量,并将其代入式(3),计算出模型末端运动的中间位置P',计算P'与设定目标位置之间的差值,基于Matlab进行迭代运算,直到差值小于设定的阈值。此时输出的末端位置P即可作为末端的求解位置,同时也可得到此时的关节变量 (θ2,θ3) 。
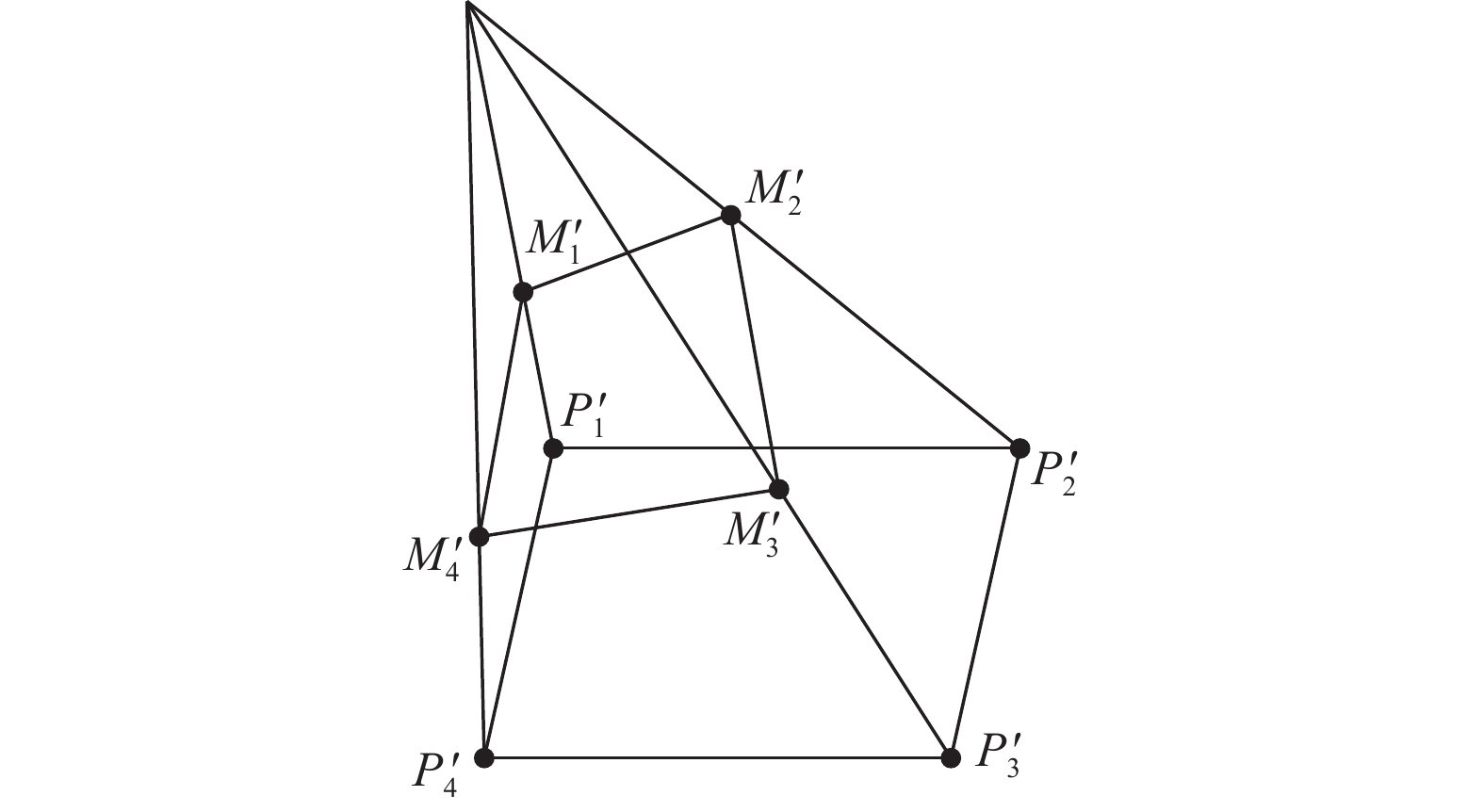
2.3 末端位置误差补偿如将仿真计算结果直接应用于舵机控制,实际机械结构与仿真模型之间的误差,会导致末端位置偏离目标位置,而且不同位置的偏差是非线性变化的,为此本文提出一种基于透视变换的误差补偿方法,即利用透视变换将仿真角度值映射至目标角度值。透视变换是一种中心投影的射影变换,在图像变换中有广泛应用[14],可以表示两个平面中点的非线性映射关系[15]。要确定透视变换矩阵,需在两个平面上确定对应的4组点(Mi'/Pi') ,如图6所示。
|
图 6 投影空间中透视变换关系 Figure 6 Perspective transformation relations in projection space |
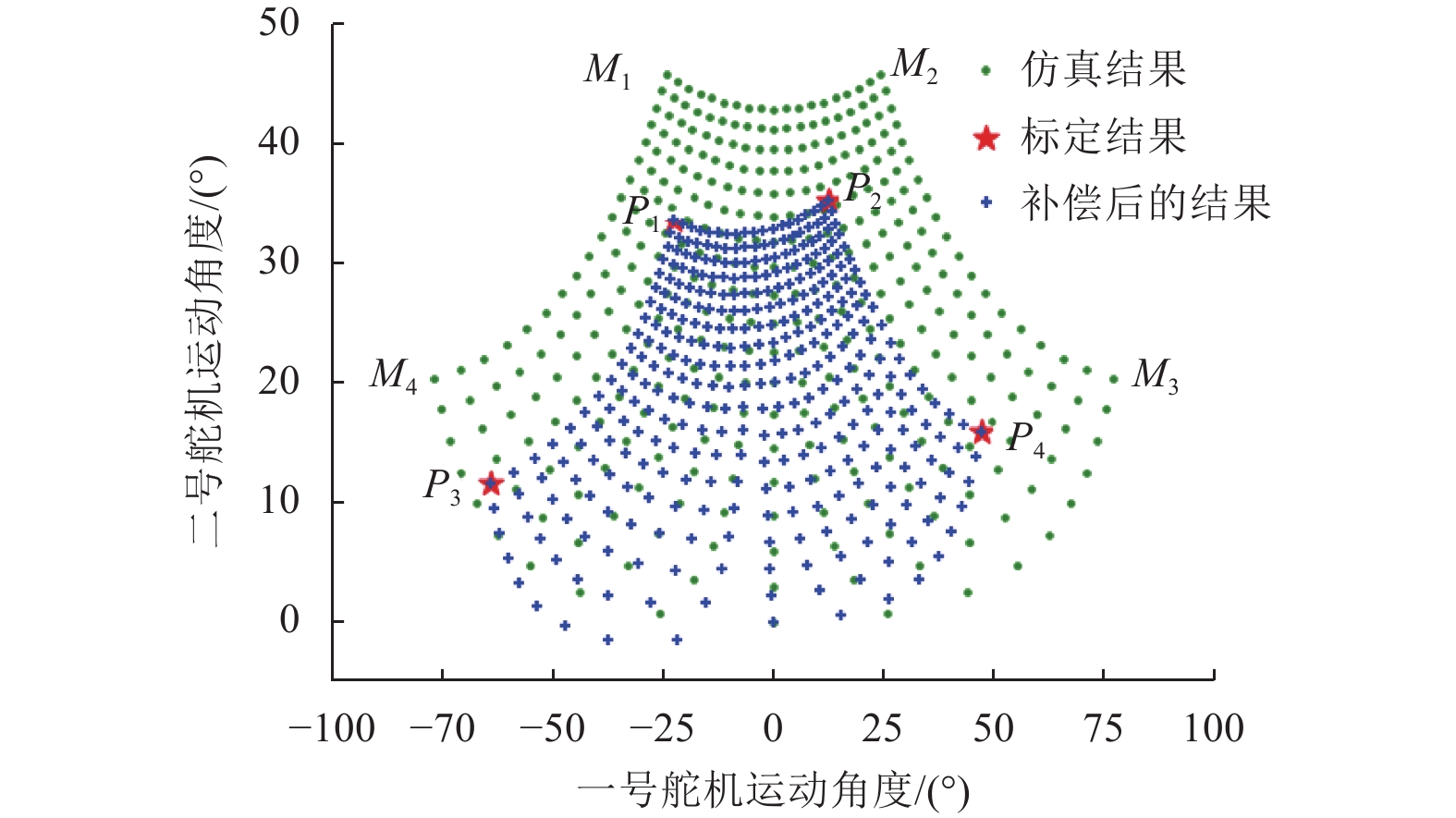
将仿真计算结果绘制到直角坐标系中,如图7中的圆点所示。定义仿真计算结果中的顶点坐标为Mi=(ui,vi) ,这4组角度值的正运动学计算结果对应于围棋棋盘格4个顶点的位置坐标。通过人工标定可以得到光点在实际棋盘格4个顶点位置对应的舵机角度值点Pi=(xi,yi) 。为了得到Mi到Pi之间的映射关系,定义投影空间中的点Mi'=(ui,vi,1),Pi'=(xi',yi',zi') 。将原始平面中的点Mi'向目标平面中投影得到Pi',根据透视变换的关系有
|
图 7 仿真角度值与补偿角度值 Figure 7 Simulation angle value and compensation angle value |
| $ \left[ {\begin{array}{*{20}{c}} {{{x}_{i}}{'}}\\ {{{y}_{i}}{'}}\\ {{{z}_{i}}{'}} \end{array}} \right]{ = {\boldsymbol{A}}}\left[ {\begin{array}{*{20}{c}} {{{u}_{i}}}\\ {{{v}_{i}}}\\ {1} \end{array}} \right],\;\;\left({\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{{a}_{{\rm{11}}}}}&{{{a}_{{\rm{12}}}}}&{{{a}_{{13}}}}\\ {{{a}_{{\rm{21}}}}}&{{{a}_{{\rm{22}}}}}&{{{a}_{{23}}}}\\ {{{a}_{{\rm{31}}}}}&{{{a}_{{\rm{32}}}}}&{{{a}_{{33}}}} \end{array}} \right]\right) $ | (4) |
式中:A为透视变换矩阵。
将(xi', yi') 转换到(ui, vi) 所在的平面,得到Pi,转换过程为
| $ {x}_{i}=\frac{{x}_{i}'}{{z}_{i}'}=\frac{{a}_{{11}}{{u}}_{{i}}+{a}_{{12}}{{v}}_{{i}}+{{a}}_{{13}}}{{{k}}_{{31}}{{u}}_{{i}}+{{k}}_{{32}}{{v}}_{{i}}+{{a}}_{{33}}} $ | (5) |
| $ {y}_{i}=\frac{{y}_{i}'}{{z}_{i}'}=\frac{{{a}}_{{21}}{{u}}_{{i}}+{{a}}_{{22}}{{v}}_{{i}}+{{a}}_{{23}}}{{{a}}_{{31}}{{u}}_{{i}}+{{a}}_{{32}}{{v}}_{{i}}+{{a}}_{{33}}} $ | (6) |
式中:a33=1, a11,a12,··· ,a32为待确定的参数。将4组原平面中的Mi和已知的Pi分别代入式(5)、(6)即可求得a11, a12, ···, a32,从而可确定仿真角度值与实际角度值之间的映射关系,由此可根据仿真结果映射得到目标角度值,如图7中星形标记点所示,进而可以确定补偿之后的围棋落子位置。
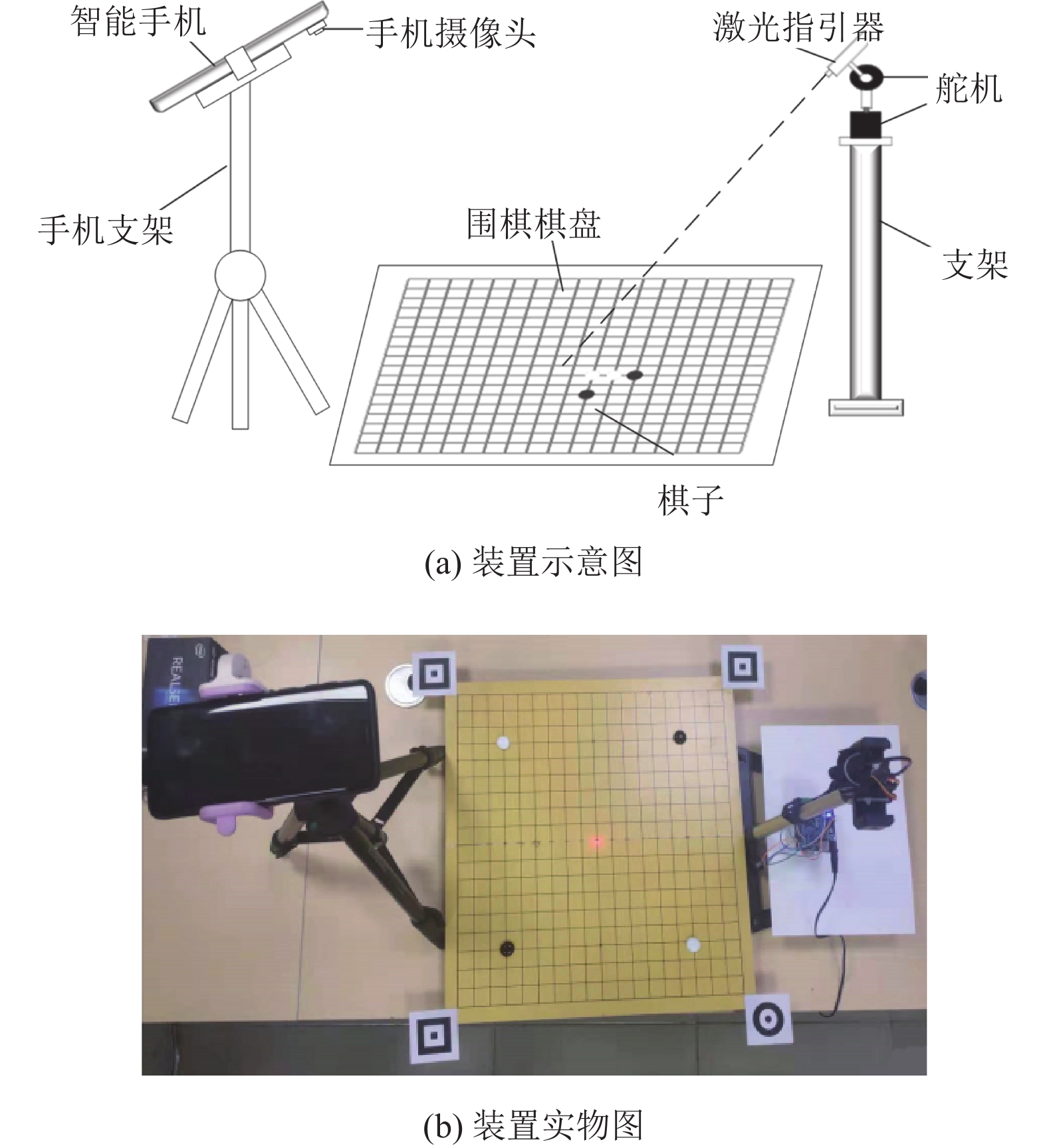
3 实验结果与分析 3.1 围棋落子指引装置所设计的围棋落子指引装置示意图与实物图如图8所示。围棋棋盘图像通过手机后置摄像头获取,分辨率为1920×1080,手机端图像处理模块基于Python3.7(OpenCV4.0) 开发;运动控制平台由Arduino微处理器搭配舵机驱动板以及通信模块组成。实验光照条件为室内正常日光灯光照。
|
图 8 围棋落子指引实验装置 Figure 8 The experiment device of Go drop guidance |
基于图8所示的围棋落子指引实验装置,分别对标准围棋棋盘图像特征提取与棋子识别效果进行测试。在实验中共完成210枚围棋棋子的落子,并在不同的光照条件下进行对比实验:(1) 光照均匀,如图9(a)所示;(2) 光照不均匀,表现为棋盘中央存在反光区域,大约覆盖90枚棋子,如图9(b)所示。其中标准棋盘图像提取的结果表现出了良好的稳定性,在所处理的约500张原始图片中,均成功获取到了标准棋盘图像。

|
图 9 不同光照条件下的棋盘 Figure 9 Chessboard under different light conditions |
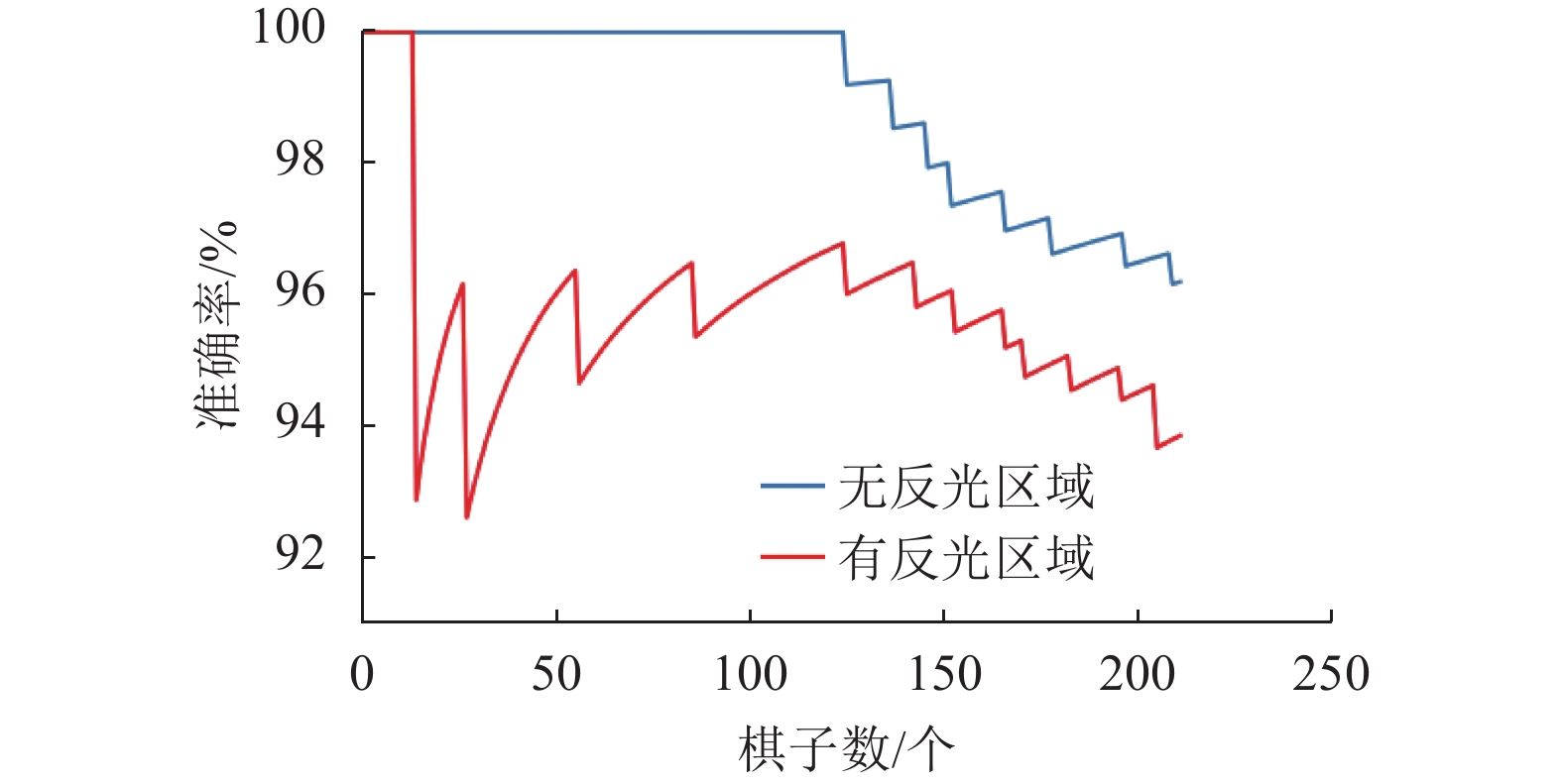
棋子识别的实验结果如图10所示,实验(1)在落第124枚棋子的时候,漏检的情况开始逐渐增多,主要原因是当棋子数目过多时,棋盘像素与棋子像素之间的阈值分割点不再明显,难以找到最佳分割阈值,即便如此,在实验(1)的条件下,棋子识别准确率仍维持在96%以上。实验(2)在落子14枚之后,开始在反光区域中出现棋子漏检的情况,导致棋子识别准确率下降。虽然在后续的落子过程中陆续出现了漏检以及误检的情况,但从总体实验结果来看,棋子检测器对棋子识别的准确率保持在92%以上。此外,若不采用棋子检测器检测,在实验(2)的条件下进行了测试,在棋盘为空的状态下便误检出了多枚棋子。这进一步证明了棋子检测器在不均匀光照条件下的有效性。
|
图 10 棋子识别准确率变化图 Figure 10 Change chart of chess recognition accuracy |
表2将3种现有的围棋棋子识别方法与本文方法进行对比,在均匀光照条件下,本文方法应用于围棋棋子识别的平均准确率为98.96%;不均匀光照条件下平均准确率为95.70%。均匀光照下,本文方法在开局与中盘阶段具有较高的稳定性,根据表2的结果可进一步发现平均准确率也优于其他方法,同时本文方法在光照不均匀的条件下,也保持了较高的识别准确率。
| 表 2 不同棋子识别方法的准确率 Table 2 Accuracy of different methods for chess recognition |
本文通过定时拍照采集图片,并对每张图片进行实时处理,表3对比了不同方法在围棋识别过程中的时间消耗,文献[6]通过神经网络提取棋子特征,从而进行棋子识别,文献[7]通过多次图像间的运算获取棋子位置,与该两种方法相比,本文在消耗较少时间的基础上获得了较高的识别准确率,可以确保指引装置运行过程的快速响应。
| 表 3 棋子识别过程的时间统计 Table 3 Time statistics of chess piece recognition process |
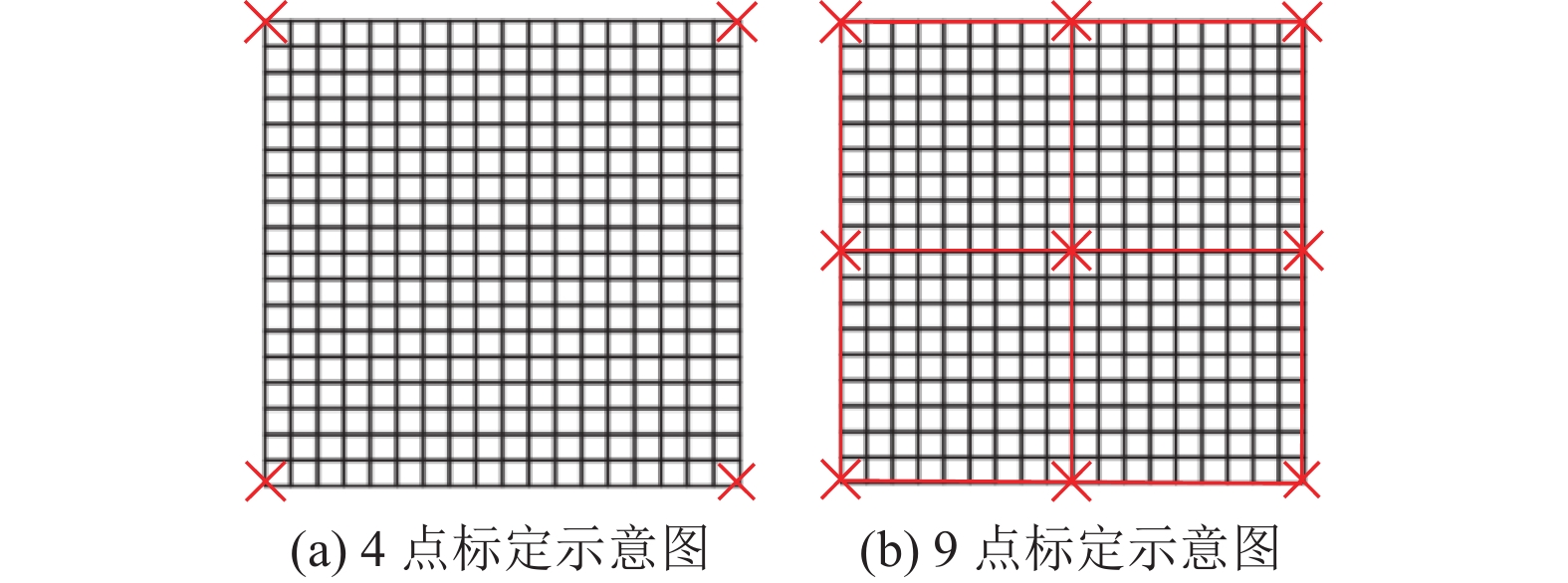
本文选择不同数目的标定点进行两组对比实验,如图11所示。图11(a)选取了4个标定点,图11(b)选取9个标定点,并对图中划分的4个区域分别进行位置误差补偿。通过设置运动程序控制舵机运动,让光点从棋盘右下运动到左上方,依次到达361个棋盘交叉点。以交叉点为中心,1/3倍棋盘格长度与宽度的矩形区域为对应交叉点周围的有效区域,在该区域中的光点记录为有效点。实验结果如表4所示。通过引入更多的标定点,可以有效地提高位置误差补偿效果,从总体上减小因数字舵机角分辨率的限制所带来的标定误差。
|
图 11 标定点选择 Figure 11 Selection of calibration points |
| 表 4 激光指引准确率 Table 4 Accuracy of laser guidance |
当设置9个标定点时,光点在棋盘交叉点位置实现了准确指引,对部分取样点的指引效果进行拼接,结果如图12 所示。

|
图 12 部分指引效果 Figure 12 Partial guidance effect |
本装置作为围棋机器人的一种辅助装置,是为后续围棋机器人的教学设计做准备,结合图像处理技术与机器人运动学完成了装置的设计。通过多尺度检测方法提取标准棋盘图像,并应用棋子检测器对反光区域的棋子单独进行检测,有效提高了检测结果的稳定性与准确性。在运动控制部分,对实际结构进行了运动学建模与仿真计算,并为仿真计算的结果建立了一个误差模型用于实际位置的修正,使得该指引装置能够有效运行。在进行实验的过程中,还发现了一些其他影响系统稳定性的因素,例如:当给定光源不在棋盘的正上方时,棋子的周围会形成阴影,此因素会在一定程度上影响棋子识别的准确性;数字舵机自身的机械间隙也会对实验结果造成一定的影响。接下来,将继续开展更深入的算法研究工作,如将基于深度学习的目标检测技术应用于图像处理,改进围棋落子指引装置的机械结构设计等,进一步提高装置运行的稳定性,并结合小型机械臂完成更加复杂的围棋教学与对弈任务。
| [1] |
张顺, 严宏志, 韩奉林, 等. 基于ARM和freeRTOS的围棋机器人控制器设计[J].
制造业自动化, 2018, 40(1): 28-32.
ZHAGN S, YAN H Z, HAN F L, et al. Design of go robot controller based on ARM and freeRTOS[J]. Manufacturing Automation, 2018, 40(1): 28-32. DOI: 10.3969/j.issn.1009-0134.2018.01.008. |
| [2] |
MATUSZEK C, MAYTON B, AIMI R, et al. Gambit: an autonomous chess-playing robotic system[C]//2011 IEEE International Conference on Robotics and Automation. Shanghai: IEEE, 2011: 4291-4297.
|
| [3] |
KOŁOSOWSKI P, WOLNIAKOWSKI A, MIATLIUK K. Collaborative robot system for playing chess[C]//2020 International Conference Mechatronic Systems and Materials (MSM) . Bialytok, Poland: IEEE, 2020.
|
| [4] |
WANG H B, SHI M. Recognizing chessboard and positioning checkboard in Chinese chess game System[C]//2014 Fourth International Conference on Communication Systems and Network Technologies (CSNT 2014) . Bhopal, India: IEEE, 2014: 1182-1186.
|
| [5] |
SONG J. LI S S. A robust algorithm for Go image recognition in Go game[C]//2018 IEEE 4th International Conference on Computer and Communications (ICCC) . Chengdu: IEEE, 2018: 1397-1401.
|
| [6] |
SONG J, YANG M Z. A calibration method for the vision system of go-robot[C]//2019 6th International Conference on Systems and Informatics (ICSAI) . Shanghai: IEEE, 2019: 1157-1162.
|
| [7] |
王亚杰, 张云博, 吴燕燕, 等. 不均匀光照下的通用棋子定位方法[J].
计算机应用, 2020, 40(12): 3490-3498.
WANG Y J, ZHANG Y B, WU Y Y, et al. General chess piece positioning method under uneven illumination[J]. Journal of Computer Applications, 2020, 40(12): 3490-3498. DOI: 10.11772/j.issn.1001-9081.2020060892. |
| [8] |
史晓佳, 张福民, 曲兴华, 等. KUKA工业机器人位姿测量与在线误差补偿[J].
机械工程学报, 2017, 53(8): 1-7.
SHI X J, ZHANG F M, QU X H, et al. Position and attitude measurement and online errors compensation for KUKA industrial robots[J]. Journal of Mechanical Engineering, 2017, 53(8): 1-7. DOI: 10.3901/JME.2017.08.001. |
| [9] |
王龙飞, 李旭, 张丽艳, 等. 工业机器人定位误差规律分析及基于ELM算法的精度补偿研究[J].
机器人, 2018, 40(6): 843-851.
WANG L F, LI X, ZHANG L Y, et al. Analysis of the positioning error of industrial robots and accuracy compensation based on ELM algorithm[J]. Robot, 2018, 40(6): 843-851. DOI: 10.13973/j.cnki.robot.170536. |
| [10] |
杨文韬, 詹军, 佘勇, 等. 工业机器人绝对定位精度优化方法综述[J].
表面工程与再制造, 2019, 19(2): 28-32.
DOI: 10.3969/j.issn.1672-3732.2019.02.012. |
| [11] |
周炜, 廖文和, 田威. 基于空间插值的工业机器人精度补偿方法理论与试验[J].
机械工程学报, 2013, 49(3): 42-48.
ZHOU W, LIAO W H, TIAN W. Theory and experiment of industrial robot accuracy compensation method based on spatial interpolation[J]. Journal of Mechanical Engineering, 2013, 49(3): 42-48. DOI: 10.3901/JME.2013.03.042. |
| [12] |
周炜, 廖文和, 田威, 等. 基于粒子群优化神经网络的机器人精度补偿方法研究[J].
中国机械工程, 2013, 24(2): 174-179.
ZHOU W, LIAO W H, TIAN W, et al. Method of industrial robot accuracy compensation based on particle swarm optimization neural network[J]. China Mechanical Engineering, 2013, 24(2): 174-179. DOI: 10.3969/j.issn.1004-132X.2013.02.007. |
| [13] |
ANGELIDIS A, VOSNIAKOS G C. Prediction and compensation of relative position error along industrial robot end-effector paths[J].
International Journal of Precision Engineering and Manufacturing, 2014, 15: 63-73.
DOI: 10.1007/s12541-013-0306-5. |
| [14] |
SHI J B, TOMASI C. Good features to track[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Seattle, WA, USA: IEEE, 1994: 593-600.
|
| [15] |
李鹏俊, 李建增, 宋瑶, 等. 基于仿真的无人机遥感图像拼接误差分析[J].
计算机应用, 2015, 35(4): 1116-1119.
LI P J, LI J Z, SONG Y, et al. Error analysis of unmanned aerial vehicle remote sensing images stitching based on simulation[J]. Journal of Computer Applications, 2015, 35(4): 1116-1119. DOI: 10.11772/j.issn.1001-9081.2015.04.1116. |
 2023, Vol. 40
2023, Vol. 40

