近年来,由于核磁共振成像(Magnetic Resonance Imaging, MRI)独特的软组织分辨能力,MRI介入下经皮穿刺手术变得越来越流行。与计算机化X线体层照相术 (Computerized Tomography, CT) 相比,MRI有更好的软组织对比效果,且无电离辐射[1],这使得它非常适合神经外科手术。
核磁共振引导的机器人系统已经得到了广泛的研究,并已经被证实可以用于前列腺活检[2-3] 、乳腺活检[4-5]、胸腹部干预[6-7]和大脑穿刺[8-9]等。然而,在MRI约束空间中的穿刺行为和强磁场环境仍然对进行穿刺机器人辅助手术提出了准确性和安全性的挑战。
为将医生工作与核磁共振空间分离,Patel 协同其小组成员使用超声波电机、机械手及其电子器械搭建了一个简单的机器人辅助系统,将消融器放进脑中进行MRI引导下的消融实验,该机器人系统的平均平移和旋转误差精度为(1.39 ± 0.64) mm和(1.27 ± 0.56)°[8]。
同时,为了应对核磁共振室的强磁场问题,如何拟定传动系统也是实现MRI设备兼容的一个重要问题。Johns Hopkins University实验室、Automation and Interventional Medicine实验室都曾经使用超声波电机来设计MRI兼容手术机器人,但稳定性和精度并不太理想[10-12],而且基于超声波电机的机器人,其信噪比(Signal Noise Ratio) 相对较高,高于10%。因此,Franco等[13]开发了一种没有任何金属材料的气动驱动机器人,其信噪比始终低于5%。后续还有很多学者开发了气动驱动器或液压驱动器。Dong等[14]设计了一款三缸液压马达,并使用该马达设计了液压驱动的手术机器人,同时结合了一种新型的磁共振无线跟踪技术,使得它能够在适当的磁共振跟踪序列下提供实时连续的机器人仪器三维定位[9]。Farimani等[15]提出了一种气动步进执行器,该执行器可以代替超声波电机作为磁共振兼容机器人的执行器。但这些驱动器的尺寸太大,无法直接应用于内径核磁共振引导活检。Frishman等[16]开发了一种带有力反馈的液压驱动MRI内孔引导活检装置,可以通过观察反馈力来区分针是否穿透膜。然而,该设备在手术过程中不能移动,它只有一个自由度(Degree of Freedom, DOF)。
因此,基于流体驱动的核磁共振兼容设备有重要的研究价值,本文重点研究了一种基于连通器原理的液压驱动穿刺手术机器人的动力学模型,以及其
MRI设备兼容穿刺手术机器人整体方案设计如图1所示。其具有的二自由度远端运动中心结构,如图2所示,可以在仅造成微小创口的情况下在人体内进行较大范围的运动。同时,本文采用了非金属材质进行搭建并采用液压的驱动方式,使该机器人可以兼容MRI设备。其主体框架主要由玻璃纤维、塑料轴承以及基于光敏树脂的3D打印件构成,并由陶瓷制成的螺丝、螺母作为紧固。此外,采用了光纤以及亚克力材质的直线光栅尺制成编码器,作为该机器人的位置反馈系统。

|
图 1 机器人整体方案设计图 Figure 1 The overview of the MRI-compatible hydraulic drive needle insertion robot |
|
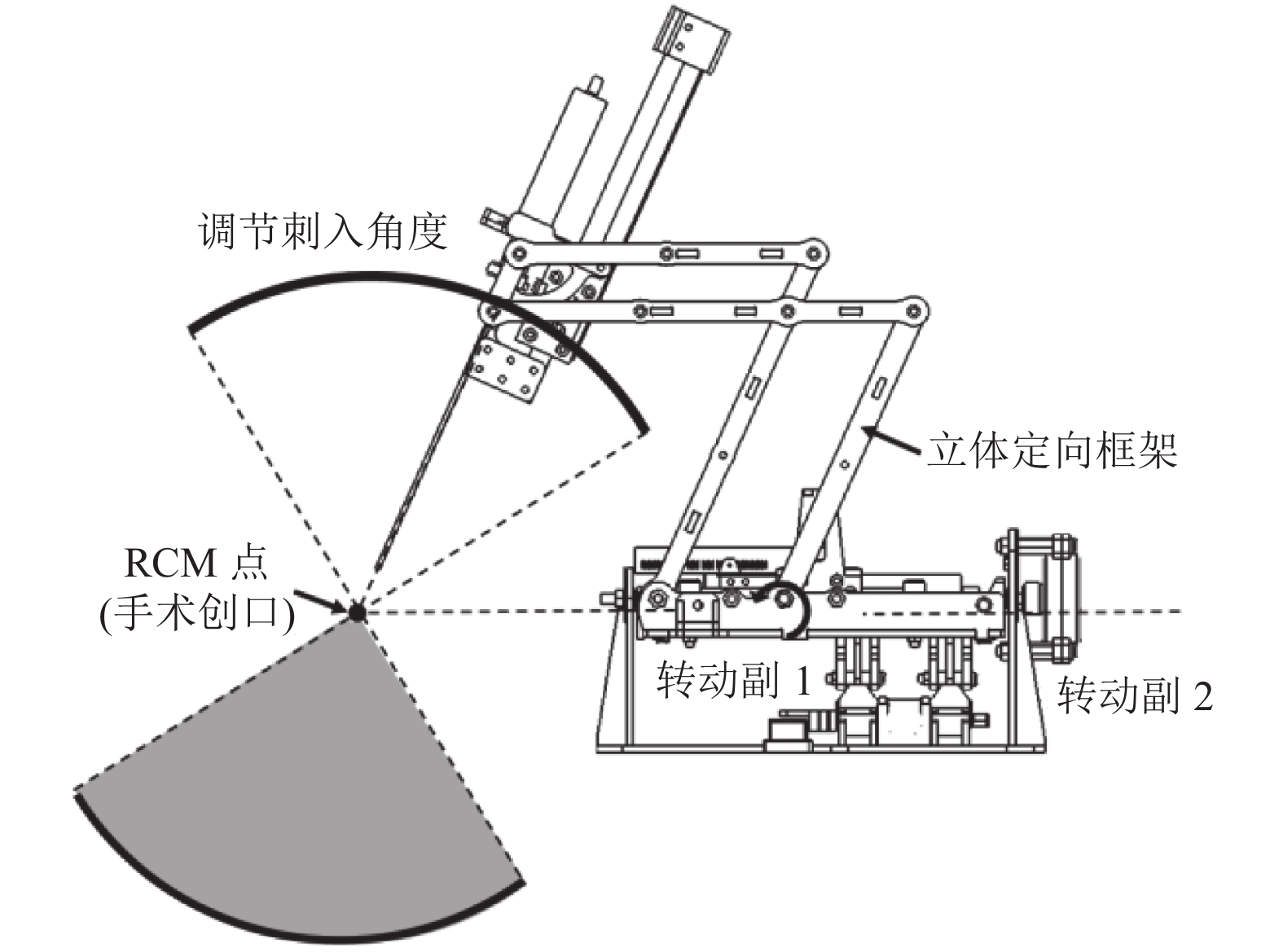
图 2 远端运动中心工作原理 Figure 2 Working principle of the RCM point and the stereotactic frame |
此六自由度机器人可以被分为4个独立的功能模块:
(1) 液压驱动模块:由位于MRI设备室外的滚珠丝杆驱动模组作为执行器,利用液压的方式进行机器人本体的控制;
(2) 穿刺点定位模块:用于将穿刺针定位在目标位置,其可以沿着坐标轴的x轴、y轴、z轴运动;
(3) 穿刺针位姿调整模块:用于调整穿刺针的位姿,以通过头颅的小孔(通常由外科医生在将患者置于扫描仪之前钻出)对患者实施穿刺手术;
(4) 穿刺针介入模块:用于调整探针刺入患者脑内的深度。
2 机器人的数学模型 2.1 机器人系统的正逆运动学模型图3 描述了机器人每个轴的名称、位置、参考坐标系,以及相应的参数。将机器人的位姿矢量定义为:L =

|
图 3 机器人运动轴参数的详细说明 Figure 3 Detailed illustration of the axis of parameters of the robot |
机器人运动学问题包括机器人正运动学和机器人逆运动学,正运动学问题为给定机器人各关节变量,求解机器人末端的位置姿态;逆运动学问题为已知机器人末端的位置姿态,求解该位姿对应的关节变量。
根据上文的描述以及机器人结构,容易推得机器人的正运动学表达式为
| $ \left\{\begin{split}&\left[ \begin{array}{c}{x}\\ {y}\\ {z}\end{array} \right]=\left[ \begin{array}{cccc}\text{1}& \text{0}& \text{0}& \dfrac{e}{{l}_{2}}\\ \text{0}& \text{1}& \text{0}& \dfrac{d}{{l}_{1}}\\ \text{0}& \text{0}& \text{1}& -\text{cos}\left(\text{arc}\text{sin}\left(\dfrac{{d}}{{{l}}_{{1}}}\right) \right) \text{cos}\left(\text{arc}\text{sin}\left(\dfrac{{e}}{{{l}}_{{2}}}\right) \right) \end{array}\right]\times\\ &\qquad\;\;\; \left[\begin{array}{c}{a}\\{b}\\ {c}\\ {f}\end{array}\right]\text+\left[\begin{array}{c}{x}_{\text{0}}\\ {y}_{\text{0}}\\ {z}_{\text{0}}\end{array}\right]\\ &{\textit{θ}}\text=\text{a}\text{r}\text{c}\text{sin}\left(\dfrac{{d}}{{{l}}_{\text{1}}}\right) \\ &{\textit{φ}}\text=\text{a}\text{r}\text{c}\text{sin}\left(\dfrac{{e}}{{l}_{\text{2}}}\right) \end{split}\right. $ | (1) |
将机器人的运动分为2个阶段:第一个阶段为机器人定位阶段,该阶段机器人的f 为0,不控制穿刺针的刺入深度,仅将远端控制中心(Remote Center of Motion, RCM)点定位到人体颅骨的某一位置,其逆运动学表达式为
| $ \left[\begin{array}{c}a\\ b\\ c\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right] \left[\begin{array}{c}x\\ y\\ {{z}}\end{array}\right]-\left[\begin{array}{c}{x}_{0}\\ {y}_{0}\\ {{z}}_{0}\end{array}\right] $ | (2) |
第二个阶段为穿刺针的刺入阶段,此时a, b, c均为0,表示机器人的RCM点不移动,仅通过穿刺针刺入深度和刺入角度的调节来控制针头末端的位置,其逆运动学表达式为
| $\left\{\begin{split}d=&\mathrm{sin}\;\theta \times (x-{x}_{0}) +\mathrm{sin}\;\varphi \times (y-{y}_{0}) -\text{c}\text{o}\text{s}\;\theta \text{c}\text{o}\text{s}\;\varphi \times \\& ({\textit{z}}-{{\textit{z}}}_{0}) \\ e=&{l}_{1} \mathrm{sin}\;\theta \\ f=&{l}_{2} \mathrm{sin}\;\varphi \end{split}\right. $ | (3) |
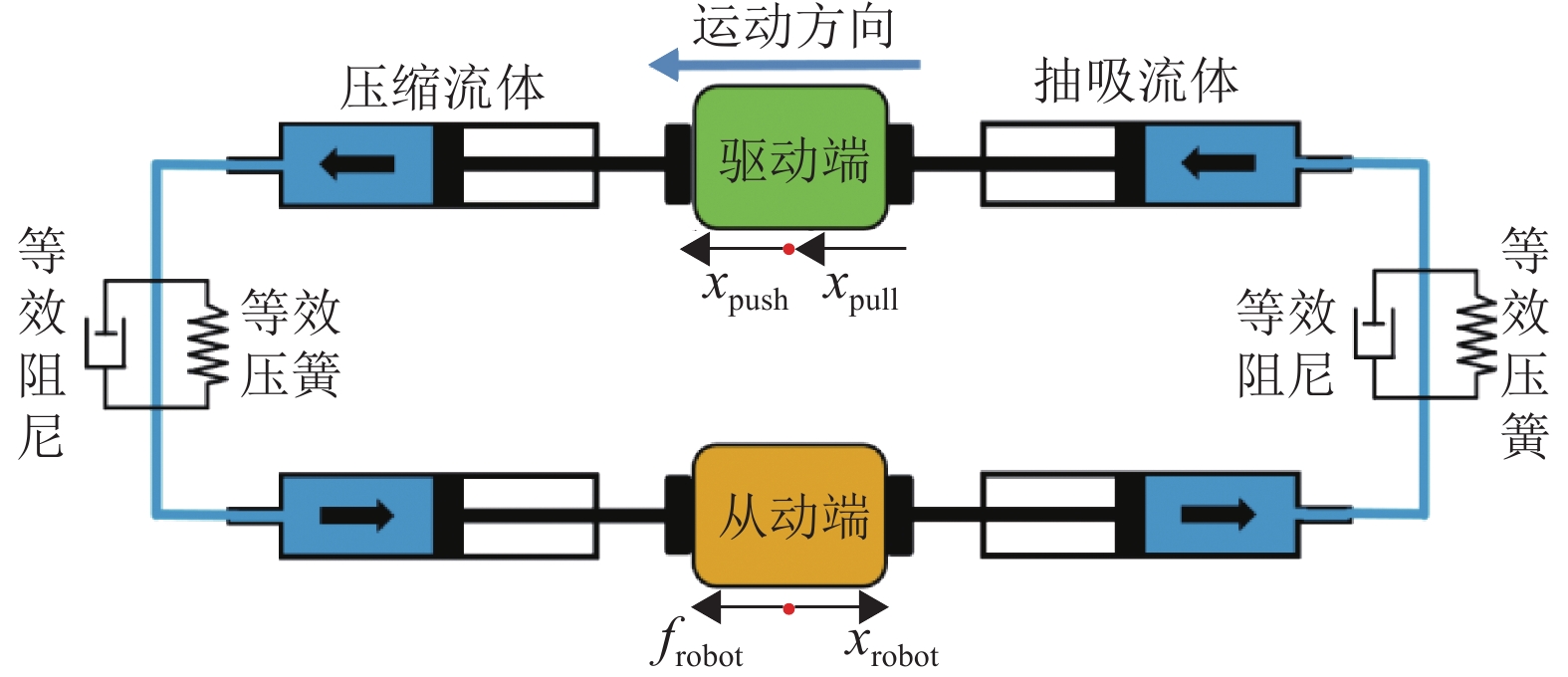
首先规定,在这一由基于活塞−缸体的液压连通器构成的液压驱动系统中,位于核磁共振室外的滚珠丝杆驱动模组的丝杆滑块,称为机器人驱动端;位于机器人上的导向轴承盒,称为机器人的从动端,如图4所示。其次,系统的输入形式为驱动端速度。这是由于采用了滚珠丝杆系统作为驱动,选用了型号为CBX1204-100ZC的滚珠丝杆滑台导轨线性滑台,其行程为10 cm,螺距为4 mm。57HS09型号步进电机,扭矩为0.9 N·m,根据滚珠丝杆扭矩计算理论驱动力,如式(4)所示,其中
|
图 4 液压驱动系统等效模型 Figure 4 Equivalent model of hydraulic drive system |
| $ {F=}\frac{\text{2}\text{π}{\textit{×η×τ}}}{I}\text=\frac{\text{2}\text{π}\text{×0.95×900}}{\text{4}}\text{=1\;343} \;{\rm{{N}}} $ | (4) |
理论驱动力为1343 N,实际机器人系统质量为2.5 kg,则加速度可达537.2 m/s²。在本模型中可以认为若驱动端滑块的速度在1 m/s的范围内,则其被视为一个可以突变的量。因此在本模型中,不以驱动端的力作为系统输入,而是以驱动端速度作为系统输入。
将该液压驱动系统等效为弹簧−阻尼模型,其中
| $ {f}_{\text{robot}}\text=\left\{\begin{array}{c}{K}\left({x}_{\text{push}}-{x}_{\text{robot}}\right) {,}\; \;{\dot{x}}_{\text{robot}}\leqslant 0\\ {f}_{\text{slide}}\text{s}\text{g}\text{n}\left({\dot{x}}_{\text{robot}}\right) \text{,}\; \;{\dot{x}}_{\text{robot}} > 0\end{array}\right. $ | (5) |
式中:sgn为符号函数,
| $ \left({m}_{\text{liquid}}\text+{m}_{\text{robot}}\right) {\ddot{x}}_{\text{robot}} = {N}{K}(x-{x}_{\text{robot}}) -{N}{C}_{\text{liquid}}\left(\dot{x} - {\dot{x}}_{\text{robot}}\right) - \text{}{f}_{\text{robot}} $ | (6) |
式中:
对于机器人中部分机构,比如z轴在运动的过程中还要受重力的影响,因此,该模型并不是可以完全照搬在机器人的每个轴上,还需要针对具体的运动方向对式(4)进行微调整:
| $ \left\{\begin{array}{l}\left({m}_{x}\right) {\ddot{x}}_{{{\rm{r}}x}}={2}{K}\left({x}_{x}-{x}_{{{\rm{r}}x}}\right) -{{2}{C}}_{{l}}\left({\dot{x}}_{x}-{\dot{x}}_{{{\rm{r}}x}}\right) -{{f}}_{{{\rm{r}}x}}\\ \left({m}_{{y}}\right) {\ddot{x}}_{{{\rm{r}}y}}={4}{K}\left({x}_{{y}}-{x}_{{{\rm{r}}y}}\right) -{{4}{C}}_{{l}}\left({\dot{x}}_{{y}}-{\dot{x}}_{{{\rm{r}}y}}\right) -{{f}}_{{{\rm{r}}y}}\\ \left({m}_{{{\textit{z}}}}\right) {\ddot{x}}_{{{\rm{r}}{\textit{z}}}}={K}\left({x}_{{{\textit{z}}}}-{x}_{{{\rm{r}}{\textit{z}}}}\right) -{{C}}_{{l}}\left({\dot{x}}_{{{\textit{z}}}}-{\dot{x}}_{{{\rm{r}}{\textit{z}}}}\right) -{{f}}_{{{\rm{r}}{\textit{z}}}}-{m}_{{{\textit{z}}}}g\\ \left({m}_{{p}}\right) {\ddot{x}}_{{{\rm{r}}p}}={K}\left({x}_{{p}}-{x}_{{{\rm{r}}p}}\right) -{{C}}_{{l}}\left({\dot{x}}_{{p}}-{\dot{x}}_{{{\rm{r}}p}}\right) -{{f}}_{{{\rm{r}}p}}\\ \left({m}_{{r}}\right) {\ddot{x}}_{{{\rm{r}}r}}={2}{K}\left({x}_{{{{r}}}}-{x}_{{{\rm{r}}r}}\right) -{{2}{C}}_{{l}}\left({\dot{x}}_{{{{r}}}}-{\dot{x}}_{{{\rm{r}}r}}\right) -{{f}}_{{{\rm{r}}r}}\\ \left({m}_{{d}}\right) {\ddot{x}}_{{{\rm{r}}d}}={K}\left({x}_{{d}}-{x}_{{{\rm{r}}d}}\right) -{{C}}_{{l}}\left({\dot{x}}_{{d}}-{\dot{x}}_{{{\rm{r}}d}}\right) -{{f}}_{{{\rm{r}}d}}\end{array}\right. $ | (7) |
式中:
本文机器人系统采用的管路为聚氨酯管,其形变可以忽略不计,因此在后续的建模中不考虑管路因液压而膨胀的情况。
首先进行流体的弹性模量,即流体刚度K的推导,流体的弹性是由流体的可压缩性决定的,流体的压缩公式为
| $ {\textit{β}}=V\frac{{\Delta }{P}}{{\Delta }{V}}{=V}\frac{{\Delta }{F}}{{\Delta }{VS}} $ | (8) |
式中:
| $ {\Delta }{F}={(} {\textit{β}}\frac{{{S}}^{{2}}}{{V}}{) }{\Delta }{h}={K} \times {\Delta }{x} $ | (9) |
式中:
一种描述气、液混合流体的等效流体刚度K的公式为
| $ {K}{= {\textit{β}}}\frac{{{S}}^{{2}}}{{V}}= {\textit{β}}_{{0}}\left[\frac{{1}+\dfrac{{{V}}_{\rm{{air}}}}{{{V}}_{\rm{{liquid}}}}}{{1}+{\left(\dfrac{{p}}{{{p}}_{{0}}}\right) }^{\dfrac{{1}}{\textit{γ}}} \times \dfrac{{{V}}_{\rm{{air}}}}{{{V}}_{\rm{{liquid}}}} \times \dfrac{ {\textit{β}}_{{0}}}{{{\textit{γ}}\text{∙}p}}}\right]\dfrac{{{S}}^{{2}}}{{V}} $ | (10) |
式中:
其次进行流体的阻力系数C的推导。流体在管道中流动时会受到沿程阻力的影响,某段管道上流体产生的总的能量损失
| $ {h}_{f}\text={\sum } {h}_{{ \lambda }}+\sum {h}_{\textit{ξ} }$ | (11) |
| $ {h}_{{ \lambda }}{= \lambda }\frac{L}{{d}}\frac{{v}^{\text{2}}}{\text{2}{g}}\text{} $ | (12) |
式中:
| $ {h}_{\textit{ξ} }={\textit{ξ} }\frac{{{v}}^{{2}}}{{2}{g}} $ | (13) |
式中:
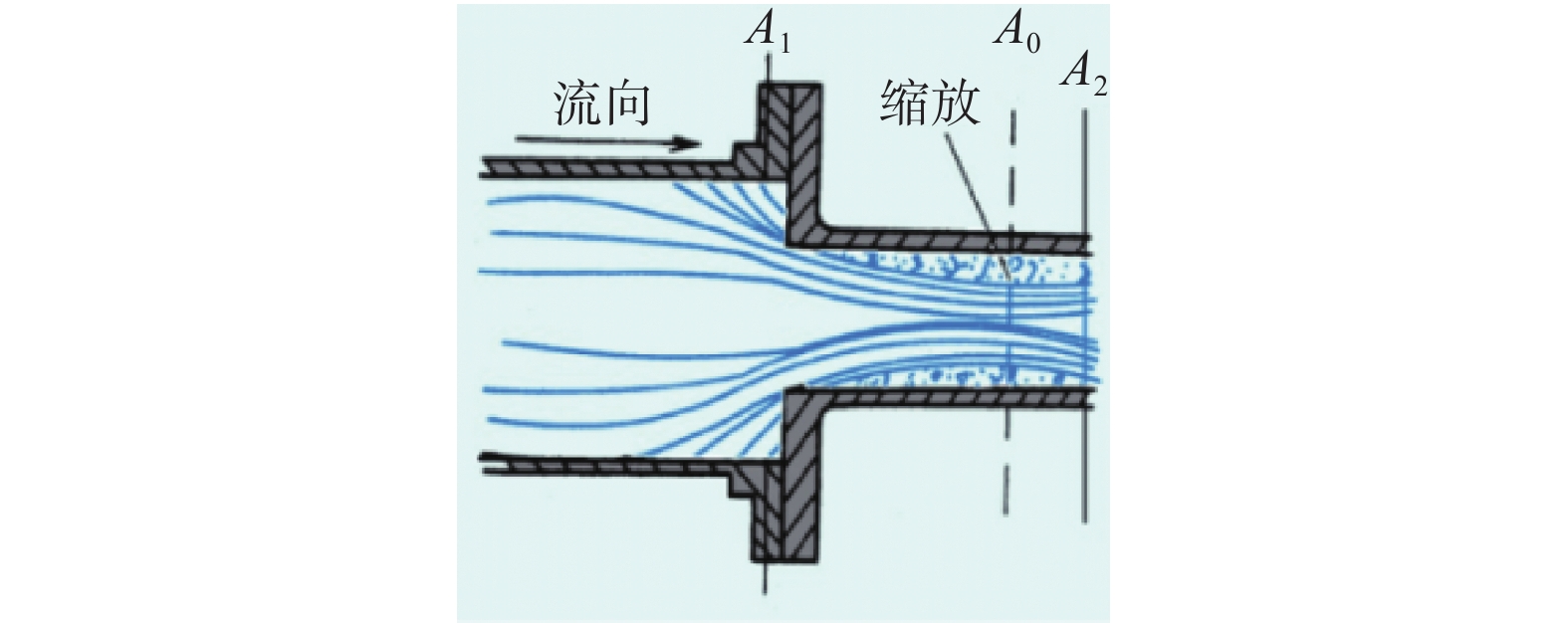
|
图 5 管路 Figure 5 Pipeline |
流体产生的总能量损失与对应摩擦力的关系可由黏性流体流动的伯努利方程得出。
| $ {\textit{z}}_{{1}}+\frac{{{p}}_{{1}}}{{\textit{ρ}}g}+{\textit{α}}_{{1}}\frac{{{V}_{{1}}}^{{2}}}{{2}{g}}={\textit{z}}_{{1}}+\frac{{{p}}_{{2}}}{{\textit{ρ}}g}+{\textit{α}}_{{2}}\frac{{{{V}}_{{2}}}^{{2}}}{{2}{g}}+{{h}}_{{f}} $ | (14) |
式中:由于该液压驱动系统两个截面相同,即
| $ {{h}}_{{f}}=\frac{{{p}}_{{1}}-{{p}}_{{2}}}{{\textit{ρ}}g} $ | (15) |
| $ {\Delta }{p}_{f}={p}_{1}-{p}_{2}={{\textit{ρ}}g}{h}_{f}=\frac{f}{S}{} $ | (16) |
因此液体流动沿程摩擦力f 可以表示为
| $ {f=S\text{∙} \Delta }{{p}}_{{f}}=\mathrm{S}\mathrm{\rho }\mathrm{g}{{h}}_{{f}} $ | (17) |
由于步进电机最大驱动速度受限在0.2 m/s内,其雷诺数Re < 2000,处于层流区。由尼古拉兹图,沿程阻力系数
| $ { \lambda =}\frac{{64}}{{Re}} $ | (18) |
由泊肃叶公式得
| $ {{h}}_{{f}}=\frac{{32}{{\textit{μ}}l}}{{{\textit{ρ}}g}{{d}}^{{2}}}{v} $ | (19) |
式中:
| $ {f=S{{\textit{ρ}}g}}{{h}}_{{f}}{=S{{\textit{ρ}}g}}\frac{{32}{{\textit{μ}}l}}{{{\textit{ρ}}g}{{d}}^{{2}}}{v=}{8}{\text{π}}{{\textit{μ}}lv} $ | (20) |
取水的黏度系数为
| $ {C}_{\text{liquid}}\text=\text{8}{\text{π}}{{\textit{μ}}l}\text{=8}\text{×}\text{3.1416}\text{×}\text{0.9} \cdot {\text{10}}^{-3}\text{×}\text{5=0.113\;1} $ | (21) |
根据式(4)描述的机器人动力学方程式,机器人的状态空间方程可以写为
| $ \left\{ \begin{array}{l}\left[\begin{array}{c}{\dot{{x}}}_{{1}}\\ {\dot{{x}}}_{{2}}\\ {\dot{{x}}}_{{3}}\end{array}\right]=\left[\begin{array}{ccc}{0}& {1}& {0}\\ -\dfrac{{2}{K}}{m}& \dfrac{{2}{C}}{m}& \dfrac{{2}{K}}{m}\\ {0}& {0}& {0}\end{array}\right]\left[\begin{array}{c}{{x}}_{{1}}\\ {{x}}_{{2}}\\ {{x}}_{{3}}\end{array}\right]+\\ \qquad\quad\;\;\; \left[\begin{array}{c}{0}\\ -\dfrac{{2}{C}}{m}\\ {1}\end{array}\right]{u}-\left[\begin{array}{c}{0}\\ \dfrac{{1}}{m}\\ {0}\end{array}\right]{f}\\ {y}=\left[\begin{array}{ccc}{1}& {0}& {0}\end{array}\right]\left[\begin{array}{c}{{x}}_{{1}}\\ {{x}}_{{2}}\\ {{x}}_{{3}}\end{array}\right]\end{array} \right. $ | (22) |
式中:K为液压驱动系统的等效弹簧模型的刚度系数,f 为机器人所受干摩擦阻尼
由式(22)得出的液压驱动系统状态方程,可转化为
| $ \left\{\begin{split}\dot{x}{(}{t}{) }=&{\boldsymbol{A}}{x}{(}{t}{) }+{\boldsymbol{{B}}}_{{1}}{u}{(}{t}{) }+{\boldsymbol{B}}_{{2}}{f}{(}{t}{) }\\ {y}{(}{t}{) }=&{\boldsymbol{C}}{x}{(}{t}{) }\end{split}\right. $ | (23) |
式中:
为了让机器人能够快速、稳定地跟踪某一输入信号,引入新的状态变量
| $ \left\{\begin{split}{\dot{\boldsymbol{x}}}_{\text{e}}\text{(}{t}\text{) }\text=&{y}_{\text{r}}\text{(}{t}\text{)}-{y}\text{(}{t}\text{) }\\ {\boldsymbol{x}}_{\text{e}}\text{(}{t}\text{) }\text=&{\int }_{\text{0}}^{t}{(}{y}_{\text{r}}\text{(}{\tau }{) -}{y}\text{(}{\tau }\text{) ) d}{\tau }\end{split}\right. $ | (24) |
式中:
| $ \left\{\begin{split}{\boldsymbol{\dot{ \varepsilon }}}\text{(}{t}\text{) }\text=&\bar{{\boldsymbol{A}}}{ \varepsilon }\text{(}{t}\text{) }\text+\bar{{{\boldsymbol{B}}}}_{\text{1}}{u}\text{(}{t}\text{) }\text+\bar{{\boldsymbol{B}}}_{\text{2}}{D}\text{(}{t}\text{) }\\ \boldsymbol{y}\text{(}{t}\text{) }\text=&\bar{{\boldsymbol{C}}}{ {\boldsymbol{\varepsilon}} }\text{(}{t}\text{) }\end{split}\right. $ | (25) |
式中:新的状态变量
| $ \begin{split} &\bar{\boldsymbol{A}}=\left[\begin{array}{cc}\boldsymbol{A}& 0\\ -\boldsymbol{C}& 0\end{array}\right],{\bar{\boldsymbol{B}}}_{1}=\left[\begin{array}{c}{\boldsymbol{B}}_{1}\\ 0\end{array}\right],{\bar{\boldsymbol{B}}}_{2}=\left[\begin{array}{cc}{\boldsymbol{B}}_{2}& 0\\ 0& 1\end{array}\right] \\ &\qquad\qquad \bar{\boldsymbol{C}}=\left[\begin{array}{cccc}1& 0& 0& 0\end{array}\right] \end{split} $ |
取控制器的性能指标项为
| $ {J=}{\int }_{{0}}^{\text{∞}}\left({{{{\boldsymbol{x}}}}_{{{\rm{e}}}}}^{\rm{{T}}}{\boldsymbol{Q}{{\boldsymbol{x}}}}_{{{\rm{e}}}}+{\boldsymbol{u}}^{\rm{{T}}}{\boldsymbol{R}}{\boldsymbol{u}}-{\textit{γ}}^{{2}}{\boldsymbol{D}}^{{{\rm{T}}}}{\boldsymbol{D}}\right) {\rm{{d}}}{t} $ | (26) |
式中:
| $ \left[\begin{array}{cccc}\bar {\boldsymbol{A}} \bar{\boldsymbol{X}}\text+{\bar{\boldsymbol{B}}}_{\text{1}}\boldsymbol{V}\text+{\text{(}\bar{\boldsymbol{A}}\bar{\boldsymbol{X}}\text+{\bar{\boldsymbol{B}}}_{\text{1}}\boldsymbol{V}\text{) }}^{\text{T}}& {\bar{\boldsymbol{B}}}_{\text{2}}& \bar{\boldsymbol{X}}{\boldsymbol{M}}^{\text{T}}& {\text{(}\boldsymbol{RV}\text{) }}^{\text{T}}\\ {{\bar{\boldsymbol{B}}}_{\text{2}}}^{\text{T}}& -{\bf{1}}\rho & \text{0}& \text{0}\\ \boldsymbol{M}\bar{\boldsymbol{X}}& \text{0}& \text−{\boldsymbol{Q}}& \text{0}\\ {\boldsymbol{R}}\boldsymbol{V}& \text{0}& \text{0}& \text−{\boldsymbol{R}}\end{array}\right] < 0 $ | (27) |
式中:
| $ \boldsymbol{u}={K{\boldsymbol{x}}}{= [}\begin{array}{cccc} {-17}& {-13.1}& {-1\;535.4}& {8\;672.1} \end{array}{]}{{[}\begin{array}{cc}{{x}}_{{1}}\; {{x}}_{{2}}\;{{x}}_{{3}}\; {{x}}_{{{\rm{e}}}}\end{array}{]}}^{\rm{{T}}} $ |
为了验证本文第三章提出的液压驱动系统的数学模型的可靠程度,需要对其进行基于Simulink的仿真验证。
根据液压驱动系统的动力学模型(式(7)),以及状态空间描述(式(22)),在Simulink中搭建出系统的框图,将不确定的摩擦阻尼,表示为一个在特定范围内取值的有界函数,作为系统的外部干扰项。通过力传感器测得该阻尼约为20 N,于是本文将边界设为30 N,作为未知干摩擦阻尼的一个上界。
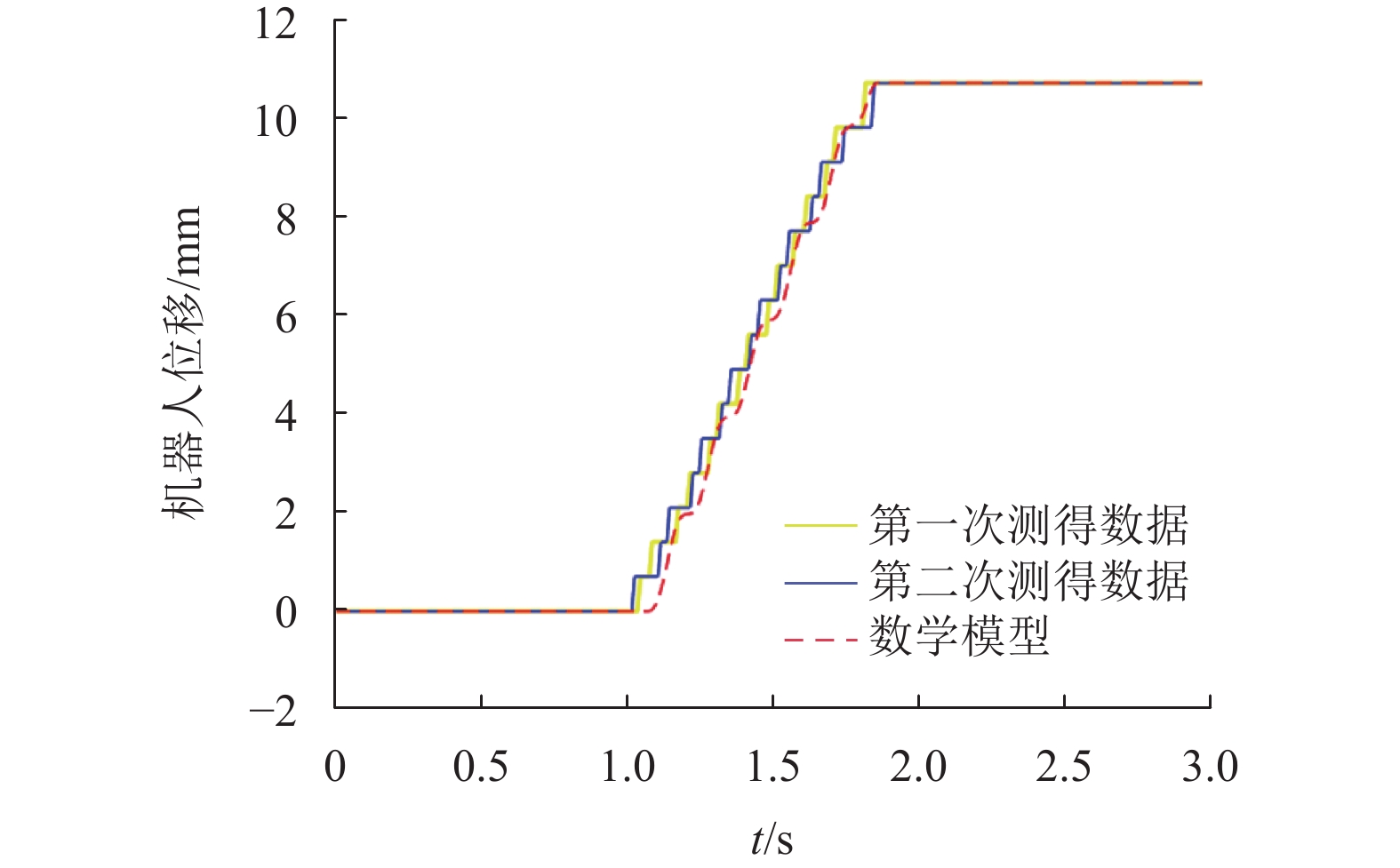
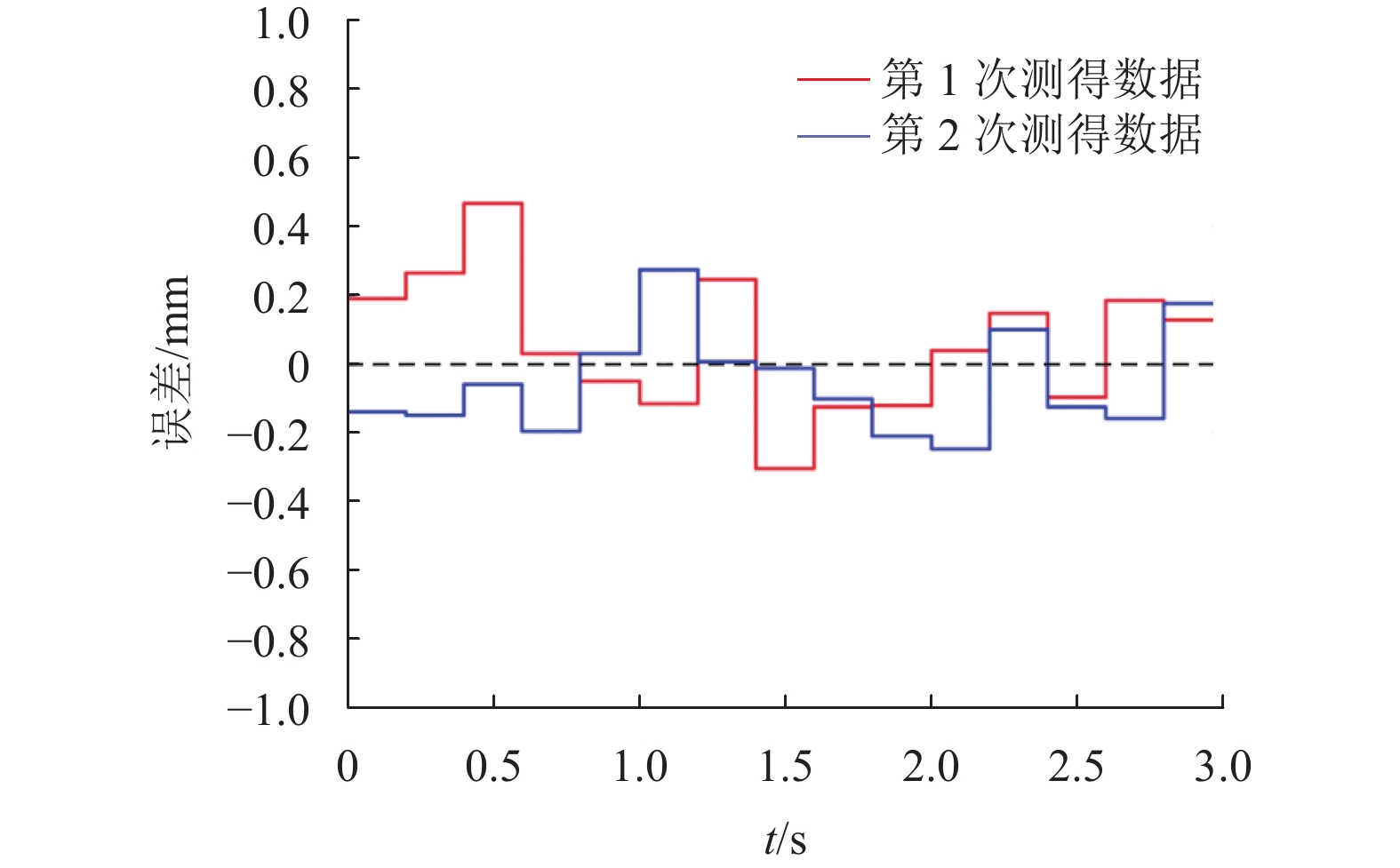
首先验证模型的准确性,本文通过STM32单片机,读取光敏二极管模组的反馈信号,得到机器人实际的运动轨迹,并且与Simulink得到的仿真轨迹相比较。仿真结果如图6所示,其中黄线表示机器人第一次实验测得的运动轨迹;蓝线表示机器人第二次实验测得的运动轨迹;红线表示仿真得出的机器人移动轨迹。图7是在单片机的每个离散的采样周期内得到的与数学模型之间的误差,模型的最大误差不超过0.5 mm,平均误差为0.38 mm。因此可以认为,机器人动力学的仿真结果与机器人实际的运动轨迹基本吻合,该数学模型基本可靠。
|
图 6 机器人在x轴上的移动轨迹和仿真结果 Figure 6 Robot trajectory on x-axis and simulation results |
|
图 7 数学模型与实物的误差对比 Figure 7 Error comparison between mathematical model and physical object |
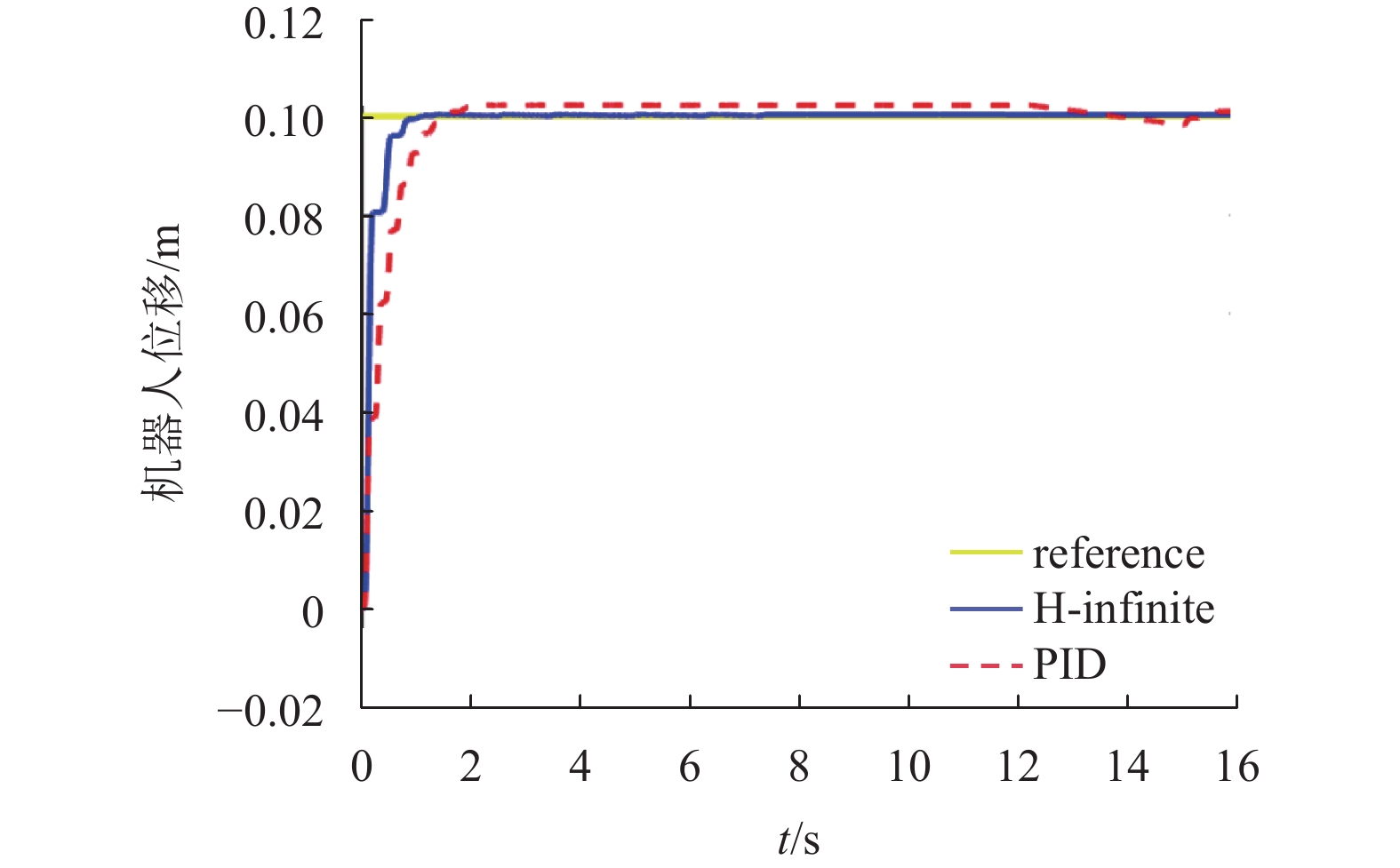
在验证了动力学模型合理的情况下,本文将继续使用Simulink以验证第三章提出的
图8展示了
|
图 8 |
|
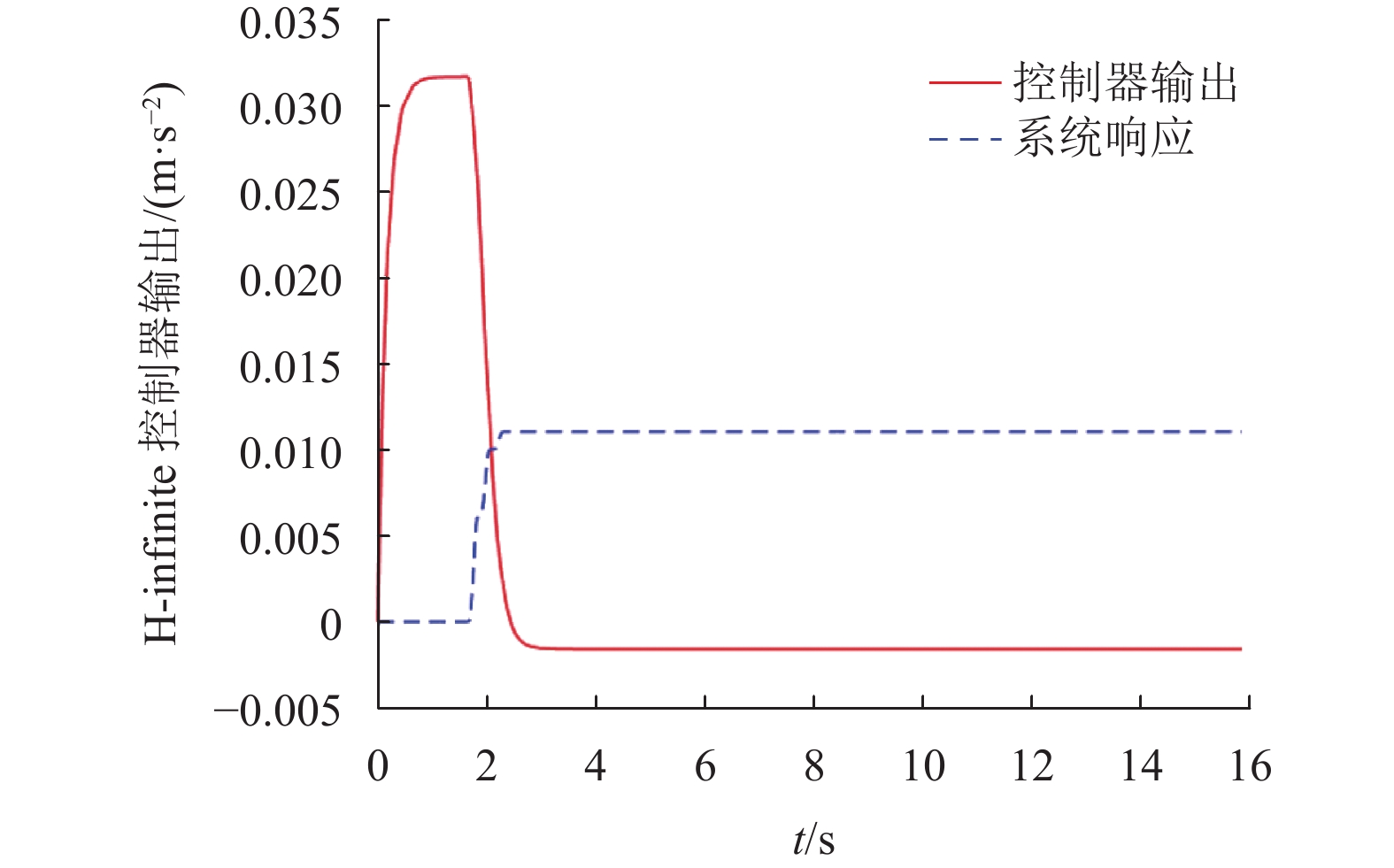
图 9 控制器输出与系统响应曲线 Figure 9 Controller output and system response curve |
本文通过分别测试机器人在x轴、y轴和z轴上的定位精度,来评估机器人的直线定位精度,结果如图10所示。通过编程使得机器人在纸片上对每条直线依次进行穿刺,并留下一系列针孔,再用游标卡尺测量针孔与目标直线之间的间距,以此得到机器人移动距离与期望值之间的误差。本文在机器人上固定一个陀螺仪模块,并利用它来测量俯仰轴和滚转轴的角度精度。规定姿态矢量L =

|
图 10 机器人实验平台 Figure 10 Experimental setup |
首先,制作了一个放置纸片的定位框架,如图10所示,使纸片边缘到机器人RCM点的距离是完全确定的。然后,根据机器人的Solidworks设计图,在纸片上打印若干条间隔10 mm的等距平行线,并确保第一条线处于RCM点的初始位置。最后,通过一个3D打印件,将陀螺仪模块固定在机器人的末端执行器上,用于传递末端执行器姿态。
4.2.2 实验过程首先执行物理复位程序,STM32单片机发送复位信号,使得滚珠丝杆滑块带动连通器活塞运动,直至滚珠丝杆滑块碰到限位开关。限位开关的摆放会确保机器人复位完成后,驱动端活塞移动到行程尽头,即内部无液体的初始状态。再由操作人员在电脑上通过上位机以及串口,给单片机发送数据,控制机器人以10 mm的步距移动,直至其工作空间边界。当机器人停止运动后,操控穿刺针进行对纸片的穿刺动作,再抬起穿刺针,发送新的目标位置点,如此往复3次。通过游标卡尺测量穿刺针留下的针孔与纸片上参考直线之间的误差,并记录下实验数据。
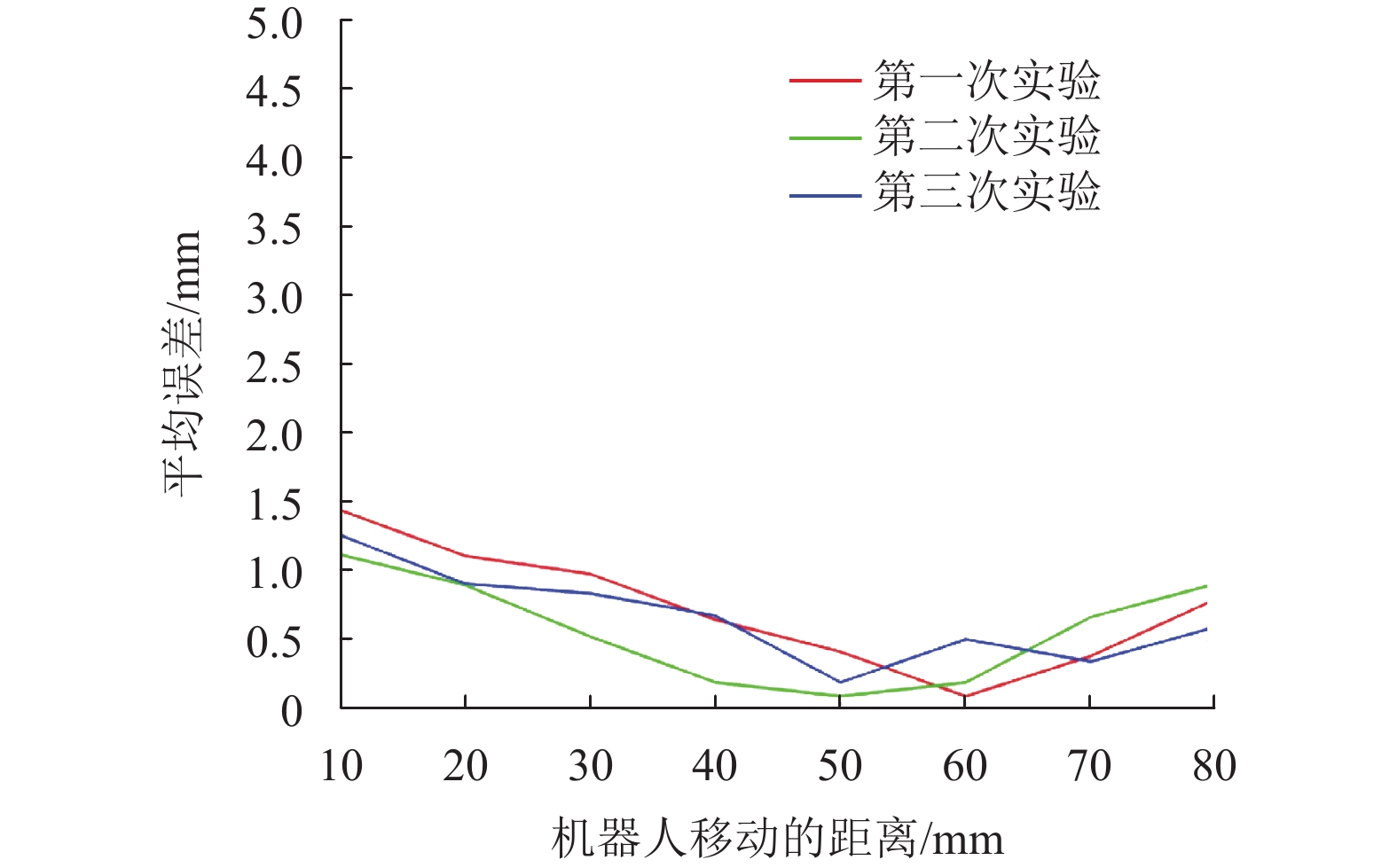
4.2.3 实验结果与分析图11~图14展示了机器人应用了
|
图 11 机器人直线定位误差(基于PID控制) Figure 11 Robot linear positioning error (based on PID controller) |
|
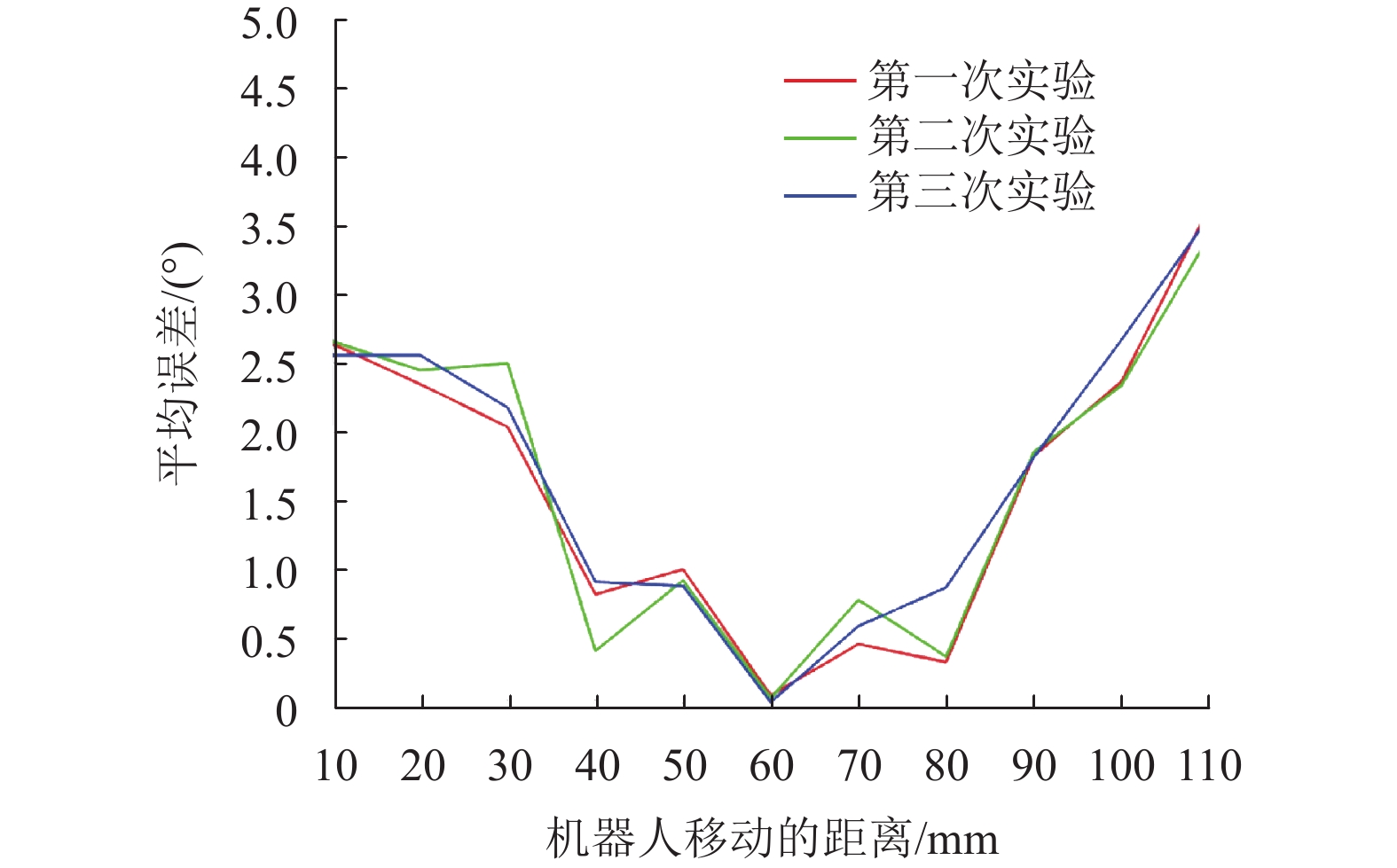
图 12 机器人旋转定位误差(基于PID控制) Figure 12 Robot rotation positioning error(based on PID controller) |
|
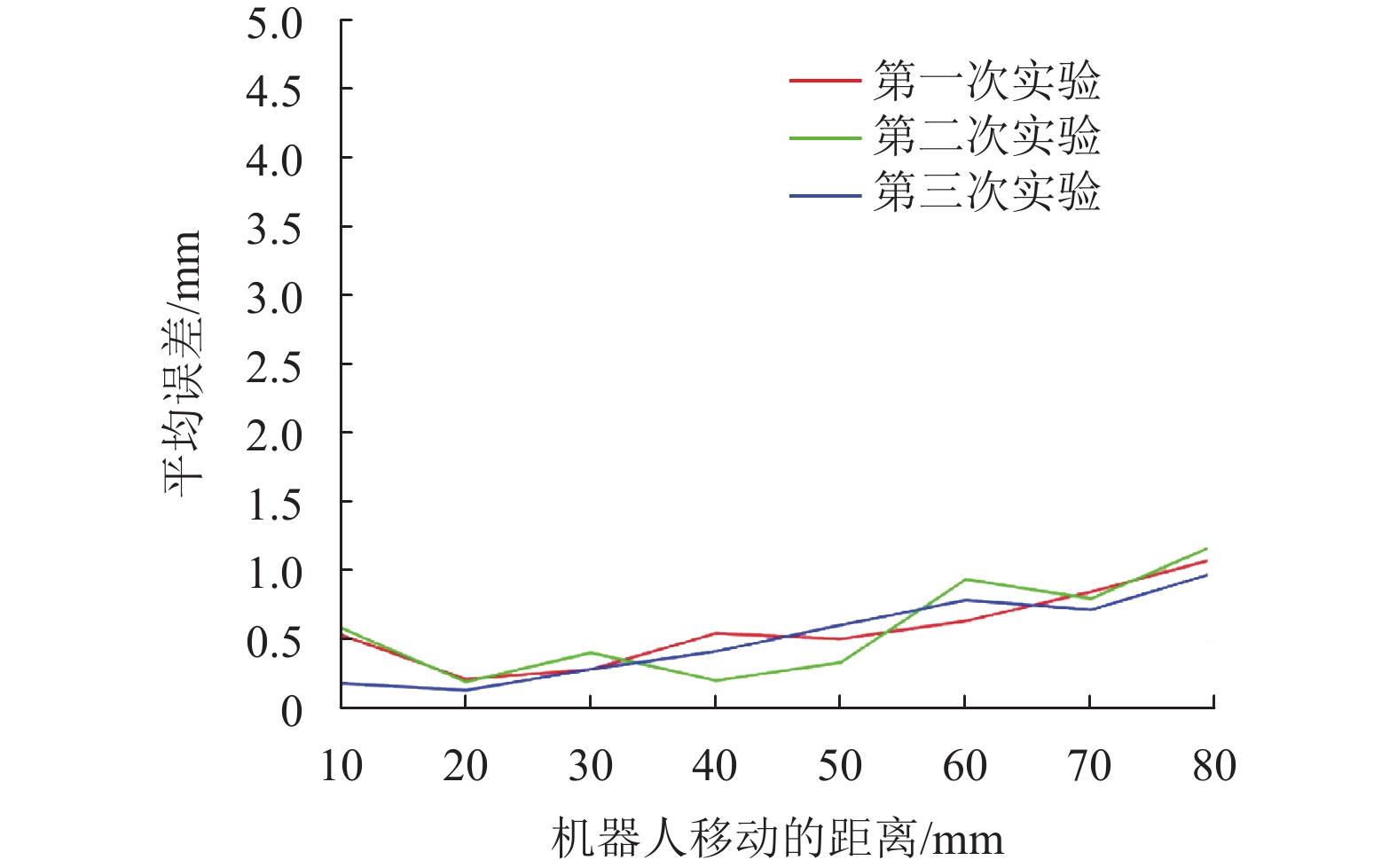
图 13 机器人直线定位误差(基于
|
|
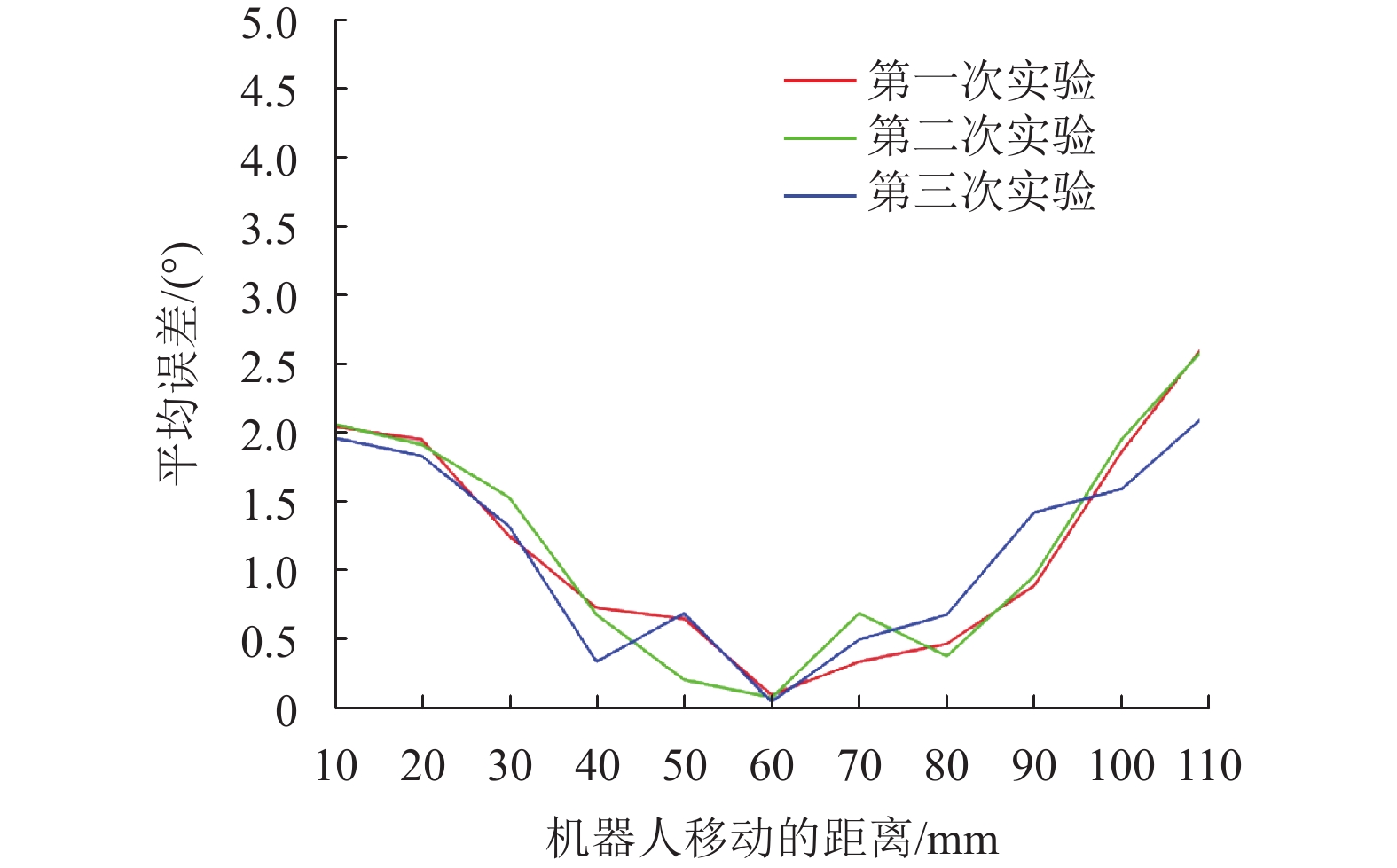
图 14 机器人旋转定位误差(基于
|
最终得到机器人系统在PID控制器下的平均线性定位误差为0.88 mm,平均角度误差为1.48°,在H∞控制器下的平均线性定位误差为0.56 mm,平均角度误差为1.03°。
通过观察,发现当目标线定位在10~60 mm时,机器人造成的相邻穿刺点之间的距离增量实际上不是太大,基本保持在0.7 mm以内,小于编码器的分辨率。然而,机器人在10和70 mm两条直线附近的定位精度不是很理想,两个穿刺点之间的距离增量和定位精度都与其他直线有很大的偏差。经过分析,其原因是当机器人运行到工作空间边缘时,气缸内的水已基本排空,剩余的空气为可压缩流体,导致液压驱动系统运行效果不理想。
在角度精度实验研究中,随着目标角度的增大,俯仰轴和滚转轴的误差越来越大。这主要是由于在RCM机构中采用了止转棒轭来驱动。当夹角θ和φ增大时,它们对应的直线长度减小,即相同的直线误差将导致夹角误差增大。
从理论上讲,机器人俯仰轴和滚转轴的角度精度与编码器的线性精度直接相关。由图11至图12可知,机器人的平均线性定位误差分别为0.88 mm和0.56 mm,根据式(1),理论上对应的角度误差应该分别为1.3°,0.82°,即最终测得的角度定位误差应在这两个值附近。最终在图13与图14中得到验证,实验测得的角度误差分别为1.48°和1.03°,基本合理。
5 结论本文首先建立了一种核磁共振兼容液压驱动穿刺手术机器人的运动学模型以及动力学模型,并针对系统具有的非线性死区特性,采用
最后,本文展示了搭建出的机器人实物,设计了基于STM32单片机的控制代码,搭建了机器人的电气系统。并且通过实验研究,验证了机器人辅助定位穿刺针的性能。机器人系统在PID控制器下的平均线性定位误差为0.88 mm,平均角度误差为1.48°,在
本文提出的模型是将液压驱动系统视为线性的弹簧−阻尼模型,叠加上一个未知的、未建模的非线性的干摩擦阻尼的结合。将非线性的干摩擦阻尼视为外部扰动,采用
| [1] |
KHIEWVAN B, TORIGIAN D A, EMAMZADEHFARD S, et al. An update on the role of PET/CT and PET/MRI in ovarian cancer[J].
European Journal of Nuclear Medicine & Molecular Imaging, 2017, 44(6): 1079-1091.
|
| [2] |
MOREIRA P, BOSKMA K J, MISRA S. Towards MRI-guided flexible needle steering using fiber Bragg grating-based tip tracking[C]// 2017 IEEE International Conference on Robotics and Automation (ICRA) . Singapore: IEEE, 2017: 4849-4854.
|
| [3] |
BALL M W, ROSS A E, GHABILI K, et al. Safety and feasibility of direct magnetic resonance imaging-guided transperineal prostate biopsy using a novel magnetic resonance imaging-safe robotic device[J].
Urology, 2017, 109: 216-221.
DOI: 10.1016/j.urology.2017.07.010. |
| [4] |
ZHANG T X, WEN Y S, LIU Y H. Developing a parallel robot for MRI-guided breast intervention[J].
IEEE Transactions on Medical Robotics and Bionics, 2020, 2(1): 17-27.
DOI: 10.1109/TMRB.2019.2957566. |
| [5] |
GROENHUIS V, SIEPEL F J, VELTMAN J, et al. Design and characterization of Stormram 4: an MRI-compatible robotic system for breast biopsy[C]// 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Vancouver: IEEE, 2017: 928-933.
|
| [6] |
HE Z, DONG Z, FANG G, et al. Design of a percutaneous MRI-guided needle robot with soft fluid-driven actuator[J].
IEEE Robotics and Automation Letters, 2020, 5(2): 2100-2107.
DOI: 10.1109/LRA.2020.2969929. |
| [7] |
LI G, NIRAVKUMAR A P, LIU W Q, et al. A fully actuated body-mounted robotic assistant for MRI-guided low back pain injection[C]// 2020 IEEE International Conference on Robotics and Automation (ICRA) . Paris: IEEE, 2020: 5495-5501.
|
| [8] |
NIRAVKUMAR A P, CHRISTOPHER J N, PAULO A C, et al. An integrated robotic system for MRI-guided neuroablation: preclinical evaluation[J].
IEEE Transactions on Biomedical Engineering, 2020, 67(10): 2990-2999.
DOI: 10.1109/TBME.2020.2974583. |
| [9] |
GUO Z Y, DONG Z Y, KIT-HANG L, et al. Compact design of a hydraulic driving robot for intra-operative MRI-guided bilateral stereotactic neurosurgery[J].
IEEE Robotics & Automation Letters, 2018, 3(3): 2515-2522.
|
| [10] |
GYEONG HU K, NIRAVKUMAR P, YAN J W, et al. Shoulder-mounted robot for MRI-guided arthrography: clinically optimized system[C]// 2019 41st Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC) . Berlin: IEEE, 2019: 1977-1980.
|
| [11] |
NIRAVKUMAR A P, YAN J W, DAVID L, et al. Body-mounted robot for image-guided percutaneous interventions: mechanical design and preliminary accuracy evaluation[C]// 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems. Madrid: IEEE, 2018: 1443-1448.
|
| [12] |
NYCZ C J, GONDOKARYONO R, CARVALHO P, et al. Mechanical validation of an MRI compatible stereotactic neurosurgery robot in preparation for pre-clinical trials[C]// 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) . Vancouver: IEEE, 2017: 875-881.
|
| [13] |
FRANCO E, BRUJIC D, REA M, et al. Needle-guiding robot for laser ablation of liver tumors under MRI guidance[J].
IEEE/ASME transactions on mechatronics:A joint publication of the IEEE Industrial Electronics Society and the ASME Dynamic Systems and Control Division, 2016, 21(2): 931-944.
|
| [14] |
DONG Z Y, GUO Z Y, KIT-HANG L, et al. High-performance continuous hydraulic motor for MR safe robotic teleoperation[J].
IEEE Robotics & Automation Letters, 2019, 4(2): 1964-1971.
|
| [15] |
FARIMANI F S, MISRA S. Introducing pneuact: parametrically-designed MRI-compatible pneumatic stepper actuator[C]// 2018 IEEE International Conference on Robotics and Automation (ICRA) . Brisbane: IEEE, 2018: 4523-4536.
|
| [16] |
FRISHMAN S, KIGHT A, PIROZZI I, et al. Enabling in-bore MRI-guided biopsies with force feedback[J].
IEEE Transactions on Haptics, 2020, 13(1): 159-166.
DOI: 10.1109/TOH.2020.2967375. |
 2023, Vol. 40
2023, Vol. 40

