单目视觉里程计是SLAM领域中的重要组成部分，其作用是对机器人的位姿进行估计^[1]。然而视觉里程计存在不少缺点，如在光照强度变化大或者特征较为单一的场景，大多数的视觉里程计都无法提供让人满意的位姿估计结果^[2]。另外，在机器人运动过快、物体发生遮挡等情况下，视觉里程计的精度会受到重大影响。有的学者采用传统图像方法增强单目视觉里程计的准确性^[3-4]，但仍然无法克服单目相机固有的缺陷。

由于单目相机的特殊性，单目视觉里程计具有尺度不确定、必须初始化和尺度漂移等特点^[5]。SLAM领域的学者们尝试使用多传感器融合技术去解决这些问题，由于惯导单元(Inertial Measurement Unit, IMU)不受各种环境因素的影响，因而成为主要研究热点。Mur-artal和Forster等^[6-7]对视觉惯导里程计进行了数学上的理论证明，Qin等^[8]研究的VINS系统是视觉惯导里程计的经典实现之一，证明了惯导与视觉融合能大幅度提高里程计的精度。

随着深度学习技术的兴起，许多新的方法进入到人们的视野，如物体检测^[9]、语义分割^[10]、深度预测^[11]。这些新技术提供了许多提高里程计精度的新思路。例如：利用深度估计技术解决单目视觉里程计存在的尺度不确定问题^[12]；采用物体检测技术构造新的多视图BA(Bundle Adjustment)约束，优化机器人位姿^[13]；使用语义分割网络获取图像语义信息，构建语义地图^[14]。受上述技术的启发，本文设计了一个基于深度特征的视觉惯导里程计，采用深度学习网络提取深度特征点和图像高维度信息，提高了特征点匹配的准确性，同时融合了传统的人工线特征，进一步提高了位姿估计的精度。另外，本文还融合了IMU信息，解决单目相机所存在的初始化难、尺度不确定等问题。

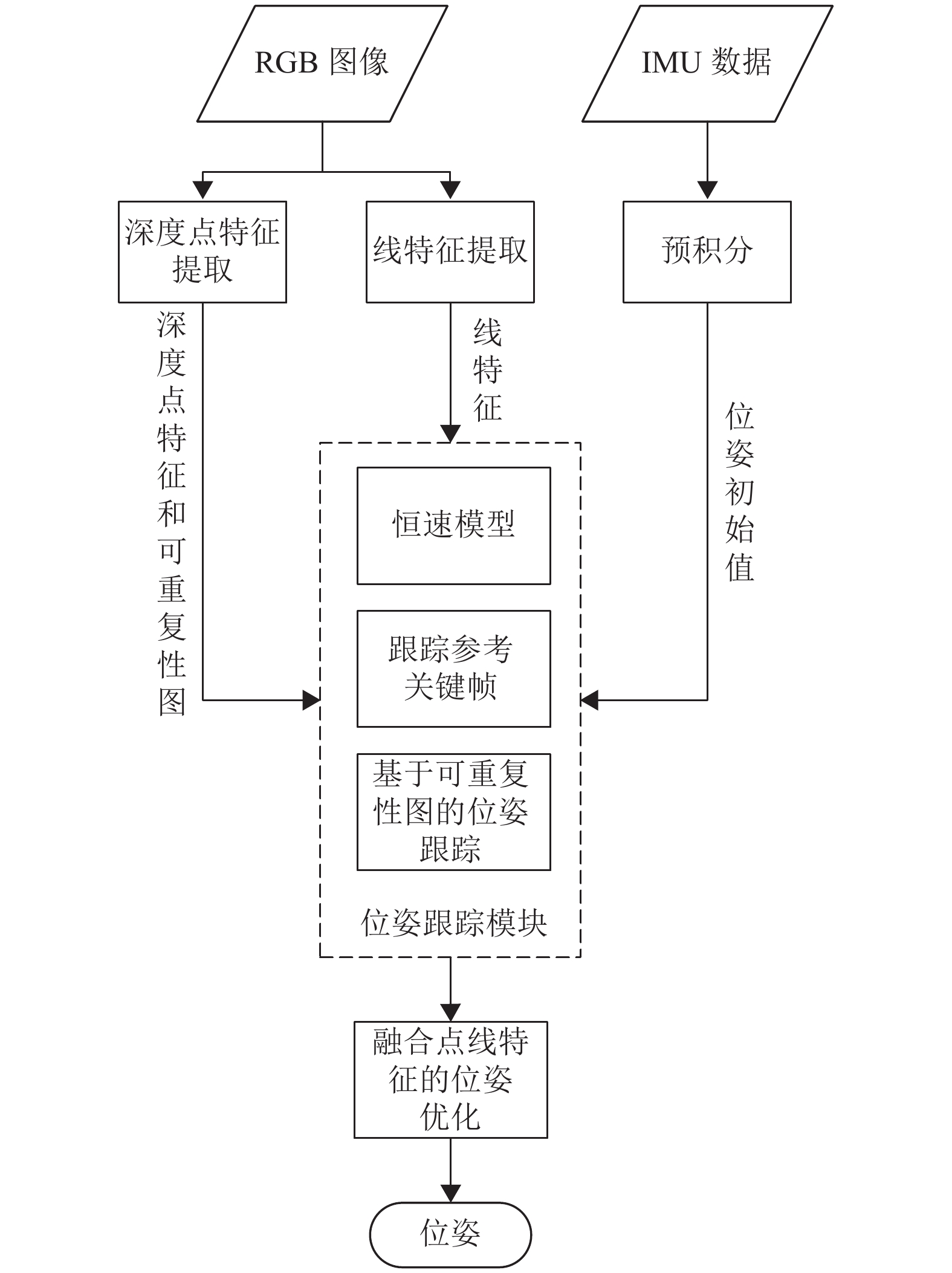
1 系统介绍 1.1 系统框架

本文提出的里程计框架如图1所示，预处理部分主要包括特征提取及IMU数据的预积分处理。提取到的图像特征被位姿跟踪模块以及位姿优化模块所使用。

在位姿跟踪部分，本系统提供了3种位姿跟踪方式：恒速模型、跟踪参考关键帧和基于可重复性图的位姿跟踪。前两种方法是视觉里程计常用的方法，本系统增加了线特征的约束，提高了位姿跟踪的精度，第三种跟踪方法是深度特征网络所特有的，它能够大大提高位姿跟踪的成功率与精度。

最后，由于跟踪参考关键帧需要稳定的光照条件，恒速模型在现实中有时也难以得到满足，因而上述的位姿跟踪方法在复杂的日常环境中难以获得一个准确的位姿初始值，进而导致位姿跟踪失败，而IMU具有与环境因素无关的特性，所以本系统也支持融合IMU信息，能够根据IMU获取的速度与加速度信息求解较为精确的位姿初始值，作为位姿跟踪的初始值，加快迭代计算效率的同时提高位姿跟踪的成功率。

1.2 特征提取

本文选用DeTone D等设计的SuperPoint网络^[15]作为特征点提取器。它先用一个共享编码器对输入图像 $I \in {\mathbb{R}^{H \times W}}$ ( $H$ 和 $W$ 分别是图像的高度和宽度)进行编码，然后分别用解码器进行解码，得到一个预测的可重复性单元 $ {\mathcal{H}\; ^\prime } \in {\mathbb{R}^{{H_c} \times {W_c} \times \left( {{C^2} + 1} \right) }} $ 和一个稠密描述子 ${\mathcal{H}\; }^{\prime }\in {\mathbb{R}}^{{H}_{c}\times {W}_{c}\times 256}$ 。其中 $C$ 是网格的大小，在本文中设置为8。 ${H_C} = \dfrac{H}{C},{W_C} = \dfrac{W}{C}$ 。 ${\mathcal{H}\; ^\prime }$ 可以标准化为

$ \mathcal{H}\left(h_{C}, w_{C}, y\right) =\frac{\exp \left(\mathcal{H} \; ^{\prime}\left(h_{C}, w_{C}, y\right) \right) }{\displaystyle\sum\nolimits_{k=1}^{\infty} \exp \left(\mathcal{H} \; ^{\prime}\left(h_{C}, w_{C}, k\right) \right) } $

(1)

式中： ${h_C},{w_C},y$ 分别为 $ {\mathcal{H} \;^\prime } $ 中3个通道中的任意一位。

其他网络的详细信息可见文献[15]。

另外，本文选用文献[16]设计的LSD线段提取算法提取线特征，以提高系统在弱纹理场景下的稳定性。为了减少短线段的误匹配对位姿跟踪精度造成影响，本文只筛选像素坐标系下长度大于30的线段。

1.3 位姿跟踪

在位姿跟踪部分，除了经典SLAM框架中的跟踪关键帧和根据恒速模型估算位姿以外，本文还采用了文献[17]中提出的基于预测的可重复性图的位姿跟踪算法，与传统的直接法直接最小化图像的光度误差不同，该方法通过最小化基于预测的可重复性图的重投影误差项来位姿跟踪。由于该方法构造的误差函数为凸函数，比传统直接法的误差函数更容易收敛到最优解，因此能够取得更高的精度。

像素级的可重复性图 $\mathcal{R}$ 和分块级的可重复性图 ${\mathcal{R}}_{\;{\rm{d}}}$ 可分别定义为

$ \begin{gathered} {\mathcal{R}} = - {\text{lg}}\left( {s\left( {\mathcal{R}\left( { \cdot , \cdot ,: - 1} \right) } \right) } \right) \\ {\mathcal{R}_{\;\rm{d}}} = \mathcal{R}( {:,:,{C^2} + 1} ) \\ \end{gathered} $

(2)

式中： $\mathcal{R} \in {\mathbb{R}}^{H\times W}$ ， $s:{\mathbb{R}}^{{H}_{C}\times {W}_{C}\times {C}^{2}}\to {\mathbb{R}}^{H\times W}$ ， $  s $ 为从可重复性图像素块到2D预测值的映射函数。

本文定义了新的基于可重复性的残差替代传统直接法的光度残差：

$ e_{i}^{\text {repeet }}=\mathcal{R}_{\;\,(\cdot) }\left(\pi_{(\cdot) }\left(\left(\xi_{k} \oplus {\boldsymbol{T}}_{k}\right) p_{i}\right) \right. $

(3)

式中： ${\mathcal{R}}_{\;\,(\cdot ) }$ 为两种不同分辨率的可重复性图之一， $ {\pi _{\left( \cdot \right) }} $ 为对应分辨率下的相机投影方程， ${{\boldsymbol{\xi}} _k}$ 为位姿增量， ${{\boldsymbol{T}}_k}$ 为当前机器人的位姿， ${p_i} $ 为3D路标点，其对应的像素点为 ${u^{\pi}_{i,k}}$ 。可重复性残差项 $e_i^{{\text{repeat}}}$ 的雅克布方程可以表示为

$ \begin{split} J_{i}= &J_{\text {repeat }}-J_{\text {proj }}-J_{\text {pose }} = \\& \dfrac{\partial \mathcal{R}_{\;\,(\cdot) }(u_{i, k}^{\pi}) }{\partial u_{i, k}^{\pi}} \cdot \dfrac{\partial u_{i, k}^{\pi}}{\partial p_{i}^{c}} \cdot \dfrac{\partial\left(\left(\xi_{k} \oplus {\boldsymbol{T}}_{i}\right) p_{i}\right) }{\partial \xi_{k}} \end{split} $

(4)

式中： ${J_{{\text{proj }}}}$ 为相机投影方程对路标点的偏导数， ${J_{{\text{pose }}}}$ 为投影点对位姿增量的偏导数， ${J_{{\text{repeat }}}} $ 为可重复性图对像素点的偏导数。

因此，误差函数可表示为

$ {\widehat {\boldsymbol{\xi}} _k} = \mathop {\arg \min }\limits_{{\xi _k}} {\sum\nolimits_{i \in {\mathcal{P}_k}} {\left\| {\mathcal{R}\left( {\pi \left( {{\xi _k} \oplus {{\boldsymbol{T}}_k}} \right) {p_i}} \right) } \right\|} _\gamma } $

(5)

式中： ${\mathcal{P}_k }$ 被初始化为上一帧跟踪到的路标点集合，若集合过小，则将其他共视程度较高的帧中的路标点加入该集合，使集合大小满足迭代的最低要求。

为了提高计算的速度，先将可重复性图上的分块级局部特征与3D路标点进行关联，然后使用列文伯格−马夸尔特法迭代优化，使得误差函数收敛，得到精度粗糙的位姿增量。

此时，在像素级的可重复性图上应用半径搜索算法，寻找与3D路标点的描述子最接近的像素点 ${\tilde u_{i,k}}$ ，随后，只要最小化重投影误差即可求出机器人当前位姿 ${{\boldsymbol{T}}_k}$ ，其对应的旋转矩阵为 ${{\boldsymbol{R}}_k}$ ，平移向量为 ${{\boldsymbol{t}}_k}$ 。对于每个3D路标点 ${p_i}$ ，重投影误差为

$ e_{i,k}^{{\text{repro }}} = \pi \left( {{{\boldsymbol{R}}_k}{p_i} + {{\boldsymbol{t}}_k}} \right) - {\tilde u_{i,k}} $

(6)

可以推导出点特征重投影误差函数为

$ {E^{{\text{point }}}} = \sum\nolimits_{i \in {\mathcal{P}_k}} {{{\left\| {{{( {e_{i,k}^{{\text{repro }}}} ) }^{\rm{T}}}{\boldsymbol{\varOmega}} _{i,k}^{ - 1}e_{i,k}^{{\text{repro }}}} \right\|}_\gamma }} $

(7)

式中： ${{\boldsymbol{\varOmega}} _{i,k}}$ 为像素点 ${\tilde u_{i,k}}$ 的协方差矩阵，它决定了特征点在优化中的权重，在ORB-SLAM框架中，它取决于特征点在图像金字塔的哪一层中被检测到，而在基于深度学习的特征提取网络中，没有图像金字塔的概念，因此本文用特征点的局部显著性作为该点的协方差矩阵，其定义为

$ \begin{split} {\boldsymbol{\varOmega}} =& E[ {( {u - {u_{{\text{peak}}}}} ) {{( {u - {u_{{\text{peak}}}}} ) }^{\rm{T}}}} ] = \\& \mathop \sum \nolimits_{i \in \mathcal{V}{\text{p}}} \frac{{\mathcal{R}( {{u_i}} ) }}{{\displaystyle\mathop \sum \nolimits_{k \in \mathcal{V}{\text{p}}} \mathcal{R}( {{u_k}} ) }}( {{u_i} - {u_{{\text{peak}}}}} ) {( {{u_i} - {u_{{\text{peak}}}}} ) ^{\rm{T}}} \end{split}$

(8)

式中： ${u_{{{i}}}}$ 为可重复性图中的第i个像素点， ${u_{{\text{peak}}}} $ 为可重复性图中的峰值像素点，而 ${\mathcal{V}_p}$ 为该点附近具有正响应值的像素点集合。

为了进一步提升视觉里程计的精度，本文还加入了线特征的信息来进行位姿估计。

假定三维空间下线特征线段的两个端点分别为 $P,Q \in {\mathbb{R}^3}$ ，相机坐标系下线特征线段的两个端点分别为 ${p_{\text{d}}},{q_{\text{d}}} \in {\mathbb{R}^2}$ ，它们对应的齐次坐标分别为 $p_{\text{d}}^{\text{h}},q_{\text{d}}^{\text{h}} \in {\mathbb{R}^3}$ ，则归一化线性系数为

$ I = \frac{{p_{\text{d}}^{\text{h}} \times q_{\text{d}}^{\text{h}}}}{{\left| {p_{\text{d}}^{\text{h}} \times q_{\text{d}}^{\text{h}}} \right|}} $

(9)

本文将线特征的重投影误差定义为线段两个端点的重投影误差之和，即

$ {E^{{\text{line}}}}({p_{\text{d}}},{q_{\text{d}}},I) = E_{{\text{pl}}}^2({p_{\text{d}}},I) + E_{{\text{pl}}}^{{2}}({q_{\text{d}}},I) $

(10)

$ {E}_{\text{pl}}^{2}({p}_{\text{d}},I)={I}^{{\rm{T}}}{p}_{\text{d}},{E}_{\text{pl}}^{{\rm{2}}}\left({q}_{\text{d}},I\right) ={I}^{{\rm{T}}}{q}_{\text{d}} $

(11)

本文将整个系统的误差函数设置为点特征的重投影误差加上线特征的重投影误差，即

$ E=E^{\text {point }}+E^{\text {line }} $

(12)

通过迭代优化重投影误差函数，即可得到更加精确的机器人位姿。

1.4 IMU融合

这部分采用与ORB_SLAM3^[18]相同的融合策略。系统的状态向量定义为 ${{\boldsymbol{S}}_i} \doteq \left\{ {{{\boldsymbol{T}}_i},{v_i},b_i^g,b_i^a} \right\}$ ，其中 ${{\boldsymbol{T}}_i}$ 是第 $i$ 帧机器人的位姿， ${{\boldsymbol{T}}_i}{\text{ = [}}{{\boldsymbol{R}}_i}{\text{,}}{p_i}{\text{]}}$ ， ${v_i}$ 是机器人对应时刻的速度， $b_i^g$ 是陀螺仪的零偏， $b_i^a$ 是加速度计的零偏。对其进行预积分，可得到测量向量信息矩阵 ${{\boldsymbol{\varOmega}} _{{\mathcal{I}_{i,i + 1}}}}$ 的预积分为

$ r_{x_{i+1}}=[r_{\Delta R_{h+1}}, r_{\Delta v_{i+1}}, r_{\Delta p_{i,+1}}] $

(13)

式中：

$ {r_{\Delta {{\text{R}}_{i,i + 1}}}} = \lg ( {\Delta {\boldsymbol{R}}_{i,i + 1}^{\text{T}}{\boldsymbol{R}}_i^{\text{T}}{{\boldsymbol{R}}_{i + 1}}} ) $

(14)

$ {r_{\Delta {v_{i,i + 1}}}} = {\boldsymbol{R}}_i^{\text{T}}\left( {{v_{i + 1}} - {v_i} - g\Delta {t_{i,i + 1}}} \right) - \Delta {v_{i,i + 1}} $

(15)

$ {r_{\Delta {p_{i,i + 1}}}} = {\boldsymbol{R}}_i^{\text{T}}\left( {{p_j} - {p_i} - {v_i}\Delta t - \frac{1}{2}g\Delta {t^2}} \right) - \Delta {p_{i,i + 1}} $

(16)

式中： $ g $ 为加速度常数。

则3D点 ${x_j}$ 在第 $i$ 帧图像的重投影误差可表示为

$ {r_{ij}} = {u_{ij}} - {\boldsymbol{\varPi}} \left( {{{\boldsymbol{T}}_{{\rm{CB}}}}{\boldsymbol{T}}_i^{ - 1} \oplus {x_j}} \right) $

(17)

式中： ${u_{ij}}$ 为3D点 ${x_j}$ 在第 $i$ 帧的投影点， ${\boldsymbol{\varPi}} $ 为相机投影矩阵， ${{\boldsymbol{T}}_{{\rm{CB}}}}$ 为机器人坐标到相机坐标的刚体变换矩阵。因此对于给定的 $k + 1$ 个关键帧及对应的状态量 ${\bar {\boldsymbol{S}}_k} \doteq \left\{ {{{\boldsymbol{S}}_{\rm{0}}}, \cdot \cdot \cdot ,{{\boldsymbol{S}}_k}} \right\}$ 和给定的 $l$ 个3D点集及其对应的状态量 $ \mathcal{X} \doteq \left\{ {{x_0}, \cdot \cdot \cdot ,{x_{l - 1}}} \right\} $ ，IMU误差函数可以表示为

$ {\min _{{{\overline S }_k},\mathcal{X}}} \bigg ( {\sum\nolimits_{i = 1}^k {{{\| {{r_{{\mathcal{I}_{i - 1,i}}}}} \|}_{{\boldsymbol{\varOmega }}_{{\mathcal{I}_{i,i + 1}}}^2}}} + \sum\nolimits_{j = 0}^{l - 1} {\sum\nolimits_{i \in {\mathcal{K}^j}} {{\rho _{{\text{Hub}}}}} } ( {{{\| {{r_{ij}}} \|}_{{{\boldsymbol{\varOmega }}_{ij}}}}} ) } \bigg ) $

(18)

式中： ${\mathcal{K}^j}$ 为第 $j$ 个3D点的观测关键帧集合， ${\rho _{{\text{Hub}}}}$ 为用于减少误匹配点对影响的鲁棒Huber核函数。

通过优化式(18)，可以得到一个比较精准的位姿初始值。

1.5 位姿优化

假设第 $j$ 个地图点表示为 ${X_j} \in {\mathbb{R}^3}$ ，对于第 $i$ 个关键帧，其相机投影方程为

$ {x_{i,j}} = \pi \left( {{X_j},{{\boldsymbol{T}}_i},{\boldsymbol{K}}} \right) $

(19)

式中： ${{\boldsymbol{T}}_i}$ 为机器人当前位姿， ${\boldsymbol{K}}$ 为相机参数，又知观测值为 ${x_{i,j}}$ ，则误差可定义为

$ {{\bf{\omega }}_{ij}} = {x_{ij}} - {x_{ijj}} $

(20)

类似的，对于线特征，假设在地图上线段的两个端点分别为 $ {P}_{j}\text{ }和\text{ }{Q}_{j} $ ，对应的投影点的齐次坐标可分别表示为

$ p_{i,j}^{\rm{h}} = \pi \left( {{P_j},{{\boldsymbol{T}}_i},{\boldsymbol{K}}} \right) $

(21)

$ q_{i,j}^{\rm{h}} = \pi \left( {{Q_j},{{\boldsymbol{T}}_i},{\boldsymbol{K}}} \right) $

(22)

因此，对于图像上对应的观测点 ${p_{i,j}}$ 和 ${q_{i,j}}$ ，误差可定义为

$ e_{i,j}^\prime = {( {{{\widetilde I}_{i,j}}} ) ^{\mathbf{T}}}( {{{\boldsymbol{K}}^{ - 1}}p_{i,j}^{\text{h}}} ) $

(23)

$ e_{i,j}^{\prime \prime } = {( {{{\widetilde I}_{i,j}}} ) ^{\mathbf{T}}}( {{{\boldsymbol{K}}^{ - {\mathbf{1}}}}q_{i,j}^{\text{h}}} ) $

(24)

式中： ${\widetilde I_{i,j}}$ 为将观测点 ${p_{i.j}}$ 和 ${q_{i,j}}$ 代入式(9) 得到的观测值。

最后，可以将误差整合为

$ \begin{gathered} C = \mathop \sum \nolimits_{i,j} \rho ( {e_{i,j}^{\text{T}}{\boldsymbol{\varOmega}} _{i,j}^{ - 1}{e_{i,j}} + e{{_{i,j}'}^{\text{T}}}{\boldsymbol{\varOmega}} {{_{i,j}'}^{ - 1}}e_{{\text{i}},{\text{j}}}' + e{{_{i,j}''}^T}{\boldsymbol{\varOmega}} {{_{i,j}''}^{ - 1}}e_{i,j}''} ) \\ \end{gathered} $

(25)

式中： $ \rho $ 为Huber核函数， ${{\boldsymbol{\varOmega}} _{i,j}},{\boldsymbol{\varOmega}} _{i,j}',{\boldsymbol{\varOmega}} _{i,j}''$ 分别为点特征和线段的两个端点的协方差矩阵。

通过迭代优化最小化误差函数 $ C $ ，即可优化机器人估计的位姿。

2 实验评估

为了更好地评估本文提出的系统在具有挑战性的场景下的鲁棒性，本文选取了EuRoC数据集^[19]来测试本文提出的系统，由于本文的系统是基于ORB_SLAM3提出的，因此将其作为对照目标，对比两个系统在EuRoC数据集上的性能。评价指标方面，本文选用了里程计的两个最重要的指标——精度与效率，对系统进行评估。

2.1 位姿跟踪精度

作为视觉里程计，位姿估计的准确度始终是放在首位的，除了需要提供准确的位姿估计以外，还需要具备较强的鲁棒性，以适应现实的场景，因此本文将两个方案在每个数据集上测试5次，取其平均值作为该数据集的轨迹误差，结果如表1所示。

从表1可以看出，在纯视觉模式下，本文提出的系统在大多数数据集上估计的位姿更加准确，得到的轨迹误差更小，这一点在标记为“difficult”的数据集上体现的更加突出，本文提出的系统在以上数据集的平均误差只有ORB_SLAM3的74.1%。这与预期相符合，由于深度点特征包含图像的高维度信息，误匹配概率较低，并且添加了线特征约束，位姿求解与优化的结果更准确，因而误差更小。

在视觉惯导的模式下，本文提出的系统在数据集上的性能仍然有所提升，但提升的幅度不是很大，这是因为在此模式下，机器人的位姿主要由IMU提供的速度与加速度来估计，位姿的精度本来就比较高，而深度点特征与线特征只是用于优化位姿，因此本文提出的方法对位姿的影响变小了。

2.2 位姿跟踪效率

实时性对于视觉里程计来讲也是一个重要的指标，为了探讨提出的方法对系统实时性的影响，本文测试了位姿跟踪时间、特征提取时间和局部光束平差法(Bundle Adjustment，BA) 时间，结果如表2所示。

从表2可以看出，本文提出的系统减少了位姿跟踪的时间，这是因为本文提出的方案增加了基于预测的可重复性图的位姿跟踪方法，在增加了位姿跟踪的成功率的同时，减少了因跟踪失败而切换至其他跟踪方法所消耗的时间。

另外，深度特征的提取时间比传统点特征提取的时间要长，再加上提取线特征的时间，约为ORB_SLAM3的提取时间的2倍。位姿优化部分由于添加了线特征约束，因而局部光束平差法的时间也有所增加，大概增加了50%。

3 结论

本文从目前视觉里程计的问题出发，设计了基于深度特征的视觉惯导里程计，并融合了线特征，提高了系统在机器人剧烈运动场景或者弱纹理场景下的鲁棒性，在EuRoC数据集上进行测试，位姿估计效果优异。在纯视觉模式下，本文提出的视觉里程计的平均轨迹误差比对比方案下降了25.9%，在惯导模式下，由于本文所提出的特征只用于优化位姿，平均轨迹误差下降了8.6%，这证明了本文提出的方法能够提高里程计的鲁棒性及准确性。

另外，本文也对里程计进行了时间测试，从测试结果可知由于本文添加了线特征约束，而且提取深度点特征和人工线特征也相对比较耗时，因此本文提出的系统的特征提取时间变成了原来的两倍，而优化时间也增加了一半，尽管依然能满足实时性的要求，但这在实时性敏感的场景可能会带来一些问题，未来可以考虑使用硬件改进来解决这一问题。