2. 广东工业大学 人事处,广东 广州 510006;
3. 广东工业大学 网络信息与现代教育技术中心,广东 广州 510006
2. Personnel Department, Guangdong University of Technology, Guangzhou 510006, China;
3. Center of Campus Network & Modern Educational Technology, Guangdong University of Technology, Guangzhou 510006, China
网约车是互联网信息技术与传统交通行业融合的新发展业态[1]。2010年以来,我国网约车从无到有并快速发展。2016年7月,交通部颁布了《网络预约出租汽车经营服务管理暂行办法》 [2],首次从国家层面出台法律法规明确网约车的合法地位并规范网约车管理和发展的文件,为网约车市场良性发展提供了政策支持[3]。
作为交通运输新业态,网约车在提高交通服务质量、给乘客带来便利的同时,也带来了隐私安全问题。中国消费者协会报告显示,信息泄露问题排在消费者最为关心的网约车行业问题的第二位[4];2016年,Uber发生用户数据泄露事件,泄露客户和驾驶员的姓名、电子邮箱和电话号码[5];2021年7月4日,国家互联网信息办公室发布通报,“滴滴出行”APP严重违法违规收集使用个人信息,从各大应用商店下架[6]。因此隐私保护问题日益重要,引起人们重视。
文献分析发现,国内外学者对网约车的研究主要集中在平台监管和个人隐私保护等方面。在平台监管方面,2015年Posen[7]回顾了出租车行业发展历程和相关监管政策,探讨了优步(Uber) 所面临的监管挑战。2020年付淑换等[8]构建网约车平台与政府监管机构的演化博弈模型,研究媒体报道对网约车行业参与主体行为偏好和策略选择的影响。2020年冯骅等[9]认为传统监管模式对于网约车这样的新业态有诸多不适,提出“政府监管网约车平台,网约车平台监管市场”的双重监管体系。2020年雷丽彩等[10]建立了平台和司机间的演化博弈模型,并对其博弈行为演化过程及演化稳定策略进行探讨。2021年张茂元等[11]提出平台监管创新需要结合互联网平台的技术特性,才能更好地降低平台治理成本、提高治理效果。
对于个人隐私保护,学者们研究了各类组织保护用户隐私的动机。2019年Al-Jabri等[12]收集了沙特阿拉伯253名在线客户数据,研究影响电商网站顾客披露个人信息意愿的因素。2021年朱侯等[13]基于保护动机理论与社会认知理论,研究了移动APP用户隐私信息设置行为影响因素。2021年周林兴等[14]采用问卷调查法,研究如何实现大数据为民服务与防止个人信息泄露、保护隐私的动态平衡,创新性地提出多元治理、技术治理、企业治理和个人治理四个治理维度。进而在网约车领域,人们开始给出改进乘客隐私保护的建议。2018年Li等[15]认为目前的法律制度和行业自治制度不够健全,无法有效保护个人数据的安全。因此提出了建立行业自治协会、制定行业对个人信息使用的具体规则等建议。2019年毛俊响等[16]认为网约车的个人信息存在敏感信息共享的不对等性、共享信息未征得个人同意、平台自我监管与政府监管之间未能实现良好衔接等问题,提出完善网约车个人信息保护的立法和行业规范、加强政府监管、严格行业自律等建议。2021年Cheng等[17]对507名网约车用户进行问卷调查,研究了网约车背景下的乘客隐私保护问题。
综上,国内外学者已经对政府监管和隐私保护问题展开了相关研究,但对于政府监管研究中已经出现的演化博弈方法尚未应用于隐私保护问题中。为此,本文基于政府和平台互相博弈的视角,考虑二者认知不够充分和需要在不断演化中寻找各自均衡策略的现实,针对网约车乘客隐私保护问题,利用演化博弈方法构建政府和网约车平台的演化博弈模型,研究双方博弈的演化机制。第1节将构建演化博弈模型;第2节将运用动态方程求出均衡点,并运用Friedman提出的判定方法判定各均衡点的演化稳定性;第3节将采用数值模拟演示不同情形下的演化趋势,并验证政府监管带来声誉提升程度
政府策略集S1={监管,不监管}。监管指政府投入大量精力对平台的乘客隐私保护行为进行监管,采取奖励或惩罚措施;不监管指政府放松对平台监管,无奖惩措施。政府选择监管和不监管策略的概率分别为
平台策略集S2={自律,不自律}。自律策略指平台企业自觉履行企业社会责任,通过改善服务协议内容、优化平台算法等积极保护乘客隐私;不自律策略指平台以利益最大化为目标,利用乘客隐私获取额外利益。平台选择自律和不自律策略的概率分别为
(1) 政府监管:如制定相关监管法律法规、投入监管资源进行市场检查等,将会产生成本
(2) 政府采取不监管策略将无需付出成本,但是公众会对政府工作产生不满,带来声誉损失
(3) 平台自律:平台具有较强的信息安全意识,在软件、硬件、人力等方面持续投入,需要投入成本
(4) 平台不自律策略将获得额外收益
根据假设,得出收益矩阵如表1所示。为了便于理解,这里整理所有参数,见表2。
| 表 1 博弈双方收益矩阵 Table 1 The payoff matrix of both sides of the game |
| 表 2 相关参数及含义 Table 2 Related parameters and their meanings |
由收益矩阵可知,政府监管期望收益为
| $ {E}_{{x}}=y({W}_{\rm{g}}-{C}_{\rm{g}}-{R}_{\rm{g}}) +(1-y) [{W}_{\rm{g}}+\alpha {F}_{\rm{g}}-(1-\alpha ) {R}_{\rm{g}}-{C}_{\rm{g}}] $ |
不监管期望收益为
| $ \begin{split} F\left(x\right) =& \frac{{\rm{d}}x}{{\rm{d}}t}=x({E}_{\rm{x}}-\overline{E}) =x\left(1-x\right) \left({E}_{{x}}-{E}_{1-x}\right) =\\ &x\left(1-x\right) [{W}_{\rm{g}}+\alpha {F}_{\rm{g}}+{L}_{\rm{g}}-(1-\alpha ) {R}_{\rm{g}}-{C}_{\rm{g}}-\\ &y(\alpha {F}_{\rm{g}}+\alpha {R}_{\rm{g}}+{L}_{\rm{g}}\left) \right] \end{split} $ |
同理,平台自律期望收益
| $ \begin{split} F\left(y\right) =&\frac{{\rm{d}}y}{{\rm{d}}t}=y({U}_{{{y}}}-\overline{U}) =y\left(1-y\right) \left({U}_{{{y}}}-{U}_{1-{{y}}}\right) =\\ &y\left(1-y\right) [{H}_{{\rm{s}}}+{H}_{{\rm{n}}}-{C}_{{\rm{r}}}-P+x\alpha ({R}_{{\rm{g}}}+{F}_{{\rm{g}}}\left) \right] \end{split} $ |
则政府和平台的复制动态方程组成一个二维动力系统,见式(1)。
| $\left\{ {\begin{array}{*{20}{l}} \begin{array}{l} F(x) = x(1 - x)[{W_{\rm{g}}} + \alpha {F_{\rm{g}}} + {L_{\rm{g}}} - (1 - \alpha ){R_{\rm{g}}} - {C_{\rm{g}}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;y(\alpha {F_{\rm{g}}} + \alpha {R_{\rm{g}}} + {L_{\rm{g}}})] \end{array}\\ {F(y) = y(1 - y)[{H_{\rm{s}}} + {H_{\rm{n}}} - {C_{\rm{r}}} - P + x\alpha ({F_{\rm{g}}} + {R_{\rm{g}}})]} \end{array}} \right.$ | (1) |
令式(1) 中两个函数同时等于零,可得到平台与政府间演化博弈5个均衡点
由于复制动态方程得到的均衡点不一定是演化稳定策略点(Evolutionarily Stable Strategy, ESS),因此Friedman提出通过演化博弈系统的雅可比矩阵判断局部均衡点的演化稳定性[19]。该系统的雅可比矩阵
| $ {\boldsymbol{J}}=\left[\begin{array}{cc}\dfrac{\partial F\left(x\right) }{\partial x}& \dfrac{\partial F\left(x\right) }{\partial y}\\ \dfrac{\partial F\left(y\right) }{\partial x}& \dfrac{\partial F\left(y\right) }{\partial y}\end{array}\right]=\left[\begin{array}{cc}{a}_{11}& {a}_{12}\\ {a}_{21}& {a}_{22}\end{array}\right] $ |
式中:
| $ \begin{split} {a}_{11}=& \left(1-2x\right) [{W}_{\rm{g}}+\alpha {F}_{\rm{g}}+{L}_{\rm{g}}-(1-\alpha ) {R}_{\rm{g}}-{C}_{\rm{g}}-\\ & y(\alpha {F}_{\rm{g}}+\alpha {R}_{\rm{g}}+{L}_{\rm{g}}\left) \right] \end{split} $ |
| $ {a}_{12}=-x\left(1-x\right) (\alpha {F}_{\rm{g}}+\alpha {R}_{\rm{g}}+{L}_{\rm{g}}) \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; $ |
| $ {a}_{21}=\alpha y\left(1-y\right) \left({R}_{\rm{g}}+{F}_{\rm{g}}\right) \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; $ |
| $ {a}_{22}=\left(1-2y\right) [{H}_{\rm{s}}+{H}_{\rm{n}}-{C}_{\rm{r}}-P+x\alpha ({R}_{\rm{g}}+{F}_{\rm{g}}\left) \right] $ |
因此5个均衡点在
| 表 3 局部均衡点雅可比矩阵元素取值 Table 3 Jacobian matrix element value of local equilibrium point |
表3中:
| $ A = - \frac{{{C_{\rm{r}}} + P - {H_{\rm{s}}} - {H_{\rm{n}}}}}{{\alpha ({R_{\rm{g}}} + {F_{\rm{g}}}) }}\left[ {1 - \frac{{{C_{\rm{r}}} + P - {H_{\rm{s}}} - {H_{\rm{n}}}}}{{\alpha ({R_{\rm{g}}} + {F_{\rm{g}}}) }}} \right]\left[ {\alpha ({R_{\rm{g}}} + {F_{\rm{g}}}) + {L_{\rm{g}}}} \right], $ |
| $ B = \alpha \left[ {\frac{{{R_{\rm{g}}} + {C_{\rm{g}}} - {W_{\rm{g}}}}}{{\alpha ({R_{\rm{g}}} + {F_{\rm{g}}}) + {L_{\rm{g}}}}}} \right]\left[ {1 - \frac{{{R_{\rm{g}}} + {C_{\rm{g}}} - {W_{\rm{g}}}}}{{\alpha ({R_{\rm{g}}} + {F_{\rm{g}}}) + {L_{\rm{g}}}}}} \right]({R_{\rm{g}}} + {F_{\rm{g}}})\;\;\;\;\; $ |
因为
| 表 4 不同情形下的系统稳定性分析结果 Table 4 System stability analysis results under different conditions |
根据表4可知,在Case 1(
最后,对于
当
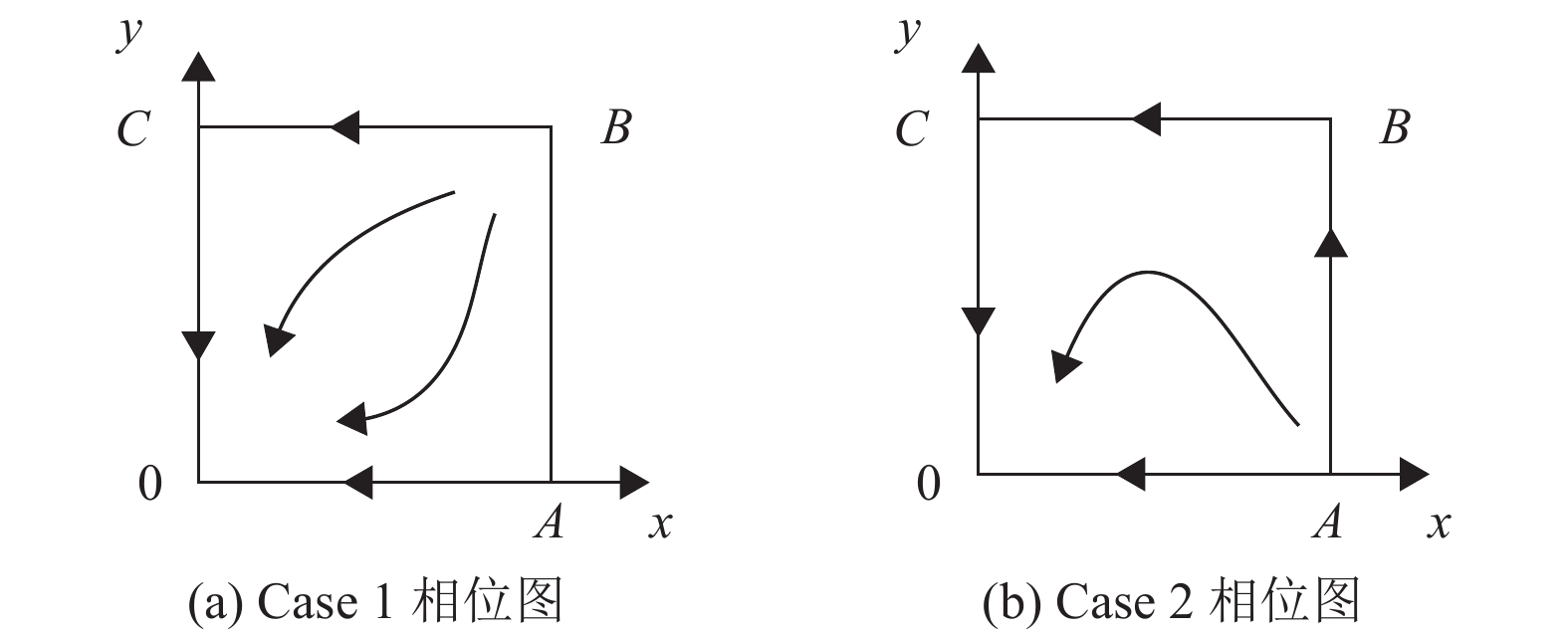
|
图 1 Case 1与Case 2相位图 Figure 1 Phase diagram of Case 1 and Case 2 |
当
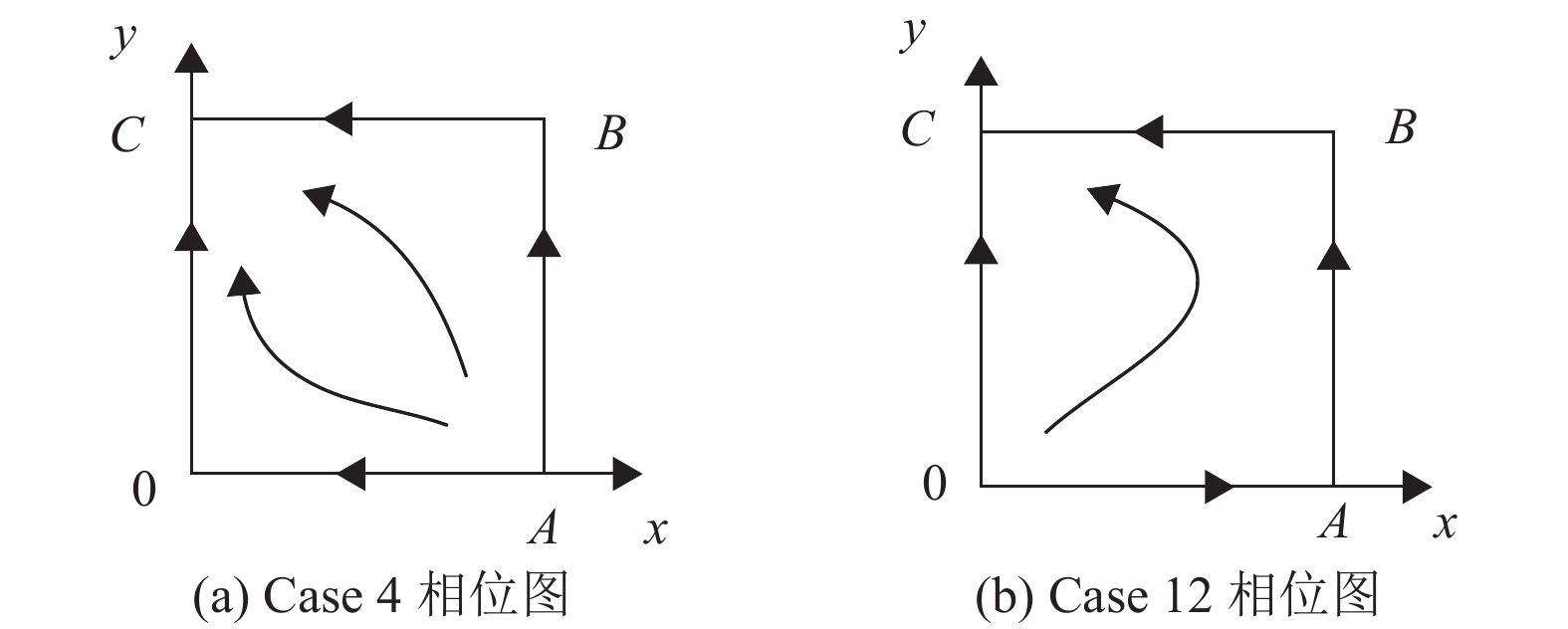
|
图 2 Case 4与Case 12相位图 Figure 2 Phase diagram of Case 4 and Case 12 |
当
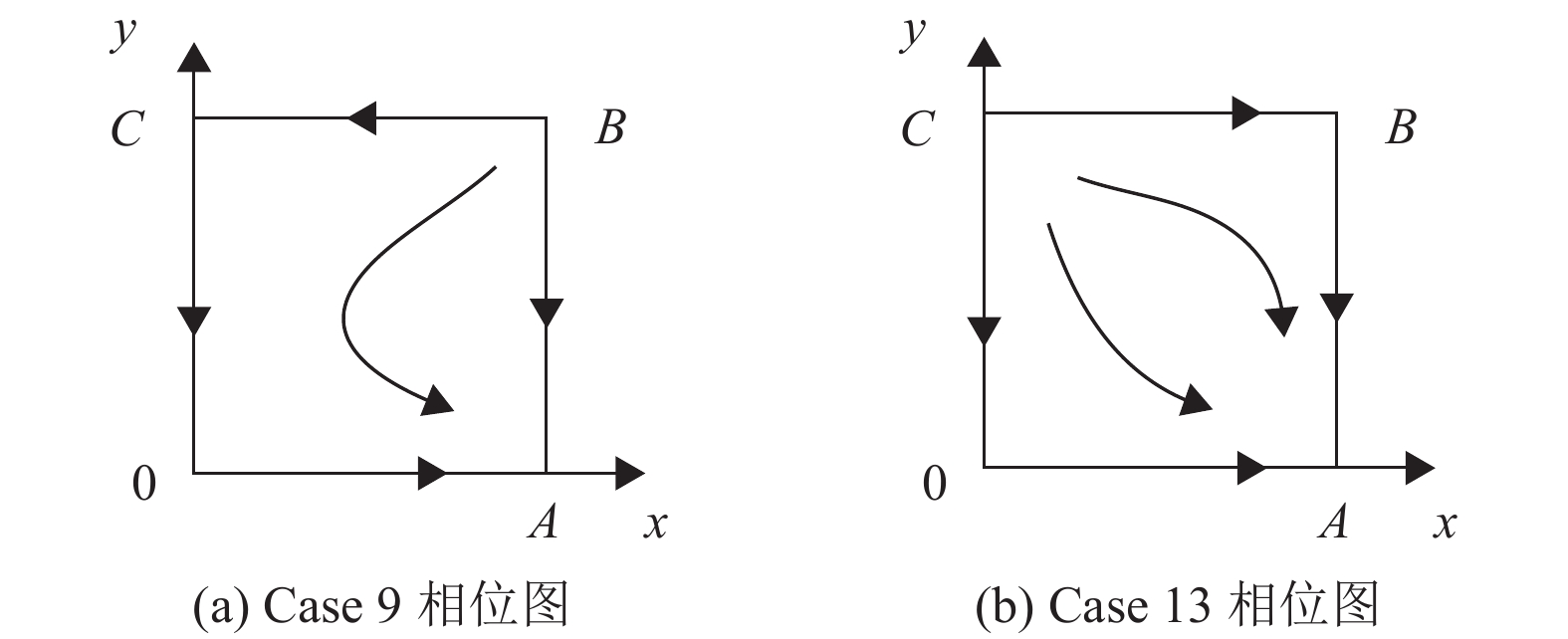
|
图 3 Case 9与Case 13相位图 Figure 3 Phase diagram of Case 9 and Case 13 |
当
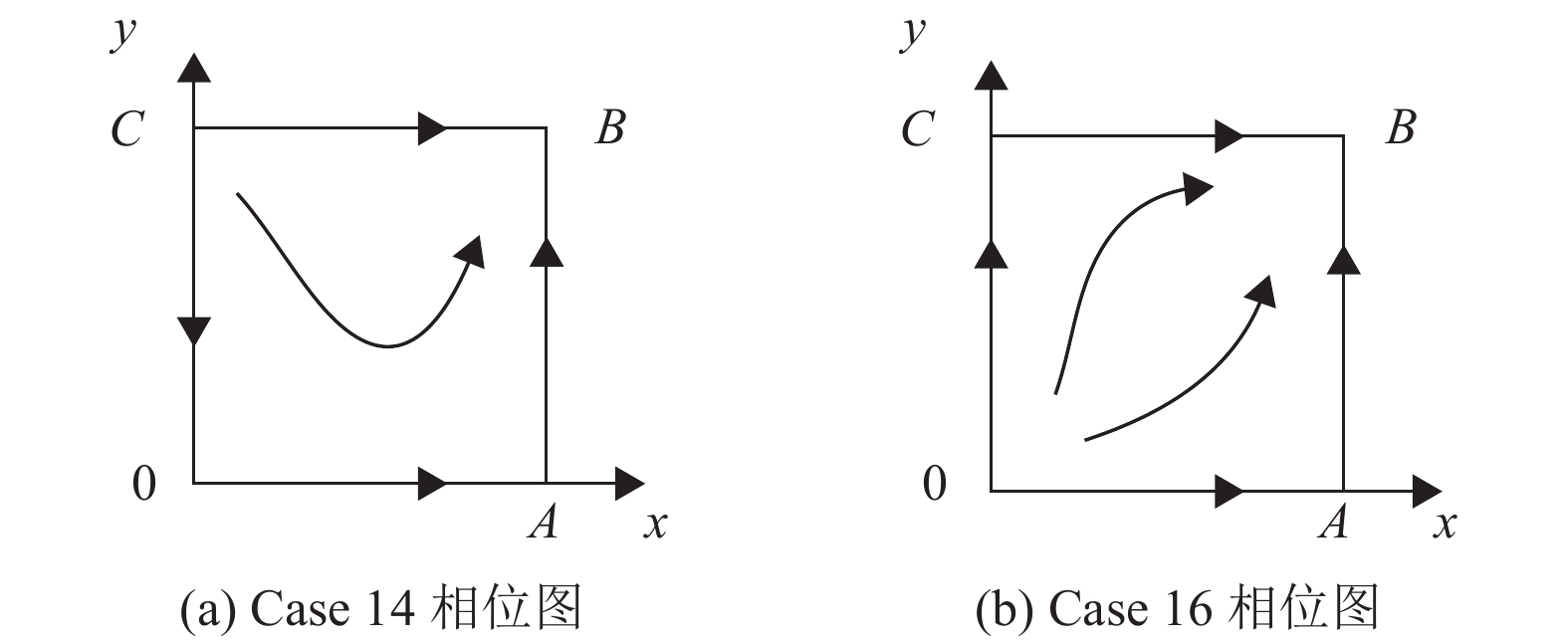
|
图 4 Case 14与Case 16相位图 Figure 4 Phase diagram of Case 14 and Case 16 |
为了直观地反映政府和平台的演化趋势,本节采用 Matlab对不同情形下的演化趋势进行模拟,以演示上述结论。其中,横坐标轴代表政府监管概率
对于Case 1,令

|
图 5 Case 1和Case 2演化路径仿真结果 Figure 5 Simulation results of evolution path of Case 1 and Case 2 |
由图5可知:无论初始概率如何设置,政府监管概率都逐渐趋近于0,同时平台自律概率也逐渐趋近于0;在Case 2下,虽然当政府监管概率较高、平台自律概率较低时,平台出现过提高自律概率的情形,但是随着政府监管概率降低,很快平台也开始不断降低自律概率;所以在这两种情形下,未来很容易出现政府不监管、平台不自律的糟糕状况,从而乘客隐私难以得到保护,最终制约行业健康发展。
3.1.2 Case 4和Case 12在Case 4,令

|
图 6 Case 4和Case 12演化路径仿真结果 Figure 6 Simulation results of evolution path of Case 4 and Case 12 |
由图6可知:无论初始概率如何设置,政府监管概率都逐渐趋近于0,同时平台自律概率逐渐趋近于1;在Case 12,虽然当政府监管和平台自律概率都较低时,政府监管概率曾经有所提高;但是随着平台自律概率提高,政府监管获得收益越来越小,也会再次不断降低监管概率;所以在这两种Case下,最终政府会不监管,但是平台会自律,这样既降低了政府监管成本,又很好地保护了乘客隐私。
3.1.3 Case 9和Case 13在Case 9,令

|
图 7 Case 9和Case 13演化路径仿真结果 Figure 7 Simulation results of evolution path of Case 9 and Case 13 |
由图7可知:无论初始概率如何设置,政府监管概率都逐渐趋近于1,同时平台自律概率逐渐趋近于0;在Case 9,当政府监管和平台自律概率都较高时,政府有降低监管概率的趋势,但是随着平台自律概率下降,政府又将提高监管概率;无论如何,最终政府会监管,但是平台仍然不自律,这样将极大推高政府监管成本,但乘客隐私仍然很难得到保护。
3.1.4 Case 14和Case 16对于Case 14,假设

|
图 8 Case 14和Case 16演化路径仿真结果 Figure 8 Simulation results of evolution path of Case 14 and Case 16 |
由图8可知:无论初始概率如何设置,政府监管和平台自律概率都逐渐趋近于1;在Case 14,当政府监管概率较低、平台自律概率较高时,平台有减少自律的可能,但是随着政府监管概率提升,平台也将不断提升自律概率;无论如何,最终将会出现政府监管、平台自律的理想结果,这样在政府的监管下,平台将很好地履行隐私保护的企业主体责任。
3.2 参数对演化路径影响的仿真分析为了更好地探究
在3.1.1节中Case 1参数设置基础上,保持其他参数不变,令
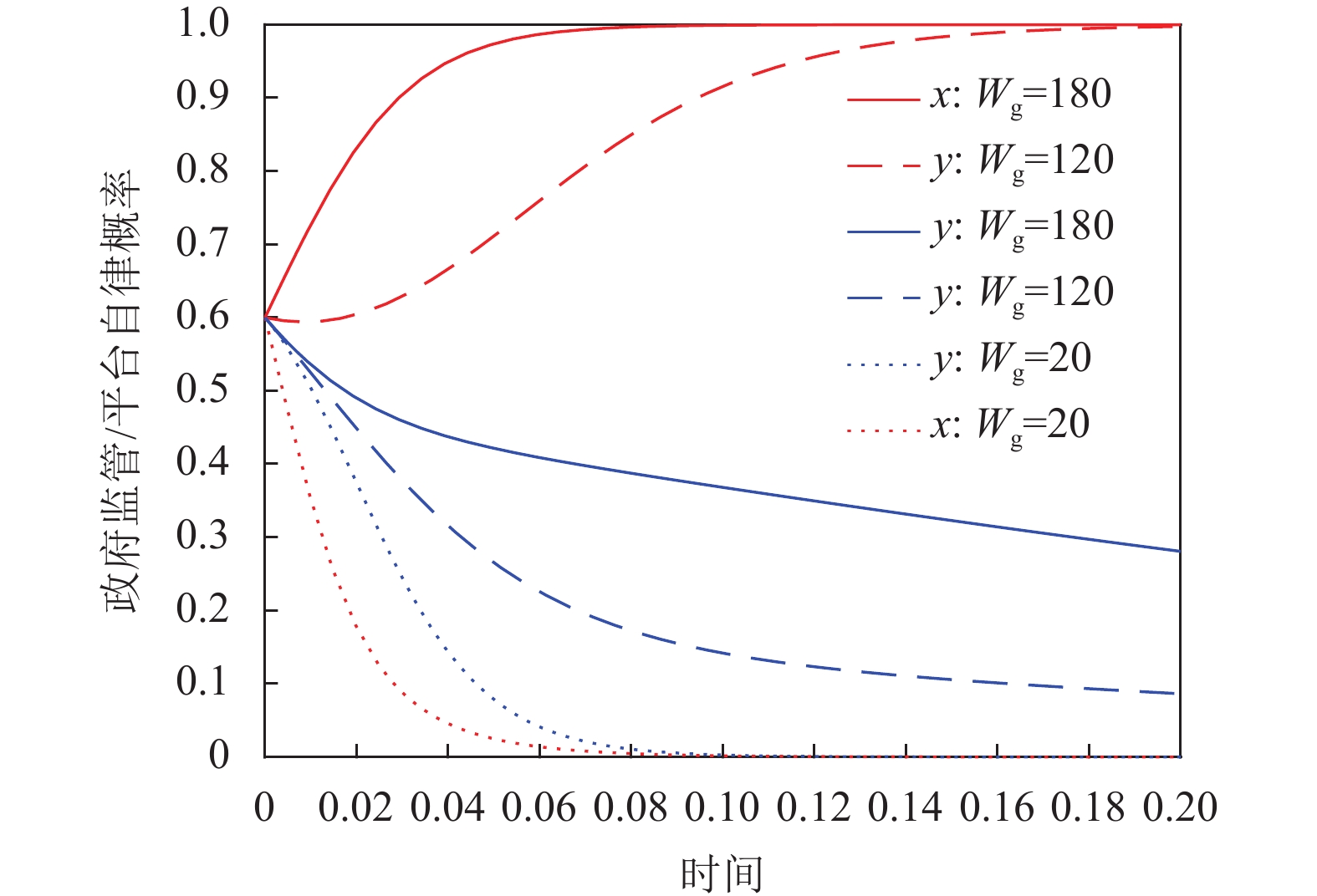
|
图 9 |
从图9可以看出,随着
同一时刻,随着
在3.1.1节Case 1参数设置基础上,令
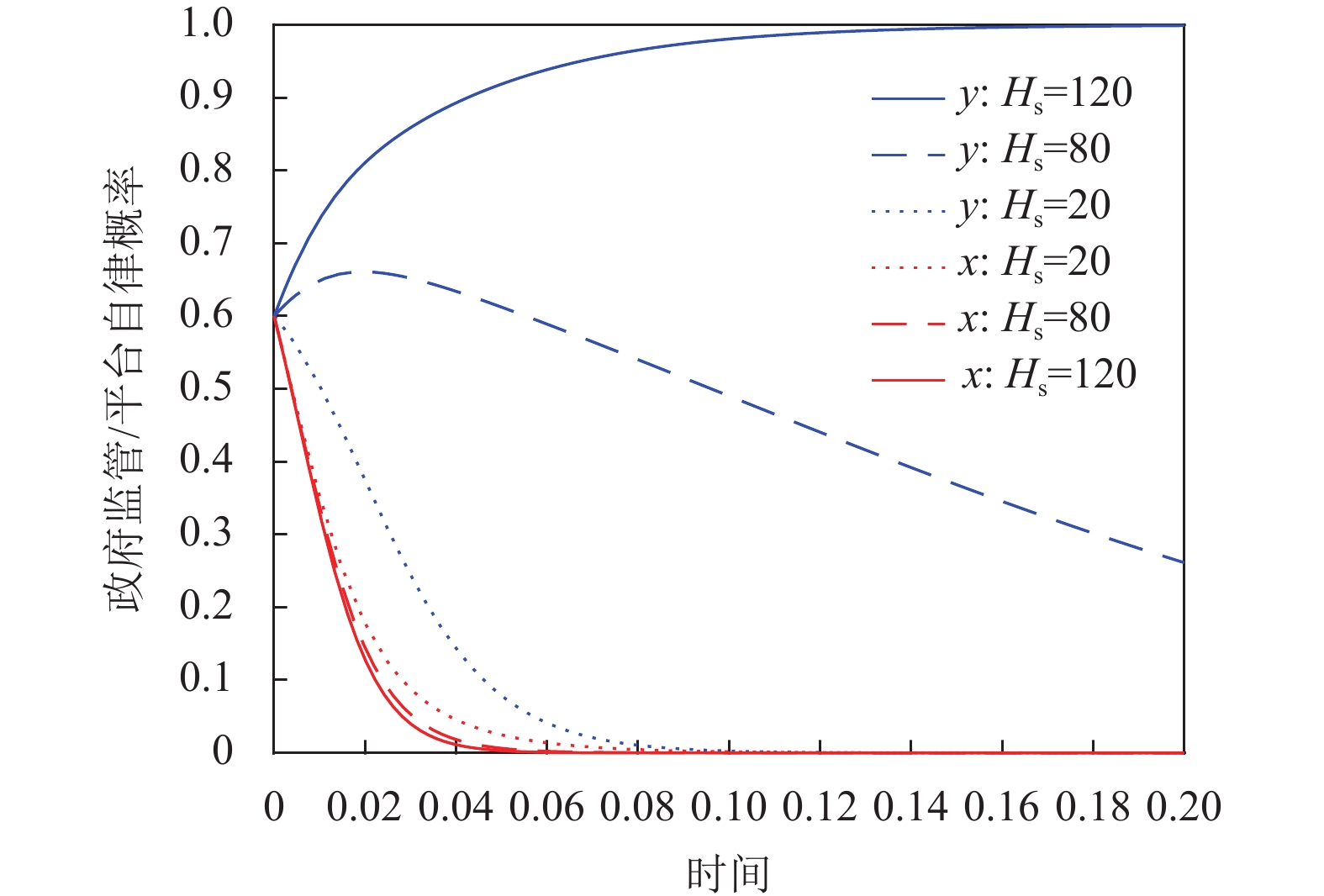
|
图 10 |
从图10看出,随着
同一时刻,随着
在3.1.2节Case 12参数设置基础上,令
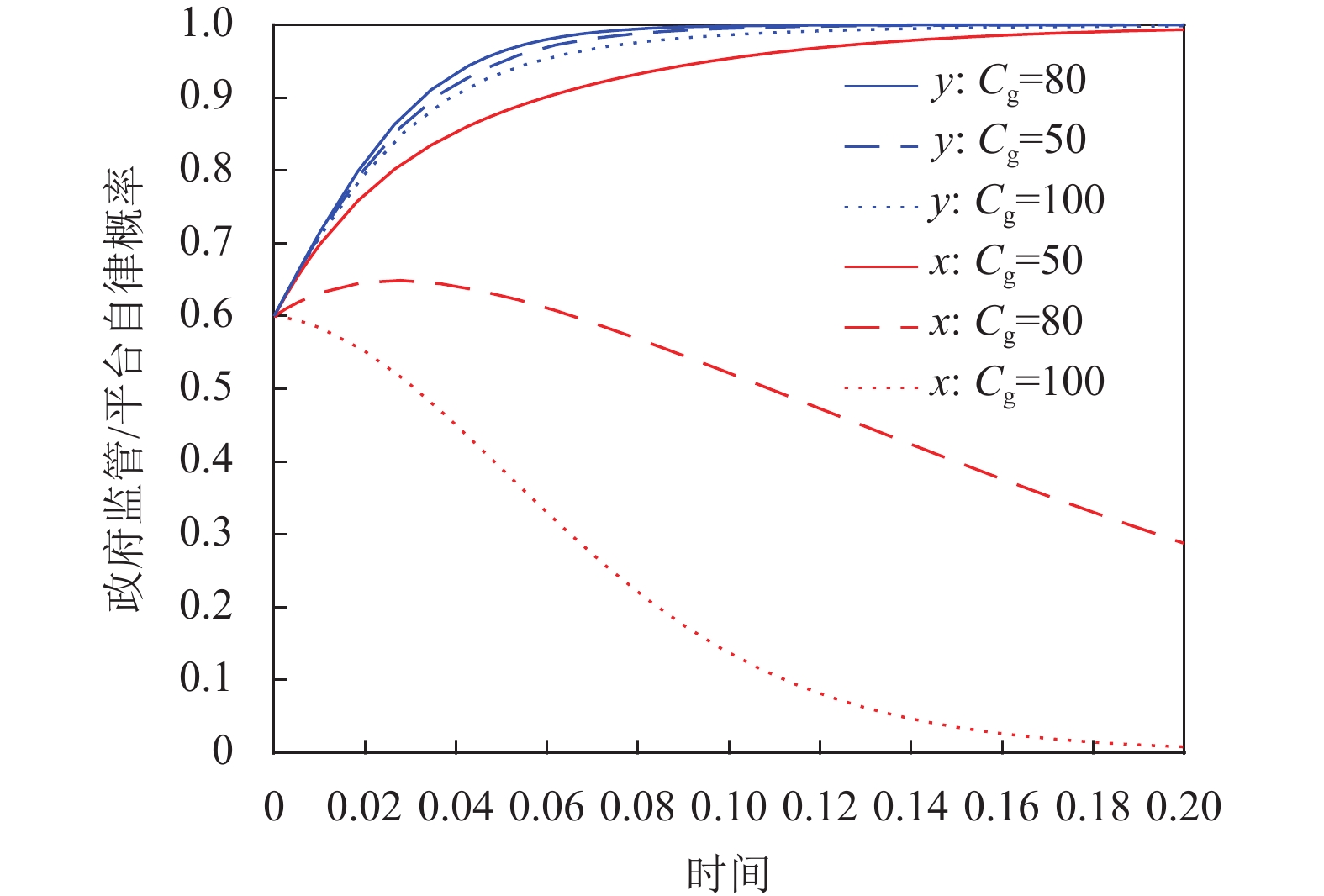
|
图 11 |
从图11可以看出,随着
同一时刻内,随着
在3.1.3节Case 13参数设置基础上,令

|
图 12 |
从图12可以看出,随着
同一时刻内,随着
本文以网约车乘客隐私保护领域的政策监管策略设计问题为研究对象,运用演化博弈理论构建了政府和平台演化博弈模型,找到不同情形下的演化稳定策略;并运用 Matlab 软件对不同情形下双方策略随时间变化的演化路径、政府监管带来声誉提升程度
研究结果显示:(1) 当政府监管收益大于不监管收益,平台自律收益大于不自律时,该博弈将演化为(监管,自律)的均衡状态,这对于保护乘客隐私是好的演化均衡;(2) 当政府监管获得声誉增加时,监管收益可能从小于不监管收益转化为大于不监管收益,从而策略选择由不监管转化为监管;(3) 当平台获得来自社会的正向收益不断增加时,平台策略将从不自律转化为自律;(4) 当政府监管成本不断减小,政府策略会从不监管转化为监管;(5) 当平台自律成本不断减少时,平台会从不自律转化为自律。
为了加强网约车行业乘客隐私保护,政府和平台应努力做到以下两点:(1) 政府不断创新监管方式,降低监管成本,提高监管效率;(2) 平台利用信息技术优势,发挥科技创新在隐私保护方面的作用,降低隐私保护成本。
| [1] |
王静. 中国网约车的监管困境及解决[J].
行政法学研究, 2016(2): 49-59.
WANG J. Regulatory quandary and its solutions of internet chauffeured car in China[J]. Administrative Law Review, 2016(2): 49-59. DOI: 10.3969/j.issn.1005-0078.2016.02.006. |
| [2] |
付淑换, 石岿然. 媒体作用下网约车平台与政府协同治理的演化博弈研究[J].
运筹与管理, 2020, 29(11): 29-36.
FU S H, SHI K R. Evolutionary game study between government and enterprises in online car-hailing under the media[J]. Operations Research and Management Science, 2020, 29(11): 29-36. |
| [3] |
侯登华. 共享经济下网络平台的法律地位——以网约车为研究对象[J].
政法论坛, 2017, 35(1): 157-164.
HOU D H. On the legal status of network platform under Shared economy —taking the online car-hailing as the research object[J]. Tribune of Political Science and Law, 2017, 35(1): 157-164. |
| [4] |
佘颖. 中国消费者协会点名网约车十大乱象[EB/OL]. [2018-05-23]. http://www.ce.cn/xwzx/gnsz/gdxw/201805/23/t20180523_29218763.shtml.
|
| [5] |
前瞻网. Uber因2016年数据泄露处理不当收到英国和荷兰共计92万英镑罚单[EB/OL]. [2018-11-28]. https://baijiahao.baidu.com/s?id=1618341655191873341&wfr=spider&for=pc.
|
| [6] |
中国长安网. 国家网信办: “滴滴出行”严重违法违规收集使用个人信息下架整改[EB/OL]. [2021-07-04]. https://baijiahao.baidu.com/s?id=1704361693953067679&wfr=spider&for=pc.
|
| [7] |
POSEN H A. Ridesharing in the sharing economy: should regulators impose Uber regulations on Uber[J].
Iowa Law Review, 2015, 101(1): 405-433.
|
| [8] |
付淑换, 石岿然. 网约车行业监管困境的演化博弈分析及优化对策[J].
经济问题, 2019(12): 8-15.
FU S H, SHI K R. Evolutionary game analysis of regulatory dilemma in online car-hailing and optimizing policy[J]. On Economic Problems, 2019(12): 8-15. DOI: 10.16011/j.cnki.jjwt.2019.12.003. |
| [9] |
冯骅, 王勇. 网约车监管的改革方向: 实施双重监管体系[J]. 企业经济, 2020(2) : 139-145.
|
| [10] |
雷丽彩, 高尚, 蒋艳, 等. 网约车新政下网约车平台与网约车司机的演化博弈分析[J].
管理工程学报, 2020, 34(1): 55-62.
LEI L C, GAO S, JIANG Y, et al. Evolutionary game analysis of car-hailing industry between platforms and drivers based on new policies of car-hailing[J]. Journal of Industrial Engineering and Engineering Management, 2020, 34(1): 55-62. |
| [11] |
张茂元, 廖安. 技术视角下的互联网平台监管研究——以网约车平台为例[J].
行政论坛, 2021, 28(6): 114-121.
|
| [12] |
AL-JABRI I M, EID M I, ABED A. The willingness to disclose personal information: trade-off between privacy concerns and benefits[J].
Information and Computer Security, 2019, 28(2): 161-181.
DOI: 10.1108/ICS-01-2018-0012. |
| [13] |
朱侯, 张明鑫. 移动APP用户隐私信息设置行为影响因素及其组态效应研究[J].
情报科学, 2021, 39(7): 54-62.
ZHU H, ZHANG M X. Influential factors and configuration effects of user privacy setting behavior in mobile app[J]. Information Science, 2021, 39(7): 54-62. |
| [14] |
周林兴, 韩永继. 大数据环境下个人信息治理研究[J].
情报科学, 2021, 39(3): 11-18.
ZHOU L X, HAN Y J. Research on personal information governance in big data environment[J]. Information Science, 2021, 39(3): 11-18. |
| [15] |
LI X, YANG Z, ZHOU S. Research on legal risk prevention and control mechanism of personal data in china's shared economy model[C]//2018 4th International Conference on Social Science and Higher Education (ICSSHE 2018) . Paris: Atlantis Press, 2018: 586-590.
|
| [16] |
毛俊响, 王思洋. 论网约车个人信息的保护[J].
探索与争鸣, 2019(6): 150-156.
MAO J X, WANG S Y. On the protection of personal information of online car-hailing industry[J]. Exploration and Free Views, 2019(6): 150-156. |
| [17] |
CHENG X, HOU T, MOU J. Investigating perceived risks and benefits of information privacy disclosure in IT-enabled ride-sharing [J]. Inf Manag, 2021, 58(6) : 103450.
|
| [18] |
TAYLOR P D, JONKER L B. Evolutionarily stable strategies and game dynamics[J].
Mathematical Biosciences, 1978, 40(1-2): 145-156.
DOI: 10.1016/0025-5564(78)90077-9. |
| [19] |
FRIEDMAN D. Evolutionary game in economics[J].
Econometrica, 1991, 59(3): 637-666.
DOI: 10.2307/2938222. |
 2023, Vol. 40
2023, Vol. 40
