2. 广东工业大学 信息工程学院,广东 广州 510006
2. School of Information Engineering, Guangdong University of Technology, Guangzhou 510006, China
随着互联网快速发展,互联网上的信息量快速增长[1-3]。人们越来越难以准确找到自己真正需要的、感兴趣的信息。推荐系统是为每个用户提供物品建议的工具和技术[4-6]。目前,推荐系统在学术界得到了广泛的研究,推荐系统可以通过统计方法和先验知识向人们推荐合适的物品,并逐渐形成了一门独立的学科[7],被广泛应用于各种场景,如网飞电影网站[8]、亚马逊和淘宝的电子商务网站[9]、YouTube视频网站等。传统推荐算法往往会陷入数据稀缺性和冷启动问题。数据稀缺性问题与数据数量有关,由于缺少大量的数据,数据的稀疏性严重地影响推荐的有效性。冷启动问题是指新加入系统的新用户没有任何相关的历史纪录,系统不能够向这些新用户提供准确的推荐(用户冷启动),同理,新物品刚进入推荐系统时也没有用户对其评价,故这些新物品也不能通过推荐系统向用户推荐(物品冷启动)。总体而言,冷启动问题得到了更多的重视,而最直接的解决办法就是对用户进行相关的问卷调查,以了解用户的喜好。目前,研究者已经提出了许多推荐算法和系统,主要可以分为基于混合的推荐[10]、基于网络的推荐[11]、基于社交的推荐[12]、基于内容的推荐和协同过滤等。
上述推荐技术主要以推荐准确性作为它们的目标,即如何让尽可能多的用户愿意接受推荐的物品[13-16]。然而,其他一些指标,如新颖性和多样性对用户也很重要。例如,兴趣广泛的用户更关注如何被推荐更多样的物品,而不是简单的高准确度推荐,它依赖于推荐物品的多样性以及准确度。此外,推荐系统通常面临严重的冷启动问题。如果没有考虑到物品的新颖性,或者没有对新物品进行特殊处理,则不能推荐没有任何评分的新物品。文献[17-18]指出,同时提高推荐的准确度、多样性、新颖性和覆盖率是困难的,需要采用多目标进化算法对传统推荐算法进行优化,才能得到更好的推荐结果[19-21]。
多目标优化技术已在诸如工程设计[22]和路线规划[23]等问题上得到应用,构建多目标优化推荐模型,就是试图同时优化多个冲突的目标。在求解多目标优化问题时,会返回许多非支配解,每个解都是不同目标之间的权衡[24]。Ribeiro等[25]建立了一个多目标推荐系统,针对精度、多样性和新颖性这三个冲突目标,试图优化得到最优的多目标解集,其中精度使用推荐列表中物品的预测评分的平均值来评估。进化算法也用于求解个性化推荐系统的多目标优化,比如文献[26]基于精度和多样性两个目标,提出了多目标优化算法。文献[27]在文献[26]基础上提出基于概率的多目标算法(Probabilistic Multi-Objective Evolutionary Algorithm, PMOEA),在性能上取得更优的结果。
推荐算法的困难之处很大程度上依赖于数据的特点。在此基础上,本文针对不同用户的分层推荐模型,采用 NSGA II (Fast Non-dominated Sorting Genetic Algorithm)作为多目标优化算法载体,利用推荐列表中物品的预测得分平均值来度量推荐准确度,以覆盖率度量推荐的多样性[28]。从算法的初始化方法、交叉操作和变异率多方面入手,对现有的多目标推荐算法进行了改进。
本文的主要创新点在于提出了基于评价次数的用户分层策略的算法初始化方案。基于评价物品的次数,把用户分为评价次数高、中、低3组,为每一组用户提供具有不同初始化方法的推荐算法。然后,基于新的算法测试得到更优的算法交叉和变异方式。本文工作的贡献点可以归纳为以下3点:
(1) 建议针对不同类型的用户,采用不同的推荐策略。例如,在评价物品较多次的情况下,推荐策略应该以偏重推荐精度的方法进行,因此初始化方案更侧重于预测评分平均值高的推荐结果,该方案在本文称为IT100方案。覆盖率越大的推荐结果对新用户越有吸引力,可以让新用户接触更多样的物品,因此对于评价次数少的用户,应重视多样性和新颖性高的推荐结果,该方案称为IC100方案。评价次数居中的用户,则采用以上两种方式分别以一半概率组合的形式进行算法初始化,称为IT50-IC50方案。
(2) 试验结果显示,在使用IT100方法进行初始化时,多目标推荐算法会找到接近于预测评分最优平均值的前沿位置点;当采用第二种初始化方法IT50-IC50时,多目标推荐算法将获得预测评分均值和覆盖率之间的折中最优值;当使用第三种初始化方法IC100时,在多目标推荐算法中可以发现左上角的边界点具有较好的覆盖率。结合上述3种初始化方法帕累托前沿的分布特性可以得到最佳的推荐列表。
(3) 调整PMOEA算法中的交叉和变异参数,算法寻优能力明显提升。进行交叉操作时,PMOEA可将其中一个交叉个体固定为Top-L中的个体或覆盖率的极值个体,交叉数量降低至3个,而变异率调整至0.05。
1 相关工作传统的推荐算法可以获取到用户对某些物品的评分,发现用户感兴趣的物品并推荐给用户,所以物品评分是推荐算法的重要基本步骤。
给定物品集 X 和用户集 Y ,物品集X包含N个物品,用户集Y包含M个用户。设评分矩阵为 R|X|×|Y|
目前,基于用户的协同过滤算法(CF_User)是应用最广泛的推荐方法之一。它首先确定不同用户之间的相似性,可以使用余弦相似度或皮尔逊相关系数来进行度量。本文将采用余弦相似度来度量不同用户之间的相似性。计算当前用户u与其他所有用户v(v
| $ {{\varphi}}{_{\text{U}}}(u,v) = \frac{{{{\boldsymbol{r}}_u} \cdot {{\boldsymbol{r}}_v}}}{{\left| {{{\boldsymbol{r}}_u}} \right| \cdot \left| {{{\boldsymbol{r}}_v}} \right|}} $ | (1) |
式中:
| $ {{R}}{_{\text{U}}}(u,i) {\text{ = }}\frac{{\displaystyle\sum\nolimits_{v \in {S_{\text{U}}}(u,K) } {{{\varphi}}{_{\text{U}}}(u,v) r(v,i) } }}{{\displaystyle\sum\nolimits_{v \in {S_{\text{U}}}(u,K) } {{{\varphi}}{_{\text{U}}}(u,v) } }} $ | (2) |
式中:r(v, i) 为用户v对物品i的评分。
1.2 基于物品的协同过滤算法(CF_Item)基于物品的协同过滤(CF_Item)与基于用户的协同过滤(CF_User)相似,可通过余弦相似度来度量不同物品间的相似性,利用用户对物品的偏好来寻找相似的物品。物品i和物品j之间的相似性采用余弦相似度来计算,具体为
| $ {{\varphi}}{_{\text{I}}}(i,j) = \frac{{{{{\boldsymbol{r}}'_i}} \cdot {{{\boldsymbol{r}}'_j}}}}{{\left| {{{{\boldsymbol{r}}'_i}}} \right| \cdot \left| {{{{\boldsymbol{r}}'_j}}} \right|}} $ | (3) |
式中:
| $ {{R}}{_{\text{I}}}(u,i) {\text{ = }}\frac{{{\displaystyle\sum}_{j \in {S_{\text{I}}}(i,K) } {{{\varphi}}{_{\text{I}}}(i,j) r(u,j) } }}{{{\displaystyle\sum}_{j \in {S_{\text{I}}}(i,K)} {{{\varphi}}{_{\text{I}}}(i,j) } }} $ | (4) |
ProbS方法[31]利用二分网络来得到物品评分,计算从物品到用户的转换资源,所有物品分配给用户u的资源计算为
| $ f(u) = \sum\nolimits_{i = 1}^N {\frac{{r(u,i)}}{{{k_i}}}} $ | (5) |
式中:ki为对物品i评分的用户数。所有用户分配到物品xi的资源计算为
| $ f'(i) = \sum\nolimits_{u = 1}^M {\frac{{r(u,i)f({u})}}{{{l_u}}}} $ | (6) |
式中:r(u,i) 为用户u对物品i的评分,lu为用户u已评分的物品数。因此,式(6) 得到的就是物品i的推荐预测评分。
1.4 推荐列表评价函数若每个用户选择评分排在前面的未评分物品组成推荐列表,则设每个用户的推荐列表都包含L个未评分物品,组成推荐列表集SL =(
| $ {{{R}}_{\rm{A}}}({S_{ L}}) = \frac{{\displaystyle\sum\nolimits_{u \in Y}\displaystyle \sum\nolimits_{i \in {S_L}} {{{R}}(u,i)} }}{{M L}} $ | (7) |
推荐物品的多样性也是评价推荐能力的重要指标。常用的多样性指标有基于覆盖率[26]的多样性指标C:
| $ {{C}}({S_{ L}}) = \frac{{N'}}{N} $ | (8) |
式中:N'为每个用户推荐L个物品所构成的推荐列表集合中非重复物品的总数。非重复的物品越多,用户推荐的物品多样性越高。
此外,还有基于推荐列表中不同主题数量的主题多样性指标D[27]:
| $ {{D}}({S_{ L}}) = \sum\nolimits_{u \in Y} {\Bigg( { - \Bigg( \sum\nolimits_{i \in {{\boldsymbol{L}}_u}} {\frac{{| {{t_{{x_i}}}} |}}{{| {{z_{{{\boldsymbol{L}}_u}}}} |}} \cdot \ln } \frac{{| {{t_{{x_i}}}} |}}{{| {{z_{{{\boldsymbol{L}}_u}}}} |}} \Bigg) {{V}} ({{\boldsymbol{L}}_u}) } \Bigg) } $ | (9) |
式中:
推荐列表的预测评分平均值和多样性评价往往是冲突的两个指标,要获得满足多个优化目标的推荐列表,采用多目标优化算法是一种可行的方法。本文基于PMOEA[27]的框架,提出了针对具有不同数据稀疏性的用户采用不同的算法初始化方法,并对算法的交叉对象和变异操作进行了改良。下面首先介绍本文算法的基本流程,然后介绍本文提出的3种初始化方法。
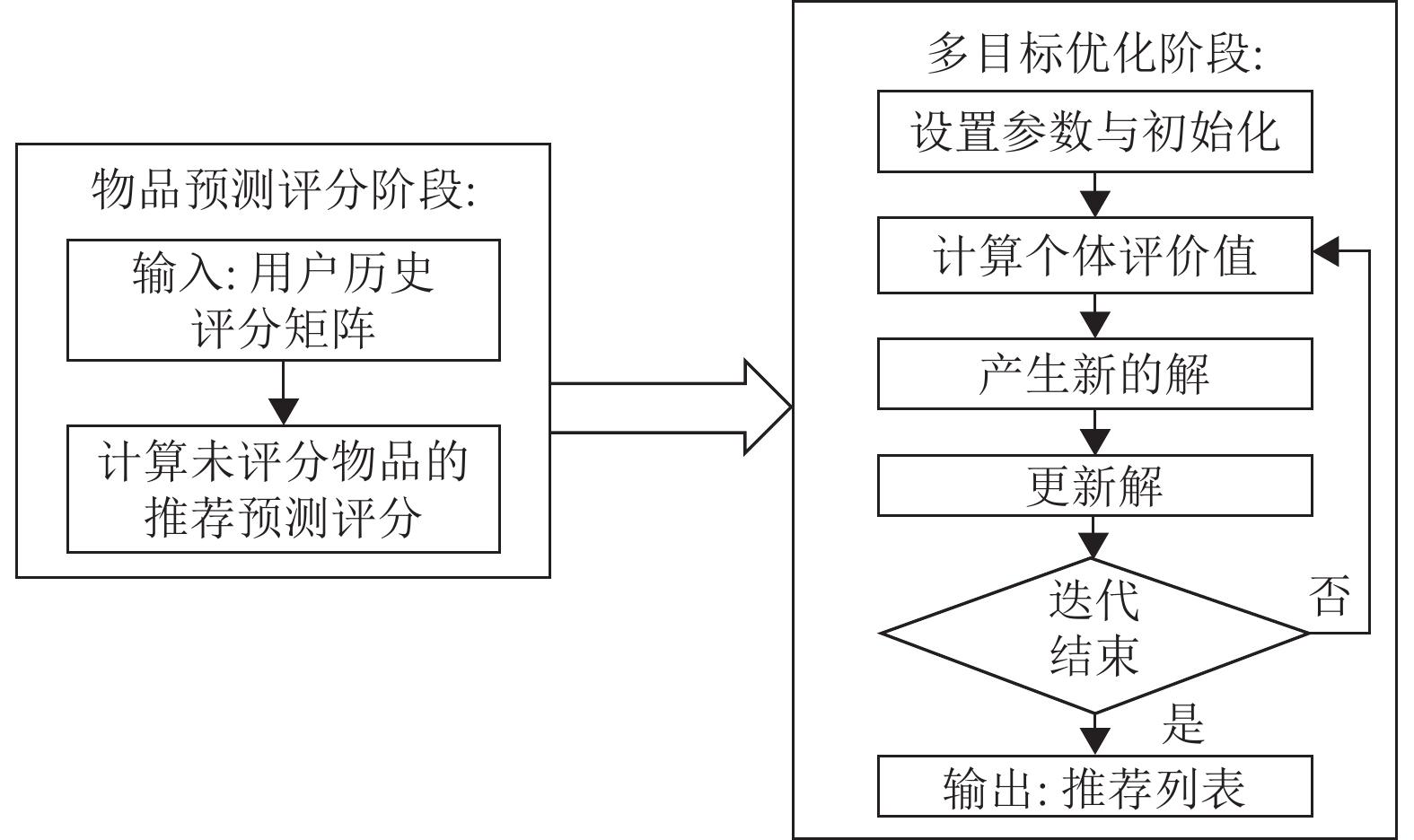
2.1 基本流程图1为一个典型的多目标推荐算法的工作流程。工作流程分为物品预测评分和多目标优化两个步骤。未被评分物品的预测得分由CF_User[29]、CF_Item[30]和 ProbS[31]等传统推荐算法来计算。多目标优化算法必须找到符合2个优化目标的帕累托最优解集合。
|
图 1 典型的多目标优化推荐算法的工作过程 Figure 1 Process of a typical multi-objective optimization recommendation algorithm |
在多目标优化阶段,先设置参数进行初始化。在循环过程中,首先对各个个体进行评估,用目标函数进行计算。该算法通过初始解的交叉、变异等操作来优化运算,生成新的解,并将其与旧的解进行比较,择优选取,从而得到新的较优解。这个周期过程一直持续到结束条件被满足为止。最后是把推荐的结果输出给用户。
2.2 编码方案算法的个体由每个用户的推荐列表组成,假设每个用户的推荐列表长度为L,有M个用户,那么一个个体解的长度为n = M×L。用Xi=

|
图 2 编码方案的结构 Figure 2 Structure of the coding scheme |
本文其中一个优化目标就是要增加推荐物品的多样性,在初始化过程中,将多样性最大化的推荐列表作为初始化个体,可以提高多目标优化算法在多样性上的求解质量。本文可以用式(8)求出覆盖率最大值;同理,用传统推荐方法获得的前 L项预测得分最高的物品所构成的推荐列表,可以通过式(7)获得最大预测得分平均值。
本文使用最大覆盖率和最大预测评分平均值的个体来进行群体的初始化。具体如下:
方法1:用传统推荐算法可得到L 项预测评分最高的物品构成的推荐列表(Top-L解),种群个体以此进行初始化。
方法2:种群中的半数个体采用Top-L解进行初始化,而另外一半则基于最大覆盖率的推荐列表解进行初始化。
方法3:种群个体全部基于覆盖率最大值对应的推荐列表解进行初始化。
在第1、3种初始群体被确定后,所有的重复个体都进行一次变异,只保留有一个原始群体不做变异操作。当第2种初始化群体被确定后,需要保留一个最大预测评分平均值的原始个体和最大覆盖率的原始个体,所有剩余的重复个体都要进行一次变异处理,所以得到的初始种群的个体基本不同。在实际实验中,考虑到种群规模为100,将以上3种初始化方案分别用代号IT100,IT50-IC50,IC100表示。
3 实验分析 3.1 实验测试数据本文采用的Movielens−100K数据集可从GroupLens Research网站下载。这份数据集包括943名用户,共对1682部影片进行了100 000次评分,每位用户都对至少20部影片进行了评分。该网站已将数据集分为训练集和测试集,测试集共有462名用户,主题种类最多为19个。
3.2 推荐质量评价指标为了评估多目标推荐算法的推荐质量,本文使用了准确率(Precision)和新颖性(Novelty)[26]作为外部评价指标。准确率的具体计算公式为
| $ {{\varGamma }}({S_{ L}}) = \frac{1}{M} \sum\nolimits_{u \in Y} {\frac{{\left| {{{\boldsymbol{L}}_u} \cap {{\boldsymbol{T}}_u}} \right|}}{L}} $ | (10) |
式中:Tu为用户u在测试数据集中评分大于2的物品集。
新颖性(用
| $ {{\varPsi }}({S_{ L}}) = \frac{1}{{M L}}\sum\nolimits_{u = 1}^M {\sum\nolimits_{i \in {{\boldsymbol{L}}_u}} {{{\log }_2}\left( {\frac{M}{{{N_i}}}} \right) } } $ | (11) |
式中:Ni为物品i的被评价次数。如果一个推荐列表的物品比较热门,那么这个推荐列表的新颖性就比较低。
准确率的范围是[0,1],新颖度的范围是[0,+∞) 。在数据集中,评分的数值是从0到5的整数,0表示没有被评分,1是最低的,5是最高的,得分越高的就越喜欢这部影片。根据式(7),CF_User和CF_Item计算得到的预测评分平均值的范围是[0,5)。Probs需要对实验数据进行预处理[26],用户对物品评分在1~2分时用0表示不喜欢,在3~5之间使用1表示喜爱,所以范围是[0,1)。
3.3 实验算法测试文献[27]介绍一种基于概率的多目标算法 PMOEA,并将 PMOEA与CF_User、CF_Item、ProbS三种传统推荐算法进行组合,分别为PMOEA + CF_User、PMOEA + CF_Item、PMOEA + ProbS。
其中,要进行优化的用户推荐列表长度L=10,推荐算法的邻居数量K=20,算法的预设群体规模都为100,交叉数目为5、变异率为0.5,以式(7)为优化目标1,以式(9)为目标2,算法的最大迭代次数为500。本文结合上述3种算法,分别从初始化、交叉运算、变异率这3个方面进行优化,再进行实验对比。
3.4 对交叉操作的改进与分析原始的PMOEA算法是使用5个随机选取的父代进行交叉的[27]。本文将一个交叉个体固定在通过传统评分法(CF_User、CF_Item、ProbS)获得的最大预测评分平均值的L项里。采用 PMOEA+CF_User-1C4来表示5个交叉个体分别为Top-L和4个随机选取。同理将交叉个数再减少到4个和3个,那么可以得到 PMOEA+CF_User-1C3和 PMOEA+CF_User-1C2算法。
如图3所示,分别将CF_User、CF_Item、ProbS与PMOEA算法相结合,利用不同的策略,得到30次运行中最优的个体分布。如果将Top-L对应的解添加到交叉运算中,可以改善主题多样性和预测评分平均值,使算法得到更优的解。从图中可以看出1C2交叉方法可以得到最优解种群分布。
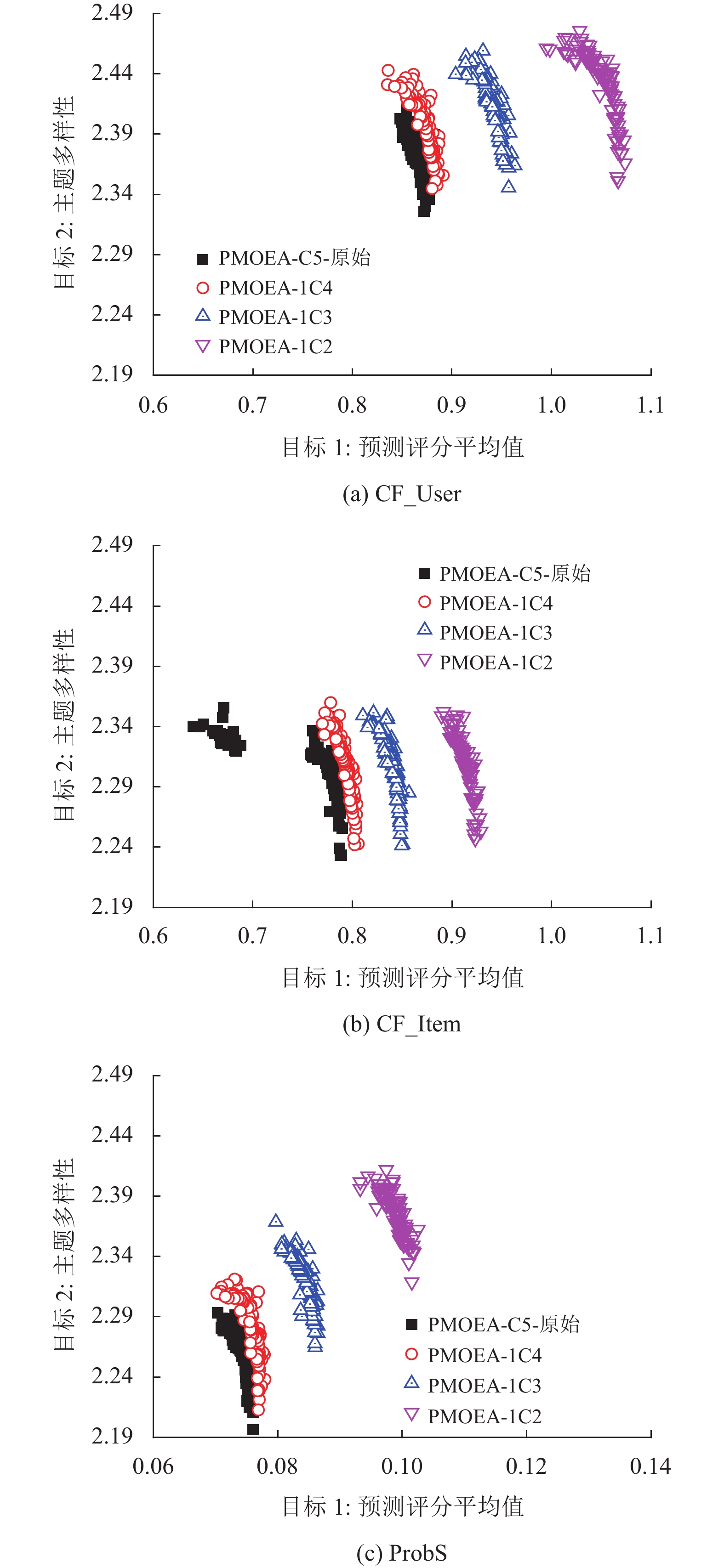
|
图 3 基于CF_User,CF_Item和ProbS方法的PMOEA在不同交叉下的迭代种群分布 Figure 3 PMOEA based on CF_User, CF_Item and ProbS method and its iterative population distribution using different crossover methods |
在其他实验参数相同的条件下,对不同的变异率进行了试验。文献[27]使用的变异率是0.5,而本实验对其进行了改良,降低变异率。图4是0.5、0.3、0.1、0.05的变异率下的实验结果。
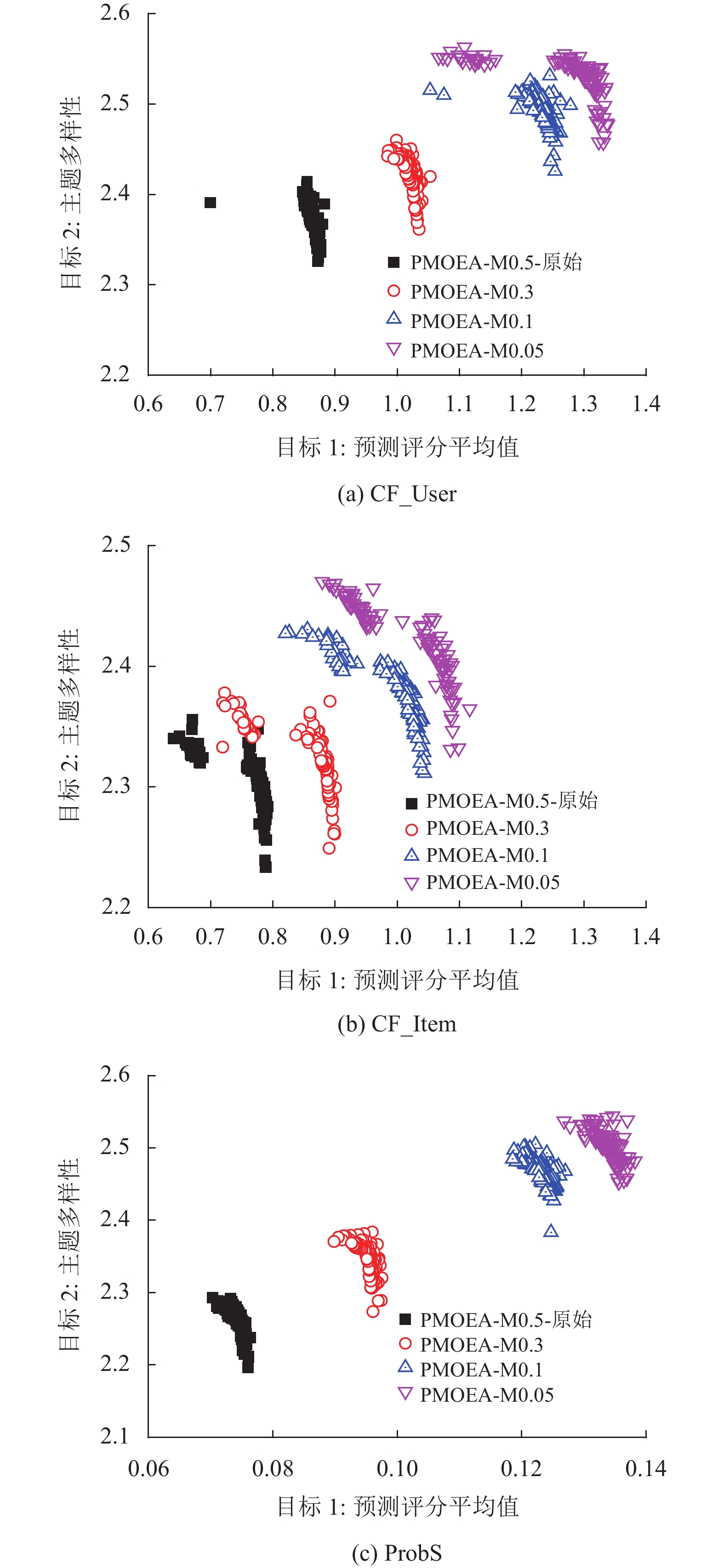
|
图 4 基于CF_User,CF_Item和ProbS方法的PMOEA在不同变异率下的迭代种群分布 Figure 4 Iterative population distribution of PMOEA based on CF_User, CF_Item and ProbS method under different variation rates |
由图4(a)可以看出,原PMOEA的变异率为0.5,其预测评分平均值在0.7~0.9,主题多样性在2.3~2.45;当变异率变为0.05时,它的预测评分平均值增长到1.25~1.35,主题多样性也增长至2.45~2.55,两个目标得到大幅提升。同样的,从图4(b)和图4(c)也可以看出,变异率设置为0.05之后,与原PMOEA变异率0.5相比,目标值都有大幅度的提升。因此,将0.05设置为最佳的变异率参数。
3.6 对多样性目标的选择分析本文对3种不同的用户初始化方法进行了实验。原始PMOEA[27]将主题多样性作为多样性的优化目标。本文将使用式(8)的覆盖率作为多样性的优化目标,对PMOEA+CF_Item算法进行测试,比较分析准确率和新颖度。本文实验将采用最优参数值进行测试,即1C2的交叉操作、0.05的变异率,30次运行中最优种群的帕累托前沿点如图5所示。
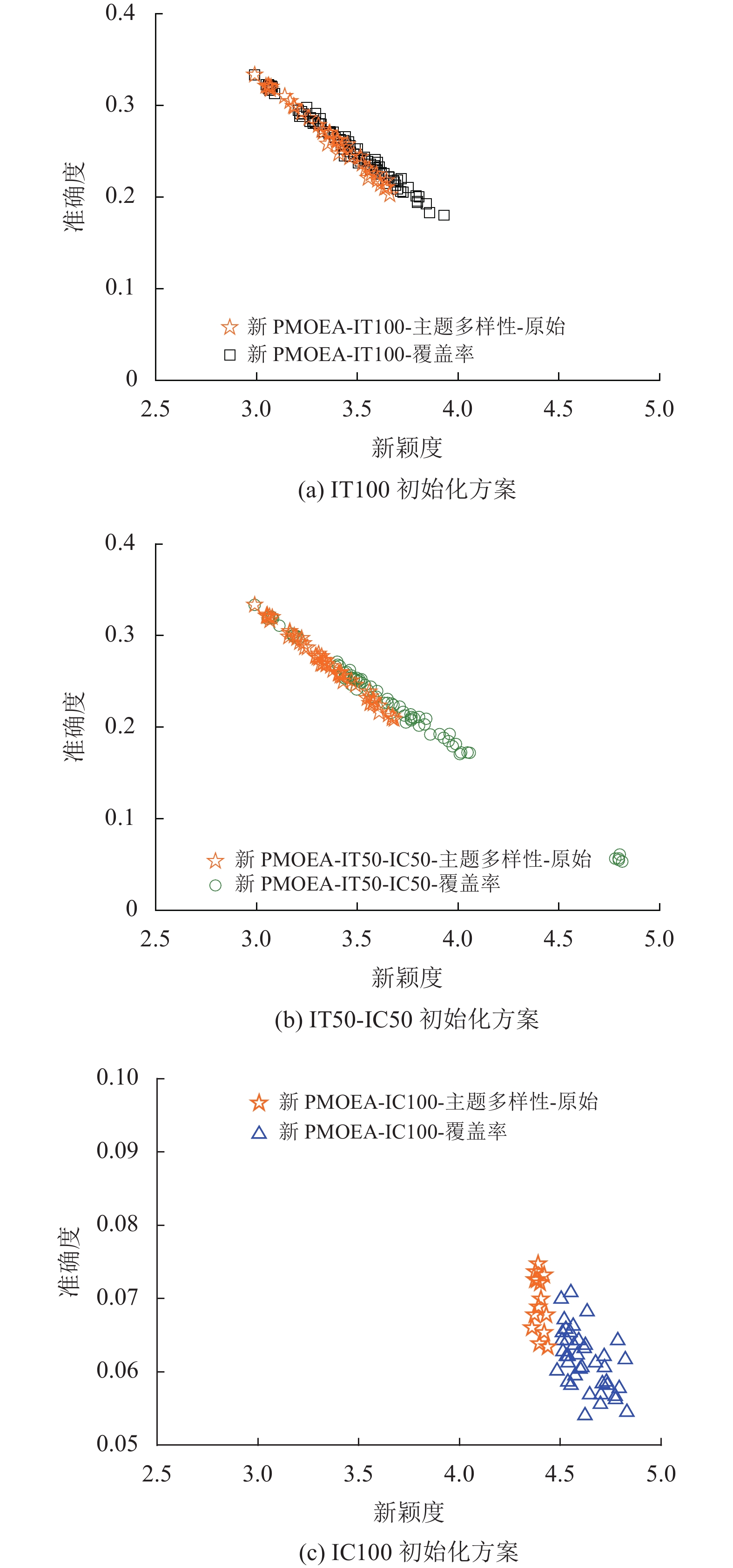
|
图 5 采用CF_Item方法的PMOEA中基于两种优化目标的推荐预测评分平均值和新颖性对比图 Figure 5 Comparison of recommendation accuracy and novelty based on two optimization objectives in PMOEA based on CF_Item |
准确率和新颖性都是越大越好。在图5(a)中,采用覆盖率为优化目标的PMOEA得到的个体不仅新颖性高,并且准确率与以主题多样性为优化目标的PMOEA相似,在图5(b)~(c)中的两种初始化方案的实验结果亦如此,所以用覆盖率为优化目标的PMOEA得到的推荐列表在准确率与新颖性上整体优于采用主题多样性为优化目标的PMOEA。
3.7 用户分层的初始化分析为检验用户分层初始化的效果,本文实验的种群规模设置为100,2个优化目标分别是预测评分平均值和覆盖率,然后利用本文所述的3个初始化方法获得初始群体。其余实验参数将采用上文实验求出的最优参数,并独立运行30次,每次运行后会汇总实验所得的帕累托前沿点再做一次快速非支配排序,得出最后的帕累托前沿点如图6所示。
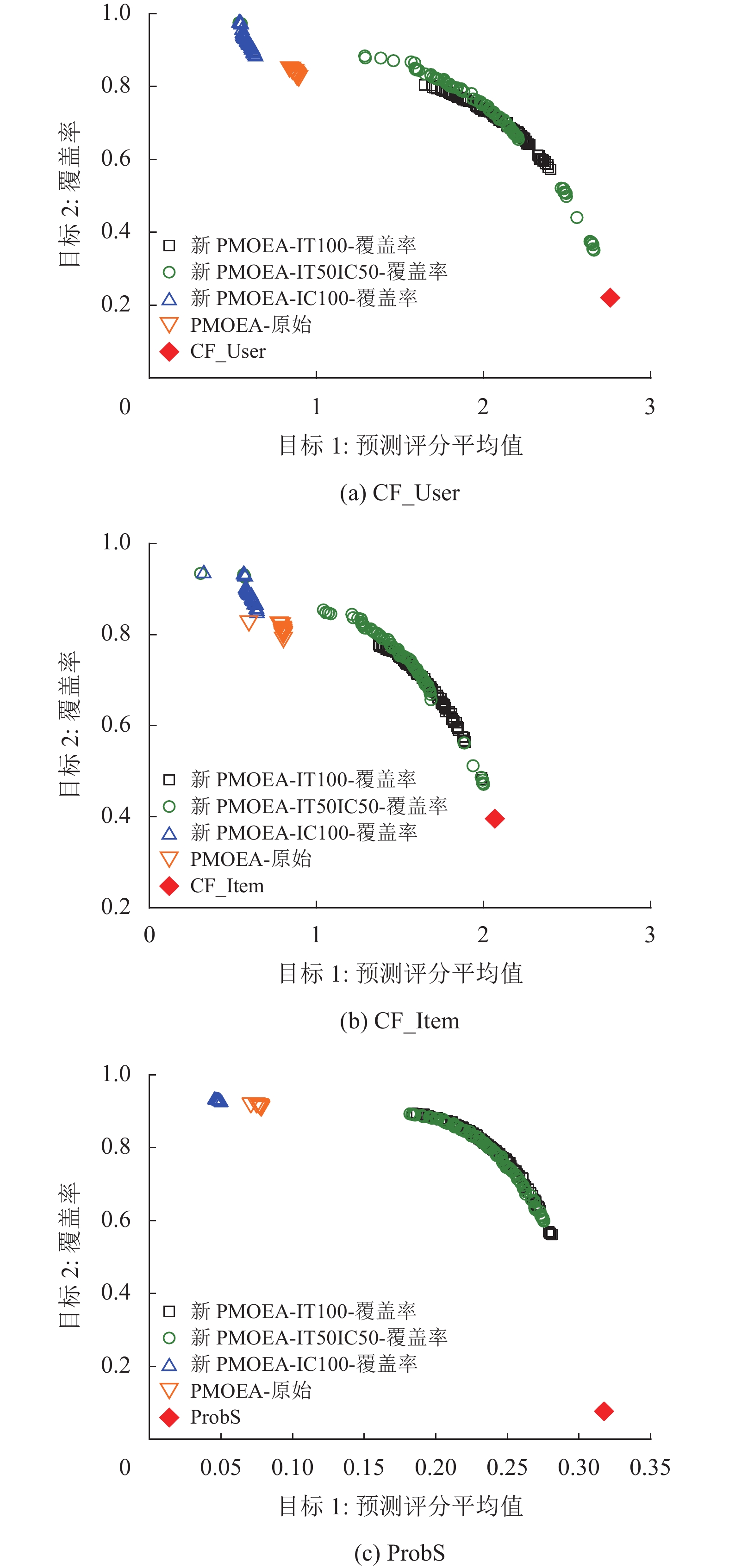
|
图 6 PMOEA基于CF_User,CF_Item,ProbS方法的帕累托前沿图 Figure 6 Pareto front diagram of PMOEA based on CF_User, CF_Item, ProbS |
采用IT100初始化方案进行初始化时,多目标推荐算法能够找到最接近预测评分最大平均值的前沿点,且覆盖度优于传统推荐方法,并与原始 PMOEA算法相比,其预测评分平均值有明显提升。当采用IT50-IC50初始化方案进行初始化时,多目标推荐算法将会找到预测评分平均值和覆盖率折中的帕累托前沿点。当采用IC100初始方案进行初始化时,即图6的左上方部分,多目标推荐算法可以找到覆盖率的最佳帕累托前沿点。
4 基于用户分层的推荐方案为检验3种初始化方法的适用性,将943个用户按照评价物品的数量依次递减排序。按递减顺序,可以将所有用户平均分为3个组,用户集1用于检验第一种初始化方案;用户集2是第316~630名用户,用作检验第二种初始化方案;用户集3是第631~943名用户,用作校验第三种初始化方案。然后,评价对比3种初始化方法的实验结果。
4.1 评价次数最多的用户(用户集1)该类用户集的用户评价物品次数最多,推荐的准确率尤为重要。从表1可以看出,IT100初始化方法相对于原始PMOEA和采用另外两种初始化方法的算法相比,得到的准确率最高,在新颖性上也比传统CF_User得到的解要高,综合两个优化目标,IT100初始化方法对用户集1适用性最高。
| 表 1 用户集1在各类算法中的评价指标 Table 1 Evaluation indexes of user set 1 in various algorithms |
该类用户集可定义为新用户,该类用户评价物品的次数最少,在没有足够的数据时很难进行精准推荐,所以该类用户更应注重覆盖率和新颖性,从表2的结果可以看出,IC100初始化方法得到的新颖性和覆盖率最高,适用于用户集3。
| 表 2 用户集3在各类算法中的评价指标 Table 2 Evaluation indexes of user set 3 in various algorithms |
用户集2有一定量的评价数据,但也不够充分。从表3的结果可以得出,IT50-IC50初始化方法得到的准确率和预测评分平均值是最高的,而新颖性和覆盖率也处于一个折中的位置,所以这类初始化方法适用于用户集2。
| 表 3 用户集2在各类算法中的评价指标 Table 3 Evaluation indexes of user set 2 in various algorithms |
同样的,3种用户集在CF_Item、ProbS中也与上面描述的情况相同。
4.4 推荐方案小结本文研究的多目标进化算法主要结论如下:
(1) 群体初始化可以分成3类,针对不同的用户集可以采用对应的初始化方案。
对于评价物品次数较多的用户可用IT100初始化方案,可以得到预测评分平均值更高的推荐列表。对于评价物品次数适中的用户可用IT50-IC50初始化方案,可以得到预测评分平均值和覆盖率折中的推荐列表。对于评价物品次数较少的用户可用IC100初始化方案,可以获取更多样的推荐结果。
(2) 在进行交叉运算时,PMOEA可以将交叉个体中的一个固定为Top-L中的或覆盖率高的个体,交叉数目减少到3个,使算法优化性能得到显著提高。
(3) 多次试验结果表明,随着变异率的降低,算法的优化性能得到了提高。
5 结论本文研究了如何基于用户对物品的评价次数实现用户分层的多目标推荐算法。基于PMOEA算法设计了面向不同用户的初始化方法,并对算法的交叉和变异操作进行了改进。实验结果表明改进后的多目标进化算法在推荐精度和多样性方面对比已有方法都能找到更优的结果。最后总结出基于用户分层的推荐方案,该方案有助于提高对不同用户的推荐效果。未来可以根据不同场景类型(例如书籍、购物评分等)的数据集和决策者的需求尝试对本文提出的3种初始化方案进行组合使用。增加不同场景类型的数据集进行实验可以验证本文提出的多目标推荐算法的适用性,而3种初始化方案的组合使用则可以满足决策者的一些需求。例如系统上架一些新物品,决策者需要将这些新物品精准地推荐给用户,那么可以先采用IC100初始化方案进行首次优化,根据上述实验结论可知,优化结果将具有较大的覆盖率和新颖性,能满足新物品的特性,广泛推荐给用户;然后根据首次的优化结果再采用IT50-IC50初始化方案进行优化,那么新物品将被精准地推荐给用户;最后再采用IT100初始化方案进行优化,进一步提高推荐精准度。根据以上实验思路,将继续完善本文提出的多目标推荐算法,在多种场景和初始化方案组合使用的前提下验证算法的有效性。
| [1] |
BOBADILLA J, ORTEGA F, HERNANDO A, et al. Recommender systems survey[J]. Knowledge-Based Systems, 2013, 46: 109-132.
|
| [2] |
王娜, 何晓明, 刘志强, 等. 一种基于用户播放行为序列的个性化视频推荐策略[J].
计算机学报, 2020, 43(1): 123-135.
WANG N, HE X M, LIU Z Q, et al. Personalized video recommendation strategy based on user’s playback behavior sequence[J]. Journal of Computer Science, 2020, 43(1): 123-135. DOI: 10.11897/SP.J.1016.2020.00123. |
| [3] |
RAE A, MURDOCK V, POPESCU A, et al. Mining the web for points of interest[C]// Proceedings of the 35th International ACM SIGIR Conference on Research and Development in Information Retrieval. New York: ACM, 2012: 711-720.
|
| [4] |
张玉洁, 董政, 孟祥武. 个性化广告推荐系统及其应用研究[J].
计算机学报, 2021, 44(3): 531-563.
ZHANG Y J, DONG Z, MENG X W. Research on personalized advertising recommendation system and their applications[J]. Journal of Computer Science, 2021, 44(3): 531-563. DOI: 10.11897/SP.J.1016.2021.00531. |
| [5] |
林穗, 郑志豪. 基于关联规则的客户行为建模与商品推荐研究[J].
广东工业大学学报, 2018, 35(3): 90-94.
LIN S, ZHENG Z H. A research of a recommender system based on customer behavior modeling by mining association rules[J]. Journal of Guangdong University of Technology, 2018, 35(3): 90-94. DOI: 10.12052/gdutxb.180015. |
| [6] |
杨洁, 朱咸军, 周献中, 等. 基于混杂社会网络的个性化Web服务推荐方法[J].
电子学报, 2020, 48(2): 341-349.
YANG J, ZHU X J, ZHOU X Z, et al. Personalized web service recommendation based on heterogeneous social network[J]. Journal of Electronics, 2020, 48(2): 341-349. DOI: 10.3969/j.issn.0372-2112.2020.02.017. |
| [7] |
RICCI F, ROKACH L, SHAPIRA B. Introduction to recommender systems handbook[M]. Berlin, Heidelberg: Springer, 2011: 1-35.
|
| [8] |
CHAI Z Y, LI Y L, HAN Y M, et al. Recommendation system based on singular value decomposition and multi-objective immune optimization[J]. IEEE Access, 2018, 7: 6060-6071.
|
| [9] |
顾立志. 协同过滤数据稀疏性问题研究[J]. 计算机光盘软件与应用, 2014, 17(8) : 101-102.
GU L Z. Research on data sparsity in collaborative filtering[J]. Computer CD Software and Applications, 2014, 17(8) : 101-102. |
| [10] |
ZHANG L, QIN T, TENG P. Using key users of social networks to solve cold start problem in collaborative recommendation systems[J].
Information Technology Journal, 2013, 12(22): 7004-7008.
DOI: 10.3923/itj.2013.7004.7008. |
| [11] |
SUN Y, HAN J, YAN X, et al. Path Sim: meta path-based top-k similarity search in heterogeneous information networks[J].
Proceedings of the VLDB Endowment, 2011, 4(11): 992-1003.
DOI: 10.14778/3402707.3402736. |
| [12] |
SEDHAIN S, SANNER S, BRAZIUNAS D, et al. Social collaborative filtering for cold-start recommendations[C]//Proceedings of the 8th ACM Conference on Recommender systems. New York: ACM, 2014: 345-348.
|
| [13] |
BEEL J, LANGER S, GENZMEHR M, et al. Research paper recommender system evaluation: a quantitative literature survey[C]//Proceedings of the International Workshop on Reproducibility and Replication in Recommender Systems Evaluation. New York: ACM, 2013: 15-22.
|
| [14] |
LIN Q, JIN G, MA Y, et al. A diversity enhanced resource allocation strategy for decomposition-based multi-objective evolutionary algorithm[J].
IEEE Transactions on Cybernetics, 2018, 48(8): 2388-2401.
DOI: 10.1109/TCYB.2017.2739185. |
| [15] |
FAN J, PAN W, JIANG L. An improved collaborative filtering algorithm combining content-based algorithm and user activity[C] //2014 International Conference on Big Data and Smart Computing (BIGC- OMP) . Bangkok: IEEE, 2014: 88-91.
|
| [16] |
ADOMAVICIUS G, KWON Y. Improving aggregate recommendation diversity using ranking-based techniques[J].
IEEE Transactions on Knowledge and Data Engineering, 2012, 24(5): 896-911.
DOI: 10.1109/TKDE.2011.15. |
| [17] |
CHU P M, TSAI H R, LEE S J, et al. Improving collaborative filtering recommendation[C] //Proceedings of 2018 3rd International Conference on Control, Automation and Artificial Intelligence (CAAI 2018). [S. l. ]: Atlantis Press, 2018: 114-116.
|
| [18] |
ZHOU T, SU R Q, LIU R R, et al. Accurate and diverse recommendations via eliminating redundant correlations[J].
New Journal of Physics, 2009, 11(12): 123008.
DOI: 10.1088/1367-2630/11/12/123008. |
| [19] |
方晨, 张恒巍, 王娜, 等. 基于随机游走和多样性图排序的个性化服务推荐方法[J].
电子学报, 2018, 46(11): 2773-2780.
FANG C, ZHANG H W, WANG N, et al. Personalized service recommendation method based on random walk and diversified graph ranking[J]. Journal of Electronics, 2018, 46(11): 2773-2780. DOI: 10.3969/j.issn.0372-2112.2018.11.027. |
| [20] |
WANG P, ZUO X, GUO C, et al. A multi-objective genetic algorithm based hybrid recommendation approach[C]//2017 IEEE Symposium Series on Computational Intelligence (SSCI) . Honolulu: IEEE, 2017: 1-6.
|
| [21] |
HOU Z, LIU J. A two-phase evolutionary algorithm for solving the accuracy-diversity dilemma in recommendation[C]//2020 IEEE Congress on Evolutionary Computation (CEC) . Glasgow: IEEE, 2020: 1-8.
|
| [22] |
LIU X F, ZHAN Z H, GAO Y, et al. Coevolutionary particle swarm optimization with bottleneck objective learning strategy for many-objective optimization[J].
IEEE Transactions on Evolutionary Computation, 2018, 23(4): 587-602.
|
| [23] |
JAMBOR T, WANG J. Optimizing multiple objectives in collaborative filtering[C] //Proceedings of the 4th ACM Conference on Recommender Systems. New York: ACM, 2010: 55-62.
|
| [24] |
WANG S, GONG M, LI H, et al. Multi-objective optimization for long tail recommendation[J]. Knowledge-Based Systems, 2016, 104: 145-155.
|
| [25] |
RIBEIRO M T, LACERDA A, VELOSO A, et al. Pareto-efficient hybridization for multi-objective recommender systems[C] //Proceedings of the 6th ACM Conference on Recommender Systems. New York: ACM, 2012: 19-26.
|
| [26] |
ZUO Y, GONG M, ZENG J, et al. Personalized recommendation based on evolutionary multi-objective optimization [Research Frontier][J].
IEEE Computational Intelligence Magazine, 2015, 10(1): 52-62.
DOI: 10.1109/MCI.2014.2369894. |
| [27] |
CUI L, PENG O, FU X, et al. A novel multi-objective evolutionary algorithm for recommendation systems[J]. Journal of Parallel and Distributed Computing, 2017, 103: 53-63.
|
| [28] |
DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-II[J].
IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.
DOI: 10.1109/4235.996017. |
| [29] |
HERLOCKER J L, KONSTAN J A, TERVEEN L G, et al. Evaluating collaborative filtering recommender systems[J].
ACM Transactions on Information Systems (TOIS), 2004, 22(1): 5-53.
DOI: 10.1145/963770.963772. |
| [30] |
SARWAR B, KARYPIS G, KONSTAN J, et al. Item-based collaborative filtering recommendation algorithms[C]//Proceedings of the 10th International Conference on World Wide Web. New York: ACM, 2001: 285-295.
|
| [31] |
ZHOU T, REN J, MEDO M, et al. Bipartite network projection and personal recommendation[J].
Physical Review E, 2007, 76(4): 046115.
DOI: 10.1103/PhysRevE.76.046115. |
 2023, Vol. 40
2023, Vol. 40

