随着科学技术的发展，大量的电力电子设备和各种非线性负荷被投入到电网中，电网中的谐波污染问题日益突出，谐波补偿在电力系统中变得越来越重要^[1-2]。有源电力滤波器(Active Power Filter，APF)具有良好的补偿特性，优越的动态响应和稳态性能，已成为谐波控制的主要方法^[3-5]。混合型有源滤波器与单纯并联或串联有源滤波器相比，能够使用较小容量的有源滤波器，且易于保护^[6-7]。文献[7-8]提出了一种并联混合有源滤波器(Shunt Hybrid Active Power Filter，SHAPF)的新结构，将有源滤波器并联到无源滤波电感，以降低逆变器的额定电流，进一步减小了SHAPF的容量。然而，人们对SHAPF的研究主要采取全补偿的控制策略，很少关注特定次谐波含量高的场合。在这些场合，有源电力滤波器只需滤除特定的谐波电流就可以使谐波满足标准规定的限值，从而降低系统的容量等级以及开关器件的耐压耐流等级^[9-10]。

目前有源电力滤波器的控制大多使用传统PI控制，但是PI控制在谐波抑制和抗干扰方面能力有限，使SHAPF在补偿性能上有较大的局限性^[11-12]。而自抗扰控制融合了传统PI技术和现代控制理论的精髓。它不依赖于被控对象的数学模型，能有效地对整个系统总扰动进行实时估计补偿，具有较强的抗干扰能力^[13-15]。文献[16]针对单相有源电力滤波器直流侧电压采用线性自抗扰控制(Linear Active Disturbance Rejection Controller，LADRC)，有效抑制和缩短非线性负载和负载突变产生的谐波和响应时间。文献[17]在有源电力滤波器的电流控制补偿中引入自抗扰控制，将有源滤波器未建模的动力学和不确定性视为系统中的扰动。文献[18]针对并联混合有源电力滤波器设计了一种LADRC双闭环控制器，相对于PI控制极大地提高了其控制性能。

针对SHAPF应用场合受限问题以及PI控制补偿性能的不足，本文在一种并联混合型有源滤波器的基础上，设计了基于线性自抗扰的特定次谐波补偿控制策略。同时将原有三阶系统控制简化成一阶自抗扰控制问题，并设计了基于LADRC的直流侧母线电压双闭环控制器。最后通过仿真实验，与传统PI控制对比，验证了方案的可行性和优越性。

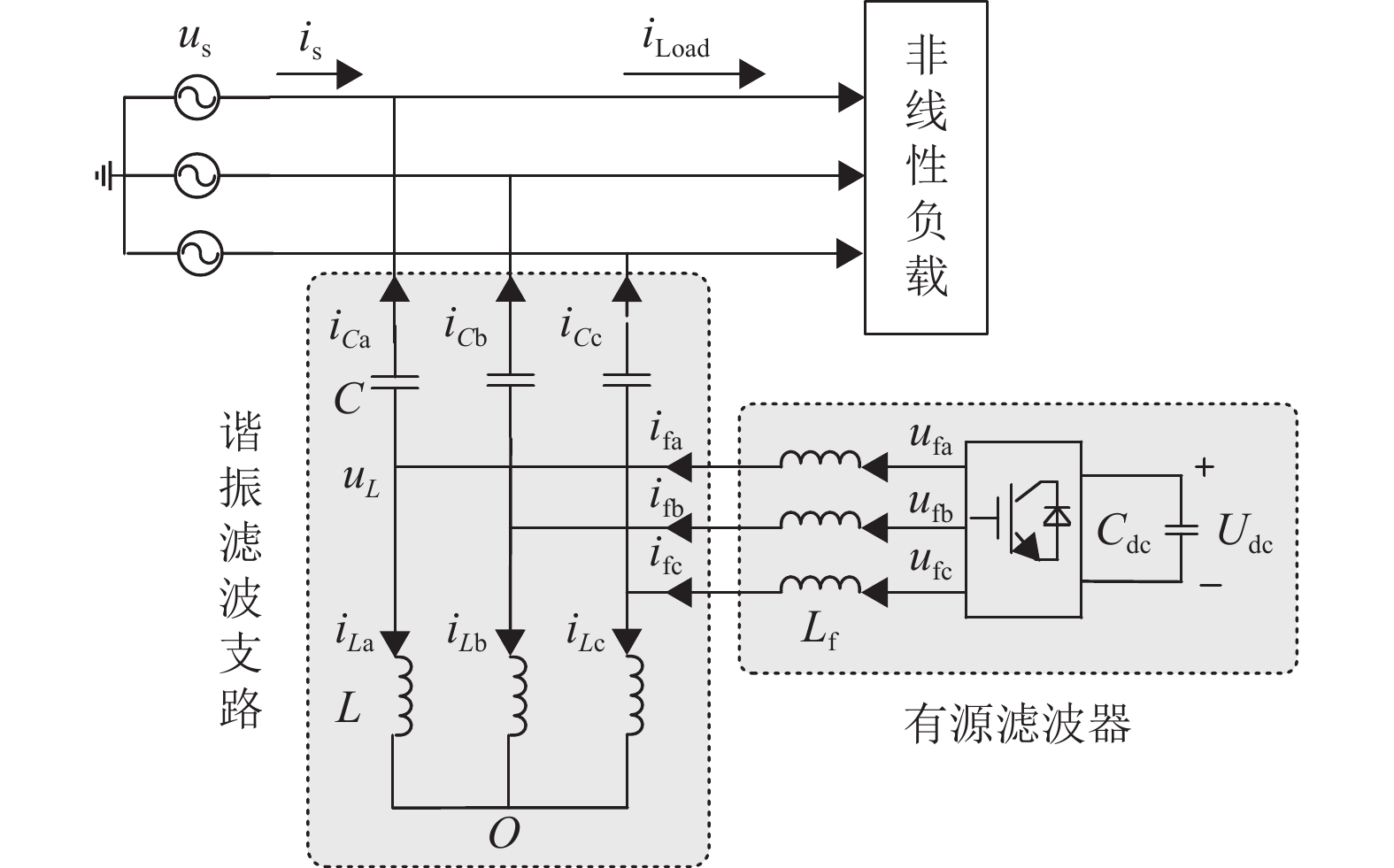
1 SHAPF的数学模型

如图1所示，C_dc表示直流侧电容，U_dc表示直流侧电压，L_f表示APF侧滤波电感，L与C共同组成谐振滤波电路，u_s表示电网侧电压，i_s表示电网侧电流，i_Ca、i_Cb、i_Cc表示三相电容C支路的注入电流，i_fa、i_fb、i_fc表示变流器的输出电流，u_fa、u_fb、u_fc表示变流器的输出电压，O表示主拓扑电路的中点，u_L表示并联电感L相对O点之间的电压，i_La、i_Lb、i_Lc表示流过并联电感L的电流。

根据图1建立并联型混合有源电力滤波器的数学模型，由交流侧电感L_f可知

$ \left\{ {\begin{array}{*{20}{l}} {{L_{\text{f}}}\dfrac{{{\text{d}}{i_{{\text{fa}}}}}}{{{\text{d}}t}} = {u_{{\text{fa}}}} - {u_{L{\text{a}}}}} \\\\ {{L_{\text{f}}}\dfrac{{{\text{d}}{i_{{\text{fb}}}}}}{{{\text{d}}t}} = {u_{{\text{fb}}}} - {u_{L{\text{b}}}}} \\\\ {{L_{\text{f}}}\dfrac{{{\text{d}}{i_{{\text{fc}}}}}}{{{\text{d}}t}} = {u_{{\text{fc}}}} - {u_{L{\text{c}}}}} \end{array}} \right. $

(1)

由谐振滤波支路电感L可知

$ \left\{ {\begin{array}{*{20}{l}} {L\dfrac{{{\text{d}}{i_{L{\text{a}}}}}}{{{\text{d}}t}} = {u_{L{\text{a}}}}} \\\\ {L\dfrac{{{\text{d}}{i_{L{\text{b}}}}}}{{{\text{d}}t}} = {u_{L{\text{b}}}}} \\\\ {L\dfrac{{{\text{d}}{i_{L{\text{c}}}}}}{{{\text{d}}t}} = {u_{L{\text{c}}}}} \end{array}} \right. $

(2)

由谐振滤波支路电容C可知

$ \left\{ {\begin{array}{*{20}{l}} {{i_{C{\text{a}}}} = C\dfrac{{\text{d}}}{{{\text{d}}t}}\left( {{u_{L{\text{a}}}} - {u_{{\text{sa}}}}} \right) } \\\\ {{i_{C{\text{b}}}} = C\dfrac{{\text{d}}}{{{\text{d}}t}}\left( {{u_{L{\text{b}}}} - {u_{{\text{sb}}}}} \right) } \\\\ {{i_{C{\text{c}}}} = C\dfrac{{\text{d}}}{{{\text{d}}t}}\left( {{u_{L{\text{c}}}} - {u_{{\text{sc}}}}} \right) } \end{array}} \right. $

(3)

将式(1~3)静止坐标系下的数学模型经过坐标变换后得到dq同步旋转坐标系下的数学模型为

$ \left\{ \begin{gathered} {L_{\text{f}}}\dfrac{{{\text{d}}{i_{{\text{f}}d}}}}{{{\text{d}}t}} - \omega {L_{\text{f}}}{i_{{\text{f}}q}} = {u_{{\text{f}}d}} - {u_{Ld}} \\ {L_{\text{f}}}\dfrac{{{\text{d}}{i_{{\text{f}}q}}}}{{{\text{d}}t}} + \omega {L_{\text{f}}}{i_{{\text{f}}d}} = {u_{{\text{f}}q}} - {u_{Lq}} \\ L\dfrac{{{\text{d}}{i_{Ld}}}}{{{\text{d}}t}} - \omega L{i_{Lq}} = {u_{Ld}} \\ L\dfrac{{{\text{d}}{i_{Lq}}}}{{{\text{d}}t}} + \omega L{i_{Ld}} = {u_{Lq}} \\ {i_{Cd}} = C\left[ {\dfrac{{\text{d}}}{{{\text{d}}t}}\left( {{u_{Ld}} - {u_{{\text{s}}d}}} \right) - \omega \left( {{u_{Lq}} - {u_{{\text{s}}q}}} \right) } \right] \\ {i_{Cq}} = C\left[ {\dfrac{{\text{d}}}{{{\text{d}}t}}\left( {{u_{Lq}} - {u_{{\text{s}}q}}} \right) + \omega \left( {{u_{Ld}} - {u_{{\text{s}}d}}} \right) } \right] \\ \end{gathered} \right. $

(4)

式中， $\omega $ 为基波角频率。

2 基于LADRC的SHAPF控制系统 2.1 自抗扰控制器原理

自抗扰控制是一种不必确定被控对象精准数学模型的控制算法，由跟踪微分器、扩张状态观测器、非线性状态误差反馈三部分组成。其中扩张状态观测器对总扰动进行观测和估计补偿。故自抗扰控制有实时估计扰动以及补偿的功能，具备较强的抗干扰能力^[19]。本文采用一阶自抗扰控制，故以一阶系统为例设计控制器。

$ \dot y = a + bu $

(5)

式中：u为对象的控制输入，y为对象的输出信号，a为扰动量之和，b为输入对输出的作用。一般由模型输入输出关系可以得到b的近似值b₀，令 $b = {b_0} + \Delta b$ 。

整理后状态空间形式为

$ \left\{ {\begin{array}{l} {{{\dot x}_1} = f + {b_0}u} \\ \;\; {y = {x_1}} \end{array}} \right. $

(6)

式中： $f = a + \Delta bu$ 。

将总扰动 f 扩张为第二个状态变量，利用线性扩张状态观测器(Linear Extended State Observer, LESO) 进行观测和估计补偿。线性扩张状态观测器的状态空间表达式为

$ \left\{ {\begin{array}{l} {\dot{\hat x} = {\boldsymbol{A}}\hat x + {\boldsymbol{B}}u + {\boldsymbol{H}}(y - \hat y) } \\ {\hat y = {\boldsymbol{C}}\hat x} \end{array}} \right. $

(7)

式中： ${\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 0&1 \\ 0&0 \end{array}} \right]$ ， ${\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{b_0}} \\ 0 \end{array}} \right]$ ， ${\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right]$ ，H为观测器输出反馈阵， ${\boldsymbol{H}} = \left[ {\begin{array}{*{20}{l}} {{\beta _1}} \\ {{\beta _2}} \end{array}} \right]$ 。

可得， $ {\boldsymbol{A}} - {\boldsymbol{HC}} = \left[ {\begin{array}{*{20}{c}} { - {\beta _1}}&1 \\ { - {\beta _2}}&0 \end{array}} \right] $ ，LESO参数采用文献[20]提出的带宽整定方法，为LESO指定一个观测器带宽ω₀，将观测器状态矩阵( $ \boldsymbol{A}-\boldsymbol{H}\boldsymbol{C} $ ) 的所有极点都配置在−ω₀处，则期望的特征多项式为

$ \begin{gathered} |s{\boldsymbol{I}} - ({\boldsymbol{A}} - {\boldsymbol{HC) }}| = \left| {\begin{array}{*{20}{c}} {s + {\beta _1}}&{ - 1} \\ {{\beta _2}}&s \end{array}} \right| = {\left( {s + {\omega _0}} \right) ^2} \\ \end{gathered} $

(8)

则 $\,{\beta _1} = 2{\omega _0}$ ， $\, {\beta _2} = \omega _0^2$ 。

对于ω₀的选取，文献[21]采用逐步加大ω₀的值，分析不同ω₀值对输入干扰抑制性能和测量噪声灵敏度的影响，从而选取合适的ω₀值。文献[22]提出了一种Fuzzy-LADRC控制方法，利用误差、误差变化率和参数之间的模糊关系来调节ω₀。

自抗扰控制律的设计分为两步：第一步是利用误差反馈抑制总扰动。第二步是使用LESO给出的被控对象的状态变量设计控制律。由于本文采用一阶线性自抗扰控制，不对各阶微分进行观测，故NLSEF简化成P控制形式为

$ {u_0} = {k_{\text{p}}}\left( {r - {{\hat x}_1}} \right) $

(9)

式中：k_p为比例常数；r为参考指令输入值。考虑到扰动补偿，LADRC最终控制量u为

$ u = \frac{{{u_0} - {{\hat x}_2}}}{{{b_0}}} $

(10)

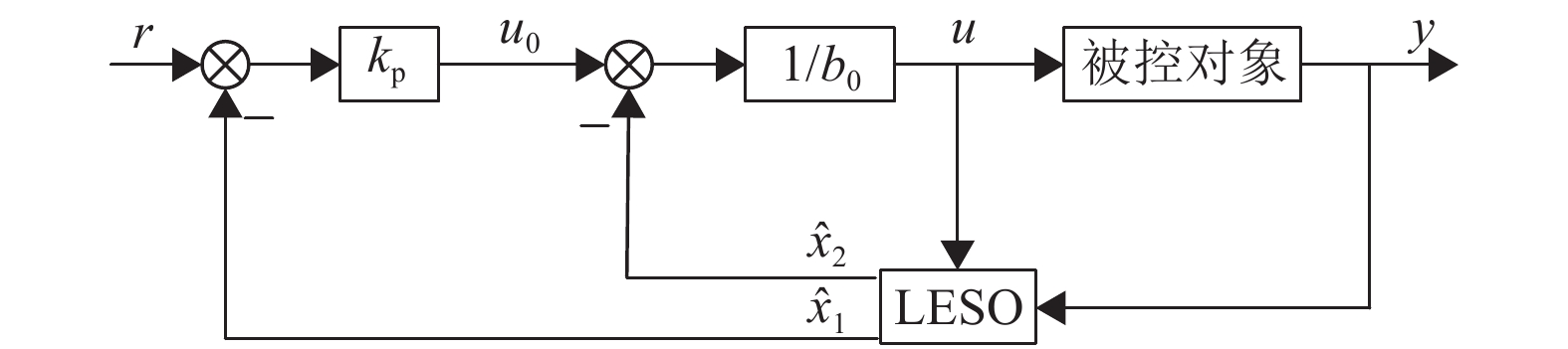
根据上述分析推导，可得一阶LADRC结构图，如图2所示。

2.2 谐波电流跟踪控制器设计

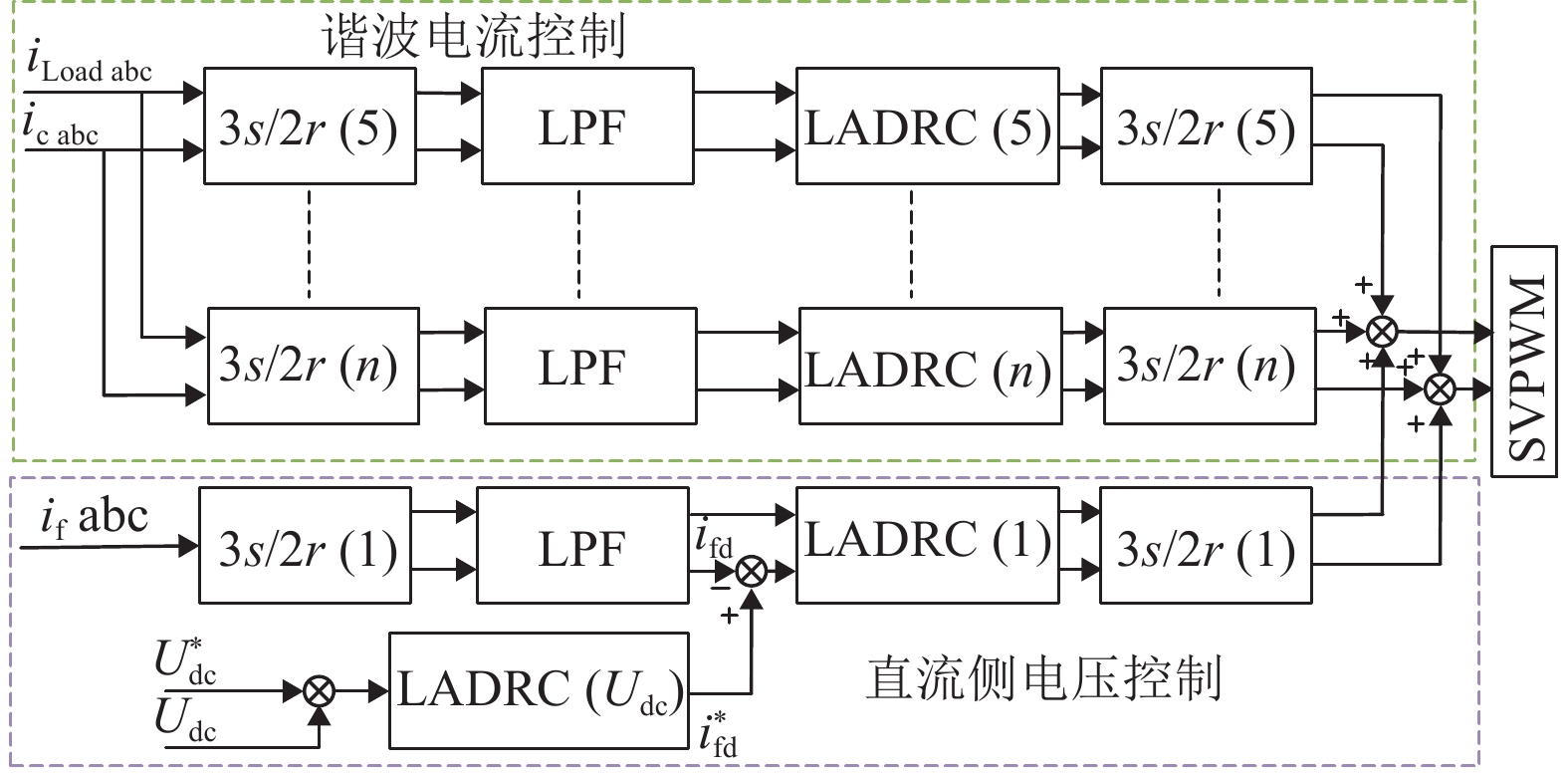
本文采用特定次谐波补偿策略，主要补偿含量较高的5，7，11，13次谐波。总体控制单元如图3所示，首先通过同步旋转坐标系提取特定次谐波参考量和反馈控制量。经过低通滤波器(Low Pass Filter，LPF)后，通过LADRC进行跟踪控制，然后将输出指令转化到两相静止坐标系，输入到SVPWM进行控制。

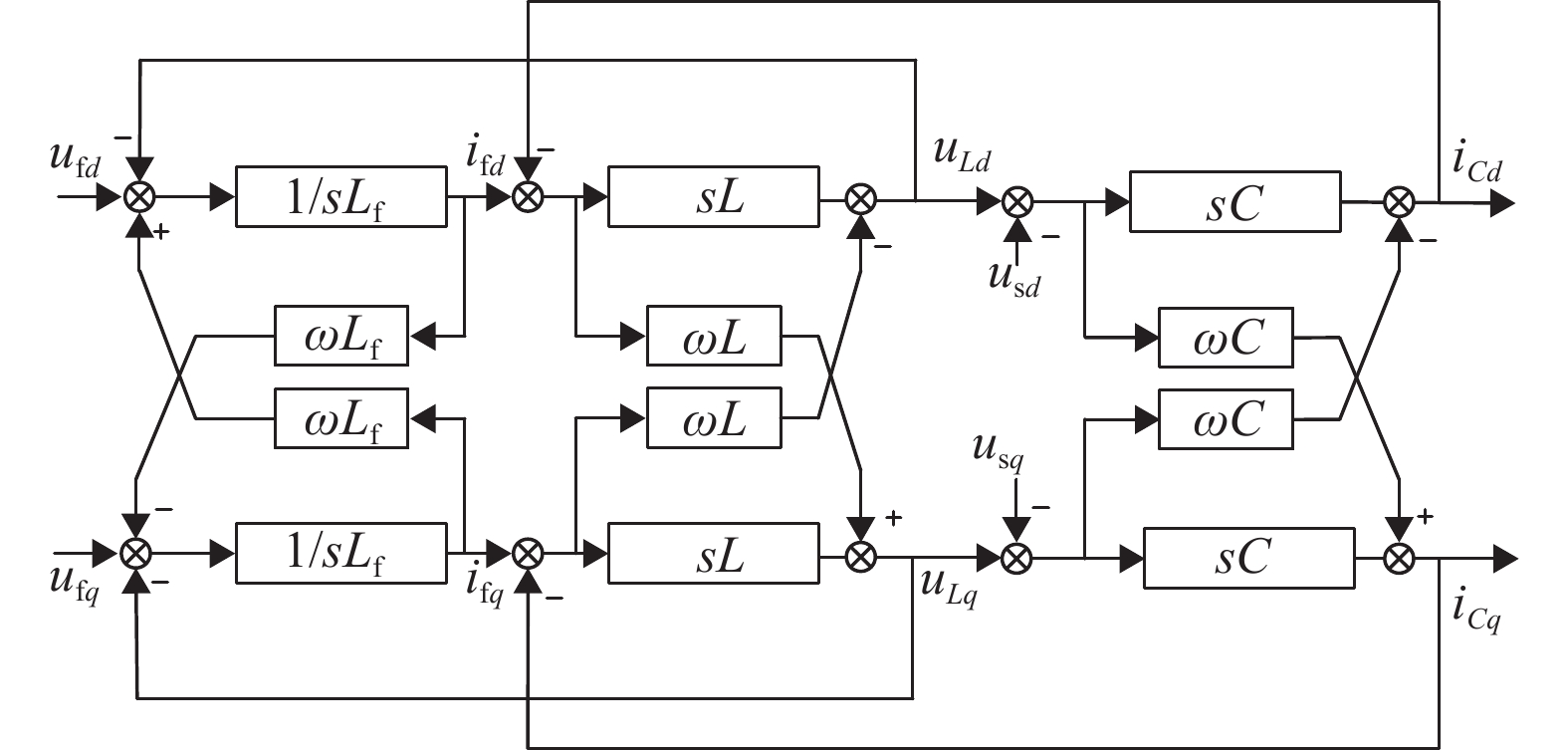
由系统数学模型可得旋转坐标系下滤波器s域数学模型，如图4所示。

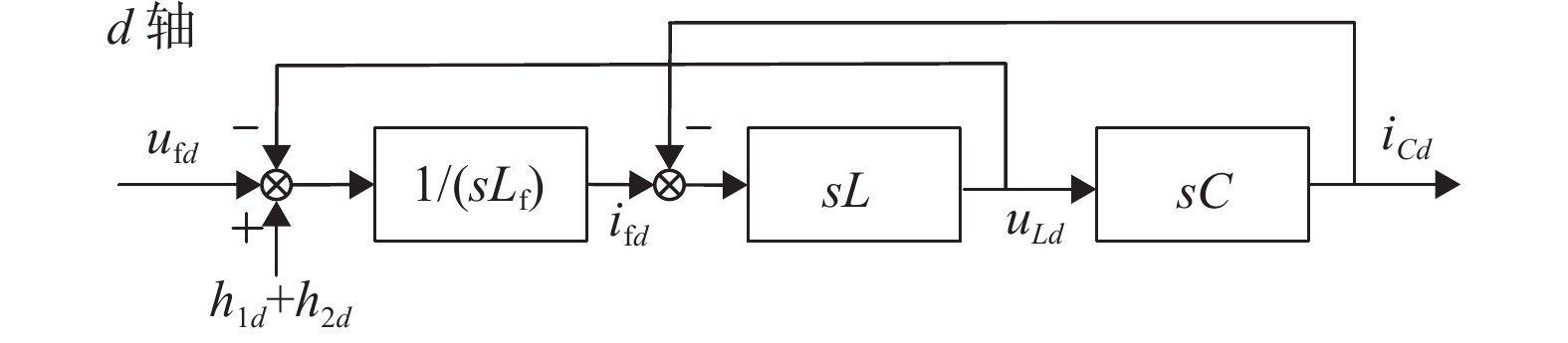
从图4可知dq轴之间存在耦合分量，然而在抗扰控制中，可以将耦合量当作内扰进行控制，故在图4的基础上，根据控制原理，将所有耦合量前移来完成解耦。以d轴为例。假设h_1d、h_1q为耦合量之和，h_2d、h_2q为电网电压前移量，如图5所示。

令 $ {f_1} = {h_{1d}} + {h_{2d}} $ ，可得输出输入传递函数为

$ G(s) = \frac{{{i_{Cd}}(s) }}{{{u_{{\text{f}}d}}(s) + {f_1}}} = \frac{{sLC}}{{{s^2}L{L_{\text{f}}} + L + {L_{\text{f}}}}} $

(11)

令 $y = {i_{Cd}}(s) $ ， $u = {u_{{\text{f}}d}}(s) $ 。可得

$ G'(s) = \frac{y}{{u + {f_1}}} = \frac{{sLC}}{{{s^2}L{L_{\text{f}}} + L + {L_{\text{f}}}}} $

(12)

令

$ \textit{z} = \frac{1}{{{s^2}L{L_{\text{f}}} + L + {L_{\text{f}}}}}(u + {f_1}) $

(13)

可得

$ \begin{gathered} \frac{{{{\text{d}}^2}\textit{z}}}{{{\text{d}}{t^2}}} = - \frac{1}{{L{L_{\text{f}}}}}\left( {L + {L_{\text{f}}}} \right) \times \textit{z} + \frac{1}{{L{L_{\text{f}}}}} \times (u + {f_1}) \\ \end{gathered} $

(14)

联立式(11~14)可得

$ \begin{gathered} \dot y = - \frac{C}{{{L_{\text{f}}}}}\left( {L + {L_{\text{f}}}} \right) \times \textit{z} + \frac{C}{{{L_{\text{f}}}}} \times (u + {f_1}) = f + {b_{01}}u \\ \end{gathered} $

(15)

式中：

$ \begin{split} &f = - (C/{L_{\text{f}}}) \left( {L + {L_{\text{f}}}} \right) \times z + (C/{L_{\text{f}}}) \times {f_1} ，\\ &{b_{01}} = C/{L_{\text{f}}} \end{split}。$

以上推导将三阶系统控制问题简化成一阶自抗扰控制问题。且自抗扰控制并不需要计算扰动的精确作用规律，可以将作用于被控对象的所有不确定因素归于总扰动进行估计补偿。故可将耦合量和电网电压归于总扰动量从而不考虑耦合量和电网电压，使其算法简单，在工程上更易实现。

2.3 直流侧电压控制器设计

直流母线电压的稳定是保证APF可靠运行的关键因素。本文直流侧电压采用电压外环和电流内环进行控制，控制方案如图3所示。测量的直流母线电压U_dc和参考电压U_dc输入电压外环LADRC。将电压外环LADRC的输出作为基波d轴i_fd的参考值再同时输入到电流内环LADRC，得到逆变器在基频处的电压命令。

电压外环设计是根据能量守恒原则，即交流侧有功功率与直流侧有功功率相等^[23]，即

$ {P_{{\text{ac}}}} = {P_{{\text{dc}}}} $

(16)

采用等量坐标变换，则

$ {P_{{\text{ac}}}} = \frac{3}{2}{u_{Ld}}{i_{{\text{f}}d}} + \frac{3}{2}{u_{Lq}}{i_{{\text{f}}q}} $

(17)

$ {P_{{\text{dc}}}} = {U_{{\text{dc}}}}{i_{{\text{dc}}}} = {u_{{\text{dc}}}}C\frac{{{\text{d}}{U_{{\text{dc}}}}}}{{{\text{d}}t}} + \frac{{U_{{\text{dc}}}^2}}{{{R_L}}} $

(18)

联立式(16~18)可得

$ \begin{gathered} {u_{{\text{dc}}}}C\frac{{{\text{d}}{U_{{\text{dc}}}}}}{{{\text{d}}t}} + \frac{{{U_{{\text{dc}}}}^2}}{{{R_L}}} = \frac{3}{2}{u_{Ld}}{i_{{\text{f}}d}} + \frac{3}{2}{u_{Lq}}{i_{{\text{f}}q}} \\ \end{gathered} $

(19)

进一步简化得

$ \begin{gathered} \frac{1}{2}C\frac{{{\text{d}}{U_{{\text{dc}}}}^2}}{{{\text{d}}t}} = - \frac{1}{{{R_L}}}{U_{{\text{dc}}}}^2 + \frac{3}{2}{u_{Ld}}{i_{{\text{f}}d}} + \frac{3}{2}{u_{Lq}}{i_{{\text{f}}q}} \\ \end{gathered} $

(20)

定义新变量 $m = \dfrac{1}{2}CU_{{\text{dc}}}^2$ 可得

$ \begin{gathered} \frac{{{\text{d}}m}}{{{\text{d}}t}} = - \frac{2}{{{R_L}{C_{{\text{dc}}}}}}m + \frac{3}{2}{u_{Ld}}{i_{{\text{f}}d}} + \frac{3}{2}{u_{Lq}}{i_{{\text{f}}q}} = f + {b_{02}}u \\ \end{gathered} $

(21)

式中： $ f = - (2/{R_L}{C_{{\text{dc}}}}) m + (3/2) {u_{Lq}}{i_{{\text{f}}q}} $ ， $ {b_{02}} = (3/2) {u_{Ld}} $ 。

直流母线电压稳定是通过控制基波电流的有功分量来达到控制结果。所以本文在设计直流母线电压控制环时，不考虑基波无功电流。

对于电流内环控制器设计。其输入输出的关系由式(2)可知，整理得

$ \begin{gathered} \frac{{{\text{d}}{i_{{\text{f}}d}}}}{{{\text{d}}t}} = \left( {{u_{{\text{f}}d}} - {u_{Ld}} + \omega {L_{\text{f}}}{i_{{\text{f}}q}}} \right) /{L_{\text{f}}} = f + {b_{03}}u \\ \end{gathered} $

(22)

式中： $f = ( - {u_{Ld}} + \omega {L_{\text{f}}}{i_{{\text{f}}q}}) /{L_{\text{f}}}$ ， ${b_{03}} = 1/{L_{\text{f}}}$ 。

3 仿真实验研究

为了验证自抗扰控制在新型SHAPF中有效性，利用Matlab中Simulink仿真平台对控制系统进行仿真验证。在保证整个系统稳定的前提下，分别采用PI控制器和LADRC进行仿真。三相不控整流器作为非线性负载，系统参数如表1所示。

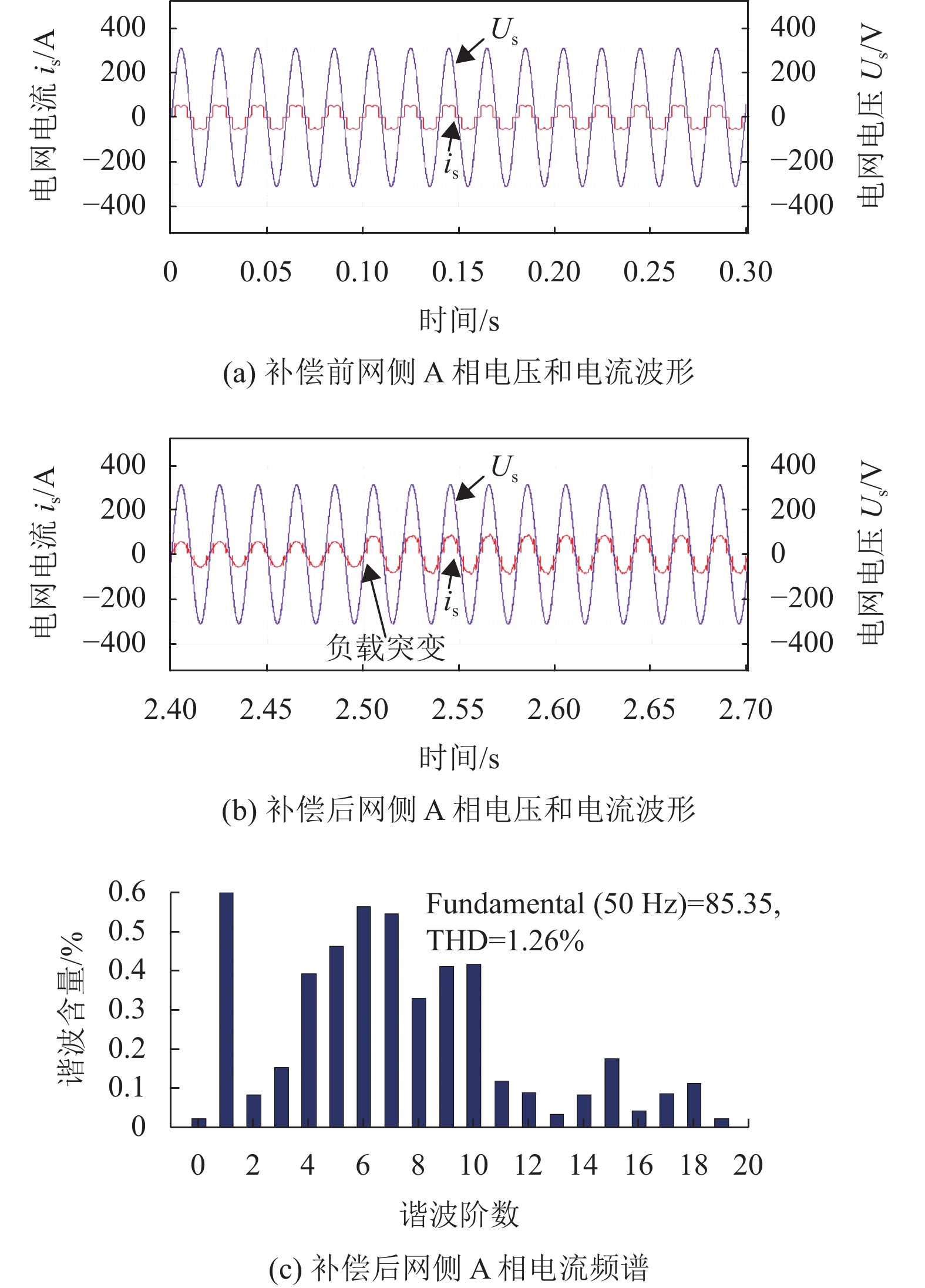
图6(a) 为补偿前电网电流A相波形。如图所示，补偿前电网电流含有大量的低次谐波，谐波畸变率27.58%。图6(b) 为LADRC补偿5，7，11，13次谐波后的电网电流波形，使用LADRC补偿后电网电流谐波畸变率(THD) 为1.26%，见图6(c)。

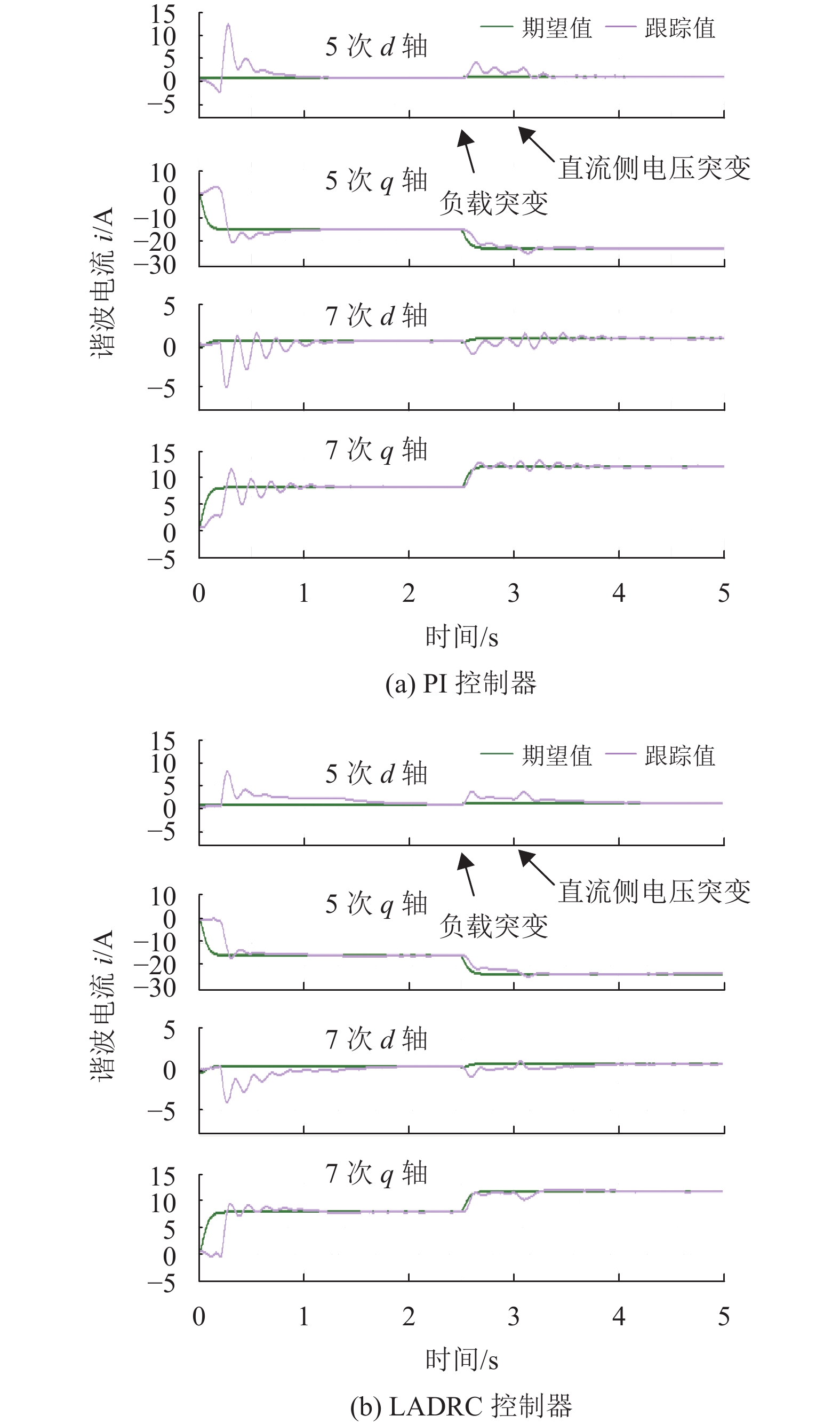
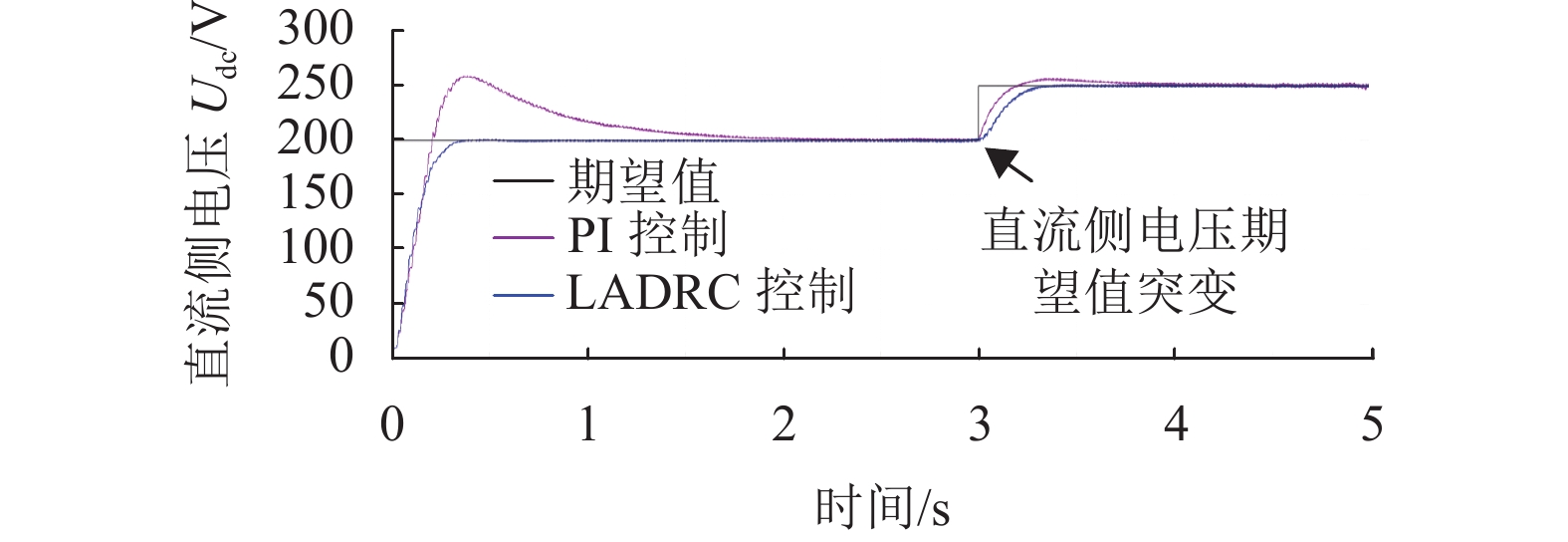
为了更好地比较在LADRC和PI控制下SHAPF对电网谐波电流的跟踪能力和抗干扰能力，以5，7次谐波dq轴为例。图7显示了PI和LADRC控制下5，7次谐波电流dq轴的跟踪控制效果。图7可知，在0.2 s时加入谐波补偿，在LADRC的控制下，SHAPF输出的补偿电流可以快速跟踪谐波电流，且超调量和振荡都小于PI控制。在2.5 s时刻减少负载，LADRC控制相对于PI控制振荡较小，有效抑制电流冲击。直流侧电压控制效果如图8所示。PI控制存在较大的超调量，而LADRC控制无超调，有效抑制了电压冲击。3 s时调整参考电压值为250 V，LADRC控制使直流母线电压更快稳定。

4 结论

为了改善有源电力滤波器控制系统的性能，采用了自抗扰控制策略取代传统PI控制。同时利用SHAPF的特点，将谐波电流三阶控制系统简化成一阶自抗扰控制问题，简化了控制器算法。考虑到APF适用场合问题，采用特定次谐波电流控制策略。最后通过仿真验证SHAPF在所提出的控制策略下系统能快速稳定地跟踪特定次谐波指令电流，直流侧电压超调为0，可以使SHAP在低冲击的条件下快速平稳运行。补偿后电网电流谐波畸变率为1.26%，符合总谐波畸变率小于5%的标准。