无人机具有功耗成本低、移动性高、可按需快速部署等独特优势，在过去十年里的商业市场规模一路攀升，广泛地应用于民用商业领域和军用领域^[1-2]。一个典型的例子，就是无人机在全球对抗新冠肺炎传播的疫情防控工作中发挥了不可或缺的作用，例如对疫区进行消毒、运送关键物资和测量体温。5G技术的发展和物联网“万物互联”的实现，对新一代无线通信提出了极大的挑战。由于通信设备小型化和无人机制造技术的进步，在无人机上加装轻型基站或中继变得越来越可行^[3]，以及在无人机和地面用户之间有很大概率可以建立起类似于视距链路(Light-of-Sight,LoS) 的高质量通信信道^[4]，这样一来创造了一个新的空中平台，让无人机在无线通信的应用中充分释放潜力以提高地面的通信质量，吸引了越来越多研究机构和学者的关注。一般来说，无人机在无线通信中的研究和应用可以分为3种类型：空中基站、移动中继、数据收集和传播^[5-6]。尽管直接链路、WiFi和卫星通信等技术在蜂窝服务中仍然发挥着重要的作用，但大数据时代需要及时、高效和成本优化的数据传输方式，这使人们相信在未来，蓬勃发展的无人机通信是最有前途和最经济的方法。

相比传统的地面通信系统，无人机通过搭建起优质的通信信道，明显地减少功率损耗和通信时延。由于受到无人机续航能力的限制，如何减少能量损耗是系统设计过程中必须考虑的重要因素。在文献[7]中，一架沿直线飞行的无人机采集一组传感器的数据，只考虑二维场景，在满足数据上传需求的前提下最小化无人机的总飞行时间。在文献[8]研究的单无人机移动中继系统和文献[9]研究的多跳无人机中继通信系统中，都通过联合优化无人机的飞行轨迹和传输功率，使得系统的端到端吞吐量最大化。为了最小化空闲侦听以减少功率损耗，文献[10]引入了睡眠/唤醒方案来调整每个传感器的睡眠和唤醒时间的比例。文献[11-14]表明了在实际应用中采用动态功率和带宽分配的自适应通信，可以与无人机轨迹设计一起提高通信性能。文献[15]通过联合优化无人机轨迹、唤醒时间分配和传感器的发射功率，权衡了空中成本(无人机的推进能量消耗和运行成本)与地面成本(所有传感器的能量消耗)，并最小化它们之间的加权和。很多工作考虑的都是延迟可容忍的应用场景，但在文献[16]研究的无人机支持的正交频分多址(Orthogonal Frequency Division Multiple Access, OFDMA) 系统中，为了最大化传感器的最小可达速率，还另外考虑了整个过程中用户需要满足最小速率约束的延迟约束情况。文献[17]提出一个多无人机支持的多链路中继系统，联合优化了无人机中继的三维飞行轨迹、源节点和无人机中继的传输功率，使得所有链路的最小吞吐量最大化。

此外，无人机在无线传感器网络中的信息采集和传播也引起了越来越多的研究兴趣。文献[18]研究了高效的物联网设备信息采集，通过对多架无人机的部署和移动性设计最小化物联网设备的传输功率。在文献[19]中，一架高度可调的无人机为它覆盖范围内的地面传感器提供能量支持并收集它们回传的信息，比较了非正交多址接入(Non-Orthogonal Multiple Access,NOMA) 和协同中继两种方案，通过优化无人机的悬停高度去降低信息采集系统的中断率。文献[20]研究了一个多无人机无线传感器网络的数据采集系统，为了最小化任务完成时间，分为悬停和飞行两种模式联合优化了无人机飞行轨迹和传感器的唤醒调度和关联。在文献[21]中，无人机和传感器之间的信道被建模为偶尔有建筑物阻挡的概率LoS信道，该文提出了一种离线−在线设计的方法联合优化了无人机的三维飞行轨迹和传感器传输调度，以最大化数据收集的最小速率。

然而，已有文献还缺乏考虑无人机需要将收集到的传感器数据转发给信息融合中心处理的情况。针对上述问题，本文考虑了一个无人机支持的多传感器信息采集系统，无人机不仅需要采集地面传感器的信息，还需要在空中飞行的过程中将采集到的信息转发给远处的信息融合中心。目标是最大化系统的端到端吞吐量，这对于无人机通信系统是十分重要的，因为在实际应用中无人机的续航能力是有限的。本文的贡献可以总结如下：

(1) 本文研究的工作主要是在一个无人机和传感器的功率可调但都有限制、无人机转发信息时满足译码−转发策略的信息采集系统中，联合优化传感器的发射功率、可用带宽的分配、无人机的传输功率和飞行轨迹，在每个传感器成功上传的数据能够达到设置的最小信息传输量的情况下，使得信息采集系统的端到端吞吐量最大化。在有限的时间里要让更多的传感器数据经过无人机传递到信息融合中心，这个问题中实际上在数据收集链路和数据转发链路之间存在着一种权衡关系，优化得到的无人机飞行轨迹必须兼顾这两段链路。然而相关的优化问题涉及到多个互相耦合的优化变量，是一个难以直接求解的非凸优化问题。

(2) 为解决这个难题，本文首先将时间离散化，使得原问题转化成一个包含有限个变量的离散问题，再利用块坐标下降法(Block Coordinate Descent, BCD) 将优化变量分成两大块，从而将原问题解耦成固定飞行轨迹优化功率带宽和固定功率带宽优化飞行轨迹两个子问题，进而交替地求解。然而这两个子问题仍然是非凸优化问题，通过引入松弛变量和一阶泰勒展开求下界之后，使用连续凸优化(Successive Convex Optimization, SCO) 方法将原本难解的问题变换为可迭代求解的问题。

(3) 提出了一种给定无人机初始局部飞行轨迹，上述两个子问题循环交替迭代求解的算法，并且文中也证明了算法的收敛性。通过Matlab得到的仿真结果显示了兼顾收集和转发两段链路而使得端到端吞吐量最大化时，无人机的飞行轨迹以及功率和带宽的瞬时分配情况。最后与其他三种基准方案的结果作对比，证明了本文提出的联合优化功率、带宽和飞行轨迹的方案能够显著地提高信息采集系统的端到端吞吐量。所提出的算法在考虑无人机和传感器的续航能力有限的实际应用中非常有意义，对于提高系统吞吐量、提高传输速率、减小任务完成时间、减少系统通信资源浪费等应用场景都可以应用其中，特别是在地质实时勘测和灾害现场监查等时效性要求比较高的大型信息采集系统中尤为重要。

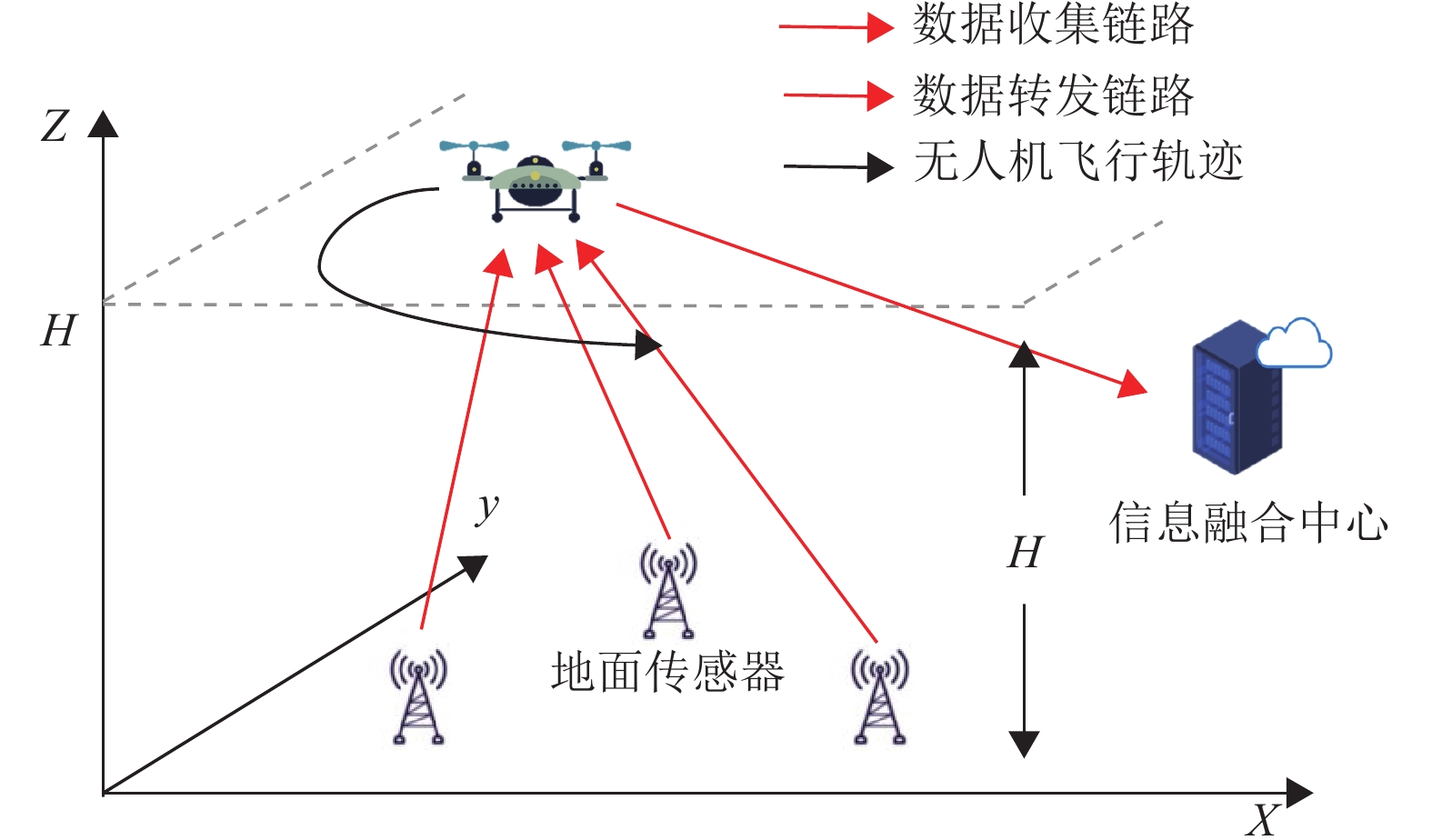
1 系统模型

如图1所示，本文考虑一个具有K≥1个传感器、一架无人机和一个信息融合中心的无人机信息采集系统。所有传感器将数据传输给无人机，无人机将收集到的数据转发给信息融合中心。本文使用三维笛卡尔坐标系来描述位置。假设无人机在固定高度H的水平面上飞行，且这个高度是不会与起伏的地表或者建筑物碰撞的最小高度，在飞行时间T里，用 ${\boldsymbol{q}}\left(t\right) \triangleq {\left[x\left(t\right) ,y\left(t\right) \right]}^{{\rm{T}}}，0\leqslant t\leqslant T$ 表示无人机飞行轨迹在地面上的投影。传感器和信息融合中心都分布在水平高度为0的地面上并且位置固定和被无人机所知，其位置坐标分别可表示为 ${{\boldsymbol{s}}}_{i}\triangleq {\left[{x}_{i},{y}_{i}\right]}^{{\rm{T}}}，i=1,\cdots ,K$ 和 ${\boldsymbol{w}}\triangleq {[{x}_{w},{y}_{w}]}^{{\rm{T}}}$ 。假设无人机的最大飞行速度为 ${V}_{{\rm{max}}}$ (m/s)，则有以下的无人机机动性约束条件

$ \left\| {{\boldsymbol{\dot{q}}}\left(t\right) } \right\|\leqslant {V}_{{\rm{max}}}\text{，}0\leqslant t\leqslant T $

(1)

式中： $\left\| {·} \right\|$ 是欧几里得范数。无人机与各个传感器和信息融合中心之间的时变距离分别表示为

$ {\tilde{s}}_{i}\left(t\right) =\sqrt{{H}^{2}+{\left\| {{\boldsymbol{q}}\left(t\right) -{{\boldsymbol{s}}}_{i}} \right\|}^{2}}\text{，}\forall i $

(2)

$ \tilde {d}\left(t\right) =\sqrt{{H}^{2}+{\left\| {{\boldsymbol{q}}\left(t\right) -{\boldsymbol{w}}} \right\|}^{2}} $

(3)

因为在地面障碍物较少和无人机飞行高度足够高的情况下，信道符合LoS模型的概率非常高，因此不妨认为系统的链路中LoS信道占主导作用，根据自由空间路径损耗模型可知负责数据收集的上行信道和负责数据转发的下行信道的功率增益分别为

$ {g}_{i}\left(t\right) ={\lambda }_{0}{{\tilde {s}}_{i}}^{-2}\left(t\right) \text{，}\forall i $

(4)

$ h\left(t\right) ={\lambda }_{0}{\tilde {d}}^{-2}\left(t\right) $

(5)

式中： $ {\lambda }_{0} $ 是单位距离的功率增益。如果总的可用带宽为B，无人机采用频分多址(Frequency Division Multiple Access, FDMA) 的方式为各链路分配带宽， $ {\alpha }_{i}\left(t\right) $ B和 $ \beta \left(t\right) $ B分别表示分配给传感器i和信息融合中心的那部分带宽，则有以下带宽分配约束条件

$ \sum \nolimits_{i=1}^{K}{\alpha }_{i}\left(t\right) +\beta \left(t\right) =1\text{，}\forall t $

(6)

$ {\alpha }_{i}\left(t\right) \geqslant 0\text{，}\beta \left(t\right) \geqslant 0\text{，}\forall i,t $

(7)

如果 $ {p}_{i}\left(n\right) $ 和 $ e\left(n\right) $ 分别表示传感器i和无人机的瞬时传输功率， $ {P}_{{\rm{aver}}-i} $ 和 $ {E}_{{\rm{aver}}} $ 分别表示它们的最大平均传输功率， $ {P}_{{\rm{peak}}-i} $ 和 $ {E}_{{\rm{peak}}} $ 分别表示它们的峰值传输功率，则传感器的传输功率约束为

$ \frac{1}{T}{\int }_{0}^{T}{p}_{i}\left(t\right) dt\leqslant {P}_{{\rm{aver}}-i}\text{，}\forall i $

(8)

$ 0\leqslant {p}_{i}\left(t\right) \leqslant {P}_{{\rm{peak}}-i},\;\;\;\forall i,t $

(9)

以及无人机的传输功率约束为

$ \frac{1}{T}{\int }_{0}^{T}e\left(t\right) {\rm{d}}t\leqslant {E}_{{\rm{aver}}} $

(10)

$ 0\leqslant e\left(t\right) \leqslant {E}_{{\rm{peak}}},\;\;\; \forall t $

(11)

结合香农公式^[22]可以得到上行信道和下行信道的瞬时可达速率(bit·s⁻¹·Hz⁻¹)可表示为

$ \begin{split} {R}_{i}\left(t\right) =&{\alpha }_{i}\left(t\right) {{{{\rm{log}}}}}_{2}\left(1+\frac{{p}_{i}\left(t\right) {g}_{i}\left(t\right) }{B{\alpha }_{i}\left(t\right) {N}_{0}}\right)= \\ &{\alpha }_{i}\left(t\right) {{\rm{log}}}_{2}\left(1+\frac{{p}_{i}\left(t\right) {\gamma }_{i}\left(t\right) }{{\alpha }_{i}\left(t\right) }\right) \text{，}\forall i \end{split} $

(12)

$ \begin{split} R\left(t\right) =&\beta \left(t\right) {{\rm{log}}}_{2}\left(1+\frac{e\left(t\right) h\left(t\right) }{B\beta \left(t\right) {N}_{0}}\right)= \\ &\beta \left(t\right) {{\rm{log}}}_{2}\left(1+\frac{e\left(t\right) \rho \left(t\right) }{\beta \left(t\right) }\right) \end{split} $

(13)

式中： $ {N}_{0} $ 是加性高斯白噪声(Additive White Gaussian Noise, AWGN) 的功率谱密度(W/Hz)，而 ${\gamma }_{i}\left(t\right) \triangleq {\gamma }_{0}/\left({H}^{2}+{\left\| {{\boldsymbol{q}}\left(t\right) -{{\boldsymbol{s}}}_{i}} \right\|}^{2}\right)$ 和 $\rho \left(t\right) \triangleq {\gamma }_{0}/\left({H}^{2}+{\left\| {{\boldsymbol{q}}\left(t\right) -{\boldsymbol{w}}} \right\|}^{2}\right)$ 分别为上行链路和下行链路的信道功率噪声比，里面 $ {\gamma }_{0}\triangleq {\lambda }_{0}/\left(B{N}_{0}\right) $ 表示单位距离参考信噪比。若无人机满足译码−转发策略，无人机在收集到传感器发来的数据后需要经过编译码等处理才能转发给信息融合中心，也就是说无人机只能转发之前已经从传感器获取到的信息，所以还必须考虑以下信息−因果约束条件

$ {\int }_{0}^{t}R\left(t\right) {\rm{d}}\tau \leqslant \sum \nolimits_{i=1}^{K}{\int }_{0}^{t}{R}_{i}\left(t\right) {\rm{d}}\tau \text{，}\forall t $

(14)

为了保证无人机对各个传感器信息采集的公平性，假设无人机需要从传感器i获取到的最小信息量都为C bits，所以有以下的最小信息传输量约束条件

$ B{\int }_{0}^{T}{R}_{i}\left(t\right) {\rm{d}}t \geqslant C\text{，}\forall i $

(15)

2 功率、带宽与飞行轨迹的联合优化

为了便于优化无人机的飞行轨迹，将飞行时间T等分为N个时隙，即 $ {t}_{n}=n{\delta }_{t}，n=1, \cdots ,N $ ,其中 $ {\delta }_{t} $ 是每个时隙的长度，要求它足够小以至于在每一个时隙里可以近似地认为无人机的位置不变。这时无人机的轨迹表示为 ${\boldsymbol{q}}\left[n\right]\triangleq {\boldsymbol{q}}\left(n{\delta }_{t}\right) ，n=1, \cdots ,N$ ，类似地对其他时变变量做同样变化。若无人机每个时隙里的最大飞行距离表示为 ${D}_{{\rm{max}}}={V}_{{\rm{max}}}{\delta }_{t}$ ，那么无人机的机动性约束条件可变为

$ {\left\| {{\boldsymbol{q}}\left[n+1\right]-{\boldsymbol{q}}\left[n\right]} \right\|}^{2}\leqslant {{D}_{{\rm{max}}}}^{2},n=1, \cdots ,N-1 $

(16)

相应地，上行信道和下行信道的瞬时可达传输速率变为

$ {R}_{i}\left[n\right]={\alpha }_{i}\left[n\right]{{\rm{log}}}_{2}\left(1+\frac{{p}_{i}\left[n\right]{\gamma }_{i}\left[n\right]}{{\alpha }_{i}\left[n\right]}\right) \text{，}\forall i,n $

(17)

$ R\left[n\right]=\beta \left[n\right]{{\rm{log}}}_{2}\left(1+\frac{e\left[n\right]\rho \left[n\right]}{\beta \left[n\right]}\right) \text{，}\forall n $

(18)

无人机收集到传感器的信息后需要足够的时间译码才能转发出去给信息融合中心，假设这个处理过程的时间延迟为一个时隙长度 $ {\delta }_{t} $ ，可知无人机和传感器分别不在第一个时隙和最后一个时隙传输信息，则有 $ \beta \left[1\right]=0，e\left[1\right]=0 $ 以及 $ {\alpha }_{i}\left[N\right]=0，{p}_{i}\left[N\right]=0 $ 。故有 $ {R}_{i}\left[N\right]=R\left[1\right]=0 $ ，则信息−因果约束条件变为

$ \sum\nolimits _{m=2}^{n}R\left[m\right]\leqslant \sum\nolimits _{i=1}^{K}\sum\nolimits _{m=1}^{n-1}{R}_{i}\left[m\right]\text{，}n=2, \cdots ,N $

(19)

本文的目标可以说成在保证每个传感器传输给无人机的数据达到目标信息传输量的情况下，通过联合优化功率、带宽和飞行轨迹，来最大化系统的端到端吞吐量。其中受到的约束条件有无人机的机动性约束(1) 、带宽分配约束(6) 和(7) 、传感器和无人机的传输功率约束(8)~(11) 、信息−因果约束条件(14) 、以及每个传感器的最小信息传输量约束(15) ，为了便于问题的描述，文中将优化变量定义为飞行轨迹 ${\boldsymbol{Q}}=\left\{{\boldsymbol{q}}\left[n\right],\forall n\right\}$ ，功率 ${\boldsymbol{P}}=\left\{{{{p}}}_{i}\left[n\right],e\left[n\right],\forall i,n\right\}$ 以及带宽 ${\boldsymbol{A}}=\left\{{\alpha }_{i}\left[n\right],\beta \left[n\right],\forall i,n\right\}$ 。所以离散形式的最大化系统端到端吞吐量的优化问题可以制定为

$ ({\rm{P}}1)\qquad \underset{{\boldsymbol{Q}},{\boldsymbol{P}},{\boldsymbol{A}}}{\mathrm{max}}\;B{\delta }_{t}\sum\nolimits _{n=2}^{N}R\left[n\right] $

$ \;\;\;\;\;{\rm{s.t.}}\;\;\; B{\delta }_{t}\sum \nolimits_{n=1}^{N-1}{R}_{i}\left[n\right] \geqslant C\text{，}\forall i $

(20)

$ \qquad\qquad \frac{1}{N}\sum\nolimits _{n=1}^{N-1}p_i\left[n\right]\leqslant {P}_{{\rm{aver-i}}}\text{，}\forall i $

(21)

$ \quad \frac{1}{N}\sum\nolimits _{n=2}^{N}e\left[n\right]\leqslant {E}_{{\rm{aver}}} $

(22)

$ \qquad 0\leqslant {p}_{i}\left[n\right]\leqslant {P}_{{\rm{peak}}-i}, \forall i,n $

(23)

$ \;\;0\leqslant e\left[n\right]\leqslant {E}_{{\rm{peak}}}, \forall n $

(24)

$\qquad\quad \sum\nolimits _{i=1}^{K}{\alpha }_{i}\left[n\right]+\beta \left[n\right]=1\text{，}\forall n $

(25)

$\begin{split} \qquad \;\;\;\; &{\alpha }_{i}\left[n\right]\geqslant 0\text{，}\beta \left[n\right]\geqslant 0\text{，}\forall i,n \\ &(16) , (19) \end{split}$

(26)

由于目标函数是非凹的而且约束条件(19) 和(20) 是非凸的，故难以求出最优解，并且问题实际上涉及到的优化变量之间存在着紧密的耦合关系，为了解耦并将问题转化成方便求解的标准凸优化问题，在接下来本文应用块坐标下降法和连续凸优化方法去交替地求解(P1) 的两个子问题，分别为固定飞行轨迹优化功率和带宽、固定功率和带宽优化飞行轨迹。

2.1 固定飞行轨迹优化功率和带宽

当给定无人机飞行轨迹Q时，原问题退化为只优化功率P和带宽分配A来最大化信息采集系统的端到端吞吐量，删除(P1) 中只与优化变量Q有关的约束条件(16) ，得到以下优化功率和带宽的子问题。

$ \begin{split} ({\rm{P}}2)\qquad \underset{{\boldsymbol{P}},{\boldsymbol{A}}}{\mathrm{max}}&B{\delta }_{t}\sum\nolimits _{n=2}^{N}R\left[n\right]\\ {\rm{s.t.}} \;\;\;&(19) \sim (26) \end{split}$

此时 $ {\gamma }_{i}\left[n\right] $ 和 $ \rho \left[n\right] $ 在这里相当于一个常数。因为目标函数是非凹的而且信息−因果约束条件(19) 相对于P和A是非凸的，这同样是一个难以求解的非凸优化问题，于是引进一个松弛变量 $ {\left\{{R}^{r}\left[n\right]\right\}}_{n=2}^{N} $ ，使得(P2) 等价为以下的优化问题。

$ ({\rm{P}}3)\qquad \underset{\left\{{R}^{r}\left[n\right]\right\},{\boldsymbol{P}},{\boldsymbol{A}}}{\mathrm{max}}B{\delta }_{t}\sum\nolimits _{n=2}^{N}{R}^{r}\left[n\right] $

$ \qquad{\rm{s.t.}}\;\;\; {R}^{r}\left[n\right] \leqslant R\left[n\right]\text{，}n=2, \cdots ,N $

(27)

$\begin{split} \qquad\qquad\qquad\;\; &\sum\nolimits _{m=2}^{n}{R}^{r}\left[m\right]\leqslant \sum\nolimits _{i=1}^{K}\sum\nolimits _{m=1}^{n-1}{R}_{i}\left[m\right]\text{，}\\& \qquad n=2, \cdots ,N\\ & \qquad (20) \sim (26) \\[-10pt] \end{split}$

(28)

可以证明对于(P3) 的最优解，约束条件(27) 中的等号总是成立，否则总可以使松弛变量 $ {R}^{r}\left[n\right] $ 增大而保持其他变量不变，直至等号成立，问题中所有的约束条件依然能够满足，并且能取得更大的函数值，也就是说引入松弛变量前后的两个问题是等价的。可以证明(P3) 中所有约束条件对于优化变量P和A都是联合凸的，因此(P3) 是一个标准凸优化问题，可以通过内点法或者CVX优化器求解。

2.2 固定功率和带宽优化飞行轨迹

当给定功率P和带宽分配A时，原问题退化为只优化无人机轨迹Q来最大化端到端吞吐量，删除(P1) 中只与优化变量P或者A有关的约束条件(21)~(26) ，得到以下优化飞行轨迹的子问题。

$ \begin{split} ({\rm{P}}4) \qquad \underset{{\boldsymbol{Q}}}{\mathrm{max}}&B{\delta }_{t}\sum\nolimits _{n=2}^{N}R\left[n\right]\\ {\rm{s.t.}}\;\;\; &(16) , (19) ,(20) \end{split} $

这个子问题也是一个非凸的优化问题，同样引入松弛变量 $ {\left\{{R}^{r}\left[n\right]\right\}}_{n=2}^{N} $ 得到以下的等价问题。

$ \begin{split} ({\rm{P}}5)\qquad \underset{\left\{{R}^{r}\left[n\right]\right\},{\boldsymbol{Q}}}{\mathrm{max}}&B{\delta }_{t}\sum\nolimits _{n=2}^{N}{R}^{r}\left[n\right]\\ {\rm{s.t.}}\;\;\;& (16) , (20) ,(27) , (28) \end{split}$

类似地，可以证明求解(P4) 等价于求解(P5) ，但是约束条件(20)、(27)、(28) 对于优化变量Q都是非凸的，则(P5) 仍然是一个难以求解的非凸优化问题。所以接下来给定一个任意的局部飞行轨迹 $ {{\boldsymbol{Q}}}^{l}\triangleq \left\{{{\boldsymbol{q}}}^{l}\left[n\right]\right\} $ ，通过一阶泰勒展开求下界，并且利用连续凸优化方法，依次最大化原问题的下界。

上行信道和下行信道的可达速率(17)、(18) 虽然对于 $ {\boldsymbol{q}}\left[n\right] $ 是非凸的，但是对于 $ {\left\| {{\boldsymbol{q}}\left[n\right]-{{\boldsymbol{s}}}_{i}} \right\|}^{2} $ 或者 $ {\left\| {{\boldsymbol{q}}\left[n\right]-{\boldsymbol{w}}} \right\|}^{2} $ 却都是凸的。如果 $ a \geqslant 0 $ 并且 $ x \geqslant -b $ ，可以证明有类似形式的函数 $f\left(x\right) \triangleq {{\rm{log}}}_{2}\left(1+\dfrac{a}{b+x}\right)$ 是一个凸函数。因为凸函数的一阶泰勒展开是原函数的下界^[23]，故有 $f\left(x\right) \geqslant f\left({x}_{0}\right) +{f}'\left({x}_{0}\right) \left(x-{x}_{0}\right) ，\forall x$ ，其中 ${f}'\left({x}_{0}\right) = -\dfrac{\left({{\rm{log}}}_{2}e\right) a}{\left(b+{x}_{0}\right) \left(a+b+{x}_{0}\right) }$ 是函数 $ f\left(x\right) $ 在 $ {x}_{0} $ 这一点的一阶导数，若令 $ {x}_{0}=0 $ 可以得到不等式

$ {{\rm{log}}}_{2}\left(1+\frac{a}{b+x}\right) \geqslant {{\rm{log}}}_{2}\left(1+\frac{a}{b}\right) -\frac{\left({{\rm{log}}}_{2}e\right) ax}{b\left(a+b\right) } $

(29)

令 ${\varepsilon }_{i}\left[n\right]\triangleq {p}_{i}\left[n\right]{\gamma }_{0}/{\alpha }_{i}\left[n\right]$ ， $ \zeta \left[n\right]\triangleq e\left[n\right]{\gamma }_{0}/\beta \left[n\right] $ ，继而对于上行信道，令上式中的 $ a={\varepsilon }_{i}\left[n\right] $ ， $b={H}^{2}+{\left\| {{{\boldsymbol{q}}}^{l}\left[n\right]-{{\boldsymbol{s}}}_{i}} \right\|}^{2}$ ，以及 $x={{\left\| {{\boldsymbol{q}}\left[n\right]-{{\boldsymbol{s}}}_{i}}\right\|}^{2}-{\left\|{{{\boldsymbol{q}}}^{l}\left[n\right]-{{\boldsymbol{s}}}_{i}} \right\|}^{2}}$ ，对于下行信道也做类似定义，代入可以得到

$ \begin{split} &{R}_{i}\left[n\right]\geqslant {R}_{i}^{lb}\left[n\right]\triangleq {\alpha }_{i}\left[n\right]{{\rm{log}}}_{2}\left(1+\frac{{\varepsilon }_{i}\left[n\right]}{{H}^{2}+{\left\| {{{\boldsymbol{q}}}^{l}\left[n\right]-{{\boldsymbol{s}}}_{i}} \right\|}^{2}}\right)- \\& {\varphi }^{l}\left[n\right]\left({\left\| {{\boldsymbol{q}}\left[n\right]-{{\boldsymbol{s}}}_{i}} \right\|}^{2}-{\left\| {{{\boldsymbol{q}}}^{l}\left[n\right]-{{\boldsymbol{s}}}_{i}} \right\|}^{2}\right) \text{，}\forall i,n \end{split} $

(30)

$ \begin{split} &R\left[n\right]\geqslant {R}^{lb}\left[n\right]\triangleq \beta \left[n\right]{{\rm{log}}}_{2}\left(1+\frac{\zeta \left[n\right]}{{H}^{2}+{\left\| {{{\boldsymbol{q}}}^{l}\left[n\right]-{\boldsymbol{w}}} \right\|}^{2}}\right)- \\ & {\phi }^{l}\left[n\right]\left({\left\| {{\boldsymbol{q}}\left[n\right]-{\boldsymbol{w}}} \right\|}^{2}-{\left\| {{{\boldsymbol{q}}}^{l}\left[n\right]-{\boldsymbol{w}}} \right\|}^{2}\right) \text{，}\forall n \end{split} $

(31)

其中：

$ {\varphi }^{l}\left[n\right] \triangleq \frac{{\alpha }_{i}\left[n\right]\left({{\rm{log}}}_{2}e\right) {\varepsilon }_{i}\left[n\right]}{\left({H}^{2} + {\left\| {{{\boldsymbol{q}}}^{l}\left[n\right] - {{\boldsymbol{s}}}_{i}} \right\|}^{2}\right) \left({H}^{2} + {\left\| {{{\boldsymbol{q}}}^{l}\left[n\right] - {{\boldsymbol{s}}}_{i}} \right\|}^{2} + {{\boldsymbol{\varepsilon}} }_{i}\left[n\right]\right) } $

(32)

$ {\phi }^{l}\left[n\right] \triangleq \frac{\beta \left[n\right]\left({{\rm{log}}}_{2}e\right) \zeta \left[n\right]}{\left({H}^{2} + {\left\| {{{\boldsymbol{q}}}^{l}\left[n\right] - {\boldsymbol{w}}} \right\|}^{2}\right) \left({H}^{2} + {\left\| {{{\boldsymbol{q}}}^{l}\left[n\right] - {\boldsymbol{w}}} \right\|}^{2} + \zeta \left[n\right]\right) } $

(33)

对于任意给定的 $ {{\boldsymbol{q}}}^{l}\left[n\right] $ ， $ {R}_{i}^{lb}\left[n\right] $ 和 $ {R}^{lb}\left[n\right] $ 分别是 $ {R}_{i}\left[n\right] $ 和 $ R\left[n\right] $ 的下界，它们都是关于 $ {\boldsymbol{q}}\left[n\right] $ 的凹函数。因此，子问题(P5) 的最优值的下界可以通过以下优化问题求解得到

$ ({\rm{P}}6) \qquad \underset{\left\{{R}^{r}\left[n\right]\right\},{\boldsymbol{Q}}}{\mathrm{max}}B{\delta }_{t}\sum\nolimits _{n=2}^{N}{R}^{r}\left[n\right] $

$ \qquad\qquad\quad\qquad\quad {\rm{s.t.}}\;\;\; B{\delta }_{t}\sum\nolimits _{n=1}^{N-1}{R}_{i}^{lb}\left[n\right] \geqslant C\text{，}\forall i $

(34)

$ {R}^{r}\left[n\right] \leqslant {R}^{lb}\left[n\right]\text{，}n=2, \cdots ,N $

(35)

$\begin{split} \qquad\qquad & \sum\nolimits _{m=2}^{n}{R}^{r}\left[m\right]\leqslant \sum\nolimits _{i=1}^{K}\sum\nolimits _{m=1}^{n-1}{R}_{i}^{lb}\left[m\right]\text{，}\\ &n=2, \cdots ,N (16) \end{split}$

(36)

需要注意的是当 $ {\boldsymbol{q}}\left[n\right]={{\boldsymbol{q}}}^{l}\left[n\right] $ 时，式(30) 和(31) 中的不等号变为等号，故代入(P6) 的最优解，(P5) 的目标函数值肯定不会小于在 $ {{\boldsymbol{q}}}^{l}\left[n\right] $ 处得到的目标函数值。实际上(P6) 的可行解集是(P5) 的可行解集的子集，并且(P6) 的最优值是(P5) 的最优值的下界。可以证明(P6) 是一个凸的二次约束二次规划问题(Quadratical Constraint Quadratic Programming, QCQP) ，故可以通过内点法或者CVX优化器求解。

3 优化算法及其收敛证明

总结上面两个子问题的处理，得到了一种有效的联合优化功率控制、带宽分配和飞行轨迹的交替优化算法，如表1所示，也就是给定初始局部飞行轨迹 ${{\boldsymbol{Q}}}^{l}$ 的情况下(P3) 和(P6) 两个子问题交替迭代求解，即在每一步迭代中一个子问题的优化结果是另一个子问题的输入，这样循环下去直到算法收敛。

在传统的块坐标下降法中，要求子问题必须得到一个准确的解，以更新优化变量。但是在本文固定功率和带宽优化无人机轨迹的子问题中，使用连续凸优化方法连续最大化原来子问题目标值的下界来得到近似解，因此此时不能简单地应用传统块坐标下降法的收敛分析，所以本文还需要结合上面的过程来证明一下所提出的交替优化算法的收敛性。

定义 $ \chi \left({\boldsymbol{P}},{\boldsymbol{A}},{\boldsymbol{Q}}\right) $ 表示原问题(P1) 的目标函数值，而 $ {\chi }_{trj}^{lb}\left({\boldsymbol{P}},{\boldsymbol{A}},{\boldsymbol{Q}}\right) $ 表示固定功率带宽优化飞行轨迹子问题(P6) 的最优值。在算法的第3步中，因为一个最大化的标准凸优化问题的最优值对比求解前肯定是非减的。所以这时可以得到

$ \chi \left({{\boldsymbol{P}}}^{l},{{\boldsymbol{A}}}^{l},{{\boldsymbol{Q}}}^{l}\right) \leqslant \chi \left({{\boldsymbol{P}}}^{l+1},{{\boldsymbol{A}}}^{l+1},{{\boldsymbol{Q}}}^{l}\right) $

(37)

在算法的第4步，有不等式关系如式(38)所示。

$ \begin{split} \;\chi \left({{\boldsymbol{P}}}^{l+1},{{\boldsymbol{A}}}^{l+1},{{\boldsymbol{Q}}}^{l}\right) &\mathop {\rm{ = }}\limits^{({\rm{a}})} {\chi }_{trj}^{lb}\left({{\boldsymbol{P}}}^{l+1},{{\boldsymbol{A}}}^{l+1},{{\boldsymbol{Q}}}^{l}\right) \mathop \leqslant \limits^{({\rm{b}})} \\& {\chi }_{trj}^{lb}\left({{\boldsymbol{P}}}^{l+1},{{\boldsymbol{A}}}^{l+1},{{\boldsymbol{Q}}}^{l+1}\right) \mathop \leqslant \limits^{({\rm{c}})} \chi \left({{\boldsymbol{P}}}^{l+1},{{\boldsymbol{A}}}^{l+1},{{\boldsymbol{Q}}}^{l+1}\right) \end{split} $

(38)

式中：等号(a) 成立是因为对于一阶泰勒展开得到的(30) 和(31) ，如果无人机飞行轨迹 $ {\boldsymbol{q}}\left[n\right] $ 等于给定的局部飞行轨迹 $ {{\boldsymbol{q}}}^{l}\left[n\right] $ 时等式成立，也就是说此时(P6) 在 $ {{\boldsymbol{q}}}^{l}\left[n\right] $ 处的最优值和问题(P5) 的一样，根据前面的证明可知和(P4) 也是一样的。而不等号(b) 能够存在主要是在算法的第4步中通过代入 $ {{\boldsymbol{P}}}^{l+1} $ 和 $ {{\boldsymbol{A}}}^{l+1} $ 优化求解(P6) 得到 $ {{\boldsymbol{Q}}}^{l+1} $ 会使目标值在迭代中保持非减。最后不等号(c) 存在的原因便是(P6) 求解得到的近似最优值是原来子问题(P4) 的下界。不等式(38) 说明(P6) 虽然只能求解得到一个近似值，但在每一次迭代中总是能够保证原问题的目标值在交替优化后是保持非减的。综合上面得到的不等式关系(37) 和(38) ，可以进一步推导得到不等式

$ \chi \left({{\boldsymbol{P}}}^{l},{{\boldsymbol{A}}}^{l},{{\boldsymbol{Q}}}^{l}\right) \leqslant \chi \left({{\boldsymbol{P}}}^{l+1},{{\boldsymbol{A}}}^{l+1},{{\boldsymbol{Q}}}^{l+1}\right) $

(39)

这证明了制定的原优化问题(P1) 的目标函数值随着提出的交替优化算法的每一步迭代都是非减的。因为问题的目标值的上界肯定是有限的，综合以上论述的内容以及推导出来的几个不等式关系，不难可以证明提出来的算法最终是会收敛的。

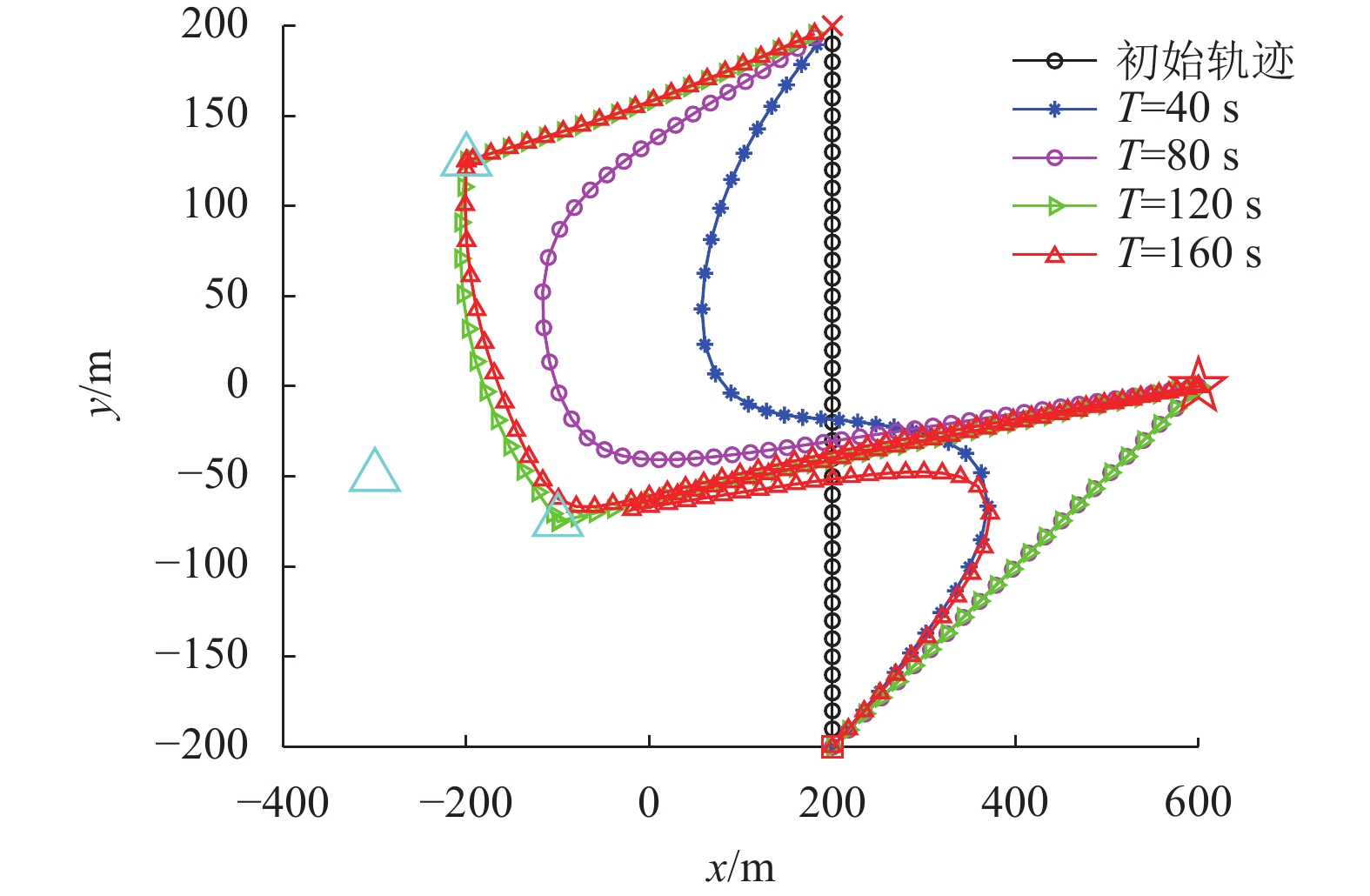
4 仿真结果

仿真过程中考虑一个有3个传感器的信息采集系统，如图2所示，用“△”、“☆”、“×”和“□”分别表示传感器位置、信息融合中心位置、无人机起始位置和最终位置。3个传感器的位置坐标分别设置为[−300,−50]，[−200,125]和[−100,−75]，信息融合中心的位置为[600,0]，无人机固定的飞行高度H=100 m，最大飞行速度 $ {V}_{{\rm{max}}} $ =20 m/s。假设步长 $ {\delta }_{t} $ =1 s，也就是飞行时间T时会被等分为 $ N=T/{\delta }_{t} $ 个时隙，则每个时隙内的最大水平飞行距离为 $ {D}_{{\rm{max}}}={V}_{{\rm{max}}}{\delta }_{t} $ =20 m。系统可用总带宽为1 MHz，加性噪声功率谱密度 $ {N}_{0} $ =−169 dBm/Hz，单位距离信道功率增益 $ {\lambda }_{0} $ =−60 dB，峰值功率和平均功率之间是4倍的关系，即 $ {P}_{{\rm{peak}}-i}=4{P}_{{\rm{aver}}-i} $ ， $ {E}_{{\rm{peak}}}=4{E}_{{\rm{aver}}} $ ，并且 $ {P}_{{\rm{aver}}-i}={E}_{{\rm{aver}}} $ =0.5 W，每个传感器所要满足的最小信息传输量为C=10⁶ bits，判断交替循环是否停止的阈值设置为 $\epsilon $ =10⁻³。

提出的交替优化算法需要设置一个初始的无人机飞行轨迹，并且其将会影响最终的收敛性。在本文中把初始飞行轨迹设置为从所有传感器位置的中点(横纵坐标分别取为所有传感器位置的横纵坐标值的平均值)到信息融合中心这两点之间连线的中垂线，无人机沿着这条中垂线自上而下匀速飞行。若假设初始轨迹的总长度为400 m，可知无人机的起始位置q₀ = [200,200]，最终位置为q_F = [200,−200]。

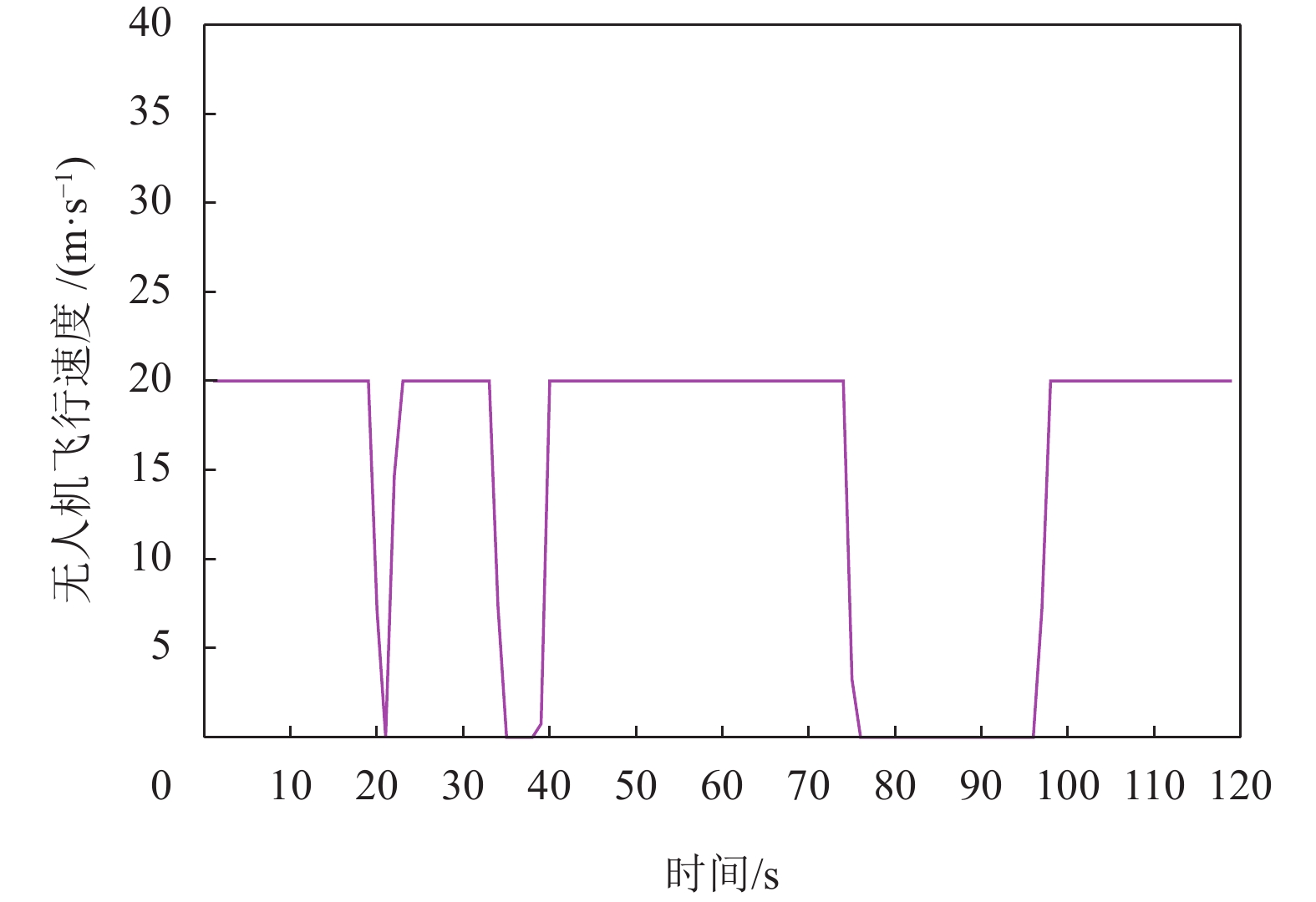
首先举例说明飞行时间T取不同值的情况下优化得到的无人机轨迹，由图2可以看出飞行时间越长，无人机飞行轨迹的自由度会越大，会趋向于飞向传感器和信息融合中心上方以获取质量最佳的通信信道。当T=40 s和T=80 s时，由于时间不足，为了维持从传感器收集到的信息量和转发给信息融合中心的信息量之间的平衡，无人机需要兼顾好靠近传感器区域或者信息融合中心的时间分配，故在这两个时间范围里无人机均无法到达任何一个传感器上方，巧合的是T=80 s时刚好可以经过信息融合中心。为了收集和转发更多的信息，这两种情况下无人机都保持着最大的速度飞行，向左靠近传感器区域，向右靠近信息融合中心，努力缩短距离减少路径损耗，并且飞行时间越长，轨迹弧线弯曲的幅度会越大。当T=120 s时间比较充足的时候，无人机经过传感器2和3，再经过信息融合中心，结合图3中无人机的瞬时速度，可以知道无人机整个过程分为最大速度飞行和悬停两种状态。将沿着轨迹飞行而剩下的时间分配在这三处地方悬停，这是因为悬停在传感器或信息融合中心上方是路径损耗最小的位置。然而当T=160 s时间更加充裕的时候，无人机宁愿在到达信息融合中心后掉头再次返回靠近传感器3继续收集信息，也没有为了遍历所有传感器而在前面的时间里经过离信息融合中心较远的传感器1，当然这样传感器1发送给无人机的数据还是会满足最小信息传输量约束。这一方面和前面所设置的位置坐标有关，另一方面无人机的飞行过程实际上依然是一种权衡收集信息和转发信息的行为。

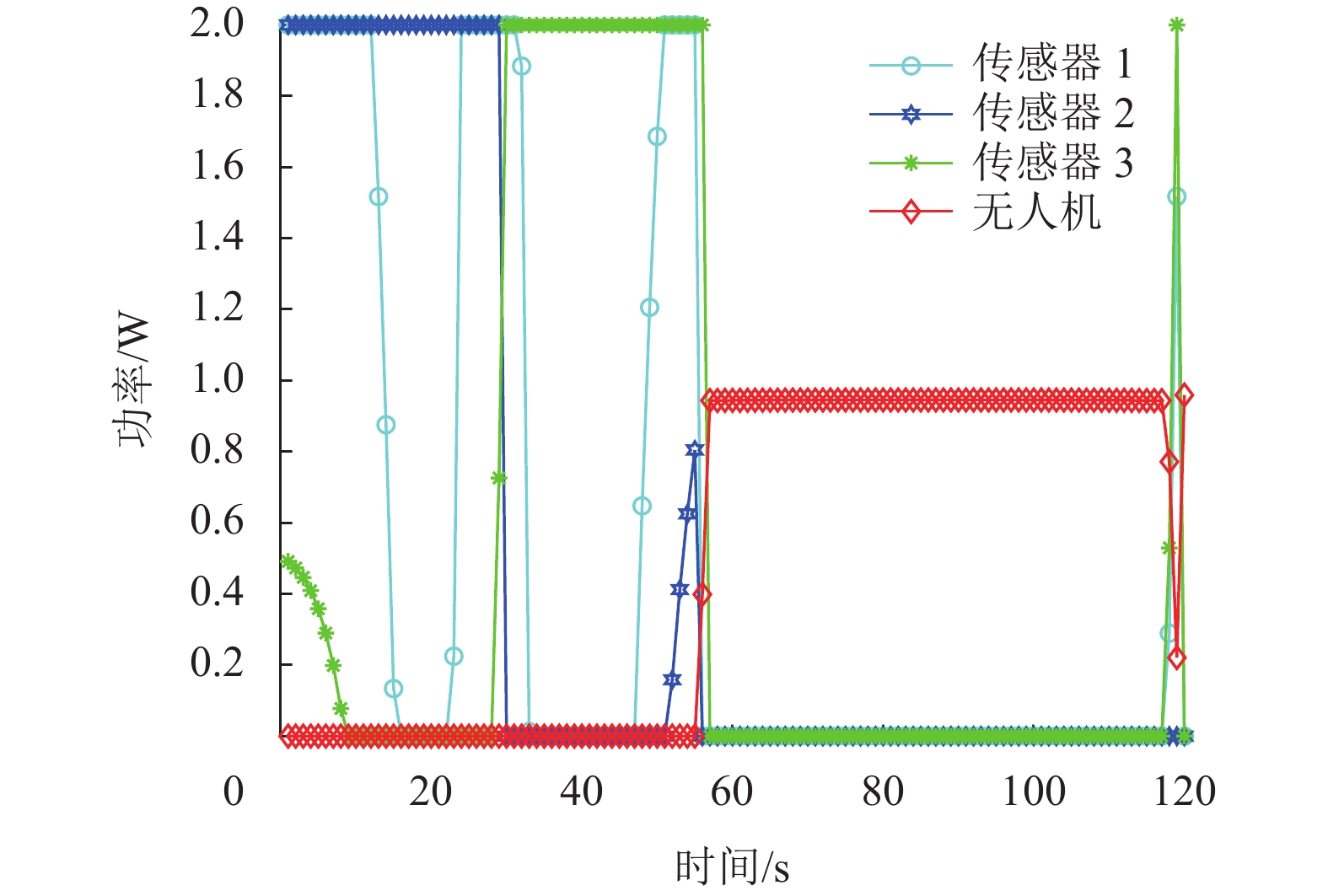
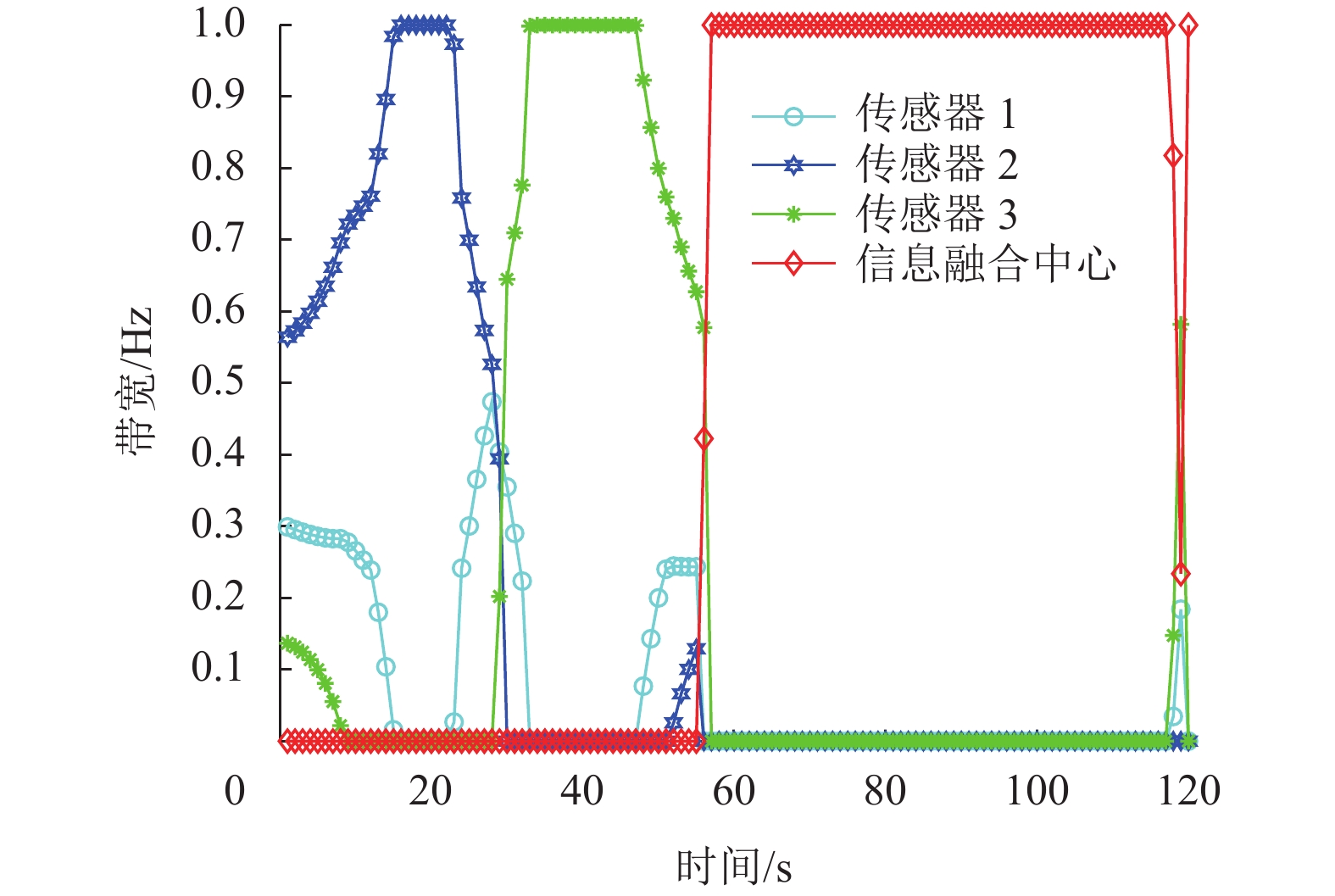
以T=120 s为例，图4和图5分别是功率和带宽的优化结果，可以看出无人机没有同时收发，而是在前一半时间里用于收集传感器数据，后一半时间里用于转发信息给信息融合中心。结合飞行轨迹，可以大致认为只有当无人机和传感器之间的距离小于一定数值时，传感器才传输数据，并且是以峰值功率传输。而带宽分配同样也是根据距离而动态分配的，无人机越靠近，分配给传感器的带宽就越多，甚至出现了在一小段时间里把所有可用带宽都分配给一个传感器的情况。可以看出不同的传感器能够同时传输数据给无人机，这是因为文中使用频分多址的方法为每条链路动态分配带宽，使得每条链路在传输数据时拥有各自的频段而不会互相干扰。

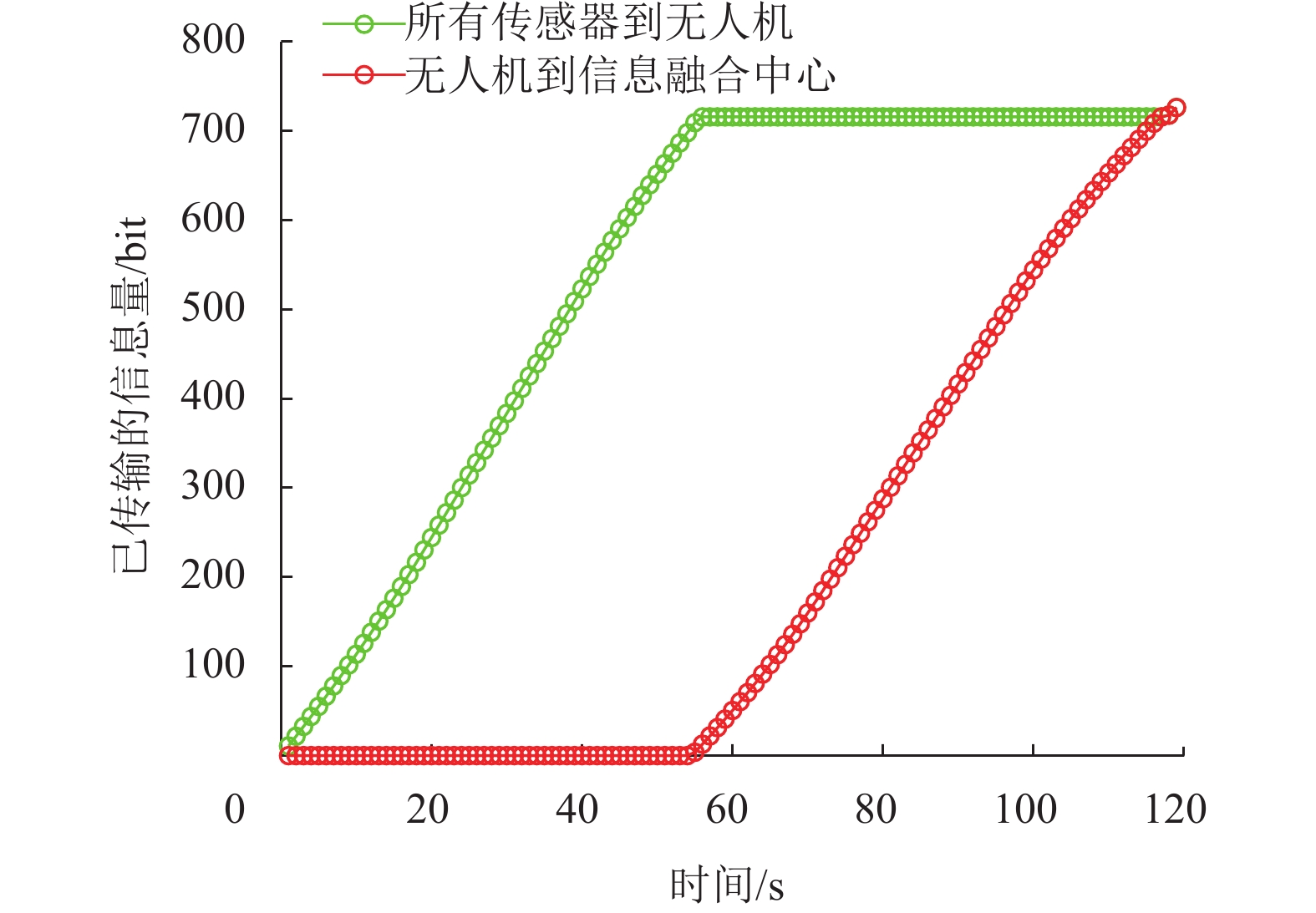
图6显示了每个时刻所有传感器已经上传给无人机的信息量和以及无人机已经转发给信息融合中心的信息量，一方面验证了仿真结果能够满足信息−因果约束条件，另一方面可以看出最终无人机转发的信息量和收集到的信息量相同，证明了本文所提出的算法确实能够有效地兼顾数据收集链路和数据转发链路之间的平衡。

为了进一步检验所提出的交替优化算法(简称T-OPT-With-PB)的有效性，接下来将考虑另外3种基准方案来做比较。

(1) PB-OPT-Without-T：有功率控制和带宽分配，但没有无人机的轨迹优化；

(2) T-OPT-Without-PB：有无人机的轨迹优化，但没有功率控制和带宽分配；

(3) Without-T-PB-OPT：没有无人机的轨迹优化，也没有功率控制和带宽分配。

在PB-OPT-Without-T方案中，将之前的中垂线初始轨迹作为固定的飞行轨迹，通过求解(P3) 最大化吞吐量。在T-OPT-Without-PB方案中，将每个传感器和无人机的传输功率都固定为平均功率，分配的带宽都是0.25 B，同样地将中垂线初始轨迹当作初始局部飞行轨迹对(P6) 进行循环迭代求解。然而在Without-T-PB-OPT方案中不做任何优化，无人机飞行轨迹为中垂线初始轨迹，带宽和功率的设置和T-OPT-Without-PB一样，直接计算此时的吞吐量。

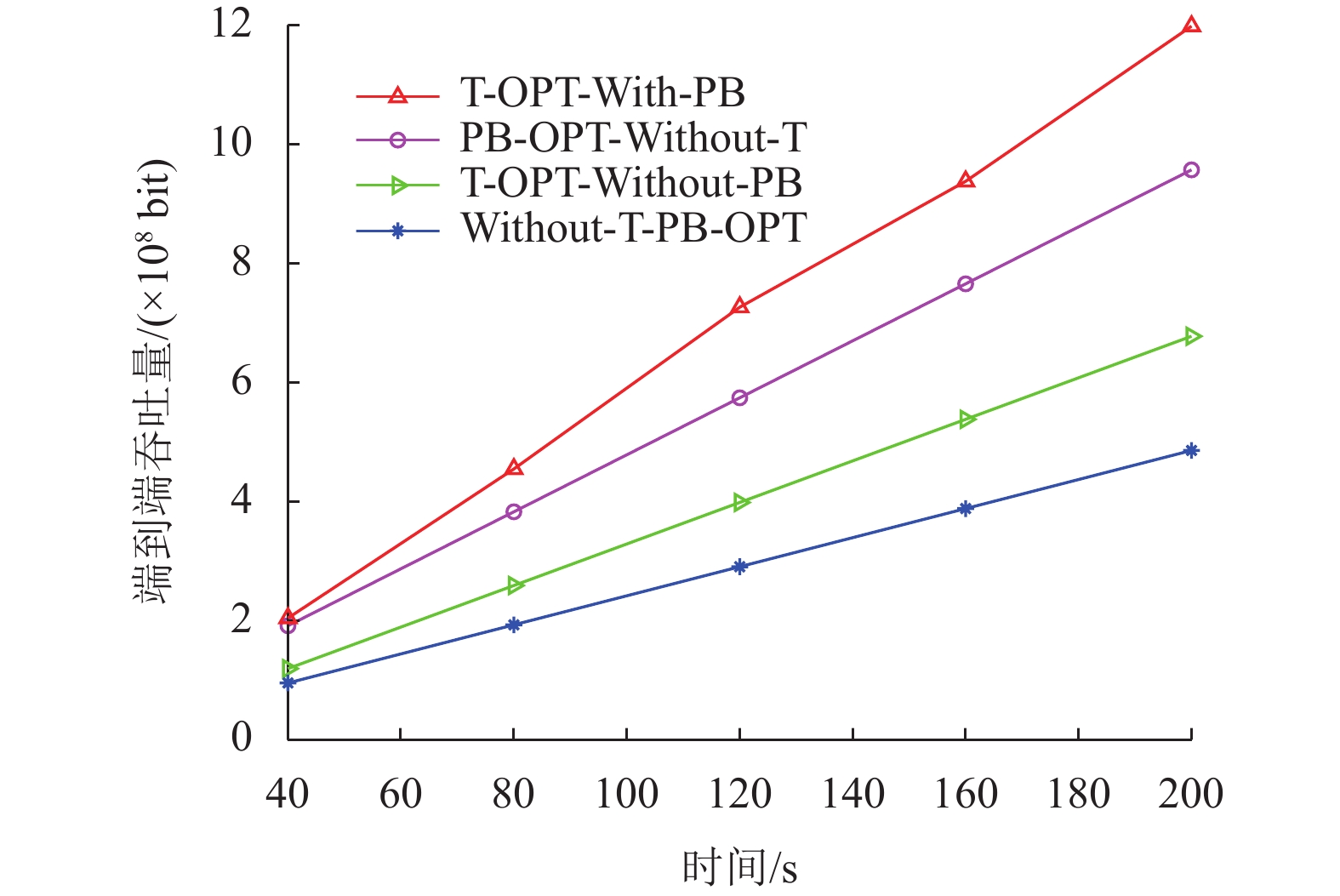
通过仿真将提出的交替优化算法和上面3种基准方案在不同飞行时间T得到的系统最大端到端吞吐量一起画在图7中，得到的结果和预期一样，提出的T-OPT-With-PB方案相比其他3种方案表现出了极好的效果，而且随着飞行时间的增加效果会越明显，而Without-T-PB-OPT在任何飞行时间都是效果最差的。PB-OPT-Without-T的效果却一直都要比T-OPT-Without-PB要好，这是因为在功率和带宽分配都固定的情况下，无论无人机怎么飞行，越靠近传感器时上行信道的通信质量越好，这势必会使下行信道的通信质量越差，反过来也是一样。而如果当飞行轨迹固定的时候，功率控制和带宽分配可以根据无人机的位置动态的调节上行信道和下行信道。

5 结论

本文研究了一个无人机支持的多传感器信息采集系统。为了最大化系统的端到端吞吐量，并且满足最小信息传输量约束、信息−因果约束、平均和峰值传输功率约束、带宽分配约束和无人机机动性约束，文中应用块坐标下降法和连续凸优化方法提出了一种联合优化传感器的发射功率、可用带宽的分配、无人机的传输功率和飞行轨迹的交替优化算法。仿真结果表明了所提出的算法有效地兼顾了数据收集链路和数据转发链路之间的平衡，显著提高了系统的端到端吞吐量。因为无人机和传感器的续航能力和发射功率实际上都是有限的，本文提出的联合优化功率、带宽和飞行轨迹的算法具有工程应用价值。在后续的工作中将会考虑例如旅行商问题来改善算法的普适性，并且可以通过最大化所有传感器之中的最小信息传输量来使得公平性更加明显。