随着无线通信网络和互联网技术的快速发展,人们能够快速地和大规模群体进行实时观点交换,其中,社会网络团体决策(Social Network Group Decision Making,SNGDM)正快速成为解释人类行为的关键工具[1-3],为学术和工程领域带来了潜在的价值,如:供应商选择[4]、公众舆情管理[5-7]、政治选举[8-10]、市场[11]等。SNGDM中包含了一组可以表达自身观点的人(智能体),这些智能体能够和其邻居进行交流并以选择最优候选解为目标。观点(Opinion)是影响和定义行为最关键的因素之一[12-13]。每个智能体通过考虑其邻居的观点来对自身观点进行修正,以此达到一致、两极化、分裂的稳定结构,这种过程被称为观点演化,又称舆情动力学(Opinion Dynamics)[12]。
在SNGDM中最具有挑战性的问题是所有智能体达成观点上的全面一致性[12, 14-16]。同时,在舆情动力学中,网络拓扑表示智能体间的交互规则,对舆情的演化起着重要的作用[17- 18]。由于社交网络拓扑中常常存在稀疏的网络连接,因此达成全面的一致性更为复杂,相关研究仍然处于初期[1]。目前,大部分上述研究仅考虑了智能体与具有相似观点的邻居之间的一跳连接,而忽略了设计更为高效的通信交流方式,以更好地在大规模场景下增强一致性。此类问题可以通过多智能体强化学习(Multi-agent Reinforcement Learning,MARL)来解决,该方法正成为一种在线解决动态复杂问题的强大技术手段[19-20]。例如,Shou等[21]提出了一种平均场表演者−评论者的MARL算法来解决在竞争场景下多驾驶员重定位的问题。Sun等[22]通过多智能体决定性策略梯度方法来解决合作场景下电压控制问题。
但目前鲜有学者将MARL的优势融入到社交网络增强舆情一致性的研究中,因此本文提出了一种全新的基于MARL的智能感知模型COEIP(Consensus Opinion Enhancement with Intelligent Perception),通过分布式的手段增强系统的舆情一致性。具体来说,在社交网络下舆情动力学模型的马尔科夫决策过程中,由于各智能体感知范围有限,在每个时刻感知到的邻居数量不定,进而导致各智能体获取的邻居状态信息不定长。因此本文设计了基于双向循环神经网络的模型来构建智能体的感知模型,使智能体具备邻域选择的能力;接着通过差分奖励的思想设计了具有3类不同舆情动力学场景目标的奖励函数,并使用基于策略梯度的多智能体探索与协同更新算法来高效训练智能体的感知模型,使智能体具备多目标权衡的邻域选择能力。大量仿真验证了本文提出的COEIP方法和差分奖励函数的有效性。同时在与3类传统方法的对比中验证了本方法可以有效增强所有智能体之间的意见一致性,即减少社交网络最终稳定时形成的簇的数量,具有一定的优越性。
1 基于MARL的增强舆情一致性方法 1.1 社交网络舆情动力学社交网络中的舆情动力学模型刻画了拥有各自观点的智能体在既定的融合规则下与其邻居进行观点演化的过程,本文针对具有时变切换拓扑的离散多智能体系统[12]进行研究。
(1) 舆情动力学模型的环境:考虑系统中的一组智能体
(2) 舆情动力学模型演化的融合规则:2个智能体
| $ \begin{array}{l} {N_i}\left( k \right) = \left\{ {j \in V:\left( {i,j} \right) \in E\left( k \right)} \right\}= \{ {j: | {{x_i}\left( k \right) - {x_j}\left( k \right)} | <{r_{\rm{c}}}} \} \end{array} $ | (1) |
根据式(1) 的定义,一个智能体永远是其自身的邻居,用
| $ {x_i}(k + 1) = \frac{{\displaystyle\sum\nolimits_{j \in {N_i}\left( k \right) } {{x_j}} (k) }}{{\displaystyle\sum\nolimits_{j \in {N_i}\left( k \right) } 1 }} $ | (2) |
式(2) 所定义的舆情动力学的融合规则表明,每个智能体通过计算可信任邻居观点的平均值来更新自身的观点。
(3) 舆情观点的表示形式:在系统中的每一个智能体
| $ \boldsymbol{X}(k+1) =\boldsymbol{L}(k) \boldsymbol{X}(k) $ | (3) |
式中:
| $ l_{ij}(k) =\left\{\begin{array}{ll} \dfrac{1}{\left|N_{i}(k) \right|}, j \in N_{i}(k) \\ 0, \;\;\;\; \;\;\;\;\; j \notin N_{i}(k) \end{array}\right. $ | (4) |
在传统舆情动力学模型(3) 的演化过程中,舆情观点的一致和网络通信拓扑有着紧密的联系,但传统模型中代表网络通信拓扑的
马尔科夫决策过程(Markov Decision Processes, MDPs)是MARL中系统建模分析的基础。根据上节的分析,扩展了Zhang等[23]提出的MARL下的马尔科夫决策过程,通过式(5) 所示的五元组来定义本文针对社交网络下舆情动力学模型的马尔科夫决策过程。
| $ \left( {{{\left\{ {{S_i}} \right\}}_{i \in V{\rm{ }}}},{{\left\{ {{A_i}} \right\}}_{i \in V}},P,{{\left\{ {{R_i}} \right\}}_{i \in V}},{{\{ G(k) \} }_{k \geqslant 0}}} \right) $ | (5) |
式中:
如图1所示,本文定义的马尔科夫决策过程的运作流程可以表述为:在时刻
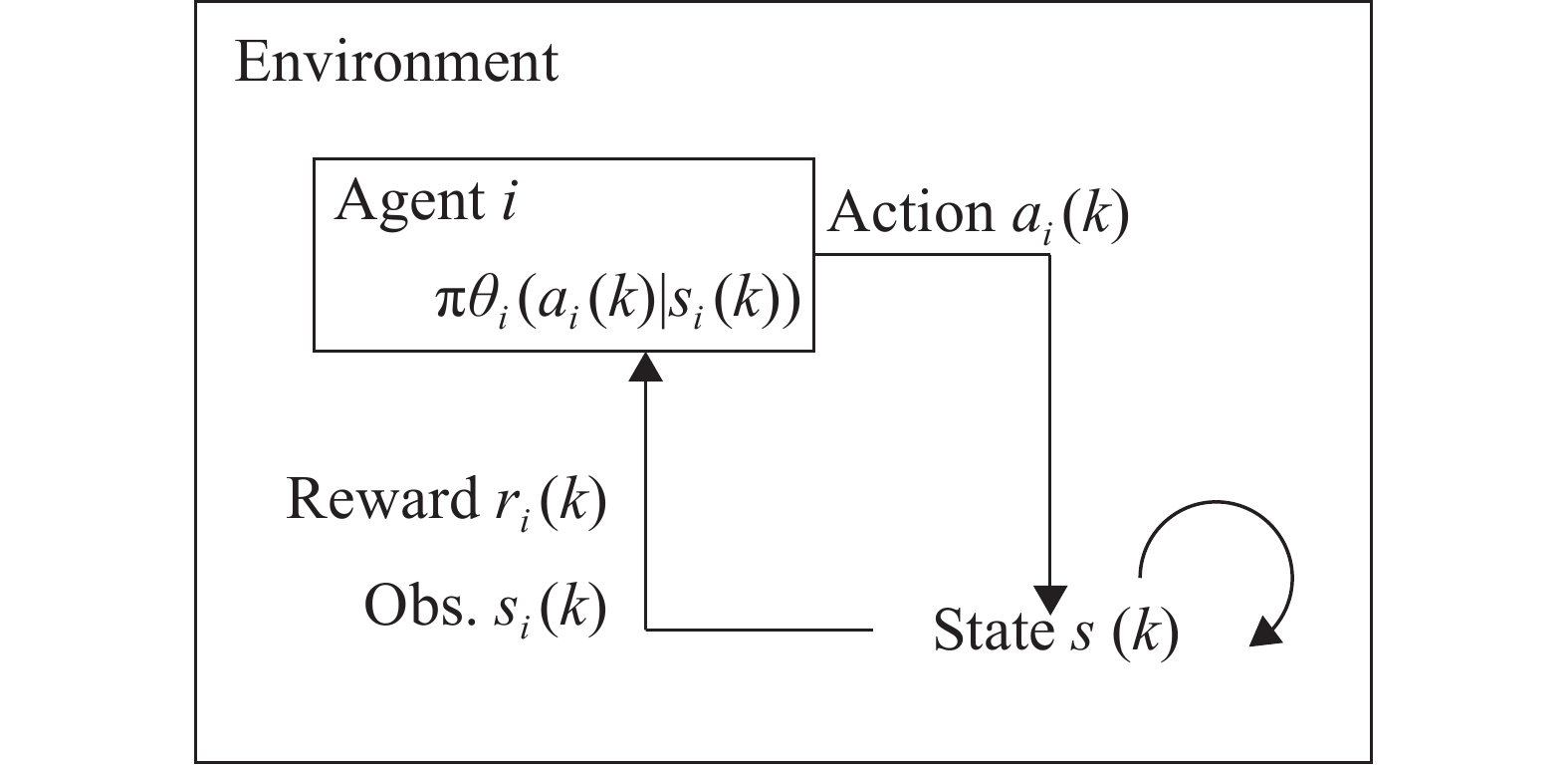
|
图 1 社交网络下舆情动力学模型的马尔科夫决策过程示意图 Figure 1 Markov decision processes in social network |
| $ U(\theta) =\mathbb{E}_{\pi_{\theta_{i}}}\Big[\sum\nolimits_{k} r_{i}(k) \mid s_{i}(k) , a_{i}(k) \Big] $ | (6) |
接下来针对智能体
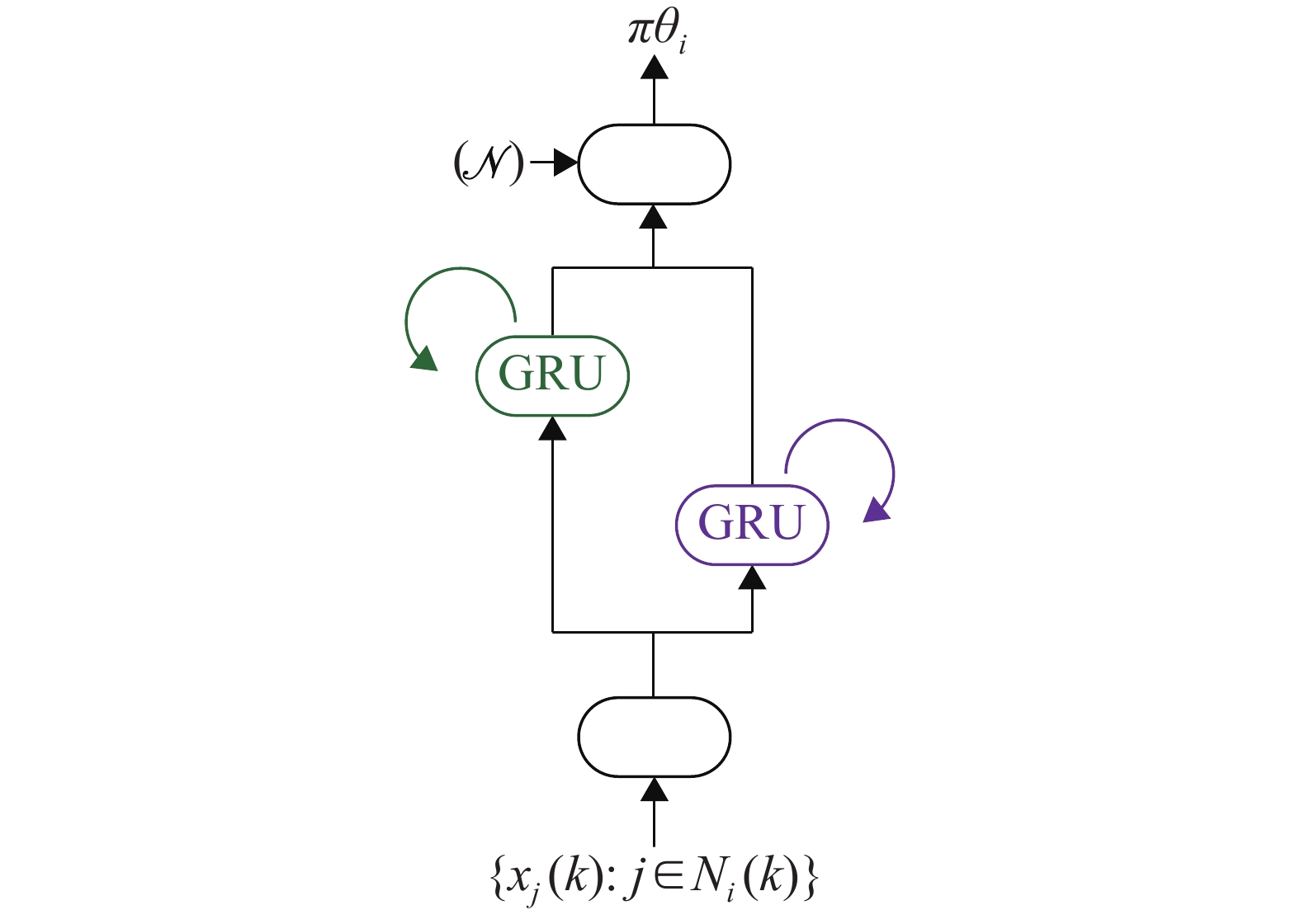
|
图 2 基于双向循环神经网络的决策模型示意图 Figure 2 Decision making model based on BGRU |
在该网络模型中,输入为智能体
| $ \widehat{N}_{i}(k) =\{j: j \in N_{i}(k) \wedge\pi _{{\theta _i}}^j>0.5\} $ | (7) |
作为一种以目标为导向的智能方法,强化学习中的目标通常采用累计奖励来表示,因此奖励函数的设计对智能体能力的学习起着至关重要的作用[25- 26]。同时,奖励函数的设计需要综合考量指标系数和可学习力之间的平衡[27- 28]。因此本文在文献的基础上,设计了舆情动力学环境下的差分奖励(Difference Reward)函数式。
| $ r_{i}(k) =R_{i}\left(s(k) , s_{-i}(k) \right) =g(s(k) ) -g\left(s_{-i}(k) \right) $ | (8) |
式中:
| $ g(s(k) ) =\alpha \cdot g_{1}(s(k) ) +\beta \cdot g_{2}(s(k) ) +\gamma \cdot g_{3}(s(k) ) $ | (9) |
式中:
(1)
| $ g_{1}(s(k) ) ={\rm{s t d}}(\boldsymbol{X}(k) ) -1 $ | (10) |
式中:
(2)
| $ g_{2}(s(k) ) =\frac{\displaystyle\sum\nolimits_{i \in V} |\widehat{N}_{i}(k) |}{n(n-1) } $ | (11) |
式中:
(3)
| $ g_{3}(s(k) ) =\frac{\displaystyle \sum\nolimits_{i \in {V}} d_{n n_{,}, i}(k) }{n(n-1) } $ | (12) |
| $ {d_{nn,i}}(k) = \frac{1}{{| {{\widehat{N}_i}(k) } |}}\sum\nolimits_{_{j \in {\widehat{N}_i}(k) }} {{d_j}(k) } $ | (13) |
式中:
值得注意的是,
基于策略梯度(Policy Gradient)的强化学习算法将智能体策略参数化,通过最大化期望累计回报来直接优化自身策略[30]。该方法能够有效地优化智能体探索过程中的迭代策略,而且可以解决动作空间连续等问题。本节在状态、动作和奖励函数的建模分析基础上,给出了完整的智能体探索和学习自身策略
输入:最大回合数
输出:智能体的策略网络参数
过程:
(1) 初始化智能体策略模型参数
(2) for episode
(3) 重置并初始化环境,得到系统全局初始状态
(4) 获取差分奖励函数的权重
(5) for
(6) 智能体根据式(1) 获取局部邻域状态
(7) 智能体通过BGRU模型计算自己的动作
(8) 根据权重
(9) 环境根据当前状态
(10) 将所有智能体
(11) if
(12) break;
(13) end if
(14) end for
(15) 从经验池
(16) 通过式(18) 和(19) 计算策略梯度
(17) 通过式(21) 更新策略参数
(18) end for
(19) return
为了方便后文的推导,使用
多智能体探索阶段:如算法中的(3) ~(14) 所示,每个智能体
| $ \left\{\begin{array}{ll} \alpha=1 ; \beta=1 ; \gamma=0, & {\rm{if}} \; {\rm{episode}} \leqslant 100 \\ \alpha=0 ; \beta=0 ; \gamma=1, & {\rm{if}}\; 100 < {\rm{episode}} < 800 \\ \alpha=0 ; \beta=0.5 ; \gamma=0.5, & {\rm{if}} \; {\rm{episode}} \geqslant 800 \end{array}\right. $ | (14) |
那么,根据式(14) 的奖励目标切换方案以及式(8) 和式(9) 所定义的差分奖励函数,即可计算出每一个时刻智能体所获取到的差分奖励
为了能够在“更新策略阶段”有效地学习更新智能体的策略参数,在本阶段中每个智能体在最长时间跨度为
更新策略阶段:如算法中的(15) ~(17) 所示,在每一回合结束时,通过均匀随机采样,从
| $ U(\theta) =\sum\nolimits_{{\tau _i}} P\left(\tau_{i} \mid \theta_{i}\right) R_{i}\left(\tau_{i}\right) $ | (15) |
| $ R_{i}\left(\tau_{i}\right) =\sum\nolimits_{k = 0}^H {{r_i}} (k) $ | (16) |
那么,针对目标函数
| $ \begin{split} \nabla_{\theta} U(\theta) =&\nabla_{\theta} \displaystyle\sum\nolimits_{{\tau _i}} P\left(\tau_{i} \mid \theta_{i}\right) R_{i}\left(\tau_{i}\right)=\\ &\sum\nolimits_{{\tau _i}} \nabla_{\theta} P\left(\tau_{i} \mid \theta_{i}\right) R_{i}\left(\tau_{i}\right)= \\ &\displaystyle\sum\nolimits_{{\tau _i}} P\left(\tau_{i} \mid \theta_{i}\right) \dfrac{\nabla_{\theta} P\left(\tau_{i} \mid \theta_{i}\right) }{P\left(\tau_{i} \mid \theta_{i}\right) } R_{i}\left(\tau_{i}\right)= \\ &\displaystyle\sum\nolimits_{\tau_{i}} P\left(\tau_{i} \mid \theta_{i}\right) \nabla_\theta {\rm{ln}} P\left(\tau_{i} \mid \theta_{i}\right) R_{i}\left(\tau_{i}\right) \end{split} $ | (17) |
从式(17) 的梯度可以发现,最终求出的
| $ \begin{split} \nabla_{\theta} U(\theta) =&\displaystyle\sum\nolimits_{\tau_{i}} P\left(\tau_{i} \mid \theta_{i}\right) \nabla_{\theta} {\rm{ln}} P\left(\tau_{i} \mid \theta_{i}\right) R_{i}\left(\tau_{i}\right) \approx \\ &\dfrac{1}{m} \displaystyle\sum\nolimits_{i=1}^{m} \nabla_{\theta} {\rm{ln}} P\left(\tau_{i} \mid \theta_{i}\right) R_{i}\left(\tau_{i}\right) \end{split} $ | (18) |
此时,式(18) 所求出的梯度可以直观地理解为算法将提高出现高奖励回报轨迹的概率,降低出现低回报轨迹的概率。接着,对式(18) 中唯一的不确定量
| $ \begin{split} {{\nabla _\theta }{\rm{ln}} P\left( {{\tau _i}\mid {\theta _i}} \right) } =& {\nabla _\theta }{\rm{ln}} \Biggr[ \prod\limits_{k = 0}^H {P\left( {{s_i}(k + 1) \mid {s_i}(k) ,{a_i}(k) } \right) \times }\Biggr. \\ &\Biggr.{{{ \pi _{{\theta _i}}}\left( {{a_i}(k) \mid {s_i}(k) } \right) } } \Biggr] =\\ &{\nabla _\theta }\left[ {\displaystyle\sum\nolimits_{k = 0}^H {\rm{ln}} P\left( {{s_i}(k + 1) \mid {s_i}(k) ,{a_i}(k) } \right) + }\right.\\ &\left.{\displaystyle\sum\nolimits_{k = 0}^H {\rm{ln}} {\pi _{{\theta _i}}}\left( {{a_i}(k) \mid {s_i}(k) } \right) } \right]=\\ &{ {\nabla _\theta }\left[ {\displaystyle\sum\nolimits_{k = 0}^H {\rm{ln}} {\pi _{{\theta _i}}}\left( {{a_i}(k) \mid {s_i}(k) } \right) } \right]= }\\ &{ \displaystyle\sum\nolimits_{k = 0}^H {{\nabla _{{\theta _i}}}} {\rm{ln}} {\pi _{{\theta _i}}}\left( {{a_i}(k) \mid {s_i}(k) } \right) } \end{split} $ | (19) |
在式(19) 的推导过程中,状态动作转移概率
| $ \nabla_{\theta} U(\theta) \approx \frac{1}{m} \sum\nolimits_{i=1}^{m} \sum\nolimits_{k=0}^{H} \nabla_{\theta} {\rm{ln}} \pi_{\theta_{i}}\left(a_{i}(k) \mid s_{i}(k) \right) r_{i}(k) $ | (20) |
最终,通过最速下降法更新智能体的策略参数。
| $ \theta \leftarrow \theta+\zeta \nabla_{\theta} U(\theta) $ | (21) |
式中:
通过以上算法流程,智能体能够在舆情动力学演化的环境中学习到在保持较低通信代价的前提下促进舆情观点一致的策略。值得注意的是,在本文的研究背景中,每个智能体在演化的过程中需要进行时间的同步,同时智能体感知到的状态、做出的动作都是局部的,这有利于模型的部署和扩展。
2 实验结果与分析 2.1 实验环境与参数设置本文实验通过Python3.6.2构建了舆情动力学的仿真环境,使用PyTorch1.6.0搭建了智能体基于BGRU的策略梯度网络。实验中涉及的相关参数如表1所示。值得注意的是,在2.2中首先验证了
| 表 1 实验参数设定 Table 1 Parameter setting of simulations |
为了全面分析本文所提出的算法和模型,除了使用CD、GD和ND 3个指标外,本文还采用了代数连通度AC(Algebraic Connectivity)[32]和边连通度EC(Edge Connectivity)[33]两个指标,它们分别表示系统的连通程度和网络鲁棒性。在图3~5中验证了单独使用某个目标奖励时模型的有效性。
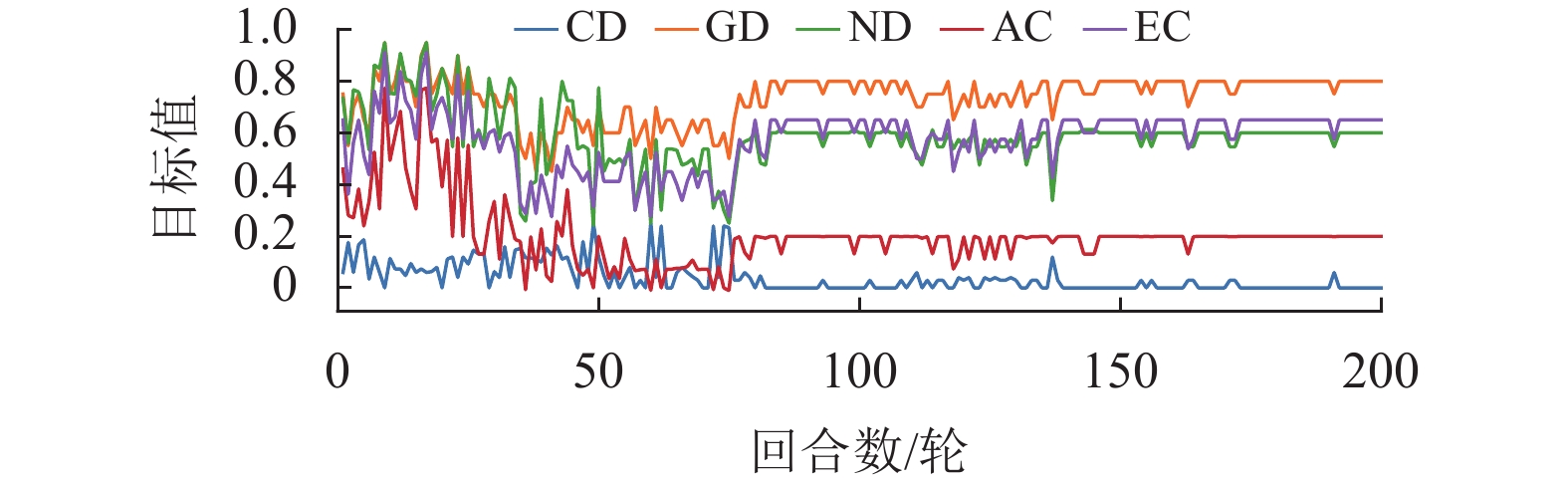
|
图 3 仅使用目标1差分奖励函数时的指标曲线
Figure 3 Indicator curve with difference reward function (
|
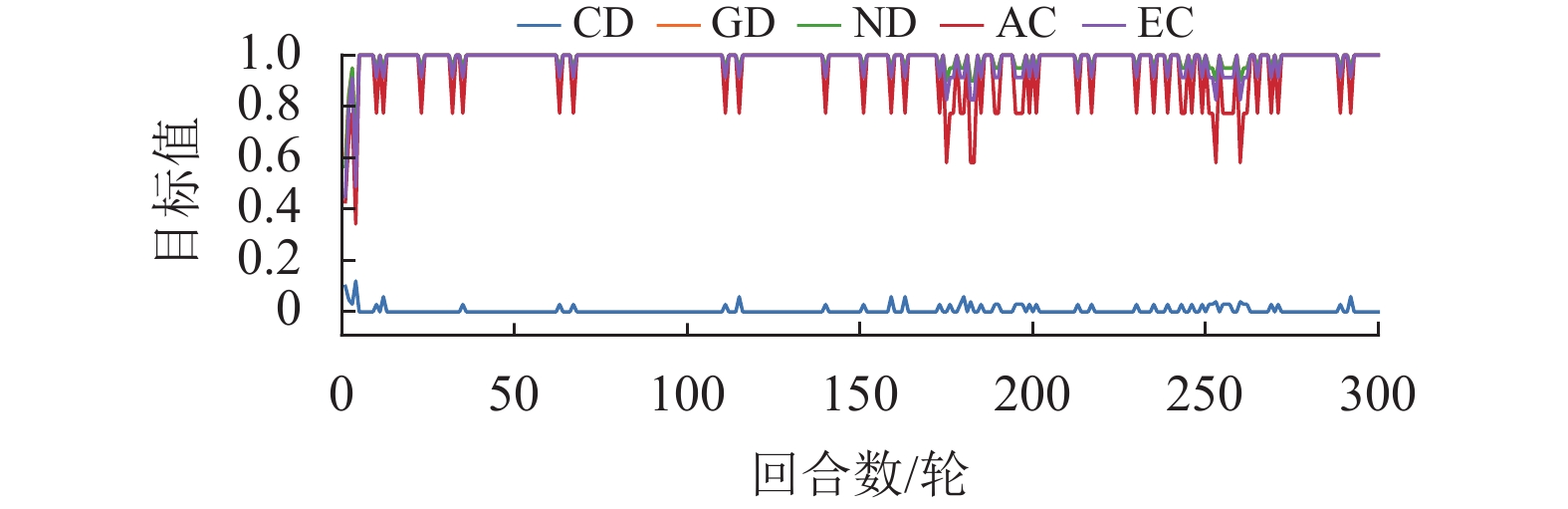
|
图 4 仅使用目标2差分奖励函数时的指标曲线
Figure 4 Indicator curve with difference reward function (
|
图3展示了单独使用目标1的差分奖励函数后的效果,即
图4展示了单独使用目标2的差分奖励函数后的效果,即
图5展示了单独使用目标3的差分奖励函数后的效果,即
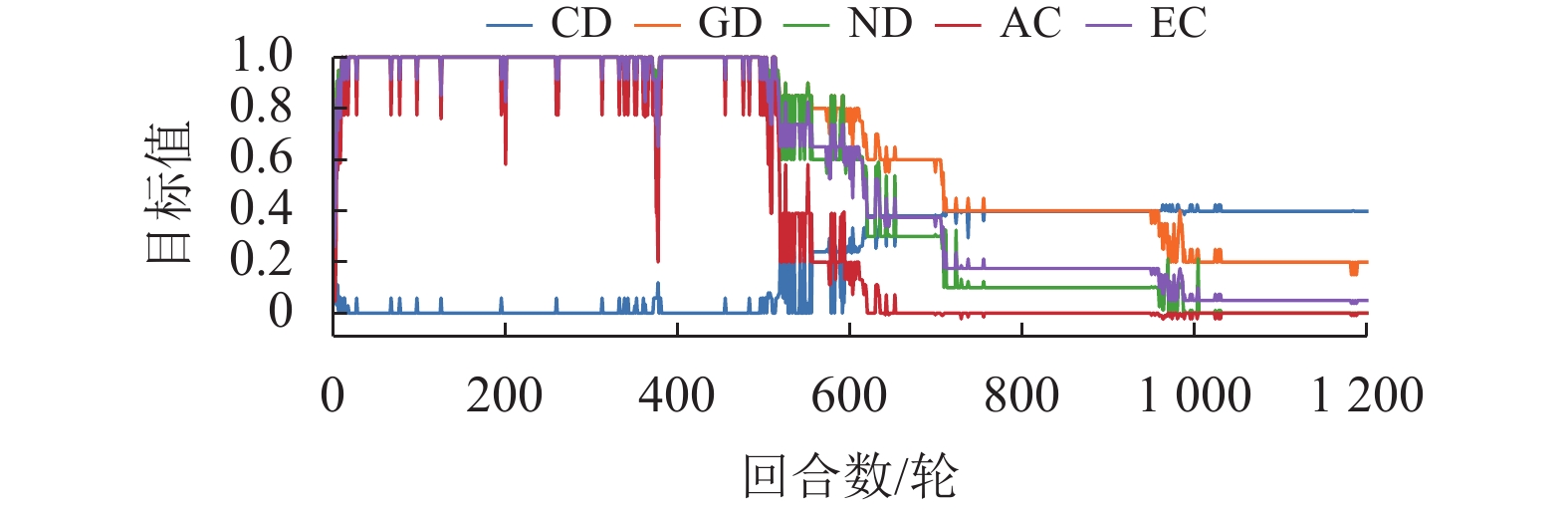
|
图 5 仅使用目标3差分奖励函数时的指标曲线
Figure 5 Indicator curve with difference reward function (
|
从图3~5的实验仿真可以总结出,智能体能够根据给定目标的奖励函数使用Policy Gradient算法优化自己的决策能力,但单个目标所设定的奖励存在一定的局限性。
因此,下面将采用渐进学习的思想,先让智能体学习较为简单的策略,然后不断叠加更多的目标奖励。以式(14) 的奖励目标切换为例,给出了其对应的指标曲线,如图6所示,其中横坐标为回合数,纵坐标为目标值。
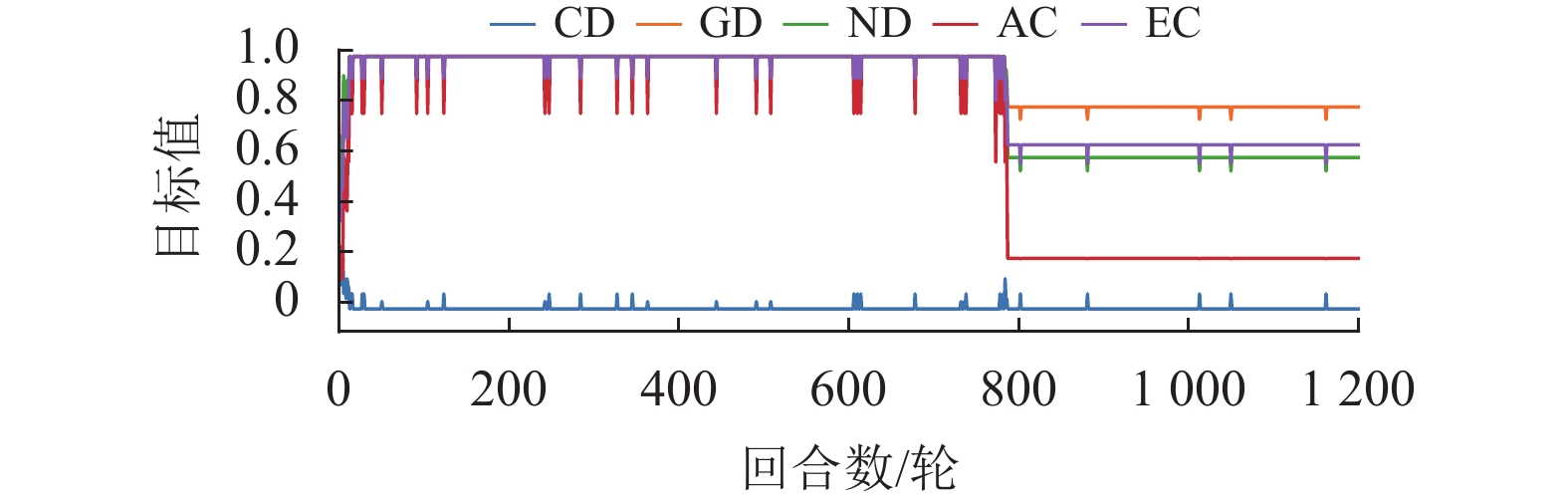
|
图 6 渐进学习混合目标差分奖励函数时的指标曲线 Figure 6 Indicator curve of progressive learning with mixed difference reward function |
从图6可以发现指标曲线中有明显的分界线,且分界线与目标切换点是带有一定的滞后性的,但总体上呈现一致性的特点。同时可以看出混合使用目标2和3,即在800回合后,各个指标趋向稳定的值可以理解为强化学习对两个目标的权衡。因此,可以总结为:通过渐进学习混合目标奖励可以自适应学习到更好的组合策略,达到各目标间的权衡。
最后,通过系统稳定时的收敛簇数、收敛步长这两类指标来衡量模型的效果,其中收敛簇数用来衡量模型增强一致性的效果,收敛步长用来衡量模型的运行步数。同时将本文所提出的COEIP模型和传统的三类模型进行了综合对比实验分析,其中包含有经典的HK模型[31]、基于共同邻居规则(Common-Neighbor Rule,CNR)模型[34]和基于组压力(Group Pressure,GP)模型[35]。由于本文研究的目标是增强一致性,换言之希望以更短的收敛步长收敛至更少的簇数。为了控制变量,CNR和GP模型中相关的参数统一设置为
实验的统计数据如表2所示。该实验场景有100个智能体,这些智能体的舆情值分别均匀分布于[0,4]和[0,10]范围内,分别对应实验编号1和2。通过表2的数据可以发现:在较小的
| 表 2 对比实验的统计数据 Table 2 Statistics of comparison simulations |
因此,可以总结为:COEIP模型通过选择适当的邻居进行舆情演化,可以有效地调和智能体间相互矛盾的观点。
3 总结本文研究了社交网络领域下舆情动力学增强一致性的问题,提出了一种基于多智能体强化学习的智能感知模型。在舆情动力学场景下的马尔科夫决策过程中,首先设计了基于双向循环神经网络来建立智能体的决策模型,接着根据舆情动力学场景中的3类目标设计了对应的差分奖励函数。最后通过基于策略梯度的多智能体探索和协同更新算法让智能体在彼此交互的过程中能够自适应地学习到高效的邻域选择策略。实验结果验证了COEIP能够让智能体决策具备多目标权衡的能力,在社交网络舆情动力学中能够高效地调和系统中差异较大的观点,以减少系统收敛稳定时簇的数量,从而促进系统一致性。未来将在本文的基础上继续研究社交网络中具有注意力机制的增强一致性方法,并验证该方法在现实场景中的有效性和泛化能力。
| [1] |
DONG Y C, ZHA Q B, ZHANG H J, et al. Consensus reaching in social network group decision making: research paradigms and challenges[J].
Knowledge-Based Systems, 2018, 162: 3-13.
DOI: 10.1016/j.knosys.2018.06.036. |
| [2] |
ZHANG Z, GAO Y, LI Z L. Consensus reaching for social network group decision making by considering leadership and bounded confidence[J].
Knowledge-Based Systems, 2020, 204: 106240.
DOI: 10.1016/j.knosys.2020.106240. |
| [3] |
SCOTT J, CARRINGTON P J. The SAGE handbook of social network analysis[M]. California: SAGE Publications, 2011.
|
| [4] |
LI Y H, KOU G, LI G X, et al. Multi-attribute group decision making with opinion dynamics based on social trust network[J].
Information Fusion, 2021, 75: 102-115.
DOI: 10.1016/j.inffus.2021.04.010. |
| [5] |
LI T Y, ZHU H M. Effect of the media on the opinion dynamics in online social networks[J].
Physica A:Statistical Mechanics and its Applications, 2020, 551: 124117.
DOI: 10.1016/j.physa.2019.124117. |
| [6] |
JIAO Y R, LI Y L. An active opinion dynamics model: the gap between the voting result and group opinion[J].
Information Fusion, 2021, 65: 128-146.
DOI: 10.1016/j.inffus.2020.08.009. |
| [7] |
DOUVEN I, HEGSELMANN R. Mis-and disinformation in a bounded confidence model[J].
Artificial Intelligence, 2021, 291: 103415.
DOI: 10.1016/j.artint.2020.103415. |
| [8] |
BISWAS K, BISWAS S, SEN P. Block size dependence of coarse graining in discrete opinion dynamics model: application to the US presidential elections[J].
Physica A:Statistical Mechanics and its Applications, 2021, 566: 125639.
DOI: 10.1016/j.physa.2020.125639. |
| [9] |
ZHU L X, HE Y L, ZHOU D Y. Neural opinion dynamics model for the prediction of user-level stance dynamics[J].
Information Processing & Management, 2020, 57(2): 102031.
|
| [10] |
BRAVO-MARQUEZ F, GAYO-AVELLO D, MENDOZA M, et al. Opinion dynamics of elections in Twitter[C]//2012 Eighth Latin American Web Congress. Colombia: IEEE, 2012: 32-39.
|
| [11] |
ZHA Q B, KOU G, ZHANG H J, et al. Opinion dynamics in finance and business: a literature review and research opportunities[J].
Financial Innovation, 2020, 6(1): 1-22.
DOI: 10.1186/s40854-019-0162-0. |
| [12] |
DONG Y C, ZHAN M, KOU G, et al. A survey on the fusion process in opinion dynamics[J].
Information Fusion, 2018, 43: 57-65.
DOI: 10.1016/j.inffus.2017.11.009. |
| [13] |
SÎRBU A, LORETO V, SERVEDIO V D P, et al. Opinion dynamics: models, extensions and external effects[M]//Participatory sensing, opinions and collective awareness. Berlin: Springer, 2017: 363-401.
|
| [14] |
URENA R, CHICLANA F, MELANCON G, et al. A social network based approach for consensus achievement in multiperson decision making[J].
Information Fusion, 2019, 47: 72-87.
DOI: 10.1016/j.inffus.2018.07.006. |
| [15] |
CABRERIZO F J, AL-HMOUZ R, MORFEQ A, et al. Soft consensus measures in group decision making using unbalanced fuzzy linguistic information[J].
Soft Computing, 2017, 21(11): 3037-3050.
DOI: 10.1007/s00500-015-1989-6. |
| [16] |
LI G X, KOU G, PENG Y. Heterogeneous large-scale group decision making using fuzzy cluster analysis and its application to emergency response plan selection[J].
IEEE Transactions on Systems, Man, and Cybernetics:Systems, 2021, 52(6): 3391-3403.
|
| [17] |
XU S, WANG P, LYU J. Iterative neighbour-information gathering for ranking nodes in complex networks[J].
Scientific reports, 2017, 7(1): 1-13.
DOI: 10.1038/s41598-016-0028-x. |
| [18] |
NEDIĆ A, OLSHEVSKY A, RABBAT M G. Network topology and communication-computation tradeoffs in decentralized optimization[J].
Proceedings of the IEEE, 2018, 106(5): 953-976.
DOI: 10.1109/JPROC.2018.2817461. |
| [19] |
ZHANG K Q, YANG Z R, BAŞAR T. Multi-agent reinforcement learning: a selective overview of theories and algorithms[J].
Handbook of Reinforcement Learning and Control, 2021: 321-384.
|
| [20] |
郑思远, 崔苗, 张广驰. 基于强化学习的无人机安全通信轨迹在线优化策略[J].
广东工业大学学报, 2021, 38(04): 59-64.
ZHENG S Y, CUI M, ZHANG G C. Reinforcement learning-based online trajectory optimization for secure UAV communications[J]. Journal of Guangdong University of Technology, 2021, 38(04): 59-64. DOI: 10.12052/gdutxb.200113. |
| [21] |
SHOU Z Y, DI X. Reward design for driver repositioning using multi-agent reinforcement learning[J].
Transportation research part C:emerging technologies, 2020, 119: 102738.
DOI: 10.1016/j.trc.2020.102738. |
| [22] |
SUN X Z, QIU J. Two-stage volt/var control in active distribution networks with multi-agent deep reinforcement learning method[J].
IEEE Transactions on Smart Grid, 2021, 12(4): 2903-2912.
DOI: 10.1109/TSG.2021.3052998. |
| [23] |
ZHANG K Q, YANG Z R, LIU H, et al. Fully decentralized multi-agent reinforcement learning with networked agents[C]//International Conference on Machine Learning. Sweden: IMLS, 2018: 5872-5881.
|
| [24] |
DEY R, SALEM F M. Gate-variants of gated recurrent unit (GRU) neural networks[C]//2017 IEEE 60th international midwest symposium on circuits and systems. Michigan: IEEE, 2017: 1597-1600.
|
| [25] |
SILVER D, SINGH S, PRECUP D, et al. Reward is enough[J].
Artificial Intelligence, 2021, 299: 103535.
DOI: 10.1016/j.artint.2021.103535. |
| [26] |
SUTTON R S, BARTO A G. Reinforcement learning: an introduction[M]. Massachusetts: MIT press, 2018.
|
| [27] |
FOERSTER J, FARQUHAR G, AFOURAS T, et al. Counterfactual multi-agent policy gradients[C]//Proceedings of the AAAI conference on artificial intelligence. Louisiana: AAAI Press, 2018, 32(1) : 2974-2982.
|
| [28] |
AGOGINO A, TURNER K. Multi-agent reward analysis for learning in noisy domains[C]//Proceedings of the fourth international joint conference on Autonomous agents and multiagent systems. Utrecht: IFAAMAS, 2005: 81-88.
|
| [29] |
BARRAT A, BARTHELEMY M, PASTOR-SATORRAS R, et al. The architecture of complex weighted networks[J].
Proceedings of the national academy of sciences, 2004, 101(11): 3747-3752.
DOI: 10.1073/pnas.0400087101. |
| [30] |
SILVER D, LEVER G, HEESS N, et al. Deterministic policy gradient algorithms[C]//International conference on machine learning. Beijing: IMLS, 2014: 387-395.
|
| [31] |
BLONDEL V D, HENDRICKX J M, TSITSIKLIS J N. On Krause's multi-agent consensus model with state-dependent connectivity[J].
IEEE transactions on Automatic Control, 2009, 54(11): 2586-2597.
DOI: 10.1109/TAC.2009.2031211. |
| [32] |
WU C W. Algebraic connectivity of directed graphs[J].
Linear and multilinear algebra, 2005, 53(3): 203-223.
DOI: 10.1080/03081080500054810. |
| [33] |
ESFAHANIAN A H. Connectivity algorithms[M]//Topics in structural graph theory. Cambridge: Cambridge University Press, 2013: 268-281.
|
| [34] |
WANG H J, SHANG L H. Opinion dynamics in networks with common-neighbors-based connections[J].
Physica A:Statistical Mechanics and its Applications, 2015, 421: 180-186.
DOI: 10.1016/j.physa.2014.10.090. |
| [35] |
CHENG C, YU C B. Opinion dynamics with bounded confidence and group pressure[J].
Physica A:Statistical Mechanics and its Applications, 2019, 532: 121900.
DOI: 10.1016/j.physa.2019.121900. |
 2022, Vol. 39
2022, Vol. 39

