暧昧性(ambiguity)描述的是市场主体在做出决策时,经济环境所具有的不确定性,有别于经典金融理论中风险的概念,暧昧不确定性无法在事前用唯一的先验概率测度来描述。暧昧性的概念最早由Knight[1]提出,他将经济环境的不确定性区分为风险和Knight不确定性两类。之后,Ellsberg[2]在其研究中又将Knight不确定性重新命名为暧昧性。此后,暧昧性被广泛引入到投资决策、市场均衡及资产定价的理论研究中,参见文献[3-5]。
再保险作为保险公司分散经营风险、控制保险责任的重要手段,在整个保险运营体系中占据非常重要的地位。同时,为了提高盈利、确保偿付能力,保险公司会将其盈余投资到金融市场。因而投资与再保险决策在保险实务中备受重视,逐渐受到越来越多专家学者的关注,暧昧厌恶的概念也被引入到投资与再保险问题中,产生了许多研究成果,例如Yi等[6]、Zeng等[7]、Zheng等[8]、Huang等[9]、Li等[10]建立了参数暧昧环境下的鲁棒最优投资与再保险优化模型,利用随机控制理论得到了鲁棒最优策略。
近年来,自Liu和Pan[11]做出了包含衍生品投资的研究以来,已有部分学者展开了包含衍生品交易的最优投资与再保险问题研究。王蕾和顾孟迪[12]在Black-Scholes模型的假设下研究了包含衍生品交易的最优投资与再保险问题。傅毅等[13]在假设风险资产服从CEV模型的条件下,探讨了保险公司的投资对象中包含欧式看涨期权的最优投资和比例再保险决策问题。Xue等[14]则在Heston随机波动率模型下,讨论了包含衍生品交易的最优投资与再保险决策问题,这些研究表明,衍生品交易可以显著提高保险公司的效用水平。
虽然上述文献为研究包含衍生品交易的投资与再保险问题提供了研究框架,但是这些文献关注的重点要么局限在模型参数的暧昧性上,要么局限在包含衍生品的投资上,忽视了将二者结合起来研究。事实上,将模型参数的暧昧性与衍生品交易结合起来研究最优投资问题的成果已经出现,例如Escobar等[15],Zeng等[16],王佩等[17]在参数暧昧环境下讨论了包含衍生品交易的最优投资问题。但纵观现有关于投资与再保险问题的相关研究中,同时考虑衍生品交易及参数暧昧的研究暂时还未见报道,因此本文在Xue等[14]、Escobar等[15]及Zeng等[16]的基础上,研究同时考虑模型参数的暧昧性与衍生品交易情形下最优投资与再保险决策问题,希望所得结果能为保险公司管理者的决策提供理论依据。
1 模型设定令
考虑一家在保险市场和金融市场同时进行交易的保险公司,该公司在保险市场上通过购买比例再保险来管理潜在风险,通过在金融市场投资来实现财富的保值增值。
参照Promislow和Young[18],用扩散过程来近似描述保险公司的索赔
| $ {\text{d}}C(t) = a{\text{d}}t - b{\text{d}}{B_0}(t) $ | (1) |
式中:
| $ {\text{d}}R(t) = {c_0}{\text{d}}t - {\text{d}}C(t) $ | (2) |
出于风险控制的需要,假设保险公司在
| $ \begin{split} {\text{d}}{R^q}(t) &=\; ({c_0} - {c_1}{\text{) d}}t - q(t) {\text{d}}C(t)= \left[ {a(\tau - \varsigma ) \;+ \;}\right. \\ & \left.{ a\varsigma q(t) } \right]{\text{d}}t + bq(t) {\text{d}}{B_0}(t) \end{split}$ | (3) |
保险公司除购买再保险外,还将其保险盈余投资于金融市场。参照Xue等[14],假设有3种资产可供保险公司进行投资选择:第一种为无风险资产(如银行存款),第二种是股票,第三种是以股票为标的资产的衍生品(如期权)。假定无风险资产在
| $ {\text{d}}{S_0}(t) = r{S_0}(t) {\text{d}}t $ | (4) |
式中:
| $ {\text{d}}S(t) = S(t) \left[ {r + \eta V(t) } \right]{\text{d}}t + S(t) \sqrt {V(t) } {\text{d}}{B_1}(t) $ | (5) |
股票收益的方差
| $\begin{split} {\text{d}}V(t) = &\kappa \left[ {\mu - V(t) } \right]{\text{d}}t +\\ &\sigma \sqrt {V(t) } \left[ {\rho {\text{d}}{B_1}(t) + \sqrt {1 - {\rho ^2}} {\text{d}}{B_2}(t) } \right] \end{split} $ | (6) |
式(5) 和(6) 中,
参照Liu和Pan[11]、Zeng等[16]及Xue等[14],假设衍生品在
| $ \begin{gathered} {\text{d}}O(t) = rO(t) {\text{d}}t + ( {{O_S}S(t) + \rho \sigma {O_V}} ) \left[ {\eta V(t) {\text{d}}t + \sqrt {V(t) } {\text{d}}{B_1}(t) } \right] + \\ \quad \quad \quad \; \sigma \sqrt {1 - {\rho ^2}} {O_V}\left[ {\xi V(t) {\text{d}}t + \sqrt {V(t) } {\text{d}}{B_2}(t) } \right] \\[-10pt] \end{gathered} $ | (7) |
式中:
考虑一个初始财富为
| $ \left\{ \begin{split} {\text{d}}{X^\pi }(t) \;= &\left[ {r{X^\pi }(t) + {\theta _1}{\text{(}}t{\text{) }}\eta V{\text{(}}t{\text{) }} + } {\theta _2}{\text{(}}t{\text{) }}\xi V{\text{(}}t{\text{) }} + \right. \\ &\left.a(\tau - \varsigma ) + a\varsigma q(t) \right]{\text{d}}t\; +\; bq(t) {\text{d}}{B_0}(t) \; +\\ &\; {\theta _1}{\text{(}}t{\text{) }}\sqrt {V{\text{(}}t{\text{) }}} {\text{d}}{B_1}(t)+ {\theta _2}{\text{(}}t{\text{) }}\sqrt {V{\text{(}}t{\text{) }}} {\text{d}}{B_2}(t) \\ {X^\pi }(0) = &{x_0} \end{split} \right. $ | (8) |
式中:
| $ \begin{split} & {\theta _1}{\text{(}}t{\text{) }} = \alpha (t) + \beta (t) \left[ {\frac{{{O_S}S(t) }}{{O(t) }} + \frac{{\rho \sigma {O_V}}}{{O(t) }}} \right] , \\ & {\theta _2}{\text{(}}t{\text{) }} = \beta (t) \sigma \sqrt {1 - {\rho ^2}} \frac{{{O_V}}}{{O(t) }} \end{split}$ | (9) |
分别表示保险公司在扩散风险
在已有投资与再保险问题的研究中,大多数研究假设保险公司是暧昧中性(ambiguity neutral)的,而现实中的保险公司多为暧昧厌恶(ambiguity averse)的,因此,本文假设保险公司是暧昧厌恶的。该保险公司使用一个参考模型去描述风险过程及资产价格动态,基于模型参数的暧昧性(例如参数估计有误差、市场的异常波动和数据采集不够等多种原因造成),暧昧厌恶的保险公司通过引入一系列替代模型来达到稳健策略,并且替代模型和参考模型间的差异通过不同概率之间的测度转换来反映。假定参考模型由概率测度
根据Girsanov定理,对每一个替换测度
| $ \begin{split} {\Lambda ^\phi }(t) =& \exp \left\{ { - \int_0^t {{\phi _0}(s) {\text{d}}{B_0}(s) } - \frac{1}{2}\int_0^t {\phi _0^{\text{2}}(s) {\text{d}}s} - \int_0^t {{\phi _1}(s) {\text{d}}{B_1}(s) - } } \right. \\ &\left. { \frac{1}{2}\int_0^t {\phi _1^2(s) {\text{d}}s} - \int_0^t {{\phi _2}(s) {\text{d}}{B_2}(s) } - \frac{1}{2}\int_0^t {\phi _2^2(s) {\text{d}}s} } \right\} \end{split} $ |
是一个
在替换测度
| $ {\text{d}}B_k^\phi (t) = {\text{d}}{B_k}(t) + {\phi _k}(t) {\text{d}}t , k \in \{ 0,\;1,\;2\} $ |
相应地,在替换测度
| $ \begin{split} {\text{d}}{R^\phi }(t) \, =& \left[ {a(\tau - \varsigma ) + a\varsigma q(t) - bq(t) {\phi _0}(t) } \right]{\text{d}}t+ \\ & bq(t) {\text{d}}B_0^\phi (t) \end{split}$ | (10) |
| $\begin{split} {\text{d}}{S^\phi }(t) =& {S^\phi }(t) \left[ {r + \eta {V^\phi }(t) - {\phi _1}(t) \sqrt {{V^\phi }(t) } } \right]{\text{d}}t +\\ & {S^\phi }(t) \sqrt {{V^\phi }(t) } {\text{d}}B_1^\phi (t) \end{split}$ | (11) |
| $ \begin{split} {\text{d}}{V^\phi }(t) = & \left[ {\kappa \left( {\mu - {V^\phi }(t) } \right) - \sigma \sqrt {{V^\phi }(t) } ( {\rho {\phi _1}(t) + \sqrt {1 - {\rho ^2}} {\phi _2}(t) } ) } \right]{\text{d}}t + \\ & \sigma \sqrt {{V^\phi }(t) } \left[ {\rho {\text{d}}B_1^\phi (t) + \sqrt {1 - {\rho ^2}} {\text{d}}B_2^\phi (t) } \right] \\[-10pt] \end{split} $ | (12) |
| $ \begin{split} {\text{d}}{O^\phi }(t) = & r{O^\phi }(t) {\text{d}}t + \left( {{O_S}{S^\phi }(t) + \rho \sigma {O_V}} \right) \left[ {\eta {V^\phi }(t) {\text{d}}t}- \right. \\ & \left.{ {\phi _1}(t)\sqrt {{V^\phi }(t) } {\text{d}}t + \sqrt {{V^\phi }(t) } {\text{d}}B_1^\phi (t) } \right] + \\ & \sigma \sqrt {1 - {\rho ^2}} {O_V}\left[ {\xi {V^\phi }(t) {\text{d}}t - {\phi _2}(t) \sqrt {{V^\phi }(t) } {\text{d}}t + }\right. \\ & \left.{\sqrt {{V^\phi }(t) } {\text{d}}B_2^\phi (t) } \right] \end{split} $ | (13) |
进一步,保险公司的财富过程
| $ \begin{split} {\text{d}}{X^{\phi ,\pi }}(t) =& \left[ {r{X^{\phi ,\pi }}(t) + \eta {\theta _1}{\text{(}}t{\text{) }}{V^\phi }{\text{(}}t{\text{) }} + \xi {\theta _2}{\text{(}}t{\text{) }}{V^\phi }{\text{(}}t{\text{) }} - } \right. \\ &\left. { {\phi _1}(t) {\theta _1}{\text{(}}t{\text{) }}\sqrt {{V^\phi }{\text{(}}t{\text{) }}} - {\phi _2}(t) {\theta _2}{\text{(}}t{\text{) }}\sqrt {{V^\phi }{\text{(}}t{\text{) }}}} +\right.\\ &\left.{ a(\tau - \varsigma ) + a\varsigma q(t) - bq(t) {\phi _0}(t) } \right]{\text{d}}t + bq(t) {\text{d}}B_0^\phi (t) + \\ &{\theta _1}{\text{(}}t{\text{) }}\sqrt {{V^\phi }{\text{(}}t{\text{) }}} {\text{d}}B_1^\phi (t) + {\theta _2}{\text{(}}t{\text{) }}\sqrt {{V^\phi }{\text{(}}t{\text{) }}} {\text{d}}B_2^\phi (t) \\[-10pt] \end{split} $ | (14) |
定义1 称策略
(i)
(ii) 对任意的
假定保险公司的目标是选择投资与再保险策略
| $ \mathop {\sup }\limits_{\pi \in \varPi } \mathop {\inf }\limits_{\phi \in \varTheta } {{\text{E}}^Q}\left[ {U\left( {{X^{\phi ,\pi }}(T) } \right) + D\left( {P\left\| Q \right.} \right) } \right] , $ | (15) |
式中:
| $ U(x) = - \frac{1}{\gamma }{{\text{e}}^{ - \gamma x}} , $ | (16) |
为了使所研究的问题存在解析解,参考Maenhout[19]的设置,假设惩罚函数具有下述形式
| $ D\left( {P\left\| Q \right.} \right) = \int_t^T {\left( {\frac{{\phi _0^2(s) }}{{2{\varPsi _0}\left( {s,x,v} \right) }} + \frac{{\phi _1^2(s) }}{{2{\varPsi _1}\left( {s,x,v} \right) }} + \frac{{\phi _2^2(s) }}{{2{\varPsi _2}\left( {s,x,v} \right) }}} \right) {\text{d}}s} $ | (17) |
式中:对
对
| $ \begin{gathered} J(t,x,v) \;=\; \mathop {\sup }\limits_{\pi \in \varPi } \mathop {\inf }\limits_{\phi \in \varTheta } {{\text{E}}^Q}\left[ { \;-\; \frac{1}{\gamma }{{\text{e}}^{ \;-\; \gamma {X^{\phi ,\pi }}(T) }} \;+\; \int_t^T {\left( {\frac{{\phi _0^2(s) }}{{2{\varPsi _0}\left( {s,x,v} \right) }} }+ \right.} } \right. \\ \quad \quad \quad\quad \left. {\left. { \frac{{\phi _1^2(s) }}{{2{\varPsi _1}\left( {s,x,v} \right) }} + \frac{{\phi _2^2(s) }}{{2{\varPsi _2}\left( {s,x,v} \right) }}} \right) {\text{d}}s} \right] \\[-15pt] \end{gathered} $ | (18) |
式中:对于
对鲁棒优化问题(15) ,利用随机动态规划原理得到相应的HJB方程可描述为
| $ \mathop {\sup }\limits_{\pi \in \varPi } \mathop {\inf }\limits_{\phi \in \varTheta } \left\{ {{\mathcal{D}^{\phi ,\pi }}J + \frac{{\phi _0^2}}{{2{\varPsi _0}}} + \frac{{\phi _1^2}}{{2{\varPsi _1}}} + \frac{{\phi _2^2}}{{{\varPsi _2}}}} \right\} = 0 $ | (19) |
边界条件为
| $ \begin{gathered} {\mathcal{D}^{\phi ,\pi }}J = {J_t} + \left[ {rx + \eta {\theta _1}v + \xi {\theta _2}v - {\phi _1}{\theta _1}\sqrt v - {\phi _2}{\theta _2}\sqrt v + }\right. \\ \quad \quad \quad \left.{a(\tau - \varsigma ) + a\varsigma q - bq{\phi _0}} \right]{J_x}+ \frac{1}{2}( {{b^2}{q^2} + \theta _1^2v + \theta _2^2v} ) {J_{xx}} + \\ \quad \quad \quad \; \left[ {\kappa (\mu - v) - \sigma \sqrt v ( {\rho {\phi _1}\;+ \sqrt {1 - {\rho ^2}} {\phi _2}} ) } \right]{J_v}\;+ \\ \quad \quad \quad \; \frac{1}{2}{\sigma ^2}v{J_{vv}} + \sigma v(\rho {\theta _1} + \sqrt {1 - {\rho ^2}} {\theta _2}) {J_{xv}} \\ \end{gathered} $ |
上节内容勾勒了保险公司面临参数暧昧下的鲁棒优化问题框架,接下来将借助动态规划原理求解该鲁棒优化问题。为了文章严谨,首先给出鲁棒优化问题的验证定理,然后再给出鲁棒最优策略的解析表达。
3.1 验证定理验证定理确保了HJB方程(19) 的解确为值函数,定理的具体内容如下。
定理1(验证定理) 如果存在实值函数
(a) 对任意的
(b) 对任意的
(c)
(d)
证明 定理1的证明类似Zheng等[8]及Zeng等[16],故这里省略。
3.2 鲁棒最优策略鲁棒最优策略的解析表达由下述定理2给出。
定理2 对鲁棒优化问题(15) ,假定保险公司采用式(16) 的指数效用函数,则HJB方程(19) 存在下述形式的解析表达
| $ J(t,x,v) = - \frac{1}{\gamma }\exp \left\{ { - \gamma x{{\text{e}}^{r(T - t) }} + g(t) v + h(t) } \right\} $ | (20) |
式中:
| $\begin{split} g(t) \;=& \frac{1}{{\kappa \;+ \;\rho \sigma \eta \;+\; \xi \sqrt {1 - {\rho ^2}} \sigma }}\left[ {\frac{{{\eta ^2}}}{{2\left( {1 + \dfrac{{{\omega _1}}}{\gamma }} \right) }} + \frac{{{\xi ^2}}}{{2\left( {1 + \dfrac{{{\omega _2}}}{\gamma }} \right) }}} \right] \times \\ & \left[ {{{\text{e}} ^ { - ( {\kappa + \rho \sigma \eta + \xi \sqrt {1 - {\rho ^2}} \sigma } ) \left( {T - t} \right) }} - 1} \right] \\[-12pt] \end{split} $ | (21) |
| $ \begin{split} h(t) =&\frac{{a( {\tau - \varsigma } ) \gamma }}{r}\left[ {{{\text{e}}^{r( {T - t} ) }} - 1} \right] + \frac{{\kappa \mu }}{{{{\left[ {\kappa + \rho \sigma \eta + \xi \sqrt {1 - {\rho ^2}} \sigma } \right]}^2}}} \times \\ &\left[ {\frac{{{\eta ^2}}}{{2\left( {1 + \dfrac{{{\omega _1}}}{\gamma }} \right) }} + \frac{{{\xi ^2}}}{{2\left( {1 + \dfrac{{{\omega _2}}}{\gamma }} \right) }}} \right] {\text{ }} \left[ {1 - {{\text{e}}^{ - ( {\kappa + \rho \sigma \eta + \xi \sqrt {1 - {\rho ^2}} \sigma } ) (T - t) }}- }\right. \\ &\left.{( {\kappa + \rho \sigma \eta + \xi \sqrt {1 - {\rho ^2}} \sigma } ) (T - t) } \right] \\[-10pt] \end{split} $ | (22) |
最优再保险策略为
| $ {q^ * }(t) = {\left( {{{\text{e}}^{ - r(T - t) }}\frac{{a\varsigma }}{{{b^2}( {\gamma + {\omega _0}} ) }} \wedge 1} \right) ^ + } $ | (23) |
式中:
最优风险敞口为
| $\begin{split} &\theta _1^ * (t) = {{\text{e}}^{ - r(T - t) }}\frac{{\eta + \left( {1 + \dfrac{{{\omega _1}}}{\gamma }} \right) \rho \sigma g}}{{\gamma + {\omega _1}}} ,\\ &\theta _2^ *(t) = {{\text{e}}^{ - r(T - t) }}\frac{{\xi + \left( {1 + \dfrac{{{\omega _2}}}{\gamma }} \right) \sqrt {1 - {\rho ^2}} \sigma g}}{{\gamma + {\omega _2}}} \end{split} $ | (24) |
此外,通过式(9) 换算得到最优投资策略为
| $ \begin{gathered} {\alpha ^ * }(t) = {{\text{e}}^{ - r(T - t) }}\Bigg\{ {\frac{{\eta + \left( {1 + \dfrac{{{\omega _1}}}{\gamma }} \right) \rho \sigma g}}{{\gamma + {\omega _1}}} - \frac{{\xi + \left( {1 + \dfrac{{{\omega _2}}}{\gamma }} \right) \sqrt {1 - {\rho ^2}} \sigma g}}{{\gamma + {\omega _2}}}\times } \Bigg. \\ \Bigg. {\quad \quad \quad \left[ {\frac{{{O_S}S(t) }}{{\sigma \sqrt {1 - {\rho ^2}} {O_V}}} + \frac{\rho }{{\sqrt {1 - {\rho ^2}} }}} \right]} \Bigg\} \\[-10pt] \end{gathered} $ | (25) |
| $ {\beta ^ * }(t) = {{\text{e}}^{ - r(T - t) }}\frac{{\xi + \left( {1 + \dfrac{{{\omega _2}}}{\gamma }} \right) \sqrt {1 - {\rho ^2}} \sigma g}}{{\gamma + {\omega _2}}}\frac{{O(t) }}{{\sigma \sqrt {1 - {\rho ^2}} {O_V}}} $ | (26) |
且最坏的测度为
| $\begin{split} &\phi _0^ * (t) = \frac{{a\varsigma {\omega _0}}}{{b\left( {\gamma + {\omega _0}} \right) }} , \phi _1^ * (t) = \frac{{{\omega _1}\eta \sqrt {V(t) } }}{{\gamma + {\omega _1}}} , \\ &\phi _2^ * (t) = \frac{{{\omega _2}\xi \sqrt {V(t) } }}{{\gamma + {\omega _2}}} \end{split}$ | (27) |
证明 假设
| $\begin{split} & \phi _0^ * = - \frac{{bq{\omega _0}{J_x}}}{{\gamma J}} , \phi _1^ * = - \frac{{\left( {{\theta _1}{J_x} + \rho \sigma {J_v}} \right) \sqrt v {\omega _1}}}{{\gamma J}} , \\ & \phi _2^ * = - \frac{{( {{\theta _2}{J_x} + \sqrt {1 - {\rho ^2}} \sigma {J_v}} ) \sqrt v {\omega _2}}}{{\gamma J}} \end{split}$ | (28) |
将式(28) 代回式(19) ,得到
| $ \begin{gathered} {J_t} + \left[ {rx + a(\tau - \varsigma ) } \right]{J_x} + \kappa (\mu - v) {J_v} + \frac{1}{2}{\sigma ^2}v{J_{vv}}+ \\ \mathop {\sup }\limits_{\pi \in \varPi } \left\{ {\left( {\eta {\theta _1}v + \xi {\theta _2}v + a\varsigma q} \right) {J_x}} \right. + \frac{1}{2}( {{b^2}{q^2} + \theta _1^2v + \theta _2^2v} ) {J_{xx}}+ \\ \sigma v(\rho {\theta _1} + \sqrt {1 - {\rho ^2}} {\theta _2}) {J_{xv}} + \frac{{{\omega _0}{b^2}{q^2}J_x^2}}{{2\gamma J}}+ \frac{{{\omega _1}{{( {{\theta _1}{J_x} + \rho \sigma {J_v}} ) }^2}v}}{{2\gamma J}}+ \\ \left. { \frac{{{\omega _2}{{( {{\theta _2}{J_x} + \sqrt {1 - {\rho ^2}} \sigma {J_v}} ) }^2}v}}{{2\gamma J}}} \right\} = 0 \\ \end{gathered} $ | (29) |
式(29) 分别对
| $ {q^ * } = - \frac{{a\varsigma {J_x}}}{{{b^2}\left( {{J_{xx}} + \dfrac{{{\omega _0}J_x^2}}{{\gamma J}}} \right) }} $ | (30) |
| $ \theta _1^ * = - \frac{{\eta {J_x} + \rho \sigma {J_{xv}} + \dfrac{{{\omega _1}\rho \sigma {J_x}{J_v}}}{{\gamma J}}}}{{{J_{xx}} + \dfrac{{{\omega _1}J_x^2}}{{\gamma J}}}} $ | (31) |
| $ \theta _2^ * = - \frac{{\xi {J_x} + \sqrt {1 - {\rho ^2}} \sigma {J_{xv}} + \dfrac{{{\omega _2}\sqrt {1 - {\rho ^2}} \sigma {J_x}{J_v}}}{{\gamma J}}}}{{{J_{xx}} + \dfrac{{{\omega _2}J_x^2}}{{\gamma J}}}} $ | (32) |
将式(30) ~(32) 代回式(29) ,得到
| $ \begin{gathered} {J_t} + \left[ {rx + a(\tau - \varsigma ) } \right]{J_x} + \kappa (\mu - v) {J_v} + \frac{1}{2}{\sigma ^2}v{J_{vv}} - \\ \frac{{{a^2}{\varsigma ^2}J_x^2}}{{2{b^2}\left( {{J_{xx}} + \dfrac{{{\omega _0}J_x^2}}{{\gamma J}}} \right) }} -\;\; \frac{{{{\left( {\eta {J_x} \;+\; \rho \sigma {J_{xv}} \;+\; \dfrac{{{\omega _1}\rho \sigma {J_x}{J_v}}}{{\gamma J}}} \right) }^2}}}{{2\left( {{J_{xx}} \;\;+\; \;\dfrac{{{\omega _1}J_x^2}}{{\gamma J}}} \right) }}v+ \\ \frac{{{\omega _1}{\rho ^2}{\sigma ^2}J_v^2}}{{2\gamma J}}v - \frac{{{{\Bigg( {\xi {J_x} + \sqrt {1 - {\rho ^2}} \sigma {J_{xv}} + \dfrac{{{\omega _2}\sqrt {1 - {\rho ^2}} \sigma {J_x}{J_v}}}{{\gamma J}}} \Bigg) }^2}}}{{2\left( {{J_{xx}} + \dfrac{{{\omega _2}J_x^2}}{{\gamma J}}} \right) }}v + \\ \frac{{{\omega _2}\left( {1 - {\rho ^2}} \right) {\sigma ^2}J_v^2}}{{2\gamma J}}v = 0 \\ \end{gathered} $ | (33) |
为了求解式(33) ,猜测
| $ J(t,x,v) = - \frac{1}{\gamma }\exp \left\{ {f(t) x + g(t) v + h(t) } \right\} $ | (34) |
式中:
由式(34) 得
| $ {J_t} = \left[ {\dot f(t) x + \dot g(t) v + \dot h(t) } \right]J , {J_x} = f(t) J , {J_v} = g(t) J , $ |
| $ {J_{xx}} = {f^2}(t) J , {J_{vv}} = {g^2}(t) J , {J_{xv}} = f(t) g(t) J $ |
将上述各式代入式(33) ,化简得到
| $ \begin{gathered} \left[ {\dot f(t) + rf(t) } \right]x + \Biggr\{ {\dot g(t) - \left[ {\kappa + \rho \sigma \eta + \sqrt {1 - {\rho ^2}} \sigma \xi } \right]g(t)-} \Biggr. \\ \left.{ \frac{{{\eta ^2}}}{{2\left( {1 + \dfrac{{{\omega _1}}}{\gamma }} \right) }} - \frac{{{\xi ^2}}}{{2\left( {1 + \dfrac{{{\omega _2}}}{\gamma }} \right) }}} \right\}v + \Biggr\{ {\dot h(t) + a(\tau - \varsigma ) f(t) + \kappa \mu g(t)- }\Biggr. \\ \left.{ \frac{{{a^2}{\varsigma ^2}}}{{2{b^2}\left( {1 + \dfrac{{{\omega _0}}}{\gamma }} \right) }}} \right\} = 0 \\ \end{gathered} $ | (35) |
式(35) 可以拆分为下述几个常微分方程
| $ \dot f(t) + rf(t) = 0 $ | (36) |
| $ \begin{split} &\dot g(t) - \left[ {\kappa + \rho \sigma \eta + \sqrt {1 - {\rho ^2}} \sigma \xi } \right]g(t) -\\ &\frac{{{\eta ^2}}}{{2\left( {1 + \dfrac{{{\omega _1}}}{\gamma }} \right) }} - \frac{{{\xi ^2}}}{{2\left( {1 + \dfrac{{{\omega _2}}}{\gamma }} \right) }} = 0 \end{split}$ | (37) |
| $ \dot h(t) + a(\tau - \varsigma ) f(t) + \kappa \mu g(t) - \frac{{{a^2}{\varsigma ^2}}}{{2{b^2}\left( {1 + \dfrac{{{\omega _0}}}{\gamma }} \right) }} = 0 $ | (38) |
结合边界条件
| $ f(t) = - \gamma {{\text{e}}^{r(T - t) }} $ | (39) |
再结合边界条件
最后将
将
| $ {q^ * } = {{\text{e}}^{ - r(T - t) }}\frac{{a\varsigma }}{{{b^2}\left( {\gamma + {\omega _0}} \right) }} $ | (40) |
| $\begin{split} &\theta _1^ * = {{\text{e}}^{ - r(T - t) }}\frac{{\eta + \left( {1 + \dfrac{{{\omega _1}}}{\gamma }} \right) \rho \sigma g}}{{\gamma + {\omega _1}}} , \\ &\theta _2^ * = {{\text{e}}^{ - r(T - t) }}\frac{{\xi + \left( {1 + \dfrac{{{\omega _2}}}{\gamma }} \right) \sqrt {1 - {\rho ^2}} \sigma g}}{{\gamma + {\omega _2}}} \end{split}$ | (41) |
由式(9) 得
| $ \begin{split} {\alpha ^ * } =& {{\text{e}}^{ - r(T - t) }}\Bigg\{ {\frac{{\eta + \left( {1 + \dfrac{{{\omega _1}}}{\gamma }} \right) \rho \sigma g}}{{\gamma + {\omega _1}}} - \frac{{\xi + \left( {1 + \dfrac{{{\omega _2}}}{\gamma }} \right) \sqrt {1 - {\rho ^2}} \sigma g}}{{\gamma + {\omega _2}}}\times} \Bigg. \\ &\Bigg. { \frac{{O(t) }}{{\sigma \sqrt {1 - {\rho ^2}} {O_V}}}\left[ {\frac{{{O_S}S(t) }}{{O(t) }} + \frac{{\rho \sigma {O_V}}}{{O(t) }}} \right]} \Bigg\} \\[-10pt] \end{split} $ | (42) |
| $ {\beta ^ * } = {{\text{e}}^{ - r(T - t) }}\frac{{\xi + \left( {1 + \dfrac{{{\omega _2}}}{\gamma }} \right) \sqrt {1 - {\rho ^2}} \sigma g}}{{\gamma + {\omega _2}}}\frac{{O(t) }}{{\sigma \sqrt {1 - {\rho ^2}} {O_V}}} $ | (43) |
最后将式(40) 和(41) 代入式(28) ,化简得
| $ \phi _0^ * = \frac{{a\varsigma {\omega _0}}}{{b\left( {\gamma + {\omega _0}} \right) }} , \phi _1^ * = \frac{{{\omega _1}\eta \sqrt v }}{{\gamma + {\omega _1}}} , \phi _2^ * = \frac{{{\omega _2}\xi \sqrt v }}{{\gamma + {\omega _2}}} $ | (44) |
定理2证毕。
4 无衍生品交易情形下的鲁棒最优策略为了比较衍生品交易的价值,本节讨论无衍生品交易情形下保险公司的鲁棒最优投资与再保险决策。
如果金融市场不包含衍生品交易,则最优的投资策略等价于对扩散风险
| $ \begin{split} {\text{d}}{X^{\tilde \phi ,\tilde \pi }}(t) =& \left[ {r{X^{\tilde \phi ,\tilde \pi }}(t) + \eta \tilde \alpha {\text{(}}t{\text{) }}{V^{\tilde \phi }}{\text{(}}t{\text{) }} - {\phi _1}(t) \tilde \alpha {\text{(}}t{\text{) }}\sqrt {{V^{\tilde \phi }}{\text{(}}t{\text{) }}} + } \right. \\ &\Biggr. {a(\tau - \varsigma ) + a\varsigma \tilde q(t)- b\tilde q(t) {\phi _0}(t) } \Biggr]{\text{d}}t + b\tilde q(t) {\text{d}}B_0^{\tilde \phi }(t)+ \\ &\tilde \alpha {\text{(}}t{\text{) }}\sqrt {{V^{\tilde \phi }}{\text{(}}t{\text{) }}} {\text{d}}B_1^{\tilde \phi }(t) \\[-10pt] \end{split} $ | (45) |
式中:
| $\begin{split} &\mathop {\sup }\limits_{\tilde \pi \in \varPi } \mathop {\inf }\limits_{\tilde \phi \in \varTheta } {{\text{E}}^Q}\left[ {U( {{X^{\tilde \phi ,\tilde \pi }}(T) } )}+\right. \\ & \left.{\int_t^T {\left( {\frac{{\tilde \phi _0^2(s) }}{{2{{\tilde \varPsi }_0}( {s,x,v} ) }} + \frac{{\tilde \phi _1^2(s) }}{{2{{\tilde \varPsi }_1}( {s,x,v} ) }}+\frac{{\tilde \phi _2^2(s) }}{{2{{\tilde \varPsi }_2}( {s,x,v} ) }}} \right) {\text{d}}s} } \right] \end{split}$ | (46) |
HJB方程变为
| $ \mathop {\sup }\limits_{\tilde \pi \in \varPi } \mathop {\inf }\limits_{\tilde \phi \in \varTheta } \left\{ {{\mathcal{D}^{\tilde \phi ,\tilde \pi }}\tilde J + \frac{{\tilde \phi _0^2}}{{2{{\tilde \varPsi }_0}}} + \frac{{\tilde \phi _1^2}}{{2{{\tilde \varPsi }_1}}} + \frac{{\tilde \phi _2^2}}{{{{\tilde \varPsi }_2}}}} \right\} = 0 $ | (47) |
| $ {\tilde \varPsi _k}(s,x,v) = - \frac{{{\omega _k}}}{{\gamma \tilde J(s,x,v) }},\quad k \in \{ 0,1,2\} $ | (48) |
边界条件为
| $ \begin{split} {\mathcal{D}^{\tilde \phi ,\tilde \pi }}\tilde J =& {{\tilde J}_t} + \left[ {rx + \eta \tilde \alpha v - {{\tilde \phi }_1}\tilde \alpha \sqrt v + a(\tau - \varsigma ) + a\varsigma \tilde q - }\right.\\ &\left.{b\tilde q{{\tilde \phi }_0}} \right]{{\tilde J}_x} + \frac{1}{2}\left( {{b^2}{{\tilde q}^2} + {{\tilde \alpha }^2}v} \right) {{\tilde J}_{xx}} + \left[ {\kappa (\mu - v) - }\right.\\ &\left.{ \sigma \sqrt v ( {\rho {{\tilde \phi }_1} + \sqrt {1 - {\rho ^2}} {{\tilde \phi }_2}} ) } \right]{{\tilde J}_v} +\frac{1}{2}{\sigma ^2}v{{\tilde J}_{vv}} + \rho \sigma \tilde \alpha v{{\tilde J}_{xv}} \\ \end{split} $ |
下述定理给出了无衍生品交易情形下最优策略及值函数的解析表达。
定理3 对无衍生品交易的鲁棒优化问题(46) ,HJB方程(47) 存在下述形式的解析表达
| $ \tilde J(t,x,v) = - \frac{1}{\gamma }\exp \left\{ { - \gamma x{{\text{e}}^{r(T - t) }} + \tilde g(t) v + \tilde h(t) } \right\} $ | (49) |
式中:
| $ \tilde g(t) = \frac{{{\nu _1}{\nu _2}\left[ {{{\text{e}}^{A\left( {{\nu _1} - {\nu _2}} \right) \left( {T - t} \right) }} - 1} \right]}}{{{\nu _2}{{\text{e}}^{A\left( {{\nu _1} - {\nu _2}} \right) \left( {T - t} \right) }} - {\nu _1}}} $ | (50) |
| $ \begin{split} \tilde h(t) = &\frac{a}{r}( {\tau - \varsigma } ) \gamma [ {1 - {{\text{e}}^{r( {T - t} ) }}} ] + \left[ {\kappa \mu {\nu _1} - \frac{{{a^2}{\varsigma ^2}}}{{2{b^2}\left( {1 + \dfrac{{{\omega _0}}}{\gamma }} \right) }}} \right]( {T - t} )+ \\ &{\text{ }} \frac{{\kappa \mu }}{A}\left[ {\ln \frac{{{\nu _2} - {\nu _1}}}{{{\nu _2}{{\text{e}}^{A( {{\nu _1} - {\nu _2}} ) ( {T - t} ) }} - {\nu _1}}} + A( {{\nu _1} - {\nu _2}} ) ( {T - t} ) } \right]\\[-10pt] \end{split} $ | (51) |
式(50) 和(51) 中的
最优再保险策略和投资策略分别为
| $ {\tilde q^ * }(t) = {\left( {{{\text{e}}^{ - r(T - t) }}\frac{{a\varsigma }}{{{b^2}( {\gamma + {\omega _0}} ) }} \wedge 1} \right) ^ + } $ | (52) |
| $ {\tilde \alpha ^ * }(t) = {{\text{e}}^{ - r(T - t) }}\frac{{\eta + \left( {1 + \dfrac{{{\omega _1}}}{\gamma }} \right) \rho \sigma \tilde g(t) }}{{\gamma + {\omega _1}}} $ | (53) |
且最坏的测度为
| $ \begin{split} &\phi _0^ * (t) = \frac{{a\varsigma {\omega _0}}}{{b( {\gamma + {\omega _0}} ) }} , \phi _1^ * (t) = \frac{{{\omega _1}\eta \sqrt {V(t) } }}{{\gamma + {\omega _1}}} , \\ &\phi _2^ * (t) = - \frac{{{\omega _2}\sqrt {1 - {\rho ^2}} \sigma \tilde g(t) \sqrt {V(t) } }}{\gamma } \end{split}$ | (54) |
定理3的证明类似定理2,囿于篇幅所限,这里不再给出证明过程。
5 数值算例为了直观地反映模型中相关参数变动对最优策略及效用函数的影响,本节将借助数值仿真算例,一方面分析模型主要参数变动对最优投资与再保险策略的影响,另一方面揭示暧昧性与衍生品交易对保险公司效用改进的影响。由于本文的工作主要是基于Xue等[14]的研究做出的,因此金融市场模型的相关参数均来自Xue等[14],而保险风险模型的相关参数来自Pun和Wong[20],参数暧昧性的相关参数来自Zeng等[16]。为表述方便,将相关参数的取值列在表1中。
| 表 1 模型的基本参数 Table 1 Base parameters of the model |
此外,为了得到相关参数变化对最优投资策略的影响,以欧式看涨期权为例来描述衍生品,期权的交割时间和执行价格分别设定为0.1和100。利用Zeng等[16]和Xue等[14]的已有结果计算可得
由式(23) 可知,模型的最优再保险策略q*受到参数a、b、r、

|
图 1 a和b对最优再保险策略q*的影响 Figure 1 Effect of a and b on q* |
|
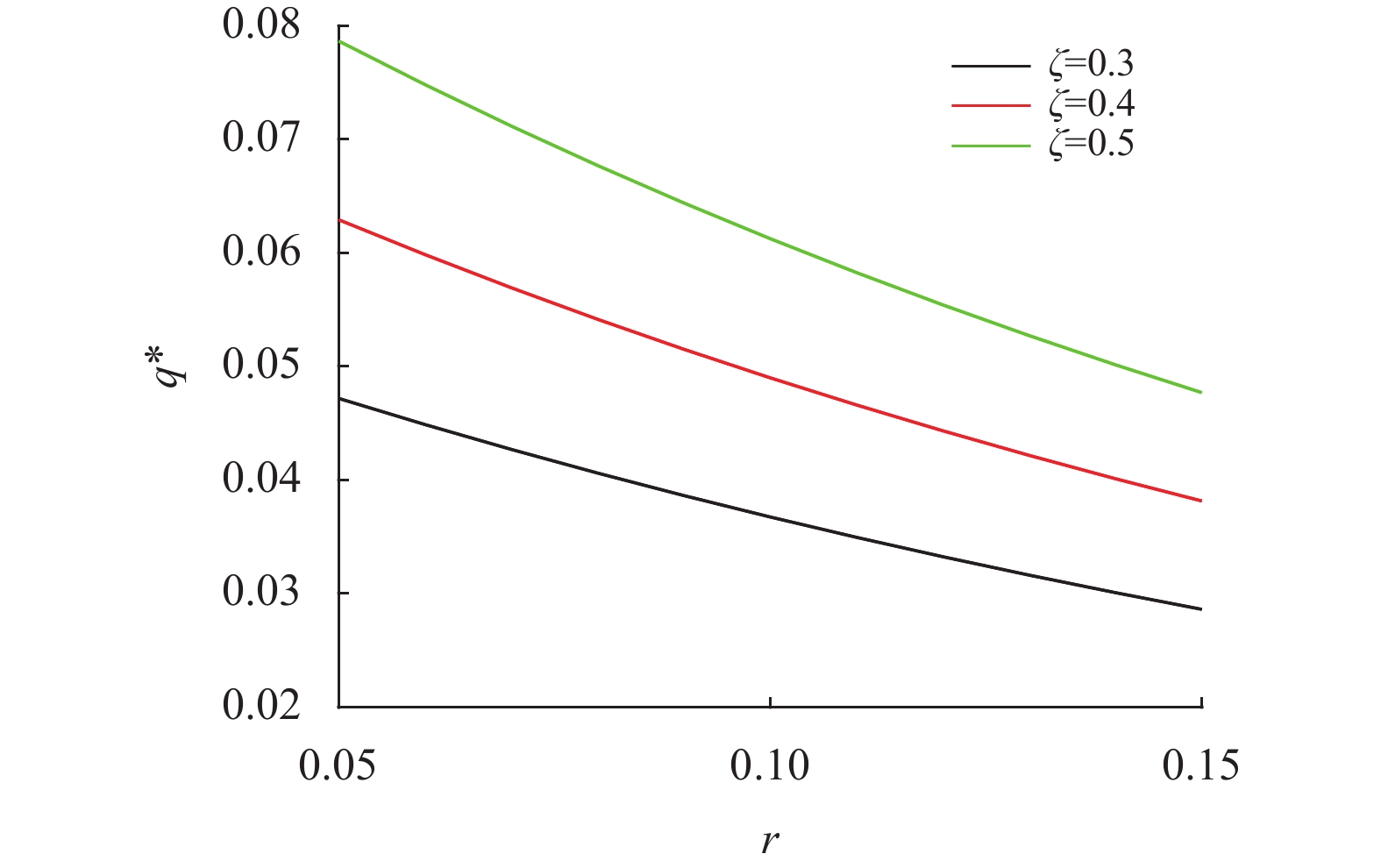
图 2 r和
|
图1揭示了索赔的期望值
图2描述了无风险利率
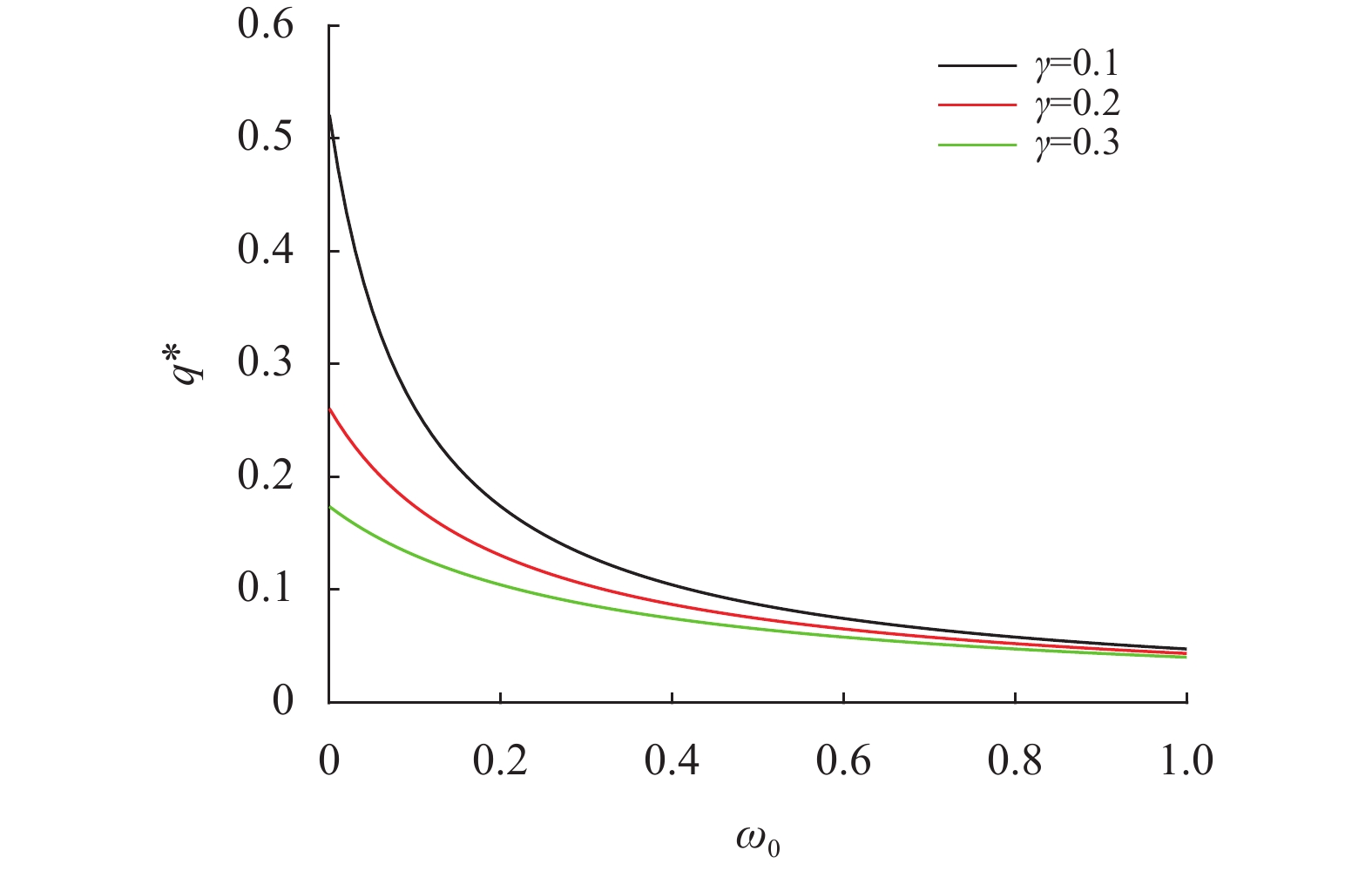
图3展示了风险厌恶系数
|
图 3 γ和ω0对最优再保险策略q*的影响 Figure 3 Effect of γ and ω0 on q* |
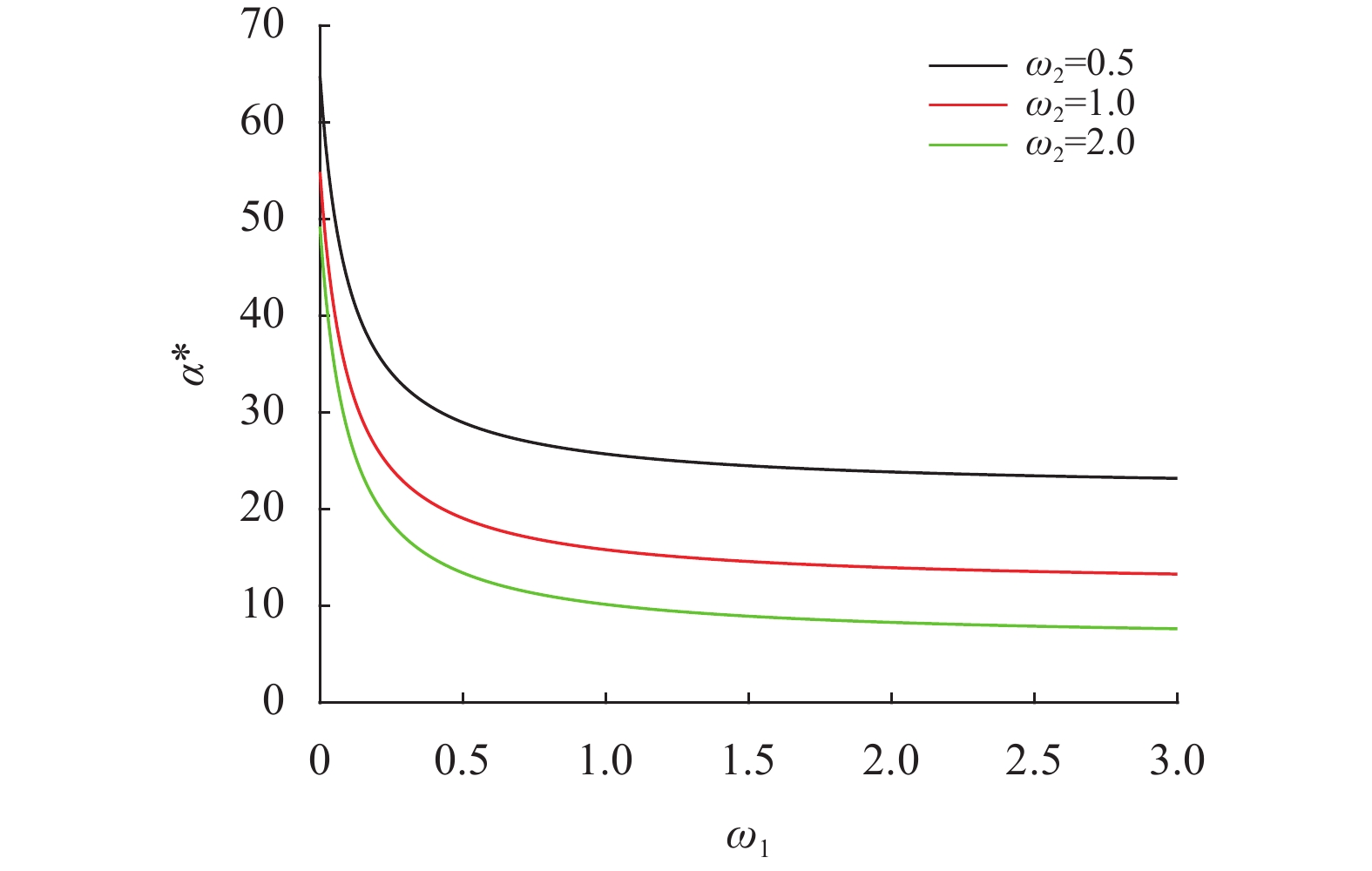
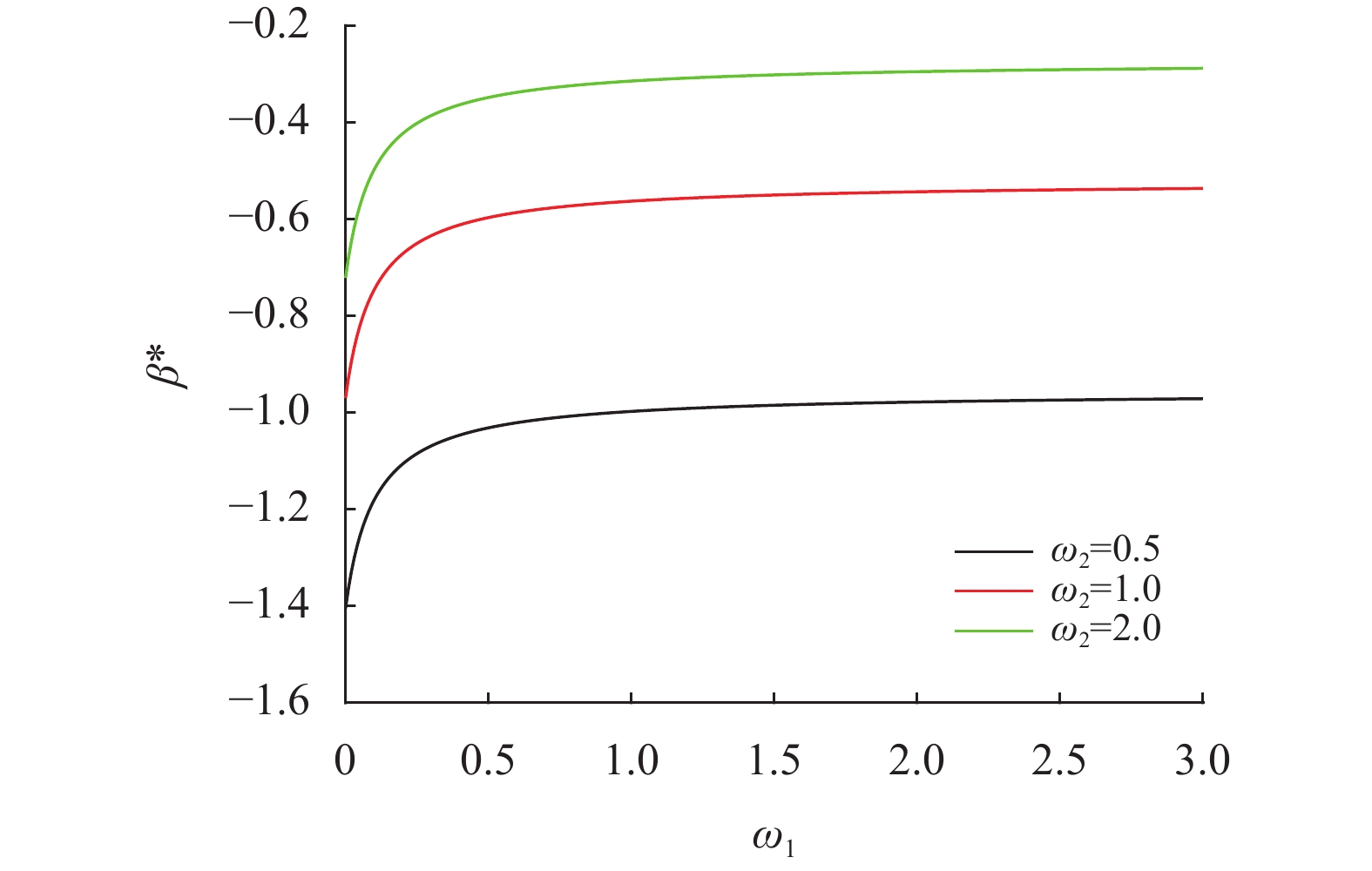
由式(25) 和(26) 可知,最优投资策略α*和β*主要受到参数κ、σ、η、ξ、ω1及ω2的影响,因此接下来考察κ、σ、η、ξ、ω1与ω2的变动基于最优投资策略α*和β*的变化,相关结果见图4~图9。
|
图 4 ω1与ω2对最优投资策略α*的影响 Figure 4 Effect of ω1 and ω2 on α* |
|
图 5 ω1与ω2对最优投资策略β*的影响 Figure 5 Effect of ω1 and ω2 on β* |
|
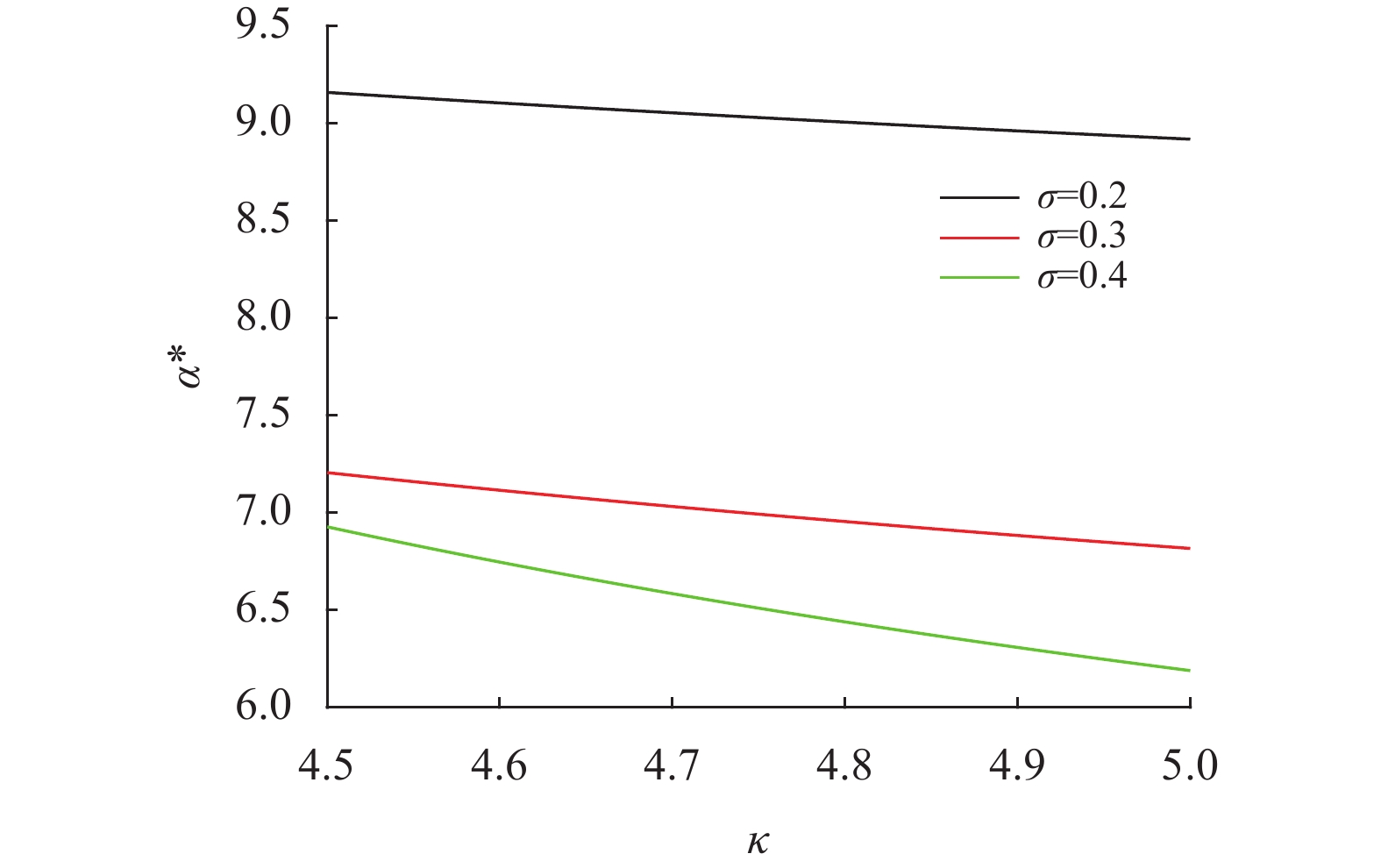
图 6 κ与σ对最优投资策略α*的影响 Figure 6 Effect of κ and σ on α* |
|
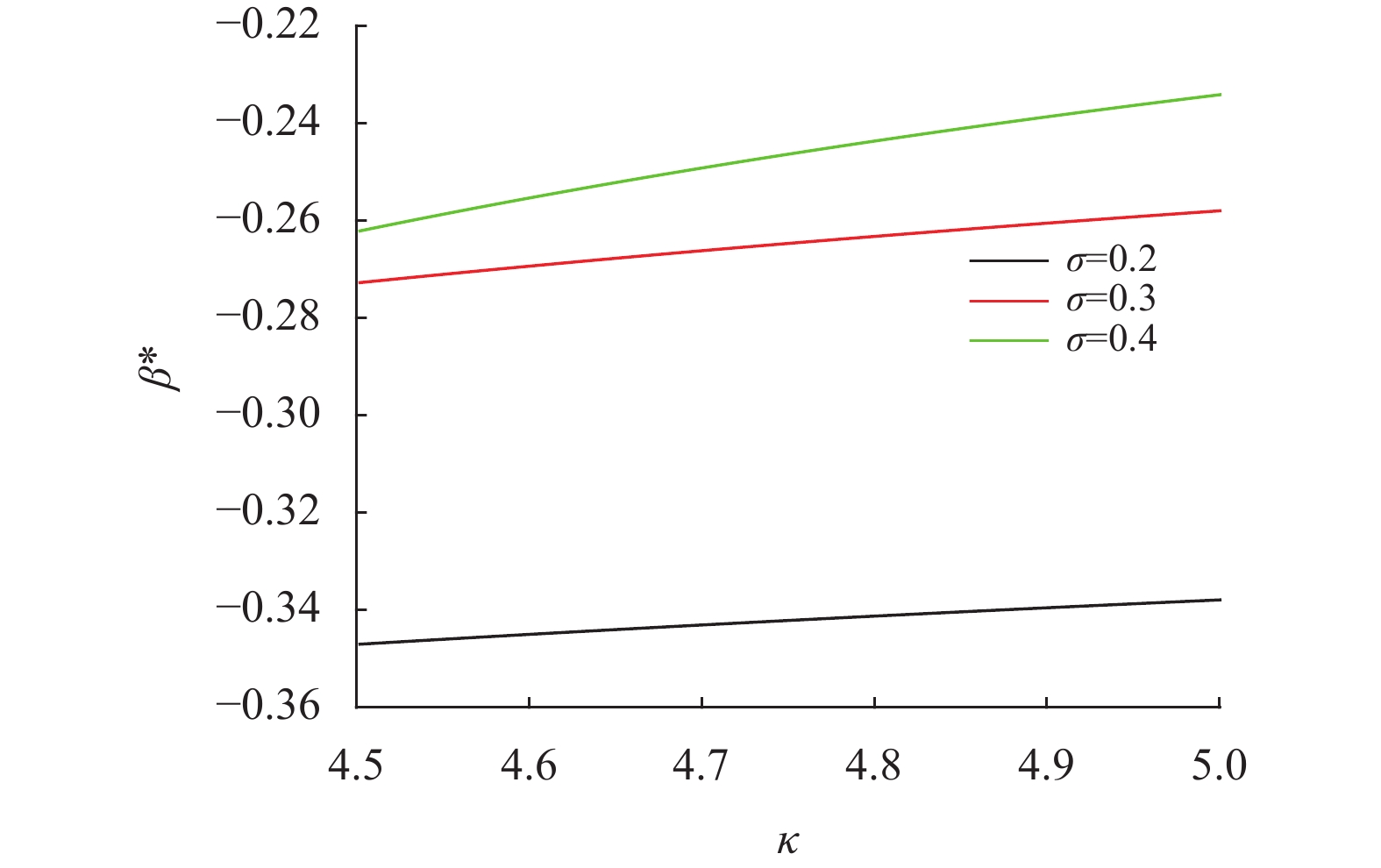
图 7 κ与σ对最优投资策略β*的影响 Figure 7 Effect of κ and σ on β* |
|
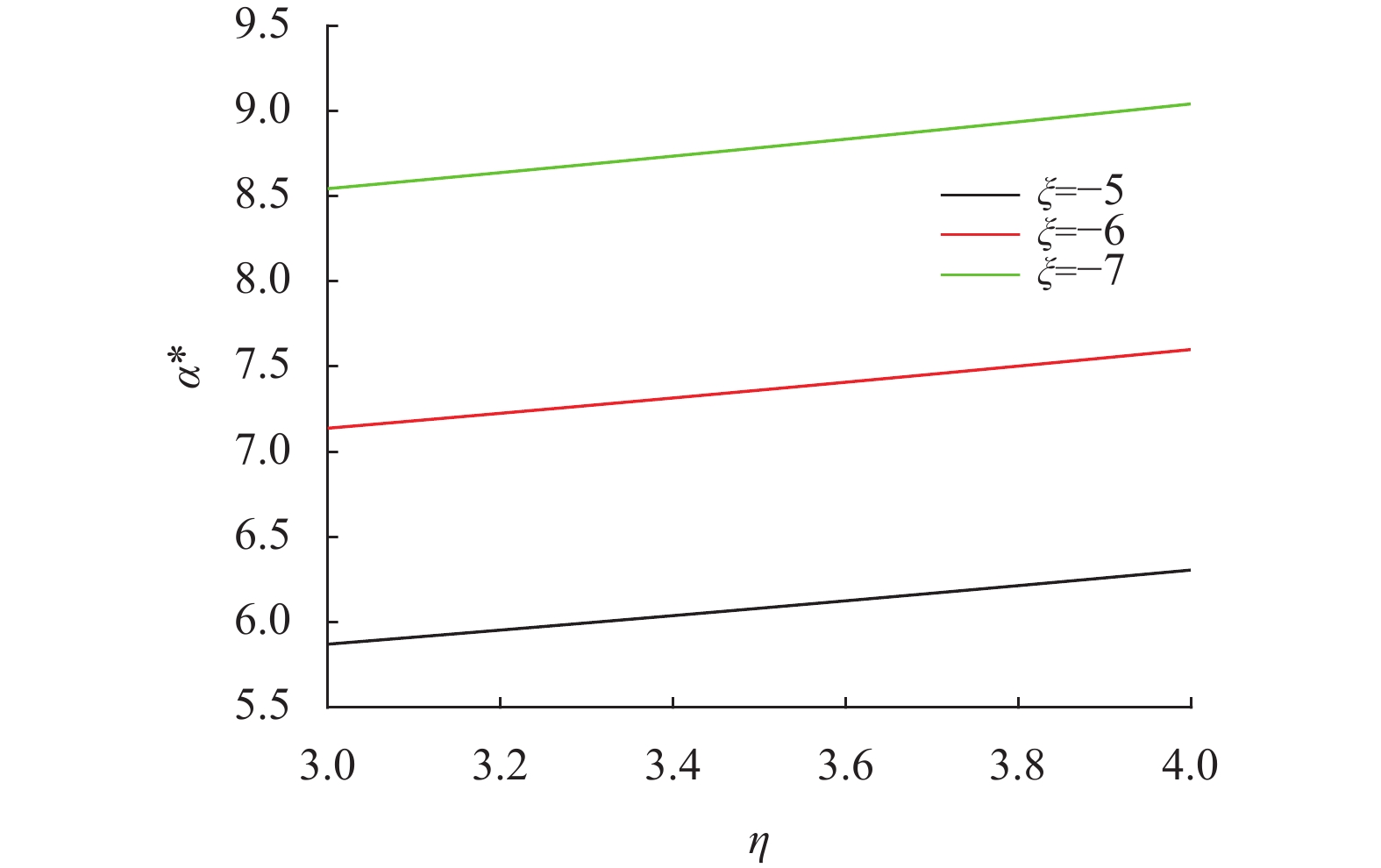
图 8 η与ξ对最优投资策略α*的影响 Figure 8 Effect of η and ξ on α* |
图4和图5揭示了暧昧厌恶系数ω1和ω2对最优投资策略α*和β*的影响。从图中可以发现,α*和β*均关于ω1和ω2单调递减。同股票上的投资头寸α*相比,期权上的投资头寸β*受ω1的影响较小。当ω1增加时,表示股票投资收益的不确定性增加,因而保险公司会购买较少头寸的股票。β*随ω2的变化趋势可类似解释,当ω2增加时,它会减少股票价格波动率的风险溢价,因而对一个风险厌恶的保险公司来说,期权的投资吸引力已变得越来越小,会引起在期权上的投资头寸变小。
图6和图7描述了均值回复速度κ和收益率方差σ对最优投资策略α*和β*的影响。从图中可以看出,随着κ的增加,α*和β*均跟着减小。因为ρ为负,股票收益的波动V(t) 和股票的价格S(t) 的运动变化方向相反,κ越大,V(t) 变化的波动相应抵消效用就越不明显,这增加了股票价格下跌的风险,因而保险公司会减少在股票和期权上的持有头寸。此外,从图中还可以看出α*和β*均随着σ的增加而减少,这是因为σ越大,投资股票的风险越大,因而保险公司则会减少在其股票和期权上的投资比例。
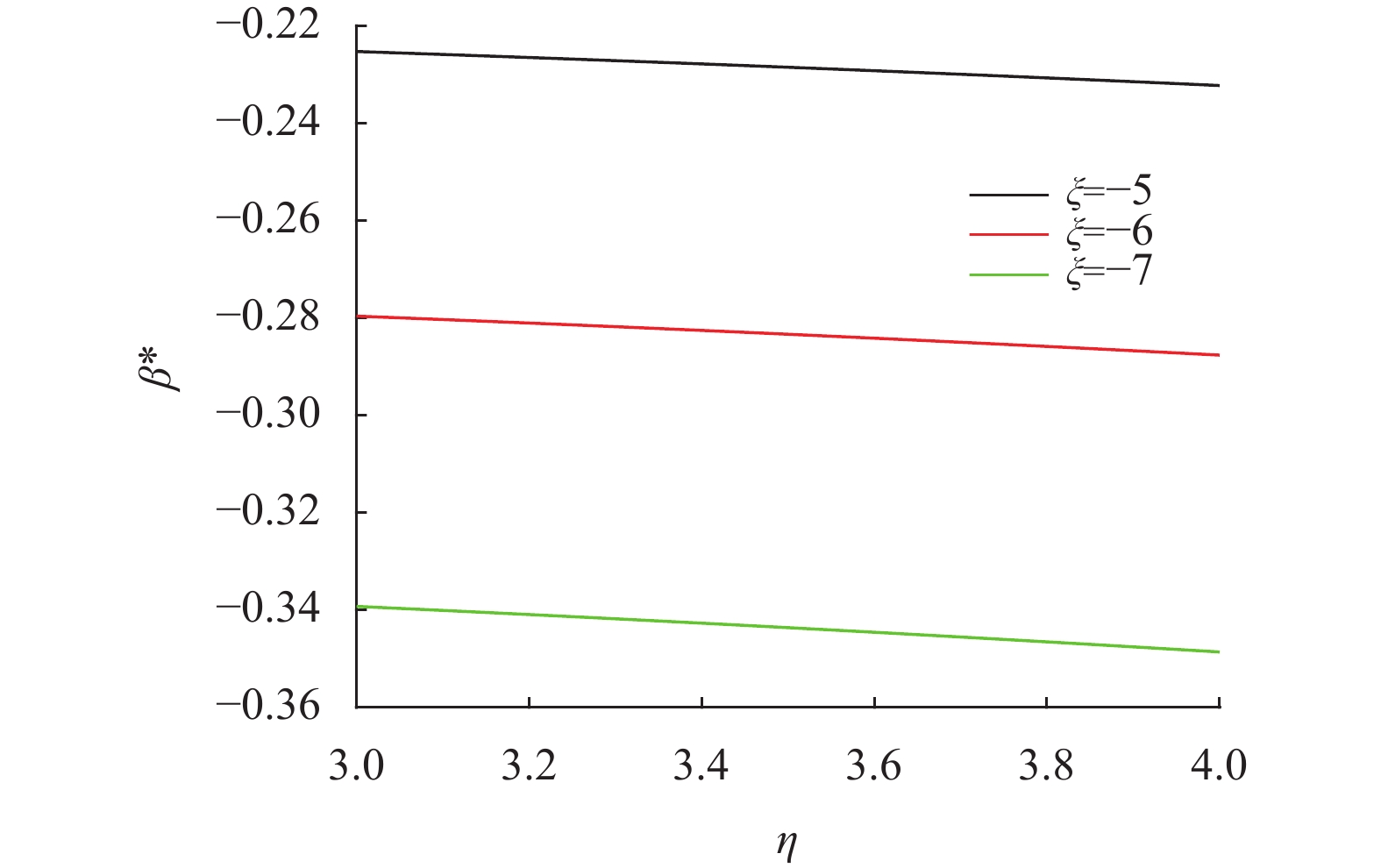
图8和图9刻画了风险溢价因子η和ξ对最优投资策略α*和β*的影响。首先从图中可以看出,α*随着η的增加而增加,而β*则几乎不受η变化的影响。这是因为随着η的增加,投资股票变得更加有利可图,因而保险公司会增持在股票上的投资额。此外,从图中还可以发现,α*和β*均是ξ的减函数,因为当ξ变小时,投资期权的吸引力越来越小,这使得保险公司减少了在股票和期权上的投资,这与Xue等[14]得到的结论是一致的。
5.3 效用改进最后研究衍生品交易对保险公司的效用改进情况。针对这种情形,通过对比考虑衍生品交易与不考虑衍生品交易两种情况下保险公司的效用函数来计算效用改进。此时相应的效用改进函数可定义为
| $ {\text{UI}}(t,x,v) = 1 - \frac{{J(t,x,v) }}{{\tilde J(t,x,v) }} = 1 - \exp \left\{ {\left[ {g(t) - \tilde g(t) } \right]v + h(t) - \tilde h(t) } \right\} $ |
式中的
|
图 9 η与ξ对最优投资策略β*的影响 Figure 9 Effect of η and ξ on β* |
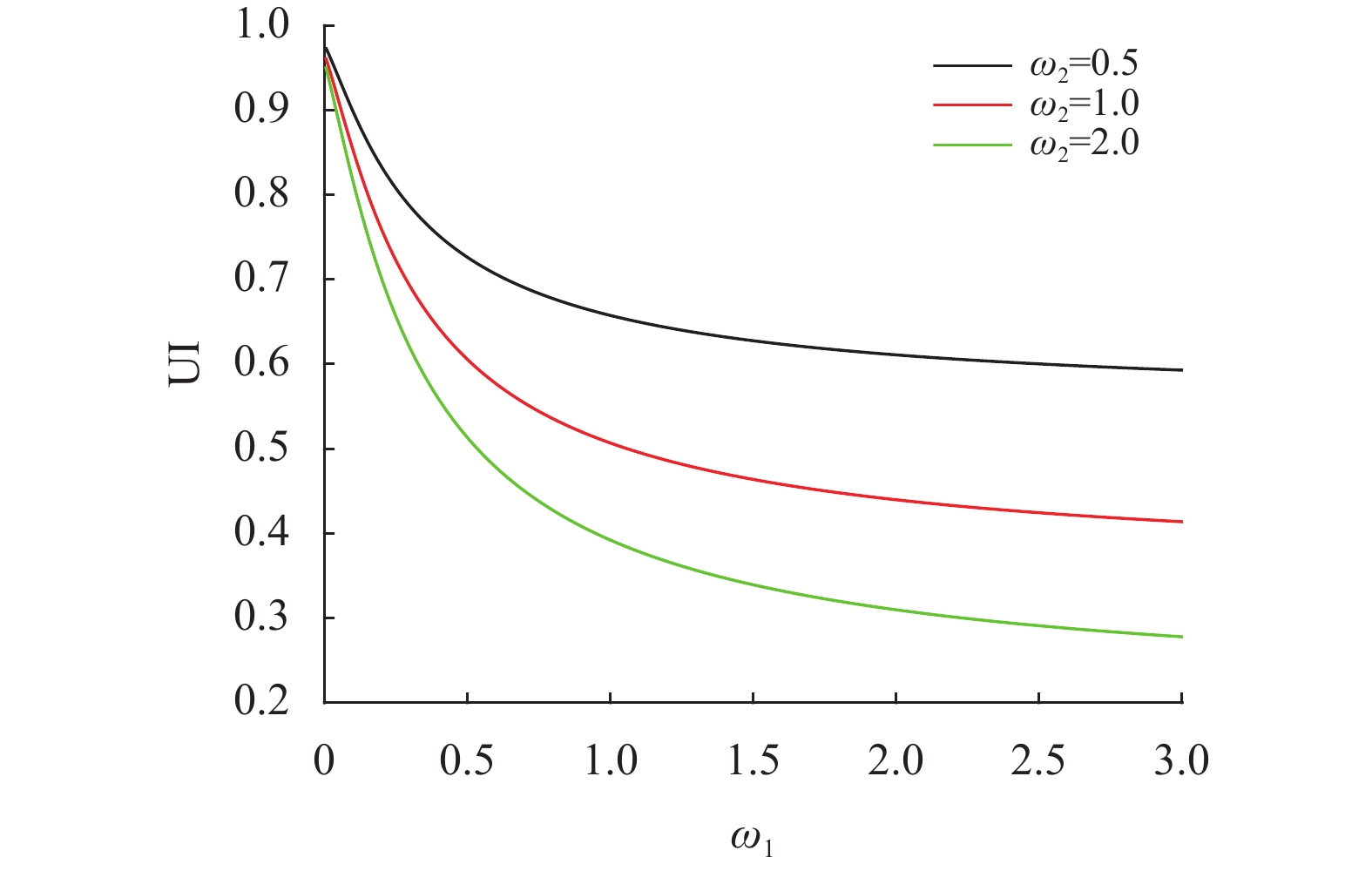
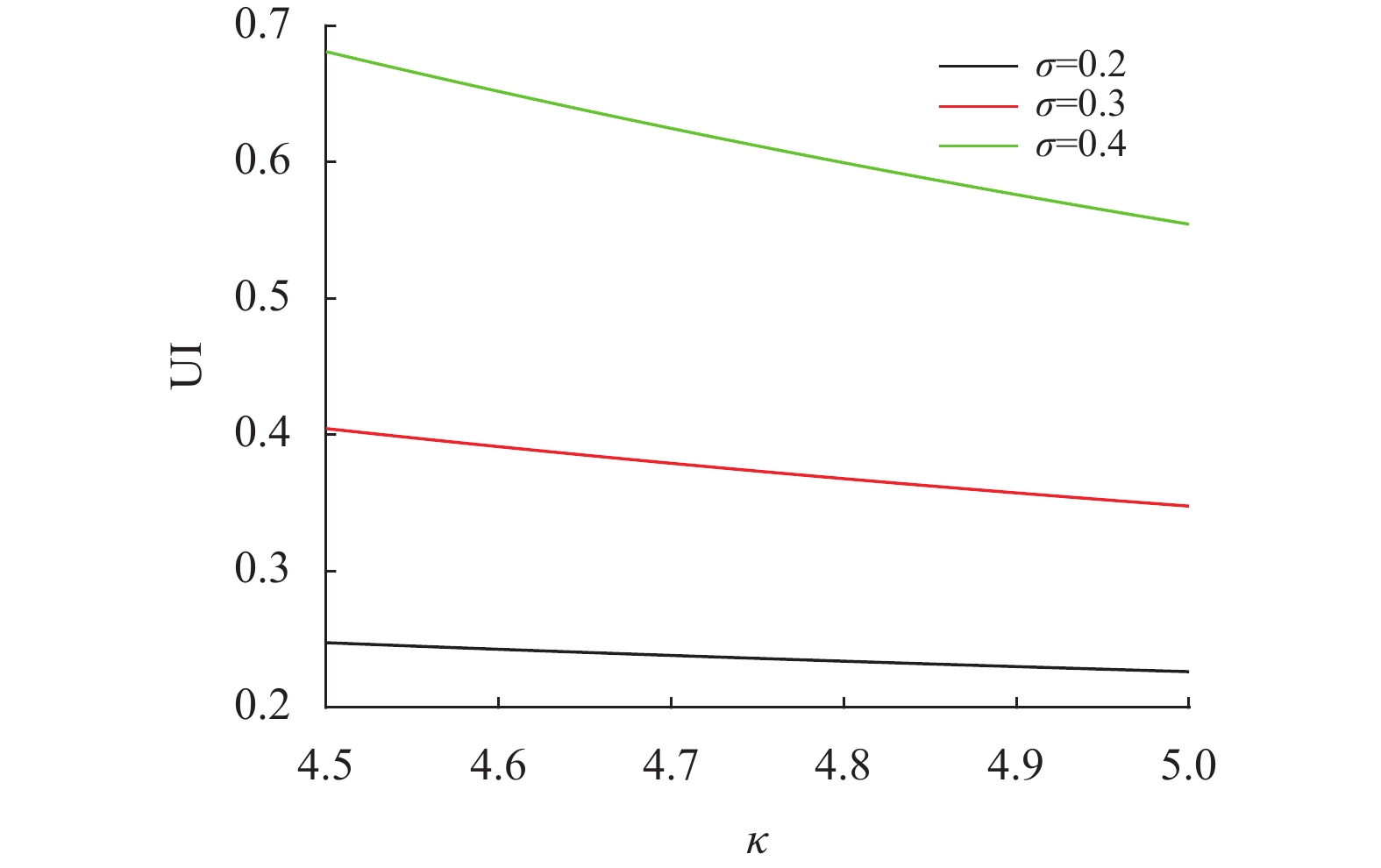
图10~图11分别给出了ω1和ω2、κ和σ对效用改进的影响。
|
图 10 ω1与ω2对效用改进的影响 Figure 10 Effect of ω1 and ω2 on utility improvement |
|
图 11 κ与σ对效用改进的影响 Figure 11 Effect of κ and σ on utility improvement |
图10描述了暧昧厌恶系数ω1和ω2对效用改进UI的影响。可以发现,随着ω1和ω2的增加,UI呈单调递减的趋势。因为随着暧昧厌恶系数的增大,保险公司对参考模型持有越大的不确定性,因而考虑期权交易可以更大地增加保险公司的效用,这与Zeng等[16]的结论是一致的。
图11刻画了均值回复速度κ和波动率方差σ对效用改进UI的影响。可以看出UI随κ单调递减而随σ单调递增。这是因为从股票价格波动的方差过程可以看出,较大的κ和较小的σ意味着股票价格波动的方差过程具有较小的不确定性。这使得保险公司面临着较小的波动率风险,因而效用改进UI关于κ单调递减,关于σ单调递增。
6 结语本文在考虑模型参数暧昧环境下,研究了含衍生品交易的鲁棒最优投资与再保险决策问题。假定保险公司的风险过程用近似扩散过程描述,保险公司通过购买比例再保险来转移索赔风险,并将其盈余投资于由无风险资产、风险股票和以股票为标的资产的衍生品3种资产构成的金融市场中。针对具有指数效用函数的保险公司构建了相应的鲁棒优化决策模型,利用动态规划方法得到了与优化问题相对应的HJB方程,然后求解HJB方程得到了最优投资与再保险策略及值函数的解析表达式。进一步,结合数值仿真算例讨论了模型主要参数变动如何影响最优投资与再保险策略及效用改进相关动态行为。通过仿真分析发现,进行衍生品交易能够显著提高保险公司的效用水平,且随着风险资产价格变化波动率的增加而增加;此外,与不考虑暧昧厌恶性相比,保险公司决策者越厌恶暧昧性(表现为暧昧厌恶系数的增加),该效用水平增加得越多,这在一定程度上为保险公司涉足衍生品交易决策提供了理论支持。
进一步的研究工作可以从以下几个方面进行考虑:一是考虑更为一般的随机波动率模型,如4/2随机波动率模型,在此基础上研究最优投资与比例再保险策略。二是考虑均值−方差准则,结合决策的时间一致性要求研究均衡投资与比例再保险策略。三是考虑市场竞争的情形,构建两家乃至多家保险公司之间的非零和投资与再保险博弈模型,利用随机控制理论求得博弈的Nash均衡策略。
| [1] |
KNIGHT F. Risk, uncertainty and profit[M]. Boston: Houghton Mifflin, 1921: 37-68.
|
| [2] |
ELLSBERG D. Risk, ambiguity, and the savage axioms[J].
The Quarterly Journal of Economics, 1961, 75(4): 643-669.
DOI: 10.2307/1884324. |
| [3] |
GHIRARDATO P, MACCHERONI F, MARINACCI M. Differentiating ambiguity and ambiguity attitude[J].
Journal of Economic Theory, 2004, 118(2): 133-173.
DOI: 10.1016/j.jet.2003.12.004. |
| [4] |
EPSTEIN L G, JI S. Ambiguous volatility and asset pricing in continuous time[J].
Review of Financial Studies, 2013, 26(7): 1740-1786.
DOI: 10.1093/rfs/hht018. |
| [5] |
ILLEDITSCH P K. Ambiguous information, portfolio inertia, and excess volatility[J].
Journal of Finance, 2011, 66(6): 2213-2247.
DOI: 10.1111/j.1540-6261.2011.01693.x. |
| [6] |
YI B, LI Z, VIENS F G, et al. Robust optimal control for an insurer with reinsurance and investment under Heston’s stochastic volatility model[J].
Insurance:Mathematics and Economics, 2013, 53(3): 601-614.
DOI: 10.1016/j.insmatheco.2013.08.011. |
| [7] |
ZENG Y, LI D, GU A. Robust equilibrium reinsurance-investment strategy for a mean-variance insurer in a model with jumps[J].
Insurance:Mathematics and Economics, 2016, 66: 138-152.
DOI: 10.1016/j.insmatheco.2015.10.012. |
| [8] |
ZHENG X, ZHOU J, SUN Z. Robust optimal portfolio and proportional reinsurance for an insurer under a CEV model[J].
Insurance:Mathematics and Economics, 2016, 67: 77-87.
DOI: 10.1016/j.insmatheco.2015.12.008. |
| [9] |
HUANG Y, OUYANG Y, TANG L, et al. Robust optimal investment and reinsurance problem for the product of the insurer’s and the reinsurer’s utilities[J].
Journal of Computational and Applied Mathematics, 2018, 344: 532-552.
DOI: 10.1016/j.cam.2018.05.060. |
| [10] |
LI D, ZENG Y, YANG H. Robust optimal excess-of-loss reinsurance and investment strategy for an insurer in a model with jumps[J].
Scandinavian Actuarial Journal, 2018, 2018(2): 145-171.
DOI: 10.1080/03461238.2017.1309679. |
| [11] |
LIU J, PAN J. Dynamic derivative strategies[J].
Journal of Financial Economics, 2003, 69(3): 401-430.
DOI: 10.1016/S0304-405X(03)00118-1. |
| [12] |
王蕾, 顾孟迪. 最优再保险与投资决策: 财富最大化和套期保值的选择[J].
系统管理学报, 2013, 22(6): 783-790.
WANG L, GU M D. Proportional reinsurance and investment strategies: maximizing the terminal wealth and hedging[J]. Journal of Systems & Management, 2013, 22(6): 783-790. DOI: 10.3969/j.issn.1005-2542.2013.06.005. |
| [13] |
傅毅, 张寄洲, 周翠. 含有期权的最优投资与比例再保险策略[J].
系统工程学报, 2015, 30(2): 181-189.
FU Y, ZHANG J Z, ZHOU C. Optimal investment and proportional reinsurance strategy with options[J]. Journal of Systems Engineering, 2015, 30(2): 181-189. |
| [14] |
XUE X, WEI P, WENG C. Derivatives trading for insurers[J].
Insurance:Mathematics and Economics, 2019, 84: 40-53.
DOI: 10.1016/j.insmatheco.2018.11.001. |
| [15] |
ESCOBAR M, FERRANDO S, RUBTSOV A. Dynamic derivative strategies with stochastic interest rates and model uncertainty[J].
Journal of Economic Dynamics and Control, 2018, 86: 49-71.
DOI: 10.1016/j.jedc.2017.09.007. |
| [16] |
ZENG Y, LI D, CHEN Z, et al. Ambiguity aversion and optimal derivative-based pension investment with stochastic income and volatility[J].
Journal of Economic Dynamics and Control, 2018, 88: 70-103.
DOI: 10.1016/j.jedc.2018.01.023. |
| [17] |
王佩, 陈峥, 张玲. 基于衍生品投资的DC型养老金计划均衡投资策略[J].
中山大学学报(自然科学版), 2021, 60(3): 147-158.
WANG P, CEHN Z, ZHANG L. Equilibrium investment strategy for a DC pension plan with derivative trading[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2021, 60(3): 147-158. |
| [18] |
PROMISLOW D S, YOUNG V R. Minimizing the probability of ruin when claims follow Brownian motion with drift[J].
North American Actuarial Journal, 2005, 9(3): 109-128.
|
| [19] |
MAENHOUT P J. Robust portfolio rules and asset pricing[J].
Review of Financial Studies, 2004, 17(4): 951-983.
DOI: 10.1093/rfs/hhh003. |
| [20] |
PUN C S, WONG H Y. Robust non-zero-sum stochastic differential reinsurance game[J].
Insurance:Mathematics and Economics, 2016, 68: 169-177.
DOI: 10.1016/j.insmatheco.2016.02.007. |
 2022, Vol. 39
2022, Vol. 39
