众所周知,大规模非线性系统通常被视为由许多相互关联的子系统组成的系统。由于控制结构的复杂性以及各子系统之间信息交换的局限性,给大规模非线性系统的控制器设计和稳定性分析带来了很大的困难。为了克服这个困难,在过去的几十年中,许多学者利用分散自适应技术控制大规模系统[1-3]。然而该控制方法有一定的局限性,即系统中的不确定非线性函数要么是参数未知的线性函数,要么是已知非线性函数。为了克服这些限制,文献[4-6]中利用神经网络或文献[7-8]中利用模糊逻辑系统来识别未知非线性函数的自适应分散控制方法得到了广泛研究。其中,在文献[8]中,针对一类具有执行器故障的非严格反馈非线性系统,利用模糊控制构造了一种改进的容错控制器,使闭环系统中的所有信号都是半全局有限时间稳定的。
另一方面,为了有效地节省通信资源,减轻通信负担,非线性系统的自适应事件触发控制也受到了广泛的关注。与传统的时间触发控制不同,事件触发控制是一种仅在系统需要时才将控制器输出应用于系统的控制机制。最近,将模糊和神经网络逼近方法与反步技术相结合,针对具有不同触发机制的非线性系统,文献[9-14]提出了一些自适应事件触发控制方案。其中,针对具有未建模动态的随机非线性系统,文献[12]提出了一种基于变阈值方案的模糊自适应有限时间事件触发控制策略。在文献[15]中,针对一类不确定严格反馈非线性系统,设计了一种新的自适应事件触发机制,使控制器和参数估计器同时触发。然而,上述控制方案不能用于控制系统的瞬态行为和稳态性能。在许多实际应用中,除了跟踪稳定性外,经常需要系统的跟踪性能满足预定的约束条件,并要求系统达到预期的稳态跟踪精度。
最近,预定义性能控制(Predefined Performance Control,PPC)技术一经在文献[16]中提出就引起了广泛关注。预定义性能控制技术通过利用规定的性能函数(Predefined Performance Function, PPF)和构造误差变化来处理预定义的性能约束[15, 17–18]。其中,文献[17]针对一类严格反馈系统,提出了一种基于有限时间性能函数的自适应模糊控制器,该控制器可以确保闭环系统的所有信号都有界,并且跟踪误差在有限时间内收敛到预定范围。然而,以上所述的基于PPF的性能控制方法取决于初始条件,这限制了其在实际中的应用。文献[19]提出了一种漏斗控制方法(Funnel Control)放宽了对初始条件的要求。近年来,利用反步技术,文献[20-21]中研究了相对度为2的非线性系统的漏斗控制问题,文献[22-24]研究了相对度大于2的非线性系统的漏斗控制问题。然而,到目前为止,对于大规模非线性系统的漏斗控制的研究还很少。因此,对于不确定大规模非线性系统,如何设计控制器,使得跟踪误差不仅在预定义的漏斗内演化,而且与初始值无关,是一个值得解决的问题。
基于上述讨论,本文研究了一类互联大规模非线性系统的自适应事件触发漏斗控制问题。本文的主要贡献如下:
(1) 与文献[15, 17-18]中基于PPF的预定义性能控制相比,本文放宽了对初始条件的约束,所提出的漏斗函数的初始值是无穷大而不是一个有界常数。
(2) 与文献[24]的研究相比,本文提出了一种新的障碍Lyapunov函数来处理漏斗约束,并确保系统的输出总是在漏斗中演化。
(3) 与文献[19-23]结果相比,利用神经网络系统、事件触发机制和反步技术设计了有限时间事件触发控制器,该控制器能有效降低控制器与执行器之间的传输负担,并大大节省通信资源。
1 问题陈述和准备工作 1.1 问题陈述本文考虑了一类具有严格反馈结构的大规模非线性系统,它由多个子系统组成,第
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot {{x}}}_{ij}} = {{{x}}_{ij + 1}} + {f_{ij}}({{{{{{{{\boldsymbol{\bar x}}}}}}_{{{{ij}}}}}}}) + {h_{ij}}({{\boldsymbol{\bar y}}})} \\ {{{\dot {{{{{{x}}}}}}}_{i{n_i}}} = {u_i} + {f_{i{n_i}}}({{\boldsymbol{{{{{{\boldsymbol{\bar x}}}}}}_{\boldsymbol{{{i}{{n}_{i}}}}}}}}) + {h_{i{n_i}}}({{\boldsymbol{\bar y}}})} \\ {{y_i} = {x_{i1}}} \end{array}} \right. $ | (1) |
式中:
假设1 参考信号
假设2 非线性函数
| $ \left|h_{i j}(\bar{{\boldsymbol{y}}})\right| \leqslant \sum\limits_{l=1}^{N} \rho_{i j l} \hbar_{i j l}\left(y_{l}\right) $ | (2) |
式中:
引理1[4] 设
| $ f({\boldsymbol{X}}) = {{\boldsymbol{W}}^{*{\rm{T}}}}{\boldsymbol{S}}({\boldsymbol{X}}) + \delta ({\boldsymbol{X}}) $ | (3) |
式中:
| $ {{\boldsymbol{W}}^*} = {\rm{arg}}\mathop {{\rm{min}}}\limits_{{\boldsymbol{W}}\in {\Lambda _X}} \left\{ {\mathop {{\rm{sup}}}\limits_{{\boldsymbol{X}} \in {\Lambda _X}} \left| {f({\boldsymbol{X}}) - {{\boldsymbol{W}}^{\rm{T}}}{\boldsymbol{S}}({\boldsymbol{X}})} \right|} \right\} $ |
引理2[25] 对于神经网络的径向基函数向量
| $ {{\boldsymbol{S}}}^{{\rm{T}}}({{\boldsymbol{\overline{{\boldsymbol{z}}}}}}_{{\boldsymbol{n}}}){\boldsymbol{S}}({{{\overline{{\boldsymbol{z}}}}}}_{{\boldsymbol{n}}})\leqslant{{\boldsymbol{S}}}^{{\rm{T}}}({{\boldsymbol{\overline{{\boldsymbol{z}}}}}}_{k}){\boldsymbol{S}}({{\boldsymbol{\overline{{\boldsymbol{z}}}}}}_{k}) $ | (4) |
式中:
基于上述假设,本文的控制目标是为大规模非线性系统(1)设计一个事件触发控制器使得:
(1) 闭环系统的所有信号都是有界的。
(2) 跟踪误差总是在预定的性能漏斗中演化。
1.3 漏斗性能首先介绍如下的漏斗性能:
| $ {F_{{\phi _i}}}: = \{ (t,{e_i}) \in {{\bf{R}}_ + } \times {{\bf{R}}^N}\mid {\phi _i}(t)\parallel {e_i}(t)\parallel < 1\} $ | (5) |
式中
(1)
(2)
(3)
备注:如果跟踪误差能够在以下的性能区域内发展,则表明所提出的控制器可以实现第二个控制目标
| $ {F_{{\phi _i}}}: = \{ (t,{e_i}) \in {{\bf{R}}_ + } \times {{\bf{R}}^N}| - {I_i}(t) < {e_i}(t) < {I_i}(t)\} $ |
式中:
|
图 1 跟踪误差预定性能示意图 Figure 1 A diagram of the prescribed tracking behavior. |
为保证跟踪误差始终在漏斗内演化,定义障碍函数为
| $ {\zeta _i}(t) = \dfrac{{{s_i}(t)}}{{1 - s_i^2(t)}} $ | (6) |
式中:
| $ {s_i}(0) = {\phi _i}(0){e_i}(0) = 0 \in ( - 1,1) $ | (7) |
从
这意味着对于跟踪误差的任意初值
在本节中,将给出事件触发控制器的设计过程。定义误差变换为
| $ \left\{ {\begin{array}{*{20}{l}} {{{{z}}_{i1}} = {\zeta _i}} \\ {{{{z}}_{ij}} = {x_{ij}} - \xi _{ij - 1}^*} \end{array}} \right. $ | (8) |
式中:
| $ {\varepsilon _{ij - 1}}\dot \xi _{ij - 1}^*(t) + \xi _{ij - 1}^*(t) = {\alpha _{ij - 1}}(t) $ | (9) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot \varsigma }_{i1}} = - {c_{i1}}{\varsigma _{i1}} + {\varsigma _{i2}} + \xi _{i1}^* - {\alpha _{i1}}} \\ {{{\dot \varsigma }_{ij}} = - {c_{ij}}{\varsigma _{ij}} + {\varsigma _{ij + 1}} + \xi _{ij}^* - {\alpha _{ij}} - {\varsigma _{ij - 1}}} \\ {{{\dot \varsigma }_{i{n_i}}} = - {\varsigma _{i{n_i} - 1}}} \end{array}} \right. $ | (10) |
式中:
| $ {\zeta }_{i}^{*}={\rm{max}}{\boldsymbol{\{}}\Vert {{\boldsymbol{W}}}_{i1}^{*}{\Vert }^{2},\cdots ,\Vert {{\boldsymbol{W}}}_{i{n}_{i}}^{*}{\Vert }^{2}{\boldsymbol{\}}} $ | (11) |
第
| $ {\dot \vartheta _{i1}}(t) = {\mu _{i2}} + {\mu _{i1}}{\phi _i}({x_{i2}} + {f_{i1}}({\bar x_{i1}}) + {h_{i1}}(\bar y) - {\dot y_{{d_i}}}) - {\dot \varsigma _{i1}} $ | (12) |
式中:
| $ \begin{array}{l}{\mu }_{i1}=\dfrac{1+{s}_{i}^{2}}{{(1-{s}_{i}^{2})}^{2}}\\ {\mu }_{i2}=\dfrac{1+{s}_{i}^{2}}{{(1-{s}_{i}^{2})}^{2}}{\dot{\phi }}_{i}{e}_{i}\end{array} $ |
选择李雅普诺夫候选函数
| $ {V_{i1}} = \dfrac{1}{2}\vartheta _{i1}^2 + \dfrac{1}{{2{r_i}}}\tilde \zeta _i^2 $ | (13) |
式中:
| $ \begin{split} {{\dot V}_{i1}} = & {\vartheta _{i1}}({\vartheta _{i2}} + {\alpha _{i1}} + {\mu _{i1}}{\phi _i}{h_{i1}}(\bar {\boldsymbol{y}}) + {g_{i1}}({{\boldsymbol{X}}_{i1}}) + \hfill \\ & {c_{i1}}{\varsigma _{i1}}) - \dfrac{1}{{{r_i}}}{{\tilde \zeta }_i}{{\dot \zeta }_i} - {\rho _i}{\vartheta _{i1}}{M_i} \end{split} $ | (14) |
式中:
| $ {\vartheta }_{i1}{\mu }_{i1}{\phi }_{i}{h}_{i1}(\overline{{\boldsymbol{y}}}) \leqslant \dfrac{1}{4}{\mu }_{i1}^{2}{\phi }_{i}^{2}{\vartheta }_{i1}^{2}+{\displaystyle \sum\limits _{l=1}^{N}{\rho }_{i1l}}{\hbar }_{i1l}({y}_{l}) $ | (15) |
由于
| $ {g_{i1}}({{\boldsymbol{X}}_{i1}}) = {\boldsymbol{W}}_{i1}^{ * {\rm{T}}}{{\boldsymbol{S}}_{i1}}({{\boldsymbol{X}}_{i1}}) + {\delta _{i1}}({{\boldsymbol{X}}_{i1}}) $ | (16) |
式中:
| $ \begin{split} &{\vartheta }_{i1}{g}_{i1}({{\boldsymbol{X}}}_{i1})\leqslant\dfrac{1}{2{a}_{i1}^{2}}{\vartheta }_{i1}^{2}{\zeta }_{i}^{*}{{\boldsymbol{S}}}_{i1}^{{\rm{T}}}{{\boldsymbol{S}}}_{i1}+\dfrac{1}{2}{a}_{i1}^{2}+\\ & \dfrac{1}{2}{\vartheta }_{i1}^{2}+\dfrac{1}{2}{\overline{\delta }}_{i1}^{2} \end{split} $ | (17) |
式中:
| $ \begin{split} &{\dot{V}}_{i1}\leqslant{\vartheta }_{i1}({\vartheta }_{i2}+{\alpha }_{i1}+\dfrac{1}{2{a}_{i1}^{2}}{\vartheta }_{i1}{\zeta }_{i}{{\boldsymbol{S}}}_{i1}^{{\rm{T}}}{{\boldsymbol{S}}}+\dfrac{1}{4}{\vartheta }_{i1}{\phi }_{i}^{2}{\mu }_{i1}^{2}+\\& {c}_{i1}{\varsigma }_{i1}+\dfrac{1}{2}{\vartheta }_{i1})+\dfrac{1}{{r}_{i}}{\tilde{\zeta }}_{i}(\dfrac{{r}_{i}}{2{a}_{i1}^{2}}{\vartheta }_{i1}^{2}{{\boldsymbol{S}}}_{i1}^{{\rm{T}}}{{\boldsymbol{S}}}-{\dot{\zeta }}_{i})-\\& {\rho }_{i}{\vartheta }_{i1}{M}_{i}+\dfrac{1}{2}{\overline{\delta }}_{i1}^{2}+\dfrac{1}{2}{a}_{i1}^{2}+{\displaystyle \sum\limits _{l=1}^{N}{\rho }_{i1l}}{\hbar }_{i1l}({y}_{l}) \end{split} $ | (18) |
此时,将虚拟控制器设计为如式(19)所示的形式。
| $ {\alpha _{i1}} = - {c_{i1}}{z_{i1}} - \dfrac{1}{{2a_{i1}^2}}{\vartheta _{i1}}{\zeta _i}{\boldsymbol{S}}_{i1}^{\rm{T}}{{\boldsymbol{S}}_{i1}} - \dfrac{1}{2}{\vartheta _{i1}} - \dfrac{1}{4}{\vartheta _{i1}}\phi _i^2\mu _{i1}^2 $ | (19) |
式中:
| $ \begin{split} &{\dot{V}}_{i1}\leqslant-{c}_{i1}{\vartheta }_{i1}^{2}+{\vartheta }_{i1}{\vartheta }_{i2}+\dfrac{1}{2}{a}_{i1}^{2}+\dfrac{1}{2}{\overline{\delta }}_{i1}^{2}+\\& {\displaystyle \sum\limits _{l=1}^{N}{\rho }_{i1l}}{\hslash }_{i1l}({y}_{l})-{\rho }_{i}{\vartheta }_{i1}{M}_{i}+\\ & \dfrac{1}{{r}_{i}}{\tilde{\zeta }}_{i}(\dfrac{{r}_{i}}{2{a}_{i1}^{2}}{\vartheta }_{i1}^2{{\boldsymbol{S}}}_{i1}^{\text{T}}{{\boldsymbol{S}}}_{i1}-{\dot{\zeta }}_{i}) \end{split} $ | (20) |
第
| $ \begin{split} {{\dot \vartheta }_{ij}}(t) = & {\vartheta _{ij + 1}} + {\varsigma _{ij - 1}} + {f_{ij}}({{\bar {\boldsymbol{x}}}_{ij}}) + {h_{ij}}(\bar {\boldsymbol{y}}) + \hfill \\ & {c_{ij}}{\varsigma _{ij}} + {\alpha _{ij}} - \dot \xi _{i,j - 1}^* \end{split} $ | (21) |
选择式(22)所示的李雅普诺夫候选函数
| $ {V_{ij}} = {V_{ij - 1}} + \dfrac{1}{2}\vartheta _{ij}^2 $ | (22) |
对
| $ \begin{split} {{\dot V}_{ij}} = & {{\dot V}_{ij - 1}} + {\vartheta _{ij}}({\vartheta _{ij + 1}} + {\alpha _{ij}} + {h_{ij}}(\bar {\boldsymbol{y}}) + \hfill \\ & {g_{ij}}({{\boldsymbol{X}}_{ij}}) + {\varsigma _{ij - 1}} + {c_{ij}}{\varsigma _{ij }}) \end{split} $ | (23) |
式中:
| $ {\vartheta }_{ij}{h}_{ij}(\overline{{\boldsymbol{y}}})\leqslant\dfrac{1}{4}{\vartheta }_{ij}^{2}+{\displaystyle \sum\limits _{l=1}^{N}{\rho }_{ijl}}{\hbar }_{ijl}({y}_{l}) $ | (24) |
由于
| $ {g_{ij}}({{\boldsymbol{X}}_{ij}}) = {\boldsymbol{W}}_{ij}^{ * {\rm{T}}}{{\boldsymbol{S}}_{ij}}({{\boldsymbol{X}}_{ij}}) + {\delta _{ij}}({{\boldsymbol{X}}_{ij}}) $ | (25) |
式中:
| $ {\vartheta }_{ij}{g}_{ij}({{\boldsymbol{X}}}_{ij})\leqslant\dfrac{1}{2{a}_{ij}^{2}}{\vartheta }_{ij}^{2}{\zeta }_{i}^{*}{{\boldsymbol{S}}}_{ij}^{{\rm{T}}}{{\boldsymbol{S}}}_{ij}+\dfrac{1}{2}{a}_{ij}^{2}+\dfrac{1}{2}{\vartheta }_{ij}^{2}+\dfrac{1}{2}{\overline{\delta }}_{ij}^{2} $ | (26) |
式中:
| $ {\alpha _{ij}} = - {c_{ij}}{{{z}}_{ij}} - \dfrac{1}{{2a_{ij}^2}}{\vartheta _{ij}}{\zeta _i}{\boldsymbol{S}}_{ij}^{\rm{T}}{{\boldsymbol{S}}_{ij}} - {{{z}}_{ij - 1}} - \dfrac{3}{4}{\vartheta _{ij}} $ | (27) |
式中:
| $ \begin{split} & {\dot{V}}_{ij}\leqslant-{\displaystyle \sum\limits _{m=1}^{j}{c}_{im}}{\vartheta }_{im}^{2}+{\vartheta }_{ij}{\vartheta }_{ij+1}+{\displaystyle \sum\limits _{m=1}^{j}{\displaystyle \sum\limits _{l=1}^{N}{\rho }_{iml}}}{\hbar }_{iml}({y}_{l})-\\& {\rho }_{i}{\vartheta }_{i1}{M}_{i}+{\displaystyle \sum\limits _{m=1}^{j}(}\dfrac{1}{2}{a}_{im}^{2}+\dfrac{1}{2}{\overline{\delta }}_{im}^{2})+\\& \dfrac{{\tilde{\zeta }}_{i}}{{r}_{i}}\left({\displaystyle \sum\limits _{m=1}^{j}\dfrac{{r}_{i}}{2{a}_{im}^{2}}}{\vartheta }_{im}^{2}{{\boldsymbol{S}}}_{im}^{{\rm{T}}}{{\boldsymbol{S}}}_{im}-{\dot{\zeta }}_{i}\right) \end{split} $ | (28) |
第
| $ \left\{ \begin{array}{l} {\omega }_{i}(t)=-(1+{k}_{i})\left({\alpha }_{i{n}_{i}}\mathrm{tanh}\dfrac{{\vartheta }_{i{n}_{i}}{\alpha }_{i{n}_{i}}}{{\epsilon_{i}}}+{\overline{\kappa }}_{i}\mathrm{tanh}\dfrac{{\vartheta }_{i{n}_{i}}{\overline{\kappa }}_{i}}{{\epsilon_{i}}}\right)\\ {u}_{i}(t)={\omega }_{i}({t}_{k}),\forall t\in [{t}_{k},{t}_{k+1}) \end{array} \right.$ | (29) |
事件触发机制为
| $ t_{k+1}=\inf \left\{t>t_{k}|| \eta_{i}\left|\geqslant k_{i}\right| u_{i} \mid+d_{i}\right\}$ | (30) |
式中:
| $ {\omega _i}(t) = (1 + {k_i}{\lambda _{{i_1}}}(t)){u_i}(t) + {\lambda _{{i_2}}}(t){d_i} $ | (31) |
式中:
| $ {u_i}(t) = \dfrac{{{\omega _i}(t)}}{{1 + {k_i}{\lambda _{{i_1}}}(t)}} - \dfrac{{{\lambda _{{i_2}}}(t){d_i}}}{{1 + {k_i}{\lambda _{{i_1}}}(t)}} $ | (32) |
由式(10)的定义,并对
| $ \dot{\vartheta}_{i n_{i}}=u_{i}+\varsigma_{i n_{i}-1}+f_{i n_{i}}\left(\overline{\boldsymbol{x}}_{i j}\right)+h_{i n_{i}}(\overline{\boldsymbol{y}})-\dot{\xi}_{i n_{i}-1}^{*} $ | (33) |
选择李雅普诺夫候选函数
| $ {V_{i{n_i}}} = {V_{i{n_i} - 1}} + \dfrac{1}{2}\vartheta _{i{n_i}}^2 $ | (34) |
| $ \begin{split} \dot{V}_{i n_{i}}= & \dot{V}_{i n_{i}-1}+\vartheta_{i n_{i}}\left(\dfrac{\omega_{i}(t)}{1+k_{i} \lambda_{i_{1}}(t)}-\dfrac{\lambda_{i_{2}}(t) d_{i}}{1+k_{i} \lambda_{i_{1}}(t)}+\right. \\ & \Bigg.\varsigma_{i n_{i}-1}+g_{i n_{i}}\left(\boldsymbol{X}_{i n_{i}}\right)+h_{i n_{i}}(\overline{\boldsymbol{y}})\Bigg) \end{split} $ | (35) |
式中:
| $ \left\{ \begin{array}{l} {\vartheta }_{i{n}_{i}}\dfrac{{\omega }_{i}(t)}{1+{k}_{i}{\lambda }_{{i}_{1}}(t)}\leqslant{\vartheta }_{i{n}_{i}}\dfrac{{\omega }_{i}(t)}{1+{k}_{i}}\\ \left|\dfrac{{\lambda }_{{i}_{2}}(t){d}_{i}}{1+{k}_{i}{\lambda }_{{i}_{1}}(t)}\right|\leqslant\dfrac{{d}_{i}}{1-{k}_{i}} \end{array} \right.$ | (36) |
根据文献[12],有不等式(37)成立。
| $ 0\leqslant\left|{x}_{i}\right|-{x}_{i}\mathrm{tanh}\left(\dfrac{{x}_{i}}{\epsilon_{i}}\right)\leqslant0.278\;5{\epsilon_{i}} $ | (37) |
式中:
| $ \begin{split} & {\dot{V}}_{i{n}_{i}}= {\dot{V}}_{i{n}_{i}-1}+{\vartheta }_{i{n}_{i}}{\alpha }_{i{n}_{i}}+{\vartheta }_{i{n}_{i}}({\varsigma }_{i{n}_{i}-1}+{h}_{i{n}_{i}}(\overline{{\boldsymbol{y}}})+\\ & {g}_{i{n}_{i}}({{\boldsymbol{X}}}_{i{n}_{i}}))+0.557{\epsilon_{i}} \end{split} $ | (38) |
利用杨氏不等式,可以得到
| $ {\vartheta }_{i{n}_{i}}{h}_{i{n}_{i}}(\overline{{\boldsymbol{y}}})\leqslant\dfrac{1}{4}{\vartheta }_{i{n}_{i}}^{2}+{\displaystyle \sum\limits _{l=1}^{N}{\rho }_{i{n}_{i}l}}{\hbar }_{i{n}_{i}l}({y}_{l}) $ | (39) |
根据引理1,利用神经网络来逼近未知的非线性函数
| $ {g_{i{n_i}}}({{\boldsymbol{X}}_{i{n_i}}}) = {\boldsymbol{W}}_{i{n_i}}^{ * {\rm{T}}}{S_{i{n_i}}}({{\boldsymbol{X}}_{i{n_i}}}) + {\delta _{i{n_i}}}({{\boldsymbol{X}}_{i{n_i}}}) $ | (40) |
式中:
| $ {\vartheta }_{i{n}_{i}}{g}_{i{n}_{i}}({{\boldsymbol{X}}}_{i{n}_{i}})\leqslant \dfrac{1}{2{a}_{i{n}_{i}}^{2}}{\vartheta }_{i{n}_{i}}^{2}{\zeta }_{i}^{*}{{\boldsymbol{S}}}_{i{n}_{i}}^{{\rm{T}}}{{\boldsymbol{S}}}_{i{n}_{i}}+\frac{1}{2}{a}_{i{n}_{i}}^{2}+\dfrac{1}{2}{\vartheta }_{i{n}_{i}}^{2}+\dfrac{1}{2}{\overline{\delta }}_{i{n}_{i}}^{2} $ | (41) |
式中:
| $ \begin{split} & {\dot{V}}_{i{n}_{i}}\leqslant{\dot{V}}_{i{n}_{i}-1}+{\vartheta }_{i{n}_{i}}\left({\alpha }_{i{n}_{i}}+\dfrac{1}{2{a}_{i{n}_{i}}^{2}}{\vartheta }_{i{n}_{i}}{\zeta }_{i}{{\boldsymbol{S}}}_{i{n}_{i}}^{{\rm{T}}}{{\boldsymbol{S}}}_{i{n}_{i}}+\dfrac{3}{4}{\vartheta }_{i{n}_{i}}+\right.\\ & \Bigg. {\varsigma }_{i{n}_{i}-1}\Bigg)+\dfrac{1}{2{a}_{i{n}_{i}}^{2}}{\vartheta }_{i{n}_{i}}^{2}{\tilde{\zeta }}_{i}{{\boldsymbol{S}}}_{i{n}_{i}}^{{\rm{T}}}{{\boldsymbol{S}}}_{i{n}_{i}}+\dfrac{1}{2}{a}_{i{n}_{i}}^{2}+\dfrac{1}{2}{\overline{\delta }}_{i{n}_{i}}^{2}+\\ & {\displaystyle \sum\limits _{l=1}^{N}{\rho }_{i{n}_{i}l}}{\hbar }_{i{n}_{i}l}({y}_{l})+0.557\epsilon_{i} \end{split} $ | (42) |
将虚拟控制器
| $ {\alpha _{i{n_i}}} = - {c_{i{n_i}}}{\vartheta _{i{n_i}}} - \dfrac{1}{{2a_{i{n_i}}^2}}{\vartheta _{i{n_i}}}{\zeta _i}{\boldsymbol{S}}_{i{n_i}}^{\rm{T}}{{\boldsymbol{S}}_{i{n_i}}} - {{{z}}_{i{n_i} - 1}} - \dfrac{3}{4}{\vartheta _{i{n_i}}} $ | (43) |
| $ {\dot \zeta _i} = \sum\limits_{m = 1}^{{n_i}} {\dfrac{{{r_i}}}{{2a_{im}^2}}} \vartheta _{im}^2{\boldsymbol{S}}_{im}^{\rm{T}}{{\boldsymbol{S}}_{im}} - {\tau _i}{\zeta _i} $ | (44) |
式中:
| $ \begin{split} & {\dot{V}}_{i{n}_{i}} \leqslant -{\displaystyle \sum\limits _{m=1}^{{n}_{i}}{c}_{im}}{\vartheta }_{im}^{2}+{\displaystyle \sum\limits _{m=1}^{{n}_{i}}{\displaystyle \sum\limits _{l=1}^{N}{\rho }_{iml}}}{\hbar }_{iml}({y}_{l})+\dfrac{{\tau }_{i}}{{r}_{i}}{\tilde{\zeta }}_{i}{\widehat{\zeta }}_{i}-\\& {\rho }_{i}{\vartheta }_{i1}{M}_{i}+{\displaystyle \sum\limits _{m=1}^{{n}_{i}}}\left(\dfrac{1}{2}{a}_{im}^{2}+\dfrac{1}{2}{\overline{\delta }}_{im}^{2}\right)+0.557\epsilon_{i} \end{split} $ | (45) |
定理1 考虑一类具有性能约束的大规模非线性系统(1),虚拟控制器(27),事件触发控制器(29)和自适应律(44)。在假设1和假设2的条件下,可以保证以下性能:
(1) 系统的输出信号在一定误差内可以追踪到参考信号;
(2) 闭环系统中所有信号都是半全局一致有界;
(3) 跟踪误差的轨迹始终在漏斗内演变。
证明 可以通过以下4个步骤来证明定理的结果。
步骤1 对整个系统构造李雅普诺夫候选函数为
| $ V = \sum\limits_{i = 1}^N {{V_{i{n_i}}}} $ | (46) |
利用杨氏不等式,能得到
| $ \dfrac{{\tau }_{i}}{{r}_{i}}{\tilde{\zeta }}_{i}{\zeta }_{i}\leqslant-\dfrac{{\tau }_{i}}{2{r}_{i}}{\tilde{\zeta }}_{i}^{2}+\dfrac{{\tau }_{i}}{2{r}_{i}}{\zeta }_{i}^{*}{}^{2} $ | (47) |
将式(47)代入式(46),并对
| $ \begin{split} &\dot{V} \leqslant- \sum\limits_{i=1}^{N} \sum\limits_{m=1}^{n_{i}} c_{i m} \vartheta_{i m}^{2}- \sum\limits_{i=1}^{N} \dfrac{\tau_{i}}{2 r_{i}} \tilde{\zeta}_{i}^{2}+ \sum\limits_{i=1}^{N} \dfrac{\tau_{i}}{2 r_{i}} \zeta_{i}^{* 2}+ \\ &h_{i}+ \sum\limits_{i=1}^{N} \sum\limits_{m=1}^{n_{i}}\left(\dfrac{1}{2} \bar{\sigma}_{i m}^{2}+\dfrac{1}{2} a_{i m}^{2}\right)+ \sum\limits_{i=1}^{N} 0.557 \epsilon_{i} \end{split}$ | (48) |
式中:
| $ {h_i} = \sum\limits_{l = 1}^N {\sum\limits_{j = 1}^{{n_l}} {{\rho _{lji}}} } {\hbar _{lji}}({y_i}) - {\rho _i}{\vartheta _{i1}}{M_i} $ |
是互连的剩余项。由于
| $ {h}_{i}\leqslant{\rho }_{i}\dfrac{{q}_{i}-{\vartheta }_{i1}^{2}}{{\vartheta }_{i1}^{2}+{q}_{i}}{\displaystyle \sum\limits _{l=1}^{N}{\displaystyle \sum\limits _{j=1}^{{n}_{l}}{\hbar }_{lji}}}({y}_{i}) $ | (49) |
通过式(49),可以得到对任意的
| $ \begin{split} &\dot{V} \leqslant- \sum\limits_{i=1}^{N} \sum\limits_{m=1}^{n_{i}} c_{i m} \vartheta_{i m}^{2}- \sum\limits_{i=1}^{N} \dfrac{\tau_{i}}{2 r_{i}} \tilde{\zeta}_{i}^{2}+ \sum\limits_{i=1}^{N} \dfrac{\tau_{i}}{2 r_{i}} \zeta_{i}^{* 2}+\bar{h}_{i}+ \\ & \sum\limits_{i=1}^{N} \sum\limits_{m=1}^{n_{i}}\left(\dfrac{1}{2} \bar{\sigma}_{i m}^{2}+\dfrac{1}{2} a_{i m}^{2}\right)+ \sum\limits_{i=1}^{N} 0.557 \epsilon_{i} \leqslant d_{1} V+d_{2} \end{split} $ | (50) |
式中:
| $ {d_2} ={\displaystyle \sum\limits _{i=1}^{N}\dfrac{{\tau }_{i}}{2{r}_{i}}}{\zeta }_{i}^{*}{}^{2}+{\displaystyle \sum\limits _{i=1}^{N}0}.557{\epsilon_{i}}+{\displaystyle \sum\limits _{i=1}^{N}{\displaystyle \sum\limits _{m=1}^{{n}_{i}}\left(\dfrac{1}{2}{a}_{im}^{2}+\dfrac{1}{2}{\overline{\sigma }}_{im}^{2}\right)}}+{\overline{h}}_{i} $ |
对式(50)进行求解,可以得到不等式(51)成立。
| $ V(t)\leqslant \left(V(0)-\dfrac{{d}_{2}}{{d}_{1}}\right){{\rm{e}}}^{-{d}_{1}t}+\dfrac{{d}_{2}}{{d}_{1}} $ | (51) |
这意味着
步骤2 定义李雅普诺夫候选函数为
| $ {V_\varsigma } = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{n_i}} {\dfrac{1}{2}} \varsigma _{ij}^2} $ | (52) |
取
| $ {\dot V_\varsigma } = - \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{n_i} - 1} {({c_{ij}}} \varsigma _{ij}^2} + {\vartheta _{ij}}(\xi _{ij}^* - {\alpha _{ij}})) $ | (53) |
基于在文献[26]中的引理有
| $ {\dot {\boldsymbol{V}}_\varsigma } = - \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{n_i} - 1} {({c_{ij}}} \varsigma _{ij}^2} + {\vartheta _{ij}}{{\overline{\boldsymbol \omega }} _{ij}}) $ | (54) |
利用杨氏不等式,得到
| $ {\overline{ \omega }}_{ij}{\varsigma }_{ij}\leqslant \dfrac{1}{2}{\varsigma }_{ij}^{2}+\dfrac{1}{2}{\overline{\boldsymbol \omega }}_{ij}^{2} $ | (55) |
将式(55)代入式(54)得到
| $ \dot{V}_{\varsigma} \leqslant- \sum\limits_{i=1}^{N} \sum\limits_{j=1}^{n_{i}-1}\left(c_{i j}-\dfrac{1}{2}\right) \varsigma_{i j}^{2}+ \sum\limits_{i=1}^{N} \sum\limits_{j=1}^{n_{i}} \dfrac{1}{2} {\overline{ \omega }}_{i j}^{2} \leqslant -l_{1} V_{\varsigma}+l_{2} $ | (56) |
式中:
步骤3 这一步证明了闭环系统的跟踪误差始终在预定义的漏斗内演化。从
步骤4 下面证明芝诺现象并不发生,即存在一个
| $ \dfrac{{{{\rm{d}}}}}{{{{\rm{d}}}}{{t}}}\left|{\eta }_{i}\right|=\mathrm{{{sgn}}}({{{\eta}} }_{i}),\;\;{\dot{{{\eta}} }}_{i}\leqslant\left|{\dot{{{\omega}} }}_{i}\right| $ | (57) |
通过式(57),可以得到
本节用一个数值例子来证明所提出的控制方法的有效性。考虑如式(58)所示的大规模非线性系统:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_{ij}} = {x_{ij + 1}} + {f_{ij}}({{\bar {\boldsymbol{x}}}_{ij}}) + {h_{ij}}(\bar {\boldsymbol{y}})} \\ {{{\dot {{x}}}_{i{n_i}}} = {u_i} + {f_{i{n_i}}}({{\bar {\boldsymbol{x}}}_{i{n_i}}}) + {h_{i{n_i}}}(\bar {\boldsymbol{y}})} \\ {{y_i} = {x_{i1}}} \end{array}} \right. $ | (58) |
式中:
| $ {f_{11}} = 0.2{x_{11}}\sin ({x_{11}}) + {x_{12}} , {f_{12}} = {x_{12}}\sin ({x_{1,1}}) $ |
| $ {f_{22}} = 0.2{x_{22}}\sin ({x_{21}}) \text{,} {f_{21}} = {x_{21}}\cos ({x_{21}}) $ |
| $ {h_{11}} = 0.1{x_{11}}\sin ({x_{21}}) + {x_{22}} , {h_{12}} = 0.5{x_{12}}{x_{21}} $ |
| $ {h_{21}} = 0.2{x_{11}}{x_{22}} , {h_{22}} = 0.5(x_{11}^2 + x_{21}^2) + {x_{12}} $ |
初始值和其他需要设计的参数选择如下:
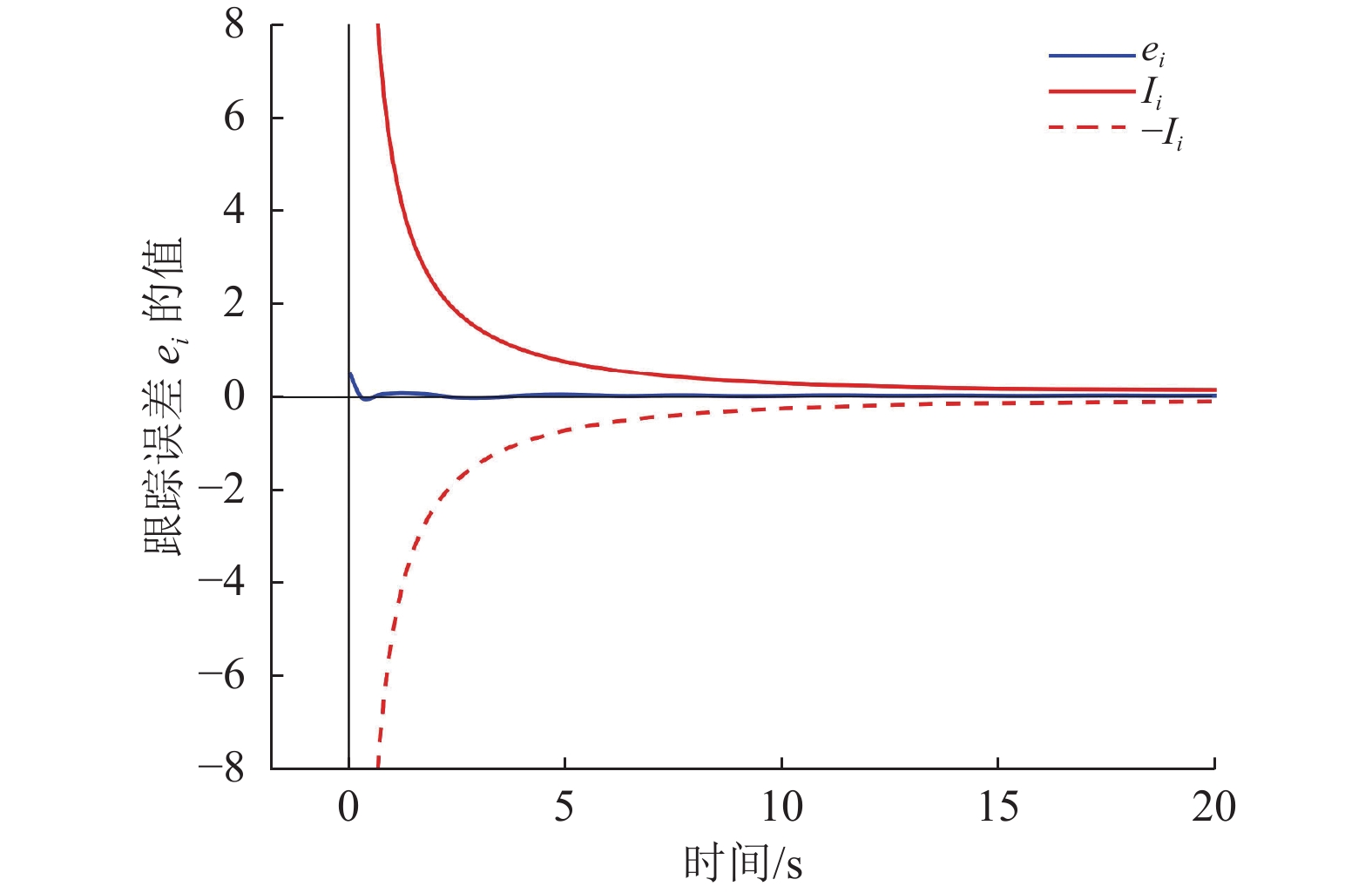
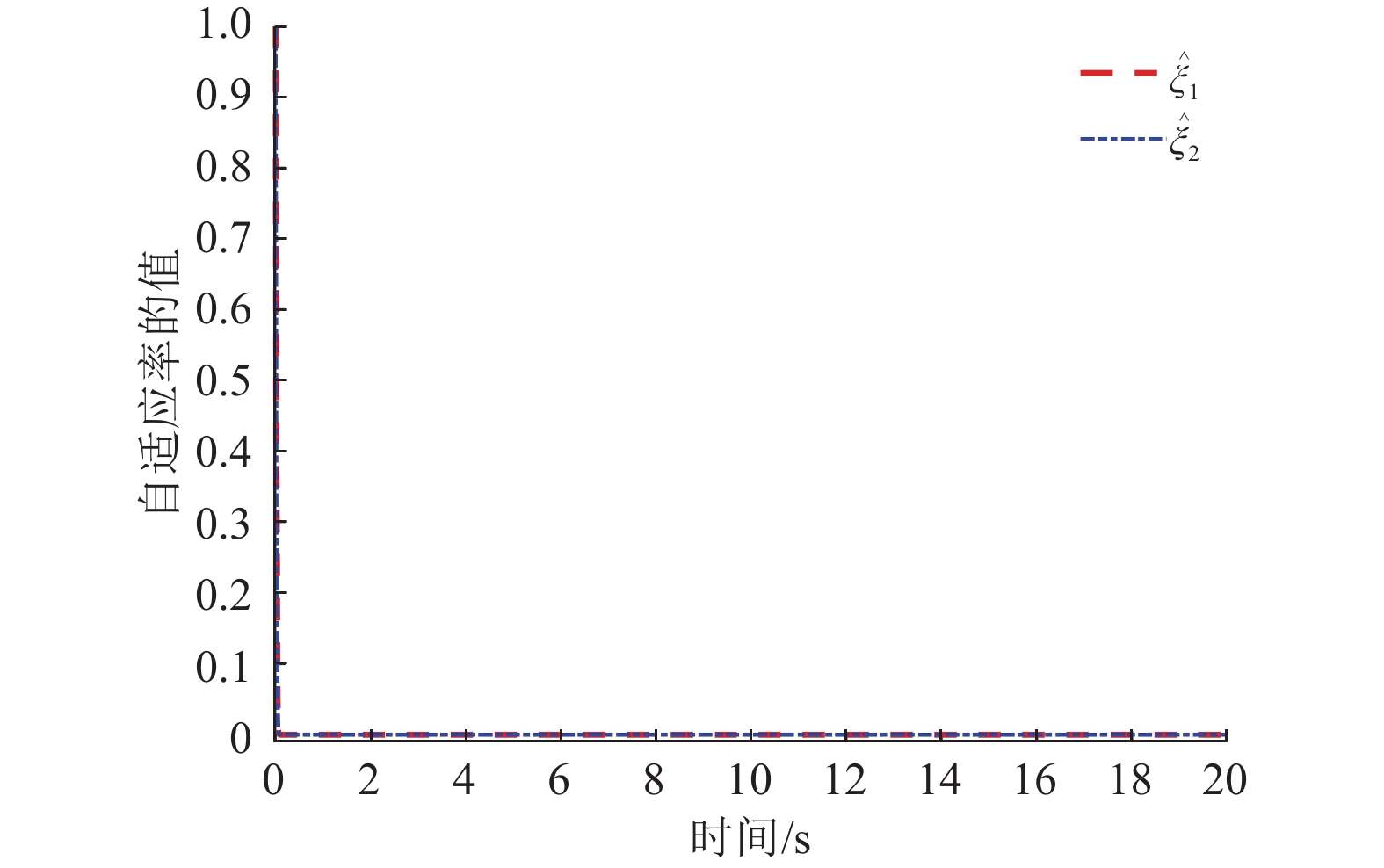
模拟结果如图2~图6所示。图2表示了系统的输出
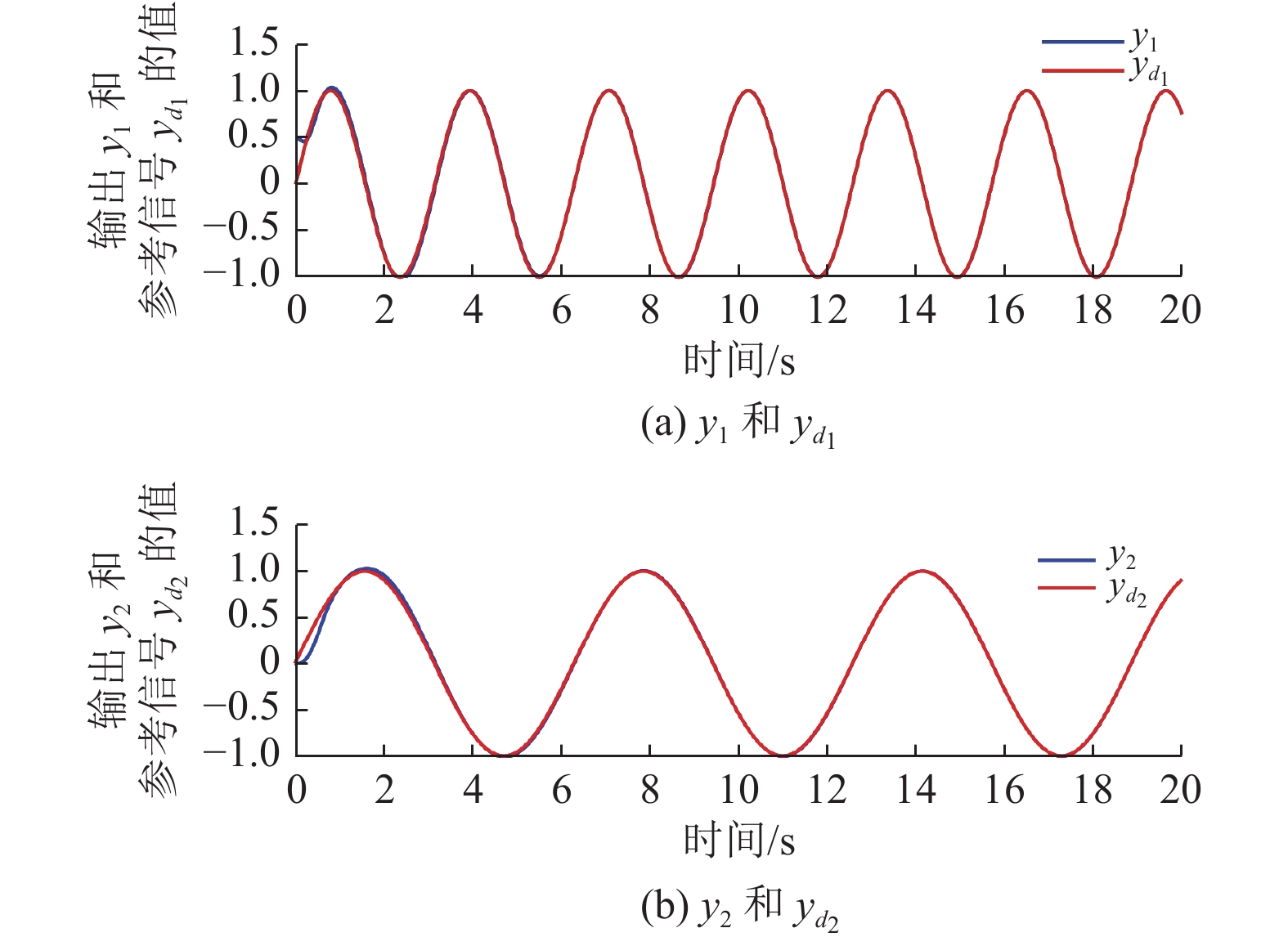
|
图 2 |
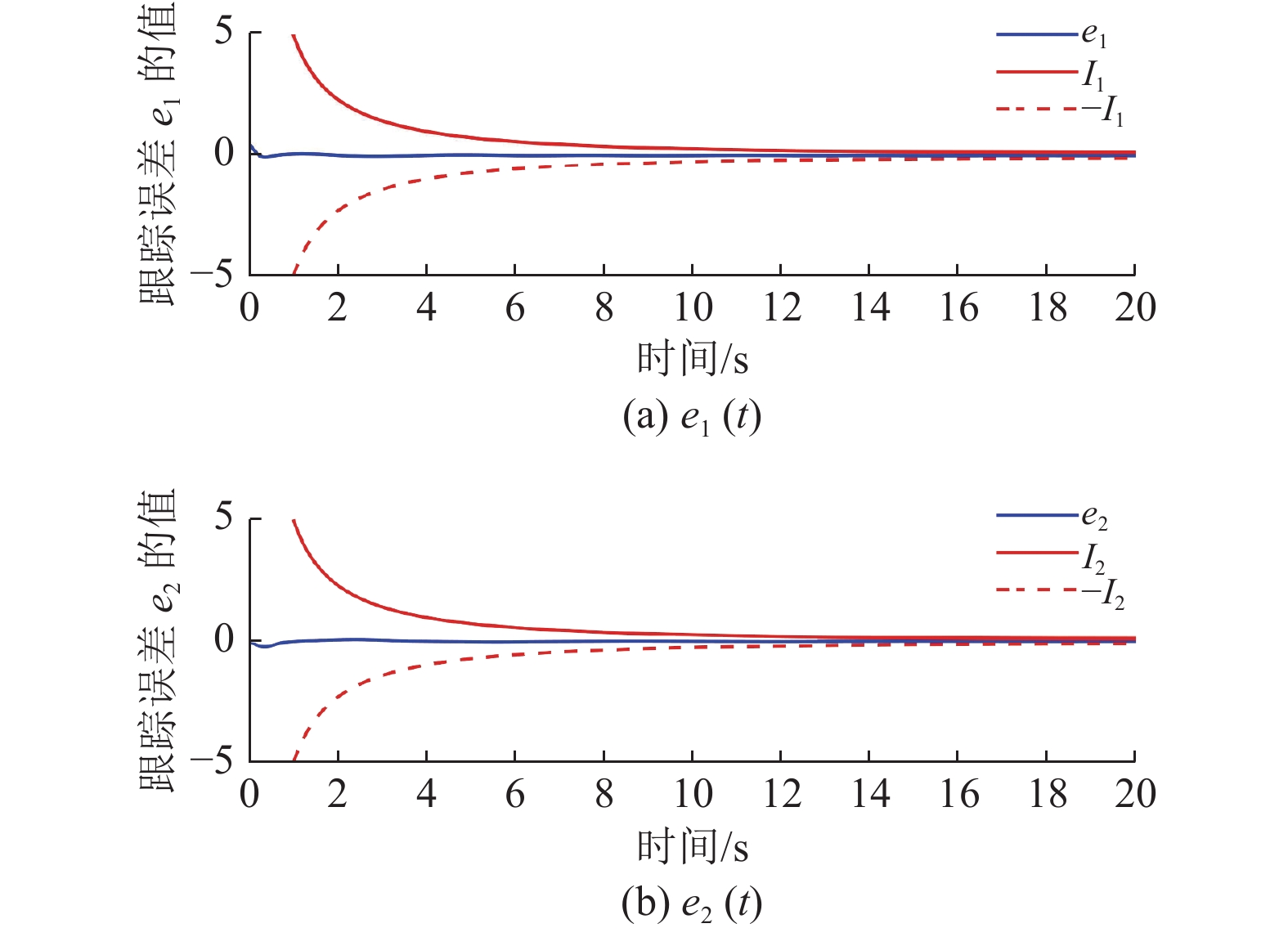
|
图 3 跟踪误差
|
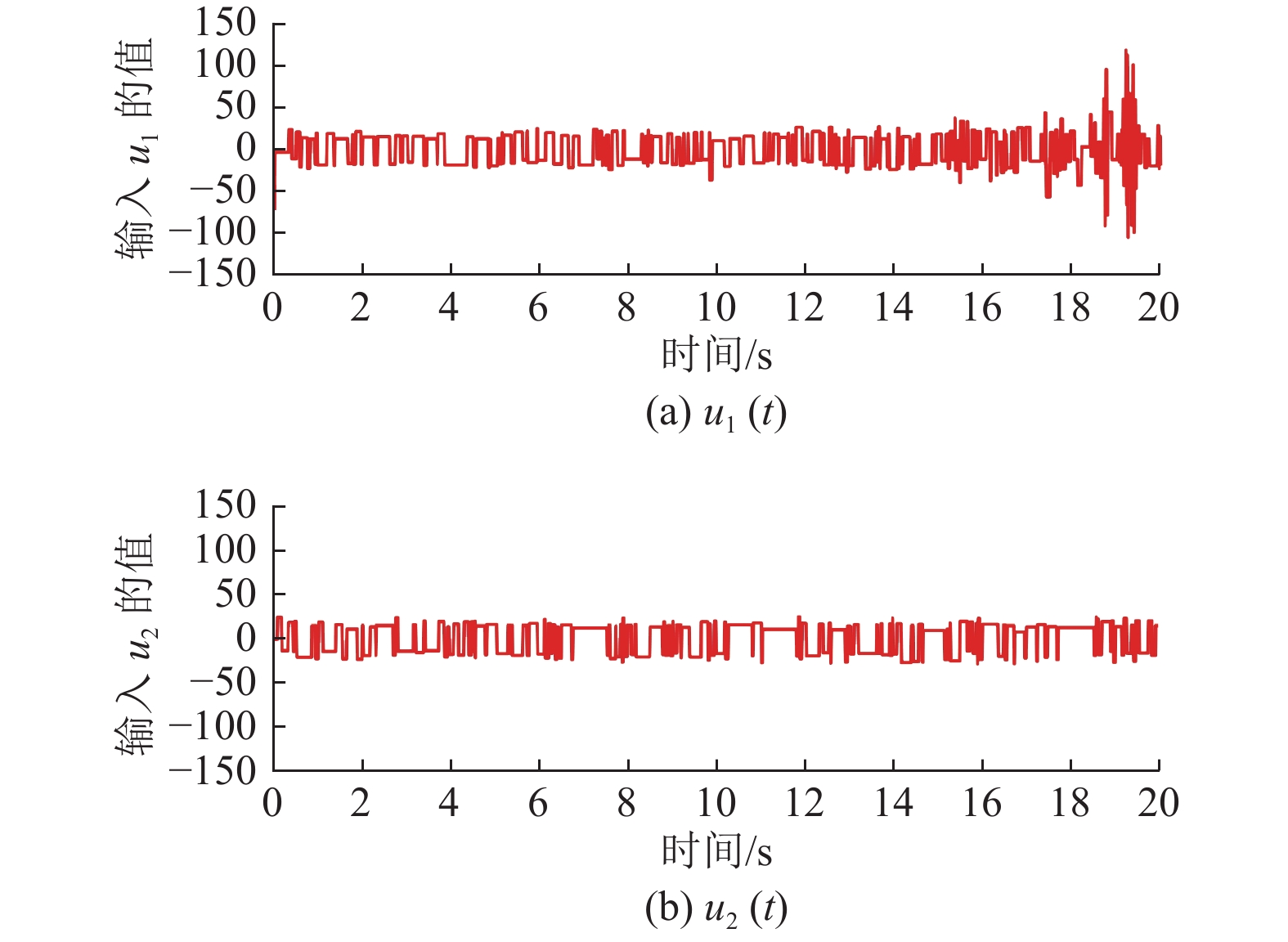
|
图 4 |
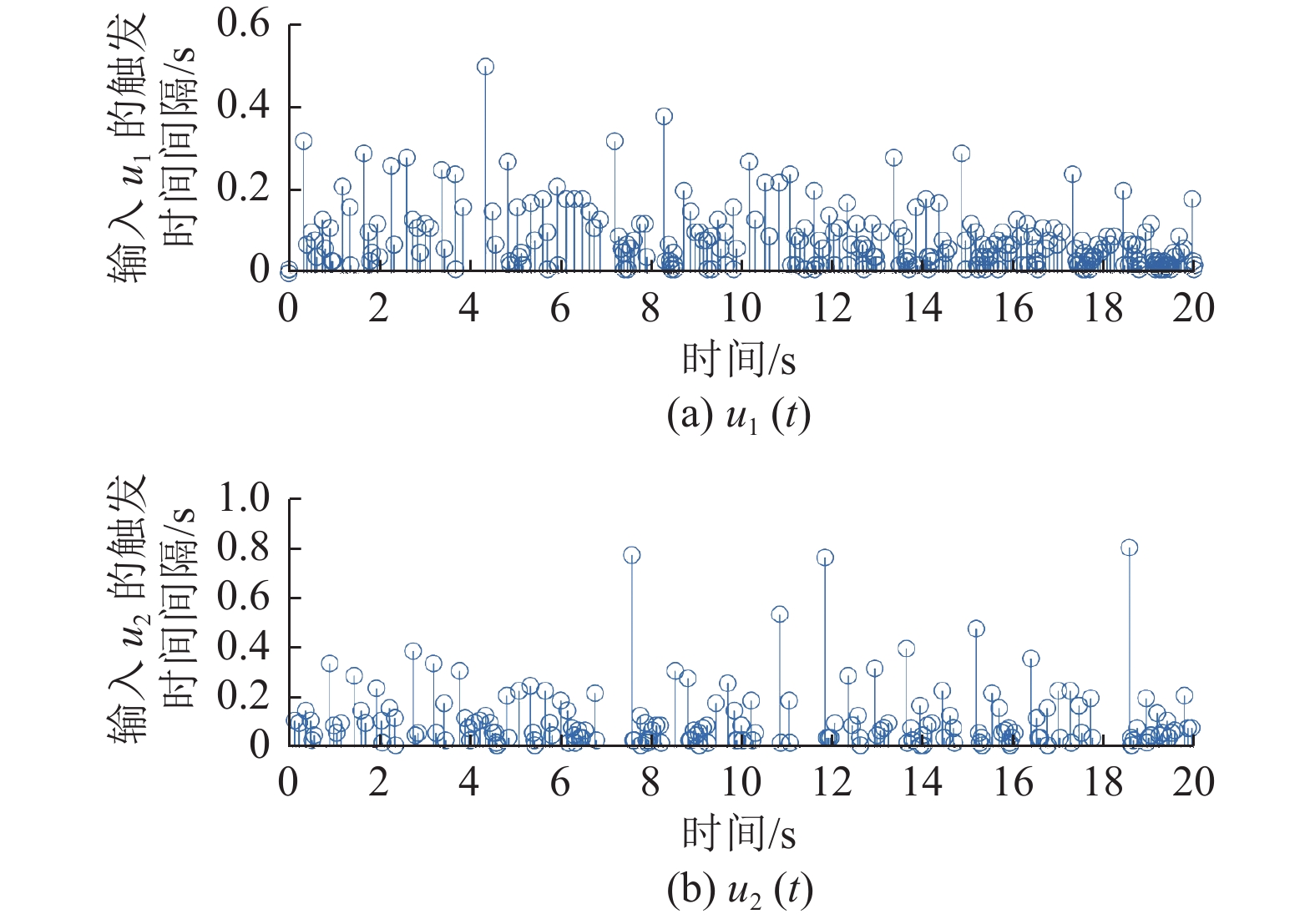
|
图 5 |
|
图 6 自适应率
|
本文研究了一类不确定大规模非线性系统的分散自适应事件触发漏斗控制问题。首先,通过障碍李雅普诺夫函数变换,递归构造了一种新的自适应分散漏斗控制器,以实现给定瞬态行为的输出跟踪。其次,为了解决控制器设计中的互联项问题,引入了一个辅助非线性函数。同时,将命令滤波技术应用到反步设计中,避免了反步过程中的“复杂性爆炸”问题。此外,还设计了一种事件触发机制,以减少控制器和执行器之间不必要的传输,从而提高资源效率。结果表明所提出的控制方案能保证闭环系统的所有信号都是有界的,并且跟踪误差总是在漏斗中演化。最后,通过一个数值系统验证了该控制方法的有效性。
| [1] |
JAIN S, KHORRAMI F. Decentralized adaptive output feedback design for large-scale nonlinear systems[J].
IEEE Transactions on Automatic Control, 1997, 42(5): 729-735.
DOI: 10.1109/9.580893. |
| [2] |
JIANG Z P. Decentralized and adaptive nonlinear tracking of large-scale systems via output feedback[J].
IEEE Transactions on Automatic Control, 2000, 45(11): 2122-2128.
DOI: 10.1109/9.887638. |
| [3] |
LIU S J, ZHANG J F, JIANG Z P. Decentralized adaptive output-feedback stabilization for large-scale stochastic nonlinear systems[J].
Automatica, 2007, 43(2): 238-251.
DOI: 10.1016/j.automatica.2006.08.028. |
| [4] |
TONG S C, LI Y M, LIU Y J. Observer-based adaptive neural networks control for large-scale interconnected systems with nonconstant control gains[J].
IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(4): 1575-1585.
DOI: 10.1109/TNNLS.2020.2985417. |
| [5] |
LI Y M, TONG S C. Adaptive neural networks prescribed performance control design for switched interconnected uncertain nonlinear systems[J].
IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(7): 3059-3068.
|
| [6] |
GONG J Y, JIANG B, SHEN Q K. Adaptive fault tolerant neural control for large-scale systems with actuator faults[J].
International Journal of Control, Automation and Systems, 2019, 17: 1421-1431.
DOI: 10.1007/s12555-018-0729-y. |
| [7] |
LI Y M, TONG S C. Fuzzy adaptive control design strategy of nonlinear switched large-scale systems[J].
IEEE Transaction on Systems, Man, and Cybernetics: Systems, 2018, 48(12): 2209-2218.
DOI: 10.1109/TSMC.2017.2703127. |
| [8] |
WANG H Q, PETER LIU X P, ZHAO X D, et al. Adaptive fuzzy finite-time control of nonlinear systems with actuator faults[J].
IEEE Transactions on Cybernetics, 2020, 50(5): 1786-1797.
DOI: 10.1109/TCYB.2019.2902868. |
| [9] |
SUI S, PHILIP CHEN L P, TONG S C. Event-trigger-based finite-time fuzzy adaptive control for stochastic nonlinear system with unmodeled dynamics[J].
IEEE Transactions on Fuzzy Systems, 2021, 29(7): 1914-1926.
DOI: 10.1109/TFUZZ.2020.2988849. |
| [10] |
LIANG H J, LIU G L, ZHANG G H, et al. Neural-network-based event-triggered adaptive control of nonaffine nonlinear multiagent systems with dynamic uncertainties[J].
IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(5): 2239-2250.
DOI: 10.1109/TNNLS.2020.3003950. |
| [11] |
HUANG J S, WANG W, WEN C Y, et al. Adaptive event-triggered control of nonlinear systems with controller and parameter estimator triggering[J].
IEEE Transactions on Automatic Control, 2020, 65(1): 318-324.
DOI: 10.1109/TAC.2019.2912517. |
| [12] |
MA H, LI H Y, LIANG H J, et al. Adaptive fuzzy event-triggered control for stochastic nonlinear systems with full state constraints and actuator faults[J].
IEEE Transactions on Fuzzy Systems, 2019, 27(11): 2242-2254.
DOI: 10.1109/TFUZZ.2019.2896843. |
| [13] |
WANG L J, PHILIP CHEN C L. Reduced-order observer-based dynamic event-triggered adaptive NN control for stochastic nonlinear systems subject to unknown input saturation[J].
IEEE Transactions on Neural Networks and Learning Systems, 2020, 32(4): 1678-1690.
|
| [14] |
JI Y H, ZHOU H L, ZONG Q. Decentralized adaptive event-triggered control for nonlinear interconnected systems in strict-feedback form[J].
International Journal of Control, Automation and Systems, 2020, 18(4): 980-990.
DOI: 10.1007/s12555-019-0461-2. |
| [15] |
BECHLIOULIS C P, ROVITHAKIS G A. Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance[J].
IEEE Transactions on Automatic Control, 2008, 53(9): 2090-2099.
DOI: 10.1109/TAC.2008.929402. |
| [16] |
ZHOU Q, LI H Y, WU C W, et al. Adaptive fuzzy control of nonlinear systems with unmodeled dynamics and input saturation using small-gain approach[J].
IEEE Transactions on Systems, Man, and Cybernetics:Systems, 2017, 47(8): 1979-1989.
DOI: 10.1109/TSMC.2016.2586108. |
| [17] |
LI Y M, SHAO X F, TONG S C. Adaptive fuzzy prescribed performance control of nontriangular structure nonlinear systems[J].
IEEE Transactions on Fuzzy Systems, 2020, 28(10): 2416-2426.
DOI: 10.1109/TFUZZ.2019.2937046. |
| [18] |
ZHANG L L, YANG G H. Adaptive fuzzy prescribed performance control of nonlinear systems with hysteretic actuator nonlinearity and faults[J].
IEEE Transactions on Systems, Man, and Cybernetics:Systems, 2018, 48(12): 2349-2358.
DOI: 10.1109/TSMC.2017.2707241. |
| [19] |
ILCHMANN A, RYAN E P, TOWNSEND P. Tracking with prescribed transient behaviour[J].
ESAIM:Control, Optimisation and Calculus of Variations, 2002, 7: 471-493.
DOI: 10.1051/cocv:2002064. |
| [20] |
HACKL M C, HOPFE N, ILCHMANN A, et al. Funnel control for systems with relative degree two[J].
SIAM Journal on Control and Optimization, 2013, 51(2): 965-995.
DOI: 10.1137/100799903. |
| [21] |
BERGER T, REIS T. Funnel control via funnel precompensator for minimum phase systems with relative degree two[J].
IEEE Transactions on Automatic Control, 2018, 63(7): 2264-2271.
DOI: 10.1109/TAC.2017.2761020. |
| [22] |
LIBERZON D, TRENN S. The bang-bang funnel controller for uncertain nonlinear systems with arbitrary relative degree[J].
IEEE Transactions on Automatic Control, 2013, 58(12): 3126-3141.
DOI: 10.1109/TAC.2013.2277631. |
| [23] |
CHOWDHURY D, KHALIL H K. Funnel control for nonlinear systems with arbitrary relative degree using high-gian observers[J].
Automatica, 2019, 105: 107-116.
DOI: 10.1016/j.automatica.2019.03.012. |
| [24] |
LIU Y H, SU C Y, LI H Y. Adaptive output feedback funnel control of uncertain nonlinear systems with arbitrary relative degree[J].
IEEE Transactions on Automatic Control, 2021, 66(6): 2854-2860.
DOI: 10.1109/TAC.2020.3012027. |
| [25] |
SUN Y M, CHEN B, LIN C, et al. Adaptive neural control for a class of stochastic nonlinear systems by backstepping approach[J].
Information Sciences, 2016, 369(10): 748-764.
|
| [26] |
FARRELL J A, POLYCARPOU M, SHARMA M, et al. Command filtered backstepping[J].
IEEE Transactions on Automatic Control, 2009, 54(6): 1391-1395.
DOI: 10.1109/TAC.2009.2015562. |
 2022, Vol. 39
2022, Vol. 39

