切换系统是由一系列的连续或离散的子系统以及协调这些子系统之间的切换规则组成的系统。在实际的生产活动中，许多控制系统常常同时含有连续时间动态和离散时间动态，而切换系统作为一种典型的混杂系统解决了许多相应的实际问题，如无人机^[1]、互联网流量分类^[2]、永磁磁通切换电机^[3]等。并且，与非切换系统的稳定性不同，切换系统不能直接继承子系统的稳定性。由于切换系统独特的稳定性特性，切换系统的稳定性问题一直是广受关注的重点内容。研究人员在对切换系统进行控制研究时，系统稳定性是亟需攻克的一大难关。目前，有关于切换系统的稳定性问题可以大致分为如下几种：切换系统在任意切换下的稳定性条件^[4-6]、切换系统在受限条件下的稳定性问题^[7-8]以及构造切换信号使得切换系统达到稳定^[9-10]。除此之外，对切换系统进行稳定性分析的方法主要有：共同Lyapunov函数方法、单Lyapunov函数方法以及多Lyapunov函数方法。值得注意的是，关于非线性切换系统的研究尚处于起步阶段。虽然近几年涌现了很多优秀的研究成果^[11-12]，但是由于实际生产活动中存在各种限制以及非线性本身固有的复杂性，为了提高控制品质，关于非线性切换系统的约束控制研究面临了很大的挑战性。

随着实际工程的发展，控制系统在工作时会受到各种限制。当系统违反这些限制而强行工作时，可能会给实际的生产活动带来巨大的财产损失，甚至威胁到生命安全。因此，在进行控制问题研究时，必须将系统的约束问题放在首要地位^[13]。尤其在非线性切换系统的控制研究中，为了使所设计的控制策略更好地解决实际问题，就必须考虑其约束控制问题。现有的约束控制研究成果主要涉及到两种类型：常数型约束^[14]和时变型约束^[15-16]。时变型约束条件随着时间的变化发生改变，控制算法的设计比常数型约束要更为复杂，设计出的控制方案更具实用性，为生产活动提供更为坚实的安全保障。在某种意义上来说，常数型约束也可以看成是特殊的时变型约束。目前，障碍Lyapunov函数是解决控制系统约束问题的一个十分有效的工具，常见的形式主要有以下几种：对数型^[17]、正切型^[18]和积分型^[19]。然而，除了约束控制问题外，随机特征也常存在于实际系统中，是影响非线性系统稳定性的一个重要因素。因此，在对非线性切换系统进行研究时，随机特征也是需要考虑的一个重要因素。

20世纪中期，为了提高系统的运行性能，保证系统的稳定性，随机稳定性的定义首次被提出^[20]。之后，一些经典的随机稳定性理论，如随机拉萨尔不变性原理^[21]和随机输入−状态稳定(Stochastic Input-to-State Stable)^[22]等也相继被提出。在过去的几十年中，随机非线性系统的控制得到了突飞猛进的发展^[23-24]。在研究过程中，为了补偿随机特征带来的不利影响，引入了ItÔ随机微分方程。与此同时，由于实际系统中常存在不确定性，采用精确的模型描述实际系统具有局限性。为了获得更好的控制效果，神经网络^[25-26]和模糊逻辑系统^[27-28]成为处理系统不确定性的重要工具，解决了很多控制难题。之后，有学者针对不确定非线性随机切换系统进行研究，涌现了很多成果，如不确定非线性随机切换系统的跟踪控制^[11-12]，不确定非线性随机切换系统的常数型输出约束控制^[29]以及不确定非线性随机切换系统的常数型全状态约束控制^[30]等。但是，上述成果未对不确定非线性随机切换系统进行时变型全状态约束控制研究。

基于上述成果的启发，为了消除随机因素对系统控制性能带来的不利影响和增强控制策略的实际应用价值，本文以不确定非线性随机切换系统为研究对象，采用神经网络处理系统中的不确定项，研究了其时变型全状态约束控制问题。基于任意切换规则，通过坐标变换技术，实现了对系统所有状态的时变型约束控制。最后，借助随机李雅普诺夫稳定性理论，实现系统稳定性分析。本文所做的主要贡献如下：

(1) 对不确定非线性随机切换系统进行全状态约束控制研究，要求被控系统的所有状态均不违反约束，控制要求更高，控制难度增大。

(2) 对系统状态采用的约束类型为时变型约束。在设计控制策略的过程中，约束条件将随着时间的改变而发生变化，控制算法更难，设计的控制方案更具有实用性。

(3) 与之前采用障碍李雅普诺夫函数解决系统状态约束问题不同，本文采用坐标变换方法，实现对系统状态的时变型约束，设计方法新颖，且能够更好地保证系统的稳定性问题。

1 系统描述和控制目标

考虑如下不确定非线性随机切换系统

$ \left\{ \begin{array}{l} \; {\text{d}}{x_i} = \left( {{x_{i + 1}} + {f_{i,\sigma \left( t \right)}}\left( {{{\bar {\boldsymbol{x}}}_i}} \right)} \right){\rm{d}}t + g_{i,\sigma \left( t \right)}^{\rm{T}}\left( {{{\bar {\boldsymbol{x}}}_i}} \right){{{\rm{d}}}}\omega, \\ \;\;\;\;\;i = 1, \cdots ,n - 1 \\ {\text{d}}{x_n} = \left( {{u_{\sigma \left( t \right)}} + {f_{n,\sigma \left( t \right)}}\left( {{{\bar {\boldsymbol{x}}}_n}} \right)} \right){\rm{d}}t + g_{n,\sigma \left( t \right)}^{\rm{T}}\left( {{{\bar {\boldsymbol{x}}}_n}} \right){{{\rm{d}}}}\omega \\ y = {x_1} \\ \end{array} \right. $

(1)

式中： $\sigma \left( t \right):\left[ {0,\infty } \right) \to {{\varGamma }} = \left\{ {1,2, \cdots ,m} \right\}$ 表示系统的切换信号， $m$ 表示切换系统(1)中子系统的数量； ${\bar {\boldsymbol{x}}_i} = {\left[ {{x_1},{x_2}, \cdots ,{x_i}} \right]^{\rm{T}}},{\text{ }}i = 1, \cdots ,n$ 表示系统的状态，并且满足 $ - {k_{ai}}\left( t \right) < {x_i} < {k_{ai}}\left( t \right)$ ， ${k_{ai}}\left( t \right)$ 是与时间 $t$ 有关的函数； $y$ 和 ${u_q}$ ， $q \in \varGamma$ 分别为系统的输出和第 $q$ 个子系统的控制输入； ${f_{i,q}}\left( {{{\bar {\boldsymbol{x}}}_i}} \right)$ 和 ${g_{i,q}}\left( {{{\bar {\boldsymbol{x}}}_i}} \right)$ 表示未知非线性函数； $\omega $ 为定义在完全概率空间 $\left( {\varOmega ,F,P} \right)$ 上的 $r$ 维标准维纳过程，其中， $\varOmega$ 为一个样本空间， $F$ 为一个 $\sigma $ 代数， $P$ 为概率测度。

控制目标：为不确定非线性随机切换系统设计一种自适应神经网络控制策略，使得闭环系统所有信号均依概率有界，系统的所有状态均不违反时变函数约束界，并且误差能够收敛到一个紧集中。

2 系统变换和预备知识

为了解决系统(1)的状态约束问题，引入非线性坐标变换

$ x_i^* = {{{x_i}} \mathord{\left/ {\vphantom {{{x_i}} {{Y_i}}}} \right. } {{Y_i}}} $

(2)

式中： ${Y_i} = \left( {{k_{ai}}\left( t \right) + {x_i}} \right)\left( {{k_{ai}}\left( t \right) - {x_i}} \right)$ 。

此时系统(1) 可以转换为

$ \left\{ \begin{array}{l} \mathrm{d} x_{i}^{*}=\Big(H_{i} x_{i+1}^{*}+f_{i, \sigma(t)}^{*}\left(Y_{i} \overline{\boldsymbol{x}}_{i}^{*}\right)-\dfrac{2}{Y_{i}} k_{a i}(t) \dot{k}_{a i}(t) \times\Big.\\ \;\;\;\;\;\;\;\;\;\;\;\Big.x_{i}^{*}\Big) \mathrm{d} t+g_{i, \sigma(t)}^{* \mathrm{~T}}\left(Y_{i} \overline{\boldsymbol{x}}_{i}^{*}\right) \mathrm{d} \omega, \\ \;\;\;\;\;i= 1, \cdots, n-1 \\ \mathrm{~d} x_{n}^{*}=\Big(H_{n} u_{\sigma(t)}+f_{n, \sigma(t)}^{*}\left(Y_{n} \overline{\boldsymbol{x}}_{n}^{*}\right)-\dfrac{2}{Y_{i}} k_{a n}(t) \times\Big.\\ \;\;\;\;\;\;\;\;\;\;\;\Big.\dot{k}_{a n}(t) x_{n}^{*}\Big) \mathrm{d} t+g_{n, \sigma(t)}^{* \mathrm{~T}}\left(Y_{n} \overline{\boldsymbol{x}}_{n}^{*}\right) \mathrm{d} \omega \\ y^{*}= Y_{1} x_{1}^{*} \end{array} \right.$

(3)

其中， ${H_i} = {{\left( {k_{ai}^2\left( t \right) + x_i^2} \right)} \mathord{\left/ {\vphantom {{\left( {k_{ai}^2\left( t \right) + x_i^2} \right)} {Y_i^2}}} \right. } {Y_i^2}},{\text{ }}i = 1, \cdots ,n$ ， $ {\dot k_{ai}}\left( t \right) = $ ${{\partial {k_{ai}}\left( t \right)} \mathord{\left/ {\vphantom {{\partial {k_{ai}}\left( t \right)} {\partial t}}} \right. } {\partial t}}$ ， $f_{i,q}^*\left( {{Y_i}\bar {\boldsymbol{x}}_i^*} \right) = {{\left( {k_{ai}^2\left( t \right) + {\boldsymbol{x}}_i^2} \right)} \mathord{\left/ {\vphantom {{\left( {k_{ai}^2\left( t \right) + x_i^2} \right)} {Y_i^2{f_{i,q}}\left( {{{\bar {\boldsymbol{x}}}_i}} \right)}}} \right. } {Y_i^2{f_{i,q}}\left( {{{\bar {\boldsymbol{x}}}_i}} \right)}}$ ， $g_{i, q}^{*}\left(Y_{i} \overline{\boldsymbol{x}}_{i}^{*}\right) = \left(k_{a i}^{2}(t)+x_{i}^{2}\right) / Y_{i}^{2} g_{i, q}({{\bar {\boldsymbol{x}}}_i})$ ， $i = 1, \cdots ,n$ 。下文将分别用 ${k_{ai}}$ 和 ${\dot k_{ai}}$ 来代替 ${k_{ai}}\left( t \right)$ 和 ${\dot k_{ai}}\left( t \right)$ 。

为了实现控制目标，本文引入了以下定义、假设和引理。

考虑随机非线性系统

$ {\rm{d}}x = f\left( {x,t} \right){\rm{d}}t + g\left( {x,t} \right){\rm{d}}\omega $

(4)

式中： $x \in {R^n}$ 为系统的状态， $f\left( x \right) \in {R^n}$ 和 $g\left( x \right) \in {R^{n \times r}}$ 为局部利普希茨函数， $\omega $ 为独立的标准维纳过程。

定义1^[31] 　对于随机非线性系统(4) 和函数 $V\left( {x,t} \right) \in {C^2}$ ，定义如下微分算子 $L$

$ L V=\dfrac{\partial V}{\partial t}+\dfrac{\partial V}{\partial x} f+\dfrac{1}{2} \operatorname{Tr}\left\{{{{g}}}^{\mathrm{T}} \dfrac{\partial^{2} V}{\partial x^{2}} {{{g}}}\right\}$

(5)

这里C²表示2次可微，且其2次微分依然连续的函数， ${\rm{T}}{\rm{r}}\left\{ \cdot \right\}$ 为矩阵的迹。

假设1^[16] 　对于 ${k_{a1}}\left( t \right):{R_ + } \to R$ ，存在函数 ${T_0}\left( t \right): {R_{\text{ + }}} \to {R_{\text{ + }}}$ 和常数 ${T_i} > 0,{\text{ }}i = 1, \cdots ,n$ ，使得期望信号 ${y_d}$ 及其导数分别满足 $\left|{y}_{d}\left(t\right)\right|\leqslant{T}_{0}\left(t\right) < {k}_{a1}\left(t\right)$ ， $\left| {y_d^i\left( t \right)} \right| < {T_{i{\text{ + }}1}}\left( t \right)$ ， $\forall t\geqslant0$ 。

引理1^[32] 　对于随机非线性系统(4) ，如果存在函数 $V\left( {x,t} \right) \in {C^2}$ ，满足

$\left\{\begin{array}{l} \psi_{1}(|x|) \leqslant V(x, t) \leqslant \psi_{2}(|x|) \\ L V(x, t) \leqslant-A V(x, t)+B \end{array}\right.$

(6)

则随机系统(4) 存在一个奇解

$ E\left(V\left(x,t\right)\right)\leqslant V\left({x}_{0}\right){{\rm{e}}}^{-At}+\dfrac{B}{A} $

(7)

式中： $A > 0$ 和 $B > 0$ 为常数， $ {\psi _1}\left( {\left| x \right|} \right) \in {K_\infty } $ ， $ {\psi _2}\left( {\left| x \right|} \right) \in {K_\infty } $ 。

引理2^[33] 　如果 $x$ ， $y$ ， $d$ 和 $h$ 是正实数，且 $\dfrac{1}{d} + \dfrac{1}{h} = 1$ ，则不等式(8) 成立。

$ xy\leqslant \dfrac{{x}^{d}}{d}+\dfrac{{y}^{h}}{h} $

(8)

引理3^[25] 　对于非线性函数 $F\left( {\boldsymbol{Z}} \right)$ ，存在相应的径向基函数神经网络(RBRNNs) ${{\boldsymbol{W}}^{\rm{T}}}{\boldsymbol{S}}\left( {\boldsymbol{Z}} \right)$ ，使得式(9) 成立。

$F(\boldsymbol{Z})=\boldsymbol{W}^{\mathrm{T}} {\boldsymbol{S}}(\boldsymbol{Z})+\delta(\boldsymbol{Z}), \delta(\boldsymbol{Z})<\varepsilon$

(9)

式中： $\delta \left( {\boldsymbol{Z}} \right)$ 为逼近误差， $\varepsilon > 0$ 为一个常数； ${\boldsymbol{W}} = {\left[ {{w_1},{w_2}, \cdots ,{w_N}} \right]^{\rm{T}}} \in {R^N}$ 为神经网络权重向量，且 $N > 1$ 为神经元节点个数； ${\boldsymbol{S}}\left( {\boldsymbol{Z}} \right) = \left[ {{s_1}\left( {\boldsymbol{Z}} \right),{s_2}\left( {\boldsymbol{Z}} \right),} \right. \cdots ,$ ${\left. {{s_N}\left( {\boldsymbol{Z}} \right)} \right]^{\rm{T}}}$ ， ${s_i}\left( {\boldsymbol{Z}} \right)$ 为神经元激活函数。本文将选取高斯函数作为基函数，形式为

$ s_{i}(\boldsymbol{Z})=\exp \left(-\dfrac{\left\|{\boldsymbol{Z}}-{\boldsymbol{\varUpsilon}}_{i}\right\|^{2}}{\mu_{i}^{2}}\right), i=1, \cdots, N $

(10)

式中： ${{\boldsymbol{\varUpsilon}} _i} = {\left[ {{\Upsilon _{i1}},{\Upsilon _{i2}}, \cdots ,{\Upsilon _{im}}} \right]^{\rm{T}}}$ 为神经网络中心， ${\mu _i}$ 为高斯型函数宽度。

3 控制器设计与稳定性分析

本节借助backstepping控制算法，针对不确定非线性随机切换系统设计一种自适应神经网络控制策略，保证系统的所有状态均不违反时变约束。

首先为了设计控制策略，本文引入如式(11)所示坐标变换。

$ \begin{aligned} {z}_{1}^{*} &=x_{1}^{*}-y_{d} \\ {{z}}_{i}^{*} &=x_{i}^{*}-\alpha_{i-1} \end{aligned} $

(11)

式中： ${y_d}$ 为期望信号， ${\alpha _{i - 1}},{\text{ }}i = 2, \cdots ,n$ 为虚拟控制函数，并将在下文的设计过程中给出。

接下来本文将借助backstepping控制算法设计控制策略。

Step 1：选取李雅普诺夫候选函数为

$ V_{1}=\dfrac{1}{4} {{z}}_{1}^{* 4}+\dfrac{1}{2 \gamma_{1}} \tilde{{{\varTheta}}}_{1}^{2} $

(12)

式中： ${\gamma _1} > 0$ 为设计参数， ${\tilde \varTheta _1} = {\varTheta _1} - {\hat \varTheta _1}$ 为估计误差， ${\hat \varTheta _1}$ 为最优权重 ${\varTheta _1}$ 的估计， ${\varTheta _1}$ 的定义将在下文中的式(19) 给出。

根据式(3) 和式(11) ，可得

$ \begin{aligned} \mathrm{d} {{z}}_{1}^{*}=& \mathrm{d} x_{1}^{*}-\mathrm{d} y_{d} =\\ &\Big(H_{1} x_{2}^{*}+f_{1, q}^{*}\left(Y_{1} x_{1}^{*}\right)-\dfrac{2}{Y_{1}} k_{a 1} \dot{k}_{a 1} x_{1}^{*}-\dot{y}_{d}\Big) \mathrm{d} t +g_{1}^{* \mathrm{~T}} \mathrm{~d} \omega \end{aligned} $

(13)

按照定义1以及式(13) ，计算 ${V_1}$ 的微分算子为

$ \begin{split} L V_{1}=& {{z}}_{1}^{* 3}\Big(H_{1} {{z}}_{2}^{*}+H_{1} \alpha_{1}+f_{1, q}^{*}\left(Y_{1} x_{1}^{*}\right)\Big.-\\ &\Big.\dfrac{2}{Y_{1}} k_{a 1} \dot{k}_{a 1} {{z}}_{1}^{*}-\dfrac{2}{Y_{1}} k_{a 1} \dot{k}_{a 1} y_{d}-\dot{y}_{d}\Big) +\\ &\dfrac{3}{2} {{z}}_{1}^{* 2}\left\|g_{1, q}^{*}\right\|^{2}-\dfrac{1}{\gamma_{1}} \tilde{\varTheta}_{1} \dot{\hat{\varTheta}}_{1} \end{split} $

(14)

借助引理2，可得

$ \dfrac{3}{2}{{{z}}}_{1}^{*}{}^{2}{\Vert {g}_{1,q}^{*}\Vert }^{2}\leqslant \dfrac{3}{4{l}_{1,q}^{2}}{z}_{1}^{*}{}^{4}{\Vert {g}_{1,q}^{*}\Vert }^{4}+\dfrac{3}{4}{l}_{1,q}^{2} $

(15)

式中： $ {l_{1,q}} > 0 $ 为一个常数。

将式(15) 代入式(14) 可得

$ \begin{split} L{V}_{1}\leqslant & {{{z}}}_{1}^{*}{}^{3}\Big({H}_{1}{\alpha }_{1}+{F}_{1}\left({{{{\boldsymbol{Z}}}}}_{1}\right)-\dfrac{2}{{Y}_{1}}{k}_{a1}{\dot{k}}_{a1}{{{z}}}_{1}^{*}\Big)+\\ &{H}_{1}{{{z}}}_{1}^{*}{}^{3}{{{z}}}_{2}^{*}+\dfrac{3}{4}{l}_{1,\mathrm{max}}^{2}-\dfrac{1}{{\gamma }_{1}}{\tilde{\varTheta }}_{1}\dot{\hat{\varTheta}}_{1} \end{split} $

(16)

式中： ${l_{1,\max }} = \max \left\{ {{l_{1,q}},q \in {{\varGamma }}} \right\}$ ， ${F_1}\left( {{{{{\boldsymbol{Z}}}}_1}} \right) = f_{1,q}^*\left( {{Y_1}x_1^*} \right) -$ $\dfrac{2}{{{Y_1}}}{k_{a1}} {\dot k_{a1}}{y_d} - {\dot y_d} + \dfrac{3}{{4l_{1,q}^2}}{{z}}_1^*{\left\| {g_{1,q}^*} \right\|^4}$ 。

应用RBFNNs对 ${F_1}\left( {{{\boldsymbol{Z}}_1}} \right)$ 进行逼近，即

$ {F_1}\left( {{{\boldsymbol{Z}}_1}} \right) = {\boldsymbol{W}}_{1,q}^{\rm{T}}{{\boldsymbol{S}}_1}\left( {{{\boldsymbol{Z}}_1}} \right) + {\delta _{1,q}}\left( {{{\boldsymbol{Z}}_1}} \right),{\text{ }}\left| {{\delta _{1,q}}\left( {{{\boldsymbol{Z}}_1}} \right)} \right| < {\varepsilon _{1,q}} $

(17)

式中： $ {\varepsilon _{1,q}} > 0 $ 为一个常数。

将式(17) 代入式(16) 得

$ \begin{split} L V_{1} \leqslant {{z}}_{1}^{* 3} &\left(H_{1} \alpha_{1}+\boldsymbol{W}_{1, q}^{\mathrm{T}} \boldsymbol{S}_{1}\left(\boldsymbol{Z}_{1}\right)+\delta_{1, q}\left(\boldsymbol{Z}_{1}\right)\right.-\\ &\left.\frac{2}{{{Y_i}}} k_{a 1} \dot{k}_{a 1} {{z}}_{1}^{*}\right)+H_{1} {{z}}_{1}^{* 3} {{z}}_{2}^{*}+\dfrac{3}{4} l_{1, \max }^{2} -\\ &\dfrac{1}{\gamma_{1}} \tilde{\varTheta}_{1} \dot{\hat{\varTheta}}_{1} \end{split} $

(18)

在引理2的基础上，对式(18) 中的 ${{z}}_{1}^{* 3} \boldsymbol{W}_{1, q}^{\mathrm{T}} \boldsymbol{S}_{1}\left(\boldsymbol{Z}_{1}\right)$ ， ${{z}}_{1}^{* 3} \delta_{1, q}\left(\boldsymbol{Z}_{1}\right)$ 和 $H_{1} {{z}}_{1}^{* 3} {{z}}_{2}^{*}$ 分别进行处理。

首先，针对 ${{z}}_{1}^{* 3} \boldsymbol{W}_{1, q}^{\mathrm{T}} \boldsymbol{S}_{1}\left(\boldsymbol{Z}_{1}\right)$ ，有

$ {{z}}_{1}^{* 3} {\boldsymbol{W}}_{1, q}^{\mathrm{T}} {\boldsymbol{S}}_{1}\left({\boldsymbol{Z}}_{1}\right) \leqslant \dfrac{1}{2 a_{1}^{2}} z_{1}^{* 6} \varTheta_{1} {\boldsymbol{S}}_{1}^{\mathrm{T}} {\boldsymbol{S}}_{1}+\dfrac{1}{2} a_{1}^{2} $

(19)

式中： ${\varTheta _1} = \max \left\{ {{{\left\| {{{\boldsymbol{W}}_{1,q}}} \right\|}^2},q \in \varGamma } \right\}$ ，并且 $ {a_1} > 0 $ 为一个常数。

其次，对于 ${{z}}_{1}^{* 3} \delta_{1, q}\left({\boldsymbol{Z}}_{1}\right)$ ，有

$ {{{z}}}_{1}^{*}{}^{3}{\delta }_{1,q}\left({{\boldsymbol{Z}}}_{1}\right)\leqslant \dfrac{1}{2}{{{z}}}_{1}^{*}{}^{6}+\dfrac{1}{2}{\varepsilon }_{1,\mathrm{max}}^{2} $

(20)

式中： ${\varepsilon _{1,\max }} = \max \left\{ {{\varepsilon _{1,q}},q \in \varGamma } \right\}$ 。

最后，关于 $H_{1} {{z}}_{1}^{* 3} {{z}}_{2}^{*}$ ，可以得到

$ {H}_{1}{{{z}}}_{1}^{*}{}^{3}{{{z}}}_{2}^{*}\leqslant \dfrac{3}{4}{H}_{1}^{\frac{4}{3}}{{{z}}}_{1}^{*}{}^{4}+\dfrac{1}{4}{{{z}}}_{2}^{*}{}^{4} $

(21)

将式(19) ~式(21) 代入式(18) 中可得

$ \begin{split} L{V}_{1}\leqslant & {{z}}_{1}^{*}{}^{3}\Big({H}_{1}{\alpha }_{1}+\dfrac{1}{2{a}_{1}^{2}}{{z}}_{1}^{*}{}^{3}{\varTheta }_{1}{{\boldsymbol{S}}}_{1}^{{\rm{T}}}{{\boldsymbol{S}}}_{1}+\dfrac{1}{2}{{z}}_{1}^{*}{}^{3}+\Big.\\& \Big.\dfrac{3}{4}{H}_{1}^{\frac{4}{3}}{{z}}_{1}^{*}{}^{4}-\dfrac{2}{{Y}_{1}}{k}_{a1}{\dot{k}}_{a1}{{z}}_{1}^{*}\Big)+\dfrac{1}{4}{{{z}}}_{2}^{*}{}^{4}+\\ & \dfrac{3}{4}{l}_{1,\mathrm{max}}^{2}-\dfrac{1}{{\gamma }_{1}}{\tilde{\varTheta }}_{1}\dot{\hat{\varTheta}}_{1}+\dfrac{1}{2}{a}_{1}^{2}+\dfrac{1}{2}{\varepsilon }_{1,\mathrm{max}}^{2} \end{split} $

(22)

设计虚拟控制器 ${\alpha _1}$ 为

$ \begin{split} {\alpha _1} = & \dfrac{1}{{{H_1}}}\left[ { - {\tau _1}{{z}}_1^* + \dfrac{2}{{{Y_1}}}{k_{a1}}{{\dot k}_{a1}}{{z}}_1^* - \dfrac{1}{2}{{z}}{{_1^*}^3}} \right. - \hfill \\ &\left. {\dfrac{3}{4}H_1^{\frac{4}{3}}{{z}}{{_1^*}^4} - \dfrac{1}{{2a_1^2}}{{z}}{{_1^*}^3}{{\hat \varTheta }_1}{\boldsymbol{S}}_1^{\rm{T}}{{\boldsymbol{S}}_1}} \right] \end{split} $

(23)

式中： ${\tau _1} > 0$ 为设计参数。

设计自适应律 ${\hat \varTheta _1}$ 为

$ \dot{\hat{\varTheta}}_{1}=-\sigma_{1} \hat{\varTheta}_{1}+\dfrac{\gamma_{1}}{2 a_{1}^{2}} {{z}}_{1}^{* 2} \boldsymbol{S}_{1}^{\mathrm{T}} \boldsymbol{S}_{1} $

(24)

式中： ${\sigma _1} > 0$ 为设计参数。

将虚拟控制器(23) 和自适应律(24) 代入式(22) 中得

$ \begin{split} L{V}_{1}\leqslant & -{\tau }_{1}{{{z}}}_{1}^{*}{}^{4}+\dfrac{1}{2}{a}_{1}^{2}+\dfrac{1}{2}{\varepsilon }_{1,\mathrm{max}}^{2}+\dfrac{3}{4}{l}_{1,\mathrm{max}}^{2}+\\ &\dfrac{{\sigma }_{1}}{{\gamma }_{1}}{\tilde{\varTheta }}_{1}\hat{\varTheta}_{1}+\dfrac{1}{4}{{{z}}}_{2}^{*}{}^{4} \end{split} $

(25)

Step ${\boldsymbol{i}}\left({\boldsymbol{2}}\leqslant {\boldsymbol{i}}\leqslant {\boldsymbol{n}}{\boldsymbol{-1}}\right)$ ：选取如下李雅普诺夫候选函数

$ V_{i}=V_{i-1}+\dfrac{1}{4} {{z}}_{i}^{*4}+\dfrac{1}{2 \gamma_{i}} \tilde{\varTheta}_{i}^{2} $

(26)

式中： ${\gamma _i} > 0$ 为设计参数， ${\tilde \varTheta _i} = {\varTheta _i} - {\hat \varTheta _i}$ 为估计误差， ${\hat \varTheta _i}$ 为最优权重 ${\varTheta _i}$ 的估计， ${\varTheta _i}$ 的定义将在下文中的式(34)给出。

根据式(3)和式(11) ，可得

$ \begin{split} L \alpha_{i-1}=& \dfrac{1}{2} \sum\limits_{j, m=1}^{i-1} \dfrac{\partial^{2} \alpha_{i-1}}{\partial x_{j}^{*} x_{m}^{*}} g_{j}^{* \mathrm{~T}} g_{m}^{*}+\\ & \sum\limits_{j=1}^{i-1} \dfrac{\partial \alpha_{i-1}}{\partial x_{j}^{*}} \dot{x}_{j}^{*}+\sum\limits_{j=1}^{i-1} \dfrac{\partial \alpha_{i-1}}{\partial \hat{\varTheta}_{j}} \dot{\hat{\varTheta}}_{j}+\\ & \sum\limits_{j=0}^{i-1} \dfrac{\partial \alpha_{i-1}}{\partial y_{d}^{(j)}} y_{d}^{(j+1)}+\sum\limits_{j=0}^{i-1} \sum\limits_{m=1}^{i-1} \dfrac{\partial \alpha_{i-1}}{\partial k_{a m}^{(j)}} k_{a m}^{(j+1)} \end{split} $

(27)

$ \begin{split} \mathrm{d} {{z}}_{i}^{*}=& \mathrm{d} x_{i}^{*}-\mathrm{d} \alpha_{i-1} =\\ &\Big(H_{i} x_{i+1}^{*}+f_{i, q}^{*}\left(Y_{i} \bar{{\boldsymbol{x}}}_{i}^{*}\right)-\frac{2}{{{Y_i}}} k_{a i} \dot{k}_{a i} x_{i}^{*}-\Big.\\ &\Big.L \alpha_{i-1}\Big) \mathrm{d} t+\Bigg(g_{i, q}^{*}-\sum\limits_{j=1}^{i-1} \dfrac{\partial \alpha_{i-1}}{\partial x_{j}^{*}} g_{j, q}^{*}\Bigg)^{\mathrm{T}} \mathrm{d} \omega \end{split} $

(28)

按照定义1，基于式(27) 和式(28) ，计算 ${V_i}$ 的微分算子为

$ \begin{split} L V_{i}=& L V_{i-1}+{{z}}_{i}^{* 3}\Big(H_{i} {{z}}_{i+1}^{*}+H_{i} \alpha_{i}+f_{i, q}^{*}\left(Y_{i} \overline{\boldsymbol{x}}_{i}^{*}\right)-\Big.\\ &\Big.\dfrac{2}{Y_{i}} k_{a i} \dot{k}_{a i} {{z}}_{i}^{*}-\dfrac{2}{Y_{i}} k_{a i} \dot{k}_{a i} \alpha_{i-1}-L \alpha_{i-1}\Big)+\\ & \dfrac{3}{2} {{z}}_{i}^{* 2}\left\|g_{i, q}^{*}-\sum\limits_{j=1}^{i-1} \dfrac{\partial \alpha_{i-1}}{\partial x_{j}^{*}} g_{j, q}^{*}\right\|^{2}-\dfrac{1}{\gamma_{i}} \tilde{\varTheta}_{i} \dot{\hat{\varTheta}}_{i} \end{split} $

(29)

基于引理2，可得

$ \begin{split} &\dfrac{3}{2} {{z}}_{i}^{* 2}\left\|g_{i, q}^{*}-\sum\limits_{j=1}^{i-1} \dfrac{\partial \alpha_{i-1}}{\partial x_{j}^{*}} g_{j}^{*}\right\|^{2}\leqslant \\ &\dfrac{3}{4 l_{i, q}^{2}} {{z}}_{i}^{* 4}\left\|g_{i, q}^{*}-\sum\limits_{j=1}^{i-1} \dfrac{\partial \alpha_{i-1}}{\partial x_{j}^{*}} g_{j, q}^{*}\right\|^{4}+\dfrac{3}{4} l_{i, q}^{2} \end{split} $

(30)

式中： $ {l_{i,q}} > 0 $ 为一个常数。

将式(30) 代入式(29) 可得

$ \begin{split} L{V}_{i}\leqslant & L{V}_{i-1}+{{{z}}}_{i}^{*}{}^{3}\Big({H}_{i}{\alpha }_{i}+{F}_{i}\left({{{{\boldsymbol{Z}}}}}_{i}\right)-\dfrac{2}{{Y}_{i}}{k}_{ai}{\dot{k}}_{ai}{{{z}}}_{i}^{*}\Big)+\\ & {H}_{i}{{{z}}}_{i}^{*}{}^{3}{{{z}}}_{i+1}^{*}+\dfrac{3}{4}{l}_{1,\mathrm{max}}^{2}-\dfrac{1}{{\gamma }_{i}}{\tilde{\varTheta }}_{i}\dot{\hat{\varTheta}}_{i} \end{split} $

(31)

式中：

$ \begin{aligned} F_{i}\left(\boldsymbol{{\boldsymbol{Z}}}_{i}\right)=& f_{i, q}^{*}\left(Y_{i} \overline{\boldsymbol{x}}_{i}^{*}\right)-\dfrac{2}{Y_{i}} k_{a i} \dot{k}_{a i} \alpha_{i-1}-L \alpha_{i-1}+\\ &\dfrac{3}{4 l_{i, q}^{2}} {{z}}_{i}^{*} \left\|g_{i, q}^{*}-\sum\limits_{j=1}^{i-1} \dfrac{\partial \alpha_{i-1}}{\partial x_{j}^{*}} g_{j, q}^{*}\right\|^{4} \\ l_{i, \max }=& \max \left\{l_{i, q}, q \in \varGamma\right\} \end{aligned} $

应用RBFNNs对 ${F_i}\left( {{{\boldsymbol{Z}}_i}} \right)$ 进行逼近，即

$ {F_i}\left( {{{\boldsymbol{Z}}_i}} \right) = {\boldsymbol{W}}_{i,q}^{\rm{T}}{{\boldsymbol{S}}_i}\left( {{{\boldsymbol{Z}}_i}} \right) + {\delta _{i,q}}\left( {{{\boldsymbol{Z}}_i}} \right),\left| {{\delta _{i,q}}\left( {{{\boldsymbol{Z}}_i}} \right)} \right| < {\varepsilon _{i,q}} $

(32)

式中： $ {\varepsilon _{i,q}} > 0 $ 为一个常数。

将式(32) 代入式(31) 得

$ \begin{split} L{V}_{i}\leqslant & L{V}_{i-1}+{{{z}}}_{i}^{*}{}^{3}({H}_{i}{\alpha }_{i}+{{\boldsymbol{W}}}_{i,q}^{{\rm{T}}}{{\boldsymbol{S}}}_{i}\left({{\boldsymbol{Z}}}_{i}\right) +\\ &{\delta }_{i,q}\left({{\boldsymbol{Z}}}_{i}\right)-2/{Y}_{i}{k}_{ai}{\dot{k}}_{ai}{{{z}}}_{i}^{*}) +\\ &{H}_{i}{{{z}}}_{i}^{*}{}^{3}{{{z}}}_{i+1}^{*}+\dfrac{3}{4}{l}_{i,\mathrm{max}}^{2}-\dfrac{1}{{\gamma }_{i}}{\tilde{\varTheta }}_{i}\dot{\hat{\varTheta}}_{i} \end{split} $

(33)

采用和Step 1中相同的方法化简式(33) 。

首先，可以得到

$ {{{z}}}_{i}^{*}{}^{3}{{\boldsymbol{W}}}_{i,q}^{{\rm{T}}}{{\boldsymbol{S}}}_{i}\left({{{{\boldsymbol{Z}}}}}_{i}\right)\leqslant \dfrac{1}{2{a}_{i}^{2}}{{{z}}}_{i}^{*}{}^{6}{\varTheta }_{i}{{\boldsymbol{S}}}_{i}^{{\rm{T}}}{{\boldsymbol{S}}}_{i}+\dfrac{1}{2}{a}_{i}^{2} $

(34)

式中： ${\varTheta _i} = \max \left\{ {{{\left\| {{{\boldsymbol{W}}_{i,q}}} \right\|}^2},q \in \varGamma } \right\}$ ，并且 $ {a_i} > 0 $ 为一个常数。

其次，计算出下面结果

$ {{{z}}}_{i}^{*}{}^{3}{\delta }_{i,q}\left({{\boldsymbol{Z}}}_{i}\right)\leqslant \dfrac{1}{2}{{{z}}}_{i}^{*}{}^{6}+\dfrac{1}{2}{\varepsilon }_{i,\mathrm{max}}^{2} $

(35)

式中： ${\varepsilon _{i,\max }} = \max \left\{ {{\varepsilon _{i,q}},q \in \varGamma } \right\}$ 。

最后，同样可以得到如下结果

$ {H}_{i}{{{z}}}_{i}^{*}{}^{3}{{{z}}}_{i+1}^{*}\leqslant \dfrac{3}{4}{H}_{i}^{\frac{4}{3}}{{{z}}}_{i}^{*}{}^{4}+\dfrac{1}{4}{{{z}}}_{i+1}^{*}{}^{4} $

(36)

将处理结果式(34) ~式(36) 代入式(33) 中可得

$ \begin{split} L V_{i} \leqslant &L V_{i-1}+{{z}}_{i}^{* 3}\Big(H_{i} \alpha_{i}+\dfrac{1}{2 a_{i}^{2}} {{z}}_{i}^{* 3} \varTheta_{i} \boldsymbol{S}_{i}^{\mathrm{T}} \boldsymbol{S}_{i}+\dfrac{1}{2} {{z}}_{i}^{*_{3}}+\Big. \\ \qquad\quad &\Big.\dfrac{3}{4} H_{i}^{\frac{4}{3}} {{z}}_{i}^{* 4}-\dfrac{2}{Y_{i}} k_{a i} \dot{k}_{c i} {{z}}_{i}^{*}\Big)+\dfrac{1}{4} {{z}}_{i+1}^{*4}+\dfrac{3}{4} l_{i, \max }^{2}- \\ \qquad\quad &\dfrac{1}{\gamma_{i}} \tilde{\varTheta}_{i} \dot{\hat{\varTheta}}_{i}+\dfrac{1}{2} a_{i}^{2}+\dfrac{1}{2} \varepsilon_{i, \max }^{2} \end{split} $

(37)

设计虚拟控制器 ${\alpha _i}$ 为

$ \begin{split} \alpha_{i}=& \dfrac{1}{H_{i}}\left[-\tau_{i} {{z}}_{i}^{*}+\dfrac{2}{Y_{i}} k_{a i} \dot{k}_{a i} {{z}}_{i}^{*}-\dfrac{1}{2} {{z}}_{i}^{*_{3}}-\right.\\ &\left.\dfrac{3}{4} H_{i}^{\frac{4}{3}} {{z}}_{i}^{* 4}-\dfrac{1}{2 a_{i}^{2}} {{z}}_{i}^{* 3} \hat{\varTheta}_{i} {\boldsymbol{S}}_{i}^{\mathrm{T}} {\boldsymbol{S}}_{i}-\dfrac{1}{4} {{z}}_{i}^{*}\right] \end{split} $

(38)

其中， ${\tau _i} > 0$ 为设计参数。

设计自适应律 ${\hat \varTheta _i}$ 为

$ \dot{\hat{\varTheta}}_{i}=-\sigma_{i} \hat{\varTheta}_{i}+\dfrac{\gamma_{i}}{2 a_{i}^{2}} {{z}}_{i}^{* 2} \boldsymbol{S}_{i}^{\mathrm{T}} \boldsymbol{S}_{i} $

(39)

其中， ${\sigma _i} > 0$ 为设计参数。

将虚拟控制器(38) 和自适应律(39) 代入式(37) 中得

$ \begin{split} L{V}_{i}\leqslant & -{\displaystyle \sum\limits _{m=1}^{i}{\tau }_{m}{{{z}}}_{m}^{*}{}^{4}}+\dfrac{1}{2}{\displaystyle \sum\limits _{m=1}^{i}{a}_{m}^{2}}+\dfrac{1}{2}{\displaystyle \sum\limits _{m=1}^{i}{\varepsilon }_{m,\mathrm{max}}^{2}}+\\ &\dfrac{3}{4}{\displaystyle \sum\limits _{m=1}^{i}{l}_{m,\mathrm{max}}^{2}}+{\displaystyle \sum\limits _{m=1}^{i}\dfrac{{\sigma }_{m}}{{\gamma }_{m}}{\tilde{\varTheta }}_{m}\hat{\varTheta}_{m}}+\dfrac{1}{4}{{{z}}}_{i+1}^{*}{}^{4} \end{split} $

(40)

Step $ {\boldsymbol{n}} $ ：选取如下李雅普诺夫候选函数

$ V_{n}=V_{n-1}+\dfrac{1}{4} {{z}}_{n}^{* 4}+\dfrac{1}{2 \gamma_{n}} \tilde{\varTheta}_{n}^{2} $

(41)

式中： ${\gamma _n} > 0$ 为设计参数， ${\tilde \varTheta _n} = {\varTheta _n} - {\hat \varTheta _n}$ 为估计误差， ${\hat \varTheta _n}$ 为最优权重 ${\varTheta _n}$ 的估计， ${\varTheta _n}$ 的定义将在式(49) 给出。

根据式(3) 和式(11) ，可得

$ \begin{split} L \alpha_{n-1}=& \sum\limits_{j=0}^{n-1} \dfrac{\partial \alpha_{n-1}}{\partial y_{d}^{(j)}} y_{d}^{(j+1)}+\sum\limits_{j=0}^{n-1} \sum\limits_{m=1}^{n-1} \dfrac{\partial \alpha_{n-1}}{\partial k_{a m}^{(j)}} k_{a m}^{(j+1)}+\\ & \sum\limits_{j=1}^{n-1} \dfrac{\partial \alpha_{n-1}}{\partial x_{j}^{*}} \dot{x}_{j}^{*}+\sum\limits_{j=1}^{n-1} \dfrac{\partial \alpha_{n-1}}{\partial \hat{\varTheta}_{j}} \dot{\hat{\varTheta}}_{j}+\\ & \dfrac{1}{2} \sum\limits_{j, m=1}^{n-1} \dfrac{\partial^{2} \alpha_{n-1}}{\partial x_{j}^{*} x_{m}^{*}} g_{j}^{* \mathrm{~T}} g_{m}^{*} \end{split} $

(42)

$ \begin{split} \mathrm{d} {{z}}_{n}^{*}=& \mathrm{d} x_{n}^{*}-\mathrm{d} \alpha_{n-1}=\\ &\Big(H_{n} u_{q}+f_{n, q}^{*}\left(Y_{n} \bar{{\boldsymbol{x}}}_{n}^{*}\right)-2 / Y_{n} k_{a n} \dot{k}_{a n} x_{n}^{*}-\Big.\\ &\Big.L \alpha_{n-1}\Big) \mathrm{d} t+\Bigg(g_{n, q}^{*}-\sum\limits_{j=1}^{n-1} \dfrac{\partial \alpha_{n-1}}{\partial x_{j}^{*}} g_{j, q}^{*}\Bigg)^{\mathrm{T}} \mathrm{d} \omega \end{split} $

(43)

按照定义1，基于式(42)和式(43) ，计算 ${V_n}$ 的微分算子为

$ \begin{split} L V_{n}=& L V_{n-1}+{{z}}_{n}^{* 3}\Big(H_{n} u_{q}+f_{n, q}^{*}\left(Y_{n} \bar{{\boldsymbol{x}}}_{n}^{*}\right)-\Big.\\ &\Big.\dfrac{2}{Y_{n}} k_{a n} \dot{k}_{a n} {{z}}_{n}^{*}-\dfrac{2}{Y_{n}} k_{a n} \dot{k}_{a n} \alpha_{n-1}-L \alpha_{n-1}\Big)+\\ & \dfrac{3}{2} {{z}}_{n}^{* 2}\left\|g_{n, q}^{*}-\sum\limits_{j=1}^{n-1} \dfrac{\partial \alpha_{n-1}}{\partial x_{j}^{*}} g_{j, q}^{*}\right\|^{2}-\dfrac{1}{\gamma_{n}} \tilde{\varTheta}_{n} \dot{\hat{\varTheta}}_{n} \end{split} $

(44)

根据引理2，可得

$ \begin{split} \dfrac{3}{2} {{z}}_{n}^{* 2}&\left\|{g_{n, q}^{*}}-\sum\limits_{j=1}^{n-1} \dfrac{\partial \alpha_{n-1}}{\partial x_{j}^{*}} g_{j, q}^{*}\right\|^{2} \leqslant \qquad\qquad\quad\\ &\dfrac{3}{4 l_{n, q}^{2}} {{z}}_{n}^{* 4}\left\|g_{n, q}^{*}-\sum\limits_{j=1}^{n-1} \dfrac{\partial \alpha_{n-1}}{\partial x_{j}^{*}} g_{j, q}^{*}\right\|^{4}+\dfrac{3}{4} l_{n, q}^{2} \end{split}$

(45)

式中： $ {l_{n,q}} > 0 $ 为一个常数。

将式(45) 代入式(44) 可得

$ \begin{split} &L{V}_{n}\leqslant L{V}_{n-1}+{{{z}}}_{n}^{*}{}^{3}\Big({H}_{n}{u}_{q}+{F}_{n}\left({{\boldsymbol{Z}}}_{n}\right)-\Big.\\ &\Big.\dfrac{2}{{Y}_{n}}{k}_{an}{\dot{k}}_{an}{{{z}}}_{n}^{*}\Big)+\dfrac{3}{4}{l}_{n,\mathrm{max}}^{2}-\dfrac{1}{{\gamma }_{n}}{\tilde{\varTheta }}_{n}\dot{\hat{\varTheta}}_{n} \end{split} $

(46)

式中 ${l_{n,\max }} = \max \left\{ {{l_{n,q}},q \in \varGamma } \right\}$ ，且

$ \begin{aligned} F_{n}\left({\boldsymbol{Z}}_{n}\right)=& f_{n, q}^{*}\left(Y_{n} \bar{{\boldsymbol{x}}}_{n}^{*}\right)-\dfrac{2}{Y_{n}} k_{a n} \dot{k}_{a n} \alpha_{n-1}-L \alpha_{n-1}+\\ & \dfrac{3}{4 l_{n, q}^{2}} {{z}}_{n}^{*}\left\|g_{n, q}^{*}-\sum\limits_{j=1}^{n-1} \dfrac{\partial \alpha_{n-1}}{\partial x_{j}^{*}} g_{j, q}^{*}\right\|^{4} \end{aligned} $

应用RBFNNs对 ${F_n}\left( {{{\boldsymbol{Z}}_n}} \right)$ 进行逼近，即

$ {F_n}\left( {{{\boldsymbol{Z}}_n}} \right) = {\boldsymbol{W}}_{n,q}^{\rm{T}}{{\boldsymbol{S}}_n}\left( {{{\boldsymbol{Z}}_n}} \right) + {\delta _{n,q}}\left( {{{\boldsymbol{Z}}_n}} \right) $

(47)

$ \left| {{\delta _{n,q}}\left( {{{{{\boldsymbol{Z}}}}_n}} \right)} \right| < {\varepsilon _{n,q}} $

式中： $ {\varepsilon _{n,q}} > 0 $ 为一个常数。

将式(47) 代入式(46) 得

$ \begin{split} L V_{n} \leqslant & L V_{n-1}+{{z}}_{n}^{* 3}\Big (H_{n} u_{q}+\boldsymbol{W}_{n, q}^{\mathrm{T}} \boldsymbol{S}_{n}\left(\boldsymbol{Z}_{n}\right)\Big.+\\ &\Big. \delta_{n, q}\left(\boldsymbol{Z}_{n}\right)-\dfrac{2}{Y_{n}} k_{a n} \dot{k}_{a n} {{z}}_{n}^{*} \Big) +\\ &\dfrac{3}{4} l_{n, \max }^{2}-\dfrac{1}{\gamma_{n}} \tilde{\varTheta}_{n} \dot{\hat{\varTheta}}_{n} \end{split} $

(48)

按照Step 1和Step $i$ 中相同的方法处理式(48) 。

首先，对于 ${{z}}_{n}^{* 3} \boldsymbol{W}_{n, q}^{\mathrm{T}} \boldsymbol{S}_{n}\left(\boldsymbol{Z}_{n}\right)$ ，可以得到

$ {{{z}}}_{n}^{*}{}^{3}{{\boldsymbol{W}}}_{n,q}^{{\rm{T}}}{{\boldsymbol{S}}}_{n}\left({{{{\boldsymbol{Z}}}}}_{n}\right)\leqslant \dfrac{1}{2{a}_{n}^{2}}{{{z}}}_{n}^{*}{}^{6}{\varTheta }_{n}{{\boldsymbol{S}}}_{n}^{{\rm{T}}}{{\boldsymbol{S}}}_{n}+\dfrac{1}{2}{a}_{n}^{2} $

(49)

式中： ${\varTheta _n} = \max \left\{ {{{\left\| {{{\boldsymbol{W}}_{n,q}}} \right\|}^2},q \in \varGamma } \right\}$ ，并且 $ {a_n} > 0 $ 为一个常数。

其次，关于 ${{z}}_{n}^{* 3} \delta_{n, q}\left({\boldsymbol{Z}}_{n}\right)$ ，有

$ {{{z}}}_{n}^{*}{}^{3}{\delta }_{n,q}\left({{\boldsymbol{Z}}}_{n}\right)\leqslant \dfrac{1}{2}{{{z}}}_{n}^{*}{}^{6}+\dfrac{1}{2}{\varepsilon }_{n,\mathrm{max}}^{2} $

(50)

式中： ${\varepsilon _{n,\max }} = \max \left\{ {{\varepsilon _{n,q}},q \in \varGamma } \right\}$ 。

最后，将处理结果式(49) 和式(50) 代入式(48) 中可得

$ \begin{split} L V_{n} \leqslant & L V_{n-1}+{{z}}_{n}^{* 3}\Big(H_{n} u_{q}+\dfrac{1}{2 a_{n}^{2}} {{z}}_{n}^{* 3} \varTheta_{n} {\boldsymbol{S}}_{n}^{\mathrm{T}} \boldsymbol{S}_{n}+\Big. \\ & \Big.\dfrac{1}{2} {{z}}_{n}^{* 3}-\dfrac{2}{Y_{n}} k_{a n} \dot{k}_{a n} {{z}}_{n}^{*}\Big)+\dfrac{3}{4} l_{n, \max }^{2}- \\ & \dfrac{1}{\gamma_{n}} \tilde{\varTheta}_{n} \dot{\hat{\varTheta}}_{n}+\dfrac{1}{2} a_{n}^{2}+\dfrac{1}{2} \varepsilon_{n, \max }^{2} \end{split} $

(51)

设计实际控制器 ${u_q}$ 为

$ \begin{split} {u_q} = & \dfrac{1}{{{H_n}}}\left[ { - {\tau _n}{{z}}_n^* + \dfrac{2}{{{Y_n}}}{k_{an}}{{\dot k}_{an}}{{z}}_n^* - \dfrac{1}{2}{{z}}{{_n^*}^3}} \right. - \hfill \\ &\left. {\dfrac{1}{{2a_n^2}}{{z}}{{_n^*}^3}{{\hat \varTheta }_n}{\boldsymbol{S}}_n^{\rm{T}}{{\boldsymbol{S}}_n} - \dfrac{1}{4}{{z}}_n^*} \right] \end{split} $

(52)

其中， ${\tau _n} > 0$ 是设计参数。

设计自适应律 ${\hat \varTheta _n}$ 为

$ \dot{\hat{\varTheta}}_{n}=-\sigma_{n} \hat{\varTheta}_{n}+\dfrac{\gamma_{n}}{2 a_{n}^{2}} {{z}}_{n}^{* 2} \boldsymbol{S}_{n}^{\mathrm{T}} \boldsymbol{S}_{n} $

(53)

式中： ${\sigma _n} > 0$ 为设计参数。

将实际控制器(52) 和自适应律(53) 代入(51) 中得

$ \begin{split} L{V}_{n}\leqslant & -{\displaystyle \sum\limits _{m=1}^{n}{\tau }_{m}{{{z}}}_{m}^{*}{}^{4}}+\dfrac{1}{2}{\displaystyle \sum\limits _{m=1}^{n}{a}_{m}^{2}}+\dfrac{1}{2}{\displaystyle \sum\limits _{m=1}^{n}{\varepsilon }_{m,\mathrm{max}}^{2}}+\\ & \dfrac{3}{4}{\displaystyle \sum\limits _{m=1}^{n}{l}_{m,\mathrm{max}}^{2}}+{\displaystyle \sum\limits _{m=1}^{n}\dfrac{{\sigma }_{m}}{{\gamma }_{m}}{\tilde{\varTheta }}_{m}\hat{\varTheta}_{m}} \end{split} $

(54)

利用引理2可得

$ {\tilde{\varTheta }}_{m}\hat{\varTheta}_{m}\leqslant -\dfrac{1}{2}{\tilde{\varTheta }}_{m}^{2}+\dfrac{1}{2}{\varTheta }_{m}^{2} $

(55)

将式(55)代入式(54)中可得

$ \begin{split} L{V}_{n}\leqslant & -{\displaystyle \sum\limits _{m=1}^{n}{\tau }_{m}{{{z}}}_{m}^{*}{}^{4}}+\dfrac{1}{2}{\displaystyle \sum\limits _{m=1}^{n}{a}_{m}^{2}}+\dfrac{1}{2}{\displaystyle \sum\limits _{m=1}^{n}{\varepsilon }_{m,\mathrm{max}}^{2}}+\\ & \dfrac{3}{4}{\displaystyle \sum\limits _{m=1}^{n}{l}_{m,\mathrm{max}}^{2}}-{\displaystyle \sum\limits _{m=1}^{n}\dfrac{{\sigma }_{m}}{2{\gamma }_{m}}{\tilde{\varTheta }}_{m}^{2}}\text+{\displaystyle \sum\limits _{m=1}^{n}\dfrac{{\sigma }_{m}}{2{\gamma }_{m}}{\varTheta }_{m}^{2}} \end{split} $

(56)

按照上述分析，选取如下共同李雅普诺夫函数

$ V = \dfrac{1}{4}\sum\limits_{i = 1}^n {{{z}}{{_i^*}^4}} + \sum\limits_{i = 1}^n {\dfrac{1}{{2{\gamma _i}}}\tilde \varTheta _i^2} $

(57)

选取参数

$ \begin{aligned} &A=\min \left\{4 \tau_{i}, \sigma_{i}: i=1, \cdots, n\right\} \\ &B=\left\{\sum_{i=1}^{n}\left[\dfrac{1}{2}\left(a_{i}^{2}+\varepsilon_{i, \max }^{2}+\dfrac{\sigma_{i}}{\gamma_{i}} \varTheta_{i}^{2}\right)+\dfrac{3}{4} l_{i, \max }^{2}\right]\right\} \end{aligned} $

根据选取的共同李雅普诺夫函数以及参数 $A,{\text{ }}B$ ，不等式(58)成立。

$ LV\leqslant -AV+B $

(58)

定理1 　对于不确定非线性随机切换系统(1)，通过利用非线性坐标变换技术，设计虚拟控制器(23)、(38)、实际控制器(52)和自适应律(24) (39) (53)，能够保证下面的结论成立。

(1) 闭环系统中所有的信号都有界。

(2) 系统中的所有状态均不违反相应的约束。

(3) 所有误差均收敛到相应的紧集中。

证明 　以引理1为依据，可以得到

$ 0\leqslant E\left[V\left(t\right)\right]\leqslant V\left(0\right){{\rm{e}}}^{-At}+B/A $

并且，当 $t \to \infty $ 时， $0\leqslant E\left[V\left(t\right)\right]\leqslant B/A$ 。

根据上述分析同样可以得到

$ \dfrac{1}{4}{{{z}}}_{i}^{*}{}^{4}\leqslant V\left(0\right){{\rm{e}}}^{-At}+B/A $

$ \dfrac{1}{2{\gamma }_{i}}{\tilde{\varTheta }}_{i}{}^{4}\leqslant V\left(0\right){{\rm{e}}}^{-At}+B/A $

又通过计算上述两个不等式可得

$ 0 \leqslant E\left[\left|z_{i}^{*}\right|\right] \leqslant \sqrt[4]{4 V(0) \mathrm{e}^{-A t}+4 B / A} $

$ 0\leqslant E\left[\left|{\tilde{\varTheta }}_{i}\right|\right]\leqslant \sqrt{2{\gamma }_{i}\left[V\left(0\right){{\rm{e}}}^{-At}+B/A\right]} $

定义如下集合

$ \begin{array}{r} \varOmega_{{{z}}_{i}^{*}}=\left\{{{z}}_{i}^{*} \mid E\left[\left|{{z}}_{i}^{*}\right|\right] \leqslant \sqrt[4]{4 V(0) \mathrm{e}^{-A t}+4 B / A}, i=1, \cdots, n\right\} \\ \varOmega_{\tilde{\varTheta}_{i}}=\left\{\tilde{\varTheta}_{i} \mid E\left[\left|\tilde{\varTheta}_{i}\right|\right] \leqslant \sqrt{2 \gamma_{i}\left[V(0) \mathrm{e}^{-A t}+B / A\right]}, i=1, \cdots, n\right\} \end{array} $

所以， ${{z}}_i^*$ 和 ${\tilde \varTheta _i}\left( {i = 1, \cdots ,n} \right)$ 均有界，并且分别收敛到相应的紧集 ${\varOmega _{{{z}}_i^*}}$ 和 ${\varOmega _{{{\tilde \varTheta }_i}}}$ 中。根据 ${\alpha _i}\left( {i = 1, \cdots ,n - 1} \right)$ 和 ${u_q}\left( {q \in \varGamma } \right)$ 的定义，可以得出 ${\alpha _i}$ 和 ${u_q}$ 有界的结论。按照文章所做的坐标变换 ${{z}}_1^* = x_1^* - {y_d}$ 以及假设1可知 $x_1^*$ 是有界的。同理， $x_i^*\left( {i = 1, \cdots ,n} \right)$ 是有界的。已知 $ {x_i} $ 和 $x_i^*$ 之间存在非线性关系 $ x_i^* = {{{x_i}} \mathord{\left/ {\vphantom {{{x_i}} {{Y_i}}}} \right. } {{Y_i}}} $ ，由此可以判断出 $ {x_i} $ 也是有界的。综合以上的分析可知闭环系统中所有信号都是有界的。

假设 $k_{b i}=\sqrt[4]{4 V(0) \mathrm{e}^{-A t}+4 B / A},\;(i=1, \cdots, n) $ ，因此 $-k_{b i}(t) < \left|{{z}}_{i}^{*}\right|< k_{b i}(t)$ 。根据假设1可知 $-T_{0}(t) \leqslant y_{d}(t) \leqslant T_{0}(t)$ 。所以

$ -k_{b 1}(t)-T_{0}(t)<x_{1}^{*}<k_{b 1}(t)+T_{0}(t) $

假设 ${F_1}\left( t \right) = {Y_1}\left( {{k_{b1}}\left( t \right) + {T_0}\left( t \right)} \right)$ ，则依据 $ {x_i} $ 和 $x_i^*\left( {i = 1,} \right.$ $\left.{\cdots ,n} \right)$ 之间的非线性关系可知 $- {F_1}\left( t \right) < {x_1} < {F_1}\left( t \right)$ 。根据 ${\alpha _i}\left( {i = 1, \cdots ,n - 1} \right)$ 的有界性，可以假设 $- {k_{ci}}\left( t \right) < {\alpha _i} < {k_{ci}}\left( t \right)$ 。根据本文所设计的坐标变换 ${{z}}_i^* = x_i^* - {\alpha _{i - 1}}, i = 2, \cdots ,n$ 可知

$ -k_{b i}(t)-k_{c, i-1}(t)< x_{i}^{*}< k_{b i}(t)+k_{c, i-1}(t) $

同样，根据 $ {x_i} $ 和 $x_i^*\left( {i = 2, \cdots ,n} \right)$ 之间的非线性关系可知

$ \begin{gathered} - {F_i}\left( t \right) = - {Y_i}\left( {{k_{bi}}\left( t \right) + {k_{c,i - 1}}\left( t \right)} \right) \hfill < {x_1} <\\ \qquad\quad{\text{ }} {Y_i}\left( {{k_{bi}}\left( t \right) + {k_{c,i - 1}}\left( t \right)} \right) = {F_i}\left( t \right) \hfill \\ \end{gathered} $

通过上述分析得出，通过调节 ${F_i}\left( t \right)$ ，可以保证系统的状态不违反相应约束。

综上所述，定理1证明完毕。

4 仿真研究

在这一部分，将提供一个数值仿真，验证设计的控制策略对具有全状态时变约束的不确定非线性随机切换系统的有效性。

例1 　考虑如下不确定非线性随机切换系统：

$\left\{\begin{array}{l} \mathrm{d} x_{1}=\left(x_{2}+f_{1, \sigma(t)}\left(\bar{{\boldsymbol{x}}}_{1}\right)\right) \mathrm{d} t+g_{1, \sigma(t)}\left(\bar{{\boldsymbol{x}}}_{1}\right) \mathrm{d} \omega \\ \mathrm{d} x_{2}=\left(u_{\sigma(t)}+f_{2, \sigma(t)}\left(\bar{{\boldsymbol{x}}}_{2}\right)\right) \mathrm{d} t+g_{2, \sigma(t)}\left(\bar{{\boldsymbol{x}}}_{2}\right) \mathrm{d} \omega \\ y=x_{1} \end{array}\right. $

(59)

式中：当 $\sigma \left( t \right) = 1$ 和 $\sigma \left( t \right) = 2$ 时，系统函数见表1。系统的期望信号为 ${y_d} = {\text{0}}{\text{.1cos}}\left( {{\text{2}}t} \right) - {\text{0}}{\text{.02sin}}\left( {{\text{2}}t} \right)$ ，并且系统状态满足约束条件 $ - {F_1} < {x_1} < {F_1}$ 和 $ - {F_2} < {x_2} < {F_2}$ ，其中 $ {F_{\text{1}}}{\text{ = 0}}{\text{.1sin}}\left( t \right){\text{ + 0}}{\text{.3}} $ , $ {F_2}{\text{ = 0}}{\text{.5 + 0}}{\text{.2}} $ $ {\text{cos}}\left( t \right) $ 。除此之外， ${Y_i} = \left( {{k_{ai}}\left( t \right) + {x_i}} \right)\left( {{k_{ai}}\left( t \right) - {x_i}} \right)$ ， $i = 1,2$ ， ${k_{a1}} = 0.63 + 0.4\cos \left( {0.9t} \right) + 0.2\sin \left( {0.9t} \right)$ ， ${k_{a2}} = 1.2 + $ $0.2\cos \left( {1.5t} \right) + 0.1\sin \left( {1.5t} \right)$ 。

通过引入非线性坐标变换 $ x_i^* = {{{x_i}} \mathord{\left/ {\vphantom {{{x_i}} {{Y_i}}}} \right. } {{Y_i}}},i = 1,2 $ ，系统(59) 可以转换成如下形式：

$ \left\{ \begin{array}{l} \mathrm{d} x_{1}^{*}=\Big(H_{1} x_{2}^{*}+f_{2, \sigma(t)}^{*}\left(Y_{1} \bar{{\boldsymbol{x}}}_{1}^{*}\right)-\dfrac{2}{Y_{1}} k_{a 1}(t)\times \Big.\\ \qquad\quad \Big. \dot{k}_{a 1}(t) x_{1}^{*}\Big) \mathrm{d} t+g_{1, \sigma(t)}^{*}\left(Y_{1} \bar{{\boldsymbol{x}}}_{1}^{*}\right) \mathrm{d} \omega \\ \mathrm{d} x_{2}^{*} =\Big(H_{2} u_{\sigma(t)}+f_{2, \sigma(t)}^{*}\left(Y_{2} \bar{{\boldsymbol{x}}}_{2}^{*}\right)-\dfrac{2}{Y_{2}} k_{a 2}(t)\times \Big.\\ \qquad\quad \Big. \dot{k}_{a 2}(t) x_{2}^{*}\Big) \mathrm{d} t+g_{2, \sigma(t)}^{*}\left(Y_{2} \bar{{\boldsymbol{x}}}_{2}^{*}\right) \mathrm{d} \omega \\ y^{*}= Y_{1} x_{1}^{*} \end{array} \right. $

(60)

式中： ${H_1} = {{\left( {k_{a1}^2\left( t \right) + x_1^2} \right)} \mathord{\left/ {\vphantom {{\left( {k_{a1}^2\left( t \right) + x_1^2} \right)} {{Y_1}}}} \right. } {{Y_1}}}$ ， ${H_2} = {{\left( {k_{a2}^2\left( t \right) + x_2^2} \right)} \mathord{\left/ {\vphantom {{\left( {k_{a2}^2\left( t \right) + x_2^2} \right)} {Y_2^2}}} \right. } {Y_2^2}}$ ，其他系统函数见表2。

仿真中，选取的初始条件为 ${x_1}\left( 0 \right) = 0.1$ ， ${x_2}\left( 0 \right) = 0.1$ ， ${\left[ {{{\hat \varTheta }_1}\left( 0 \right),{{\hat \varTheta }_2}\left( 0 \right)} \right]^{\rm{T}}} = {\left[ {0.02,0.01} \right]^{\rm{T}}}$ ，选取的各设计参数为 ${\tau _1} = 100$ ， ${\tau _2} = 50$ ， ${a_1} = 20$ ， ${a_2} = 10$ ， ${\sigma _1}{\text{ = }}2$ ， ${\sigma _2} = 1$ ， ${\gamma _1} = 0.1$ ， ${\gamma _2} = 0.2$ 。

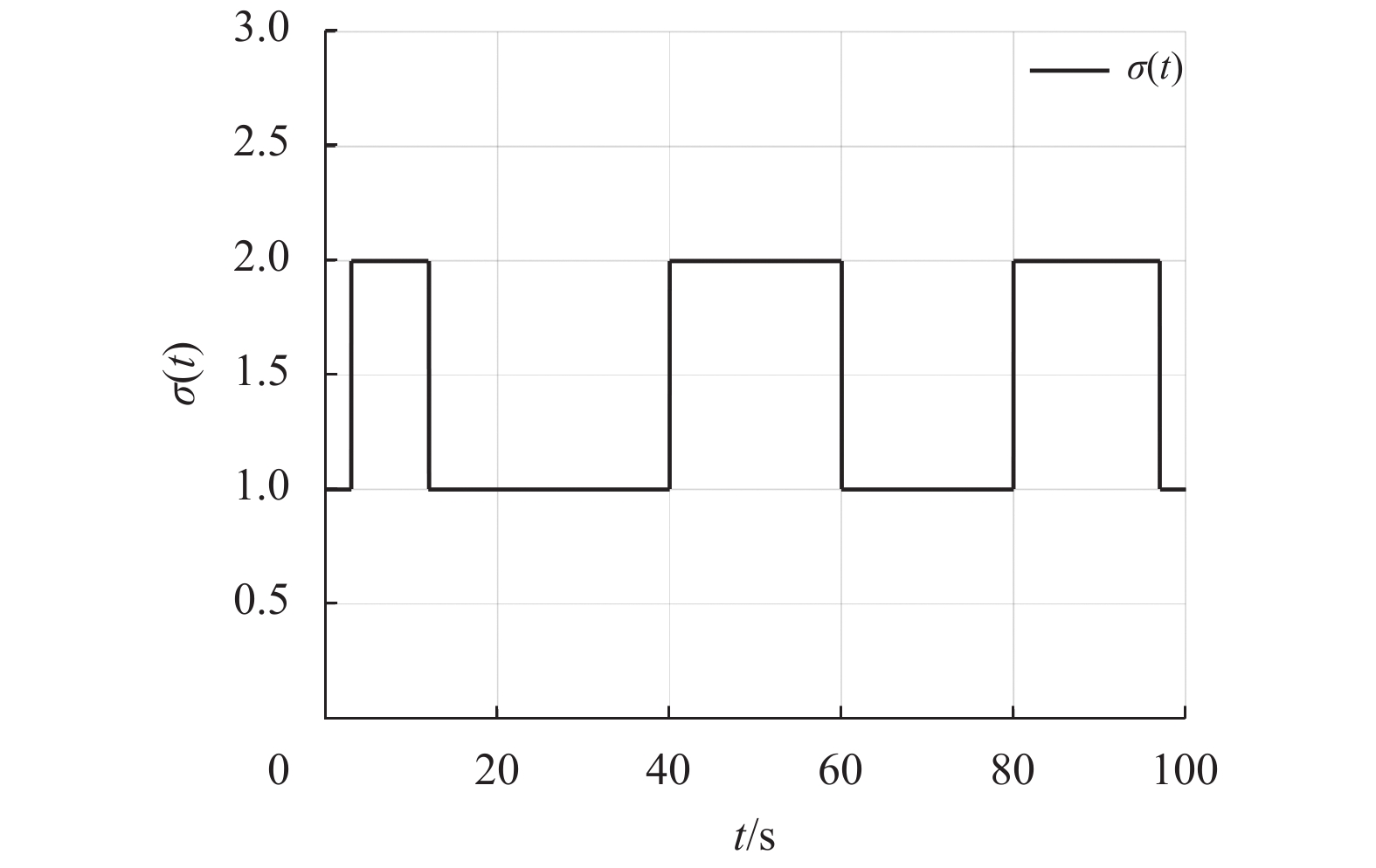
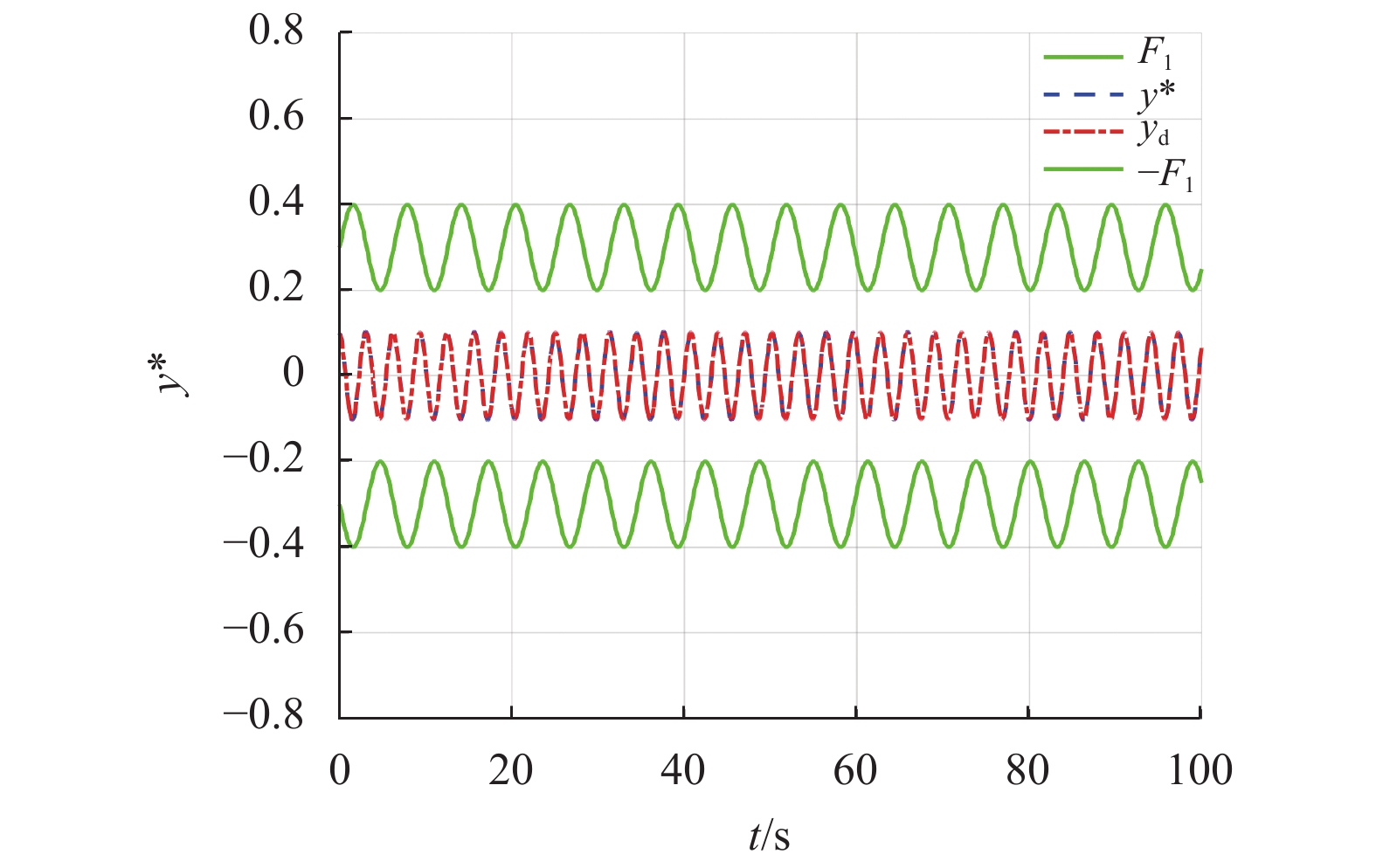
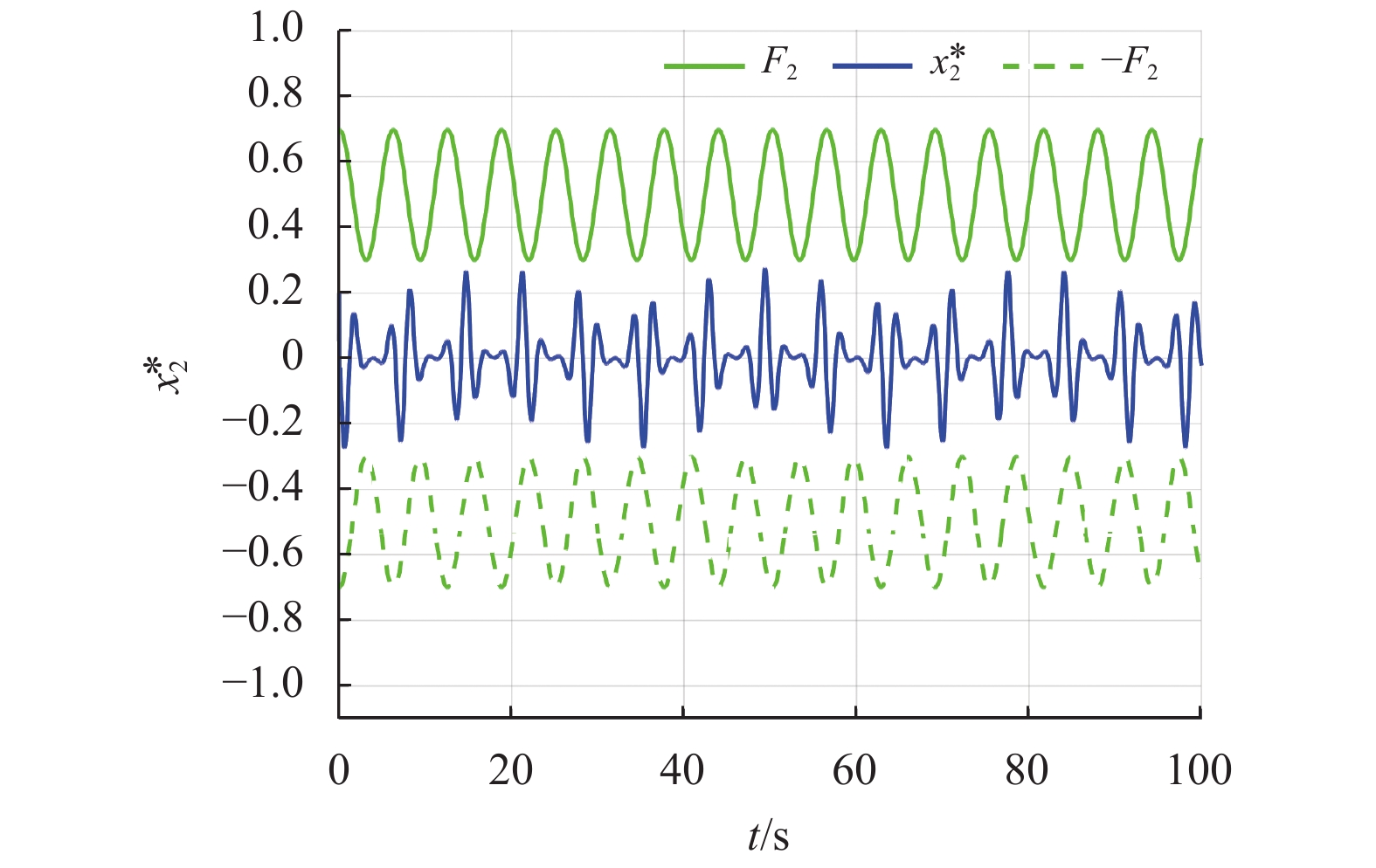
图1~5为仿真结果。图1展示了切换信号的轨迹。图2给出了控制系统的跟踪性能，从图中可以看出系统输出跟踪效果非常好，并且不违反相应的约束条件。图3说明系统的状态 $x_2^{\text{*}}$ 不违反其相应的约束条件。图4和图5分别是系统的自适应律和控制器的轨迹，从图中不难看出自适应律和控制器均有界。

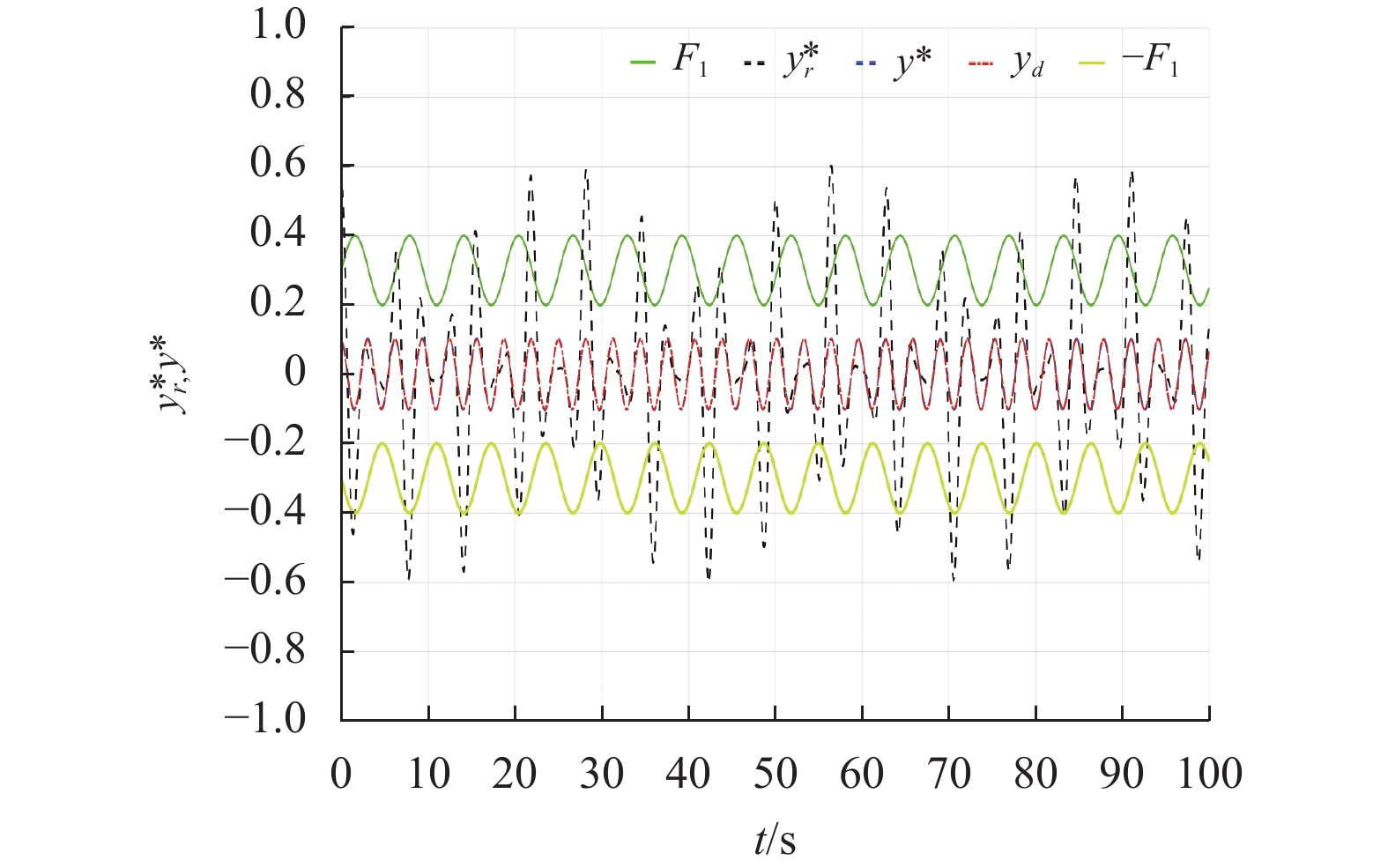
以例1中的系统为背景，将本文设计的控制策略与文献[29]中的做了比较，结果如图6所示。其中， $y_r^*$ 是文献[29]中的输出， ${y^*}$ 是本文中的输出， ${y_d}$ 是期望信号， ${F_{11}}$ 和 $ - {F_{11}}$ 是相应的约束条件。从图6中可以看出，文献[29]中的控制方案的跟踪性能较差，且违反了约束条件。

5 结论

本文针对一类不确定非线性随机切换系统进行了全状态约束控制研究，基于任意切换规则，设计了一种自适应神经网络控制策略。所针对的约束类型为时变型约束，约束条件将随着时间而发生改变，在设计控制方案的过程中涉及到的控制算法较复杂。除此之外，本文采用了坐标变换技术来解决系统的状态约束问题，方法新颖且更好地解决了系统状态约束问题。最后，通过数值仿真实验可知本文所设计的控制策略能够达到较好的控制效果。