塑料制品因其良好的可塑性、化学稳定性以及质量轻等特点被广泛应用于航空航天、电力电子以及汽车制造等各个领域^[1]。而注塑成型作为注塑件生产过程中的重要一环，将直接影响注塑件的成品质量。注塑成型是一种间歇性的生产过程工艺，一般包括合模、注射、保压、冷却以及脱模等5个阶段。首先，颗粒状或粉末状树脂材料经由料斗倒入料筒体中。塑料颗粒在螺杆旋转摩擦以及筒壁加热带的作用下被加热至熔融状态，并填充满螺杆前的物料空腔。然后在伺服电机的驱动作用下，注射座前移至指定位置，注塑模具在机械结构的作用下夹紧。螺杆在伺服阀的驱动作用下沿筒腔向前做往复运动，迫使熔融树脂以较快的速度注入封闭模具并保持稳定的注射压力。随后，模腔内压力被进一步升高，更多的熔料被压入模具中并填充因熔融塑料凝固收缩而形成的空腔。在经过一定时间冷却后，模具打开并将定型的注塑件弹出。在不同的注塑成型阶段，注射速度、筒腔温度、模具压力等各项参数有着不同的要求，各项参数的变化都会不同程度地影响产品的最终质量^[2-3]。然而受限于注塑成型技术底蕴不足，国内现有的注塑成型控制技术已越来越难以满足当下高效化、精确化、响应快、高稳定性的生产需求，并且与国际先进水平仍存在一定的技术差距。

近年来，国内外研究团队围绕注塑成型过程控制策略展开相关研究，并取得了大量研究成果。例如，文献[4]提出一种基于迭代学习控制(Iterative Learning Control, ILC)的注塑机注射速度控制方法。文献[5]将PI(Proportion Integration)控制与ILC控制相结合，通过复合控制结构提高控制性能。文献[6]提出一种基于离散预期学习控制的注塑控制策略，该策略拥有较好的抗干扰能力。文献[7]采用模型预测控制(Model Predictive Control, MPC)策略，考虑树脂材料PVT(Pressure Volume Temperature)特性，实现对注塑机模腔压力的自适应控制。文献[8]结合循环交换领域人工蜂群算法与PID(Proportion Integration Differentiation)控制实现对料筒温度的快速、精确控制。模型预测控制作为一种考虑约束的有限时域最优控制方法，能够快速地对跟踪轨迹的变化做出响应，在解决注塑成型过程控制等复杂问题时更具优势^[9]。而随着模型复杂度的提升，MPC控制器往往需要消耗更长的计算时间，这使得注塑控制过程的实时性要求越来越难以得到保障。针对这一问题，不少学者展开了相关研究，常见的处理方式是将MPC转化为显式模型预测控制以降低计算的复杂度，通过离线计算、在线查询的方式替换原有的在线求解过程。然而此类方法存在一定的局限性，一般仅适用于处理较小规模的控制问题^[10-12]。

深度学习方法拥有较强的辨识与学习能力，目前被广泛应用于目标识别、文本翻译以及路径规划等研究领域^[13-15]。而现有研究表明，将深度学习与控制理论相结合的策略能够较好地简化复杂控制过程^[16-17]。文献[18]提出一种通过深度神经网络(Deep Neural Network, DNN)学习实时状态和最优控制输入之间变化关系的策略，实现小行星着陆器的实时最优控制。文献[19]将DNN与预测控制相结合，实现对谐振功率转换器实时预测控制。文献[20]设计并训练深度信念网络，实现对直流电机的在线PID控制。

本文组织结构如下：第1节介绍了注塑机注射过程速度模型的建模过程以及约束条件；第2节介绍了本文所使用的方法，包括MPC控制器的设计、数据集采集以及DNN控制器的设计与优化；第3节通过仿真实验验证了该方法的有效性，并对仿真结果进行比较；第4节对本文所提出的基于DNN的注塑机过程预测控制方法进行了总结。

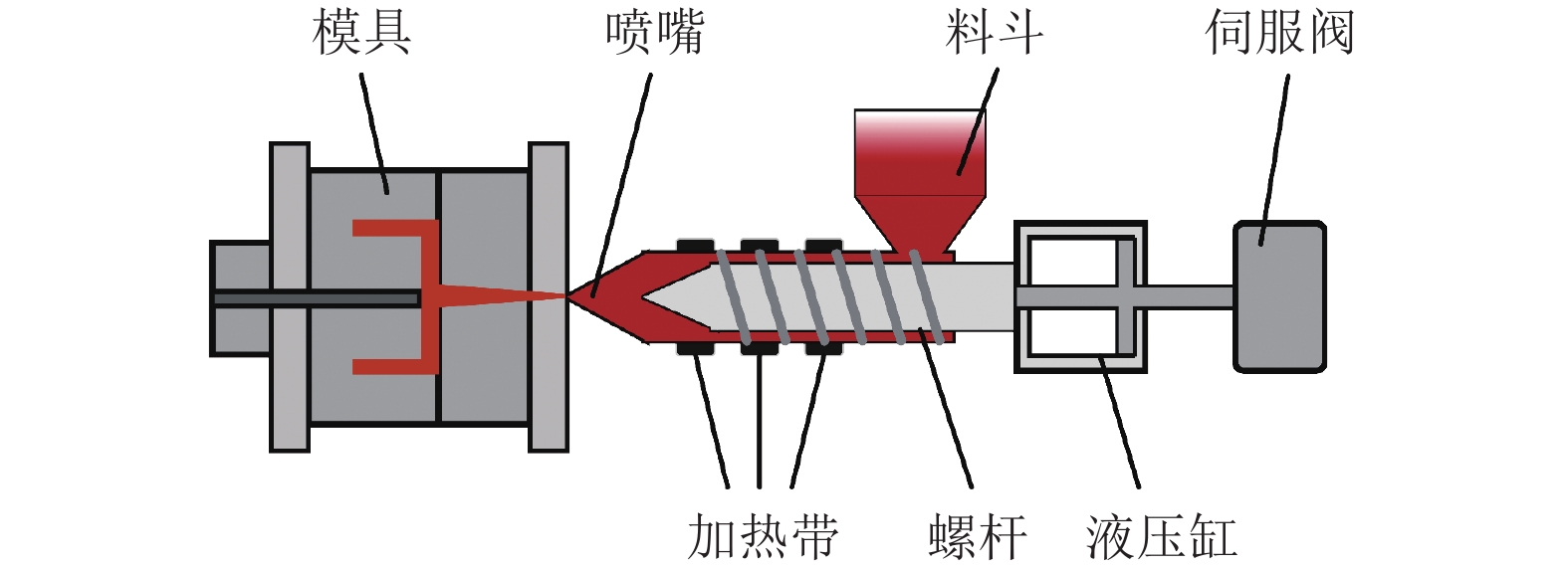
1 注塑机注射速度过程建模

注塑机注塑成型系统由多个复杂模块共同组成，包括伺服阀、注射液压缸、螺杆、控制器以及电子传感器等。简化注塑机注射结构如图1所示。在注塑机运行过程中，位移、速度等传感器不断收集系统各项状态数据，并发送至注塑机控制器模块。控制器根据实时的状态数据，调整伺服阀的输入电压大小并调节伺服阀的开度，实现对注塑机注射速度的控制。

注塑机注射速度控制过程是一个间歇性的控制过程。在不同的控制阶段，注射速度的取值需跟随参考轨迹的变化而发生改变，这对控制器的控制精度提出了较高要求。本文使用式(1)所示四阶注塑机线性模型^[21]，该传递函数为注射速度与伺服阀开度大小之比。

$ G(s) = \frac{p}{{(s + {s_1})(s + {s_2})( {{{(s + {s_3})}^2} + s_4^2} )}} $

(1)

式中： $ p $ 、 $ {s_1} $ 、 $ {s_2} $ 、 $ {s_3} $ 、 $ {s_4} $ 为注塑机系统配置参数，可根据不同的注塑机模型系统进行设置。在本文中， $p{\text{ = }} $ $ 2.144 \times {10^{11}} $ ， $ {s_1}{\text{ = }}125 $ ， $ {s_2}{\text{ = }}1\;138 $ ， $ {s_3}{\text{ = 383}} $ ， $ {s_4}{\text{ = 1\;135}} $ 。

对上述传递函数进行变换并采用零阶保持法离散状态方程，取采样周期为 $ T{\text{ = }}0.005\; {\text{s}} $ ，可得如式(2)所示的离散状态空间表达式。

$ \left\{ \begin{array}{l} {\boldsymbol{x}}(k + 1) = {\boldsymbol{Ax}}(k) + {\boldsymbol{B}}u(k) \hfill \\ y(k) = {\boldsymbol{Cx}}(k) \end{array} \right. $

(2)

式中： $ {\boldsymbol{x}} $ 为离散状态方程的状态变量， $ u $ 为注塑机伺服阀控制信号， $ y $ 为注塑机注射速度， $ k $ 为当前采样时刻。并且有

$ {{\boldsymbol{A}} = \left[\begin{array}{cccc}0.107 & 66.512 & -6.689\times {10}^{4} & -1.024\times {10}^{7}\\ 5.015\times {10}^{-5} & 0.208 & 194.135 & 2.947\times {10}^{4}\\ -1.444\times {10}^{-7} & -2.428\times {10}^{-4} & -0.159 & -83.289\\ 4.081\times {10}^{-10} & 6.835\times {10}^{-7} & 7.955\times {10}^{-4} & 0.625\end{array}\right]，} $

$ {\begin{split} \\ {\boldsymbol{B}}=\left[\begin{array}{c}5.015\times {10}^{-5}\\ -1.444\times {10}^{-7}\\ 4.081\times {10}^{-10}\\ 1.838\times {10}^{-12}\end{array}\right]，{\boldsymbol{C}}=\left[\begin{array}{cccc}0& 0& 0& 2.144\times {10}^{11}\end{array}\right] \end{split}}$

在注塑控制过程中，注塑机性能表现受限于自身的硬件条件，一般需要满足相应的约束条件并在合理范围内安全运行，注塑机模型的约束条件给定如式(3)所示。

$ \left\{ \begin{array}{l} {u_{\min }} \leqslant u \leqslant {u_{\max }} \hfill \\ {y_{\min }} \leqslant y \leqslant {y_{\max }} \hfill \\ \end{array} \right. $

(3)

式中： $ {u_{\min }} $ 、 $ {u_{\max }} $ 为注塑机伺服阀控制信号的最小值和最大值， $ {y_{\min }} $ 、 $ {y_{\max }} $ 为注射机注射速度的最小值和最大值。

传统MPC控制器可以通过配置参考注射速度轨迹，结合注射速度数学模型实现对注射速度的精确预测控制，而预测控制较为复杂的计算过程使得控制的实时性难以保障。因此，本文提出结合DNN与MPC的学习预测控制方法以实现对注塑机注射速度的快速精准跟踪控制。

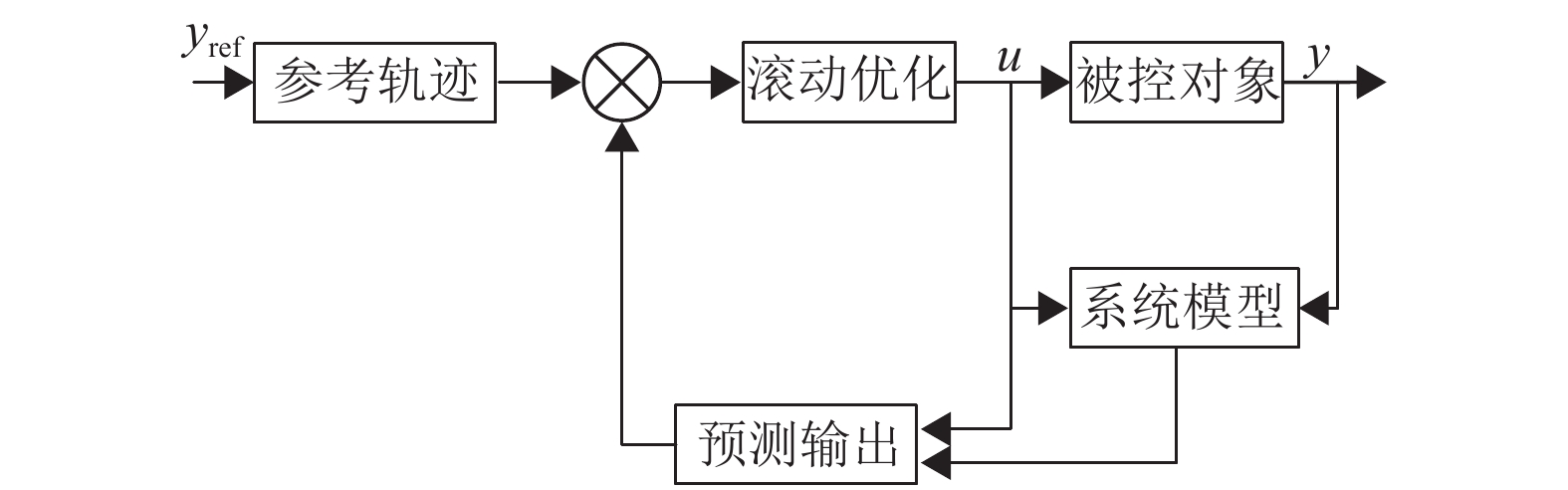
2 本文方法 2.1 模型预测控制器设计

注射速度控制过程是一个间歇性的、不断循环的、时变的变化过程。相较于传统PID控制，基于模型预测控制的注塑机控制器在拥有较高控制精度的同时有着较好的抗扰动性。MPC控制结构如图2所示。控制器经由传感器获取实时状态数据 $ {\boldsymbol{x}} $ 与注射速度 $ y $ ，系统模型用以预测有限时间域内注射速度的变化情况。设置合适的参考轨迹 $ {y_{{\text{ref}}}} $ ，控制器通过求解有限时域内的最优控制问题获得最优控制序列，并将序列首项作为控制输入 $ u $ 作用于伺服阀。

模型预测控制的实现过程具体可分为3个部分，即预测模型的构建、目标函数的确定以及滚动优化。考虑系统增广状态形式，对注塑机注射系统离散状态空间表达式(2)进行整理，可得如下增广状态空间表达式

$ \left\{ \begin{array}{l} {{\boldsymbol{x}}_{\text{s}}}(k + 1) = {{\boldsymbol{A}}_{\text{s}}}{{\boldsymbol{x}}_{\text{s}}}(k) + {{\boldsymbol{B}}_{\text{s}}}\Delta u(k) \hfill \\ y(k) = {{\boldsymbol{C}}_{\text{s}}}{{\boldsymbol{x}}_{\text{s}}}(k) \end{array} \right. $

(4)

式中：

${{\boldsymbol{A}}}_{{\rm{s}}}=\left[\begin{array}{cc}{\boldsymbol{A}}&{\boldsymbol{B}}\\ {{\boldsymbol{0}}}_{{N}_{u}\times {{{N}}}_{{\boldsymbol{x}}}}&{{\boldsymbol{I}}}_{{N}_{{\boldsymbol{x}}}}\end{array}\right]，{{\boldsymbol{B}}}_{\text{s}}=\left[\begin{array}{c}{\boldsymbol{B}}\\ {{\boldsymbol{I}}}_{{N}_{{\boldsymbol{x}}}}\end{array}\right]，{{\boldsymbol{C}}}_{\text{s}}=\left[\begin{array}{cc}{\boldsymbol{C}}&{{\boldsymbol{0}}}_{{N}_{{\boldsymbol{x}}}}\end{array}\right]$ $ {{\boldsymbol{x}}_{\text{s}}}(k) = {[ {\begin{array}{*{20}{c}} {{\boldsymbol{x}}(k)}&{u(k - 1)} \end{array}} ]^{\text{T}}} $ ， $ {{{N}}_{\boldsymbol{x}}} $ 和 $ {{{N}}_u} $ 分别为状态变量 $ {\boldsymbol{x}} $ 和控制变量 $ u $ 的个数， $ {\boldsymbol{I}} $ 为单位矩阵。

目标函数能够衡量实际输出与参考值间的误差大小，注射速度的变化过程应迅速且平滑，目标函数设定式(5)所示。

$ \begin{split} \mathop {\min }\limits_{\Delta u(k)} J =& \sum\nolimits_{k = 1}^{{N_{\text{p}}}} {{{(y(k) - {y_{{\text{ref}}}}(k))}^{\text{T}}}{\boldsymbol{Q}}(y(k) - {y_{{\text{ref}}}}(k)) + } \hfill \\& \sum\nolimits_{k = 1}^{{N_{\text{c}}}} {\Delta u{{(k)}^{\text{T}}}{\boldsymbol{R}}\Delta u(k)} \end{split} $

(5)

式中： $ {y_{{\text{ref}}}} $ 为目标注射速度参考轨迹， $ {\boldsymbol{Q}} $ 、 ${\boldsymbol{ R}} $ 为权重矩阵， $ {N_{\text{p}}} $ 为预测时域， $ {N_{\text{c}}} $ 为控制时域， $\Delta u(k) = u(k) - $ $ u(k - 1) $ 。由式(3)~(5)可得式(6)所示注塑机有限时域内的最优控制问题。

$ \begin{split} & \mathop {\min }\limits_{\Delta u(k)} J = \sum\nolimits_{k = 1}^{{N_{\text{p}}}} {{{(y(k) - {y_{{\text{ref}}}}(k))}^{\text{T}}}{\boldsymbol{Q}}(y(k) - {y_{{\text{ref}}}}(k)) + } \hfill \\& \qquad \qquad {\text{ }}\sum\nolimits_{k = 1}^{{N_{\text{c}}}} \Delta u{(k)^{\text{T}}}{\boldsymbol{R}}\Delta u(k) \hfill \\& \text { s.t. }\left\{\begin{array}{l} \boldsymbol{x}_{\mathrm{s}}(k+1)=\boldsymbol{A}_{\mathrm{s}} \boldsymbol{x}_{\mathrm{s}}(k)+\boldsymbol{B}_{\mathrm{s}} \Delta u(k) \\ y(k)=\boldsymbol{C}_{\mathrm{s}} \boldsymbol{x}_{\mathrm{s}}(k) \\ u_{\min } \leqslant u(k) \leqslant u_{\max } \\ y_{\min } \leqslant y(k) \leqslant y_{\max } \end{array}\right. \end{split}$

(6)

对上述最优控制问题(6)进行整理，可得式(7)所示二次型规划(Quadratic Programming, QP)问题。

$ \begin{split} & \mathop {\min }\limits_{\Delta {\boldsymbol{U}}} \frac{1}{2}\Delta {{\boldsymbol{U}}^{\text{T}}}{\boldsymbol{H}}\Delta {\boldsymbol{U}} + {{\boldsymbol{f}}^{\text{T}}}\Delta {\boldsymbol{U}} \hfill \\& {\text{s}}{\text{.t}}{\text{. }}{\boldsymbol{E}}\Delta {\boldsymbol{U}} \leqslant {\boldsymbol{D}} \end{split}$

(7)

式中： ${\boldsymbol{H}} = {{\boldsymbol{\varPhi}} ^{\text{T}}}{\boldsymbol{Q}}{\boldsymbol{\varPhi}} + {\boldsymbol{R }}$ , ${\boldsymbol{ f }}= {{\boldsymbol{\varPhi}} ^{\text{T}}}{\boldsymbol{Q}}\left( {{\boldsymbol{\varGamma}} {{\boldsymbol{x}}_{\text{s}}}(k) - {{\boldsymbol{Y}}_{{\text{ref}}}}} \right)$

$ \quad \Delta {\boldsymbol{U}} = {[ {\begin{array}{*{20}{c}} {\Delta u(k)}& {\Delta u(k + 1)}& \cdots & {\Delta u(k + {N_{\text{c}}} - 1)} \end{array}} ]^{\text{T}}}$

$ \quad {{\boldsymbol{Y}}_{{\text{ref}}}} = {[ {\begin{array}{*{20}{c}} {{y_{{\text{ref}}}}(k + 1)}& {{y_{{\text{ref}}}}(k + 2)}& \cdots & {{y_{{\text{ref}}}}(k + {N_{\text{p}}})} \end{array}} ]^{\text{T}}}$

${\boldsymbol{\varPhi}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{C}}_{\text{s}}}{{\boldsymbol{B}}_{\text{s}}}}& 0& \cdots & 0 \\ {{{\boldsymbol{C}}_{\text{s}}}{{\boldsymbol{A}}_{\text{s}}}{{\boldsymbol{B}}_{\text{s}}}}& {{{\boldsymbol{C}}_{\text{s}}}{{\boldsymbol{B}}_{\text{s}}}}& \cdots & 0 \\ \vdots & \vdots & & \vdots \\ {{{\boldsymbol{C}}_{\text{s}}}{\boldsymbol{A}}_{\text{s}}^{{N_{\text{p}}} - 1}{\boldsymbol{B}}}& {{{\boldsymbol{C}}_{\text{s}}}{\boldsymbol{A}}_{\text{s}}^{{N_{\text{p}}} - 2}{\boldsymbol{B}}}& \cdots & {{{\boldsymbol{C}}_{\text{s}}}{\boldsymbol{A}}_{\text{s}}^{{N_{\text{p}}} - {N_{\text{c}}} - 1}{\boldsymbol{B}}} \end{array}} \right] $

${\boldsymbol{\varGamma }} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{C}}_{\text{s}}}{{\boldsymbol{A}}_{\text{s}}}} \\ {{{\boldsymbol{C}}_{\text{s}}}{\boldsymbol{A}}_{\text{s}}^{\text{2}}} \\ \vdots \\ {{{\boldsymbol{C}}_{\text{s}}}{\boldsymbol{A}}_{\text{s}}^{{N_{\text{p}}}}} \end{array}} \right],\;{\boldsymbol{ E}} = \left[ {\begin{array}{*{20}{c}} {\boldsymbol{L}} \\ { - {\boldsymbol{L}}} \\ {\boldsymbol{ \varPhi}} \\ { - {\boldsymbol{\varPhi }}} \end{array}} \right],\;{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{U}}_{\max }} - {\boldsymbol{U}}(k - 1)} \\ { - {{\boldsymbol{U}}_{\min }} + {\boldsymbol{U}}(k - 1)} \\ {{{\boldsymbol{Y}}_{\max }} - {\boldsymbol{\varGamma}} {{\boldsymbol{x}}_{\text{s}}}(k)} \\ { - {{\boldsymbol{Y}}_{\min }} + {\boldsymbol{\varGamma }}{{\boldsymbol{x}}_{\text{s}}}(k)} \end{array}} \right] $

$ {\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} 1& 0& \cdots & 0 \\ 1& 1& \cdots & 0 \\ \vdots & \vdots & & \vdots \\ 1& 1& \cdots & 1 \end{array}} \right]$

使用QP求解器对问题(7)进行求解，得到当前采样时刻的有限时域最优控制序列。在滚动优化过程中，MPC控制器在各采样时刻对问题(7)进行重新计算，并将序列首项作为控制输入作用于被控系统。

2.2 训练数据集的建立

DNN的反向传播是一种有监督的训练方法，需要使用大量运行数据用于学习。为更好地训练DNN控制器，让网络充分地收敛并实现对注射速度的快速预测控制，所采集的仿真运行数据应尽可能覆盖各种不同的情况。在实际运行过程中，受限于生产任务不同以及注塑机内外部环境的干扰，注射机的初始条件与注射速度的参考轨迹往往并不固定，需要根据不同任务进行调整以满足不同生产需求。本文首先通过收集注塑模型的开环运行数据，获取系统状态变量的变化范围。在数据采集过程中，随机生成注塑机系统的初始状态，设置不同的注射速度参考轨迹，采集控制器输出与系统状态数据，最后将采集的数据整理、存储为预测控制数据集，用以训练DNN控制器。

本文共生成1000组注塑机仿真运行轨迹，每组轨迹包含200个采样时刻在内的预测控制输入、系统状态变量以及参考注射速度等仿真运行数据，共计200000组运行数据。80%的数据作为DNN控制器的训练集，20%的数据作为DNN的验证集。

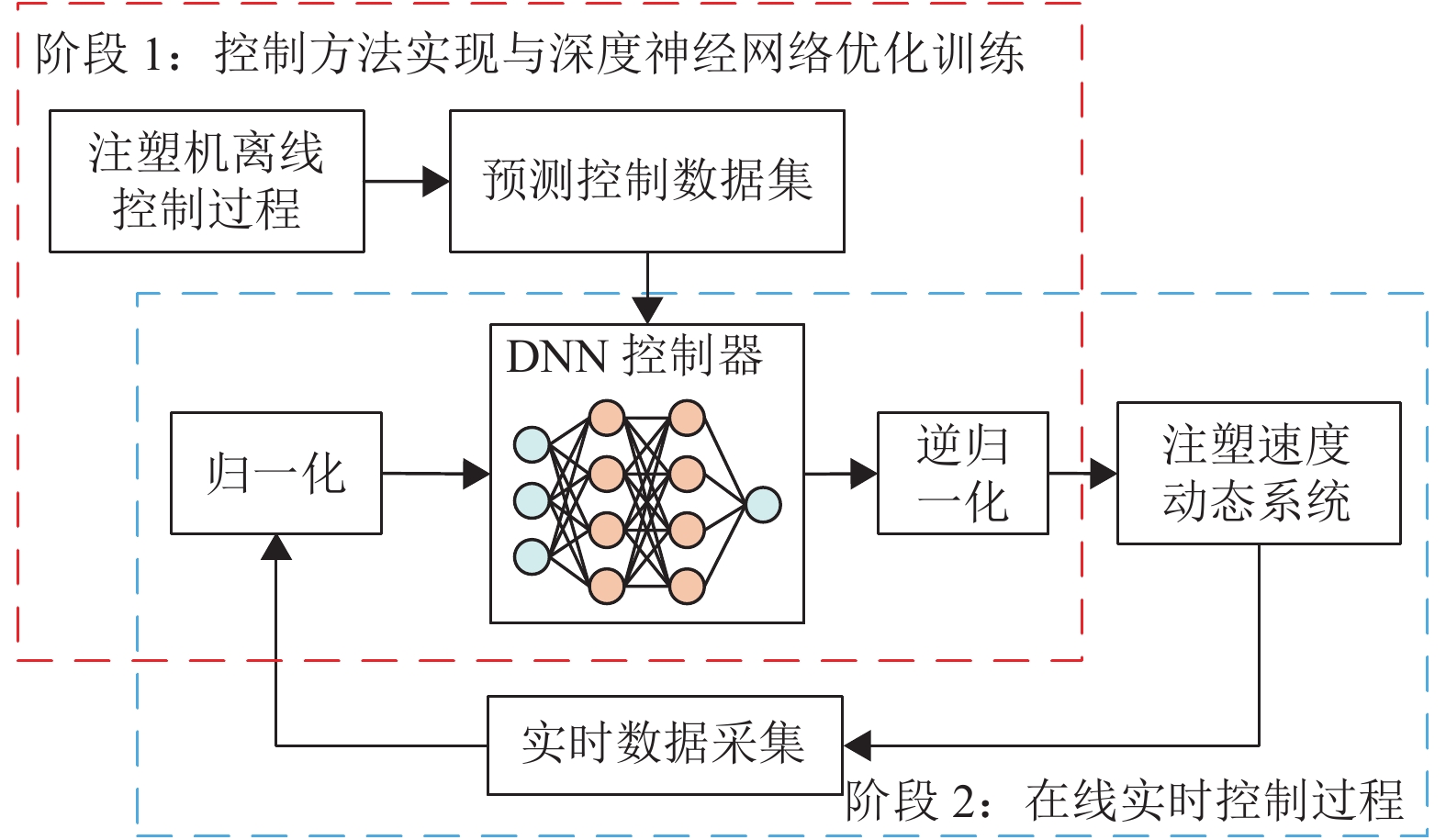
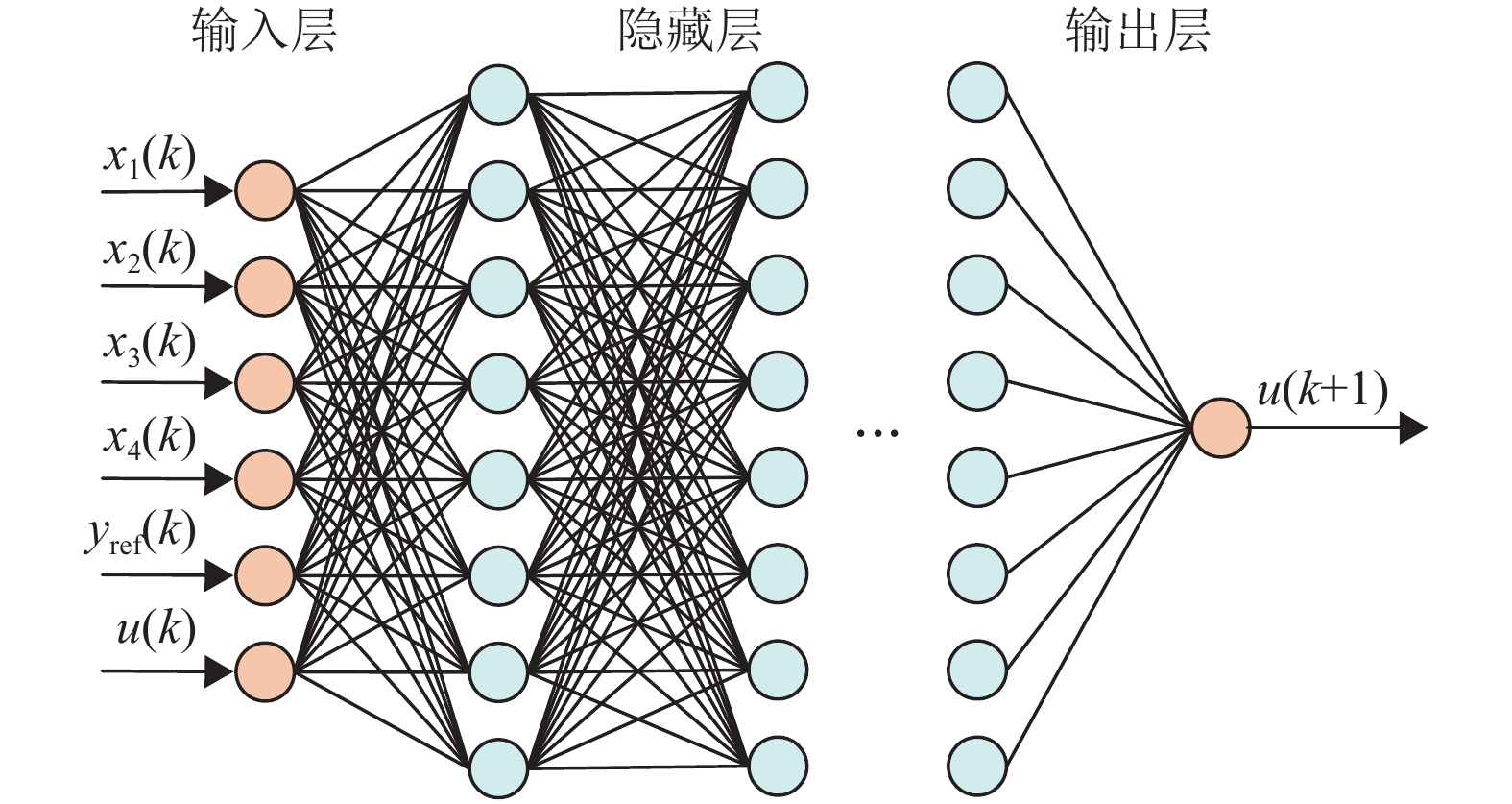
2.3 深度神经网络设计与优化

基于DNN的MPC控制过程流程图如图3所示，控制流程主要可分为2个阶段。首先是控制方法的实现与DNN的优化训练。在离散数据集的基础上对DNN控制器进行训练与优化。通过这一过程，使DNN能够映射系统状态输入—预测输出的内部联系。然后通过在线实时控制，验证并比较不同控制器的控制效果。注塑动态系统深度神经网络的结构如图4所示，DNN由多层神经网络相互连接构成，能够表示由输入到输出之间复杂的内部映射关系，并根据注塑机系统状态输出当前有限时间域内的最优控制量。

DNN主要由输入层、输出层以及隐藏层3个部分组成，分别为DNN的第一层、最后一层以及输入层与输出层之间的其余中间层。每一层神经网络都由多个神经元共同组成，DNN数学表达式见式(8)。

$ \left\{ \begin{gathered} {\sigma _{ij}} = {g_j}({{\boldsymbol{\omega}} _{ij}}{\sigma _{j - 1}} + {b_{ij}}) \hfill \\ {\sigma _{j - 1}} = \sum\nolimits_{i = 1}^{N_i^{j - 1}} {{g_{j - 1}}({{\boldsymbol{\omega}} _{i,j - 1}}{\sigma _{i,j - 1}} + {b_{i,j - 1}})} \hfill \\ \end{gathered} \right. $

(8)

式中： $ g $ 、 $ {\boldsymbol{\omega }}$ 、 $ b $ 分别为DNN的激活函数、权重矩阵以及偏置， $ {\sigma _j} $ 为第 $ j $ 层神经网络， $ {\sigma _{ij}} $ 为第 $ j $ 层、第 $ i $ 个神经元， $ i = 1,2, \cdots ,{N_{\sigma }} $ ， $ j = 1,2, \cdots ,{N_{\text{L}}} $ 。网络输入为 ${\boldsymbol{X}} = $ $ {\left[ {x_1^{(k)},x_2^{(k)},x_3^{(k)},x_4^{(k)},y_{{\text{ref}}}^{(k)},{u^{(k)}}} \right]^{\text{T}}} $ ， ${N_\sigma } $ 为各层神经网络的神经元个数， ${N_{\rm{L}}} $ 为DNN的层数。输出为MPC控制器的预测结果 $ {u^{(k + 1)}} $ ，网络的激活函数为ReLU函数，网络的优化算法为Adam算法^[22]。与Sigmoid、tanh等激活函数相比，ReLU函数结构简单，能够使DNN获得更快的收敛速度与计算速度。

为使网络尽可能地收敛并实现精确预测，需要最小化DNN输出结果与MPC控制器预测输出 $ u $ 之间的误差，因此选用均方误差函数(Mean Square Error, MSE)作为网络的损失函数，数学表达式见式(9)。

$ L({\boldsymbol{\delta}} ) = \frac{1}{N}\sum\nolimits_{i = 1}^N {\left| {{\rm{Net}}({{\boldsymbol{X}}_i}|{\boldsymbol{\delta}} ) - u_i^*} \right|^2} $

(9)

式中： ${\boldsymbol{ \delta}} $ 为单次输入的训练数据集， $ {\rm{Net}}({{\boldsymbol{X}}_i}|{\boldsymbol{\delta}} ) $ 为DNN在输入为 $ {{\boldsymbol{X}}_i} $ 下网络输出的预测控制量， $ u_i^* $ 为预测控制参考取值。

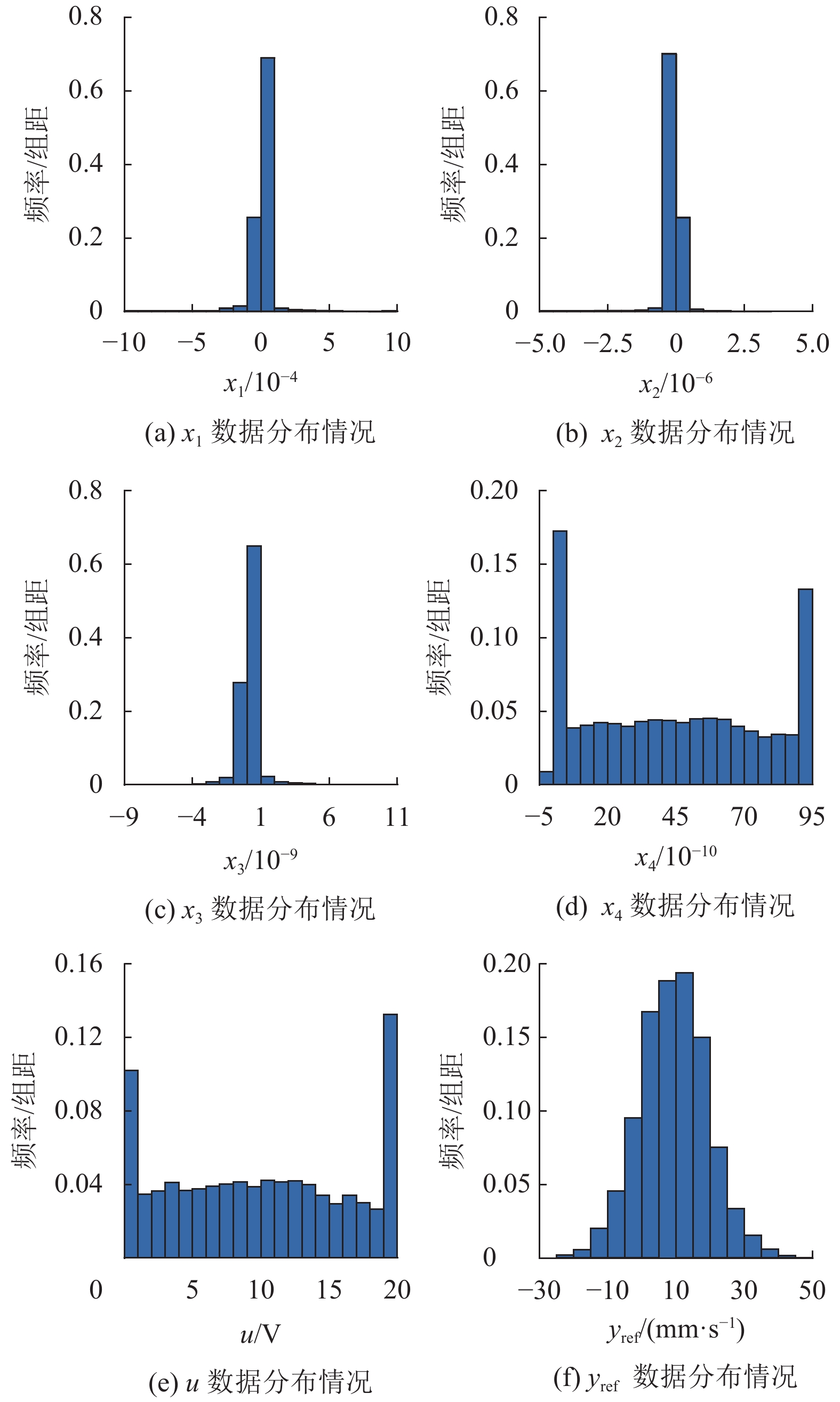
MPC控制过程数据分布如图5所示，分别为 $ {x_1} $ 、 $ {x_2} $ 、 $ {x_3} $ 、 $ {x_4} $ 、 $ {y_{{\rm{ref}}}} $ 以及 $ u $ 的分布情况。图中x轴为各项数据的分布区间，y轴为数据的分布频率。由图5可知，各项数据的分布范围差异较大，尤其是数据分布的数量级不同，这会造成DNN在训练过程中难以收敛，或是需要消耗更多的迭代次数。为此，需要对训练数据集进行标准化处理，本文使用Min-Max标准化方法将数据映射至[0,1]区间内，该方法能够提高DNN的收敛速度与预测精度，Min-Max标准化算式见式(10)。

$ {{\boldsymbol{X}}_{{\text{norm}}}} = \frac{{{\boldsymbol{X}} - {{\boldsymbol{X}}_{\min }}}}{{{{\boldsymbol{X}}_{\max }} - {{\boldsymbol{X}}_{\min }}}}$

(10)

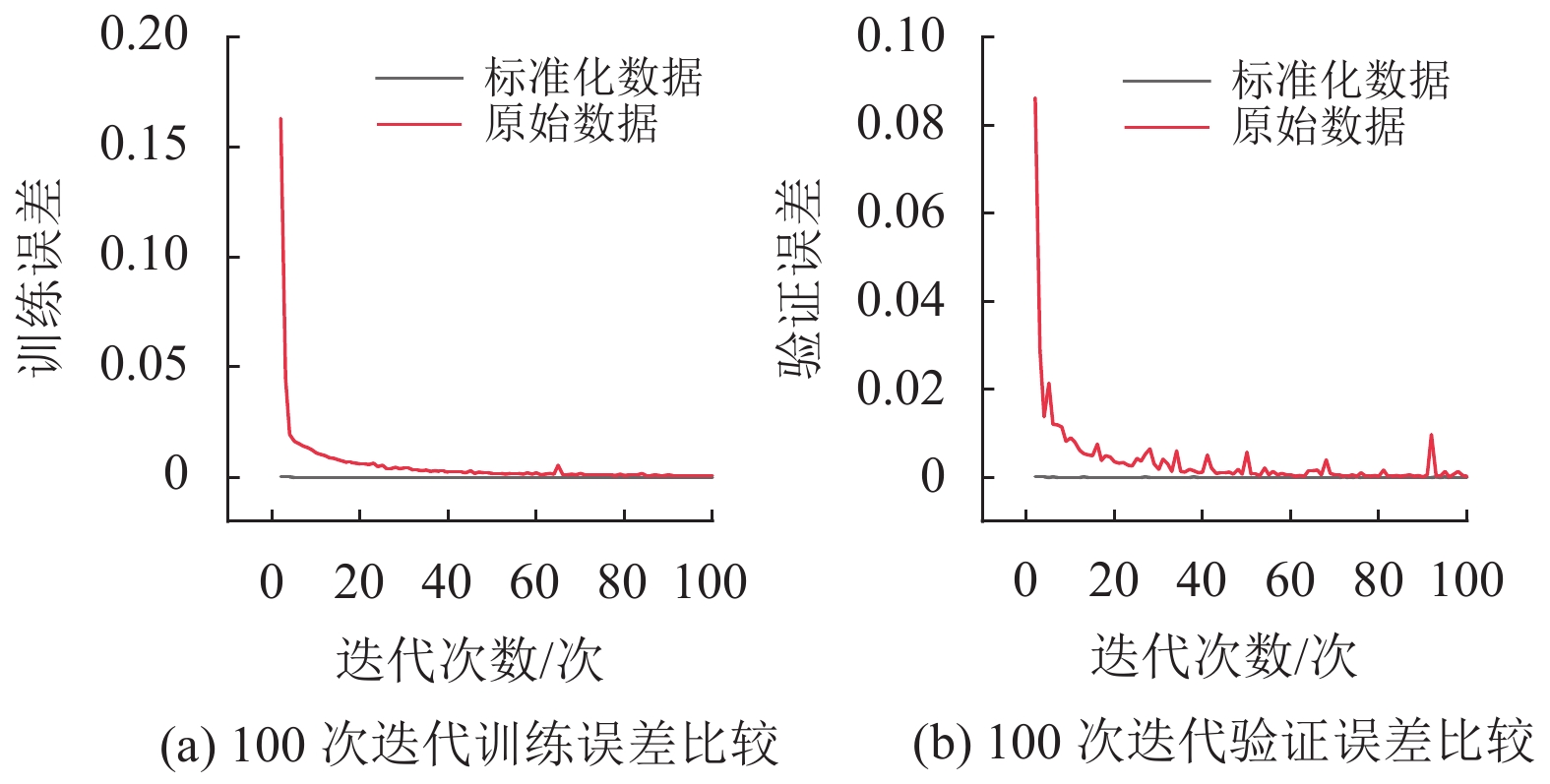
图6分别为使用原始数据集和标准化数据集在相同条件下对DNN进行100次迭代训练后的结果。训练误差衡量了网络对训练集的收敛情况，验证误差用以评估不同网络的预测效果。网络的误差越小，则DNN的预测结果与MPC控制器越接近。相较于未处理的原始数据集，标准化后的数据集能够使模型更快地收敛，并且收敛至更小的训练与验证误差。而由于网络的输入输出被线性映射至新的区间，因此在使用DNN进行预测控制时，需对网络的输入输出进行标准化与反标准化处理。

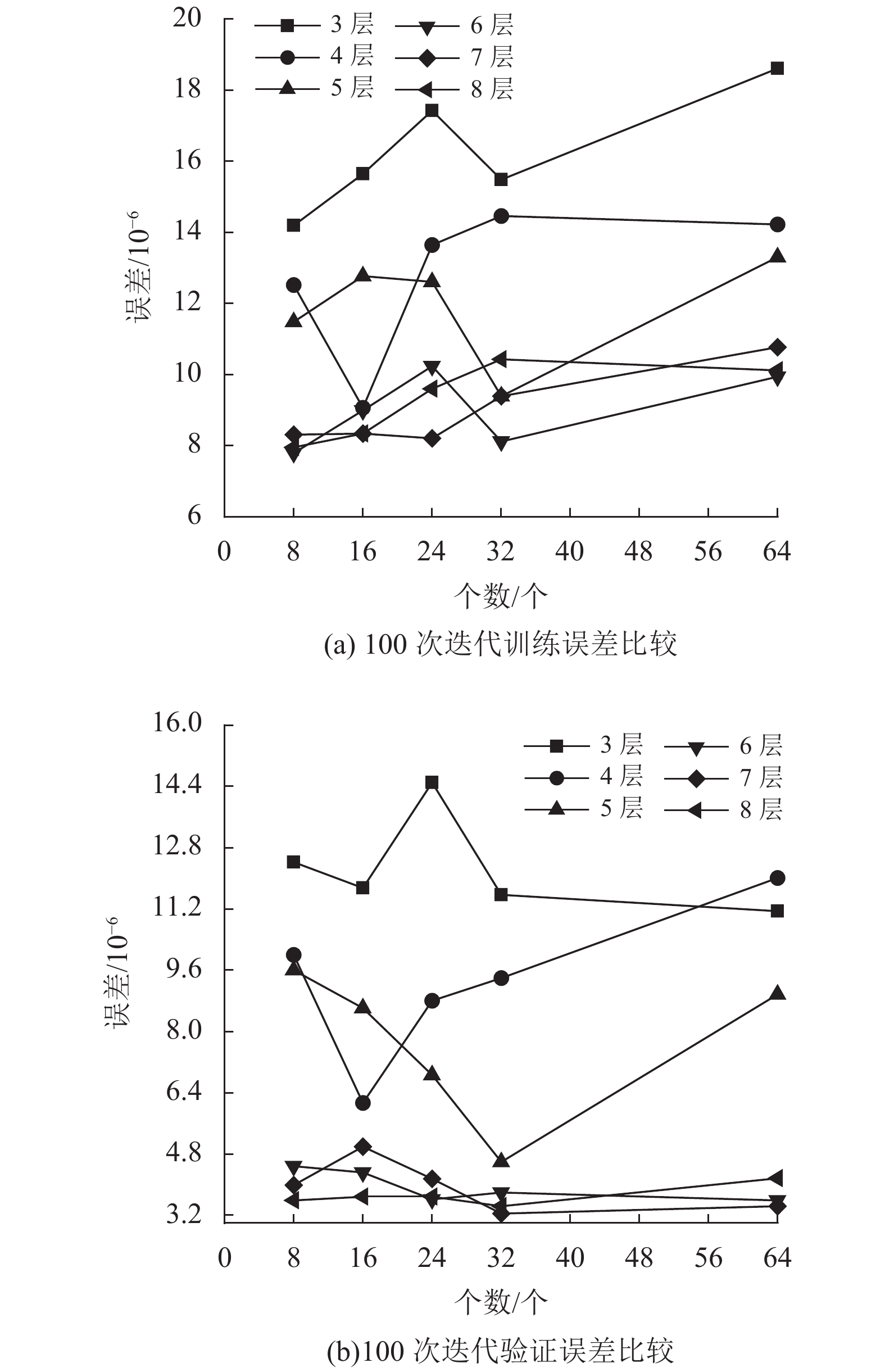
相较于单层神经网络，DNN的主要优势在于网络规模的扩大与层数增加所带来的更强学习能力。然而随着网络规模的扩大，更多的层数与神经元个数往往会造成网络训练困难以及计算耗时增加等问题^[23-24]。在神经元个数相同的情况下，层数较多的DNN往往能够拥有相较于层数较少的DNN更好的收敛能力，并拥有更小的训练与验证误差。而随着规模的不断扩大，网络也需要消耗更多训练时间以收敛至更小的误差。因此，在网络结构的设计上应根据任务的不同选择合适的规模，让DNN拥有更高预测精度的同时所需耗时也相对较小。为此，本文通过设计比较实验，比较不同DNN在相同条件下进行100轮迭代的收敛情况。图7为训练与验证误差比较。表1为不同网络在100次随机初始条件下与MPC控制器的平均预测误差。实验结果表明，随着层数的增多，DNN的误差相对更小；而随着规模的扩大，DNN需要消耗更多的迭代次数才能够收敛至更小的误差值。本文选用8层、单层8个神经元的深度神经网络作为DNN控制器，该网络在拥有更小的训练与验证误差的同时，网络结构相对较小，能够快速处理注射速度的预测控制问题。

3 仿真结果

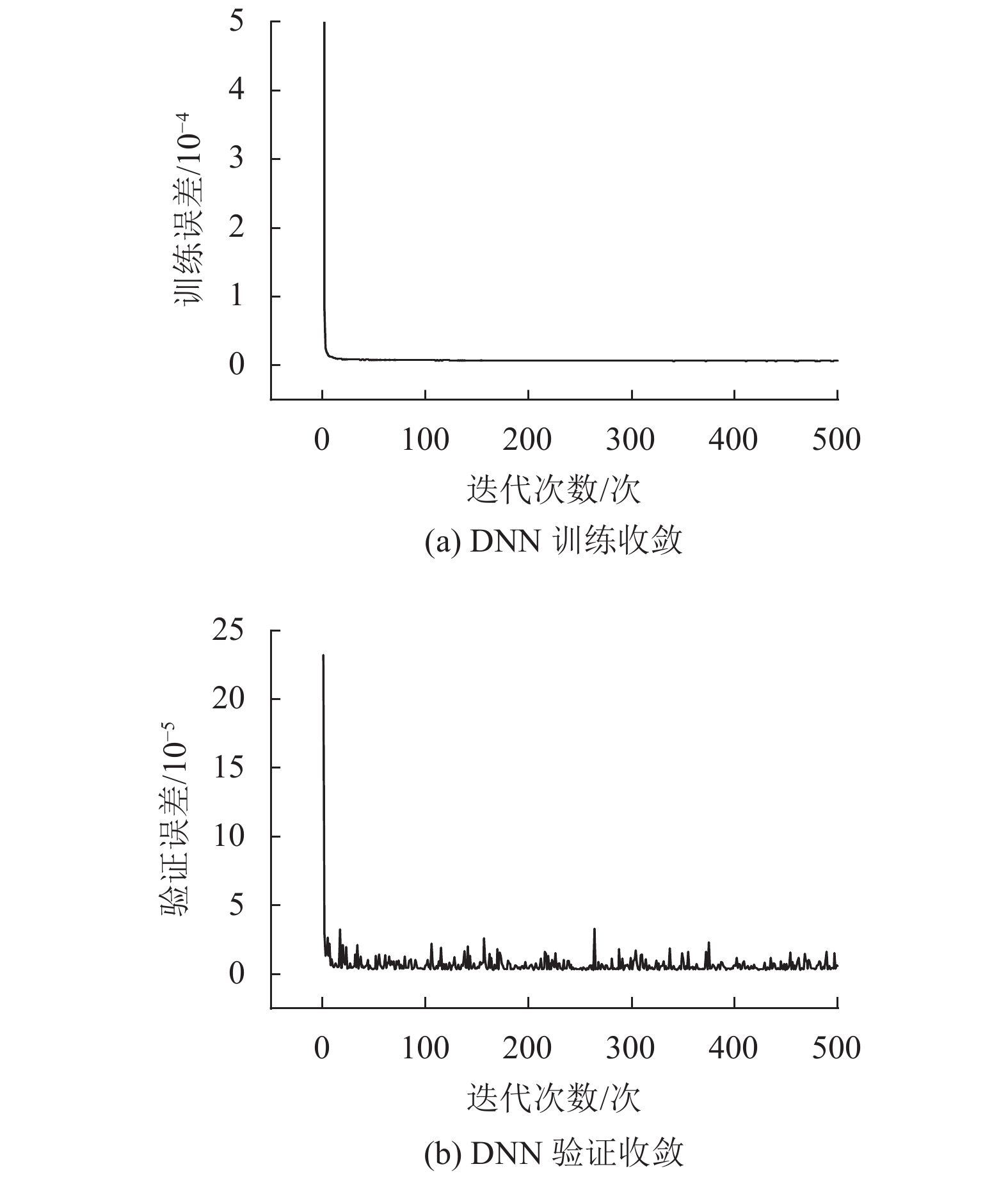
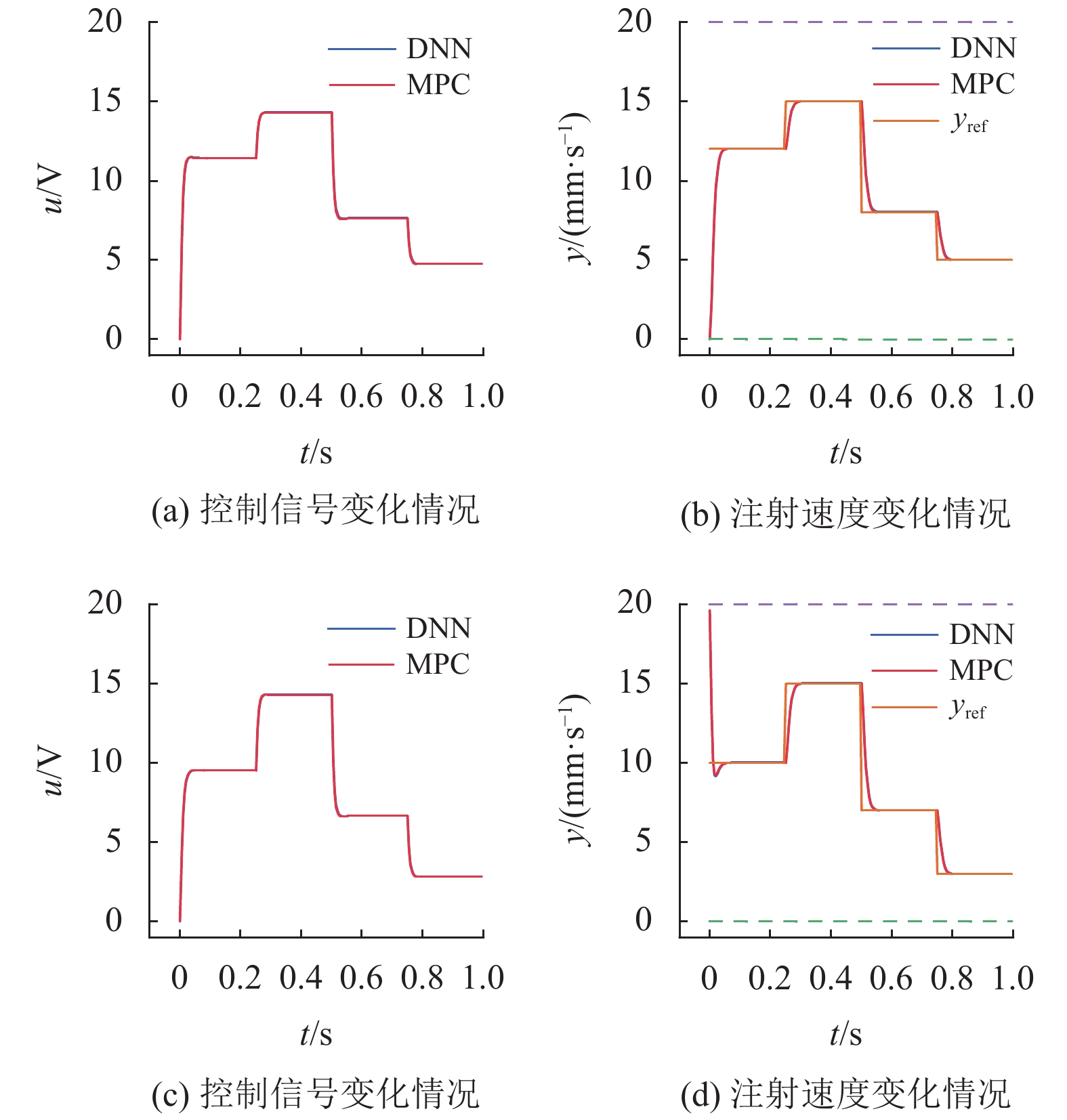
训练与仿真实验均运行在配置为Intel Core i7-8700、16GB内存的Windows计算机平台上，使用Python/Pytorch编写MPC算法以及DNN控制器的训练与验证代码。通过Adam算法调整优化网络权重与偏置，选取误差最小的网络模型作为控制器。图8为设计的DNN训练迭代500次的收敛曲线。网络在迭代10次后便趋于平缓并缓慢下降，并逐渐收敛至较小的误差值。表2为训练完成后网络的训练误差与验证误差。表3为DNN控制器与MPC控制器在相同条件下分别运行100次的平均计算耗时与平均预测误差。实验结果表明，训练完成的深度神经网络控制器有着与MPC控制器基本一致的控制效果，且二者之间的平均误差较小。前者平均计算耗时为0.32 ms，要小于后者12.62 ms的平均计算耗时，且小于5 ms的采样周期，满足在线实时预测控制要求。图9中(a)~(b)和(c)~(d)分别为DNN与MPC两种控制器在零初始条件以及随机初始条件下的预测控制仿真结果，二者输出的控制曲线基本一致。且无论是在随机初始条件或是零初始条件下，DNN控制器都能够迅速收敛至参考轨迹并跟随轨迹变化迅速做出响应。因此，本文提出的基于深度神经网络的模型预测控制器能够较好地完成注塑机注射速度的控制任务，在降低预测控制所需计算耗时的同时，实现了对目标注射速度的快速跟踪，且在不同条件下仍具备可行性与稳定性。

4 结论与展望

本文提出了一种基于DNN的注塑机注塑过程预测控制方法。该方法结合深度学习与模型预测控制理论，在MPC控制的基础上设计DNN网络学习注塑机的预测控制过程。训练完成的DNN控制器能够根据实时注塑机系统状态，输出相应的预测控制结果。实验结果表明该方法具有可行性，并且相较于传统预测控制方法，所需计算耗时更短。在确保预测控制精确度的同时，该方法能够较好地完成注塑机系统复杂控制任务并快速输出预测控制结果，满足实时性要求。由于DNN控制器结构相对较为简单，前向计算所需计算时间较短，该方法同样适用于如嵌入式设备等计算资源相对紧缺的硬件平台上，并实现对动态系统的在线预测控制。

在后续的工作中，将继续围绕深度学习与预测控制方法展开研究，并对本文实验方法中的不足进行完善，如考虑数据集规模对DNN学习效率的影响、比较不同激活函数以及标准化方法的效果等。此外，将尝试使用本文方法应用于更复杂的注塑机非线性系统，结合网络压缩、网络剪枝等方法，实现更高效的实时预测控制。