2. 上海电子信息职业技术学院 中德工程学院,上海 201411;
3. 东北石油大学 黑龙江省网络化与智能控制重点实验室,黑龙江 大庆 163318;
4. 东北石油大学 三亚海洋油气研究院,海南 三亚 572024
2. Sino German Institute of Sngineering, Shanghai Technical Institute of Electronics & Information, Shanghai 201411, China;
3. Heilongjiang Provincial Key Laboratory of Networking and Intelligent Control, Northeast Petroleum University, Daqing 163318, China;
4. Sanya Offshore Oil & Gas Research Institute, Northeast Petroleum University, Sanya 572024, China
在过去的几十年里,多智能体系统由于在化学制造业、地质勘探、楼宇自动化以及航空航天等各个领域的广泛应用而吸引了大量学者的目光[1-4]。作为多智能体系统的主要研究课题之一,一致性控制问题持续受到关注[5-8],其目标是通过利用邻居节点的信息设计一致性算法(或协议),使多智能体的状态达到某些共同特征(如位置、相位、速度和姿态),目前在该方面已经涌现了大批优秀成果。例如,文献[5]研究了拓扑结构变化的多智能体系统,考虑了在受到模型不确定性和外部扰动影响下的一致性控制问题。文献[7]对离散时间多智能体系统,同时考虑了外部干扰和测量丢失,并深入研究了测量丢失对一致性行为的影响。此外,为了提高通信可靠性,引入了冗余信道,并构建了相应的冗余信道信息传输协议。文献[8]使用相对输出测量的方法解决了具有一般线性节点的动态多智能体系统的分布式H∞一致性控制问题。
值得注意的是,现有的大多数控制器设计方法都依赖于一个假设,即所设计的控制器可以精确地实现。然而,由于复杂和多变的环境会对控制器执行过程造成一定程度的干扰[9-13],导致这一假设在现实中并不总是成立的。为了解决这一问题,学者们设计了非脆弱控制器来容忍控制器增益中的扰动项。在文献[9]中,基于切换有向网络拓扑,提出了一种非脆弱控制方案,以确保具有时变输入时滞的线性连续时间多智能体系统实现有限时间一致性控制。文献[10]分别针对有时滞和无时滞的分数阶记忆(Bidirectional Associative Memory, BAM)神经网络,给出了分数阶BAM神经网络的非脆弱状态估计方法,引入了一种新的变换,将分数阶BAM神经网络转换为带有参数不确定的系统。文献[11]研究了连续时间广义多智能体系统在Lipschitz非线性动力学下的非脆弱一致性控制问题。考虑了相关的非线性多智能体在无向图中通信的情况,最终所有智能体的状态通过所设计控制协议达成一致。更多相关结果见文献[12-16]。
在复杂的实际系统中,不同的信号往往根据其物理特性采用不同的采样率进行采样,也就是说更多的工程系统实际上是多速率系统[17-21]。例如,在机器人和制造业系统中,测量是通过图像处理来进行视觉反馈,它们都需要较长的时间才能实现采样,这就导致了大的采样周期。因此,对于不同的元件采用不同的采样率(即多速率采样)能够使系统性能和资源消耗达到一个恰当的平衡状态,所以研究多速率系统具有很好的理论意义和工业价值。由于多速率采样带来的复杂性,关于多速率系统的分析与综合已经受到了广泛关注,如稳定性分析、H∞一致性控制、模型预测控制及故障检测[22-36]。文献[24]讨论了一类时变时滞网络化控制系统的镇定问题,其中随机时滞小于一个传感器周期或大于一个传感器周期但有界。文中提出了一种新的多速率方法来建立短随机时滞和长随机时滞的联合模型。文献[28]针对带有随机噪声、未知输入以及执行器和传感器故障的系统,解决了多速率多传感器融合系统的故障检测问题和最优滤波问题。值得指出的是,虽然多速率采样问题已经被大量研究,但在多智能体系统中少有考虑。因此,本文的第一个研究动机是探索多速率采样对多智能体系统非脆弱一致性控制问题的影响。
众所周知,在恶劣的环境下智能体的通信资源和运算能力通常是被限制的[37-38],为了降低资源的损耗,基于事件触发的通信方式进入了人们的视野[39-44]。瑞典学者Åarzén于20世纪90年代末第一次提出了基于事件触发机制的PID控制策略[45],并对事件触发机制进行了详细的分析。与时间触发机制不同,事件触发机制的核心思想是“按需”触发,而不再是“按时”触发。根据实际需求预先设定触发条件,只有系统的当前信息满足触发条件,才执行当前触发任务。显而易见,事件触发机制的应用会降低资源的消耗。在文献[39]中,作者清楚地描述了时间触发和事件触发的区别,并阐述了事件触发在节约通信资源方面的优势。值得注意的是,目前基于事件触发机制的多智能体系统一致性控制问题的研究大多数聚焦于单速率采样,本文将研究事件触发机制对多速率多智能体系统一致性控制问题的影响,并提出相应的一致性控制方案。
基于以上讨论,本文将针对多速率多智能体系统,研究其在事件触发机制下的非脆弱H∞一致性控制问题。具体贡献如下:(1) 首次研究了一类多速率多智能体系统的非脆弱H∞一致性控制问题;(2) 与时间触发机制相比,引入的事件触发机制在节约通信资源方面更具优势并且采用了相对触发的形式来动态调整阈值,使系统的性能和资源的消耗达到恰当的平衡;(3) 获得了增广系统渐近稳定且满足给定H∞一致性控制约束的充分条件。
1 预备知识 1.1 图论首先,通过使用有向图
引理1[46] 给定3个适当维数的矩阵
| $ \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{S}_1}}&{\boldsymbol{S}_3^{\text{T}}} \\ {{\boldsymbol{S}_3}}&{{\boldsymbol{S}_2}} \end{array}} \right] \lt 0 或 \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{S}_2}}&{{\boldsymbol{S}_3}} \\ {\boldsymbol{S}_3^{\text{T}}}&{{\boldsymbol{S}_1}} \end{array}} \right] \lt 0 $ | (1) |
成立。
对于具有
| $ {\boldsymbol{W}} = {\boldsymbol{U}}\left[ {\begin{array}{*{20}{c}} {\boldsymbol{\theta}} \\ {\bf{0}} \end{array}} \right]{\boldsymbol{V}^{\text{T}}} = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{U}_1}}&{{\boldsymbol{U}_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\boldsymbol{\theta}} \\ {\bf{0}} \end{array}} \right]{{{\boldsymbol{V}}}^{\text{T}}} = {\boldsymbol{U}_1}{\boldsymbol{\theta}} {\kern 1pt} {\kern 1pt} {\boldsymbol{V}^{\text{T}}} $ | (2) |
式中:
根据式(2)可得以下引理:
引理2[47] 如果矩阵
| $ \begin{split} {\boldsymbol{B}_Q} &= \left[ {{\boldsymbol{U}_1}}\;\;{{\boldsymbol{U}_2}} \right]{\text{diag}}\{ {\boldsymbol{B}_Q}_1,{\boldsymbol{B}_Q}_2\} {\left[ {{\boldsymbol{U}_1}}\;\;{{\boldsymbol{U}_2}} \right]^{\text{T}}} =\hfill \\ & {\boldsymbol{U}_1}{\boldsymbol{B}_Q}_1{\boldsymbol{U}}_1^{\text{T}} + {\boldsymbol{U}_2}{\boldsymbol{B}_Q}_2{\boldsymbol{U}}_2^{\text{T}} \hfill \end{split} $ | (3) |
式中:
引理3[46] 给定适当维数的实矩阵
| $ {\boldsymbol{\varPhi}} + {\boldsymbol{\varGamma}} {\boldsymbol{\varUpsilon}} {\boldsymbol {Z}} + {{\boldsymbol Z}^{\text{T}}}{\boldsymbol{\varUpsilon} ^{\text{T}}}{\boldsymbol{\varGamma} ^{\text{T}}} \lt 0 $ |
当且仅当存在一个常数
| $ {\boldsymbol{\varPhi}} + {\varepsilon} {\kern 1pt} {\boldsymbol{\varGamma}} {\boldsymbol{\varGamma} ^{\text{T}}} + {\varepsilon ^{ - 1}}{{\boldsymbol Z}^{\text{T}}}{\boldsymbol Z} \lt 0 $ | (4) |
首先,考虑由以下状态空间模型描述的多智能体系统
| $ \left\{ \begin{array}{l}{\boldsymbol{x}}_{i}({T}_{m+1})={\boldsymbol{Ax}}_{i}({T}_{m})+{\boldsymbol{Bu}}_{i}({T}_{m})+{\boldsymbol{Ew}}_{i}({T}_{m})\\ {\boldsymbol{z}}_{i}({T}_{m})={\boldsymbol{Dx}}_{i}({T}_{m})\end{array} \right.$ | (5) |
式中:
在采样时刻
| $ {\boldsymbol{y}_i}({{t}_{m}}) = {\boldsymbol{Cx}_i}({{t}_{m}}) + {\boldsymbol{Fv_i}}({t_m}) $ | (6) |
式中:
通过提升技术,将式(5)提升为时间尺度为
| $ \left\{ \begin{array}{l}{\boldsymbol{x}}_{i}({t}_{m+1})={\boldsymbol{A}}^{b}{\boldsymbol{x}}_{i}({t}_{m})+{\overline{\boldsymbol{B}}}_{1}{\overline{\boldsymbol{u}}}_{i}({t}_{m})+{\overline{\boldsymbol{E}}}_{1}{\overline{\boldsymbol{w}}}_{i}({t}_{m})\\ {\boldsymbol{x}}_{i}({t}_{m+1}-h)={\boldsymbol{A}}^{b-1}{\boldsymbol{x}}_{i}({t}_{m})+{\overline{\boldsymbol{B}}}_{2}{\overline{\boldsymbol{u}}}_{i}({t}_{m})+{\overline{\boldsymbol{E}}}_{2}{\overline{\boldsymbol{w}}}_{i}({t}_{m})\\ \qquad \qquad \qquad \qquad \qquad \vdots \\ {\boldsymbol{x}}_{i}({t}_{m+1}-(b-1)h)={\boldsymbol{A}}{\boldsymbol{x}}_{i}({t}_{m})+{\overline{\boldsymbol{B}}}_{b}{\overline{\boldsymbol{u}}}_{i}({t}_{m})+{\overline{\boldsymbol{E}}}_{b}{\overline{\boldsymbol{w}}}_{i}({t}_{m})\end{array}\right. $ | (7) |
式中:
| $ \begin{array}{l}{\overline{\boldsymbol{B}}}_{l}\triangleq [{\overline{\boldsymbol{B}}}_{l1} \quad {\bf{0}}],{\overline{\boldsymbol{E}}}_{l}\triangleq [{\overline{\boldsymbol{E}}_{l1}} \quad {\bf{0}}],\text{}\text{}\text{}\text{}{\bf{0}}\triangleq [\underset{l-1}{\underbrace{0\quad \cdots \quad0}}]\\ {\overline{\boldsymbol{B}}}_{l1}\triangleq [\underset{b-l+1}{\underbrace{\begin{array}{cccc}{\boldsymbol{A}}^{b-l}{\boldsymbol{B}}& \cdots & {\boldsymbol{AB}}& {\boldsymbol{B}}\end{array}}}],l\triangleq 1,2,\cdots ,b\text{}\text{}\\ {\overline{\boldsymbol{E}}}_{l1}\triangleq [\underset{b-l+1}{\underbrace{\boldsymbol{A}^{b-l}{\boldsymbol{E}}\cdots {\boldsymbol{AE\quad E}}}}]\end{array} $ |
接下来,定义:
| $ \begin{array}{l}{\overline{\boldsymbol{x}}}_{i}({t}_{m})\triangleq {\text{col}}_{1}^{b}\{{\boldsymbol{x}}_{i}({t}_{m}-(l-1)h)\}\\ {\overline{\boldsymbol{u}}}_{i}({t}_{m})\triangleq {\text{col}}_{1}^{b}\{{\boldsymbol{u}}_{i}({t}_{m}+(l-1)h)\}\\ {\overline{\boldsymbol{w}}}_{i}({t}_{m})\triangleq {\text{col}}_{1}^{b}\{{\boldsymbol{w}}_{i}({t}_{m}+(l-1)h)\}\\ {\overline{\boldsymbol{v}}}_{i}({t}_{m})\triangleq {\text{col}}_{1}^{b}\{{\boldsymbol{v}}_{i}({t}_{m}+(l-1)h)\}\\ {\overline{\boldsymbol{z}}}_{i}({t}_{m})\triangleq {\text{col}}_{1}^{b}\{{\boldsymbol{z}}_{i}({t}_{m}-(l-1)h)\}\end{array} $ |
得到一个新的采样时刻为
| $ \left\{\begin{array}{l}{\overline{\boldsymbol{x}}}_{i}({t}_{m+1})=\hat{\boldsymbol{A}}{\overline{\boldsymbol{x}}}_{i}({t}_{m})+\hat{\boldsymbol{B}}{\overline{\boldsymbol{u}}}_{i}({t}_{m})+\hat{\boldsymbol{E}}{\overline{\boldsymbol{w}}}_{i}({t}_{m})\\ {\boldsymbol{y}}_{i}({t}_{m})=\overline{\boldsymbol{C}}{\overline{\boldsymbol{x}}}_{i}({t}_{m})+\overline{\boldsymbol{F}}{\overline{\boldsymbol{v}}}_{i}({t}_{m})\\ {\overline{\boldsymbol{z}}}_{i}({t}_{m})=\overline{\boldsymbol{D}}{\overline{\boldsymbol{x}}}_{i}({t}_{m})\end{array}\right. $ | (8) |
式中:
为了表述方便,进一步表示
本部分将基于系统状态设计控制器,因此,首先针对多智能体
| $ {\boldsymbol{\xi} _i}(k + 1) = \hat {\boldsymbol{A}}{\boldsymbol{\xi} _i}(k) + \hat {\boldsymbol{B}}{\overline {\boldsymbol{u}}_i}(k) + {\boldsymbol{H}}({\boldsymbol{y}_i}(k) - \overline {\boldsymbol{C}}{\boldsymbol{\xi} _i}(k)) $ | (9) |
式中:
考虑到智能体之间的通信受限情况,采用事件触发机制决定它们之间的通信时刻,其中触发时刻由式(10)决定。
| $k_{s+1}^{i}=\inf \left\{k>k_{s}^{i} \mid\left[\hat{\boldsymbol{\xi}}_{i}(k)-\boldsymbol{\xi}_{i}(k)\right]^{\mathrm{T}}\left[\hat{\boldsymbol{\xi}}_{i}(k)-\boldsymbol{\xi}_{i}(k)\right] \geqslant \boldsymbol{\sigma}_{i} \boldsymbol{\xi}_{i}^{\mathrm{T}}(k) \boldsymbol{\xi}_{i}(k)\right\}$ | (10) |
式中:
基于事件触发机制,为智能体
| $ {\overline {\boldsymbol{u}}_i}(k) = \hat{\boldsymbol{K}}\sum\nolimits_{j \in {\mathbb{N}_i}} {{q_{ij}}} ({\hat{\boldsymbol{\xi}} _j}(k) - {\hat {\boldsymbol{\xi}}_i}(k)) $ | (11) |
式中:
| $ \Delta {\boldsymbol{K}}{\text{ = }}{\boldsymbol{K}}{\boldsymbol{H}_1}{\boldsymbol{F}_1}{\boldsymbol{G}_1} $ | (12) |
式中:
注解1 在触发时刻
为方便以下分析,先做出如下定义:
| $ \begin{array}{l}{\boldsymbol{\delta} }_{i}(k)\triangleq {\boldsymbol{\xi} }_{i}(k)-{\overline{\boldsymbol{x}}}_{i}(k)\\ {\boldsymbol{e}}_{i}(k)\triangleq {\hat{\boldsymbol{\xi} }}_{i}(k)-{\boldsymbol{\xi} }_{i}(k) \\ \overline{\boldsymbol{x}}(k)\triangleq {[}{{\overline{\boldsymbol{x}}}_{1}^{\text{T}}}(k)\;\; {{\overline{\boldsymbol{x}}}_{2}^{\text{T}}}(k)\;\; \cdots\;\; {{\overline{\boldsymbol{x}}}_{N}^{\text{T}}}(k){]}^{\text{T}} \\ {\boldsymbol{\xi}} (k)\triangleq {[}{{\boldsymbol{\xi} }_{1}^{\text{T}}}(k)\;\;{{\boldsymbol{\xi} }_{2}^{\text{T}}}(k)\;\;\cdots\;\;{{\boldsymbol{\xi} }_{N}^{\text{T}}}(k){]}^{\text{T}} \\ \hat{\boldsymbol{\xi} }(k)\triangleq {[}{{\hat{\boldsymbol{\xi} }}_{1}^{\text{T}}}(k)\;\;{{\hat{\boldsymbol{\xi} }}_{2}^{\text{T}}}(k)\;\;\cdots\;\;{{\hat{\boldsymbol{\xi} }}_{N}^{\text{T}}}(k){]}^{\text{T}} \\ {\boldsymbol{e}}(k)\triangleq {[}{{\boldsymbol{e}}_{1}^{\text{T}}}(k)\;\;{{\boldsymbol{e}}_{2}^{\text{T}}}(k)\;\;\cdots\;\;{{\boldsymbol{e}}_{N}^{\text{T}}}(k){]}^{\text{T}} \\ \overline{\boldsymbol{w}}(k)\triangleq {[}{{\overline{\boldsymbol{w}}}_{1}^{\text{T}}}(k)\;\;{{\overline{\boldsymbol{w}}}_{2}^{\text{T}}}(k)\;\;\cdots\;\;{{\overline{\boldsymbol{w}}}_{N}^{\text{T}}}(k){]}^{\text{T}} \\ {\boldsymbol{v}}(k)\triangleq {[}{{\overline{\boldsymbol{v}}}_{1}^{\text{T}}}(k)\;\;{{\overline{\boldsymbol{v}}}_{2}^{\text{T}}}(k)\;\;\cdots\;\;{{\overline{\boldsymbol{v}}}_{N}^{\text{T}}}(k){]}^{\text{T}} \\ {\boldsymbol{\delta}} (k)\triangleq {[}{{\boldsymbol{\delta} }_{1}^{\text{T}}}(k)\;\;{{\boldsymbol{\delta} }_{2}^{\text{T}}}(k)\;\;\cdots\;\;{{\boldsymbol{\delta} }_{N}^{\text{T}}}(k){]}^{\text{T}} \\ \overline{\boldsymbol{z}}(k)\triangleq {[}{{\overline{\boldsymbol{z}}}_{\text{1}}^{\text{T}}}(k)\;\;{{\overline{\boldsymbol{z}}}_{\text{2}}^{\text{T}}}(k)\;\;\cdots\;\;{{\overline{\boldsymbol{z}}}_{{N}}^{\text{T}}}(k){]}^{\text{T}} \end{array} $ |
那么系统(8)可重写为
| $ \left\{ \begin{array}{l}\overline{\boldsymbol{x}}(k+1)=[{\boldsymbol{I}}_{N}\otimes \hat{\boldsymbol{A}}-{\boldsymbol{L}}\otimes (\hat{\boldsymbol{B}}\hat{\boldsymbol{K}})]\overline{\boldsymbol{x}}(k)\text{}\text{ }-[{\boldsymbol{L}}\otimes (\hat{\boldsymbol{B}}\hat{\boldsymbol{K}})]{\boldsymbol{e}}(k)-\\ \qquad\qquad [{\boldsymbol{L}}\otimes (\hat{\boldsymbol{B}}\hat{\boldsymbol{K}})]{\boldsymbol{\delta}} (k) \text{}\text{ }+({\boldsymbol{I}}_{N}\otimes \hat{\boldsymbol{E}})\overline{\boldsymbol{w}}(k)\\ {\boldsymbol{\delta}} (k+1)=[{\boldsymbol{I}}_{N}\otimes \hat{\boldsymbol{A}}-{\boldsymbol{I}}_{N}\otimes (\boldsymbol{H}\overline{\boldsymbol{C}})]{\boldsymbol{\delta}} (k)+[{\boldsymbol{I}}_{N}\otimes ({\boldsymbol{H}}\overline{\boldsymbol{F}})]{\boldsymbol{v}}(k)-\\ \qquad\qquad ({\boldsymbol{I}}_{N}\otimes \hat{\boldsymbol{E}})\overline{\boldsymbol{w}}(k)\\ \overline{\boldsymbol{z}}(k)=({\boldsymbol{I}}_{N}\otimes \overline{\boldsymbol{D}})\overline{\boldsymbol{x}}(k)\end{array} \right. $ | (13) |
式中:
通过定义变量
| $ \left\{ \begin{array}{l}{\boldsymbol{\eta}} (k+1)={\boldsymbol{A}}_{1}{\boldsymbol{\eta}} (k)+{\boldsymbol{B}}_{1}{\boldsymbol{e}}(k)+{\boldsymbol{E}}_{1}{\boldsymbol{\omega}} (k)\\ \overline{\boldsymbol{z}}(k)={\boldsymbol{D}}_{1}{\boldsymbol{\eta}} (k)\end{array} \right. $ | (14) |
式中:
| $ \begin{array}{l}{{\boldsymbol{ A}}}_{1}\triangleq {\overline{\boldsymbol{A}}}_{1}\text+\Delta {\overline{\boldsymbol{A}}}_{1},{\boldsymbol{B}}_{1}\triangleq {\overline{\boldsymbol{B}}}_{1}\text+\Delta {\overline{\boldsymbol{B}}}_{1}\\ {\overline{\boldsymbol{A}}}_{1}\triangleq \left[\begin{array}{cc}{\boldsymbol{I}}_{N}\otimes \hat{\boldsymbol{A}}-{\boldsymbol{L}}\otimes (\hat{\boldsymbol{B}}{\boldsymbol{K}})& -{\boldsymbol{L}}\otimes (\hat{\boldsymbol{B}}{\boldsymbol{K}})\\ {\boldsymbol{0}}& {\boldsymbol{I}}_{N}\otimes \hat{\boldsymbol{A}}-{\boldsymbol{I}}_{N}\otimes ({\boldsymbol{H}}\overline{\boldsymbol{C}})\end{array}\right]\\ \Delta {\overline{\boldsymbol{A}}}_{1}\triangleq \left[\begin{array}{cc}-{\boldsymbol{L}}\otimes (\hat{\boldsymbol{B}}\Delta {\boldsymbol{K}})& -{\boldsymbol{L}}\otimes (\hat{\boldsymbol{B}}\Delta {\boldsymbol{K}})\\ {\boldsymbol{0}}& {\boldsymbol{0}}\end{array}\right]\\ {\boldsymbol{E}}_{1}\triangleq \left[\begin{array}{cc}{\boldsymbol{I}}_{N}\otimes \hat{\boldsymbol{E}}& {\boldsymbol{0}}\\ -{\boldsymbol{I}}_{N}\otimes \hat{\boldsymbol{E}}& {\boldsymbol{I}}_{N}\otimes ({\boldsymbol{H}}\overline{\boldsymbol{F}})\end{array}\right],{\overline{\boldsymbol{B}}}_{1}\triangleq \left[\begin{array}{c}-{\boldsymbol{L}}\otimes (\hat{\boldsymbol{B}}{\boldsymbol{K}})\\ {\boldsymbol{0}}\end{array}\right]\\ \Delta {\overline{\boldsymbol{B}}}_{1}\triangleq \left[\begin{array}{c}-{\boldsymbol{L}}\otimes (\hat{\boldsymbol{B}}\Delta {\boldsymbol{K}})\\ {\boldsymbol{0}}\end{array}\right],{\boldsymbol{D}}_{1}\triangleq \left[\begin{array}{cc}{\boldsymbol{I}}_{N}\otimes \overline{\boldsymbol{D}}& {\boldsymbol{0}}\end{array}\right]\end{array} $ |
由以上结果可知,式(10)中的事件触发条件为
| $ {{\boldsymbol{e}}^{\text{T}}}(k){\boldsymbol{e}}(k) \lt {{\boldsymbol{\eta}} ^{\text{T}}}(k){\boldsymbol{M}}{\boldsymbol{\eta}} (k) $ | (15) |
式中:
| $ \begin{array}{l}{\boldsymbol{M}}\triangleq {\left[\begin{array}{cc}{\boldsymbol{I}}_{bN{n}_{x}}& {\boldsymbol{I}}_{bN{n}_{x}}\end{array}\right]}^{\text{T}}\left({\boldsymbol{\Lambda}} \otimes {\boldsymbol{I}}_{b{n}_{x}}\right)\left[\begin{array}{cc}{\boldsymbol{I}}_{bN{n}_{x}}& {\boldsymbol{I}}_{bN{n}_{x}}\end{array}\right]\\ {\boldsymbol{\Lambda}} \triangleq \text{diag}\{{\boldsymbol{\sigma }}_{1},{\boldsymbol{\sigma} }_{2},\cdots ,{\boldsymbol{\sigma} }_{N}\}\end{array} $ |
注解2 在式(10)中事件触发条件是起到判断触发时刻的作用,如果其成立,则表示事件被触发。而式(15)指触发时刻(包括该触发时刻)与下一个触发时刻之间的时间段处于不触发状态,即
定义:对于给定的干扰抑制水平
| $ {\displaystyle \sum\nolimits _{k=0}^{\infty }\Vert \overline{\boldsymbol{z}}(}k)-{\ell} \overline{\boldsymbol{z}}(k){\Vert }^{2} \lt {\gamma }^{2}{\displaystyle \sum\nolimits _{k=0}^{\infty }\Vert {\boldsymbol{\omega}} (k){\Vert }^{2}} $ | (16) |
式中:
本文旨在设计非脆弱控制器(11)使得:
(a)
(b) 零初始条件下,增广系统(14)满足给定
定理1将给出使增广系统(14)渐近稳定并满足
定理 1 给定干扰抑制水平
| $ \overline{\boldsymbol{\varOmega} }\triangleq \left[\begin{array}{ccc}{\overline{\boldsymbol{\varOmega} }}_{11}& \ast & \ast \\ {\overline{\boldsymbol{\varOmega} }}_{21}& {\overline{\boldsymbol{\varOmega} }}_{22}& \ast \\ {\overline{\boldsymbol{\varOmega} }}_{31}& {\overline{\boldsymbol{\varOmega} }}_{32}& {\overline{\boldsymbol{\varOmega} }}_{33}\end{array}\right] \lt 0 $ | (17) |
则增广系统(14)在
| $ \begin{array}{l} {\overline{\boldsymbol{\varOmega} }}_{11}\triangleq {\boldsymbol{A}}_{1}^{\text{T}}\;{\boldsymbol{PA}}_{1}+{\overline{\boldsymbol{D}}}_{1}-{\boldsymbol{P}}+\rho {\boldsymbol{M}},{\overline{\boldsymbol{\varOmega} }}_{21}\triangleq {\boldsymbol{B}}_{1}^{\text{T}}{\boldsymbol{PA}}_{1}\\ {\overline{\boldsymbol{\varOmega} }}_{22}\triangleq {\boldsymbol{B}}_{1}^{\text{T}}{\boldsymbol{PB}}_{1}-\rho {\boldsymbol{I}}_{bN{n}_{x}},{\overline{\boldsymbol{\varOmega} }}_{31}\triangleq {\boldsymbol{E}}_{1}^{\text{T}}{\boldsymbol{PA}}_{1}\\ {\overline{\boldsymbol{\varOmega} }}_{32}\triangleq {\boldsymbol{E}}_{1}^{\text{T}}{\boldsymbol{PB}}_{1},{\overline{\boldsymbol{\varOmega} }}_{33}\triangleq {\boldsymbol{E}}_{1}^{\text{T}}{\boldsymbol{PE}}_{1}-{\gamma }^{2}{\boldsymbol{I}}_{bN{n}_{x}}\\ {\overline{\boldsymbol{D}}}_{1}\triangleq {({\boldsymbol{D}}_{1}-{\ell} {\boldsymbol{D}}_{1})}^{\text{T}}({\boldsymbol{D}}_{1}-{\ell} {\boldsymbol{D}}_{1}) \end{array} $ |
式(17)中
证明 首先,构造如下Lyapunov函数
| $ V(k) = {\boldsymbol{\eta} ^{\text{T}}}(k){\boldsymbol{P}}{\boldsymbol{\eta}} (k) $ | (18) |
然后,计算
| $ \begin{split} \Delta V(k) =& {{\boldsymbol{\eta}} ^{\rm{T}}}(k + 1){\boldsymbol{P}}{\boldsymbol{\eta}} (k + 1)) - {{\boldsymbol{\eta}} ^{\rm{T}}}(k){\boldsymbol{P}}{\boldsymbol{\eta}} (k) =[ {{\boldsymbol{A}}_1}{\boldsymbol{\eta}} (k) +\\ & {{\boldsymbol{B}}_1}{\boldsymbol{e}}(k) + {{\boldsymbol{E}}_1}{\boldsymbol{\omega}} (k) ]^{\rm{T}}{\boldsymbol{P}} \times \left[ {{{\boldsymbol{A}}_1}{\boldsymbol{\eta}} (k) + {{\boldsymbol{B}}_1}{\boldsymbol{e}}(k) + {{\boldsymbol{E}}_1}{\boldsymbol{\omega}} (k)} \right] -\\ & {{\boldsymbol{\eta}} ^{\rm{T}}}(k){\boldsymbol{P}}{\boldsymbol{\eta}} (k) = {{\boldsymbol{\eta}} ^{\rm{T}}}(k){{\boldsymbol{A}}_1^{\rm{T}}}{\boldsymbol{P}}{{\boldsymbol{A}}_1}{\boldsymbol{\eta}} (k) + {{\boldsymbol{e}}^{\rm{T}}}(k){{\boldsymbol{B}}_1^{\rm{T}}}{\boldsymbol{P}}{{\boldsymbol{B}}_1}{\boldsymbol{e}}(k) +\\ &{\boldsymbol{\omega} ^{\rm{T}}}(k){{\boldsymbol{E}}_1^{\rm{T}}}{\boldsymbol{P}}{{\boldsymbol{E}}_1}{\boldsymbol{\omega}} (k) - {{\boldsymbol{\eta}} ^{\rm{T}}}(k){\boldsymbol{P}}{\boldsymbol{\eta}} (k) + 2{{\boldsymbol{\eta}} ^{\rm{T}}}(k){{\boldsymbol{A}}_1^{\rm{T}}}{\boldsymbol{P}}{{\boldsymbol{B}}_1}{\boldsymbol{e}}(k) + \\ & 2{{\boldsymbol{\eta}} ^{\rm{T}}}(k){{\boldsymbol{A}}_1^{\rm{T}}}{\boldsymbol{P}}{{\boldsymbol{E}}_1}{\boldsymbol{\omega}} (k) + 2{{\boldsymbol{e}}^{\rm{T}}}(k){{\boldsymbol{B}}_1^{\rm{T}}}{\boldsymbol{P}}{{\boldsymbol{E}}_1}{\boldsymbol{\omega}} (k) \\[-10pt] \end{split}$ | (19) |
当
| $ \rho \left[ {{{\boldsymbol{\eta}} ^{\rm{T}}}(k){\boldsymbol{M\eta}} (k) - {{\boldsymbol{e}}^{\rm{T}}}(k){\boldsymbol{e}}(k)} \right] > 0 $ | (20) |
由式(19)可知
| $ \begin{split} \Delta {V_{\boldsymbol{\omega}} }(k) & < {{\boldsymbol{\eta}} ^{\rm{T}}}(k){{\boldsymbol{A}}_1^{\rm{T}}}{\boldsymbol{P}}{{\boldsymbol{A}}_1}{\boldsymbol{\eta}} (k) + {{\boldsymbol{e}}^{\rm{T}}}(k){{\boldsymbol{B}}_1^{\rm{T}}}{\boldsymbol{P}}{{\boldsymbol{B}}_1}{\boldsymbol{e}}(k)-\\ & {{\boldsymbol{\eta}} ^{\rm{T}}}(k){\boldsymbol{P\eta}} (k) + 2{{\boldsymbol{\eta}} ^{\rm{T}}}(k){{\boldsymbol{A}}_1^{\rm{T}}}{\boldsymbol{P}}{{\boldsymbol{B}}_1}{\boldsymbol{e}}(k)+\\ & \rho \left[ {{{\boldsymbol{\eta}} ^{\rm{T}}}(k){\boldsymbol{M\eta}} (k) - {{\boldsymbol{e}}^{\rm{T}}}(k){\boldsymbol{e}}(k)} \right]= \\ & {{\bar {\boldsymbol{\eta}} }^{\rm{T}}}(k){\boldsymbol{\varOmega }}\bar {\boldsymbol{\eta}} (k) \end{split}$ | (21) |
式中:
| $ \begin{array}{l}{\boldsymbol{\varOmega}} \triangleq \left[\begin{array}{cc}{{\boldsymbol{\varOmega}} }_{11}& \ast \\ {\overline{{\boldsymbol{\varOmega}} }}_{21}& {\overline{\boldsymbol{\varOmega}} }_{22}\end{array}\right],\overline{{\boldsymbol{\eta}} }(k)\triangleq \left[\begin{array}{c}{\boldsymbol{\eta}} (k)\\ {\boldsymbol{e}}(k)\end{array}\right],\\ {{\boldsymbol{\varOmega}} }_{11}\triangleq {\boldsymbol{A}}_{1}^{\text{T}}{\boldsymbol{P}}{\boldsymbol{A}}_{1}-{\boldsymbol{P}}+ \rho {\boldsymbol{M}}\end{array} $ |
根据式(17)可知
在零初始条件下且
| $ \begin{split} \Delta V(k) \lt& {\kern 1pt} {\kern 1pt} {{\boldsymbol{\eta}} ^{\text{T}}}(k){{\boldsymbol{A}}_1^{\text{T}}}{\boldsymbol{P}}{{\boldsymbol{A}}_1}{\boldsymbol{\eta}} (k) + {{\boldsymbol{e}}^{\text{T}}}(k){{\boldsymbol{B}}_1^{\text{T}}}{\boldsymbol{P}}{{\boldsymbol{B}}_1}{\boldsymbol{e}}(k)+ {{\boldsymbol{\omega}} ^{\text{T}}}(k) \times \hfill \\ & {{\boldsymbol{E}}_1^{\text{T}}}{\boldsymbol{P}}{{\boldsymbol{E}}_1}{\boldsymbol{\omega}} (k) - {{\boldsymbol{\eta}} ^{\text{T}}}(k){\boldsymbol{P}}{\boldsymbol{\eta}} (k)+ 2{{\boldsymbol{\eta}} ^{\text{T}}}(k){{\boldsymbol{A}}_1^{\text{T}}}{\boldsymbol{P}}{{\boldsymbol{B}}_1}{\boldsymbol{e}}(k)+ \hfill \\ & 2{{\boldsymbol{\eta}} ^{\text{T}}}(k){{\boldsymbol{A}}_1^{\text{T}}}{\boldsymbol{P}}{{\boldsymbol{E}}_1}{\boldsymbol{\omega}} (k)+ 2{{\boldsymbol{e}}^{\text{T}}}(k){{\boldsymbol{B}}_1^{\text{T}}}{\boldsymbol{P}}{{\boldsymbol{E}}_1}{\boldsymbol{\omega}} (k)+ \hfill \\ & \rho \left[ {{{\boldsymbol{\eta}} ^{\text{T}}}(k){\boldsymbol{M}}{\boldsymbol{\eta}} (k) - {{\boldsymbol{e}}^{\text{T}}}(k){\boldsymbol{e}}(k)} \right] \hfill \\[-10pt] \end{split} $ | (22) |
将
| $ \begin{split} \Delta V(k) + & {{\boldsymbol{\eta}} ^{\text{T}}}(k){\overline {\boldsymbol{D}} _1}{\boldsymbol{\eta}} (k) - {\gamma ^2}{\boldsymbol{\omega}} {(k)^{\text{T}}}{\boldsymbol{\omega}} (k) \lt {{\boldsymbol{\eta}} ^{\text{T}}}(k){{\boldsymbol{A}}_1^{\text{T}}}{\boldsymbol{P}}{{\boldsymbol{A}}_1}{\boldsymbol{\eta}} (k) + \hfill \\ & {{\boldsymbol{e}}^{\text{T}}}(k){{\boldsymbol{B}}_1}^{\text{T}}{\boldsymbol{P}}{{\boldsymbol{B}}_1}{\boldsymbol{e}}(k) + {{\boldsymbol{\omega}} ^{\text{T}}}(k){{\boldsymbol{E}}_1^{\text{T}}}{\boldsymbol{P}}{{\boldsymbol{E}}_1}{\boldsymbol{\omega}} (k) - {{\boldsymbol{\eta}} ^{\text{T}}}(k){\boldsymbol{P}}{\boldsymbol{\eta}} (k) + \hfill \\ & 2{{\boldsymbol{\eta}} ^{\text{T}}}(k){{\boldsymbol{A}}_1^{\text{T}}}{\boldsymbol{P}}{{\boldsymbol{B}}_1}{\boldsymbol{e}}(k) + 2{{\boldsymbol{\eta}} ^{\text{T}}}(k){{\boldsymbol{A}}_1^{\text{T}}}{\boldsymbol{P}}{{\boldsymbol{E}}_1}{\boldsymbol{\omega}} (k)+ \hfill \\ & 2{{\boldsymbol{e}}^{\text{T}}}(k){{\boldsymbol{B}}_1^{\text{T}}}{\boldsymbol{P}}{{\boldsymbol{E}}_1}{\boldsymbol{\omega}} (k) + \rho \left[ {{{\boldsymbol{\eta}} ^{\text{T}}}(k){\boldsymbol{M}}{\boldsymbol{\eta}} (k) - {{\boldsymbol{e}}^{\text{T}}}(k){\boldsymbol{e}}(k)} \right]+ \hfill \\ & {{\boldsymbol{\eta}} ^{\text{T}}}(k){\overline {\boldsymbol{D}} _1}{\boldsymbol{\eta}} (k) - {\gamma ^2}{\boldsymbol{\omega}} {(k)^{\text{T}}}{\boldsymbol{\omega}} (k) = {{\tilde {\boldsymbol{\eta}} }^{\text{T}}}(k){{\overline {\boldsymbol{\varOmega}} }}\tilde {\boldsymbol{\eta}} (k){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \end{split} $ | (23) |
式中:
根据式(17)中
| $ \Delta V(k) \lt - {\left( {\overline {\boldsymbol{z}}(k) - {\ell} \overline {\boldsymbol{z}}(k)} \right)^{\text{T}}}\left( {\overline {\boldsymbol{z}}(k) - {\ell} \overline {\boldsymbol{z}}(k)} \right) + {\gamma ^2}{{\boldsymbol{\omega}} ^{\text{T}}}(k){\boldsymbol{\omega}} (k) $ | (24) |
进一步可知
| $ \begin{split} \sum\nolimits_{k = 0}^\infty \Delta V(k) =& {{\boldsymbol{\eta}} ^{\text{T}}}(\infty ){\boldsymbol{P}}{\boldsymbol{\eta}} (\infty ) - {{\boldsymbol{\eta}} ^{\text{T}}}(0){\boldsymbol{P}}{\boldsymbol{\eta}} (0) \lt - \sum\nolimits_{k = 0}^\infty \big[ \overline {\boldsymbol{z}}(k) -\big.\hfill \\ & \big. {\ell} \overline {\boldsymbol{z}}(k) \big]^{\text{T}} \left[ {\overline {\boldsymbol{z}}(k) - {\ell} \overline {\boldsymbol{z}}(k)} \right] + \sum\nolimits_{k = 0}^\infty {{\gamma ^2}} {{\boldsymbol{\omega}} ^{\text{T}}}(k){\boldsymbol{\omega}} (k) \hfill \\ \end{split} $ | (25) |
由于
| $ {{\boldsymbol{\eta}} }^{\text{T}}(\infty ){\boldsymbol{P}}{\boldsymbol{\eta}} (\infty ) \gt 0\text{,}{{\boldsymbol{\eta}} }^{\text{T}}(0){\boldsymbol{P}}{\boldsymbol{\eta}} (0)=0 $ | (26) |
进而可以得到
| $ {\displaystyle \sum\nolimits _{k=0}^{\infty }\Vert \overline{\boldsymbol{z}}(}k)-{\ell} \overline{\boldsymbol{z}}(k){\Vert }^{2} \lt {\gamma }^{2}{\displaystyle \sum\nolimits _{k=0}^{\infty }\Vert {\boldsymbol{\omega}} (k){\Vert }^{2}} $ | (27) |
证明结束。
3.2 增益求解本部分将求解观测器增益和控制器增益。
定理 2 对于给定的干扰抑制水平
| $ \left[ {\begin{array}{*{20}{c}} {{\hat {\boldsymbol {\varXi} }}}&*&* \\ {\hat {\boldsymbol{R}}_1^{\rm{T}}}&{ - \varepsilon {\boldsymbol{P}}}&* \\ {{{\overline {\boldsymbol{R}}}_2}}&{\boldsymbol{0}}&{ - {\varepsilon ^{ - 1}}{{\boldsymbol{I}}_{bN{n_x}}}} \end{array}} \right] \lt 0 $ | (28) |
式中:
| $ \begin{array}{l}\hat{{\boldsymbol{\varXi}} }\triangleq \left[\begin{array}{cccc}{\boldsymbol{A}}_{11}& *& *& *\\ {\boldsymbol{0}}& -\rho {\boldsymbol{I}}_{bN{n}_{x}}& *& *\\ {\boldsymbol{0}}& {\boldsymbol{0}}& -{\gamma }^{2}{\boldsymbol{I}}_{bN{n}_{x}}& *\\ {\boldsymbol{A}}_{51}& {\boldsymbol{A}}_{52}& {\boldsymbol{A}}_{53}& -{\boldsymbol{P}}\end{array}\right]\\ {\boldsymbol{A}}_{11}\triangleq {\overline{\boldsymbol{D}}}_{1}-{\boldsymbol{P}}+\rho {\boldsymbol{M}},{\boldsymbol{P}}\triangleq \text{diag}\{{\boldsymbol{I}}_{N}\otimes \overline{{\boldsymbol{P}}},{\boldsymbol{I}}_{N}\otimes \overline{{\boldsymbol{P}}}\}\\ {\boldsymbol{A}}_{51}\triangleq \left[ \begin{array}{cc}{\boldsymbol{I}}_{N}\otimes (\overline{{\boldsymbol{P}}}\hat{\boldsymbol{A}})-{\boldsymbol{L}}\otimes (\hat{\boldsymbol{B}}\tilde{K})& -{\boldsymbol{L}}\otimes (\hat{\boldsymbol{B}}\tilde{{\boldsymbol{K}}})\\ {\boldsymbol{0}}& {\boldsymbol{I}}_{N}\otimes (\overline{\boldsymbol{P}}\hat{\boldsymbol{A}})-{\boldsymbol{I}}_{N}\otimes (\tilde{\boldsymbol{H}}\overline{\boldsymbol{C}})\end{array} \right] \end{array} $ |
| $\begin{array}{l} {\boldsymbol{A}}_{52}\triangleq \left[\begin{array}{c}-{\boldsymbol{L}}\otimes (\hat{\boldsymbol{B}}\tilde{\boldsymbol{K}})\\ {\boldsymbol{0}}\end{array}\right],{\boldsymbol{A}}_{53}\triangleq \left[\begin{array}{cc} {\boldsymbol{I}}_{N}\otimes (\overline{\boldsymbol{P}}\hat{\boldsymbol{E}})& {\boldsymbol{0}}\\ -{\boldsymbol{I}}_{N}\otimes (\overline{\boldsymbol{P}}\hat{\boldsymbol{E}})& {\boldsymbol{I}}_{N}\otimes (\tilde{\boldsymbol{H}}\overline{\boldsymbol{F}})\end{array}\right]\\ {\hat{\boldsymbol{R}}}_{1}\triangleq \left[\begin{array}{ccc}{\boldsymbol{0}}& {\boldsymbol{0}}& {\boldsymbol{0}}\\ {\boldsymbol{0}}& {\boldsymbol{0}}& {\boldsymbol{0}}\\ -{\boldsymbol{L}}\otimes (\hat{\boldsymbol{B}}\tilde{\boldsymbol{K}}{\boldsymbol{H}}_{1})& -{\boldsymbol{L}}\otimes (\hat{\boldsymbol{B}}\tilde{\boldsymbol{K}}{\boldsymbol{H}}_{1})& -{\boldsymbol{L}}\otimes (\hat{\boldsymbol{B}}\tilde{\boldsymbol{K}}{\boldsymbol{H}}_{1})\\ {\boldsymbol{0}}& {\boldsymbol{0}}& {\boldsymbol{0}}\end{array}\right]\\ {\overline{\boldsymbol{R}}}_{2}\triangleq \left[\begin{array}{cc}{\boldsymbol{R}}_{2}& {\boldsymbol{0}}\end{array}\right],{\boldsymbol{R}}_{2}\triangleq \text{diag}\left\{{\boldsymbol{I}}_{N}\otimes {\boldsymbol{G}}_{1},{\boldsymbol{I}}_{N}\otimes {\boldsymbol{G}}_{1},{\boldsymbol{I}}_{N}\otimes {\boldsymbol{G}}_{1}\right\} \end{array} $ |
如果(28)是可行的,观测器增益
| $ {\boldsymbol{H}}={\overline{\boldsymbol{P}}}\,^{-1}\tilde{\boldsymbol{H}}\text{,}{\boldsymbol{K}}={\tilde{\boldsymbol{P}}}^{-1}\tilde{\boldsymbol{K}}={\boldsymbol{V}}{\boldsymbol{\theta} }^{{-1}}{\overline{\boldsymbol{P}}}\,^{-1}_{1}{\boldsymbol{\theta}} {\boldsymbol{V}}^{\text{T}}\tilde{\boldsymbol{K}} $ | (29) |
式中:
证明 根据引理1及式(17)可得
| $ {\overline{\boldsymbol{\varXi} }}{\text{ + }}\Delta {\boldsymbol{\varXi }} \lt 0 $ | (30) |
式中:
| $ \begin{array}{l}\overline{\boldsymbol{\varXi}}\triangleq \left[\begin{array}{cccc}{\boldsymbol{A}}_{11}& *& *& *\\ {\boldsymbol{0}}& -\rho {\boldsymbol{I}}_{bN{n}_{x}}& *& *\\ {\boldsymbol{0}}& {\boldsymbol{0}}& -{\gamma }^{2}{\boldsymbol{I}}_{bN{n}_{x}}& *\\ {\overline{{\boldsymbol A}}}_{1}& {\overline{\boldsymbol{B}}}_{1}& {\boldsymbol{E}}_{1}& -{\boldsymbol{P}}^{-1}\end{array}\right] \\ {\boldsymbol{R}}_{1}\triangleq \left[\begin{array}{ccc}-{\boldsymbol{L}}\otimes (\hat{\boldsymbol{B}}{\boldsymbol{KH}}_{1})& -{\boldsymbol{L}}\otimes (\hat{\boldsymbol{B}}{\boldsymbol{KH}}_{1})& -{\boldsymbol{L}}\otimes (\hat{\boldsymbol{B}}{\boldsymbol{KH}}_{1})\\ {\boldsymbol{0}}& {\boldsymbol{0}}& {\boldsymbol{0}}\end{array}\right]\\ {\overline{\boldsymbol{F}}}_{1}\triangleq \text{diag}\{{\boldsymbol{I}}_{N}\otimes {\boldsymbol{F}}_{1},{\boldsymbol{I}}_{N}\otimes {\boldsymbol{F}}_{1},{\boldsymbol{I}}_{N}\otimes {\boldsymbol{F}}_{1}\}\\ \Delta {\boldsymbol{\varXi}} \triangleq \left[\begin{array}{cc}{\boldsymbol{0}}& *\\ {\boldsymbol{R}}_{1}{\overline{\boldsymbol{F}}}_{1}{\boldsymbol{R}}_{2}&{\boldsymbol{0}}\end{array}\right]\end{array} $ |
定义
| $ \overline {\boldsymbol{\varXi}} + {\overline {\boldsymbol{R}}_1}{\overline {\boldsymbol{F}}_1}{\overline {\boldsymbol{R}}_2} + {\overline {\boldsymbol{R}}^{\text{T}}_2}{\overline {\boldsymbol{F}}^{\text{T}}_1}{\overline {\boldsymbol{R}}^{\text{T}}_1} \lt 0 $ | (31) |
根据引理3可得
| $ \overline {\boldsymbol{\varXi}} + {\varepsilon ^{ - 1}}{\overline {\boldsymbol{R}}_1}{\overline {\boldsymbol{R}}_1^{\text{T}}} + \varepsilon {\overline {\boldsymbol{R}}^{\text{T}}_2}{\overline {\boldsymbol{R}}_2} \lt 0 $ | (32) |
由此可知不等式(33)成立
| $ \left[\begin{array}{ccc}\overline{\boldsymbol{\varXi}}& *& *\\ {\overline{\boldsymbol{R}}}_{1}^{{\rm{T}}}& -\varepsilon {\boldsymbol{I}}_{bN{n}_{x}}& *\\ {\overline{\boldsymbol{R}}}_{2}^{}& {\boldsymbol{0}}& -{\varepsilon }^{-1}{\boldsymbol{I}}_{bN{n}_{x}}\end{array}\right] \lt 0 $ | (33) |
利用
注解3 本文建立了一个统一的框架来处理多速率多智能体系统在事件触发机制下的非脆弱一致性控制问题。多速率采样、事件触发机制以及控制器执行过程中的扰动大大增加了系统分析与控制器设计的困难,这些因素所带来的影响最终都反映在了确保控制器存在的充分条件中。
4 仿真结果本节将提供一个数值仿真例子来验证所提出控制方法的有效性。
考虑由3个智能体组成的多智能体系统,其邻接矩阵
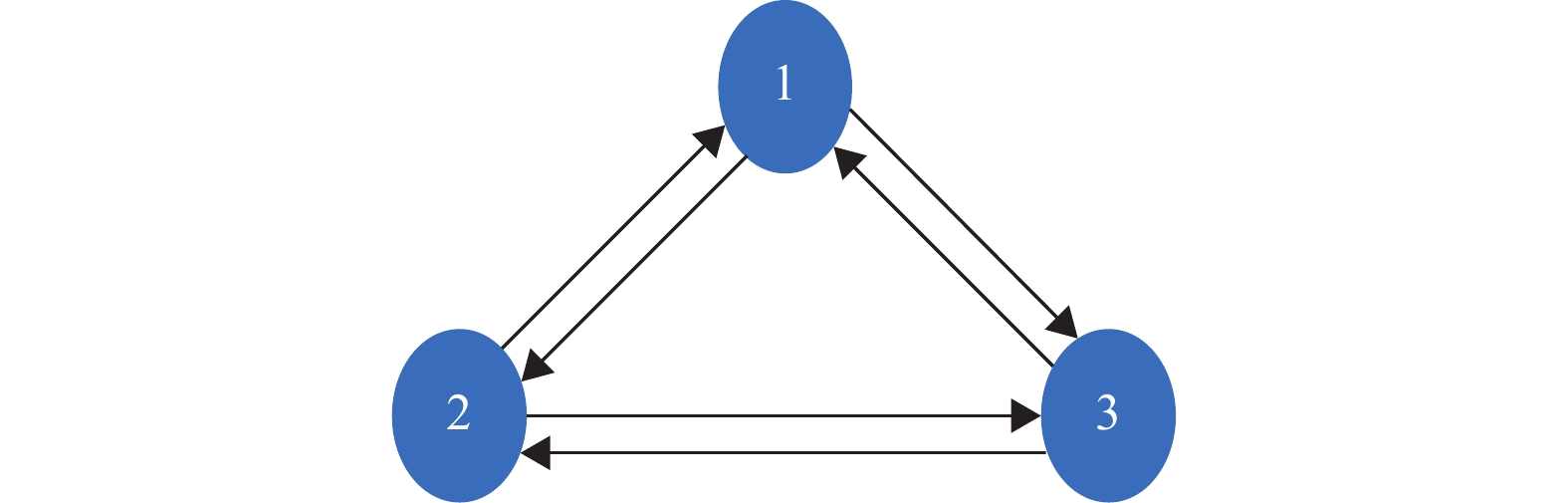
|
图 1 拓扑结构 Figure 1 Topology |
| $ {\boldsymbol{Q}}_{Q}=\left[\begin{array}{ccc}0& 1& 1\text{} \\ 1& 0& 1\\ 1& 1& 0\end{array}\right] $ |
多智能体系统参数如下
| $ \begin{array}{l}{\boldsymbol{A}}=\left[\begin{array}{cc}0.947\;2& -0.059\;8\\ 0.126\;0& 0.952\;5\end{array}\right],{\boldsymbol{B}}=\left[\begin{array}{c}0.432\;0\\ 0.184\;5\end{array}\right]\\ {\boldsymbol{E}}=\left[\begin{array}{c}0.099\;1\\ 0.102\;3\end{array}\right],{\boldsymbol{C}}=\left[\begin{array}{cc}0.5& 0\\ 0& 0.5\end{array}\right]\\ {\boldsymbol{F}}=\left[\begin{array}{c}0.1\\ 0.1\end{array}\right],{\boldsymbol{D}}=\left[\begin{array}{cc}0.5& 0.1\end{array}\right]\end{array} $ |
设置
控制器增益扰动的相关参数为
| $ {\boldsymbol{H}}_{1}=\left[\begin{array}{cccc}1.0& 1.0& 1.0& 1.0\\ 0.6& 0.6& 0.6& 0.6\\ 0.9& 0.9& 0.9& 0.9\\ 0.5& 0.5& 0.5& 0.5\end{array}\right] $ |
| $ {{\boldsymbol{G}}_1} = \left[ {\begin{array}{*{20}{c}} {0.4}&{0.4}&{0.4}&{0.4} \\ {0.3}&{0.3}&{0.3}&{0.3} \\ {0.5}&{0.5}&{0.5}&{0.5} \\ {0.6}&{0.6}&{0.6}&{0.6} \end{array}} \right] $ |
根据定理2并利用MATLAB工具箱,观测器增益
| ${\boldsymbol{H}}={\left[\begin{array}{cccc}1.168\;7& -0.419\;5& 1.194\;4& -0.600\;1\\ -0.226\;7& 1.815\;3& -0.105\;2& 1.932\;3\end{array}\right]}^{\text{T}} $ |
| ${\boldsymbol{K}} = \left[ {\begin{array}{*{20}{l}} {0.003\;2}&{0.009\;9}&{ - 0.006\;5}&{ - 0.006\;6}\\ { - 1.508\;5 \times {{10}^{ - 7}}}&{ - 3.171\;7 \times {{10}^{ - 7}}}&{2.678\;5 \times {{10}^{ - 7}}}&{2.001\;7 \times {{10}^{ - 7}}} \end{array}} \right] $ |
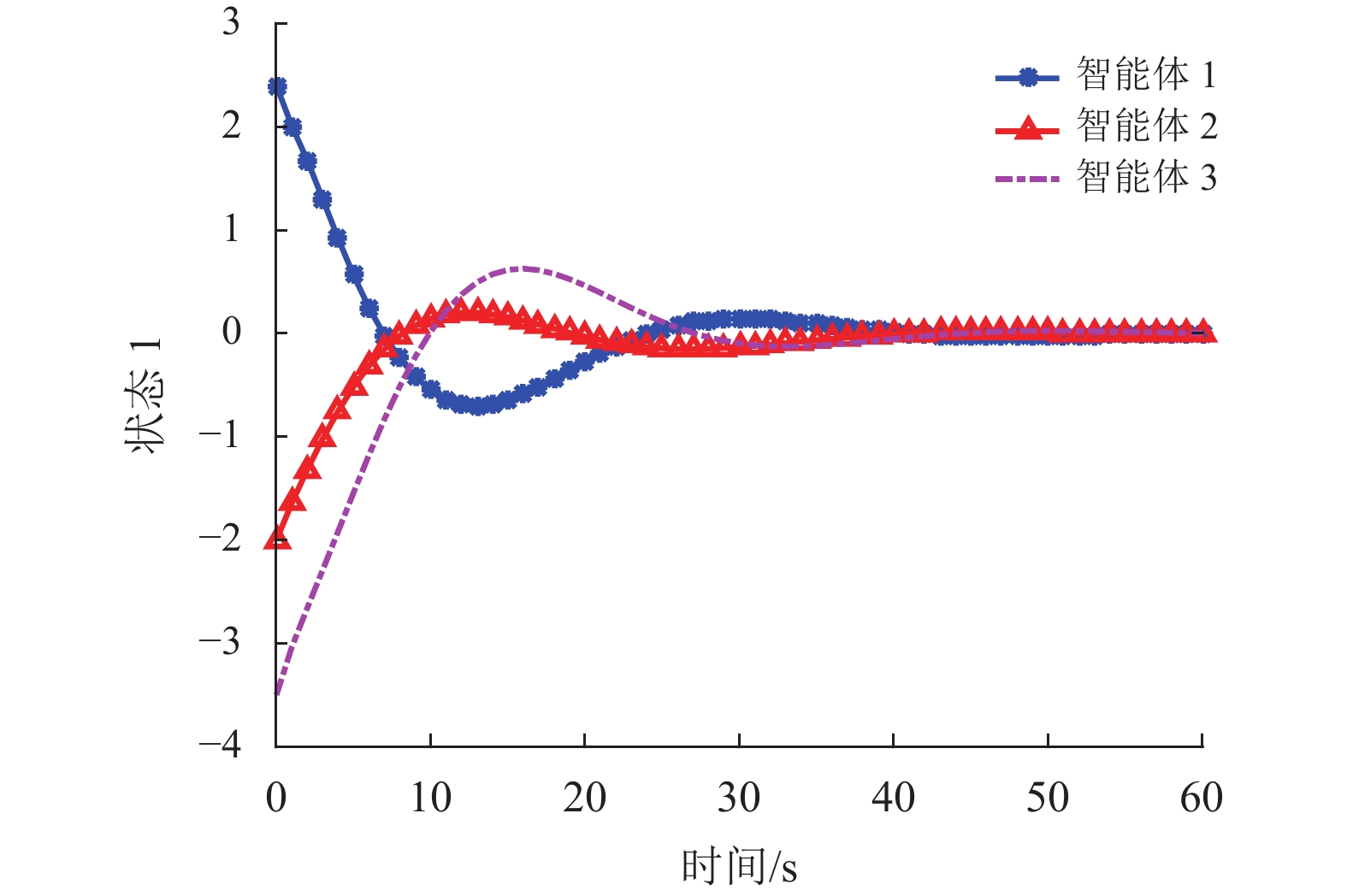
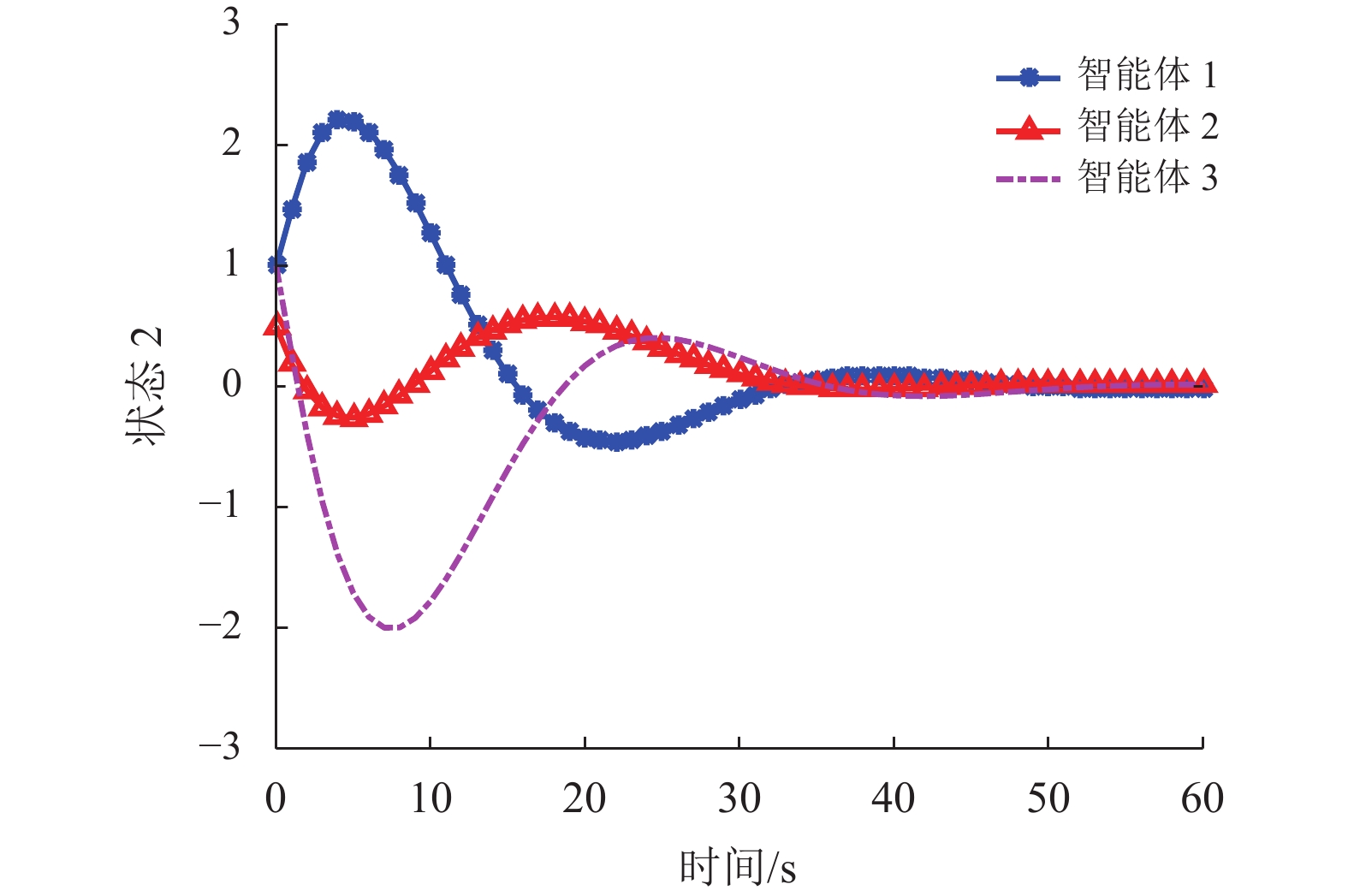
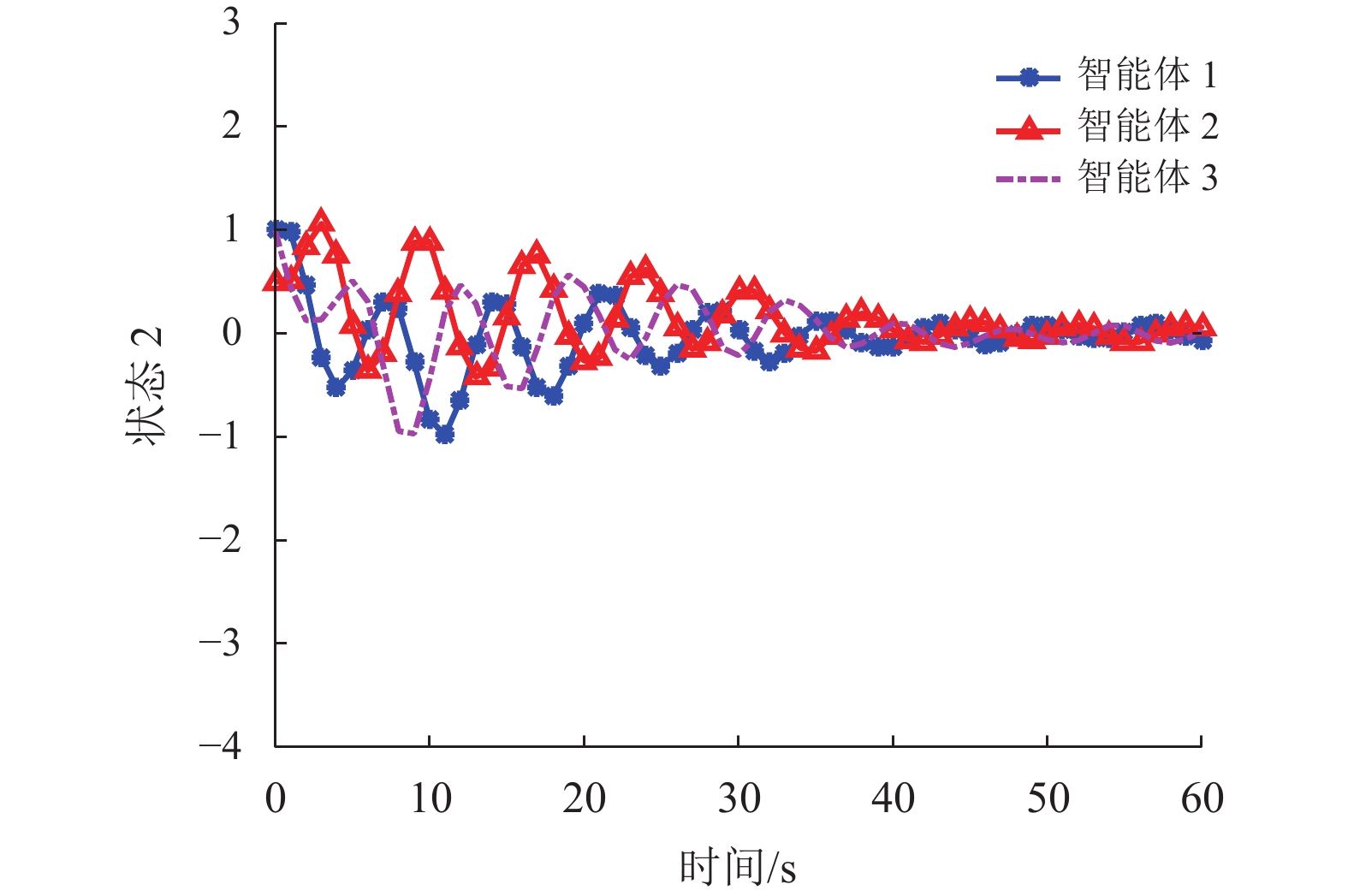
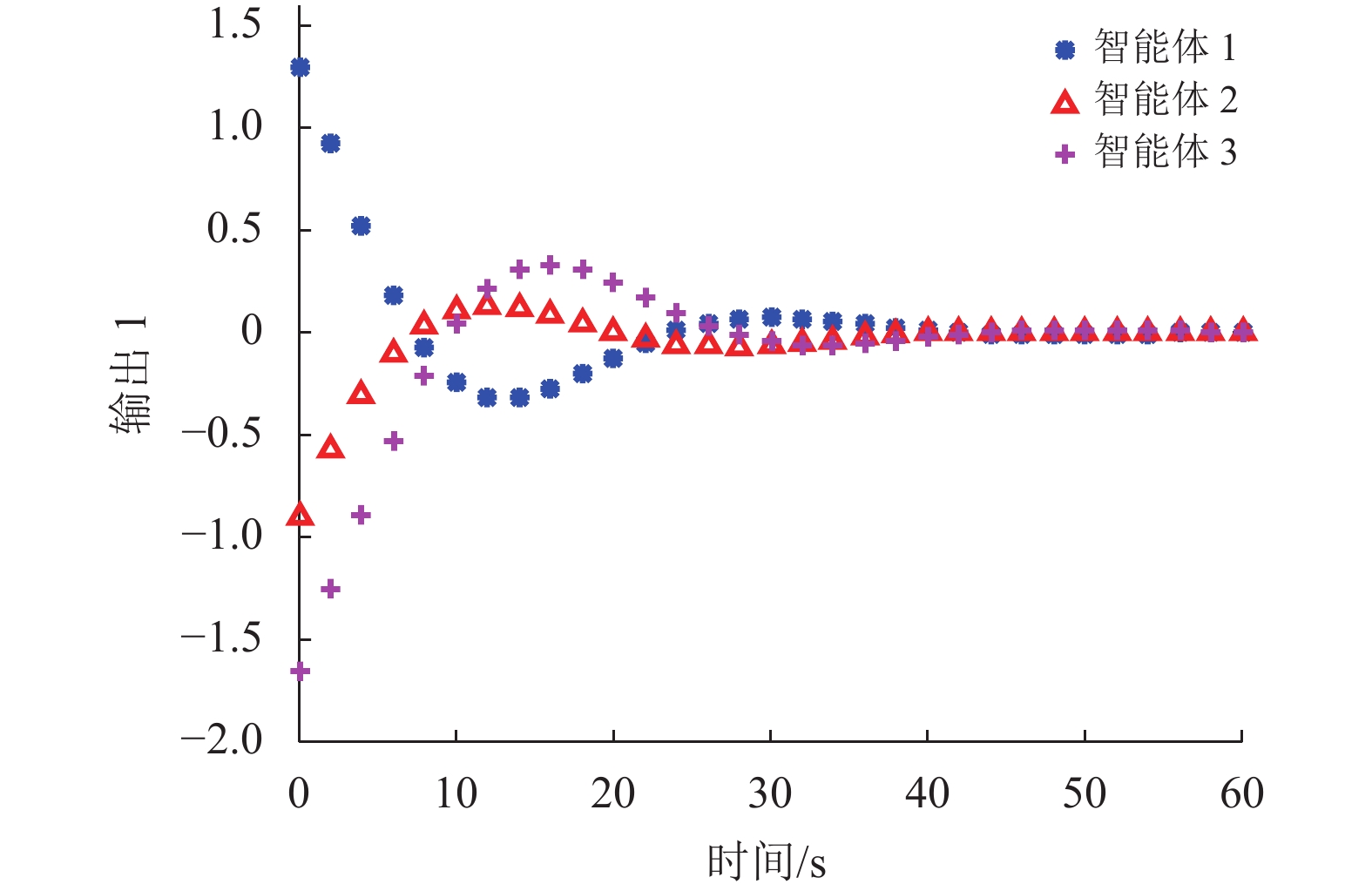
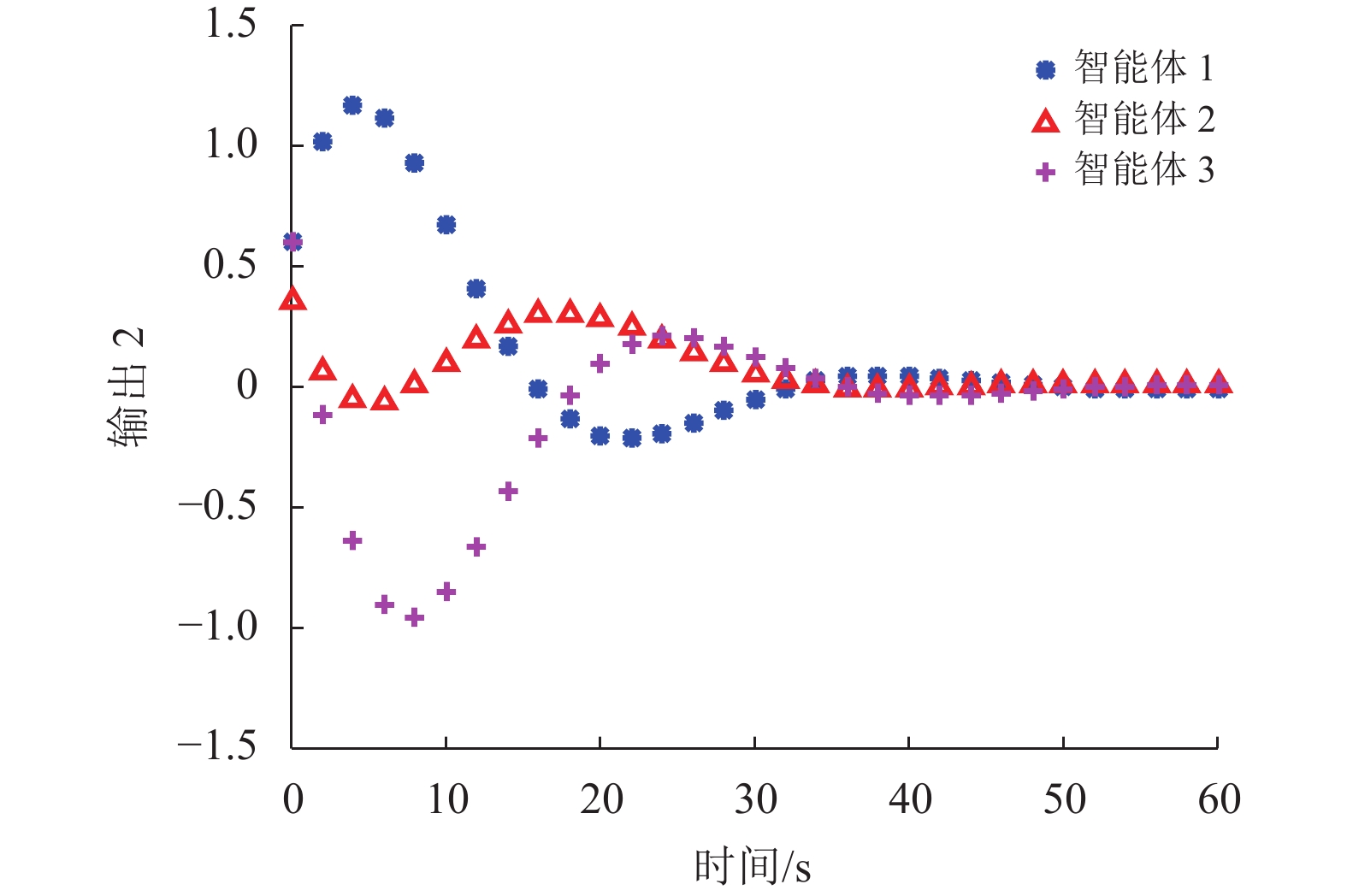
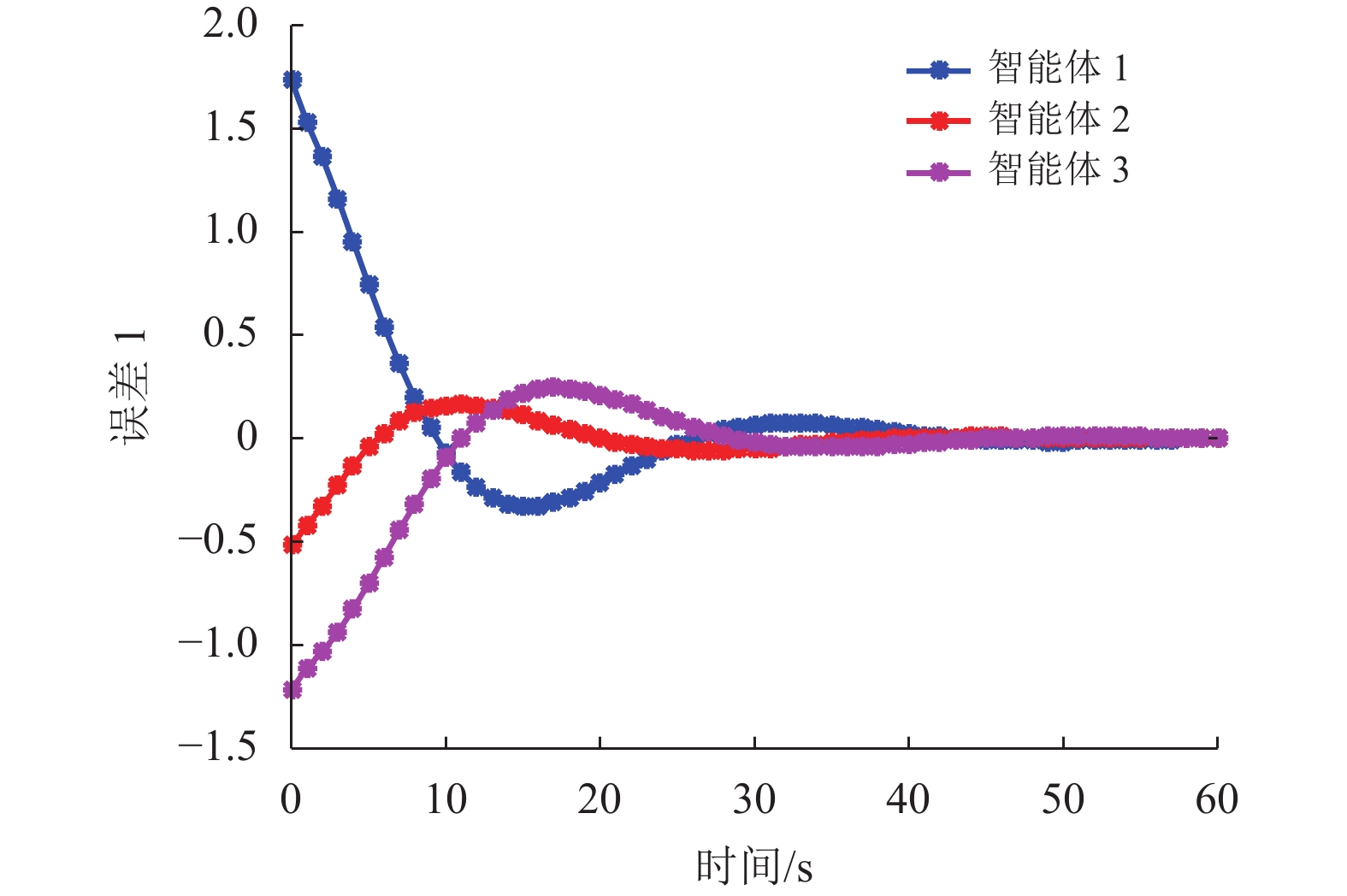
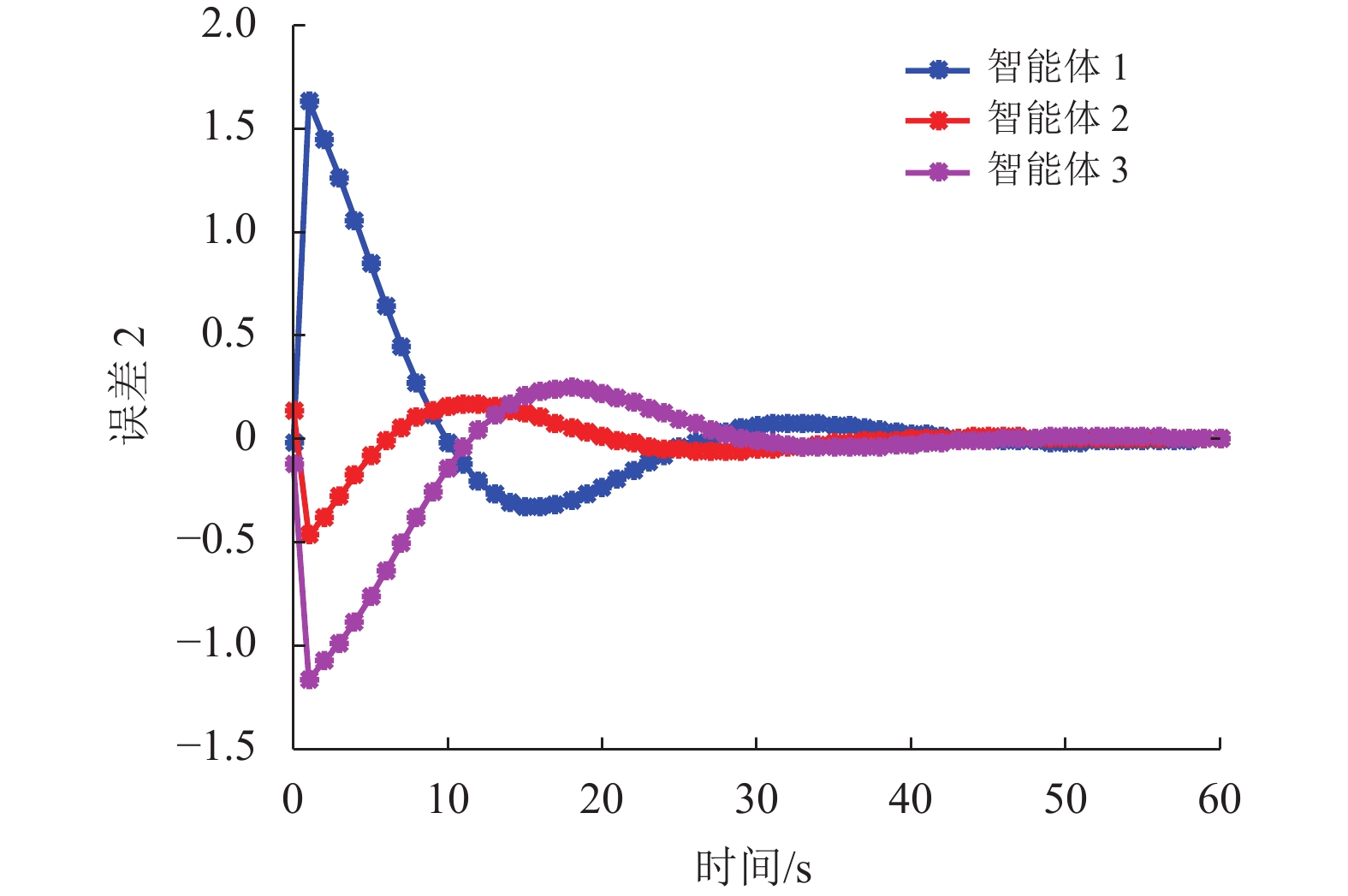
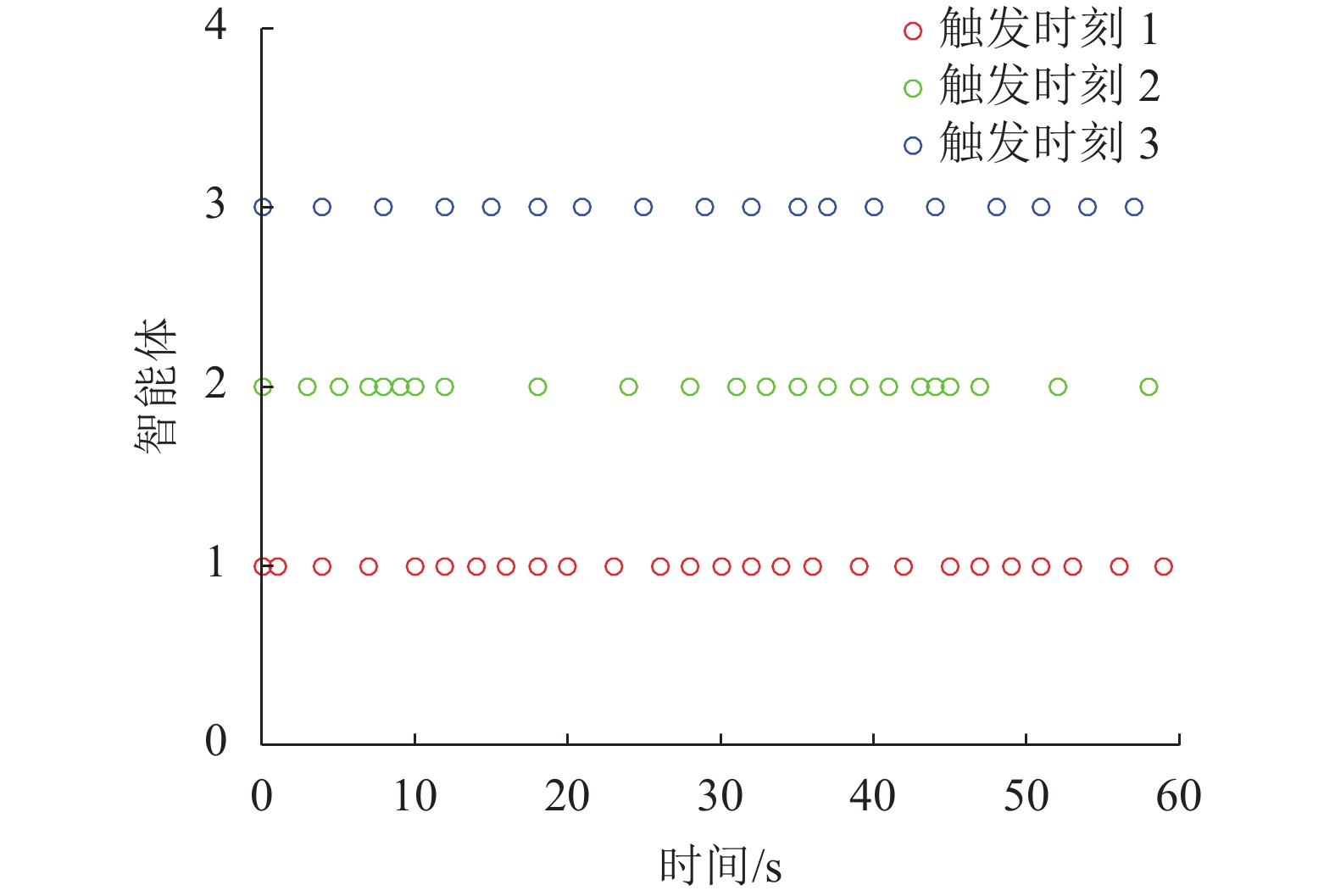
仿真结果见图2~10。图2~3绘制了在非脆弱控制器控制下3个智能体的状态轨迹,其中
|
图 2 非脆弱控制器下3个智能体的状态轨迹
|
|
图 3 非脆弱控制器下3个智能体的状态轨迹
|
|
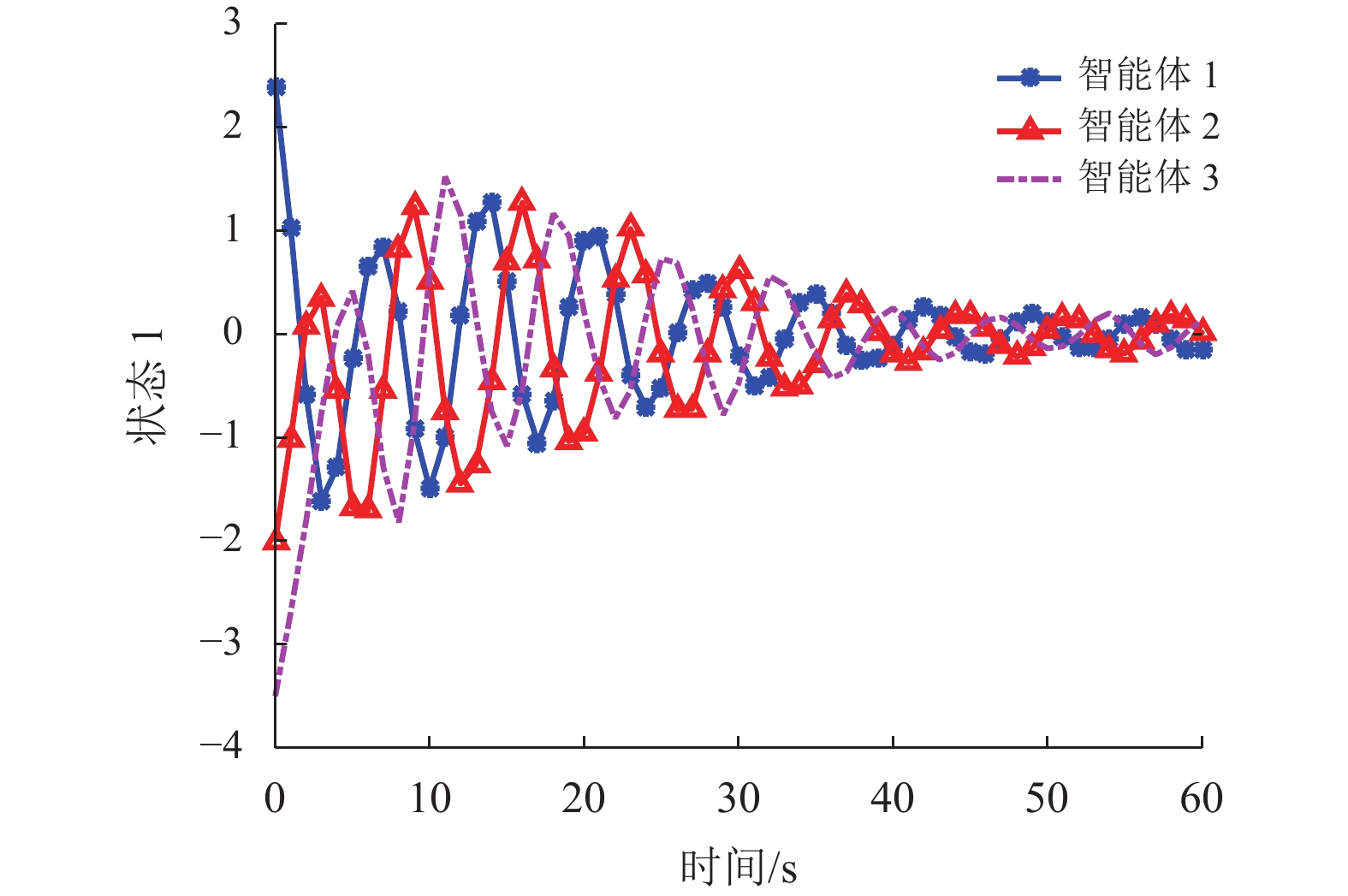
图 4 一般控制器下3个智能体的状态轨迹
|
|
图 5 一般控制器下3个智能体的状态轨迹
|
|
图 6 3个智能体的测量输出
|
|
图 7 3个智能体的测量输出
|
|
图 8 一致性误差1 Figure 8 Consensus error 1 |
|
图 9 一致性误差2 Figure 9 Consensus error 2 |
|
图 10 3个智能体的触发时刻 Figure 10 Triggering instants of three agents |
本文针对一类多速率多智能体系统,研究了在事件触发机制下的非脆弱H∞一致性控制问题。首先,利用提升技术将多速率多智能体系统统一为单速率多智能体系统。接下来,对比时间触发机制,提出了一种基于相对事件触发机制的分布式一致性控制方案,并且所设计的控制器具有非脆弱性。然后,利用Lyapunov稳定性理论,获得了增广系统渐近稳定且满足给定H∞一致性控制约束的充分条件。最后,通过数值例子验证了所提出控制方案的有效性。论文未来潜在的研究方向总结如下:(1) 提升技术的使用造成了大量计算负担,寻找更有效的方法来处理多速率系统;(2) 将研究结果扩展到更复杂的系统,如时滞系统、马尔可夫跳变系统、T-S模糊系统和传感器网络;(3) 研究信道衰落、编码解码机制等对多智能体系统一致性控制问题的影响。
| [1] |
DU H, WEN G, WU D, et al. Distributed fixed-time consensus for nonlinear heterogeneous multi-agent systems[J].
Automatica, 2020, 113: 108797.
DOI: 10.1016/j.automatica.2019.108797. |
| [2] |
ZOU W, SHI P, XIANG Z, et al. Finite-time consensus of second-order switched nonlinear multi-agent systems[J].
IEEE Transactions on Neural Networks and Learning Systems, 2019, 31(5): 1757-1762.
|
| [3] |
DUNBAR W B. Distributed receding horizon control of dynamically coupled nonlinear systems[J].
IEEE Transactions on Automatic Control, 2007, 52(7): 1249-1263.
DOI: 10.1109/TAC.2007.900828. |
| [4] |
FRANCO E, MAGNI L, PARISINI T, et al. Cooperative constrained control of distributed agents with nonlinear dynamics and delayed information exchange: a stabilizing receding-horizon approach[J].
IEEE Transactions on Automatic Control, 2008, 53(1): 324-338.
DOI: 10.1109/TAC.2007.914956. |
| [5] |
LIN P, JIA Y, LI L. Distributed robust H∞ consensus control in directed networks of agents with time-delay
[J].
Systems & Control Letters, 2008, 57(8): 643-653.
|
| [6] |
WANG J, DUAN Z, WEN G, et al. Distributed robust control of uncertain linear multi-agent systems[J].
International Journal of Robust and Nonlinear Control, 2015, 25(13): 2162-2179.
DOI: 10.1002/rnc.3199. |
| [7] |
XU W, WANG Z, HO D W C. Finite-horizon H∞ consensus for multiagent systems with redundant channels via an observer-type event-triggered scheme
[J].
IEEE Transactions on Cybernetics, 2017, 48(5): 1567-1576.
|
| [8] |
ZHAO Y, DUAN Z, WEN G, et al. Distributed H∞ consensus of multi-agent systems: a performance region-based approach
[J].
International Journal of Control, 2012, 85(3): 332-341.
DOI: 10.1080/00207179.2011.652181. |
| [9] |
SAKTHIVEL R, KANAKALAKSHMI S, KAVIARASAN B, et al. Finite-time consensus of input delayed multi-agent systems via non-fragile controller subject to switching topology[J].
Neurocomputing, 2019, 325: 225-233.
DOI: 10.1016/j.neucom.2018.10.030. |
| [10] |
BAO H, PARK J H, CAO J. Non-fragile state estimation for fractional-order delayed memristive BAM neural networks[J].
Neural Networks, 2019, 119: 190-199.
DOI: 10.1016/j.neunet.2019.08.003. |
| [11] |
JIANG X, XIA G, FENG Z. Non-fragile consensus control for singular multi-agent systems with Lipschitz nonlinear dynamics[J].
Neurocomputing, 2019, 351: 123-133.
DOI: 10.1016/j.neucom.2019.03.038. |
| [12] |
WANG Z, DING D, SHU H. Non-fragile H∞ control with randomly occurring gain variations, distributed delays and channel fadings
[J].
IET Control Theory & Applications, 2015, 9(2): 222-231.
|
| [13] |
MA L, WANG Z, LAM H K. Mean-square H∞ consensus control for a class of nonlinear time-varying stochastic multiagent systems: the finite-horizon case
[J].
IEEE Transactions on Systems, Man, and Cybernetics:Systems, 2016, 47(7): 1050-1060.
|
| [14] |
BU X, DONG H, WANG Z, et al. Non-fragile distributed fault estimation for a class of nonlinear time-varying systems over sensor networks: the finite-horizon case[J].
IEEE Transactions on Signal and Information Processing over Networks, 2018, 5(1): 61-69.
|
| [15] |
LI J, DONG H, LIU H, et al. Sampled-data non-fragile state estimation for delayed genetic regulatory networks under stochastically switching sampling periods[J].
Neurocomputing, 2021, 463: 168-176.
DOI: 10.1016/j.neucom.2021.07.093. |
| [16] |
LIU L, MA L, ZHANG J, et al. Distributed non-fragile set-membership filtering for nonlinear systems under fading channels and bias injection attacks[J].
International Journal of Systems Science, 2021, 52(6): 1192-1205.
DOI: 10.1080/00207721.2021.1872118. |
| [17] |
GENG H, LIANG Y, LIU Y, et al. Bias estimation for asynchronous multi-rate multi-sensor fusion with unknown inputs[J].
Information Fusion, 2018, 39: 139-153.
DOI: 10.1016/j.inffus.2017.03.002. |
| [18] |
QU B, WANG Z, SHEN B. Fusion estimation for a class of multi-rate power systems with randomly occurring SCADA measurement delays[J].
Automatica, 2021, 125: 109408.
DOI: 10.1016/j.automatica.2020.109408. |
| [19] |
HUA C, GE C, GUAN X. Synchronization of chaotic Lur’e systems with time delays using sampled-data control[J].
IEEE Transactions on Neural Networks and Learning Systems, 2014, 26(6): 1214-1221.
|
| [20] |
SHEN Y, WANG Z, DONG H, et al. Multi-sensor multi-rate fusion estimation for networked systems: advances and perspectives[J]. Information Fusion, 2022, 82: 19-27.
|
| [21] |
马伟伟, 贾新春, 张大伟. 双率采样系统的基于观测器的网络化H∞控制
[J].
自动化学报, 2015, 41(10): 1788-1797.
MA W W, JIA X C, ZHANG D W. Observer-based networked H∞ control for dualrate sampling systems [J]. Acta Automatica Sinica, 2015, 41(10): 1788-1797. |
| [22] |
WEI G, WANG L, LIU Y. H∞ control for a class of multi-agent systems via a stochastic sampled-data method
[J].
IET Control Theory & Applications, 2015, 9(14): 2057-2065.
|
| [23] |
JU Y, TIAN X, LIU H, et al. Fault detection of networked dynamical systems: a survey of trends and techniques[J].
International Journal of Systems Science, 2021, 52(16): 3390-3409.
DOI: 10.1080/00207721.2021.1998722. |
| [24] |
GUAN Z H, YANG C, HUANG J. Stabilization of networked control systems with short or long random delays: a new multirate method[J].
International Journal of Robust and Nonlinear Control, 2010, 20(16): 1802-1816.
|
| [25] |
MOARREF M, RODRIGUES L. Stability and stabilization of linear sampled-data systems with multi-rate samplers and time driven zero order holds[J].
Automatica, 2014, 50(10): 2685-2691.
DOI: 10.1016/j.automatica.2014.08.037. |
| [26] |
OHSHIMA M, HASHIMOTO I, OHNO H, et al. Multirate multivariable model predictive control and its application to a polymerization reactor[J].
International Journal of Control, 1994, 59(3): 731-742.
DOI: 10.1080/00207179408923102. |
| [27] |
GENG H, LIANG Y, YANG F, et al. Model-reduced fault detection for multi-rate sensor fusion with unknown inputs[J].
Information Fusion, 2017, 33: 1-14.
DOI: 10.1016/j.inffus.2016.04.002. |
| [28] |
GENG H, LIANG Y, YANG F, et al. The joint optimal filtering and fault detection for multi-rate sensor fusion under unknown inputs[J].
Information Fusion, 2016, 29: 57-67.
DOI: 10.1016/j.inffus.2015.10.003. |
| [29] |
IZADI I, ZHAO Q, CHEN T. An H∞ approach to fast rate fault detection for multirate sampled-data systems
[J].
Journal of Process Control, 2006, 16(6): 651-658.
DOI: 10.1016/j.jprocont.2005.10.004. |
| [30] |
ZHANG P, DING S X, WANG G Z, et al. Fault detection for multirate sampled-data systems with time delays[J].
International Journal of Control, 2002, 75(18): 1457-1471.
DOI: 10.1080/0020717021000031475. |
| [31] |
ZHONG M, YE H, DING S X, et al. Observer-based fast rate fault detection for a class of multirate sampled-data systems[J].
IEEE Transactions on Automatic Control, 2007, 52(3): 520-525.
DOI: 10.1109/TAC.2006.890488. |
| [32] |
ZHANG Y, WANG Z, ZOU L, et al. Fault detection filter design for networked multi-rate systems with fading measurements and randomly occurring faults[J].
IET Control Theory & Applications, 2016, 10(5): 573-581.
|
| [33] |
LIANG Y, CHEN T, PAN Q. Multi-rate optimal state estimation[J].
International Journal of Control, 2009, 82(11): 2059-2076.
DOI: 10.1080/00207170902906132. |
| [34] |
YAN L, JIANG L, XIA Y, et al. State estimation and data fusion for multirate sensor networks[J].
International Journal of Adaptive Control and Signal Processing, 2016, 30(1): 3-15.
DOI: 10.1002/acs.2569. |
| [35] |
ZHANG H, BASIN M V, SKLIAR M. It–Volterra optimal state estimation with continuous, multirate, randomly sampled, and delayed measurements[J].
IEEE Transactions on Automatic Control, 2007, 52(3): 401-416.
DOI: 10.1109/TAC.2007.892383. |
| [36] |
GENG H, LIANG Y, ZHANG X. Linear-minimum-mean-square-error observer for multi-rate sensor fusion with missing measurements[J].
IET Control Theory & Applications, 2014, 8(14): 1375-1383.
|
| [37] |
ZOU L, WANG Z, HU J, et al. Communication-protocol-based analysis and synthesis of networked systems: progress, prospects and challenges[J].
International Journal of Systems Science, 2021, 52(14): 3013-3034.
DOI: 10.1080/00207721.2021.1917721. |
| [38] |
HU J, ZHANG H, LIU H, et al. A survey on sliding mode control for networked control systems[J].
International Journal of Systems Science, 2021, 52(6): 1129-1147.
DOI: 10.1080/00207721.2021.1885082. |
| [39] |
WEI G, LIU L, WANG L, et al. Event-triggered control for discrete-time systems with unknown nonlinearities: an interval observer-based approach[J].
International Journal of Systems Science, 2020, 51(6): 1019-1031.
DOI: 10.1080/00207721.2020.1746441. |
| [40] |
ZHANG P, YUAN Y, GUO L. Fault-tolerant optimal control for discrete-time nonlinear system subjected to input saturation: a dynamic event-triggered approach[J].
IEEE Transactions on Cybernetics, 2019, 51(6): 2956-2968.
|
| [41] |
SUN Y, DING D, DONG H, et al. Event-based resilient filtering for stochastic nonlinear systems via innovation constraints[J].
Information Sciences, 2021, 546: 512-525.
DOI: 10.1016/j.ins.2020.08.007. |
| [42] |
HU J, WANG Z, ALSAADI F E, et al. Event-based filtering for time-varying nonlinear systems subject to multiple missing measurements with uncertain missing probabilities[J].
Information Fusion, 2017, 38: 74-83.
DOI: 10.1016/j.inffus.2017.03.003. |
| [43] |
DING D, WANG Z, HAN Q L. A set-membership approach to event-triggered filtering for general nonlinear systems over sensor networks[J].
IEEE Transactions on Automatic Control, 2019, 65(4): 1792-1799.
|
| [44] |
NOWZARI C, GARCIA E, CORTÉS J. Event-triggered communication and control of networked systems for multi-agent consensus[J].
Automatica, 2019, 105: 1-27.
DOI: 10.1016/j.automatica.2019.03.009. |
| [45] |
ÅARZÉN K E. A simple event-based PID controller[J].
IFAC Proceedings Volumes, 1999, 32(2): 8687-8692.
DOI: 10.1016/S1474-6670(17)57482-0. |
| [46] |
BOYD S, EL GHAOUI L, FERON E, et al. Linear matrix inequalities in system and control theory[M]. Philadelphia: Society for Industrial and Applied Mathematics, 1994: 55-87.
|
| [47] |
HAN F, WEI G, DING D, et al. Finite-horizon H∞-consensus control for multi-agent systems with random parameters: the local condition case
[J].
Journal of the Franklin Institute, 2017, 354(14): 6078-6097.
DOI: 10.1016/j.jfranklin.2017.07.010. |
 2022, Vol. 39
2022, Vol. 39

