永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)具有转矩惯量比高、温升低、功率因素高以及动态特性好等显著特点,在日常生活、工业生产、农业生产、航空航天中得到了日益广泛的应用[1-4]。随着工艺要求不断提高,往往需要增加系统中电机的数量以提高控制性能。两台电机协调驱动可以增加系统的灵活性、减小电机体积、减少能耗,在电动汽车、输送带和风力发电等工业生产中得到广泛应用。因此,研究双永磁同步电机系统协调控制具有广阔的应用前景和重要学术价值。
在双电机同步控制系统中保证两电机转速同步和转矩同步非常重要,倘若系统在运行中出现严重的转速差或转矩差,那么会造成断带、打滑甚至电机损坏[5-9]。针对双电机协调控制精度的问题,国内外学者将控制结构和先进的控制算法相结合以确保系统的同步性。传统的控制结构主要有并行控制、主从控制、交叉耦合控制、偏差耦合控制、虚拟主轴控制等;控制算法有滑模控制、神经网络控制、自适应控制和预测控制等[10-15]。滑模变结构控制(Sliding Mode Control, SMC)主要是利用控制量的高频切换使得被控对象沿着滑模面运动,对外界扰动抑制和系统不确定性体现出很强的鲁棒性,非常适用于PMSM系统,很多学者在单电机控制中引入滑模控制,而忽略了在多电机系统中引入滑模控制以设计优化协调控制器[16-20]。
为了提高双永磁同步电机驱动系统对于负载扰动的鲁棒性,本文研究双电机协调控制问题。首先,利用胡克定律刻画柔性联接的耦合特性,并考虑采用d轴电流为零的策略对系统带来的不确定性,初步建立了双电机系统数学模型。接着,引入交叉耦合控制和PI算法且将系统扰动分为匹配扰动和非匹配扰动,建立了具有不确定性和非匹配扰动的双电机数学模型。然后,针对系统的不确定性和非匹配扰动提出一种基于干扰观测器的积分滑模控制方法。最后,在基于dSPACE的多电机平台上进行半实物仿真实验。实验结果表明,该方法能有效提高系统在启动和负载突变时的转速同步和转矩同步性能。
1 双永磁同步电机系统数学模型如图1所示为双永磁同步电机的物理结构示意图,驱动滚筒之间通过皮带或齿轮中间连接器联接,两电机分别驱动两端的滚筒使得系统同步运行,通常应用于输送机、起重机及电梯等场合[21-24]。在该类系统中,通常情况下两电机的转速处在同步协调状态下,但是,在实际应用场景中系统会受到外界环境的未知干扰,使得系统内部电流和转速出现差异,造成皮带或齿轮的张力波动过大,这样两电机之间的耦合作用力将会出现并且进一步引发两电机相互影响,出现皮带或齿轮断裂,转矩差过大会导致电机的发热烧毁[25-28]。因此,双电机系统中保证转速同步和转矩平衡是协调控制的重要目标。
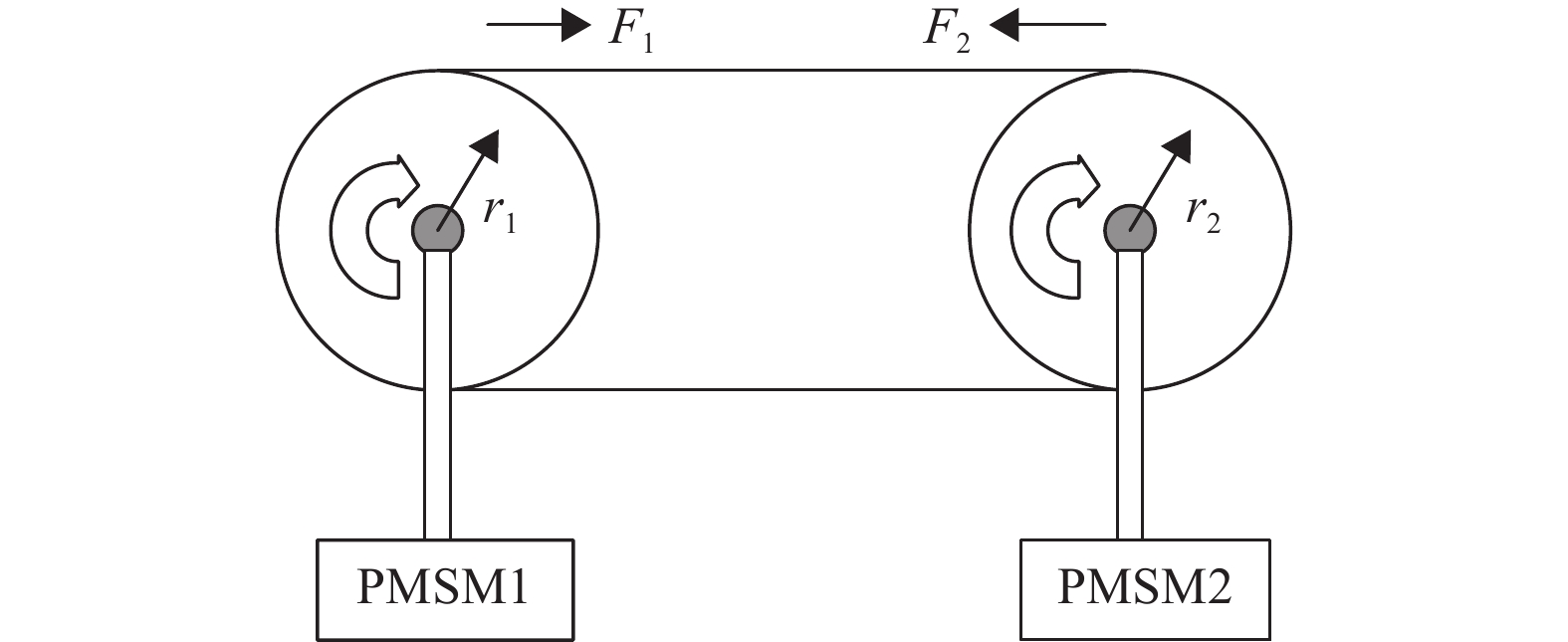
|
图 1 双永磁同步电机系统物理结构示意图 Figure 1 Physical structure diagram of dual permanent magnet synchronous motor system |
若受干扰两电机转子角度出现差异时,根据胡克定律可得到如下表达式:
| $ \left\{ \begin{gathered} {{{F}}_{\text{1}}}{\text{ = }}{r_1}k\int_0^t {\left( {{{\boldsymbol{\omega}} _2} - {{\boldsymbol{\omega}} _1}} \right){\rm{d}}\tau } \hfill \\ {{{F}}_{\text{2}}}{\text{ = }}{r_2}k\int_0^t {\left( {{{\boldsymbol{\omega}} _1} - {{\boldsymbol{\omega}} _2}} \right){\rm{d}}\tau } \hfill \\ \end{gathered} \right. $ | (1) |
式中:
记两电机各自承受的负载分别为
| $\left\{\begin{array}{l} {{T}^{\prime}_{{\rm{l}} 1}}={{T}}_{{\rm{l}} 1}+r^{2} k \displaystyle \int_{0}^{t}\left(\omega_{1}-\omega_{2}\right) {\rm{d}} \tau \\ {{T}}_{{\rm{l}} 2}^{\prime}={{T}}_{{\rm{l}} 2}+r^{2} k \displaystyle \int_{0}^{t}\left(\omega_{2}-\omega_{1}\right) {\rm{d}} \tau \end{array}\right. $ | (2) |
根据图2所示PMSM坐标矢量图得到永磁同步电机在(d-q)坐标系上的数学模型:
| $ \left\{ \begin{gathered} \frac{{{\rm{{\rm{d}}}}{i_{{d}}}}}{{{\rm{d}}t}} = - \frac{{{R_{\rm{s}}}}}{{{{{L}}_{{\rm{s}}{{d}}}}}}{i_{{d}}} + \frac{{{L_{{{{\rm{s}}q}}}}}}{{{L_{{\rm{s}}{{d}}}}}}\omega {i_{{q}}} + \frac{1}{{{L_{{\rm{s}}{{d}}}}}}{u_{{d}}} \hfill \\ \frac{{{\rm{d}}{i_{{q}}}}}{{{\rm{d}}t}} = - \frac{{{L_{{\rm{s}}{{d}}}}}}{{{{{L}}_{{{{\rm{s}}q}}}}}}\omega {i_{{d}}} - \frac{{{R_{\rm{s}}}}}{{{L_{{{{\rm{s}}q}}}}}}{i_{{q}}} - \frac{1}{{{L_{{{{\rm{s}}q}}}}}}\omega {\varphi _{\rm{f}}} + \frac{1}{{{L_{{{{\rm{s}}q}}{{}}}}}}{u_{{q}}} \hfill \\ \end{gathered} \right. $ | (3) |
式中:
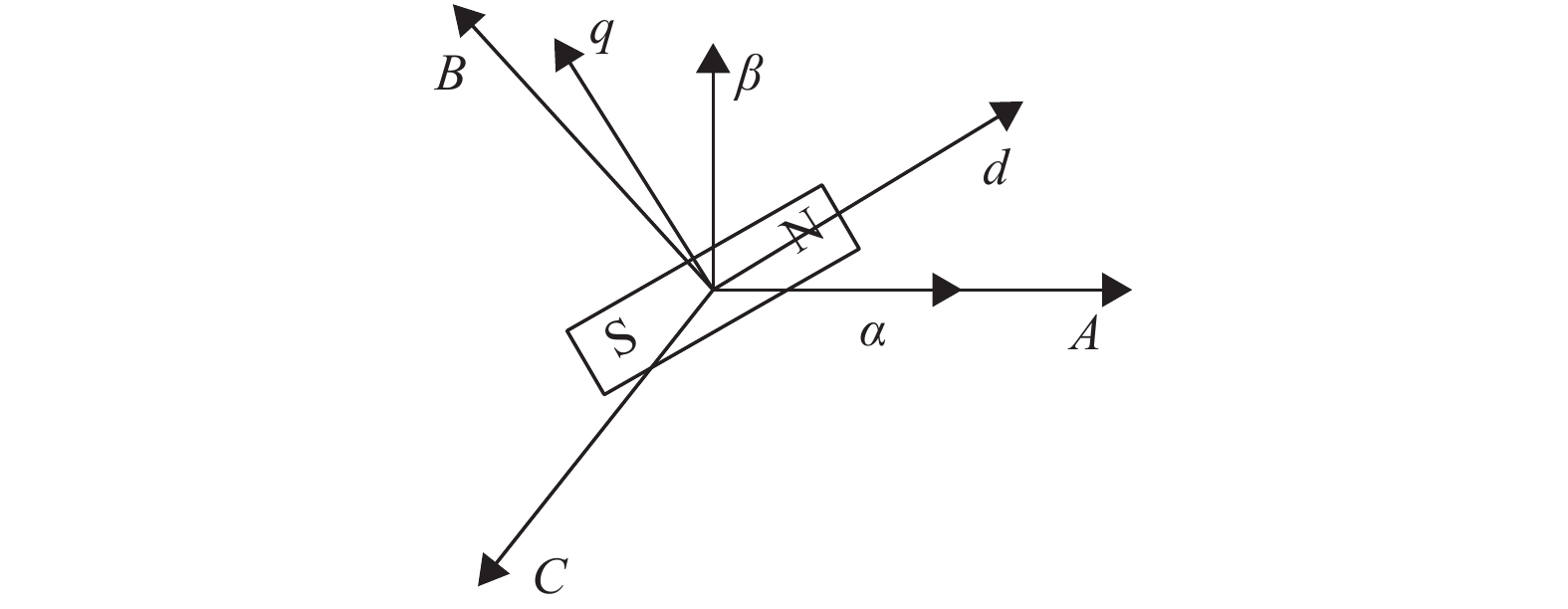
|
图 2 PMSM坐标矢量图 Figure 2 Clock-phase diagram of PMSM |
本文电机为表贴式永磁同步电机,其电磁转矩方程为
| $ {T_{\rm{e}}} = \frac{3}{2}{n_{\rm{p}}}{i_{{q}}}\left( {{\varphi _{\rm{f}}} + \left( {{L_{{{{\rm{s}}d}}}} - {L_{{{{\rm{s}}{{q}}}}}}} \right){i_{{d}}}} \right) $ | (4) |
式中:
本文选择
| $ {T_{\rm{e}}} = \frac{3}{2}{n_{\rm{p}}}{\varphi _{\rm{f}}}{i_{{q}}} $ | (5) |
根据力学平衡条件可得到PMSM的运动方程为
| $ {T_{\rm{e}}} - {T_{\rm{l}}} = \frac{J}{{{n_{\rm{p}}}}}\frac{{{\rm{d}}\omega }}{{{\rm{d}}t}} + \frac{B}{{{n_{\rm{p}}}}}\omega $ | (6) |
式中:
将式(6)与式(3)、(5)相结合,得到
| $ \frac{{{\rm{d}}\omega }}{{{\rm{d}}t}} = \frac{{n_{\rm{p}}^2}}{J}{\varphi _{\rm{f}}}{i_{{q}}} - \frac{{{n_{\rm{p}}}}}{J}{T_{\rm{l}}} - \frac{B}{J}\omega $ | (7) |
因此,单台PMSM数学模型可以简化为
| $ \left\{ \begin{gathered} \frac{{{\rm{d}}{i_{{q}}}}}{{{\rm{d}}t}} = - \frac{{{R_{\rm{s}}}}}{{{L_{{{{\rm{s}}q}}}}}}{i_{{q}}} - \frac{1}{{{L_{{{{\rm{s}}q}}}}}}\omega \left( {{\varphi _{\rm{f}}} + \delta } \right) + \frac{1}{{{L_{{{{\rm{s}}q}}}}}}{u_{{q}}} \hfill \\ \frac{{{\rm{d}}\omega }}{{{\rm{d}}t}} = \frac{{n_{\rm{p}}^2{\varphi _{\rm{f}}}}}{J}{i_{{q}}} - \frac{{{n_{\rm{p}}}}}{J}{T_{\rm{l}}} - \frac{B}{J}\omega \hfill \\ \end{gathered} \right. $ | (8) |
式中:
结合式(1)、(2)和(8)得到双永磁同步电机数学模型:
| $ \left\{ \begin{gathered} \frac{{{\rm{d}}{i_{{{q}}1}}}}{{{\rm{d}}t}} = - \frac{{{R_{{\rm{s1}}}}}}{{{L_{{{{\rm{s}}{{q}}}}1}}}}{i_{{{q}}1}} - \frac{1}{{{L_{{{{\rm{s}}{{q}}}}1}}}}{\omega _1}\left( {{\varphi _{{\rm{f}}1}} + {\delta _1}} \right) + \frac{1}{{{L_{{{{\rm{s}}{{q}}}}1}}}}{u_{{{q}}1}} \hfill \\ \frac{{{\rm{d}}{\omega _1}}}{{{\rm{d}}t}} = \frac{{n_{{\rm{p}}1}^2{\varphi _{{\rm{f}}1}}}}{{{J_1}}}{i_{{{q}}{\text{1}}}} - \frac{{{n_{{\rm{p}}1}}}}{{{J_1}}}({T_{{\rm{l}}1}} + {r^2}k\int_0^t {({\omega _1} - {\omega _2})} {\rm{d}}\tau ) - \frac{{{B_1}}}{{{J_1}}}{\omega _1} \hfill \\ \frac{{{\rm{d}}{i_{{{q}}2}}}}{{{\rm{d}}t}} = - \frac{{{R_{{\rm{s2}}}}}}{{{L_{{{{\rm{s}}{{q}}}}2}}}}{i_{{{q}}2}} - \frac{1}{{{L_{{{{\rm{s}}{{q}}}}2}}}}{\omega _2}\left( {{\varphi _{{\rm{f}}2}} + {\delta _2}} \right) + \frac{1}{{{L_{{{{\rm{s}}{{q}}}}2}}}}{u_{{{q}}2}} \hfill \\ \frac{{{\rm{d}}{\omega _2}}}{{{\rm{d}}t}} = \frac{{n_{{\rm{p2}}}^2{\varphi _{{\rm{f}}2}}}}{{{J_2}}}{i_{{{q}}{\text{2}}}} - \frac{{{n_{{\rm{p2}}}}}}{{{J_2}}}({T_{{\rm{l}}2}} + {r^2}k\int_0^t {({\omega _2} - {\omega _1})} {\rm{d}}\tau ) - \frac{{{B_2}}}{{{J_2}}}{\omega _2} \hfill \\ \end{gathered} \right. $ | (9) |
交叉耦合控制是一种耦合控制方式,其结构简单很适用于双电机控制系统,两电机的q轴电流输出作差后反馈至电流环控制器前,若其中一台电机受到负载扰动整个系统会作出响应以抵抗扰动的影响。为保证双永磁同步电机系统的同步性能采用如图3所示控制结构,转速环和电流环都采用PI控制算法。图中ASR1、ASR2分别为电机1、2的转速调节器,ACQR1、ACQR2分别为电机1、2的q轴电流调节器,ACDR1、ACDR2分别电机1、2的d轴电流调节器,
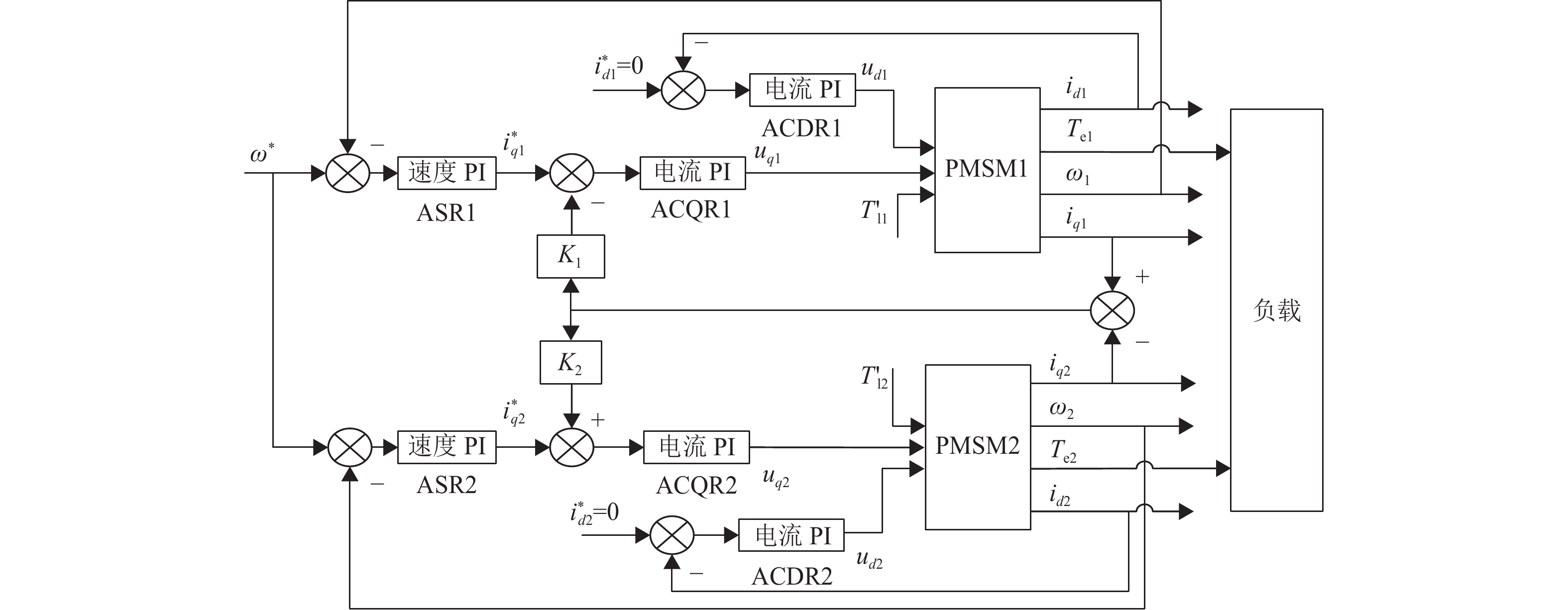
|
图 3 双永磁同步电机系统交叉耦合控制结构 Figure 3 Cross coupling control structure of flexible coupling dual permanent magnet synchronous motor system |
根据图3双电机系统交叉耦合控制结构,给定角速度和反馈的角速度作差经两电机转速调节器的输出,以及其输出与反馈的q轴电流差经q轴电流调节器的输出表达式如式(10)、(11)所示。
| $ \left\{ \begin{array}{l} i_{{{q}}1}^* = {k_{{\rm{PS}}1}}\left( {{\omega ^*} - {\omega _1}} \right) + {k_{{\rm{IS}}1}}\displaystyle \int_0^t {\left( {{\omega ^*} - {\omega _1}} \right){\rm{d}}\tau } \\ i_{{{q}}2}^* = {k_{{\rm{PS}}2}}\left( {{\omega ^*} - {\omega _2}} \right) + {k_{{\rm{IS}}2}}\displaystyle \int_0^t {\left( {{\omega ^*} - {\omega _2}} \right){\rm{d}}\tau } \end{array} \right. $ | (10) |
| $ \left\{ \begin{array}{l} {u_{{{q}}1}} = {k_{{\rm{{\rm{PQ}}}}1}}\left[ {i_{{{q}}1}^* - {K_1}\left( {{i_{{{q}}1}} - {i_{{{q}}2}}} \right)} \right] + {k_{{\rm{IQ}}1}}\displaystyle \int_0^t {\left[ {i_{{{q}}1}^* - {K_1}\left( {{i_{{{q}}1}} - {i_{{{q}}2}}} \right)} \right] {\rm{d}}\tau + {v_1}} \\ {u_{{{d}}1}} = {k_{{\rm{PD}}1}}\left( {i_{{{d}}1}^* - {i_{{{d}}1}}} \right) + {k_{{\rm{ID}}1}}\displaystyle \int_0^t {\left( {i_{{{d}}1}^* - {i_{{{d}}1}}} \right){\rm{d}}\tau } \\ {u_{{{q}}2}} = {k_{{\rm{{\rm{PQ}}}}2}}\left[ {i_{{{q}}2}^* + {K_2}\left( {{i_{{{q}}1}} - {i_{{{q}}2}}} \right)} \right] + {k_{{\rm{{\rm{IQ}}}}1}}\displaystyle \int_0^t {\left[ {i_{{{q}}1}^* + {K_2}\left( {{i_{{{q}}1}} - {i_{{{q}}2}}} \right)} \right] {\rm{d}}\tau + {v_2}} \\ {u_{{{d}}2}} = {k_{{\rm{PD}}2}}\left( {i_{{{d}}2}^* - {i_{{{d}}2}}} \right) + {k_{{\rm{ID}}2}}\displaystyle \int_0^t {\left( {i_{{{d}}2}^* - {i_{{{d}}2}}} \right){\rm{d}}\tau } \end{array} \right. $ | (11) |
式中:
定义新变量如式(12)和(13)所示。
| $ \left\{ \begin{array}{l} {m_1} = \displaystyle \int_0^t {[ {i_{{{q1}}}^* - {K_1}\left( {{i_{{{q1}}}} - {i_{{{q2}}}}} \right)} ]{\rm{d}}\tau } \\ {m_2} = \displaystyle \int_0^t {[ {i_{{{q1}}}^* + {K_2}\left( {{i_{{{q1}}}} - {i_{{{q2}}}}} \right)} ]{\rm{d}}\tau } \\ {{\dot m}_1} = i_{{{q1}}}^* - {K_1}\left( {{i_{{{q1}}}} - {i_{{{q2}}}}} \right)\\ {{\dot m}_2} = i_{{{q1}}}^* + {K_2}\left( {{i_{{{q1}}}} - {i_{{{q2}}}}} \right) \end{array} \right. $ | (12) |
| $ \left\{ \begin{array}{l} {w_1} = \displaystyle \int_0^t {\left( {{\omega ^*} - {\omega _1}} \right){\rm{d}}\tau } \\ {w_2} = \displaystyle \int_0^t {\left( {{\omega ^*} - {\omega _2}} \right){\rm{d}}\tau } \\ {{\dot w}_1} = {\omega ^*} - {\omega _1}\\ {{\dot w}_2} = {\omega ^*} - {\omega _2} \end{array} \right. $ | (13) |
将式(10)~(13)代入式(9)中,整理化简具有不确定性的双永磁同步电机系统的数学模型,写成状态空间形式如式(14)所示。
| $ \dot {\boldsymbol{x}} = \left( {{\boldsymbol{A}} + \Delta {\boldsymbol{A}}} \right)x + {\boldsymbol{Bu}} + {{\boldsymbol{B}}_1}{{{d}}_1} + {{\boldsymbol{B}}_2}{{\boldsymbol{d}}_2} $ | (14) |
其中,
| ${\boldsymbol{ A}} + \Delta {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}&{\dfrac{{{k_{{\rm{PQ}}1}}{K_1}}}{{{L_{{{{\rm{s}}q}}1}}}}}&0&{\dfrac{{{k_{{\rm{IQ}}1}}}}{{{L_{{{{\rm{s}}q}}1}}}}}&0&{\dfrac{{{k_{{\rm{PQ}}1}}{k_{{\rm{IS}}1}}}}{{{L_{{{{\rm{s}}q}}1}}}}}&0\\ {{a_7}}&{ - \dfrac{{{{\boldsymbol{B}}_1}}}{{{J_1}}}}&0&0&0&0&{{a_3}}&{ - {a_3}}\\ {\dfrac{{{k_{{\rm{PQ}}2}}{K_2}}}{{{L_{{{{\rm{s}}q}}2}}}}}&0&{{a_4}}&{{a_5}}&0&{\dfrac{{{k_{{\rm{IQ}}2}}}}{{{L_{{{{\rm{s}}q}}2}}}}}&0&{\dfrac{{{k_{{\rm{PQ}}2}}{k_{{\rm{IS}}2}}}}{{L{}_{{{{\rm{s}}q}}2}}}}\\ 0&0&{{a_8}}&{ - \dfrac{{{{\boldsymbol{B}}_2}}}{{{J_2}}}}&0&0&{ - {a_6}}&{{a_6}}\\ { - {K_1}}&{ - {k_{{\rm{PS}}1}}}&{{K_1}}&0&0&0&{{k_{{\rm{IS}}1}}}&0\\ {{K_2}}&0&{ - {K_2}}&{ - {k_{{\rm{PS}}2}}}&0&0&0&{{k_{{\rm{IS}}2}}}\\ 0&{ - 1}&0&0&0&0&0&0\\ 0&0&0&{ - 1}&0&0&0&0 \end{array}} \right] $ | (15) |
| $ \begin{split} \\ {a_1} = - \frac{{{R_{{\rm{s}}1}} + {k_{{\rm{PQ}}1}}{K_1}}}{{{L_{{{{\rm{s}}q}}1}}}},{a_2} = - \frac{{{\varphi _{{\rm{f}}1}} + {k_{{\rm{PQ}}1}}{k_{{\rm{PS}}1}} + {\delta _1}}}{{{L_{{{{\rm{s}}q1}}}}}},{a_3} = \frac{{{n_{{\rm{p}}1}}{r^2}k}}{{{J_1}}} \end{split}$ |
| $\begin{array}{*{20}{c}} {a_4} = - \dfrac{{{R_{{\rm{s}}2}} + {k_{{\rm{PQ}}2}}{K_2}}}{{{L_{{{{\rm{s}}q}}2}}}},{a_5} = - \dfrac{{{\varphi _{{\rm{f}}2}} + {k_{{\rm{PQ}}2}}{k_{{\rm{PS}}2}} + {\delta _2}}}{{{L_{{{{\rm{s}}q}}2}}}}\\{a_6} = \dfrac{{{n_{{\rm{p}}2}}{r^2}k}}{{{J_2}}},{a_7} = \dfrac{{n_{{\rm{p}}1}^2{\varphi _{{\rm{f}}1}}}}{{{J_1}}} \end{array}$ |
| $ {a_8} = \frac{{n_{{\rm{p}}2}^2{\varphi _{{\rm{f}}2}}}}{{{J_2}}},{\boldsymbol{B}} = \mathop {\left[ {\begin{array}{*{20}{c}} {1/{L_{{{{\rm{s}}q}}1}}}&0&0& 0& 0& 0& 0& 0\\ 0&0&{1/{L_{{{{\rm{s}}q}}2}}}& 0& 0& 0& 0& 0 \end{array}} \right]}\nolimits^{\rm{T}} $ |
| $ {\boldsymbol{g}} = \mathop {\left[ {\begin{array}{*{20}{c}} {\dfrac{{{k_{{\rm{PQ}}1}}{k_{{\rm{PS}}1}}}}{{{L_{{{{\rm{s}}q}}1}}}}{\omega ^*}}& { - \dfrac{{{n_{{\rm{p}}1}}}}{{{J_1}}}{T_{{\rm{l}}1}}}& 0& { - \dfrac{{{n_{{\rm{p}}2}}}}{{{J_2}}}{T_{{\rm{l}}2}}}& {{k_{{\rm{PS}}1}}{\omega ^*}}& 0& {{\omega ^*}}& 0 \end{array}} \right]}\nolimits^{\rm{T}} $ |
| $ {{\boldsymbol{B}}_1} = \mathop {\left[ {\begin{array}{*{20}{c}} {\dfrac{{{k_{{\rm{PQ}}1}}{k_{{\rm{PS}}1}}}}{{{L_{{{{\rm{s}}q}}1}}}}}&0&0&0&{{k_{{\rm{PS}}1}}}&0&1&0 \end{array}} \right]}\nolimits^{\rm{T}} ,{{{d}}_1} = {\omega ^ * } $ |
| $ {{\boldsymbol{B}}_2} = \mathop {\left[ {\begin{array}{*{20}{c}} 0& { - \dfrac{{{n_{{\rm{p}}1}}}}{{{J_1}}}}& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& { - \dfrac{{{n_{{\rm{p}}2}}}}{{{J_2}}}}& 0& 0& 0& 0 \end{array}} \right]}\nolimits^{\rm{T}} ,{{{{\boldsymbol{d}}}}_2} = {\left[ {\begin{array}{*{20}{c}} {{T_{{\rm{l}}1}}}& {{T_{{\rm{l}}2}}} \end{array}} \right]^{\rm{T}}} $ |
| $ {\boldsymbol{x}} = \mathop {\left[ {\begin{array}{*{20}{c}} {{i_{q1}}}& {{\omega _1}}& {{i_{q2}}}& {{\omega _2}}& {{m_1}}& {{m_2}}& {{w_1}}& {{w_2}} \end{array}} \right]}\nolimits^{\rm{T}} ,{\boldsymbol{u}} = \mathop {\left[ {\begin{array}{*{20}{c}} {{v_1}}& {{v_2}} \end{array}} \right]}\nolimits^{\rm{T}} $ |
假设1 系统(14)的不确定性
| $ \Delta {{\boldsymbol{A}}_{2 * 2}} = {\boldsymbol{M}}\Delta {\boldsymbol{\delta}} {\boldsymbol{N}} $ | (16) |
式中:
| $ {{\boldsymbol{M}}_{8 * 2}} = {\left[ {\begin{array}{*{20}{c}} {{\raise0.7ex\hbox{$1$} \mathord{\left/ {\vphantom {1 {{L_{{{q}}1}}}}}\right.} \lower0.7ex\hbox{${{L_{{{q}}1}}}$}}}&0&0&0&0&0&0&0 \\ 0&0&{{\raise0.7ex\hbox{$1$} \mathord{\left/ {\vphantom {1 {{L_{{{q}}2}}}}}\right.} \lower0.7ex\hbox{${{L_{{{q}}2}}}$}}}&0&0&0&0&0 \end{array}} \right]^{\rm{T}}} $ |
| $\begin{split} \\ \Delta {\boldsymbol{\delta}} = \left[ {\begin{array}{*{20}{c}} {{\delta _1}}&0 \\ 0&{{\delta _2}} \end{array}} \right],{{\boldsymbol{N}}_{2 * 8}} = \left[ {\begin{array}{*{20}{c}} 0&1&0&0&0&0&0&0 \\ 0&0&0&1&0&0&0&0 \end{array}} \right] \end{split} $ |
在传统的交叉耦合控制中,速度同步和转矩同步并没有达到最优效果,因此本文提出如图4所示的交叉耦合控制和滑模控制结合的双电机协调控制结构。
2.2 双永磁同步电机系统滑模协调控制器设计滑模变结构对外界扰动、负载频繁变化的系统具有较好的鲁棒性,能够克服系统的不确定性,当其中一台电机受到干扰时通过滑模控制可以使系统迅速作出响应,选择合适的滑模面和控制律,合理设计控制器增益可使系统满足到达条件和稳定性,并且沿着滑模面滑动。但是系统状态轨迹运动到滑模面后滑向平衡点是不可严格控制的。由于符号函数的存在系统一般沿滑模面做切换运动,这便会造成抖振,在实际应用中需选取合适的控制律削弱抖振[30-34]。本文将非匹配干扰估计值考虑在内设计积分滑模控制器,控制器采用欧几里德范数替换传统的符号函数有效抑制了抖振,利用
结合式(14)将带有干扰的双永磁同步电机系统写为
| $ \left\{ \begin{gathered} \dot {\boldsymbol{x}}\left( t \right) = \left( {{\boldsymbol{A}} + \Delta {\boldsymbol{A}}} \right){\boldsymbol{x}}\left( t \right) + {\boldsymbol{Bu}}\left( t \right) + {{\boldsymbol{B}}_1}{d_1}\left( t \right) + {{\boldsymbol{B}}_2}{{\boldsymbol{d}}_2}\left( t \right) \hfill \\ {\boldsymbol{y}} = {\boldsymbol{Cx}}\left( t \right) \hfill \\ \end{gathered} \right. $ | (17) |
式中:
| $ {\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {{c_1}}& 0& { - {c_1}}& 0& 0& 0& 0& 0 \\ 0& {{c_2}}& 0& { - {c_2}}& 0& 0& 0& 0 \end{array}} \right],{c_1} \in {{\bf{R}}^ + },{c_2} \in {{\bf{R}}^ + } $ |
受到文献[40]启示,干扰观测器设计为
| $ \left\{ \begin{array}{l} \dot {\boldsymbol{v}}\left( t \right) ={\boldsymbol{ \varLambda}} {{\hat {\boldsymbol{d}}}_2}\left( t \right) + {\boldsymbol{\varLambda }}{\boldsymbol{B}}_2^ + \left( {\left( {{\boldsymbol{A}} + \Delta{\boldsymbol{ A}}} \right){\boldsymbol{x}}\left( t \right) + {\boldsymbol{Bu}}\left( t \right) + {{\boldsymbol{B}}_1}{d_1}\left( t \right)} \right) \\ {{\hat {\boldsymbol{d}}}_2}\left( t \right) = {\boldsymbol{v}}\left( t \right) - {\boldsymbol{\varLambda}} {\boldsymbol{B}}_2^ + {\boldsymbol{x}}\left( t \right) \\ \end{array} \right.$ | (18) |
式中:
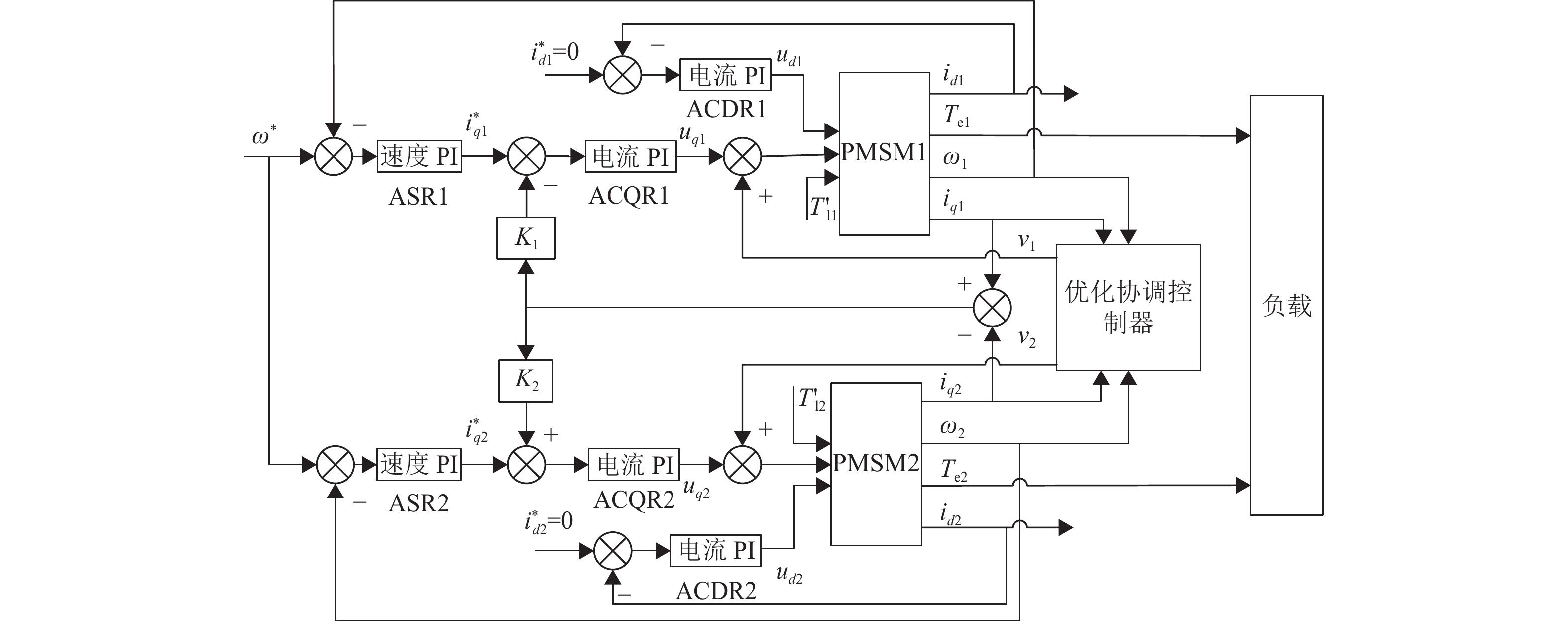
|
图 4 双永磁同步电机系统滑模协调控制结构 Figure 4 Sliding mode coordination control structure of dual permanent magnet synchronous motor system |
引理1[40] 假设
那么,可以得到以下结果。
引理2 对于给定的干扰观测器式(18),干扰估计误差
证明 由式(18)得
| $ {\dot {\tilde {\boldsymbol{d}}}_2}\left( t \right) = {\dot {\boldsymbol{d}}_2}\left( t \right) + {\boldsymbol{\varLambda}} {\tilde {\boldsymbol{d}}_2}\left( t \right) $ | (19) |
进一步
| $ \begin{split} \| {{{\tilde {\boldsymbol{d}}}_2}\left( t \right)} \| \leqslant &\| {{{\rm{e}}^{{\boldsymbol{\varLambda}} t}}{{\boldsymbol{d}}_2}\left( 0 \right)} \| + \left\| {\int_0^t {{{\rm{e}}^{{\boldsymbol{\varLambda}} \left( {t - s} \right)}}} {{\dot {\boldsymbol{d}}}_2}\left( s \right){\rm{d}}s} \right\| \leqslant \\& \| {{{\rm{e}}^{{\boldsymbol{\varLambda}} t}}} \|\left\| {{{\boldsymbol{d}}_2}\left( 0 \right)} \right\| + \int_0^t {\| {{{\rm{e}}^{{\boldsymbol{\varLambda}} \left( {t - s} \right)}}} \|} \| {{{\dot {\boldsymbol{d}}}_2}\left( s \right)} \|{\rm{d}}s \leqslant\\& c\alpha {{\rm{e}}^{\tfrac{{{\lambda _{\max }}\left( {\boldsymbol{\varLambda}} \right)}}{2}t}} + c\beta \int_0^t {{\rm{e}}\frac{{{\lambda _{\max }}\left( {\boldsymbol{\varLambda}} \right)}}{2}} \left( {t - s} \right){\rm{d}}s = \\& c\alpha {{\rm{e}}^{\tfrac{{{\lambda _{\max }}\left( {\boldsymbol{\varLambda}} \right)}}{2}t}} + c\beta \frac{2}{{{\lambda _{\max }}\left( {\boldsymbol{\varLambda}} \right)}}\left( {{{\rm{e}}^{\tfrac{{{\lambda _{\max }}\left( {\boldsymbol{\varLambda}} \right)}}{2}t}} - 1} \right) \leqslant\\& c\alpha - c\beta \frac{2}{{{\lambda _{\max }}\left( {\boldsymbol{\varLambda}} \right)}} \end{split} $ | (20) |
通过定义
注释1 由引理2得到在干扰观测器式(1)中参数矩阵
设计如下基于干扰观测器的积分滑模面:
| $ \begin{gathered} {\boldsymbol{ \sigma}} ( t ) = {{\boldsymbol{B}}^ + }( {\begin{array}{*{20}{c}} \end{array}{\boldsymbol{x}}(t) - {\boldsymbol{x}}(0) - } \\ {\int_0^t {( {( {{\boldsymbol{A}} + \Delta {\boldsymbol{A}}} ){\boldsymbol{x}}(s) + {\boldsymbol{B}}{{\boldsymbol{u}}_1}(s) + {{\boldsymbol{B}}_1}{{{d}}_1}( s ) + {{\boldsymbol{B}}_2}{{\hat {\boldsymbol{d}}}_2}(s)} )} {\rm{d}}s\begin{array}{*{20}{c}} \end{array}} ) \\ \end{gathered} $ | (21) |
式中:
注释2 与传统的积分滑模面不同,用干扰观测器式(18)中的干扰估计
若
| $ {\boldsymbol{u}}(t) = {{\boldsymbol{u}}_1}(t) + {{\boldsymbol{B}}^ + }{{\boldsymbol{B}}_2}{{\boldsymbol{u}}_N}(t) $ | (22) |
式中:
接下来,讨论滑模面
定理1 在积分滑模控制器式(22)的作用下,系统满足滑模运动的可达性条件,即闭环系统的状态轨迹将在有限时间内到达滑模面
证明 定义如下的李雅普诺夫函数为
| $ \begin{split} \dot {\boldsymbol{\sigma }}(t) &= {{\boldsymbol{B}}^ + }( {( {{\boldsymbol{A}} + \Delta {\boldsymbol{A}}} ){\boldsymbol{x}}( t ) + {\boldsymbol{Bu}}( t ) + {{\boldsymbol{B}}_1}{{{d}}_1}( t ) + {{\boldsymbol{B}}{\boldsymbol{}}_2}{{\boldsymbol{d}}_2}( t )} -\\ & { ( {( {{\boldsymbol{A}} + \Delta {\boldsymbol{A}}} ){\boldsymbol{x}}( t ) + {\boldsymbol{B}}{{\boldsymbol{u}}_1}( t ) + {{\boldsymbol{B}}_1}{{{d}}_1}( t ) + {{\boldsymbol{B}}_2}{{\hat {\boldsymbol{d}}}_2}( t )} )} )=\\ & {\boldsymbol{u}}( t ) - {{\boldsymbol{u}}_1}( t ) + {{\boldsymbol{B}}^ + }{{\boldsymbol{B}}_2}{{\tilde {\boldsymbol{d}}}_2}( t ) =\\ & {{\boldsymbol{B}}^ + }{{\boldsymbol{B}}_2}( {{{\boldsymbol{u}}_{\rm{N}}}( t ) + {{\tilde {\boldsymbol{d}}}_2}( t )} ) \end{split}$ | (23) |
于是
| $ \begin{split} \dot {\boldsymbol{V}}\left( t \right) =& {{\boldsymbol{\sigma}} ^{\rm T}}\left( t \right)\left( { - ({{\rho}} + \varpi )\frac{{{{\boldsymbol{B}}^ + }{{\boldsymbol{B}}_2}{\boldsymbol{B}}_2^{\rm T}{{\boldsymbol{B}}^{ + {\rm T}}}{\boldsymbol{\sigma}} (t)}}{{\left\| {{\boldsymbol{B}}_{\rm{d}}^{\rm T}{{\boldsymbol{B}}^{ + {\rm T}}}{\boldsymbol{\sigma}} (t)} \right\|}} + {{\boldsymbol{B}}^ + }{{\boldsymbol{B}}_2}{{\tilde {\boldsymbol{d}}}_2}\left( t \right)} \right) =\\& - \left( {{{\rho}} + \varpi } \right)\| {{\boldsymbol{B}}_2^{\rm T}{{\boldsymbol{B}}^{ + {\rm T}}}{\boldsymbol{\sigma}} (t)} \| + {{\boldsymbol{\sigma}} ^{\rm T}}\left( t \right){{\boldsymbol{B}}^ + }{{\boldsymbol{B}}_2}{{\tilde {\boldsymbol{d}}}_2}\left( t \right) \leqslant\\& - {{\rho}} \| {{\boldsymbol{B}}_2^{\rm T}{{\boldsymbol{B}}^{ + {\rm T}}}{\boldsymbol{\sigma}} (t)} \| \\[-15pt] \end{split} $ | (24) |
由
综上所述,基于干扰观测器的的积分滑模控制框图如图5所示。
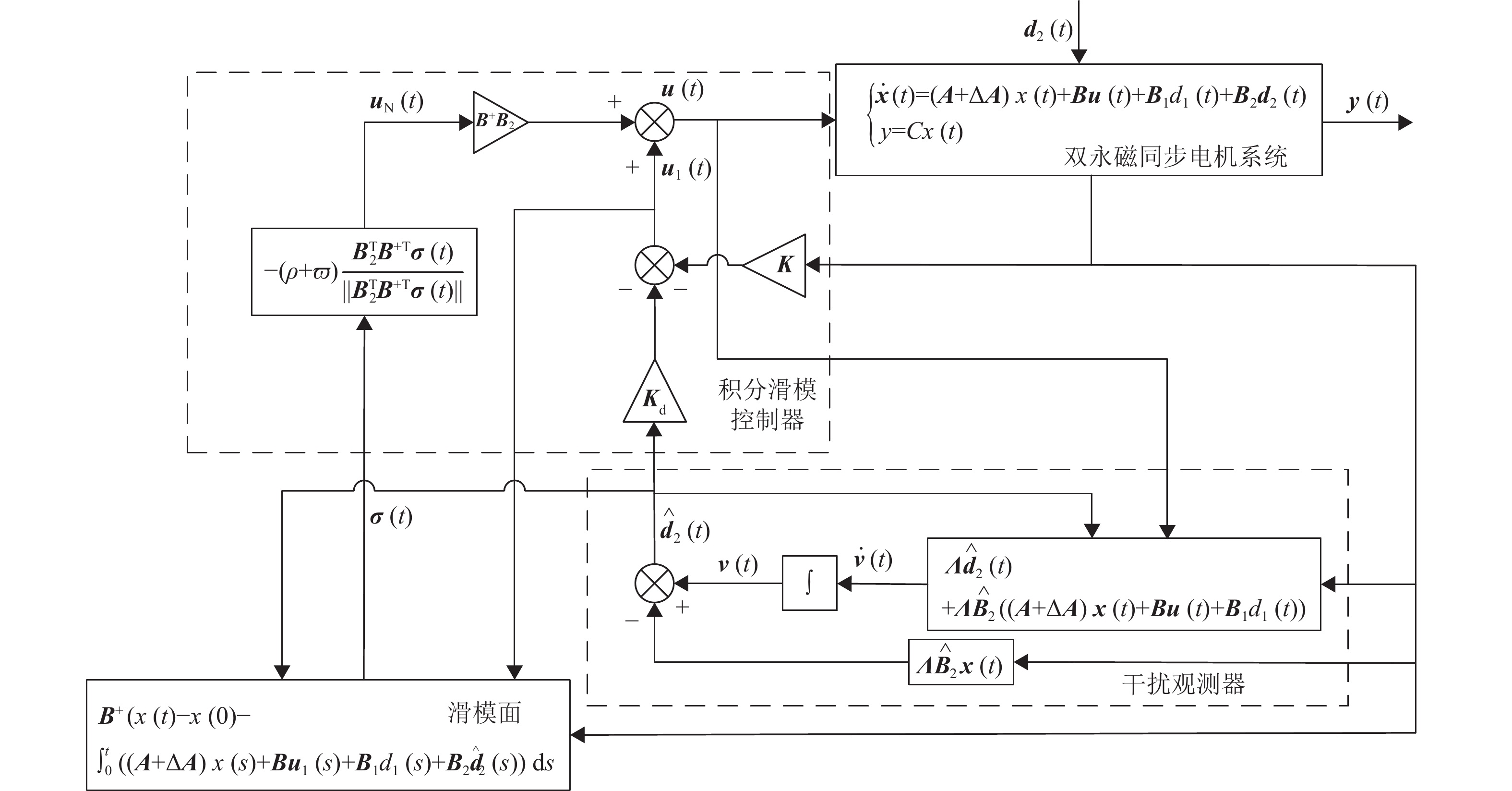
|
图 5 基于干扰观测器的积分滑模控制框架 Figure 5 Integral sliding mode control framework based on disturbance observer |
接下来,用等效控制方法确定滑模运动方程,并进行滑动运动的稳定性分析。
求解方程
| $ \begin{split} \dot {\boldsymbol{x}}\left( t \right) =& \left( {{\boldsymbol{A}} + \Delta {\boldsymbol{A}}} \right){\boldsymbol{x}}\left( t \right) + {\boldsymbol{B}}{{\boldsymbol{u}}^{{\rm{eq}}}}\left( t \right) + {{\boldsymbol{B}}_2}{{\boldsymbol{d}}_2}\left( t \right) =\\& \left( {{\boldsymbol{A}} + \Delta {\boldsymbol{A}}} \right){\boldsymbol{x}}\left( t \right) \begin{array}{*{20}{c}} \end{array} + {\boldsymbol{B}}\left( {{{\boldsymbol{u}}_1}\left( t \right) + {{\boldsymbol{B}}^ + }{{\boldsymbol{B}}_2}{\boldsymbol{u}}_{\rm{N}}^{{\rm{eq}}}\left( t \right)} \right) + {{\boldsymbol{B}}_2}{{\boldsymbol{d}}_2}\left( t \right) = \\& \left( {{\boldsymbol{A}} + \Delta {\boldsymbol{A}} - {\boldsymbol{BK}}} \right)x\left( t \right) - {\boldsymbol{B}}{{\boldsymbol{K}}_{\rm{d}}}{{\hat {\boldsymbol{d}}}_2}\left( t \right) - \\& \begin{array}{*{20}{c}} \end{array}{\boldsymbol{B}}{{\boldsymbol{B}}^ + }{{\boldsymbol{B}}_2}{{\tilde {\boldsymbol{d}}}_2}\left( t \right) + {{\boldsymbol{B}}_2}{{\boldsymbol{d}}_2}\left( t \right) \\[-10pt] \end{split} $ | (25) |
接着,使用
| $ \begin{split} \dot{\boldsymbol{ x}}( t ) & = ( {{\boldsymbol{A}} + \Delta {\boldsymbol{A}} - {\boldsymbol{BK}}} ){\boldsymbol{x}}( t ) \begin{array}{*{20}{c}} \end{array} - {\boldsymbol{B}}{{\boldsymbol{B}}^ + }{{\boldsymbol{B}}_2}( {{{\hat {\boldsymbol{d}}}_2}( t ) + {{\tilde {\boldsymbol{d}}}_2}( t )} ) + {{\boldsymbol{B}}_2}{{\boldsymbol{d}}_2}( t ) =\\& ( {{\boldsymbol{A}} + \Delta {\boldsymbol{A}} - {\boldsymbol{BK}}} )x( t ) \begin{array}{*{20}{c}} \end{array} - ( {{{\boldsymbol{I}}_{\rm{n}}} - {{\boldsymbol{B}}^ \bot }{{\boldsymbol{B}}^{ \bot + }}} ){{\boldsymbol{B}}_2}{{\boldsymbol{d}}_2}( t ) + {{\boldsymbol{B}}_2}{{\boldsymbol{d}}_2}( t ) =\\& ( {{\boldsymbol{A}} + \Delta {\boldsymbol{A}} - {\boldsymbol{BK}}} ){\boldsymbol{x}}( t ) + {{\boldsymbol{B}}^ \bot }{{\boldsymbol{B}}^{ \bot + }}{{\boldsymbol{B}}_2}{{\boldsymbol{d}}_2}( t ) \\[-10pt] \end{split} $ | (26) |
定义
| $ \dot {\boldsymbol{x}}\left( t \right) = \left( {{\boldsymbol{A}} + \Delta {\boldsymbol{A}} - {\boldsymbol{BK}}} \right){\boldsymbol{x}}\left( t \right) + {\tilde {\boldsymbol{B}}_2}{{\boldsymbol{d}}_2}\left( t \right) $ | (27) |
根据
| $ {\int_0^\infty {\left\| {{\boldsymbol{y}}\left( t \right)} \right\|} ^2}{\rm{d}}t \leqslant {\gamma ^2}{\int_0^\infty {\left\| {{{\boldsymbol{d}}_2}\left( t \right)} \right\|} ^2}{\rm{d}}t $ | (28) |
定理1 给定
| $ \left[ {\begin{array}{*{20}{c}} \begin{gathered} {{\boldsymbol{P}}^{\rm T}}{{\boldsymbol{A}}^{\rm T}} - {{\boldsymbol{F}}^{\rm T}}{\boldsymbol{B}} + {\boldsymbol{A}}{\boldsymbol{P}} \\ - {\boldsymbol{B}}{\boldsymbol{F}} + \mu {{\boldsymbol{P}}^{\rm T}} + {\boldsymbol{M}}{{\boldsymbol{M}}^{\rm T}} \\ \end{gathered} &{{{\tilde {\boldsymbol{B}}}_2}}&{{{\boldsymbol{P}}^{\rm T}}{{\boldsymbol{C}}^{\rm T}}}&{{{\boldsymbol{P}}^{\rm T}}{{\boldsymbol{N}}^{\rm T}}} \\ *&{ - {\gamma ^2}{\boldsymbol{I}}}&0&0 \\ * &*&{ - {\boldsymbol{I}}}&0 \\ * &*&*&{ - {\boldsymbol{I}}} \end{array}} \right] \lt 0 $ | (29) |
那么,控制器增益为
证明 选择李雅普诺夫函数为
| $ {{\boldsymbol{V}}_x}\left( t \right) = {{\boldsymbol{x}}^{\rm T}}\left( t \right){{\boldsymbol{P}}^{ - 1}}{\boldsymbol{x}}\left( t \right) $ | (30) |
引理3 对于任意具有适当维数的常数矩阵
| $ {\boldsymbol{Q}}_1^{\rm T}{{\boldsymbol{Q}}_2} + {\boldsymbol{Q}}_2^{\rm T}{{\boldsymbol{Q}}_1} \leqslant {\boldsymbol{Q}}_1^{\rm T}{{\boldsymbol{Q}}_1} + {\boldsymbol{Q}}_2^{\rm T}{{\boldsymbol{Q}}_2} $ | (31) |
根据引理3可以得到:
| $ \begin{gathered} \Delta {{\boldsymbol{A}}^{\rm T}}{{\boldsymbol{P}}^{ - 1}} + {{\boldsymbol{P}}^{ - {\rm T}}}\Delta {\boldsymbol{A}} = {{\boldsymbol{N}}^{\rm T}}\Delta {{\boldsymbol{\delta}} ^{^{\rm T}}}{{\boldsymbol{M}}^{\rm T}}{{\boldsymbol{P}}^{ - 1}} + {{\boldsymbol{P}}^{ - {\rm T}}}{\boldsymbol{M}}\Delta {\boldsymbol{\delta}} {\boldsymbol{N}} \leqslant\\ {{\boldsymbol{N}}^{\rm T}}\Delta {{\boldsymbol{\delta}} ^{^{\rm T}}}\Delta {\boldsymbol{\delta}} {\boldsymbol{N}} + {{\boldsymbol{P}}^{ - {\rm T}}}{\boldsymbol{M}}{{\boldsymbol{M}}^{\rm T}}{{\boldsymbol{P}}^{ - 1}} \leqslant {{\boldsymbol{N}}^{\rm T}}{\boldsymbol{N}} + {{\boldsymbol{P}}^{ - {\rm T}}}{\boldsymbol{M}}{{\boldsymbol{M}}^{\rm T}}{{\boldsymbol{P}}^{ - 1}} \\ \end{gathered} $ | (32) |
于是,可以得到以下不等式成立:
| $ \begin{split} {{\boldsymbol{V}}_x}\left( t \right) &+ {{\boldsymbol{y}}^{\rm T}}\left( t \right){\boldsymbol{y}}\left( t \right) - {\gamma ^2}{\boldsymbol{d}}_2^{\rm T}\left( t \right){{\boldsymbol{d}}_2}\left( t \right) + \mu {{\boldsymbol{V}}_x}\left( t \right) =\hfill \\& {{\dot {\boldsymbol{x}}}^{\rm T}}\left( t \right){{\boldsymbol{P}}^{ - 1}}{\boldsymbol{x}}\left( t \right) + {{\boldsymbol{x}}^{\rm T}}\left( t \right){{\boldsymbol{P}}^{ - 1}}\dot {\boldsymbol{x}}\left( t \right) + {{\boldsymbol{y}}^{\rm T}}\left( t \right){\boldsymbol{y}}\left( t \right) \hfill -\\& \begin{array}{*{20}{c}} \end{array} {\gamma ^2}{\boldsymbol{d}}_2^{\rm T}\left( t \right){{\boldsymbol{d}}_2}\left( t \right) + \mu {x^{\rm T}}\left( t \right){{\boldsymbol{P}}^{ - 1}}{\boldsymbol{x}}\left( t \right) = \hfill \\& {\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{x}}\left( t \right)} \\ {{{\boldsymbol{d}}_2}\left( t \right)} \end{array}} \right]^{\rm T}}{\boldsymbol{\varXi}} \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{x}}\left( t \right)} \\ {{{\boldsymbol{d}}_2}\left( t \right)} \end{array}} \right] \leqslant \hfill \\& {\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{x}}\left( t \right)} \\ {{{\boldsymbol{d}}_2}\left( t \right)} \end{array}} \right]^{\rm T}}{\boldsymbol{\varOmega}} \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{x}}\left( t \right)} \\ {{{\boldsymbol{d}}_2}\left( t \right)} \end{array}} \right] \end{split} $ | (33) |
式中:
| $ {\boldsymbol{\varXi}} = \left[ {\begin{array}{*{20}{c}} \begin{gathered} {\left( {{\boldsymbol{A}} + \Delta {\boldsymbol{A}} - {\boldsymbol{BK}}} \right)^{\rm T}}{{\boldsymbol{P}}^{ - 1}} \\ + {{\boldsymbol{P}}^{ - {\rm T}}}\left( {{\boldsymbol{A}} + \Delta {\boldsymbol{A}} - {\boldsymbol{BK}}} \right) + \mu {{\boldsymbol{P}}^{ - 1}} + {{\boldsymbol{C}}^{\rm T}}{\boldsymbol{C}} \\ \end{gathered} &{{{\boldsymbol{P}}^{ - {\rm T}}}{{\tilde {\boldsymbol{B}}}_2}} \\ {{{\tilde {\boldsymbol{B}}}^{\rm T}}_2{{\boldsymbol{P}}^{ - 1}}}&{ - {\gamma ^2}{\boldsymbol{I}}} \end{array}} \right] $ |
| $ {\boldsymbol{\varOmega}} = \left[ {\begin{array}{*{20}{c}} \begin{gathered} {\left( {{\boldsymbol{A}} - {\boldsymbol{B}}K} \right)^{\rm T}}{{\boldsymbol{P}}^{ - 1}} + {{\boldsymbol{P}}^{ - {\rm T}}}\left( {{\boldsymbol{A}} - {\boldsymbol{B}}K} \right) + \rho {{\boldsymbol{P}}^{ - 1}} \\ + {{\boldsymbol{C}}^{\rm T}}{\boldsymbol{C}} + {{\boldsymbol{N}}^{\rm T}}{\boldsymbol{N}} + {{\boldsymbol{P}}^{ - {\rm T}}}{\boldsymbol{M}}{{\boldsymbol{M}}^{\rm T}}{{\boldsymbol{P}}^{ - 1}} \\ \end{gathered} &{{{\boldsymbol{P}}^{ - {\rm T}}}{{\tilde {\boldsymbol{B}}}_2}} \\ {{{\tilde {\boldsymbol{B}}}^{\rm T}}_2{{\boldsymbol{P}}^{ - 1}}}&{ - {\gamma ^2}{\boldsymbol{I}}} \end{array}} \right] $ |
对
| ${\boldsymbol{ \varSigma}} = \left[ {\begin{array}{*{20}{c}} \begin{gathered} {{\boldsymbol{P}}^{\rm T}}{{\boldsymbol{A}}^{\rm T}} + {{\boldsymbol{P}}^{\rm T}}{K^{\rm T}}{{\boldsymbol{B}}^{\rm T}} + {\boldsymbol{A}}{\boldsymbol{P}} + {\boldsymbol{B}}K{\boldsymbol{P}} + \mu {{\boldsymbol{P}}^{\rm T}} +\\ {{\boldsymbol{P}}^{\rm T}}{{\boldsymbol{C}}^{\rm T}}{\boldsymbol{C}}{\boldsymbol{P}} + {{\boldsymbol{P}}^{\rm T}}{{\boldsymbol{N}}^{\rm T}}{\boldsymbol{N}}{\boldsymbol{P}} + {\boldsymbol{M}}{{\boldsymbol{M}}^{\rm T}} \\ \end{gathered} &{{{\tilde {\boldsymbol{B}}}_2}} \\ {{{\tilde {\boldsymbol{B}}}^{\rm T}}_2}&{ - {\gamma ^2}{\boldsymbol{I}}} \end{array}} \right] $ | (34) |
运用Schur补引理[41],
| $ {\boldsymbol{\varTheta}} = \left[ {\begin{array}{*{20}{c}} \begin{gathered} {{\boldsymbol{P}}^{\rm T}}{{\boldsymbol{A}}^{\rm T}} + {{\boldsymbol{P}}^{\rm T}}{K^{\rm T}}{{\boldsymbol{B}}^{\rm T}} + {\boldsymbol{A}}{\boldsymbol{P}} +\hfill \\ {\boldsymbol{B}}K{\boldsymbol{P}} + \mu {{\boldsymbol{P}}^{\rm T}} + {\boldsymbol{M}}{{\boldsymbol{M}}^{\rm T}} \hfill \\ \end{gathered} & {\tilde {\boldsymbol{B}}_2^{\rm T}}& {{{\boldsymbol{P}}^{\rm T}}{{\boldsymbol{C}}^{\rm T}}}& {{{\boldsymbol{P}}^{\rm T}}{{\boldsymbol{N}}^{\rm T}}} \\ *& { - {\gamma ^2}{\boldsymbol{I}}}& 0& 0 \\ *& *& { - {\boldsymbol{I}}}& 0 \\ *& *& *& { - {\boldsymbol{I}}} \end{array}} \right] \lt 0 $ | (35) |
可以看出,将
| $ {{\boldsymbol{V}}_x}\left( t \right) + {{\boldsymbol{y}}^{\rm T}}\left( t \right){\boldsymbol{y}}\left( t \right) - {\gamma ^2}{\boldsymbol{d}}_2^{\rm T}\left( t \right){{\boldsymbol{d}}_2}\left( t \right) + \mu {{\boldsymbol{V}}_x}\left( t \right) \lt 0 $ | (36) |
当
| $ {\dot {\boldsymbol{V}}_x}\left( t \right) + \mu {\boldsymbol{V}}\left( t \right) \lt 0 $ | (37) |
分别定义
| $ 0 \lt {\lambda _{\min }}( {{{\boldsymbol{P}}^{ - 1}}} ){\left\| {{\boldsymbol{x}}\left( t \right)} \right\|^2} \leqslant {\boldsymbol{V}}\left( t \right) \leqslant {\lambda _{\max }}( {{{\boldsymbol{P}}^{ - 1}}} ){\left\| {{\boldsymbol{x}}\left( t \right)} \right\|^2} $ | (38) |
根据不等式(36)和(37),有
| $ \left\| {{\boldsymbol{x}}\left( t \right)} \right\| \lt \sqrt {\frac{{{\lambda _{\max }}\left( {{{\boldsymbol{P}}^{ - 1}}} \right)}}{{{\lambda _{\min }}\left( {{{\boldsymbol{P}}^{ - 1}}} \right)}}} {{{{\rm{e}}}}^{ - \tfrac{\mu }{2}t}}\left\| {{\boldsymbol{x}}\left( 0 \right)} \right\| $ | (39) |
这表明系统式(27)是指数稳定的。从不等式(36)可知
| $ {{\boldsymbol{V}}_x}\left( t \right) + {{\boldsymbol{y}}^{\rm T}}\left( t \right){\boldsymbol{y}}\left( t \right) - {\gamma ^2}{\boldsymbol{d}}_2^{\rm T}\left( t \right){{\boldsymbol{d}}_2}\left( t \right) \lt 0 $ | (40) |
对于
| $ \int_0^\infty {{{\boldsymbol{y}}^{\rm T}}\left( t \right){\boldsymbol{y}}\left( t \right)} {\rm{d}}t \leqslant {\gamma ^2}\int_0^\infty {{\boldsymbol{d}}_2^{\rm T}\left( t \right){{\boldsymbol{d}}_2}\left( t \right)} {\rm{d}}t $ | (41) |
这表明闭环系统满足
本节基于dSPACE的双永磁同步电机半实物仿真实验平台进行实验,通过两电机在交叉耦合控制和滑模协调控制下的角速度和q轴电流的对比情况,分析本文所设计的滑模协调控制器的优越性。
利用基于dSPACE的双永磁同步电机实验平台验证所设计的协调控制器的实际运行效果。表贴式永磁同步电机选取的型号为ACSM60-G00630LZ,具体参数如表1所示,电机尾部带有编码器反馈电机的位置信号;扭矩传感器用以输出电机扭矩;减速箱用以实现电机等比减速;输送带是采用橡胶制成的,中间配有张紧装置;电磁粉末制动器选取的型号为FZ-6-K,并和其中一台电机同轴连接用以模拟添加负载;张力控制器选取型号为TB-200A,其有4种工作模式可供选用,分别为可循环切换恒流(恒电流输出),恒压(恒电压输出)、恒功率输出、外接电位器(外部电压控制)。机械实验装置实物如图6所示。
| 表 1 PMSM参数 Table 1 PMSM parameters |

|
图 6 机械实验装置 Figure 6 Mechanical test device |
实验平台主要由变流器、转接板、变流器、调压器、MicroLabBox控制器、上位机、刚柔耦合多电机实验装置等组成,实物如图7所示。

|
图 7 双永磁同步电机半实物仿真硬件系统 Figure 7 Hardware-in-the-loop simulation system of dual-PMSM |
实验硬件设计完成后进行实验。其中,
| $ {\boldsymbol{K}} = \left[ {\begin{array}{*{20}{c}} {0.14}& {0.29}& { - 0.24}& { - 0.3}& {0.23}& { - 0.4}& {0.36}& {0.233} \\ {0.46}& {0.7}& { - 1.234}& {0.045}& {0.45}& {0.0243}& {0.5034}& {0.33} \end{array}} \right] $ |
| $ {{\boldsymbol{K}}_{\rm{d}}} = \left[ {\begin{array}{*{20}{c}} {3.26}& {0.39}& {3.68}& {4.21}& { - 0.954}& {6.32}& {2.98}& {1.88} \\ { - 6.33}& { - 0.35}& {3.77}& {4.65}& { - 0.23}& { - 3.46}& {7.32}& {2.342} \end{array}} \right] $ |
在10 s时突加8
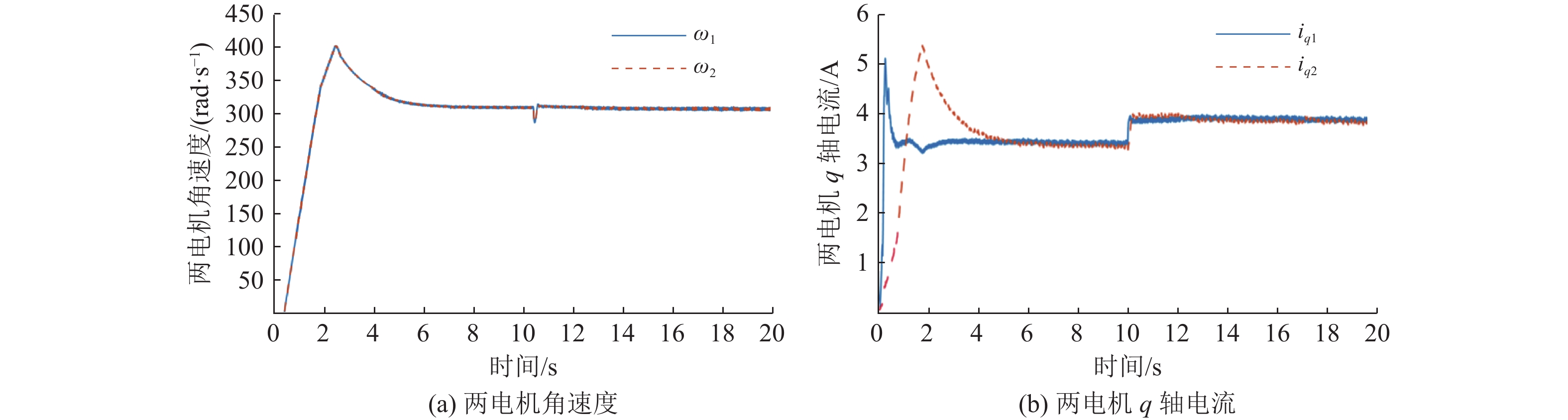
|
图 8 交叉耦合控制下两电机角速度和q轴电流 Figure 8 The angular velocity and q-axis current of the two motors are controlled by cross coupling |
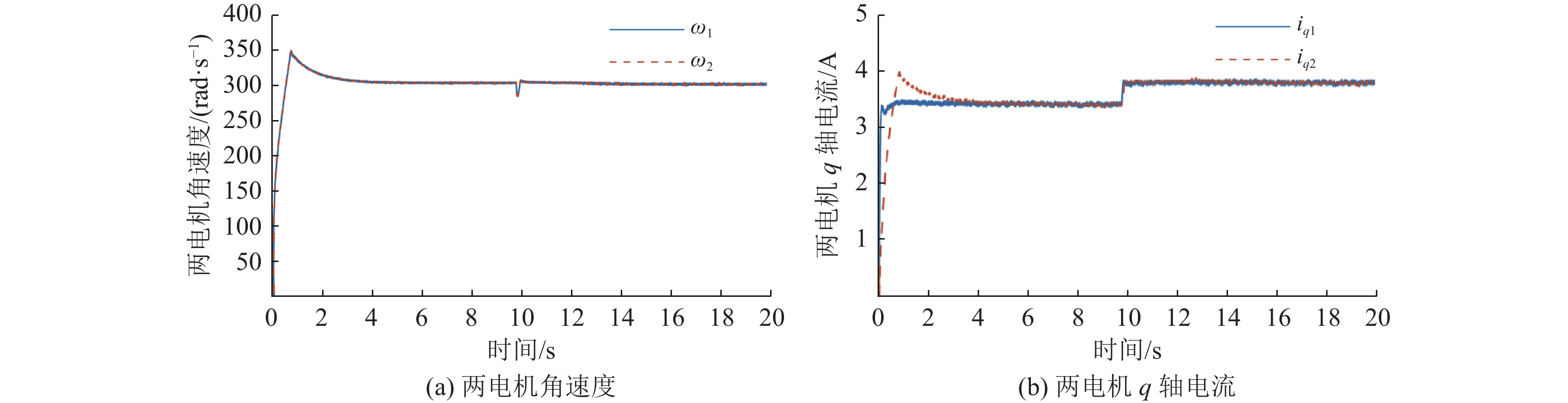
|
图 9 滑模协调控制下两电机角速度和 q 轴电流 Figure 9 The angular velocity and q-axis current of the two motors are controlled by sliding mode coordination |
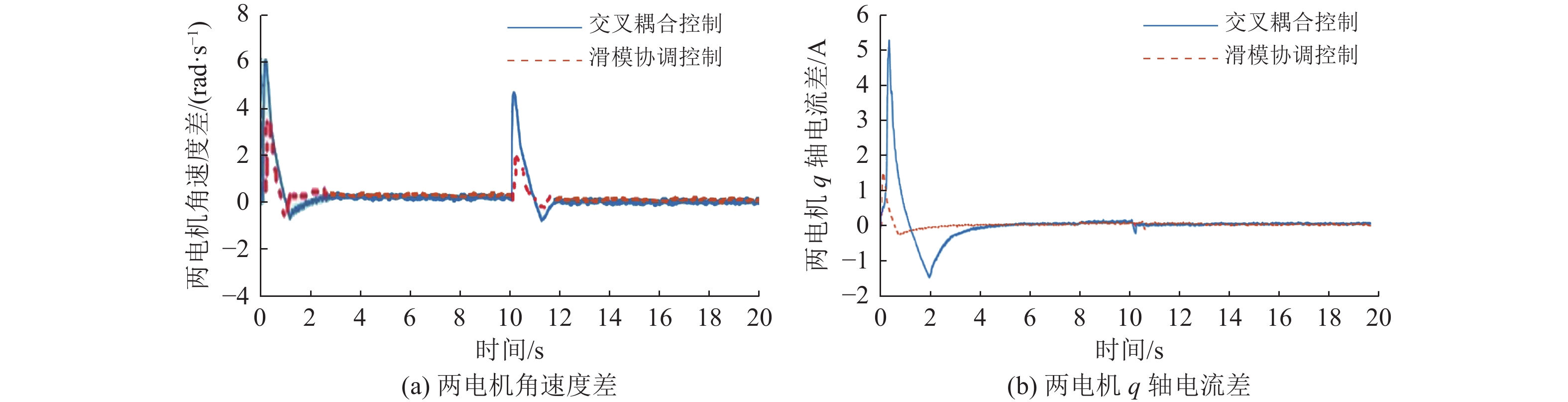
|
图 10 两电机角速度差和 q 轴电流差比较 Figure 10 Comparison of angular velocity difference and q-axis current difference between two motors |
综上所述,本文针对双永磁同步电机所设计的基于干扰观测器的积分滑模控制器相比于传统的交叉耦合控制具有更好的鲁棒性,启动阶段和突加负载阶段波动更小,恢复至平稳状态更快,角速度差和q轴电流差更小。
4 结语本文针对具有不确定性和非匹配扰动的双永磁同步电机系统提出了一种基于干扰观测器的积分滑模控制方法,研究双电机系统的协调控制,通过实验成功地证明了所设计的优化协调控制器在转速平衡和转矩平衡方面具有更好的控制性能。总的来说,所提的同步协调控制方法整体性能比交叉耦合控制优越,不但表现在系统拥有更好的动态特性,而且在启动阶段和负载突变时转速和转矩误差更小,具有很强的抗扰动能力,系统结构简单、易实现、可靠性高。
| [1] |
余章, 高军礼. 一种双三相永磁同步电机无速度传感器控制的实现方法研究[J].
广东工业大学学报, 2019, 36(3): 83-90.
YU Z, GAO J L. A research on an implementation method of speed sensorless control for dual three-phase permanent magnet synchronous motor[J]. Journal of Guangdong University of Technology, 2019, 36(3): 83-90. DOI: 10.12052/gdutxb.180092. |
| [2] |
周林娜, 金南南, 王海, 等. 永磁同步电动机控制半实物仿真系统设计[J].
实验室研究与探索, 2022, 41(2): 89-93.
ZHOU L N, JIN N N, WANG H, et al. Design of permanent magnet synchronous motor control semi-physical simulation system[J]. Research and Exploration in Laboratory, 2022, 41(2): 89-93. |
| [3] |
CHEN Q, YU X, SUN M, et al. Adaptive repetitive learning control of PMSM servo systems with bounded nonparametric uncertainties: theory and experiments[J].
IEEE Transactions on Industrial Electronics, 2020, 68(9): 8626-8635.
|
| [4] |
WU G, HUANG S, WU Q, et al. Robust predictive torque control of N* 3-phase PMSM for high-power traction application[J].
IEEE Transactions on Power Electronics, 2020, 35(10): 10799-10809.
DOI: 10.1109/TPEL.2020.2981914. |
| [5] |
LIU X, YU H. Continuous adaptive integral-type sliding mode control based on disturbance observer for PMSM drives[J].
Nonlinear dynamics, 2021, 104(2): 1429-1441.
DOI: 10.1007/s11071-021-06360-z. |
| [6] |
WANG M, DONG X, REN X, et al. SDRE based optimal finite-time tracking control of a multi-motor driving system[J].
International Journal of Control, 2021, 94(9): 2551-2563.
DOI: 10.1080/00207179.2020.1717632. |
| [7] |
SUN X, HU C, ZHU J, et al. MPTC for PMSMs of EVs with multi-motor driven system considering optimal energy allocation[J].
IEEE Transactions on Magnetics, 2019, 55(7): 1-6.
|
| [8] |
周林娜, 王众, 刘金浩, 等. 基于dSPACE的刚柔耦合多电机控制实验平台[J].
实验技术与管理, 2020, 37(11): 120-124.
ZHOU L N, WANG Z, LIU J H, et al. Rigid-flexible coupling multi-motor control experiment platform based on dSPACE[J]. Experiment Technology and Management, 2020, 37(11): 120-124. |
| [9] |
杨春雨, 孟凡仪, 许一鸣, 等. 大惯量负载多电机驱动系统协调控制方法综述[J].
电机与控制应用, 2019, 46(3): 1-7.
YANG C Y, MENG F Y, XU Y M, et al. Coordinated control Methods for multi-motor drive systems of large inertia load: a survey[J]. Electric Machines and Control Application, 2019, 46(3): 1-7. DOI: 10.3969/j.issn.1673-6540.2019.03.001. |
| [10] |
SHI T, LIU H, GENG Q, et al. Improved relative coupling control structure for multi-motor speed synchronous driving system[J].
IET Electric Power Applications, 2016, 10(6): 451-457.
DOI: 10.1049/iet-epa.2015.0515. |
| [11] |
TLV Y, REN X, NA J. Online Nash-optimization tracking control of multi-motor driven load system with simplified RL scheme[J].
ISA Transactions, 2020, 98(3): 251-262.
|
| [12] |
SANT A V, KHADKIKAR V, XIAO W, et al. Four-axis vector-controlled dual-rotor PMSM for plug-in electric vehicles[J].
IEEE Transactions on Industrial Electronics, 2015, 62(5): 3202-3212.
DOI: 10.1109/TIE.2014.2387094. |
| [13] |
CHU X, NIAN X, WANG H, et al. Distributed fault tolerant tracking control for large-scale multi-motor web-winding systems[J].
IET Control Theory & Applications, 2019, 13(4): 543-553.
|
| [14] |
SAGITOV P I, ALMURATOVA N K, TOYGOZHINOVA Z Z, et al. Mathematical modeling and optimization of the control system for multi-motor electric drive of conveyor belt[J].
Int. J of Engineering Research and Technology, 2019, 12(6): 899-911.
|
| [15] |
LUO X, TANG Q, SHEN A, et al. PMSM sensorless control by injecting HF pulsating carrier signal into estimated fixed-frequency rotating reference frame[J].
IEEE Transactions on Industrial Electronics, 2016, 63(4): 2294-2303.
DOI: 10.1109/TIE.2015.2505679. |
| [16] |
UTKIN V, POZNYAK A, ORLOV Y, et al. Conventional and high order sliding mode control[J].
Journal of the Franklin Institute, 2020, 357(15): 10244-10261.
DOI: 10.1016/j.jfranklin.2020.06.018. |
| [17] |
HU J, ZHANG H, LIU H, et al. A survey on sliding mode control for networked control systems[J].
International Journal of Systems Science, 2021, 52(6): 1129-1147.
DOI: 10.1080/00207721.2021.1885082. |
| [18] |
QU S, ZHAO L, XIONG Z. Cross-layer congestion control of wireless sensor networks based on fuzzy sliding mode control[J].
Neural Computing and Applications, 2020, 32(17): 13505-13520.
DOI: 10.1007/s00521-020-04758-1. |
| [19] |
WANG S, NA J, CHEN Q. Adaptive predefined performance sliding mode control of motor driving systems with disturbances[J].
IEEE Transactions on Energy Conversion, 2020, 36(3): 1931-1939.
|
| [20] |
WANG Y, XIE X, CHADLI M, et al. Sliding-mode control of fuzzy singularly perturbed descriptor systems[J].
IEEE Transactions on Fuzzy Systems, 2020, 29(8): 2349-2360.
|
| [21] |
TU Z, FEI F, DENG X. Untethered flight of an at-scale dual-motor hummingbird robot with bio-inspired decoupled wings[J].
IEEE Robotics and Automation Letters, 2020, 5(3): 4194-4201.
|
| [22] |
ZOU M, FANG P, PENG H, et al. Study on synchronization characteristics for self-synchronous vibration system with dual-frequency and dual-motor excitation[J].
Journal of Mechanical Science and Technology, 2019, 33(3): 1065-1078.
DOI: 10.1007/s12206-019-0206-4. |
| [23] |
KHALIFEH J M, DIBBLE C F, DY C J, et al. Cost-effectiveness analysis of combined dual motor nerve transfers versus alternative surgical and nonsurgical management strategies to restore shoulder function following upper brachial plexus injury[J].
Neurosurgery, 2019, 84(2): 362-377.
DOI: 10.1093/neuros/nyy015. |
| [24] |
ZHENG W, WANG Y, JIAN C, et al. Fault-tolerant control of NPC three-level inverters-fed double-stator-winding PMSM drives based on vector space decomposition[J].
IEEE Transactions on Industrial Electronics, 2017, 64(99): 8446-8458.
|
| [25] |
MYNAR Z, VESELY L, VACLAVEK P. PMSM model predictive control with field-weakening implementation[J].
IEEE Transactions on Industrial Electronics, 2016, 63(8): 5156-5166.
DOI: 10.1109/TIE.2016.2558165. |
| [26] |
FENG G, LAI C, MUKHERJEE K, et al. Current injection-based online parameter and VSI nonlinearity estimation for PMSM drives using current and voltage DC components[J].
IEEE Transactions on Transportation Electrification, 2016, 2(2): 119-128.
DOI: 10.1109/TTE.2016.2538180. |
| [27] |
BELDA K, VOMIK D. Explicit generalized predictive control of speed and position of PMSM drives[J].
IEEE Transactions on Industrial Electronics, 2016, 63(6): 3889-3896.
DOI: 10.1109/TIE.2016.2515061. |
| [28] |
KONTARCEK A, BAJEC P, NEMEC M, et al. Cost-effective three-phase PMSM drive tolerant to open-phase fault[J].
IEEE Transactions on Industrial Electronics, 2015, 62(11): 6708-6718.
DOI: 10.1109/TIE.2015.2437357. |
| [29] |
MAZZOLETTI M A, BOSSIO G R, ANGELO C, et al. A model-based strategy for interturn short-circuit fault diagnosis in PMSM[J].
IEEE Transactions on Industrial Electronics, 2017, 64(9): 7218-7228.
DOI: 10.1109/TIE.2017.2688973. |
| [30] |
JIAN H, YANG Q, HUI L. Adaptive robust nonlinear feedback control of chaos in PMSM system with modeling uncertainty[J].
Applied Mathematical Modelling, 2016, 40(19-20): 8265-8275.
DOI: 10.1016/j.apm.2016.04.019. |
| [31] |
WEI W, ZHANG J, MING C. A Dual-Level Hysteresis current control for one five-leg VSI to control two PMSMs[J].
IEEE Transactions on Power Electronics, 2016, 32(1): 804-814.
|
| [32] |
SHI T, WANG Z, XIA C. Speed measurement error suppression for PMSM control system using self-adaption kalman observer[J].
IEEE Transactions on Industrial Electronics, 2015, 62(5): 2753-2763.
DOI: 10.1109/TIE.2014.2364989. |
| [33] |
WIBOWO W K, JEONG S K. Improved estimation of rotor position for sensorless control of a PMSM based on a sliding mode observer[J].
Journal of Central South University, 2016, 23(7): 1643-1656.
DOI: 10.1007/s11771-016-3219-5. |
| [34] |
ULLAH S, MEHMOOD A, KHAN Q, et al. Robust integral sliding mode control design for stability enhancement of under-actuated quadcopter[J].
International Journal of Control, Automation and Systems, 2020, 18(7): 1671-1678.
DOI: 10.1007/s12555-019-0302-3. |
| [35] |
SAMAT A A, ISHAK D, IQBAL S, et al. Comparison between takagi sugeno FIS and PI controller: an adaptation scheme of MRAS for speed sensorless control of PMSM[J].
Applied Mechanics & Materials, 2015, 785(2): 193-197.
|
| [36] |
SALEH, KAMEL, SUMNER, et al. Modeling and simulation of sensorless control of four-leg inverter PMSM drives in the case of a single-phase open circuit fault.[J].
Turkish Journal of Electrical Engineering & Uter Sciences, 2016, 24(5): 3807-3820.
|
| [37] |
周琪, 陈广登, 鲁仁全, 等. 基于干扰观测器的输入饱和多智能体系统事件触发控制[J].
中国科学:信息科学, 2019, 49(11): 1502-1516.
ZHOU Q, CHEN G D, LU R Q, et al. Disturbance-observer-based event-triggered control for multi-agent systems with input saturation[J]. Sci Sin Inform, 2019, 49(11): 1502-1516. DOI: 10.1360/SSI-2019-0105. |
| [38] |
VADIVEL R, JOO Y H. Reliable fuzzy H∞ control for permanent magnet synchronous motor against stochastic actuator faults[J].
IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2019, 51(4): 2232-2245.
|
| [39] |
杨彬, 周琪, 曹亮, 等. 具有指定性能和全状态约束的多智能体系统事件触发控制[J].
自动化学报, 2019, 45(8): 1527-1535.
YANG B, ZHOU Q, CAO L, et al. Event-triggered control for multi-agent systems with prescribed performance and full state constraints[J]. Acta Automatica Sinica, 2019, 45(8): 1527-1535. |
| [40] |
XIA J, LI Z, YU D, et al. Robust speed and current control with parametric adaptation for surface-mounted PMSM considering system perturbations[J].
IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 9(3): 2807-2817.
|
| [41] |
GAO Y, SUN B, LU G. Passivity-based integral sliding-mode control of uncertain singularly perturbed systems[J].
IEEE Transactions on Circuits & Systems II Express Briefs, 2011, 58(6): 386-390.
|
 2022, Vol. 39
2022, Vol. 39

