2. 青岛大学 山东省工业控制技术重点实验室,山东 青岛 266071
2. Shandong Key Laboratory of Industrial Control Technology, Qingdao University, Qingdao 266071, China
近年来,多智能体系统(Multi-agent Systems, MASs)的协同控制问题在无人机[1]、多机器人系统[2]等领域的广泛应用引起了学界极大的研究兴趣。与传统的控制系统相比,MASs具有分布式、协作、自治、容错、高效、低成本等优点。一般来说,协同控制主要有3个目标,即趋同控制、跟踪控制和包容控制。趋同控制的目标是使所有智能体的输出最终达成一致。跟踪控制的目标是在趋同控制目标的基础上跟踪期望的输出。包容控制的目标是使一群追随者能够到达并停留在由多个领导者形成的凸包上。目前,已经有许多基于模型的MASs趋同控制方法[3-8]、跟踪控制方法[9-12]和包容控制方法[13-19]。
值得说明的是上述研究都是基于系统模型的。然而,在实际系统中,经常无法得到系统的准确模型。因此,学界已经有几种数据驱动的控制方法来完成MASs的各种控制任务[20-22]。作为一种新颖的数据驱动方法,文献[23-27]提出的无模型自适应控制(Model-free Adaptive Control, MFAC)不需要任何系统模型,只需要利用系统的输入输出信号。在MFAC框架中,可以利用动态线性化技术将非线性系统变换为线性数据模型,可分为紧格式动态线性化(Compact Form Dynamic Linearization, CFDL)、偏格式动态线性化(Partial Form Dynamic Linearization, PFDL)和全格式动态线性化(Full Form Dynamic Linearization,FFDL)。需要指出的是,CFDL只使用一个参数来捕捉非线性系统的复杂行为,如非线性和时延等。PFDL和FFDL通过使用多个参数来更好地捕捉复杂非线性系统的复杂行为。文献[25]和文献[26]分别研究了单输入单输出(Single-input Single-output,SISO)和多输入多输出(Multiple-input Multiple-output,MIMO)非线性系统的CFDL-MFAC和PFDL-MFAC问题。此外,文献[27]研究了FFDL-MFAC问题。
最近,MFAC方法已被引入MASs以实现协同控制目标。文献[28]使用MFAC算法研究了一致性跟踪控制问题,其中提出了分布式无模型自适应控制(Distributed Model-free Adaptive Control,DMFAC)算法来保证所有智能体都可以跟踪参考信号。文献[29]研究了在切换拓扑下使用MFAC算法应对非线性MASs的输出编队问题。分布式无模型自适应迭代学习控制的问题在文献[30]中得到解决。进一步扩展应用该结果使所有智能体在有限时间内实现趋同跟踪目标[31]。文献[32]研究了非线性MASs的编队控制问题,其中设计了无模型自适应迭代学习控制算法来实现编队控制目标。此外,文献[33]研究了具有有界扰动的非线性MASs的鲁棒无模型自适应迭代学习编队控制问题。文献[34]研究了使用MFAC算法的MASs的中继协同跟踪控制问题。文献[35]使用无模型自适应迭代学习控制方法解决了具有未知干扰的MASs的一致性跟踪控制问题。文献[36]研究了多输入多输出MASs的鲁棒迭代学习一致性跟踪控制问题。
需要指出的是,上述无模型自适应控制器设计中采用了网络拓扑,即无模型自适应控制器参数依赖于拉普拉斯矩阵的特征值。为了更好地展示MFAC算法在MASs框架中的优越性,有必要仅使用MASs的输入/输出(input/output,I/O)数据来研究新的DMFAC算法。主要困难是如何建立一个新的MASs的DMFAC框架。因此,需要在现有的单智能体数据模型的基础上,探索一个合理的MASs数据模型。
随着网络通信技术的发展,MASs遭受网络攻击时的安全性问题受到广泛关注。众所周知,恶意网络攻击是不可避免的,而且会对MASs造成严重影响。有两种常见的网络攻击,即拒绝服务(Denial-of-Service,DoS)和虚假数据注入(False Data Injection,FDI)攻击。目前,有分别考虑DoS攻击[37-38]和FDI攻击[39-40]的基于模型的分布式MASs控制器。此外,文献[41]研究了受到DoS攻击的MASs协同控制问题,并开发了一种基于学习的DMFAC来抵抗DoS攻击。然而,考虑FDI网络攻击的DMFAC问题并没有得到很好的解决,还缺乏相关的研究。
为了解决上述问题,本文首先建立了一种新的分布式紧格式动态线性化(Distributed CFDL,DCFDL)MASs数据模型。然后,基于DCFDL数据模型,研究了分布式无模型自适应控制器,以实现遭受FDI攻击的MASs分布式协同控制目标。
1 预备知识和DMFAC框架制定本节旨在DCFDL数据模型的基础上建立非线性MASs的DMFAC框架。
1.1 预备知识首先展示一些图论相关知识。拓扑图
| $ L_{ii} = \sum\nolimits_{j = 1, j \neq i}^Na_{ij},\; L_{ij} = - a_{ij}(i \neq j) $ |
考虑一类异构非线性MASs,第
| $ y_i(k + 1) = f_i(y_i(k), u_i(k)) $ | (1) |
式中:
以下假设和引理将会在本文中使用。
假设1[25]
假设2[25] 非线性系统式(1)满足广义Lipschitz条件,即如果
假设3 拓扑图
引理1[25] 如果非线性MASs式(1)满足假设1、2,而且对于所有
| $ \Delta y_i(k + 1) = \phi_i^{\rm{c}}(k)\Delta u_i(k) $ | (2) |
式中:
假设4[25] 对所有
注释1 假设1是非线性系统的一般约束条件。假设2意味着有界输入产生有界输出,这在实际系统中是满足的。假设3是达成趋同控制目标的充分必要条件。假设4意味着当输入增加时,系统的输出不会减少,这被认为是一种“类线性”特性。在基于模型的控制方法中的控制方向可以找到类似的假设。
注释2 引理1提出了一种新的线性化方法,其广泛应用于无模型自适应控制方法中[23-27]。与现有的线性化方法不同,这种线性化方法仅使用系统的I/O数据。此外,可以通过设计估计器来估计PPD参数。
为了将MFAC框架引入MASs,定义分布式量测输出为
| $ \xi_i(k + 1) = \sum\nolimits_{j\in N_i}a_{ij}(y_i(k + 1) - y_j(k + 1)) $ | (3) |
然后,将式(1)代入式(3),得到
| $ \xi_i(k + 1) = \sum\nolimits_{j\in N_i}a_{ij}(f_i(y_i(k), u_i(k)) - f_j(y_j(k), u_j(k)) $ | (4) |
可以观察到,
基于引理1,引理2给出了MASs的DCFDL数据模型。
引理2 对于满足假设1~3且
| $ \Delta \xi_i(k + 1) = \phi_i(k) \Delta u_i(k) $ | (5) |
式中:
证明 基于系统式(4),
| $\begin{split} & \Delta\xi_i(k+1) = \sum\nolimits_{j\in N_i}a_{ij}(f_i(y_i(k),u_i(k))-f_j(y_j(k),u_j(k))- \\ & f_i(y_i(k-1),u_i(k-1))+f_j(y_j(k-1),u_j(k-1)) + \\ & f_i(y_i(k),u_i(k-1))-f_i(y_i(k),u_i(k-1))) \end{split}$ |
然后,将
| $ \Delta\xi_i(k+1) = \sum\nolimits_{j\in N_i}a_{ij}\left(\frac{\partial f^*}{\partial u_i(k)}\Delta u_i(k)+\varPsi(k)\right) $ |
式中:
根据文献[24]中的动态线性化技巧可以得到等式
此外,一方面由于实际系统中的执行器不能变化太快[42],所以控制输入的增量是有界的,即
| $ \begin{split}& |\Delta \xi_i(k+1)| \leqslant \\& \left| \sum\nolimits_{j\in N_i} a_{ij}\overline{b}_i\Delta u_i(k)\right|+\left|\sum\nolimits_{j\in N_i}a_{ij}\overline{b}_j\Delta u_j(k)\right| \leqslant \\& \left| \sum\nolimits_{j\in N_i}a_{ij}\overline{b}_i\right||\Delta u_i(k)|+\left|\sum\nolimits_{j\in N_i}a_{ij}\overline{b}_j\right||\Delta u_j(k)| \leqslant \\& \left|\sum\nolimits_{j\in N_i}a_{ij}\overline{b}_i\right||\Delta u_i(k)|+\left|\sum\nolimits_{j\in N_i}a_{ij}\overline{b}_j\right|\frac{\overline{\varepsilon}_j}{\underline{\varepsilon}_i}|\Delta u_i(k)| = \\& b_i|\Delta u_i(k)| \end{split}$ |
式中:
注释3 值得注意的是,
需要注意的是实际的PPD参数
| $ \hat{\xi}_i(k + 1) = \hat{\xi}_i(k) + \hat{\phi}_i(k)\Delta u_i(k) + K_i(\xi_i(k) - \hat{\xi}_i(k)) $ | (6) |
式中:
| $ \hat{\phi}_i(k) = \hat{\phi}_i(k - 1) + \frac{\eta_i\Delta u_i(k - 1)(\Delta \xi_i(k) - \hat{\phi}_i(k - 1)\Delta u_i(k - 1))}{\Delta u_i^2(k - 1) + \mu_i} $ | (7) |
式中:
为了设计分布式趋同无模型自适应控制器,定义式(8)性能函数。
| $ J_2[u_i(k)] = |\hat{\xi}_i(k + 1)|^2 + \lambda_i |u_i(k) - u_i(k - 1)|^2 $ | (8) |
式中:
令
| $ u_i(k) = u_i(k - 1) - \frac{\rho_i\hat{\phi}_i(k)}{\hat{\phi}_i^2(k) + \lambda_i}(\hat{\xi}_i(k) + K_i(\xi_i(k) - \hat{\xi}_i(k))) $ | (9) |
注释4 性能函数式(8)由两部分组成,即估计的分布输出
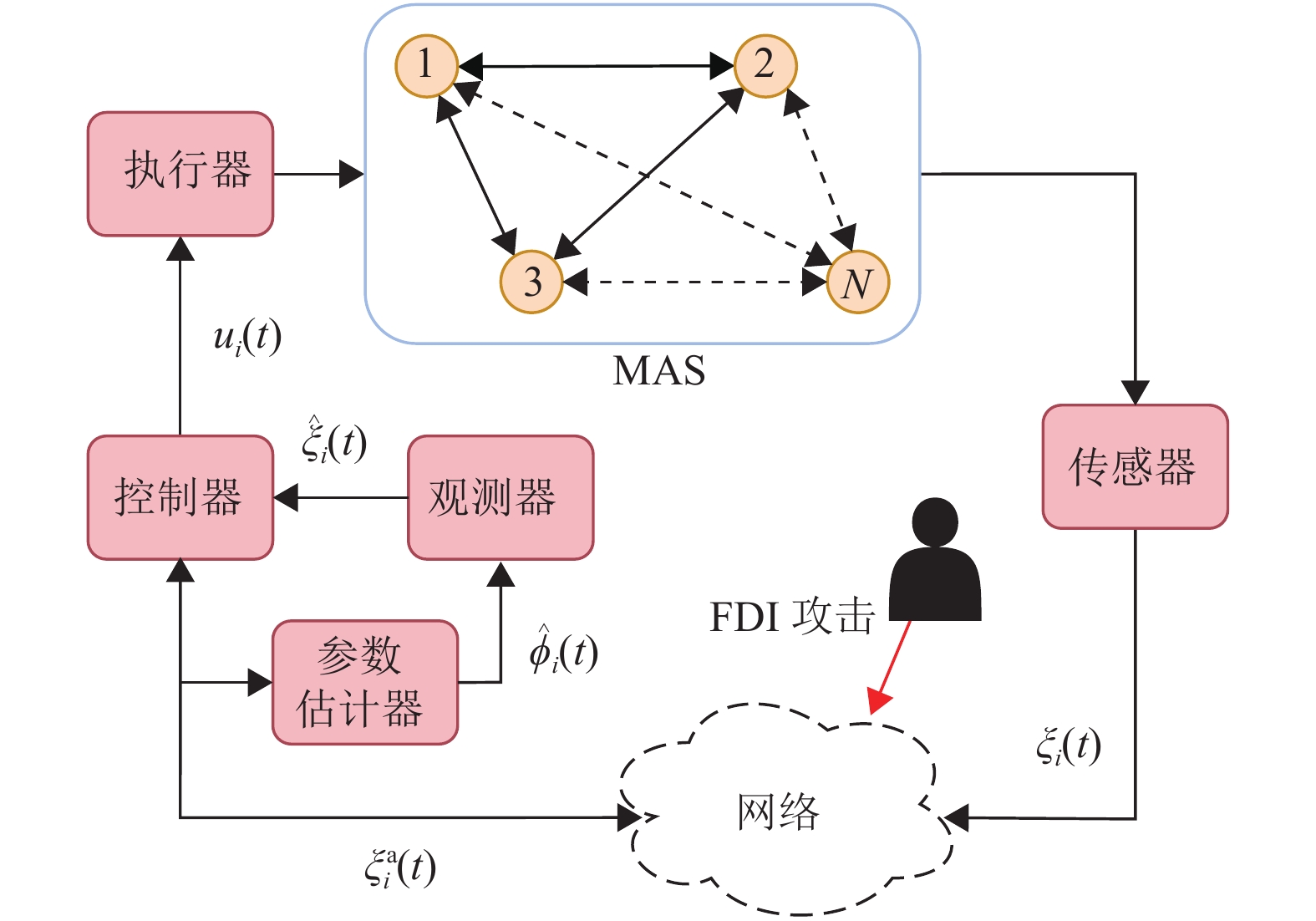
FDI攻击旨在通过将虚假数据注入传输网络来破坏系统性能。假设攻击者会随机对从传感器到控制器的传输网络发起FDI攻击,如图1所示。因此,当传输网络中发生FDI攻击时,观测器和控制器接收到的数据包为
|
图 1 具有FDI攻击的MASs的DMFAC系统框图 Figure 1 System block diagram of the DMFAC for MASs with FDI attacks |
| $ \xi_i^{\rm{a}}(k) = \xi_i(k) + \beta_i(k) \omega_i(k) $ | (10) |
式中:
将式(6)和式(9)结合并考虑到传输网络遭受FDI攻击,得到受FDI攻击的DMFAC算法为
| $ \hat{\xi}_i(k + 1) = \hat{\xi}_i(k) + \hat{\phi}_i(k)\Delta u_i(k) + K_i(\xi_i^{\rm{a}}(k) - \hat{\xi}_i(k)) $ | (11) |
| $ \begin{split}& \hat{\phi}_i(k) = \hat{\phi}_i(k - 1) + \\& \frac{\eta_i(\xi_i^{\rm{a}}(k) - \xi_i(k - 1) - \hat{\phi}_i(k - 1)\Delta u_i(k - 1))\Delta u_i(k - 1)}{\Delta u_i^2(k - 1) + \mu_i} \end{split}$ | (12) |
| $ u_i(k) = u_i(k - 1) - \frac{\rho_i\hat{\phi}_i(k)}{\hat{\phi}_i^2(k) + \lambda_i}(\hat{\xi}_i(k) + K_i(\xi_i^{\rm{a}}(k) - \hat{\xi}_i(k))) $ | (13) |
问题1 对于受FDI攻击的非线性MASs式(1),本文旨在设计由式(11)~(13)构成的仅使用I/O数据的DMFAC算法,在均方意义上实现有界趋同控制目标,即
本节讨论了MASs的稳定性分析,并得到了DMFAC算法的参数。以下定理是保证趋同控制目标能够实现的主要结果。
定理1 对于受到FDI攻击的非线性MASs式(1),如果满足假设1~4,而且存在
| $ \hat{\xi}_i(k + 1) = \hat{\xi}_i(k) + \hat{\phi}_i(k) \Delta u_i(k) + K_i(\xi_i^{\rm{a}}(k) - \hat{\xi}_i(k)) $ | (14) |
| $ {\hat \phi _i}(k) = \left\{ \begin{array}{l} {{\hat \phi }_i}(k - 1)+({\eta _i}\Delta {u_i}(k - 1)(\xi _i^a(k) - {\xi _i}(k - 1) - \\ {{\hat \phi }_i}(k - 1)\Delta {u_i}(k - 1)))/({{\Delta u_i^2(k - 1) + {\mu _i}}}), 其他\\ {{\hat \phi }_i}(1),如果|{{\hat \phi }_i}(k)| \leqslant {\sigma _i}或|\Delta {u_i}(k - 1)| \leqslant {\sigma _i} \end{array} \right. $ | (15) |
| $ u_i(k) = u_i(k - 1) - \frac{\rho_i \hat{\phi}_i(k)}{\hat{\phi}_i^2(k) + \lambda_i}(\hat{\xi}_i(k) + K_i(\xi_i^{\rm{a}}(k) - \hat{\xi}_i(k))) $ | (16) |
证明 过程将分为2个步骤,即PPD参数的估计误差和趋同误差分别在均方意义上有界。
(1) 证明PPD参数的估计误差在均方意义上有界。
将PPD参数的估计误差定义为
| $ \begin{split} & e_{\phi_i}(k) = \hat{\phi}_i(k - 1) - \phi_i(k) + \frac{\eta_i\Delta u_i(k - 1)}{\Delta u_i^2(k - 1) + \mu_i} \times \\ & (\phi_i(k - 1) \Delta u_i(k - 1) + \beta_i(k) \omega_i(k) - \hat{\phi}_i(k - 1)\Delta u_i(k - 1)) = \\ & e_{\phi_i}(k - 1) + \phi_i(k - 1) - \phi_i(k) - \frac{\eta_i\Delta u_i^2(k - 1)}{\Delta u_i^2(k - 1) + \mu_i}e_{\phi_i}(k - 1) + \\ & \frac{\eta_i \Delta u_i(k - 1)}{\Delta u_i^2(k - 1) + \mu_i}\beta_i(k)\omega_i(k) = \left(1 - \frac{\eta_i\Delta u_i^2(k - 1)}{\Delta u_i^2(k - 1) + \mu_i}\right)e_{\phi_i}(k - 1) + \\ &\;\phi_i(k - 1) - \phi_i(k) + \frac{\eta_i\Delta u_i(k - 1)}{\Delta u_i^2(k - 1) + \mu_i}\beta_i(k)\omega_i(k) \end{split} $ | (17) |
然后,在式(17)两边取绝对值和期望得到
| $ \begin{split} {{{\rm{E}}}}\{|e_{\phi_i}(k)|\}\leqslant & \left|1 - \frac{\eta_i\Delta u_i^2(k - 1)}{\Delta u_i^2(k - 1) + \mu_i}\right| {{{\rm{E}}}}\{|e_{\phi_i}(k - 1)|\} +\\& \left|\frac{\eta_i\Delta u_i(k - 1)}{\Delta u_i^2(k - 1) + \mu_i}\right|\beta_i|\omega_i(k)| + |\phi_i(k - 1) - \phi_i(k)| \end{split} $ | (18) |
根据式(15),函数
| $ 0\leqslant\left|1 - \frac{\eta_i\Delta u_i^2(k - 1)}{\Delta u_i^2(k - 1) + \mu_i}\right|\leqslant 1 - \frac{\eta_i\sigma_i^2}{\mu_i + \sigma_i^2} \mathop{=}\limits^\Delta d_1<1 $ | (19) |
另外有
| $ 0\leqslant\left|\frac{\eta_i\Delta u_i(k - 1)}{\Delta u^2_i(k - 1) + \mu_i}\right|\leqslant\frac{\eta_i\Delta u_i(k - 1)}{2\Delta u_i(k - 1)\sqrt{\mu_i}} = \frac{\eta_i}{2\sqrt{\mu_i}} \mathop{=}\limits^\Delta d_2 < 1 $ | (20) |
根据引理2,有
| $ \begin{split} {\rm{E}}\{|e_{\phi_i}(k)|\} \leqslant& d_1{\rm{E}}\{|e_{\phi_i}(k - 1)|\} + 2b_i + d_2\beta_i c_i \leqslant \cdots \leqslant \\& d_1^{k - 1}{\rm{E}}\{|e_{\phi_i}(1)|\} + \frac{(2b_i + d_2\beta_i c_i)(1 - d_1^{k - 1})}{1 - d_1} \end{split}\qquad $ |
所以,
(2) 证明趋同误差在均方意义上有界,即
首先基于
| $ \begin{split}& e_{\xi_i}(k + 1) = \\& \xi_i(k) + \phi_i(k) \Delta u_i(k) - \hat{\xi}_i(k) - \hat{\phi}_i(k) \Delta u_i(k) - K_i(\xi_i^{\rm{a}}(k) - \hat{\xi}_i(k)) = \\& e_{\xi_i}(k) + (\phi_i(k) - \hat{\phi}_i(k))\Delta u_i(k) - K_i(\xi_i^{\rm{a}}(k) - \hat{\xi}_i(k)) = \\& e_{\xi_i}(k) - e_{\phi_i}(k) \Delta u_i(k) - K_i(\xi_i(k) + \beta_i(k) \omega_i(k) - \hat{\xi}_i(k)) = \\& (1 - K_i)e_{\xi_i}(k) - e_{\phi_i}(k)\Delta u_i(k) - K_i \beta_i(k) \omega_i(k) \\[-10pt] \end{split}$ | (21) |
在式(21)两侧同时取期望和绝对值,可得
| $\begin{split} {\rm{E}}\{|e_{\xi_i}(k + 1)|\} \leqslant &|1 - K_i| {\rm{E}}\{|e_{\xi_i}(k)|\} + |e_{\phi_i}(k) \Delta u_i(k)| + \\& |K_i \beta_i \omega_i(k)| = |1 - K_i| {\rm{E}}\{|e_{\xi_i}(k)|\} + \varUpsilon_i(k) \\[-10pt] \end{split} \qquad $ | (22) |
式中:
根据定理1中
| $ \begin{split} {\rm{E}}\{|e_{\xi_i}(k + 1)|\} \leqslant& |1 - K_i| {\rm{E}}\{|e_{\xi_i}(k)|\} + \upsilon_i \leqslant \cdots \leqslant \\ & {|1 - K_i|}^k {\rm{E}}\{|e_{\xi_i}(1)|\} + \frac{\upsilon_i(1 - |1 - K_i|^k)}{1 - |1 - K_i|} \\[-10pt] \end{split}\qquad $ | (23) |
很显然
| $ \left\{ e_{\xi_i}(k) | {\rm{E}}\{|e_{\xi_i}(k + 1)|\} \leqslant \frac{\upsilon_i}{1 - |1 - K_i|} \right\} $ | (24) |
然后证明
| $ \hat{\xi}_i(k + 1) = \left(1 - \frac{\rho_i \hat{\phi}_i^2(k)}{\hat{\phi}_i^2(k) + \lambda_i}\right)(\hat{\xi}_i(k) + K_i(\xi_i^a(k) - \hat{\xi}_i(k))) $ | (25) |
考虑式(10),得到
| $ \begin{split}& \hat{\xi}_i(k + 1) = \left(1 - \frac{\rho_i \hat{\phi}_i^2(k)}{\hat{\phi}_i^2(k) + \lambda_i}\right)(\hat{\xi}_i(k) + K_i( \xi_i(k) + \beta_i(k) \omega_i(k) -\\& \hat{\xi}_i(k))) = \left(1 - \frac{\rho_i \hat{\phi}_i^2(k)}{\hat{\phi}_i^2(k) + \lambda_i}\right)(\hat{\xi}_i(k) + K_i(e_{\xi_i}(k) + \beta_i(k) \omega_i(k))) \end{split} $ | (26) |
在式(26)两边取绝对值和期望,得到
| $ {\rm{E}}\{|\hat{\xi}_i(k + 1)|\} \leqslant \left|1 - \frac{\rho_i \hat{\phi}_i^2(k)}{\hat{\phi}_i^2(k) + \lambda_i}\right|({\rm{E}}\{|\hat{\xi}_i(k)|\} + \varPsi_i(k)) $ | (27) |
式中:
根据定理1中
| $ 0 < \left|1 - \frac{\rho_i \hat{\phi}_i^2(k)}{\hat{\phi}_i^2(k) + \lambda_i}\right| = 1 - \frac{\rho_i \hat{\phi}_i^2(k)}{\hat{\phi}_i^2(k) + \lambda_i} \mathop{=}\limits^\Delta d_3 < 1 $ | (28) |
根据式(28),可以从式(27)中得到不等式
| $ \begin{split} {\rm{E}}\{|\hat{\xi}_i(k + 1)|\} \leqslant& d_3 {\rm{E}}\{|\hat{\xi}_i(k)|\} + d_3 \varphi_i \leqslant \cdots \leqslant\\& d_3^k {\rm{E}}\{|\hat{\xi}_i(1)|\} + \frac{d_3 \varphi_i(1 - d_3^k)}{1 - d_3} \end{split}\qquad \qquad $ |
很显然
| $ \{ \hat{\xi}_i(k) | {\rm{E}}\left\{|\hat{\xi}_i(k + 1)|\} \leqslant \frac{d_3 \varphi_i}{1 - d_3} \right\} $ | (29) |
结合式(24)与式(29)可以得到,当
| $ \{ \xi_i(k) | {\rm{E}}\{|\xi_i(k)|\} \leqslant | \hat{\xi}_i(k) + e_{\xi_i}(k) | \leqslant \varsigma_i \} $ | (30) |
式中:
另外结合假设3中的有向生成树的条件,可以解决问题1,即趋同误差在均方意义上是有界的。
注释5 所设计的DMFAC算法式(14)~(16)仅使用系统的I/O数据,没有使用模型参数。另外,所设计的控制算法并不需要知道MASs拓扑结构的全局信息。
4 仿真在本节中,提供了仿真示例,以验证所提出的DMFAC算法的有效性。
考虑以下异构非线性MASs。
| $ \left\{ {\begin{array}{*{20}{l}} {{y_1}(k + 1) = \dfrac{{{y_1}(k)}}{{1 + y_1^2(k)}} + u_1^2(k)}\\ {{y_2}(k + 1) = \dfrac{{{y_2}(k){u_2}(k)}}{{1 + y_2^3(k)}} + 0.5{u_2}(k)}\\ {{y_3}(k + 1) = 0.7\sin({y_3}(k)) + {u_3}(k)}\\ {{y_4}(k + 1) = 0.4\cos({y_4}(k)) + 0.7{u_4}(k)} \end{array}} \right. $ |
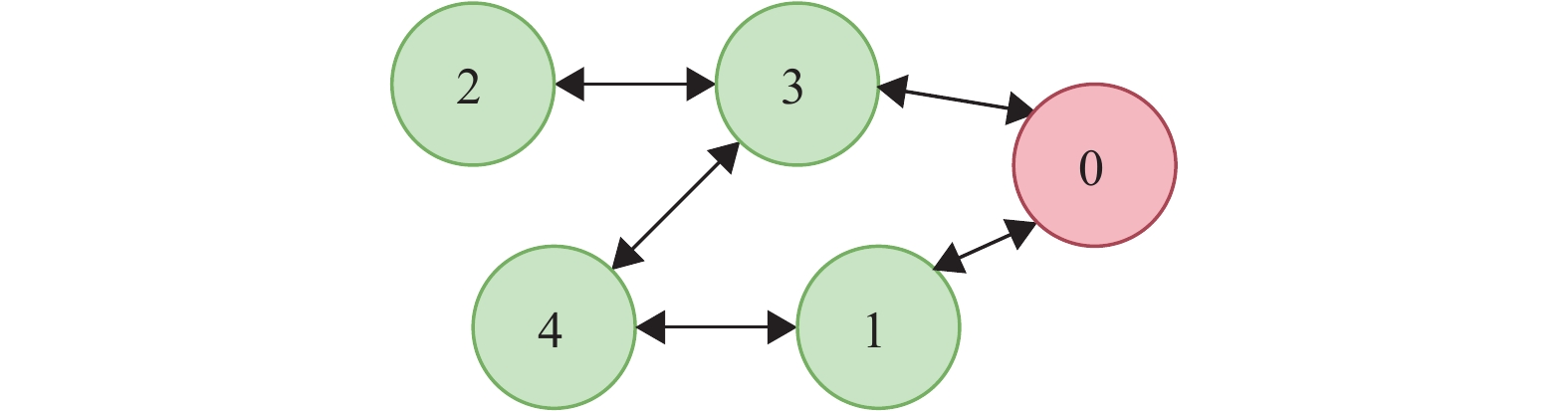
趋同控制的拓扑图如图2所示。在不考虑领导者的情况下,得到拉普拉斯矩阵为
| $ {\boldsymbol{L}} = \left[ {\begin{array}{*{20}{r}} 1&0&0&{ - 1}\\ 0&1&{ - 1}&0\\ 0&{ - 1}&1&0\\ { - 1}&0&{ - 1}&2 \end{array}} \right] $ |
初始值为
|
图 2 趋同控制的拓扑图 Figure 2 The topology graph for the consensus control |
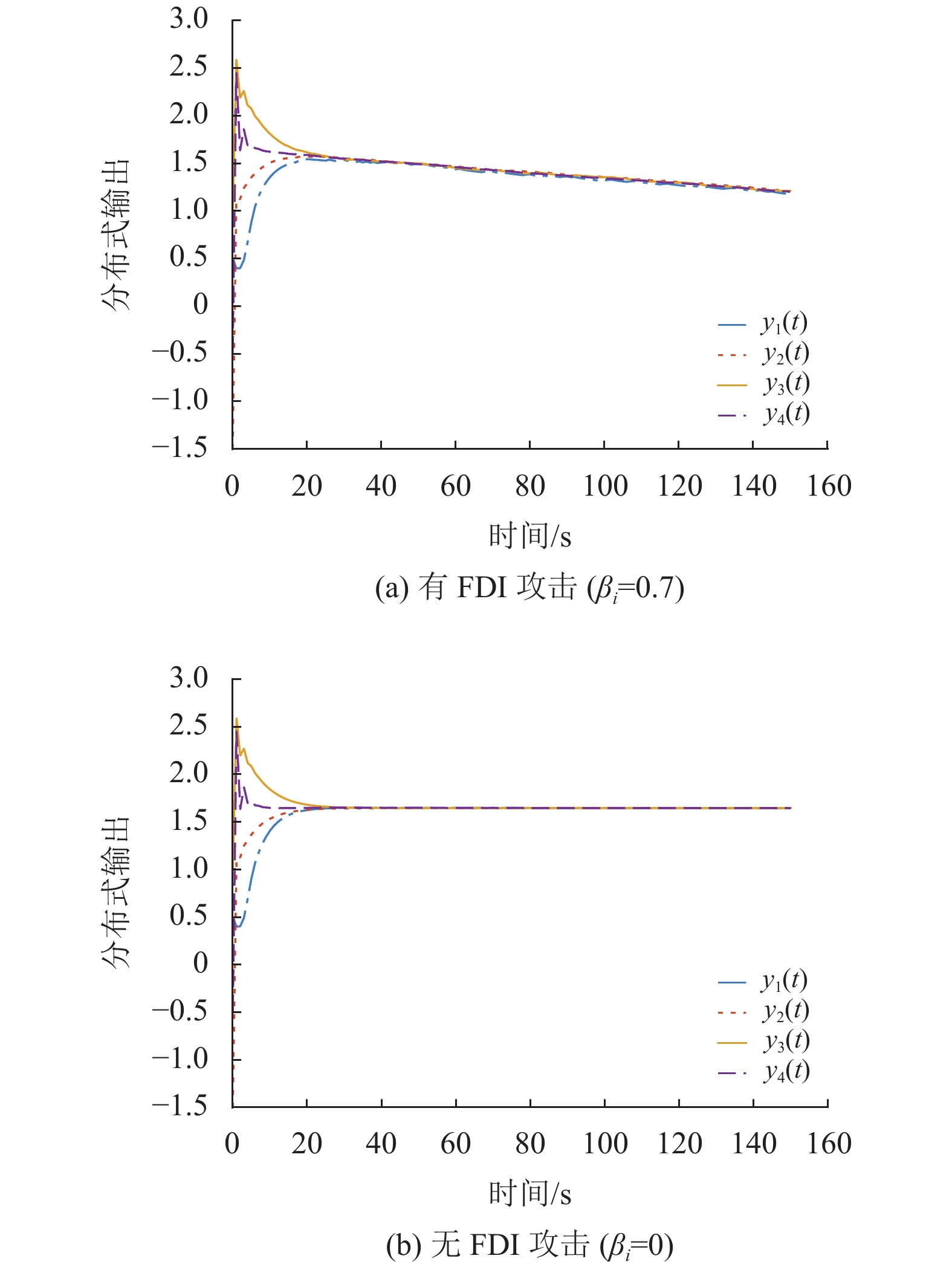
仿真结果如图3所示。可以观察到,当通信网络受到FDI攻击时,所有智能体的输出都是有界趋同的。
|
图 3 有和无FDI攻击的趋同控制算法的性能 Figure 3 The performance of the consensus control algorithm with(left) and without(right) FDI attacks |
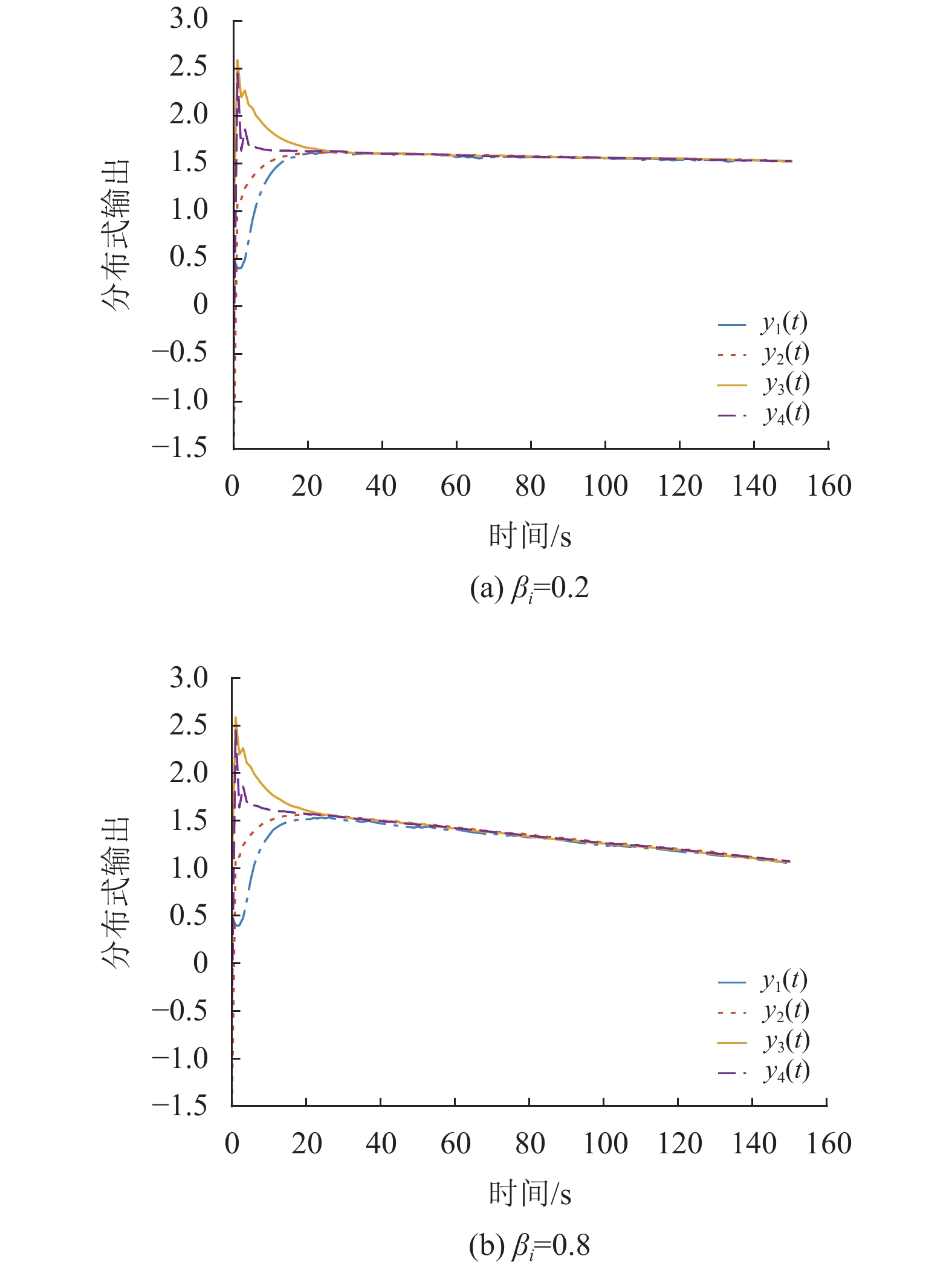
图4展示了在保持其他初始值不变,
|
图 4 不同攻击成功概率下趋同控制算法的性能 Figure 4 The performance of the consensus control algorithm with different attacks possibility |
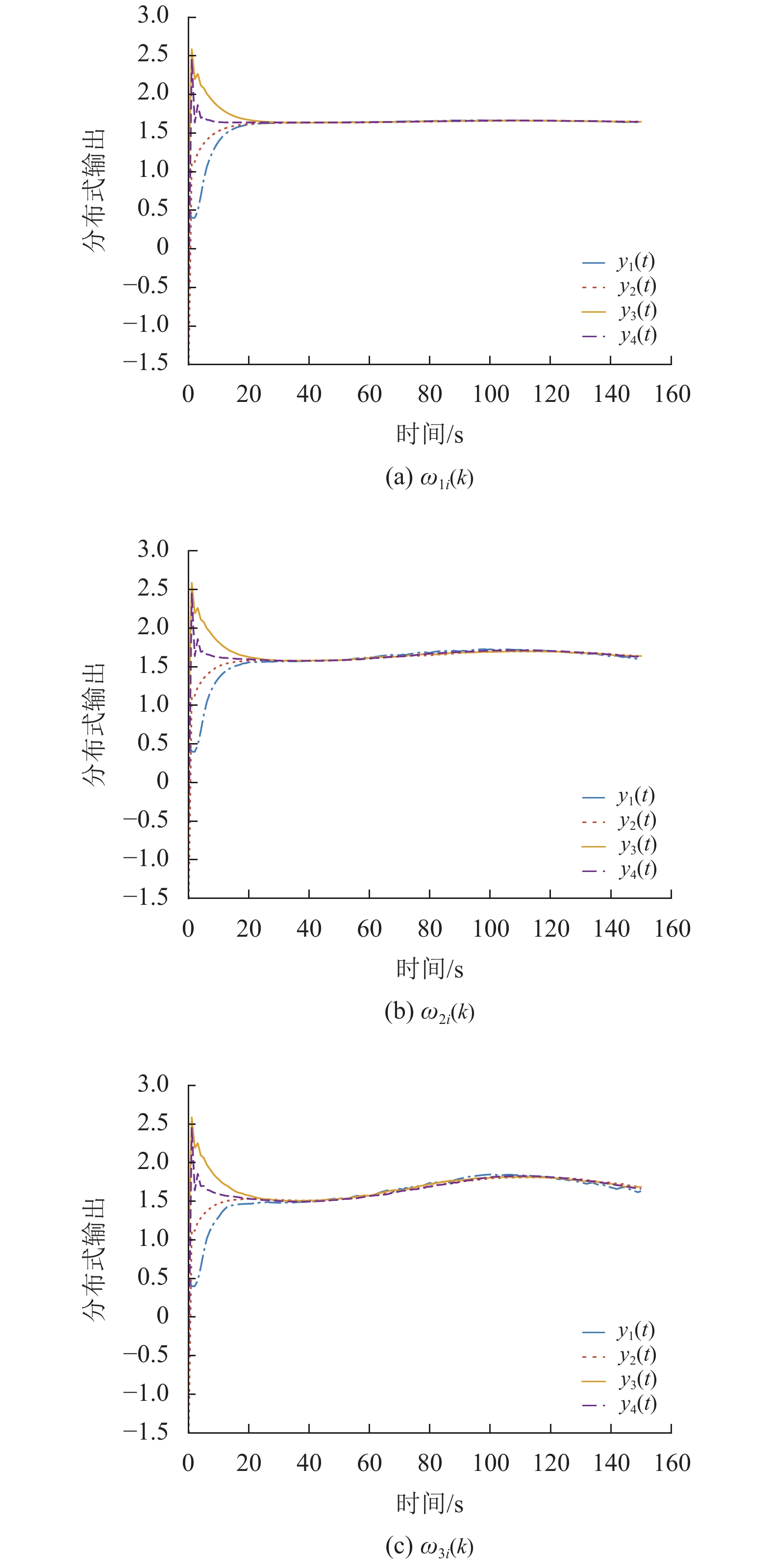
|
图 5 不同虚假数据下趋同控制算法的性能 Figure 5 The performance of the consensus control algorithm with different false data |
本文研究了受FDI攻击的非线性异构MASs的分布式趋同MFAC问题,在文献[25]中设计的单智能体CFDL数据模型的基础上,提出了一种新颖的DCFDL数据模型设计方法,通过改进的动态线性化方法,使用非线性MASs的I/O数据获得等效线性数据模型。基于DCFDL数据模型,设计了一种新的DMFAC算法来实现受FDI攻击的MASs分布式趋同控制。所提出的DMFAC算法既不需要系统模型,也不需要网络拓扑结构。仿真结果表明,所设计的ET-MFAC算法可以很好地实现分布式趋同控制目标。
| [1] |
TANG Y, XING X, KARIMI H R, et al. Tracking control of networked multi-agent systems under new characterizations of impulses and its applications in robotic systems[J].
IEEE Transactions on Industrial Electronics, 2015, 63(2): 1299-1307.
|
| [2] |
DONG X, HUA Y, ZHOU Y, et al. Theory and experiment on formation-containment control of multiple multirotor unmanned aerial vehicle systems[J].
IEEE Transactions on Automation Science and Engineering, 2018, 16(1): 229-240.
|
| [3] |
OLFATI-SABER R, MURRAY R M. Consensus problems in networks of agents with switching topology and time-delays[J].
IEEE Transactions on Automatic Control, 2004, 49(9): 1520-1533.
DOI: 10.1109/TAC.2004.834113. |
| [4] |
HE W, XU B, HAN Q L, et al. Adaptive consensus control of linear multiagent systems with dynamic event-triggered strategies[J].
IEEE Transactions on Cybernetics, 2019, 50(7): 2996-3008.
|
| [5] |
DENG C, CHE W W, WU Z G. A dynamic periodic event-triggered approach to consensus of heterogeneous linear multiagent systems with time-varying communication delays[J].
IEEE Transactions on Cybernetics, 2021, 51(4): 1812-1821.
DOI: 10.1109/TCYB.2020.3015746. |
| [6] |
DENG C, CHE W W. Fault-tolerant fuzzy formation control for a class of nonlinear multiagent systems under directed and switching topology[J].
IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(9): 5456-5465.
DOI: 10.1109/TSMC.2019.2954870. |
| [7] |
JIN X Z, CHE W W, WU Z G, et al. Adaptive consensus and circuital implementation of a class of faulty multiagent systems[J].
IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2022, 52(1): 226-237.
DOI: 10.1109/TSMC.2020.2995802. |
| [8] |
JIANG C, CHEN Z, GUO Y. Multi-robot formation control: a comparison between model-based and learning-based methods[J].
Journal of Control and Decision, 2020, 7(1): 90-108.
DOI: 10.1080/23307706.2019.1697970. |
| [9] |
DENG C, CHE W W, SHI P. Cooperative fault-tolerant output regulation for multiagent systems by distributed learning control approach[J].
IEEE Transactions on Neural Networks and Learning Systems, 2019, 31(11): 4831-4841.
|
| [10] |
YANG H, YE D. Observer-based fixed-time secure tracking consensus for networked high-order multiagent systems against dos attacks[J].
IEEE Transactions on Cybernetics, 2022, 52(4): 2018-2031.
DOI: 10.1109/TCYB.2020.3005354. |
| [11] |
XU W, HO D W, LI L, et al. Event-triggered schemes on leader-following consensus of general linear multiagent systems under different topologies[J].
IEEE Transactions on Cybernetics, 2015, 47(1): 212-223.
|
| [12] |
YANG Y, LI Y, YUE D, et al. Distributed secure consensus control with event-triggering for multiagent systems under dos attacks[J].
IEEE Transactions on Cybernetics, 2021, 51(6): 2916-2928.
DOI: 10.1109/TCYB.2020.2979342. |
| [13] |
AMINI A, ASIF A, MOHAMMADI A. Formation-containment control using dynamic event-triggering mechanism for multi-agent systems[J].
IEEE/CAA Journal of Automatica Sinica, 2020, 7(5): 1235-1248.
|
| [14] |
ZUO S, YUE D. Resilient output formation containment of heterogeneous multigroup systems against unbounded attacks[J].
IEEE Transactions on Cybernetics, 2022, 52(3): 1902-1910.
DOI: 10.1109/TCYB.2020.2998333. |
| [15] |
DENG C, YANG G H. Distributed adaptive fault-tolerant containment control for a class of multi-agent systems with non-identical matching non-linear functions[J].
IET Control Theory & Applications, 2016, 10(3): 273-281.
|
| [16] |
CHEN W, DING D, GE X, et al.
|
| [17] |
WANG D, WANG Z, WANG Z, et al. Design of hybrid event-triggered containment controllers for homogeneous and heterogeneous multiagent systems[J].
IEEE Transactions on Cybernetics, 2021, 51(10): 4885-4896.
DOI: 10.1109/TCYB.2020.3007500. |
| [18] |
WANG W, LONG J, WEN C, et al. Recent advances in distributed adaptive consensus control of uncertain nonlinear multi-agent systems[J].
Journal of Control and Decision, 2020, 7(1): 44-63.
DOI: 10.1080/23307706.2019.1693913. |
| [19] |
FATTAHI M, AFSHAR A. Controller-based observer design for distributed consensus of multi-agent systems with fault and delay[J].
Journal of Control and Decision, 2019, 6(4): 217-235.
DOI: 10.1080/23307706.2018.1458659. |
| [20] |
ZHANG H, YUE D, DOU C, et al. Data-driven distributed optimal consensus control for unknown multiagent systems with input-delay[J].
IEEE Transactions on Cybernetics, 2018, 49(6): 2095-2105.
|
| [21] |
JIANG H, HE H. Data-driven distributed output consensus control for partially observable multiagent systems[J].
IEEE Transactions on Cybernetics, 2018, 49(3): 848-858.
|
| [22] |
WANG S, DUAN J, SHI D, et al. A data-driven multi-agent autonomous voltage control framework using deep reinforcement learning[J].
IEEE Transactions on Power Systems, 2020, 35(6): 4644-4654.
DOI: 10.1109/TPWRS.2020.2990179. |
| [23] |
HOU Z, JIN S. Model free adaptive control: theory and applications[M]. Boca Raton: CRC press, 2019.
|
| [24] |
HOU Z, CHI R, GAO H. An overview of dynamic-linearization-based data-driven control and applications[J].
IEEE Transactions on Industrial Electronics, 2016, 64(5): 4076-4090.
|
| [25] |
HOU Z, JIN S. A novel data-driven control approach for a class of discrete-time nonlinear systems[J].
IEEE Transactions on Control Systems Technology, 2010, 19(6): 1549-1558.
|
| [26] |
HOU Z, JIN S. Data-driven model-free adaptive control for a class of mimo nonlinear discrete-time systems[J].
IEEE Transactions on Neural Networks, 2011, 22(12): 2173-2188.
DOI: 10.1109/TNN.2011.2176141. |
| [27] |
HOU Z, XIONG S. On model-free adaptive control and its stability analysis[J].
IEEE Transactions on Automatic Control, 2019, 64(11): 4555-4569.
DOI: 10.1109/TAC.2019.2894586. |
| [28] |
BU X, HOU Z, ZHANG H. Data-driven multiagent systems consensus tracking using model free adaptive control[J].
IEEE Transactions on Neural Networks and Learning Systems, 2017, 29(5): 1514-1524.
|
| [29] |
SONG W, FENG J, SUN S. Data-based output tracking formation control for heterogeneous mimo multiagent systems under switching topologies[J].
Neurocomputing, 2021, 422: 322-331.
DOI: 10.1016/j.neucom.2020.10.017. |
| [30] |
BU X, YU Q, HOU Z, et al. Model free adaptive iterative learning consensus tracking control for a class of nonlinear multiagent systems[J].
IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2017, 49(4): 677-686.
|
| [31] |
BU X, ZHU P, HOU Z, et al. Finite-time consensus for linear multi-agent systems using data-driven terminal ilc[J].
IEEE Transactions on Circuits and Systems II: Express Briefs, 2019, 67(10): 2029-2033.
|
| [32] |
BU X, CUI L, HOU Z, et al. Formation control for a class of nonlinear multiagent systems using model-free adaptive iterative learning[J].
International Journal of Robust and Nonlinear Control, 2018, 28(4): 1402-1412.
DOI: 10.1002/rnc.3961. |
| [33] |
REN Y, HOU Z. Robust model-free adaptive iterative learning formation for unknown heterogeneous non-linear multi-agent systems[J].
IET Control Theory & Applications, 2019, 14(4): 654-663.
|
| [34] |
ZHANG J, CHAI S, ZHANG B, et al. Relay cooperative tracking control of networked nonlinear multi-agent systems with communication delays: a data-driven method[J].
Neurocomputing, 2019, 363: 9-16.
DOI: 10.1016/j.neucom.2019.05.057. |
| [35] |
WANG Y, LI H, QIU X, et al. Consensus tracking for nonlinear multi-agent systems with unknown disturbance by using model free adaptive iterative learning control[J].
Applied Mathematics and Computation, 2020, 365: 124701.
DOI: 10.1016/j.amc.2019.124701. |
| [36] |
FENG J, SONG W, ZHANG H, et al. Data-driven robust iterative learning consensus tracking control for mimo multiagent systems under fixed and iteration-switching topologies[J].
IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2022, 52(2): 1331-1344.
DOI: 10.1109/TSMC.2020.3017289. |
| [37] |
DENG C, WEN C. Distributed resilient observer-based fault-tolerant control for heterogeneous multiagent systems under actuator faults and dos attacks[J].
IEEE Transactions on Control of Network Systems, 2020, 7(3): 1308-1318.
DOI: 10.1109/TCNS.2020.2972601. |
| [38] |
FENG Z, HU G. Secure cooperative event-triggered control of linear multiagent systems under dos attacks[J].
IEEE Transactions on Control Systems Technology, 2019, 28(3): 741-752.
|
| [39] |
HE W, MO Z, HAN Q L, et al. Secure impulsive synchronization in lipschitz-type multi-agent systems subject to deception attacks[J].
IEEE/CAA Journal of Automatica Sinica, 2020, 7(5): 1326-1334.
|
| [40] |
HE W, GAO X, ZHONG W, et al. Secure impulsive synchronization control of multi-agent systems under deception attacks[J].
Information Sciences, 2018, 459: 354-368.
DOI: 10.1016/j.ins.2018.04.020. |
| [41] |
MA Y S, CHE W W, DENG C, et al. Distributed model-free adaptive control for learning nonlinear mass under dos attacks[J/OL]. IEEE Transactions on Neural Networks and Learning Systems, 2021: 1-10. (2021-08-24) [2022-03-20]. https://doi.org/10.1109/TNNLS.2021.3104978.
|
| [42] |
XU D, JIANG B, SHI P. A novel model-free adaptive control design for multivariable industrial processes[J].
IEEE Transactions on Industrial Electronics, 2014, 61(11): 6391-6398.
DOI: 10.1109/TIE.2014.2308161. |
 2022, Vol. 39
2022, Vol. 39

