新一代信息技术与制造业的深度融合催生了工业互联网，使其成为推动我国制造业新工业革命的重要基石。为此，我国加快推进了发展工业互联网这一关键基础设施的布局。工业互联网要求控制系统具有高实时性和高可靠性^[1]。传统的控制策略为时间触发模式，其特点是控制律按时间周期性更新，这一控制模式使得各设备之间需要保持数据的实时互联^[2]，即使生产稳定、控制指令无需更新时，系统依然需要占用大量的通信资源^[3-4]。当前，我国制造业大力建设工业互联网，传统时间触发控制模式显然将带来巨大的网络通讯负担，严重时容易导致信道堵塞，使控制器失效^[5-6]。

为顺应制造业工业互联网的新发展，事件触发控制模式被提出，其根据所设计的事件触发机制，使控制器仅在符合某种触发机制(如，控制误差较大)时触发，进而刷新控制律^[7-9]。事件触发控制模式以不影响控制系统性能为前提，使系统不再依赖信号的实时通讯，而是按“需”执行控制任务，从而显著降低系统内部的通讯量，并减少计算负荷^[10-12]。

近些年，一系列事件触发控制方法被相继提出^[13-16]。文献[17]通过设计一种基于自适应估计模型的事件触发控制器，改变了状态变量、控制律以及神经网络权值的更新时间。文献[18]针对连续时间线性系统，提出了一种基于事件触发机制的输出反馈自适应控制方法，利用数据重构了不可测状态，通过基于事件的反馈策略减少了控制更新次数。文献[19]针对不确定离散线性系统，提出了一种数据驱动的事件触发输出反馈控制方法，解决了系统在只有输出信息时的自适应最优输出调节问题。文献[20]提出了非线性离散系统的事件触发最优控制方法，通过神经网络辨识系统模型与事件触发机制，实现了神经网络模型参数的非周期性矫正。

复杂过程工业中，生产系统往往由多个工序或多个设备串并联组成，由于不同工序或设备的功能和特性迥异，以及各类检测仪表信息处理快慢特性鲜明，控制系统必然存在采样周期和控制律更新周期不一致的情况。因此复杂工业控制系统往往具有多速率的特性^[21]。此外，随着控制系统的发展，复杂过程工业系统要求采集更精确、更多样化的数据，这导致设备间通讯的内容不仅包含大量系统运行的状态数据，还包含视频、音频和图像等信号。随着工业互联网的发展，各设备间信息交互显著增多，给系统通讯带来了极大的负担。因此，在工业系统控制方法中引入事件触发控制模式，可有效减少系统信息传输量^[22]，符合工业互联网高实时性的要求。

本文针对互联网环境下工业过程多速率控制系统的特点，提出一种事件触发机制下的工业过程多速率模型预测控制方法。其首先将提升技术与模型预测控制(Model Predictive Control, MPC)方法相结合，设计多速率MPC控制器；进而基于Lyapunov稳定性理论，设计了事件触发机制，有效地减少了通信资源和计算资源的消耗；最后以湿式磨矿过程为背景，通过仿真实验验证了所提方法的有效性。

1 多速率模型预测控制器设计

本文以如下的一类连续时间工业过程为被控对象

$ \left\{ \begin{gathered} {\dot{\boldsymbol x}}\left( t \right) = {{\boldsymbol{A}}_c}{\boldsymbol{x}}\left( t \right) + {{\boldsymbol{B}}_c}{\boldsymbol{u}}\left( t \right) \hfill \\ {\boldsymbol{y}}\left( t \right) = {{\boldsymbol{C}}_c}{\boldsymbol{x}}\left( t \right) + {{\boldsymbol{D}}_c}{\boldsymbol{u}}\left( t \right) \hfill \\ \end{gathered} \right. $

(1)

式中： ${\boldsymbol{x}} \in {{\mathbf{R}}^{{n_{\boldsymbol{x}}}}}$ 为过程状态， ${\boldsymbol{u}} \in {{\mathbf{R}}^{{n_{\boldsymbol{u}}}}}$ 为控制输入， ${\boldsymbol{y}} \in {{\mathbf{R}}^{{n_{\boldsymbol{y}}}}}$ 为控制输出； ${n_{\boldsymbol{x}}}$ 、 ${n_{\boldsymbol{u}}}$ 和 ${n_{\boldsymbol{y}}}$ 分别为相应变量的维数； ${{\boldsymbol{A}}_{{c}}}$ 、 ${{\boldsymbol{B}}_{{c}}}$ 、 ${{\boldsymbol{C}}_{{c}}}$ 和 ${{\boldsymbol{D}}_{{c}}}$ 为系统矩阵。

定义 ${T_h}$ 为基周期，控制周期 ${T_a} = a{T_h}$ ，采样周期 ${T_b} = b{T_h}$ ， $a < b$ 且互为质数。为实现过程模型在一个周期内进行描述，定义框架周期 ${T_0}{{ = }}ab{T_h}$ ，为 ${T_a}$ 和 ${T_b}$ 的最小公倍数，具体关系如图1所示。

按照基周期 ${T_h}$ ，将连续系统(1)进行离散化,可得

$ \left\{ {\begin{array}{*{20}{l}} {{\boldsymbol{x}}\left( {k + 1} \right) = {{\boldsymbol{A}}_f}{\boldsymbol{x}}\left( k \right) + {{\boldsymbol{B}}_f}{\boldsymbol{u}}\left( k \right)} \\ {{\boldsymbol{y}}\left( k \right) = {{\boldsymbol{C}}_f}{\boldsymbol{x}}\left( k \right) + {{\boldsymbol{D}}_f}{\boldsymbol{u}}\left( k \right)} \end{array}} \right. $

(2)

式中： ${{{\boldsymbol{A}}} _f} = {{\rm{e}}^{{{{\boldsymbol{A}}} _{{c}}}{T_h}}}$ ， ${{{\boldsymbol{B}}} _f} ={{{\boldsymbol{B}}} _c} \int_0^{{T_h}} {{{\rm{e}}^{{{{\boldsymbol{A}}} _c}t}}{{\rm{d}}t}}$ ， ${{\boldsymbol{C}}_f} = {{\boldsymbol{C}}_c}$ ， ${{\boldsymbol{D}}_{f} } = {{\boldsymbol{D}}_c}$ 。

采用提升技术，以“堆叠”的思想对系统(2)进行变换，将框架周期 ${T_0}$ 内的 $b$ 个控制输入进行向量堆叠，得到增维后的控制输入 $\bar {\boldsymbol{u}}$ ；同时堆叠 $a$ 个控制输出，得到增维后的控制输出 $\bar {\boldsymbol{y}}$ ，即

$ {\overline{\boldsymbol u}}(m) = {L_b}{\boldsymbol{u}}(m{T_0}) = \left[ \begin{gathered} {\boldsymbol{u}}(m{T_a}) \\ {\boldsymbol{u}}(m{T_0} + {T_a}) \\ \vdots \\ {\boldsymbol{u}}(m{T_0} + (b - 1){T_a}) \\ \end{gathered} \right] \in {{\mathbf{R}}^{{N_{\boldsymbol{u}}}}} $

$ {\overline{\boldsymbol y}}(m) = {L_a}{\boldsymbol{y}}(m{T_0}) = \left[ \begin{gathered} {\boldsymbol{y}}(m{T_b}) \\ {\boldsymbol{y}}(m{T_0} + {T_b}) \\ \vdots \\ {\boldsymbol{y}}(m{T_0} + (a - 1){T_b}) \\ \end{gathered} \right] \in {{\mathbf{R}}^{{N_{\boldsymbol{y}}}}} $

式中： $m$ 为框架周期 ${T_0}$ 下的控制拍数， ${N_{\boldsymbol{u}}} = b{n_{\boldsymbol{u}}}$ ， ${N_{\boldsymbol{y}}} = a{n_{\boldsymbol{y}}}$ 。

整理可得提升后的状态空间模型如下

$ \left\{ {\begin{array}{*{20}{l}} {{\boldsymbol{x}}(m + 1) = {\overline{\boldsymbol A}}{\boldsymbol{x}}(m) + {\overline{\boldsymbol B}}{\overline {\boldsymbol{u}}}(m)} \\ {{\overline{\boldsymbol y}}(m) = {\overline{\boldsymbol C}}{\boldsymbol{x}}(m) + {\overline{\boldsymbol D}}{\overline {\boldsymbol{u}}}(m)} \end{array}} \right. $

(3)

式中： $\overline {\boldsymbol{A}},\overline {\boldsymbol{B}},\overline {\boldsymbol{C}},\overline {\boldsymbol{D}}$ 为提升后系统参数矩阵，详细描述可参考文献[21]。

本文采用MPC方法设计控制器，预测时域设为 $p$ ，控制时域设为 $q$ ，在控制时域外，控制量不变，即， ${\boldsymbol{u}}\left( {k + q - 1} \right) = {\boldsymbol{u}}\left( {k + i} \right),i = q,q + 1, \cdots ,p - 1$ 。根据式(3)可得预测模型为

$ \boldsymbol{x}\left(m+i|m\right)=\left\{ \begin{array}{l} {\overline{\boldsymbol A }}^{i}\boldsymbol{x}\left(m\right)+\\ {\displaystyle {\sum} _{\varepsilon =0}^{i-1}{\overline{\boldsymbol A }}^{i-1-\varepsilon }\overline{\boldsymbol B}\overline{\boldsymbol u}\left(m+\varepsilon \right)},\;1 \leqslant i \leqslant q\\ {\overline{\boldsymbol A }}^{i}\boldsymbol{x}\left(m\right)+{\displaystyle {\sum} _{\varepsilon =0}^{q-1}{\overline{\boldsymbol A }}^{i-\varepsilon -1}\overline{\boldsymbol B}\overline{\boldsymbol u}\left(m+\varepsilon \right)}+\\ {\displaystyle {\sum} _{\varepsilon =1}^{p-q}{\overline{\boldsymbol A }}^{p-q-\varepsilon }\overline{\boldsymbol B}\overline{\boldsymbol u}\left(m+q-1\right)},\;q+1 \leqslant i \leqslant p\ \end{array} \right.$

(4)

$ \overline{\boldsymbol y}\left(m+i|m\right)=\left\{ \begin{array}{l} {\overline{\boldsymbol C}}\;{\overline{\boldsymbol A}}^{i}\boldsymbol{x}\left(m\right)+\overline{\boldsymbol D}\overline{\boldsymbol u}\left(m+i\right)+\\ \overline{\boldsymbol C}{\displaystyle {\sum} _{\varepsilon =0}^{i-1}{\overline{A}}^{i-1-\varepsilon }\overline{\boldsymbol B}\overline{\boldsymbol u}\left(m+\varepsilon \right)},1 \leqslant i \leqslant q\\ {\overline{\boldsymbol C}}\;{\overline{\boldsymbol A}}^{i}\boldsymbol{x}\left(m\right)+\overline{\boldsymbol D}\overline{\boldsymbol u}\left(m+q-1\right)+\\ \overline{\boldsymbol C}{\displaystyle {\sum} _{\varepsilon =0}^{q-1}{\overline{\boldsymbol A}}^{i-\varepsilon -1}\overline{\boldsymbol B}\overline{\boldsymbol u}\left(m+\varepsilon \right)}+\\ \overline{\boldsymbol C}{\displaystyle {\sum} _{\varepsilon =1}^{p-q}{\overline{\boldsymbol A}}^{p-q-\varepsilon }\overline{\boldsymbol B}\overline{\boldsymbol u}\left(m+q-1\right)},q+1 \leqslant i \leqslant p\ \end{array} \right.$

(5)

定义 $p$ 步预测输出向量和 $q$ 步输入向量分别如下

$ {\overline{\boldsymbol Y}}\left( {\left. {m + 1} \right|m} \right) = \left[ \begin{gathered} {\overline{\boldsymbol y}}\left( {\left. {m + 1} \right|m} \right) \\ {\overline{\boldsymbol y}}\left( {\left. {m + 2} \right|m} \right) \\[-3pt] \vdots \\ {\overline{\boldsymbol y}}\left( {\left. {m + p} \right|m} \right) \\ \end{gathered} \right]，{\overline{\boldsymbol U}}\left( m \right) = \left[ \begin{gathered} {\overline{\boldsymbol u}}\left( m \right) \\ {\overline{\boldsymbol u}}\left( {m + 1} \right) \\[-3pt] \vdots \\ {\overline{\boldsymbol u}}\left( {m + q - 1} \right) \\ \end{gathered} \right] $

则式(5)改写为

$ {\overline{\boldsymbol Y}}(m + 1\left| m \right.) = {{\boldsymbol{S}}_{\boldsymbol{x}}}{\boldsymbol{x}}(m) + {{\boldsymbol{S}}_{\boldsymbol{u}}}{\overline{\boldsymbol U}}(m) $

(6)

式中：

$ {{\boldsymbol{S}}_{\boldsymbol{x}}} = \left[ \begin{gathered} {\overline{\boldsymbol C}}\;{\overline{\boldsymbol A}} \\ {\overline{\boldsymbol C}}\;{\overline{\boldsymbol A}}^{2} \\ \vdots \\ {\overline{\boldsymbol C}}\;{\overline{\boldsymbol A}}^p \\ \end{gathered} \right], {{\boldsymbol{S}}_{\boldsymbol{u}}} = \\ \left[ {\begin{array}{*{20}{c}} {\overline {\boldsymbol{C}}\;\overline {\boldsymbol{B}}}&{\overline {\boldsymbol{D}}}&{\bf{0}}& \cdots &{\bf{0}}&{\bf{0}}\\ {{\overline{\boldsymbol C}}\;{\overline{\boldsymbol A}}\;\overline {\boldsymbol{B}}}&{\overline {\boldsymbol{C}}\;\overline {\boldsymbol{B}}}&{\overline {\boldsymbol{D}}}& \ldots &{\bf{0}}&{\bf{0}}\\ \vdots & \vdots & \vdots& & \vdots & \vdots \\ {{\overline{\boldsymbol C}}\;{\overline{\boldsymbol A}}^{{{{q}} - 2}}\overline {\boldsymbol{B}}}&{{\overline{\boldsymbol C}}\;{\overline{\boldsymbol A}}^{{{{q}} - 3}}\overline {\boldsymbol{B}}}&{{\overline{\boldsymbol C}}\;{\overline{\boldsymbol A}}^{{{{q}} - 4}}\overline {\boldsymbol{B}}}& \cdots &{\overline {\boldsymbol{C}}\;\overline {\boldsymbol{B}}}&{\overline {\boldsymbol{D}}}\\ {{\overline{\boldsymbol C}}\;{\overline{\boldsymbol A}}^{{{{q}} - 1}}\overline {\boldsymbol{B}}}&{{\overline{\boldsymbol C}}\;{\overline{\boldsymbol A}}^{{{{q}} - 2}}\overline {\boldsymbol{B}}}&{{\overline{\boldsymbol C}}\;{\overline{\boldsymbol A}}^{{{{q}} - 3}}\overline {\boldsymbol{B}}} &\cdots &{{\overline{\boldsymbol C}}\;{\overline{\boldsymbol A}}\;\overline {\boldsymbol{B}}}&{\overline {\boldsymbol{C}}\;\overline {\boldsymbol{B}} + \overline {\boldsymbol{D}}}\\ \vdots & \vdots & \vdots && \vdots & \vdots\\ {{\overline{\boldsymbol C}}\;{\overline{\boldsymbol A}}^{{{{p}} - 1}}\overline {\boldsymbol{B}}}&{{\overline{\boldsymbol C}}\;{\overline{\boldsymbol A}}^{{{{p}} - 2}}\overline {\boldsymbol{B}}}&{{\overline{\boldsymbol C}}\;{\overline{\boldsymbol A}}^{{{{p}} - 3}}\overline {\boldsymbol{B}}} & \cdots &{{\overline{\boldsymbol C}}\;{\overline{\boldsymbol A}}^{{{{p - q}} + 1}}\overline {\boldsymbol{B}}}&{{\overline{\boldsymbol C}}\;{\overline{\boldsymbol A}}^{{{{p - q}}}}\overline {\boldsymbol{B}} + \overline {\boldsymbol{C}}\displaystyle\sum\nolimits_{\varepsilon = 1}^{{{p - q}}} {{{\overline {\boldsymbol{A}}}^{{{p - q - }}\varepsilon }}\overline {\boldsymbol{B}} + \overline {\boldsymbol{D}}} } \end{array}} \right] $

在工业过程中， ${{\boldsymbol{y}}^*}$ 为系统设定值，定义 ${\boldsymbol{\alpha }} = {\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{I}}_{{n_{\boldsymbol{y}}} \times {n_{\boldsymbol{y}}}}}}& \cdots &{{{\boldsymbol{I}}_{{n_{\boldsymbol{y}}} \times {n_{\boldsymbol{y}}}}}} \end{array}} \right]^{\rm{T}}} \in {{\mathbf{R}}^{{N_{\boldsymbol{y}}} \times {n_{\boldsymbol{y}}}}}$ 为将设定值 ${{\boldsymbol{y}}^*}$ 的维度提升至与 $\overline {\boldsymbol{y}}$ 相同的系数矩阵。定义加权因子 ${{\boldsymbol{\varGamma}} _{{\overline{\boldsymbol y}}}}$ 和 ${{\boldsymbol{\varGamma}} _{{\overline{\boldsymbol u}}}}$ 为

$ \begin{split} {{\boldsymbol{\varGamma }}_{{\overline{\boldsymbol y}}}}: = {{\rm{diag}}} \left\{ {{\varGamma _{{{\overline y}_1}}},{\varGamma _{{{\overline y}_2}}}, \cdots ,{\varGamma _{{{\overline y}_{{N_{\boldsymbol{y}}}}}}}} \right\} \in {{\mathbf{R}}^{{N_{\boldsymbol{y}}} \times {N_{\boldsymbol{y}}}}}\\ {{\boldsymbol{\varGamma }}_{{\overline{\boldsymbol u}}}}: = {{\rm{diag}}} \left\{ {{\varGamma _{{{\overline u}_1}}},{\varGamma _{{{\overline u}_2}}}, \cdots ,{\varGamma _{{{\overline u}_{{N_{\boldsymbol{u}}}}}}}} \right\} \in {{\mathbf{R}}^{{N_{\boldsymbol{u}}} \times {N_{\boldsymbol{u}}}}} \end{split} $

其中， ${\rm{diag}}\left\{ \cdot \right\}$ 为对角矩阵。

实际工业过程中，由于控制输入的大小(如，电振机频率)直接影响生产能耗，因此在保证系统输出能够跟踪设定值的前提下，希望控制输入 $\overline {\boldsymbol{U}}$ 尽可能小，故定义性能指标函数 $J$ 为

$ J = \sum\nolimits_{i = 1}^p {{{\left\| {{{\boldsymbol{\varGamma}} _{{\overline{\boldsymbol Y}}}}( {{\overline{\boldsymbol Y}}\left( {m + i\left| m \right.} \right) - {\boldsymbol{\delta }}{{\boldsymbol{Y}}^*}\left( {m + i} \right)} )} \right\|}^2}} + {\left\| {{{\boldsymbol{\varGamma}} _{{\overline{\boldsymbol U}}}}{\overline{\boldsymbol U}}\left( m \right)} \right\|^2} $

(7)

式中： $\left\| {\;} \right\|$ 为矩阵的范数， ${\boldsymbol{\delta }} = {\left[ {{{\boldsymbol{\alpha }}^{{\rm{T}}} } \cdots {{\boldsymbol{\alpha }}^{{\rm{T}}} }} \right]^{{\rm{T}}} } \in {{\mathbf{R}}^{p{N_{\boldsymbol{y}}} \times {n_{\boldsymbol{y}}}}}$ 表示将 ${{\boldsymbol{Y}}^*}$ 的维度提升至与 $\overline {\boldsymbol{Y}}$ 相同的系数矩阵， ${{\boldsymbol{Y}}^*}\left( {m + 1} \right) = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{y}}^*}\left( {m + 1} \right)}&{{{\boldsymbol{y}}^*}\left( {m + 2} \right)}& \cdots \end{array}} \right.{\left. {{{\boldsymbol{y}}^*}\left( {m + p} \right)} \right]^{\rm{T}}}$ ， ${{\boldsymbol{\varGamma}} _{{\overline{\boldsymbol Y}}}}$ 和 ${{\boldsymbol{\varGamma}} _{{\overline{\boldsymbol U}}}}$ 分别为预测控制输出和控制输入的加权因子，其中，

$ {\boldsymbol{\varGamma} _{{\overline{\boldsymbol Y}}}}: = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{\varGamma} _{{\overline{\boldsymbol y}}}}}&{{\boldsymbol{\varGamma} _{{\overline{\boldsymbol y}}}}}& \cdots &{{\boldsymbol{\varGamma} _{{\overline{\boldsymbol y}}}}} \end{array}} \right] \in {{\mathbf{R}}^{{N_{\boldsymbol{y}}} \times p{N_{\boldsymbol{y}}}}} $

$ {\boldsymbol{\varGamma} _{{\overline{\boldsymbol U}}}}: = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{\varGamma} _{{\overline{\boldsymbol u}}}}}&{{\boldsymbol{\varGamma} _{{\overline{\boldsymbol u}}}}}& \cdots &{{\boldsymbol{\varGamma} _{{\overline{\boldsymbol u}}}}} \end{array}} \right] \in {{\mathbf{R}}^{{N_{\boldsymbol{u}}} \times q{N_{\boldsymbol{u}}}}} $

则MPC优化问题转变为

$ \mathop {\min }\limits_{{\overline{\boldsymbol U}}\left( m \right)} J({\boldsymbol{x}}(m),{\overline{\boldsymbol U}}(m),p,q) $

(8)

为解决上述优化问题，定义辅助变量

$ {\boldsymbol{\sigma }}: = \left[ \begin{gathered} {{\boldsymbol{\varGamma }}_{{\overline{\boldsymbol Y}}}}({\overline{\boldsymbol Y}}(m + 1\left| m \right.) - {\boldsymbol{\delta }}{{\boldsymbol{Y}}^*}(m + 1)) \\ {{\boldsymbol{\varGamma }}_{{\overline{\boldsymbol U}}}}{\overline{\boldsymbol U}}(m) \\ \end{gathered} \right] $

(9)

则性能指标函数 $J$ 改写为

$ J = {{\boldsymbol{\sigma }}^{\rm{T}}}{\boldsymbol{\sigma }} $

(10)

将式(6)代入式(9)，可得

$ {\boldsymbol{\sigma }} = \left[ \begin{gathered} {{\boldsymbol{\varGamma}} _{{\overline{\boldsymbol Y}}}}{{\boldsymbol{S}}_{\boldsymbol{u}}} \\ {{\boldsymbol{\varGamma}} _{{\overline{\boldsymbol U}}}} \\ \end{gathered} \right]{\overline{\boldsymbol U}}(m) - \left[ \begin{gathered} {{\boldsymbol{\varGamma}} _{{\overline{\boldsymbol Y}}}}({\boldsymbol{\delta }}{{\boldsymbol{Y}}^*}(m + 1) - {{\boldsymbol{S}}_{\boldsymbol{x}}}{\boldsymbol{x}}(m)) \\ {\bf{0}} \\ \end{gathered} \right] $

(11)

对 $J$ 求极值，即 $\dfrac{{{{\rm{d}}} {{\boldsymbol{\sigma }}^{{\rm{T}}} }{\boldsymbol{\sigma }}}}{{{{\rm{d}}} {\overline{\boldsymbol U}}(m)}} = 0$ ，可得到所需的最优控制序列 ${\overline{\boldsymbol U}}(m)$

$ {\overline{\boldsymbol U}}(m) = {\boldsymbol{K}}({\boldsymbol{\delta }}{{\boldsymbol{Y}}^*}(m + 1) - {{\boldsymbol{S}}_{\boldsymbol{x}}}{\boldsymbol{x}}(m)) $

(12)

式中： ${\boldsymbol{K}} = {({\boldsymbol{S}}_{\boldsymbol{u}}^{{\rm{T}}} {\boldsymbol{\varGamma}} _{\overline {\boldsymbol{Y}}}^{{\rm{T}}} {{\boldsymbol{\varGamma}} _{\overline {\boldsymbol{Y}}}}{{\boldsymbol{S}}_{\boldsymbol{u}}} + {\boldsymbol{\varGamma}} _{\overline {\boldsymbol{U}}}^{{\rm{T}}} {{\boldsymbol{\varGamma}} _{\overline {\boldsymbol{U}}}})^{ - 1}}{\boldsymbol{S}}_{\boldsymbol{u}}^{{\rm{T}}} {\boldsymbol{\varGamma}} _{\overline {\boldsymbol{Y}}}^{{\rm{T}}} {{\boldsymbol{\varGamma}} _{\overline {\boldsymbol{Y}}}}$ 。

由于在实际工业过程中，设定值一般由工艺工程师根据原料和生产需要进行定期调整，具有慢时间尺度的特性，故在一定时间内保持不变，因此可假设 ${{\boldsymbol{Y}}^*}(m)$ = ${{\boldsymbol{Y}}^*}(m + 1)$ ，从而得到控制律

$ {\overline{\boldsymbol U}}(m) = {\boldsymbol{K}}({\boldsymbol{\delta }}{{\boldsymbol{Y}}^*}(m) - {{\boldsymbol{S}}_{\boldsymbol{x}}}{\boldsymbol{x}}(m)) $

(13)

2 事件触发机制

工业互联网环境下，每一时刻都求解控制律并进行更新将带来较大的计算和通信负担。为此本文引入事件触发机制，首先定义一个单调递增的子序列 $\left\{ {{k_s}} \right\}_{s = 0}^\infty $ 作为采样时刻(或事件触发时刻)，控制器仅在离散点 ${k_0},{k_1},{k_2} \cdots$ 更新。

定义跟踪误差如下

$ {\boldsymbol{d}}\left( k \right) = {\boldsymbol{y}}\left( k \right) - {{\boldsymbol{y}}^*}\left( k \right) $

(14)

式中： $k$ 为基周期 ${T_h}$ 下的控制拍数。

并定义 ${\boldsymbol{v}}\left( k \right)$ 为

$ {\boldsymbol{v}}\left( k \right) = {\boldsymbol{y}}\left( k \right) - {{\boldsymbol{y}}^*}\left( {{k_s}} \right) $

(15)

式中： ${{\boldsymbol{y}}^*}\left( {{k_s}} \right)$ 为第 $s$ 个触发时刻的设定值。

定义事件触发误差如下

$ {\boldsymbol{e}}\left( k \right) = {\boldsymbol{v}}\left( k \right) - {\boldsymbol{d}}\left( k \right) $

(16)

对于系统(2)，定义事件触发阈值为

$ {{\boldsymbol{e}}_{\rm{T}}} = \left( { {1/\beta } - 1} \right)\left\| {{\boldsymbol{d}}\left( k \right)} \right\| $

(17)

式中： $\beta $ 为待设计的系数。本文提出两个事件触发条件，组成一个事件触发条件组

$ \left\| {{\boldsymbol{e}}\left( k \right)} \right\| > {{\boldsymbol{e}}_{\rm{T}}} $

(18)

$ \left\| {{\boldsymbol{d}}\left( {k + 1\left| k \right.} \right)} \right\| > \beta \left\| {{\boldsymbol{e}}\left( k \right)} \right\| + \beta \left\| {{\boldsymbol{d}}\left( k \right)} \right\| $

(19)

式中： ${{\boldsymbol{e}}_{\rm{T}}}$ 为所设计的事件触发阈值， ${\boldsymbol{d}}\left( {k + 1\left| k \right.} \right)$ 为下一时刻的跟踪误差估计值。式(18)描述了触发误差与触发阈值的数量关系；式(19)描述下一时刻跟踪误差估计值与上一触发时刻跟踪误差值和触发误差的关系。

当事件触发条件式(18)和式(19)至少有一个满足时，事件被触发，更新控制律，并经零阶保持器(Zero-Order Holder, ZOH)保持。当式(18)和式(19)都不满足时，事件未被触发，控制律不更新。此时，系统的控制输入是ZOH中保存的控制律。下面给出系统稳定性分析。

定理1 　控制器仅当不等式(18)或不等式(19)成立时更新控制律，反之，不更新控制策略，则该系统在平衡点处是Lyapunov稳定的。

证明 　定义该离散时间系统的Lyapunov函数为

$ L\left( k \right) = {{\boldsymbol{d}}^{\rm{T}}}\left( k \right){{\boldsymbol{d}}^{{\rm{T}}} }\left( k \right) + {{\boldsymbol{u}}^{\rm{T}}}\left( k \right){{\boldsymbol{u}}^{\rm{T}}}\left( k \right) $

(20)

其一阶差分方程为

$ \begin{split} \Delta L\left( k \right) =& {{\boldsymbol{d}}^{\rm{T}}}\left( {k + 1} \right){{\boldsymbol{d}}^{\rm{T}}}\left( {k + 1} \right) - {{\boldsymbol{d}}^{\rm{T}}}\left( k \right){{\boldsymbol{d}}^{\rm{T}}}\left( k \right) +\\ & {{\boldsymbol{u}}^{\rm{T}}}\left( {k + 1} \right){{\boldsymbol{u}}^{\rm{T}}}\left( {k + 1} \right) - {{\boldsymbol{u}}^{\rm{T}}}\left( k \right){{\boldsymbol{u}}^{\rm{T}}}\left( k \right) \end{split} $

(21)

当触发条件式(18)和式(19)均不满足时，事件未被触发，控制律不更新，则Lyapunov函数的一阶差分方程可简化为

$ \Delta L\left( k \right) = {{\boldsymbol{d}}^{{\rm{T}}} }\left( {k + 1} \right){{\boldsymbol{d}}^{\rm{T}}}\left( {k + 1} \right) - {{\boldsymbol{d}}^{\rm{T}}}\left( k \right){{\boldsymbol{d}}^{\rm{T}}}\left( k \right) $

(22)

由于式(19)不满足，故

$ \Vert \boldsymbol{d}\left(k+1|k\right)\Vert \leqslant \beta \Vert \boldsymbol{e}\left(k\right)\Vert +\beta \Vert \boldsymbol{d}\left(k\right)\Vert $

(23)

将式(23)代入式(21)，可得

$ \Delta L\left(k\right) \leqslant {\left(\beta \Vert \boldsymbol{e}\left(k\right)\Vert +\beta \Vert \boldsymbol{d}\left(k\right)\Vert \right)}^{2}-{\Vert \boldsymbol{d}\left(k\right)\Vert }^{2} $

(24)

由于式(18)不满足，可得

$ \Vert \boldsymbol{e}\left(k\right)\Vert \leqslant \left(1/\beta -1\right)\Vert \boldsymbol{d}\left(k\right)\Vert $

(25)

将式(25)代入式(24)中，可以得到

$ \Delta L\left(k\right) \leqslant 0 $

(26)

由上述分析可知，当事件未被触发时，系统是Lyapunov稳定的。当触发条件式(18)和式(19)至少有一个满足时，事件被触发，系统的稳定性由MPC方法来保证。

3 仿真实验 3.1 磨矿过程工艺流程

为了验证所提方法的有效性，本文以工业湿式磨矿过程为背景开展仿真实验。工业湿式磨矿过程为典型的矿物分选过程，其将大颗粒矿石研磨成小颗粒，进而通过重力分选，将有用矿物从脉石中分离出来。本文以一段闭路磨矿过程为对象，其工艺流程如图2所示，图中实线表示物质流，虚线表示信息流。主要包括球磨机和水力旋流器两个主要磨选设备。磨矿生产过程中，原矿首先和一定比例的水被输送至球磨机，通过球磨机自身旋转带动内置钢球对矿石进行研磨。研磨后的矿浆从球磨机出口处排出流入泵池，经稀释后由底流泵打入水力旋流器进行粒度分级，形成含有细颗粒物的溢流矿浆和含有粗颗粒物的底流矿浆。溢流矿浆为产品进入下一工序，底流矿浆返回至球磨机再进行研磨，形成循环负荷。

磨矿过程通常设置磨机给矿和泵池补水两个基础回路。其中，磨机给矿回路通过调节电振机给矿频率 $f$ (Hz)来实现给矿量 $o$ (t/h)跟踪设定值 ${o^*}$ (t/h)；泵池补水回路通过调节补水阀门开度 $l$ (%)来实现补水量 $w$ (m³/h)跟踪设定值 ${w^*}$ (m³/h)。由此可得，设定值 ${{\boldsymbol{y}}^{\boldsymbol{*}}} = $ ${\left[ {y_1^*,y_2^*} \right]^{\rm{T}}} = {\left[ {{o^*},{w^*}} \right]^{{\rm{T}}} }$ 。

根据文献[23]，磨矿过程模型用式(27)来模拟

$ \left\{ {\begin{array}{*{20}{l}} {\boldsymbol{\dot x}\left( t \right) = \left[ {\begin{array}{*{20}{c}} { - 0.065\;4}&0\\ 0&{ - 0.082\;3} \end{array}} \right]\boldsymbol{x}\left( t \right) + }\\ {\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {0.145\;7}&0\\ 0&{0.180\;7} \end{array}} \right]\boldsymbol{u}\left( t \right)}\\ {\boldsymbol{y}\left( t \right) = \left[ {\begin{array}{*{20}{l}} 1&0\\ 0&1 \end{array}} \right]\boldsymbol{x}\left( t \right)} \end{array}} \right.$

(27)

式中： ${\boldsymbol{y}} = {\left[ {{y_1},{y_2}} \right]^{\rm{T}}} = {\left[ {o,w} \right]^{{\rm{T}}} }$ ， ${\boldsymbol{u}} = {\left[ {{u_1},{u_2}} \right]^{\rm{T}}} = {\left[ {f,l} \right]^{{\rm{T}}} }$ 。

3.2 仿真实验研究

为了验证本文所提方法，将电振机给矿频率 $f$ 和补水阀门开度 $l$ 的控制周期 ${T_a}$ 设置为2 s，给矿量 $o$ 和补水量 $w$ 的采样周期 ${T_b}$ 设置为3 s。根据本文所提的方法，可以得到基周期 ${T_h}$ 为1 s，框架周期 ${T_0}$ 为6 s，事件触发机制中参数 $\beta $ 设为0.9。在实际工业过程中，由于物料的特性并不会发生突变，因此设定值往往不会频繁变化，为模拟实际磨矿过程中设定值的调整，设置其每300 s变化一次，预测时域和控制时域均设置为1。

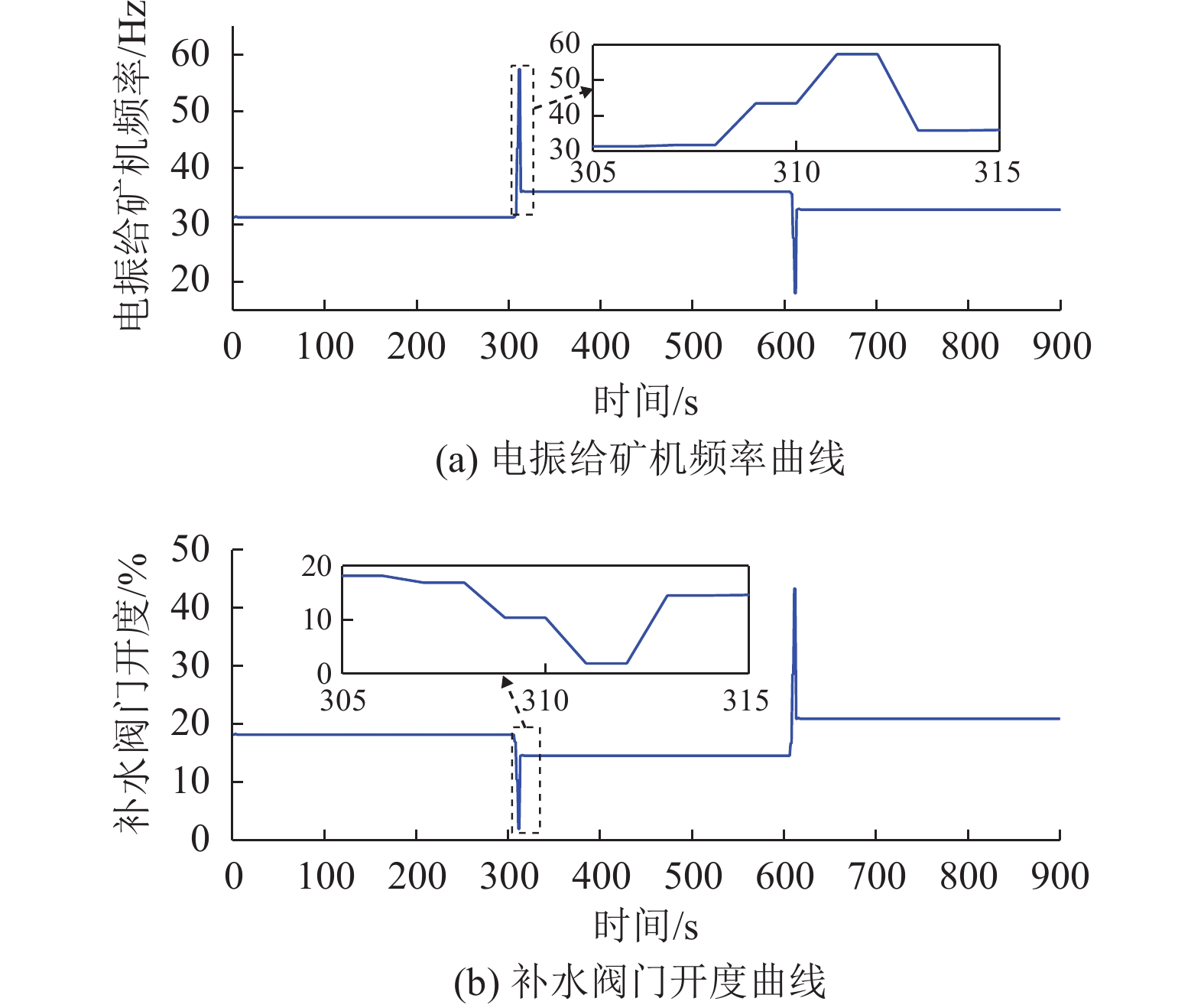
采用本文方法的控制效果如图3～5所示。图3(a)和(b)分别给出了给矿量和补水量的控制曲线，其中标注“○”的点为触发时刻；图4是电振机给矿频率和补水阀门开度的变化曲线。图5给出给矿量和补水量的控制误差。

为进一步验证本文方法的有效性，本文加快给矿量设定值和补水量设定值的变化，每90 s变化一次，以验证当设定值频繁变化时算法的有效性。仿真结果如图6所示。可以看出，本文所提算法仍可获得较好的效果。实际上，当设定值每一时刻都在变化时，事件也每一时刻都在触发，此时事件触发接近于传统时间触发。

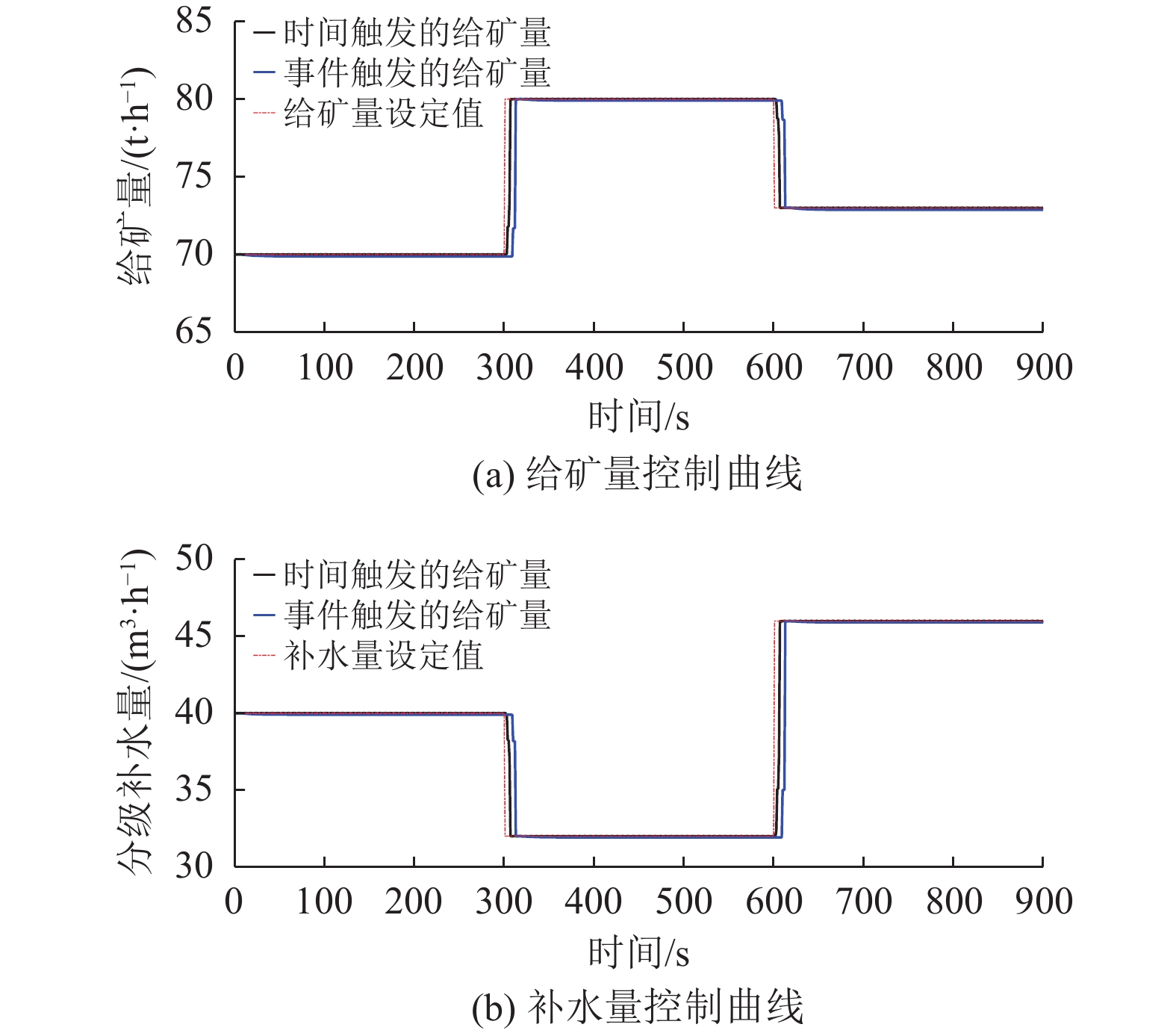
图7为事件触发控制与传统时间触发控制下的给矿量和补水量控制曲线，其中时间触发控制律由式(13)给出，与事件触发控制方法相同。图8给出两种模式下的控制律更新频次。时间触发控制方法要求控制器在每个框架周期 ${T_0} = 6\;{\rm{s}}$ 都需要进行一次计算并更新控制律，则在900 s的仿真时间里，时间触发需要更新150次，而事件触发方法则在同样仿真时间里仅更新了5次，但仍可以有效地跟踪设定值。由此可以看出，本文所提方法能够以较少的更新次数获得良好的跟踪效果。

4 结语

本文针对一类多速率工业过程，创新性地将模型预测与提升技术、事件触发方法相结合，提出了一种事件触发机制下的工业过程多速率模型预测控制方法。该方法通过提升技术构建多速率系统模型，采用MPC设计控制器以跟踪设定值，并引入事件触发机制，减小了信息的计算量和传输量。以磨矿过程为对象的仿真表明该方法能够在维持控制系统性能的前提下，显著减少控制器的更新次数，对工业互联网环境下控制器的设计具有一定的参考价值。