车辆路径问题(Vehicle Routing Problem,VRP)由Dantzig和Ramser于1959年首次提出^[1]，VRP作为经典的组合优化问题，得到了广大学者的研究。带容量的车辆路径问题(Capacitated Vehicle Routing Problem, CVRP)是VRP的一类，广泛存在交通运输、物流配送等方面，同时，当今社会推行绿色低碳发展，绿色车辆路径问题受到了重视。在上述背景下，研究绿色带容量的车辆路径问题(Green Capacitated Vehicle Routing Problem, GCVRP)具有重要的现实意义。由于VRP为NP-hard问题，而VRP可归约为GCVRP，故GCVRP也属于NP-hard问题，对其展开研究具有较大的理论价值。

VRP的求解方法可以分为两类，一类为智能优化算法，如遗传算法、蚁群算法和禁忌搜索算法等^[2-4]，该类算法通过建立问题的排序模型进行求解，一般不能保证得到全局最优解以及无法判断所求解的优劣程度；另一类为精确算法，如分支定界、列生成和拉格朗日松弛算法等^[5-10]，该类算法通过建立问题严格的数学模型，能在合理时间内求得小规模问题最优解，针对大规模问题，该类算法能在合理时间内求得问题的精确下界，由于该类算法所求解为问题最优解或逼近最优解的下界，能较大程度保证解的求解质量，同时求解时间也基本合理。

近年来，相关学者对VRP及其拓展问题的精确算法或基于精确算法的混合算法进行了研究。Bouzid等^[11]针对CVRP，以最小化路径成本为优化目标，建立了整数规划模型，并提出一种拉格朗日分裂(Lagrangian Split, LS)与变邻域搜索(Variable Neighbourhood Search, VNS)结合的混合算法进行求解。Singh等^[5]针对具有模糊需求的CVRP，建立了该问题的数学模型，并以最小化成本为优化目标，提出一种分支定界算法(Branch and Bound, B&B)进行求解。Lysgaard等^[6]针对累积容量车辆路径问题(Cumulative Capacitated Vehicle Routing Problem, CCVRP)，建立了问题的集划分模型，以最小化路径总成本为优化目标，采用(Branch-and-Cut-and-Price, BCP)进行求解。Majid等^[7]针对随机需求的车辆路径问题(Vehicle Routing Problem with Stochastic Demands, VRPSD)，建立了该问题的数学模型，以最小化总费用为优化目标，采用整数L形(L-shaped)算法在分支切割框架下求解VRPSD，实验结果验证了所提算法的有效性。Christiansen等^[8]针对VRPSD，以最小化成本为求解目标，提出了一种分支定价算法(Branch-and-price, B&P)进行求解。

当今社会持续推进节能减排，坚持绿色发展，考虑燃油消耗和碳排放等因素的绿色车辆路径问题(Green Vehicle Routing Problem, GVRP)受到了重视。Andelmin等^[9]针对求解目标为最小化行驶总距离的GVRP，并将该问题建模为集合划分问题，提出了一种结合K-路(K-path)切割的列生成(Column Generation, CG)算法进行求解。Dabia等^[10]研究污染路径问题(Pollution-routing Problem, PRP)，以最小化运送成本为求解目标，运用CG算法对主问题进行了求解，并提出一种定制的标记算法解决了定价问题，实验结果验证了所提算法的有效性。Çağrı等^[12]提出了GCVRP的混合整数规划模型(Mixed Integer Programming, MIP)，并以最小化行驶距离为求解目标，同时提出了一种基于模拟退火(Simulated Annealing, SA)的精确解方法进行求解，作者运用改进B&P算法改进下界，并引用了一种基于SA的启发式算法来获得上界，实验结果验证了所提算法的有效性。Qiu等^[13]研究碳排放限额交易下的污染生产路径问题(Pollution Production-routing Problem, PPRP)，建立了该问题的数学模型并以最小化运营成本为求解目标，提出一种分支定价启发式算法进行求解，仿真实验证明了该模型具有降低二氧化碳排放水平和运营成本的潜力。由文献调研可知，目前求解GCVRP的精确算法或与精确算法相结合的算法相对较少。

拉格朗日松弛算法(Lagrange Relaxation, LR)是一种求解复杂组合优化问题的有效方法，LR主要思想是将问题的难约束引入目标函数得到松弛问题，再通过不断更新迭代乘子，逐步求得松弛问题的解。运用传统LR求解GCVRP，往往只能求得问题的下界，该下界一般为不可行解。因此，本文综合LR和启发式算法优势，采用两者相结合的算法求解GCVRP，首先运用LR求得问题下界，再根据问题性质，设计相应启发式算法对下界进行修复及优化，得到问题的上界，通过上界和下界的间隙(Gap)，可以衡量算法性能，是一种求解GCVRP的有效方法。

综上，本文针对实际生活中广泛存在的GCVRP，建立以最小化运输成本为优化目标的混合整数规划模型，并提出一种改进拉格朗日算法进行求解，具体为运用拉格朗日松弛算法得到GCVRP的松弛问题，进而得到原问题的对偶模型，并采用一种次梯度法求解该对偶模型，得到原问题的一个下界；然后，采用修复算法及邻域搜索算法对下界进行修复和优化，得到原问题的一个上界。最后，通过上下界的间隙大小以及对比Gurobi求解器所求解来衡量所提算法的有效性。

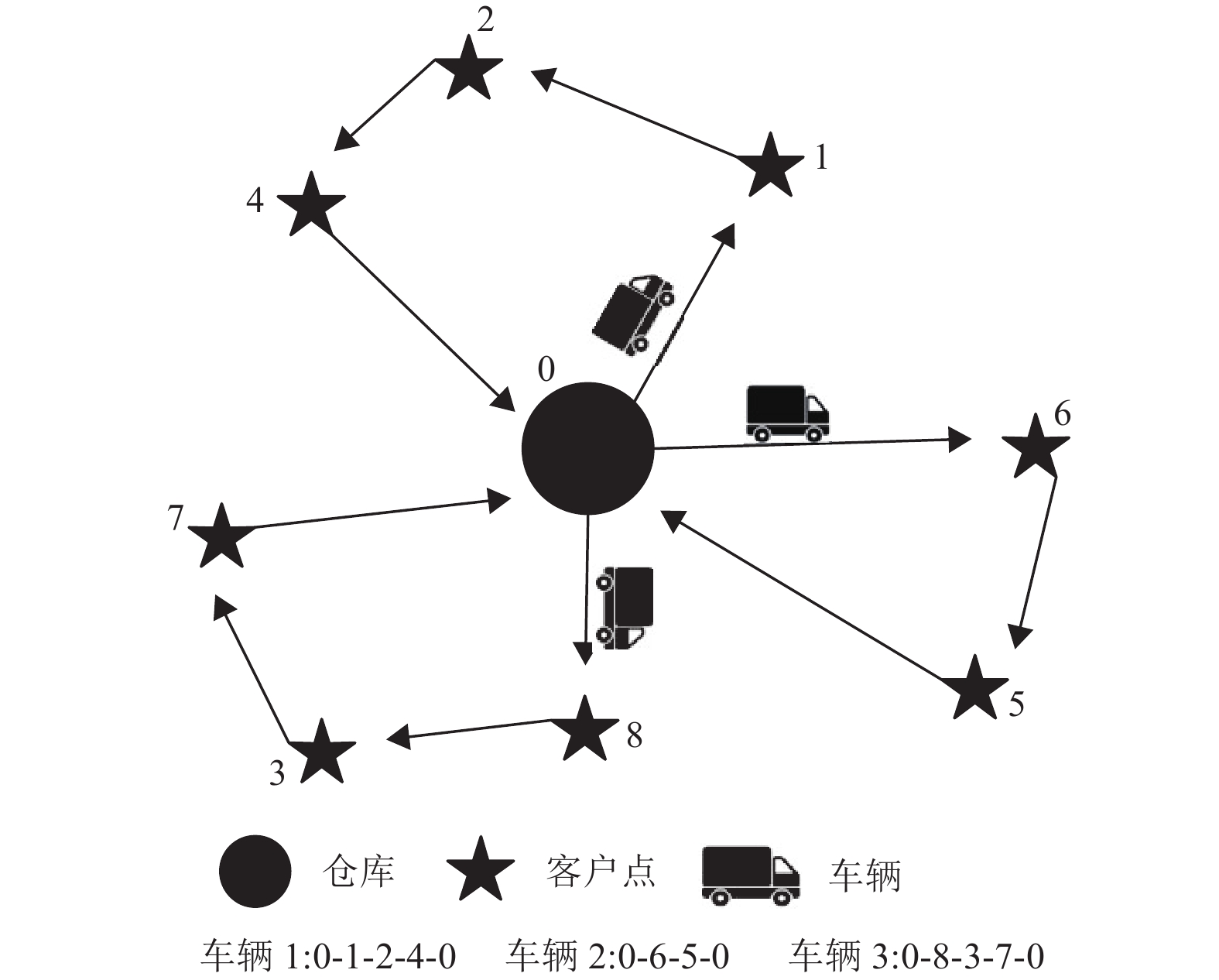
1 GCVRP问题描述与数学模型 1.1 GCVRP问题描述

GCVRP是在CVRP的基础上进一步考虑了绿色因素，该问题建立在已知仓库和客户点坐标(坐标以km为单位)、客户需求及车辆载重条件下，合理调度仓库中的车辆为客户送货，使运输费用最小。图1为问题示意图。

问题相关假设如下：

(1) 仓库内所有车辆均参与配送；

(2) 每辆车仅执行一次配送任务；

(3) 车辆从仓库出发，完成服务后返回原仓库；

(4) 每个客户只能被一辆车服务一次；

(5) 每辆车配送的货物总量不能超过其载重；

(6) 车辆在配送过程中保持匀速行驶，忽略道路等因素对车辆的影响。

GCVRP相关符号定义见表1。

1.2 GCVRP混合整数规划模型

目标函数

$ \begin{split} {\rm{min}}{{Z}}=&\sum\nolimits_{m = 1}^M {\sum\nolimits_{i = 0}^N {\sum\nolimits_{j = 0}^N {{c_1}{x_{mij}}{d_{ij}}} } } + \sum\nolimits_{m = 1}^M {\sum\nolimits_{j = 0}^N {{c_2}{x_{m0j}}} } + \hfill \\ & \sum\nolimits_{m = 1}^M {\sum\nolimits_{i = 0}^N {\sum\nolimits_{j = 0}^N {{c_m}{E_{ij}}} } } {x_{mij}} \hfill \\[-15pt] \end{split} $

(1)

约束条件：

$ \sum\nolimits_{m = 1}^M {\sum\nolimits_{j = 1}^N {{x_{m0j}}} } = \sum\nolimits_{m = 1}^M {\sum\nolimits_{j = 1}^N {{x_{mj0}}} } $

(2)

$ \sum\nolimits_{j = 1}^N {{x_{m0j}}} = \sum\nolimits_{j = 1}^N {{x_{mj0}}} = 1,\forall m \in C $

(3)

$ \sum\nolimits_{m = 1}^M {\sum\nolimits_{i = 0}^N {{x_{mij}}} } = 1,i \ne j,\forall j \in V\backslash \{ 0\} $

(4)

$ \sum\nolimits_{m = 1}^M {\sum\nolimits_{j = 0}^N {{x_{mij}}} } = 1,i \ne j,\forall i \in V\backslash \{ 0\} $

(5)

$ \sum\nolimits_{m = 1}^M {\sum\nolimits_{i = 0}^N {\sum\nolimits_{j = 0}^N {{x_{mij}}} } } = 0,i = j $

(6)

$ \sum\nolimits_{i = 0}^N {{x_{mij}}} = \sum\nolimits_{i = 0}^N {{x_{mji}}} ,i \ne j,\forall m \in C,\forall j \in V\backslash \{ 0\} $

(7)

$ \sum\nolimits_{i = 0}^N {\sum\nolimits_{j = 0}^N {{x_{mij}} \cdot {q_i}} } \leqslant Q,i \ne j,\forall m \in C $

(8)

$ \begin{gathered} {u_i} - {u_j} + 1 - N(1 - {x_{mij}}) \leqslant 0, \hfill \\ i \ne j,\forall m \in C,\forall i \in V\backslash \{ 0\} ,\forall j \in V\backslash \{ 0\} \hfill \\ \end{gathered} $

(9)

$ \sum\nolimits_{i = 0}^N {\sum\nolimits_{j = 0}^N {{x_{mij}}} } {q_i} = \sum\nolimits_{j = 1}^N {{w_{m0j}}{x_{m0j}}} ,\forall m \in C $

(10)

$ \sum\nolimits_{j = 0}^N {{w_{mj0}}} = 0,\forall m \in C $

(11)

$ \begin{gathered} \sum\nolimits_{i = 0}^N {{w_{mij}}{x_{mij}}} - {q_j}\sum\nolimits_{i = 0}^N {{x_{mij}}} = \sum\nolimits_{i = 0}^N {{w_{mji}}{x_{mji}}} , \hfill \\ i \ne j,\forall j \in V\backslash \left\{ 0 \right\},\forall m \in C \hfill \\ \end{gathered} $

(12)

$ {w_{mij}} \geqslant 0,\forall i \in V,\forall j \in V,\forall m \in C $

(13)

$ \begin{array}{l} {x}_{mij}=\left\{ {\begin{array}{*{20}{l}}{1,}& {若仓库的第m辆车从节点i移动到节点j} \\ {0,}& {其他}\end{array}} \right.\\ i\ne j,\forall i\in V,\forall j\in V,\forall m\in C\end{array} $

(14)

其中：式(1)为目标函数；式(2)要求从仓库出入车辆数目相等；式(3)要求仓库内所有车均参与配送，且配送完返回原仓库；式(4)~(6)要求每个客户只能被一辆车服务一次；式(7)为流平衡约束；式(8)要求仓库的每辆车的载货量不能超过其额定载重；式(9)为MTZ子环消除约束；式(10)表示车辆从仓库出发时的载货量等于所服务客户的总需求量；式(11)表示车辆完成服务任务，返回仓库的载货量为0；式(12)表示某辆车服务完当前客户点后的货物量等于从该客户点离开的货物量；式(13)和(14)为决策变量。

1.3 碳排放量计算方法

车辆行驶过程中的碳排放与燃油的消耗直接相关，影响燃油消耗的因素较多，计算也相对复杂。本文在计算碳排放量上，采用文献[14-16]中的计算方法，相关参数定义见表2。计算公式为

$ {E_{ij}} = e\tau (\zeta {N_0}{V_s} + \gamma W\alpha v + \gamma {w_{mij}}\alpha v + \gamma \beta {v^3}){d_{ij}}/v $

(15)

式中： $ \beta = 0.5{C_d}\rho A $ ， $ \tau = \varphi /\mu \psi $ ， $ \alpha = a + g\sin \theta + g{C_r}\cos \theta $ ， $ \gamma = 1/1\;000\varepsilon \eta $ 。

2 改进拉格朗日松弛算法

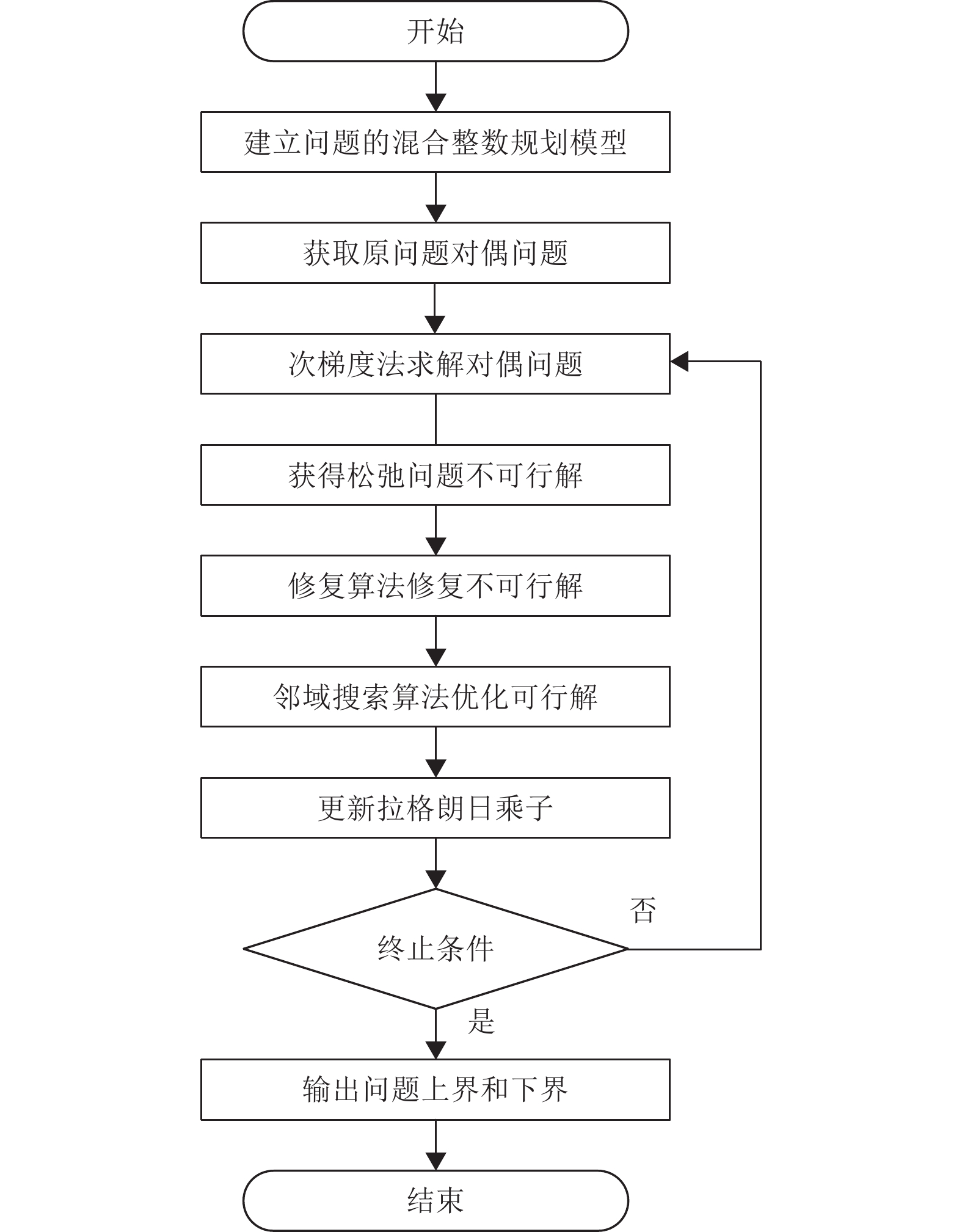
本节针对上节所提问题模型，提出一种结合拉格朗日松弛算法与启发式算法的改进拉格朗日松弛算法进行求解。GCVRP求解流程如图2所示。

2.1 松弛载重约束

由于上节所提GCVRP具有NP难属性，直接求解其最优解非常困难，但求取该问题的下界较为简单。LR是一种求解问题下界的有效方法，通过松弛问题中的难约束，可以大大减小问题的求解难度。通过对GCVRP进行分析，车辆的载重约束(8)影响了车辆的行驶距离，会影响目标值的求取，松弛这条约束会使原问题容易求解。本节将约束条件(8)松弛到目标函数中，得到拉格朗日松弛模型为

$ \begin{split} L(\lambda )=&\sum\nolimits_{m = 1}^M {\sum\nolimits_{i = 0}^N {\sum\nolimits_{j = 0}^N {{c_1}{x_{mij}}{d_{ij}}} } } + \sum\nolimits_{m = 1}^M {\sum\nolimits_{j = 0}^N {{c_2}{x_{m0j}}} } + \hfill \\ & \sum\nolimits_{m = 1}^M {\sum\nolimits_{i = 0}^N {\sum\nolimits_{j = 0}^N {{c_m}{E_{ij}}} } } {x_{mij}} + \\ & \sum\nolimits_{m = 1}^M {{\lambda _m}\left(\sum\nolimits_{i = 0}^N {\sum\nolimits_{j = 0}^N {{x_{mij}} {q_i}} } - Q\right)} \\[-15pt] \end{split} $

(16)

$ {\rm{s}}.{\rm{t}}.(2) \sim (7)、(9) \sim (14)以及 {\lambda _m} \geqslant 0,\forall m \in C $

式中： $ {\lambda _m} \in \lambda = \{ {\lambda _1}, \cdot \cdot \cdot ,{\lambda _m}\} $ ， $ {\lambda _m} $ 是拉格朗日乘子，最大化 $ L(\lambda ) $ 可以求解拉格朗日对偶(Lagrange dual,LD)问题，如下所示。

$ \mathop {\max }\limits_{\lambda \in [0, + \infty )} L(\lambda ) $

(17)

$ {\rm{s}}.{\rm{t}}.(2) \sim (7)、(9) \sim (14)以及 {\lambda _m} \geqslant 0,\forall m \in C $

通过求解LD问题可以得到原问题的一个下界。

2.2 构造可行解

求解对偶问题所得解一般是不可行解，因为可能违反车辆的载重约束条件，因此需要先对不可行解进行修复，得到原问题的可行解，再运用局部搜索操作对可行解进行优化，得到原问题高质量解。本小节采用修复算法和邻域搜索算法对不可行解进行修复及优化。

2.2.1 修复算法

1) 解的转化。

上述不可行解为二进制编码解，需要转化成排序解。转化方法为：设不可行解为 $ {x_{m0{j_1}}} = 1 $ 、 $ {x_{m{j_1}{j_2}}} = 1 $ 、 $ {x_{m{j_2}0}} = 1 $ ，其表示车辆 $ m $ 从仓库出发，依次服务完客户 $ {j_1} $ 、 $ {j_2} $ ，再回到仓库，则相应的排序解为 $ {\varPi _m} = \left\{ {0,{j_1},{j_2},0} \right\} $ ，表示意义与二进制编码解相同，多个客户点转化方法相同。

2) 修复不可行解。

针对上述获得的不可行解，运用以下算法进行修复，设车辆数为 $ M $ ，车辆编号为 $ m $ ，算法步骤如下：

(1) 将二进制编码解转换成排序解。

(2) 依次判断车辆 $ m $ ( $ m = 1,2, \cdots ,M $ )是否满足载重约束，若满足，将车辆 $ m $ 放入可行车辆集合 $ X $ ；否则，将车辆 $ m $ 中超过其服务能力的客户点按服务先后顺序摘出，放入剩余客户点集合 $ Y $ 中，操作后，车辆 $ m $ 满足载重约束，将车辆 $ m $ 放入可行车辆集合 $ X $ 中。直至判断完所有车辆。

(3) 以最小化行驶距离为目标，并以车辆载重为约束条件，将剩余客户点插入所有车辆( $ M $ 辆)的所有位置，找出最佳插入点，将客户插入，对剩余客户按顺序逐个执行步骤3。若剩余客户均分配完，输出修复后的可行解，执行步骤7；否则，执行步骤4。

(4) 选出 $ M $ 辆车中剩余容量最大的车 $ {m_1} $ ，将剩余客户插入车 $ {m_1} $ 的最后一个位置，同时，从车 $ {m_1} $ 中选出某一客户点插入车 $ {m_2} $ ( $ {m_2} = 1,2, \cdots ,M,{m_1} \ne {m_2} $ )的最后一个位置，使两车均满足容量约束。对剩余客户按顺序逐个执行步骤4。

(5) 若剩余客户点分配完，输出修复后的可行解，执行步骤(7)；否则，执行步骤(6)。

(6) 将剩余客户点插入车辆 $ m $ ( $ m = 1,2,\cdots,M $ )的最后一个位置，同时，从车辆 $ m $ 选出某一客户插入除车辆 $ m $ 的其他车辆的最后一个位置，使两车均满足容量约束。如果满足，则插入；否则，直至判断完所有车辆。对剩余客户点按顺序逐个执行步骤(6)。

(7) 程序结束。

2.2.2 邻域搜索算法

本小节针对上述获得的可行解，设计了车辆间和车辆内两类共4种邻域搜索操作，以进一步提高可行解的质量。算法步骤如下：

(1) 设可行解为 $ \varPi $ ，令当前最优解 $ {\varPi ^*} = \varPi $ ，局部搜索次数为 $ {\max _{\text{s}}} $ ，车辆间搜索次数为 $ {v_{{\text{out}}}} $ ，车辆内搜索次数为 $ {v_{{\rm{in}}}} $ ，车辆数为 $ M $ ，循环参数： $ {\text{loop}} = 1 $ 、 $ {N_{{\text{out}}}} = 1 $ 、 $ {N_{{\text{in}}}} = 1 $ 、 $ {N_{\text{v}}} = 1 $ ，标志位 $ {\text{SI}} = 1 $ 。

(2) 在 $ \varPi $ 中随机选取两辆车，在两辆车中分别随机选取一个客户，得到客户 $ r $ 和 $ t $ ，将 $ t $ 客户插到 $ r $ 客户之前，若不满足载重约束条件，令 $ \varPi = {\varPi ^*} $ ，执行步骤(3)；反之，若获得更优解 $ \varPi ' $ ，则令 $ {\varPi ^*} = \varPi ' $ ， $ \varPi = \varPi ' $ ，执行步骤(4)，若没获得更优解，执行步骤(3)。

(3) 在 $ \varPi $ 中随机选取两辆车，在两辆车中分别随机选取一个客户进行交换，若不满足载重约束条件，令 $ \varPi = {\varPi ^*} $ ，执行步骤(4)；反之，若获得更优解 $ \varPi ' $ ，则令 $ {\varPi ^*} = \varPi ' $ ， $ \varPi = \varPi ' $ ，执行步骤(4)。

(4) $ {N_{{\text{out}}}} = {N_{{\text{out}}}} + 1 $ ，如果 $ {N_{{\text{out}}}} \leqslant {v_{{\text{out}}}} $ ，执行步骤(2)，否则，令 $ \varPi = {\varPi ^*} $ ，执行步骤(5)。

(5) 如果 $ {\text{SI}} = 1 $ ，则对第 $ {N_{\text{v}}} $ 辆车，选出其中一客户点 $ b $ ，依次与车 $ {N_{\text{v}}} $ 中所有客户点进行交换后，若获得更优解 $ \varPi ' $ ，则令 $ {\varPi ^*} = \varPi ' $ ， $ \varPi = \varPi ' $ 。重复执行这一操作，直至所有客户点被考虑。若此过程获得更优解，则令 $ {\text{SI}} = 1 $ ，执行步骤(7)；否则，令 $ {\text{SI}} = 2 $ ，执行步骤(6)。

(6) 如果 $ {\text{SI}} = 2 $ ，则对第 $ {N_{\text{v}}} $ 辆车，选出其中一客户点 $ h $ ，重新插入到车 $ {N_{\text{v}}} $ 中所有可能位置，若获得更优解 $ \varPi ' $ ，则令 $ {\varPi ^*} = \varPi ' $ ， $ \varPi = \varPi ' $ 。重复执行这一操作，直至所有客户点被考虑。若此过程获得更优解，则令 $ {\text{SI}} = 2 $ ，否则，令 $ {\text{SI}} = 1 $ 。执行步骤(7)。

(7) 如果步骤(5)或(6)均未获得更好解，则执行步骤(8)；反之， $ {N_{{\text{in}}}} = {N_{{\text{in}}}} + 1 $ ，如果 $ {N_{{\text{in}}}} \leqslant {v_{{\text{in}}}} $ ，执行步骤(5)；否则，执行步骤(8)。

(8) 令 $ {N_{{\text{in}}}} = 1 $ ， $ {N_{\text{v}}} = {N_{\text{v}}} + 1 $ ，如果 $ {N_{\text{v}}} \leqslant M $ ，执行步骤(5)；否则， $ {\text{loop}} = {\text{loop}} + 1 $ ， $ {N_{\text{v}}} = 1 $ ， $ {N_{{\text{out}}}} = 1 $ ， $ {N_{{\text{in}}}} = 1 $ ， $ {\text{SI}} = 1 $ ，执行步骤(9)。

(9) 如果 $ {\text{loop}} \leqslant {\max _{\text{s}}} $ ，执行步骤(2)；否则，输出 $ {\varPi ^*} $ 。

2.3 次梯度算法

针对上述所提的拉格朗日对偶问题，本文采用次梯度算法进行求解。其求解基本思想是：根据已知条件，求解对偶问题，获得问题的下界和决策变量值，进而计算更新次梯度以及拉格朗日乘子，通过不断更新迭代求解对偶问题，直到找到满足条件的对偶值。用次梯度算法求解对偶问题时，拉格朗日乘子 $ {\lambda _m}(m \in C) $ 更新公式为

$ \lambda _m^{n + 1} = {\rm{max}}\{ 0,\lambda _m^n + {\rm{Ste}}{{\rm{p}}^n} \cdot {g_m}({x^n})\} $

(18)

式中： $ g({x^n}) $ 是 $ n $ 次迭代的次梯度，计算公式为

$ {g_m}({x^n}) = \sum\nolimits_{i = 0}^N {\sum\nolimits_{j = 0}^N {{x_{mij}}} } {q_i} - Q,\forall m \in C $

(19)

步长更新公式为

$ {\rm{Ste}}{{\rm{p}}^n} = \frac{{({\rm{UB}} - {\rm{L}}{{\rm{B}}^n})}}{{\displaystyle\sum\nolimits_{m = 1}^M {{{({g_m}({x^n}))}^2}} }}\omega $

(20)

式中： $ {\rm{UB}} $ 为 $ n $ 次迭代的最佳上界， $ {\rm{L}}{{\rm{B}}^n} $ 为 $ n $ 次迭代的下界，参数 $ \omega $ 值取0.2。

2.4 改进拉格朗日松弛算法步骤

整个求解算法步骤如下：

(1) 初始化拉格朗日乘子 $ {\lambda _0} = 0 $ ，迭代次数 $ n = 0 $ ，设初始上界 $ {\rm{UB}} $ 为原问题较大的可行目标值。

(2) 求解对偶问题(17)，获得决策变量 $ {x^n} $ 及下界 $ {\rm{L}}{{\rm{B}}^n} $ 。

(3) 运用2.2.1中的修复算法对下界进行修复，若能修复得可行解 $ \varPi $ ，执行步骤(4)；否则上界 $ {\rm{UB}} $ 保持不变，执行步骤(5)。

(4) 运用2.2.2中的二阶段算法对可行解 $ \varPi $ 进行优化，获得优化后的解 $ {\varPi ^*} $ ，如果优化后的目标值 $ Z({\varPi ^*}) < {\rm{UB}} $ ，则令 $ {\rm{UB}} = Z({\varPi ^*}) $ ；否则保持 $ {\rm{UB}} $ 不变。

(5) 运用公式(18)、(19)和(20)更新次梯度、步长和拉格朗日乘子。

(6) 判断是否满足终止条件，若满足，输出最佳上界 $ {\rm{UB}} $ 和下界 $ {\rm{L}}{{\rm{B}}^n} $ ，程序结束；否则继续执行步骤(2)~(5)。

3 实验结果与分析 3.1 实验环境及数据

本节将改进拉格朗日松弛算法所求解与基于Gurobi求解器所求MIP的解进行对比，通过两者所求解与改进拉格朗日松弛算法所求下界的间隙( $ {\rm{Gap}} $ )来衡量算法的性能。本文实验算法均采用Python3.8编程实现，操作系统为windows10，电脑内存为8 G，CPU为Intel i5-4258U，主频频率为2.4 GHz。本文测试算例来源于网站( http://www.bernabe.dorronsoro.es/vrp/)的CVRP中Set P数据集。根据算例规模大小，设置Gurobi求解器最大运行时间分别为1800，3600，7200 s，改进拉格朗日松弛算法最大运行时间为2500 s或最大迭代10次，且在相同实验环境下独立重复运行10次。其中，平均间隙 $ {\rm{Gap}} = \dfrac{{{\rm{UB}} - {\rm{LB}}}}{{{\rm{LB}}}} \times 100\% $ ，用来衡量Gurobi求解器的解和改进拉格朗日松弛算法的解与下界在平均值上的偏离程度， $ {\rm{UB}} $ 为改进拉格朗日松弛算法所求可行解的平均值或Gurobi所求的可行解，即问题上界， $ {\rm{LB}} $ 为改进拉格朗日松弛算法所求下界， $ {\rm{WST}} $ 为10次测试结果中的最差值， $ {\rm{BST}} $ 为10次测试结果中的最好值， $ {\rm{AVG}} $ 为10次测试结果中的平均值， $ T $ 为10次测试的平均求解时间(单位：s)， $ O $ 为客户和仓库总数。求解结果如表3所示。

3.2 结果分析

本文提出一种改进拉格朗日松弛算法求解GCVRP，与商业求解器Gurobi所求解进行了对比，求解结果见表3，从表可以看出：针对编号1~7的小规模算例，Gurobi求解器在1800 s内能求得4个算例的最优解。小规模算例所求解平均 $ {\rm{Gap}} $ 为5.78%，求解平均时间为825.277 s。改进拉格朗日松弛算法在合理时间内求得了问题的满意解，求解平均 $ {\rm{Gap}} $ 为7.17%，求解平均时间为219.896 s。这也体现Gurobi求解器在求解小规模问题的优势，能大概率求解问题的最优解，但求解时间较长。改进拉格朗日松弛算法求解效率较高，在较短时间内能求得问题的上下界，能求得问题的满意解。

针对编号为8~19的中大规模算例，随着问题规模的变大，解空间更加复杂，Gurobi求解器弊端凸显，12个算例的平均 $ {\rm{Gap}} $ 为21.12%，平均求解时间为5100 s，求解质量和求解效率不高。而改进拉格朗日松弛算法通过松弛难约束，使问题变得容易求解，求解效率更高，求解质量令人满意，所求12个算例的平均 $ {\rm{Gap}} $ 为7.87%，平均求解时间为2422.016 s，求解质量远优于Gurobi求解器。

综合来看，针对19个不同规模的算例，改进拉格朗日松弛算法能较好地求解GCVRP，在合理时间内，所有算例的平均 $ {\rm{Gap}} $ 为7.61%。其在求得问题上界的同时，也能为原问题提供一个下界，可以衡量所求解的质量，综合了传统拉格朗日松弛算法与启发式算法的优势，是求解GCVRP的有效算法。

4 结论

本文在VRP的基础上，进一步考虑车辆载重和绿色因素，建立了GCVRP的混合整数规划模型，并以总费用最小为求解目标，提出一种改进拉格朗日松弛算法进行求解。首先，采用次梯度法求解对偶问题，得到原问题的下界；其次利用修复算法和邻域操作对下界进行修复及优化，得到原问题高质量下界，实现上界下界并行求解。实验结果表明，本文算法的综合求解性能优于Gurobi，是一种求解GCVRP的有效方法。后续将进一步考虑多车场多车型因素，并设计有效求解算法。