在实际系统运行过程中，突然的外部环境变化、子零部件失效等因素导致系统参数或结构不可避免地发生变化。为了精确、合理地模拟该类系统的实时运行状态，Markov跳变系统理论已经被广泛应用在实际系统中，并涌现出大量的研究成果^[1-4]。然而，在Markov跳变系统理论中，驻留时间遵循指数分布且具有无记忆性。这种无记忆性分布极大地限制了Markov跳变系统理论的应用。随后，一些学者提出了semi-Markov跳变系统理论，改善了Markov跳变系统理论的应用前景^[5-7]。文献[8]针对含奇异摄动的离散semi-Markov跳变系统模型，提出了一种基于离散时间semi-Markov核方法的慢状态反馈镇定问题。文献[9]考虑离散线性semi-Markov跳变系统转换率是部分已知的情况，引入了不完全semi-Markov核的概念，并提出了动态输出反馈控制方案。进一步，文献[10]考虑了非线性特征和参数不确定性对semi-Markov跳变系统性能的影响，引入了区间二型方法，建立了非线性semi-Markov跳变系统模型，并提出了故障诊断策略。

在上述关于semi-Markov跳变系统的研究成果中，都是假设系统的模态信息能够实时捕获，以实现系统与控制器/滤波器/观测器之间的模态信息传递。然而，在实际系统的信息传输过程中，由于信号传输时延、信息测量不及时等情况时有发生，这使得实时捕捉系统模态信息的任务是很难实现的。因此，许多专家学者提出了隐Markov/semi-Markov过程的概念，以保障控制器/滤波器/观测器的性能免受异步模态信息的影响^[11-17]。在这些研究成果中，文献[11]针对连续型semi-Markov跳变系统，设计了异步线性滤波器，并提出了Energy-to-Peak滤波方法。文献[14]考虑系统在信号传输时欺骗攻击对传输网络的影响，基于事件触发策略，提出了具有安全性的无源控制器设计方法。值得注意的是，上述研究成果在处理系统异步模态信息时，主要采用已知的条件概率进行描述，但实际系统通常是在极其复杂的环境下进行信息传输的，难以准确测量系统与控制器/滤波器之间的转移概率。

在此基础上，文献[18]引入了模态转移概率与时变发射概率模型，提出了基于异步观测器设计方法的稳定控制策略，极大地降低了先前成果的保守性。然而，现有研究成果对时变发射概率方法只是进行了初步探索，基于semi-Markov跳变系统模型的线性跳变系统，借助时变发射概率方法，如何设计一个有效的非同步静态输出反馈控制器还没有被彻底解决。本文基于semi-Markov理论构建线性跳变系统模型，提出基于时变发射概率方法的非同步静态输出反馈控制器的设计策略。

符号说明： ${\text{E(}} \cdot {\text{)}}$ 表示数学期望。 ${\text{He(}}{\boldsymbol{A}}{\text{)}}$ 表示矩阵 ${\boldsymbol{A}}$ 与其转置的和。 ${{\boldsymbol{A}}^{\rm{T}}}$ 表示矩阵 ${\boldsymbol{A}}$ 的转置。

1 问题描述 1.1 线性跳变系统模型

考虑外界环境因素会使实际系统的参数、结构发生变化等现象，在本节中使用semi-Markov跳变系统模型去模拟这类系统的实际运行状态。首先，给定概率空间 $(\varOmega ,\text{ }{F}\text{, }{P})$ ，其中 $\varOmega$ 、 $ {F} $ 和 $ {P} $ 分别表示样本空间、样本空间子集的代数和事件概率。基于semi-Markov跳变系统模型，线性跳变系统模型如式(1)所示。

$ \left\{ \begin{gathered} {\boldsymbol{\dot x}}{\text{(}}t{\text{)}} = {{\boldsymbol{A}}_{\alpha {\text{(}}{t} {\text{)}}}}{\boldsymbol{x}}{\text{(}}t{\text{)}} + {{\boldsymbol{B}}_{\alpha {\text{(}}{t} {\text{)}}}}{\boldsymbol{u}}{\text{(}}t{\text{)}} + {{\boldsymbol{C}}_{\alpha {\text{(}}{t} {\text{)}}}}{\boldsymbol{w}}{\text{(}}t{\text{)}} \hfill \\ {\boldsymbol{y}}{\text{(}}t{\text{)}} = {{\boldsymbol{D}}_{\alpha {\text{(}}{t} {\text{)}}}}{\boldsymbol{x}}{\text{(}}t{\text{)}} \hfill \\ \end{gathered} \right. $

(1)

式中： ${\boldsymbol{x}}{\text{(}}t{\text{)}} \in {{\bf{R}}^{{n_{\text{x}}}}}$ 为随机跳变系统的状态向量， ${\boldsymbol{u}}{\text{(}}t{\text{)}} \in {{\bf{R}}^{{n_{\text{u}}}}}$ 为系统的控制输入， ${\boldsymbol{w}}{\text{(}}t{\text{)}} \in {{\bf{R}}^{{n_{\text{w}}}}}$ 为外部干扰信号且属于 $ {{L} _{\text{2}}}{\text{[0}},\infty {\text{)}} $ ， ${\boldsymbol{y}}{\text{(}}t{\text{)}} \in {{\bf{R}}^{{n_{\text{y}}}}}$ 为系统的测量输出信号， $ \alpha {\text{(}}{t} {\text{)}} $ 为连续时间的齐次semi-Markov过程且取值在有限集合 ${N} = {\text{\{ 1, 2, }}\cdots{\text{, }}{{N} _{\text{1}}}{\text{\} }}$ 内， $ {{N} _{\text{1}}} $ 为系统的模态总数。 $ {{\boldsymbol{A}}_{\alpha {\text{(}}{t} {\text{)}}}} $ 、 $ {{\boldsymbol{B}}_{\alpha {\text{(}}{t} {\text{)}}}} $ 、 $ {{\boldsymbol{C}}_{\alpha {\text{(}}{t} {\text{)}}}} $ 和 $ {{\boldsymbol{D}}_{\alpha {\text{(}}{t} {\text{)}}}} $ 为具有适当维数的常数系统矩阵。为了符号简化，定义 $ \alpha {\text{(}}{t} {\text{)}} = {i} $ ，系统模型(1)可表示为

$ \left\{ \begin{gathered} {\boldsymbol{\dot x}}{\text{(}}t{\text{)}} = {{\boldsymbol{A}}_i}{\boldsymbol{x}}{\text{(}}t{\text{)}} + {{\boldsymbol{B}}_i}{\boldsymbol{u}}{\text{(}}t{\text{)}} + {{\boldsymbol{C}}_i}{\boldsymbol{w}}{\text{(}}t{\text{)}} \hfill \\ {\boldsymbol{y}}{\text{(}}t{\text{)}} = {{\boldsymbol{D}}_i}{\boldsymbol{x}}{\text{(}}t{\text{)}} \hfill \\ \end{gathered} \right. $

(2)

对于semi-Markov过程， $ \alpha {\text{(}}{t} {\text{)}} $ 的转移率满足

$ {{{\rm{Pr}}\{ }}\alpha {\text{(}}{t} {\text{ + }}\varDelta {\text{)}} = {j} |\alpha {\text{(}}{t} {\text{)}} = {i} {\text{\} = }}\left\{ \begin{gathered} {\pi _{ij}^{h} }\varDelta + o{\text{(}}\varDelta {\text{), }}{i} \ne j \hfill \\ {\text{1}} + {\pi_{i{i} } ^{h} }\varDelta + o{\text{(}}\varDelta {\text{), }}{i} = j{\text{ }} \hfill \\ \end{gathered} \right. $

式中： ${\pi _{ij}^{h} }{\text{ (}}{\pi _{ij}^{h} } \geqslant {\text{0, }}{i} \ne {j} {\text{)}}$ 表示系统从 $ {t} $ 时刻的模态 $ {i} $ 跳跃到 ${t} + \varDelta$ 时刻的模态 $ {j} $ 的转移速率， $\varDelta$ 表示无穷小的转移时间区间且满足

$ \mathop {{\rm{lim}}}\limits_{\varDelta \to {\rm{0}}} \frac{{o(\varDelta )}}{\varDelta } = {\rm{0}} $

注释1 　由上述可知，系统的模态转移速率 ${\pi_{ij} ^{h} }$ 仅取决于参数 $ {h} $ 。参数 $ {h} $ 表示驻留时间且不同于时间 $ {t} $ ，即系统最近一次跳变所消耗的时间。因此，当系统模态发生变化时，驻留时间 $ {h} $ 设置为0。

1.2 模态受限下线性跳变系统的控制器设计

基于上述线性跳变系统模型(2)，设计静态输出反馈控制器为

$ {\boldsymbol{u}}{\text{(}}{t} {\text{)}} = {{\boldsymbol{K}}_i}{\boldsymbol{y}}{\text{(}}{t} {\text{)}} $

(3)

式中：参数 $ {{{\boldsymbol{K}}} _i} $ 为待确定的控制器增益。根据控制器(3)，不难发现控制器的设计依赖于系统模态 $ {i} $ 且与系统模态是实时匹配的。因此，需要确保系统的模态变化是实时可观测的。然而，在实际系统中，其模态信息可能不是连续可接收的，这使得系统模态与控制器模态并不是实时匹配的。针对这种模态受限现象，引入隐semi-Markov过程去模拟系统模态的变化。根据文献[18]可知,在隐semi-Markov过程中，所有的状态是隐藏的且能够发射一些可观测的信号。为了更清晰地描述该过程，引入以下概念：(1) 转移概率：描述隐藏状态之间的转移规律；(2) 发射概率：描述隐藏状态所发射可观测信号之间的转移规律。

定义可观测信号为 $ \kappa {\text{(}}{t} {\text{) (}}{t} \geqslant {\text{0)}} $ ，而且取值在集合 ${{N} ^\diamondsuit } = {\text{\{ 1, 2, }}\cdots{\text{, }}{{N} _{\text{2}}}{\text{\} }}$ 内。 $ {{N} _{\text{2}}} $ 表示控制器的模态总数。然后，对于 $ \kappa {\text{(}}{t} {\text{)}} = {m} $ ， $ \forall {i} \in {N} $ ， $ \forall {m} \in {{N} ^\diamondsuit } $ 和 ${\text{Pr\{ }}\kappa {\text{(}}{t} {\text{)}} = {m} |\alpha {\text{(}}{t} {\text{)}} = {i} {\text{\} }} = {\varphi _{im}^t}$ ，定义时变发射概率矩阵为 ${\boldsymbol{\varPhi }}{\text{(}}{t} {\text{)}} = {[ {{\varphi _{im}^t}} ]_{{N_{\text{1}}} \times {N_{\text{2}}}}}$ ，其中 ${\varphi_{im} ^t} \in {\text{[0,1]}}$ ， $\displaystyle\sum\nolimits_{m \in {N^\diamondsuit }}{{\varphi _{im}^t}} = {\text{1}}$ 。由文献[18]可知，可以假设时变发射概率满足： ${\boldsymbol{\varPhi }}{\text{(}}{t} {\text{)}} = \displaystyle\sum\nolimits_{\beta = {\text{1}}}^{{\beta _0}} {{\eta _\beta }{\text{(}}{t} {\text{)}}} {{\boldsymbol{\varPhi }}_\beta }$ ，其中 $\displaystyle\sum\nolimits_{\beta = {\text{1}}}^{{\beta _0}} {{\eta _\beta }{\text{(}}{t} {\text{)}}} = {\text{1}}$ ， $ {\eta _\beta }{\text{(}}{t} {\text{)}} \geqslant {\text{0}} $ ， ${{\boldsymbol{\varPhi }}_\beta } = {[ {{\varphi _{im}^\beta }} ]_{{N_{\text{1}}} \times {N_{\text{2}}}}}$ 。

基于上述内容，构造非同步静态输出反馈控制器，如式(4)所示。

$ {\boldsymbol{u}}{\text{(}}{t} {\text{)}} = {{\boldsymbol{K}}_{m} }{\boldsymbol{y}}{\text{(}}{t} {\text{)}} $

(4)

结合系统模型(2)和控制器(4)，能够得到闭环线性随机跳变系统为

$ \left\{ \begin{gathered} {\boldsymbol{\dot x}}{\text{(}}t{\text{)}} = {\text{(}}{{\boldsymbol{A}}_i} + {{\boldsymbol{B}}_i}{{\boldsymbol{K}}_m}{{\boldsymbol{D}}_i}{\text{)}}{\boldsymbol{x}}{\text{(}}{t} {\text{)}} + {{\boldsymbol{C}}_i}{\boldsymbol{w}}{\text{(}}t{\text{)}} \hfill \\ {\boldsymbol{y}}{\text{(}}t{\text{)}} = {{\boldsymbol{D}}_i}{\boldsymbol{x}}{\text{(}}t{\text{)}} \hfill \\ \end{gathered} \right. $

(5)

注释2 　根据闭环系统(5)，不难发现当矩阵 $ {{\boldsymbol{D}}_i} $ 是单位矩阵时，本文所解决的非同步静态输出反馈控制器设计问题将转换为非同步状态反馈控制器设计问题。同时，当 $ {{N} ^\diamondsuit } = {\text{\{1\} }} $ 时，非同步静态输出反馈控制器设计问题将转换为模态不依赖静态输出反馈控制器设计问题；当 $ {{N} ^\diamondsuit } = {N} $ 且 ${\text{Pr }}\{ \kappa {\text{(}}{t} {\text{)}} = {i} |\alpha {\text{(}}{t} {\text{)}} = {i} \} = {\varphi _{i{i} }^t}$ 时，非同步静态输出反馈控制器设计问题将转换为同步静态输出反馈控制器设计问题。

在进行系统稳定性分析与控制器设计之前，首先给出以下引理与定理。

引理1^[19] 　如果存在标量 $ {v} $ 和适当维数矩阵 $ {\boldsymbol{Q}} $ , $ {\boldsymbol{R}} $ , $ {\boldsymbol{M}} $ 和 $ {\boldsymbol{S}} $ 满足 $\left[ {\begin{array}{*{20}{c}} {\boldsymbol{Q}}&{{\boldsymbol{M}} + v{{\boldsymbol{S}}^{\rm{T}}}} \\ *&{ - v{\boldsymbol{R}} - v{{\boldsymbol{R}}^{\rm{T}}}} \end{array}} \right] \lt {\text{0}}$ ，则存在不等式 ${\boldsymbol{Q}} + {\boldsymbol{M}}{{\boldsymbol{R}}^{ - {\text{1}}}}{\boldsymbol{S}} + {{\boldsymbol{S}}^{\rm{T}}}{({{\boldsymbol{R}}^{ - {\rm{1}}}})^{\rm{T}}}{{\boldsymbol{M}}^{\rm{T}}} \lt {\text{0}}$ 成立。

定义1^[20] 　如果下列条件同时满足，则称线性跳变系统(5)是随机稳定的且满足 $ {{H} _\infty } $ 的性能指标 $\gamma $ 。

(1) 对于任意初始条件 $ {{{\boldsymbol{x}}} _{\text{0}}} $ ， $ {\alpha _{\text{0}}} \in {N} $ 和 $ {\kappa _{\text{0}}} \in {{N} ^\diamondsuit } $ ，当 $ {\boldsymbol{w}}{\text{(}}{t} {\text{)}} = {\text{0}} $ 时，如果满足

$ \parallel {\boldsymbol{x}}{\text{(}}{t} {\text{)}}\parallel _{\text{2}}^{\text{2}} = \int_{\text{0}}^\infty {{\text{E\{ }} \parallel {\boldsymbol{x}}{\text{(}}{t} {\text{)}}{\parallel ^2}|{\text{(}}{{\boldsymbol{x}}_{\text{0}}}{\text{,}}{\alpha _{\text{0}}}{\text{,}}{\kappa _{\text{0}}}{\text{)\} }}} {\text{d}}t \lt \infty $

那么，线性跳变系统(5)是随机稳定的。

(2) 对于任意 $ {{H} _\infty } $ 性能指标 $\gamma $ 大于0以及干扰信号 $ {\boldsymbol{w}}{\text{(}}{t} {\text{)}} $ 属于 $ {{L} _{\text{2}}}{\text{[0}},\infty {\text{)}} $ ，有

$ {\text{E}}\left\{ {\int_{\text{0}}^\infty {{{\boldsymbol{y}}^{\rm{T}}}{\text{(}}t{\text{)}}{\boldsymbol{y}}{\text{(}}t{\text{)d}}{t} } } \right\} \leqslant {\gamma ^{\text{2}}}{\text{E}}\left\{ {\int_{\text{0}}^\infty {{{\boldsymbol{w}}^{\rm{T}}}{\text{(}}t{\text{)}}{\boldsymbol{w}}{\text{(}}t{\text{)d}}{t} } } \right\} $

成立，则称闭环系统(5)满足 $ {{H} _\infty } $ 性能。

2 主要结论

在本节中，主要讨论闭环线性跳变系统随机稳定的充分条件以及在时变发射概率方法下非同步静态输出反馈控制器的设计过程。

定理1 　对于 $ {i} \in {N} $ ， $ {m} \in {{N} ^\diamondsuit } $ 以及所有可容许的不确定性，如果存在正定矩阵 $ {{\boldsymbol{P}}_i} $ 和适当维数矩阵 $ {{\boldsymbol{K}}_{m} } $ ，以及 $ {{H} _\infty } $ 性能指标 $\gamma $ 大于0，使得不等式(6)成立，则称闭环线性跳变系统是随机稳定的且满足 $ {{H} _\infty } $ 性能指标。

$ {{\boldsymbol{\varPsi}} _{\text{1}}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{\varPhi}} _{{\text{11}}}}}&{{{\boldsymbol{P}}_i}{{\boldsymbol{C}}_{i} }} \\ * &{ - {\gamma ^{\text{2}}}{\boldsymbol{I}}} \end{array}} \right] \lt {\text{0}} $

(6)

$ {{\boldsymbol{\varPhi}} _{{\text{11}}}} = {\boldsymbol{\sum\nolimits}}_{{j} = {\text{1}}}^{{N_{\text{1}}}} {\pi _{ij}^*{{\boldsymbol{P}}_j} + {\text{2}}{{\boldsymbol{P}}_i}{{\left({{\boldsymbol{A}}_i} + {\boldsymbol{\sum\nolimits}}_{{m} = {\text{1}}}^{{{N} _{\text{2}}}} {{\varphi_{im} ^t}{{\boldsymbol{B}}_i}{{\boldsymbol{K}}_{m} }{{\boldsymbol{D}}_i}} \right) + }}{{{\boldsymbol{D}}}}_{i} ^{\rm{T}}{{\boldsymbol{D}}_i}} $

$ \pi _{ij}^* = \int_{\text{0}}^\infty {\pi _{ij}^h} {q} _i^h{{{{\rm{d}}}}h} $

式中： $q_i^h $ 为系统在模态i上的概率密度函数。

证明 　首先，对于任意 $ {i} \in {N} $ ， $ {m} \in {{N} ^\diamondsuit } $ ，构造依赖于系统模态变化的Lyapunov函数。

$ {V}({\boldsymbol{x}}({t}),\alpha ({t}),{t})={{\boldsymbol{x}}}^{{\rm{T}}}({t}){{\boldsymbol{P}}}_{a({t})}{\boldsymbol{x}}({t}) $

根据文献[18]，对于 $ \alpha {\text{(}}{t} {\text{)}} = {i} $ ，使用条件概率公式得到函数 ${V}({\boldsymbol{x}}({t}),\alpha ({t}),{t})$ 的无穷小算子为

$ \begin{aligned}&\quad{L} ( {{V} ( {{\boldsymbol{x}}({t} ),\alpha ({t} ),{t} } )} ) =\\ &\mathop {{\text{lim}}}\limits_{\varDelta \to {\text{0}}} \frac{{\text{1}}}{\varDelta }\left( {\sum\nolimits_{{j} = {\text{1}},{j} \ne {i} }^{{N_{\text{1}}}} {{{q} _{ij}}\frac{{{{G} _i}{\text{(}}{h} + \varDelta {\text{)}} - {{G} _i}{\text{(}}{h} {\text{)}}}}{{{\text{1}} - {{G} _i}{\text{(}}{h} {\text{)}}}}{{\boldsymbol{x}}^{\rm{T}}}({t} + \varDelta ){{\boldsymbol{P}}_j}} } \right. \times\\ &\quad{\boldsymbol{x}}({t} + \varDelta ) + \frac{{{\text{1}} - {{G} _i}{\text{(}}{h} + \varDelta {\text{)}}}}{{{\text{1}} - {{G} _i}{\text{(}}{h} {\text{)}}}}{{\boldsymbol{x}}^{\rm{T}}}({t} + \varDelta ){{\boldsymbol{P}}_i}{\boldsymbol{x}}({t} + \varDelta ) -\\ &\quad\bigg.{{\boldsymbol{x}}^{\rm{T}}}({t} ){{\boldsymbol{P}}_i}{\boldsymbol{x}}({t} )\bigg) \end{aligned}$

式中： $ {{G} _i}{\text{(}}{h} {\text{)}} $ 为系统在模态 $ \alpha {\text{(}}{t} {\text{)}} = {i} $ 上驻留时间的累积分布函数， $ {{q} _{ij}} $ 为系统从模态 $ {i} $ 跳跃到模态 $ {j} $ 的概率密度函数。

此外，对于满足条件 $\mathop {{\rm{lim}}}\limits_{\varDelta \to {\rm{0}}}{\varDelta ^{\text{2}}}/\varDelta = {\text{0}}$ 的参数 $\varDelta$ ，可得

$ {\boldsymbol{x}}({t} + \varDelta ) = \varDelta {\boldsymbol{\dot x}}{\text{(}}{t} {\text{)}} + {\boldsymbol{x}}{\text{(}}{t} {\text{)}} + o{\text{(}}\varDelta {\text{)}} $

结合上述 ${V} ( {{\boldsymbol{x}}( t ),\alpha ( t ),t} )$ 、 ${\boldsymbol{x}}( {{t} + \varDelta } )$ 、系统模型(5)以及累积分布函数与概率密度函数的性质，可得

$ \begin{split} &{\text{E}}\left( {{L} \left( {{V} \left( {{\boldsymbol{x}}\left( {t} \right),\alpha \left( {t} \right),{t} } \right)} \right)} \right) ={\text{2}}{{\boldsymbol{x}}^{\rm{T}}}{\text{(}}{t} {\text{)}}{{\boldsymbol{P}}_i}{\text{[(}}{{\boldsymbol{A}}_i} + {{\boldsymbol{B}}_i}{{\boldsymbol{K}}_{m} }{{\boldsymbol{D}}_i}{\text{)}}{\boldsymbol{x}}{\text{(}}{t} {\text{)}} +\\ & {{\boldsymbol{C}}_i}{\boldsymbol{w}}{\text{(}}t{\text{)]}} + \sum\nolimits_{{j} = {\text{1}}}^{{N_{\text{1}}}} {{{\boldsymbol{x}}^{\rm{T}}}{\text{(}}{t} {\text{)}}\pi _{ij}^h{{\boldsymbol{P}}_j}{\boldsymbol{x}}{\text{(}}{t} {\text{)}}} =\\ &{\rm{2}}{{\boldsymbol{x}}^{\rm{T}}}{\rm{(}}t{\rm{)}}{{\boldsymbol{P}}_i}\left[ {({{\boldsymbol{A}}_i} + \sum\nolimits_{m = {\rm{1}}}^{{N_{\rm{2}}}} {{\varphi_{im} ^t}{{\boldsymbol{B}}_i}{{\boldsymbol{K}}_m}{{\boldsymbol{D}}_i}} {\rm{)}}{\boldsymbol{x}}{\rm{(}}t{\rm{)}} + {{\boldsymbol{C}}_i}{\boldsymbol{w}}{\rm{(}}t)} \right] + \\ &\sum\nolimits_{{j} = {\text{1}}}^{{N_{\text{1}}}} {{{\boldsymbol{x}}^{\rm{T}}}{\text{(}}{t} {\text{)}}\pi _{ij}^*{{\boldsymbol{P}}_j}{\boldsymbol{x}}{\text{(}}{t} {\text{)}}} \end{split}$

当 $ {\boldsymbol{w}}{\text{(}}{t} {\text{)}} = {\text{0}} $ 时，可得

$ \begin{aligned} &{\text{E}}( {{L} ( {{V} ( {{\boldsymbol{x}}( {t} ),\alpha ( {t} ),{t} } )} )} ) = \sum\nolimits_{{j} = {\text{1}}}^{{N_{\text{1}}}} {{{\boldsymbol{x}}^{\rm{T}}}{\text{(}}{t} {\text{)}}\pi _{ij}^*{{\boldsymbol{P}}_j}{\boldsymbol{x}}{\text{(}}{t} {\text{)}}}+\\ &{\text{2}}{{\boldsymbol{x}}^{\rm{T}}}{\text{(}}{t} {\text{)}}{{\boldsymbol{P}}_i}\left({{\boldsymbol{A}}_i} + \sum\nolimits_{{m} = {\text{1}}}^{{N_{\text{2}}}} {{\varphi _{im}^t}{{\boldsymbol{{ B}}}_i}{{\boldsymbol{K}}_{m} }{{\boldsymbol{D}}_i}} \right){\boldsymbol{x}}{\text{(}}{t} {\text{)}}\end{aligned} $

然后，由不等式(6)可知， ${\text{E}}( {{L} ( {{V} ( {{\boldsymbol{x}}( {t} ),\alpha ( {t} ),{t} } )} )} )$ 是小于0的。借助定义1以及文献[5]中的定理1，可以称在 $ {\boldsymbol{w}}{\text{(}}{t} {\text{)}} = {\text{0}} $ 的情况下闭环系统(5)是随机稳定的。

进一步，考虑 $ {\boldsymbol{w}}{\text{(}}{t} {\text{)}} \ne {\text{0}} $ 以及定义1给出的 $ {{H} _\infty } $ 性能指标，可得

$ \begin{aligned} &{\text{E}}\left( {{L} \left( {{V} \left( {{\boldsymbol{x}}\left( {t} \right),\alpha \left( {t} \right),{t} } \right)} \right)} \right) \leqslant\\ &{\text{2}}{{\boldsymbol{x}}^{\rm{T}}}{\text{(}}{t} {\text{)}}{{\boldsymbol{P}}_i}{\text{(}}{{\boldsymbol{A}}_i} + {{\boldsymbol{B}}_i}{{\boldsymbol{K}}_{m} }{{\boldsymbol{D}}_i}{\text{)}}{\boldsymbol{x}}{\text{(}}{t} {\text{)}} + \sum\nolimits_{{j} = {\text{1}}}^{{N_{\text{1}}}} {{{\boldsymbol{x}}^{\rm{T}}}{\text{(}}{t} {\text{)}}\pi _{ij}^*{{\boldsymbol{P}}_j}{\boldsymbol{x}}{\text{(}}{t} {\text{)}}} +\\ &{\text{2}}{{\boldsymbol{x}}^{\rm{T}}}{\text{(}}{t} {\text{)}}{{\boldsymbol{P}}_i}{{\boldsymbol{C}}_{i} }{\boldsymbol{w}}{\text{(}}t{\text{) + }}{{\boldsymbol{y}}^{\rm{T}}}{\text{(}}t{\text{)}}{\boldsymbol{y}}{\text{(}}t{\text{)}} - {\gamma ^{\text{2}}}{{\boldsymbol{w}}^{\rm{T}}}{\text{(}}t{\text{)}}{\boldsymbol{w}}{\text{(}}t{\text{)}} =\\ &{{\boldsymbol{\xi }}^{\rm{T}}}{\text{(}}{t} {\text{)}}{\boldsymbol{\varPsi \xi }}{\text{(}}{t} {\text{)}} \end{aligned}$

式中：

$ {{\boldsymbol{\xi }}^{\rm{T}}}{\text{(}}{t} {\text{)}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{x}}^{\text{T}}}{\text{(}}{t} {\text{)}}}&{{{\boldsymbol{w}}^{\text{T}}}{\text{(}}{t} {\text{)}}} \end{array}} \right] $

$ {\boldsymbol{\varPsi }} = \left[ {\begin{array}{*{20}{c}} {\displaystyle\sum\nolimits_{{j} = {\text{1}}}^{{N_{\text{1}}}} {\pi _{ij}^*{{\boldsymbol{P}}_j} + {\text{2}}{{\boldsymbol{P}}_i}{\text{(}}{{\boldsymbol{A}}_i} + {{\boldsymbol{{ Z}}}_{im}}{\text{) + }}{\boldsymbol{D}}_{i} ^{\rm{T}}{{\boldsymbol{D}}_i}} }&{{{\boldsymbol{P}}_i}{{\boldsymbol{C}}_{i} }} \\ * &{ - {\gamma ^{\text{2}}}{\boldsymbol{I}}} \end{array}} \right] $

$ {{\boldsymbol{{ Z}}}_{im}} = \sum\nolimits_{{m} = {\text{1}}}^{{N_{\text{2}}}} {{\varphi _{im}^t}{{\boldsymbol{B}}_i}{{\boldsymbol{K}}_{m} }{{\boldsymbol{D}}_i}} $

由不等式(6)可知 ${\boldsymbol{\varPsi }} \lt {\text{0}}$ 。综上所述，满足定义1中的条件，可以称闭环随机跳变系统(5)是随机稳定的且满足 $ {{H} _\infty } $ 性能指标 $\gamma $ 。证毕。

注释3 　基于线性矩阵不等式方法与Lyapunov函数方法，定理1给出了系统的随机稳定性条件。然而，在定理1所给的不等式中，存在时变的发射概率以及耦合项 $ {{\boldsymbol{P}}_i}{{\boldsymbol{B}}_i}{{\boldsymbol{K}}_{m} }{{\boldsymbol{D}}_i} $ ，这导致不等式(6)不是数值可解的，即通过定理1并不能够直接求解出控制器增益 $ {{\boldsymbol{K}}_{m} } $ 。因此，给出定理2以确保控制器增益 $ {{\boldsymbol{K}}_{m} } $ 的求解。

定理2 　对于 $ {i} \in {N} $ ， $ {m} \in {{N} ^\diamondsuit } $ 以及给定的参数 $ \varepsilon $ ，如果存在具有适当维数的矩阵 $ {{\boldsymbol{P}}_i} $ 大于0， $ {{\boldsymbol{X}}_m} $ 、 $ {{\boldsymbol{Y}}_{m} } $ 、 $ {{\boldsymbol{W}}_{im}} $ 以及 $ {{H} _\infty } $ 性能指标 $\gamma $ 大于0，有

$ {\mathop {\boldsymbol{\varPsi_{\text{1}} }}\limits^ \wedge } = \left[ {\begin{array}{*{20}{c}} {{{\mathop {\boldsymbol{\varPhi }}\limits^ \wedge }_{{\text{11}}}}}&{{{\boldsymbol{P}}_i}{{\boldsymbol{C}}_{i} }} \\\\ * &{ - {\gamma ^{\text{2}}}{\boldsymbol{I}}} \end{array}} \right] < {\text{0}} $

(7)

$ \left[ {\begin{array}{*{20}{c}} {{\text{He(}}{{\boldsymbol{B}}_i}{{\boldsymbol{Y}}_{m} }{{\boldsymbol{D}}_i}{\text{)}} - {{\boldsymbol{W}}_{im}}}&{\boldsymbol{\varXi }} \\\\ *&{ - \varepsilon {{\boldsymbol{X}}_m} - \varepsilon {{\boldsymbol{X}}_m^{\rm{T}}}} \end{array}} \right] \lt {\text{0}} $

(8)

式中：

$ {\boldsymbol{\varXi }} = {\text{(}}{{\boldsymbol{P}}_i}{{\boldsymbol{B}}_i} - {{\boldsymbol{B}}_i}{{\boldsymbol{X}}_m}{\text{)}} + \varepsilon {{\text{(}}{{\boldsymbol{Y}}_{m} }{{\boldsymbol{D}}_i}{\text{)}}^{\rm{T}}} $

$ {{{\mathop {\boldsymbol{\varPhi }}\limits^ \wedge }_{{\text{11}}}}} = \sum\nolimits_{{j} = {\text{1}}}^{{N_{\text{1}}}} {\pi _{ij}^*{{\boldsymbol{P}}_j} + {\text{2}}{{\boldsymbol{P}}_i}{{\boldsymbol{A}}_i} + \sum\nolimits_{\beta = {\text{1}}}^{{\beta _0}} {\sum\nolimits_{{m} = {\text{1}}}^{{N_{\text{2}}}} {\varphi _{im}^\beta {{\boldsymbol{W}}_{im}}} } + {\boldsymbol{D}}_{i} ^{\rm{T}}{{\boldsymbol{D}}_i}} $

则可称闭环线性跳变系统是随机稳定的且满足 $ {{H} _\infty } $ 性能指标。此外，非同步静态输出反馈控制器增益能够被确定为

$ {{\boldsymbol{K}}_{m} } = {\boldsymbol{X}}_m^{ - {\text{1}}}{{\boldsymbol{Y}}_{m} } $

证明 　首先，为了解决定理1中的耦合项 $ {{\boldsymbol{P}}_i}{{\boldsymbol{B}}_i} {{\boldsymbol{K}}_{m} }{{\boldsymbol{D}}_i} $ ，引入辅助项 $ {{\boldsymbol{W}}_{im}} $ 满足

$ {{\boldsymbol{P}}_i}{{\boldsymbol{B}}_i}{{\boldsymbol{K}}_{m} }{{\boldsymbol{D}}_i} + {{\text{(}}{{\boldsymbol{P}}_i}{{\boldsymbol{B}}_i}{{\boldsymbol{K}}_{m} }{{\boldsymbol{D}}_i}{\text{)}}^{\rm{T}}} < {{\boldsymbol{W}}_{im}} $

由于 ${\varphi _{im}^t} \in {\text{[0,1]}}$ ，于是有

$ {\mathop {\boldsymbol{\varPsi_{\text{1}} }}\limits^ \to } = \left[ {\begin{array}{*{20}{c}} {{{\mathop {\boldsymbol{\varPhi }}\limits^ \to }_{{\text{11}}}}}&{{{\boldsymbol{P}}_i}{{\boldsymbol{C}}_{i} }} \\\\ * &{ - {\gamma ^{\text{2}}}{\boldsymbol{I}}} \end{array}} \right] < {\text{0}} $

式中：

$ {{{\mathop {\boldsymbol{\varPhi }}\limits^ \to }_{{\text{11}}}}} = \sum\nolimits_{{j} = {\text{1}}}^{{N_{\text{1}}}} {\pi _{ij}^*{{\boldsymbol{P}}_j} + {\text{2}}{{\boldsymbol{P}}_i} {{\boldsymbol{A}}_i} + \sum\nolimits_{{m} = {\text{1}}}^{{N_{\text{2}}}} {{\varphi _{im}^t}{{\boldsymbol{W}}_{im}}} + {\boldsymbol{D}}_{i} ^{\rm{T}}{{\boldsymbol{D}}_i}} $

考虑时变发射概率满足 ${\boldsymbol{\varPhi }}{\text{(}}{t} {\text{)}} = \displaystyle\sum\nolimits_{\beta = {\text{1}}}^{{\beta _0}} {{\eta _\beta }} {\text{(}}t{\text{)}}{{\boldsymbol{\varPhi }}_\beta }$ 且 $ {\eta _\beta }{\text{(}}{t} {\text{)}} \geqslant {\text{0}} $ ，由此可得

$ {\mathop {\boldsymbol{\varPsi_{\text{1}} }}\limits^ \wedge } = \left[ {\begin{array}{*{20}{c}} {{{\mathop {\boldsymbol{\varPhi }}\limits^ \wedge }_{{\text{11}}}}}&{{{\boldsymbol{P}}_i}{{\boldsymbol{C}}_{i} }} \\\\ * &{ - {\gamma ^{\text{2}}}{\boldsymbol{I}}} \end{array}} \right] < {\text{0}} $

式中：

$ {{{\mathop {\boldsymbol{\varPhi }}\limits^ \wedge }_{{\text{11}}}}} = \sum\nolimits_{{j} = {\text{1}}}^{{N_{\text{1}}}} {\pi _{ij}^*{{\boldsymbol{P}}_j} + {\text{2}}{{\boldsymbol{P}}_i}{{\boldsymbol{A}}_i} + \sum\nolimits_{\beta = {\text{1}}}^{{\beta _0}} {\sum\nolimits_{{m} = {\text{1}}}^{{N_{\text{2}}}} {\varphi _{im}^\beta {{\boldsymbol{W}}_{im}}} } + {\boldsymbol{D}}_{i} ^{\rm{T}}{{\boldsymbol{D}}_i}} $

然后， ${{\boldsymbol{P}}_i}{{\boldsymbol{B}}_i}{{\boldsymbol{K}}_{m} }{{\boldsymbol{D}}_i} + {{\text{(}}{{\boldsymbol{P}}_i}{{\boldsymbol{B}}_i}{{\boldsymbol{K}}_{m} }{{\boldsymbol{D}}_i}{\text{)}}^{\rm{T}}} - {{\boldsymbol{W}}_{im}} < {\text{0}}$ 可改写为

$ {{\boldsymbol{B}}_i}{{\boldsymbol{Y}}_{m} }{{\boldsymbol{D}}_i} + {{\text{(}}{{\boldsymbol{B}}_i}{{\boldsymbol{Y}}_{m} }{{\boldsymbol{D}}_i}{\text{)}}^{\rm{T}}} - {{\boldsymbol{W}}_{im}} +{\text{2(}}{{\boldsymbol{P}}_i}{{\boldsymbol{B}}_i} - {{\boldsymbol{B}}_i}{{\boldsymbol{X}}_m}{\text{)}}{\boldsymbol{X}}_m^{ - {\text{1}}}{{\boldsymbol{Y}}_{m} }{{\boldsymbol{D}}_i} \lt {\text{0}} $

通过使用引理1，可得

$ \left[ {\begin{array}{*{20}{c}} {{\text{He(}}{{\boldsymbol{B}}_i}{{\boldsymbol{Y}}_{m} }{{\boldsymbol{D}}_i}{\text{)}} - {{\boldsymbol{W}}_{im}}}&{{\text{(}}{{\boldsymbol{P}}_i}{{\boldsymbol{B}}_i} - {{\boldsymbol{B}}_i}{{\boldsymbol{X}}_m}{\text{)}} + \varepsilon {{{\text{(}}{{\boldsymbol{Y}}_{m} }{{\boldsymbol{D}}_i}{\text{)}}}^{\rm{T}}}} \\\\ *&{ - \varepsilon {{\boldsymbol{X}}_m} - \varepsilon {{\boldsymbol{X}}_m}^{\rm{T}}} \end{array}} \right] \lt {\text{0}} $

因此，如果找到 $ {{\boldsymbol{Y}}_{m} } = {{\boldsymbol{X}}_{m} }{{\boldsymbol{K}}_{m} } $ ，则不等式(7)和(8)成立。证毕。

注释4 　在现有线性跳变系统非同步输出反馈控制的研究成果中，文献[21]对于线性跳变系统使用Markov跳变系统模型进行建模，而且通过一种固定转移概率描述系统模态之间、系统模态与控制器模态之间的关系，进而提出了非同步静态输出反馈控制器的设计方法。因此，与文献[21]相比，本文的研究成果进一步降低了其保守性，而且更加适用于实际系统。

3 数值算例

在本节中，旨在通过数值仿真分析验证所提基于时变发射概率方法的线性跳变系统非同步静态输出反馈控制策略的有效性与正确性。首先，考虑含有两个模态变化的线性跳变系统(2)。

$ 模态1：\left\{ \begin{gathered} {\boldsymbol{\dot x}}{\text{(}}t{\text{)}} = {{\boldsymbol{A}}_{\text{1}}}{\boldsymbol{x}}{\text{(}}t{\text{)}} + {{\boldsymbol{B}}_{\text{1}}}{\boldsymbol{u}}{\text{(}}t{\text{)}} + {{\boldsymbol{C}}_{\text{1}}}{\boldsymbol{w}}{\text{(}}t{\text{)}} \hfill \\ {\boldsymbol{y}}{\text{(}}t{\text{)}} = {{\boldsymbol{D}}_{\text{1}}}{\boldsymbol{x}}{\text{(}}t{\text{)}} \hfill \\ \end{gathered} \right. $

$ 模态2：\left\{ \begin{gathered} {\boldsymbol{\dot x}}{\text{(}}t{\text{)}} = {{\boldsymbol{A}}_{\text{2}}}{\boldsymbol{x}}{\text{(}}t{\text{)}} + {{\boldsymbol{B}}_{\text{2}}}{\boldsymbol{u}}{\text{(}}t{\text{)}} + {{\boldsymbol{C}}_{\text{2}}}{\boldsymbol{w}}{\text{(}}t{\text{)}} \hfill \\ {\boldsymbol{y}}{\text{(}}t{\text{)}} = {{\boldsymbol{D}}_{\text{2}}}{\boldsymbol{x}}{\text{(}}t{\text{)}} \hfill \\ \end{gathered} \right. $

对于上述系统，两个操作模态下的系统参数为

$ \begin{array}{*{20}{l}} {{{\boldsymbol{A}}_1} = \left[ {\begin{array}{*{20}{c}} 0&2\\ 2&{ - 3} \end{array}} \right]，}&{{{\boldsymbol{A}}_2} = \left[ {\begin{array}{*{20}{c}} { - 1}&1\\ 1&{ - 4} \end{array}} \right]}\\ {{{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}} 0\\ { - 2} \end{array}} \right]，}&{{{\boldsymbol{B}}_2} = \left[ {\begin{array}{*{20}{c}} 0\\ { - 10/8} \end{array}} \right]}\\ {{{\boldsymbol{C}}_1} = \left[ {\begin{array}{*{20}{c}} 1\\ 0 \end{array}} \right]，}&{{{\boldsymbol{C}}_2} = \left[ {\begin{array}{*{20}{c}} 1\\ 0 \end{array}} \right]}\\ {{{\boldsymbol{D}}_1} = {{\left[ {\begin{array}{*{20}{c}} { - 3}\\ 0 \end{array}} \right]}^{\rm{T}}}，}&{{{\boldsymbol{D}}_2} = {{\left[ {\begin{array}{*{20}{c}} 0\\ 3 \end{array}} \right]}^{\rm{T}}}} \end{array}$

假设模态的驻留时间服从Weibull分布。根据文献[22]，转移概率矩阵及其数学期望可表示为

$ [ {\pi _{ij}^h} ] = \left[ {\begin{array}{*{20}{c}} { - {\text{2}}{h} }&{{\text{2}}{h} } \\\\ {{\text{3}}{{h} ^{\text{2}}}}&{ - {\text{3}}{{h} ^{\text{2}}}} \end{array}} \right] $

$ {\text{E}}[ {\pi _{ij}^h} ] = \left[ {\begin{array}{*{20}{c}} { - {\text{1}}{\text{.772 5}}}&{\;\;{\text{1}}{\text{.772 5}}} \\\\ {\;\;{\text{2}}{\text{.708 2}}}&{ - {\text{2}}{\text{.708 2}}} \end{array}} \right] $

考虑控制器也存在两个模态变化。假设时变发射概率由具有两个顶点的多面体表征。

$ \varphi _{im}^{\text{1}} = \left[ {\begin{array}{*{20}{c}} {{\text{0}}{\text{.3}}}&{{\text{0}}{\text{.7}}} \\\\ {{\text{0}}{\text{.6}}}&{{\text{0}}{\text{.4}}} \end{array}} \right] \text{，} \varphi _{im}^{\text{2}} = \left[ {\begin{array}{*{20}{c}} {{\text{0}}{\text{.2}}}&{{\text{0}}{\text{.8}}} \\\\ {{\text{0}}{\text{.4}}}&{{\text{0}}{\text{.6}}} \end{array}} \right] $

给出参数 $ \varepsilon = {\text{1}} $ 。通过MATLAB线性矩阵不等式工具箱，求解不等式(7)~(8)，可得控制器参数为

$ {{\boldsymbol{K}}_{\text{1}}} = - {\text{0}}{\text{.333 2}} \text{，} {{\boldsymbol{K}}_{\text{2}}} = - {\text{0}}{\text{.280 0}} $

假设外部干扰信号为

$ {\boldsymbol{w}}\text{(}t\text{)=}\left\{\begin{array}{l}\text{6,} \qquad\,{3}\leqslant \mathrm{t}\leqslant \text{5 }\\\\ \text{5sin}\;{t},\text{ 5} < \mathrm{t}\leqslant \text{10}\\\\ \text{0,} \quad\;\;\;\;\,\text{其他}\end{array}\right. $

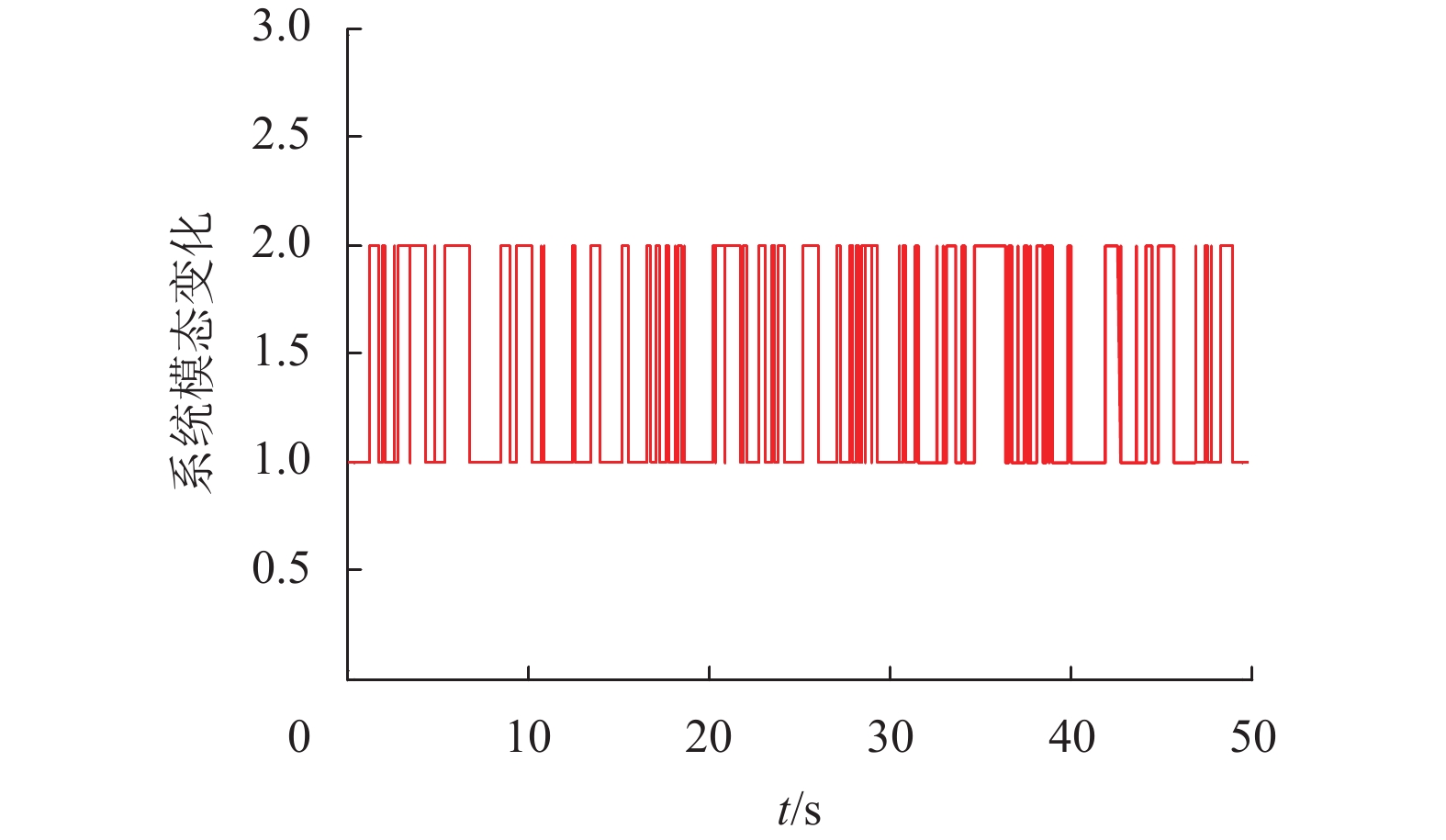
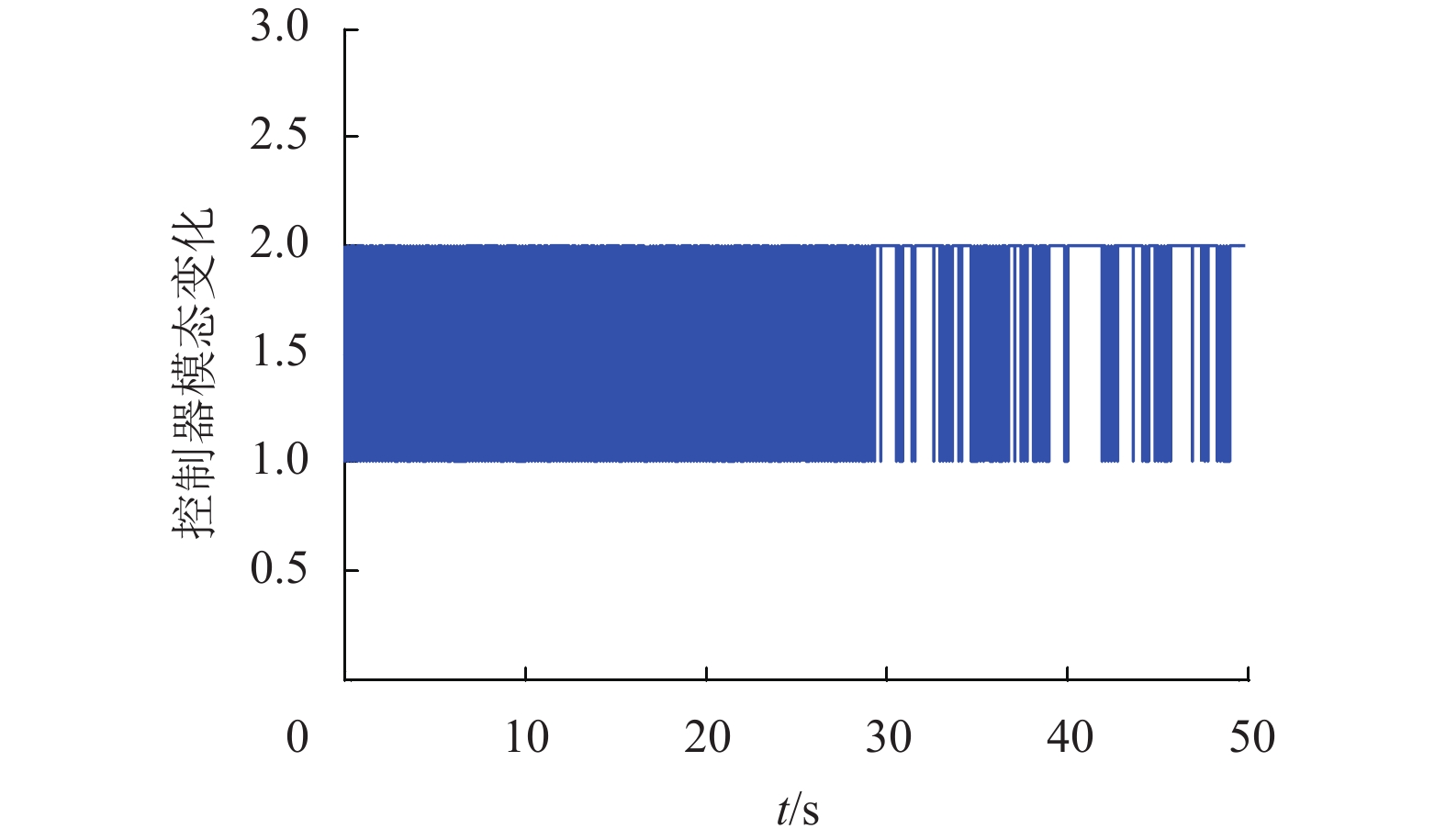
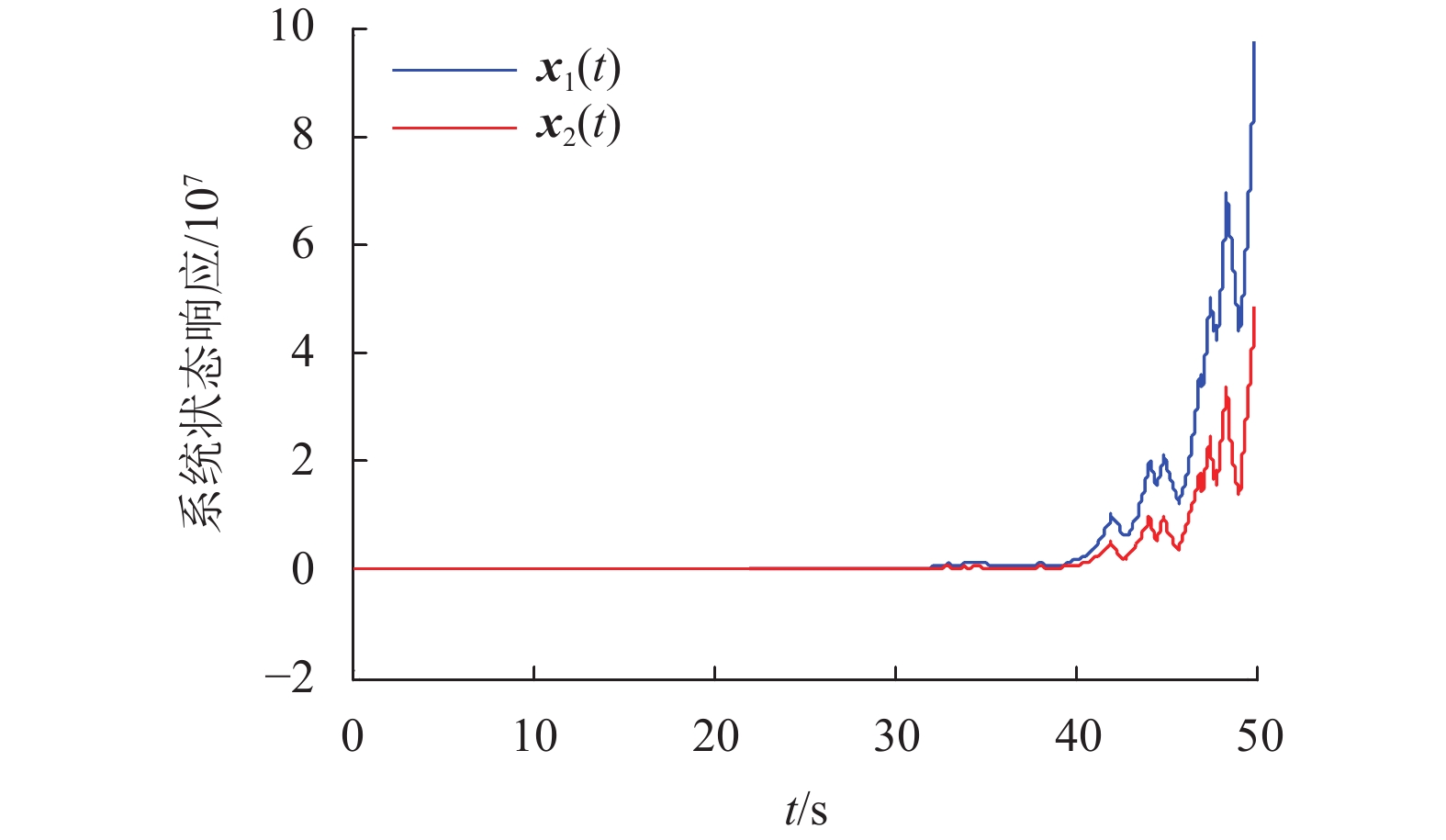
依据上述理论以及数值信息，对系统进行0~50 s的仿真测试，仿真结果如图1~4所示。图1表示线性跳变系统的模态变化情况。图2表示在时变发射概率下非同步静态输出反馈控制器的模态变化情况。系统的状态变化如图3~4所示。图3表示开环线性跳变系统的状态变化。图4表示闭环线性跳变系统的状态变化。从图3~4可以看出，本文所提的控制方法能够保障系统的稳定运行。因此，该控制方法是有效且正确的。

4 结论

本文基于时变发射概率方法，研究了模态受限线性跳变系统的静态输出反馈控制器的设计问题。考虑外部环境使系统参数与结构发生变化的现象，本文充分发挥了semi-Markov跳变系统模型的优势，建立了基于semi-Markov理论的线性跳变系统模型。为了保障系统的稳定运行，设计了一个非同步静态输出反馈控制器。考虑系统模态受限的情况，本文采用了隐semi-Markov转移概率模型与时变发射概率模型模拟系统与控制器之间的模态关系。此外，通过使用Lyapunov稳定性理论与线性矩阵不等式方法，给出了系统稳定性条件以及非同步静态输出反馈控制器的存在条件。最后，通过数值仿真验证了所提控制方法的有效性与正确性。基于上述内容，本文的贡献点包括以下几个方面：(1) 考虑一类基于semi-Markov跳变系统模型的线性随机跳变系统，设计了基于时变发射概率方法的非同步静态输出反馈控制器；(2) 提出了semi-Markov跳变系统的输出反馈控制新框架；(3) 提出了闭环semi-Markov跳变系统新的稳定性条件以及控制器存在条件。与一些现有模态受限系统稳定控制策略相比，所提方法能够克服时不变发射概率的保守性。在将来的工作中，希望所提控制方法能够应用到更多系统模型中^[23-24]。