列车运行控制策略在列车行驶过程中发挥着重要作用[1]。现有列车运行控制研究根据列车运行动静态参数建立列车运行模型,求解得到列车运行控制策略[2-4]。按求解方法的不同,可以分为传统控制方法和优化方法。传统控制方法侧重于给出问题的解析解,例如设计列车运行反馈控制器跟踪列车运行曲线[5-7]。Khmelnitsky等[8]研究在运行条件不确定及速度受限情况下的列车运行控制问题,利用极大值原理给出了牵引制动策略。Zhuan等[9]设计了输出反馈控制器,根据列车预设速度曲线调整列车运行速度。Li等[10]设计了鲁棒高速列车巡航控制器,实现列车速度跟踪。随着计算机技术的发展和计算效率的提升,优化方法得到了学者们的关注。优化方法通过构建列车运行模型,以运行能耗、准点到站等为目标求解得到列车运行控制策略[11-13]。Wang等[14]研究了速度、牵引力受约束下列车最优运行控制问题,并将其转化为混合整数规划问题进行求解。Lin等[15]采用凸优化方法求解列车运行最优控制输入。随着高铁里程不断增加,列车运行控制问题的规模不断增大,有必要引入合适的算法提升此类优化问题的求解效率。
交替方向乘子法(Alternating Direction Multiplier Method,ADMM)在1976 年由Gabay等提出,是一种适用于可分离凸优化问题的简单有效方法[16]。该方法将对偶上升法的可分解性与乘子法的优越收敛性结合起来,可以看作是在增广拉格朗日算法基础上发展起来的算法。Boyd等[17]将交替方向乘子法引入分布式优化和统计学习中,在此之后,ADMM受到了越来越多研究者的关注。Fu等[18]通过ADMM设计控制系统的最优反馈增益。Li等[19]将ADMM应用于多列车分布式最优控制,目的是使每辆列车在干扰作用下跟踪预设运行曲线。作为ADMM的拓展,He等[20]进一步研究了对称交替方向乘子法(Symmetric Alternating Direction Multiplier Method,SADMM)。对称交替方向乘子法相比于交替方向乘子法在一次迭代过程中多更新一次对偶变量,可以在较短时间内给出高精度解。与ADMM相比,该方法具有更快的收敛速率[21-23],适用于求解大规模优化问题,包括列车运行控制问题。
本文考虑单列车在多站点间的运行优化问题,以旅客乘坐舒适度、列车运行能耗以及列车准点到站为优化目标,将列车运行动力学方程、站点发车时间、运行速度和牵引力限制等作为约束条件,构建列车最优运行控制模型。采用对称交替方向乘子法进行求解,利用目标函数决策变量的可分性将优化问题分为2个独立的子问题:包含等式与不等式约束的二次型规划问题和无约束混合
本节关注列车运行控制模型的构建。在列车运行控制的理论研究和工程设计中,常常对列车运行过程进行适当近似。为方便模型的构建,首先对单列车最优控制模型作以下假设。(1) 将包含多个车厢的列车简化为具有相同位置及速度信息的单质点,而忽略列车本身的车长。列车运动过程符合牛顿第二定律。(2) 列车牵引力可在牵引约束上下限范围内任意取值。(3) 本文假设列车运行中所受阻力为定值。(4) 假设每个站点区间长度与相邻站点间的距离相比,站点区间长度非常小,因此可以将其视为一个质点。
1.1 单列车运行动力学模型根据牛顿动力学方程,列车的动力学方程可以表示为
| $ \left\{ {\begin{array}{*{20}{l}} {\dot x(t) = v(t)} \\ {m\dot v(t) = ma(t) = F(t) - f} \end{array}} \right. $ | (1) |
式中:
在实际运行中,列车不能在预设出站时间
| $ x({t_{j,{\text{out}}}}) \leqslant {l_j},{\text{ }}j = 1,2, \cdots ,J $ | (2) |
式中:
列车的速度约束可以表示为
| $ 0 \leqslant v \leqslant {v_{\max }} $ | (3) |
式中:
牵引力约束可以表示为
| $ {F_{\min }} \leqslant F(t) \leqslant {F_{\max }} $ | (4) |
式中:
高速列车运行需要满足安全、准点、舒适等目标,同时希望尽量节能运行。本节讨论兼顾旅客乘坐舒适度的列车节能运行控制,给出乘坐舒适度相关数学定义。列车加速率(加速度的一阶导数)、列车车厢温度、座位类型、车厢拥挤度等都会影响旅客乘坐体验。将列车运行加速度变化率作为乘坐舒适度标准,因此旅客乘坐舒适度函数可以表示为
| $ \dot a(t) = \frac{1}{m}\dot F(t) $ | (5) |
考虑乘坐舒适度的列车节能运行控制目标函数为
| $ \begin{split} \psi = & {\alpha _1}\int_{t = {t_0}}^{{t_l}} {{F^2}(t){\text{d}}t} + \beta \sum\nolimits_{j = 1}^J {{{(x({t_{j,{\text{in}}}}) - {l_j})}^2}} +\hfill \\ & \theta \sum\nolimits_{j = 1}^J {{v^2}({t_{j,{\text{in}}}})} + {\gamma _{\Delta a}}\int_{t = {t_0}}^{{t_l}} {\left| {\dot a(t)} \right|} {\text{d}}t \end{split} $ | (6) |
式中:
将上述连续时间模型转化为离散时间模型,假设采样周期是
| $ \left\{ {\begin{array}{*{20}{l}} {x(k + 1) - x(k) = v(k)d + \dfrac{{{d^2}}}{{2m}}(F(k) - f)} \\ {v(k + 1) - v(k) = \dfrac{d}{m}(F(k) - f)} \end{array}} \right. $ | (7) |
约束(2)转换为
| $ x({k_{j,{\text{out}}}}) \leqslant {l_j},{\text{ }}j = 1,2, \cdots ,J $ | (8) |
式中:
约束(3)转换为
| $ 0 \leqslant v(k) \leqslant {v_{\max }} $ | (9) |
约束(4)转换为
| $ {F_{\min }} \leqslant F(k) \leqslant {F_{\max }} $ | (10) |
乘坐舒适度函数表示为
| $ a(k + 1) - a(k) = \frac{1}{m}\left( {F(k + 1) - F(k)} \right) $ | (11) |
因此目标函数可以表示为
| $ \begin{split} \psi = & \sum\nolimits_{k = 0}^{N - 1} {\alpha {F^2}(k)} + \sum\nolimits_{j = 1}^J {(\beta {{(x({k_{j,{\text{in}}}}) - {l_j})}^2}} + \theta ({v^2}({k_{j,{\text{in}}}}))) +\hfill \\ & \sum\nolimits_{k = 0}^{N - 2} {\gamma \left| {F(k + 1) - F(k)} \right|}\\[-15pt] \end{split} $ | (12) |
式中:
整理上述目标函数和约束条件,最优运行控制优化问题可表示为
| $\begin{aligned} \min \psi= \sum_{k=0}^{N-1} \alpha F^{2}(k)+\sum_{j=1}^{J}\left(\beta\left(x\left(k_{j, \text { in }}\right)-l_{j}\right)^{2}+\right.\\\left.\theta\left(v^{2}\left(k_{j, \text { in }}\right)\right)\right)+\sum_{k=0}^{N-2} \gamma|F(k+1)-F(k)| \\ x(k+1)-x(k)=v(k) d+\frac{d^{2}}{2 m}(F(k)-f) \\ v(k+1)-v(k)=\frac{d}{m}(F(k)-f) \\ x\left(k_{j, \text { out }}\right) \leqslant l_{j}, j=1,2, \cdots, J \\ 0 \leqslant v(k) \leqslant v_{\max } \\ F_{\min } \leqslant F(k) \leqslant F_{\max } \end{aligned}$ | (13) |
接下来将该最优控制模型转化为对称交替方向乘子法可求解形式。首先列车运行动力学方程(7)可以写为
| $ {\boldsymbol{\zeta}} (k + 1) = {\boldsymbol{C\zeta}} (k) + {\boldsymbol{D}}F(k) + {\boldsymbol{E}} $ | (14) |
式中:
| $ {\boldsymbol{\zeta}} (k)={\left[x(k),\text{ }v(k)\right]}^{\text{T}},{\boldsymbol{C}}=\left[\begin{array}{cc}1& d\\ 0& 1\end{array}\right] $ |
| $ {\boldsymbol{D}}=\left[\begin{array}{c}\dfrac{{d}^{2}}{2m}\\ \dfrac{d}{m}\end{array}\right],{\boldsymbol{E}}\text=\left[\begin{array}{l}-\dfrac{{d}^{2}f}{2m}\\ -\dfrac{df}{m}\end{array}\right] $ |
将状态量
| $\begin{array}{c} {\boldsymbol{w}} = {[F(0),{\rm{ }}F(1),{\rm{ }} \cdots ,{\rm{ }}F(N - 1),{\rm{ }}{\boldsymbol{\zeta}} {(1)^{\rm{T}}},{\rm{ }} \cdots ,{\rm{ }}{\boldsymbol{\zeta}} {(N)^{\rm{T}}}]^{\rm{T}}} \hfill \\ {\text{ }}{\boldsymbol{w}} \in {\mathbb{R}^{3N}} \hfill \\ \end{array} $ |
结合式(14),关于向量
| $ {\boldsymbol{Aw}} = {\boldsymbol{B}} $ |
式中:
| $ {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{r}} { - {\boldsymbol{D}}} & {\boldsymbol{O}} & {\boldsymbol{O}} & \cdots & {\boldsymbol{O}} & {\boldsymbol{I}} & {\boldsymbol{O}} & \cdots & {\boldsymbol{O}} & {\boldsymbol{O}} \\ {\boldsymbol{O}} & {- {\boldsymbol{D}}} & {\boldsymbol{O}} & \cdots & {\boldsymbol{O}} & { - {\boldsymbol{C}}} & {\boldsymbol{I}} & \cdots & {\boldsymbol{O}} & {\boldsymbol{O}} \\ {\boldsymbol{O}} & {\boldsymbol{O}} & { - {\boldsymbol{D}}} & \cdots & {\boldsymbol{O}} & {\boldsymbol{O}} & { - {\boldsymbol{C}}} & \cdots & {\boldsymbol{O}} & {\boldsymbol{O}} \\ \vdots & \vdots & \vdots & & \vdots & \vdots & \vdots & & \vdots & \vdots \\ {\boldsymbol{O}} & {\boldsymbol{O}} & {\boldsymbol{O}} & \cdots & { - {\boldsymbol{D}}} & {\boldsymbol{O}} & {\boldsymbol{O}} & \cdots & { - {\boldsymbol{C}}} & {\boldsymbol{I}} \end{array}} \right] \in {\mathbb{R}^{2N \times 3N}} $ |
| $ {\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{C\zeta}} (0) + {\boldsymbol{E}}} \\ {\boldsymbol{E}} \\ {\boldsymbol{E}} \\ \vdots \\ {\boldsymbol{E}} \end{array}} \right]{\text{ }} \in {\mathbb{R}^{2N}} $ |
其中,O为零矩阵。
当采样时刻满足约束
| $ \begin{array}{c} {\overline{{\boldsymbol{U}}}}_{j}={\left[{l}_{j},\text{ }{v}_{\mathrm{max}},\text{ }\cdots ,\text{ }{l}_{j},\text{ }{v}_{\mathrm{max}}\right]}^{{\rm{T}}}\in {\mathbb{R}}^{2{\kappa }_{j}},{\underline {{\boldsymbol{U}}} _j} = {{\boldsymbol{O}}_{2{\kappa _j} \times 1}}\\ {\kappa _j} = {k_{j,{\text{out}}}} - {k_{j - 1,{\text{out}}}},{\text{ }}\displaystyle\sum\nolimits_{j = 1}^J {{\kappa _j}} = N \end{array} $ |
于是
| $ \underline{{\boldsymbol{w}}} \leqslant {\boldsymbol{w}} \leqslant \overline {\boldsymbol{w}} $ |
式中:
| $\overline {\boldsymbol{w}} = {[{\boldsymbol{F}}_{{\rm{total}}\_{\rm{max}}}^{\rm{T}},{\overline {\boldsymbol{U}}_1^{\rm{T}}},{\overline {\boldsymbol{U}}_2^{\rm{T}}},\; \cdots ,\;{\overline {\boldsymbol{U}}_J^{\rm{T}}}]^{\rm{T}}}\in {\mathbb{R}^{3N}} $ |
| $ \underline{{\boldsymbol{w}}} = {[ {\boldsymbol{F}}_{{\text{total\_min}}}^{\text{T}},{\text{ }}{{\underline{{\boldsymbol{U}}} }_1^{\text{T}}},{\text{ }}{{\underline{{\boldsymbol{U}}} }_2^{\text{T}}},{\text{ }} \cdots ,{\text{ }}{{\underline{{\boldsymbol{U}}} }_J^{\text{T}}} ]^\text{T}} \in {\mathbb{R}^{3N}} $ |
| $ \begin{split} &{{\boldsymbol{F}}_{{\text{total\_max}}}} = {\left[ {{F_{\max }},{\text{ }} \cdots ,{\text{ }}{F_{\max }}} \right]^{\text{T}}} \in {\mathbb{R}^N}\\ &{{\boldsymbol{F}}_{{\text{total\_min}}}} = {\left[ {{F_{\min }},{\text{ }} \cdots ,{\text{ }}{F_{\min }}} \right]^{\text{T}}} \in {\mathbb{R}^N} \end{split} $ |
除此之外,对目标函数也进行相应转化,可以表示为
| $ \psi = {({\boldsymbol{w}} - {\boldsymbol{p}})^{\text{T}}}{\boldsymbol{Q}}({\boldsymbol{w}} - {\boldsymbol{p}}) + \gamma {\left\| {{\boldsymbol{Lw}}} \right\|_1} $ |
式中:
| $ {\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{c}} {\boldsymbol{R}}&{\boldsymbol{O}}&{\boldsymbol{ O}}& \cdots &{\boldsymbol{O}} \\ {\boldsymbol{O}}&{{{\boldsymbol{Q}}_1}}&{\boldsymbol{O}}& \cdots &{\boldsymbol{O}} \\ {\boldsymbol{O}}&{\boldsymbol{O}}&{{{\boldsymbol{Q}}_2}}& \cdots &{\boldsymbol{O}} \\ \vdots & \vdots & \vdots & & \vdots \\ {\boldsymbol{O}}&{\boldsymbol{O}}&{\boldsymbol{O}}& \cdots &{{{\boldsymbol{Q}}_J}} \end{array}} \right] \in {\mathbb{R}^{3N \times 3N}},{\boldsymbol{R}}{\text{ = }}\alpha {I_N} $ |
| $ {{\boldsymbol{Q}}_j} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{O}}_{{{{\mu }}_{{j}}}}}}&{\boldsymbol{O}}&{\boldsymbol{O}} \\ {\boldsymbol{O}}&{\boldsymbol{\varOmega }}&{\boldsymbol{O}} \\ {\boldsymbol{O}}&{\boldsymbol{O}}&{{{\boldsymbol{O}}_{{{{\eta }}_{{j}}}}}} \end{array}} \right] \in {\mathbb{R}^{2{\kappa _j} \times 2{\kappa _j}}},{\text{ }}{\boldsymbol{\varOmega }} = \left[ {\begin{array}{*{20}{c}} \beta &0 \\ 0&\theta \end{array}} \right] \in {\mathbb{R}^{2 \times 2}} $ |
| $ \begin{array}{c} {\mu _j} = 2({k_{j,{\text{in}}}} - {k_{j - 1,{\text{out}}}} - 1{\text{), }}{\eta _j} = 2({k_{j,{\text{out}}}} - {k_{j,{\text{in}}}}) \hfill \\ {\mu _j} + {\eta _j} + 2 = 2{\kappa _j} \hfill \\ \end{array} $ |
| $ \tilde {\boldsymbol{L}} = \left[ {\begin{array}{*{20}{r}} { - 1}&1&0&0& \cdots &0&0 \\ 0&{ - 1}&1&0& \cdots &0&0 \\ 0&0&{ - 1}&1& \cdots &0&0 \\ \vdots & \vdots & \vdots & \vdots & & \vdots & \vdots \\ 0&0&0&0& \cdots &{ - 1}&1 \end{array}} \right] \in {\mathbb{R}^{(N - 1) \times N}} $ |
| $ {\boldsymbol{L}} = [ {{\boldsymbol{\tilde L}},{\text{ }}{{\boldsymbol{O}}_{(N - 1) \times 2N}}} ] \in {\mathbb{R}^{(N - 1) \times 3N}} $ |
| $ {\text{ }}{{\boldsymbol{\hat p}}_j} = {[ {{{\boldsymbol{O}}_{1 \times {\mu _j}}},{\text{ }}{l_j},{\text{ }}0,{\text{ }}{{\boldsymbol{O}}_{1 \times {\eta _j}}}} ]^{\text{T}}} \in {\mathbb{R}^{2{\kappa _j}}} $ |
| $ {\boldsymbol{p}} = {[ {{{\boldsymbol{O}}_{1 \times N}},{\text{ }}{\boldsymbol{\hat p}}_1^{\text{T}},{\text{ }}{\boldsymbol{\hat p}}_2^{\text{T}},{\text{ }} \cdots ,{\text{ }}{\boldsymbol{\hat p}}_J^{\text{T}}} ]^{\text{T}}} \in {\mathbb{R}^{3N}} $ |
综上所述,将离散最优运行控制问题(13)表述为
| $ \begin{split} & \min {\text{ }}\psi = {({\boldsymbol{w}} - {\boldsymbol{p}})^{\text{T}}}{\boldsymbol{Q}}({\boldsymbol{w}} - {\boldsymbol{p}}) + \gamma {\left\| {{\boldsymbol{Lw}}} \right\|_1} \hfill \\ &\qquad {\rm{s}}.{\rm{t}}.\left\{ \begin{array}{l} {\boldsymbol{Aw}} = {\boldsymbol{B}} \hfill \\ {\text{ }}\underline{{\boldsymbol{w}}} \leqslant {\boldsymbol{w}} \leqslant \overline {\boldsymbol{w}} \end{array} \right.\\ \\ \end{split} $ | (15) |
在上一节得到了考虑乘坐舒适度的列车最优运行控制模型。本节给出基于对称交替方向乘子法求解该模型的具体步骤。首先最优控制问题(15)可以转化为
| $ \begin{split} & \min {\text{ }}\psi = f({\boldsymbol{w}}) + g({\boldsymbol{Z}}) = {({\boldsymbol{w}} - {\boldsymbol{p}})^{\text{T}}}{\boldsymbol{Q}}({\boldsymbol{w}} - {\boldsymbol{p}}) + \gamma {\left\| {\boldsymbol{Z}} \right\|_1} \hfill \\ &\qquad {\rm{s}}.{\rm{t}}.\left\{ \begin{array}{l} {\boldsymbol{Lw}} = {\boldsymbol{Z}} \hfill \\ {\text{ }}{\boldsymbol{w}} \in W \end{array} \right.\\ \\ \end{split} $ | (16) |
式中:
问题(16)的增广拉格朗日形式可以表示为
| $\begin{split} {\psi _\rho }({\boldsymbol{w}},{\boldsymbol{Z}},{\boldsymbol{\lambda }}) =& {({\boldsymbol{w}} - {\boldsymbol{p}})^{\rm{T}}}{\boldsymbol{Q}}({\boldsymbol{w}} - {\boldsymbol{p}}) + \gamma {\left\| {\boldsymbol{Z}} \right\|_1}+\\ & {{\boldsymbol{\lambda }}^{\rm{T}}}({\boldsymbol{Lw}} - {\boldsymbol{Z}}) + \frac{\rho }{2}\left\| {{\boldsymbol{Lw}} - {\boldsymbol{Z}}} \right\|_2^2,{\boldsymbol{w}} \in W \end{split}$ | (17) |
式中:
| $ {{\boldsymbol{w}}^{k + 1}} = \arg \mathop {\min }\limits_{{\boldsymbol{w}} \in W} {\text{ }}{\psi _\rho }({\boldsymbol{w}},{{\boldsymbol{Z}}^k},{{\boldsymbol{\lambda }}^k}) $ | (18) |
| $ {{\boldsymbol{\lambda }}^{k + {1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}} = {{\boldsymbol{\lambda }}^k} + \rho ({\boldsymbol{L}}{{\boldsymbol{w}}^{k + 1}} - {{\boldsymbol{Z}}^k}) $ | (19) |
| $ {{\boldsymbol{Z}}^{k + 1}} = \arg \mathop {\min }\limits_Z {\text{ }}{\psi _\rho }({{\boldsymbol{w}}^{k + 1}},{\boldsymbol{Z}},{{\boldsymbol{\lambda }}^{k + {1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}) $ | (20) |
| $ {{\boldsymbol{\lambda }}^{k + 1}} = {{\boldsymbol{\lambda }}^{k + {1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}} + \rho ({\boldsymbol{L}}{{\boldsymbol{w}}^{k + 1}} - {{\boldsymbol{Z}}^{k + 1}}) $ | (21) |
直到
对称交替方向乘子法将
| $ \begin{split} {{\boldsymbol{w}}^{k + 1}} = & \arg \mathop {\min }\limits_{{\boldsymbol{w}} \in W} {\text{ }}{{\boldsymbol{w}}^{\text{T}}}({\boldsymbol{Q}} + \frac{\rho }{2}{{\boldsymbol{L}}^{\text{T}}}{\boldsymbol{L}}){\boldsymbol{w}} -\hfill \\ & (2{{\boldsymbol{p}}^{\text{T}}}{\boldsymbol{Q}} - \rho (\frac{1}{\rho }{({{\boldsymbol{\lambda }}^k})^{\text{T}}} - {({{\boldsymbol{Z}}^k})^{\text{T}}}){\boldsymbol{L}}){\boldsymbol{w}} \end{split}$ |
内点法是解决这类问题的有效方法。详细步骤可以参考文献[24]。
2.2 软阈值法求解Z最小化问题利用软阈值法[25]可求解混合
| $ \begin{array}{c} {{\boldsymbol{\lambda }}^{\text{T}}}({\boldsymbol{Lw}} - {\boldsymbol{Z}}) + \dfrac{\rho }{2}\left\| {{\boldsymbol{Lw}} - {\boldsymbol{Z}}} \right\|_2^2 = {{\boldsymbol{\lambda }}^{\text{T}}}{\boldsymbol{r}} + \dfrac{\rho }{2}\left\| {\boldsymbol{r}} \right\|_2^2 = \hfill \\ \dfrac{\rho }{2}\left\| {{\boldsymbol{r}} + \dfrac{\boldsymbol{\lambda }}{\rho }} \right\|_2^2 - \dfrac{\rho }{2}\left\| \dfrac{\boldsymbol{\lambda }}{\rho } \right\|_2^2 \end{array} $ |
于是Z最小化迭代步骤可以表示为
| $ {{\boldsymbol{Z}}^{k + 1}} = \arg \mathop {\min }\limits_{\boldsymbol{Z}} {\text{ }}\gamma {\left\| {\boldsymbol{Z}} \right\|_1} + \frac{\rho }{2}\left\| {{\boldsymbol{Z}} - {\boldsymbol{Lw}} -\frac{\boldsymbol{\lambda }}{\rho }}\right\|_2^2 $ | (22) |
令
| $ z_{g,{\text{opt}}}^{k + 1} = \arg \mathop {\min }\limits_{{z_g}} {\text{ }}\gamma | {{z_g}} | + \frac{\rho }{2}{({z_g} - {u_g})^2} $ |
式中:
| $ h({z_g}) = {({z_g} - {u_g})^2}{\text{ + }}\frac{{2\gamma }}{\rho }| {{z_g}} | $ | (23) |
的最小值。对式(23)求导有
| $ \frac{{{\text{d}}h({z_g})}}{{{\text{d}}{z_g}}} = 2({z_g} - {u_g}) + \frac{{2\gamma }}{\rho }{{\rm{sgn}}} ({z_g}) $ |
令
| $ {z_g} = {u_g} - \frac{\gamma }{\rho }{{\rm{sgn}}} ({z_g}) $ |
分3种情况进行讨论,分别为
| $ z_{g,{\rm{opt}}}^{k + 1} = {\text{soft}}({u_g},\frac{\gamma }{\rho }) = \left\{ {\begin{array}{*{20}{l}} {{u_g} + \dfrac{\gamma }{\rho },{\text{ }}{u_g} \lt - \dfrac{\gamma }{\rho }} \\ {0,{\text{ }}| {{u_g}} | \leqslant \dfrac{\gamma }{\rho }} \\ {{u_g} - \dfrac{\gamma }{\rho },{\text{ }}{u_g} \gt \dfrac{\gamma }{\rho }} \end{array}} \right. $ |
由此,子问题变量Z最优值可以表示为
| $ {{\boldsymbol{Z}}^{k + 1}} = [ {\begin{array}{*{20}{c}} {z_{1,{\text{opt}}}^{k + 1}}&{z_{2,{\text{opt}}}^{k + 1}}& \cdots &{z_{N - 1,{\text{opt}}}^{k + 1}} \end{array}} ] = {\text{soft}}({{\boldsymbol{u}}^{k + 1}},\frac{\gamma }{\rho }) $ |
综上所述,在对称交替方向乘子法的一次迭代求解过程中,分别利用内点法更新
SADMM迭代的终止准则是原始可行性残差和对偶可行性残差必须小于给定值
| $ {\| {{{\boldsymbol{r}}^k}} \|_2} \leqslant {\varepsilon ^{{\text{pri}}}}和{\| {{{\boldsymbol{s}}^k}} \|_2} \leqslant {\varepsilon ^{{\text{dual}}}} $ |
式中:
| $ {\varepsilon ^{{\text{pri}}}} = \sqrt N {\varepsilon ^{{\text{abs}}}} + {\varepsilon ^{{\text{rel}}}}\max \{ {\| {{\boldsymbol{L}}{{\boldsymbol{w}}^k}} \|_2},{\text{ }}{\| {{{\boldsymbol{Z}}^k}} \|_2}\} $ |
| $ {\varepsilon ^{{\text{dual}}}} = \sqrt N {\varepsilon ^{{\text{abs}}}} + {\varepsilon ^{{\text{rel}}}}{\| {{{\boldsymbol{\lambda}} ^k}} \|_2} $ |
| $ {\| {{{\boldsymbol{r}}^k}} \|_2} = \frac{1}{\rho }{\| {{\boldsymbol{L}}{{\boldsymbol{w}}^k} - {{\boldsymbol{Z}}^k}} \|_2} $ | (24) |
| $ {\| {{{\boldsymbol{s}}^k}} \|_2} = N{\rho ^2}\| {{{\boldsymbol{Z}}^k} - {{\boldsymbol{Z}}^{k - 1}}} \|{}_2 $ | (25) |
式(24)~(25)中:
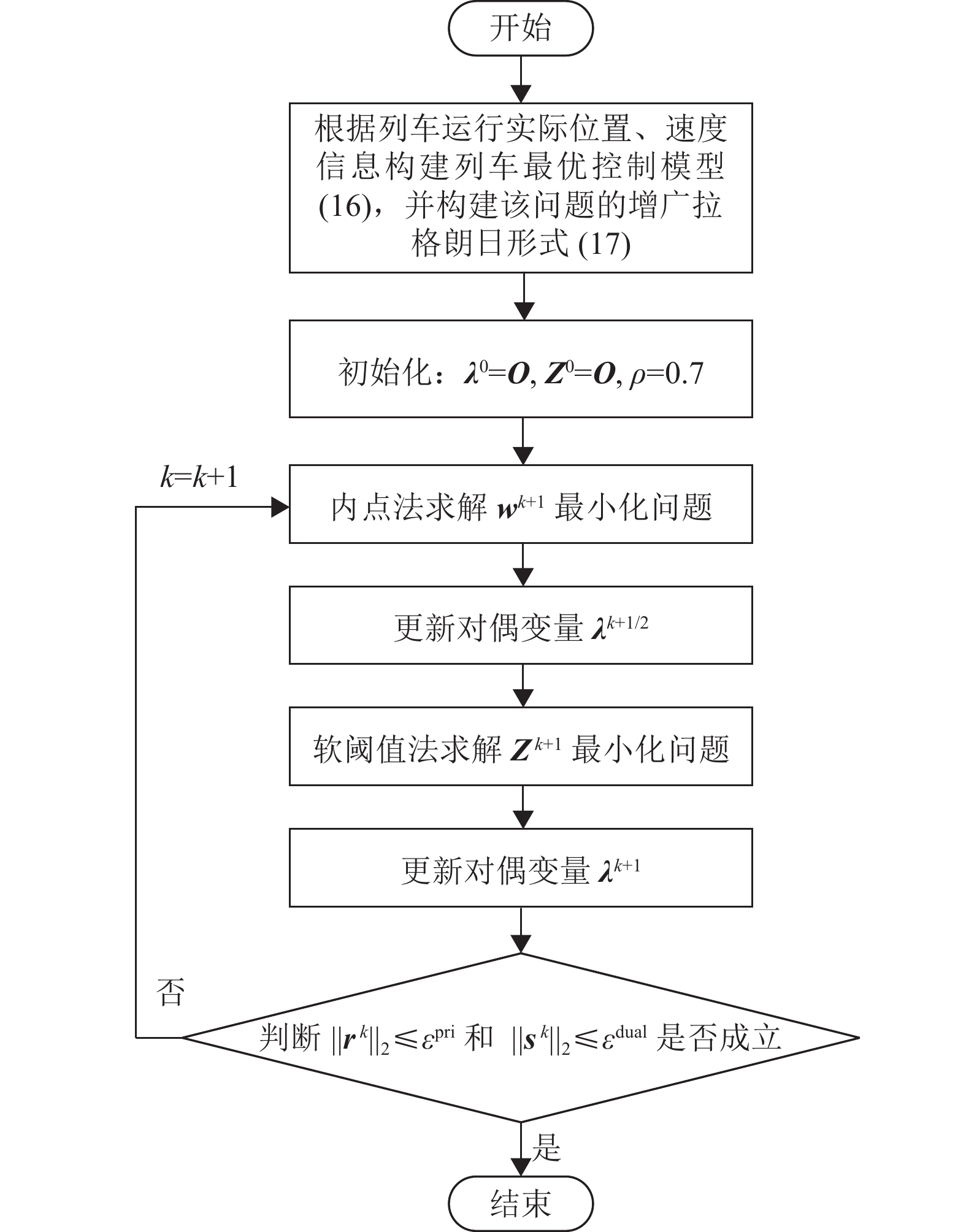
步骤1:根据列车实际运行情况,构建列车最优控制模型(16),并构建该问题的增广拉格朗日形式(17)。
步骤2:初始化
步骤3:利用内点法求解
| $ \begin{split} {{\boldsymbol{w}}^{k + 1}} = & \arg \mathop {\min }\limits_{{\boldsymbol{w}} \in W} {\rm{ }}{{\boldsymbol{w}}^{\rm{T}}}({\boldsymbol{Q}} + \frac{\rho }{2}{{\boldsymbol{L}}^{\rm{T}}}{\boldsymbol{L}}){\boldsymbol{w}}-\\ & (2{{\boldsymbol{p}}^{\rm{T}}}{\boldsymbol{Q}} - \rho (\frac{1}{\rho }{({{\boldsymbol{\lambda }}^k})^{\rm{T}}} - {({{\boldsymbol{Z}}^k})^{\rm{T}}}){\boldsymbol{L}}){\boldsymbol{w}} \end{split} $ |
步骤4:更新对偶变量
| $ {{\boldsymbol{\lambda }}^{k + {1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}} = {{\boldsymbol{\lambda }}^k} + \rho ({\boldsymbol{L}}{{\boldsymbol{w}}^{k + 1}} - {{\boldsymbol{Z}}^k}) $ |
步骤5:利用软阈值法求解Z最小化问题
| $ {{\boldsymbol{Z}}^{k + 1}} = {\rm{soft}}({{\boldsymbol{u}}^{k + 1}},{\gamma \mathord{\left/ {\vphantom {\gamma \rho }} \right. } \rho }) $ |
步骤6:更新对偶变量
| $ {{\boldsymbol{\lambda }}^{k + 1}} = {{\boldsymbol{\lambda }}^{k + {1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}} + \rho ({\boldsymbol{L}}{{\boldsymbol{w}}^{k + 1}} - {{\boldsymbol{Z}}^{k + 1}}) $ |
步骤7:若满足迭代终止条件
|
图 1 对称交替方向乘子法求解列车运行控制问题流程图 Figure 1 Train operation control via SADMM |
本节给出2个算例来说明算法的有效性。算例一采用对称交替方向乘子法求解得到列车运行曲线。算例二权衡旅客乘坐舒适度及列车运行能耗,生成不同
选定的线路包括4个车站,路段限速为300 km/h。列车G1的运行时刻表如表1所示。假设列车G1在S1站的出发时间为8:30,相邻两个车站之间的距离为100 km。列车参数如表2所示。权重系数
| 表 1 G1计划时刻表 Table 1 The scheduled timetable of train G1 |
| 表 2 列车基本参数 Table 2 Parameters of train G1 |
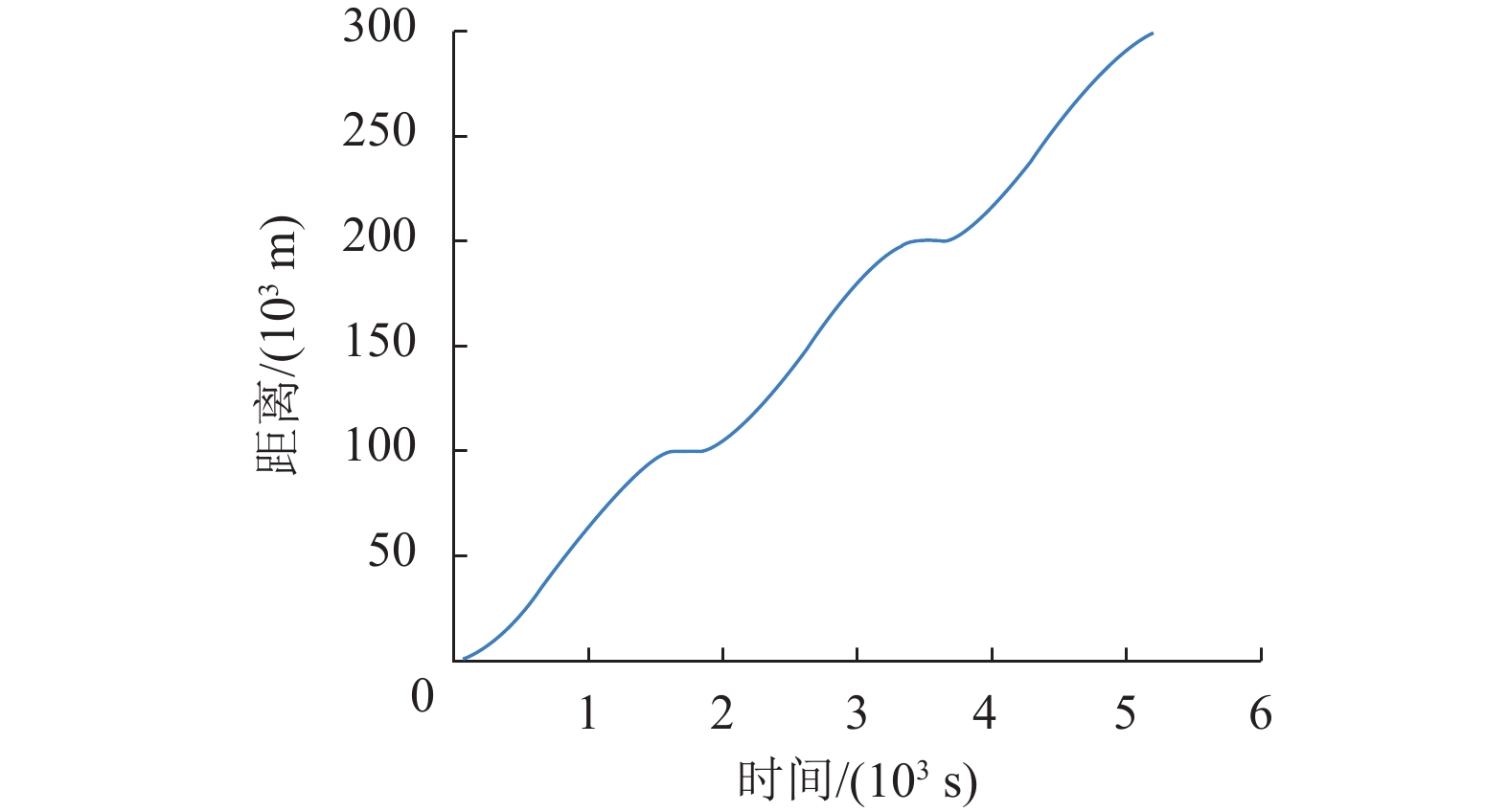
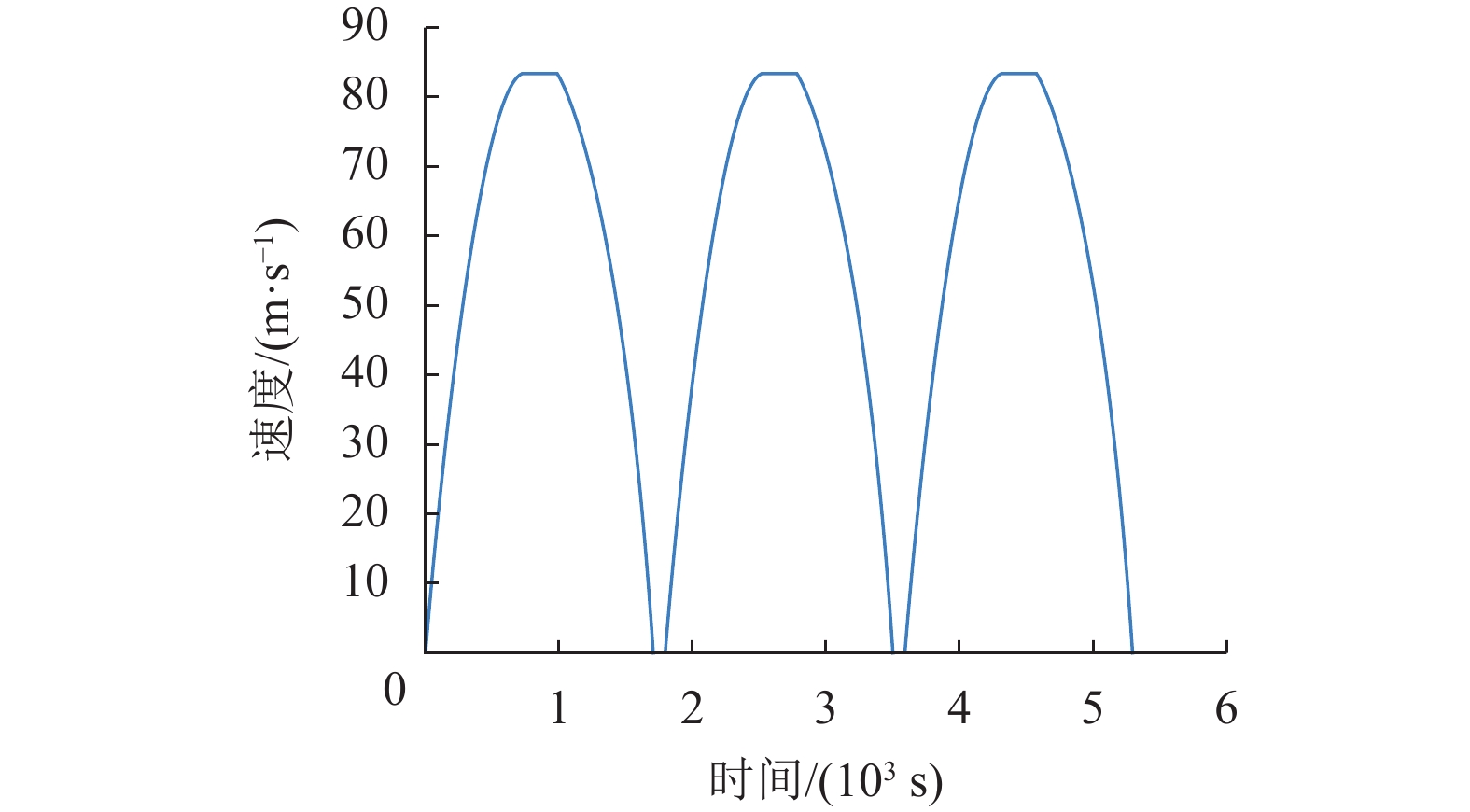
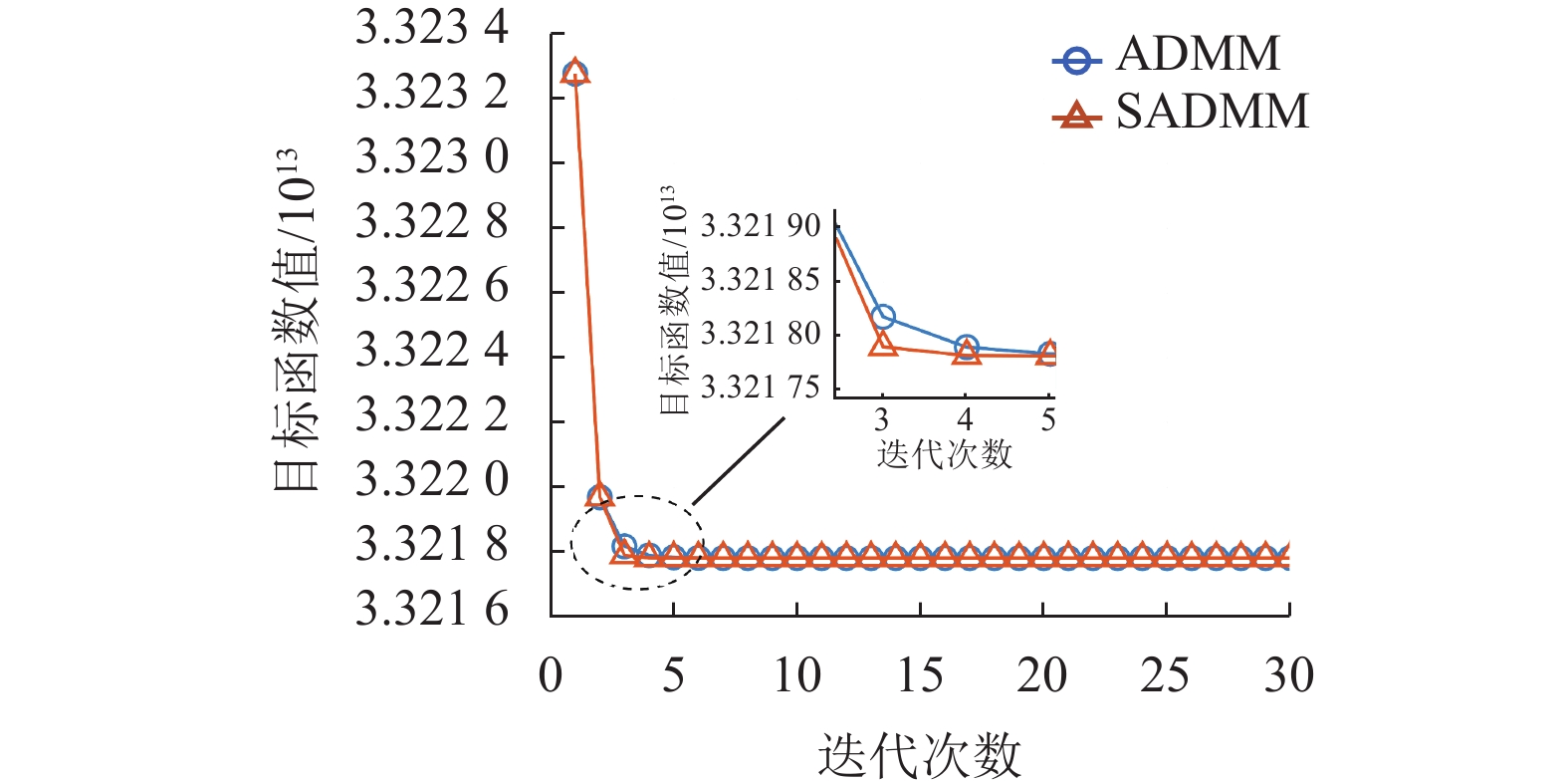
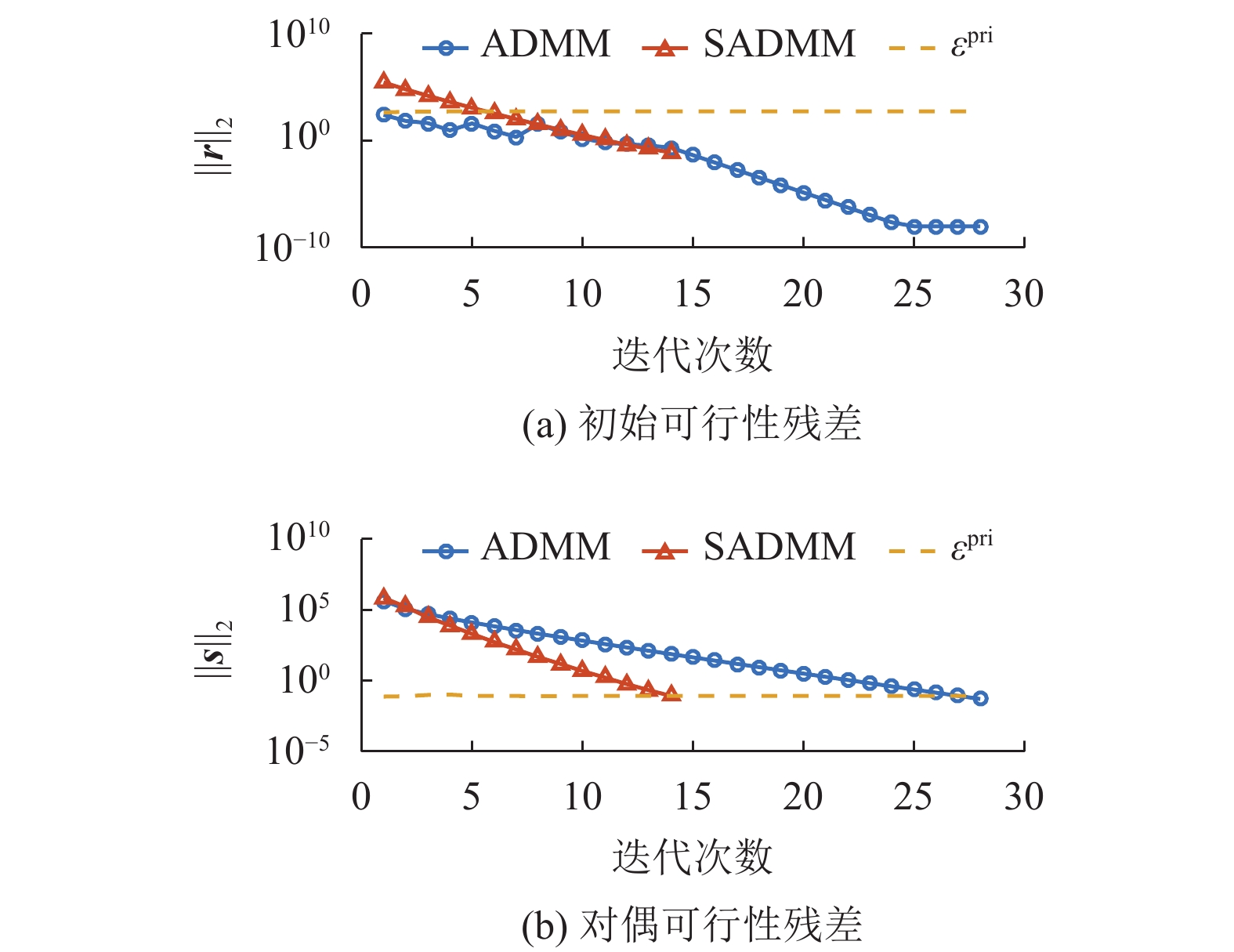
采用对称交替方向乘子法求解得到列车运行距离和列车运行速度随时间变化的曲线分别如图2和图3所示。列车先加速至300 km/h,保持匀速运行一段时间之后开始减速运行。该方案能够保证列车在预定时间内到站。图4和图5分别是交替方向乘子法和对称交替方向乘子法求解列车运行控制问题的收敛曲线图。图4对比了使用两种算法时目标函数值随迭代步数的变化,可以看出对称交替方向乘子法收敛速度更快。图5对比了使用两种算法时初始可行性残差和对偶可行性残差随迭代步数的变化,其中黄色虚线代表算法退出阈值。如图所示两种算法在迭代约5次后均达到初始可行性残差阈值,对称交替方向乘子法在迭代约14次达到对偶可行性残差阈值,交替方向乘子法需要迭代约28次。从图5中可以看出ADMM较快收敛至初始可行性残差阈值,但SADMM比ADMM更快收敛至对偶可行性残差阈值。综合初始可行性残差和对偶可行性残差随迭代次数的变化,可以看出SADMM先满足算法退出条件,求解效率更高。
|
图 2 G1列车运行距离曲线 Figure 2 The position trajectory of train G1 |
|
图 3 G1列车运行速度曲线 Figure 3 The velocity trajectory of train G1 |
|
图 4 基于ADMM和SADMM求解的目标函数值随迭代次数的变化 Figure 4 Evolution of the objective function value for ADMM and SADMM |
|
图 5 ADMM和SADMM收敛误差随迭代次数的变化 Figure 5 Evolution of the convergence residual for ADMM and SADMM |
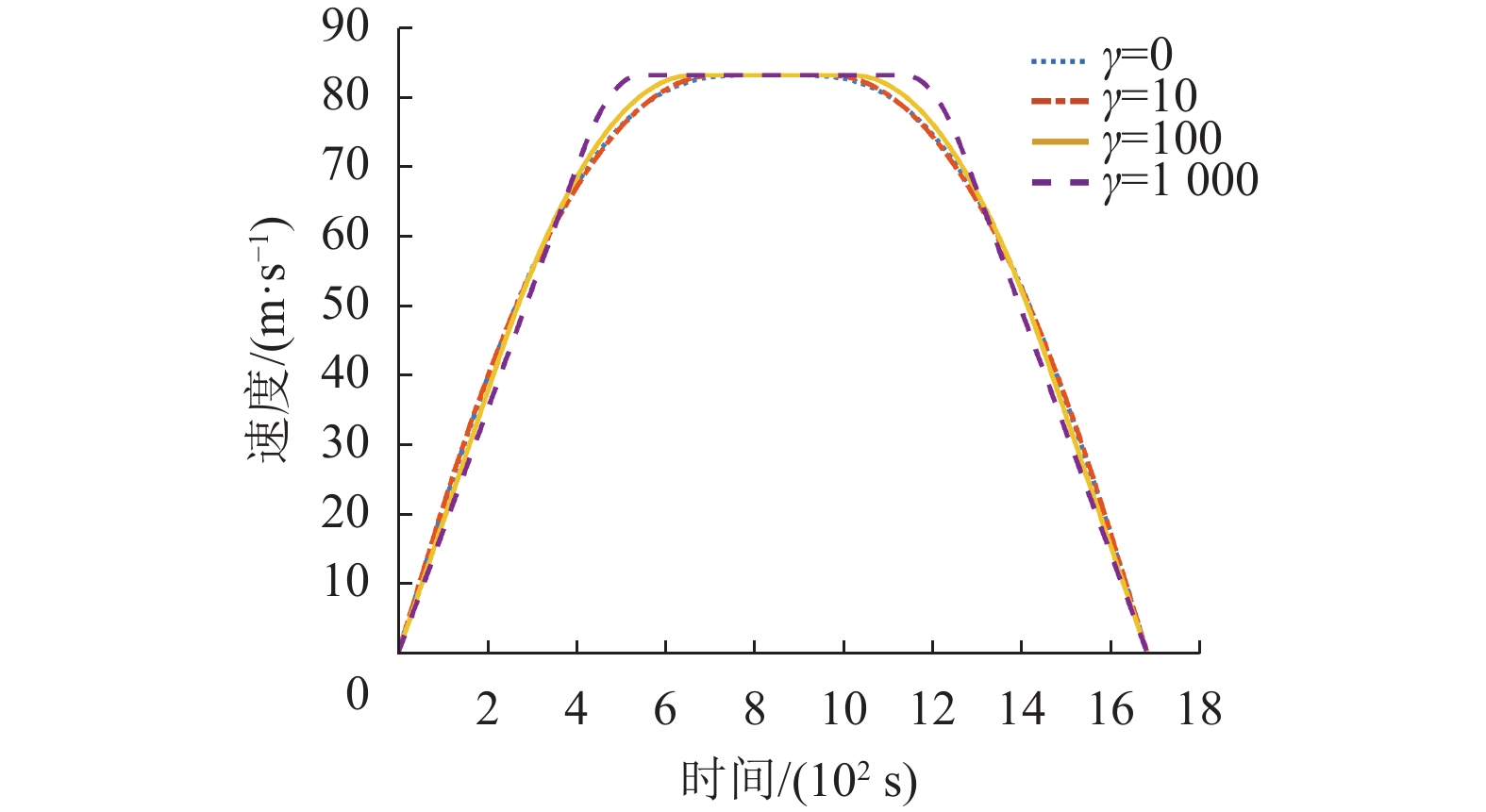
接下来讨论不同
|
表 3 不同
|
|
表 4 不同
|
|
图 6 不同
|
针对单列车在多个站点间的运行控制问题,本文提出一种基于对称交替方向乘子法的单列车最优运行控制方案。该方案有以下特点:(1) 在对称交替方向乘子法的求解框架下,分别采用内点法和软阈值法交替更新目标函数的两个决策变量。(2) 将当前列车运行位置、速度信息作为初始条件,可以快速求解得到列车运行曲线。(3) 通过调整惩罚系数,可以得到满足不同列车运行能耗和乘客舒适度需求的列车运行曲线。本文提出的方法可以为列车运行控制提供辅助决策,提升列车运行效率。
| [1] |
宁滨, 董海荣, 郑伟, 等. 高速铁路运行控制与动态调度一体化的现状与展望[J].
自动化学报, 2019, 45(12): 2208-2217.
NING B, DONG H R, ZHENG W, et al. Integration of train control and inline rescheduling for high-speed railways: challenges and future[J]. Acta Automatica Sinica, 2019, 45(12): 2208-2217. |
| [2] |
SONG Q, SONG Y, TANG T, et al. Computationally inexpensive tracking control of high-speed trains with traction/braking saturation[J].
IEEE Transactions on Intelligent Transportation Systems, 2011, 12(4): 1116-1125.
DOI: 10.1109/TITS.2011.2143409. |
| [3] |
AMIE R, ALBRECHT, HOWLETT P G, et al. Energy-efficient train control: from local convexity to global optimization and uniqueness[J].
Automatica, 2013, 49(10): 3072-3078.
DOI: 10.1016/j.automatica.2013.07.008. |
| [4] |
DONG H, NING B, CAI B, et al. Automatic train control system development and simulation for high-speed railways[J].
IEEE Circuits and Systems Magazine, 2010, 10(2): 6-18.
DOI: 10.1109/MCAS.2010.936782. |
| [5] |
DONG H, ZHU H, LI Y, et al. Parallel intelligent systems for integrated high-speed railway operation control and dynamic scheduling[J].
IEEE Transactions on Cybernetics, 2018, 48: 3381-3389.
DOI: 10.1109/TCYB.2018.2852772. |
| [6] |
FAIEGHI M, JALALI A, MASHHADI K E D M. Robust adaptive cruise control of high-speed trains[J].
ISA Transactions, 2014, 53(2): 533-541.
DOI: 10.1016/j.isatra.2013.12.007. |
| [7] |
MAO Z, TAO G, JIANG B, et al. Adaptive Actuator compensation of position tracking for high-speed trains with disturbances[J].
IEEE Transactions on Vehicular Technology, 2018, 67(7): 5706-5717.
DOI: 10.1109/TVT.2018.2808360. |
| [8] |
KHMELNITSKY E. On an optimal control problem of train operation[J].
IEEE Transactions on Automatic Control, 2000, 45(7): 1257-1266.
DOI: 10.1109/9.867018. |
| [9] |
ZHUAN X, XIA X. Speed regulation with measured output feedback in the control of heavy haul trains[J].
Automatica, 2008, 44(1): 242-247.
DOI: 10.1016/j.automatica.2007.05.002. |
| [10] |
LI S, YANG L, GAO Z. Robust sampled-data cruise control scheduling of high speed train[J].
Transportation Research Part C:Emerging Technologies, 2014, 46(46): 274-283.
|
| [11] |
BOTTE M, D’ACIERNO L. Dispatching and rescheduling tasks and their interactions with travel demand and the energy domain: models and algorithms[J].
Urban Rail Transit, 2018, 4(4): 163-197.
DOI: 10.1007/s40864-018-0090-8. |
| [12] |
FENANDEZ P M, SANCHIS I V, YEPES V, et al. A review of modelling and optimisation methods applied to railways energy consumption[J].
Journal of Cleaner Production, 2019, 222(10): 153-162.
|
| [13] |
LU S, HILLMANSEN S, HO T K, et al. Single-train trajectory optimization[J].
IEEE Transactions on Intelligent Transportation Systems, 2013, 14(2): 743-750.
DOI: 10.1109/TITS.2012.2234118. |
| [14] |
WANG Y, SCHUTTER B D, BOOM T, et al. Optimal trajectory planning for trains—a pseudospectral method and a mixed integer linear programming approach[J].
Transportation Research Part C:Emerging Technologies, 2013, 29(4): 97-114.
|
| [15] |
LIN F, FARDAD M, JOVANOVIC M R. Optimal control of vehicular formations with nearest neighbor interactions[J].
IEEE Transactions on Automatic Control, 2012, 57(9): 2203-2218.
DOI: 10.1109/TAC.2011.2181790. |
| [16] |
GABAY D, MERCIER B. A dual algorithm for the solution of nonlinear variational problems via finite element approximation[J].
Computers & Mathematics with Applications, 1976, 2(1): 17-40.
|
| [17] |
BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J].
Foundations & Trends in Machine Learning, 2010, 3(1): 1-122.
|
| [18] |
FU L, FARDAD M, JOVANOVIC M R. Design of optimal sparse feedback gains via the alternating direction method of multipliers[J].
IEEE Transactions on Automatic Control, 2013, 58(9): 2426-2431.
DOI: 10.1109/TAC.2013.2257618. |
| [19] |
LI S, YANG L, GAO Z. Distributed optimal control for multiple high-speed train movement: an alternating direction method of multipliers[J].
Automatica, 2020, 112: 108646-108652.
DOI: 10.1016/j.automatica.2019.108646. |
| [20] |
HE B, LIU H, WANG Z, et al. A strictly contractive Peaceman-Rachford splitting method for convex programming[J].
SIAM Journal on Optimization, 2014, 24(3): 1011-1040.
DOI: 10.1137/13090849X. |
| [21] |
HE B, MA F, YUAN X. Convergence study on the symmetric version of ADMM with larger step sizes[J].
SIAM Journal on Imaging Sciences, 2016, 9(3): 1467-1501.
DOI: 10.1137/15M1044448. |
| [22] |
JIAO Y, JIN Q, LU X, et al. Alternating direction method of multipliers for linear inverse problems[J].
SIAM Journal on Numerical Analysis, 2016, 54(4): 2114-2137.
DOI: 10.1137/15M1029308. |
| [23] |
YANG L, LUO J, XU Y, et al. A distributed dual consensus ADMM based on partition for DC-DOPF with carbon emission trading[J].
IEEE Transactions on Industrial Informatics, 2019, 16(3): 1858-1872.
|
| [24] |
NOCEDAL J, WRIGHT S J, MIKOSCH T V, et al. Numerical Optimization[M]. New York: Springer, 1999.
|
| [25] |
DONOHO D L, JOHNSTONE J M. Ideal spatial adaptation by wavelet shrinkage[J].
Biometrika, 1994, 81(3): 425-455.
DOI: 10.1093/biomet/81.3.425. |
 2022, Vol. 39
2022, Vol. 39
