2. 山东鲁软数字科技有限公司 智慧能源分公司,山东 济南 250000;
3. 山东正中信息技术股份有限公司,山东 济南 250014
2. Shaodong Luruan Digital Technology Co., Ltd., Smart Energy Branch, Jinan 250000, China;
3. Shandong Zhengzhong Information Technology Co., Ltd., Jinan 250014, China
PD/PID控制方法具有结构简单、易于工程实现的优点,因此被广泛应用于主动式悬架[1]、航天器[2]、机械臂[3]、轮椅外骨骼机器人[4]、双足机器人[5]、伺服机构[6]等工业领域。作为一类典型的线性控制方法,PD/PID方法与模型无关,其控制增益可单独调节。一个简单的PD/PID控制方法和适当的控制增益可保证实际应用中令人满意的控制性能。
众所周知,滑模控制(Sliding Mode Control, SMC)方法针对系统模型不确定性以及外界干扰具有较强的鲁棒性。为充分利用这些显著优势,学者们针对主动式悬架系统设计了几种类型的SMC方法[7-10]。值得指出的是,文献[7]通过估计不确定弹簧、阻尼器、载荷振动以及道路扰动的信息,构造了一种基于扰动观测器的SMC方法,不过该方法需要准确的簧上质量信息。在文献[8]中,针对模型未知项、时变位移以及速度约束的问题,提出了一种自适应SMC方法。在文献[9]中,为了减小驾驶员和乘客的头部加速度,提出了一种分数阶终端SMC方法。在文献[10]中,提出了可在有限时间内将系统状态轨迹驱动到指定的滑模面上的SMC方法,不过该方法依赖系统参数。综上可知,现有SMC方法仍存在需要一定的系统参数信息的问题,因此很难计算出其等效控制部分。因此,为了避免等效控制部分的计算,考虑了将PD部分替代SMC控制的等效部分。
在主动式悬架系统中,非线性因素如非线性刚度、阻尼等是不可避免的。现有的控制方法直接消除由悬架组件中的固有非线性传递的振动能量来改善乘坐舒适性,这会导致消耗额外的能量。然而,研究结果表明充分利用有益的非线性因素可以获得比线性系统更好的悬架性能[11]。此外,在不影响悬架性能的条件下,利用这些有益的非线性因素可以大大减少能量消耗[11-13]。因此,在本文之前的工作中,针对主动式悬架系统,设计了几种节能的鲁棒控制方法。更准确地说,在文献[11]中,针对主动式悬架系统设计了自适应模糊SMC方法,该方法可有效补偿系统参数不确定性、外部干扰和输入饱和的影响。然而,所设计的控制方法结构复杂,很难应用于实际工程中。在文献[12]中,充分利用好的扰动响应,设计了一种基于切换逻辑的饱和跟踪控制方法,该方法可以显著提高系统的暂态控制性能。然而,由于所设计的控制方法不连续,不可避免地会出现抖振现象,即控制器输出的高频振荡导致轨迹在滑模面附近快速振荡。在文献[13]中,采用神经网络方法处理未知/不确定的动力学模型。但是,所设计的控制方法不能保证控制输入在允许范围内,与实际应用相差甚远。不过这些结果清楚地表明,可以利用系统中有利的非线性并且在较少的能量消耗下达到控制目的。
在主动式悬架系统方面,性能改进一直是现有研究最受关注的课题。然而,至今为止易于工程实现、输入饱和以及减少能耗等实际问题并未很好地解决。针对上述几个问题,本文提出了一种新颖的饱和PD型滑模控制(饱和PD-SMC)方法。具体来说,通过利用独特的仿生X型参考模型中有益的非线性刚度和阻尼特性,在较少能耗的情况下实现主动式悬架系统卓越的隔振性能。为了增强鲁棒性,设计了具有简单结构的PD-SMC跟踪控制方法。此外,为防止控制输入超出允许范围,在控制器中引入了饱和函数。最后,实验结果验证了所提控制方法的有效性以及强鲁棒性。该方法的优点可描述如下。
(1) 充分利用主动式悬架系统固有的非线性特性,并有意地引入有益的仿生非线性刚度和阻尼特性,可以极大地提高悬架性能,并大大降低能耗。
(2) 该控制方法不需要精确的系统参数(如簧上/簧下质量),因此对不同/不确定的系统参数具有较强的鲁棒性。此外,所提出的饱和PD-SMC跟踪方法只包含跟踪误差、跟踪误差的时间导数以及簧上质量和簧下质量的名义值,易于工程实现。
(3) 所设计的控制方法具有PD控制方法的简单结构、SMC方法对扰动的强鲁棒性等特点。同时该方法充分考虑了控制输入的实际约束问题。
2 问题描述四分之一主动式悬架系统见图1,其动力学模型可描述为
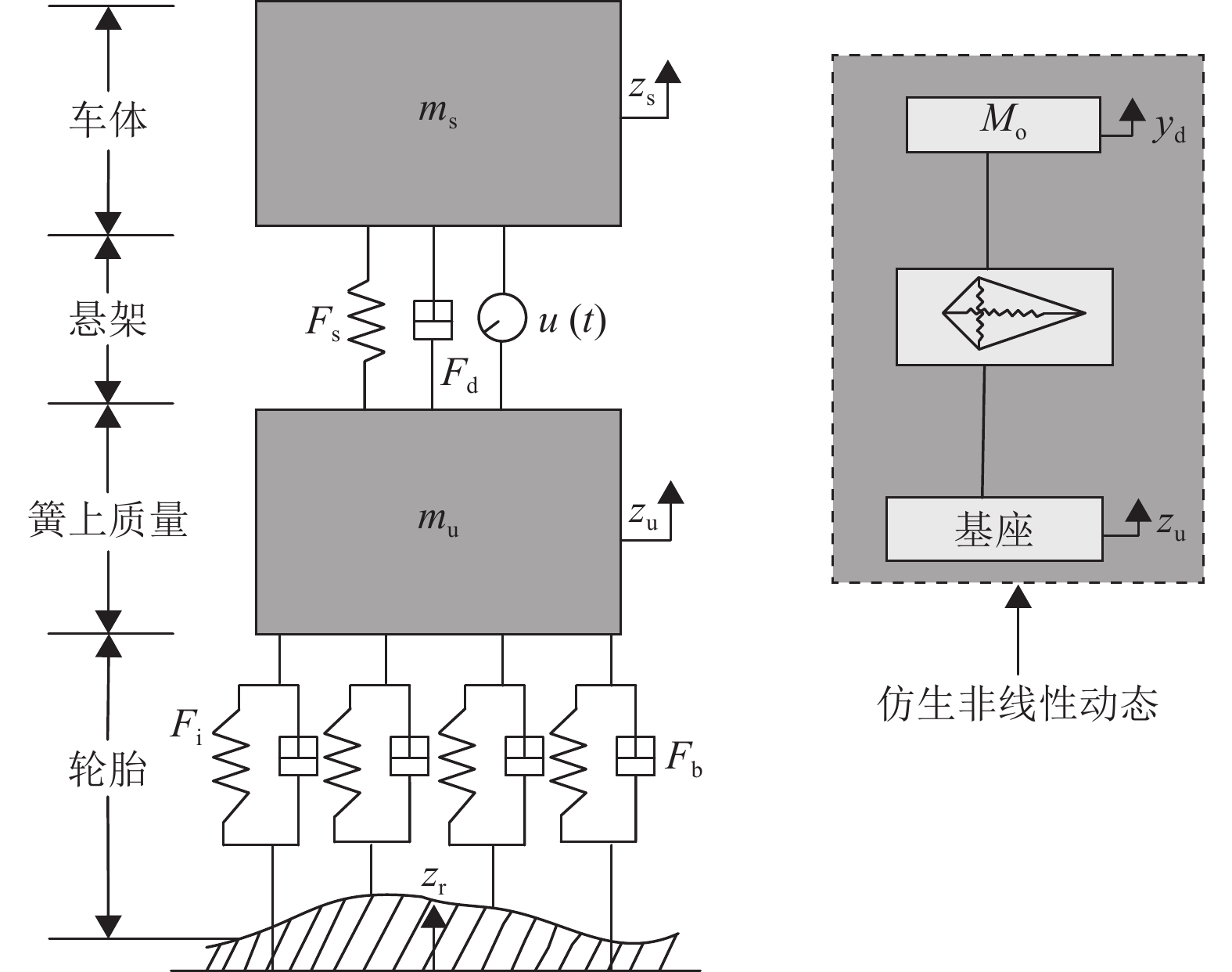
|
图 1 四分之一主动式悬架系统框图 Figure 1 Structure of a quarter-vehicle active suspension system |
| $ {m_{\rm{s}}}{\ddot z_{\rm{s}}} = - {F_{\rm{s}}}\left( {{z_{\rm{s}}},{z_{\rm{u}}}} \right) - {F_{\rm{d}}}\left( {{{\dot z}_{\rm{s}}},{{\dot z}_{\rm{u}}}} \right) + {d_1} + u\left( t \right) $ | (1) |
| $ \begin{split} {m_{\rm{u}}}{{\ddot z}_{\rm{u}}} =& {F_{\rm{s}}}\left( {{z_{\rm{s}}},{z_{\rm{u}}}} \right) + {F_{\rm{d}}}\left( {{{\dot z}_{\rm{s}}},{{\dot z}_{\rm{u}}}} \right) - {F_{\rm{t}}}\left( {{z_{\rm{u}}},{z_{\rm{r}}}} \right) \hfill -\\& {F_{\rm{b}}}\left( {{{\dot z}_{\rm{u}}},{{\dot z}_{\rm{r}}}} \right) + {d_2} - u\left( t \right) \end{split} $ | (2) |
式中:
本文的一个重要目标是构建一个具有理想非线性准零刚度的仿生隔振参考模型(如图1右侧所示),然后设计一种新颖的饱和PD-SMC跟踪控制方法使悬架行程
| $ \begin{split} & \frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}{{\ddot z}_{\rm{e}}}{\text{ = }} - \left[ {{F_{\rm{s}}}\left( {{z_{\rm{s}}},{z_{\rm{u}}}} \right){\text{ + }}{F_{\rm{d}}}\left( {{{\dot z}_{\rm{s}}},{{\dot z}_{\rm{u}}}} \right)} \right] + \frac{{{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}{d_1} \hfill -\\& \frac{{{m_{\rm{s}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}{d_2}{\text{ + }}\frac{{{m_{\rm{s}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}\left[ {{F_{{t}}}\left( {{z_{\rm{u}}},{z_{\rm{r}}}} \right) + {F_{\rm{b}}}\left( {{{\dot z}_{\rm{u}}},{{\dot z}_{\rm{r}}}} \right)} \right] \hfill +\\& u\left( t \right) ={\varDelta _1} + u\left( t \right) \\[-15pt] \end{split} $ | (3) |
式中:
| $ \begin{split} {\varDelta _1}{\text{ = }}& - \left[ {{F_{\rm{s}}}\left( {{z_{\rm{s}}},{z_{\rm{u}}}} \right){\text{ + }}{F_{\rm{d}}}\left( {{{\dot z}_{\rm{s}}},{{\dot z}_{\rm{u}}}} \right)} \right] + \frac{{{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}{d_1} - \\& \frac{{{m_{\rm{s}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}{d_2}{\text{ + }}\frac{{{m_{\rm{s}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}\left[ {{F_{\rm{t}}}\left( {{z_{\rm{u}}},{z_{\rm{r}}}} \right) + {F_{\rm{b}}}\left( {{{\dot z}_{\rm{u}}},{{\dot z}_{\rm{r}}}} \right)} \right] \end{split}$ | (4) |
为了更好地评估主动式悬架系统的控制性能,引入车体加速度
| $ {\text{RMS}}\left( {{{\ddot z}_{\rm{s}}}} \right) = \frac{1}{T}\int_0^T {\ddot z_{\rm{s}}^2} {\rm{d}}t $ | (5) |
| $ {\text{RMS}}\left( E \right) = \frac{1}{T}\int_0^T {\left( {{E^ + }\left( \tau \right)} \right)} {\rm{d}}\tau $ | (6) |
式中:
| $ {E^ + }\left( t \right) = \left\{ \begin{gathered} u\left( t \right){{\dot z}_{\rm{e}}},{\text{ if }}u\left( t \right){{\dot z}_{\rm{e}}} \gt 0 \hfill \\ 0,{\text{ else}} \hfill \\ \end{gathered} \right. $ | (7) |
假设1 针对主动式悬架系统,未知干扰
本节将构造饱和PD-SMC方法的整个框架。首先,建立仿生X型结构非线性系统模型。紧接着,设计饱和PD-SMC方法。最后,给出严格的稳定性证明。
3.1 仿生X型结构非线性系统模型由弹簧、旋转接头、连杆组成的多层仿生结构如图2所示,相应的系统参数如表1所示。
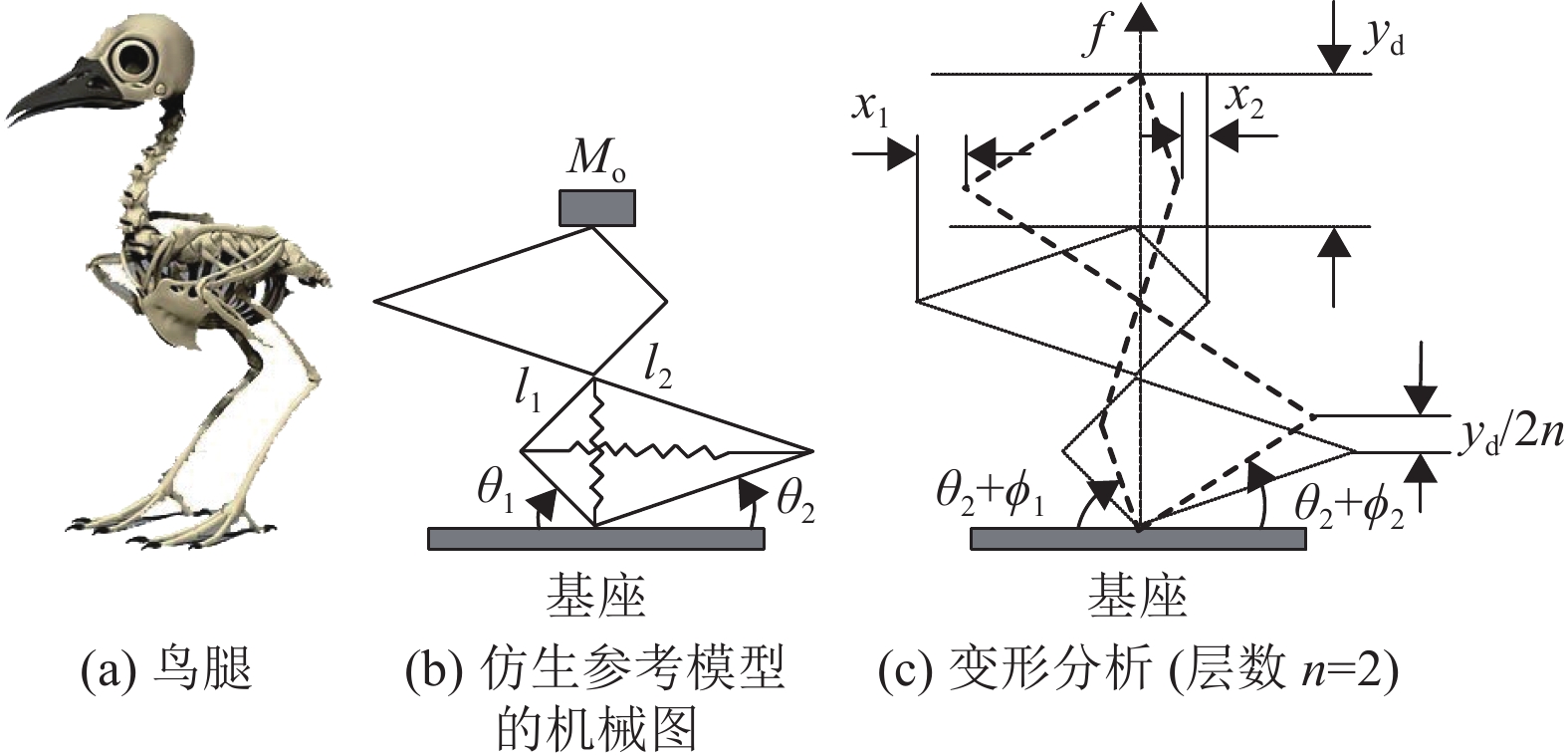
|
图 2 仿生参考模型 Figure 2 Bioinspired reference model |
| 表 1 仿生X型结构非线性系统模型 Table 1 Parameters of the bioinspired X-structured nonlinear system |
| $ {M_{\rm{o}}}{\ddot y_{\rm{d}}} + {p_1} + \frac{{{k_{\rm{v}}}}}{{{n^2}}}{y_{\rm{d}}} + {\mu _1}{\dot y_{\rm{d}}} + {\mu _2}{n_{\rm{x}}}{p_2}{\dot y_{\rm{d}}} = - {M_{\rm{o}}}{\ddot z_{\rm{u}}} $ | (8) |
式中:
| $ \begin{gathered} {p_1} = \frac{{{k_{\rm{h}}}\vartheta }}{{2n}}\left( {{l_1}\cos {\theta _1} - \sqrt {l_1^2 - {\vartheta ^2}} + {l_{\text{2}}}\cos {\theta _{\text{2}}} - \sqrt {l_2^2 - {\vartheta ^2}} } \right) \times\\ \qquad \Bigg( {\frac{1}{{\sqrt {l_1^2 - {\vartheta ^2}} }} + \frac{1}{{\sqrt {l_2^2 - {\vartheta ^2}} }}} \Bigg) \hfill \\ {p_2} = {\Bigg( {\frac{{{l_1}}}{{2n\sqrt {l_1^2 - {\vartheta ^2}} }} + \frac{{{l_2}}}{{2n\sqrt {l_2^2 - {\vartheta ^2}} }}} \Bigg)^2} \hfill \\ \end{gathered} $ |
式中:
为保证
| $ \left\{ \begin{gathered} {{\ddot y}_{\rm{d}}} = {\gamma _1}{\text{, }}{{\ddot y}_{\rm{d}}} \lt {\gamma _1}{\text{ }} \hfill \\ {M_{\rm{o}}}{{\ddot y}_{\rm{d}}} + {p_1} + \frac{{{k_{\rm{v}}}}}{{{n^2}}}{y_{\rm{d}}} + {\mu _1}{{\dot y}_{\rm{d}}} + {\mu _2}{n_{\rm{x}}}{p_2}{{\dot y}_{\rm{d}}} = - {M_{\rm{o}}}{{\ddot z}_{\rm{u}}}{\text{, }}{\gamma _1} \leqslant {{\ddot y}_{\rm{d}}} \leqslant {\gamma _2} \hfill \\ {{\ddot y}_{\rm{d}}} = {\gamma _2}{\text{, }}{{\ddot y}_{\rm{d}}} \gt {\gamma _2}{\text{ }} \hfill \\ \end{gathered} \right. $ | (9) |
备注1 受生物肢体运动启发的仿生肢状非线性结构(也称为X形结构)的特殊几何非线性会产生非常有益的等效非线性刚度和阻尼。现有研究已经证明,此仿生结构模型始终可以提供非常出色的准零刚度特性,具有高负载、低固有频率和宽隔振范围的优点[11-13]。与现有控制方法不同的是,所设计的控制方法以仿生非线性模型的动态输出作为参考轨迹,这样既可以避免消除主动式悬架系统有益的非线性响应,又可以在很大程度上发挥这些有益的因素来抑制振动。此外,所提出的控制方法可以消耗更少的控制能量,从而有助于提高系统的节能性能。
3.2 饱和PD-SMC方法设计为促进接下来控制器的设计,定义系统状态误差为
| $ e = {z_{\rm{e}}} - {y_{\rm{d}}} $ | (10) |
构造滑模面
| $ s = \dot e + 2\lambda \arctan e $ | (11) |
式中:
由式(3)和式(10)可得
| $ \begin{split} & \frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}\ddot e{\text{ = }}{\varDelta _1} + \frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}{{\ddot y}_{\rm{d}}} + u\left( t \right) = \\& \left( {{\varDelta _1} + \left( {\frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}} - \frac{{{{\overline m}_{\rm{s}}}{{\overline m}_{\rm{u}}}}}{{{{\overline m}_{\rm{s}}}{\text{ + }}{{\overline m}_{\rm{u}}}}}} \right){{\ddot y}_{\rm{d}}}} \right) + \frac{{{{\overline m}_{\rm{s}}}{{\overline m}_{\rm{u}}}}}{{{{\overline m}_{\rm{s}}}{\text{ + }}{{\overline m}_{\rm{u}}}}}{{\ddot y}_{\rm{d}}} + u\left( t \right) = \\& {\varGamma _1} + \frac{{{{\overline m}_{\rm{s}}}{{\overline m}_{\rm{u}}}}}{{{{\overline m}_{\rm{s}}}{\text{ + }}{{\overline m}_{\rm{u}}}}}{{\ddot y}_{\rm{d}}} + u\left( t \right) = {\varGamma _1} + \overline m{{\ddot y}_{\rm{d}}} + u\left( t \right) \\[-15pt] \end{split} $ | (12) |
式中:
| $ {\varGamma _1} = {\varDelta _1} + \left( {\frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}} - \overline m} \right){\ddot y_{\rm{d}}} $ | (13) |
由假设1以及式(9),不难得出
| $ \left| {{\varGamma _1}} \right| \leqslant \beta $ | (14) |
式中:
定理1 针对主动式悬架系统,饱和PD-SMC跟踪控制方法设计为
| $ u\left( t \right) = - \frac{{2{k_{\rm{p}}}}}{{\text{π}} }\arctan e - \frac{{2{k_{\rm{d}}}}}{{\text{π}} }\arctan {\dot e} - {k_{\rm{s}}}{{\rm{sgn}}} s - \overline m{\ddot y_{\rm{d}}} $ | (15) |
式中:
| $ \mathop {\lim }\limits_{t \to \infty } e = 0,{\text{ }}\mathop {\lim }\limits_{t \to \infty } \dot e = 0 $ | (16) |
与此同时,控制输入始终保持在允许的范围内:
| $ \left| {u\left( t \right)} \right| \leqslant {u_{\max }} $ | (17) |
式中
| $ \left\{ \begin{gathered} \lambda \lt \frac{1}{2} \hfill \\ {k_{\rm{p}}} \gt \lambda {\text{π}} \frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}} + \omega \hfill \\ {k_{\rm{s}}} \gt \beta \hfill \\ {k_{\rm{p}}} \gt \frac{1}{2}{\text{π}} {k_{\rm{d}}} \hfill \\ {k_{\rm{d}}} \geqslant \frac{{{{\text{π}} ^2}\lambda {m_{\rm{s}}}{m_{\rm{u}}}}}{{\left( {2 - \lambda } \right)\left( {{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}} \right)}}{\left( {1 + \sqrt {\frac{{2V\left( {{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}} \right)}}{{\left( {1 - 2\lambda } \right){m_{\rm{s}}}{m_{\rm{u}}}}}} } \right)^2} \hfill \\ \frac{{2{k_{\rm{p}}}}}{{\text{π}} } + \frac{{2{k_{\rm{d}}}}}{{\text{π}} } + {k_{\rm{s}}}{{\rm{sgn}}} \left( s \right) + \bar m\left\{ {\max \left( {\left| {{\gamma _1}} \right|,{\text{ }}\left| {{\gamma _2}} \right|} \right)} \right\} \leqslant {u_{\max }} \hfill \\ \end{gathered} \right. $ | (18) |
式中:
首先,引入李雅普诺夫候选函数
| $ \begin{split} V\left( t \right) =& \frac{1}{2}\frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}{{\dot e}^2} + \frac{{2{k_{\rm{p}}}}}{{\text{π}} }\left[ {e\arctan \left( e \right) - \frac{1}{2}\ln \left( {1 + {e^2}} \right)} \right] + \\& 2\lambda \frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}\dot e\arctan \left( {\dot e} \right) \hfill \\[-10pt] \end{split}$ | (19) |
紧接着,将证明以上函数是非负的。为此,整理式(19)的第2项:
| $ \begin{split} & \frac{{2{k_{\rm{p}}}}}{{\text{π}} }\left[ {e\arctan \left( e \right) - \frac{1}{2}\ln ( {1 + {e^2}} )} \right] = \\& \frac{{2\left( {{k_{\rm{p}}} - \omega } \right) + 2\omega }}{{\text{π}} }\left[ {e\arctan \left( e \right) - \frac{1}{2}\ln ( {1 + {e^2}} )} \right] \hfill \geqslant\\& \frac{{{k_{\rm{p}}} - \omega }}{{\text{π}} }{\arctan ^2}\left( e \right) + \frac{{2\omega }}{{\text{π}} }\left[ {e\arctan \left( e \right) - \frac{1}{2}\ln ( {1 + {e^2}} )} \right] \end{split} $ | (20) |
式中:
与此同时,计算式(19)的最后一项为
| $ \begin{split} & 2\lambda \frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}\dot e\arctan \left( {\dot e} \right) \geqslant - \lambda \frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}{\dot e^2} -\\& \lambda \frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}{\arctan ^2}\left( {\dot e} \right) \end{split} $ | (21) |
将式(20)、(21)代入式(19),可得
| $ \begin{split} V\left( t \right) =& \frac{1}{2}\frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}{{\dot e}^2} + \frac{{2{k_{\rm{p}}}}}{{\text{π}} }\left[ {e\arctan \left( e \right) - \frac{1}{2}\ln ( {1 + {e^2}} )} \right] + \\& 2\lambda \frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}\dot e\arctan \left( {\dot e} \right) \hfill \geqslant \frac{1}{2}\frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}\left( {1 - 2\lambda } \right){{\dot e}^2} + \\&\left( {\frac{{{k_{\rm{p}}} - \omega }}{{\text{π}} } - \lambda \frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}} \right){\arctan ^2}\left( e \right) + \\& \frac{{2\omega }}{{\text{π}} }\left[ {e\arctan \left( e \right) - \frac{1}{2}\ln ( {1 + {e^2}} )} \right] \\[-10pt] \end{split} $ | (22) |
由式(18)不难得出李雅普诺夫候选函数
| $ V\left( t \right) \geqslant 0 $ | (23) |
对式(19)两端关于时间求导,并将式(12)、(15)的结论代入所得结果,可得
| $ \begin{split} \dot V\left( t \right) = &\frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}\dot e\ddot e + \frac{{2{k_{\rm{p}}}}}{{\text{π}} }\dot e\arctan \left( e \right) + 2\lambda \frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}} {\text{ + }} {m_{\rm{u}}}}}\ddot e\arctan \left( e \right) +\hfill \\& {\text{ }} 2\lambda \frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}\frac{{{{\dot e}^2}}}{{1 + {{\dot e}^2}}} = \\& {\text{ }} \dot e\left( { - \frac{{2{k_{\rm{p}}}}}{{\text{π}} }\arctan \left( e \right) - \frac{{2{k_{\rm{d}}}}}{{\text{π}} }\arctan \left( {\dot e} \right) - {k_{\rm{s}}}{{\rm{sgn}}} \left( s \right) + {\varGamma _1}} \right) + \\& {\text{ }} \frac{{2{k_{\rm{p}}}}}{{\text{π}} }\dot e\arctan \left( e \right) + 2\lambda \frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}\frac{{{{\dot e}^2}}}{{1 + {{\dot e}^2}}} + 2\lambda \arctan \left( e \right) \times \\& \left( - \frac{{2{k_{\rm{p}}}}}{{\text{π}} }\arctan \left( e \right) - \frac{{2{k_{\rm{d}}}}}{{\text{π}} }\arctan \left( {\dot e} \right) - {k_{\rm{s}}}{{\rm{sgn}}} \left( s \right) + {\varGamma _1} \right) = \\& - \frac{{2{k_{\rm{d}}}}}{{\text{π}} }\dot e\arctan \left( {\dot e} \right) - \frac{{4\lambda {k_{\rm{p}}}}}{{\text{π}} }{\arctan ^2}\left( e \right) - \\& \frac{{4\lambda {k_{\rm{d}}}}}{{\text{π}} }\arctan \left( e \right)\arctan \left( {\dot e} \right) + 2\lambda \frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}\frac{{{{\dot e}^2}}}{{1 + {{\dot e}^2}}} +\\& s\left( {{\varGamma _1} - {k_{\rm{s}}}{{\rm{sgn}}} \left( s \right)} \right) \\[-10pt] \end{split}$ | (24) |
接下来,将讨论
| $ \begin{split} s\left( {{\varGamma _1} - {k_{\rm{s}}}{sgn} \left( s \right)} \right) &= s{\varGamma _1} - {k_{\rm{s}}}\left| s \right| \leqslant\hfill \\& \left| s \right|{\varGamma _1} - {k_{\rm{s}}}\left| s \right| \leqslant \hfill \\& \left| s \right|\left( {{\varGamma _1} - {k_{\rm{s}}}} \right) \leqslant 0 \end{split} $ | (25) |
除此之外,式(24)的第3项可计算为
| $ \begin{split} & - \frac{{4\lambda {k_{\rm{d}}}}}{{\text{π}} }\arctan \left( e \right)\arctan \left( {\dot e} \right) \leqslant 2\lambda {k_{\rm{d}}}{\arctan ^2}\left( e \right) +\\& \frac{{2\lambda {k_{\rm{d}}}}}{{{{\text{π}} ^2}}}{\arctan ^2}\left( {\dot e} \right) \end{split} $ | (26) |
随后,通过利用
| $ - \frac{{2{k_{\rm{d}}}}}{{\text{π}} }\dot e\arctan \left( {\dot e} \right) \leqslant - \frac{{4{k_{\rm{d}}}}}{{{{\text{π}} ^2}}}{\arctan ^2}\left( {\dot e} \right) $ | (27) |
由于
| $ 2\lambda \frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}\frac{{{{\dot e}^2}}}{{1 + {{\dot e}^2}}} \leqslant 2\lambda \frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}{\dot e^2} $ | (28) |
将式(25)~(28)代入式(24),可得
| $ \begin{split} \dot V\left( t \right) \leqslant & - \frac{{4{k_{\rm{d}}}}}{{{{\text{π}} ^2}}}{\arctan ^2}\left( {\dot e} \right) - \frac{{4{k_{\rm{p}}}\lambda }}{{\text{π}} }{\arctan ^2}\left( e \right) + 2{k_{\rm{d}}}\lambda {\arctan ^2}\left( e \right) + \\& \frac{{2{k_{\rm{d}}}\lambda }}{{{{\text{π}} ^2}}}{\arctan ^2}\left( {\dot e} \right) + 2\lambda \frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}{{\dot e}^2} \leqslant \\& - \left( {\frac{{4{k_{\rm{d}}} - 2{k_{\rm{d}}}\lambda }}{{{{\text{π}} ^2}}}} \right){\arctan ^2}\left( {{{\dot e}_{{{{\phi}}}} }} \right) + 2\lambda \frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}{{\dot e}^2} - \\& \left( {\frac{{4{k_{\rm{p}}}\lambda }}{{\text{π}} } - 2{k_{\rm{d}}}\lambda } \right){\arctan ^2}\left( e \right) \\[-10pt] \end{split} $ | (29) |
由式(18)、(29)可知,若以下不等式成立:
| $ - \left( {\frac{{4{k_{\rm{d}}} - 2{k_{\rm{d}}}\lambda }}{{{{\text{π}} ^2}}}} \right){\arctan ^2}\left( {\dot e} \right) + 2\lambda \frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}{\dot e^2} \leqslant 0 $ | (30) |
那么,不难得到
为证明式(30),考虑如下两种情况。
(1)
(2)
| $ \frac{{{{\dot e}^2}}}{{{{\arctan }^2}\left( {\dot e} \right)}} \leqslant \frac{{\left( {2 - \lambda } \right){k_{\rm{d}}}\left( {{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}} \right)}}{{{{\text{π}} ^2}\lambda {m_{\rm{s}}}{m_{\rm{u}}}}} $ | (31) |
由文献[14],可知以下结论:
| $ \frac{{{{\dot e}^2}}}{{{{\arctan }^2}\left( {\dot e} \right)}} \leqslant {\left( {1 + \left| {\dot e} \right|} \right)^2} $ | (32) |
为保证式(31)始终成立,一个充分条件是选择
| $ \frac{{\left( {2 - \lambda } \right){k_{\rm{d}}}\left( {{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}} \right)}}{{{{\text{π}} ^2}\lambda {m_{\rm{s}}}{m_{\rm{u}}}}} \geqslant {\left( {1 + \left| {\dot e} \right|} \right)^2} $ | (33) |
由式(18)、(22),不难得出
| $ V\left( t \right) \geqslant \frac{1}{2}\frac{{{m_{\rm{s}}}{m_{\rm{u}}}}}{{{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}}}\left( {1 - 2\lambda } \right){\dot e^2} $ | (34) |
由式(34),易得
| $ {\dot e^2} \leqslant \frac{{2V\left( {{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}} \right)}}{{\left( {1 - 2\lambda } \right){m_{\rm{s}}}{m_{\rm{u}}}}} \Rightarrow \left| {\dot e} \right| \leqslant \sqrt {\frac{{2V\left( {{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}} \right)}}{{\left( {1 - 2\lambda } \right){m_{\rm{s}}}{m_{\rm{u}}}}}} $ | (35) |
将式(35)代入式(33),有
| $ \begin{gathered} \frac{{\left( {2 - \lambda } \right){k_{\rm{d}}}\left( {{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}} \right)}}{{{{\text{π}} ^2}\lambda {m_{\rm{s}}}{m_{\rm{u}}}}} \geqslant {\Bigg( {1 + \sqrt {\frac{{2V\left( {{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}} \right)}}{{\left( {1 - 2\lambda } \right){m_{\rm{s}}}{m_{\rm{u}}}}}} } \Bigg)^2} \hfill \\ \Rightarrow {k_{\rm{d}}} \geqslant \frac{{{{\text{π}} ^2}\lambda {m_{\rm{s}}}{m_{\rm{u}}}}}{{\left( {2 - \lambda } \right)\left( {{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}} \right)}}{\Bigg( {1 + \sqrt {\frac{{2V\left( {{m_{\rm{s}}}{\text{ + }}{m_{\rm{u}}}} \right)}}{{\left( {1 - 2\lambda } \right){m_{\rm{s}}}{m_{\rm{u}}}}}} } \Bigg)^2} \hfill \\ \end{gathered} $ | (36) |
若式(36)成立,则式(29)可重写为
| $ \dot V\left( t \right) \leqslant - {\alpha _1}{\arctan ^2}\left( {\dot e} \right) - {\alpha _2}{\arctan ^2}\left( e \right) $ | (37) |
式中:
| $ V\left( t \right) \in {L_\infty } \Rightarrow e,{\text{ }}\dot e \in {L_\infty } \Rightarrow s,{\text{ }}u \in {L_\infty } $ | (38) |
以及
| $ \mathop {\lim }\limits_{t \to \infty } e = 0,{\text{ }}\mathop {\lim }\limits_{t \to \infty } \dot e = 0 \Rightarrow \mathop {\lim }\limits_{t \to \infty } {z_{\rm{e}}} = {y_{\rm{d}}},{\text{ }}\mathop {\lim }\limits_{t \to \infty } {\dot z_{\rm{e}}} = {\dot y_{\rm{d}}} $ | (39) |
由式(15),易得
| $ \begin{split} u\left( t \right) &= - \frac{{2{k_{\rm{p}}}}}{{\text{π}} }\arctan \left( e \right) - \frac{{2{k_{\rm{d}}}}}{{\text{π}} }\arctan \left( {\dot e} \right) - {k_{\rm{s}}}{{\rm{sgn}}} \left( s \right) - \bar m{{\ddot y}_{\rm{d}}} \leqslant\hfill \\ & {\text{ }} \frac{{2{k_{\rm{p}}}}}{{\text{π}} } + \frac{{2{k_{\rm{d}}}}}{{\text{π}} } + {k_{\rm{s}}} + \bar m\left\{ {\max \left( {\left| {{\gamma _1}} \right|,{\text{ }}\left| {{\gamma _2}} \right|} \right)} \right\} \leqslant {u_{\max }} \end{split}$ | (40) |
由式(39)、(40)的结果可知定理1得证。
备注2 为避免抖震现象,用双曲正切函数替代式(15)中的符号函数,将其进一步修改为
| $ u\left( t \right) = - \frac{{2{k_{\rm{p}}}}}{{\text{π}} }\arctan \left( e \right) - \frac{{2{k_{\rm{d}}}}}{{\text{π}} }\arctan \left( {\dot e} \right) - {k_{\rm{s}}}\tanh \left( s \right) - \bar m{\ddot y_{\rm{d}}} $ | (41) |
为进一步验证所提控制方法的实际控制性能以及节能效果,将在一个四分之一主动式悬架平台上进行几组实验。实验平台见图3,其模型参数的名义值见表2。

|
图 3 主动式悬架实验平台 Figure 3 Active suspension setup |
| 表 2 四分之一主动式悬架系统的模型参数的名义值 Table 2 Parameters of the quarter-vehicle active suspension system |
为更好地测试所提跟踪控制方法的控制性能,考虑两种路面输入:正弦和随机路形,见图4及图5。
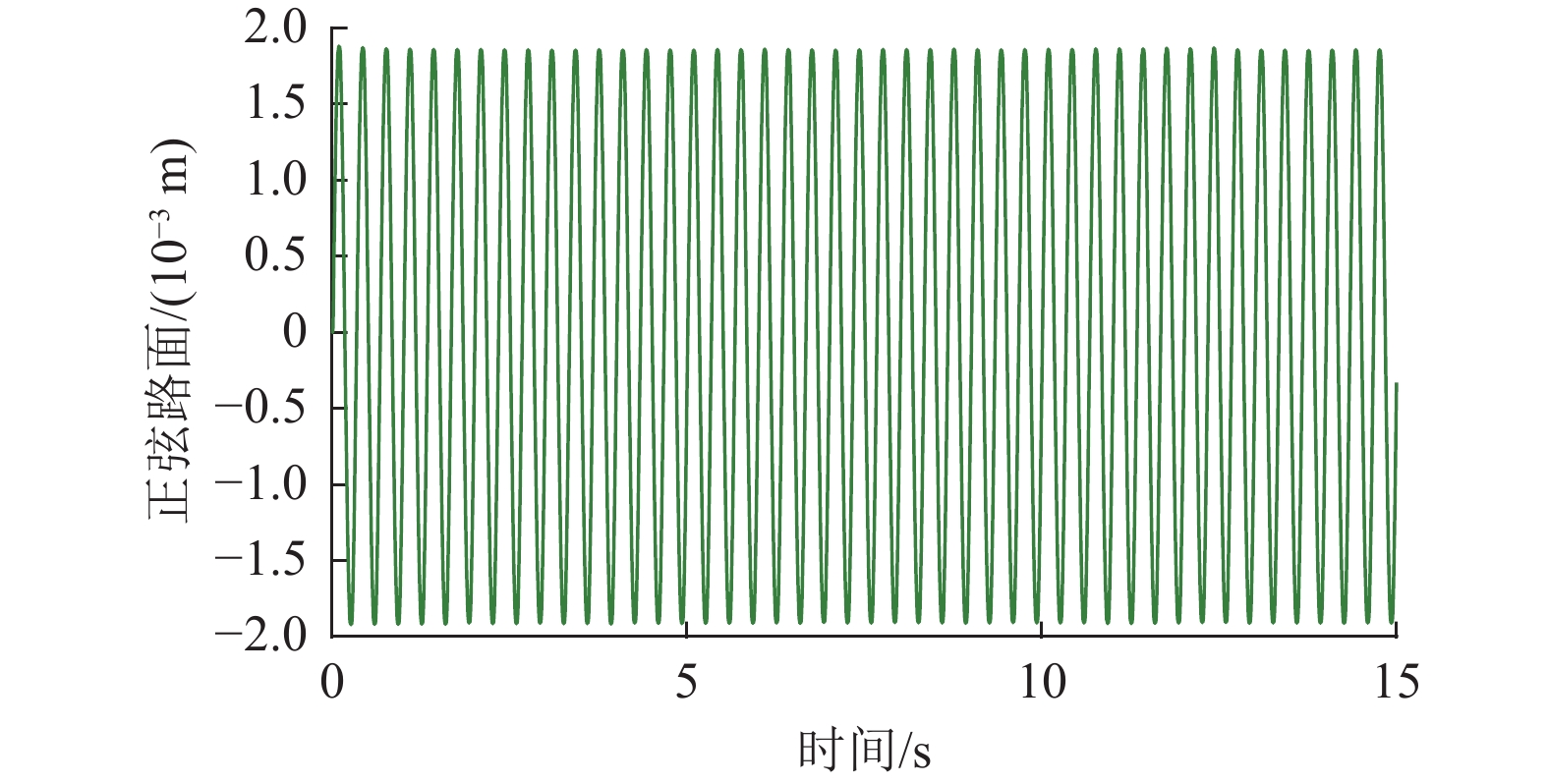
|
图 4 正弦路面的图形 Figure 4 Sinusoidal road profile |
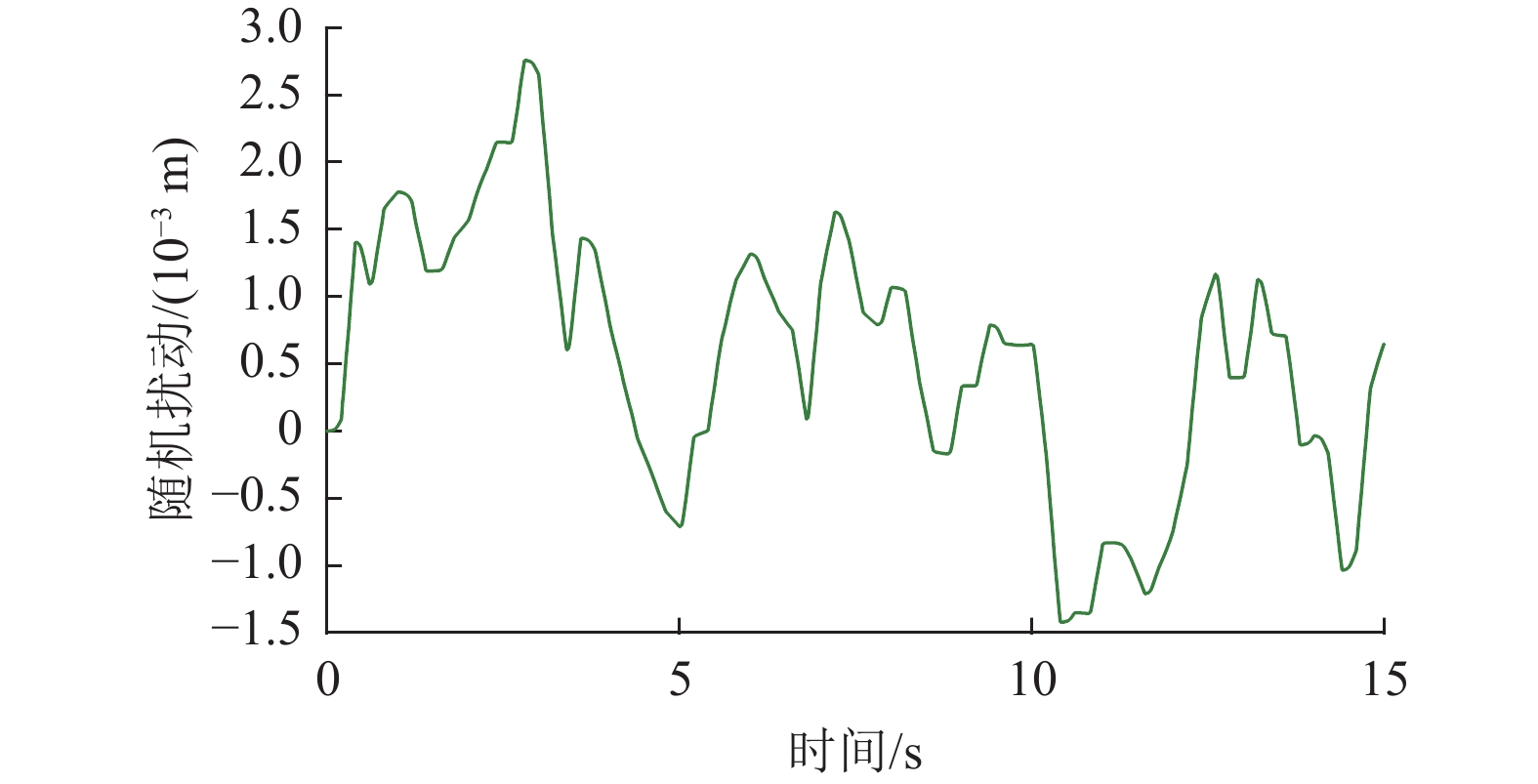
|
图 5 随机路面的图形 Figure 5 Random road profile |
采用谐波平衡法,分析得到的位移传递率在不同参数下的曲线,最终确定仿生非线性动力学模型参数,如表3所示。
| 表 3 仿生X结构参考模型的参数 Table 3 Parameters of the bioinspired X-structured reference model |
此外,弹簧、阻尼器以及轮胎的动力学模型描述如下:
| $ {F_{\rm{s}}}\left( {{z_{\rm{s}}},{z_{\rm{u}}}} \right) = {k_{s1}}\left( {{z_{\rm{s}}} - {z_{\rm{u}}}} \right) + {k_{{\rm{s}}2}}{\left( {{z_{\rm{s}}} - {z_{\rm{u}}}} \right)^3} $ | (42) |
| $ {F_{\rm{d}}}\left( {{{\dot z}_{\rm{s}}},{{\dot z}_{\rm{u}}}} \right) = \left\{ \begin{gathered} {k_{{\rm{d}}1}}\left( {{{\dot z}_{\rm{s}}} - {{\dot z}_{\rm{u}}}} \right),{\text{ }}{{\dot z}_{\rm{s}}} - {{\dot z}_{\rm{u}}} \gt 0 \hfill \\ {k_{{\rm{d}}2}}\left( {{{\dot z}_{\rm{s}}} - {{\dot z}_{\rm{u}}}} \right),{\text{ }}{{\dot z}_{\rm{s}}} - {{\dot z}_{\rm{u}}} \leqslant 0 \hfill \\ \end{gathered} \right. $ | (43) |
| $ {F_{\rm{t}}}\left( {{z_{\rm{u}}},{z_{\rm{r}}}} \right) = {k_{\rm{t}}}\left( {{z_{\rm{u}}} - {z_{\rm{r}}}} \right) $ | (44) |
| $ {F_{\rm{b}}}\left( {{{\dot z}_{\rm{u}}},{{\dot z}_{\rm{r}}}} \right) = {k_{\rm{b}}}\left( {{{\dot z}_{\rm{u}}} - {{\dot z}_{\rm{r}}}} \right) $ | (45) |
式中:
主动式悬架系统状态的初始值设置为0。与此同时,簧上质量、簧下质量以及不确定参数
为了更好地比较,考虑如下3种情形。
情形1:被动式悬架系统;
情形2:基于拓展状态观测器的跟踪控制方法(ESOT)[15];
情形3:本文所设计的控制方法,见式(15)。
根据试凑法,所设计的跟踪控制方法以及ESOT控制方法的控制增益分别为:
| 表 4 不同控制器的车体加速度的均方根 Table 4 RMS of the vehicle body acceleration with respect to different controllers |
| 表 5 不同控制器的控制输入的均方根 Table 5 RMS of the energy consumption with respect to different controllers |
|
图 6 正弦路面下的车体加速度及其频率分量 Figure 6 Vehicle body acceleration and its frequency component for sinusoidal road profile |
|
图 7 正弦路面下的控制输入及其频率分量 Figure 7 Control force and its frequency component for sinusoidal road profile |
|
图 8 正弦路面下的悬架行程及轮胎行程 Figure 8 Suspension stroke and tire deflection for sinusoidal road profile |
|
图 9 随机路面下的车体加速度及其频率分量 Figure 9 Vehicle body acceleration and its frequency component for random road profile |
|
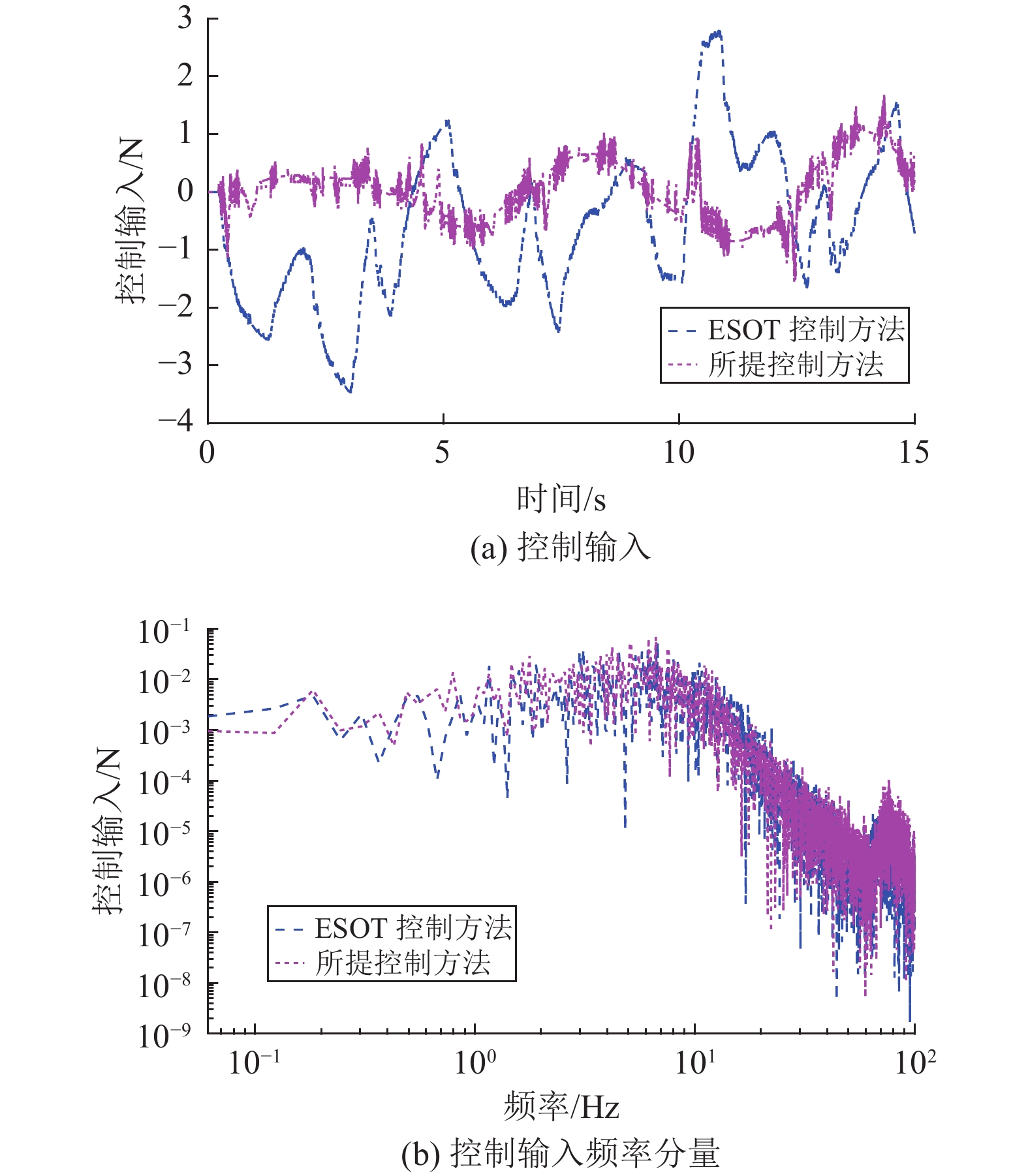
图 10 随机路面下的控制输入及其频率分量 Figure 10 Control force and its frequency component for random road profile |
|
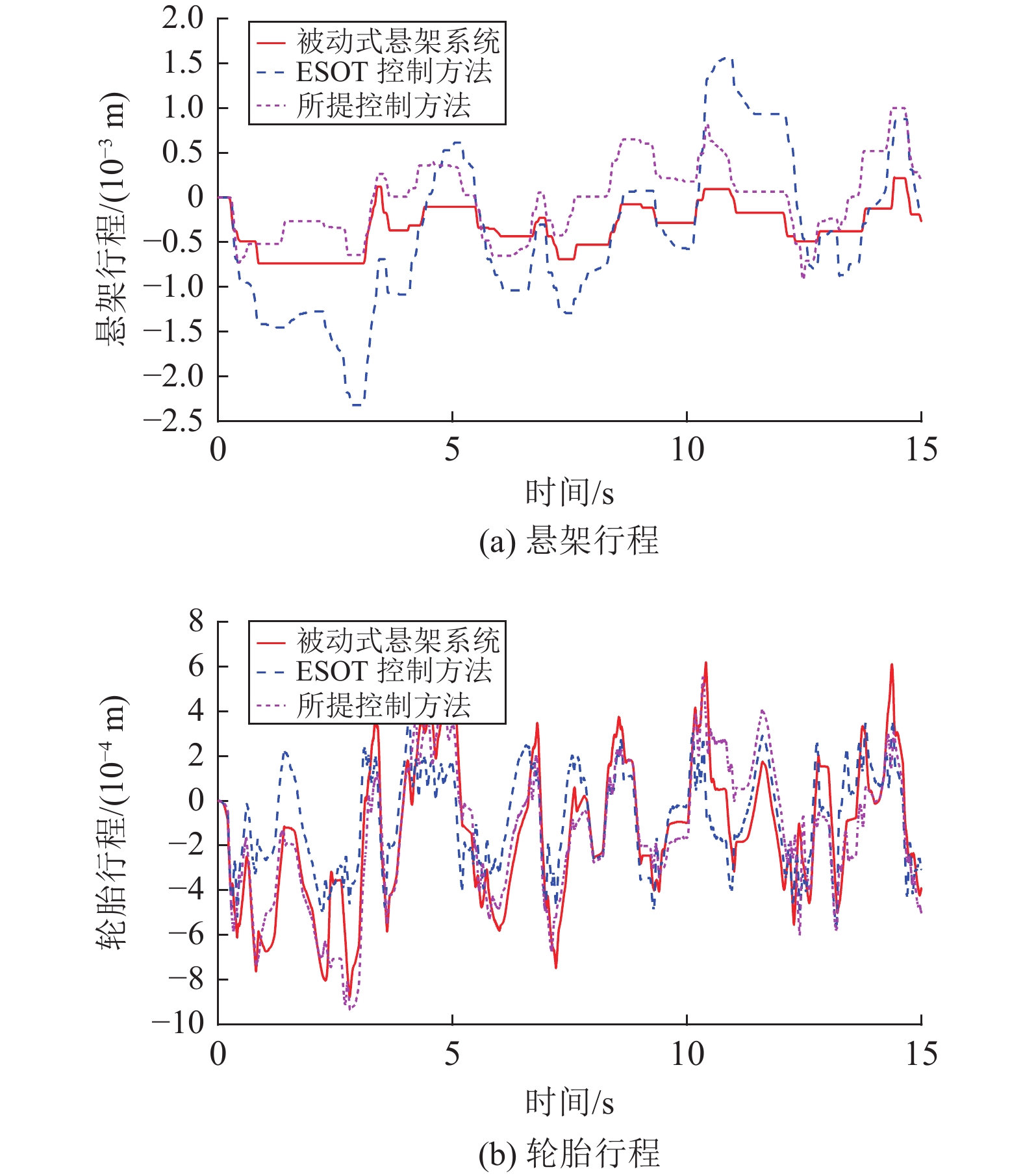
图 11 随机路面下的悬架行程及轮胎行程 Figure 11 Suspension stroke and tire deflection for sinusoidal road profile |
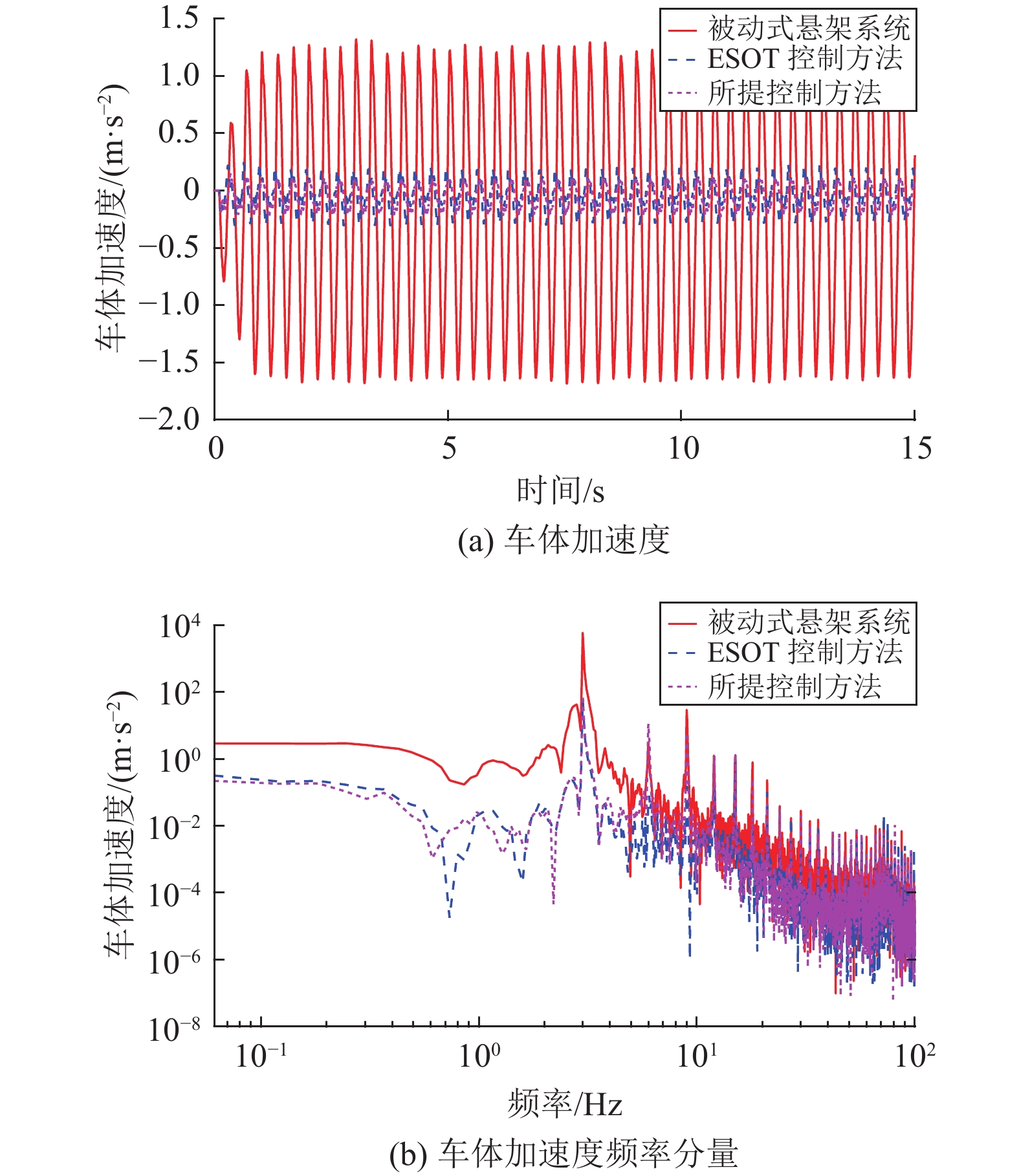
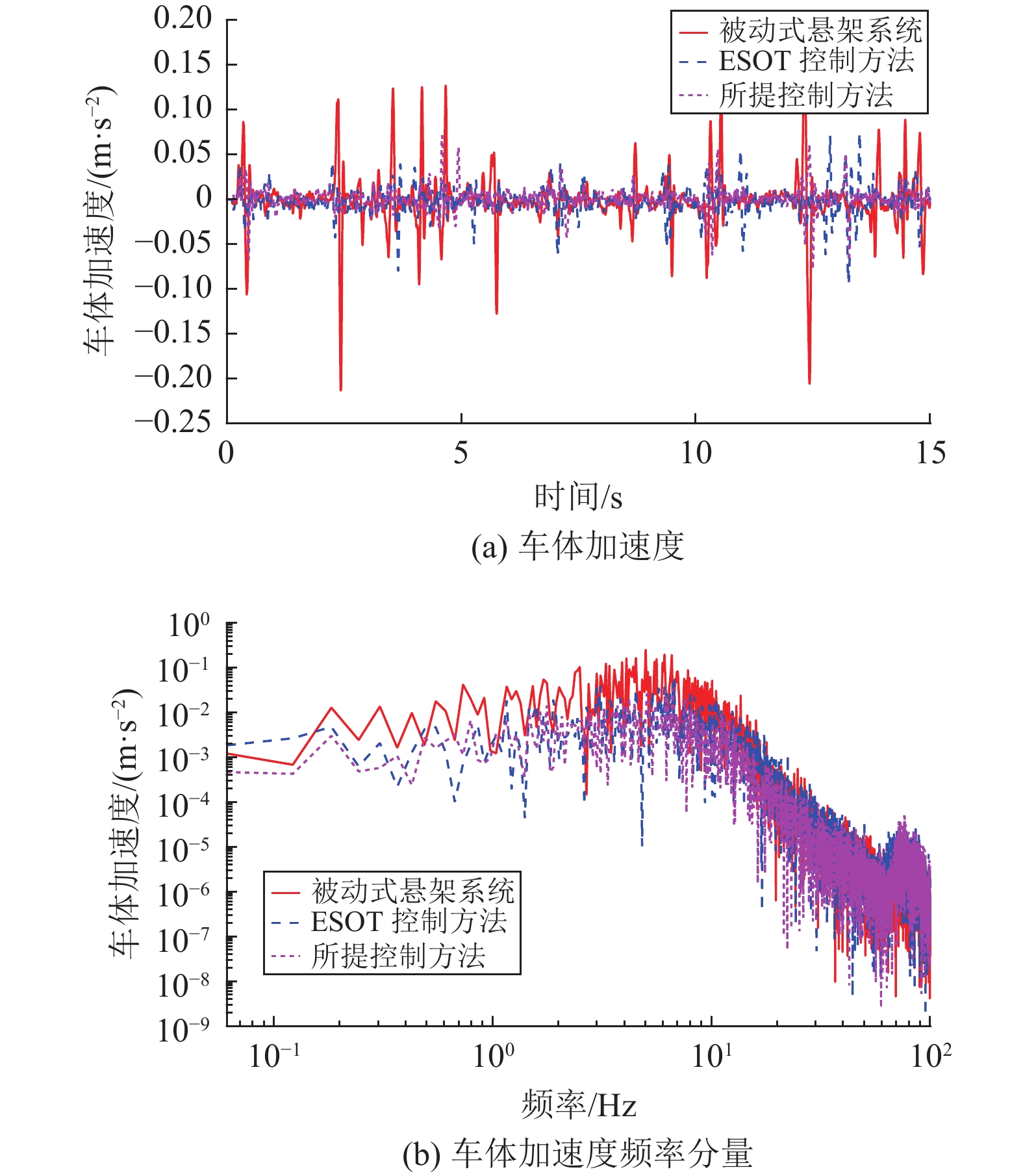
图6和图9分别为被动式悬架系统、ESOT控制器以及所设计的跟踪控制器在正弦和随机路面下车体加速度的时间响应和频率响应的对比。表4总结了两种不同路面输入下的车体加速度的均方根。从图6和图9可以明确地看出,与被动式悬架系统相比,ESOT控制方法以及本文所设计控制方法的车体加速度大大减少,同时这也表明ESOT控制器以及本文所设计跟踪控制器可以有效地隔离模型参数不确定性以及外部扰动引起的振动。相应地,ESOT控制器和所设计的跟踪控制器的乘坐舒适性得到了明显的提高。具体来说,从表4可以看出,与被动式悬架系统相比,ESOT控制器针对正弦和随机路面,车体加速度的均方根值分别减少了85.93%,47.42%。而所设计的跟踪控制器针对正弦和随机路面,车体加速度的均方根值分别下降了90.58%,51.55%。
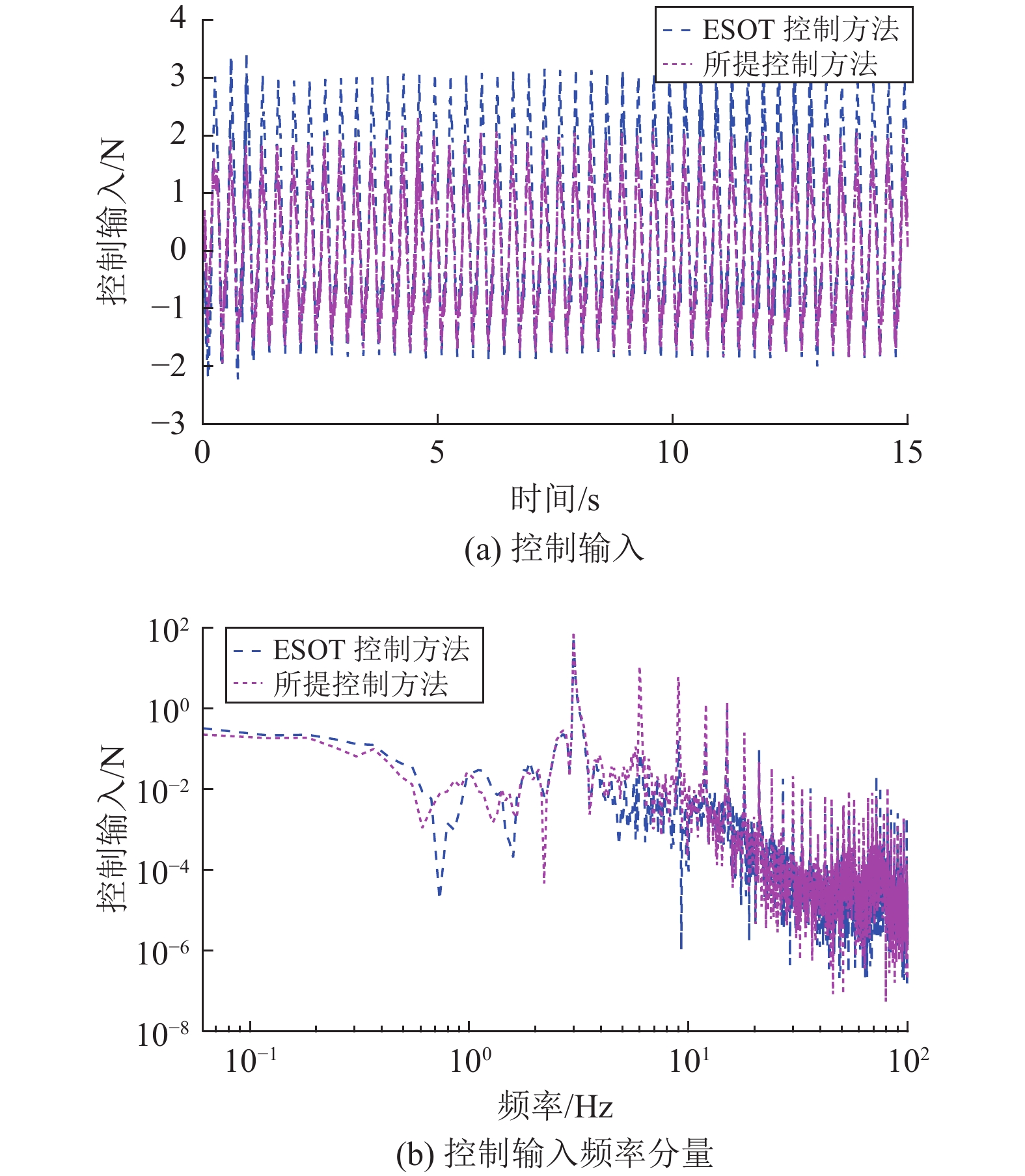
图7 (a)和图10 (a)分别为正弦和随机路面下,ESOT控制器及所设计跟踪控制器的控制输入的时间响应图。相应的频率响应分别见图7 (b)和图10(b)。表5给出了ESOT控制器和所设计跟踪控制器的控制输入的均方根值。从图7 (a)和图10 (a)可以看出,所设计的跟踪控制器的控制输入比ESOT控制器的控制输入要小得多。另外,ESOT控制器的高频分量比所设计的跟踪控制器要大得多。众所周知,执行器的高带宽要求会增加被控主动悬架系统的成本和输入饱和的可能性。然而,在实际应用中,执行机构的带宽总是有限的。因此,与ESOT控制器相比,所设计的跟踪控制器具有较高的能效和较低的执行器带宽特性。这个结论由表5也可以得到证实,与ESOT控制器相比,所设计的跟踪控制方法针对正弦路面和随机路面的能耗均方根值分别降低了30.65%和66.67%。
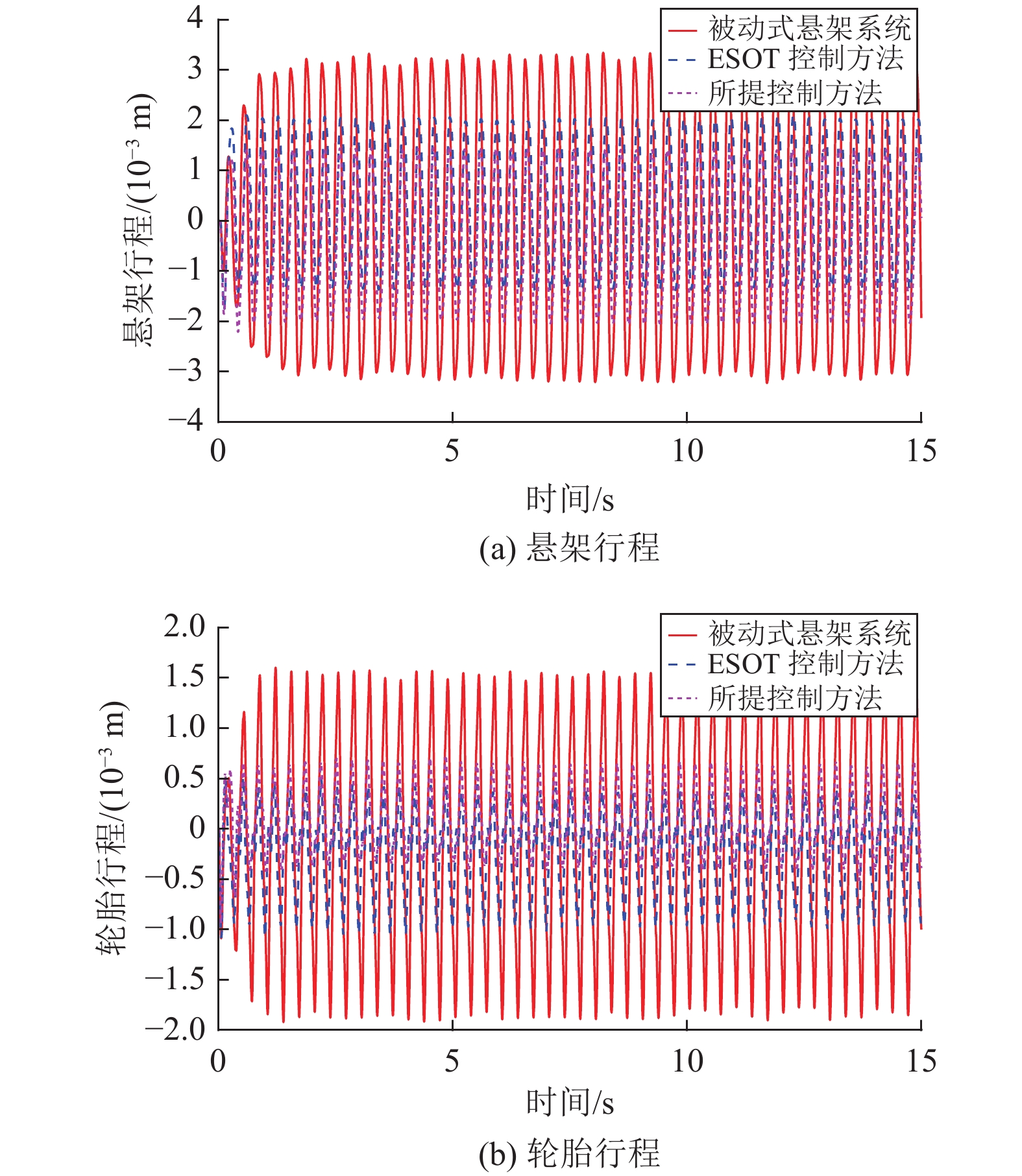
由图8和图11可知,被动式悬架系统、ESOT控制器和所设计的跟踪控制器的悬架行程和轮胎行程均被保持在允许的范围内。这些结果均表明,所设计的跟踪控制器能保证驾驶员和乘员的安全。
5 结论为提高主动式悬架系统的暂态控制性能和能量效率,设计了一种基于仿生动力学的饱和PD-SMC跟踪控制方法,该方法考虑了系统的输入约束、鲁棒性、稳定性、易实现性以及良好的非线性特性。为了节约能量消耗,应充分利用主动式悬架控制有益的非线性特性,为此,引入了仿生动力学系统对这些非线性因素进行合理的利用。所设计的控制方法将饱和PD控制方法、SMC方法和仿生参考模型相结合,具有结构简单、鲁棒性强、能耗小等优点。基于李雅普诺夫的分析方法验证了所设计的控制方法的控制性能。实验结果表明,与现有的几种控制方法相比,该控制方法具有较好的隔振性能和较低的能耗。
| [1] |
KUMAR V, RANA K P S, KUMAR J, et al. Self-tuned robust fractional order fuzzy PD controller for uncertain and nonlinear active suspension system[J].
Neural Computing and Applications, 2018, 30(6): 1827-1843.
DOI: 10.1007/s00521-016-2774-x. |
| [2] |
SU Y, ZHENG C. Single saturated PD control for asymptotic attitude stabilization of spacecraft[J].
IET Control Theory and Applications, 2020, 14(19): 3338-3343.
DOI: 10.1049/iet-cta.2020.0598. |
| [3] |
ZHANG Y, KIM D G, ZHAO Y, et al. PD control of a manipulator with gravity and inertia compensation using an RBF neural network[J].
International Journal of Control, Automation and Systems, 2020, 18(12): 3083-3092.
DOI: 10.1007/s12555-019-0482-x. |
| [4] |
TENG L, GULL M A, BAI S P. PD-based fuzzy sliding mode control of a wheelchair exoskeleton robot[J].
IEEE/ASME Transactions on Mechatronics, 2020, 25(5): 2546-2555.
DOI: 10.1109/TMECH.2020.2983520. |
| [5] |
KOLATHAYA S. Local stability of PD controlled bipedal walking robots[J]. Automatica, 2020, 114: 108841
|
| [6] |
ZHENG C, SU Y, MERCORELLI P. A simple nonlinear PD control for faster and high-precision positioning of servomechanisms with actuator saturation[J].
Mechanical Systems and Signal Processing, 2019, 121: 215-226.
DOI: 10.1016/j.ymssp.2018.11.017. |
| [7] |
DESHPANDE V S, MOHAN B, SHENDGE P D, et al. Disturbance observer based sliding mode control of active suspension systems[J].
Journal of Sound and Vibration, 2014, 333: 2281-2296.
DOI: 10.1016/j.jsv.2014.01.023. |
| [8] |
CHEN H, LIU Y, LIU L, et al. Anti-saturation-based adaptive sliding-mode control for active suspension systems with time-varying vertical displacement and speed constraints[J]. IEEE Transactions on Cybernetics, in press, doi: 10.1109/TCYB.2020.3042613.
|
| [9] |
RAJENDIRAN S, LAKSHMI P. Performance analysis of fractional order terminal SMC for the half car model with random road input[J].
Journal of Vibration Engineering and Technologies, 2020, 8(4): 687-597.
|
| [10] |
SONG J, NIU Y, ZOU Y. A parameter-dependent sliding mode approach for finite-time bounded control of uncertain stochastic systems with randomly varying actuator faults and its application to parallel active suspension system[J].
IEEE Transactions on Industrial Electronics, 2018, 65(10): 8124-8132.
DOI: 10.1109/TIE.2018.2801801. |
| [11] |
LI J, JING X, LI Z. Fuzzy adaptive control for nonlinear suspension systems based on a bioinspired reference model with deliberately designed nonlinear damping[J].
IEEE Transactions on Industrial Electronics, 2019, 66(11): 8713-8723.
DOI: 10.1109/TIE.2018.2884219. |
| [12] |
ZHANG M, JING X. Switching logic-based saturated tracking control for active suspension systems based on disturbance observer and bioinspired X-dynamics[J].
Mechanical Systems and Signal Processing, 2021, 155: 107611.
DOI: 10.1016/j.ymssp.2021.107611. |
| [13] |
ZHANG M, JING X, WANG G. Bioinspired nonlinear dynamics-based adaptive neural network control for vehicle suspension systems with uncertain/unknown dynamics and input delay[J]. IEEE Transactions on Industrial Electronics, in press, doi: 10.1109/TIE.2020.3040667.
|
| [14] |
SUN N, FANG Y, CHEN H. Tracking control for magnetic-suspension systems with online unknown mass identification[J].
Control Engineering Practice, 2017, 58: 242-253.
DOI: 10.1016/j.conengprac.2016.09.003. |
| [15] |
PAN H, SUN W, GAO H, et al. Nonlinear tracking control based on extended state observer for vehicle active suspensions with performance constraints[J].
Mechatronics, 2015, 30: 363-370.
DOI: 10.1016/j.mechatronics.2014.07.006. |
 2022, Vol. 39
2022, Vol. 39
