目前，我国已经成为了一个工业制造体系完备的制造大国，随着“中国制造2025”战略的实施和推进，我国正逐渐由制造大国向制造强国迈进^[1]。大力推进工业生产的智能化、信息化，大力发展机器人技术，促进我国制造业的产业升级，是国家未来工业化发展主攻的方向，也是国家“十四五”规划的重要内容^[2]。作为机器人领域中最具代表性的一类机械设备，机械臂在工业上的广泛应用可以说是人类社会工业化水平近50年来快速发展的重要因素。由此可见，机械臂控制技术的不断发展和提高是实现制造强国这一目标的重要基石。

现如今，在工业生产、航空航天、军事医疗、冶炼勘探等多个应用场景中均可见到机械臂的身影。在这些应用场景中，机械臂被用来代替人类从事劳动强度大、重复性高、安全风险高、操作环境复杂的工作，这大大提高了工业生产的工作效率和安全性^[3-4]。机械臂是由关节和连杆所组成的机械系统。传统机械臂的关节和连杆均采用刚性的结构和材料设计，这类机械臂被称为刚性机械臂。然而，绝对刚性的机械臂实际上是不存在的，机械臂的结构和材料总会存在一定的柔性。在高负载高加速度运动中，这些柔性的特征会给机械臂带来弹性振动。为最大程度地降低系统的弹性振动，刚性机械臂普遍采用刚度较大的材料制造且设计非常笨重。这导致该类机械臂存在基座沉重、连杆粗短、工作范围有限、运动灵活性差、功耗大、运动速度慢等缺点^[5]。

这些缺点使得刚性机械臂难以适用于一些应用场景，如空间机械臂^[6]、手术机械臂^[7]、人机交互式机械臂等^[8]。随着我国空间站“天和”核心舱的升空，国产空间机械臂在神舟十二号、神舟十三号的出舱任务中得到了成功的应用，如图1所示。为了获得较大的工作空间，空间机械臂往往采用细长的连杆结构，这导致其结构和材料的柔性无法被忽视。手术机械臂为了能够灵巧运动，完成精细化的手术任务，往往需要采用柔性的连续型骨架^[9]。而人机交互式机械臂为了避免机械臂与人的刚性碰撞，需要确保机械臂运动的柔顺性，这使其需要采用一定的柔性材料和结构来设计^[10]。这些机械臂可以被认为是柔性机械臂，此外，在生活中，一些具有大跨度连杆结构的工程机械臂也可以被认为是柔性机械臂，如塔吊旋转臂^[11]、空间桁架^[12]等。

由于传统刚性机械臂的运动控制方法未考虑对系统的弹性振动进行有效抑制，当其被用于控制柔性机械臂时，连杆结构和材料的柔性所导致的弹性振动只能等待其自行衰减消失，这会严重降低此类机械臂的工作效率和控制精度。此外，在一些高精密的应用场景中，机械臂末端细微的弹性振动也无法被容忍，需要对振动进行主动的抑制^[13]。因此，柔性机械臂及其运动控制方法引起了国内外学者们的广泛关注与兴趣^[14-15]。

机械臂的主要任务是把一个物体从一个位置搬运到另一个位置，因此，机械臂末端负载从任意初始位置到任意目标位置的点对点位置控制(以下简称“位置控制”)是机械臂主要的运动控制目标。对于一个常规的机械臂系统来说，仅在每个关节处有一个驱动器(即关节电机)。若要实现刚性机械臂的位置控制，仅需利用关节电机实现系统各连杆的角度控制。但若要实现柔性机械臂的位置控制，利用关节电机，不仅需要实现系统各连杆的角度控制，还需要实现系统柔性连杆的振动抑制。然而，关节电机无法对连杆振动进行直接控制，这使得柔性机械臂的运动控制要比刚性机械臂的运动控制难得多。而且柔性机械臂是一类分布参数系统^[16]，其系统自由度个数为无限个，而其控制输入个数为有限个，这意味着该机械系统存在欠驱动特性^[17]。这些因素使得柔性机械臂的运动控制成为一个具有挑战性的研究课题。

在实际控制中，机械臂的驱动器可能会发生各种类型的故障情况，轻则驱动器的性能无法达到预期，驱动能力部分失效，重则系统的某个驱动器可能完全损坏，驱动能力完全失效。一旦系统的驱动器发生故障，原有的运动控制方法可能无法继续实现系统的控制目标，此时，机械臂需要停止工作，等待检查和维修。同时，机械臂运动控制过程中突发的驱动器故障可能会降低系统的控制性能，甚至可能直接破坏系统原有的稳定性，导致系统失稳、机械臂失控等危险情况。

由于柔性机械臂的驱动器需要同时兼顾机械臂连杆的角度控制和振动抑制，即便是程度较小的驱动器故障也可能会导致严重的后果，轻者可能导致振动无法得到完全抑制造成机械臂末端负载在目标点附近抖振，重者甚至可能激发柔性连杆的共振导致振幅过大，柔性机械臂机械结构损坏等。对于像空间机械臂这样维修难度大、耗时长的柔性机械臂系统，停机维修发生故障的驱动器将严重影响系统的后续工作计划。而对于像手术机械臂、人机交互式机械臂等对控制精度和安全性有较高要求的柔性机械臂系统，控制过程中突发的驱动器故障可能直接威胁到患者及操作员的人身安全。故而，有必要研究驱动器故障影响下的柔性机械臂运动控制方法，这将有助于提高柔性机械臂系统的可靠性和安全性。

研究驱动器故障影响下的柔性机械臂运动控制方法，通常需要在常规柔性机械臂运动控制方法的基础上对驱动器故障加以考虑并克服。鉴于此，本文首先概述常规柔性机械臂的运动控制问题，并对其研究现状进行综述。然后对驱动器故障影响下的柔性机械臂运动控制研究现状进行总结和归纳。最后基于已有考虑驱动器故障的柔性机械臂运动控制研究成果，对未来需要进一步解决的挑战性控制问题进行讨论，并对研究的前景方向进行展望。

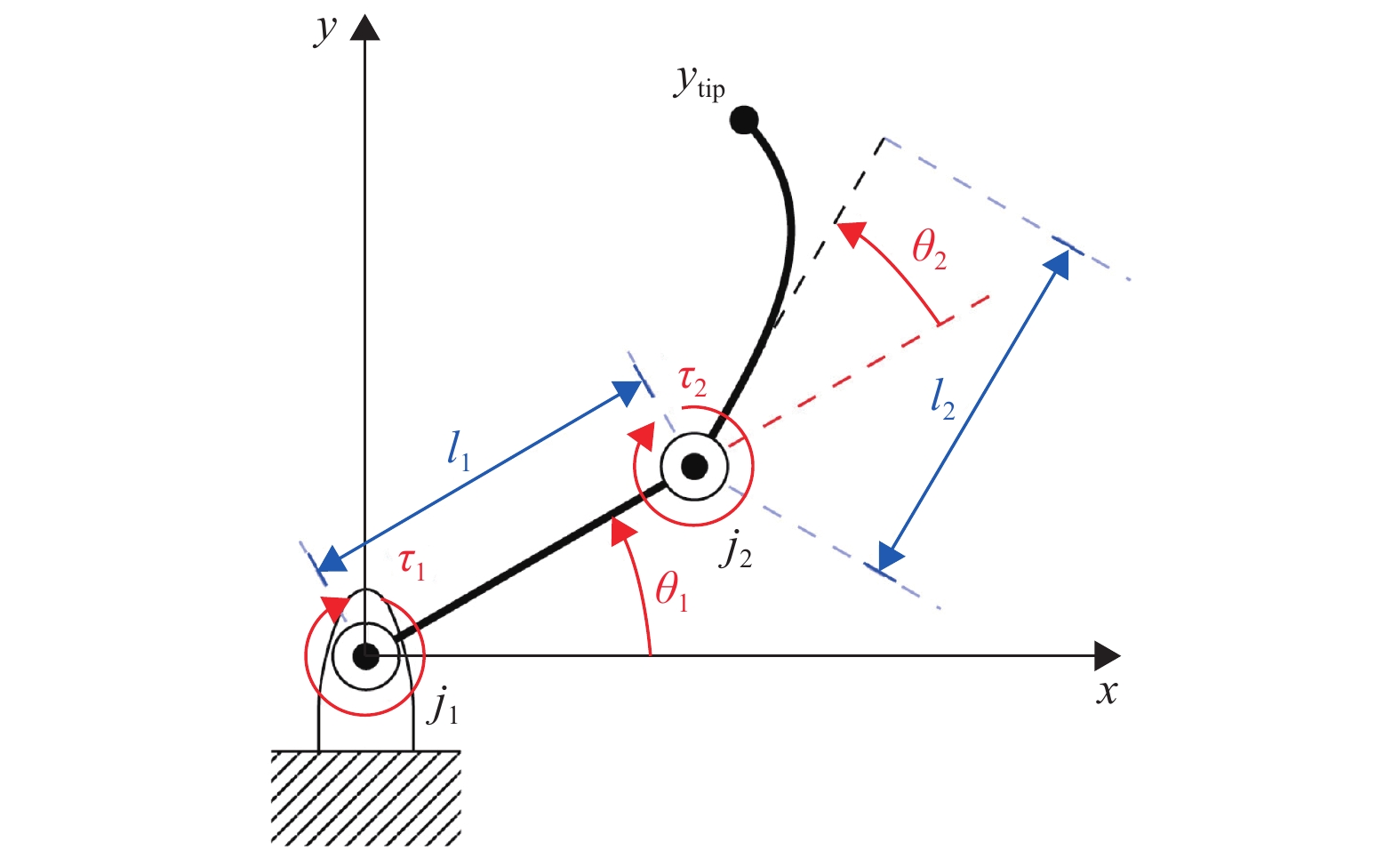
1 柔性机械臂运动控制方法研究现状

在工业生产中，机械臂的主要运动控制目标是末端负载的位置控制。在刚性机械臂的位置控制中，只需先根据末端负载的目标位置求取机械臂各连杆的目标角度，然后将机械臂各连杆稳定到各自的目标角度上即可。但对于柔性机械臂来说，如图2所示两连杆刚柔机械臂结构示意图^[18]，若只将系统各连杆稳定到目标角度，机械臂的柔性连杆可能存在振动^[19]。柔性连杆的振动会使系统末端负载在目标位置附近来回摆动，从而无法实现位置控制目标^[20]。

因此，柔性机械臂的位置控制不仅包含各连杆的角度控制，还包含柔性连杆的振动抑制。一般而言，机械臂的每个关节处均有一个驱动器，即关节电机，这样，连杆的角度控制可以通过控制机械臂关节处的电机转动来实现，这与刚性机械臂相似。而柔性连杆的振动抑制没有对应的驱动器来直接实现，需要设计相应的振动抑制控制方法，因此，振动抑制是实现该类系统控制目标所需要解决的关键问题。

早期柔性连杆的振动抑制方法为被动抑制，通过设计或改良机械臂的材料和结构，使所有连杆到达目标角度后，系统残余的能量可以逐渐被耗散或储存，以此来抑制振动。其中，增大系统阻尼^[21]和设计减振机构^[22]是较为常用的柔性机械臂振动被动抑制方法。然而，振动被动抑制方法虽然可以在一定程度上降低弹性振动，但效率不高。例如，航天飞机的遥控机械臂系统，虽然使用了阻尼较大的材料且有一定的减振设计，但仍约有三分之一的工作时间被用来等待弹性振动的衰减，严重影响了机械臂的工作效率^[23]。因此，国内外的学者开始研究柔性机械臂弹性振动的主动抑制方法。

最直接的方法是给柔性机械臂安装额外的驱动器来主动抑制其弹性振动。文献[24]和文献[25]分别以压电陶瓷和形状记忆合金作为振动抑制驱动器，对一类柔性机械臂进行了振动主动抑制的研究。文献[26]则是将压电材料与应变传感器共同应用到了柔性机械臂上，提出了基于线性二次调节器与线性二次高斯最优状态调节器的控制方法，实现了系统的控制目标。此外，一些学者针对柔性机械臂，提出了一类边界控制方法^[27-29]。该方法需要在柔性连杆末端边界处施加一个边界控制力来主动抑制柔性连械臂的弹性振动，而边界控制力需要在柔性连杆末端处安装一个驱动器来提供。

这些方法虽然可以对柔性机械臂的弹性振动进行直接的抑制，但安装额外的驱动器意味着，柔性机械臂必须根据控制方法进行重新的结构设计和组装。对于常规的柔性机械臂来说，系统的驱动器只有每个关节处的关节电机，研究如何利用已有的驱动器来主动抑制系统的振动更具普适性和实用价值。

对此，针对仅以关节电机作为驱动器的柔性机械臂，文献[30]针对单连杆柔性机械臂提出了滑模变结构控制方法，实现了系统的末端负载位置控制。在此基础上，文献[31]进一步研究了单连杆柔性机械臂的滑模变结构控制方法，克服了文献[30]中选择的切换面不能保证系统稳定性的缺陷。此外，文献[32]提出了具有模糊补偿的滑模控制方法，解决了两连杆柔性机械臂的位置控制问题。奇异摄动方法也是一种常用的柔性机械臂控制方法，该方法将柔性机械臂分解为两个时间尺度下的子系统来研究，通过对这两个子系统进行不同的控制器设计，实现不同子系统各自的控制目标，以此实现原系统的控制目标^[33]。文献[34]基于奇异摄动方法将柔性机械臂分解为具有刚性运动特征的慢变子系统和具有柔性振动特征的快变子系统。然后，分别针对这两个子系统设计鲁棒控制器和全局最优控制器，实现了机械臂连杆的角度控制和振动抑制。而文献[35]则是针对两个子系统，分别设计了滑模控制器和最优振动抑制控制器，使系统最终稳定。然而，当柔性机械臂的柔性连杆数量众多、模型复杂且耦合性强时，很难设计合适的滑模切换面保证系统所有状态的收敛性，也很难将系统的模型分解为两个时间尺度下的子系统。因此，这些控制方法适用于结构较为简单的系统。文献[36]提出了一种基于系统能量的控制方法，该方法在控制系统柔性连杆稳定到目标角度之后，通过使系统总能量收敛为零，来主动抑制柔性连杆的弹性振动，具有很好的普适性。

近些年来，一些学者将柔性机械臂的位置控制问题转化为轨迹规划和跟踪控制问题来研究，取得了很好的控制效果^[37]。文献[38]针对两连杆刚柔机械臂提出了一种基于粒子群算法的轨迹优化方法，使机械臂各连杆在到达目标角度后振动最小化。文献[39]采用三次样条插值方法为两连杆刚柔机械臂规划了一条连续轨迹，并利用差分进化算法对轨迹进行优化，从而使系统位置控制中的能耗和弹性形变达到满意的指标。文献[40]则是结合双向轨迹规划方法和遗传算法，对两连杆刚柔机械臂进行了轨迹规划。规划的轨迹可以使机械臂各连杆在到达目标角度的同时，柔性连杆的振动恰好消失。这样，通过设计滑模轨迹跟踪控制器，使机械臂各连杆高精度地跟踪规划轨迹，实现了系统的控制目标。

此外，为克服实际控制中柔性机械臂存在的参数摄动、外界扰动以及未建模动力学等不确定因素影响，一些自适应控制方法被提出，如神经网络控制方法^[41]、模糊控制方法^[42]、迭代学习控制方法^[43]等。这些方法可以在一定程度上克服因建模不准确而导致的模型不确定性，提高系统的控制精度。文献[44]将柔性机械臂受到的时变约束也考虑在内，提出了一种基于径向基函数(Radial Basis Function, RBF)神经网络的控制方法，来对系统的振动进行抑制并实现系统的控制目标。文献[45]考虑了柔性连杆末端振幅约束的问题，提出了一种基于运动规划与自适应神经网络的控制方法，实现了具有模型不确定性的两连杆刚柔机械臂的位置控制。

由此可见，针对柔性机械臂的运动控制方法，国内外的研究学者们已经开展了广泛的研究，取得了较为丰硕的研究成果。但这些方法均假设系统的驱动器是完好的，即驱动器给机械臂提供的控制扭矩与所设计控制方法期望的控制扭矩完全相等。但在实际控制中，机械臂的驱动器可能因为各种原因发生故障^[46]。驱动器故障会破坏驱动器的驱动能力，从而使得这些控制方法无法继续实现系统的控制目标。在这种情况下，需要对机械臂的驱动器进行检查和维修。但对于像空间机械臂这样维修难度大，维修周期长的机械系统，这将严重影响机械臂的工作计划，因此，有必要研究驱动器故障下的柔性机械臂运动控制方法。

2 驱动器故障及克服方法

当柔性机械臂的某个驱动器发生故障时，该驱动器无法根据期望信号为系统提供控制扭矩，此时驱动器的实际输出扭矩可以描述为

$\tau =\psi \left(\tilde {\tau }\right)$

(1)

式中： $\tau$ 为驱动器的实际输出扭矩， $\tilde {\tau }$ 为驱动器的期望输出扭矩， $\psi \left(*\right)$ 为未知的故障描述函数。

故障成因的不同或故障严重程度的不同会导致驱动器故障具有不同的特征。本节以驱动器故障的特征为分类依据，从驱动器性能故障、驱动器完全损坏故障，以及驱动器突发故障3个方面分别介绍当前考虑驱动器故障的柔性机械臂运动控制方法相关研究。

2.1 驱动器性能故障

在实际情况中，可能因轴承进灰、缺油，传动装置损坏等原因，导致驱动器的驱动能力受损，无法达到原本的预期性能。这类情况可以被界定为驱动器发生了性能故障，驱动能力受到约束。在式(1)中，驱动器性能故障的描述函数 $\psi \left(*\right)$ 是一个不恒为零、整体趋势正向增长的线性或非线性函数。该类驱动器故障对系统的影响可以被认为是系统存在输入约束。由于导致驱动器性能故障的成因不同，系统存在的输入约束种类也不同，常见的输入约束有增益、死区、迟滞和饱和等。

2.1.1 增益约束

增益约束指的是系统的实际输入与期望输入之间存在近似正比例关系，对于驱动器故障来说，增益约束往往源于驱动器内部绝缘老化所导致的驱动能力弱化，其故障描述函数可以表示为^[47]

$\tau =\psi \left(\tilde{\tau }\right)=\kappa \tilde{\tau }+\varpi \left(t\right)$

(2)

式中： $\kappa$ 为故障增益因子，是一个正的常数，满足 $0 < \kappa < 1$ ； $\varpi \left(t\right)$ 为故障偏置因子，满足 $\left|\varpi \left(t\right)\right|\leqslant {\varpi }^{\mathrm{m}\mathrm{a}\mathrm{x}}$ ，其中 ${\varpi }^{\mathrm{m}\mathrm{a}\mathrm{x}}$ 是一个正常数。故障偏置因子可以理解为驱动器故障所导致的有界输入扰动。

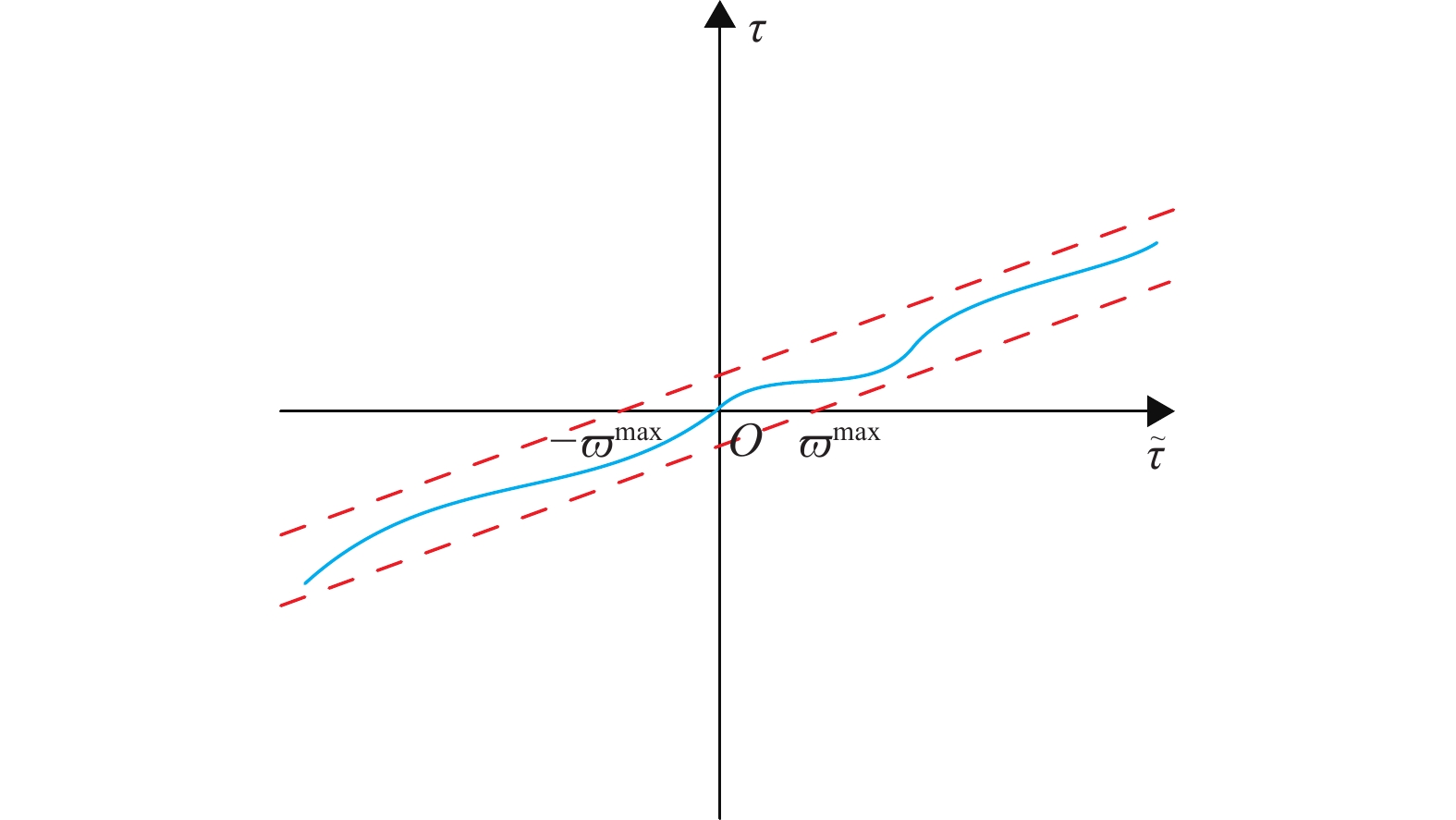
由于存在驱动器性能故障的系统，其输入约束往往具有不确定性，因此，式(2)中的 $\kappa$ 和 $\varpi \left(t\right)$ 均为未知的量。式(2)所示故障描述函数可以表示为图3。

对于该类输入约束，故障偏置因子 $\varpi \left(t\right)$ 对系统的影响可以等效为系统的外部扰动，故而可以将其和外部扰动视为一类问题来处理^[48]。因此，如何补偿故障增益因子 $\kappa$ 对系统的影响是克服式(2)所示输入增益约束的关键。

针对这一问题，文献[49]提出了一种自适应神经网络容错控制策略，利用神经网络的逼近特性对系统中负载质量、轮毂惯量和弯曲刚度造成的不确定性进行了逼近，并设计了一种自适应方法对系统的输入增益约束进行了补偿，实现了具有不确定项的柔性机械臂系统的控制目标。文献[50]针对移动双柔性机械臂，通过构造自适应律对增益故障描述函数(2)中的增益因子 $\kappa$ 进行在线估计，设计了一种容错控制方法实现了系统的振动抑制和协调运行。此外，文献[51]针对一类系统模型由常微分方程和柔性Euler-Bernoulli梁级联描述的系统，设计了一种鲁棒自适应容错控制方法，采用李雅普诺夫直接法设计控制方案并证明闭环系统的稳定性，在输入增益约束、参数不确定性和外部扰动的情况下实现了系统的跟踪控制目标。

2.1.2 死区约束

死区约束表现为驱动器对较小信号的不敏感，它通常是由驱动器机械结构中存在的库仑摩擦引起的^[52-53]，广泛存在于机械系统中。但驱动器因轴承进灰或缺油而发生的驱动器性能故障往往会使系统的死区约束效果更加明显，并具有复杂未知的非线性特征。导致系统存在死区约束的驱动器性能故障描述函数可以表示为^[54]

$\tau =\psi \left(\tilde{\tau }\right)=\left\{\begin{array}{ll}{\varphi }_{r}\left(\tilde{\tau }-{\varrho }_{r}\right),& \tilde{\tau }\geqslant {\varrho }_{r}\\ 0,& -{\varrho }_{l} < \tilde{\tau } < {\varrho }_{r}\\ {\varphi }_{l}(\tilde{\tau }+{\varrho }_{l}),& \tilde{\tau }\leqslant -{\varrho }_{l}\end{array}\right.$

(3)

式中： ${\varphi }_{r}$ 和 ${\varphi }_{l}$ 为死区函数左右两侧未知的正斜率， ${\varrho }_{r}$ 和 ${\varrho }_{l}$ 是死区函数左右两侧的断点，为未知的有界的正常数。

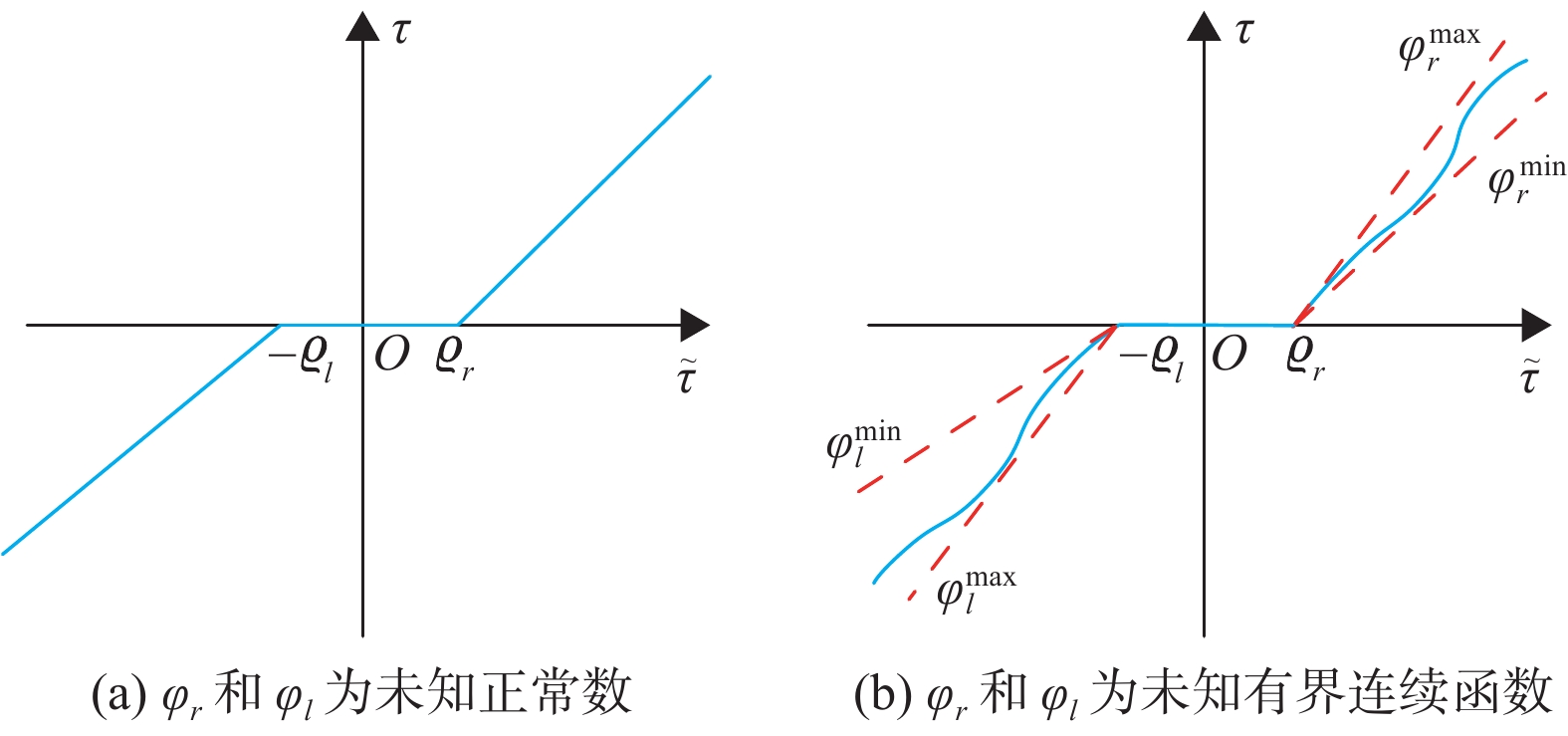
在一些研究中，如文献[55-57]中，死区函数左右两侧的斜率 ${\varphi }_{r}$ 和 ${\varphi }_{l}$ 被假设是未知的正常数，此时，式(3)所示的死区函数可以表示为图4(a)。但驱动器性能故障所导致的系统死区约束往往具有复杂的非线性特征，为了充分考虑实际环境中死区约束对系统的影响，一些学者假设 ${\varphi }_{r}$ 和 ${\varphi }_{l}$ 为未知有界的连续函数，即 ${\varphi }_{r}$ 和 ${\varphi }_{l}$ 满足下列约束

${\varphi }_{r}^{\mathrm{m}\mathrm{i}\mathrm{n}}\leqslant {\varphi }_{r}\left(t\right)\leqslant {\varphi }_{r}^{\mathrm{m}\mathrm{a}\mathrm{x}},{\varphi }_{l}^{\mathrm{m}\mathrm{i}\mathrm{n}}\leqslant {\varphi }_{l}\left(t\right)\leqslant {\varphi }_{l}^{\mathrm{m}\mathrm{a}\mathrm{x}}$

(4)

式中： ${\varphi }_{r}^{\mathrm{m}\mathrm{i}\mathrm{n}}$ ， ${\varphi }_{r}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ ， ${\varphi }_{l}^{\mathrm{m}\mathrm{i}\mathrm{n}}$ 和 ${\varphi }_{l}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ 均为正的常数。此时，式(3)所示的死区函数可以表示为图4(b)。

针对具有死区约束的柔性机械臂，研究学者们提出了一些有效的运动控制方法，其中，克服死区约束最直接的方法是构造死区约束的描述函数，然后对描述函数求逆来对死区约束进行逆补偿^[58]，但这往往需要死区描述函数的各项参数。一些学者将死区约束与模型不确定性统一作为系统的不确定项来处理，在针对存在死区约束的柔性机械臂研究中，文献[59]提出了一种自适应模糊控制方法，克服了系统输入死区约束和模型不确定性对系统的影响。文献[60]提出了一种基于运动、振动一体化的积分滑模神经网络自适应控制方法，克服了斜率与边界参数未知的死区约束对系统的影响。

2.1.3 迟滞约束

迟滞约束表现为驱动器的输出扭矩相对控制信号存在滞后，它往往是由驱动器机械传动装置的齿隙导致的^[61]。迟滞约束所对应的故障描述函数可以表示为^[62]

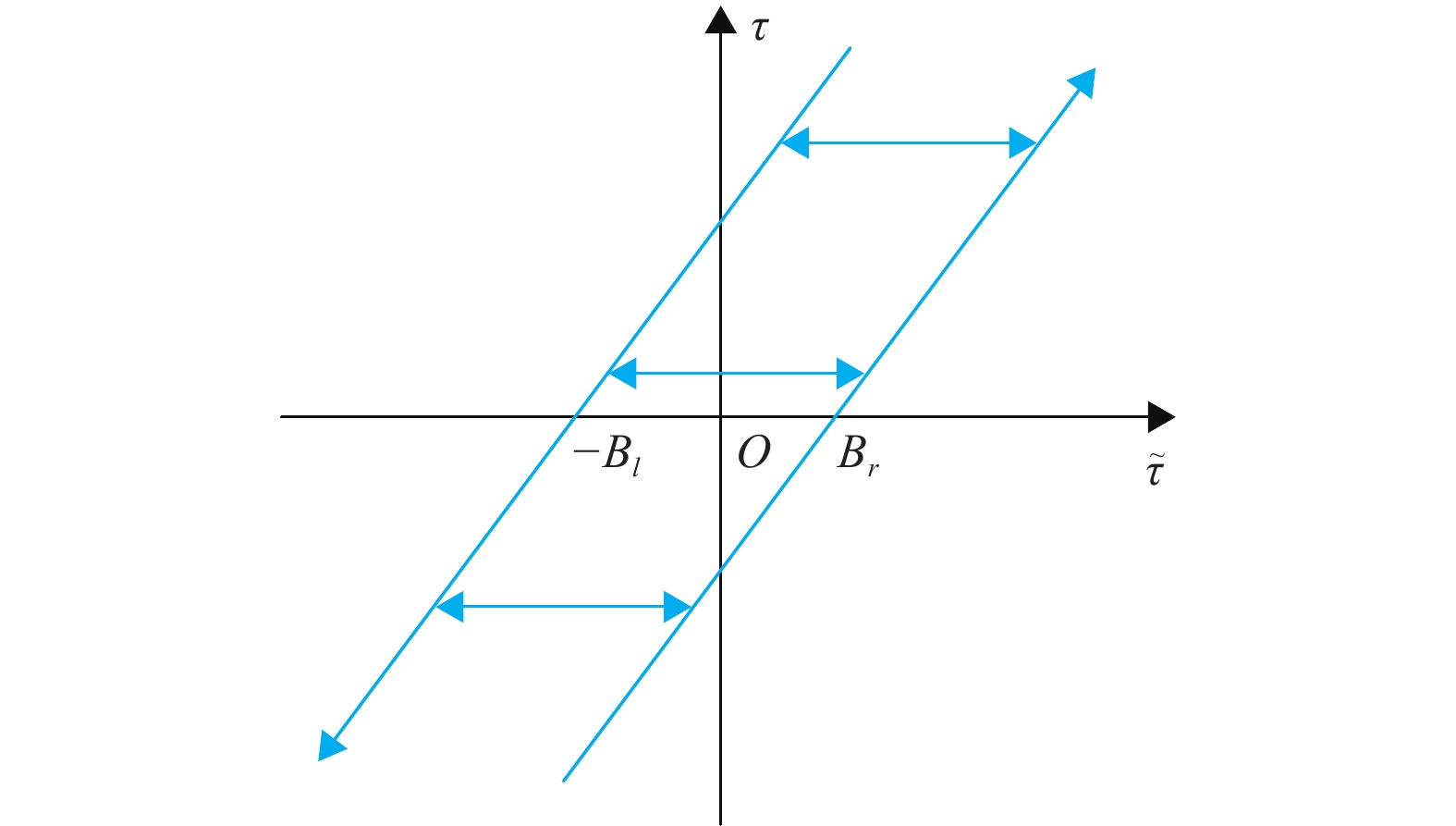
$\tau =\psi \left(\tilde{\tau }\right)=\left\{\begin{array}{ll}m\left(\tilde{\tau }-{B}_{r}\right),& \dot{\tilde{\tau }} > 0\&\tau =m(\tilde{\tau }-{B}_{r})\\ m(\tilde{\tau }+{B}_{l}),& \dot{\tilde{\tau }} < 0\&\tau =m(\tilde{\tau }+{B}_{l})\\ \tau \left({t}_-\right),& \mathrm{其}\mathrm{他}\end{array}\right.$

(5)

式中： $m$ 为迟滞函数的斜率， ${B}_{l}$ 和 ${B}_{r}$ 是齿隙参数， $\tau \left({t}_{-}\right)$ 表示 $\tau$ 相对前一时刻没有改变。 $m$ ， ${B}_{l}$ 和 ${B}_{r}$ 均为正常数。式(5)所示的迟滞函数可以表示为图5。

对于一个伺服电机来说，当其工作正常时，迟滞约束对系统的影响微弱，可以忽略不计。但当驱动器因碰撞、结构松动等原因发生驱动器性能故障时，其传动转置的齿隙可能发生异常，这使得系统的迟滞约束往往具有复杂的不确定性和非线性，可能会导致系统控制性能降低、振荡、甚至是不稳定。为克服这一问题，一种方法是构造迟滞约束的描述函数，然后设计自适应逆补偿控制策略来克服迟滞约束的影响^[63]。利用这一方法，文献[64]克服了非线性迟滞约束对单连杆柔性机械臂的影响，并利用输出反馈控制方法实现了柔性连杆的角度控制和振动抑制。文献[65]针对单连杆柔性机械臂，提出了一种基于自适应逆补偿的边界振动控制方法。

还有一种方法是直接利用迟滞约束的描述函数，将不确定的迟滞约束转化成为一个确定的线性部分和一个不确定的非线性部分，然后将不确定的非线性部分当作扰动来处理。文献[66]利用这一方法，通过设计一种基于神经网络的自适应控制器，实现了不确定输入迟滞约束下单连杆柔性机械臂的位置控制。文献[67]针对一类具有迟滞约束的可变长度旋转柔性机械臂，提出了一种自适应神经网络输出约束控制策略。文献[68]则针对具有迟滞约束的两连杆刚柔机械臂，研究了一种基于干扰观测器的自适应边界迭代学习控制策略。

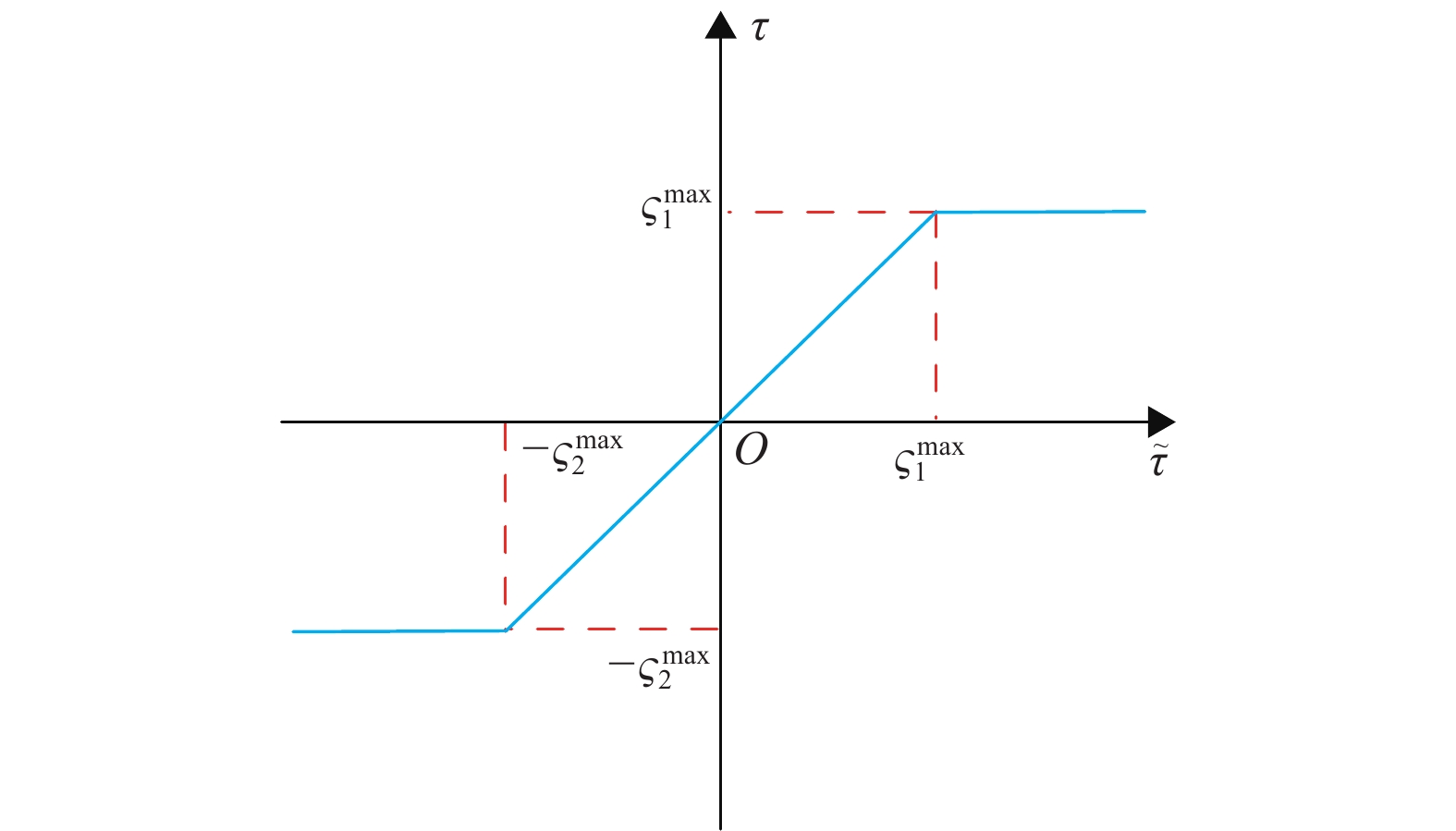
2.1.4 饱和约束

饱和约束是一种常见的输入约束，它表现为驱动器的输出扭矩存在最大值，当控制信号大于该最大值时，驱动器的实际输出扭矩将维持在该最大值不变^[69]。饱和约束可以表示为如下驱动器性能故障描述函数^[70]

$\tau =\psi \left(\tilde{\tau }\right)=\left\{\begin{array}{ll}{\varsigma }_{1}^{\mathrm{m}\mathrm{a}\mathrm{x}},& \tilde{\tau }\geqslant {\varsigma }_{1}^{\mathrm{m}\mathrm{a}\mathrm{x}}\\ \tilde{\tau },& -{\varsigma }_{2}^{\mathrm{m}\mathrm{a}\mathrm{x}} < \tilde{\tau } < {\varsigma }_{1}^{\mathrm{m}\mathrm{a}\mathrm{x}}\\ -{\varsigma }_{2}^{\mathrm{m}\mathrm{a}\mathrm{x}},& \tilde{\tau }\leqslant -{\varsigma }_{2}^{\mathrm{m}\mathrm{a}\mathrm{x}}\end{array}\right.$

(6)

式中： ${\varsigma }_{1}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ ， ${\varsigma }_{2}^{\mathrm{m}\mathrm{a}\mathrm{x}} > 0$ 分别为驱动器实际可以输出的正反最大扭矩。式(6)所描述的饱和约束中 $\tau$ 与 $\tilde{\tau }$ 之间的关系可以表示为图6。

理想情况下，驱动器输出扭矩的最大值 ${\varsigma }_{1}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ 和 ${\varsigma }_{2}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ 是已知的，与驱动器的额定最大输出有关。为了克服此类已知的饱和约束，一些学者利用双曲正切函数对系统的反馈信号进行处理，并通过设置相应的控制器参数，使控制过程中 $\left|\tilde{\tau }\right| < {\varsigma }_{*}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ ，其中 ${\varsigma }_{*}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ 为 ${\varsigma }_{1}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ 和 ${\varsigma }_{2}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ 中的最小值，从而避免饱和约束对系统的影响。基于该方法，文献[71]在饱和约束下实现了一种三维空间运动的两连杆刚柔机械臂的位置控制；文献[72]提出了一种偏微分方程边界控制方法实现了单连杆柔性机械臂的位置控制；而文献[73]则进一步结合高阶扰动观测器，实现了具有输入扰动和饱和函数的单连杆柔性机械臂的位置控制。

此外，一些学者将饱和约束对系统的影响当作输入端的扰动来处理。为解决图6所示饱和函数非光滑的问题，文献[74]先利用双曲正切函数对系统的饱和约束进行了光滑逼近，然后将逼近误差当作系统的输入扰动，利用反步法设计控制器，实现了一类单连杆柔性Euler-Bernoulli机械臂的振动抑制。

然而，当驱动器因轴承进灰、缺油等原因而存在驱动器性能故障时，其传动装置往往存在较大的摩擦，此时，系统的输入饱和约束将存在不确定性，也就是式(6)中的 ${\varsigma }_{1}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ 和 ${\varsigma }_{2}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ 未知。文献[75]针对这一未知的饱和约束，提出了一种带有辅助系统的边界控制方法，通过设计辅助系统对未知的饱和约束进行补偿，解决了非线性输入饱和对系统的影响，实现了单连杆柔性Timoshenko机械臂的角度控制和振动抑制。文献[76]针对具有输入饱和约束的两连杆柔性机械臂，设计了两个辅助系统用于补偿未知饱和约束对系统的影响。文献[77]则是利用了双曲正切函数对反馈信号进行处理，通过设计自适应律对驱动器所能输出的最大值进行估计，从而克服了未知饱和约束对系统的影响。

注释1 　驱动器性能故障可能会导致系统存在输入约束，但这并不意味着所有存在输入约束的系统都可以被认为是驱动器发生故障的系统。事实上，即便是一些正常工作的驱动器，也会存在饱和约束和轻微的死区与迟滞约束。这些输入约束不应被界定为驱动器故障。

2.2 驱动器完全损坏故障

性能故障虽然会导致一个驱动器的驱动能力部分失效，但该驱动器仍然可以驱动机械臂的连杆转动，即该驱动器所对应的机械臂关节仍然是可驱动关节。但在实际控制中，还存在一种驱动器故障会导致驱动器的驱动能力完全失效，这就是完全损坏故障，在式(1)中，驱动器完全损坏故障所对应的描述函数为

$\tau =\psi \left(\tilde{\tau }\right)\equiv 0$

(7)

当柔性机械臂的某一驱动器完全损坏时，该驱动器无法继续为系统提供控制扭矩，其所在的机械臂关节成为自由转动的欠驱动关节，所对应的机械臂连杆被称为“欠驱动连杆”^[17]。相应地，可以由驱动器直接驱动的机械臂连杆被称为“驱动连杆”。欠驱动关节会使得欠驱动连杆没有与之对应的控制输入来控制其转动，这样一来，该类系统的动力学模型相对全关节驱动系统的动力学模型，存在额外的状态约束方程^[78]。这表明，驱动器完全损坏故障会导致柔性机械臂的运动特性发生根本性的变化，若要继续实现该类系统的位置控制，则需要利用系统剩余的驱动器在实现驱动连杆角度控制的同时，实现欠驱动连杆的角度控制和系统所有柔性连杆的振动抑制，这无疑是一个极具挑战性的研究课题。

对于某一驱动器完全损坏的柔性机械臂系统，文献[79]针对第二关节欠驱动的两连杆刚柔机械臂进行了建模，并对系统的运动特性进行了分析。文献[80]分析了该类系统的振动可控性，文献[81]进一步对该类系统的动力学耦合展开了分析。文献[82]分析了具有完全损坏驱动器的柔性机械臂内共振现象，并在实验中应用该现象使柔性连杆的振幅最小化。然而，该方法在欠驱动关节处安装有锁死装置。

针对第二关节欠驱动的两连杆刚柔机械臂，文献[83]利用欠驱动关节处的关节锁死装置，分3个阶段实现了系统的运动控制目标。文献[84]提出一种分段位置控制策略，将系统的运动控制分成两个阶段，通过控制欠驱动关节处关节锁死装置的开闭实现了驱动连杆和欠驱动连杆控制目标。文献[85]提出一种基于神经网络的控制方法，解决了柔性机械臂系统动力学方程难以准确建立的问题。然而，这些控制方法同样需要在欠驱动关节处增加冗余的锁死装置。

文献[86]研究了第一关节欠驱动的两连杆刚柔机械臂的运动控制问题，发现该系统的速度状态间存在约束关系。利用这种约束关系，该研究提出了一种基于能量与智能优化的控制方法，同时实现了驱动连杆和欠驱动连杆的角度控制，以及柔性连杆的振动抑制。然而，该方法仅对第一关节欠驱动的两连杆刚柔机械臂有效，如何推广到其他存在某一驱动器完全损坏故障的柔性机械臂系统，还需要进一步研究。

2.3 驱动器突发故障

上述考虑了驱动器故障的柔性机械臂运动控制方法研究中，大多假设驱动器的故障发生在控制之前，并且已知故障的类型。这样就可以在设计控制器的过程中，对驱动器故障加以分析和考虑，并利用专门的方法来克服故障的影响，从而实现系统的控制目标。然而，在实际环境中，驱动器的故障可能发生在控制的过程中，为克服该类故障，需要设计的控制器具有一定的容错性。

对此，文献[87]针对三维空间运动的两连杆刚柔机械臂，提出了一种自适应容错控制方法，而文献[88]和文献[89]中则是针对单连杆柔性机械臂，提出了一种自适应边界容错控制方法和一种自适应补偿控制方法。此外，文献[90]针对单连杆柔性机械臂，提出了一种自适应PID控制策略，文献[91]针对两连杆刚柔机械臂提出了一种基于比例微分反馈控制器、扰动观测器和容错算法的控制方法。这些控制方法虽然可以克服控制过程中突发的驱动器故障，但这些研究均假设突发的故障类型已知。然而，控制过程中突发的驱动器故障往往具有类型未知性，它可能是驱动器性能故障，也可能是驱动器完全损坏故障。这些不同类型的故障对系统运动特性的影响截然不同。显然，这些方法无法完全应对控制过程中突发的驱动器故障。

3 挑战与展望

根据上述对驱动器故障影响下的柔性机械臂运动控制方法研究现状综述可知，虽然目前已经有一些柔性机械臂的运动控制方法考虑了驱动器故障对系统的影响，但总的来说，仍然存在以下问题需要得到进一步的解决。

(1) 因轴承进灰、缺油，传动装置损坏等原因造成的驱动器性能故障可能导致柔性机械臂存在输入约束，不同类型的输入约束具有不同的特性。目前，大部分针对输入约束下柔性机械臂的控制方法研究往往单独考虑某一类输入约束，然后设计专门的控制器来克服所考虑的输入约束。这就使得这些方法仅对某一类输入约束有效，缺乏普适性。此外，一些研究假设故障描述函数的参数先验已知，这使得这些方法存在一定的局限性。事实上，驱动器性能故障不仅可能导致柔性机械臂存在不同种类的输入约束，还可能导致系统存在多种输入约束混杂的情况，并且此类驱动器故障所导致的系统输入约束往往具有复杂的非线性和不确定性。因此，有必要针对驱动器的性能故障研究一种具有普适性的控制方法，当柔性机械臂因驱动器性能故障而存在不同种类输入约束，甚至是混杂型输入约束时，可以克服这些约束对系统的影响，实现系统的控制目标。

(2) 目前，柔性机械臂的运动控制方法，大多基于系统所有驱动器均具有驱动能力的前提条件。而当系统某一驱动器完全损坏时，该驱动器的驱动能力完全失效，这意味着，柔性机械臂原有的控制方法无法在该类驱动器故障影响下实现系统的控制目标。现有的一些考虑了驱动器完全损坏故障的研究，有的仅仅分析了该情况下系统的运动特性，有的需要在完全损坏驱动器处增加关节锁死装置来辅助实现系统的控制目标。然而，增加关节锁死装置意味着需要对系统的结构进行改造，并不具备普适性。文献[86]中的方法虽然仅对完全损坏驱动器在第一关节处的刚柔机械臂有效，但该方法提供了一种控制思路，那就是利用驱动连杆和欠驱动连杆之间的动力学耦合关系来实现系统所有连杆的角度控制和振动抑制。未来需要对完全损坏驱动器在不同关节处的柔性机械臂进行运动特性分析，以期可以发现这些系统驱动连杆和欠驱动连杆之间的动力学耦合关系，并提出有效的运动控制方法，利用剩余的驱动器实现系统的控制目标。

(3) 控制过程中发生的驱动器故障往往具有突发性和未知性，一般无法在设计控制器时，对控制过程中是否会发生故障，以及故障发生的时间进行预判。这就导致所设计的控制器无法针对驱动器故障进行预处理。一旦驱动器故障在控制的过程中发生，若不及时对控制方法进行调整，轻则导致控制目标无法实现，重则导致系统不稳定和机械臂损坏等情况。已有的一些容错控制方法虽然可以应对突发的驱动器故障，但这些方法往往假设驱动器故障的类型先验已知。对于突发的驱动器故障来说，它可能是任意一种驱动器性能故障，也可能是驱动器完全损坏故障，甚至可能是驱动器性能故障和驱动器完全损坏故障交替发生的情况。因此，需要研究一种可以对驱动器故障进行实时在线检测、诊断和克服的运动控制方法，来应对控制过程中突发的未知驱动器故障，实现柔性机械臂的运动控制。

4 结语

随着人类科技的不断发展，空间探索、人机交互等领域对机械臂控制精度、运动灵活性、工作空间范围的需求不断提高，传统刚性机械臂逐渐难以满足这些需求，这使得柔性机械臂及其运动控制方法研究成为机械臂控制领域的研究热点之一。其中，研究可以有效克服驱动器故障对系统影响的柔性机械臂运动控制方法将是提供系统运行可靠性和安全性的有效手段。虽然当前针对驱动器故障下柔性机械臂运动控制问题的研究已经取得了一定的研究成果，但这些研究往往仅对某一类驱动器故障有效。由于驱动器故障的种类繁多，且不同种类故障对系统的影响也不同，具有普适性的控制方法还有待进一步研究。因此，总体来说，驱动器故障影响下的柔性机械臂运动控制仍然是一个开放性的研究课题。为存在驱动器故障的柔性机械臂提出一套有效的运动控制解决方案，不仅可以有效克服驱动器性能故障导致的系统不同种类输入约束，甚至是混杂型输入约束，还能在系统某一驱动器完全损坏，甚至是控制过程中突发未知驱动器故障时，依旧保障系统控制目标的实现，这是当前柔性机械臂运动控制亟待解决的关键问题。攻克该项难题，将极大促进柔性机械臂运动控制理论的进一步完善和发展，并能有效带动空间机械臂控制技术的发展，具有重要而现实的理论意义和应用前景。