近年来,随着智能应用需求的深化,许多具有高维变量、强非线性并伴随明显的不确定性、随机性等影响因素的问题不断呈现,如复杂环境下机器人任务动态规划、无人驾驶动态环境目标识别、智能电网中用电行为辨识与负荷预测等。针对这些问题,基于机理驱动的传统方法不免受到制约,而基于数据驱动的智能方法日益受到关注。特别是,深度学习在很多传统的识别任务上识别率显著提升,显示了其处理复杂任务的能力,在学术界和工业界发展迅猛。
深度学习面临的问题多种多样,其中一个核心的科学问题是:给定一组输入−输出样本数据集
| $ {f^*} = \arg \mathop {\min }\limits_{f \in \varOmega } \left\{ {{l_D}(f(x),y) + \lambda p(f(x)} \right\} $ | (1) |
式中:
| $ {\omega ^*} = \arg \mathop {\min }\limits_\omega \left\{ {{l_D}({f_\omega }(x),y) + \lambda p({f_\omega }(x))} \right\} $ | (2) |
2021年在杭州召开的全球人工智能技术大会上,徐宗本院士作了《如何突破机器学习的先验假设?》的精彩演讲,将上述科学问题存在的瓶颈归纳为5个先验假设的选择[1]。一是,损失函数的选择是否应该与实际问题无关,谓之独立性假设;二是,函数空间
为了解上述问题,一方面,希望函数簇
然而在已有的大量实践中,数据密集型的成功应用较多,而在数据集很小时常受到阻碍。本质上讲,人类的学习是基于小样本的,学到的知识是可以迁移的,且在掌握一种学习能力后可以拓展新的学习。所以,基于受限或不完备的样本数据集
2019年,Wang 等[2]对小样本学习(Few-shot Learning, FSL)进行了综述,将不同的FSL方法分为数据、模型、算法3个方面:使用先验知识来增强样本(数据),将小样本转化为大样本[3-4];通过先验知识来约束假设空间(模型),使得小样本是相对够用的[5-6];使用先验知识来改变搜索策略(算法),弥补小样本的不充分搜索[7-8]。近两年,将FSL与强化学习、元学习相结合成为一个新的途径。Hong 等[9]在骨架网络里加入一个注意力代理,该代理通过强化学习进行训练,在强化注意力的帮助下,嵌入网络能够在小样本学习中逐步生成更具辨别力的特征表示。Elsken等[10]提出MetaNAS,将需要大样本的神经架构搜索 (Network Architecture Search, NAS)与元学习结合,可以与任意模型不可知元学习算法和任意基于梯度的 NAS 方法一起使用。
本文假设样本是受限的,不对样本扩增方面的研究进行阐述。实际上,将小样本转化为大样本不利于模型的快速学习;另外,提前用先验知识来增强样本学习与人的学习过程不尽一致,这种先验知识更合适刻画在模型中。目前受限样本的深度学习取得了一定进展,本文对迁移学习模型、元学习模型和课程与自步学习模型进行回顾。
1.1 迁移学习模型迁移学习,就是希望把大样本领域习得的知识和方法迁移到小样本领域中,这样计算机也可以“举一反三”“触类旁通”。近些年,迁移学习成为了一个热门的研究方向[11-12]。迁移学习的核心问题是找到两个领域的相似性,为此形成了4种迁移方式:基于实例的迁移[13-15],通过度量源域与目标域样本之间的相似度,加大对训练目标模型有利的源域训练样本(相似度大的)的权重;基于特征的迁移[16-18],识别出源域与目标域中共有的特征表示,利用共有的特征来训练一个通用的分类器;基于参数的迁移[19-20],假定源任务和目标任务共享模型的部分参数或参数分布;基于关系的迁移[21-22],假设源域和目标域中某些数据之间关系是相似的,一般采用统计关系技术进行学习。源域和目标域相差不大时,迁移学习效果不错,相差较远时,会出现较大的负迁移影响。为了克服负迁移的影响,Tan等[23-24]提出分段迁移学习,以一个课程为基础再转到下一个课程,形成多步传导式的迁移,取得了较好的效果。另外,可以尝试多个预训练模型进行迁移,为了找到合适的预训练模型,对各种预训练模型进行评估是一个关键,You等[25]提出最大证据对数(Log Maximum Evidence, LogME)用于评估迁移学习的预训练模型,其快速性、准确性、通用性都得到一定提高。
从理论层面上看,迁移学习目前主要关注什么条件下可进行迁移。Ben等[26]定义了分布之间的距离,此距离与领域适应性有关,并且给出了在有限VC (Vapnik-Chervonenkis)维情况下领域适应性问题推广性的界。随后,Blitzer 等[27]进一步界定了在特定的经验风险最小化的情形下的误差率;Ben等[28]进一步研究了在什么条件下一个分类器能在目标领域里很好地完成分类任务,还研究了给定目标领域少量的已标注的样本,如何在训练过程中把它们与大量的已标注的源数据相结合,以实现目标误差最小。
1.2 元学习模型元学习是一种模仿人类利用先前已有的知识快速学习新的未知事物的一种学习方式,即学会学习。元学习研究目前大致分为3个方向[29-30]:基于相似度度量的方法、基于记忆功能模型的方法、基于优化策略的方法。
基于相似度度量的方法,是假定支持集样本与查询集样本在低维嵌入空间可以通过某种度量进行相似度对比,从而快速地比对出查询集样本的分类信息。该方法包括3个部分:支持集到嵌入空间的映射
具有记忆功能是人类能够进行快速学习新事物的重要基础。基于记忆功能模型的方法是将任务中有用的信息编码储存到记忆模块中,以便在下次遇到新任务时可以快速准确地检索相关信息。CNN在学习后可以有效提取样本特征,其特征信息分布在网络参数中,当样本撤消后其特征向量不再显式存在,因而不便于应用到新事物的快速学习上。为此,Santoro 等[35]提出MANN(Meta-Learning with Memory-Augmented Neural Networks)模型,引入具有存储模块的神经图灵机(Neural Turing Machine, NTM),可将某种类型的特征向量显式地存储起来实现记忆增强,在下次遇到同类图片时就能快速识别出来,存储模块的读写由LSTM(Long Short-Term Memory)网络作为控制器来实施,以最少最近使用的规则(Least Recently Used Access, LRUA)对存储单元进行覆盖操作,从而节省存储空间与查询开支。
实际上,元学习的目标是试图建立一个通用的框架桥梁,这需要找到与问题无关的元信息,以此快速归纳偏差,修正当前任务空间中的模型设置(参数)。Munkhdalai 等[36]提出MetaNet(Meta Networks)模型,由基学习器(Base Learner)和带有记忆模块的元学习器(Meta Learner)组成,选择损失梯度信息作为元信息,其训练包括3个主要过程:元数据的获取、快速权重的生成和慢速权重的优化。基学习器分析支持集的任务并将元信息反馈给元学习器,元学习器则快速归纳偏差生成权重,实现快速概括,并记录到存储模块,供新样例检索使用,再结合查询集中的任务对慢速权重进行优化。该方法将存储的类别特征信息升级为直接保存的权重信息,并且使用一种层增强技术,可同时利用快速权重和慢速权重得到预测结果。
结合快速查询和相似度比对,Cai 等[37]提出MM-Net(Memory Matching Networks for One-Shot Image Recognition)模型,将支持集的特征与对应类别标签构成“键−值对”储存在记忆模块中,然后提取查询集的特征,并与记忆模块中的特征进行比对,选择相似程度最高的作为查询图片的类别,在此过程中利用Bi-LSTM (Bi-directional Long Short Term Memory)网络,根据记忆模块中存储的特征信息学习特征,提取网络的卷积核参数,这一点类似于MetaNet中的快速参数化。
在监督学习的方式下,梯度信息直接影响模型参数的学习,建立以它为基础的元学习能力是有意义的,这就是基于优化策略的方法。Finn等[38]提出MAML(Model-Agnostic Meta-Learning)模型,创造性地给出双循环的优化策略,针对随机采样的学习任务,其内循环与通常的预训练模型一样,利用支撑集的梯度信息更新参数,此过程是在网络副本上进行的,谓之第一次梯度更新过程,实现基学习的任务;外循环是以内循环的结果来测试查询集,再以这个损失的梯度信息真正更新网络参数,谓之第二次梯度更新过程,即Gradient by Gradient,其目的就是找到一个尽量满足所有任务的网络参数,实现元学习的任务。如此多次循环后作为新任务的网络初始化参数,再用少量的样本进行微调(Fine-tune)便可快速拟合。MAML的元学习实际上是一个双循环的框架,与基学习的模型无关,这一特点使MAML类模型成为了众多元学习算法的基础框架,其适用范围扩展至强化学习、回归预测等领域[39–43]。
基于优化策略的元学习,其目的是学习到梯度的更新规则。Ravi 等[7]注意到梯度更新的迭代序列与LSTM的序列学习记忆过程是同构相似的,因而构建了一个基于LSTM的梯度优化器,以它作为元学习者(Meta-learner)训练另一个只有小样本的基学习者(Learner),换言之,通过一个网络更新另一个网络。通常基学习者的网络参数是大量的,若元学习者LSTM网络的隐藏单元一一对应基学习者的网络参数,将引起元学习者的参数爆炸,为此使用了一种参数共享机制,即LSTM的隐藏单元只有一个,基学习者的每个参数都共享这个LSTM,即它们的更新规则一样,但各自的历史隐藏信息不同,因而它们的每个参数的更新量是不一样的。
1.3 课程与自步学习模型样本数据集的完备程度影响深度学习的效果,但现实中样本数据常常会有噪声不同、异常值、不平衡等情况,即样本有“难”“易”之分,若不加处理同等对待全部提供给机器学习,即使有足够量的样本数据,其效果也会受到制约。为此,出现了课程−自步学习理论。
2009年,Bengio 等[44]首次提出了课程学习的概念,尝试模拟“从易到难”的学习机制,预先将数据按照某种预设“课程”从易到难排序,然后按此顺序将数据逐步输入学习模型进行增量式学习。虽然课程学习在一些应用中体现出良好的性能,但其性能依赖于预先主观制定的课程质量,这需要用户对领域拥有足够全面的先验知识;另一方面,对于人类容易的课程未必对于模型也是容易的。
为了能自适应设置课程,Kumar等[45]在2010年提出了自步学习(Self-paced Learning),将课程的难易程度以正则化项嵌入到目标函数中,动态地调整参与学习的样本的难易系数。由于正则项独立,不会因为任务的改变而改变,自步学习被广泛用于不同的任务,并获得了良好的应用效果[46–49]。Meng等[50]从理论上证明了自步学习的迭代算法与一个鲁棒损失函数的迭代过程是对应的,并在此后证明了自步学习的收敛性[51],这项工作揭示了自步学习具有鲁棒学习的本质内涵。随后,Liu等[52]阐明了自步学习模型与凹共轭形式是本质等价的,并在此框架下诱导出更具一般性的自步正则。
然而,所有这些工作都敏感地依赖于正则项中超参数的选择。若选择不当,可能导致进入学习的训练样本过快过多,使异常样本或者无意义的噪声样本过早侵入,从而产生训练效果的偏差;或者导致进入样本过少,使学习速度过慢等。为此,束俊等[53]提出一种元自步学习算法,将元学习与自步学习相融合,构建了超参数的自动学习策略。
近几年,课程与自步学习在深度和广度方面都有新推进[54],如采取老师−学生共同学习的方式[55–57]、与弱监督迁移学习相结合[58-59]、与贝叶斯优化器相结合[60]、用动态损失函数分类课程[61]等。上述成果印证了课程与自步学习是具有广泛有效性的,但Zhang等[62]发现在神经机器翻译任务上,“由难到易”的反课程效果更好,随后,Hacohen等[63]和Wang等[64]也有类似结论。这提示了如何根据任务与模型的不同设置合适的课程体系仍是一个待解决的问题。
借鉴“仿人学习”而提出的小样本学习、迁移学习、元学习、课程与自步学习等,尽管有各自的出发点,但相互嵌入融合成为了目前一个新的发展趋势,为改善神经网络泛化能力,提高快速响应能力,加强通用性带来新机。
2 进一步研究的思考前面的分析表明,解决式(2)的科学问题面临的挑战仍在两方面:一是函数簇
从目前对大脑的研究看,人的认知过程在大脑中是分区域的,每个区域担负的功能是不同的,因而,对每个区域功能的训练(生化过程)也应该是有差异的。因此,网络结构
此外,对于每个功能模块的训练应该是“进阶”式的,类似人的大脑从婴儿到成人有一个从发育至成熟的过程。在这个过程中,有些功能模块需要先训练,有些功能模块需要后训练;不同功能的实现,应提供不同的“课程”(样本),采用不同的教法(优化策略)等。
鉴于此,本文给出一种分区分层多种功能模块的网络结构设想,并初步研究“进阶”式的功能模块训练方法,以期探求“仿人学习”的新路径。
2.1 分区分层多种功能模块的网络结构为了简化描述,本文以图像分类问题为例进行阐述。令
若属于同一类,则
| $ \begin{array}{*{20}{c}} {f({x_i},\omega ) = f({x_j},\omega ) = f({x_i} + \Delta x,\omega )},&{{x_i},{x_j} \in {D_k}} \end{array}\quad $ | (3) |
若不属于同类,则
| $ \begin{array}{*{20}{c}} {f({x_i},\omega ) \ne f({x_j},\omega ) = f({x_i} + \Delta x,\omega )},&{{x_i} \in {D_k},{x_j} \in {D_{k'}}} \end{array} $ | (4) |
网络模型应做到“同类相吸、异类相斥”,或者对于类内差异
为了实现“同类相吸、异类相斥”,网络模型
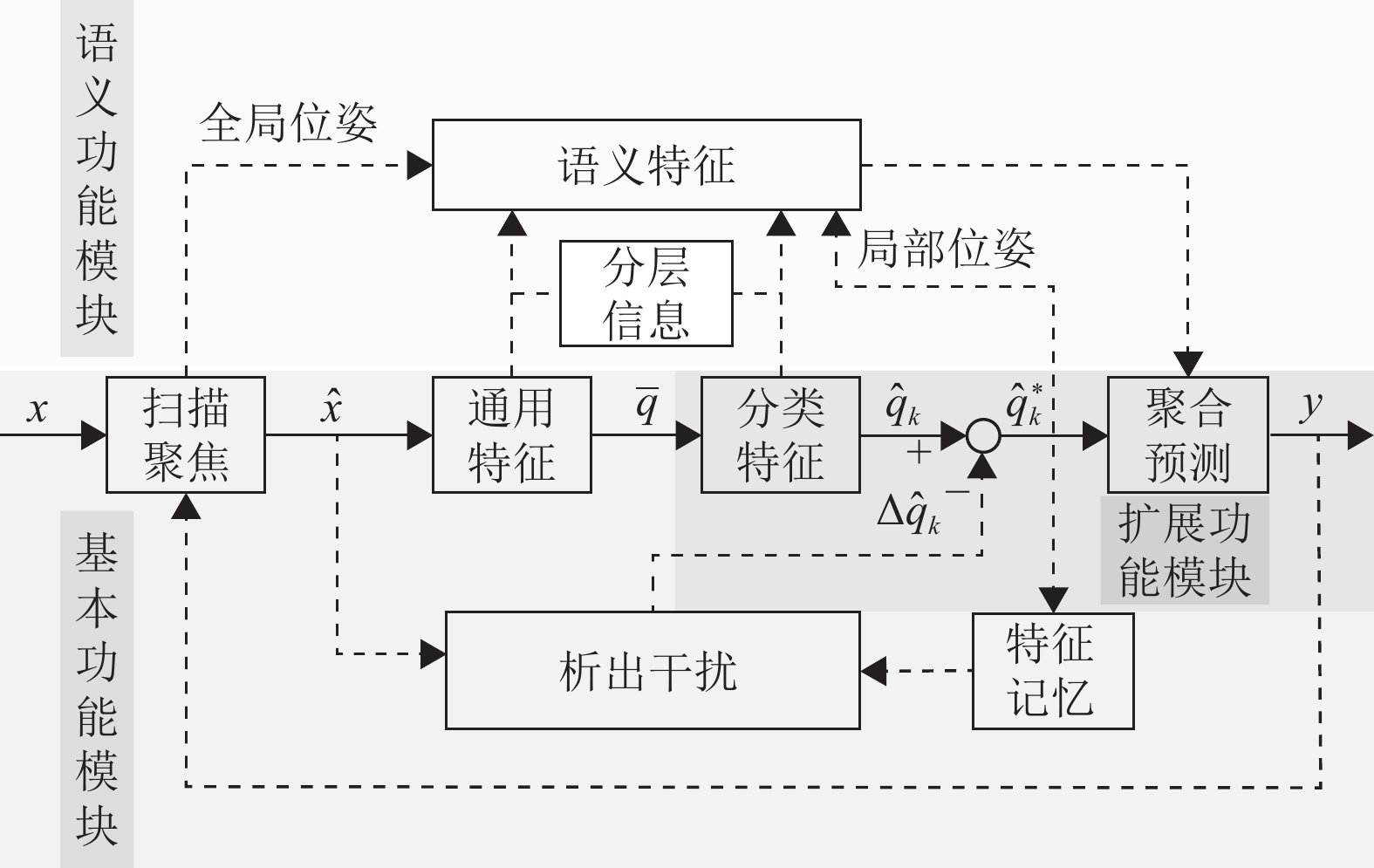
|
图 1 分区分层多种功能模块的网络结构 Figure 1 Network structure with partitioned and hierarchical multi-functional modules |
(1) 基本功能模块。该模块处理标准尺寸的图像(
(2) 扩展功能模块。该模块需实现三方面功能:一是,构建长期记忆模块存储各类的特征信息;二是,构建扫描聚焦模块,将输入的大图
(3) 语义功能模块。该模块归纳出图像多层次多尺度的语义特征。一是,研究从扫描聚焦模块抽出全局(图像)位姿信息;二是,研究从扩展功能模块抽出局部(图像)位姿信息;三是,研究从通用特征、分类特征模块的分层信息和前面的位姿信息中归纳出各级语义信息。由于位姿信息的存在,可以锚定通用特征、分类特征模块中的信息,使语义特征更加明确。构造网络模型实现式(4)的要求相对容易,而实现式(3)的要求相对困难,有了语义特征后,再聚合数据特征,便能很好地实现式(3)的要求。
2.2 训练样本集的构建要实现“功能进阶式”的训练,构建不同功能的训练样本集是一个重点。可大致将样本集分为:基本集、扩展集、语义级。
(1) 对于基本集,重点是训练如何提取数据特征,样本应尽量不含背景噪声等干扰因素。由于原型样本量小,所以研究对原型样本的遮蔽方法,形成大量残缺样本,增强基本集,以训练特征提取的鲁棒性。
(2) 对于扩展集,重点是训练如何析出与原型样本的差异信息。研究在基本集的样本上自动进行平移、缩放、旋转、视点变换的增强方法,形成1级扩展集;再研究在1级扩展集的基础上,引入各种背景噪声,形成2级扩展集;再研究借助Web等易得资源扩充多类多变的复杂样本,形成3级扩展集。
(3) 对于语义级,重点是训练如何提取语义特征,样本可在基本集和扩展集中筛选,再对其实施各种掩蔽,用以生成语义信息和建立它们之间的关联。
3 结论受限样本的深度学习旨在模仿人类学习的方式,通过将学习到的不同模态间的通用知识刻画在模型里,然后快速迁移到小样本的新任务中。本文从深度学习的优化问题出发,总结出依赖不完备样本数据集的深度学习模型更接近人类的学习,然后对迁移学习模型、元学习模型和课程与自步学习模型在受限样本下的深度学习进行了分类综述。进一步地,针对受限样本的深度学习所面临的挑战,给出了一种分区分层多种功能模块的网络结构设想,并构建相应的数据集,以探索“仿人学习”的新路径。
| [1] |
徐宗本. 人工智能的十个重大数理基础问题[J].
中国科学:信息科学, 2021, 51(12): 1967-1978.
XU Z B. Ten fundamental problems for artificial intelligence: mathematical and physical aspects[J]. Scientia Sinica(Informationis), 2021, 51(12): 1967-1978. |
| [2] |
WANG Y, YAO Q, KWOK J T, et al. Generalizing from a few examples: a survey on few-shot learning[J].
ACM Computing Surveys (Csur), 2020, 53(3): 1-34.
|
| [3] |
LIU B, WANG X D, DIXIT M, et al. Feature space transfer for data augmentation[C] //Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE, 2018: 9090-9098.
|
| [4] |
TSAI Y H H, SALAKHUTDINOV R. Improving one-shot learning through fusing side information[EB/OL]. (2018-01-23)[2022-05-13]. https://arxiv.org/abs/1710.08347.
|
| [5] |
TRIANTAFILLOU E, ZEMEL R, URTASUN R. Few-shot learning through an information retrieval lens[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2017, 30: 2252-2262.
|
| [6] |
YAN L M, ZHENG Y H, CAO J. Few-shot learning for short text classification[J].
Multimedia Tools and Applications, 2018, 77(22): 29799-29810.
DOI: 10.1007/s11042-018-5772-4. |
| [7] |
RAVI S, LAROCHELLE H. Optimization as a model for few-shot learning[C] //Proceedings of the International Conference on Learning Representations. Cambridge: ICLR, 2017: 1-11.
|
| [8] |
YOO D, FAN H, BODDETI V N, et al. Efficient k-shot learning with regularized deep networks[EB/OL]. (2017-10-06) [2022-05-13]. https://arxiv.org/abs/1710.02277.
|
| [9] |
HONG J, FANG P, LI W, et al. Reinforced attention for few-shot learning and beyond [C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE, 2021: 913-923.
|
| [10] |
ELSKEN T, STAFFLER B, METZEN J H, et al. Meta-learning of neural architectures for few-shot learning[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE, 2020: 12365-12375.
|
| [11] |
PAN S J, YANG Q. A survey on transfer learning[J].
IEEE Transactions on Knowledge and Data Engineering, 2009, 22(10): 1345-1359.
|
| [12] |
ZHUANG F, QI Z, DUAN K, et al. A comprehensive survey on transfer learning[J].
Proceedings of the IEEE, 2020, 109(1): 43-76.
|
| [13] |
JIANG J, ZHAI C. Instance weighting for domain adaptation in NLP[C]// Proceedings of the Annual Meeting of the Association for Computational Linguistics. Stroudsburg: ACL, 2007: 264-271.
|
| [14] |
DAI W, YANG Q, XUE G R, et al. Boosting for transfer learning[C]// Proceedings of the International Conference on Machine Learning. New York: PMLR, 2007: 193-200.
|
| [15] |
SUGIYAMA M, NAKAJIMA S, KASHIMA H, et al. Direct importance estimation with model selection and its application to covariate shift adaptation[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2007, 20: 1433-1440.
|
| [16] |
SAITO K, USHIKU Y, HARADA T. Asymmetric tri-training for unsupervised domain adaptation[C]//Proceedings of the International Conference on Machine Learning. New York: PMLR, 2017: 2988-2997.
|
| [17] |
DUAN L, TSANG I W, XU D. Domain transfer multiple kernel learning[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(3): 465-479.
DOI: 10.1109/TPAMI.2011.114. |
| [18] |
ZHUANG F, LUO P, YIN P, et al. Concept learning for cross-domain text classification: a general probabilistic framework[C]//Twenty-Third International Joint Conference on Artificial Intelligence. Amsterdam: Elsevier, 2013: 1960-1966.
|
| [19] |
BONILLA E V, CHAI K, WILLIAMS C. Multi-task Gaussian process prediction[C] //Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2007, 20: 153-160.
|
| [20] |
SCHWAIGHOFER A, TRESP V, YU K. Learning Gaussian process kernels via hierarchical Bayes[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2004, 17: 1209-1216.
|
| [21] |
MIHALKOVA L, MOONEY R J. Transfer learning by mapping with minimal target data[C] //Proceedings of the AAAI-08 Workshop on Transfer Learning for Complex Tasks. Palo Alto: AAAI Press, 2008: 1163-1168.
|
| [22] |
DAVIS J, DOMINGOS P. Deep transfer via second-order markov logic [C]//Proceedings of the International Conference on Machine Learning. New York: PMLR, 2009: 217-224.
|
| [23] |
TAN B, SONG Y, ZHONG E, et al. Transitive transfer learning[C] //Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2015: 1155-1164.
|
| [24] |
TAN B, ZHANG Y, PAN S, et al. Distant domain transfer learning [C]//Proceedings of the AAAI Conference on Artificial Intelligence. Palo Alto: AAAI Press, 2017, 31: 2604-2610.
|
| [25] |
YOU K C, LIU Y, WANG J M, et al. Logme: practical assessment of pre-trained models for transfer learning[C]//Proceedings of the International Conference on Machine Learning. New York: PMLR, 2021: 12133-12143.
|
| [26] |
BEN-DAVID S, BLITZER J, CRAMMER K, et al. Analysis of representations for domain adaptation[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2006, 19: 137-144.
|
| [27] |
BLITZER J, CRAMMER K, KULESZA A, et al. Learning bounds for domain adaptation[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2007, 20: 129-136.
|
| [28] |
BEN-DAVID S, BLITZER J, CRAMMER K, et al. A theory of learning from different domains[J].
Machine learning, 2010, 79(1): 151-175.
|
| [29] |
HUISMAN M, VANRIJN J N, PLAAT A. A survey of deep meta-learning[J].
Artificial Intelligence Review, 2021, 54(6): 4483-4541.
DOI: 10.1007/s10462-021-10004-4. |
| [30] |
HOSPEDALES T, ANTONIOU A, MICAELLI P, et al. Meta-learning in neural networks: a survey[EB/OL]. https://arxiv.org/abs/2004.05439.
|
| [31] |
KOCH G, ZEMEL R, SALAKHUTDINOV R. Siamese neural networks for one-shot image recognition[C] //ICML deep learning workshop. New York: PMLR, 2015, 2: 1-8.
|
| [32] |
VINYALS O, BLUNDELL C, LILLICRAP T, et al. Matching networks for one shot learning[C]//Advances in Neural Information Processing Systems. Cambridge, Massachusetts: MIT Press, 2016, 29: 3637-3645.
|
| [33] |
SNELL J, SWERSKY K, ZEMEL R. Prototypical networks for few-shot learning[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2017, 30: 4080-4090.
|
| [34] |
SUNG F, YANG Y, ZHANG L, et al. Learning to compare: Relation network for few-shot learning[C] //Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE, 2018: 1199-1208.
|
| [35] |
SANTORO A, BARTUNOV S, BOTVINICK M, et al. Meta-learning with memory-augmented neural networks[C]//Proceedings of the International Conference on Machine Learning. New York: PMLR, 2016: 1842–1850.
|
| [36] |
MUNKHDALAI T, YU H. Meta networks[C]//Proceedings of the International Conference on Machine Learning. New York: PMLR, 2017: 2554-2563.
|
| [37] |
CAI Q, PAN Y, YAO T, et al. Memory matching networks for one-shot image recognition[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE, 2018: 4080-4088.
|
| [38] |
FINN C, ABBEEL P, LEVINE S. Model-agnostic meta-learning for fast adaptation of deep networks[C]//Proceedings of the International Conference on Machine Learning. New York: PMLR, 2017: 1126-1135.
|
| [39] |
RUSU A A, RAO D, SYGNOWSKI J, et al. Meta-learning with latent embedding optimization[EB/OL]. (2019-03-26)[2022-05-13]. https://arxiv.org/abs/1807.05960v3.
|
| [40] |
LEE Y, CHOI S. Gradient-based meta-learning with learned layerwise metric and subspace[C]//Proceedings of the International Conference on Machine Learning. New York: PMLR, 2018: 2927-2936.
|
| [41] |
Al-SHEDIVAT M, BANSAL T, BURDA Y, et al. Continuous adaptation via meta-learning in nonstationary and competitive environments[EB/OL]. (2018-02-23)[2022-05-13]. https://arxiv.org/abs/1710.03641.
|
| [42] |
GRANT E, FINN C, LEVINE S, et al. Recasting gradient-based meta-learning as hierarchical bayes[EB/OL]. (2018-01-26)[2022-05-13]. https://arxiv.org/abs/1801.08930v1.
|
| [43] |
NAGABANDI A, CLAVERA I, LIU S, et al. Learning to adapt in dynamic, real-world environments through meta-reinforcement learning[EB/OL]. (2019-02-27)[2022-05-13]. https://arxiv.org/abs/1803.11347v6.
|
| [44] |
BENGIO Y, LOURADOUR J, COLLOBERT R, et al. Curriculum learning[C] //Proceedings of the International Conference on Machine Learning. New York: PMLR, 2009: 41-48.
|
| [45] |
KUMAR M P, PACKER B, KOLLER D. Self-paced learning for latent variable models[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2010, 23: 1189-1197.
|
| [46] |
JIANG L, MENG D Y, MITAMURA T, et al. Easy samples first: self-paced reranking for zero-example multimedia search[C]// Proceedings of the ACM International Conference on Multimedia. New York: ACM, 2014: 547-556.
|
| [47] |
ZHANG D W, MENG D Y, HAN J W. Co-saliency detection via a self-paced multiple-instance learning framework[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 39(5): 865-878.
|
| [48] |
JIANG L, MENG D Y, ZHAO Q, et al. Self-paced curriculum learning[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Palo Alto, CA: AAAI Press, 2015: 2694-2700.
|
| [49] |
SUPANCIC J S, RAMANAN D. Self-paced learning for long-term tracking[C] //Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE, 2013: 2379-2386.
|
| [50] |
MENG D Y, ZHAO Q, JIANG L. A theoretical understanding of self-paced learning[J].
Information Sciences, 2017, 414: 319-328.
DOI: 10.1016/j.ins.2017.05.043. |
| [51] |
MA Z L, LIU S Q, MENG D Y, et al. On convergence properties of implicit self-paced objective[J].
Information Sciences, 2018, 462: 132-140.
DOI: 10.1016/j.ins.2018.06.014. |
| [52] |
LIU S Q, MA Z L, MENG D Y, et al. Understanding self-paced learning under concave conjugacy theory[J].
Communications in Information and Systems, 2018, 1(1): 1-27.
|
| [53] |
束俊, 孟德宇, 徐宗本. 元自步学习[J].
中国科学: 信息科学, 2020, 50(6): 781-793.
SHU J, MENG D Y. XU Z B, Meta self-paced learning[J]. Scientia Sinica (Informationis), 2020, 50(6): 781-793. |
| [54] |
WANG X, CHEN Y D, ZHU W W. A survey on curriculum learning [J/OL]. IEEE Transactions on Pattern Analysis and Machine Intelligence. (2021-03-31)[2022-05-13]. https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=9392296.
|
| [55] |
JIANG L, ZHOU Z, LEUNG T, et al. Mentornet: learning data-driven curriculum for very deep neural networks on corrupted labels[C]//Proceedings of the International Conference on Machine Learning. New York: PMLR, 2018: 2304-2313.
|
| [56] |
KIM T-H, CHOI J. Screenernet: learning self-paced curriculum for deep neural networks [EB/OL]. (2018-01-03)[2022-05-13]. https://arxiv.org/abs/1801.00904.
|
| [57] |
WU L, TIAN F, XIA Y, et al. Learning to teach with dynamic loss functions[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2018, 31: 6467-6478.
|
| [58] |
GUO S, HUANG W, ZHANG H, et al. Curriculumnet: weakly supervised learning from large-scale web images [C] // Computer Vision – ECCV 2018.Munich: European Conference on Computer Vision (ECCV), 2018: 135-150.
|
| [59] |
SHU Y, CAO Z, LONG M, et al. Transferable curriculum for weakly-supervised domain adaptation[C]// Proceedings of the AAAI Conference on Artificial Intelligence. Palo Alto: AAAI Press, 2019, 33(1): 4951-4958.
|
| [60] |
TSVETKOV Y, FARUQUI M, LING W, et al. Learning the curriculum with bayesian optimization for task-specific word representation learning[C] //Proceedings of the Annual Meeting of the Association for Computational Linguistics. Stroudsburg: ACL, 2016: 130-139.
|
| [61] |
SAXENA S, TUZEL O, DECOSTE D. Data parameters: a new family of parameters for learning a differentiable curriculum[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2019, 32: 11095-11105.
|
| [62] |
ZHANG X, KUMAR G, KHAYRALLAH H, et al. An empirical exploration of curriculum learning for neural machine translation[EB/OL]. (2018-11-02)[2022-05-13]. https://arxiv.org/abs/1811.00739.
|
| [63] |
HACOHEN G, WEINSHALL D. On the power of curriculum learning in training deep networks[C]// Proceedings of the International Conference on Machine Learning. New York: PMLR, 2019: 2535-2544.
|
| [64] |
WANG W, CASWELL I, CHELBA C. Dynamically composing domain-data selection with clean-data selection by "co-curricular learning" for neural machine translation[C]//Proceedings of the Annual Meeting of the Association for Computational Linguistics. Stroudsburg: ACL, 2019: 1282-1292.
|
 2022, Vol. 39
2022, Vol. 39

