自然界中“泥而不滓”的荷叶,“飞檐走壁”的壁虎,“水上漂”的水黾等,给予了我们启示,构造不同的微纳粗糙表面可以获取特殊的润湿行为[1]。自然界中存在如下3种典型的润湿态:Wenzel润湿态、Cassie疏水态和Cassie-Baxter(CB)超疏水态。仿生材料获取特殊润湿行为的研究中,主要通过调控粗糙表面化学组成和固体粗糙表面的几何结构实现,用于自清洁、油水分离、防雾、防霜和减阻等诸多领域[1]。
微米尺度效应下的液滴润湿行为几乎吻合理论分析及宏观实验规律[2-3],纳米粗糙表面可以实现显著的润湿态[4],但是由于纳米尺度粗糙表面加工难度大以及纳米尺度粗糙表面对实验设备的超高要求,目前对于粗糙表面化学组成和固体粗糙表面几何结构调控研究主要集中在微米尺度或者微纳米双尺度。Berendjchi等[5]采用实验的方法,制备了具有多重微纳米复合结构的棉织品,其表面是掺杂有 Cu 纳米粒子的硅溶胶,通过表面低能化处理,该样品呈现显著的疏水性。Liu等[6]通过3D打印技术分别用硬质硅和柔质聚酰亚胺制备了柱状和多级T形再入几何结构的微米粗糙表面,研究了正全氟辛烷、水、正十二烷、乙醇、己烷和硅油6种不同表面能的液滴在粗糙结构上的润湿性,发现引入各种表面能的液滴,柱状粗糙结构接触角都小;针对单级T形再入结构,只有水滴疏水,其他表面能的液滴均亲水;而以上6种液体都无法穿透双级和三级T形再入几何结构,表明这两种T形再入几何结构提高了固体表面疏水性。重心悬垂的微纳米粗糙结构可以有效调控其表面液滴的润湿行为[4,7],比如“T”形或蘑菇形。
关于纳米尺度下的润湿行为,现有学者就纳米结构高度、间距和相面积分数以及固液间相互作用参数对不同的几何形貌展开了相关研究,主要包括矩形、T形和蘑菇形,特别是矩形粗糙表面。Yong等[8]采用分子动力学模拟方法,分析了纳米尺度下沟槽中不同的粗糙度因子和相面积分数对汞液滴润湿行为的作用。结果表明,对于疏水表面,接触角、粗糙度因子和相面积分数之间的函数服从Wenzel理论和Cassie理论的预测;而少量液体发生渗透时,接触角出现轻微偏差,不能使用Cassie或Wenzel的理论来精确地预测;对于亲水表面,只观察到润湿态且接触角常高于Wenzel预测。Berim等[9]用密度泛函理论研究了接触角与粗糙度的关系,发现在纳米疏水表面上,接触角随粗糙度的增加而增大的趋势并不是普遍有效的,而是取决于固液间的相互作用、柱高、柱间距以及滴度的大小,王宝和等[10]的研究也证实了这点。颜笑等[11]采用分子动力学模拟,构建矩形纳米粗糙表面,研究其表面二维液滴在不同能量系数、矩形结构高度以及宽度等多重因素作用下的润湿行为,表明矩形结构高度对润湿行为的作用存在一个临界值(0.6 nm),超过该值,纳米结构高度对润湿行为的影响较小,这与Hirvi等[12]和Jeong等[13]的模拟结果一致;可见,粗糙表面纳米结构的高度对液滴润湿性的调控幅度较小;在本征疏水性较弱的表面,宽度较小时纳米结构上存在结构化的水分子阻碍上部水分子沿着缝隙渗透从而影响润湿态的转变[11]。这与Chen等[2,14]的研究结果一致,他们指出由于纳米结构上存在水分子结构化,Cassie状态仅存在于纳米结构的表面。Ambrosia等[15]采用分子动力学模拟,构建具有矩形纳米结构的石墨表面,分析润湿行为在不同矩形纳米结构高度作用下所呈现的规律,同样表明,高度对润湿性的改变存在局限性。
综上所述,在纳米粗糙表面润湿行为的研究中,几何尺寸的调控能力存在一定的局限性。固−液之间的相互作用系数对纳米粗糙表面液滴润湿行为的调控更有效。而大区间内能量系数作用下,纳米尺度粗糙表面呈现的润湿规律报道甚少。因此,本文采用分子动力学模拟的方法,探讨倒三角形纳米实心悬垂结构表面液滴的润湿性随着能量系数区间的不同所呈现的规律,为设计并调控人造粗糙表面液滴润湿性提供依据。
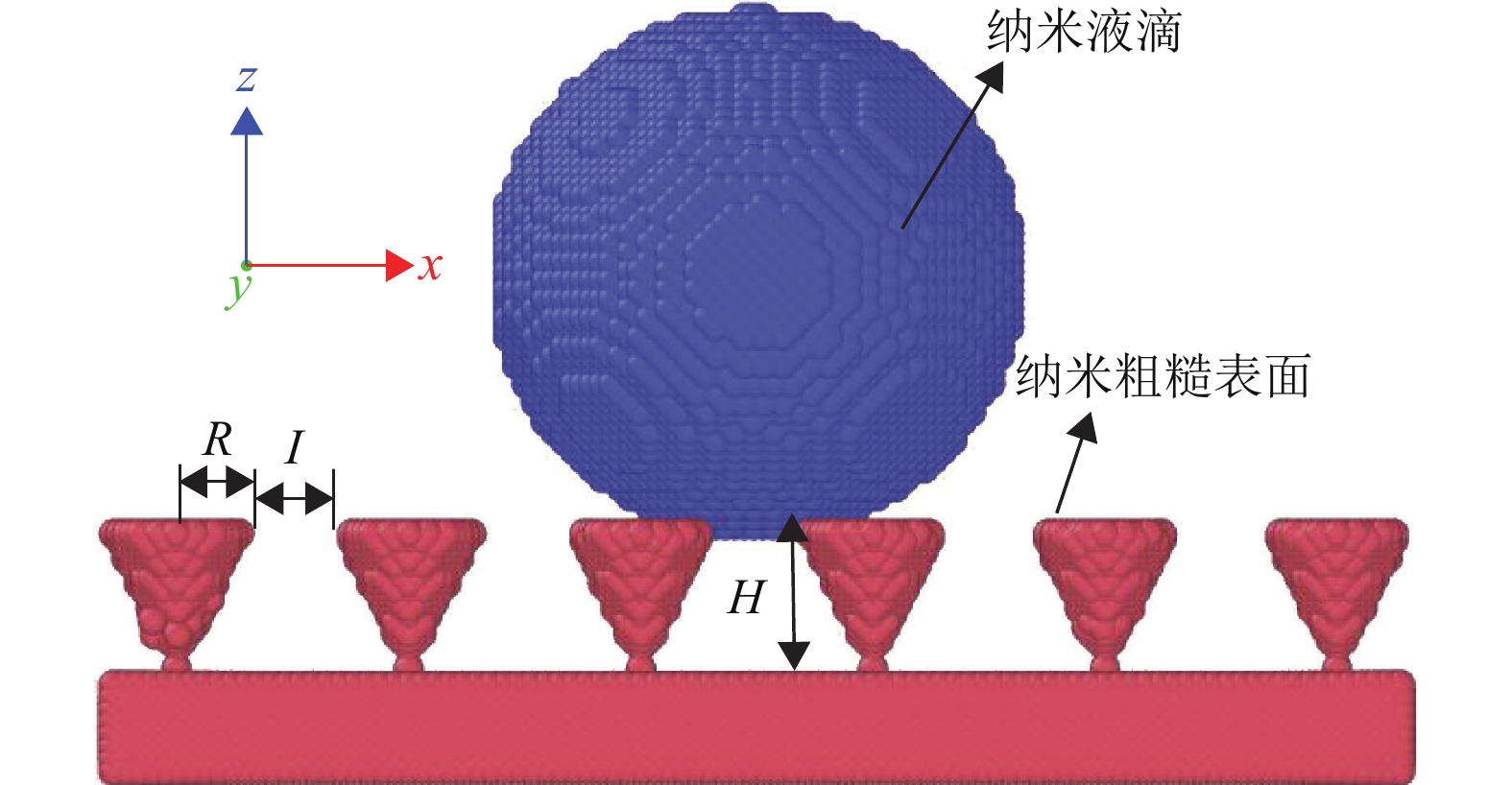
1 物理模型和模拟方法不同能量系数下倒三角形纳米粗糙表面润湿态分子动力学模型如图1所示,固体壁面底层一共八层原子,按面心立方结构(FCC)排列,固体壁面长度和宽度均为161.5σ(对应55 nm),高13.6σ(对应4.63 nm),壁面顶层为倒三角形纳米结构,间距I为11.9σ(对应4.05 nm),高度H为17σ(对应5.79 nm),半径R为17σ(对应5.79 nm)。倒三角形纳米粗糙表面上构建半径为32.3σ(对应11 nm)的液滴。液氩原子也按照面心立方结构(FCC)排列,尺寸参数σf=σ=0.3405 nm,能量参数εf=1.670×10−21 J。模拟时间用t表示,单位为τ,可由式(1)获得时间单位τ等于2.16 ps[16]。
|
图 1 模拟盒子示意图 Figure 1 Sketch of simulation box |
| $ \tau =\sqrt{m{{\sigma }_{f}}^{2}/{\varepsilon }_{f}} $ | (1) |
同类原子间势能φ(r)采用Lennard-Jones(LJ)势能模型描述,见式(2)。
| $ \varphi \left(r\right)=4\varepsilon \left[{\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^{6}\right] $ | (2) |
式中:r为原子间距离,σ为尺寸参数,ε为能量参数。固体原子尺寸参数σs=0.73σf=0.2475 nm,能量参数εs=50εf。液体原子尺寸参数σf,能量参数εf。不同类原子间(即固液原子间)相互作用根据Lorentz-Berthelot混合规则[17],见式(3)、(4),采用修正后Lennard-Jones(LJ)势能模型,见式(5)。
| $ {\varepsilon }_{fs}^{*}=\sqrt{\frac{{\varepsilon }_{f}}{{\varepsilon }_{f}}\times \frac{{\varepsilon }_{s}}{{\varepsilon }_{f}}} $ | (3) |
| $ {\sigma }_{fs}^{*}=0.5\times \left(\frac{{\sigma }_{f}}{{\sigma }_{f}}+\frac{{\sigma }_{s}}{{\sigma }_{f}}\right) $ | (4) |
| $ {\varphi }_{fs}\left(r\right)=4a{\varepsilon }_{fs}^{*}\left[{\left(\frac{{\sigma }_{fs}^{*}}{r}\right)}^{12}-{\left(\frac{{\sigma }_{fs}^{*}}{r}\right)}^{6}\right] $ | (5) |
式(5)中引入修正系数a调节固液原子间能量系数,近似模拟了不同化学组分的固体壁面。以液氩的系数为单位,
引入渗透率λ衡量润湿程度,模拟过程中,当倒三角形纳米粗糙表面液滴达到平衡时,渗入沟槽中的液体原子总数与沟槽中液体原子的最大容纳量之比即为λ,本文润湿行为的定义中,包括如下3种状态:Wenzel态(λ>0.6),Cassie态(λ<0.1),余下的均为过渡态(0.1<λ<0.6)。
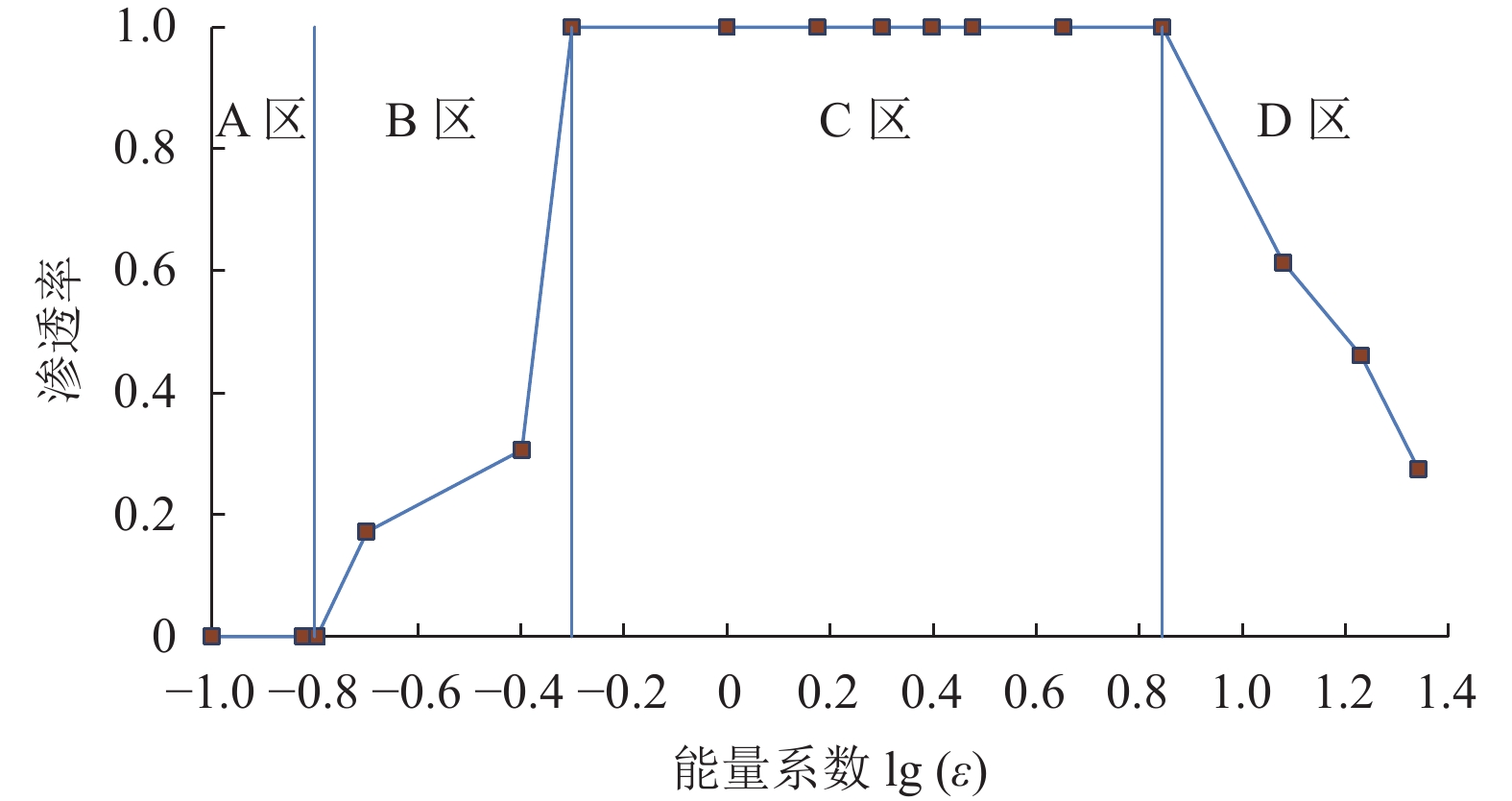
2 结果与讨论普遍地,固—液原子之间相互作用系数越大,液体浸润壁面的现象越显著,相应地,λ越大。图2是给定间距11.9,高度H=17,渗透率在能量系数ε为0.1,0.15,0.16,0.2,0.5,1,1.5,2,2.5,3,4.5,7,12,17和22共15种不同数值下的变化规律,对应的lg(ε)分别为−1.00, −0.82, −0.80, −0.70, −0.40, −0.30, 0.00, 0.18, 0.30, 0.40, 0.48, 0.65, 0.85, 1.08, 1.23以及1.34,发现:渗透率随能量系数的变化可以划分为4个子区域,首先,随着能量系数的增加,渗透率几乎不变,对应图2中的A区;接着,继续增大固液原子间的能量系数,lg(ε)在区间[−0.80,−0.30)内,渗透率增长迅速,随后缓慢增长,最后急剧增大到1,对应图2中的B区;随着能量系数增加,lg(ε)在区间[−0.30,0.85)内,即是图2中C区,渗透率为恒定值1;当能量系数继续增加,超过临界值(~7,对应lg(7)=0.85),lg(ε)在区间[0.85,1.34)内,即是图2中D区,渗透率从最大值1开始迅速下降。下面针对4个区作具体的讨论。
|
图 2 渗透率与能量系数lg(ε)的关系 Figure 2 Penetrating rate varying with lg(ε) |
本文模拟了固液相互作用强度lg(ε)=(−7,−1,−0.92,−0.82,−0.80)5种工况下的润湿行为,发现渗透率趋于0,液滴近似悬浮在倒三角形纳米粗糙表面,呈现显著的疏水态。给定间距11.9,高度H=17,以固液相互作用强度ε=0.12为例,对应lg(ε)=−0.92,液滴的逐时润湿态如图3所示,整个时间段内均呈现显著的Cassie态,具备显著的水平运动能力,如图3(c)~(e)所示,最终近似惯性作用下而趋向于x轴负方向,见图3(f)~(g)。当ε>0.16,对应lg(ε)>−0.8,改变固体壁面对液体的作用系数,液滴的润湿行为发生了明显的变化,开始由水平运动转向竖直向下运动,渗透率由0迅速增加,这种变化随着ε的增大而愈加显著。

|
图 3 ε=0.12时,液滴在不同时刻的润湿态 Figure 3 Evolution of wetting state for droplet with ε=0.12 over time |
当能量系数ε=0.5,液滴迅速占据了正下方的整个纳米沟槽,并浸入相邻的纳米沟槽,在壁面铺展开,呈现Wenzel态。给定纳米粗糙结构间距11.9,高度H=17,固液间相互作用系数为0.5时,液滴的逐时润湿状态,如图4所示,一旦克服竖直向下的阻力,液滴便迅速向下运动,并且铺展到沟槽底部,渗透率增长到1。随后一定范围内增大能量系数未见液滴在纳米粗糙表面的渗透率发生明显变化,而是维持在恒定值1。

|
图 4 ε=0.5时,液滴在不同时刻的润湿态 Figure 4 Evolution of wetting state for droplet with ε=0.5 over time |
一旦能量系数越过临界值7,渗透率随着固液原子之间能量系数的变化不再是恒定值1,而是近似线性减小,对应的润湿态逐渐趋向于Cassie态。固液相互作用系数为22的液滴润湿性随时间的演绎过程如图5所示。可见,较大的固液相互作用强度使得倒三角形纳米粗糙表面液滴达到平衡态所需的时间大大缩短,整个润湿过程,液滴几乎维持形状不变,掉进纳米沟槽中的原子几乎可以忽略不计,展示出较强的疏水特性。此时,液滴在倒三角形纳米粗糙表面的润湿行为发生了逆向渗出,呈现出与宏观尺度下该有Wenzel态显著不同的Cassie态。
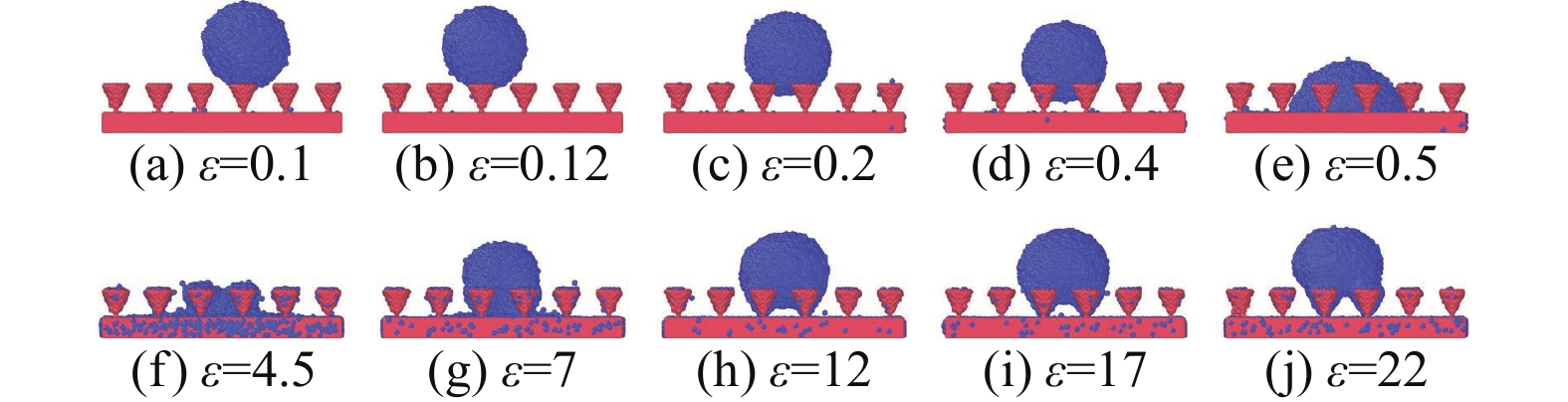
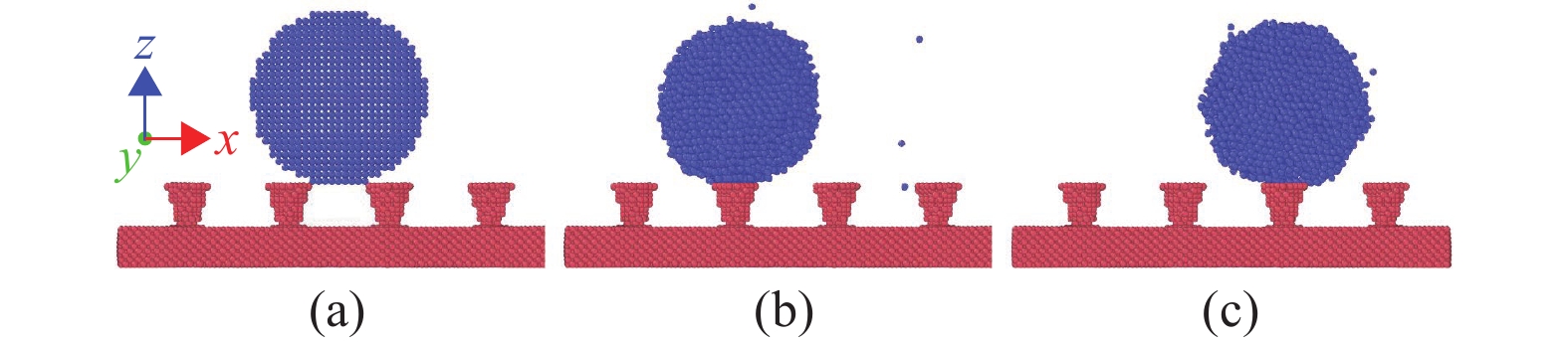
可见,较大的区间范围内,随着能量系数的增加,纳米粗糙表面液滴渗透率在不同区间的能量系数作用下不是单调递增,也不是逐渐增加然后趋于最大值1,而是先增大到最大值,然后迅速减少,对应的润湿态如图6所示,总体上可以概括为Cassie态到Wenzel态过渡,Wenzel态再到Cassie态过渡。图6是给定倒三角形纳米粗糙结构间距11.9,高度17,分析能量系数ε=(0.1,0.12,0.2,0.4,0.5,4.5,7,12,17,22)时,倒三角形纳米粗糙表面液滴呈现的润湿态。比较小的ε不足以让液滴克服向沟槽渗入的阻力,而是在系统热涨落效应下,在粗糙壁面发生水平方向的随机运动,如图6(a)和图6(b)所示。为了进一步证实上述随机运动的存在,图7给定纳米粗糙结构间距7,沟槽高5,上半径为3,液滴半径为11.5,固液间能量系数为0.12,液液间能量系数为1.5,相同的初始构型,见图7(a),采用两种不同的随机种子数,纳米粗糙表面的液滴发生方向不同的两种随机运动,对应图7(b)和图7(c)。

|
图 5 ε=22时,液滴在不同时刻的润湿态 Figure 5 Evolution of wetting state for droplet with ε=22 over time |
|
图 6 液滴在不同ε下的润湿态 Figure 6 Droplet wetting states under the different energy parameters |
|
图 7 液滴在较小能量系数作用下发生随机运动 Figure 7 Random movement of droplet with weak ε |
图6(c)中ε=0.2,液滴原子受到其下固体原子的向下的作用力足以克服向下的阻力后,逐渐渗入倒三角形纳米沟槽中;进一步增大能量系数,见图6(d),ε=0.4时,较多的液滴原子逐渐渗入倒三角形纳米沟槽;当ε=0.5时,液滴在较强的固液相互作用下,浸润倒三角形纳米粗糙表面,图6(e)即是其所呈现的亲水的Wenzel态;ε在(1,4.5)区间内,液滴原子在更大的能量系数作用下几乎全部浸入纳米沟槽中,如图6(f)所示;而图6(g)中,继续增大固液间能量系数(ε=7),液滴原子渗入纳米沟槽的总数明显变小;ε取12和17两个数值时,渗入沟槽中的液体原子个数变得更少,如图6(h)~(i)所示,液滴整体悬挂在沟槽上方,呈现Cassie态。进一步增大ε至22时,仅有极少数液体原子附着在倒三角形纳米沟槽表面,呈现显著的Cassie态,如图6(j)所示。
可见,增大固液间相互作用能量系数可以获得亲水态,大幅度增大能量系数同样可以获得理想的疏水态,这是固液相互作用强度直接作用的结果。
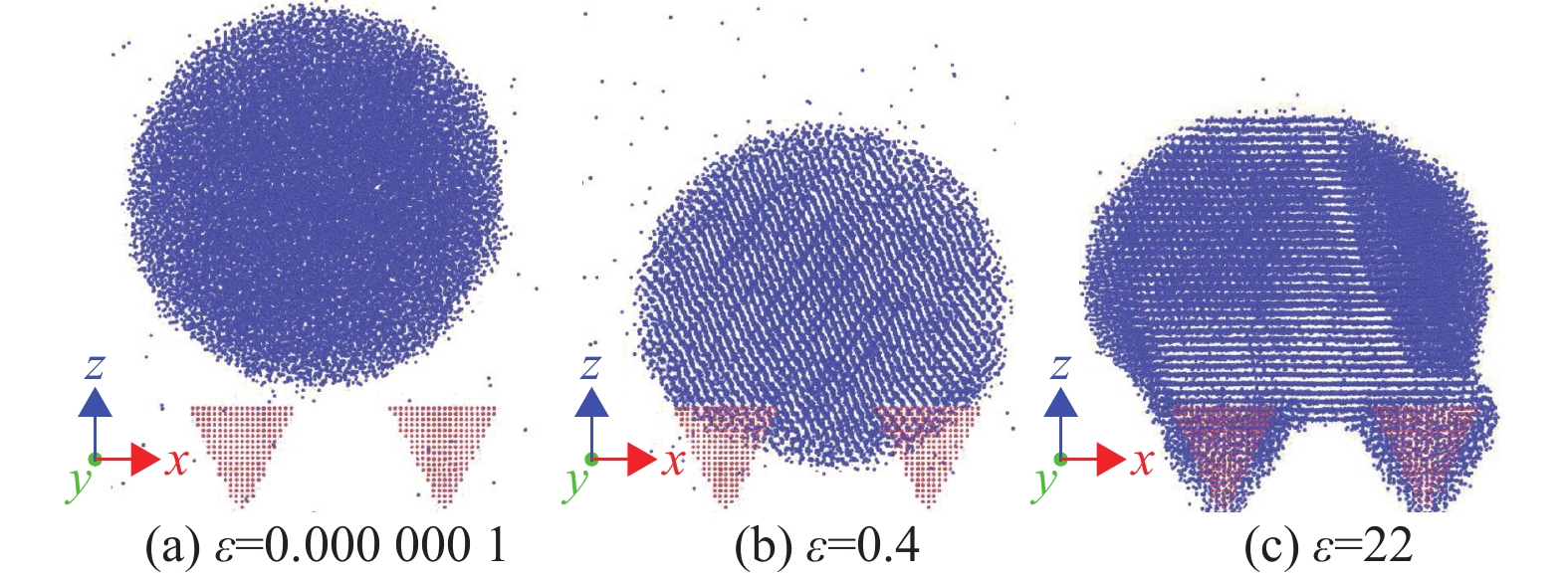
通过分析xyz 3个方向上液滴的空间分布,结果表明,较小的ε对液体原子的束缚较小,无法让其停留在特定区域,因此分布混乱;而随着ε的增加,液滴受到的束缚逐渐增大,其空间分布也呈现出一定的规律性。采用相同几何尺寸的物理模型,间距11.9,高度17,研究不同ε对液滴原子空间分布的影响规律,如图8所示。图8(a)中ε=0.0000001,固液相互作用较弱,液滴原子在空间上受到的固体壁面对其束缚作用较小而随机排列;而图8(b)中ε=0.4时,固体原子对液滴原子有着较强的束缚力而使得液滴原子在空间排列上逐渐有序化;当ε增大至22时,上述液滴原子这种有序程度愈加显著,水平方向上甚至出现平行于x-y平面的分层现象,如图8(c)所示,离固体壁面最近的液滴原子分布规律最明显。
|
图 8 液滴原子在不同能量系数作用下的空间排列 Figure 8 Spatial arrangement of droplet atoms under the different energy parameters |
为了进一步剖析液滴原子呈现的上述两种显著不同的空间分布,图9(a)和图10(a)中分别取以上两种状态中在空间排列上距离固体壁面最近的七层液体原子为讨论对象,划定的空间尺寸为Δx×Δy×Δz=8.76×9.1×0.4,上下两层液体原子之间间隔Δz取0.8,剖析液滴原子在每层空间的排列规律。为了对比分析,规定:竖直方向上距离固体原子最近的一层液滴原子颜色为绿色,近壁面7层液体原子颜色从下往上依次是绿色、碧蓝色、黄色、青紫色、蔚蓝色、蓝色和暗紫色。而图9(c)和图10(c)中菱形图标为晶格线或晶面中点位置的液滴原子。

|
图 9 液滴原子的空间排列(ε=0.4) Figure 9 Spatial arrangement of droplet atoms with ε=0.4 |

|
图 10 液滴原子的空间排列(ε=22) Figure 10 Spatial arrangement of droplet atoms with ε=22 |
图9呈现了ε=0.4时液滴原子在空间上的排列规律,图9(b)展示了上述靠近固体壁面的7层液滴原子的空间分布,每层空间液体原子较为稀疏。相应的俯视图见图9(c),图中液体原子分布不均。通过统计,可知,从下往上,每层液滴原子的个数n依次为25、56、64、53、41、48和55,可见随着层数的递增,相应层的液体原子总数呈现先增后减再增的曲线变化,见图9(d);而分布在晶格线或晶面中点位置的液滴原子依次为9、15、8、5、2、6和3,见图9(c)中菱形小方框所示,其余绝大多数液滴原子在上述中心位置以外的区域任意分布。
图10描述了固液相互作用能量系数ε=22时液滴原子的空间分布,近壁面7层液滴原子的空间排列如图10(b)所示。相比于图9(b),图10(b)呈现的每层空间原子的排列更加密集,水平分层显著,特别是近壁面5层空间的液体原子均匀分布,而且单位面积的液体原子密度更大。图10(c) 是每层空间相应的俯视图,图中可见近壁面第1层空间液体原子的个数为107个,第2至第7层依次是117、113、113、110、72和20个;可见,随着层数的递增,每层空间中液体原子的总数呈现起始几乎不变,直到第5层,近似线性下降的趋势,见图10(d)。显然,能量系数为22时,近壁面第1层空间液滴原子总数是能量系数为0.4时的4倍;第2至第5层则是是能量系数为0.4时的2倍;第6层是1.5倍,第7层却比能量系数为0.4时的第7层少,仅是能量系数为0.4时的0.36倍。每层空间中,分布在晶格线或晶面中点位置的液体原子个数如图10(c)中菱形小方框所示,从近壁面第1层空间往上,每层空间中菱形小方框个数依次是86、13、17、16、15、9和5。可见,能量系数为22时,近壁面第1层空间中,分布在晶格线或晶面中点位置的液体原子个数是能量系数为0.4时的9倍,同时至少是相同能量系数下其余层空间中的5倍。
由此可见,较强的固液相互作用系数使得近壁面5层空间的液体原子受到较强的束缚而分层排列。特别是第1层空间中液体原子,因受到较强的束缚,大部分则有规律地分布在晶格线或晶面中点位置;随着层数的递增,这种中点位置分布规律才被逐渐打破,呈现出一定的随机性。
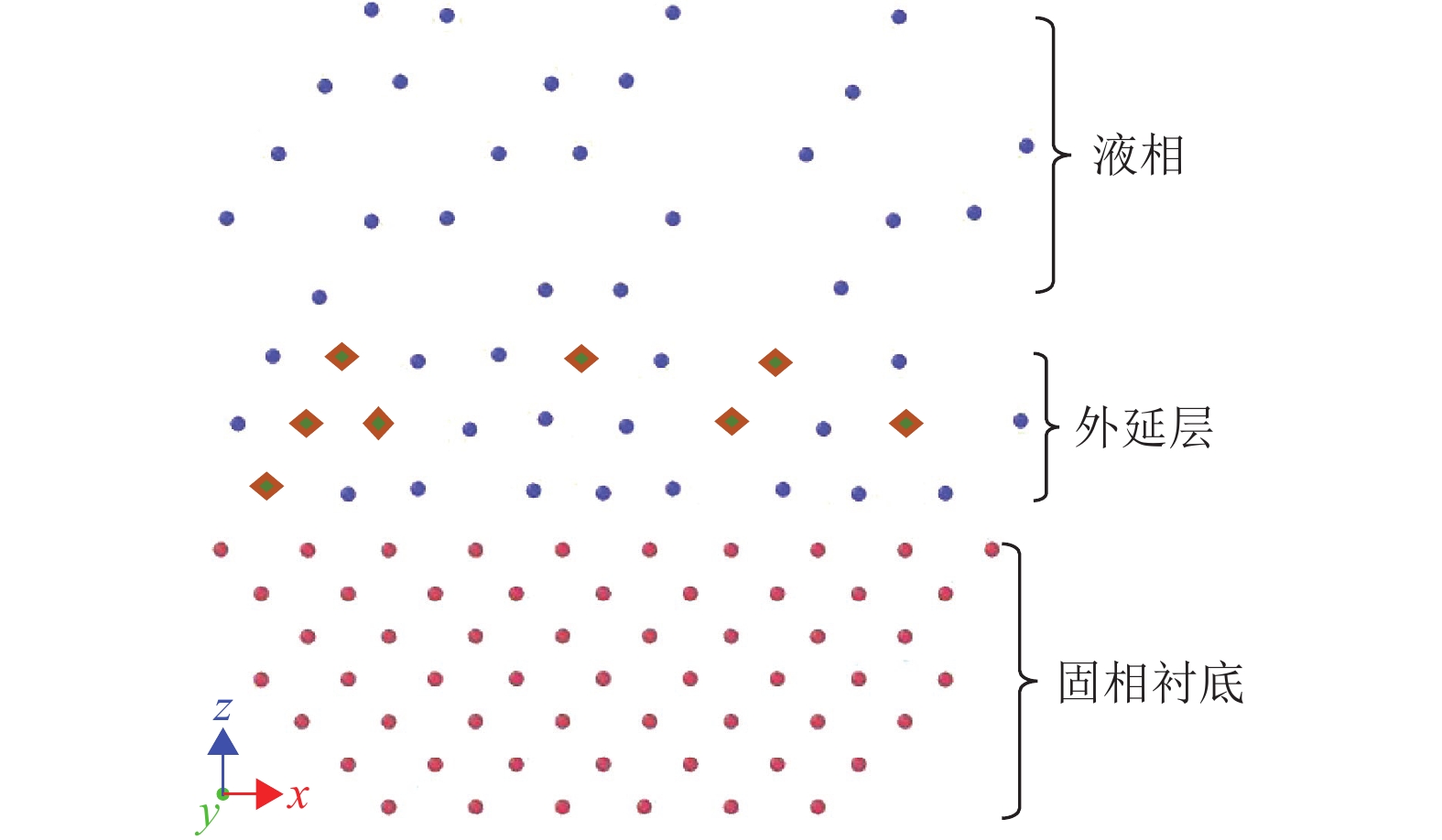
综上所述,较强的固液相互作用系数不仅使得近壁面多层空间原子分层排列,甚至使得近壁面第1层空间中的液体原子绝大部分打破曾经的随机性,按着固体衬底的晶向,有规律地分布在晶格线或者晶面中心位置,形成外延层[18],近似壁面固体原子的外延生长,见图11。较强的固液相互作用下,近壁面3层液体空间的原子出现结构化现象,形成图中所示的外延层,其中深绿色的菱形小方框可以衡量该外延层的均匀性,可见近壁面第1层液体原子可以形成较好的外延层,而近壁面第2、3层空间中液体原子受到的固体壁面的作用力小于近壁面第1层液体原子所受的的作用力,因此形成的外延层具有一定的瑕疵。3层以上的空间中液体原子在内外作用力的抗衡下努力维持液相不变。正是上述外延层的形成,使得即便是较强固液相互作用下的液滴本体原子,也难以穿过多层结构化的原子空间,无法深入倒三角形纳米沟槽中,渗透率急剧下降。这进一步解释了大幅度增加固液间能量系数后,疏水Cassie态的形成机制,阐明了倒三角形纳米粗糙表面液体润湿行为出现反转的主要原因。
|
图 11 外延示意图 Figure 11 Sketch of epitaxis |
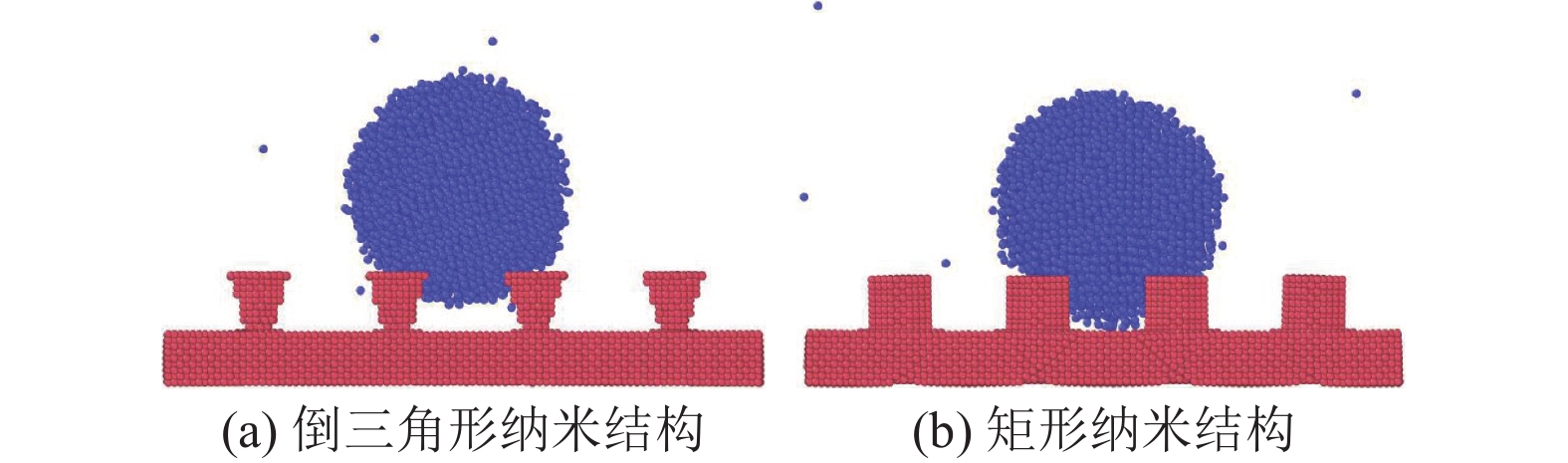
为了直观展示倒三角形纳米粗糙表面的具有更好的疏水性,图12给出了液滴在倒三角形粗糙表面以及柱状粗糙表面的润湿状态,在纳米沟槽高5,间距为7,倒三角形(圆锥)下半径0.1,上半径为3,圆柱半径为3,固液相互作用为0.3,液液相互作用为1.5时,当系统达到平衡后(t=7.43 ns),倒三角形纳米粗糙表面液滴渗入沟槽的原子数为175,对应的润湿态如图12(a)所示;而柱状纳米粗糙表面液滴渗入沟槽的原子数为400,对应的润湿态如图12(b)所示。可见,倒三角形纳米粗糙表面比柱状纳米粗糙表面具有更好的疏水性。
|
图 12 不同形状的纳米结构表面液滴润湿性 Figure 12 Wettability of droplet on different nanostructure shapes |
本文通过LAMMPS分子动力学模拟的方法,建立了倒三角形纳米粗糙表面液滴的润湿模型,分析了液滴在倒三角形纳米结构表面的润湿行为,考察了较大区间内能量系数对纳米结构表面液滴润湿行为的影响,得到如下结论:
1) 液滴渗透率在不同区间的能量系数作用下,呈现的规律不同,大致可以归纳为4类:(1) A区中渗透率随着能量系数的增加,几乎维持在恒定值0;(2) B区中渗透率随着能量系数的增加而增加,并且较快达到最大值1;(3) C区中渗透率不再随着能量系数的增加而发生变化,而是保持恒定值1;(4) D区中渗透率随着能量系数的增加而近似线性减小,其中渗透率开始变小时对应的能量系数临界值(~7)。相应地,液滴的润湿状态也发生了变化,在润湿特性状态空间中表示为疏水的Cassie态逐渐过渡到亲水的Wenzel态,接着润湿特性出现反转,又由Wenzel态过渡到Cassie态。可见,增大能量系数不仅可以获得Wenzel态,一定程度上也可以获得显著的Cassie态。
2) 超高固液相互作用强度下,液滴分子空间分布呈现明显的规律性,近壁面五层液滴原子水平分层排列,特别是近壁面第1层液滴原子,形成外延层,出现结构化现象,近似固体壁面的外延生长,诱发Cassie态的形成。
| [1] |
YONG J, CHEN F, YANG Q, et al. A review of femtosecond-faser-induced underwater superoleophobic surfaces[J].
Advanced Materials Interfaces, 2018, 5(7): 1701370.
DOI: 10.1002/admi.201701370. |
| [2] |
CHEN S, WANG J, CHEN D. States of a water droplet on nanostructured surfaces[J].
The Journal of Physical Chemistry C, 2014, 118(32): 18529-18536.
DOI: 10.1021/jp504070e. |
| [3] |
HIRVI J T, PAKKANEN T A. Nanodroplet impact and sliding on structured polymer surfaces[J].
Surface Science, 2008, 602(10): 1810-1818.
DOI: 10.1016/j.susc.2008.03.020. |
| [4] |
MACGREGON-RAMIASA M N, VASILEV K. Questions and answers on the wettability of nano-engineered surfaces[J].
Advanced Materials Interfaces, 2017, 4(16): 1700381.
DOI: 10.1002/admi.201700381. |
| [5] |
BERENDJCHI A, KHAJAVI R, YAZDANSHENAS M E. Fabrication of superhydrophobic and antibacterial surface on cotton fabric by doped silica-based sols with nanoparticles of copper[J].
Nanoscale Research Letters, 2011, 6(1): 594.
DOI: 10.1186/1556-276X-6-594. |
| [6] |
LIU X, GU H, WANG M, et al. 3D printing of bioinspired liquid superrepellent structures[J].
Advanced Materials, 2018, 30(22): 1800103.
DOI: 10.1002/adma.201800103. |
| [7] |
LIU J L, FENG X Q, WANG G, et al. Mechanisms of superhydrophobicity on hydrophilic substrates[J].
Journal of Physics:Condensed Matter, 2007, 19(35): 356002.
DOI: 10.1088/0953-8984/19/35/356002. |
| [8] |
YONG X, ZHANG L T. Nanoscale wetting on groove-patterned surfaces[J].
Langmuir, 2009, 25(9): 5045-5053.
DOI: 10.1021/la804025h. |
| [9] |
BERIM G O, RUCKENSTEIN E. Contact angle of a nanodrop on a nano rough solid surface[J].
Nanoscale, 2015, 7(7): 3088-3099.
DOI: 10.1039/C4NR06591C. |
| [10] |
王宝和, 强伟丽, 王甜, 等. 纳米水滴在纳米粗糙壁面上润湿行为的分子动力学模拟[J].
高校化学工程学报, 2017, 31(5): 1169-1176.
WANG B H, QIANG W L, WANG T, et al. Molecular dynamics simulation on wetting behaviors of water nanodroplets on nanotextured rough surfaces[J]. Journal of Chemical Engineering of Chinese Universities, 2017, 31(5): 1169-1176. |
| [11] |
颜笑, 陈凤, 张勤昭, 等. 纳米沟槽表面润湿特性的分子动力学模拟[J]. 原子能科学技术, 2015, 49(增刊1): 342-348.
YAN X, CHEN F, ZHANG Q Z, et al. Molecular dynamics simulations on wettability of nano-grooved surface[J]. Atomic Energy Science and Technology, 2015, 49 (Suppl 1): 342-348. |
| [12] |
HIRVI J T, PAKKANEN T A. Enhanced hydrophobicity of rough polymer surfaces[J].
The Journal of Physical Chemistry B, 2007, 111(13): 3336-3341.
DOI: 10.1021/jp067399j. |
| [13] |
JEONG W J, HA M Y, YOON H S, et al. Dynamic behavior of water droplets on solid surfaces with pillar-type nanostructures[J].
Langmuir, 2012, 28(12): 5360-5371.
DOI: 10.1021/la205106v. |
| [14] |
CHEN S, WANG J, MA T, et al. Molecular dynamics simulations of wetting behavior of water droplets on polytetrafluorethylene surfaces[J].
The Journal of Chemical Physics, 2014, 140(11): 114704.
DOI: 10.1063/1.4868641. |
| [15] |
AMBROSIA M S, HA M Y, Balachandar S. The effect of pillar surface fraction and pillar height on contact angles using molecular dynamics[J].
Applied Surface Science, 2013, 282: 211-216.
DOI: 10.1016/j.apsusc.2013.05.104. |
| [16] |
ZHANG L Y, XU J L, CHENQ C, et al. Switchable heat transfer in nano Janus-interface-system[J].
International Journal of Heat and Mass Transfer, 2018, 127: 761-771.
DOI: 10.1016/j.ijheatmasstransfer.2018.07.090. |
| [17] |
DELHOMMELLE J, MILLIÉ P. Inadequacy of the Lorentz-Berthelot combining rules for accurate predictions of equilibrium properties by molecular simulation[J].
Molecular Physics, 2001, 99(8): 619-625.
DOI: 10.1080/00268970010020041. |
| [18] |
李薇薇, 王胜利, 刘玉岭. 微电子工艺基础[M]. 北京: 化学工业出版社, 2006: 169-176.
|
 2022, Vol. 39
2022, Vol. 39

