2. 东南大学 土木工程学院,江苏 南京 210096
2. School of Civil Engineering, Southeast University, Nanjing 210096, China
多胞材料或多孔材料兼有功能与结构双重属性,具有超轻质,良好的吸音、阻热,较高的能量耗散力和抗冲击强度等特性,其在航空航天、舰船以及交通运输等工程领域的应用前景引起人们的极大兴趣[1]。金属空心球结构(Metallic Hollow Sphere Structures,MHSS)[2] 是由完全相同的薄壁金属空心球按一定的堆积形式连接而制成的超轻质多孔金属材料,其空隙均匀且大小容易控制,力学性能稳定且容易测定,有利于实现材料功能与结构最优化,因而极具发展潜力[3]。
在传统金属空心球结构中,两球之间连接通常采用3种方式[4]。(1) 通过各种黏结剂材料,使其充满在相邻小球缝隙中;(2) 通常利用液体张力在局部形成连接颈粘结小球;(3) 采用对小球进行“焊接”,即在连接处通过加热加压方式使其形成扩散粘接。关于金属空心球多孔材料的静动态力学性能已有许多研究。利用原子规则排列的概念,Sanders和Gibson[5-6]对体心立方和面心立方堆积的金属空心球材料的弹性模量和初应力强度进行了数值模拟分析,发现金属空心球材料与现有的开孔和闭孔金属泡沫材料相比,在许多方面具有更加优异的性能。Fiedler和Öchsner 等[7-9]研究了简单立方体排列的复合金属空心球结构和部分胶合金属空心球结构的力学性能,以及烧结金属空心球材料的力学性能和尺寸效应。Shufrin等[10]推导了一种三维连续体理论模型,研究了空心球结构的负泊松比行为,并利用数值模拟方法分析了空心球排列方式对结构负泊松比行为的影响。Song等[11]通过实验并结合数值模拟研究了球壁微孔隙对薄壁金属空心球弹性行为和屈服行为的影响。Gao等[12-13]对烧结金属空心球材料的冲击动力学行为进行实验和数值模拟研究,并提出了弹性模量、屈服强度和平台应力的计算公式。以乒乓球作为实验对象,余同希等[14-15]对单球、多球阵列进行了一系列静动态压缩实验,推导了球体堆叠压缩变形模式。吴承伟等[16]研究了乒乓球单球自由压缩、被胶结于两个平行板间压缩和胶结成列阵压缩的力学行为。杨姝等[17]利用乒乓球阵列验证了空心球结构有限元模型的有效性,在此基础上利用有限元方法研究了梯度空心球结构的抗冲击性能。众多学者对空心球结构/材料的静动态力学性能取得了诸多研究成果,但是大多数研究均采用理想的堆积、连结形式,得出的理论公式与实验对比在某些情况下差异较大,这主要是因为传统工艺制备中无法保证空心球的堆积形式和球体之间的连接方式或接触状态保持一致。
增材制造技术或3D打印技术作为一种新兴制造技术,不受结构形状的限制可以直接成型比较复杂的构件,为空心球材料的制备提供了新的途径[18-21]。由于大多数3D打印技术的局限性,打印后结构内部会残留粉末材料,为便于后处理中除去结构内部多余的粉末材料[22],需要对空心球结构进行开孔或穿孔设计,从而形成开孔空心球结构。目前,研究人员分别利用光敏树脂,PLA塑料以及尼龙材料,通过光固化(Stereo Lithography Apparatus, SLA)[18]、熔融沉积(Fused Deposition Modeling, FDM)[19-20]以及多射流熔融(Multi-Jet Fusion, MJF)[21]等增材技术制备了不同开孔方式的空心球结构,开展了一系列压缩实验和数值模拟研究。结果表明,开孔或穿孔不仅减轻了空心球结构的重量,且具有与传统空心球结构相似的力学行为。然而,关于空心球结构中球体之间的连接方式或连接部位的几何形状对不同排列方式结构压缩力学性能尤其是大变形的影响尚不清楚。本文基于MJF 3D打印技术,通过实验并结合有限元数值模拟研究开孔空心球结构准静态压缩下的力学行为,主要探讨胞元个数、开孔孔径、空心球连接方式以及排列方式(简单立方(Simple Cubic, SC)、体心立方(Body Centered Cubic, BCC)以及面心立方(Face Centered Cubic, FCC))对开孔空心球结构力学性能以及能量吸收的影响,为3D打印空心球材料的轻量化工程应用提供一定参考。
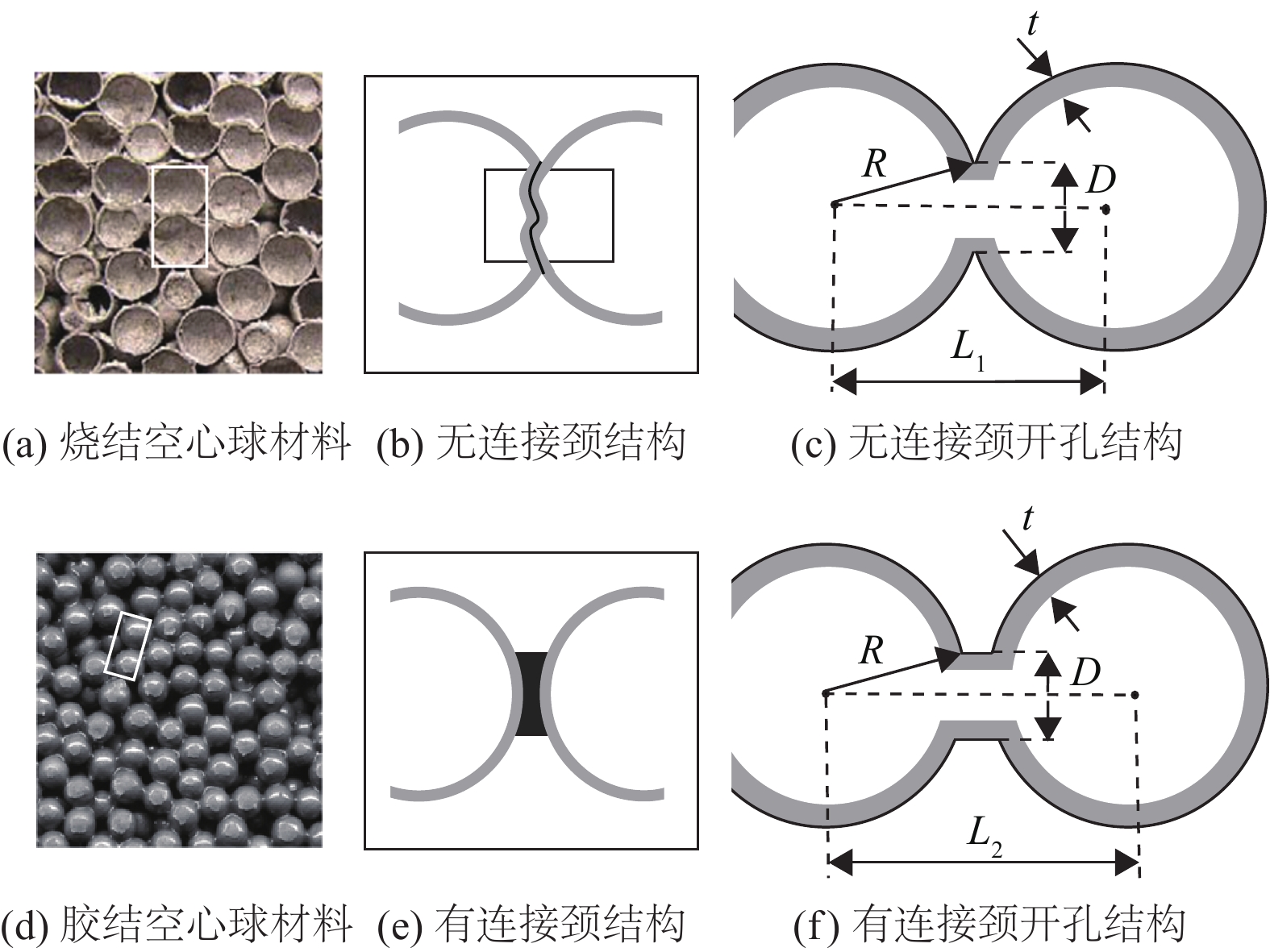
1 开孔空心球结构的几何模型图1展示了空心球材料的两种连接方式。其中,图1(a) 是通过加压加热导致扩散粘接而形成的空心球材料,两球之间的连接方式如图1(b)所示。图1(d)是通过液体在局部形成连接颈粘结小球形成的空心球材料,两球之间的连接颈如图1(e)所示。基于3D打印成型方法对结构内部连通性的要求,对实心的连接结构以及与其粘接的球壁进行开孔,如图1(c)和图1(f)所示。这样,一方面使得空心球结构内部不再有封闭的孔穴,便于3D打印成型后除去内部多余的材料,另一方面减轻了实体材料重量,提高了结构的孔隙率。除空心球的空间排布方式外,主要的几何参数还包括空心球外径R与壁厚t,开孔外径D及不带连接颈两相邻球心距为L1,带连接颈为L2,见图1(c)和图1(f)。
|
图 1 空心球连接方式 Figure 1 Connections between hollow spheres |
在研究连接方式(有无连接颈)对此类结构力学性能的影响时,包括开孔孔径D在内的其他几何参数需保持一致。但由于无连接颈结构中,孔径D随球心距L1改变而变化,二者之间的关系满足式(1),所以只要确定开孔孔径D,无连接颈结构的球心距L1可由式(1)计算得到。在研究孔径大小对结构力学性能影响时,对于带连接颈结构只要改变孔径大小D,球心距L2无需改变,本文中均取20.5 mm,而无连接颈结构则通过改变L1改变D。
| $ {L}_{1}=2\times \sqrt{\left({R}^{2}-{\left(\frac{D}{2}\right)}^{2}\right)} $ | (1) |
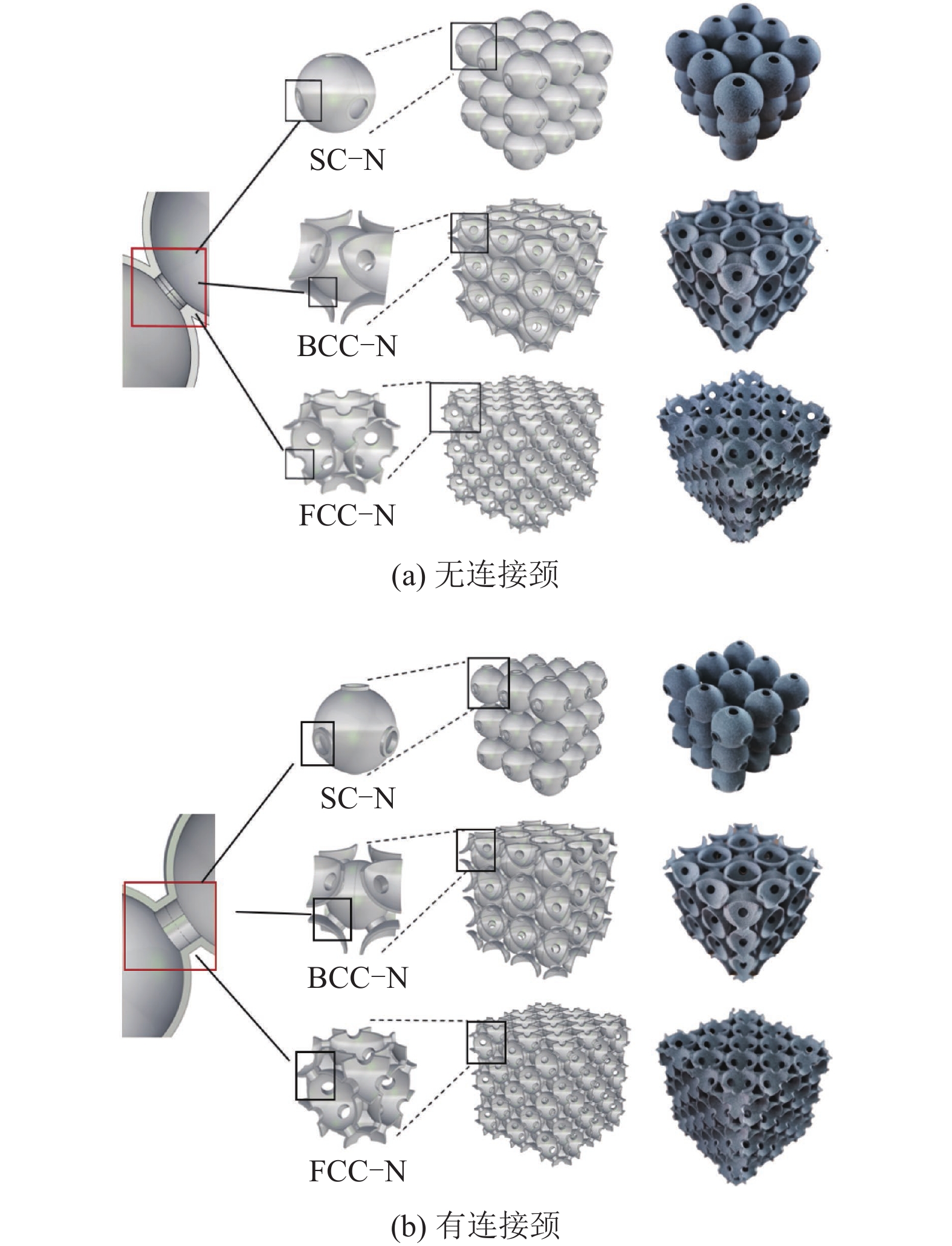
利用rhino6.5三维建模软件建立3×3×3的不同排列方式的空心球结构几何模型,包括简单立方体(SC)、体心立方体(BCC)以及面心立方体(FCC) 3种排列方式,并生成“stl”格式文件进行3D打印。所采用的打印方法为惠普MJF 3D打印技术,材料为惠普尼龙P12粉末,模型中的几何参数:R=10 mm,D=5.5 mm,t=0.8 mm,L1=18.98 mm,L2=20.50 mm,几何模型及对应的实验样品如图2所示。为了便于对比和分析,在不带连接颈的结构名称后面加−N,带连接颈的结构名称后面为−CN,例如:无连接颈的简单立方结构简称SC−N,有连接颈的简单立方结构简称SC−CN。
|
图 2 不同连接方式的开孔空心球结构 Figure 2 Perforated hollow-sphere structures with different connections |
由于所有样品的材料与打印条件一致,本文将仅对其中一种结构BCC−CN同时进行准静态压缩实验和数值模拟,并将实验和模拟结果进行对比来验证数值模拟的有效性。
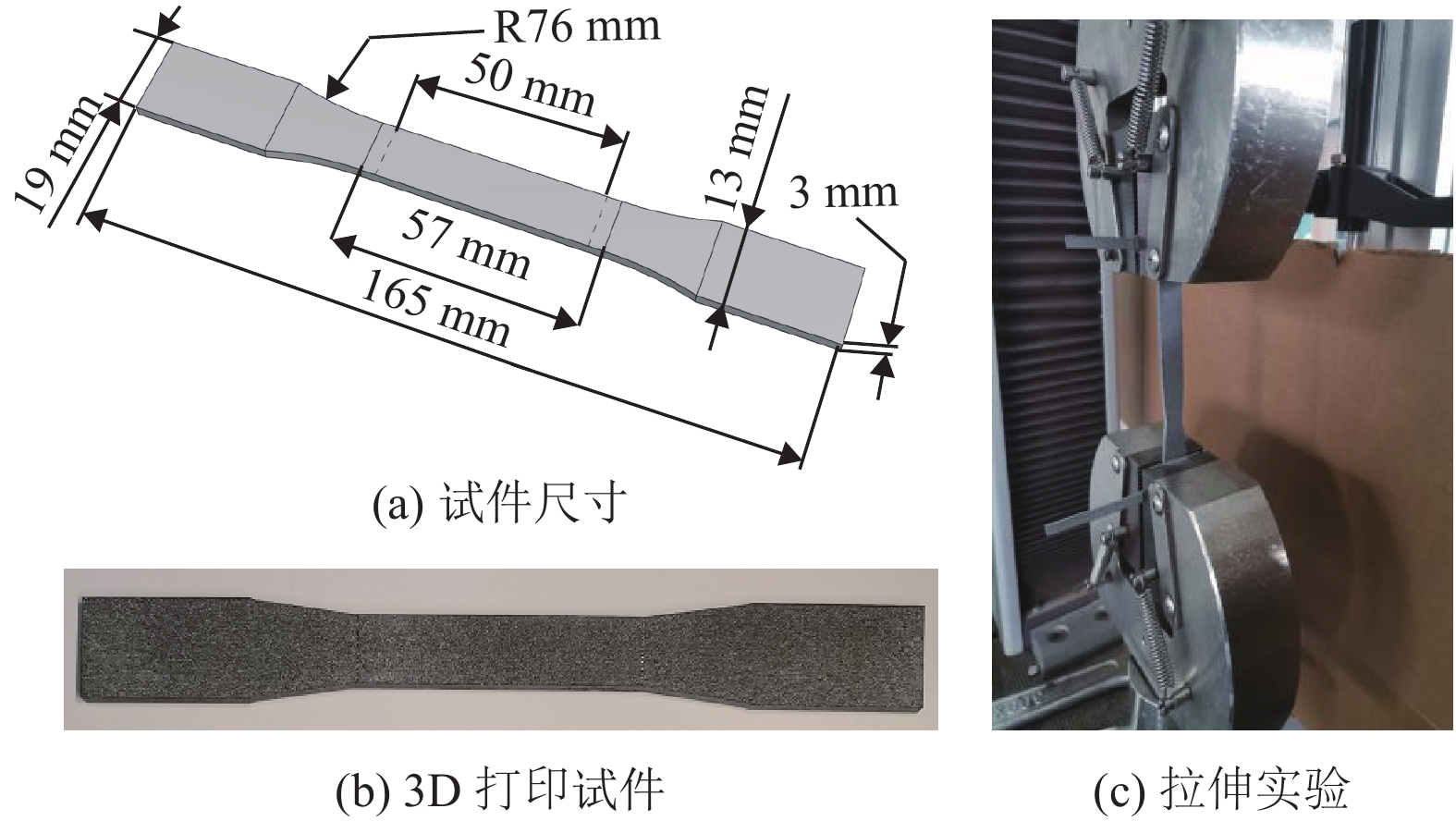
实验中,将3D打印的有连接颈空心球结构BCC−CN放在万能试验机(AI−7000M/GT−7001−HC6, 10 kN量程)的两个刚性平板之间进行准静态单轴压缩实验,加载速度设为10 mm/min,压缩实验装置如图3所示。为确定3D打印实体材料的力学性能,采用美国材料试验协会(American Society for Testing and Materials, ASTM)提供的D638−10标准[23],制备标准拉伸试件,具体尺寸如图4(a)所示,在相同的打印条件下打印拉伸试件,见图4(b),并利用万能试验机对试件进行拉伸实验,如图4(c)所示。

|
图 3 压缩实验装置 Figure 3 Compression experiment setup |
|
图 4 试件与拉伸实验 Figure 4 Specimen and tensile test |
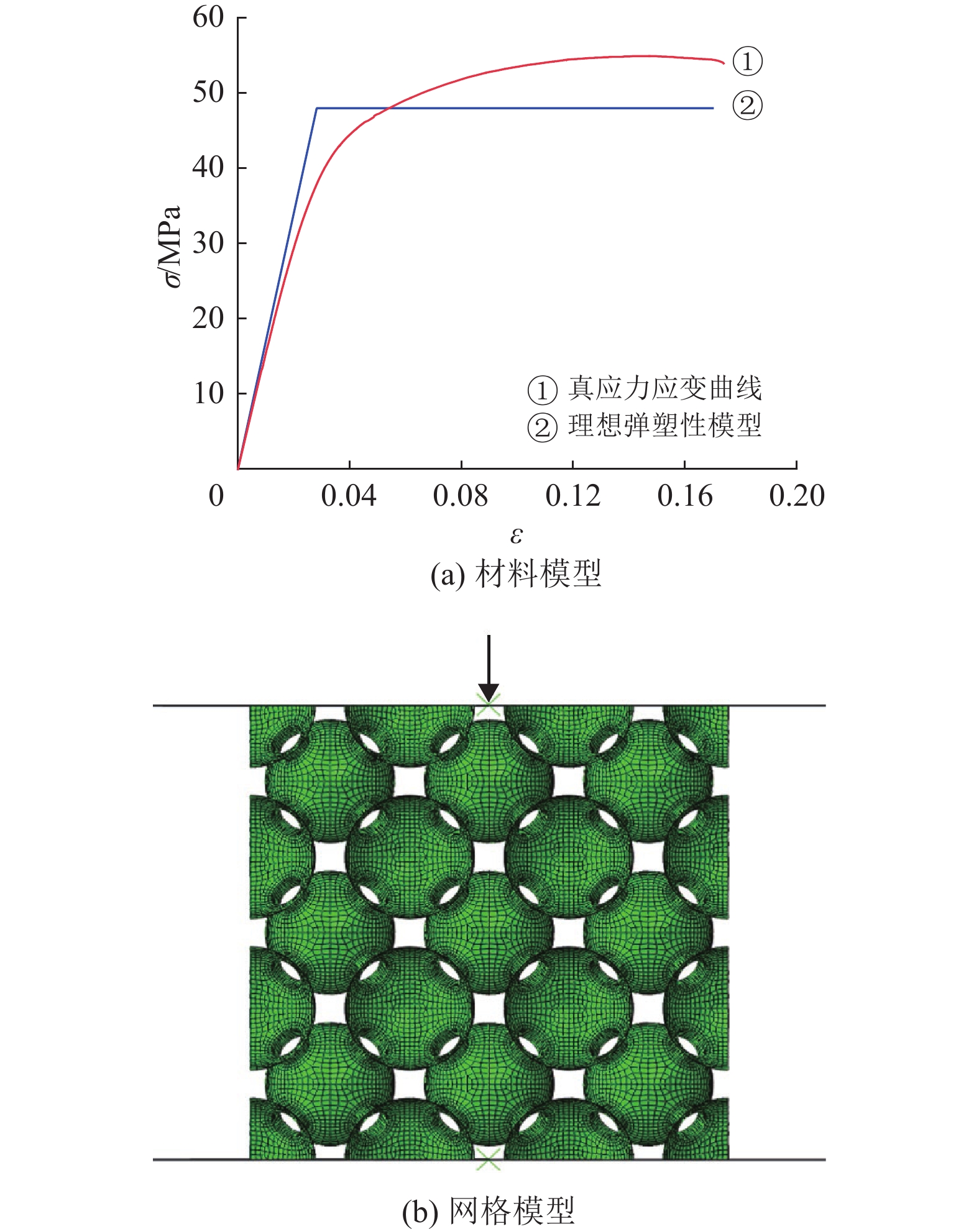
在进行数值模拟时,采用两种材料模型:①是采用实验获得的真应力−应变曲线,如图5(a)中红色曲线所示;②是根据3D打印平台提供的信息,假设的理想弹塑性模型,如图5(a)中蓝色曲线所示,其杨氏模量为1700 MPa,屈服强度为48 MPa。此外,两种材料模型的泊松比均设为0.3。利用Abaqus有限元软件建立与实验对应的数值模型。由于空心球是一种薄壁结构,在建立有限元网格模型时,采用缩减积分壳单元S4R进行网格划分,如图5(b)所示,结构底部平板采用固定约束,在顶部平板设置垂直向下的位移荷载。将刚性平板与结构之间定义为面−面接触,其中法向行为采用硬接触算法,切向行为考虑摩擦系数(取0.1)。大变形结构由于自身的自接触行为自身设置为通用接触,加载位移取模型高度的90%约为64 mm。最后,利用Abaqus显式分析方法进行准静态压缩模拟计算。
|
图 5 有限元模型 Figure 5 Finite element model |
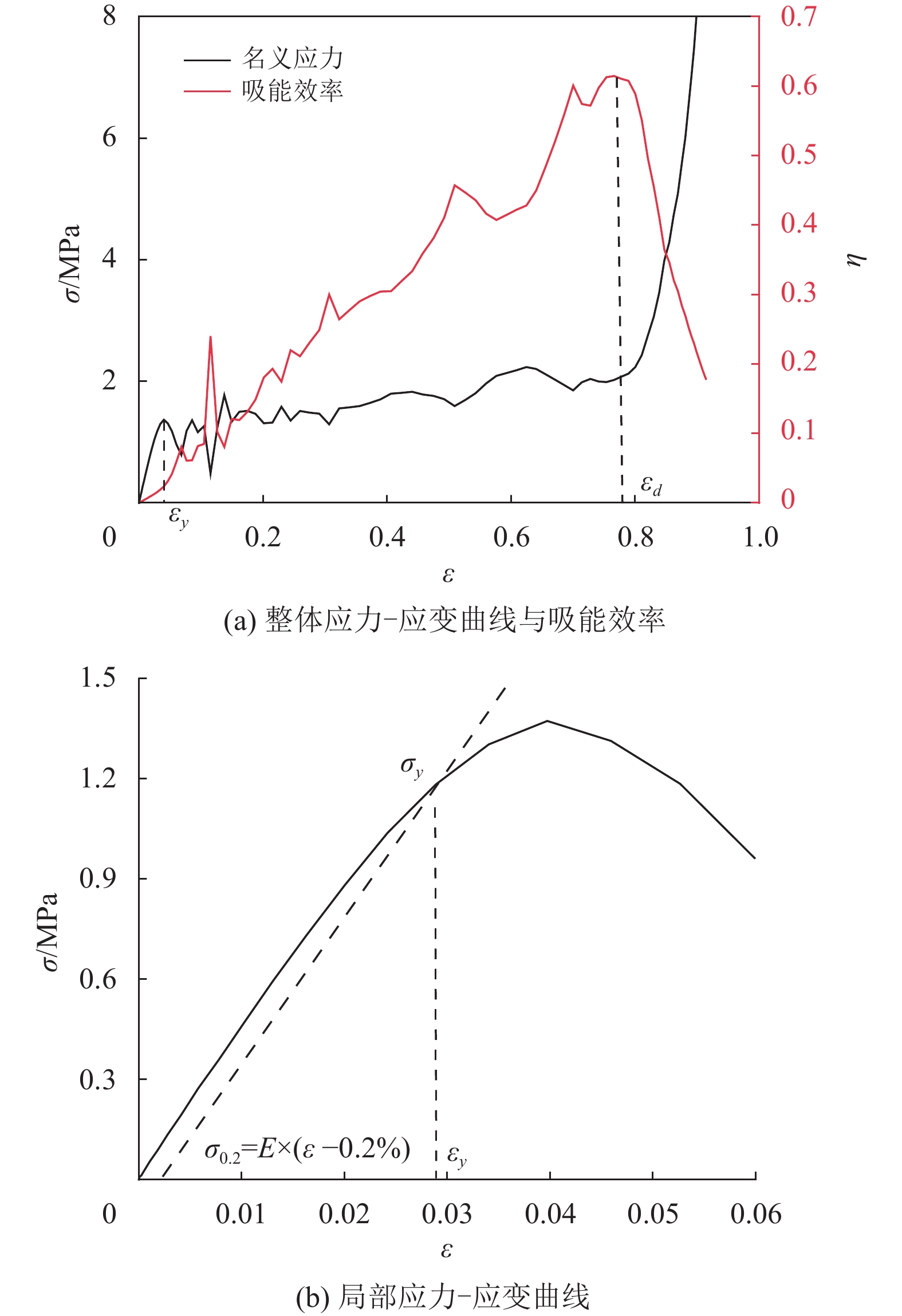
为便于分析,定义名义应力σ为平板压力除以结构在平面上的投影面积,名义应变ε定义为加载位移与结构初始高度的比值。典型多胞材料的名义应力−应变曲线如图6(a)所示,其变形过程可以分为线弹性阶段、塑性大变形阶段以及致密化阶段。
|
图 6 典型名义应力−应变曲线与吸能效率曲线 Figure 6 Typical nominal stress-strain curve and energy absorption efficiency curve |
平均压溃应力[22]
| $ {\sigma }_{p}=\frac{{\displaystyle\int }_{{\varepsilon }_{y}}^{{\varepsilon }_{d}}\sigma \left(\varepsilon \right)\mathrm{d}{\varepsilon}}{{\varepsilon }_{d}-{\varepsilon }_{y}} $ | (2) |
式中:
| $ {\left.\frac{\mathrm{d}\eta \left(\varepsilon \right)}{\mathrm{d}{\varepsilon }}\right|}_{{\varepsilon }_{d}}=0 $ | (3) |
式中:
| $ \eta \left(\varepsilon \right)=\frac{1}{\sigma \left(\varepsilon \right)}{\int }_{0}^{\varepsilon }\sigma \left(\varepsilon \right){\rm{d}}\varepsilon $ | (4) |
多胞材料在单轴压缩下会出现层层塌缩现象,在较小的一段应变里,应力会发生剧烈改变,所以在大形变阶段多胞材料会出现多个局部密实化应变点。对于结构整体性而言,最后一个能量吸收效率峰值且之后一直呈下降趋势的应变点为绝对密实化应变点。
在多胞材料的轻量化防护工程应用中,比吸能(SEA)[22],即单位质量的能量吸收率,是对能量吸收能力最重要的一个的评价指标,定义为
| $ \mathrm{S}\mathrm{E}\mathrm{A}={W}_{m}=\frac{{\displaystyle\int } F\mathrm{d}\delta }{m}=\frac{{\displaystyle\int }_{0}^{{\varepsilon }_{d}}\sigma \left(\varepsilon \right)\mathrm{d}\varepsilon }{\rho } $ | (5) |
式中:F为作用力,δ为加载端或冲击端的位移,m为多胞材料的质量,ρ为密度,表示为实体材料密度与相对密度的乘积。
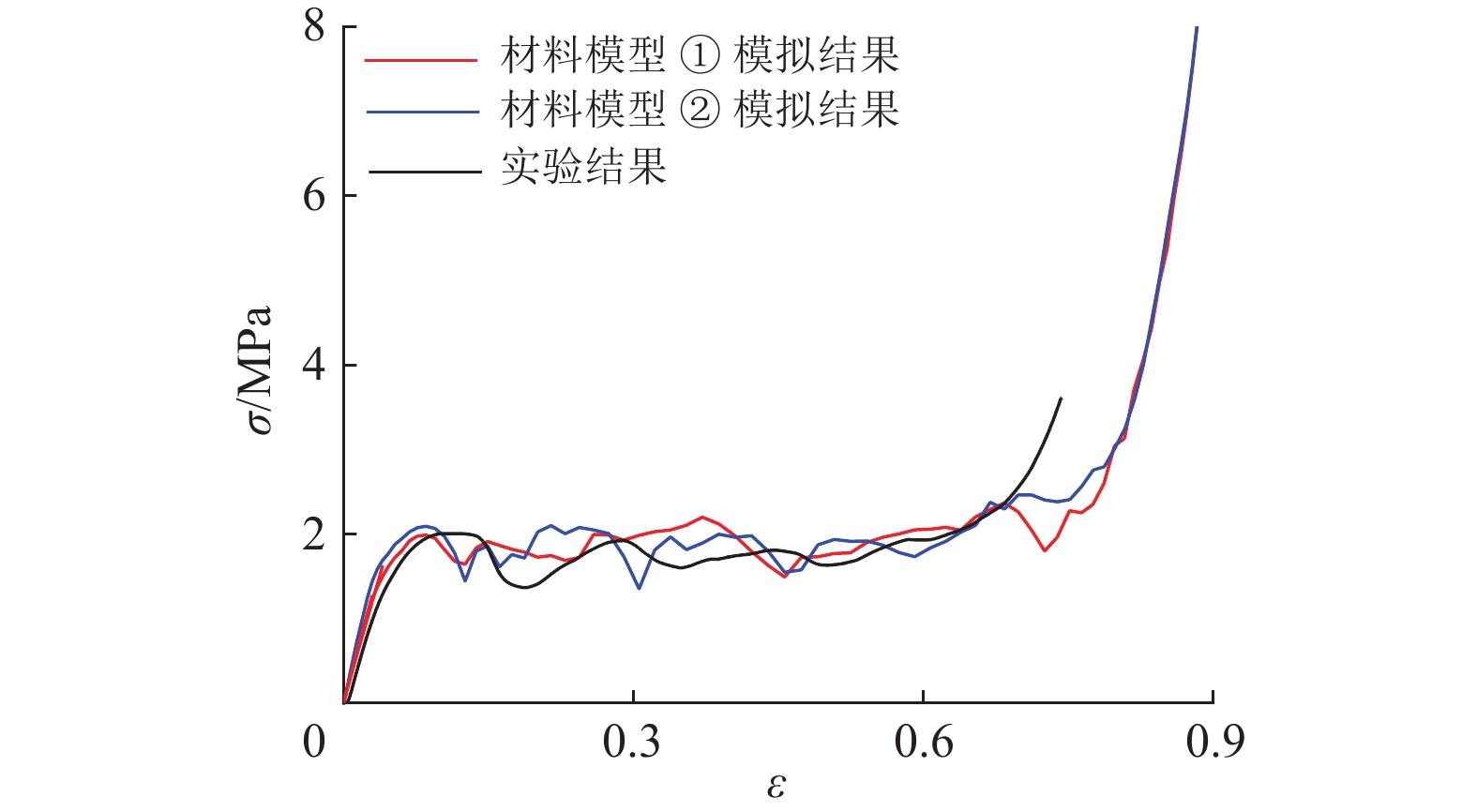
图7是实验和数值模拟得到的BCC−CN结构准静态压缩下的名义应力−应变曲线。表1为得到的弹性模量、屈服强度、平均压溃应力以及密实化应变的结果。可以看出,采用理想弹塑性材料模型得到的结果与采用拉伸应力应变曲线得到的结果总体上是比较接近的。而弹性模量相对来说差别比较大,这主要是因为实际打印材料的杨氏模量比3D打印平台给出的值要小。与实验结果对比还可以看出,数值模拟得到的密实化应变明显大于实验结果。这可能是因为3D打印的空心球结构中存在未固化的粉末。数值模拟的结果总体上与实验结果趋势一致,而且采用拉伸试件材料模型的数值结果更接近实验结果,因此本文所建立的有限元模型是有效的。后续研究中将采用拉伸实验得到的材料模型进行数值模拟。
| 表 1 实验与数值模拟结果 Table 1 Results from experiment and simulation |
|
图 7 实验与有限元结果比较 Figure 7 Comparison between experimental and finite element results |
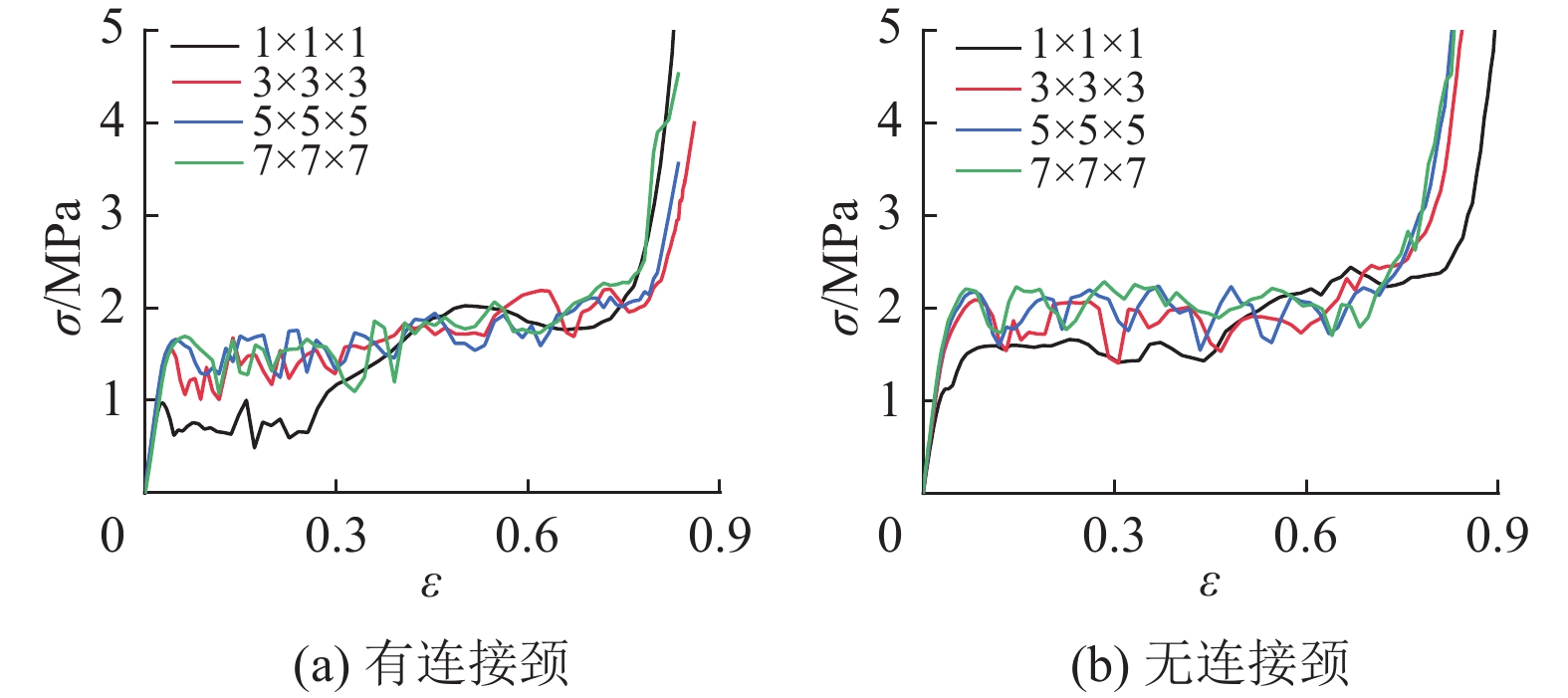
胞元数量对整体材料力学性能的影响,也称为尺寸效应,主要是因为立方体结构的外围自由胞壁所受到的约束较少。该部分承载能力较弱,受外力时易于变形,对整体结构受力产生影响,而当单胞数量变多,自由壁占比变小,整体结构力学性能趋于稳定。如图2所示,在相同胞元个数的立方体中,SC结构自由壁占比相较于BCC结构更少,所以其力学性能受胞元个数影响更小;而FCC结构最外层胞壁占比略多于BCC结构,但是由于FCC结构复杂,结构外层胞壁之间相互连通,相互约束,其尺寸效应并不明显。因此,本研究仅分析基于2种连接方式的BCC结构的尺寸效应,将分别由1×1×1,3×3×3,5×5×5,7×7×7胞元构成的BCC结构进行准静态压缩的数值模拟。图8是4种不同胞元数量BCC−N,BCC−CN结构的名义应力−应变曲线。
|
图 8 不同胞元数量的BCC结构 名义应力−应变曲线 Figure 8 Nominal stress-strain curves of BCC structures with different cell numbers |
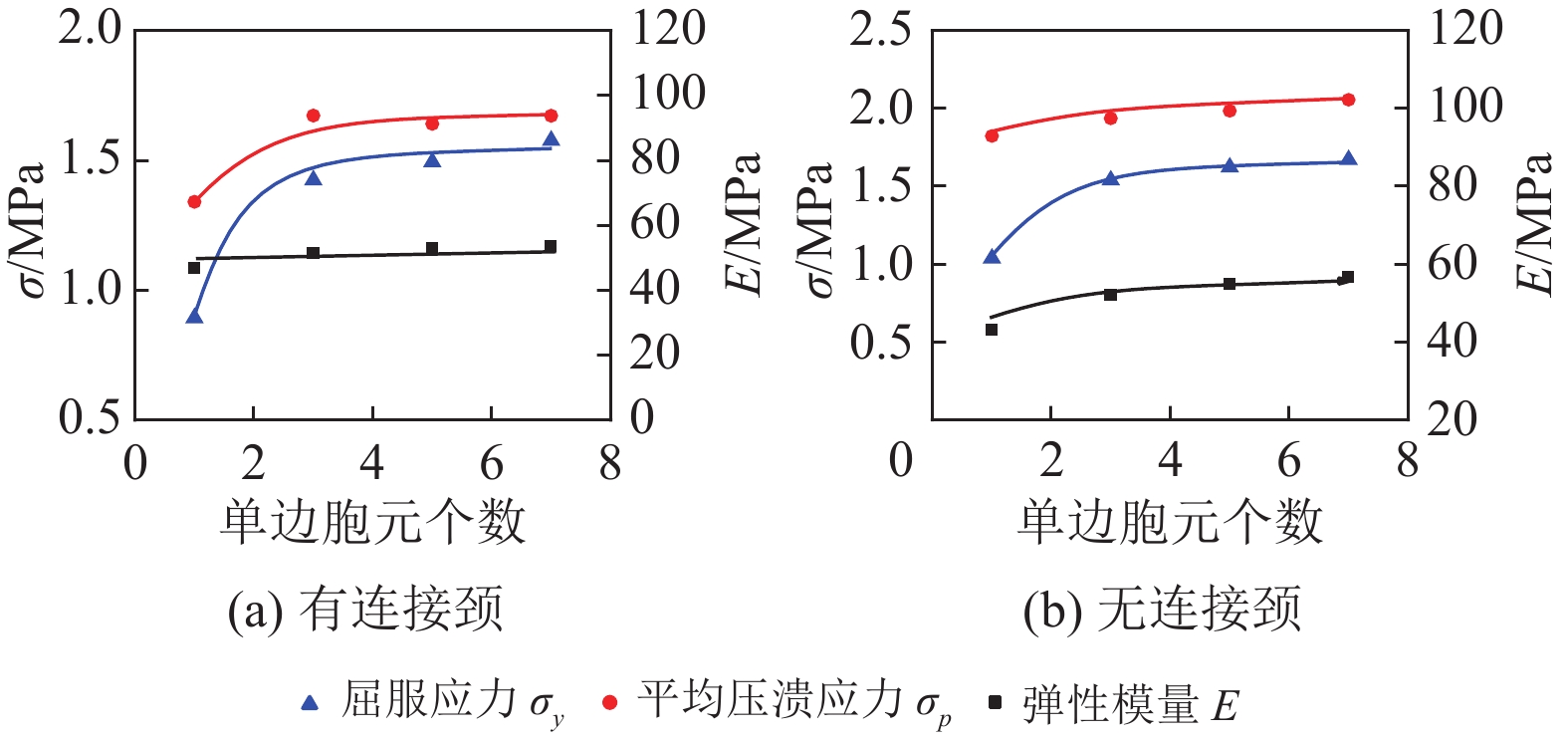
图9展示了单边胞元数量对BCC−N和BCC−CN结构弹性模量、屈服应力以及平均压溃应力的影响。可以看出,此类结构单边胞元个数达到3以后,其结果趋于稳定。虽然结构中胞元个数越多,其结果越接近整体材料,但是相应会导致计算量剧增,因此,为简化计算,将采用5×5×5胞元结构进行以下参数研究。
|
图 9 胞元数量对BCC结构力学行为的影响 Figure 9 The influence of cell number on the mechanical behaviors of BCC structures |
在研究连接方式与孔径大小的影响时,开孔外径D分别取4.3 mm,6.3 mm,8.3 mm,空心球厚度t=0.8 mm以及半径R=10 mm均保持不变。采用无连接颈方式连接时,两球心距L1由式(1)计算出分别为19.52 mm,18.98 mm,18.20 mm;在此基础上分析孔径大小对有连接颈结构力学性能的影响时,两球心距L2均取20.50 mm。表2为不同结构的详细参数及对应的密度。由表2可知,SC结构的密度受孔径大小影响比较小,FCC结构受孔径影响比较明显,BCC结构介于两者之间。这可能是因为SC结构中单个球体中包含的孔比较少,而FCC结构最多。SC−N结构的密度基本不受孔径大小影响,而其他空心球结构的密度与孔径基本上都是线性相关的,并且随着孔径的增大而减小。在相同孔径条件下,无连接颈结构的密度略大于有连接颈结构。
| 表 2 空心球结构的几何参数与密度 Table 2 Geometric parameters and densities of hollow-sphere structures |
由于在相同几何参数下,不同连接方式、不同孔径大小或不同排列方式的结构具有不同的密度。因此,在探讨孔径大小对空心球结构力学性能的影响时,采用不同结构的比强度、比模量以及比吸能等参数进行比较分析。比强度和比模量是衡量材料承载能力的重要指标,比强度σ'y定义为材料的屈服强度除以密度,比模量E'定义为材料的弹性模量除以密度。
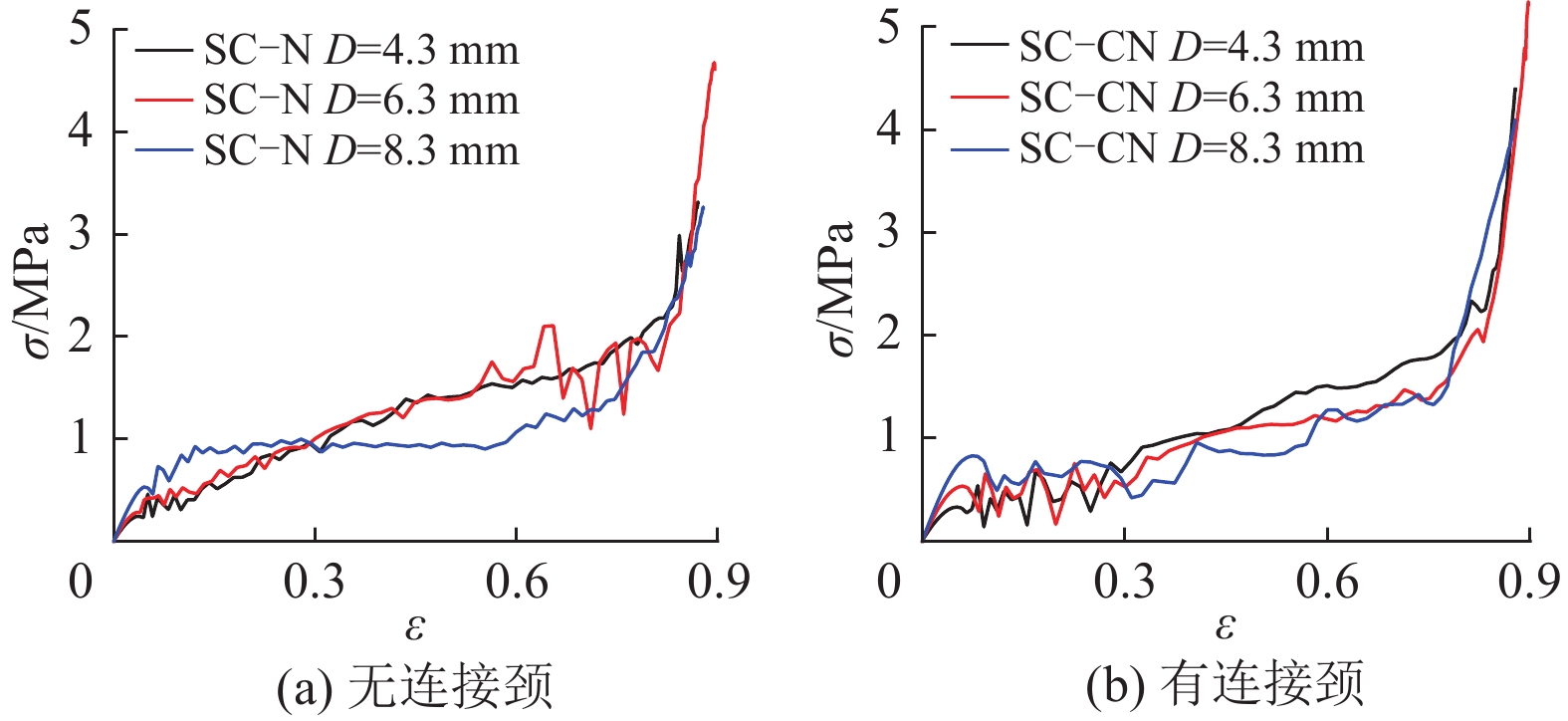
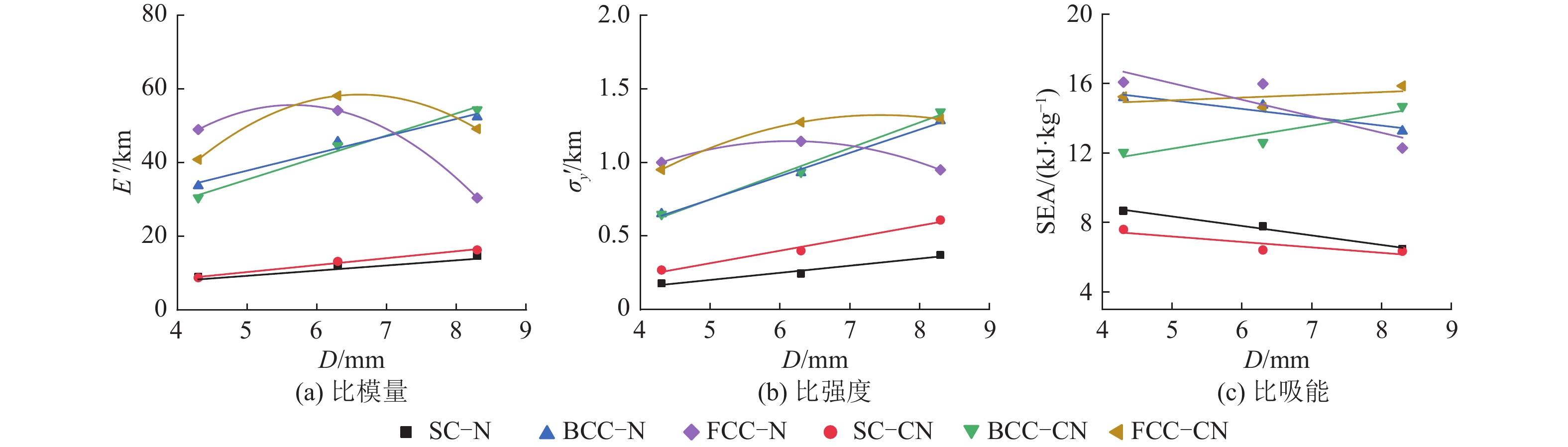
图10、11、12分别是通过数值模拟得到的不同连接方式与不同孔径大小条件下,简单立方(SC)、体心立方(BCC)以及面心立方(FCC)结构在准静态压缩下的名义应力−应变曲线。图13的(a)、(b)和(c)分别为不同空心球结构在准静态压缩下的比模量、比强度以及比吸能随孔径变化的曲线。由图10~12可知,与传统多胞材料的压缩力学行为相似,此类开孔空心球结构的变形过程都可以分为典型的三阶段,即:线弹性阶段、塑性大变形阶段以及致密化阶段。
|
图 10 不同连接方式SC结构采用不同孔径的名义应力−应变曲线 Figure 10 Nominal stress-strain curves of the SC structures with different connections and hole diameters |
|
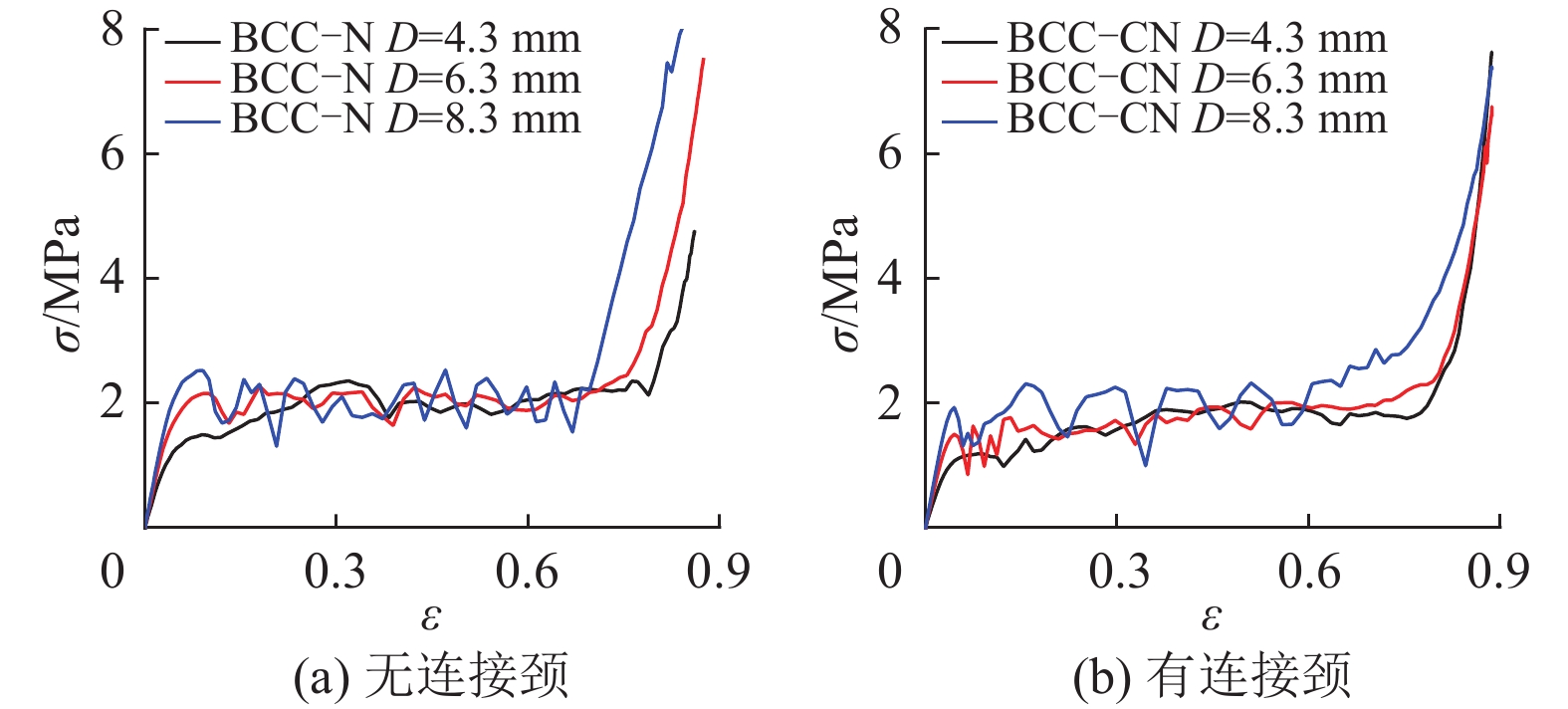
图 11 不同连接方式BCC结构采用不同孔径的名义应力−应变曲线 Figure 11 Nominal stress-strain curves of the BCC structures with different connections and hole diameters |
|
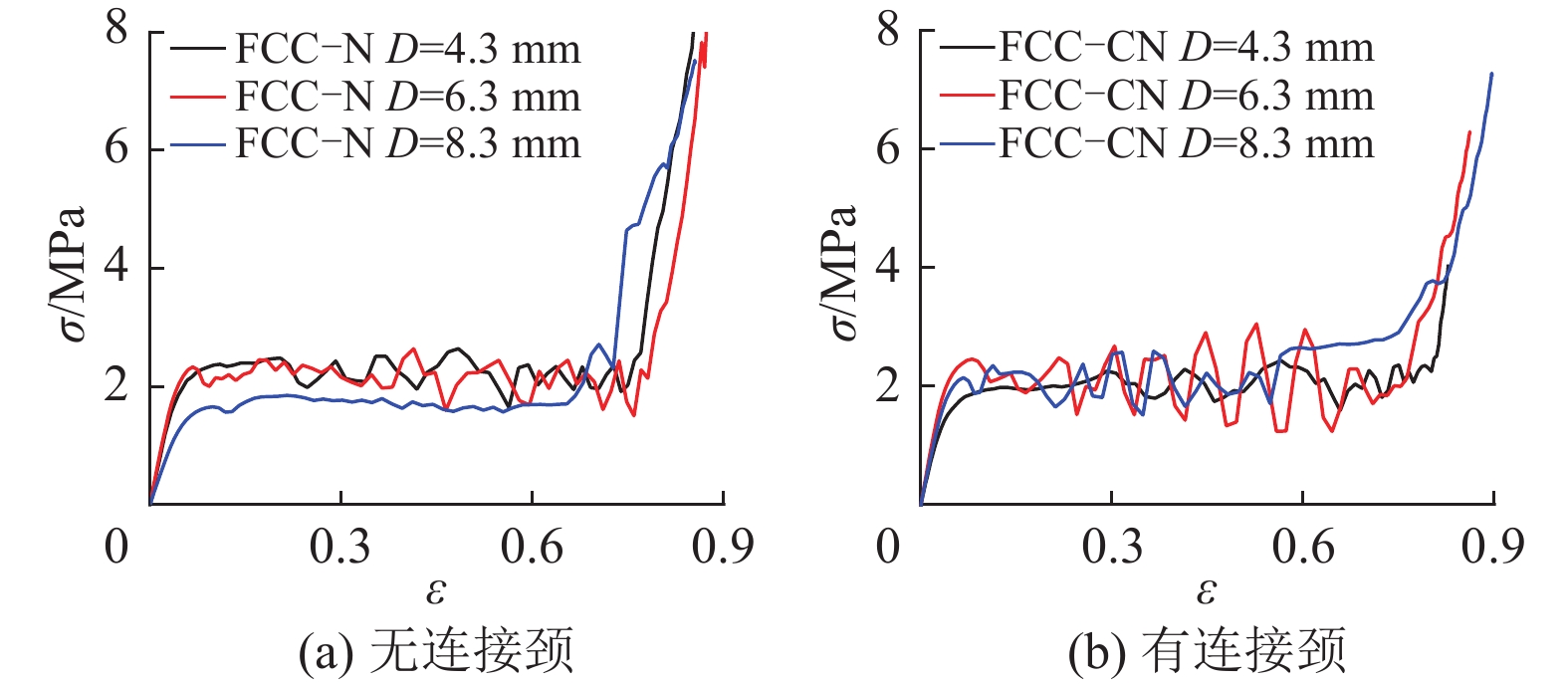
图 12 不同连接方式FCC结构采用不同孔径的名义应力−应变曲线 Figure 12 Nominal stress-strain curves of the FCC structures with different connections and hole diameters |
|
图 13 开孔孔径对比模量、比强度以及比吸能的影响 Figure 13 Influence of hole diameter on the specific modulus, specific strength and specific energy absorption |
由结果可知,无连接颈SC−N和有连接颈SC−CN结构的比模量和比强度均随着孔径的增大而增大,而比吸能随着孔径的增大而减小。2种连接方式下,SC结构的应力−应变曲线展现一定的应变硬化效应。这是因为SC结构受到压缩时,上下空心球相互挤压,其中一个空心球率先屈曲形成塑性圆环(见图14(a)、(b)),塑性圆环的半径随着压缩位移的增大而增大(见图14(c)、(d)),从而压缩应力得到强化。对于有连接颈的SC−CN结构来说,在上下空心球相互接触挤压之前经历了一段层层连续坍塌的变形行为(见图14(b))。此时应力−应变曲线剧烈波动(见图10(b))。当所有上下空心球紧密接触之后(见图14(d))应力逐渐上升;对于无连接颈的SC−N结构来说,相邻空心球之间本来就紧密相接(见图14(a)),应变硬化效应更加明显。而随着孔径的增大这种应变硬化效应也逐渐减弱,由图10可知,当孔径为8.3 mm时,SC−N和SC−CN结构的应力−应变曲线具有较为平坦的大变形阶段。总体上,在相同几何参数条件下,有连接颈SC−CN结构的比模量和比强度比无连接颈的SC−N结构大,且孔径越小两者越接近;而有连接颈的SC−CN结构的比吸能比无连接颈的SC−N结构小,且孔径越大两者越接近。因此无连接颈的SC−N结构具有更好的吸能减震能力,并且孔径越小吸能效果越好。

|
图 14 孔径D=6.3 mm时SC结构不同阶段的变形图 Figure 14 Deformations of SC structures with D of 6.3 mm at different stages |
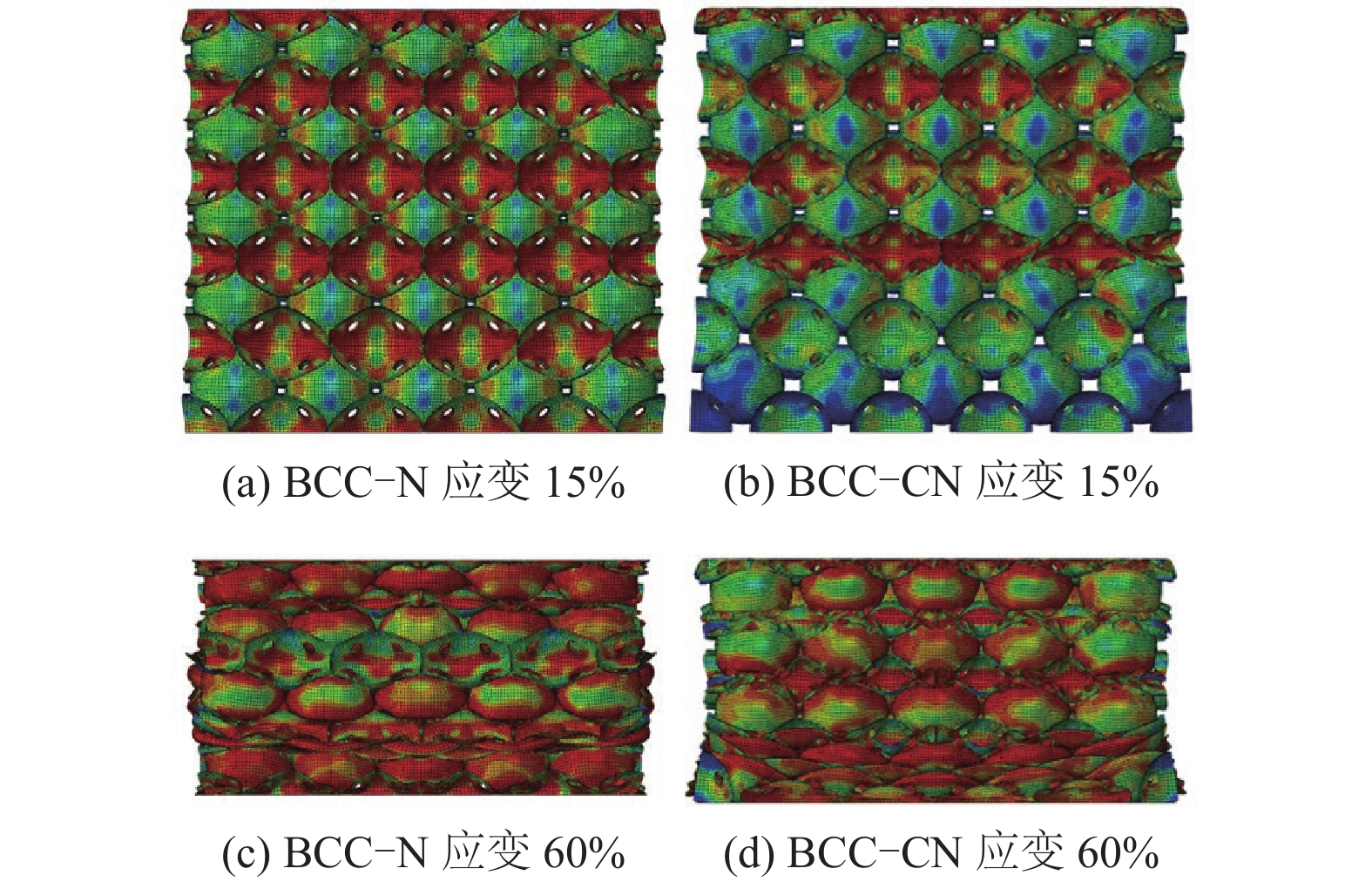
对于体心立方结构,无连接颈BCC−N和有连接颈BCC−CN结构的比模量和比强度均随着孔径的增大而增大,有连接颈BCC−CN结构的比吸能随着孔径的增大而增大,而无连接颈BCC−N结构的比吸能随着孔径的增大而减小。这主要是因为BCC−N结构的密实化应变随着孔径的增大而明显减小(见图11(a))。总体上,无连接颈结构BCC−N的比模量和比强度低于有连接颈BCC−CN结构,且孔径越小两者越接近,而无连接颈结构的比吸能高于有连接颈结构。由变形过程可知,无连接颈BCC−N结构由于空心球之间紧密相连,其变形一开始是整体性的,而有连接颈BCC−CN结构在大变形初期具有局部化的特点,如图15(a)、(b)所示。主要是因为在挤压作用下连接颈处球壁出现了应力集中的现象,较弱的同层空心球率先在此处屈服而凹陷。随后,结构内部空心球之间相互接触挤压从而进入一种初步密实的状态,这种现象也会随着孔径的增大而减弱。当所有空心球紧密接触,在相互挤压作用下,整体结构进入层层坍缩密实的大变形阶段,如图15(c)(d)所示。
|
图 15 孔径D=4.3 mm时BCC结构不同阶段的变形图 Figure 15 Deformations of BCC structures with D of 4.3 mm at different stages |
对于面心立方结构,无连接颈FCC−N结构和有连接颈FCC−CN结构的比模量和比强度均随着孔径的增大先增大后减小。无连接颈FCC−N结构的比吸能随着孔径的增大而减小,而有连接颈FCC−CN结构的比吸能随着孔径的增大先减小后增大(数值上相差并不大)。当孔径较小的时候(4.3 mm左右),无连接颈FCC−N结构的比模量、比强度以及比吸能均略优于有连接颈FCC−CN结构;而当孔径比较大(8.3 mm左右)的时候,有连接颈FCC−CN结构的比模量、比强度以及比吸能均优于无连接颈FCC−N结构。不同于SC和BCC排列方式,2种不同连接方式的FCC结构的大变形模式基本相同:由薄弱层开始引发的层层坍塌密实的大变形过程,如图16所示。

|
图 16 孔径D=6.3 mm时FCC结构应变60%的变形图 Figure 16 Deformations of FCC structures with D of 6.3 mm at strain 60% |
由图13可知,2种连接方式下,当孔径较小的时候(如4.3 mm,6.3 mm),FCC结构的比模量、比强度以及比吸能最高,SC结构最弱,BCC结构介于二者之间;而当孔径较大的时候(如8.3 mm),BCC结构的比模量、比强度均高于FCC结构。总体上来说,FCC结构的综合性能较为优越。
5 结论增材制造技术或3D打印技术为空心球材料的制备提供了新途径。利用实验和有限元数值模拟对3D打印开孔空心球结构的准静态压缩力学行为进行了研究,实验结果验证了有限元模型的有效性;并分析了胞元个数、开孔孔径、空心球连接方式以及排列方式对此类结构力学性能的影响,为3D打印空心球材料的轻量化工程应用提供一定参考。研究主要得到以下结论:
(1) 与传统空心球结构类似,开孔空心球结构的准静态压溃过程主要分为弹性变形阶段、塑性大变形阶段以及密实化阶段。
(2) 胞元个数对开孔空心球结构的准静态压缩力学性能具有一定影响,当胞元数大于3×3×3时,其力学性能基本上对胞元个数不敏感。
(3) 总体上看,有连接颈结构的比模量和比强度高于无连接颈结构, 而无连接颈结构的比吸能高于有连接颈结构。
(4) FCC结构的综合性能最优,SC结构最弱,BCC结构介于二者之间。
(5) SC和BCC结构的压缩力学性能与孔径之间是线性关系,而FCC结构的力学性能与孔径之间是非线性关系。
| [1] |
ZHU J, ZHOU H, WANG C, et al. A review of topology optimization for additive manufacturing: Status and challenges[J].
Chinese Journal of Aeronautics, 2020, 34: 91-110.
|
| [2] |
ANDREAS ÖCHSNER. Multifunctional metallic hollow sphere structures: manufacturing, properties and application[M]. Springer Science & Business Media, Berlin, 2009, 2-29.
|
| [3] |
余为. 金属空心球材料组元力学性能及结构设计[D]. 秦皇岛: 燕山大学, 2011: 48-67.
|
| [4] |
LIU Y, WU H, ZHANG X, et al. The influence of lattice structure on the dynamic performance of metal hollow sphere agglomerates[J].
Mechanics Research Communications, 2011, 38(8): 569-573.
DOI: 10.1016/j.mechrescom.2011.07.011. |
| [5] |
SANDERS W S, GIBSON L J. Mechanics of BCC and FCC hollow-sphere foams[J].
Materials Science and Engineering:A, 2003, 352(1-2): 150-161.
DOI: 10.1016/S0921-5093(02)00890-0. |
| [6] |
SANDERS W S, GIBSON L J. Mechanics of hollow sphere foams[J].
Materials Science and Engineering:A, 2003, 347(1-2): 70-85.
DOI: 10.1016/S0921-5093(02)00583-X. |
| [7] |
FIEDLER T, ÖCHSNER A. On the anisotropy of adhesively bonded metallic hollow sphere structures[J].
Scripta Materialia, 2008, 58(8): 695-698.
DOI: 10.1016/j.scriptamat.2007.12.005. |
| [8] |
FIEDLER T, VEYHL C, BELOVA I V, et al. Mechanical properties and micro-deformation of sintered metallic hollow sphere structure[J].
Computational Materials Science, 2013, 74(6): 143-147.
|
| [9] |
AMANI Y, ÖCHSNER A. Finite element simulation of arrays of hollow sphere structures[J].
Materialwissenschaft Und Werkstofftechnik, 2015, 46(4-5): 462-476.
DOI: 10.1002/mawe.201500422. |
| [10] |
SHUFRIN I, PASTERNAK E, DYSKIN A V. Negative Poisson's ratio in hollow sphere materials[J].
International Journal of Solids & Structures, 2015, 54: 192-214.
|
| [11] |
SONG J, SUN Q, YANG Z, et al. Effects of microporosity on the elasticity and yielding of thin-walled metallic hollow spheres[J].
Materials Science & Engineering:A, 2017, 688: 134-145.
|
| [12] |
GAO Z Y, YU T X, ZHAO H. Mechanical behavior of metallic hollow sphere materials: experimental study[J].
Journal of Aerospace Engineering, 2008, 21(4): 206-216.
DOI: 10.1061/(ASCE)0893-1321(2008)21:4(206). |
| [13] |
GAO Z Y, YU T X, KARAGIOZOVA D. Finite element simulations on the mechanical properties of MHS materials[J].
Acta Mechanica Sinica, 2007, 23(1): 65-75.
DOI: 10.1007/s10409-006-0049-y. |
| [14] |
RUAN H H, GAO Z Y, YU T X. Crushing of thin-walled spheres and sphere arrays[J].
International Journal of Mechanical Sciences, 2006, 48: 117-133.
DOI: 10.1016/j.ijmecsci.2005.08.006. |
| [15] |
DONG X L, GAO Z Y, YU T X. Dynamic crushing of thin-walled spheres: an experimental study[J].
International Journal of Impact Engineering, 2008, 35(8): 717-726.
DOI: 10.1016/j.ijimpeng.2007.11.004. |
| [16] |
吴承伟, 张鹏程, 周平. 薄壁球壳超轻质结构力学行为研究[J].
大连理工大学学报, 2008, 48(5): 625-630.
WU C W, ZHANG P C, ZHOU P. Research on mechanical behavior of super-lightweight structure made of thin-walled spheres[J]. Journal of Dalian University of Technology, 2008, 48(5): 625-630. DOI: 10.7511/dllgxb200805001. |
| [17] |
杨姝, 刘国平, 亓昌, 等. 金属空心球梯度泡沫结构抗冲击特性仿真与优化[J].
浙江大学学报(工学版), 2016, 50(8): 1593-1599.
YANG S, LIU G P, QI C, et al. Simulation and optimization for anti-shock performances of graded metal hollow sphere foam structure[J]. Journal of Zhejiang University (Engineering Science), 2016, 50(8): 1593-1599. DOI: 10.3785/j.issn.1008-973X.2016.08.023. |
| [18] |
DAI M, MA Y, YANG F, et al. Experimental and numerical studies on compressive mechanical properties of hollow-sphere structures with perforations[J].
Mechanics of Materials, 2019, 134: 193-203.
DOI: 10.1016/j.mechmat.2019.04.013. |
| [19] |
ALI N B, KHLIF M, HAMMAMI D, et al. Mechanical and morphological characterization of spherical cell porous structures manufactured using FDM process[J].
Engineering Fracture Mechanics, 2019, 216: 106527.
DOI: 10.1016/j.engfracmech.2019.106527. |
| [20] |
吴少杰. 球壳胞元轻质多孔材料力学性能的多参数影响分析[D]. 秦皇岛: 燕山大学, 2019: 36-48.
|
| [21] |
DAI M, JIANG H, DAI X, et al. Investigations of the compressive mechanical properties of open-cell hollow-sphere structures[J].
Mechanics of Materials, 2020, 148: 103517.
DOI: 10.1016/j.mechmat.2020.103517. |
| [22] |
唐超兰, 张伟祥, 陈志茹, 等. 3D打印用钛合金粉末制备技术分析[J]. 广东工业大学学报, 2019, 140(3): 91-98.
TANG C L, ZHANG W X, CHEN Z R, et al. Analysis of preparation technology of titanium alloy powder for 3D printing [J] Journal of Guangdong University of Technology, 2019, 140 (3): 91-98. |
| [23] |
ASTM International. Standard test method for tensile properties of plastics: ASTM D638-10[S]. West Conshohocken, MI, US: ASTM International, 2010: 1-17.
|
| [24] |
夏元明, 张威, 崔天宁, 等. 金属多级类蜂窝的压溃行为研究[J].
力学学报, 2019, 51(3): 873-883.
XIA Y M, ZHANG W, CUI T N, et al. Study on the crushing behavior of multi-level honeycomb[J]. Acta Mechanica Sinica, 2019, 51(3): 873-883. DOI: 10.6052/0459-1879-18-434. |
 2022, Vol. 39
2022, Vol. 39
