形变是普遍存在于自然界事物中的一种现象,它是指形变体在各种载荷作用下,其形状、尺寸与位置在空间域与时间域中的变化。所谓形变监测,是对形变体的形变现象采用精密测量仪器设备和测量方法进行监视观测的过程,其目的是确定形变体在各种载荷与外力作用下,形状、尺寸及位置变化的空间状态与时间特征。
形变监测技术包括常规大地测量技术、特殊形变测量技术和全球导航卫星系统(Global Navigation Satellite System,GNSS)技术。常规大地测量,是采用经纬仪、水准仪、测距仪、全站仪等常规测量仪器测定点的形变值,其优点是:(1) 能够提供形变体整体的形变状态;(2) 适用于不同的监测精度要求、不同形式的形变体和不同的监测环境;(3) 可以提供绝对形变信息[1]。特殊形变测量技术是指随着光、电、机技术的发展,人们利用专门研制的一些特殊和专用的监测仪器对事物、建筑物进行形变监测,具有测量过程简单、可监测形变体内部的形变、容易实现自动化监测等优点,但通常只能提供局部的和相对的形变信息,如文献[2-3]中提到的两种特殊测量方法和仪器。常规大地测量技术与特殊形变测量技术受限于巨大的设备成本和精密的设备要求,难以长时间在恶劣环境中工作。GNSS在形变监测上的应用随着时代的发展和技术的进步,变得更加广泛。GNSS能够很好地应对前两种技术在形变监测中难以适应的场景,包括滑坡在内的自然灾害,用于桥梁、轨道等的形变监测。有助于专家更好地了解建筑物的形变状态与趋势,进而提前预防灾害,如文献[4-5]中提出的两种GNSS的应用情况。然而在运用GNSS对形变体进行定位监测时,需要对形变体监测位置的三维空间坐标进行一段时间的采样,并将这段观测时长内的所有采样数据进行解算得到一个相对更加精确的坐标值。而在缩短观测时长的情况下,采样数据的减少导致采样数据解算过程中,一些多路径误差难以消除,使定位精度下降。本文就此问题提出一种通过粒子滤波算法,建立形变体监测点的状态空间模型,结合GNSS观测值,得到监测点的最优状态估计。通过对高铁铁轨路基的形变监测验证方法的可行性。
1 BDS数据采集与处理 1.1 数据采集方案为了开展基于BDS形变监测的高铁铁轨路基沉降形变的研究分析,本文利用了位于广东省内广州市与汕头市之间广汕高速铁路搭建的BDS形变监测系统。其中,基准站B001位于主控楼楼顶,主控楼的持力层为中等风化凝灰层,同时在施工桩基前做了强化夯实处理,基桩深度达30 m,成为整个广汕高铁的BDS形变监测系统项目中最稳固的地方。监测站M001、M002、M003、M004、M005、M006以及基准站B001均位于该铁路路段的一侧,6个监测站均位于地面,距离基准站最近的是监测站M001,距离为60 m,距离基准站最远的监测站是M006,距离为350 m,同时M006监测站也最靠近铁轨。6个监测站底座安装位置的路基接触点即为一一对应的M1、M2、M3、M4、M5、M6监测点,基准站对应的基准点为B1。基准站和监测站的位置分布如图1所示。基准站和监测站接收机都采用上海司南导航M300 Plus北斗/GNSS高精度形变接收机,同时各测站上均配置了AT340测量型天线,天线安装在观测墩上,观测墩严格水平。

|
图 1 基准站和监测站分布情况 Figure 1 Distribution of reference stations and monitoring stations |
只在特殊情形下,高速铁路路基上才会发生瞬间对路基的沉降形变量造成突变的情况(如山体滑坡、地震及突然施工等)。一般场景下,高速铁路路基形变体的形变极为缓慢,其在局部时间域内可以认为是稳定的,即时间域内形变体的形变量可忽略不计,高铁路基形变体的局部时间域为半年。故对于在局部时间域内的高铁路基的形变监测就可以根据监测出的数据分析达到预警的目的。本文中广汕高铁路基形变监测的监测周期为1个月(2018年5月15日-2018年6月15日)。该监测系统为24 h实时在线监测系统。监测站与基准站的采集BDS定位数据的采样间隔为15 s。
1.3 数据传输数据传输网络使用星形拓扑结构,当监控系统某一个网点发生故障时,不会影响其他网点的正常工作。监测站主机与各监测站的接受机进行实时数据交换,并转为RINEX文件储存[6],其主要流程如图2所示。

|
图 2 系统结构图 Figure 2 System structure diagram |
形变监测集成软件(Dam Deformation Monitoring Software,DDMS)由总控、数据处理、数据分析和数据库管理4个模块组成,主要功能包括 BDS基线解算、坐标估计、形变量提取以及精度分析、基准稳定性分析、形变过程线显示、预警报警等[7]。基于形变监测系统中基线短的特点,且需保证实时性和高精度的要求,广汕高铁路基BDS形变监测系统项目中关于BDS基线解算模型软件的开发主要借鉴参考了文献[7]中GPS基线解算软件的开发。具体模型以及处理策略受篇幅限制在这里不再详述。
广汕高铁路基监测的一个月周期处在局部时间域内,同时在此周期内的项目范围5公里未发生会导致路基产生突变式形变的特殊情况,因此认为在监测周期内项目的所有监测点与基准点的空间位置坐标不变。
本文分别收集了M006监测站与B001基准站于2018年5月30日(0:00~24:00)采集的BDS定位数据,M001监测站与B001基准站于2018年5月28日(0:00~24:00)采集的BDS定位数据,M003监测站与B001基准站于2018年5月29日(0:00~24:00)采集的BDS定位数据。选取M006监测站与B001基准站之间收集的BDS定位数据,结合开发的BDS基线解算模型软件将定位数据按每小时解算一次,解算出24个M6监测点的三维空间坐标值。将M6监测点的24个坐标值取平均,均值坐标即作为M6监测点的真值坐标。由此统计出M6监测点的水平方向(径向A、切向B)精度在3 mm内,高程H方向的精度在5 mm内。其误差序列如图3所示。其横轴

|
图 3 BDS每小时解算误差序列 Figure 3 BDS solving the error sequence every 1h |

|
图 4 BDS每15 min解算误差序列 Figure 4 BDS solving the error sequence every 15 min |
由图3与图4比较,能明显看到由于解算时取用的采样数据减少,其在解算过程中消去的多路径误差变少,导致解算坐标值的精度明显下降。对于这种情形,本文尝试采用一种粒子滤波算法,结合对监测点解算坐标值(此处解算坐标值即粒子滤波算法中的观测数据)的分析,构建监测点坐标值数据的系统模型。在系统模型中引入观测数据,递推出观测数据同时刻的最优估计值,达到减少多路径误差并提升精度的目的。
2 研究方法 2.1 粒子滤波的基本原理与公式粒子滤波是通过寻找一组在状态空间中传播的随机样本对后验概率密度函数进行近似模拟,然后以样本均值代替积分运算,从而获得状态最小方差估计的过程,而这些样本即被称为“粒子”[8-9]。是一种通过非参数化蒙特卡洛模拟方法实现递推贝叶斯估计的算法,可以通过状态模型与观测模型由前一时刻的状态值递推得到当前时刻的状态值[10-11]。
对于高铁铁轨路基形变监测系统,采用粒子滤波算法递推的方式。其采用系统本身的状态转移方程和在缩短观测时长的观测资料之间,求得系统所处时刻的最优估计值。因而在一定程度上使用粒子滤波器可以解决由于BDS观测时长减少引起监测点定位精度下降的问题。
粒子滤波算法的数学模型包含状态转移方程和观测方程,其模型一般形式如下
状态转移方程
| $ {\boldsymbol{X}}_{K}=f\left({\boldsymbol{X}}_{K-1}\right)+{\boldsymbol{Q}}_{K} $ | (1) |
观测方程
| $ {\boldsymbol{Y}}_{K}=h\left({\boldsymbol{X}}_{K}\right)+{\boldsymbol{R}}_{K} $ | (2) |
式(1)~(2)中:正整数
假设状态噪声与观测噪声均服从高斯分布,可以得到粒子滤波递推公式如下:
(1) 给初值
(2) 粒子初始化:由先验概率分布
(3) 预测步。生成
| $ {\boldsymbol{x}}_{1}^{\left(i\right)}=f({\boldsymbol{x}}_{0}^{\left(i\right)})+{\boldsymbol{q}}^{\left(i\right)} $ | (3) |
式中:
(4) 更新步。
假设观测噪声为服从方差
| $ {\boldsymbol{w}}_{1}^{\left(i\right)}={f}_{\boldsymbol{R}}\left[{\boldsymbol{Y}}_{1}-\boldsymbol{h}({\boldsymbol{x}}_{1}^{\left(i\right)})\right]\times {\boldsymbol{w}}_{0}^{\left(i\right)} =\frac{1}{\sqrt{2\text{π }\boldsymbol{R}}}\times {\mathrm{e}}^{-\frac{{\left[{\boldsymbol{Y}}_{1}-\boldsymbol{h}\left({\boldsymbol{x}}_{1}^{\left(i\right)}\right)\right]}^{2}}{2\boldsymbol{R}}}\times {\boldsymbol{w}}_{0}^{\left(i\right)} $ | (4) |
(5) 权重归一化。
| $ {\boldsymbol{w}}_{1}^{\left(i\right)}=\frac{{\boldsymbol{w}}_{1}^{\left(i\right)}}{\displaystyle\sum {\boldsymbol{w}}_{1}^{\left(i\right)}} $ | (5) |
(6) 粒子重采样。
对于粒子滤波算法应用过程中存在粒子退化的问题,即算法经过几次迭代后,绝大多数粒子权重变到很小甚至可忽略,而只有少部分粒子所占权重很大。随着无效采样粒子数目的增加,使得大量的计算浪费在对后验滤波概率分布几乎不起作用的粒子估计上,使算法估计性能下降[12-14]。
重采样思路:在保持粒子数目不变的同时,将那些权重极小的不起作用的粒子舍去,用一些新的粒子来取代它们。通过将剩余不同权重的粒子按照它们自身权重在总权重中所占的比例复制。大权重粒子多复制,相对较小权重粒子少复制,最后粒子数补充恢复到原来粒子数。过程如下:
从均匀分布中
| $ \sum\nolimits _{j=1}^{i-1}{\boldsymbol{w}}_{1}^{\left(j\right)} < {\boldsymbol{u}}_{1}^{\left(n\right)}\leqslant \sum\nolimits _{j=1}^{i}{\boldsymbol{w}}_{1}^{\left(j\right)} $ | (6) |
最终可获得重采样之后的
(7) 状态最优估计值求取:由上述步骤(1)~(6)可得
| $ \widehat{{\boldsymbol{X}}_{1}}=\sum\nolimits_{i=1}^{{L}}{\boldsymbol{w}}_{1}^{\left(i\right)}\times {\boldsymbol{x}}_{1}^{\left(i\right)} $ | (7) |
以上步骤通过粒子滤波求

|
图 5 粒子滤波的递归过程 Figure 5 Recursive process of particle filter |
在本文中,BDS是作为三维铁轨形变监测自动化系统的工具,使用BDS监测铁轨形变时,监测点的位置是工程本身独立坐标系中的坐标
根据粒子滤波 (Particle Filter,PF)模型,状态空间模型的建立是应用粒子滤波算法在实际问题中处理预测的基础。铁轨形变体的形变在局部时间域内铁轨的空间状态是稳定的情况下,本文观测系统BDS观测值的时间序列包含于这个局部时间域中。
本文采用一阶自回归模型作为局部时间域内铁轨形变的状态空间方程,采用一元线性回归模型作为铁轨形变的观测方程。具体的系统模型如下:
状态转移方程
| $ {{\boldsymbol{X}}_{K}={\boldsymbol{\varphi }}_{1}{\boldsymbol{X}}_{K-1}+{\boldsymbol{Q}}_{K}\text{,}\boldsymbol{Q}}_{K} \sim N\left({\bf{0}},{\boldsymbol{\sigma }}_{{\boldsymbol{Q}}_{K}}^{2}\right) $ | (8) |
观测方程
| $ {\boldsymbol{Y}}_{K}={\boldsymbol{\varphi }}_{2}{\boldsymbol{X}}_{K}+{\boldsymbol{R}}_{K},{\boldsymbol{R}}_{K} \sim N({\bf{0}},{\boldsymbol{\sigma }}_{{\boldsymbol{R}}_{K}}^{2}) $ | (9) |
式(8)~(9)中:
初始参数的设置对PF模型的预测具有重要作用,合适的模型参数可以快速捕捉系统状态,提高跟踪效率[14]。其中主要的初始化参数包括
本文原始采样数据分别来自广汕高铁铁轨路基BDS形变监测系统于2018年5月30日(0:00~24:00)时间段对此段高铁的M6监测点持续采样收集,2018年5月28日(0:00~24:00)时间段M1监测点持续采样收集和2018年5月29日(0:00~24:00)时间段对M3监测点持续采样收集。
首先对M6的采集数据进行解算仿真;从使用观测时长为1 h的采样数据解算出一个解到使用观测时长为15 min的采样数据解算出一个解后,解算出96组有效数据。数据结果包含有监测点的三维空间位置信息:径向方向(
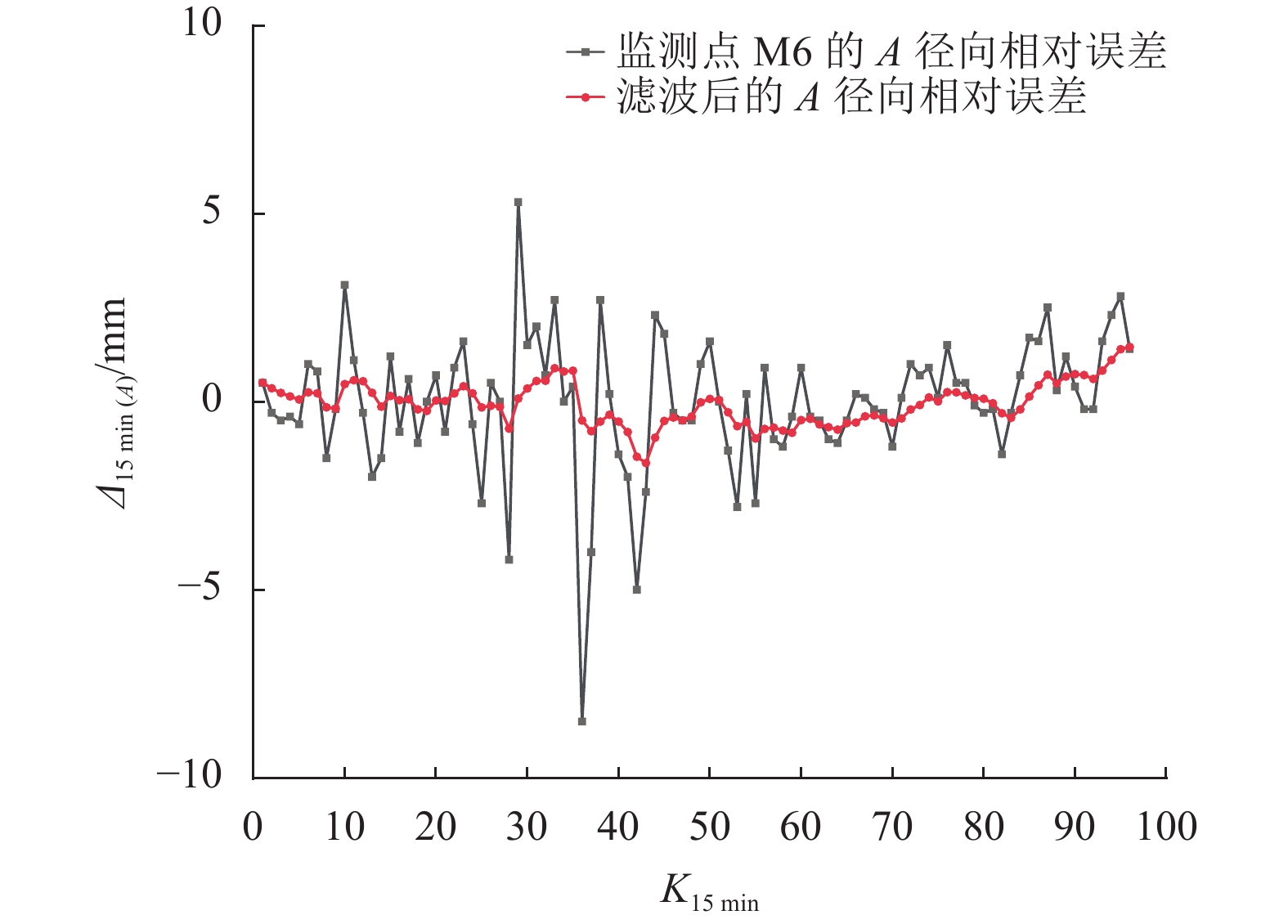
|
图 6 |
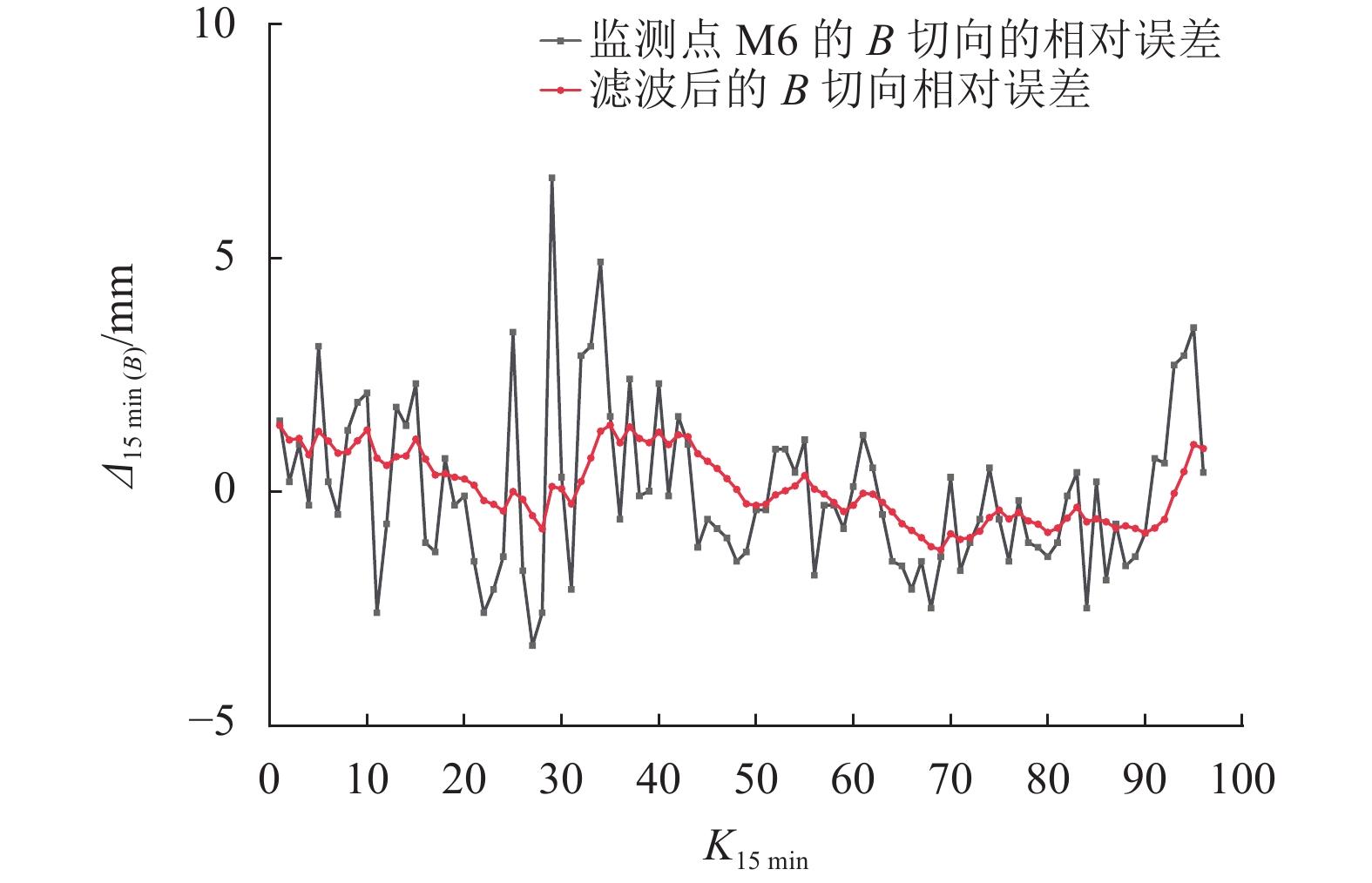
|
图 7 |
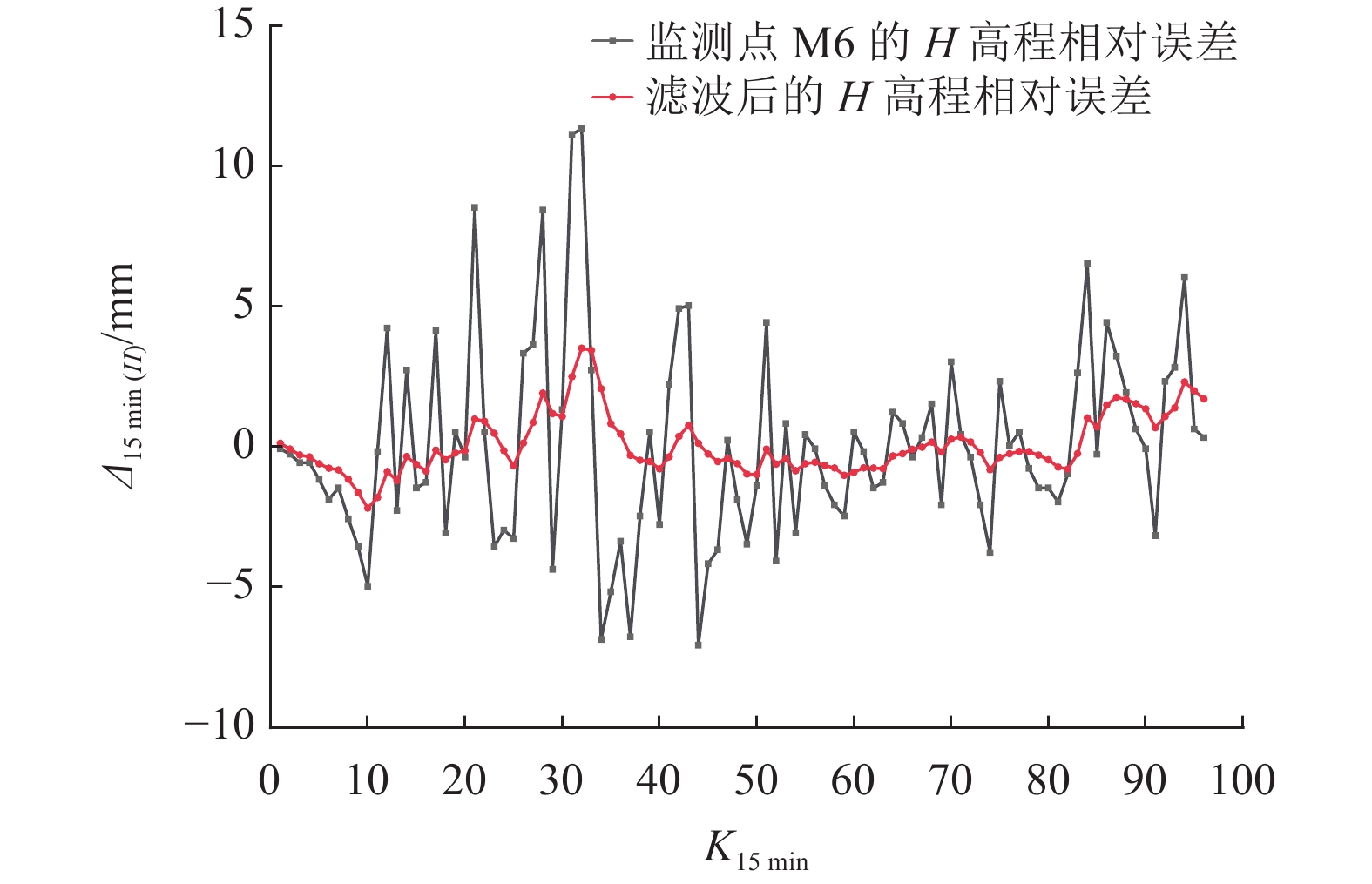
|
图 8 |
由图6~8显示效果可知,建立的粒子滤波模型是合理可靠的,从图中能明显看到滤波估计值的精度比原始解算观测值精度有所提高。监测点每15 min解算一次的原始解算观测值
为进一步验证方法的可靠性,本文在此仿真的基础上分别对2018年5月28日(0:00~24:00)时间段M1监测点的采样数据以及2018年5月29日(0:00~24:00)时间段M3监测点的采样数据以相同的观测时长15 min的采样数据解算一次的方式加入算法进行仿真验证,得到的监测点监测误差范围变化情况如表1所示。
| 表 1 监测误差对比 Table 1 Comparison of monitoring errors |
表1中的
本文利用粒子滤波算法较好地解决了由于观测时长减少,监测点采样数据量减少而带来的监测点解算坐标值精度下降的问题。通过建立与监测点状态空间向量契合的状态转移方程同BDS采样数据的解算观测值相结合,去除了某些周期性误差的影响,求得监测点最优估计向量,从而提高了定位精度。通过对广汕高铁铁轨路基的实测数据进行分析,验证了该方法的可行性,为减少高铁空窗期维护时间以提升高铁运行效率提供有效方法。
| [1] |
胡友健, 梁新美, 许成功. 论GPS变形监测技术的现状与发展趋势[J].
测绘科学, 2006(5): 155-157.
HU Y J, LIANG X M, XU C G. On the status quo and development trend of GPS technology for deformation monitoring[J]. Science of Surveying and Mapping, 2006(5): 155-157. |
| [2] |
王勇刚, 周俊萍, 李永江, 等. 基于惯性定位定向的高铁轨检仪分析研究[J].
导航定位与授时, 2018, 5(2): 70-74.
WANG Y G, ZHOU J P, LI Y J, et al. Analytical research of the inspecting instrument for high speed railway track based on the inertial position and azimuth determining technology[J]. Navigation Positioning and Timing, 2018, 5(2): 70-74. |
| [3] |
代志宏, 卢鹏, 张志芳, 等. 基于PS-InSAR技术的南宁地表沉降监测与分析[J].
大地测量与地球动力学, 2021, 41(5): 491-496.
DAI Z H, LU P, ZHANG Z F, et al. Surface subsidence monitoring and analysis of Nanning based on PS-InSAR technology[J]. Journal of Geodesy and Geodynamics, 2021, 41(5): 491-496. |
| [4] |
方新建. 基于GPS/BDS组合的矿区地表变形监测高精度解算模型构建及实现[D]. 淮南: 安徽理工大学, 2019.
|
| [5] |
徐纵, 黄陆明, 李博, 等. 采用北斗卫星导航系统的超高压变电站GIS变形监测精度分析[J].
浙江电力, 2021, 40(4): 101-107.
XU Z, HUANG L M, LI B, et al. Analysis of GIS deformation monitoring accuracy in EHV substation using Beidou satellite navigation system[J]. Zhejiang Electric Power, 2021, 40(4): 101-107. |
| [6] |
陈锋. GPS测量技术在桥梁工程变形观测中的应用研究[J].
建材与装饰, 2016(44): 272-273.
|
| [7] |
姜卫平, 刘鸿飞, 刘万科, 等. 西龙池上水库GPS变形监测系统研究及实现[J].
武汉大学学报(信息科学版), 2012, 37(8): 949-952.
JIANG W P, LIU H F, LIU W K, et al. CORS development for Xilongchi dam deformation monitoring[J]. Geomatics and Information Science of Wuhan University, 2012, 37(8): 949-952. |
| [8] |
李岚, 张云, 史宝明. 融合Mean-shift与粒子滤波改进算法的自适应人脸跟踪[J].
工业仪表与自动化装置, 2016(1): 82-85.
LI L, ZHANG Y, SHI B M. Improved adaptive algorithm in face tracking of fusing Mean-shift and particle filtering[J]. Industrial Instrumentation and Automation Device, 2016(1): 82-85. |
| [9] |
李会莹. 鲁棒滤波问题的若干研究[D]. 南京: 南京理工大学, 2007.
|
| [10] |
郝晶晶. 基于贝叶斯推理的故障诊断方法研究[D]. 北京: 北京交通大学, 2012.
|
| [11] |
朱福利, 曾碧, 曹军. 基于粒子滤波的SLAM算法并行优化与实现[J].
广东工业大学学报, 2017, 34(2): 92-96.
ZHU F L, ZENG B, CAO J. Parallel optimization and implementation of SLAM algorithm based on particle filter[J]. Journal of Guangdong University of Technology, 2017, 34(2): 92-96. |
| [12] |
张亚楠, 孙丰财, 史旭华. 一种改进RBPF激光SLAM算法[J].
无线通信技术, 2017, 26(4): 16-20.
ZHANG Y N, SUN F C, SHI X H. An improved RBPF-laser-SLAM algorithm[J]. Wireless Communication Technology, 2017, 26(4): 16-20. |
| [13] |
蔡登禹, 刘以安. 一种基于遗传算法的改进粒子滤波器[J].
计算机仿真, 2018, 35(7): 221-225.
CAI D Y, LIU Y A. Improved particle filter based on genetic algorithm[J]. Computer Simulation, 2018, 35(7): 221-225. |
| [14] |
霍富功, 王诗琴. 基于多特征融合的转移粒子滤波红外小目标跟踪算法研究[J].
信息与电脑(理论版), 2018(12): 56-59.
HUO F G, WANG S Q. Research on infrared small target tracking algorithm based on multi feature fusion[J]. Information & Computer (Theoretical Edition), 2018(12): 56-59. |
| [15] |
谢宏远, 刘逸, 候权, 等. 基于粒子滤波和遗传算法的氢燃料电池剩余使用寿命预测[J].
东北电力大学学报, 2021, 41(1): 56-64.
XIE H Y, LIU Y, HOU Q, et al. Prediction of PEMFC based on particle filter and genetic algorithm[J]. Journal of Northeast Electric Power University, 2021, 41(1): 56-64. |
| [16] |
孟庆旭. 粒子滤波算法研究及其在非线性估计中的应用[D]. 武汉: 华中科技大学, 2019.
|
 2022, Vol. 39
2022, Vol. 39

