介质阻挡放电(Dielectric Barrier Discharge, DBD)也称无声放电,是将绝缘物质插入放电空间的一种气体放电。当在放电电极间施加足够高的激励电压时,电极间的气体会被击穿而在微放电通道中发生微放电[1-2]。这一放电结构使得DBD能在很宽的激励电压频率和气压范围内能产生放电现象。大气压介质阻挡放电(Atmospheric Pressure Dielectric Barrier Discharge, APDBD)是一种典型的常压低温等离子体产生方式[3]。由于APDBD装置可以在接近室温的条件下产生大量的活性粒子,而且不需要昂贵、操作缓慢的抽真空设备。因此,近年来APDBD在生物医学、材料表面改性、挥发性有机气体(Volatile Organic Compounds, VOCs)处理及臭氧合成等领域发展迅速[4-5]。
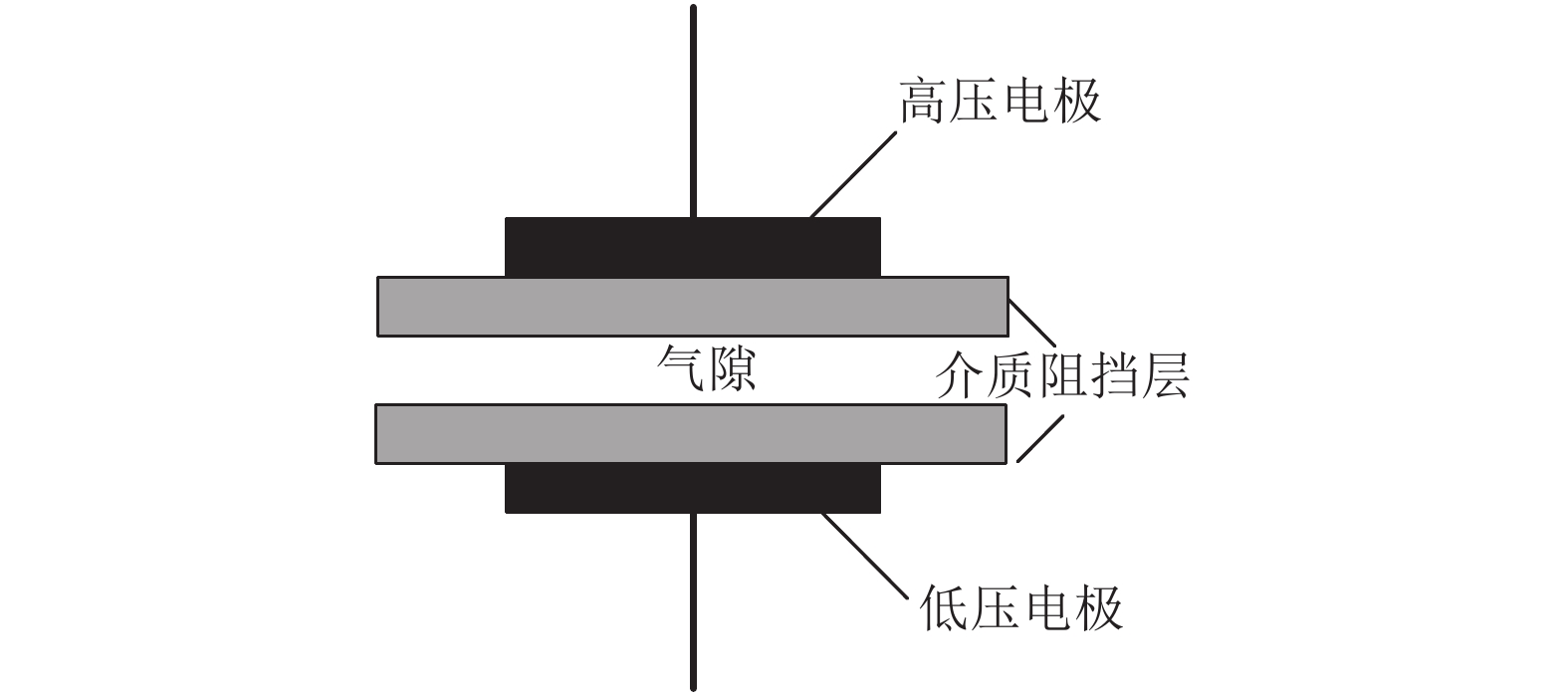
APDBD一般由高压电极、介质阻挡层、气隙、低压电极组成,它们之间的连接关系如图1所示[6]。在高低压电极之间施加适当幅值的交变电压,就能在气隙间形成放电现象[7]。
|
图 1 APDBD的常用结构 Figure 1 Common structure of APDBD |
很显然,当APDBD的结构参数确定及外部环境稳定后,激励电源类型及其参数就成为影响APDBD性能的关键因素[8]。目前常用的激励电源主要有正弦型激励电源和脉冲型激励电源[9]。众多的实验结果表明,APDBD在脉冲型激励电源作用下,会表现出比在正弦型激励电源作用下更优异的性能[10-12]。相比电流型脉冲激励,电压型脉冲激励具有实现便利的优势,电源工程师研制脉冲激励时往往采用电压型脉冲激励。然而,作为一种典型的容性负载[13],如将电压型脉冲激励直接施加于APDBD时,至少会存在如下两个缺陷:
(1) 负载端会出现不受控制的电流尖峰(尖峰大小与负载等效电流和施加电压上升率有关),该电流尖峰轻则造成保护电路动作,重则导致电路损坏。
(2) 很难对与APDBD的目标产物(如臭氧发生器中的臭氧产量、介质阻挡放电灯的紫外线的光通量)存在密切联系的注入电流进行有效控制。
此外,由于学科的交叉性,对放电机理进行研究的研究人员,一般都是直接使用由电源工程师研制的电压型脉冲激励。这也造成了现阶段少有研究人员对电流型脉冲激励下的APDBD特性进行研究。因此,不论在理论研究还是在实际应用中都非常有必要对电流型脉冲激励下的APDBD特性进行研究[14-16],这项研究不仅会为提高APDBD性能提供一种新的视角,而且可以为APDBD研制新型的供电电源提供有益的帮助。
考虑到气体放电现象的相似性以及现有实验方式不能从微观上获得APDBD的特性(如微观粒子的时空分布特性、击穿电压、电场分布等),本文将以板—板圆形电极结构的APDBD装置(腔体内填充氦气)为研究对象,通过构建一维流体模型来对电流型脉冲激励下的APDBD性能展开分析。分析结果表明,He+与He*的数密度与外施电流幅值存在近似的正相关性、与气隙宽度存在近似的负相关性;如要优化APDBD的目标产物(一般与处于激发态的原子数密度存在密切联系),则需要综合考虑外施脉冲电流的幅值、气隙宽度和其他电源波形参数等因素。
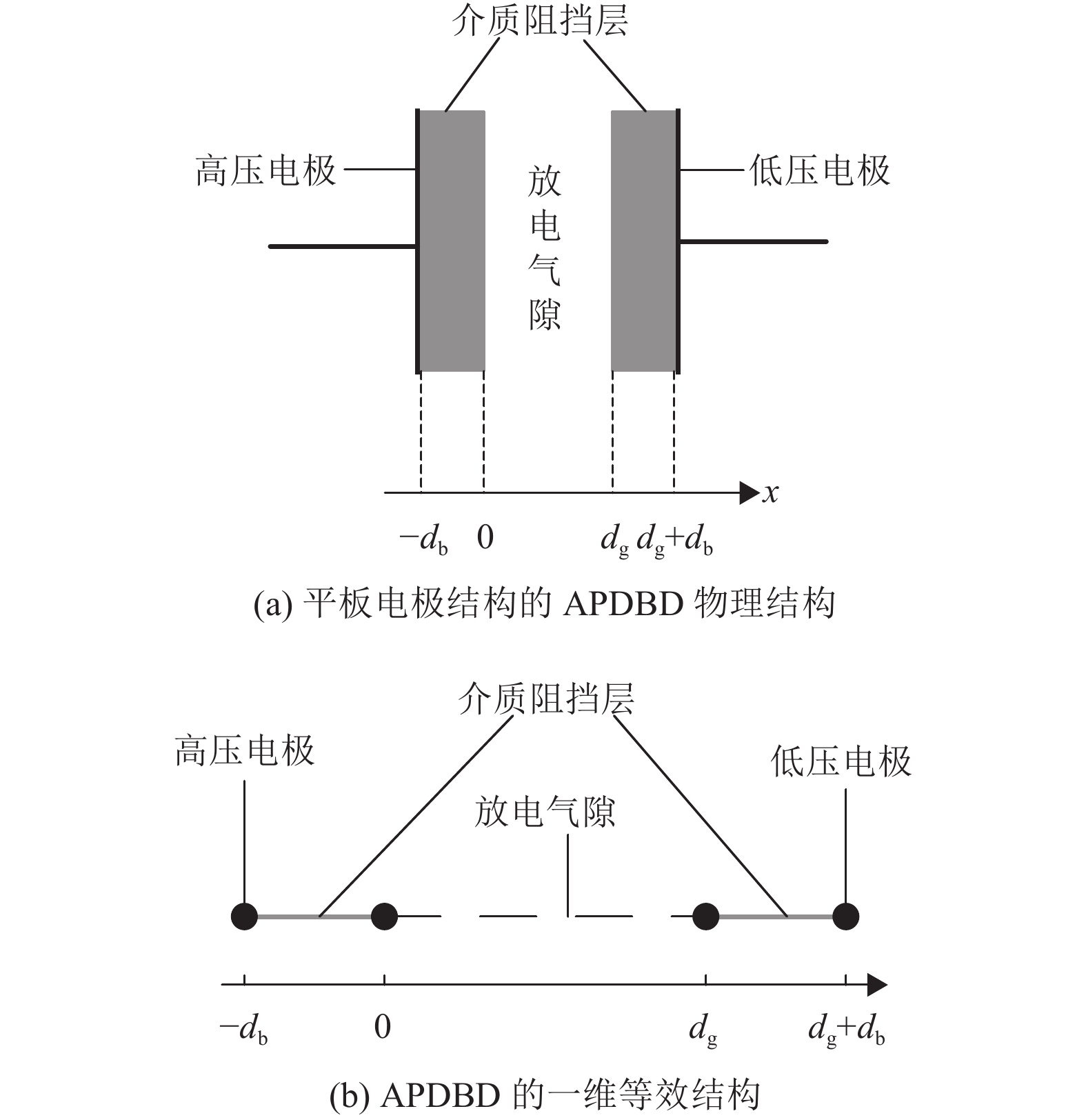
1 APDBD流体模型的建立及验证 1.1 APDBD的一维模型图2(a)给出了在本文中使用的平板电极结构的APDBD的物理结构示意图。其中,高压电极和低压电极上都覆盖有厚度为db的介质阻挡层,介质阻挡层之间有宽度为dg的放电气隙,气隙中充满氦气。在构建APDBD的一维模型时可以将重要物理量(如介质阻挡层、放电气隙等)一维简化成线段,而不做研究的物理量(如电极)则简化成点[17]。图2(b)给出由图2(a)得到的APDBD一维模型。
|
图 2 APDBD的物理结构及其一维等效结构 Figure 2 The physical structure and one-dimension equivalent structure of APDBD |
描述APDBD的流体模型主要由一系列的控制方程及其边界条件构成,其中控制方程包含有电子对流扩散方程、电子能量密度守恒方程、重粒子的连续性方程以及泊松方程,具体形式为
| $ \frac{{\partial {n_e}}}{{\partial t}} + \nabla \cdot [ - {n_e}({\mu _e} \cdot {\boldsymbol{E}}) - {D_e}\nabla {n_e}] = {R_e} $ | (1) |
| $ \frac{{\partial {n_\varepsilon }}}{{\partial t}} + \nabla \cdot [ - {n_\varepsilon }({\mu _\varepsilon } \cdot {\boldsymbol{E}}) - {D_\varepsilon }\nabla {n_\varepsilon }] = {R_\varepsilon } $ | (2) |
| $ \rho \frac{{\partial {\omega _k}}}{{\partial t}} + \rho ({\boldsymbol{u}}\nabla ){\omega _k} = \nabla \cdot {{\boldsymbol{j}}_k} + {R_k} $ | (3) |
| $ - \nabla {\varepsilon _0}{\varepsilon _{\rm{r}}}\nabla V = {\rho _q} $ | (4) |
| $ {\rho _q} = e\Bigg(\sum\nolimits_{k = 1}^N {{Z_k}{n_k} - {n_e}} \Bigg) $ | (5) |
式中:t 为时间,ne、nε和nk分别为电子数密度、电子能量密度和重粒子数密度,μe、με、De和Dε分别为电子迁移率、电子能量迁移率、电子扩散率和电子能量扩散率,Re和Rε分别为电子化学源项和电子能量源项,ρ为混合气体密度,ωk为重粒子质量分数,u为质量平均流体速度矢量,jk为扩散通量矢量,Rk为重粒子k 的产生速率,ε0和εr分别为真空介电常数与相对介电常数,ρq为空间电荷密度,e为元电荷,Zk 为粒子k所带电荷量,E为电场矢量,V为所加电势,N为重粒子的种类数。
控制方程的边界条件包括:放电电极表面散射与吸收过程中的电子通量边界条件,电极表面处的电子平均能量边界条件,电子、平均电子能量和重粒子在间隙处的边界条件和泊松方程的边界条件。式(6)~(11)依次给出了除泊松方程边界条件以外的边界条件表达式。
| $ {{\boldsymbol{\varGamma}} _e} \cdot {\boldsymbol{n}} = \frac{{1 - {\gamma _e}}}{{1 + {\gamma _e}}}\left[( - 2{a_e} + 1){n_e}{\mu _e}E{\boldsymbol{n}} + \frac{1}{2}{v_e}{n_e}\right] $ | (6) |
| $ {{\boldsymbol{\varGamma}} _\varepsilon } \cdot {\boldsymbol{n}} = \frac{1}{3}{v_e}\bar \varepsilon {n_e} $ | (7) |
| $ - {\boldsymbol{n}} \cdot {{\boldsymbol{\varGamma}} _e} = 0 $ | (8) |
| $ - {\boldsymbol{n}} \cdot {{\boldsymbol{\varGamma}} _\varepsilon } = 0 $ | (9) |
| $ - {\boldsymbol{n}} \cdot {{\boldsymbol{\varGamma}} _k} = 0 $ | (10) |
| $ {{\boldsymbol{\varGamma}} _k} \cdot {\boldsymbol{n}} = \frac{{{\gamma _k}}}{4}\sqrt {\frac{{8{k_{\rm{B}}}{T_k}}}{{{\text{π }}{m_k}}}} {n_k} $ | (11) |
式中:Γe为电子通量矢量,Γε为电子能量通量矢量,Γk为重粒子通量矢量,n为电极法向矢量,γe为电子在电极表面的反射系数,γk为激发态粒子和正,负离子与电极表面发生碰撞变为中性粒子的反应系数。ae为电子通量的方向指向,当电子通量的方向指向电极时,ae=1,否则ae =0;kB为玻尔兹曼常数,Tk为第k类粒子的温度,mk为第 k类粒子的质量、
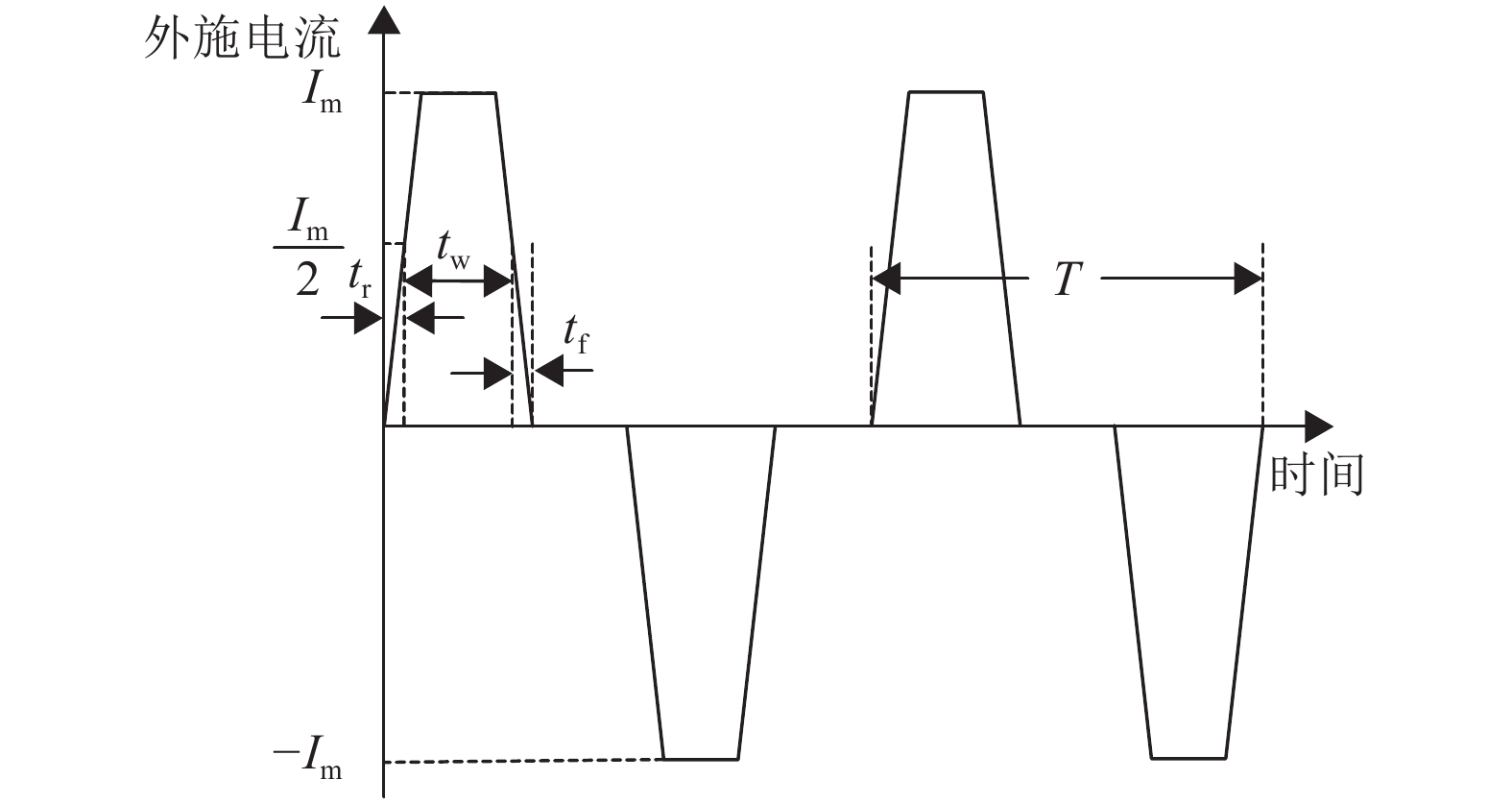
对于泊松方程的边界条件,可以认为是:在高压电极外施双极性电流型脉冲激励,低压电极接地。其中外施的双极性电流型脉冲激励的波形示意图如图3所示。
|
图 3 双极性电流型脉冲激励 Figure 3 Bipolar current pulse power |
在图3中,Im为脉冲电流激励幅值,tr为脉冲电流激励的上升时间,tf为脉冲电流激励的下降时间,不失一般性有tr=tf,tw为电流脉宽,T为脉冲电流激励周期。关于这种双极性电流型脉冲激励的具体实现方式,笔者将另行撰文进行叙述。
1.2.2 等离子体化学设定DBD的实质是在气隙间施加交变的电场,从而引起微观粒子的相互作用。因此等离子体所涉及的化学反应与激励的类型无关,在这里直接采用从电压源激励得出的化学反应及其速率。本文选取包含6种微观粒子(电子e,背景气体分子He,氦的两种离子态He+、He2+和氦的两种激发态
| 表 1 化学反应方程及其速率常数 Table 1 Chemical reaction and its rate constant |
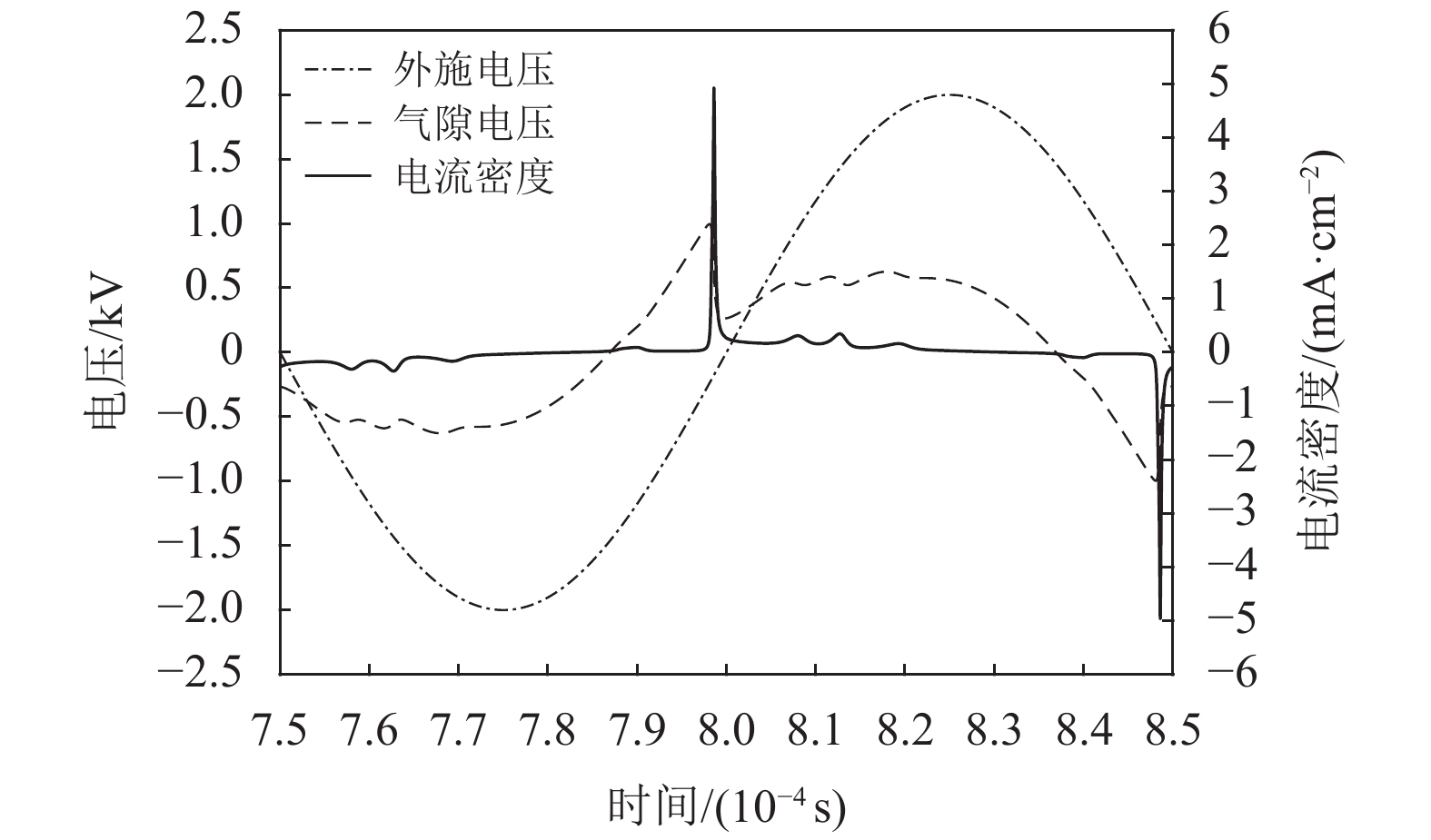
由于笔者未找到使用高频电流源作为激励来研究APDBD特性的文献,故在验证本文构建的APDBD一维流体模型是否正确时,选择大多数文献中使用的正弦电压作为激励,如图4所示,给出了V=Vmsin (2πft)的激励波形。其中:Vm为正弦电压峰值,其值为2000 V,f 为电源频率,其值为10 kHz。
|
图 4 伏安-时间特性 Figure 4 Comparison of voltammetry property |
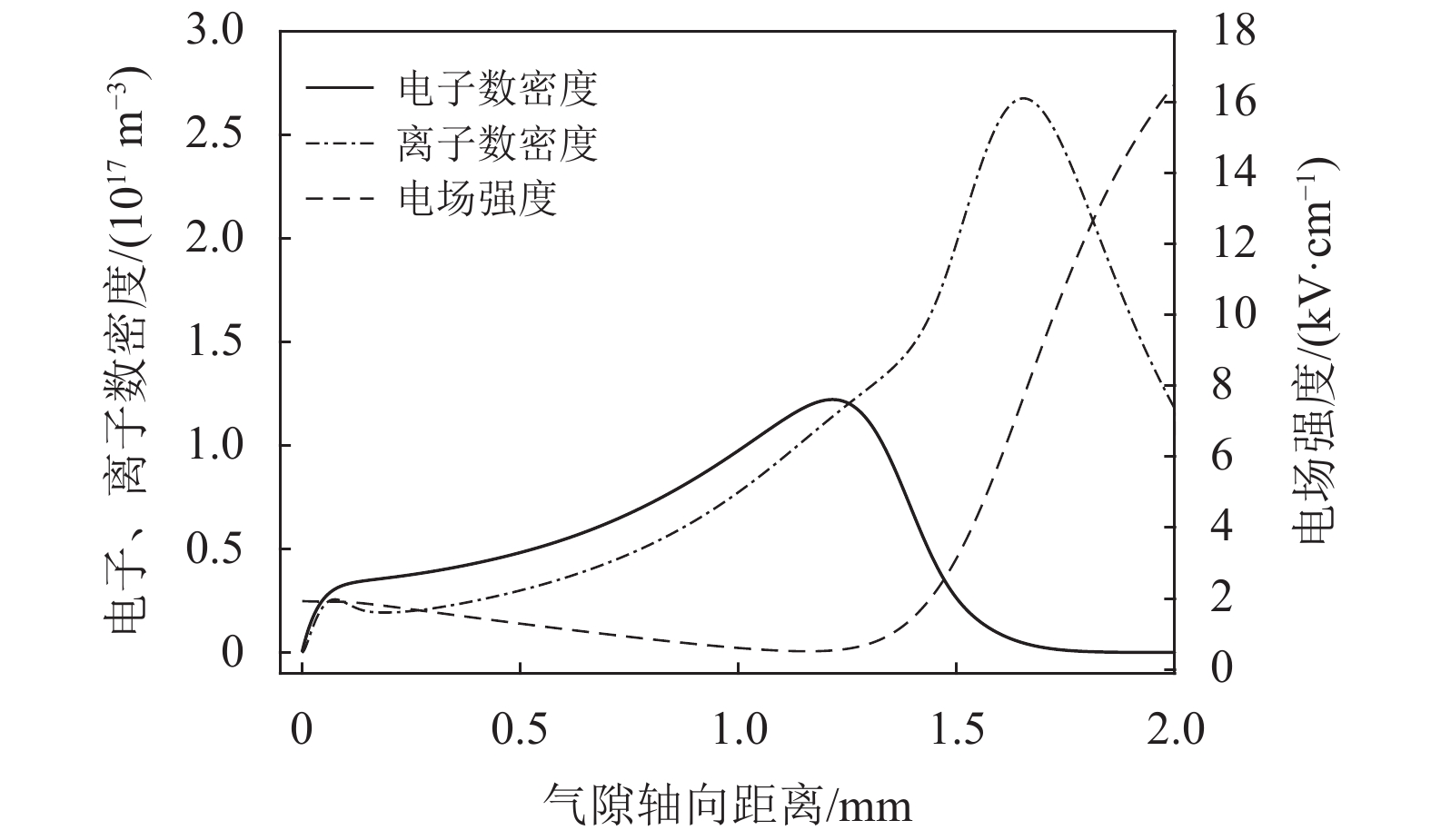
图4和图5给出了本文所构建模型的特性曲线。通过与文献[19]所给出的模型进行对比,可以得知二者的结果具有较好的一致性。这直接验证了本文构建的APDBD流体模型的正确性。很显然,如果将正弦激励更换成电流型脉冲激励,就可以对电流型脉冲激励下APDBD特性进行分析。
|
图 5 空间粒子数密度与电场强度分布 Figure 5 Comparison of spatial particle number density and electric field intensity distribution |
考虑到电子器件发展迅速以及APDBD在高频条件下会有更佳特性,因此本文在研究过程中使用的激励频率设定为50 kHz。此外,考虑到COMSOL Multiphysics在分析多物理场方面的优异性能,本文后续的分析结果均由该仿真软件获得。图6给出了电流脉冲激励的频率f =50 kHz、电流幅值Im=70 mA、电流脉宽tw=4 μs,电流的上升、下降时间tr=tf=1 μs,圆形介质板厚度db=1 mm、介质板直径dplate=50 mm和阻挡介质的相对介电常数εr=7.5时,APDBD在不同气隙宽度dg下的伏安−时间曲线及其气隙击穿电压曲线。从图6(a)中可以看出,气隙电压会经历如下4个阶段:(1) 在电流的正半周期中,随着注入电荷的增加,气隙电压快速上升,然后在某一稳定值(击穿电压Vth)附近进行数次振荡(表明气隙进行了数次击穿);(2) 当外施电流进入稳定阶段后,气隙电压维持在击穿电压处;(3) 当外施电流进入电流下降阶段时,气隙电压也逐渐下降;(4) 当外施电流等于零时,气隙电压也降至零。负半周期内APDBD的工作状态与正半周期内的工作状态相同,这里不再赘述。

|
图 6 APDBD在不同dg时的特性曲线 Figure 6 The characteristic curve of APDBD at different dg |
出现这一现象的原因可简述如下:外施电流增加,靠近阳极处的阻挡介质和气隙上开始累积正电荷,阻挡介质和气隙的电压快速上升;当气隙电压达到击穿电压后,放电过程开始,正电荷迅速转移到低压电极,气隙电压降低,本次放电过程结束;由于电流持续注入,正电荷还将继续在气隙上继续累积,这将在后续形成多次放电。但随着电流不断注入,在阻挡介质中累积的电荷形成的内部反向电场将逐步抵消外施电流的影响,使得气隙不再击穿,气隙电压维持为击穿电压;当外施电流减少时,累积在阻挡介质上和气隙中的正电荷开始逐步向电流源转移,阻挡介质电压和气隙电压逐步降低到零。这一过程也可从图7中得到验证。

|
图 7 阻挡介质和气隙中的电势及电场的时空分布 Figure 7 Temporal-spatial distribution of electric potential and electric field in barrier and air gap |
此外,从图6(b)中还可看出,气隙击穿电压与气隙宽度基本呈正相关的关系。造成这一现象的原因是:随着气隙宽度的增加,整个气隙的空间平均电场强度会逐渐减小,使得微观粒子发生碰撞、电离的概率减小,电子获得的能量降低,高能电子数目减少。如要出现放电现象,电子需要运动更长的距离,即击穿气隙需要达到更高的击穿电压。
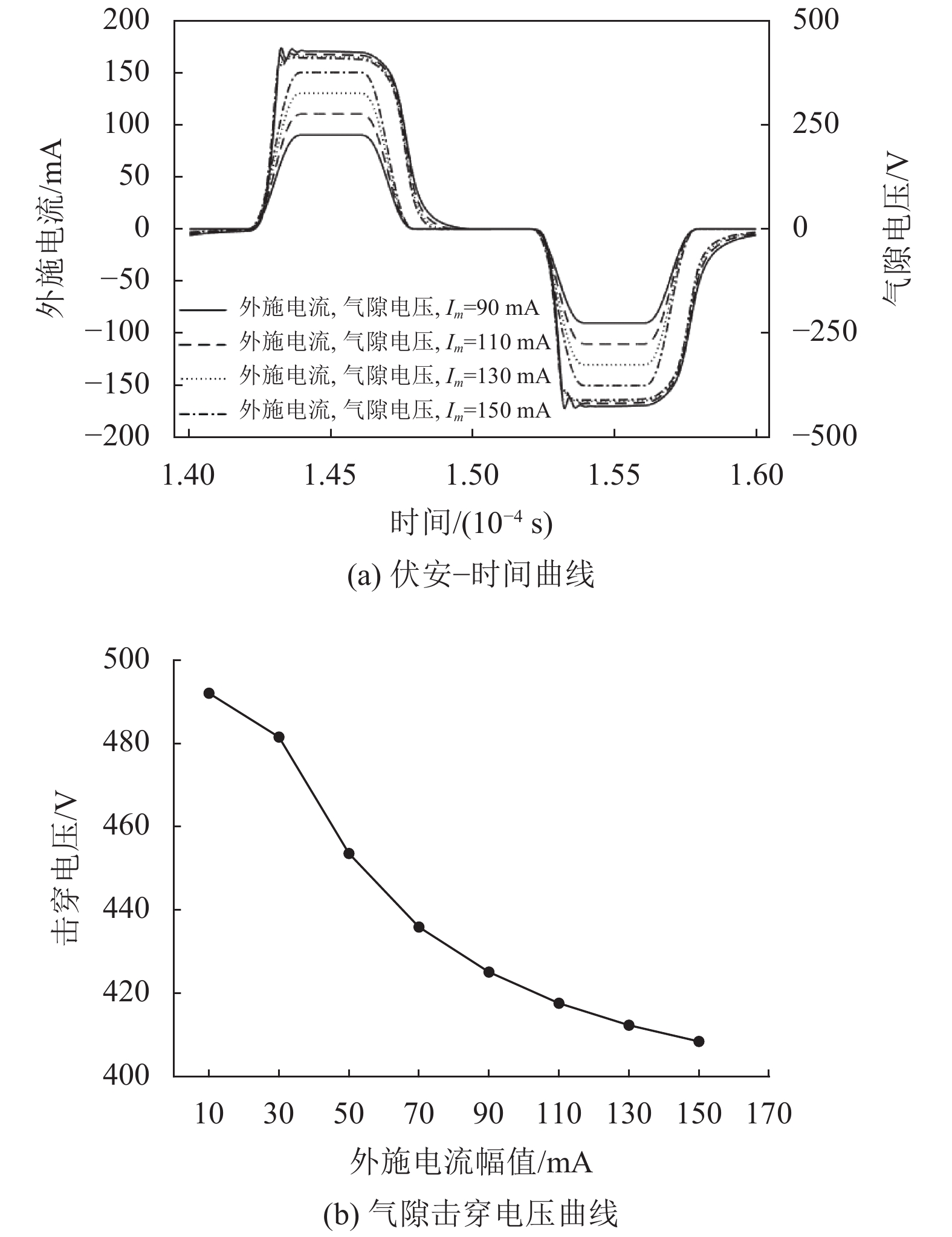
图8则给出了当dg=2 mm时,APDBD在不同外施电流幅值Im作用下的伏安−时间曲线及气隙击穿电压曲线。从图中可以看出,气隙击穿电压与Im呈现负相关。这一现象的原因可解释为:在更大的Im作用下,气隙内的电场会更强,微观粒子从外部电场获得的能量更多、高能电子数目大幅增加。这就增加了气隙内的微观粒子发生碰撞电离或激发的概率,这使得在无需更高的击穿电压条件下气隙也能被击穿。
|
图 8 APDBD在不同Im时的特性曲线 Figure 8 APDBD’s characteristics at different Im |
在众多微观粒子中,由于氦离子He+与各类反应密切相关、激发态的氦原子He*则是决定APDBD性质的重要微观粒子(如气体发光特性),因此非常有必要对这两类微观粒子的时空变化规律进行分析。图9和图10分别给出了在电流脉冲激励频率 f =50 kHz、电流幅值 Im=70 mA、电流脉宽 tw=4 μs,电流的上升、下降时间 tr=tf =1 μs,圆形介质板厚度db=1 mm、介质板直径 dplate=50 mm、气隙宽度dg=2 mm和阻挡介质的相对介电常数εr=7.5时的He+与He*数密度与激励波形的关系曲线图及时空分布图。

|
图 9 He+数密度跟随外施电流的时空变化情况 Figure 9 Variation of He+ number density with applied current and its temporal-spatial distribution |
|
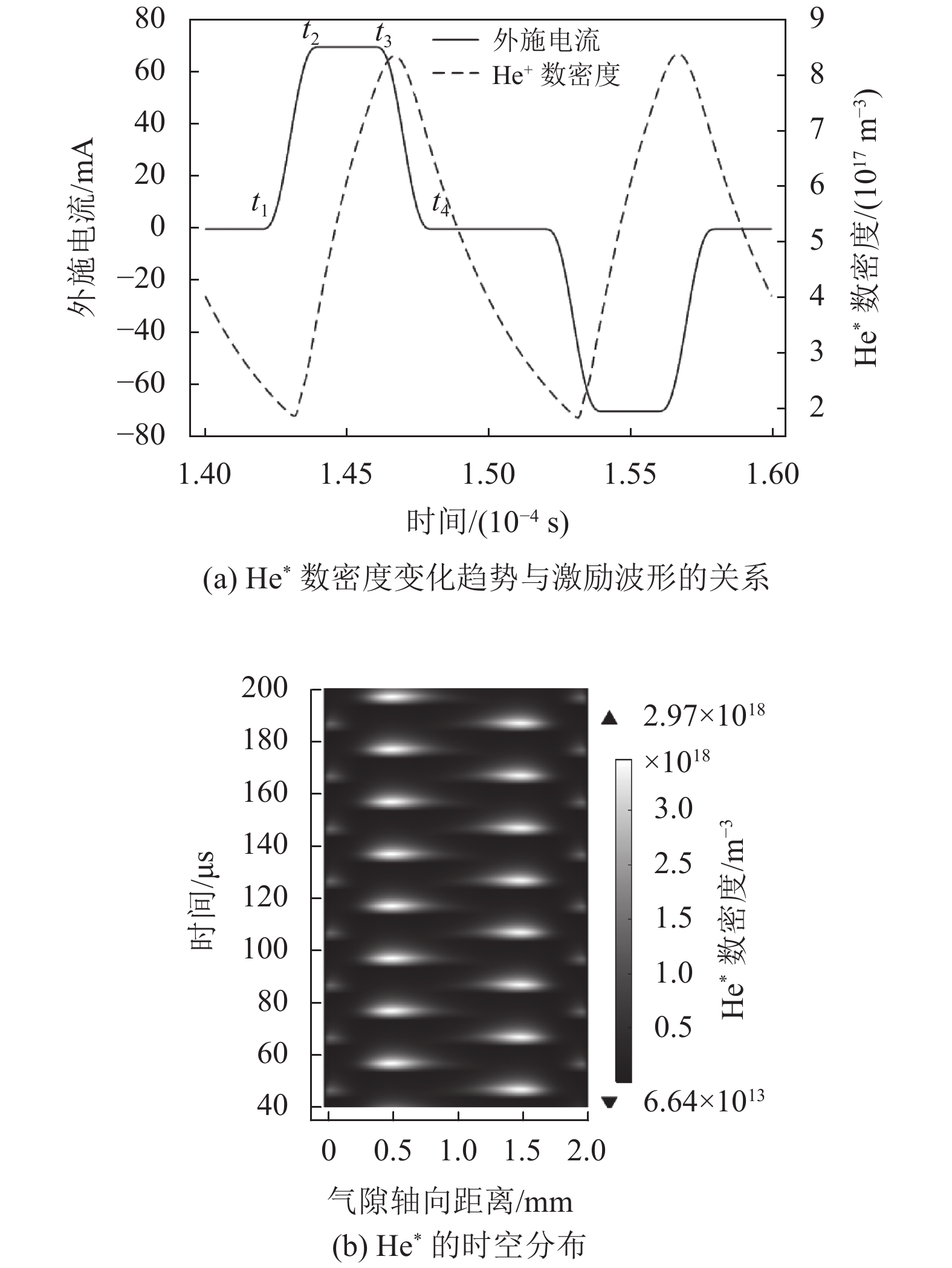
图 10 He*数密度随外施电流的变化情况及时空分布 Figure 10 Variation of He* number density with applied current and its temporal-spatial distribution |
从图9(a)可以看出,在外施电流上升阶段(t1−t2),电流的不断注入加速了高能电子的产生,使得反应R3、反应R4加快,He+数密度急剧增加;当电流处于恒定阶段(t2−t3),高能电子数目维持在稳定阶段,He+数密度基本保持不变;当电流处于下降阶段(t3−t4),高能电子数目将大幅降低,He+数密度随之下降。图9(b)所示的He+的时空分布图展示了He+数密度的变化过程。
从图10(a)可以看出,由于高能电子与背景气体的剧烈碰撞会增加He*的数目,因此在外施电流上升阶段(t1−t2),He*数密度持续增加;在(t2−t3) 阶段,由于反应R7、R12、R13的发生,部分He+转换为He*,He*数密度继续增加;在电流下降阶段(t3−t4),虽然高能电子运动导致的碰撞趋缓,但原子间相互碰撞依然在进行着(如反应R18~R24),这些反应都将消耗He*的数目,使得He*数密度持续下降。He*数密度变化情况可在图10(b)的He*的时空分布图得到验证。
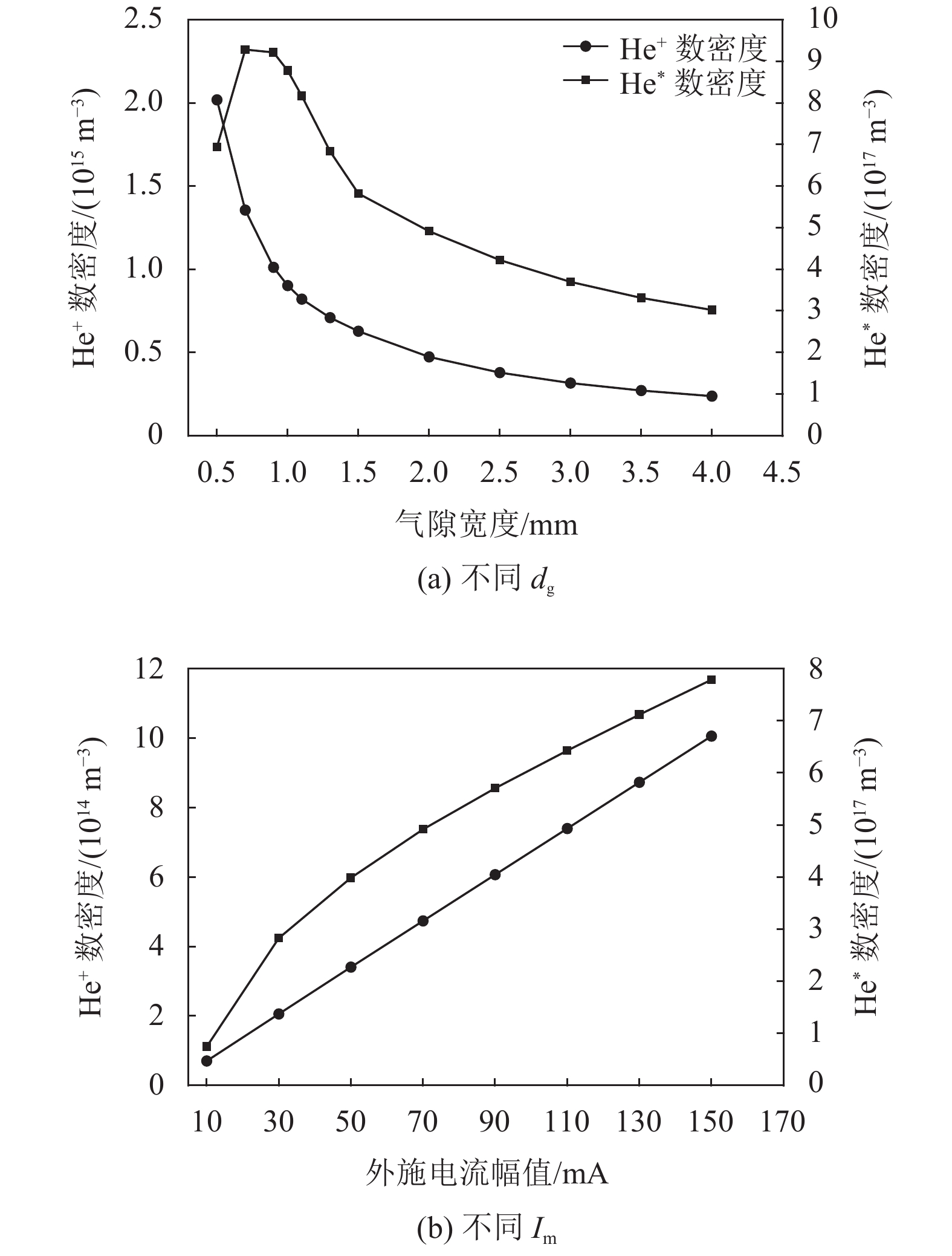
图11则给出了,He+、He*数密度与dg和Im的关系曲线。从图11(a)可以看出,当dg<1 mm时,He*数密度随着气隙宽度的增加而增加;当dg>1 mm时,He*数密度随着气隙宽度的增加而减少。造成这一现象的原因可能是:dg的增大将使气隙内的平均电场减小、高能电子数减少、碰撞电离减弱,从而减少He*的生成。但如果在足以引起电子雪崩的前提下略微增加气隙宽度,会促进碰撞电离的发生,He*数密度随之增加。然而,He+数密度却没有遵循这一规律,可能是由于化学反应合集的完善度不够及反应速率不准确造成的。从图11(b)可以得出,He+与He*数密度是随着电流幅值增加而基本呈线性增加。出现这一现象的原因是,更高的电流幅值将产生更多的高能电子,使得其与气隙内的各种粒子碰撞几率增加、碰撞程度加剧,从而生成更多的He+与He*。
|
图 11 He+与He*数密度分别在不同dg和Im的变化 Figure 11 The change of He+ and He* number density at different dg andIm, respectively |
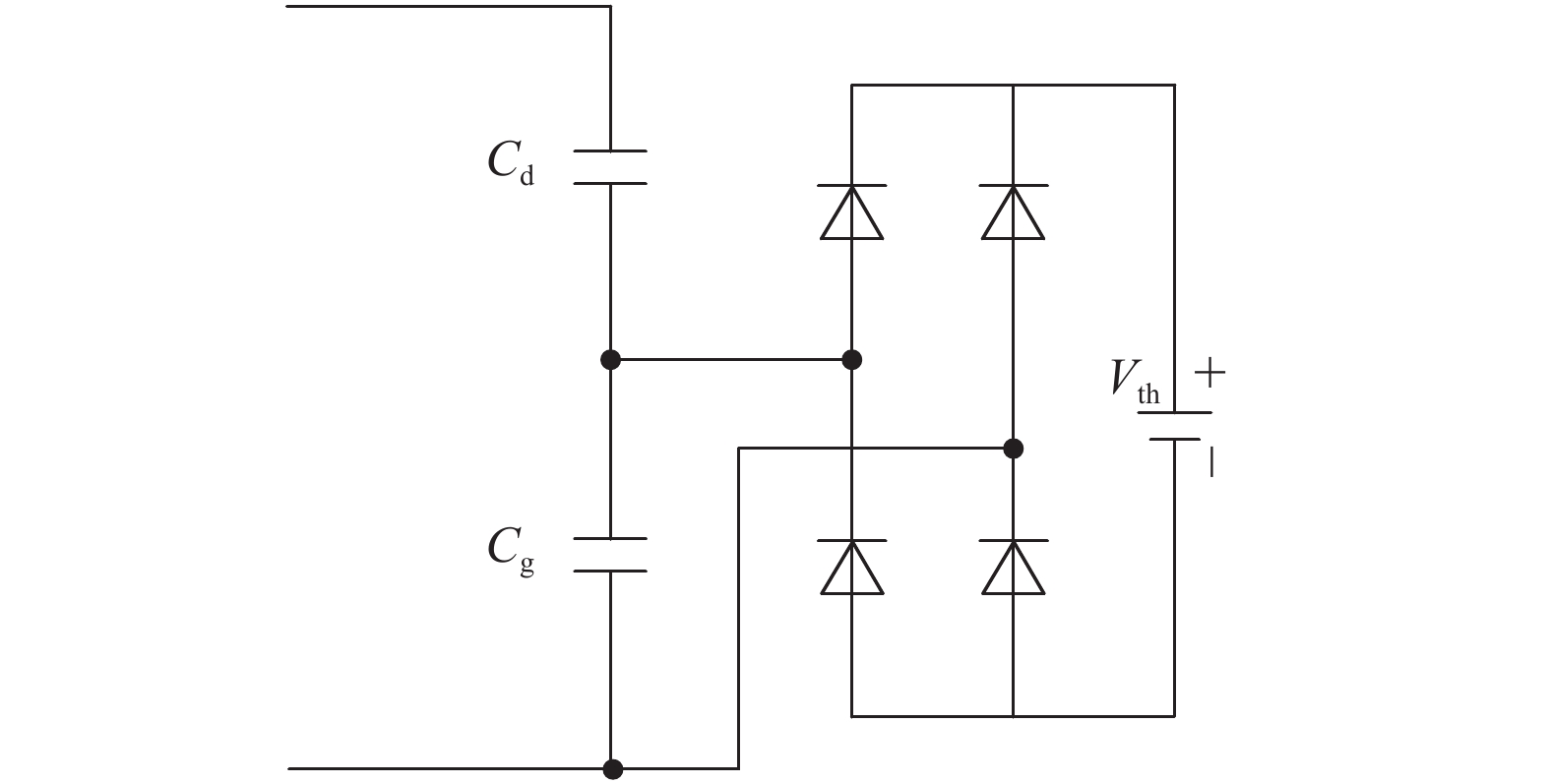
APDBD的电气等效电路已有很多文献进行探讨[21-22],图12给出了一种广为使用的等效电路。在这种等效电路电路中,当气隙未出现放电现象时,APDBD可视为由介质阻挡电容Cd和气隙电容Cg串联而成;当气隙电压达到击穿电压Vth时,APDBD可等效为介质阻挡电容Cd和击穿电压Vth串联构成。
|
图 12 一种广为使用的APDBD的电气等效电路 Figure 12 A widely used electrical equivalent circuit of APDBD |
这种电气等效电路源自于APDBD的“电荷−电压”李萨如图形,因而这种等效电路本质上是一种平均模型。通过对比图4和图6(a)中气隙电压波形可以发现,APDBD只有在电流源作用下,才能用图12所示的电气等效电路进行近似。因此,如要采用图12所示的等效电路对供电电源的特性进行时域分析,必须确保APDBD的激励源为电流型激励,否则将会产生较大的误差。
3.2 气隙宽度的选择He*数密度直接影响APDBD的某些重要性质(例如发光特性),虽然图11(a)给出了He*数密度与dg大小的关系,但未给出He*数密度随dg变化的空间分布变化趋势,也就不能为APDBD设计合理宽度的气隙提供指导。图13(a)~(h)给出了He*数密度随气隙宽度变化的时空分布。从图中可以看出,随着dg的增加,He*密集区越来越分散,这对得到足够集中的光照强度非常不利。当dg=1 mm时,正负两个半周期生成的He*密集区在气隙中点处出现了重叠。因此,对于论文进行分析的APDBD,1 mm的dg是一个比较好的取值。

|
图 13 He*数密度随气隙宽度变化的时空分布 Figure 13 Temporal-spatial distribution of He* number density varying with gap width |
图14(a)~(h)给出了He*数密度随Im大小变化的时空分布图。从图中可以得出:(1) 随着Im增大,He*密集区域将朝对应半周期的阴极板移动;(2) 当Im达到一定数值后(如文中Im>110 mA),He*密集区域位置基本保持不变;(3) 随着Im增大,He*数密度的最大值逐渐增加。这就意味着,如将APDBD应用于发光领域,一味通过提高Im数值来提高APDBD的发光亮度不是一个最优方案。因为提高Im大小不仅会使得APDBD的发光区域更为分散,而且会提高APDBD的承受电压值。在本文中,Im=90 mA就是一个合适的选择。

|
图 14 He*数密度随外施电流幅值变化的时空分布 Figure 14 Temporal-spatial distribution of He* number density varying with amplitude of the applied current |
图15给出了不同电流脉宽对APBDB承受电压以及He*数密度的影响情况,从图中可以得出:随着电流脉宽的增加,APDBD承受的电压随之增加;He*数密度随流脉冲持续时间线性增长。这些特性意味着增加电流脉宽可有效提高相关粒子数密度,但在增加电流脉宽时必须考虑APDBD的耐压情况,以免造成APDBD装置的损坏。

|
图 15 电流脉宽对APDBD特性的影响 Figure 15 The influence of current pulse width on the characteristics of APDBD |
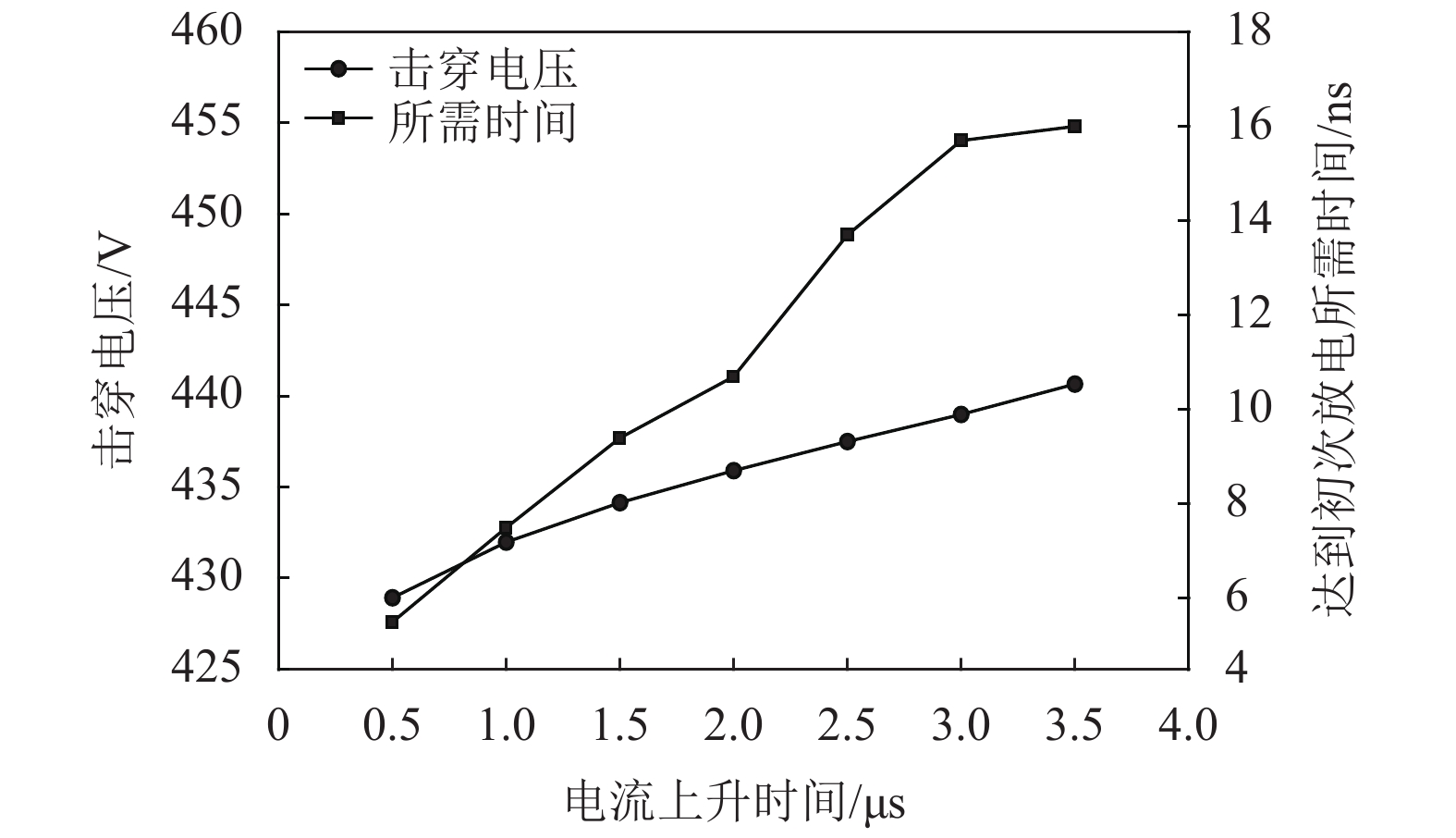
图16给出了击穿电压和达到初次放电所需时间与电流上升时间的关系。从图中得知:电流上升时间越长会导致击穿气隙需要更高电压和更长时间。产生这一现象的原理与图6(b)的解释类似,这里不再进行赘述。需要指出的是,更短的电流上升时间虽然会提高APDBD的性能,但前者会受到电源制作工艺的限制,一味缩短电流上升时间不仅难以实现且得不偿失。
|
图 16 电流上升时间对APDBD击穿过程的影响 Figure 16 The influence of current rise time on APDBD breakdown process |
在图3所示激励下,频率的增加意味着电流脉冲占空比增加。这使得两个相邻周期的时间间隔缩短,留给带电粒子之间进行复合反应的时间缩短,导致气隙内的剩余电子数增加。这些电子会在外施电场的作用下聚集在靠近阳极处的介质表面上,从而削弱气隙的电场,进而使放电变弱。但相关研究表明,外施电源频率的增加有利于增大等离子体面积及提高等离子体的均匀度[23]。因此合理选择电源工作频率是非常有挑战性的一项工作,不仅需要在放电均匀度和强度上进行考虑,还需要综合考虑电流源的电路拓扑结构的特性和现有器件的发展水平。
4 结论本文通过一维流体模型对双极性电流源激励下的大气压氦气介质阻挡放电进行分析,研究发现:
(1) 当给APDBD施加交变电流时,气隙电压会先后经过快速上升、振荡和维持稳定3个阶段。在对电流源作用下的APDBD进行时域分析时,APDBD可用经典的电压钳位型等效电路来替代。
(2) APDBD的气隙击穿电压与气隙宽度呈正相关,与外施电流幅值呈负相关。
(3) He+数密度的时间演化走势与外施电流的走势基本保持一致;而He*的数密度在外施电流上升、恒定的阶段保持增长,在外施电流下降、为零的阶段保持下降。
(4) 气隙宽度的增加会使He*密集区在空间上更加分散,外施电流幅值的增加会使He*密集区朝对应半周期的阴极板移动。如将APDBD应用于发光领域,应该综合考虑气隙宽度和外施电流幅值。
(5) 电流脉冲宽度、电流上升时间、电源频率等电源波形参数对APBDB的特性均存在较大影响,应对它们进行精心设计以满足实际运行需求。
| [1] |
戴栋, 宁文军, 邵涛. 大气压低温等离子体的研究现状与发展趋势[J].
电工技术学报, 2017, 32(20): 1-9.
DAI D, NING W J, SHAO T. A review on the state of art and future trends of atmospheric pressure low temperature plasmas[J]. Transactions of China Electrotechnical Society, 2017, 32(20): 1-9. |
| [2] |
HUANG X T, ZHOU S M, LIU M H. Investigation of the coupled volume dielectric barrier discharge for ozone formation in open atmospheric air[J].
IEEE Transactions on Plasma Science., 2018, 46(8): 2887-2893.
DOI: 10.1109/TPS.2018.2847285. |
| [3] |
李超. 介质阻挡放电技术处理挥发性有机物的研究进展[J].
化工进展, 2020, 39(5): 1964-1973.
LI C. Research progress on VOCs degradation using dielectric barrier discharge plasma[J]. Chemical Industry and Engineering Progress, 2020, 39(5): 1964-1973. |
| [4] |
马良军, 王佳媚, 黄明明, 等. 不同处理条件对介质阻挡放电低温等离子体杀菌效果及影响机理研究[J].
微生物学报, 2019, 59(4): 1513-1521.
MA L J, WANG J M, HUANG M M, et al. Sterilization by dielectric barrier discharge low temperature plasma under different treatment conditions[J]. Acta Microbiologica Sinica, 2019, 59(4): 1513-1521. |
| [5] |
SHAO T, LIU F, HAI B, et al. Surface modification of epoxy using an atmospheric pressure dielectric barrier discharge to accelerate surface charge dissipation[J].
IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(3): 1557-1565.
DOI: 10.1109/TDEI.2017.006321. |
| [6] |
徐学基, 诸定昌. 气体放电物理[M]. 上海: 复旦大学出版社, 1996.
|
| [7] |
郑殿春. 气体放电数值仿真方法[M]. 北京: 科学出版社, 2016.
|
| [8] |
史曜炜, 周若瑜, 崔行磊, 等. 不同电源激励下共面介质阻挡放电特性实验[J].
电工技术学报, 2018, 33(22): 5371-5380.
SHI Y W, ZHOU R Y, CUI X L, et al. Experimental investigation on characteristics of coplanar dielectric barrier discharge driven by different power supplies[J]. Transactions of China Electrotechnical Society, 2018, 33(22): 5371-5380. |
| [9] |
ZHAO Z L, WANG W C, YANG D Z, et al. Nanosecond pulsed array wire-to-wire surface dielectric barrier discharge in atmospheric air: electrical and optical emission spectra characters influenced by quantity of electrodes[J].
IEEE Transactions on Plasma Science., 2019, 47(8): 4219-4224.
DOI: 10.1109/TPS.2019.2922739. |
| [10] |
陈紫蒙, 马天鹏, 赵琼, 等. 大气压空气介质阻挡放电的数值模拟[J].
东华大学学报(自然科学版), 2018, 44(3): 485-494.
CHEN Z M, MA T P, ZHAO Q, et al. Numerical simulation of atmospheric air dielectric barrier discharges[J]. Journal of Donghua University (Natural Science), 2018, 44(3): 485-494. |
| [11] |
PAN J, LI L, WANG Y N. Particle densities of the atmospheric-pressure argon plasmas generated by the pulsed dielectric barrier discharges[J].
Plasma Science and Technology, 2016, 18(11): 1081-1088.
DOI: 10.1088/1009-0630/18/11/05. |
| [12] |
FANG Z, JI S C, PAN J, et al. Electrical model and experimental analysis of the atmospheric-pressure homogeneous dielectric barrier discharge in He[J].
IEEE Transactions on Plasma Science, 2012, 40(3): 883-891.
DOI: 10.1109/TPS.2011.2180544. |
| [13] |
DIEZ R, PIQUET H, FLOREZ D, et al. Current-mode approach in power supplies for DBD excilamps: review of 4 topologies[J].
IEEE Transactions on Plasma Science, 2015, 43(1): 452-460.
DOI: 10.1109/TPS.2014.2370796. |
| [14] |
RUEDA V, WIESNER A, DIEZ R, et al. Power estimation of a current supplied DBD considering the transformer parasitic elements[J].
IEEE Transactions on Industry Applications, 2019, 55(6): 6567-6575.
DOI: 10.1109/TIA.2019.2933519. |
| [15] |
FLOREZ D, DIEZ R, PIQUET H, et al. Square-shape current-mode supply for parametric control of the DBD excilamp power[J].
IEEE Transactions on Industrial Electronics, 2015, 62(3): 1451-1460.
DOI: 10.1109/TIE.2014.2361601. |
| [16] |
EI-DEIB A A, DAWSON F, EERDEN G V, et al. Analysis and experimental validation of a new current-controlled driver for a dielectric barrier discharge lamp[J].
IEEE Transactions on Industry Applications, 2011, 47(4): 1974-1982.
|
| [17] |
张雨晖. 大气压氦气介质阻挡放电中典型非线性现象的仿真研究[D]. 广州: 华南理工大学, 2019.
|
| [18] |
SANTOS M, NOEL C, BELMONTE T. Microwave capillary plasmas in helium at atmospheric pressure[DB]. (2017-11-14)[2020-07-28]. https://www.lx-cat.net/.
|
| [19] |
万静, 宁文军, 张雨晖, 等. 气隙宽度对大气压氦气介质阻挡放电多脉冲特性影响的仿真研究[J].
电工技术学报, 2019, 34(4): 871-879.
WAN J, NING W J, ZHANG Y H, et al. Influence of gap width on the multipeak characteristics of atmospheric pressure helium dielectric barrier discharges-a numerical approach[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 871-879. |
| [20] |
LAZAROU C, BELMONTE T, CHIPER A S, et al. Numerical modelling of the effect of dry air traces in a helium parallel plate dielectric barrier discharge[J].
Plasma Sources Science and Technology, 2016, 25(5): 1-20.
DOI: 10.1088/0963-0252/25/5/055023. |
| [21] |
TANG X, LI Z, ZHANG M. A wide-range frequency model for dielectric barrier discharge type ozone generators powered by series resonant inverters[J]. IEEE Access, 2019, 7: 124309-124314.
|
| [22] |
王帅, 邱祁, 刘星亮, 等. 大气压短间隙介质阻挡放电等效负载模型[J].
电工电能新技术, 2018, 37(11): 9-14.
WANG S, QIU Q, LIU X L, et al. Equivalent load model of dielectric barrier discharge in short gap at atmospheric pressure[J]. Advanced Technology of Electrical Engineering and Energy, 2018, 37(11): 9-14. |
| [23] |
潘光胜, 谭震宇, 王晓龙, 等. 高氧浓度下大气压Ar/O2脉冲介质阻挡放电频率特性数值研究
[J].
电工技术学报, 2017, 32(20): 71-81.
PAN G S, TAN Z Y, WANG X L, et al. A numerical study on the frequency effects of the electrical characteristics of the pulsed dielectric barrier discharge in Ar/O2 with high oxygen concentration at atmospheric pressure [J]. Transactions of China Electrotechnical Society, 2017, 32(20): 71-81. |
 2022, Vol. 39
2022, Vol. 39

