近年来,随着物联网以及人工智能应用的高速发展,涌现了计算密集型的新型低时延物联网应用,如增强现实、虚拟现实、远程手术、车联网等[1]。这些新型应用需要海量无线设备(如智能手机、可穿戴设备和智能传感器)的实时通信和计算能力。传统的云计算技术,受限于核心网络传输拥塞和抖动,难以满足这些新型物联网应用的低时延要求。作为第五代通信的关键技术,移动边缘计算(Mobile Edge Computing, MEC)成为物联网低时延应用的重要使能技术,受到了学术界和工业界的广泛关注[2-3]。
在MEC系统中,通过计算卸载(Computation Offloading, CO)技术,无线设备将计算任务传输到附近网络边缘设备或者基站,由其代理计算。由此,MEC系统能为终端用户提供在网络边缘(如无线接入点和蜂窝基站)的类云计算服务,这为满足时延敏感的计算密集型移动端应用的需求提供了较好的解决方案。在MEC计算卸载应用中,存在着无线资源和计算资源的权衡关系。因此,无线资源和计算资源联合配置是提高MEC系统性能的重要研究课题。
基于用户能耗最小化、计算时延最小化、能耗与时延的折中以及计算速率最大化等计算卸载性能指标,国内外研究团队对MEC系统的通信和计算资源联合优化配置进行了深入研究[4-11]。此外,基于设备直联(Device-to-Device, D2D)通信的MEC协同计算技术,使无线设备之间共享/贡献其未使用的计算资源,能显著提高整体计算性能[12-14]。值得注意的是,已有的针对无线设备储能研究是静态的场景[4-14]。然而,在可再生能量收集系统中,可再生能量通常以时空动态变化的方式到达用户[15-16]。
为此,基于计算吞吐量最大化的系统性能准则,本文重点研究能量收集用户的在线MEC系统设计难题。基站侧部署MEC服务器,无线设备配置可再生能量收集电路。该系统将卸载的工作时间划分为多个等长度的时隙。特别地,本文考虑了在给定任务下基于MEC服务器的用户协同通信和计算,增加动态任务到达和随机能量收集[17-19]。假设到达每个用户的可再生能量是动态的,能量在每个时隙的开始时收集并储存于电池。此外,本文考虑部分计算卸载技术,计算任务分割为独立的两部分,分别由无线设备的本地计算和计算卸载完成任务处理。
本文的主要贡献总结如下:(1) 建立了多时隙计算框架,建模任务因果关系、能量约束和完成约束条件,基于计算吞吐量最大化准则,联合优化基站帮助用户在不同时隙的本地计算和任务交换(卸载)决策;(2) 为了刻画系统性能上界,考虑信道状态信息和能量到达已知的离线场景,利用凸优化技术,推导了多时隙本地计算和计算卸载的资源配置最优解的解析形式;(3) 基于离线最优解结构,在信道状态信息和能量到达信息预测条件下,提出了基于滑动窗的多时隙在线资源联合配置方案;(4) 本文实现了大量的数值仿真实验,验证了在线方案的有效性,相较于已有基准设计方案,本文所提方案具有显著的性能增益。
1 系统模型与问题构造如图1所示,本文考虑基于能量收集的多用户MEC系统。该系统包含一个基站和K个无线设备,其中基站集成了MEC服务器,每个无线设备的可再生能量随机动态到达。无线设备具备能量收集功能,其收集的可再生能量储存于本地电池用于本地计算和计算卸载。每个无线设备配置单天线,所有用户都可以通过任务卸载和本地计算执行任务。记用户设备序号为
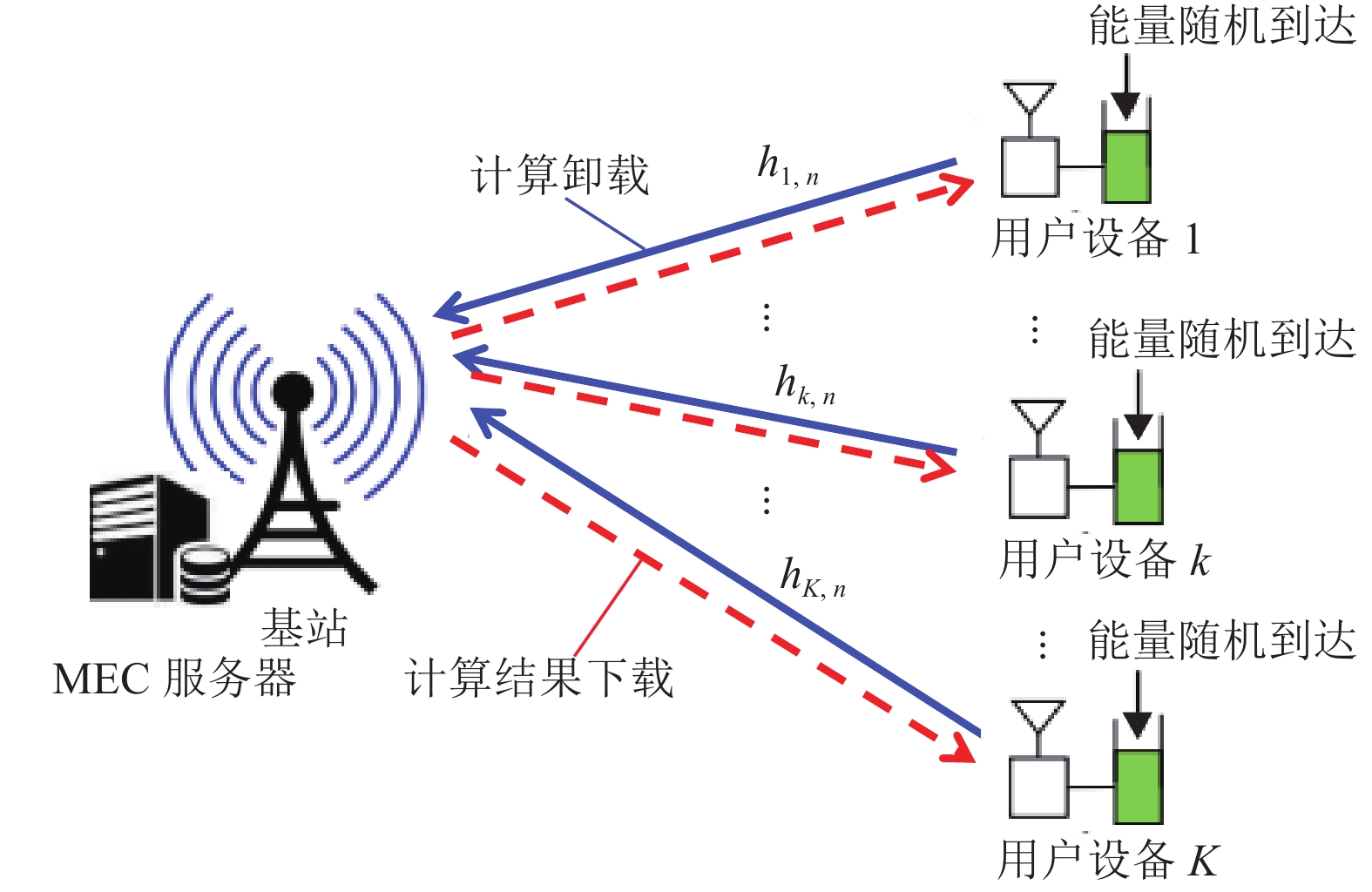
|
图 1 基于能量采集的多用户MEC系统模型 Figure 1 Energy-harvesting based multi-user MEC system |
考虑一个时间跨度为
记
| $ \sum\nolimits_{j = 1}^n {{E_{k,j}}} - \sum\nolimits_{j = 1}^n {E_{k,j}^{{\text{loc}}}} - \sum\nolimits_{j = 1}^n {E_{k,j}^{{\text{off}}}} \geqslant 0,{\text{ }}n ={1,\cdots,N-1} $ | (1) |
| $ \sum\nolimits_{j = 1}^N {{E_{k,j}} - \sum\nolimits_{j = 1}^N {E_{k,j}^{{\text{loc}}}} } - \sum\nolimits_{j = 1}^N {E_{k,j}^{{\text{off}}}} = 0 $ | (2) |
式中:
记
| $ {E}_{k,n}^{\text{loc}}={C}_{k}{l}_{k,n}^{\text{loc}}{\gamma }_{k}{\left(\frac{{C}_{k}{l}_{k,n}^{\text{loc}}}{\tau }\right)}^{2}\text=\frac{{\gamma }_{k}{C}_{k}{}^{3}{\left({l}_{k,n}^{\text{loc}}\right)}^{3}}{{\tau }^{2}} $ | (3) |
式中:
考虑用户k向基站进行计算卸载的上行链路信道服从半静态衰落信道模型,即上行链路信道功率增益在每个时隙内保持不变,但在不同的时隙可能有变化。令
| $ {r_{k,n}} = {B_k}{\log _2}\left( {1 + \frac{{{p_{k,n}}{h_{k,n}}}}{{\sigma _0^2}}} \right) $ | (4) |
式中:
| $ E_{k,n}^{{\text{off}}} = \tau {p_{k,n}} = \frac{{\sigma _0^2\tau }}{{{h_{k,n}}}}\left( {{2^{{{l_{k,n}^{{\text{off}}}} \mathord{\left/ {\vphantom {{l_{k,n}^{{\text{off}}}} {\left( {\tau {B_k}} \right)}}} \right. } {\left( {\tau {B_k}} \right)}}}} - 1} \right) $ | (5) |
式中:
在给定能量因果约束条件,本文以该多用户MEC系统的计算吞吐量最大化为准则,联合设计多时隙的本地计算和计算卸载,优化配置无线资源和通信资源。具体的,就是建立能量因果约束条件下的计算吞吐量最大化设计问题:
| $ \begin{gathered} \left( {{\text{P}}1} \right):{\text{ }}\mathop {\max }\limits_{l_{k,n}^{{\text{loc}}} \geqslant 0,l_{k,n}^{{\text{off}}} \geqslant 0} {\text{ }}F: = \sum\nolimits_{k = 1}^K {\sum\nolimits_{n = 1}^N {( {l_{k,n}^{{\text{loc}}} + l_{k,n}^{{\text{off}}}} )} } \hfill \\ {\text{s}}{\text{.t}}{\text{.}}\left\{ \begin{gathered} \sum\nolimits_{j = 1}^n {{E_{k,j}}} - \sum\nolimits_{j = 1}^n {E_{k,j}^{{\text{loc}}}} - \sum\nolimits_{j = 1}^n {E_{k,j}^{{\text{off}}}} \geqslant 0,{\text{ }}n = {1,\cdots,N-1} \hfill \\ \sum\nolimits_{j = 1}^N {{E_{k,j}} - \sum\nolimits_{j = 1}^N {E_{k,j}^{{\text{loc}}}} } - \sum\nolimits_{j = 1}^N {E_{k,j}^{{\text{off}}}} = 0,{\text{ }}k={1,\cdots,K} \hfill \\ E_{k,n}^{{\text{loc}}} = \frac{{{\gamma _k}C_k^3{{( {l_{k,n}^{{\text{loc}}}} )}^3}}}{{{\tau ^2}}},{\text{ }}k={1,\cdots,K};\;n={1,\cdots,N} \hfill \\ E_{k,n}^{{\text{off}}} = \frac{{\sigma _0^2\tau }}{{{h_{k,n}}}}( {{2^{{{l_{k,n}^{{\text{off}}}} \mathord{\left/ {\vphantom {{l_{k,n}^{{\text{off}}}} {\left( {\tau {B_k}} \right)}}} \right. } {\left( {\tau {B_k}} \right)}}}} - 1} ),{\text{ }}k={1,\cdots,K};\;n={1,\cdots,N} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $ |
对问题(P1)作如下说明:用户采集的能量将全部用于处理计算任务,问题(P1)的优化目标F是所有K个用户设备的计算比特数目总和最大化。在离线情况下,优化问题(P1)是凸优化问题,可采用经典拉格朗日对偶理论,推导出最优解的解析形式[20]。然而,针对在线设计场景,优化问题(P1)的求解非常复杂,需要预测未来时刻的信道/能量状态信息,实时动态调整本地计算和计算卸载的资源配置方案。
2 问题(P1)优化分析与求解在本节中,首先基于拉格朗日对偶理论[20],推导离线场景下优化设计问题(P1)的最优解结构,然后,针对在线场景下,基于滑动窗口算法,提出优化问题(P1)的在线优化设计方案。
2.1 离线场景下的最优解结构在离线场景下,信道状态信息以及能量状态信息
离线场景凸优化问题(P1)满足Slater条件[20]。因此,优化问题(P1)与其拉格朗日对偶问题之间存在强对偶性。对优化问题(P1)的能量因果约束条件引入拉格朗日乘子
| $ \mu _{k,n}^*\left( {\sum\nolimits_{j = 1}^n {{E_{k,j}}} - \sum\nolimits_{j = 1}^n {E_{k,j}^{{\text{loc*}}}} - \sum\nolimits_{j = 1}^n {E_{k,j}^{{\text{off*}}}} } \right) = 0 $ | (6) |
式中:
基于互补松弛条件(6)和拉格朗日函数一阶导数为零的性质,推导离线场景时凸优化问题(P1)的最优解[20]。因此,问题(P1)的最优解表达式推导如式(7)所示。
| $ \left\{ \begin{gathered} l_{k,n}^{{\text{loc*}}}{\text{ = }}\sqrt {{{{\tau ^2}} \mathord{\left/ {\vphantom {{{\tau ^2}} {\left( {3\left( {\sum\nolimits_{j = n}^N {\mu _{k,j}^*} } \right){\gamma _k}C_k^3} \right)}}} \right. } {\left( {3\left( {\sum\nolimits_{j = n}^N {\mu _{k,j}^*} } \right){\gamma _k}C_k^3} \right)}}} \hfill \\ l_{k,n}^{{\text{off}}*} = \tau {B_k}{\log _2}\Bigg( {\frac{{{B_k}{h_{k,n}}}}{{\left( {\displaystyle \sum\nolimits_{j = n}^N {\mu _{k,j}^*} } \right)\sigma _0^2\ln 2}}} \Bigg) \hfill \\ \end{gathered} \right. $ | (7) |
式中:
算法1 离线优化问题(P1)的次梯度求解算法
1) 输入:给定初始对偶变量
2) 迭代:
(a) 给定
(b) 更新次梯度:
(c) 更新对偶变量:
(d) 更新迭代次数:
(e) 更新步长:
3) 直到:
4) 输出:得到
在每时隙
为此,本小节基于离线问题(P1)的最优解(7),提出在线滑动窗设计方案。具体地,本文建模信道状态信息的预测误差
首先,定义窗口长度为M的滑动窗,M是从1至N中的任意整数。在时隙n,考虑M个时隙{
值得注意的是,在线滑动窗口不能超出N时隙范围,即
| $ \begin{gathered} {\text{OW}}\left( i \right):{\text{ }}\mathop {\max }\limits_{l_{k,n}^{{\text{loc}}\left( i \right)} \geqslant 0,l_{k,n}^{{\text{off}}\left( i \right)} \geqslant 0} {\text{ }}F\left( i \right): = \sum\nolimits_{k = 1}^K {\sum\nolimits_{n = i}^M {( {l_{k,n}^{{\text{loc}}\left( i \right)} + l_{k,n}^{{\text{off}}\left( i \right)}} )} } \hfill \\ {\text{s}}{\text{.t}}{\text{.}}\left\{ \begin{gathered} {E_{k,i}} + \sum\nolimits_{j = i + 1}^n {{{\hat E}_{k,j}}} - \sum\nolimits_{j = i}^n {E_{k,j}^{{\text{loc}}}} - \sum\nolimits_{j = i}^n {E_{k,j}^{{\text{off}}}} \geqslant 0 \hfill \\ {E_{k,i}} + \sum\nolimits_{j = i + 1}^{i + M - 1} {{{\hat E}_{k,j}}} - \sum\nolimits_{j = i}^{i + M - 1} {E_{k,j}^{{\text{loc}}}} - \sum\nolimits_{j = i}^{i + M - 1} {E_{k,j}^{{\text{off}}}} = 0 \hfill \\ E_{k,n}^{{\text{loc}}} = \frac{{{\gamma _k}{C_k}^3{{( {l_{k,n}^{{\text{loc}}\left( i \right)}} )}^3}}}{{{\tau ^2}}},\forall k,n \in \left\{ {i,\cdots,i + M - 1} \right\} \hfill \\ E_{k,n}^{{\text{off}}} = \frac{{\sigma _0^2\tau }}{{{{\hat h}_{k,n}}}}( {{2^{{{l_{k,n}^{{\text{off}}\left( i \right)}} \mathord{\left/ {\vphantom {{l_{k,n}^{{\text{off}}\left( i \right)}} {\left( {\tau {B_k}} \right)}}} \right. } {\left( {\tau {B_k}} \right)}}}} - 1} ), \forall k,n \in \left\{ {i + 1,\cdots,i + M - 1} \right\} \hfill \\ E_{k,i}^{{\text{off}}} = \frac{{\sigma _0^2\tau }}{{{h_{k,i}}}}( {{2^{{{l_{k,i}^{{\text{off}}\left( i \right)}} \mathord{\left/ {\vphantom {{l_{k,i}^{{\text{off}}\left( i \right)}} {\left( {\tau {B_k}} \right)}}} \right. } {\left( {\tau {B_k}} \right)}}}} - 1} ),\forall k \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $ |
根据次梯度算法1,将N替换成M,离线的信道/能量状态信息替换成在线滑动窗的信道/能量状态信息预测值,快速求解该在线设计问题OW(i)。
该在线滑动窗设计问题OW(i)的最优解表示为
| $ \tilde l_{k,i}^{{\text{loc}}} = l_{k,i}^{{\text{loc}}\left( i \right)*},\tilde l_{k,i}^{{\text{off}}} = l_{k,i}^{{\text{off}}\left( i \right)*} $ |
在线滑动窗优化设计算法如下所示。
算法2 基于滑动窗的在线优化设计算法
1) 开始:设置滑动窗长度M,滑动窗序号i=1
2) 迭代:
(a) 在第i个时隙时,获取当前时隙i以及时隙{
(b) 采用算法一计算在线优化问题OW(i),得到最优解
(c) 设置:
(d) 更新:
3) 直到i = N
4) 输出:滑动窗在线设计最优解
值得注意的是,在该在线滑动窗算法中,窗口大小M值在信道状态信息和能量状态信息预测误差以及MEC系统性能上起着关键作用。一方面,在预测误差较小的情况下,设置较大窗口长度M,能够充分利用长期信道及能量状态信息。另一方面,随着M值的减小,能量状态信息的预测和信道状态信息的预测作用有限,在较大信道状态信息及能量状态信息预测误差情况下,需要选取较小M值。因此,通过调整滑动窗长度M,可以适配多用户MEC系统的不同信道状态信息和能量状态信息预测特征。本文提出的在线滑动窗优化设计方案具有较低的计算复杂度。
3 仿真结果分析与对比本节将提供计算机数值仿真结果来验证所提算法方案的有效性,评估针对无线多用户联合MEC系统计算吞吐量性能。令
本文考虑3种系统吞吐量最大化的基准方案,用于基于能量采集的多用户MEC系统性能比较。
(1) 基准方案1:完全本地计算,每个用户只通过本地计算处理计算任务,即
(2) 基准方案2:完全计算卸载,每个用户只通过计算卸载处理计算任务,即
(3) 基准方案3:比例混合计算,每个用户将每时隙采集的能量,按照既定比例分别用于其本地计算和计算卸载。本文考虑3种比例,即“1/2计算卸载+1/2本地计算”、“2/3计算卸载+1/3本地计算”、“1/3计算卸载+2/3本地计算”。
在本文仿真实验中,每个用户在每时隙采集的能量大小独立同分布,服从均匀分布。而未作额外说明时,该多用户MEC系统参数设置如下:时隙长度τ为0.2 s,时隙数目N=20,基站接收机的噪声功率
图2显示了不同时隙数目N下的系统计算吞吐量性能曲线,其中用户数设备目K=20,信道和能量状态信息预测误差的归一化方差均为0.2,滑动窗口实习数目设置为M=5。随着时隙数目N增大,所有方案的计算吞吐量均单调上升。离线最优方案是基于算法1在无信道/能量状态信息预测误差下的性能曲线。相比于基准方案,本文提出的在线滑动窗方案能显著地提高系统计算吞吐量。此外,3种比例混合计算的基准方案明显优于完全本地计算和完全计算卸载的基准方案。这表明了本地计算和计算卸载联合设计的必要性。
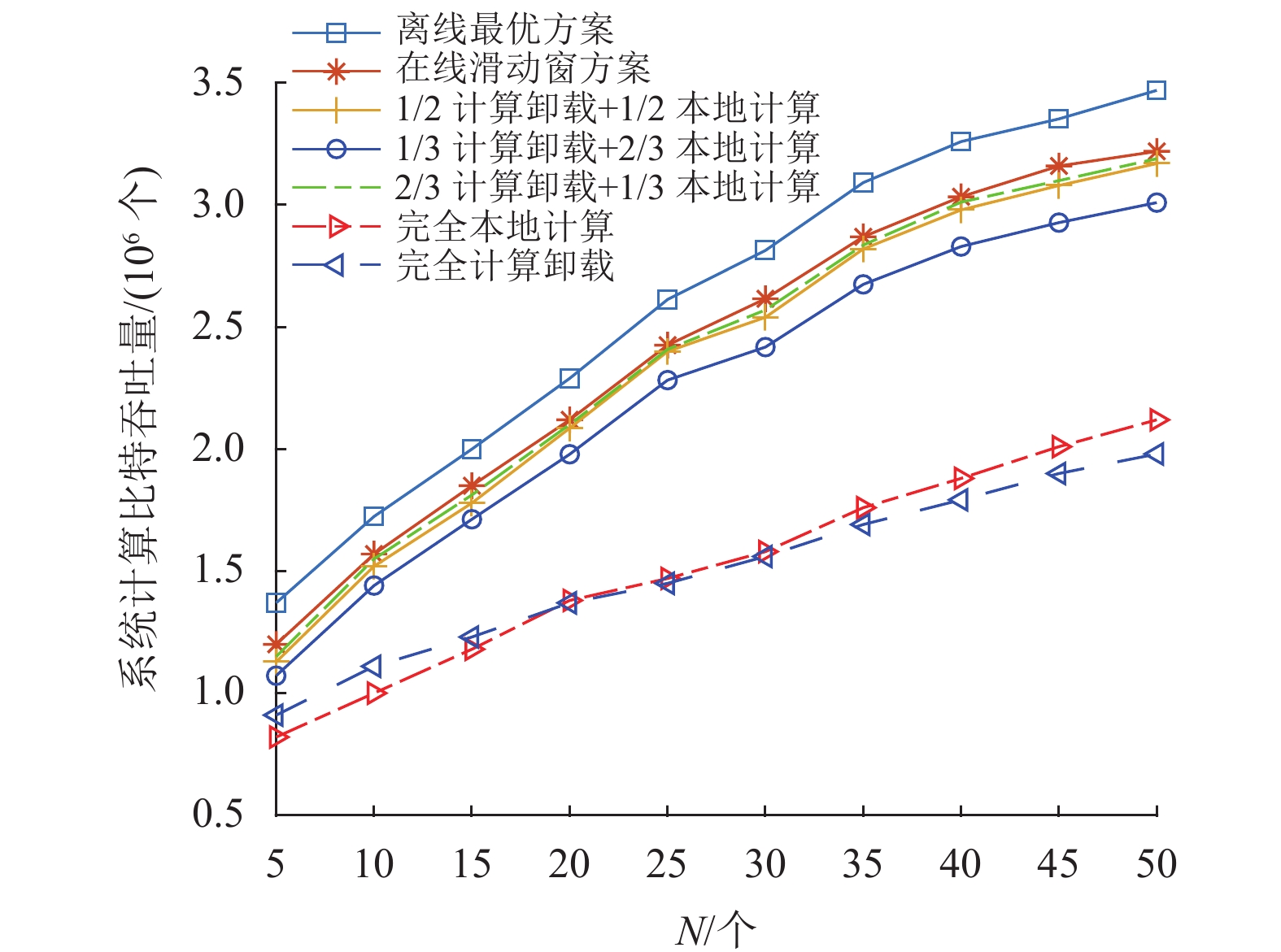
|
图 2 不同时隙数目N下的系统计算吞吐量性能 Figure 2 Computational throughput performance under different number N of time slots |
图3显示了不同时隙长度τ下的系统计算吞吐量性能曲线,其中时隙数目N=20,滑动窗时隙数目M=10,信道及能量状态信息预测误差的归一化方差均为0.2。随着时隙长度τ增大,所有方案的计算吞吐量均单调增大。本文提出的在线滑动窗方案优于已有的基准方案,并逐渐逼近离线最优方案。“2/3计算卸载+1/3本地计算”基准方案性能逼近在线滑动窗方案。类似于图2,3种比例混合计算的基准方案明显优于完全本地计算和完全计算卸载的基准方案,能取得更好的系统计算吞吐量性能。

|
图 3 不同时隙长度τ下的系统计算吞吐量性能 Figure 3 Computational throughput performance under different slot duration τ |
图4显示了不同用户设备数量K下的系统计算吞吐量性能曲线,其中滑动窗时隙数目M=10,信道状态信息预测误差的归一化方差
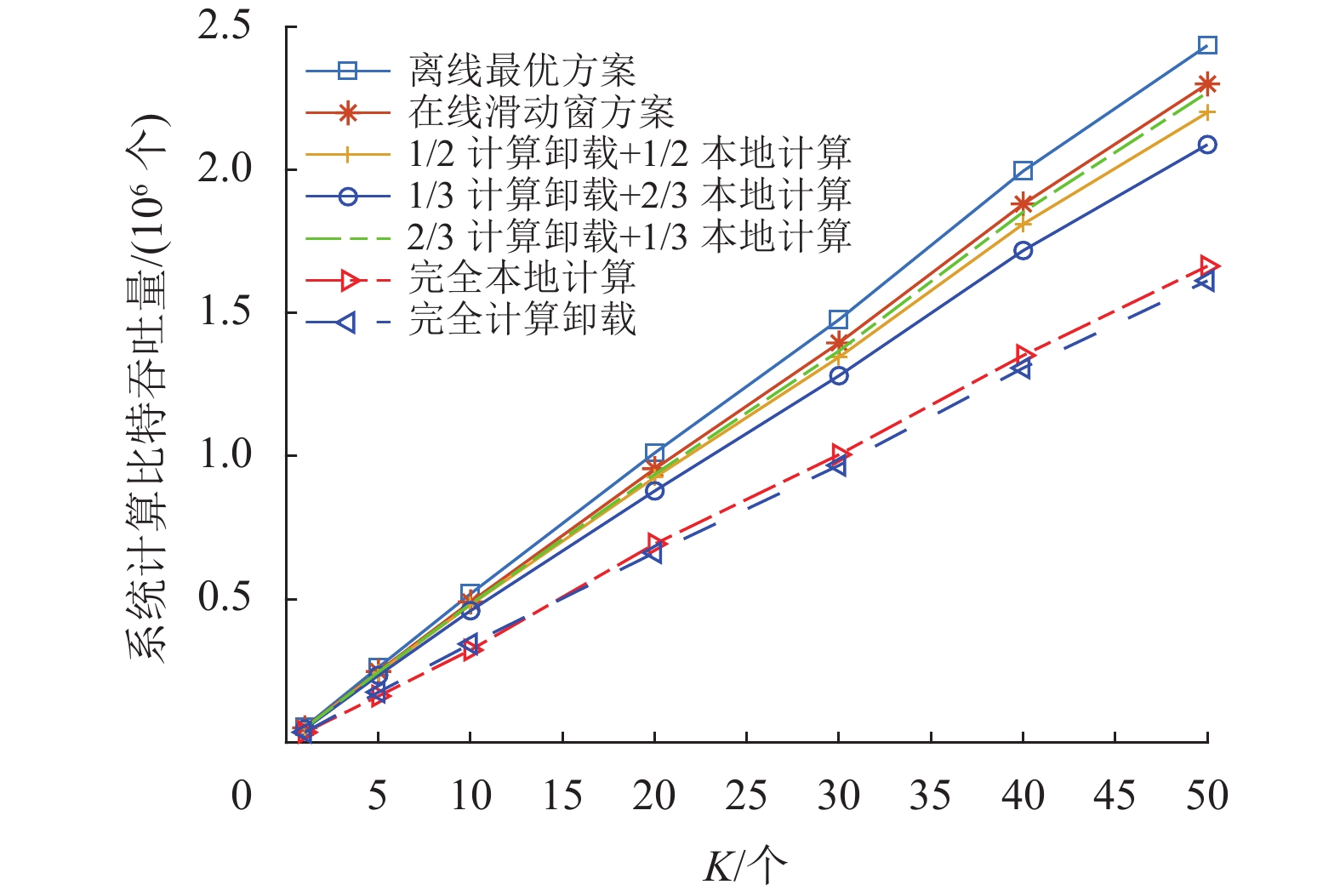
|
图 4 不同用户设备数量K下的系统吞吐量性能 Figure 4 Computation throughput performance under different user number K |
图5显示了滑动窗时隙数目M对系统计算吞吐量的影响,其中时隙数目N=20,信道/能量状态信息预测误差的归一化方差
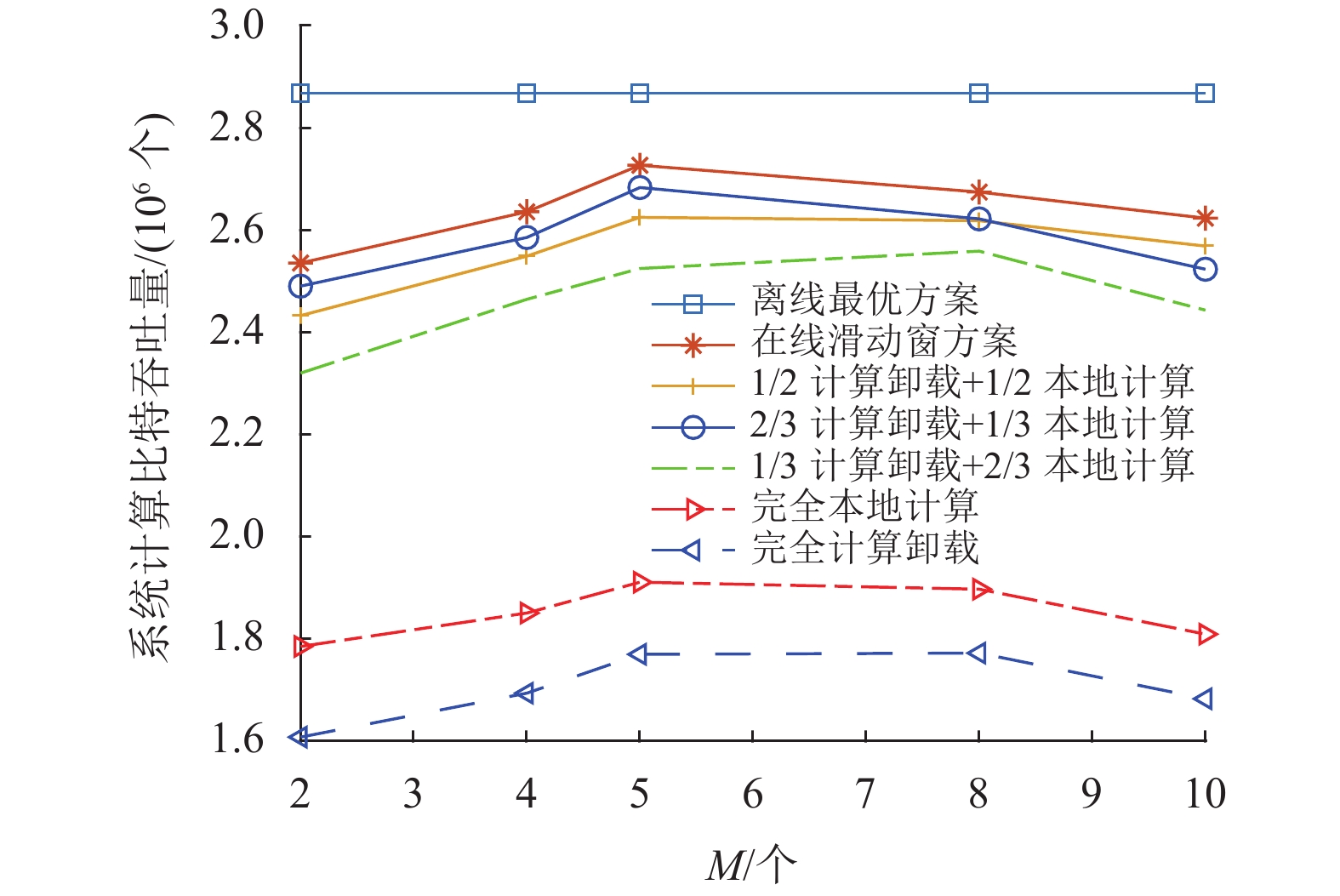
|
图 5 滑动窗时隙数目M对系统计算吞吐量的影响 Figure 5 Effect of sliding-window size M on computation throughput performance |
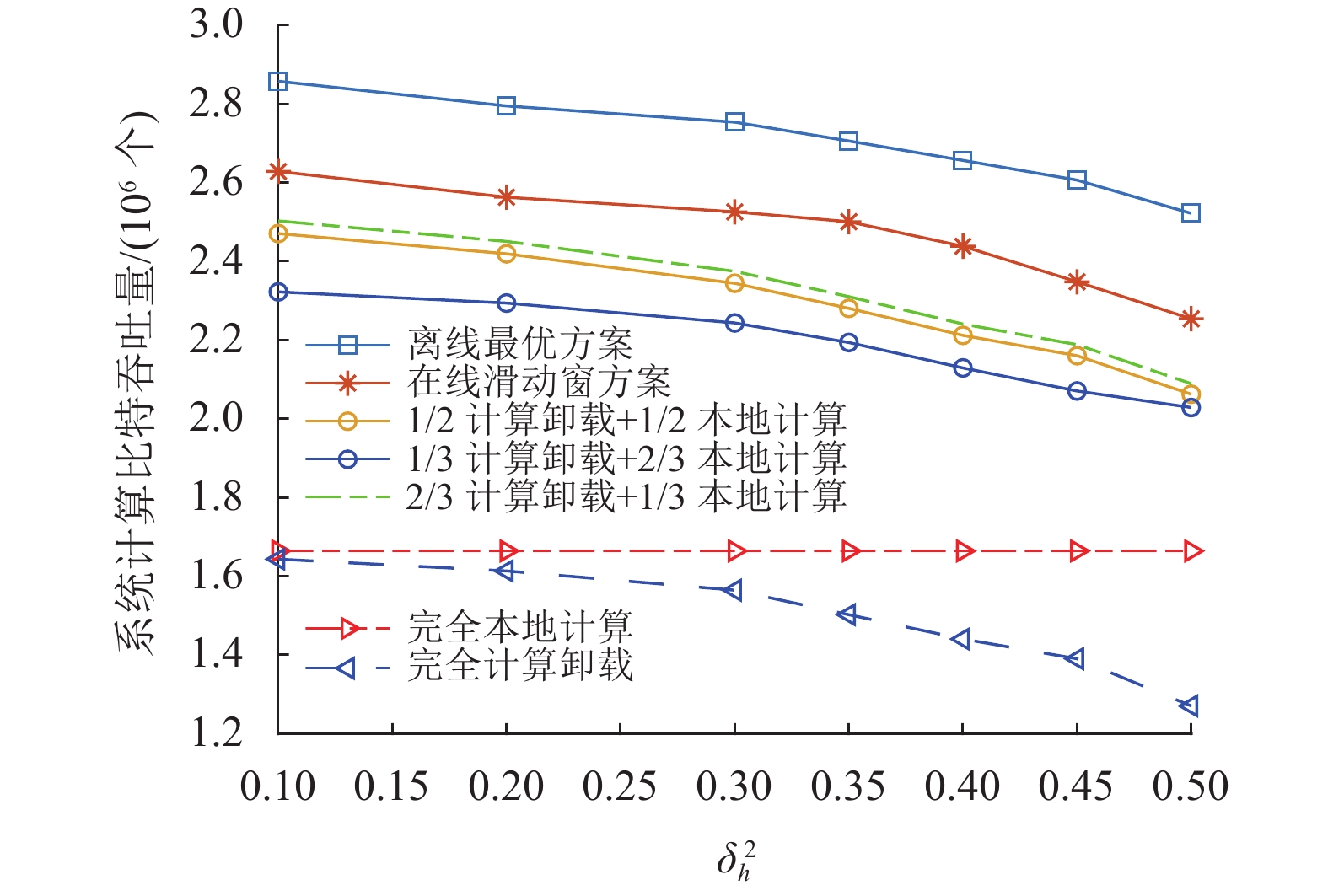
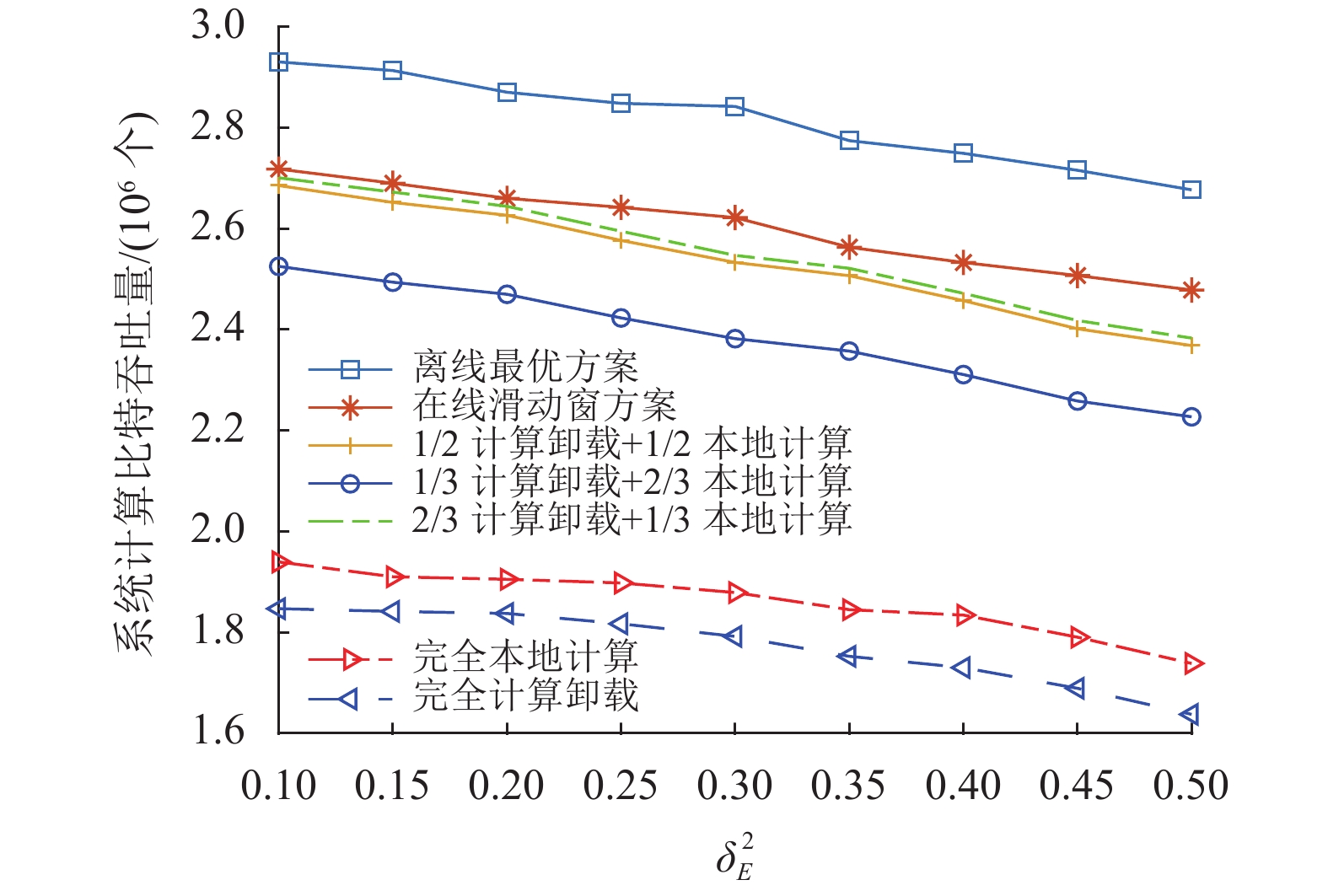
图6和图7分别显示了信道和能量状态信息预测误差情况下的系统计算吞吐量性能曲线,其中用户设备数目K=10,滑动窗时隙数目M=10,时隙总数目N=20,每个时隙长度τ=0.01 s。如图6所示,完全本地计算基准方案的系统计算吞吐量保持不变,而其他方案的系统性能随着信道状态信息预测误差的归一化方差增大而变差。这是因为信道状态信息预测的准确度决定了用户计算卸载的能耗情况。用户的本地计算无需信道状态信息,故完全本地计算方案的计算吞吐量与信道预测误差无关。如图7所示,随着能量预测误差的归一化方差的增大,所有方案的系统计算吞吐量性能显著变差,这表明了能量状态信息对于保证系统性能的重要性。综合图6和图7,与基准方案相比,本文所提出的在线滑动窗设计方案的系统计算吞吐量下降幅度较小,显示了更好的抗误差鲁棒性能。
|
图 6 系统计算吞吐量与信道状态预测误差关系 Figure 6 Computation throughput performance under different energy predication errors |
|
图 7 系统计算吞吐量与能量状态预测误差关系 Figure 7 Computation throughput performance under different energy predication errors |
本文研究了基于能量收集的多用户MEC系统的多时隙在线资源优化配置问题。在用户采集能量动态随机到达场景下,以系统计算吞吐量最大化为准则,根据用户能量收集和信道时变条件,联合优化了多用户本地计算和计算卸载的任务分配方案,推导了离线情况下的无线及计算资源最优管控结构。针对在能量因果关系及其未来信道/能量状态信息具有预测误差的情况下,基于离线最优结构求解一系列凸优化问题,提出了基于滑动窗的在线优化设计方案,实现了系统资源的动态管控。数值结果验证了本文提出在线滑动窗设计方案优于完全本地计算、完全计算卸载设计或固定能量分配的基准方案,具有显著的计算吞吐量性能增益。本文研究结果有望为多用户MEC系统的动态能量管理和资源集成提供一种新方法。
| [1] |
MACH P, BECVAR Z. Mobile edge computing: a survey on architecture and computation offloading[J].
IEEE Communications Surveys and Tutorials, 2017, 19(3): 1628-1656.
DOI: 10.1109/COMST.2017.2682318. |
| [2] |
MAO Y, YOU C, ZHANG J, et al. A survey on mobile edge computing: the communication perspective[J].
IEEE Communications Surveys and Tutorials, 2017, 19(4): 2322-2358.
DOI: 10.1109/COMST.2017.2745201. |
| [3] |
高志鹏, 尧聪聪, 肖楷乐. 移动边缘计算: 架构、应用和挑战[J].
中兴通讯技术, 2019, 25(3): 23-30.
GAO Z P, YAO C C, XIAO K L. Mobile edge computing: architecture, applications, and challenges[J]. ZTE Technology Journal, 2019, 25(3): 23-30. |
| [4] |
WANG F, XU J, DING Z. Multi-antenna NOMA for computation off loading in multiuser mobile edge computing systems[J].
IEEE Transactions on Communications, 2019, 67(3): 2450-2463.
DOI: 10.1109/TCOMM.2018.2881725. |
| [5] |
YOU C, HUANG K, CHAE H. Energy efficient mobile cloud computing powered by wireless energy transfer[J].
IEEE Journal on Selected Areas in Communications, 2016, 34(5): 1757-1771.
DOI: 10.1109/JSAC.2016.2545382. |
| [6] |
WANG F, XU J, WANG X, et al. Joint offloading and computing optimization in wire-less powered mobile-edge computing systems[J].
IEEE Transactions on Wireless Communications, 2018, 17(3): 1784-1797.
DOI: 10.1109/TWC.2017.2785305. |
| [7] |
BI S Z, ZHANG Y J. Computation rate maximization for wireless powered mobile-edge computing with binary computation offloading[J].
IEEE Transactions on Wireless Communications, 2018, 17(6): 4177-4190.
DOI: 10.1109/TWC.2018.2821664. |
| [8] |
WANG Y, SHENG M, WANG X, et al. Mobile edge computing: partial computation offloading using dynamic voltage scaling[J].
IEEE Transactions on Communications, 2016, 64(10): 4268-4282.
|
| [9] |
CHEN X, JIAO L, LI W, et al. Efficient multi-user computation offloading for mobile-edge cloud computing[J].
IEEE/ACM Transactions on Networking, 2016, 24(5): 2795-2808.
DOI: 10.1109/TNET.2015.2487344. |
| [10] |
AO Y, ZHANG J, LETAIEF K. Dynamic computation offloading for mobile-edge computing with energy harvesting devices[J].
IEEE Journal on Selected Areas in Communications, 2016, 34(12): 3590-3605.
DOI: 10.1109/JSAC.2016.2611964. |
| [11] |
XU J, CHEN L, REN S. Online learning for offloading and autoscaling in energy harvesting mobile edge computing[J].
IEEE Transactions on Cognitive Communications and Net- working, 2017, 3(3): 361-373.
DOI: 10.1109/TCCN.2017.2725277. |
| [12] |
LIN Q, WANG F, XU J. Optimal task offloading scheduling for energy efficient D2D cooperative computing[J].
IEEE Communications Letters, 2019, 23(10): 1816-1820.
DOI: 10.1109/LCOMM.2019.2931719. |
| [13] |
WANG F, XU J, CUI S. Optimal energy allocation and task offloading policy for wire-less powered mobile edge computing systems[J].
IEEE Transactions on Wireless Communications, 2020, 19(4): 2443-2459.
DOI: 10.1109/TWC.2020.2964765. |
| [14] |
ZHOU F, WU F, HU R, et al. Computation rate maximization in UAV-enabled wireless- powered mobile-edge computing systems[J].
IEEE Journal on Selected Areas in Communications, 2018, 36(9): 1927-1941.
DOI: 10.1109/JSAC.2018.2864426. |
| [15] |
OZEL O, TUTUNCUOGLU K, YANG J, et al. Transmission with energy harvesting nodes in fading wireless channels: optimal policies[J].
IEEE Journal on Selected Areas in Communications, 2011, 29(8): 1732-1743.
DOI: 10.1109/JSAC.2011.110921. |
| [16] |
HO C, ZHANG R. Optimal energy allocation for wireless communications with energy harvesting constraints[J].
IEEE Transactions on Signal Processing, 2012, 60(9): 4808-4818.
DOI: 10.1109/TSP.2012.2199984. |
| [17] |
MIN M, XIAO L, CHEN Y, et al. Learning based computation offloading for IoT devices with energy harvesting[J].
IEEE Transactions on Vehicular Technology, 2019, 68(2): 1930-1941.
DOI: 10.1109/TVT.2018.2890685. |
| [18] |
ZHANG G, CHEN Y, SHEN Z, et al. Distributed energy management for multiuser mobile edge computing systems with energy harvesting devices and QoS constraints[J].
IEEE Internet of Things Journal, 2019, 6(3): 4035-4048.
DOI: 10.1109/JIOT.2018.2875909. |
| [19] |
ZHANG J, DU J, SHEN Y, et al. Dynamic computation offloading with energy harvesting devices: a hybrid-decision-based deep reinforce- ment learning approach[J].
IEEE Internet of Things Journal, 2020, 7(10): 9303-9317.
DOI: 10.1109/JIOT.2020.3000527. |
| [20] |
BOYD S, VANDENBERGHE L. Convex optimization[M]. Cambridge: Cambridge University Press, 2004.
|
 2022, Vol. 39
2022, Vol. 39
