随着移动互联网的发展,出现了越来越多的计算密集型任务,例如增强现实、人脸识别和导航应用等[1]。与此同时,移动设备的综合能力也在显著提升。移动设备体积小、重量轻,相对于服务器来说,移动设备的计算能力和续航能力相对有限。当移动设备的处理能力不能有效地执行一个应用时,会降低用户的体验质量(Quality of Experience, QoE)。
移动云计算是解决上述问题的一种有效方式。通过将计算密集型的任务卸载到计算能力更强的远程服务器中进行处理,移动设备的能耗和任务的完成时间将会大大减少[2]。然而,云计算中心往往分布在离用户比较远、电价较低的地方,这样不可避免地带来了较长的通信时延。虽然移动云计算能够在很大程度上提升移动设备的综合性能,但它仍然不是最有效的一种解决方案。为此,Satyanarayanan等[3]提出了微云的概念:“微云是靠近用户侧的,可信的,与互联网有很好连接的一台计算资源丰富的计算机或者计算机集群”。移动设备可以通过无线网络接入微云,获取对应的计算、网络通信等服务。移动边缘计算的概念类似微云;此外,它能够支持多种无线网络(Wi-Fi,4G等)。移动边缘计算技术部署边缘服务器在靠近用户的网络边缘,为移动设备提供超低延迟的网络通信服务和云一样的计算能力。因此,相比移动云计算而言,移动边缘计算是一种更加有效的解决方案[4]。
目前,已有很多关于移动边缘计算环境下任务的调度问题的研究[5-9]。这些研究普遍关注移动边缘计算环境下的任务卸载和资源分配问题。问题的优化目标往往是移动设备的任务的完成时间、移动设备的能耗,或者是两者之间权衡。文献[10]针对只包含一个边缘服务器和一个移动设备的边缘计算环境,提出了一种基于李雅普诺夫优化的调度策略。该策略能够有效地减少任务完成时间,同时降低任务错误率。文献[11]针对包含一个边缘计算节点和多个物联网设备的移动边缘计算环境,考虑了信道的随机波动,提出了一种随机优化算法,降低了多个设备的平均能耗。Chen等[12]提出了一种基于博弈论的分布式算法,同时优化了移动设备的任务能耗和任务的完成时间两个目标。Mazouzi等[13]构建了一个包含多个微云的移动边缘计算环境模型,并针对该模型下的任务卸载问题,提出了一种微云选择策略用来减少移动设备的能耗。文献[14]针对包含多个边缘服务器和单个用户的移动边缘计算环境,提出了一种基于半定松弛算法的任务调度算法。文献[15]针对包含一种边缘计算节点和一个中心云的移动边缘计算环境,考虑单用户具有多个任务的情况,提出了一种基于粒子群算法的任务卸载策略。文献[16]针对包含多个边缘服务器和多个用户的移动边缘计算场景,考虑每个用户具有多个任务的情况,提出了一种基于深度学习的方法优化了任务的完成时间和移动设备的能耗的权衡值。
综上所述,这些工作并没有针对包含多个用户和多个边缘服务器的移动边缘计算环境,同时优化移动设备任务的完成时间、能耗以及通信成本3个目标。此外,本文考虑每个用户具有多个任务的场景。为了更好地解决上述问题,本文首先对该问题的优化目标进行了归一化,然后通过加权将多目标优化问题转化为一种单目标优化问题。最后,提出了一种基于多种群进化算法的任务调度算法。
1 移动边缘计算模型与问题描述 1.1 场景描述令Nq={1, 2, 3
|
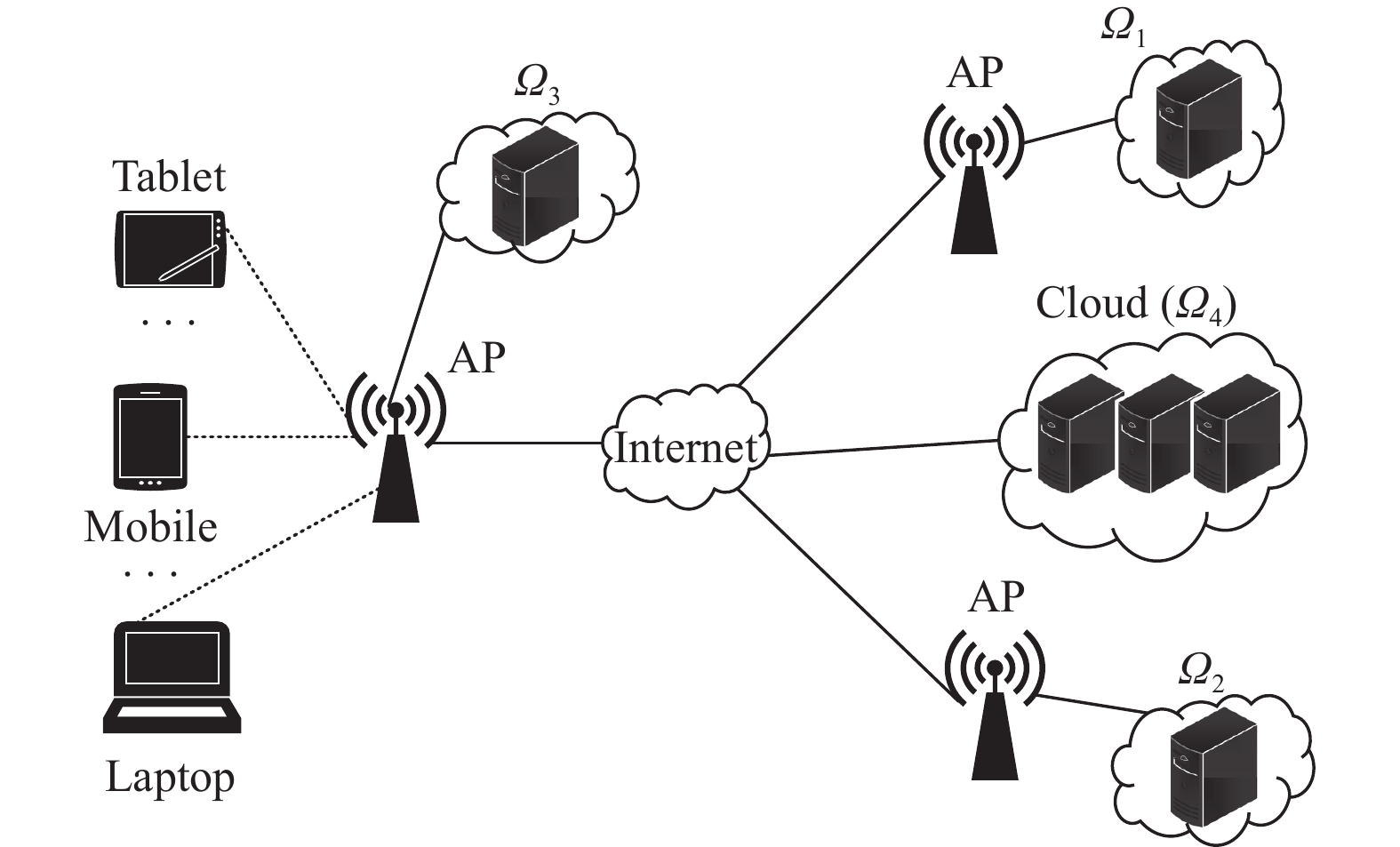
图 1 包含3个微云和一个中心云的移动边缘计算环境 Figure 1 An MEC environment with three cloudlets and a central cloud |
移动设备具有一定计算能力和通信能力,例如手机、平板、笔记本电脑等。
| $ {P_{{\text{cm}}}}(n) = \beta \times {({r_n})^3} $ | (1) |
式中:
移动设备通过无线通信网络与AP进行通信,AP通过高速有线网络与边缘服务器进行连接。相比于AP与移动设备之间的通信时延,AP与边缘服务器之间的时延很小。因此,本文忽略了AP与边缘服务器之间的通信时延。矩阵
令m表示边缘计算环境中每台移动设备运行任务的数量。
| $ W(t_n^i) = {D_{{\text{in}}}}{\text{(}}t_n^i) \times A $ | (2) |
式中:A是一个常量,表示任务负载与输入数据量之间的比例常数,单位为Cycle/byte。参考文献[17],将A设定为1900 Cycle/byte。
1.2 时间计算模型完成任务的时间包含移动设备的通信时间和任务的计算时间。L(n)表示
| $ {T}_{\text{com}}(n\text{,}i)=\left\{ \begin{array}{l}\dfrac{{D}_{\text{in}}({t}_{n}^{i})}{{B}_{\text{up}}}\text+\dfrac{{D}_{\text{out}}({t}_{n}^{i})}{{B}_{\text{dl}}}\text{, }{x}_{n}^{i}\text=L(n)\\ \text{0, }{x}_{n}^{i}\text{=0 }\\ \dfrac{{D}_{\text{in}}({t}_{n}^{i})}{{B}_{\text{up}}}\text+\dfrac{{D}_{\text{out}}({t}_{n}^{i})}{{B}_{\text{dl}}}\text+\dfrac{{D}_{\text{in}}({t}_{n}^{i})}{{B}_{{x}_{n}^{i},L(n)}}\text+\dfrac{{D}_{\text{out}}({t}_{n}^{i})}{{B}_{{x}_{n}^{i},L(n)}}\text{, }\small{\text{其他}}\end{array}\right. $ | (3) |
| $ {T_{{\text{pro}}}}(n,i) = W(t_n^i)/r(n,i,x_n^i) $ | (4) |
| $ {T}_{\text{up}}(n,i)=\left\{ \begin{array}{l}0,{x}_{n}^{i}=0\\ \dfrac{{D}_{\text{in}}({t}_{n}^{i})}{{B}_{\text{up}}},{x}_{n}^{i} > 0\end{array}\right. $ | (5) |
| $ {T}_{\text{dl}}(n,i)=\left\{ \begin{array}{l}0,{x}_{n}^{i}=0\\ \dfrac{{D}_{\text{out}}({t}_{n}^{i})}{{B}_{\text{dl}}},{x}_{n}^{i} > 0\end{array}\right. $ | (6) |
| $ T(n,i) = {T_{{\text{com}}}}{\text{(}}n{\text{,}}i{\text{)}} + {T_{{\text{pro}}}}{\text{(}}n{\text{,}}i{\text{)}} $ | (7) |
| $ T(n) = \sum\nolimits_{i = 1}^m {T(n,i)} $ | (8) |
| $ \overline T = \sum\nolimits_{n = 1}^u {T(n)/u} $ | (9) |
式中:u为移动设备的数量。
1.3 能耗计算模型移动设备的能耗包含3个部分:计算能耗、通信能耗以及空闲能耗。
| $ {E}_{\text{loc}}(n,i)=\left\{ \begin{array}{l}\beta \times {r}_{n}\times {r}_{n}\times W\text{(}{t}_{n}^{i}\text{), }{x}_{n}^{i}\text{=0}\\ \text{0, }{x}_{n}^{i} > 0\end{array}\right. $ | (10) |
| $ {E_{{\text{loc}}}}(n) = \sum\nolimits_{i = 1}^m {{E_{{\text{loc}}}}(n,i)} $ | (11) |
| $ {E_{{\text{up}}}}(n,i) = {P_{{\text{up}}}} \times {T_{{\text{up}}}}(n,i) $ | (12) |
| $ {E_{{\text{dl}}}}(n,i) = {P_{{\text{dl}}}} \times {{{T}}_{{\text{dl}}}}(n,i) $ | (13) |
| $ {E_{{\text{up}}}}(n) = \sum\nolimits_{i = 1}^m {{E_{{\text{up}}}}(n,i)} $ | (14) |
| $ {E_{{\text{dl}}}}(n) = \sum\nolimits_{i = 1}^m {{E_{{\text{dl}}}}(n,i)} $ | (15) |
| $ E(n) = {E_{{\text{dl}}}}(n) + {E_{{\text{up}}}}(n) + {E_{{\text{loc}}}}(n) $ | (16) |
| $ \overline E = \sum\nolimits_{n = 1}^u {E(n)/u} $ | (17) |
| $ C(n,i)=\left\{ \begin{array}{l}{P}_{c}\times ({D}_{\text{in}}({t}_{n}^{i})+{D}_{\text{out}}({t}_{n}^{i})),\text{ }{x}_{n}^{i} > 0\\ 0,{x}_{n}^{i}=0\end{array} \right.$ | (18) |
| $ C(n) = \sum\nolimits_{i = 1}^m {C(n,i)} $ | (19) |
| $ \overline C = \sum\nolimits_{n = 1}^u {C(n)/u} $ | (20) |
为了避免各个优化目标量纲不一致的问题,本文对当前的多个优化目标进行了归一化处理。此外,用户对于任务的完成时间、能耗、通信成本关注程度不同。线性加权是权衡多个目标的一种常用处理方式[18]。一个目标的权重因子越大,表示用户对这个目标的关注程度越高。例如,当用户想要花费更少的通信成本时,就会将通信成本的权重因子设置为较大的值。本文采用线性加权的方式该多目标优化问题转化成单目标优化问题。建立模型表示该问题,如式(21)所示。
| $ \mathop {{\text{min}}}\limits_{{\boldsymbol{X,R}}} {\text{: }}f\left( {{\boldsymbol{X}},{\boldsymbol{R}}} \right) = {w_1} \times \overline T /{\overline T _{{\text{loc}}}} + {w_2} \times \overline E /{\overline E _{{\text{loc}}}} + {w_3} \times \overline C /{\overline C _{{\text{ao}}}} $ | (21) |
约束条件为
| $ \begin{array}{l}(\text{a})\text{ }{x}_{n}^{i}\in \left\{0\right\}\cup {N}_{\text{|}{\mathit{\Omega}} \text{|}}\\ \text{(b) }r(n,i,{x}_{n}^{i})\leqslant {r}_{n}\text{, }\small{\text{当}}{x}_{n}^{i}\text=0\\ \text{(c) }{{\displaystyle \sum }_{i=1}^{m}{{\displaystyle \sum} _{n=1}^{u}r(n,i,{x}_{n}^{i})}\leqslant {f}_{{x}_{n}^{i}}}\text{, }\forall {x}_{n}^{i}\in {N}_{\text{|}{\mathit{\Omega}} \text{|}}\end{array} $ |
式中:
编码方式主要2种: 实数编码和二进制编码。二进制编码方式一般适用于问题的解精度较小的问题。对于精度较高和维度较大的问题,二进制编码会占用大量存储空间。为了更好地求解提出的问题,采用实数编码的方式。
2.1.3 种群更新进化种群通过一定更新方式迭代寻优,从而得到问题的解。例如,遗传算法通过交叉、变异和选择更新种群,从而得到问题的最优解或者次优解。
2.1.4 移民操作简单来说,移民操作就是使用当前子种群中的最优个体替换掉目标子种群中的适应度最差的个体。移民操作能够实现子种群之间的信息交流,增强算法的全局寻优能力,从而避免算法过早收敛。
2.2 不同算法的更新流程 2.2.1 基于精英保留的遗传算法遗传算法(Genetic Algorithm, GA)是一种通过模拟自然进化过程探索最优解的方法。基于精英保留的遗传算法(Elitism Genetic Algorithm, EGA)在GA的基础上增加了精英保留机制[18]。EGA算法种群更新操作如下。
(1) 交叉:交叉是为了将两个个体人工结合生成新的个体。模拟二进制交叉算子对连续优化问题具有很好的性能[19]。因此,采用模拟二进制交叉算子。
(2) 变异:变异是对现有种群中的个体进行随机调整,这可以改变原始的个体特性,从而引入新的特征。本算法采用多项式变异算子作为变异算子[20]。
(3) 选择:选择操作用来模拟生物界“物竞天择,适者生存”的自然选择机制。从每次迭代产生的个体中,选择适应度函数值比较好的个体作为下一代迭代的父代种群。本文使用轮盘赌选择算子。
(4) 精英保留:种群中迄今适应度最好的个体不参与种群的更新迭代过程,直接保留进入下一代父代种群。
2.2.2 粒子群算法粒子群(Particle Swarm Optimization, PSO)算法是一种具有个体改进、种群合作和竞争机制的启发式算法,它受启发于自然界中成群鸟类或成群鱼类的捕食行为[21]。PSO算法更新操作主要包括速度更新和位置更新。
| $ {{\boldsymbol{Q}}_l}(h + 1) = {{\boldsymbol{Q}}_l}(h) + {{\boldsymbol{V}}_l}(h + 1){\text{ }} $ | (22) |
| $ \begin{split} {{\boldsymbol{V}}_l}(h + 1) =& w \times {{\boldsymbol{V}}_l}(h) + {c_1} \times {G_1} \times {\text{ }}({{\boldsymbol{p}}_{l,{\rm{best}}}}(h) - {{\boldsymbol{Q}}_l}(h)) +\\& {c_2} \times {\text{ }}{G_2} \times ({{\boldsymbol{p}}_{{\rm{gbest}}}}(h) - {{\boldsymbol{Q}}_l}(h)) \end{split} $ | (23) |
| $ w{\text{ = }}{w_{\max }}{{ - }}\frac{{{w_{\max }} - {w_{\min }}}}{{{h_{\max }}}} \times h $ | (24) |
式中:
布谷鸟 (Cuckoo Search, CS) 算法是一种用来解决优化问题的元启发式算法。该算法模拟了布谷鸟独特的寻窝产卵的行为,并引入了自然界一些鸟类和果蝇的Levy飞行机制[22]。布谷鸟算法更新操作主要包括更新鸟巢和丢弃鸟蛋。
(1) 更新鸟巢。种群中个体的位置更新如式(25)所示。
| $ {{\boldsymbol{Q}}_l}(h + 1) = {{\boldsymbol{Q}}_l}(h) + \alpha \times Y(\lambda ) $ | (25) |
式中:
(2) 丢弃鸟蛋。表示鸟蛋被丢弃的概率。遍历当前种群中的个体,以概率
本文对不同约束采用了不同处理方式:对于约束(a), 在算法流程中如果有元素超出了边界,使用边界值进行替代。对于约束(b), 如果
| $ g({\boldsymbol{X}},{\boldsymbol{R}}) = \sum\nolimits_{x_n^i \in {\mathit{\Lambda}} }^{} {\left(\sum\nolimits_{i = 1}^m {\sum\nolimits_{n = 1}^u {r(n,i,x_n^i)} } - {f_{x_n^i}}\right)} $ | (26) |
| $ {\text{ }}H({\boldsymbol{X}},{\boldsymbol{R}}) = \theta (q({\boldsymbol{X}},{\boldsymbol{R}})) \times {(q({\boldsymbol{X}},{\boldsymbol{R}}))^{\psi (q({\boldsymbol{X}},{\boldsymbol{R}}))}}{\text{ }} $ | (27) |
| $ {\text{ }}q({{\boldsymbol{X}}},{{\boldsymbol{R}}}){\text{ = }}\max \{ 0,g({{\boldsymbol{X}}},{{\boldsymbol{R}}})\} {\text{ }} $ | (28) |
| $ \psi (q({{\boldsymbol{X}}},{{\boldsymbol{R}}})) = \left\{ \begin{gathered} 1,{\boldsymbol{ }}q({{\boldsymbol{X}}},{{\boldsymbol{R}}}) < 1 \hfill \\ 2,{\boldsymbol{ }}q({{\boldsymbol{X}}},{{\boldsymbol{R}}}) \geqslant 1 \hfill \\ \end{gathered} \right.{\text{ }} $ | (29) |
| $ \theta (q(\boldsymbol{X},\boldsymbol{R}))=\left\{ \begin{array}{l}5, q(\boldsymbol{X},\boldsymbol{R}) < 0.001\\ 10, 0.001\leqslant q(\boldsymbol{X},\boldsymbol{R})\leqslant 0.1\\ 15\text{, }\text{0}{.1 < }q(\boldsymbol{X},\boldsymbol{R})\leqslant 1\\ 30,\text{ }\small{\text{其他}}\end{array}\right. $ | (30) |
| $ \delta (h) = h\sqrt h {\text{ }} $ | (31) |
式(26)中,
| $ F({\boldsymbol{X}},{\boldsymbol{R}}) = f({\boldsymbol{X}},{\boldsymbol{R}}) + \delta (h) \times H({\boldsymbol{X}},{\boldsymbol{R}}) $ | (32) |
步骤1 初始化算法参数。按照算法参数初始化3个子种群。按照式(27)~(31)初始化约束,并设置h=1。
步骤2 对种群1进行模拟二进制交叉和多项式变异。
步骤3 按照式(32)对种群1进行适应度计算,将最优个体保存为种群1的第一个个体。
步骤4 按照式(22)对种群2的每个个体进行更新。
步骤5 按照式(25),对种群3中的每一个个体进行更新得到新种群,如果新种群的个体的适应度函数值小于种群3对应个体的适应度函数值,使用新种群的个体替换掉种群3中的对应个体。
步骤6 遍历种群3,以一定的概率
步骤7 在种群1~3之间进行移民操作。
步骤8 按照式(32)计算整个种群的适应度,获得整个种群中的最优个体,将种群1的第一个个体替换为整个种群的最优个体。
步骤9 按照式(27)~(31)更新约束。
步骤10 h=h+1;如果h < hmax,返回步骤2,否则停止迭代。
3 实验 3.1 实验环境参数设置计算机配置:CPU为Core(TM) i9-9900K CPU@3.60 GHz型号, 内存容量32 GB。表1为移动边缘计算环境参数表。实验考虑包含3个异构微云和一个中心云的移动边缘计算环境。参考文献[16],将3个微云的处理频率分别设置为3.5,5,6.5 GHz。将中心云的处理速率设置为10 GHz。参考文献[24],将移动设备的通信成本
| 表 1 MEC环境参数 Table 1 MEC environment parameters |
EGA算法参数设置为:种群规模为60,交叉概率为0.8,变异概率为0.02。
CS算法参数设置为:种群规模为60,丢弃概率
GA-PSO-CS算法参数设置为:对于种群1,种群规模为15,交叉概率为0.8, 变异概率0.005。对于种群2,种群规模15,
为了更好地对比提出的GA-PSO-CS算法的性能,选择CS算法和EGA算法作为对比算法。为了保证实验结果的公平性,每次运行算法时设置迭代次数为200,独立运行每个算法20次,取结果的平均值。为了更好地说明算法的有效性,针对三组不同优化目标权重因子设置进行了实验。权重因子设置如下:
(I)
(II)
(III)
|
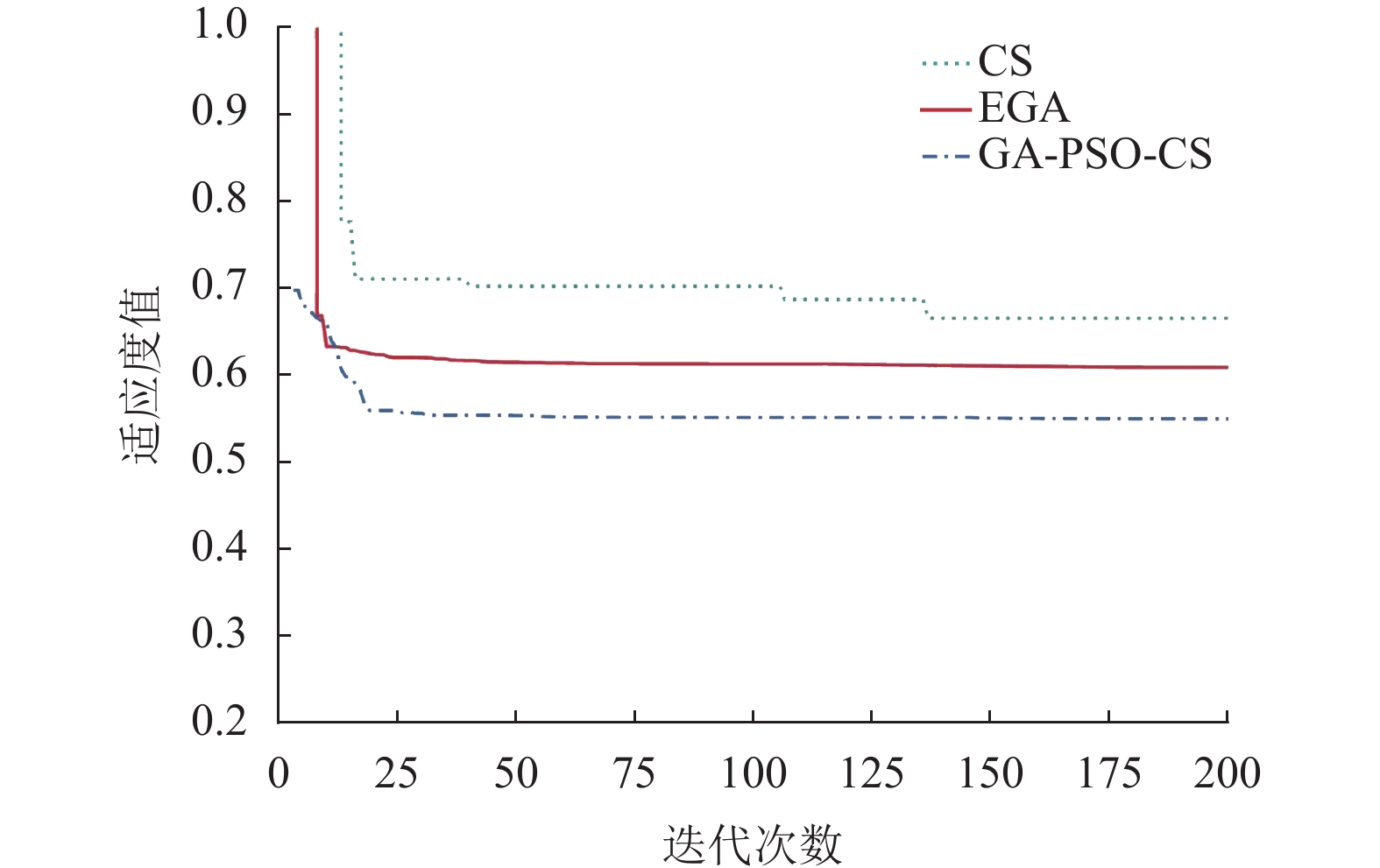
图 2 设置(I)下的不同算法的收敛结果 Figure 2 Convergence of different algorithms under setting (I) |
|
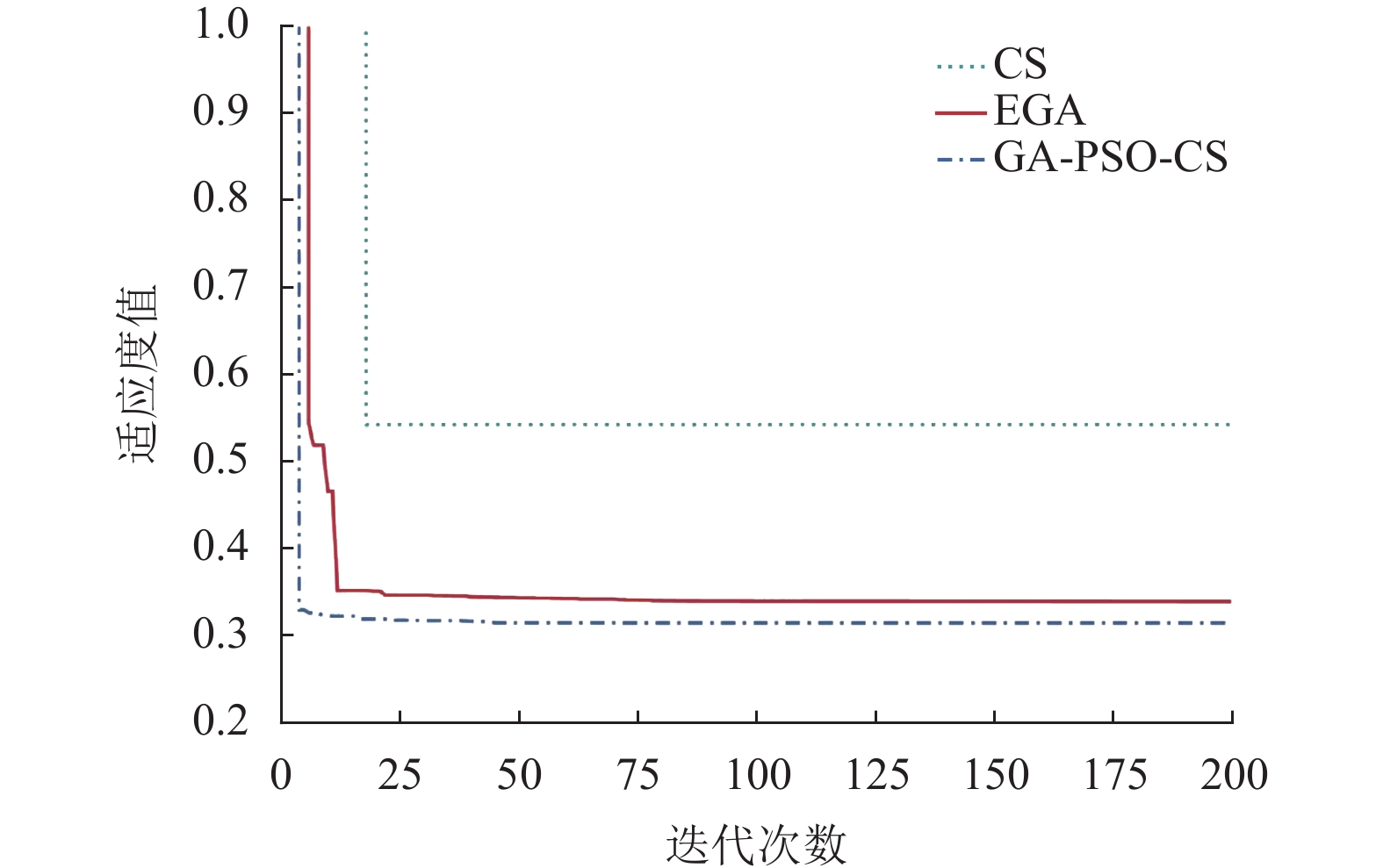
图 3 设置(II)下的不同算法的收敛结果 Figure 3 Convergence of different algorithms under setting (II) |
|
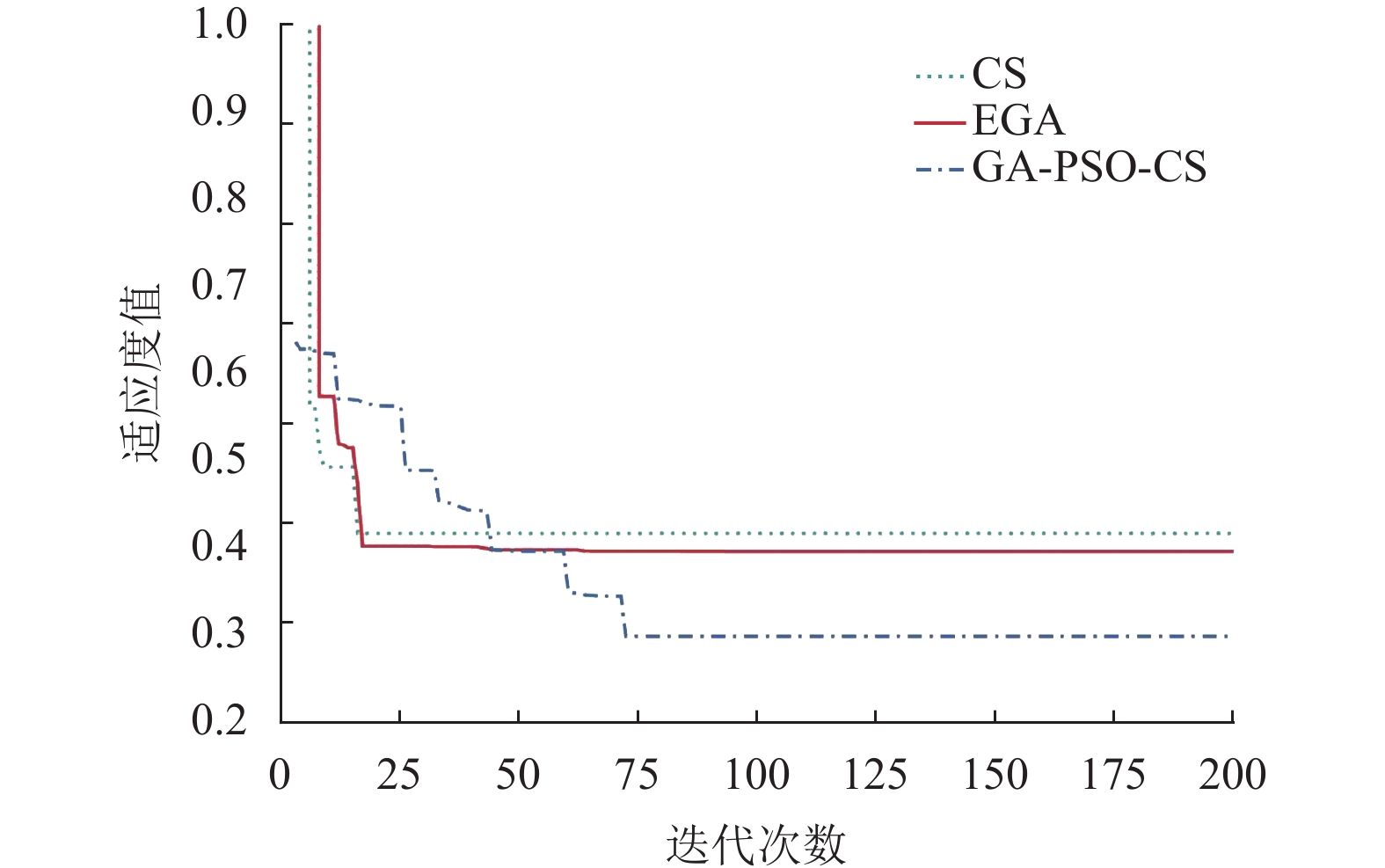
图 4 设置(III)下的不同算法的收敛结果 Figure 4 Convergence of different algorithms under setting (III) |
表2是设置(I)下不同算法收敛时的平均任务完成时间、平均能耗、平均通信成本以及对应的综合成本。由表2可以看出,GA-PSO-CS能够得到最小的综合成本、平均任务完成时间和平均能耗。设置(II)和(III)下的结果不再展示。
| 表 2 设置(I)下的不同算法的目标对比 Table 2 Comparison of objectives of different algorithms under setting (I) |
从图2~4可以看出,GA-PSO-CS算法能够得到更优的适应度值,这表明该算法具有更好的全局寻优结果。在设置(I)下,GA-PSO-CS最先收敛且收敛结果优于CS和EGA。在设置(II)下,CS最先收敛,但很快陷入局部最优。GA-PSO-CS收敛速度适中,但收敛结果优于CS和EGA。在设置(III)下,GA-PSO-CS收敛速度最慢,但能够得到最好的收敛结果。综上所述,GA-PSO-CS相比于EGA和CS,具有更好的收敛性能。
3.3.2 综合指标分析为了评估算法的性能,选取20次收敛结果的平均值、最优值、最差值以及标准差作为算法的评估指标。表3对应设置(I)~(III)下不同算法的综合指标结果。
| 表 3 不同设置下的不同算法的收敛结果指标对比 Table 3 Comparison of convergence result indicators of different algorithms under different settings |
从表3可以看出,在设置(I)和(II)下,GA-PSO-CS算法得到的收敛结果的最优值、平均值、最差值均优于EGA和CS。在设置(III)下,GA-PSO-CS算法的收敛结果具有最好的最优值、平均值、最差值以及标准差。综上所述,GA-PSO-CS算法具有最强的收敛性,且具有较强的稳定性。
4 总结与展望本文针对包含多个异构微云和一个中心云的移动边缘计算环境下任务卸载与资源分配问题,考虑了多用户、多任务的场景。提出了在满足资源约束情况,同时优化包含任务的完成时间、移动设备的能耗以及移动设备的平均通信成本多个目标的任务调度问题。针对该问题,提出了一种基于多种群进化算法的任务调度算法。该算法通过合理地对任务卸载位置和计算资源分配进行决策,提升了移动设备的综合性能。仿真实验结果表明,相比于CS和EGA,提出的改进多种群进化算法GA-PSO-CS具有更好的综合性能。在未来工作中,笔者将针对有数据依赖的应用任务进行研究,同时使用深度强化学习或者基于单解的启发式算法求解问题。
| [1] |
MAHMOODI S E, UMA R N, SUBBALAKSHMI K P. Optimal joint scheduling and cloud offloading for mobile applications[J].
IEEE Transactions on Cloud Computing, 2019, 7(2): 301-313.
DOI: 10.1109/TCC.2016.2560808. |
| [2] |
CHEN M, GUO S, LIU K, et al. Robust computation offloading and resource scheduling in cloudlet-based mobile cloud computing[J].
IEEE Transactions on Mobile Computing, 2021, 20(5): 2025-2040.
DOI: 10.1109/TMC.2020.2973993. |
| [3] |
SATYANARAYANAN M, BAHL P, CACERES R, et al. The case for VM-based cloudlets in mobile computing[J].
IEEE Pervasive Computing, 2009, 8(4): 14-23.
DOI: 10.1109/MPRV.2009.82. |
| [4] |
MACH P, BECVAR Z. Mobile edge computing: a survey on architecture and computation offloading[J].
IEEE Communications Surveys & Tutorials, 2017, 19(3): 1628-1656.
|
| [5] |
XU Y, GU B, HU R Q, et al. Joint computation offloading and radio resource allocation in MEC-based wireless-powered backscatter communication networks[J].
IEEE Transactions on Vehicular Technology, 2021, 70(6): 6200-6205.
DOI: 10.1109/TVT.2021.3077094. |
| [6] |
MUKHERJEE A, DE D, ROY D G. A power and latency aware cloudlet selection strategy for multi-cloudlet environment[J].
IEEE Transactions on Cloud Computing, 2019, 7(1): 141-154.
DOI: 10.1109/TCC.2016.2586061. |
| [7] |
BI J, YUAN H, DUANMU S, et al. Energy-optimized partial computation offloading in mobile-edge computing with genetic simulated-annealing-based particle swarm optimization[J].
IEEE Internet of Things Journal, 2021, 8(5): 3774-3785.
DOI: 10.1109/JIOT.2020.3024223. |
| [8] |
BOZORGCHENANI A, MASHHADI F, TARCHI D, et al. Multi-objective computation sharing in energy and delay constrained mobile edge computing environments[J].
IEEE Transactions on Mobile Computing, 2021, 20(10): 2992-3005.
DOI: 10.1109/TMC.2020.2994232. |
| [9] |
LI H, XU H, ZHOU C, et al. Joint optimization strategy of computation offloading and resource allocation in multi-access edge computing environment[J].
IEEE Transactions on Vehicular Technology, 2020, 69(9): 10214-10226.
DOI: 10.1109/TVT.2020.3003898. |
| [10] |
MAO Y, ZHANG J, LETAIEF K B. Dynamic computation offloading for mobile-edge computing with energy harvesting devices[J].
IEEE Journal on Selected Areas in Communications, 2016, 34(12): 3590-3605.
DOI: 10.1109/JSAC.2016.2611964. |
| [11] |
CHEN Y, ZHANG N, ZHANG Y, et al. Energy efficient dynamic offloading in mobile edge computing for internet of things[J].
IEEE Transactions on Cloud Computing, 2021, 9(3): 1050-1060.
DOI: 10.1109/TCC.2019.2898657. |
| [12] |
CHEN X, JIAO L, LI W, et al. Efficient multi-user computation offloading for mobile-edge cloud computing[J].
IEEE/ACM Transactions on Networking, 2015, 24(5): 2795-2808.
|
| [13] |
MAZOUZI H, ACHIR N, BOUSSETTA K. Dm2-ecop: an efficient computation offloading policy for multi-user multi-cloudlet mobile edge computing environment[J].
ACM Transactions on Internet Technology (TOIT), 2019, 19(2): 1-24.
|
| [14] |
DINH T Q, TANG J, LA Q D, et al. Offloading in mobile edge computing: task allocation and computational frequency scaling[J].
IEEE Transactions on Communications, 2017, 65(8): 3571-3584.
|
| [15] |
WU J, CAO Z, ZHANG Y, et al. Edge-cloud collaborative computation offloading model based on improved partical swarm optimization in MEC[C]//IEEE 25th International Conference on Parallel and Distributed Systems (ICPADS). TianJin: IEEE, 2019: 959-962.
|
| [16] |
HUANG L, FENG X, ZHANG L, et al. Multi-server multi-user multi-task computation offloading for mobile edge computing networks[J].
Sensors, 2019, 19(6): 1446.
DOI: 10.3390/s19061446. |
| [17] |
CHEN M H, LIANG B, DONG M. Joint offloading decision and resource allocation for multi-user multi-task mobile cloud[C]//2016 IEEE International Conference on Communications (ICC). Kuala Lumpur: IEEE, 2016: 1-6.
|
| [18] |
杨天, 杨军. 移动边缘计算中的卸载决策与资源分配策略[J].
计算机工程, 2021, 47(2): 19-25.
YANG T, YANG J. Offloading decision and resource allocation strategy in mobile edge computing[J]. Computer Engineering, 2021, 47(2): 19-25. |
| [19] |
DEB K, AGRAWAL R B. Simulated binary crossover for continuous search space[J].
Complex Systems, 1995, 9(2): 115-148.
|
| [20] |
DEB K, GOYAL M. A combined genetic adaptive search (GeneAS) for engineering design[J].
Computer Science and Informatics, 1996, 26(4): 30-45.
|
| [21] |
KENNEDY J, EBERHART R. Particle swarm optimization[C]// Proceedings of International Conference on Neural Networks (ICNN'95). Perth: IEEE, 1995, 4: 1942-1948.
|
| [22] |
YANG X S, DEB S. Cuckoo search via Lévy flights[C]//2009 World Congress on Nature & Biologically Inspired Computing (NaBIC). Coimbatore: IEEE, 2009: 210-214.
|
| [23] |
PARSOPOULOS K E, VRAHATIS M N. Particle swarm optimization method for constrained optimization problems[J].
Intelligent Technologies–Theory and Application:New Trends in Intelligent Technologies, 2002, 76(1): 214-220.
|
| [24] |
ZHANG C, LIU Z, GU B, et al. A deep reinforcement learning based approach for cost- and energy-aware multi-flow mobile data offloading[J].
IEICE Transactions on Communications, 2018, E101.B(7): 1625-1634.
DOI: 10.1587/transcom.2017CQP0014. |
 2022, Vol. 39
2022, Vol. 39
