概率规划[1]是人工智能主要的研究方向之一。概率规划问题的特点是并行性和概率性。并行性表示动作可以并行执行,概率性表示动作的效果具有概率性[2]。并且概率规划更加注重求解的过程,即最大累计奖励值,所以被广泛用于现实问题的处理当中。对于现实问题中动作执行需要一定时间的问题,使用考虑动作执行时间的时态规划[3]对该类问题进行求解。文献[4]将概率规划用于股票指数模拟与分析当中,使用基于抽样的方法进行模拟,最终的模拟效果可以贴近真实的股票变化趋势。
概率规划描述的是一类具有大状态空间的马尔可夫决策问题,文献[5]研究了概率规划中计算的复杂性。而蒙特卡洛方法[6-7]是能够接近最优解的方法之一,文献[8]使用了蒙特卡洛规划处理大规模部分可观察的马尔科夫决策问题。目前主流的规划器都是基于UCT[9](Upper Confidence Bounds on Trees)算法实现的。UCT将强盗算法的上置信区间应用到基于蒙特卡洛树搜索的规划算法中。文献[10]使用受UCT算法启发的随机搜索策略,在复杂空间中可以渐进收敛。当前表现最好的规划器为SOGBOFA[11],其使用聚合模拟推导出计算图,并通过基于梯度的搜索选择最优动作,可以动态平衡蒙特卡洛搜索和梯度搜索,加快收敛速度同时提高求解性能。文献[12]提出了一种概率机器人规划框架,使用一系列的生成程序构建领域文件,并在框架中集成了最新的SOGBOFA规划器,进一步提高了概率规划和机器人系统的集成度。
众包技术[13]早已在商业上实现,主要的思想是将任务分派出去,利用不同的个体独立处理任务。受此启发将众包概念和概率规划结合,通过集成多个规划器处理复杂的概率规划问题。由于概率规划中存在约束条件,拆分和合并规划任务非常困难,所以对于每个规划器来说,都需要独立处理完整的规划任务,即根据输入状态计算出可行动作集。
目前概率规划问题的求解存在很多的困难和挑战。概率规划问题具有并行和概率的特性,这导致其具有很大的状态空间;随着领域实例规模的增大,状态空间也会呈指数的趋势增大。同时越复杂领域,验证动作的约束条件和状态的演化过程也越慢,使得基于模拟的算法无法获取最优策略[14]。由于概率规划的动作是并行的,并且需要统一进行动作集的约束检查,所以很难拆分概率规划问题。同时,概率规划领域现有的规划器都是单线程求解,也缺乏众包结合概率规划问题的相关研究。针对以上问题本文提出了基于蒙特卡洛树搜索的众包概率规划算法,主要的工作如下:
(1) 提出了一个通用的众包概率规划框架,通过集成多个规划器共同处理规划问题。该框架可以整合多个规划器的信息,并将最优解信息共享给所有规划器,提高求解效率。
(2) 提出了一种基于蒙特卡洛树搜索的评价算法,使用改进的蒙特卡洛采样构建前瞻树,并计算状态−动作对的评价值,用于选择最优动作。
(3) 对众包框架和评价算法进行优化操作,提高框架的扩展性和求解效率。
1 概率规划第四届国际规划比赛首次引入了概率规划的比赛项目[15],即国际概率规划比赛(International Probabilistic Planning Competitions,IPPC),在原有状态转移的过程中加入了随机性。概率规划描述的是抽象的马尔科夫决策过程(Factored Markov Decision Process,Factored MDP)[16]。使用六元组T=<V, A, P, R, h, S0>[17]来表示Factored MDP问题,其中V为状态集;S0为初始状态;h为迭代步数,可为任意实数;P为转移函数用于计算动作A由状态S转移至S'的概率;R为奖励值计算函数[18]。概率规划的目标是在完成指定次数的迭代后最大化累计奖励值表示为
| $ {\text{maximize}}\sum\nolimits_{h = 0}^{{\text{horizon}}} {{r_h}} $ | (1) |
其中:rh为迭代步h的奖励值,horizon为总迭代次数。
为了更高效地表示概率规划问题中动作的并发和效果的概率性,在IPPC-2011开始,RDDL(Relational Dynamic Influence Diagram Language)[15]被用作概率规划的描述语言。RDDL使用动态贝叶斯网络(Dynamic Bayes Net,DBN)来表示Factored MDP问题中的动作、状态和概率转换。RDDL可以支持多种变量类型和多层的动态贝叶斯网络,更好地支持动作的并发。IPPC官方提供了RDDL文件的解析和模拟工具rddlsim (RDDL Simulator)[19]进行相关约束检查和模拟状态演化等操作。也有PlanVerb[20]这样可以将RDDL文件和规划器的输出转化为更容易理解的自然语言描述和因果解释的方法。为保证公平性,IPPC中使用在线的方式评估参赛规划器,其由调用rddlsim的服务端和调用规划器客户端组成[21],在线评价方法如算法1所示。
算法1 IPPC在线评价算法
输入 RDDL领域文件、客户端及规划器
输出 平均奖励值Avg_Reward
1.客户端和服务端初始化相关参数,并解析RDDL领域文件
2. for r←0
3. 初始化当前状态S←S0
4. for h←0
5. 发送当前状态S给客户端
6. 客户端接收状态S,调用规划器计算出状态S的可执行动作集A
7. 将动作集A返回给服务端
8. 服务端根据动作集A计算出后继状态S'和即时奖励值R
9.进行状态迭代S←S'、记录累计奖励值Reward←Reward + R
10. end
11.end
12.计算Avg_Reward←Reward / round
算法1中round为执行轮次,服务端通过多轮执行求得平均奖励值,避免小概率的极值影响整体评价的准确性。客户端的主要作用是初始化领域文件,同时将规划器计算的结果发送给服务端,服务端和客户端共同组成了在线评价算法。算法1输入的客户端负责调用规划器,规划器需要根据当前状态S找到可执行动作集。为了保证求得的动作满足约束条件,规划器和客户端都会进行约束检查,防止错误的解影响后续的迭代过程。步骤4~9是一轮完整的概率规划过程,horizon为规划的步长,在领域的初始参数中给出。
2 算法设计 2.1 众包概率规划框架受众包的启发,在概率规划中引入众包的概念,利用不同形式计算资源处理规划问题。该框架通过集成多个规划器共同参与计算,并根据状态−动作评价算法选择评价值最优的动作,以便获得最优解。同时该框架可以整合不同规划器返回的结果,将当前最优解信息共享给其他的规划器,在多个规划器之间共享求解信息,从而增加跳出局部最优解的能力,提高算法的求解性能。参考IPPC在线评价过程,众包概率规划框架由发布规划任务的服务端和调用规划器的客户端两部分组成。与算法1相比,众包概率规划框架中的服务端需要同时连接多个客户端共同求解规划问题。其中每个客户端调用一个规划器,规划器的功能保持不变,依然是求解当前状态下的可行动作集。众包概率规划框架如算法2所示。
算法2 众包概率规划框架
输入 RDDL领域文件、n个客户端及规划器
输出 平均奖励值Avg_Reward
1.客户端和服务端初始化相关参数,并解析RDDL领域文件
2. for r←0
3. 初始化当前状态S←S0
4. for h←0
5. 发送当前状态S给每个客户端
6. foreach客户端i do
7. 接收状态S,并调用规划器计算出状态S的可执行动作集Ai
8. 计算出后继状态S'i、即时奖励值Ri、状态动作评价值Ei
9. 将S'i、Ai、Ri、Ei返回给服务端
10. end
11. 服务端选择最优Emax对应的客户端max
12. 进行状态迭代S←S'max、记录累计奖励值Reward←Reward + Rmax、记录执行动作Amax
13. end
14. end
15. 计算Avg_Reward←Reward / round
2.1.1 服务端流程服务端主要负责与客户端进行交互,并存储迭代过程中产生的信息。为了分担服务端的计算压力,将后继状态演化的过程放在客户端。这样的任务分配可以使服务端有更好的扩展性,客户端数量的增减不会影响服务端的效率。同时也可以保证每个客户端拥有固定的计算任务,客户端之间也互不影响。服务端的主要3个功能为对每个客户端分派规划任务,根据客户端返回的信息和选择最优的动作集并更新相应的迭代信息。众包概率规划服务端的流程图如图1所示。
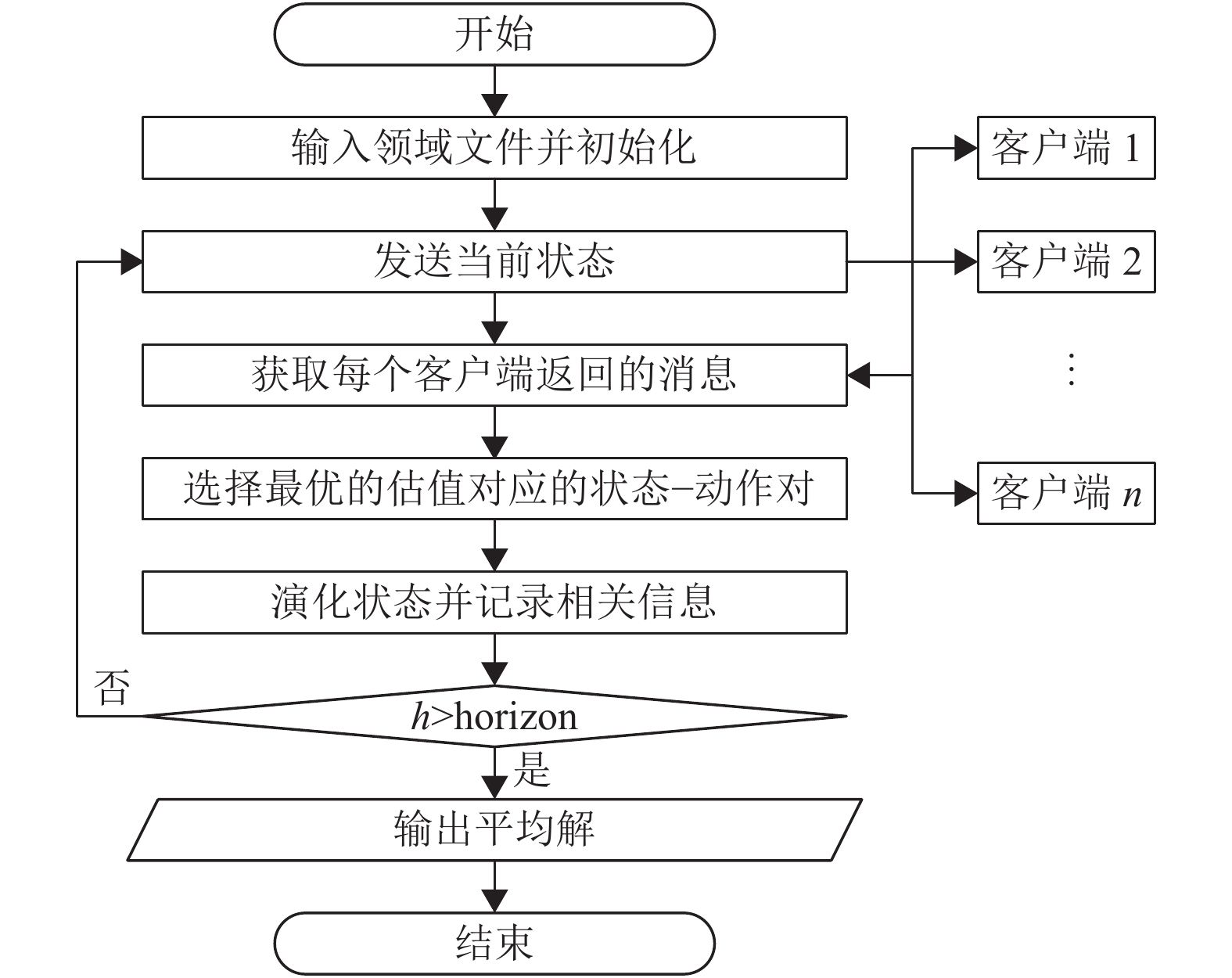
|
图 1 众包概率规划服务端流程图 Figure 1 Flow chart of crowdsourcing based probabilistic planning server |
客户端主要负责调用规划器求解规划问题,进行状态演化和适应度计算。每个客户端都调用一个特定规划器参与计算。客户端首先通过规划器,找到当前状态下的可执行动作集;然后使用rddlsim进行约束检查、奖励值计算,并根据领域描述随机生成后继状态;计算对应的状态−动作对的评价值;最后将可执行动作集、奖励值、后继状态、评价值等参数返回给服务端。众包概率规划客户端的流程图如图2所示。
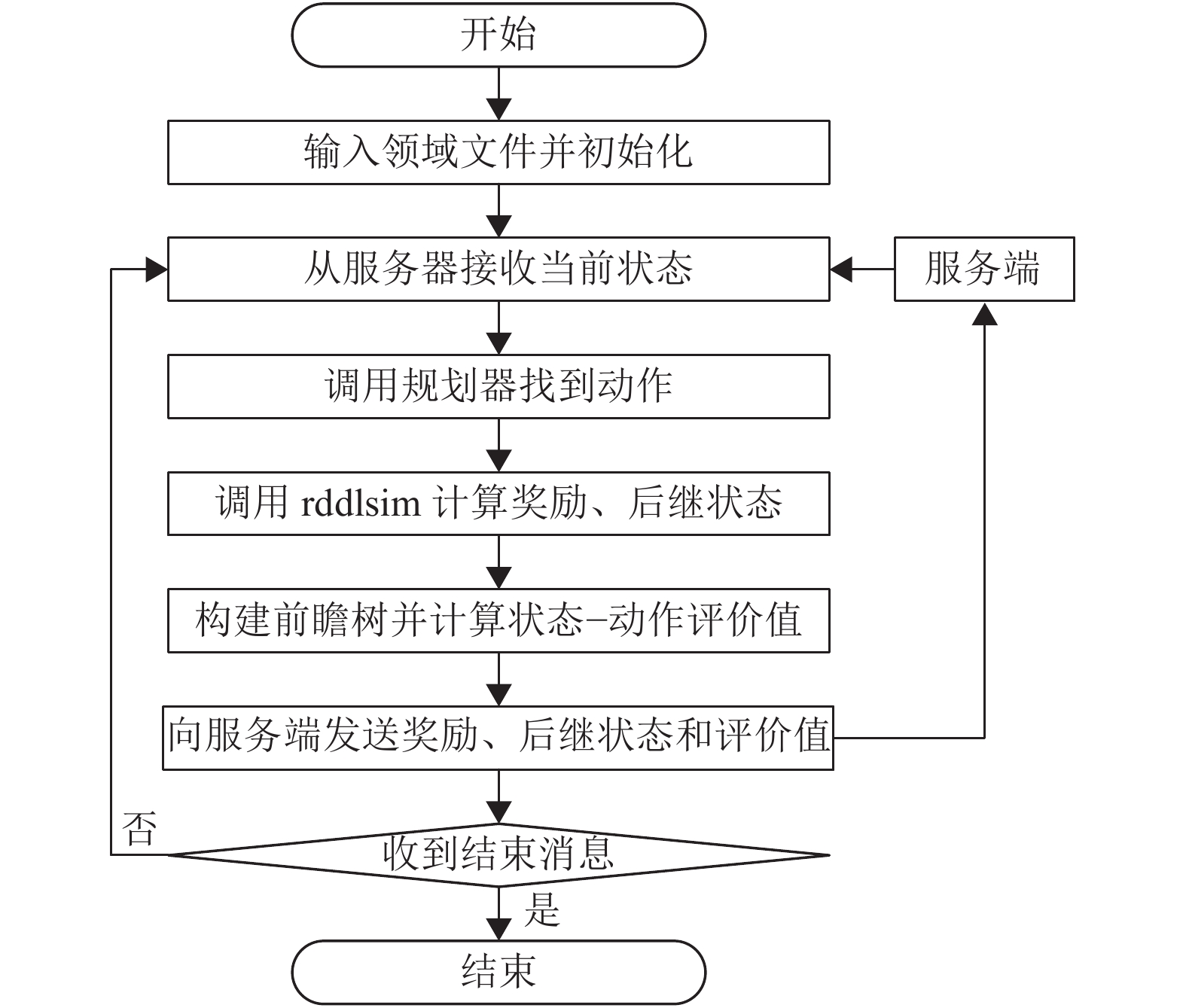
|
图 2 众包概率规划客户端流程图 Figure 2 Flow chart of crowdsourcing based probabilistic planning client |
相比于IPPC中的消息传输,本框架中的交互次数和每次传输的信息量都有所增加。为了统一格式,本文参考IPPC的通信协议[21],并在此基础上使用二进制编码方法,对状态和动作进行编码和解码操作。通过传输编码减少消息的大小,减少通信的时间消耗。众包概率规划中增加了客户端的数量,所以服务端之间的通信次数也有所增加。但由于客户端和服务端可以并行收发消息,和IPPC在线评价过程相比,通信的代价并没有增加。
服务端需要接收所有客户端返回的计算结果,用于下一次的迭代操作。其中就包含状态的演化结果、所执行的动作集、状态−动作对的评价值以及动作的奖励值等信息。服务端接收消息后更新迭代信息,并进入到下一次迭代。在下一次迭代开始时,服务端会选择上一次迭代的最优动作对应的后继状态,并发送给所有的客户端,共享全局的求解信息。客户端需要独立完成一步的规划过程,需要从服务端接收上一步的最优解和迭代步数等信息。图3使用顺序图表示众包概率规划框架中服务端与每个客户端的交互过程,不同客户端之间是独立且并行的。
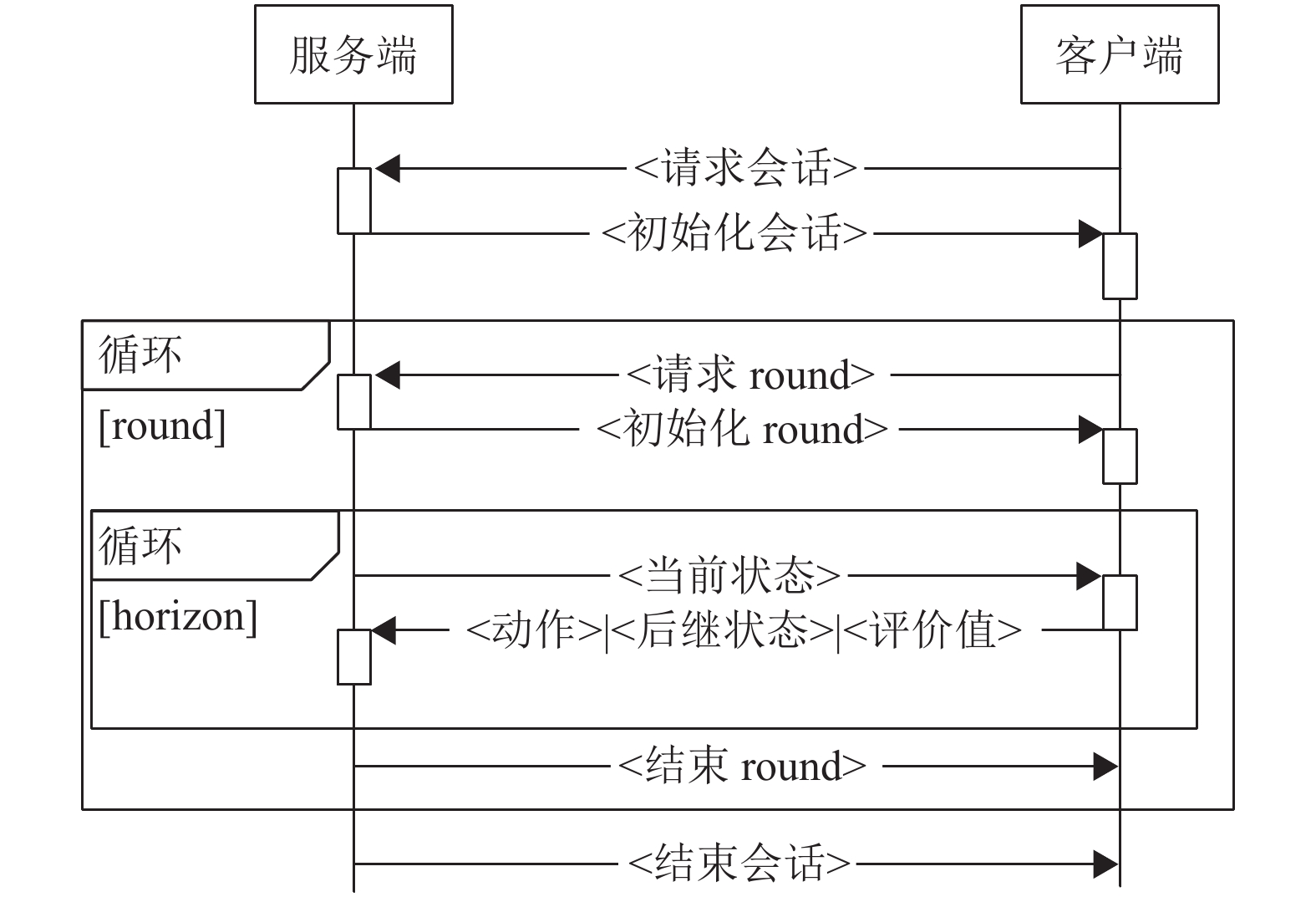
|
图 3 众包概率规划框架顺序图 Figure 3 Sequence diagram of crowdsourcing based probabilistic planning framework |
在消息传输过程中,不可避免地会出现消息传输异常的情况。如在运行过程中服务端接收客户端异常消息,会直接忽略对应客户端的消息,使用剩下客户端返回的信息进行计算。如遇到以下异常情况会重启客户端和服务端:在会话开始的阶段发生消息传输异常、客户端和服务端连接异常以及会影响到求解过程的异常情况。
2.2 状态−动作评价算法对于多个客户端返回的迭代信息,本文使用统一的评价算法,用于评价并选择最优的迭代信息。概率规划中即时奖励值只能体现当前状态和动作的即时效果,并不能反映当前动作对后续结果的影响[22]和后继状态概率分布的期望。所以不能使用即时奖励值作为评价的唯一标准。由于概率规划的目标为最大化累计奖励,估计当前动作对后续产生的影响,将是评价算法重要的部分。动作对后续的影响主要表现为后续几步迭代中状态概率分布的期望。所以本文提出了统一的状态−动作对评价算法,使用当前动作的即时奖励值和状态期望的估计值共同作为状态−动作对的评价值,用于对客户端返回信息进行评估。
状态−动作的评价值为基于蒙特卡洛树搜索算法计算出的状态估计值和执行当前动作的即时奖励值的加权和。其中的权值为一个自适应参数,在迭代初期估计值所占权重更大,有利于全局搜索;而在迭代后期即时奖励所占比重更大,有利于局部搜索;动态地平衡全局和局部搜索,可以增加找到最优解的概率。评价值计算公式为
| $ {\rm{evaluat}}{{\rm{e}}_{ij}} = \alpha {r_i} + (1 - \alpha ) {\rm{avg}}\_{e_j} $ | (2) |
| $ \alpha {\text{ = }}\frac{h}{{{\text{horizon}}}} $ | (3) |
式中:ri为动作i的即时奖励值,avg_ej为状态j基于蒙特卡洛树搜索的平均估计值,h为当前的迭代步数,horizon为总的迭代次数。估计值的计算主要分为构建前瞻树和回溯更新估计值两部分。
2.2.1 构建前瞻树估计值是对动作产生的影响进行估计,也是对状态的期望进行估计。使用基于蒙特卡洛树搜索算法的超前搜索建立前瞻树,然后从前瞻树叶子结点回溯,逐步计算状态的估计值。本文将模拟规划执行的步数定义为搜索深度,将每个状态的后继状态个数称为分支因子数。前瞻树中的节点表示状态,边表示执行的动作,产生的奖励值为边的权值。
本文采用了改进的蒙特卡洛树搜索方法,蒙特卡洛树搜索是基于抽样的搜索算法,有很强的通用性,可以应用到有不同的领域需求和变量类型的领域中。为了更好地对当前状态的概率分布进行估计,需要有足够多的后继状态,这就需要多次对当前状态进行采样,模拟出尽可能多的后继状态。
蒙特卡洛树搜索算法是通过多次模拟,构建搜索树。但这种方式得到的分支因子较小,不能准确评价状态的期望。同时这种模拟优先进行深度探索,但概率规划中深度越大估计值的随机性就越强,进而导致估值不准。本文使用改进的蒙特卡洛树搜索构建前瞻树,优先对分支因子进行扩展而不是深度搜索。足够大的分支因子可以降低后继状态概率分布期望的估值误差[23],在保证当前估值准确的前提下进行深度搜索。构建前瞻树步骤如算法3所示。
算法3 构建前瞻树
输入 状态搜索列表List←{S0}
输出 前瞻树
1.取出状态搜索列表List中第一个状态S
2.从状态搜索列表List中删除状态S
3.如果前瞻树中存在S对应的节点,返回步骤1
4.使用随机策略找到当前状态S的一个可执行动作A
5.模拟执行动作A,获得后继状态集合S'1并加入到状态搜索列表List中
6.记录奖励值、后继状态和执行动作,并更新前瞻树
7.重复执行步骤4,直到后继状态数大于设定的分支因子数
8.计算后继状态{S'1, S'2, S'3
9.重复执行步骤1,直到状态搜索列表List为空或时间消耗完或达到最大搜索深度
算法3的输入为状态搜索列表List,每次会扩展状态搜索列表List中第一个节点,直到时间结束。输出的前瞻树只在第一次迭代的时候才会初始化,在后续的迭代过程中不断地更新前瞻树。
图4表示的是前瞻树构建过程中的一步,当前状态为S1,对应算法3中步骤4、5。步骤4通过使用增强的随机搜索策略和自适应的时间限制,找到一个动作a1。步骤5为调用rddlsim执行动作a1生成后继状态S'2,并计算奖励值r12。步骤5允许执行重复的动作,这时如果得到的后继状态不同就会出现图4的S'3和S'4这种情况,而奖励值只受动作和当前状态影响,所以r13和r14是相同的。重复执行步骤4~6就会得到图4中的状态{S'2, S'3, S'4, S'5}及对应的节点。
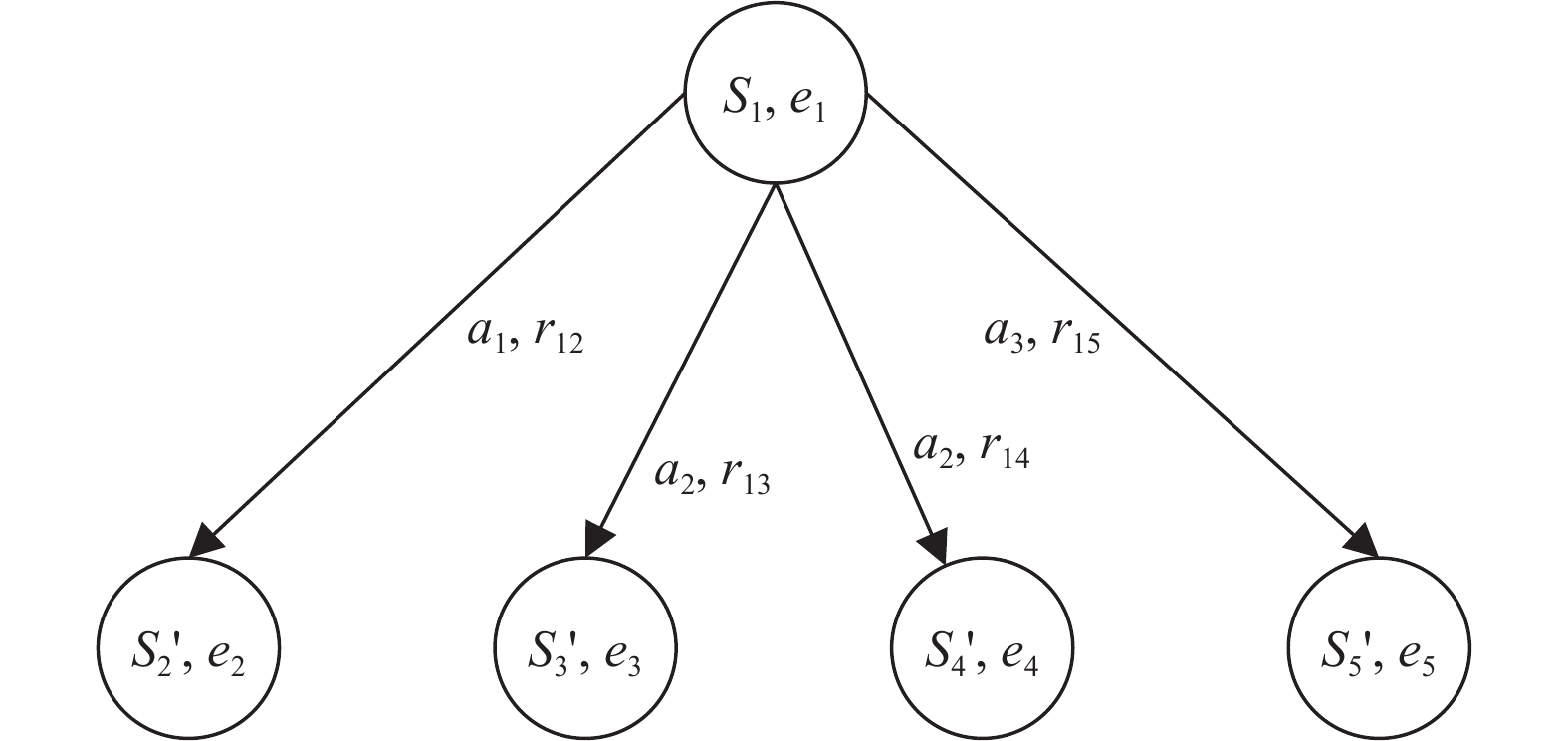
|
图 4 构建前瞻树 Figure 4 Building the lookahead tree |
算法3的步骤2和步骤8中都可能会出现状态重复的情况,这时就需要消除重复状态。为了减小存储前瞻树所消耗的空间,使用2.1.3节中的二进制编码方式,在节点和边中存储动作和状态的编码。为了防止前瞻树无限增长,对其最大节点数也做了限制。当超过最大节点数时,会删除那些长时间未访问的节点。在步骤2中遇到重复状态时,就可以直接使用之前计算的结果,减少计算次数,加快收敛速度。步骤8使用实际采样的结果计算概率分布。
受时间的限制,需要在有限时间内优先扩展分支因子,所以扩展的深度是动态变化的。步骤9中的最大深度限制仅用于迭代后期,目的是防止采样深度超过剩余迭代次数,而浪费计算资源。
2.2.2 回溯计算估计值采用对前瞻树回溯的方式,从叶子结点开始计算节点的估计值。节点i的估计值为边的权值和对应后继状态估计值的加权平均,计算公式为
| $ {e_i} = \sum\nolimits_j^{{\rm{NS}}} {({r_{ij}} + {e_j}) {p_j}} $ | (4) |
式中:NS为节点i的子节点的集合;rij为节点i和j之间的边的权值,为执行动作的即时奖励值;pj为节点j对应状态出现的概率;叶子结点初始适应度为0。
节点的概率为其中的状态出现的次数/总采样次数。如图4所示,其中没有出现重复状态的情况,那么每个状态的概率为0.25。所以状态S1的估计值计算公式为e1=0.25 ( r12 + e2 ) + 0.25 ( r13 + e3 ) + 0.25 ( r14 + e4 ) + 0.25 ( r15 + e5 )。
受时间的影响,不同的客户端计算的搜索的深度不确定,所以使用平均估值作最终的状态估值,即
| $ {\rm{avg}}\_{e_j} = {e_j}/{\rm{deep}} $ | (5) |
式中:deep为节点j的深度,ej为节点j的估计值。
使用随机抽样的方式进行模拟,将模拟过程的奖励值作为状态的估计值,用于评价动作对后续规划的“影响”。当模拟的分支因子足够大就可以近似估计后继状态的概率分布;模拟搜索深度越大时,估计值就越接近于动作的真实奖励值。在时间充裕的极限情况下,本算法可以遍历所有的情况,得到的估计值就是实际概率分布的期望值。
3 实验结果分析 3.1 实验设置实验采用IPPC中的基准领域作为测试,包括IPPC-2014[24]的4个领域(Elevators、Skill teaching、Tamarisk、Traffic)和IPPC-2018[25]的4个领域(Academic Advising、Cooperative Recon、Manufacturer、Red-finned Blue-eye)作为实验的测试集。每个领域有10个实例,每个实例运行75轮,记录平均的奖励值和每轮奖励值的标准差,用于结果分析。实验环境为Ubuntu 20.04.3,Intel Core(TM) i7-11700 @2.5GHz,31.2 GB RAM,使用java1.8实现算法。实验分为不同策略之间的性能对比和本算法的扩展性对比两部分。
3.2 策略对比实验本节主要对比本文方法在最优参数设定下和其他策略之间的性能差异。由于目前没有众包结合概率规划的相关工作,本文使用最优的SOGBOFA规划器和使用最广泛的Random规划器作为客户端的规划器,同时使用单一客户端的SOBBOFA和Random共同作为基准策略。采用IPC得分[11]作为评价指标,将每个策略的平均累计奖励进行归一化处理。使用同一实例中表现最优和最差的策略返回的解计算得分,奖励值最高的策略对应的得分为1,最低的得分为0。IPC得分提供了一个标准化分数,已经成为对比不同策略的标准方法。奖励值得分
| $ {{{s}}_i^r} = \frac{{{r_i} - {r_{\min }}}}{{{r_{\max }} - {r_{\min }}}} $ | (6) |
式中:ri为当前策略的奖励值,rmax为最优策略对应的奖励值,rmin为最差策略对应的奖励值。
为了比较不同策略的求解稳定性,同时计算每个策略75轮的标准差,并计算标准差得分
| $ {{{s}}_i^d} = \frac{{{d_{\max }} - {d_i}}}{{{d_{\max }} - {d_{\min }}}} $ | (7) |
式中:di为当前策略的奖励值标准差,dmax为所有策略中最大的标准差,dmin为所有策略中最小的标准差。
表1为对比的策略名以及对应的参数设置。其中的Rand和SOG使用单一客户端的策略,测试随机(Random)规划器和SOGBOFA规划器的性能;GCR(Greedy Crowdsourcing Based Probabilistic Planning with Random)和GCS(Greedy Crowdsourcing Based Probabilistic Planning with SOGBOFA)使用即时奖励作为评价值的贪心众包概率规划框架策略;ECR(Evaluation Based Crowdsourcing Based Probabilistic Planning with Random)和ECS(Evaluation Based Crowdsourcing Based Probabilistic Planning with SOGBOFA)使用状态−动作评价算法的众包概率规划框架策略,后面的数字为客户端的个数;ECRS是ECR和ECS两个策略的融合,使用混合客户端的策略。实验结果如表2所示,为不同策略的平均奖励值得分和标准差得分情况。
| 表 1 不同策略的参数设置 Table 1 Parameter settings of different policies |
| 表 2 不同策略的平均奖励值得分和标准差得分 Table 2 The reward scores and deviation scores of different policies |
首先对比Rand、GCR、ECR-5三个策略,从得分来看,使用了众包框架的GCR和ECR两个策略相较于Rand都有一定的提升,分别获得了4.35和32.64的得分。而对比GCR和ECR发现,由于ECR使用了评价算法,结果远远优于使用即时奖励为评价值的GCR的策略。
为了保证对比的公平性,对于SOG策略设定单步的时间限制为2.5 s;使用5个客户端的GCS和ECS-5,单步时间总限制为0.5 s。假设在相同的硬件条件下,1个策略运行2.5 s和5个相同策略运行0.5 s消耗了同样的计算资源。由表2可知,在相同资源限制下,使用了贪心众包规划框架的GCS取得了和SOG相近的分数。虽然ECS-5加入了评价算法,进一步压缩了每个客户端中SOGBOFA的单步时间,但求解效果远远领先同样条件下的SOG和GCS策略。表明本众包概率规划框架有着很小的性能损失,同时基于蒙特卡洛树搜索的状态−动作评价算法具有很小评价误差,对算法性能的提升有正向的作用。
表2中GCR、ECS-5的标准差相对Rand和SOG有一定的提升。而带有评价算法的众包概率规划策略ECR和ECS-5在标准差方面又有进一步的提升。说明众包概率规划框架和状态−动作评价算法在求解稳定性上也有一定提升。
为了测试众包概率规划对不同规划器的兼容性和求解能力,利用有限的资源,进行了ECS-10和ECRS两组额外的实验。在ECS-10中,放宽了资源的限制,使用10个客户端从而得到了当前策略中的最高分,并在7个领域中都取得了最高分。在ECRS的客户端使用了Random和SOGBOFA两种不同的规划器,虽然最终的效果不如ECS-5,但也说明了使用不同种类规划器混合处理规划问题的可行性。
3.3 扩展性实验本节对众包概率规划框架的扩展性进行检测,测试随着客户端数量的增加,算法的整体求解效果以及运行时间的差异。使用性能最低的策略作为本实验的基准策略,计算其他策略的性能提升比例。提升比例可以清晰展现求解性能相对于基准策略的好坏。使用式(8)计算不同策略的提升比例。
| $ {\rm{rati}}{{\rm{o}}_i} = \frac{{{r_i} - {r_{{\rm{base}}}}}}{{{r_{{\rm{base}}}}}} $ | (8) |
式中:ri表示当前策略的奖励值,rbase为基准策略的奖励值。
提升比例可以直观地表示不同参数设置对于求解效果的影响,采用效果最差的Random规划器,即客户端数量为1的策略作为计算比例的基准。实验结果如表3所示。
| 表 3 对比不同客户端个数的提升比例 Table 3 Comparison the increase ratio of different client numbers |
表3的cooperative-recon领域中,Random规划器求解到的累计奖励值为零,出现无法计算提升比例的情况;对于剩下的策略来说,随着客户端数量的增加,有一定概率找到可执行动作并取得正的奖励值,所以在cooperative-recon领域中剩下的策略不会差于Random规划器。在academic-advising中随着客户端数量增加,性能提升并不明显,甚至在manufacturer领域中还有降低,说明在这两个领域中目前的评价算法还存在很大的改进空间。但综合来看随着客户端数量的上升,求解性能也不断增加;客户端个数为10相比于Random规划器有着平均68%的提升。随着客户端数量的增加,服务端的计算压力并没有明显增加,说明调用不同规划器的客户端之间可以保持并行,扩展性不受影响。
4 结语本文针对概率规划的求解困难,提出了基于蒙特卡洛树搜索的众包概率规划算法,成功将众包和概率规划结合。根据众包的思想,使用多个规划器共同处理概率规划问题,同时充分利用有限的计算资源。实验结果表明本算法有着很小的性能损失,在相同资源限制下,求解效果和稳定性方面都有优势。在计算资源充足的情况下可以加快问题的求解,同时提升求解质量。在今后的工作中可以继续对评价算法进行改进,改进实验中表现较差的manufacturer领域,提高评价算法的效率,尽可能降低评价误差。
| [1] |
KLößNER T, HOFFMANN J, STEINMETZ M, et al. Pattern databases for goal-probability maximization in probabilistic planning[C]//Proceedings of the International Conference on Automated Planning and Scheduling. Palo Alto, CA: AAAI Press, 2021: 201-209.
|
| [2] |
KUSHMERICK N, HANKS S, WELD D S. An algorithm for probabilistic planning[J].
Artificial Intelligence, 1995, 76(1-2): 239-286.
DOI: 10.1016/0004-3702(94)00087-H. |
| [3] |
饶东宁, 杨锦鹏, 刘越畅. 时态规划综述及研究现状[J].
广东工业大学学报, 2021, 38(3): 9-16.
RAO D N, YANG J P, LIU Y C. A survey of temporal planning[J]. Journal of Guangdong University of Technology, 2021, 38(3): 9-16. DOI: 10.12052/gdutxb.200127. |
| [4] |
饶东宁, 郭海峰, 蒋志华. 基于并行概率规划的股票指数模拟[J].
计算机学报, 2019(6): 1334-1350.
RAO D N, GUO H F, JIANG Z H. Stock index simulation based on parallel probabilistic planning[J]. Chinese Journal of Computers, 2019(6): 1334-1350. DOI: 10.11897/SP.J.1016.2019.01334. |
| [5] |
LITTMAN M L, GOLDSMITH J, MUNDHENK M. The computational complexity of probabilistic planning[J].
Journal of Artificial Intelligence Research, 1998, 9: 1-36.
DOI: 10.1613/jair.505. |
| [6] |
GELLY S, SILVER D. Monte-Carlo tree search and rapid action value estimation in computer Go[J].
Artificial Intelligence, 2011, 175(11): 1856-1875.
DOI: 10.1016/j.artint.2011.03.007. |
| [7] |
BROWNE C B, POWLEY E, WHITEHOUSE D, et al. A survey of monte carlo tree search methods[J].
IEEE Transactions on Computational Intelligence and AI in Games, 2012, 4(1): 1-43.
DOI: 10.1109/TCIAIG.2012.2186810. |
| [8] |
SILVER D, VENESS J. Monte-Carlo planning in large POMDPs[C]//Proceedings of the 23rd International Conference on Neural Information Processing Systems. La Jolla, California: NIPS, 2010: 2164-2172.
|
| [9] |
SRINIVASAN S, TALVITIE E, BOWLING M. Improving exploration in UCT using local manifolds[C]//Twenty-Ninth AAAI Conference on Artificial Intelligence. Palo Alto, CA: AAAI Press, 2015: 3386-3392.
|
| [10] |
PATRA S, MASON J, GHALLAB M, et al. Deliberative acting, planning and learning with hierarchical operational models[J].
Artificial Intelligence, 2021, 299: 103523.
DOI: 10.1016/j.artint.2021.103523. |
| [11] |
CUI H, KELLER T, KHARDON R. Stochastic planning with lifted symbolic trajectory optimization[C]//Proceedings of the International Conference on Automated Planning and Scheduling. Palo Alto, CA: AAAI Press, 2019: 119-127.
|
| [12] |
RAO D, HU G, JIANG Z. PRobPlan: a framework of integrating probabilistic planning into ROS[J].
IEEE Access, 2020, 8: 106516-106530.
DOI: 10.1109/ACCESS.2020.3000293. |
| [13] |
KAZEMI L, SHAHABI C. Geocrowd: enabling query answering with spatial crowdsourcing[C]// Proceedings of the 20th International Conference on Advances in Geographic Information Systems. New York: ACM, 2012: 189-198.
|
| [14] |
JEONG J, JAGGI P, SANNER S. Symbolic dynamic programming for continuous state MDPs with linear program transitions[C]//Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence. Amsterdam: Elsevier, 2021: 4083-4089.
|
| [15] |
YOUNES H L S, LITTMAN M L. PPDDL1.0: an extension to PDDL for expressing planning domains with probabilistic effects[J/OL]. CMU-CS, 2004 [2022-2-20]http://reports-archive.adm.cs.cmu.edu/anon/anon/home/ftp/usr0/ftp/2004/CMU-CS-04-167.pdf
|
| [16] |
BELLMAN R E. A markov decision process[J].
Journal of Mathematical Mechanics, 1957, 6: 679-684.
|
| [17] |
KELLER T, EYERICH P. PROST: Probabilistic planning based on UCT[C]//Twenty-Second International Conference on Automated Planning and Scheduling. Palo Alto, CA: AAAI Press, 2012: 119-127.
|
| [18] |
GUESTRIN C, KOLLER D, PARR R, et al. Efficient solution algorithms for factored MDPs[J].
Journal of Artificial Intelligence Research, 2003, 19: 399-468.
DOI: 10.1613/jair.1000. |
| [19] |
COLES A, COLES A, OLAYA A G, et al. A survey of the seventh international planning competition[J].
AI Magazine, 2012, 33(1): 83-88.
DOI: 10.1609/aimag.v33i1.2392. |
| [20] |
CANAL G, KRIVIĆ S, LUFF P, et al. PlanVerb: domain-independent verbalization and summary of task plans[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Palo Alto, CA: AAAI Press, 2022.
|
| [21] |
YOUNES H L S, LITTMAN M L, WEISSMAN D, et al. The first probabilistic track of the international planning competition[J].
Journal of Artificial Intelligence Research, 2005, 24: 851-887.
DOI: 10.1613/jair.1880. |
| [22] |
KAUR J, CHATTERJEE I, LIKHACHEV M. Speeding up search-based motion planning using expansion delay heuristics[C]//Proceedings of the International Conference on Automated Planning and Scheduling. Palo Alto, CA: AAAI Press, 2021: 528-532.
|
| [23] |
SINGH A, LIPOVETZKY N, RAMIREZ M, et al. Approximate novelty search[C]//Proceedings of the International Conference on Automated Planning and Scheduling. Palo Alto, CA: AAAI Press, 2021: 349-357.
|
| [24] |
VALLATI M, CHRPA L, GRZEŚ M, et al. The 2014 international planning competition: Progress and trends[J].
AI Magazine, 2015, 36(3): 90-98.
DOI: 10.1609/aimag.v36i3.2571. |
| [25] |
GEIßER F, SPECK D, KELLER T. An analysis of the probabilistic track of the IPC 2018[C]//ICAPS 2019 Workshop on the International Planning Competition (WIPC). Palo Alto, CA: AAAI Press, 2019: 27-35.
|
 2022, Vol. 39
2022, Vol. 39

