随着能源短缺与全球变暖状况的日益加剧,发展电动汽车被认为是解决这些难题的有效方法,而动力电池则是电动汽车最重要的部件[1-3]。除了续航里程,电池模组的热安全也在阻碍着电动汽车的推广[4-5]。过高的温度和过大的温差加快了动力电池的寿命衰减,甚至可能引发热失控[6-7]。近几年,随着电动汽车行业的需求,各种电池热管理技术纷纷出现,旨在解决动力电池充放电过程中的散热问题,达到控制电池模组的温度和温差的目的[8-9]。相变材料(Phase Change Material, PCM)以其自身的高潜热、均温性好、结构简单紧凑等特性,逐渐成为行业研究的热点[10-12]。
目前,相变材料应用于电池热管理系统的研究主要集中在导热系数、抗泄漏、阻燃等材料性能的研究,对其结构设计方面的研究较少[13]。为了满足实际需求,相变材料往往在添加稳定剂(如环氧树脂、低密度聚乙烯等)后制备为复合相变材料(Composite PCM, CPCM)[14-15]。所得到的CPCM比较容易被制备成板状结构,并且夹在方形电池的两侧,达到冷却的目的。然而,由于圆柱型电池是弯曲表面,其冷却结构往往更加复杂。在大多数的研究中,CPCM都被制备为块状的结构,随后在其表面钻孔,从而配合圆柱型电池的弯曲表面。虽然这种结构依旧能达到冷却电池模组的目的,然而,巨大的块状结构容易导致散热面积小,不利于电池模组的二次散热。
因此,在本研究中提出了一种新型的管状复合相变材料(tubular Composite PCM, t-CPCM)结构,来替代传统的块状复合相变材料(block-shaped Composite PCM, b-CPCM)结构,不仅提高了散热面积,同时优化了流道。首先使用数值仿真的方法,分析这两种电池模组所对应的简化二维模型的流场分布;随后通过这两种电池模型仿真得出流场数据,使用热阻分析法定量/定性计算其导热热阻和对流换热热阻;最后采用实验研究的方法,在高温工况下(40 ℃)对这两种电池模组进行高倍率充放电的测试,验证和评估这两种电池模组的控温和均温效果,为后续热管理系统的设计提供理论和数据支撑。
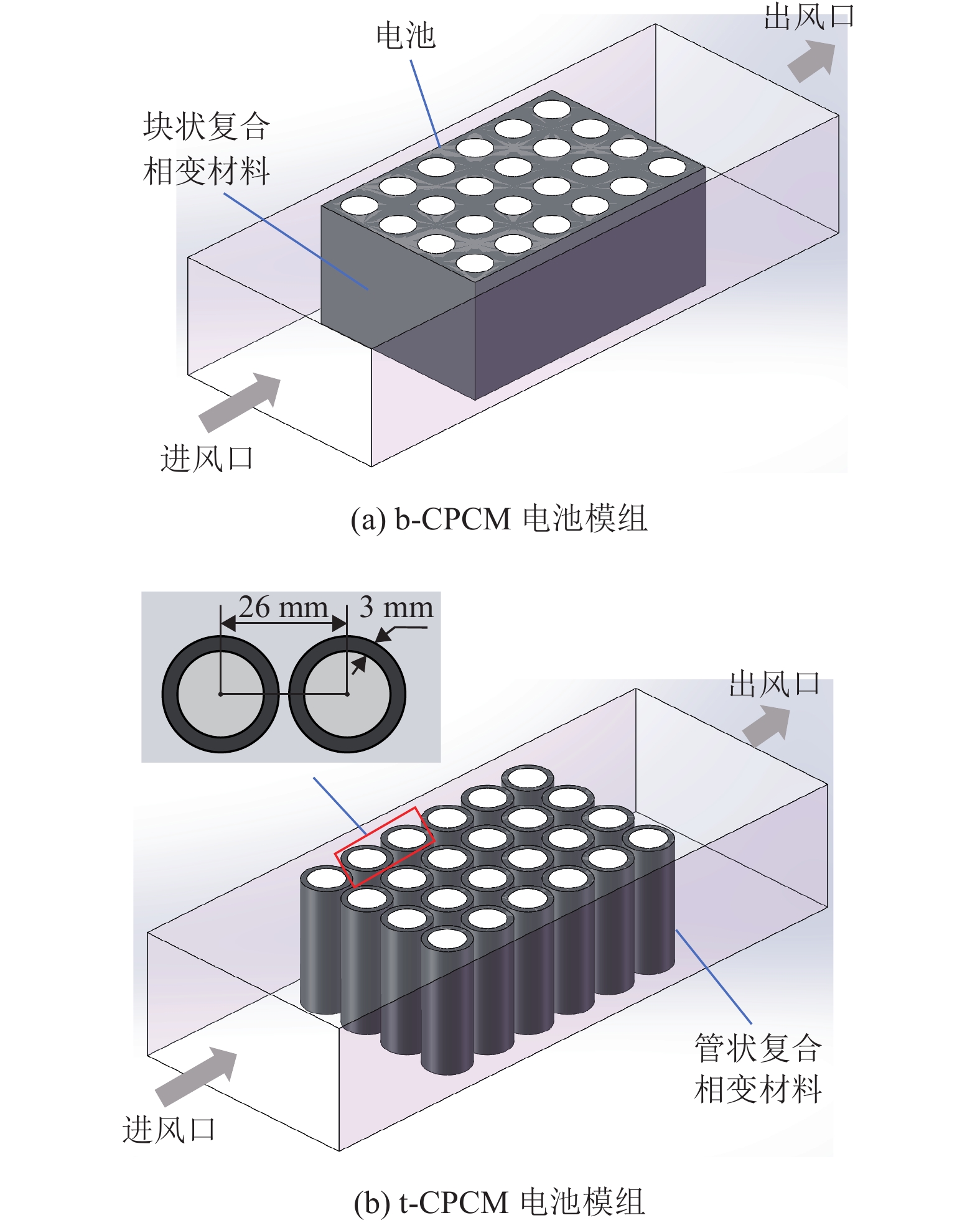
1 电池热管理系统的结构与仿真模型建立 1.1 电池热管理系统的结构如图1所示,电池模组分别按照b-CPCM和t-CPCM耦合强制对流的结构进行设计。所选电池为18650型磷酸铁锂动力电池,电池之间的中心间距为26 mm,具体参数如表1所示。在b-CPCM电池模组中,模块的尺寸为156 mm×104 mm×55 mm;在t-CPCM电池模组中,所选用的CPCM厚度为3 mm,高度为55 mm,进出风口的尺寸均为124 mm×55 mm。
|
图 1 电池模组耦合强制对流示意图 Figure 1 Battery module coupled with forced convection diagram |
| 表 1 b-CPCM模型和t-CPCM模组具体参数 Table 1 Specific parameters of b-CPCM module t-CPCM module |
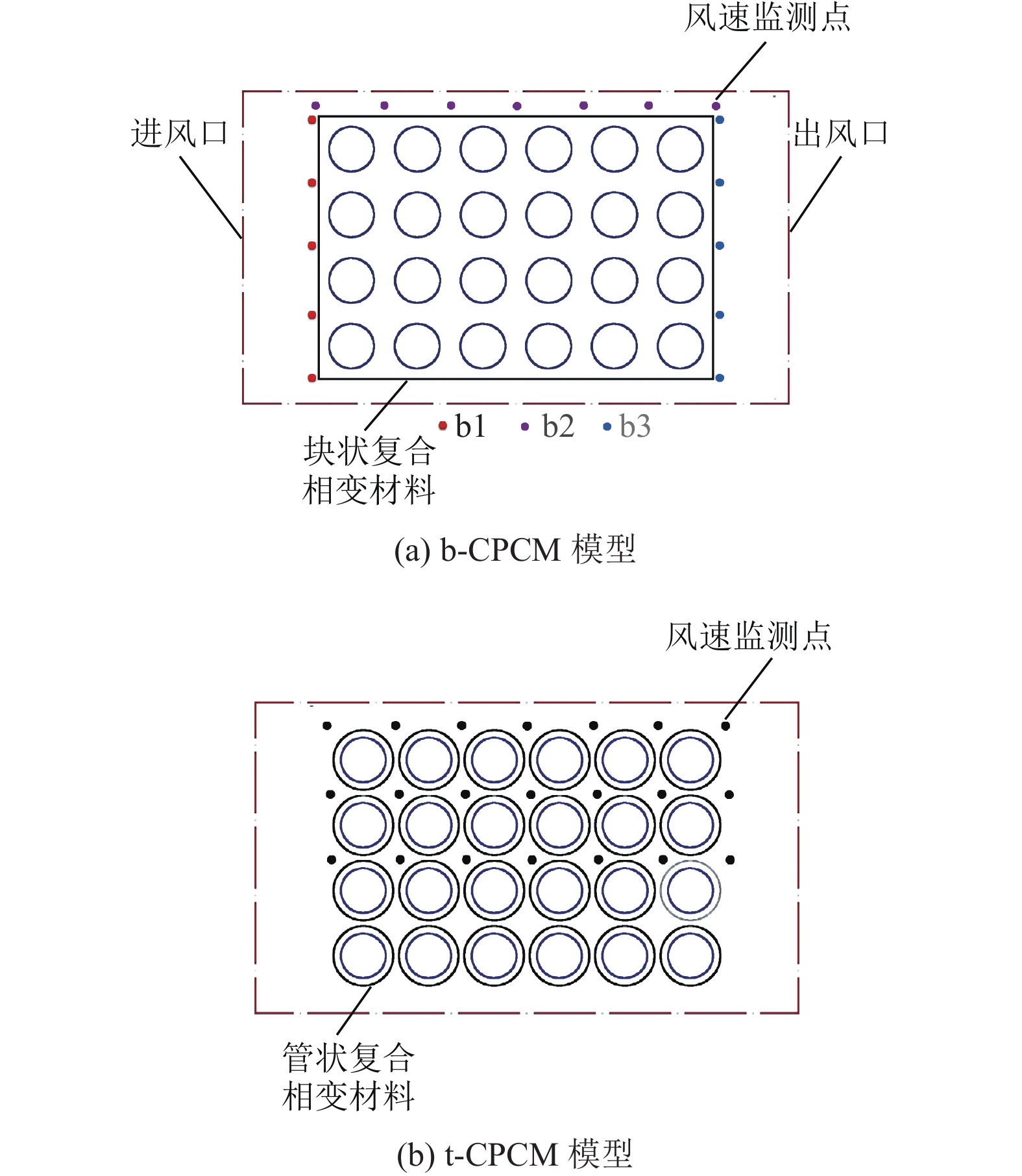
为了简化计算,使用CAD将b-CPCM和t-CPCM两个仿真模型绘制成了如图2所示的二维平面图像,将进风口的风速设置为1 m/s,并使用Ansys仿真软件来研究两个模型在强制对流过程中的流场分布情况。
|
图 2 流场仿真计算模型与风速监测点 Figure 2 Flow field simulation calculation model and velocity monitoring point |
空气的连续性方程为
| $ {\rho }_{{\rm{a}}}\left(\frac{\partial {\boldsymbol{v}}}{{\partial {{t}}}}+\nabla {{\boldsymbol{v}}}\right)=0 $ | (1) |
式中:ρa为空气的平均密度,v为空气的速度矢量。
空气的动量守恒方程为
| $ {\rho }_{{\rm{a}}}\left[\left(\frac{\partial {\boldsymbol{v}}}{{\partial {{t}}}}+\nabla {{\boldsymbol{v}}}\right)\right]{{\boldsymbol{v}}}=-\nabla P+\mu {\nabla}^{2}{{\boldsymbol{v}}} $ | (2) |
式中:P为空气的静态压强,μ为空气的动力黏度。
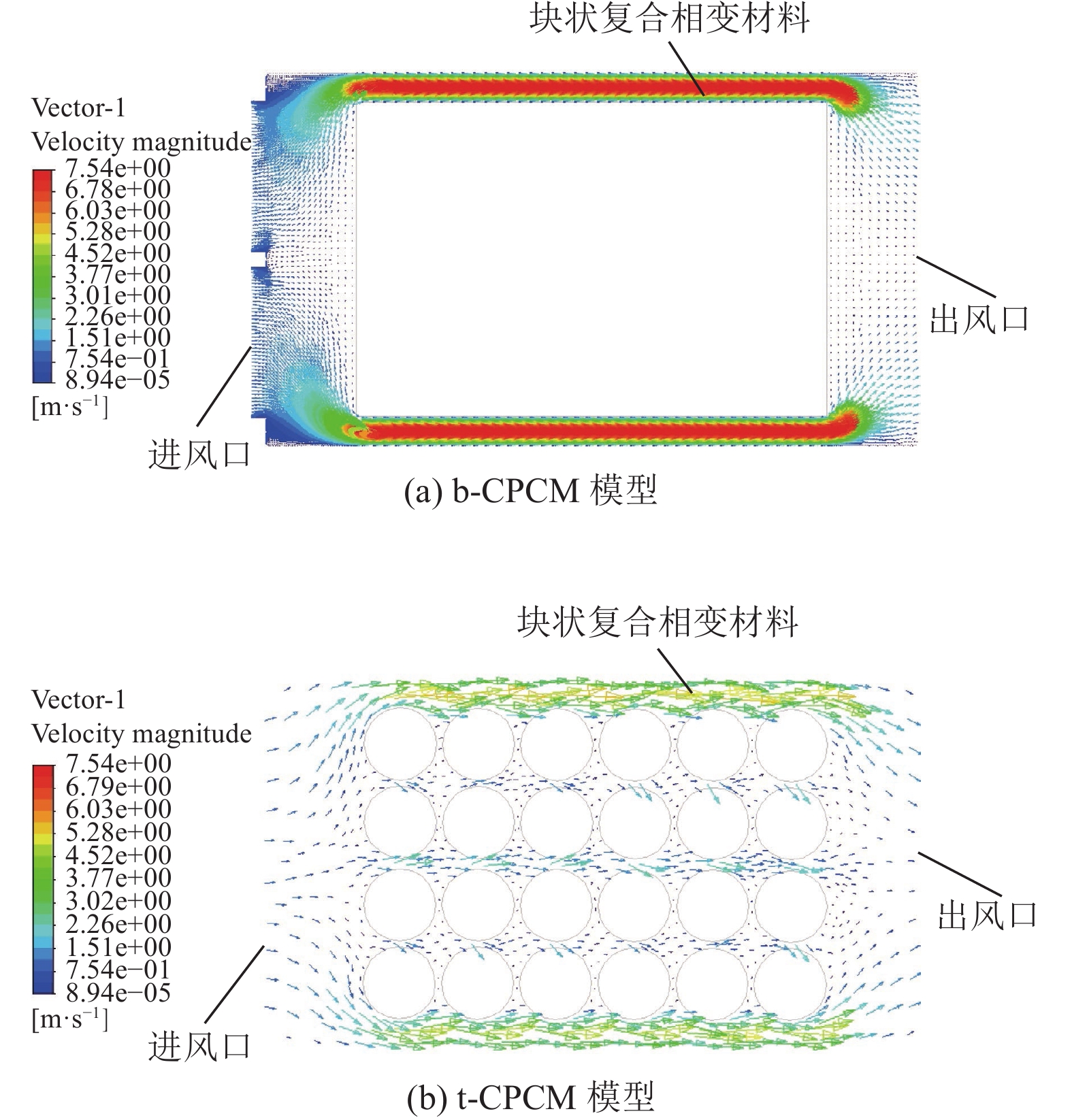
2 结果与讨论 2.1 b-CPCM仿真模型与t-CPCM仿真模型的流场分布如图3(a)所示,b-CPCM仿真模型在600 s时流场集中于模型的两侧。虽然通过数据分析后发现其局部空气流速可达到7.6 m/s,然而这种流场只能快速地通过对流换热的方式冷却模型的外侧,中心位置的热量却需要通过热传导的方式逐渐传递至外侧。这种不均匀的换热方式极易导致模组内部产生严重的温差,甚至有引发热失控的风险;而t-CPCM仿真模型(见图3(b))在600 s时的流场虽然两侧的空气流速依旧较高,但却在仿真模型的中心形成了均匀的流道,进而使电池的中心区域也可以进行强制对流换热,这无异于在提升电池模组散热效果的同时,也提升了模组内部的均温性。
|
图 3 600 s后,仿真模型的流场分布 Figure 3 After 600 s, flow field distribution of simulation model |
由传热学的基本机理可知,在使用相变材料冷却时,电池产生的热量首先由相变材料吸收,随后再传递至空气中。因此,上述b-CPCM和t-CPCM两个仿真模型的热阻可以分为如图4和式(3)所示的两部分:热量由电池表面传递至CPCM外侧的导热热阻R1,以及热量从CPCM外侧传递至外部空气的对流换热热阻R2。R1和R2的值可以通过式(4)和式(5)计算得出[16]。
| $ R={R}_{1}+{R}_{2} $ | (3) |
| $ {R}_{1}=\frac{\delta }{{{A}_{{\rm{SA}}}\lambda }_{{\rm{CPCM}}}} $ | (4) |
| $ {R}_{2}=\frac{1}{{A}_{{\rm{SB}}}h} $ | (5) |
式中:δ为CPCM的当量厚度,λCPCM为CPCM的导热系数,h为外部空气的对流换热系数,ASA为CPCM的内部热传导面积,ASB为CPCM外侧与外部空气的对流换热面积。
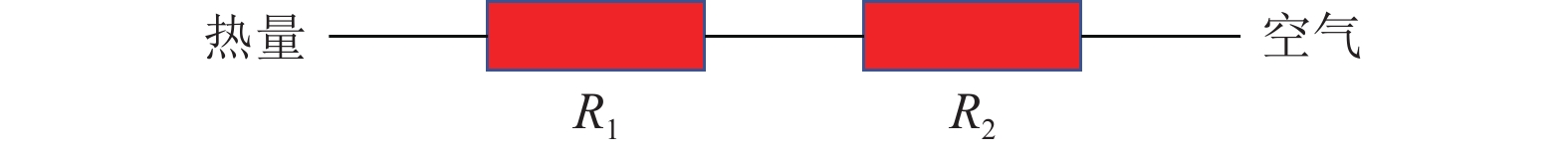
|
图 4 CPCM的换热热阻 Figure 4 Thermal resistance of CPCM |
由前文可知,b-CPCM电池模组中处于边缘的电池的当量厚度δ与t-CPCM电池模组的近似相等;而处于b-CPCM电池模组中心区域的电池的当量厚度δ则远比t-CPCM模型的大。另外,两者的ASA近似相等,λCPCM相等。因此根据上述式(4),t-CPCM仿真模型的R1远小于b-CPCM仿真模型的。
而根据式(5),对流换热热阻R2的值由ASB与h决定。ASB已在表1中给出,只需计算两个仿真模型与外部空气之间的对流换热系数h。在b-CPCM仿真模型的流场分布符合管内强制对流模型,因此h可以通过式(6)~(11)获得[17]。
| $\begin{split} &\text{Nu}=\dfrac{h{l}_{{\rm{c}}}}{\lambda } = \dfrac{\dfrac{f}{8\left({\rm{Re}}-1\,000\right){{\rm{Pr}}}_{{\rm{f}}}}}{1+12.7\sqrt{\dfrac{f}{8}}\left({{{\rm{Pr}}}_{{\rm{f}}}}^{\tfrac{2}{3}}-1\right)}\left[1+{\left(\dfrac{d}{{l}_{{\rm{c}}}}\right)}^{\tfrac{2}{3}}\right]{c}_{{\rm{t}}} \;\;,\\ &\qquad ({\rm{Re}} \leqslant {10}^{6}) \end{split}$ | (6) |
| $ \text{Re}=\frac{v{l}_{{\rm{c}}}}{u} $ | (7) |
| $ {{{\rm{Pr}}}_{{\rm{f}}}}=\frac{u}\alpha $ | (8) |
| $ f={\left(1.82\mathrm{lg}{\rm{Re}}-1.64\right)}^{-2} $ | (9) |
| $ {d}=\frac{4{A}_{{\rm{c}}}}{C} $ | (10) |
| $ {c}_{{\rm{t}}}={\left(\frac{{T}_{{\rm{f}}}}{{T}_{{\rm{w}}}}\right)}^{0.45}(0.5\leqslant {c}_{{\rm{t}}}\leqslant 1.5) $ | (11) |
式中:Nu为努赛尔数,Re为雷诺数,Prf为空气的普朗特数,lc为特征长度,λ为空气导热系数,f为“Darcy”阻力系数,d为当量直径,ct为修正系数,v为空气流速,u为动力黏度,α为热扩散率,Ac为流动截面积,C为润湿周长,Tf为流体平均温度,Tw为壁面平均温度。
由图3(a)可看出,由于b-CPCM仿真模型的流场是对称分布的,因此可以通过计算仿真模型的一半区域,以相加的方式来获得b-CPCM电池模组整体的R2(R2-b)。本文根据模型内外部空气流速的不同,将b-CPCM仿真模型划分成如图5所示的3个区域,并分别命名为R2-b1,R2-b2,R2-b3。由于3个区域之间的热阻是并联的关系,因此可以使用式(12)来计算R2-b。
| $ \frac{1}{{R}_{2-{\rm{b}}}}=2\times (\frac{1}{{R}_{2-{\rm{b}}1}}+\frac{1}{{R}_{2-{\rm{b}}2}}+\frac{1}{{R}_{2-{\rm{b}}3}}) $ | (12) |
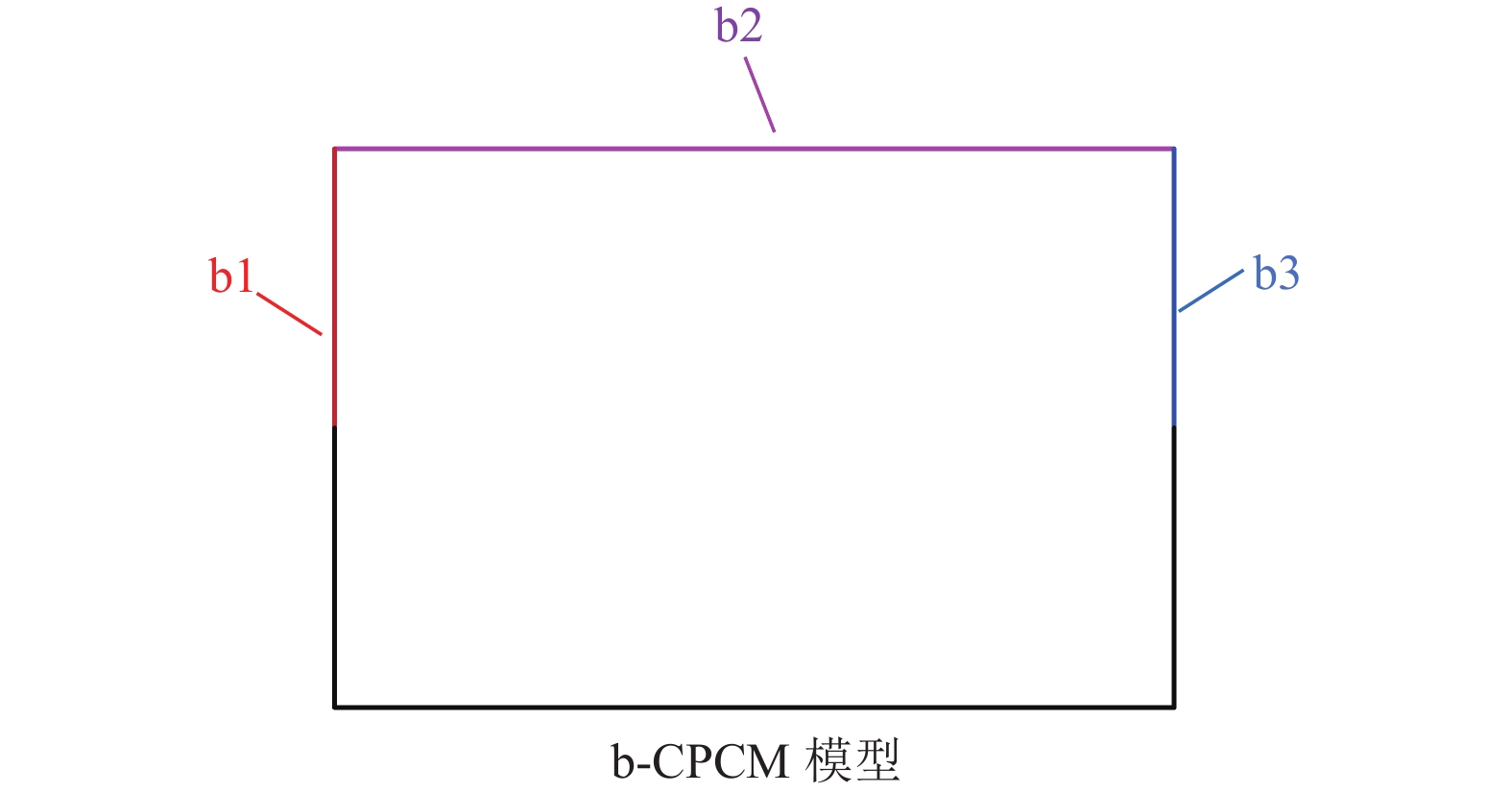
|
图 5 不同外部空气流速下,b-CPCM仿真模型的3个热阻计算区域 Figure 5 At different flow rates, the three thermal resistance calculation areas of the b-CPCM model |
另外,在t-CPCM仿真模型中仿真模型的流场分布符合流体横掠顺排管束模型,因此可以根据式(13)计算h[17]:
| $ {\rm{Nu}}= \frac{h{l}_{{\rm{c}}}}{\lambda } = 0.27\varepsilon {{{\rm{Re}}}^{0.63}{\rm{Pr}}}_{{\rm{f}}}^{0.36}{({{\rm{Pr}}}_{{\rm{f}}}/{{\rm{Pr}}}_{{\rm{w}}})}^{0.25} $ | (13) |
式中:ε为修正系数,Prw为管壁的普朗特数。
通过上述公式的计算后,将b-CPCM仿真模型与t-CPCM仿真模型所使用的参数与计算结果列于表2和表3中。需要特别强调的是,b-CPCM仿真模型中,由于3个计算区域的雷诺数Re的计算结果均小于106,因此可以根据式(6)可以来计算Nu和h。
| 表 2 b-CPCM仿真模型各计算参数 Table 2 b-CPCM model calculation parameters |
| 表 3 t-CPCM仿真模型各计算参数 Table 3 t-CPCM model calculation parameters |
比较表2与表3的计算结果可知,根据式(5)和式(12)计算后可得出b-CPCM仿真模型的R2-b为16.4 K·W−1,而t-CPCM仿真模型的R2-t仅为0.8 K·W−1,是R2-b的1/20。因此,结合前面对导热热阻R1的讨论结果后可以得出,t-CPCM仿真模型的总热阻R远小于b-CPCM模型的R。
2.3 电池热管理系统的建立与测试对b-CPCM和t-CPCM仿真模型的流场和热阻分析后,依据图1所设计的电池热管理系统结构,建立了如图6所示的b-CPCM电池模组与t-CPCM电池模组,以验证这两种电池模组在实际工况下的热管理性能。为了验证两个电池模组在高温工况下的散热性能,将环境温度设定为40 ℃,风速设定为5 m/s,使用1 C倍率充电−搁置20 min−3 C倍率放电(1~3 C)的工步进行测试,并记录如图7所示的4个电池的温度。同时使用式(14)~(16)来定义中心温度,边缘温度和温差,用于评估两个模组的电池热管理性能。

|
图 6 电池模组耦合强制对流实物图 Figure 6 Physical diagram of battery module coupled with forced convection |

|
图 7 温度监测点 Figure 7 Temperature monitoring point |
| $ \mathrm{边}\mathrm{缘}\mathrm{温}\mathrm{度}=\frac{{T}_{1}+{T}_{4}}{2} $ | (14) |
| $ \mathrm{中}\mathrm{心}\mathrm{温}\mathrm{度}=\frac{{T}_{2}+{T}_{3}}{2} $ | (15) |
| $ 温差=中心温度-边缘温度 $ | (16) |
图8为两个电池模组在充放电过程中的温度变化图像。明显可以看出,b-CPCM电池模组的中心温度最高达51.0 ℃,超过了行业推荐的标准[18](≤50 ℃)。而t-CPCM电池模组的中心温度仅为46.9 ℃。而另外一项的温差评估标准,b-CPCM电池模组的最大温差接近5.0 ℃,而t-CPCM电池模组的最大温差仅为0.8 ℃。更低的温差意味着电池模组具有更加优良的温度一致性,对于提升电池模组的寿命至关重要。
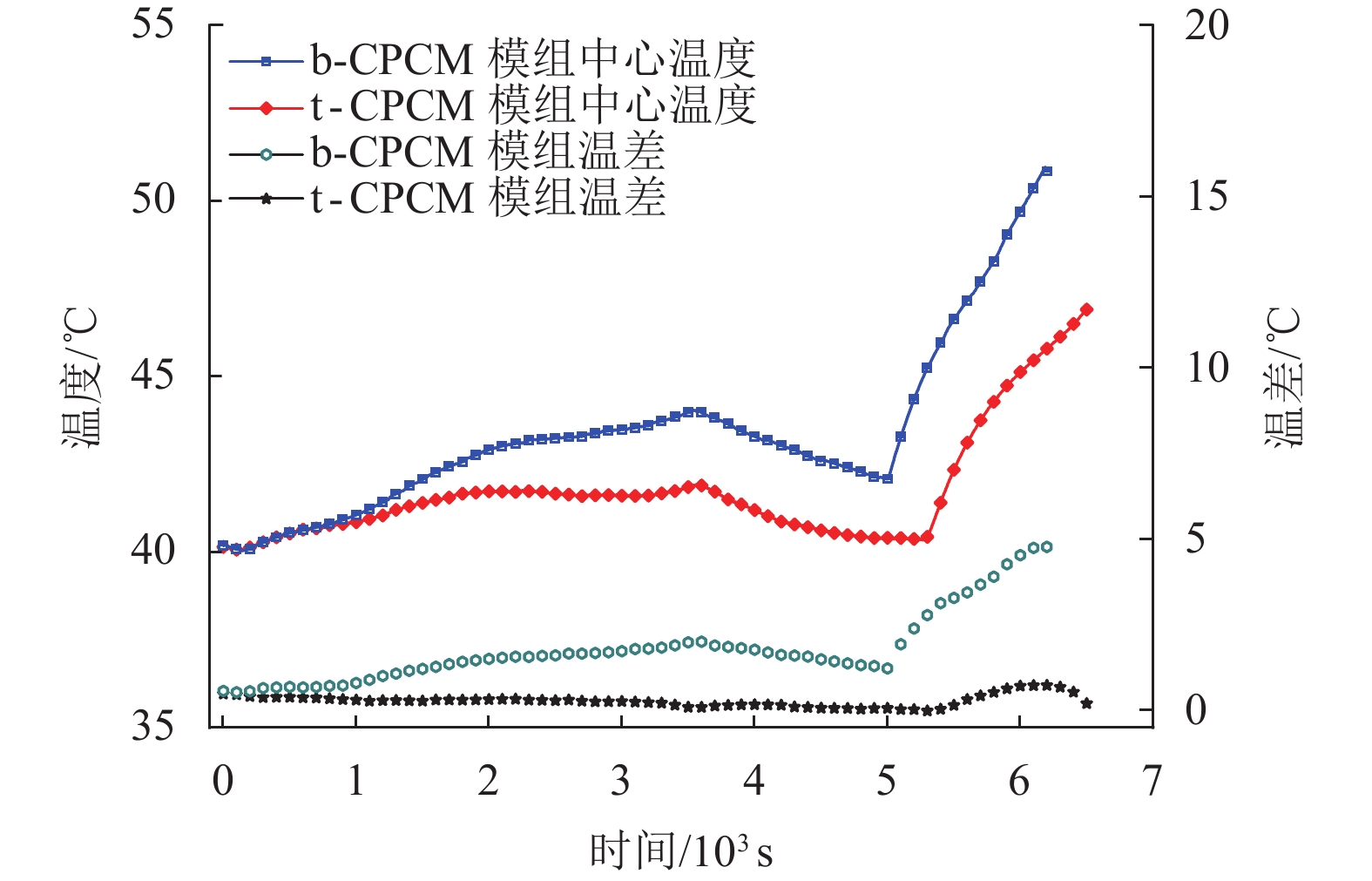
|
图 8 1~3 C充放电工步下,b-CPCM电池模组与t-CPCM电池模组温度变化图 Figure 8 At 1~3C charging and discharging rate, b-CPCM battery module and t-CPCM battery module temperature change diagram |
本文设计了传统的块状复合相变材料(b-CPCM)电池模组与新型的管状复合相变材料(t-CPCM)电池模组,分别耦合强制对流作为电池热管理系统,并采用数值仿真和实验研究的方法评估这两种模组的散热性能。仿真结果表明,相比于b-CPCM仿真模型,更高的散热面积和更均匀的流场分布让t-CPCM仿真模型的换热热阻更低,有利于提高热传导和对流换热的能力。实验结果表明,在40 ℃的高温环境中,t-CPCM电池模组即使在高倍率充放电下也能有效地控制电池温度,例如,t-CPCM电池模组的最高温度仅为46.9 ℃,最大温差仅为0.8 ℃;而传统的b-CPCM电池模组的最高温度则高达51 ℃,最大温差也接近5 ℃,在控温与均温方面均优于传统相变材料的热管理效果。本研究所采用的管状复合相变材料不仅在动力电池领域具有重要的实用价值,而且在其他储能领域也有良好的应用前景。
| [1] |
SHAHBAZ M, RAGHUTLA C, CHITTEDI K R, et al. The effect of renewable energy consumption on economic growth: evidence from the renewable energy country attractive index[J].
Energy (Oxford), 2020, 207: 118162.
DOI: 10.1016/j.energy.2020.118162. |
| [2] |
BUTTURI M A, LOLLI F, SELLITTO M A, et al. Renewable energy in eco-industrial parks and urban-industrial symbiosis: a literature review and a conceptual synthesis[J].
Applied Energy, 2019, 255: 113825.
DOI: 10.1016/j.apenergy.2019.113825. |
| [3] |
LIU Z, HAO H, CHENG X, et al. Critical issues of energy efficient and new energy vehicles development in China[J].
Energy Policy, 2018, 115: 92-97.
DOI: 10.1016/j.enpol.2018.01.006. |
| [4] |
LIN B, WU W. Why people want to buy electric vehicle: an empirical study in first-tier cities of China[J].
Energy Policy, 2018, 112: 233-241.
DOI: 10.1016/j.enpol.2017.10.026. |
| [5] |
WU W, WANG S, WU W, et al. A critical review of battery thermal performance and liquid based battery thermal management[J].
Energy Conversion and Management, 2019, 182: 262-281.
DOI: 10.1016/j.enconman.2018.12.051. |
| [6] |
XU Y, LI X, LIU X, et al. Experiment investigation on a novel composite silica gel plate coupled with liquid-cooling system for square battery thermal management[J].
Applied Thermal Engineering, 2021, 184: 116217.
DOI: 10.1016/j.applthermaleng.2020.116217. |
| [7] |
饶中浩, 汪双凤, 洪思慧, 等. 电动汽车动力电池热管理实验与数值分析[J].
工程热物理学报, 2013(6): 1157-1160.
RAO Z H, WANG S F, HONG S H, et al. Thermal management experiment and numerical analysis of electric vehicle power battery[J]. Journal of Engineering Thermophysics, 2013(6): 1157-1160. |
| [8] |
罗庆凯, 王志荣, 刘婧婧, 等. 18650型锂离子电池热失控影响因素[J].
电源技术, 2016, 40(2): 277-279.
LUO Q K, WANG Z R, LIU J J, et al. Influencing factors of thermal runaway of 18650 lithium-ion battery[J]. Power Supply Technology, 2016, 40(2): 277-279. DOI: 10.3969/j.issn.1002-087X.2016.02.013. |
| [9] |
李惠, 吉维肖, 曹余良, 等. 锂离子电池热失控防范技术[J].
储能科学与技术, 2018, 35(3): 17-24.
LI H, JI W X, CAO Y L, et al. Thermal runaway prevention technology for lithium-ion batteries[J]. Energy Storage Science and Technology, 2018, 35(3): 17-24. |
| [10] |
JILTE R D, KUMAR R, AHMADI M H, et al. Battery thermal management system employing phase change material with cell-to-cell air cooling[J].
Applied Thermal Engineering, 2019, 161: 114199.
DOI: 10.1016/j.applthermaleng.2019.114199. |
| [11] |
IANNICIELLO L, BIWOLÉ P H, ACHARD P. Electric vehicles batteries thermal management systems employing phase change materials[J].
Journal of Power Sources, 2018, 378: 383-403.
DOI: 10.1016/j.jpowsour.2017.12.071. |
| [12] |
TENG T P, CHENG C M, CHENG C P. Performance assessment of heat storage by phase change materials containing MWCNTs and graphite[J].
Applied Thermal Engineering, 2013, 50(1): 637-644.
DOI: 10.1016/j.applthermaleng.2012.07.002. |
| [13] |
LYU Y, LIU G, ZHANG G, et al. A novel thermal management structure using serpentine phase change material coupled with forced air convection for cylindrical battery modules[J].
Journal of Power Sources, 2020, 468: 228398.
DOI: 10.1016/j.jpowsour.2020.228398. |
| [14] |
MILLS A, FARID M, SELMAN J R, et al. Thermal conductivity enhancement of phase change materials using a graphite matrix[J].
Applied Thermal Engineering, 2006, 26(14-15): 1652-1661.
DOI: 10.1016/j.applthermaleng.2005.11.022. |
| [15] |
LYU Y, YANG X, LI X, et al. Experimental study on a novel battery thermal management technology based on low density polyethylene-enhanced composite phase change materials coupled with low fins[J].
Applied Energy, 2016, 178: 376-382.
DOI: 10.1016/j.apenergy.2016.06.058. |
| [16] |
JIANG Z Y, QU Z G, ZHANG J F, et al. Rapid prediction method for thermal runaway propagation in battery pack based on lumped thermal resistance network and electric circuit analogy[J].
Applied Energy, 2020, 268: 115007.
DOI: 10.1016/j.apenergy.2020.115007. |
| [17] |
杨世铭, 陶文铨. 传热学: 第4版[M]. 北京: 高等教育出版社, 2006.
|
| [18] |
靳鹏超, 王世学. 一种使用相变材料的新型电动汽车电池热管理系统[J].
化工进展, 2014(10): 2608-2612.
JIN P C, WANG S X. A new electric vehicle battery thermal management system using phase change materials[J]. Chemical Industry Progress, 2014(10): 2608-2612. |
 2022, Vol. 39
2022, Vol. 39

