随着社会的飞速发展,如何高效、准确地进行身份认证变得越来越重要。和传统的身份识别技术相比,基于生物特征[1]的识别技术由于具有方便、安全、可靠等优点而受到广泛关注。过去的十几年里,掌纹、人脸、字迹、步态、指纹、DNA和声音等[1-6]生物识别技术已在民用领域中广泛使用。和其他生物特征识别技术相比,掌纹[7-11]主要有以下优势:(1) 稳定的特征:掌纹不会像人脸一样随着年龄的变化而变化,也不会像指纹一样被磨损;(2) 识别率高:掌纹不仅包含主线、褶皱和纹理特征等特征,还包含手型特征和静脉特征;(3) 唯一性:研究人员在研究双胞胎的掌纹特征时,发现掌纹可以将双胞胎100%区分开来。
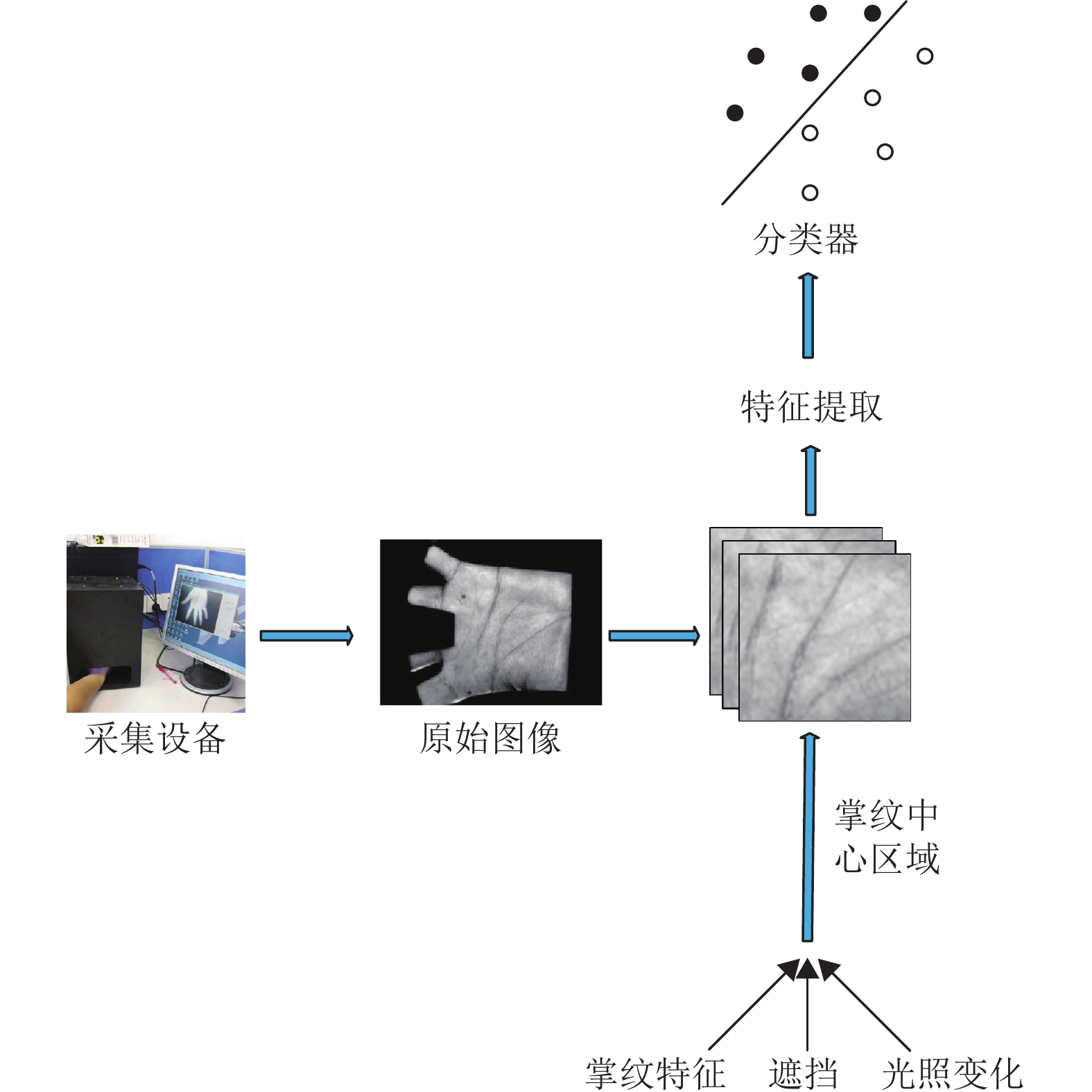
图1为掌纹识别系统的工作流程,主要包含4个部分。(1) 掌纹图像采集:掌纹采集设备用于采集掌纹图像,以便构建掌纹图像数据库。不同的掌纹采集设备可以采集到不同类型的掌纹图像:二维掌纹图像[10-11]、多光谱掌纹图像[12-14]和三维掌纹图像[15-16]。(2) 掌纹图像预处理:在提取掌纹特征和识别之前需要对掌纹进行中心区域[17](region of interest)提取。原始掌纹图像包含很多不必要信息,如背景区域和手指。除了将无用信息去除外,提取掌纹中心区域有利于掌纹对齐,以便后续的特征提取。(3) 掌纹特征提取:掌纹图像除了包含掌纹的特征信息外,还包含遮挡和光照变化等噪音。如何将掌纹特征从掌纹图像中分离出来对后续掌纹分类的准确性有很大影响。(4) 掌纹分类:大部分掌纹数据库提供的掌纹图像都进行了预处理,本文将注意力集中在掌纹特征提取和分类上。
|
图 1 掌纹识别系统的工作流程 Figure 1 Work flow of palmprint recognition system |
过去的20年来,很多学者提出了多种有效的掌纹识别算法。大致可以把这些算法分为2大类:手工提取图像特征的掌纹识别算法和基于学习的掌纹识别算法。
手工提取掌纹图像特征的算法利用先验知识设计一个效果良好的特征提取模型。掌纹图像中最显著的特征就是3条主线,即生命线,智慧线,感情线。因此基于手工提取特征的掌纹识别算法旨在通过边缘检测算子来提取掌纹主线特征。如Huang等[18]提出了一种基于掌纹主线的掌纹识别算法。特征提取阶段,采用改进的有限Radon变换(Modified Finite Radon Transform, MFRT)来提取掌纹的主线特征并使用一种新的掌纹匹配算法(pixel-to-area)来计算2个掌纹之间的相似度。然而掌纹主线特征单一且在数据量大的时候容易出现主线特征相似的2个不同掌纹。因此,近期许多工作专注于提取掌纹的褶皱和纹理特征。如,Sun等[19]使用Gabor滤波器来提取相交2条线的响应值并使用序数的方法对其进行编码。Kong等[20]提出竞争编码算法,即用6个方向的Gabor滤波器去提取掌纹中每一个点的方向,将响应最大的方向设为该点主方向。由于竞争编码采取赢者通吃的方法,使得它不能准确地提取到线特征的主方向。针对这个问题,Xu等[21]提出了区分性和鲁棒性竞争编码(Discriminative and Robust Competitive Code, DRCC),使得提取的掌纹方向特征更加准确。Guo等[22]提出二进制方向向量(Binary Orientation Co-occurrence Vector, BOCV)算法来改进算法的性能。Zheng等[23]从二维掌纹图像中提取三维特征来用于掌纹识别。Fei等[24]提出显性和隐性方向编码(Apparent and Latent Direction Code, ALDC)提取掌纹的双层方向信息。后来,Jia等[25]提出线方向直方图(Histogram of Oriented Lines,HOL)算法将提取到的掌纹线特征转换成直方图描述子用于掌纹的识别。
虽然手工提取的掌纹特征取得了很好效果,但是它不具备可扩展性。这些手工的图像特征一般是由数据科学家根据特定的机器学习任务进行设计,这就要求数据科学家必须具有丰富的领域知识。手工提取特征是人去寻找特征,而基于学习的掌纹识别算法是让机器从训练样本中学习数据的内在特征。Zhao等[26]从掌纹中提取局部方向特征(Complete Local Direction Feature, CLDF)和卷积差异特征(Salient Convolution Difference Feature, SCDF),并从CLDF和SCDF中学习掌纹的判别性特征。Fei等[27]通过最大化类间距离和最小化类内距离,从掌纹的方向特征和纹理特征中学习判别性特征。一些子空间的方法,比如说独立主成分分析[28-29]和局部保留映射[30]等也被用于掌纹识别中。得益于计算能力的飞速进步,近年来神经网络算法得到了快速的发展。深度学习也被用于掌纹识别的任务中[31-32]。神经网络虽然在人脸识别,图像检索、自然语言处理中取得很好的效果,然而神经网络的效果依赖于数据库的大小和图像分辨率。而现有的掌纹数据库的数据量都比较小且分辨率低,是一个典型的小样本问题,因此神经网络并不能取得最好的效果。
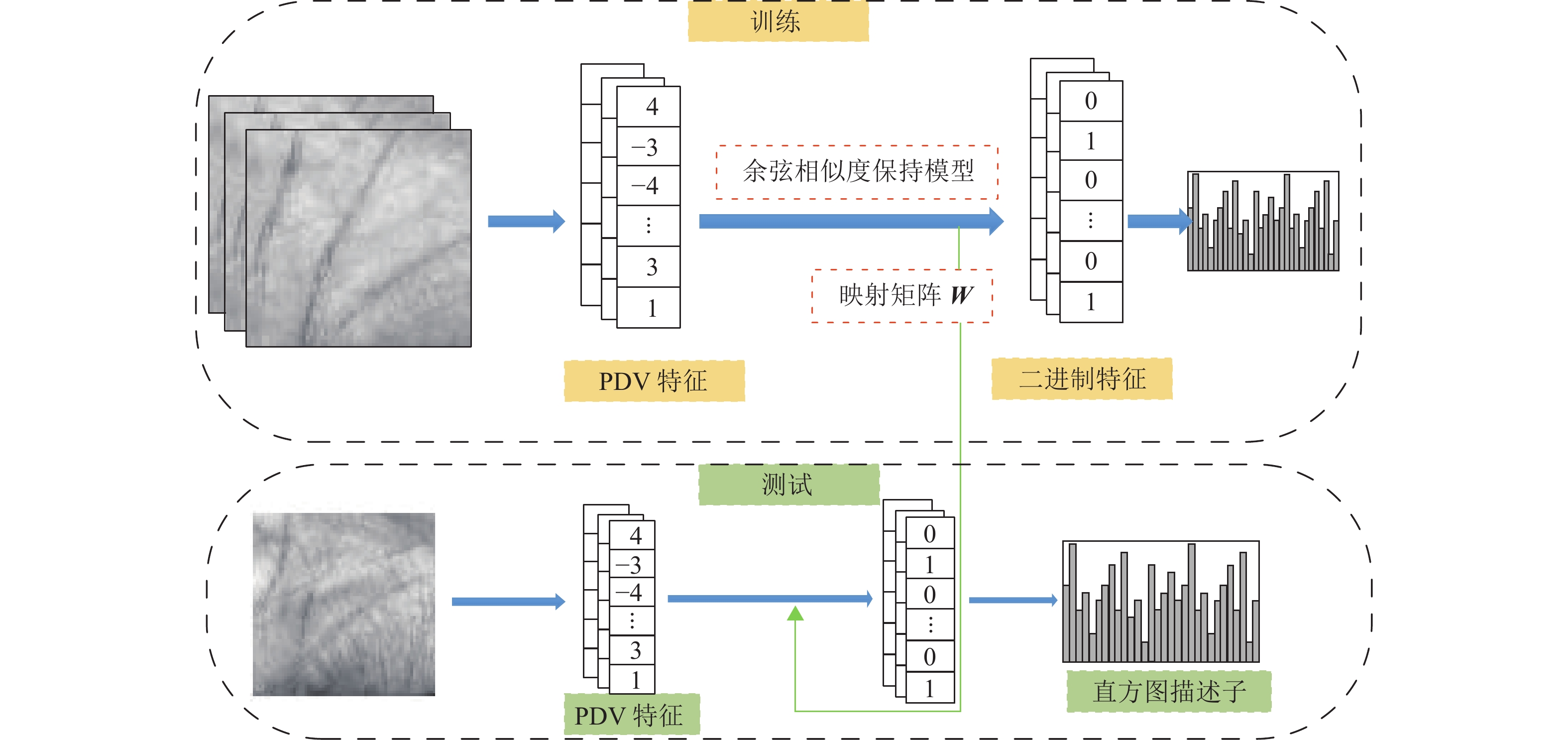
本文提出了一种基于余弦相似度保留的掌纹识别算法。图2给出了算法的流程。对于训练过程,首先提取掌纹的PDV (Pixel Different Vector)特征,然后通过余弦相似度保持模型(Cosine Similarity Preserving Learning, CSPL)同时学习PDV特征的二进制表示及其映射函数以减少PDV特征中的信息冗余。为了处理掌纹位置偏移和光照变化等噪音,将学习得到的二进制特征编码成直方图描述子。对于测试过程,利用学习到的映射函数将测试掌纹图像的PDV特征快速编码成二进制特征编码,并将其转化成直方图描述子。通过比较训练样本和测试样本的直方图描述子可以识别相似的掌纹图像。
|
图 2 算法流程 Figure 2 Flowchart of algorithm |
本节先介绍提取PDV[33]特征的方法,然后介绍如何通过余弦相似度保持模型将PDV特征映射为二进制特征,最后给出了将二进制特征编码成直方图描述子的过程。
1.1 PDV特征学习PDV特征可以很好地刻画图像的局部特征,被广泛应用于计算机视觉算法中。
本文用
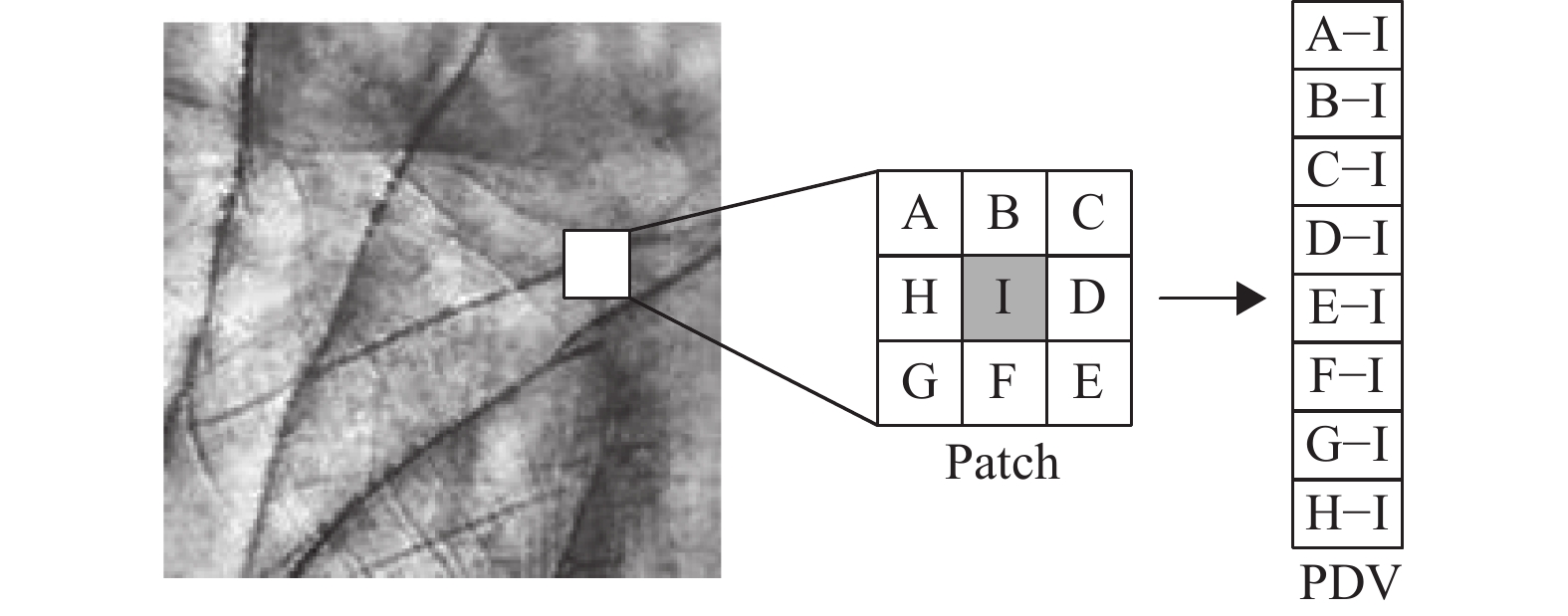
(1) 对于训练样本的每个像素点,先计算该像素和周围正方形区域像素的差值,接着以左上角为起点,以顺时针的方向将像素差值连接起来形成PDV特征。图3是提取像素I的PDV特征过程。
(2) 对于一个维度为
|
图 3 PDV的提取过程 Figure 3 PDV extraction process |
和实值特征(real-valued feature)相比,二进制特征对光照变化具有鲁棒性。为了去除PDV特征中的冗余信息并获得更加鲁棒性的特征,本文将实值的PDV特征转化为二进制特征
余弦相似度通过计算两个向量之间的夹角来衡量向量之间的相似度,即
| $ \left\{ \begin{array}{l} {{{O}}_{{\text{obj}}}} = \mathop {\min }\limits_{{\boldsymbol{B}}} {\displaystyle\sum\nolimits_{i,j = 1}^{n \times d} {\left( {\dfrac{{{{{\boldsymbol{u}}}_i}{{\boldsymbol{u}}}_j^{{\rm{T}}} }}{{{{\| {{{{\boldsymbol{u}}}_i}} \|}_2}{{\| {{{{\boldsymbol{u}}}_j}} \|}_2}}} - \dfrac{1}{r}\dfrac{{{{{\boldsymbol{b}}}_i}{{\boldsymbol{b}}}_j^{{\rm{T}}} }}{{{{\| {{{{\boldsymbol{b}}}_i}} \|}_2}{{\| {{{{\boldsymbol{b}}}_j}} \|}_2}}}} \right)} ^2} \\ {\text{s}}.{\text{t}}.{\text{ }}{{{\boldsymbol{b}}}_i} \in {\{ - 1,1\} ^{1 \times k}},{{{\boldsymbol{b}}}_i} = {\text{sgn}}({{{\boldsymbol{u}}}_i}{\boldsymbol{W}}) \end{array} \right. $ | (1) |
式中:
| $ \left\{ \begin{array}{l} {{{O}}_{{\text{obj}}}} = \mathop {\min }\limits_{{\boldsymbol{B}}} ||{{\boldsymbol{U}}}{{{\boldsymbol{U}}}^{\text{T}}} - \dfrac{1}{r}{{\boldsymbol{B}}}{{{\boldsymbol{B}}}^{\text{T}}}|{|^2} \hfill \\ {\text{s}}.{\text{t}}.\;\;{{\boldsymbol{B}}} \in {\{ - 1,1\} ^{(n \times d) \times k}} ,\; {{\boldsymbol{B}}} = {\text{sgn(}}{{\boldsymbol{UW}}}{\text{)}} \end{array} \right. $ | (2) |
式中:
| $\left\{ \begin{array}{l} {{{O}}_{{\text{obj}}}} = \mathop {\min }\limits_{{\boldsymbol{B}}} {\lambda _1}||{{\boldsymbol{U}}}{{{\boldsymbol{U}}}^{\text{T}}} - \dfrac{1}{r}{{\boldsymbol{B}}}{{\text{(}}{{\boldsymbol{UW}}}{\text{)}}^{\text{T}}}|{|^2} + {\lambda _2}||{{\boldsymbol{B}}} - {{\boldsymbol{UW}}}|{|^2} \hfill \\ {\text{s}}.{\text{t}}.\;\;{{\boldsymbol{B}}} \in {\{ - 1,1\} ^{(n \times d) \times k}}\end{array} \right. $ | (3) |
式中:
在这个部分,主要介绍对目标函数求解的优化算法。首先对变量
W子问题:固定等式(3)中的二进制特征矩阵
| $ \left\{ \begin{array}{l} \mathop {\min }\limits_{{\boldsymbol{W}}} {\lambda _1}{\text{tr}}( - \dfrac{2}{r}{{\boldsymbol{U}}}{{{\boldsymbol{U}}}^{\text{T}}}{{\boldsymbol{B}}}{{{\boldsymbol{W}}}^{\text{T}}}{{{\boldsymbol{U}}}^{\text{T}}} + \frac{1}{{{r^2}}}{{\boldsymbol{UW}}}{{{\boldsymbol{B}}}^{\text{T}}}{{\boldsymbol{B}}}{{{\boldsymbol{W}}}^{\text{T}}}{{{\boldsymbol{U}}}^{\text{T}}}) + \hfill \\ {\lambda _2}{\text{tr}}( - 2{{{\boldsymbol{W}}}^{\text{T}}}{{{\boldsymbol{U}}}^{\text{T}}}{{\boldsymbol{B}}} + {{{\boldsymbol{W}}}^{\text{T}}}{{{\boldsymbol{U}}}^{\text{T}}}{{\boldsymbol{UW}}}) \hfill \\ {\text{s}}.{\text{t}}.\;\;{{\boldsymbol{B}}} \in {\{ - 1,1\} ^{(n \times d) \times k}} \end{array} \right. $ | (4) |
使式(4)的导数为零,可以得到投影矩阵的解为
| $ \begin{split} & {\nabla _{{\boldsymbol{W}}}}{\lambda _1}{\text{tr}}( - \frac{2}{r}{{\boldsymbol{U}}}{{{\boldsymbol{U}}}^{\text{T}}}{{\boldsymbol{B}}}{{{\boldsymbol{W}}}^{\text{T}}}{{{\boldsymbol{U}}}^{\text{T}}} + \frac{1}{{{r^2}}}{{\boldsymbol{UW}}}{{{\boldsymbol{B}}}^{\text{T}}}{{\boldsymbol{B}}}{{{\boldsymbol{W}}}^{\text{T}}}{{{\boldsymbol{U}}}^{\text{T}}}) + \hfill \\ & {\lambda _2}{\text{tr}}( - 2{{{\boldsymbol{W}}}^{\text{T}}}{{{\boldsymbol{U}}}^{\text{T}}}{{\boldsymbol{B}}} + {{{\boldsymbol{W}}}^{\text{T}}}{{{\boldsymbol{U}}}^{\text{T}}}{{\boldsymbol{UW}}}) = - \frac{2}{r}{\lambda _1}{{{\boldsymbol{U}}}^{\text{T}}}{{\boldsymbol{U}}}{{{\boldsymbol{U}}}^{\text{T}}}{{\boldsymbol{B}}} +\hfill \\ & \frac{2}{{{r^2}}}{\lambda _1}{{{\boldsymbol{U}}}^{\text{T}}}{{\boldsymbol{UW}}}{{{\boldsymbol{B}}}^{\text{T}}}{{\boldsymbol{B}}} - 2{\lambda _2}{{{\boldsymbol{U}}}^{\text{T}}}{{\boldsymbol{B}}} + 2{\lambda _2}{{{\boldsymbol{U}}}^{\text{T}}}{{\boldsymbol{UW}}} \hfill \end{split} $ | (5) |
| $\boldsymbol{W}=\left(\boldsymbol{U}^{\mathrm{T}} \boldsymbol{U}\right)^{-1}\left(\frac{2}{r} \lambda_{1} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{U} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{B}+2 \lambda_{2} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{B}\right)\left(\frac{2}{r^{2}} \lambda_{1} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{B}+\lambda_{2} \boldsymbol{I}\right)^{-1}$ | (6) |
B子问题:对于式(3),固定投影矩阵
| $ \left\{ \begin{array}{l} \mathop {\min }\limits_{{\boldsymbol{B}}} \dfrac{{\text{1}}}{{{r^2}}}{\lambda _1}||{{\boldsymbol{B}}}{{\text{(}}{{\boldsymbol{UW}}}{\text{)}}^{\text{T}}}|{|^2} - \dfrac{2}{r}{\lambda _1}{\text{tr}}({{{\boldsymbol{B}}}^{\text{T}}}({{\boldsymbol{U}}}{{{\boldsymbol{U}}}^{\text{T}}}{{\boldsymbol{UW}}})) - \hfill \\ 2{\lambda _2}{\text{tr}}({{{\boldsymbol{B}}}^{\text{T}}}{{\boldsymbol{UW}}}) \hfill \\ {\text{s}}.{\text{t}}.\;\;{{\boldsymbol{B}}} \in {\{ - 1,1\} ^{(n \times d) \times k}} \end{array} \right. $ | (7) |
为了求解离散编码
| $\left\{ \begin{array}{l} \mathop {\min }\limits_{{\boldsymbol{B}}} \dfrac{1}{{{r^2}}}{\lambda _1}||{{\boldsymbol{B}}}{{{\boldsymbol{V}}}^{\text{T}}}|{|^2} - 2{\text{tr}}({{{\boldsymbol{B}}}^{\text{T}}}{{\boldsymbol{Q}}}) \hfill \\ {\text{s}}.{\text{t}}.\;\;{{\boldsymbol{B}}} \in {\{ - 1,1\} ^{(n \times d) \times k}}\end{array} \right. $ | (8) |
式中:
这里分别用
| $ ||{{\boldsymbol{B}}}{{{\boldsymbol{V}}}^{\text{T}}}|{|^2}{\text{ = tr}}({{\boldsymbol{V}}}{{{\boldsymbol{B}}}^{\text{T}}}{{\boldsymbol{B}}}{{{\boldsymbol{V}}}^{\text{T}}}) = {\text{const}} + 2{{{\boldsymbol{v}}}^{\text{T}}}{{{\boldsymbol{V}}}'}{{{\boldsymbol{B}}'}^{{\text{T}}}}{{\boldsymbol{b}}} $ | (9) |
同样的可以得到
| $ {\text{tr}}({{{\boldsymbol{B}}}^{\text{T}}}{{\boldsymbol{Q}}}) = {\text{const}} + {{{\boldsymbol{q}}}^{\text{T}}}{{\boldsymbol{b}}} $ | (10) |
将式(8)~(10)结合在一起可以得到
| $ \mathop {\min }\limits_{{\boldsymbol{b}}} (\frac{1}{{{r^2}}}{\lambda _1}{{{\boldsymbol{B}}}'}{{{\boldsymbol{V}}'}^{{\text{T}}}}{{\boldsymbol{v}} } - {{{\boldsymbol{q}}}^{\text{T}}}){{\boldsymbol{b}}} $ | (11) |
最后根据式(11)求解得到
| $ {{\boldsymbol{b}}} = {{\boldsymbol{q}}} - \frac{1}{{{r^2}}}{\lambda _1}{{{\boldsymbol{v}}}^{\text{T}}}{{{\boldsymbol{V}}}'}{{{\boldsymbol{B}}'}^{{\text{T}}}} $ | (12) |
直方图是一个统计学上的概念,反映了相应变量的分布情况,所以变量的微小变化对直方图的影响微乎其微。一些掌纹识别算法,比如ALDC[24]和HOL[25]使用直方图描述子来处理掌纹图像中光照,平移和旋转等噪音。为了提高算法的鲁棒性,本文将学习到的二进制特征编码成直方图描述子,相应的计算过程包括:
(1) 将掌纹图像分成
(2) 对于每个block,使用K-means聚类算法将学习到的二进制特征聚类成
| $ {\bf{HB}} = [{\text{F}}{{\text{N}}_1},{\text{F}}{{\text{N}}_2}, \cdots ,{\text{F}}{{\text{N}}_N}] $ |
(3) 将每个block的直方图连接起来为最终的直方图描述子(Histogram of Graph, HG)。
| $ {\bf{HG}} = [{\text{H}}{{\text{B}}_1},{\text{H}}{{\text{B}}_2}, \cdots ,{\text{H}}{{\text{B}}_{m \times m}}]。$ |
在这一节中,使用3个掌纹数据库:polyU接触式掌纹数据库,ITTD非接触式掌纹数据库和CASIA非接触式掌纹数据库对本文提出的算法进行有效性验证。在实验中使用余弦相似度来进行识别。
2.1 掌纹数据库polyU掌纹数据集包含193名师生(每名师生提供左右手,即一共386个不同的掌纹)的7752张掌纹图像。掌纹的采集过程分为2个阶段,每个阶段对每个志愿者的左右手分别采集10张掌纹图像。经过ROI图像裁剪后,每张掌纹图像的分辨率为64×64。
ITTD掌纹数据库包含2601张掌纹图像。对于每个手掌,分别收集5~7张不同手部姿势变化的掌纹图像。并且这些掌纹图像的ROI(150×150分辨率掌纹图像)以位图的格式提供给大众。
CASIA非接触式掌纹数据库是由中国科学院自动化研究所收集的。所有掌纹图像均使用研究中心开发的掌纹识别系统采集,每个手掌分别采集6~18张掌纹图像。CASIA掌纹数据库一共包含5501张来自310名志愿者的掌纹图像(128×128分辨率掌纹图像)。
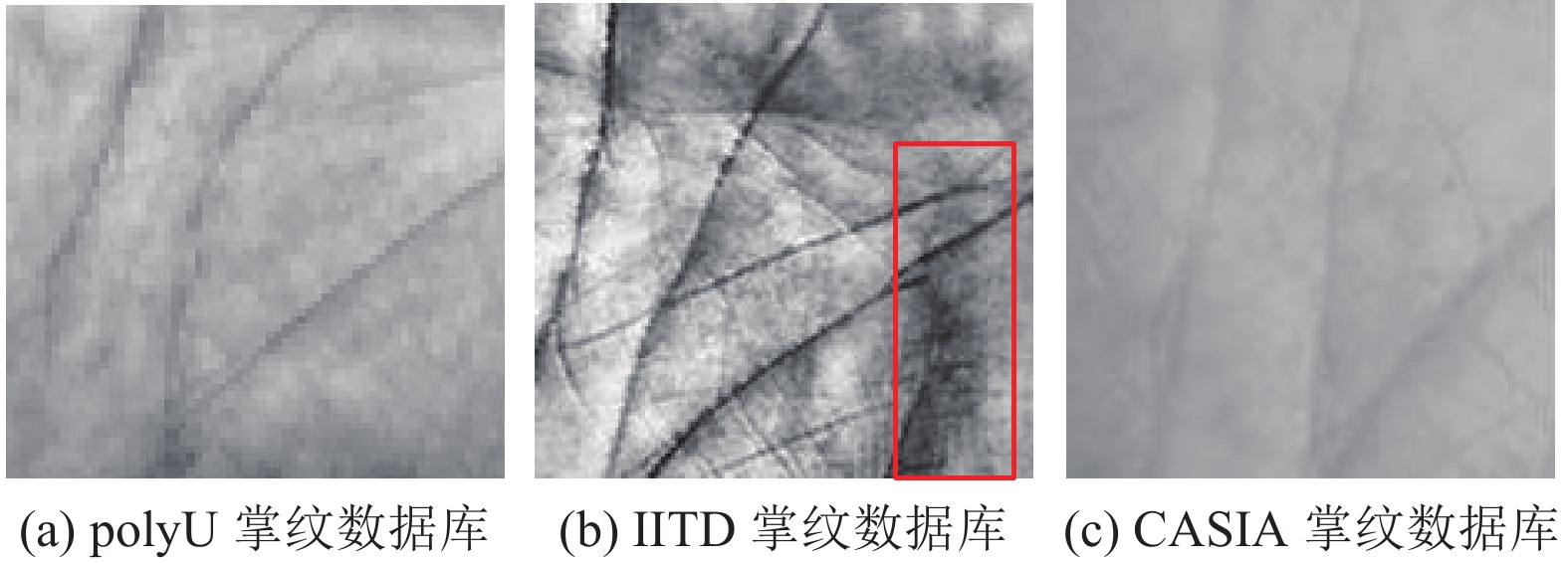
图4中从左到右的掌纹分别来自polyU、IITD和CASIA掌纹数据库。从图中可以看出polyU数据库中的掌纹线特征清晰且表面没有干扰的噪点。IITD中的掌纹虽然线特征清晰,但是从图4(b)中红框处可看出IITD掌纹表面有明显阴影。CASIA数据库中的掌纹图像则是整体偏白,线特征不够清晰。
|
图 4 来自不同掌纹数据库的掌纹图像 Figure 4 Palmprint images from different palmprint databases |
图5为接触式掌纹采集设备,在采集掌纹的时候需要用户将手掌和采集设备接触。接触式的掌纹采集设备可以很方便地获得清晰的掌纹图像,但是对用户不友好。图6为非接触式掌纹采集设备,在采集过程中,用户只需将手掌对着采集设备即可。由于非接触式的掌纹采集设备具有携带方便、对用户友好等优点,成为近年来研究的一个热点。但受到光照和手掌位置偏移的影响,采集到的掌纹图像常常出现偏移、噪音污染等情况。

|
图 5 接触式掌纹采集设备 Figure 5 Contact palmprint collection device |
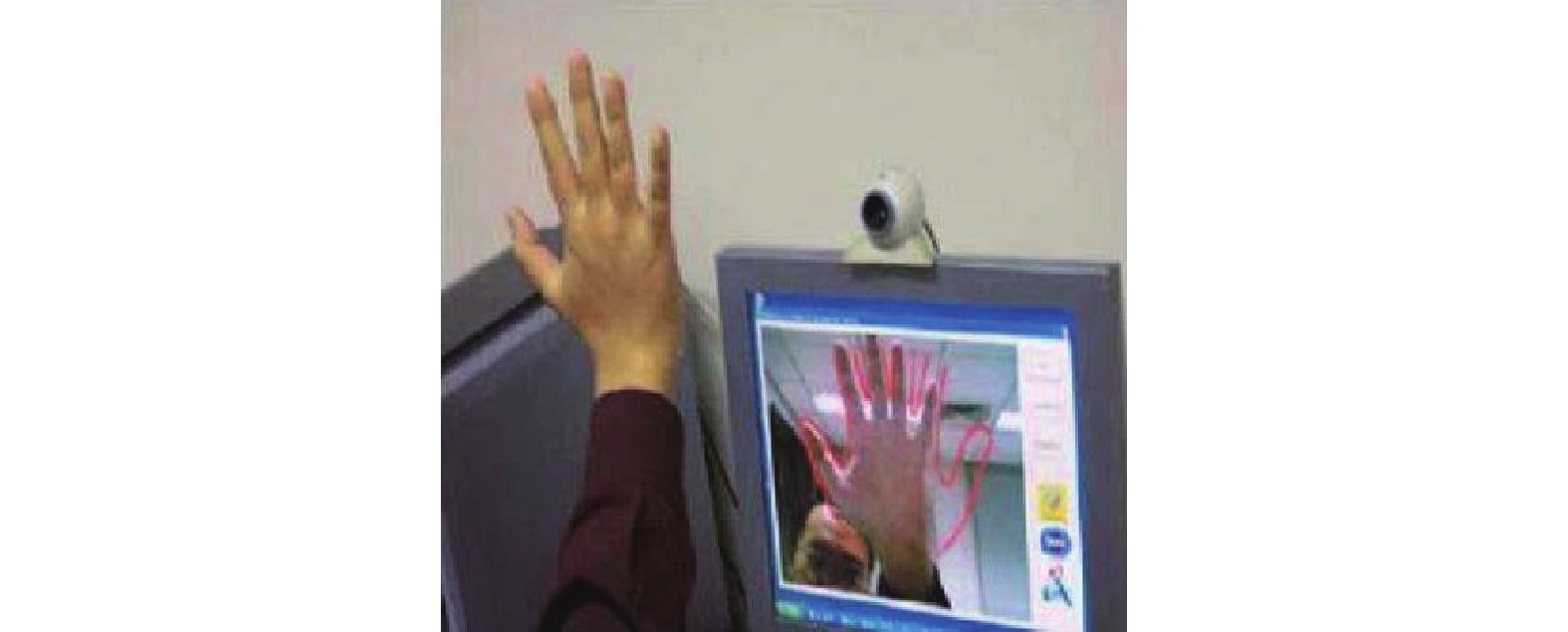
|
图 6 非接触式掌纹采集设备 Figure 6 Contactless palmprint collection device |
掌纹识别是将一个待查询的图像与训练集中的其他图像进行比较,并确定该图像与数据库中的哪一类图像最接近。实验过程中,随机选取每个掌纹的3张图像作为训练集,其余的图像作为测试集。即在polyU掌纹数据库中选取1158张掌纹图像作为训练集,6594张掌纹图像作为测试集。IITD掌纹数据库中选取1380张掌纹图像作为训练集,1221张掌纹图像作为测试集。CASIA掌纹数据库中选取1860张掌纹图像作为训练集,3641张掌纹图像作为测试集。
在实验中,使用DRCC[21],DoN[23], ALDC[24], HOL[25],Ordinal[19]和VGG-F[35]6种比较有代表性的算法来进行对比实验。表1给出了本文算法和其他算法在polyU,IITD和CASIA 3个掌纹数据库中的实验结果。
| 表 1 算法识别率 Table 1 Algorithm recognition rate |
由于polyU接触式掌纹数据库中的掌纹图像清晰,受到的噪声干扰小。所有的算法都实现了较高的识别率,其中本文算法和ALDC的准确率最高。
同时,在非接触式掌纹数据库(IITD掌纹数据库和CASIA掌纹数据库)中,除了HOL算法、ALDC算法和本文的算法外,其他掌纹识别算法的表现大大不如在接触式掌纹数据库中的表现。即使在polyU数据库中表现优异的DRCC算法,在这两个数据库中的识别率下降了20%左右。由图4可以看出,IITD和CASIA数据库中普遍出现噪音干扰和线特征不清晰等问题[36],所以在接触式掌纹数据库上表现优秀的算法在非接触式掌纹数据库中不一定能取得一样的效果。而本文的算法在得到掌纹的二进制的特征的时候将其编码成直方图特征,和没有使用直方图特征的DRCC、DoN和Ordinal算法相比具有更好的抗干扰性。和同样使用了直方图的HOL和ALDC算法相比,本文的算法在提取了PDV特征后,通过学习将PDV特征的冗余信息去除后得到二进制特征,而HOL和ALDC是直接使用手工提取的特征。这表明本文的算法和手工提取特征的算法相比有更好的表现。
2.3 掌纹认证掌纹认证(Palmprint Verification)是通过比较来确定两张掌纹图像是否属于同一个人。通常先设定一个阈值,如果两张图片的相似度大于这个阈值则将判断这两张图片来自同一个个体,否则将这两张图片判断为来自不同个体。
图7~9分别表示在3个数据库中不同算法的表现。横坐标表示错误接受率(False Accept Rate, FAR),纵坐标表示错误拒绝率(False Reject Rate, FRR)。表2中给出的是等错误率(Equal Error Rate, EER)。从图7~9和表2中可看出,在polyU数据库中所有的算法的表现都非常接近。而在非接触式数据库(IITD和CASIA掌纹数据库)中,本文提出的算法取得最好的性能。

|
图 7 算法在CASIA数据集上的ROC曲线 Figure 7 ROC curves on the CASIA database |
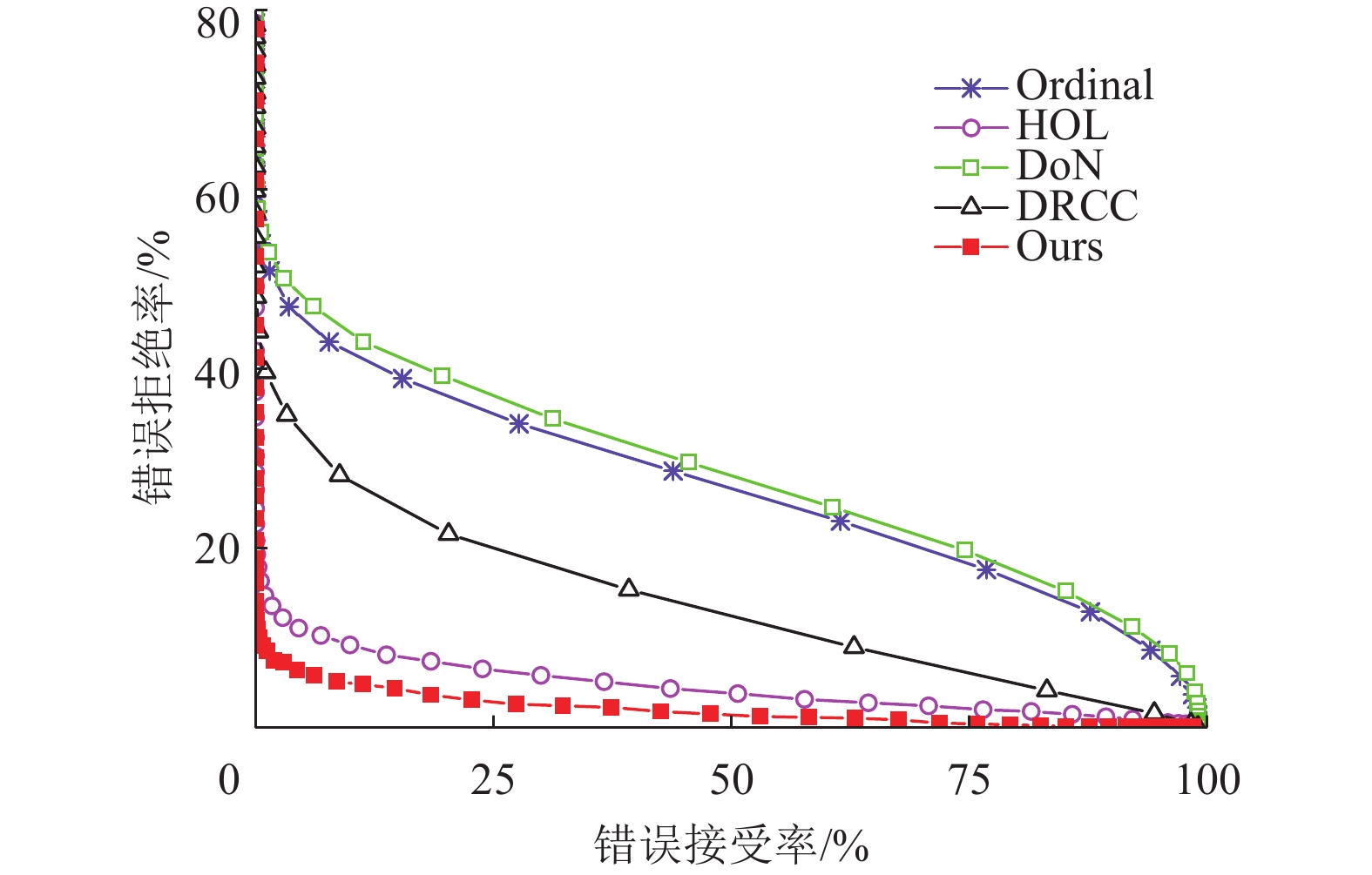
|
图 8 算法在IITD数据集上的ROC曲线 Figure 8 ROC curves on the IITD database |
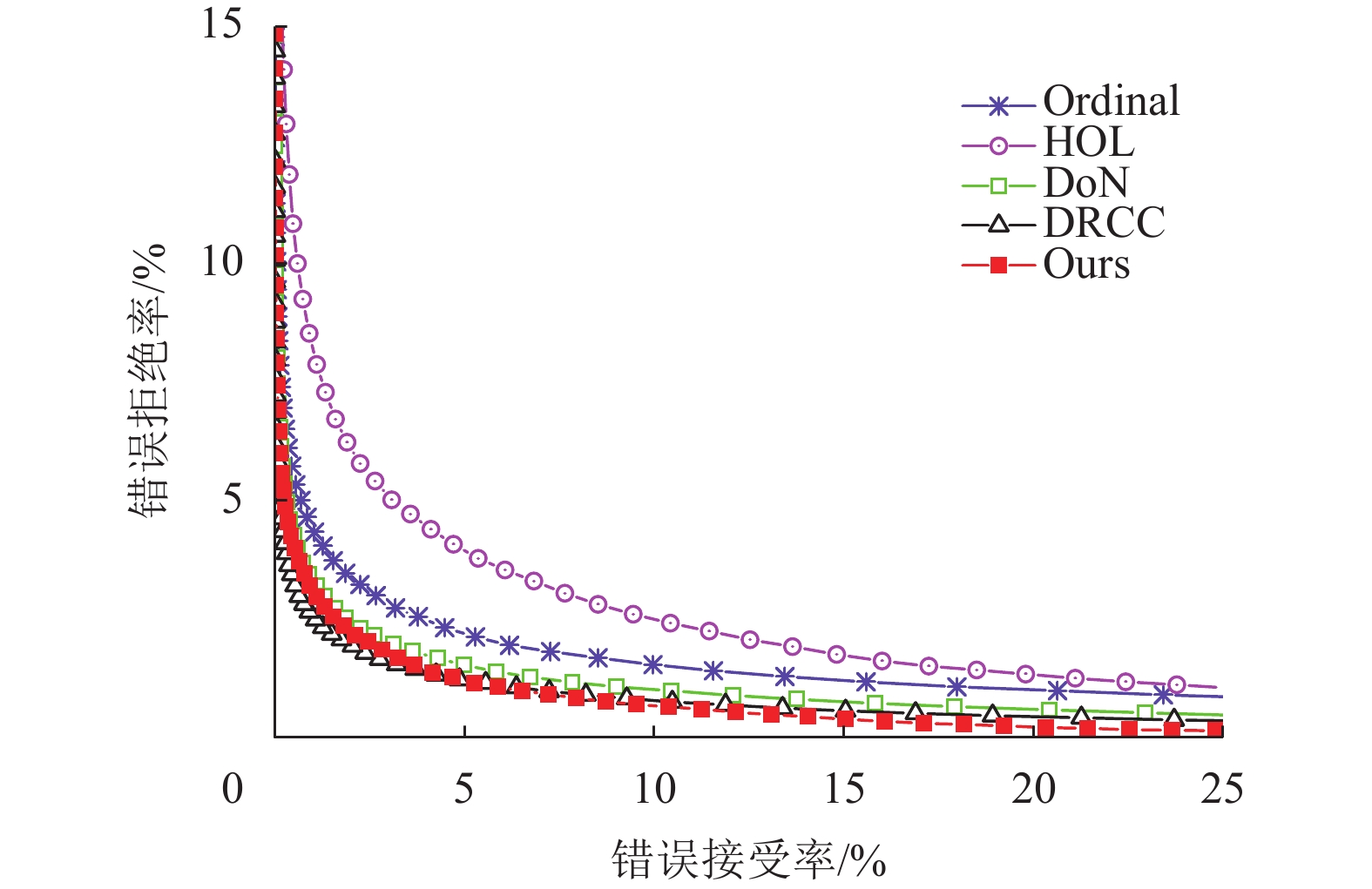
|
图 9 算法在polyU数据集上的ROC曲线 Figure 9 ROC curves on the polyU database |
| 表 2 等错误率 Table 2 Equal error rate |
本文所提算法首先提取了掌纹的PDV特征,然后使用余弦相似度保持模型(CSPL)将学习到的PDV特征映射为二进制特征,最后将其计算为直方图特征。为了验证余弦相似度保持模型(CSPL)的有效性,将使用局部二进制编码[37](Local Binary Pattern, LBP)处理PDV特征、直接使用PDV向量作为特征表示与使用余弦相似度保持模型(CSPL)三者进行对比。
(1) LBP:对掌纹图像提取了PDV特征后,使用LBP将其映射为二进制特征,最后将二进制特征计算为直方图特征。
(2) PDV:对掌纹图像提取了PDV特征后,直接将其计算成直方图特征。
(3) CSPL:对掌纹图像提取了PDV特征后,使用余弦相似度保持模型将其映射为二进制特征,最后将学习到的二进制特征计算为直方图特征。
相关的实验结果如表3所示。
| 表 3 算法识别率 Table 3 Algorithm recognition rate |
从表3可知,相对于使用LBP将PDV特征映射为二进制特征和不将PDV特征映射为二进制特征,使用余弦相似度保持模型(CSPL)比前两者效果更好。
2.5 特征长度的敏感性余弦相似度保持模型(CSPL)将PDV特征映射为二进制特征,不同长度的二进制特征包含不同的信息量。为了测试不同长度的二进制特征对算法准确率的影响,在IITD掌纹数据库中测试了5,10,15,20,25这5种不同长度的二进制编码对算法识别率的影响。图10显示了不同的二进制特征长度对算法准确率的影响。
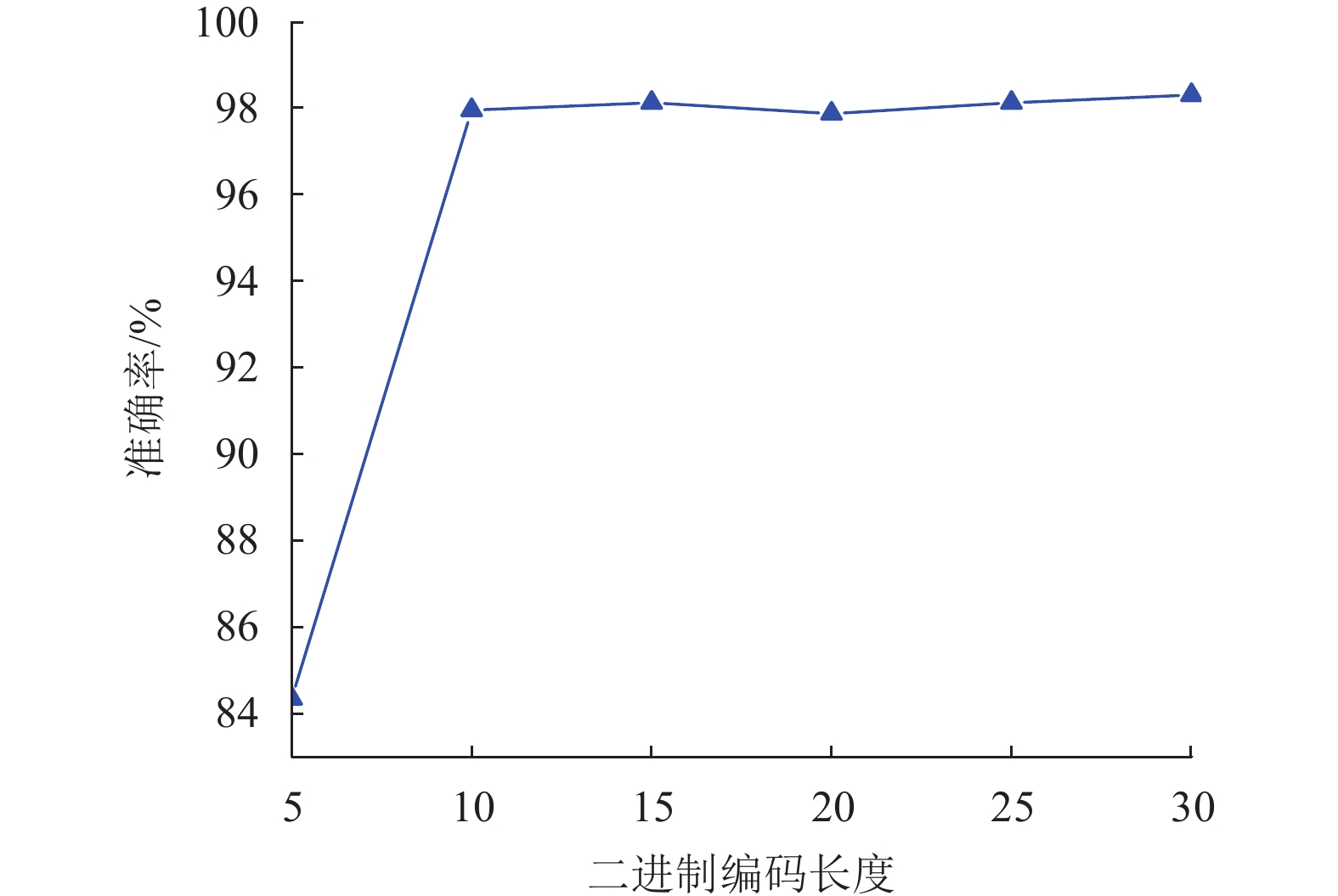
|
图 10 二进制编码长度对实验结果的影响 Figure 10 Influence of binary coding length |
从图10可以看出,将二进制编码的长度设置为5的时候,算法的准确率可以达到84.3%。当二进制编码的长度大于等于10的时候,算法的准确率呈缓慢上升的趋势。但是二进制编码的长度增加意味着训练时间的增加,且当二进制编码长度大于15的时候,准确率变化不大。综合性能和时间成本,将最优的二进制编码的长度设置为15。
3 结论本文设计了一种基于余弦相似度保持的掌纹识别算法。主要贡献可以总结如下:
(1) 通过让学习到的二进制特征的余弦值和原始特征的余弦值保持一致,使得学习得到的二进制特征保留原始空间结构。
(2) 在3个广泛使用的掌纹数据库上进行了大量实验,结果表明:和其他掌纹识别算法相比,本文提出的算法能更好地挖掘掌纹的潜在信息,体现了更高的精度和抗干扰性,验证了本文算法的优越性和有效性。
| [1] |
ANIL K, KARTHIK N, ARUN R. 50 years of biometric research: accomplishments, challenges, and opportunities[J].
Pattern Recognition Letters, 2016, 79(1): 80-105.
|
| [2] |
钟德星, 朱劲松, 杜学峰. 掌纹识别综述[J].
模式识别与人工智能, 2019, 32(5): 436-445.
ZHONG D X, ZHU J S, DU X F. Progress of palmprint recognition: a review[J]. Pattern Recognition and Artificial Intelligence, 2019, 32(5): 436-445. |
| [3] |
DING Y H, ZHUANG D, WANG K. A study of hand vein recognition method[C]//IEEE International Conference Mechatronics and Automation. Niagara Falls: IEEE, 2005: 2106-2110.
|
| [4] |
KUMAR A, WONG D C M, SHEN H C, et al. Personal verification using palmprint and hand geometry biometric[C]// International Conference on Audio and Video Based Biometric Person Authentication. Berlin: Springer, 2003: 668-678.
|
| [5] |
ZHOU M, ZHANG X, YIN F, et al. Discriminative quadratic feature learning for handwritten Chinese character recognition[J].
Pattern Recognition, 2016, 49(1): 7-18.
|
| [6] |
SARKAR S, PHILLIPS P J, LIU Z, et al. The humanoid gait challenge problem: data sets, performance, and analysis[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(2): 162-177.
DOI: 10.1109/TPAMI.2005.39. |
| [7] |
SHU W, ZHANG D. Automated personal identification by palmprint[J].
Optical Engineering, 1998, 37(8): 2359-2362.
DOI: 10.1117/1.601756. |
| [8] |
ZHANG D, SHU W. Two novel characteristics in palmprint verification: datum point invariance and line feature matching[J].
Pattern Recognition, 1999, 32(4): 691-702.
DOI: 10.1016/S0031-3203(98)00117-4. |
| [9] |
ZHANG D, KONG W K, YOU J, et al. Online palmprint identification[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(9): 1041-1050.
DOI: 10.1109/TPAMI.2003.1227981. |
| [10] |
DAI J, ZHOU J, MEMBER S. Multifeature-based high-resolution palmprint recognition[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(5): 945-957.
DOI: 10.1109/TPAMI.2010.164. |
| [11] |
FEI L, TENG S, WU J. Enhanced minutiae extraction for high-resolution[J].
International Journal of Image and Graphics, 2017, 17(4): 1-15.
|
| [12] |
BOUNNECHE M, BOUBCHIR L, BOURIDANE A, et al. Multi-spectral palmprint recognition based on oriented multiscale log-gabor filters[J].
Neurocomputing, 2016, 205(9): 274-286.
|
| [13] |
GUO Z, ZHANG D, ZHANG L, et al. Feature band selection for online multispectral palmprint recognition[J].
IEEE Transactions on Information Forensics and Security, 2012, 7(3): 1094-1099.
DOI: 10.1109/TIFS.2012.2189206. |
| [14] |
ZHANG D, GUO Z, LU G, et al. An online system of multispectral palmprint verification[J].
IEEE Transactions on Instrumentation and Measurement, 2010, 59(2): 480-490.
DOI: 10.1109/TIM.2009.2028772. |
| [15] |
ZHANG D, LU G, LI W, et al. Palmprint recognition using 3-d information[J].
IEEE Transactions on Systems Man and Cybernetics-Part C, 2009, 39(5): 505-519.
DOI: 10.1109/TSMCC.2009.2020790. |
| [16] |
ZHANG D, KANHANGAD V, LUO N, et al. Robust palmprint verification using 2D and 3D features[J].
Pattern Recognition, 2010, 43(1): 358-368.
DOI: 10.1016/j.patcog.2009.04.026. |
| [17] |
林森, 苑玮琦. 掌纹感兴趣区域定位与选择方法[J].
计算机工程与应用, 2011, 47(14): 21-24.
LIN S, YUAN W Q. Survey on orientation and selection methods for palmprint region of interest[J]. Computer Engineering and Applications, 2011, 47(14): 21-24. DOI: 10.3778/j.issn.1002-8331.2011.14.007. |
| [18] |
HUANG D, JIA W, ZHANG D. Palmprint verification based on principal lines[J].
Pattern Recognition, 2008, 41(4): 1316-1328.
DOI: 10.1016/j.patcog.2007.08.016. |
| [19] |
SUN Z, TAN T, WANG Y, et al. Ordinal palmprint representation for personal identification[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego: IEEE, 2005: 279-284.
|
| [20] |
KONG A W K, ZHANG D. Competitive coding scheme for palmprint verification[C] //Proceedings of 17th International Conference on Pattern Recognition. Cambridge: IEEE, 2004: 520-523.
|
| [21] |
XU Y, FEI L K, WEN J, et al. Discriminative and robust competitive code for palmprint recognition[J].
IEEE Transactions on Systems Man and Cybernetics Systems, 2018, 48(2): 232-241.
DOI: 10.1109/TSMC.2016.2597291. |
| [22] |
GUO Z H, ZHANG D, ZHANG L, et al. Palmprint verification using binary orientation co-occurrence vector[J].
Pattern Recognition Letter, 2009, 30(13): 1219-1227.
DOI: 10.1016/j.patrec.2009.05.010. |
| [23] |
ZHENG Q, KUMAR A, PAN G. A 3D feature descriptor recovered from a single 2D palmprint image[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(6): 1272-1279.
DOI: 10.1109/TPAMI.2015.2509968. |
| [24] |
FEI L, ZHANG B, ZHANG W, et al. Local apparent and latent direction extraction for palmprint recognition[J].
Information Sciences, 2019, 473: 59-72.
DOI: 10.1016/j.ins.2018.09.032. |
| [25] |
JIA W, HU R X, LEI Y K, et al. Histogram of oriented lines for palmprint recognition[J].
IEEE Transactions on Systems Man and Cybernetics:Systems, 2013, 44(3): 385-395.
|
| [26] |
ZHAO S P, ZHANG B. Learning complete and discriminative direction pattern for robust palmprint recognition[J].
IEEE Transactions on Image Processing, 2021, 30(6): 1001-1014.
|
| [27] |
FEI L K, ZHANG B, ZHANG L. Learning compact multifeature codes for palmprint recognition from a single training image per palm[J].
IEEE Transactions on Multimedia, 2020, 44(3): 385-395.
|
| [28] |
LU G M, ZHANG D, WANG K Q. Palmprint recognition using eigenpalms features[J].
Pattern Recognition Letters, 2003, 24(9): 1463-1467.
|
| [29] |
裴昱, 温洁嫦. 基于独立分量分析的一种改进的掌纹识别算法[J].
广东工业大学学报, 2010, 27(1): 51-54.
PEI Y, WEN J C. An improved method of palmprint recognition based on independent component analysis[J]. Journal of Guangdong University of Technology, 2010, 27(1): 51-54. DOI: 10.3969/j.issn.1007-7162.2010.01.013. |
| [30] |
HU D W, FENG G Y, ZHOU Z T. Two-dimensional locality preserving projections (2DLPP) with its application to palmprint recognition[J].
Pattern Recognition, 2007, 40(1): 339-342.
DOI: 10.1016/j.patcog.2006.06.022. |
| [31] |
SVOBODA J, MASCI J, BRONSTEIN M M. Palmprint recognition via discriminative index learning[C] //International Conference on Pattern Recognition. Cancun: IEEE, 2017: 4232-4237.
|
| [32] |
ZHANG L, CHENG Z X, SHEN Y, et al. Palmprint and palmvein recognition based on DCNN and a new large-scale contactless palmvein dataset[J].
Symmetry, 2018, 10(4): 78-92.
DOI: 10.3390/sym10040078. |
| [33] |
LU J W, LIONG V E, ZHOU X Z, et al. Learning compact binary face descriptor for face recognition[J].
IEEE Transaction on Pattern Analysis Machine Intelligence, 2015, 37(10): 2041-2056.
DOI: 10.1109/TPAMI.2015.2408359. |
| [34] |
SHEN F M, SHEN C H, LIU W, et al. Supervised discrete hashing[C] //IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 2015: 37-45.
|
| [35] |
SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[EB/OL].(2015-04-10)[2019-12-11].https://arxiv.org/pdf/1409.1556.pdf
|
| [36] |
贾梦琦. 非接触式掌纹识别算法研究[D]. 青岛: 青岛大学, 2017.
|
| [37] |
HUANG D, SHAN C F. Local binary patterns and its application to facial image analysis: a survey[J].
IEEE Transactions on Systems Man and Cybernetics-Part C, 2011, 41(6): 765-781.
DOI: 10.1109/TSMCC.2011.2118750. |
 2022, Vol. 39
2022, Vol. 39

