近年来,可重构智能表面(Reconfigurable Intelligent Surface, RIS)作为一种新技术,引起了学者的关注[1-4]。具体来说,RIS是一个由大量低成本、无源的反射元件组成的平面,每个无源反射元件能够独立地改变入射信号的相移,从而协同形成无源反射波束。RIS已被公认为未来无线网络的强力前沿技术[4]。有了RIS这种新的自由度,当发射机和接收器被障碍物阻挡时,可以部署RIS来创建一个额外的反射链路[5]。非正交多址接入技术(Non-Orthogonal Multiple Access, NOMA)作为5G的关键技术之一,因其能够显著提高无线通信系统的频谱效率而得到广泛研究。NOMA利用功率域复用技术给具有相同时频资源块的多个用户提供服务,提高了频谱效率[6-7]。预计RIS与NOMA的结合可以进一步提高网络性能。文献[8]考虑一个RIS辅助下行NOMA的多输入单输出(Multiple Input Single Output, MISO)系统,基站由RIS辅助向通信盲区中的2个用户发送信号,通过优化基站的波束形成和RIS的反射相移实现系统最大的能量效率。文献[9]研究了RIS辅助下行的通信系统,联合优化解码顺序、功率分配和RIS的反射相移,使K个用户的总吞吐量最大化。文献[10]考虑在基站与用户之间没有直接链路情况下的RIS增强毫米波NOMA系统,提出了一种基于交替优化和连续凸近似的联合优化算法,使系统的和速率最大。
另一方面,RIS会形成无源波束使通信信号增强,同时也带来了新的物理层安全(Physical Layer Security,PLS)问题。PLS作为一种促进无线系统安全通信的技术,已成为人们聚焦的研究方向。为了最大限度地提高通信保密率,人们提出各种技术,如人工噪声干扰和多天线波束形成等[11-14]。一些具有创新性的工作已经投入到RIS辅助安全无线通信的研究中[15-17]。文献[11]最先将RIS运用到辅助安全通信中,通过交替来优化基站的波束形成和RIS的反射相移,优化的方案与无RIS辅助通信的系统对比,一定程度上提高了系统的保密率。文献[15-16]研究的发射机人工噪声干扰可以与RIS无源波束形成联合设计,进一步降低窃听者的速率,而不损害合法用户的速率。文献[17]提出了一种鲁棒优化波束形成的方案来保护RIS辅助的NOMA传输系统,利用人工噪声干扰减少多天线窃听者的信息泄露,针对发射功率最小化的问题,提出并求解了联合有源无源波束形成优化问题。文献[18]研究了一种RIS辅助的MIMO窃听信道,提出了一种联合优化基站发射波束形成和RIS反射相移的交替优化算法,使系统保密率最大。然而,在文献[8-10]的研究工作中,只考虑了利用RIS创建一个额外的反射链路来辅助解决基站与用户之间没有直接链路通信的问题,而RIS能有效提高系统保密率的优势尚未考虑。文献[11,15-16]集中研究了RIS辅助安全通信,但是未考虑用户的信息传输速率,用户的服务质量(Quality of Service, QoS)无法得到保障。
综上所述,针对以上RIS辅助传输和信息安全问题,本文考虑了RIS辅助上行多用户安全通信系统,主要贡献和创新点如下。
(1) 用RIS创建一个额外的反射链路辅助通信的同时考虑基站处存在窃听者,部署的RIS既能辅助通信,还能提高系统通信安全。所考虑的模型具有实际应用价值,但暂时还没有相关文献研究。
(2) 考虑的优化问题具有非凸性,变量之间高度耦合,难以求解。本文通过引入辅助变量、一阶泰勒展开、半定松弛(Semi Definite Relaxation, SDR)和连续凸近似等方法,将原问题中的非凸目标函数和非凸约束转化成凸的形式,然后使用交替优化算法求得原非凸问题的次优解。在变量解耦合、子问题等价变换等方面具有创新性。
(3) 仿真结果表明,与基准策略(“固定功率,优化相移”和“固定相移,优化功率”)相比,本文使用的算法一定程度上提高了系统的安全性,体现了联合优化RIS相移和功率的优越性。
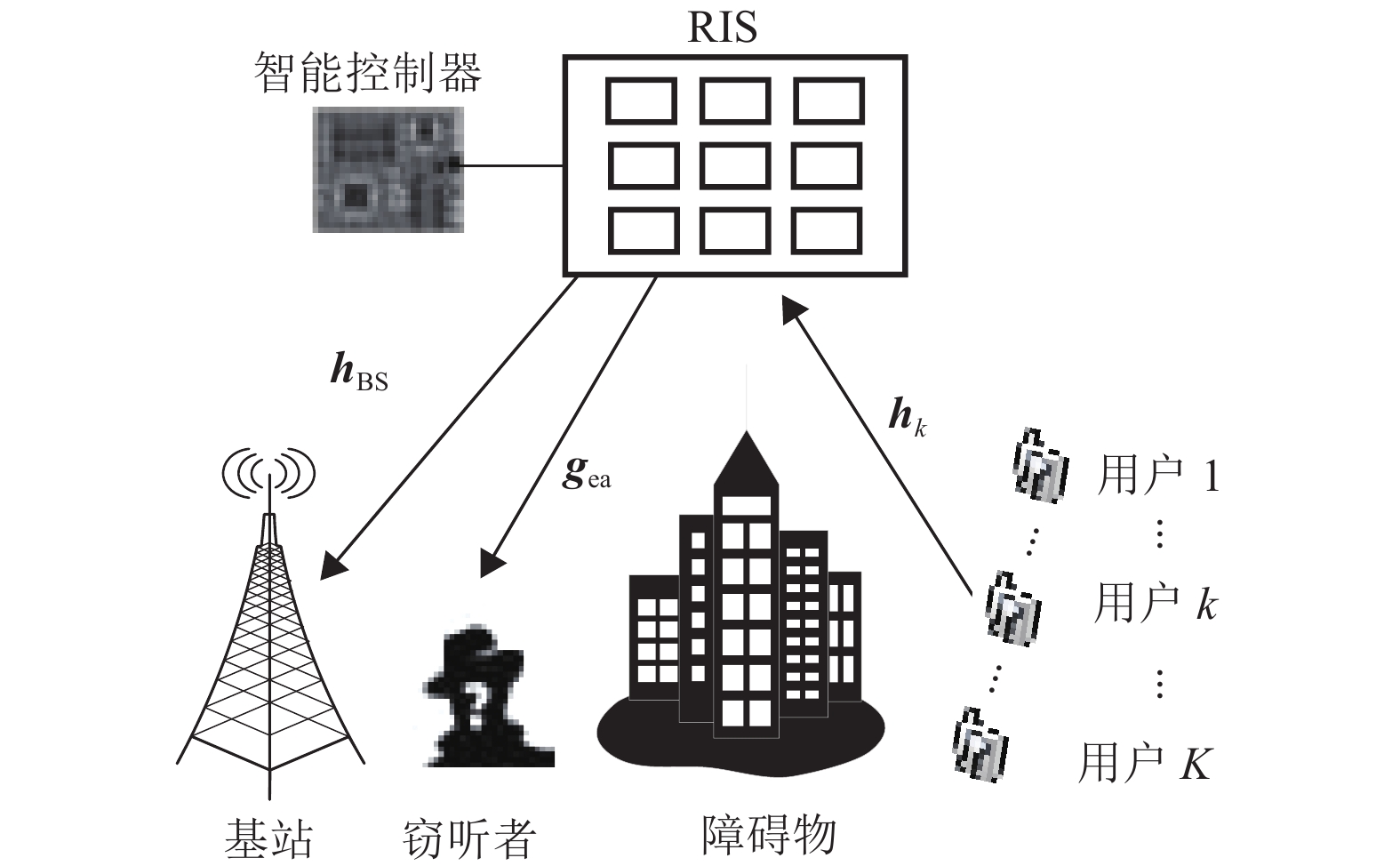
1 系统模型如图1所示,本文考虑RIS辅助的上行NOMA通信系统,它由K个用户、1个基站和1个窃听者构成。
|
图 1 RIS辅助的多用户上行NOMA通信系统 Figure 1 A RIS-assisted multi-user NOMA uplink communication system |
其中,K个用户、基站和窃听者都是单天线。大型建筑物的阻碍使用户与基站之间不存在直接通信链路。因此,这种通信方式是通过具有N个反射元素的RIS辅助进行。从用户k到RIS、RIS到基站和RIS到窃听者的信道分别表示为:
| $ {y_{{\rm{BS}}}} = \sum\nolimits_{k = 1}^K {{\boldsymbol{h}}_{{\rm{BS}}}^{\rm{H}}{\boldsymbol{\varPhi}} {{\boldsymbol{h}}_k}{s_k}\sqrt {{P_k}} } + {n_{\rm{B}}} $ | (1) |
| $ {y_{{\rm{e}}{\rm{a}},k}} = \sum\nolimits_{k = 1}^K {{\boldsymbol{g}}_{{\rm{e}}{\rm{a}}}^{\rm{H}}{\boldsymbol{\varPhi}} {{\boldsymbol{h}}_k}{{{s}}_k}\sqrt {{P_k}} } + {n_{{\rm{ea}}}} $ | (2) |
式中:
由式(1)可以看出,用户
| $ | {{\boldsymbol{h}}_{{\text{BS}}}^{\text{H}}{{{\boldsymbol{\varPhi}}}} {{\boldsymbol{h}}_1}} | \geqslant \cdots \geqslant |{{\boldsymbol{h}}_{{\text{BS}}}^{\text{H}}{\boldsymbol{\varPhi}} {{\boldsymbol{h}}_K}} | $ | (3) |
根据NOMA协议,用户
| $ {\gamma _k} = \frac{{{{| {{\boldsymbol{h}}_{{\text{BS}}}^{\text{H}}{\boldsymbol{\varPhi}} {{\boldsymbol{h}}_k}} |}^2}{P_k}}}{{\displaystyle \sum\nolimits_{i = k + 1}^K {{{| {{\boldsymbol{h}}_{{\text{BS}}}^{\text{H}}{\boldsymbol{\varPhi}} {{\boldsymbol{h}}_i}} |}^2}{P_i} + \sigma _{\rm{B}}^2} }} $ | (4) |
式中:当
| $ {R_k} = {\log _2}\left( {1 + {\gamma _k}} \right) $ | (5) |
本文假设了一种最坏的情况,即窃听者具有很强的多用户检测能力,并且可以消除NOMA保密协议中的用户间干扰[21],那么窃听者窃听每个用户的窃听率为
| $ {R_{{\text{ea}},k}} = {\log _2}\Bigg( {1 + \frac{{{{| {{\boldsymbol{g}}_{{\rm{e}}{\text{a}}}^{\text{H}}{\boldsymbol{\varPhi}} {{\boldsymbol{h}}_k}} |}^2}{P_k}}}{{\sigma _{{\rm{e}}{\text{a}}}^2}}} \Bigg) $ | (6) |
因此,从用户k到基站的保密率(bps/Hz)为[17]
| $ {R_{\sec ,k}}{\text{ = }}{[ {{R_k} - {R_{{\rm{e}}{\text{a}},k}}} ]^ + } $ | (7) |
式中:
| $ {R_{\sec }} = \sum\nolimits_{k = 1}^K {{{[ {{R_k} - {R_{{\rm{e}}{\text{a}},k}}} ]}^ + }} $ | (8) |
本文的目标是通过优化用户的发射功率和RIS的反射相移,使整个系统K个用户的总保密率最大,因此所考虑的问题1具体描述为
| $\mathop {\max }\limits_{{\boldsymbol{P,\varPhi}} } {\text{ }}\sum\nolimits_{k = 1}^K {{{[ {{R_k} - {R_{{\rm{e}}{\text{a}},k}}} ]}^ + }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; $ | (9) |
| $ \quad\quad\quad\quad\quad{\rm{s}}{\rm{.t}}{. } \left\{ {\begin{array}{*{20}{l}} {{\rm}{{\log }_2}\left( {1 + {\gamma _k}} \right)\geqslant R_k^{\min }\quad\quad\quad\quad\quad\quad\;\;\,(10)}\\ {{P_k}\leqslant P_k^{\max },\forall k \in \left\{ {1, \cdots ,K} \right\}\quad\quad\quad\;\;\;\,(11)}\\ {\left| {{\phi _i}} \right| = 1,\forall i \in \left\{ {1, \cdots ,N} \right\}\quad\quad\quad\quad\quad(12)} \end{array}} \right. $ |
式(10)~(12)中:
首先,
| $ \begin{split} {R_{{\text{sum}}}} =&\displaystyle \sum\nolimits_{k = 1}^K {{{\log }_2}\Bigg( {1 + \frac{{{{| {{\boldsymbol{h}}_{{\text{BS}}}^{\text{H}}{\boldsymbol{\varPhi}} {{\boldsymbol{h}}_k}} |}^2}{P_k}}}{{\displaystyle \sum\nolimits_{i = k + 1}^K {{{| {{\boldsymbol{h}}_{{\text{BS}}}^{\text{H}}{\boldsymbol{\varPhi}} {{\boldsymbol{h}}_i}} |}^2}{P_i} + \sigma _{\rm{B}}^2} }}} \Bigg)}= \\& {\text{ lo}}{{\text{g}}_2}\Bigg( {1 + \frac{{\displaystyle \sum\nolimits_{k = 1}^K {{{| {{\boldsymbol{h}}_{{\text{BS}}}^{\text{H}}{\boldsymbol{\varPhi}} {{\boldsymbol{h}}_k}} |}^2}{P_k}} }}{{\sigma _{\rm{B}}^2}}} \Bigg) \end{split} $ | (13) |
从式(13)可以看出总可达速率是关于
为了更好地处理
| $ {| {{\boldsymbol{h}}_{{\text{BS}}}^{\text{H}}{\boldsymbol{\varPhi}} {{\boldsymbol{h}}_k}} |^2}{\text{ = }}{| {{{\boldsymbol{\varphi}} ^{\text{H}}}{{\hat {\boldsymbol{h}}}_k}} |^2} $ | (14) |
| $ {| {{\boldsymbol{g}}_{{\rm{e}}{\text{a}}}^{\text{H}}{\boldsymbol{\varPhi}} {{\boldsymbol{h}}_k}} |^2}{\text{ = }}{| {{{\boldsymbol{\varphi}} ^{\text{H}}}{{\hat {\boldsymbol{g}}}_{{\rm{ea}},k}}} |^2} $ | (15) |
而式(10)并非一个凸约束,本文将它转为式(16)的形式变成凸的约束。
| $ {| {{{\boldsymbol{\varphi}} ^{\text{H}}}{{\hat {\boldsymbol{h}}}_k}}|^2}{P_k} \geqslant ( {{2^{R_k^{\min }}} - 1} )\left( {\sum\nolimits_{i = k + 1}^K {{{| {{{\boldsymbol{\varphi}} ^{\rm{H}}}{{\hat {\boldsymbol{h}}}_i}} |}^2}{P_i} + \sigma _{\rm{B}}^2} } \right) $ | (16) |
问题1进一步化简得到问题2,如式(17)~(20)所示。
| $ {\text{ }}\mathop {\max }\limits_{{\boldsymbol{P}},{\boldsymbol{\varphi}} } {\text{ lo}}{{\text{g}}_2}\Bigg( {1 + \frac{{\displaystyle \sum\nolimits_{k = 1}^K {{{| {{{\boldsymbol{\varphi}} ^{\text{H}}}{{\hat {\boldsymbol{h}}}_k}} |}^2}{P_k}} }}{{\sigma _{\rm{B}}^2}}} \Bigg) - \sum\nolimits_{k = 1}^K {{{\log }_2}\Bigg( {1 + \frac{{{{| {{{\boldsymbol{\varphi}} ^{\text{H}}}{{\hat {\boldsymbol{g}}}_{{\rm{e}}{\text{a}},k}}} |}^2}{P_k}}}{{\sigma _{{\text{ea}}}^2}}} \Bigg)} $ | (17) |
| $ {\rm{s}}{\rm{.t}}{\rm{. }}\left\{ {\begin{array}{*{20}{l}} {{{| {{{\boldsymbol{\varphi}} ^{\rm{H}}}{{\hat {\boldsymbol{h}}}_k}} |}^2}{P_k} \geqslant ({2^{R_k^{\min }}} - 1)\left(\displaystyle \sum\nolimits_{i = k + 1}^K {{{| {{{\boldsymbol{\varphi}} ^{\rm{H}}}{{\hat {\boldsymbol{h}}}_i}} |}^2}{P_i} + \sigma _{\rm{B}}^2} \right) \;\;\;\,(18)}\\ {{P_k}\leqslant P_k^{\max },\;\forall k \in \left\{ {1, \cdots ,K} \right\}\quad\quad\quad\quad\quad\quad\quad\quad\,\;\;(19)}\\ {\left| {{{{\varphi}} _i}} \right| = 1,\;\forall i \in \left\{ {1, \cdots ,N} \right\}\;\;\quad\quad\quad\quad\quad\quad\quad\quad \quad\;(20)} \end{array}} \right. $ |
从问题2可以明显看出,式(19)是只关于变量
固定
| $ {\text{ }}\mathop {\max }\limits_{\boldsymbol{P}} {\text{ lo}}{{\text{g}}_2}\Bigg( {1 + \frac{{\displaystyle \sum\nolimits_{k = 1}^K {{{| {{{\boldsymbol{\varphi}} ^{\text{H}}}{{\hat {\boldsymbol{h}}}_k}} |}^2}{P_k}} }}{{\sigma _{\rm{B}}^2}}} \Bigg)- \sum\nolimits_{k = 1}^K {{{\log }_2}\Bigg( {1 + \frac{{{{| {{{\boldsymbol{\varphi}} ^{\text{H}}}{{\hat {\boldsymbol{g}}}_{{\rm{e}}{\text{a}},k}}} |}^2}{P_k}}}{{\sigma _{{\text{ea}}}^2}}} \Bigg)} $ | (21) |
| $ \text{s}\text{.t}\text{. }式\left(18\right),式\left(19\right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; $ | (22) |
可以注意到目标函数中的第1项
根据凸函数的一阶泰勒展开式是它的全局下估计量,而凹函数的一阶泰勒展开是它的全局上估计量[22]。因此将目标函数的第2项进行一阶泰勒展开,进行连续凸近似得到式(23)。
| $ \begin{split}& \sum\nolimits_{k = 1}^K {{{\log }_2}\Bigg( {1 + \frac{{{{| {{{\boldsymbol{\varphi}} ^{\text{H}}}{{\hat {\boldsymbol{g}}}_{{\rm{e}}{\text{a}},k}}} |}^2}{P_k}}}{{\sigma _{{\text{ea}}}^2}}} \Bigg)} \leqslant \sum\nolimits_{k = 1}^K {{{\log }_2}\Bigg( {1 + \frac{{{{| {{{\boldsymbol{\varphi}} ^{\text{H}}}{{\hat {\boldsymbol{g}}}_{{\rm{ea}},k}}} |}^2}P_k^{\left( 0 \right)}}}{{\sigma _{{\text{ea}}}^2}}} \Bigg)} + \hfill \\& \sum\nolimits_{k = 1}^K {\frac{{{{| {{{\boldsymbol{\varphi}} ^{\text{H}}}{{\hat {\boldsymbol{g}}}_{{\rm{ea}},k}}} |}^2}}}{{( {{{ { |{{\boldsymbol{\varphi}} ^{\text{H}}}{{\hat {\boldsymbol{g}}}_{{\rm{ea}},k}}} |}^2}P_k^{\left( 0 \right)} + \sigma _{{\text{ea}}}^2} )}}} ( {{P_k} - P_k^{( 0 )}} ){\text{ = }}X\\[-15pt] \end{split} $ | (23) |
式中:
| $ {\text{ }}\mathop {\max }\limits_{\boldsymbol{P}} {\text{ lo}}{{\text{g}}_2}\Bigg( {1 + \frac{{ \displaystyle \sum\nolimits_{k = 1}^K {{{| {{{\boldsymbol{\varphi}} ^{\text{H}}}{{\hat {\boldsymbol{h}}}_k}} |}^2}{P_k}} }}{{\sigma _{\rm{B}}^2}}} \Bigg) - X $ | (24) |
| $ \text{s}\text{.t}\text{. }式\left(22\right) \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ | (25) |
可以注意到经过连续凸近似后,问题4的目标函数为凹函数。因此,问题4是一个凸优化问题,可以通过内点法进行优化求解[23]。
2.3 固定对于给定
| $ {\text{ }}\mathop {\max }\limits_{\boldsymbol{\varphi}} {\text{ lo}}{{\text{g}}_2}\Bigg( {1 + \frac{{ \displaystyle \sum\nolimits_{k = 1}^K {{{| {{{\boldsymbol{\varphi}} ^{\text{H}}}{{\hat {\boldsymbol{h}}}_k}} |}^2}{P_k}} }}{{\sigma _{\rm{B}}^2}}} \Bigg)- \sum\nolimits_{k = 1}^K {{{\log }_2}\Bigg( {1 + \frac{{{{| {{{\boldsymbol{\varphi }}^{\text{H}}}{{\hat {\boldsymbol{g}}}_{{\rm{e}}{\text{a}},k}}} |}^2}{P_k}}}{{\sigma _{{\text{ea}}}^2}}} \Bigg)} $ | (26) |
| $ \text{s}\text{.t}\text{. }式\left(18\right),式\left(20\right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; $ | (27) |
同样,可以明显地看到目标函数是非凹的,并且式(18)和式(20)都是非凸约束。首先,将问题转化成矩阵迹的形式为后面运用SDR方法做好铺垫。令
| $ {| {{{\boldsymbol{\varphi}} ^{\text{H}}}{{\hat {\boldsymbol{h}}}_k}} |^2}{P_k}{\text{ = }}{{\boldsymbol{\varphi}} ^{\text{H}}}{P_k}{{\hat {\boldsymbol{h}}}_k}\hat {\boldsymbol{h}}_k^{\text{H}}{\boldsymbol{\varphi}} {\text{ = }} {{\boldsymbol{\varphi}} ^{\text{H}}}{{\boldsymbol{H}}_k}{\boldsymbol{\varphi}} {\text{ = tr}}( {{{\boldsymbol{\varphi}} ^{\text{H}}}{{\boldsymbol{H}}_k}{\boldsymbol{\varphi }}} ){\text{ = tr}}\left( {{{\boldsymbol{H}}_k}{\boldsymbol{\varTheta}} } \right) $ | (28) |
| $ \begin{split}& {| {{{\boldsymbol{\varphi}} ^{\text{H}}}{{\hat {\boldsymbol{g}}}_{{\rm{e}}{\text{a}},k}}} |^2}{P_k}{\text{ = }}{{\boldsymbol{\varphi}} ^{\text{H}}}{P_k}{{\hat {\boldsymbol{g}}}_{{\rm{ea}},k}}\hat {\boldsymbol{g}}_{{\text{ea}},k}^{\text{H}}{\boldsymbol{\varphi}} {\text{ = }} \hfill \\& {{\boldsymbol{\varphi}} ^{\text{H}}}{{\boldsymbol{G}}_k}{\boldsymbol{\varphi }}{\text{ = tr}}( {{{\boldsymbol{\varphi}} ^{\text{H}}}{{\boldsymbol{G}}_k}{\boldsymbol{\varphi}} } ){\text{ = tr}}\left( {{{\boldsymbol{G}}_k}{\boldsymbol{\varTheta}} } \right) \hfill \\ \end{split} $ | (29) |
问题5可重新表示为问题6,如式(30)~(33)所示。
| $ {\text{ }}\mathop {\max }\limits_{\boldsymbol{\varTheta}} {\text{ lo}}{{\text{g}}_2}\Bigg( {1 + \frac{{ \displaystyle \sum\nolimits_{k = 1}^K {{\text{tr}}\left( {{{\boldsymbol{H}}_k}{\boldsymbol{\varTheta}} } \right)} }}{{\sigma _{\rm{B}}^2}}} \Bigg) - \sum\nolimits_{k = 1}^K {{{\log }_2}\Bigg( {1 + \frac{{{\text{tr}}\left( {{{\boldsymbol{G}}_k}{\boldsymbol{\varTheta}} } \right)}}{{\sigma _{{\text{ea}}}^2}}} \Bigg)} $ | (30) |
| $ {\rm{s}}{\rm{.t}}. \left\{ {\begin{array}{*{20}{l}} {{\rm{ tr}}\left( {{{\boldsymbol{H}}_k}{\boldsymbol{\varTheta}} } \right) \geqslant ( {{2^{R_k^{\min }}} - 1} )\left( {\displaystyle \sum\nolimits_{i = k + 1}^K {{\rm{tr}}\left( {{{\boldsymbol{H}}_i}{\boldsymbol{\varTheta}} } \right) + \sigma _{\rm{B}}^2} } \right)\quad\;\;\,\,(31)}\\ {{\boldsymbol{\varTheta}} \succeq {\bf{0}}\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\;\;\;\;\;\;\;(32)}\\ {{\rm{rank}}\left( {\boldsymbol{\varTheta}} \right){\rm{ = }}1\qquad\qquad\qquad\qquad\qquad\qquad\quad\,\,\;\;\;\;\;(33)} \end{array}} \right. $ |
式(32)表示
可以看到,问题6仍然难以解决,因为它的目标函数是非凹的,并且秩一约束是非凸的。因此,下文将目标函数的第2项进行一阶泰勒展开得到式(34)为
| $ \begin{split}& \sum\nolimits_{k = 1}^K {{{\log }_2}\Bigg( {1 + \frac{{{\text{tr}}\left( {{{\boldsymbol{G}}_k}{\boldsymbol{\varTheta}} } \right)}}{{\sigma _{{\text{ea}}}^2}}} \Bigg)} \leqslant \sum\nolimits_{k = 1}^K {{{\log }_2}\Bigg( {1 + \frac{{{\text{tr}}\left( {{{\boldsymbol{G}}_k}{{\boldsymbol{\varTheta}} ^{\left( 0 \right)}}} \right)}}{{\sigma _{{\text{ea}}}^2}}} \Bigg)}+ \hfill \\& \sum\nolimits_{k = 1}^K {{\text{tr}}\Bigg( {\frac{{{\boldsymbol{G}}_k^{\rm{H}}}}{{\left( {{\text{tr}}\left( {{{\boldsymbol{G}}_k}{{\boldsymbol{\varTheta}} ^{\left( 0 \right)}}} \right) + \sigma _{{\text{ea}}}^2} \right){\rm{I}}{\text{n}}( 2 )}}( {{\boldsymbol{\varTheta}} - {{\boldsymbol{\varTheta}} ^{\left( 0 \right)}}} )} \Bigg)} {\text{ = }}Y \hfill \\ \end{split} $ | (34) |
式中:
| $ {\text{ }}\mathop {\max } \limits_{\boldsymbol{\varTheta}} {\text{ lo}}{{\text{g}}_2}\Bigg( {1 + \frac{{ \displaystyle \sum\nolimits_{k = 1}^K {{\text{tr}}\left( {{{\boldsymbol{H}}_k}{\boldsymbol{\varTheta}} } \right)} }}{{\sigma _{\rm{B}}^2}}} \Bigg) - Y \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\[-15pt]$ | (35) |
| $\;\;\;{\rm{s}}{\rm{.t}}.\left\{ {\begin{array}{*{20}{l}} {{\rm{ tr}}\left( {{{\boldsymbol{H}}_k}{\boldsymbol{\varTheta}} } \right) \geqslant ( {{2^{R_k^{\min }}} - 1} )\left( { \displaystyle \sum\nolimits_{i = k + 1}^K {{\rm{tr}}\left( {{{\boldsymbol{H}}_i}{\boldsymbol{\varTheta}} } \right) + \sigma _{\rm{B}}^2} } \right)\;\;\;\;\;\,(36)}\\ {{\rm{tr}}\left( {{{\boldsymbol{E}}_i}{\boldsymbol{\varTheta}} } \right){\rm{ = }}1,\;\forall i \in \left\{ {1, \cdots ,N} \right\} \quad \quad \quad \quad \quad \quad \quad \;\;\; (37)}\\ {{\boldsymbol{\varTheta}} \succeq {\bf{0}} \quad \quad \quad \quad \quad \quad \qquad \qquad \quad \qquad \qquad\;\;\;\;\;(38)}\\ {{\rm{rank}}\left( {\boldsymbol{\varTheta}} \right){\rm{ = }}1 \quad \quad \quad \quad \quad \qquad \qquad \qquad \quad \quad\;\;\;\;(39)} \end{array}} \right.$ |
| $ {\text{ }}\mathop {\max }\limits_{\boldsymbol{\varTheta}} {\text{ lo}}{{\text{g}}_2}\Bigg( {1 + \frac{{ \displaystyle \sum\nolimits_{k = 1}^K {{\text{tr}}\left( {{{\boldsymbol{H}}_k}{\boldsymbol{\varTheta}} } \right)} }}{{\sigma _{\rm{B}}^2}}} \Bigg) - Y\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; $ | (40) |
| $\;\;\;\;{\rm{s}}{\rm{.t}}.\left\{ {\begin{array}{*{20}{l}} {{\rm{ tr}}\left( {{{\boldsymbol{H}}_k}{{{\boldsymbol{\varTheta}}}} } \right) \geqslant ( {{2^{R_k^{\min }}} - 1} )\left( { \displaystyle \sum\nolimits_{i = k + 1}^K {{\rm{tr}}\left( {{{\boldsymbol{H}}_i}{{{\boldsymbol{\varTheta}}}} } \right) + \sigma _{\rm{B}}^2} } \right)\;\;\;\;\;(41)}\\ {{\rm{tr}}\left( {{{\boldsymbol{E}}_i}{{{\boldsymbol{\varTheta}}}} } \right){\rm{ = }}1,\;\forall i \in \left\{ {1, \cdots ,N} \right\}\qquad\qquad\qquad\quad\;\;\,(42)}\\ {{{{\boldsymbol{\varTheta}}}} \succeq {\boldsymbol{0}} \qquad\qquad\qquad\qquad\qquad\qquad\qquad \quad\;\;\;\,\,{\rm{(43)}}} \end{array}} \right. $ |
此时,问题已经转化为一个凸优化问题,可以使用内点法解决。但是问题8得出的最优解并不是一个秩一解。因此,为了解决问题8省略的秩一约束,本文运用标准高斯随机化方法来获得问题的近似解,具体的方法见文献[2]。
综上所述,算法的求解过程如下:
步骤1:初始化
步骤2:令
步骤3:固定
步骤4:固定
步骤5:求得
步骤6:如果
此节主要通过计算机MATLAB仿真实验验证本文算法性能,仿真的参数设置如下:假设有3个用户,RIS与基站之间的距离和RIS与用户之间的距离都是40 m,窃听者与RIS之间的距离为30 m。RIS与基站、RIS与用户和RIS与窃听者的信道都是小尺度衰落的瑞利信道模型。同时,这2个通道对应的大尺度路径损失分别为
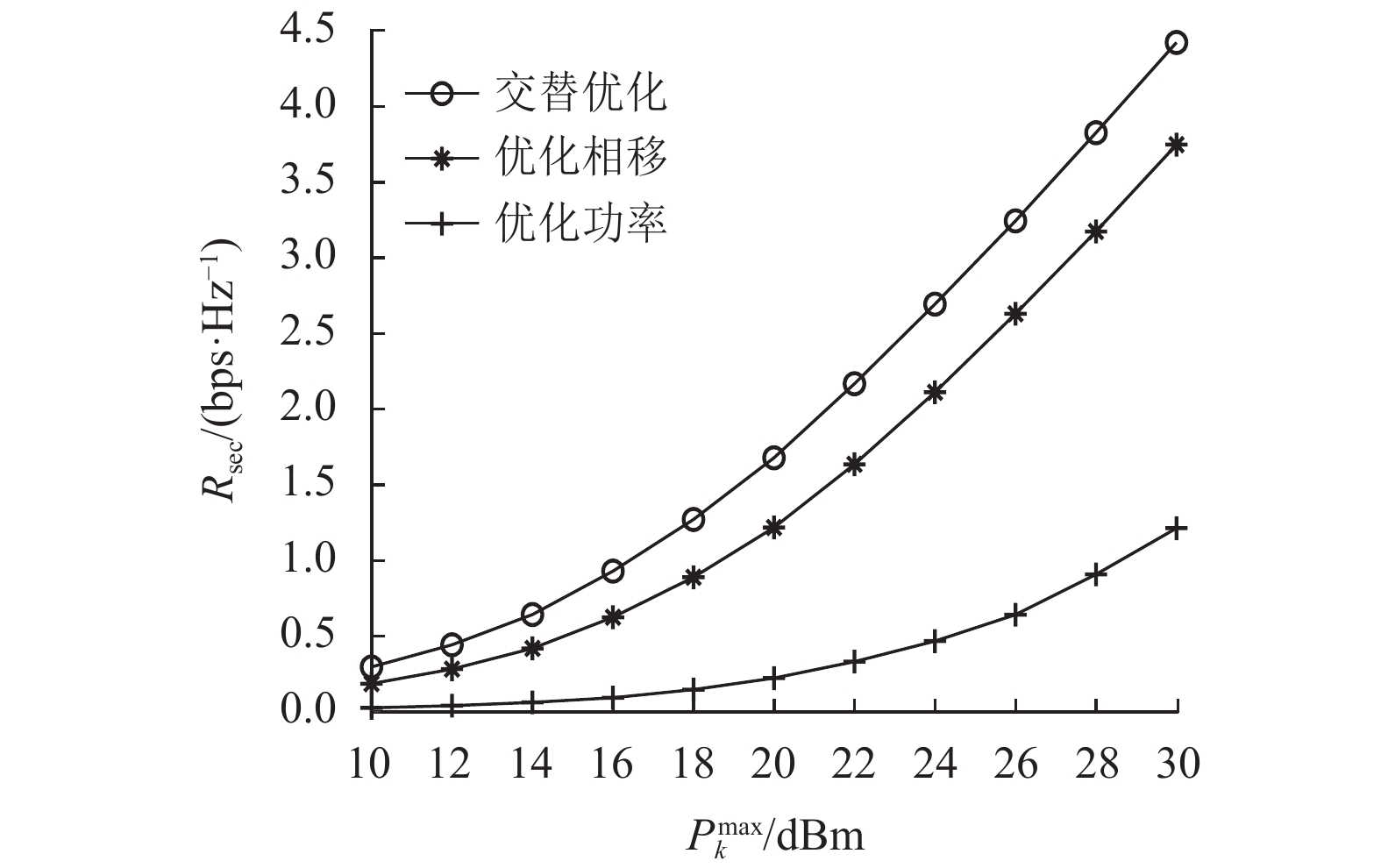
图2显示的是在不同基准方案下用户最大发射功率和K个用户的总保密率之间的关系。其中,系统的总保密率随着用户最大发射功率的增大而增大。可以明显地看出交替优化算法在性能上比只优化功率和只优化相移的方案有较大的提升。当
|
图 2 不同方案下系统总保密率与
|
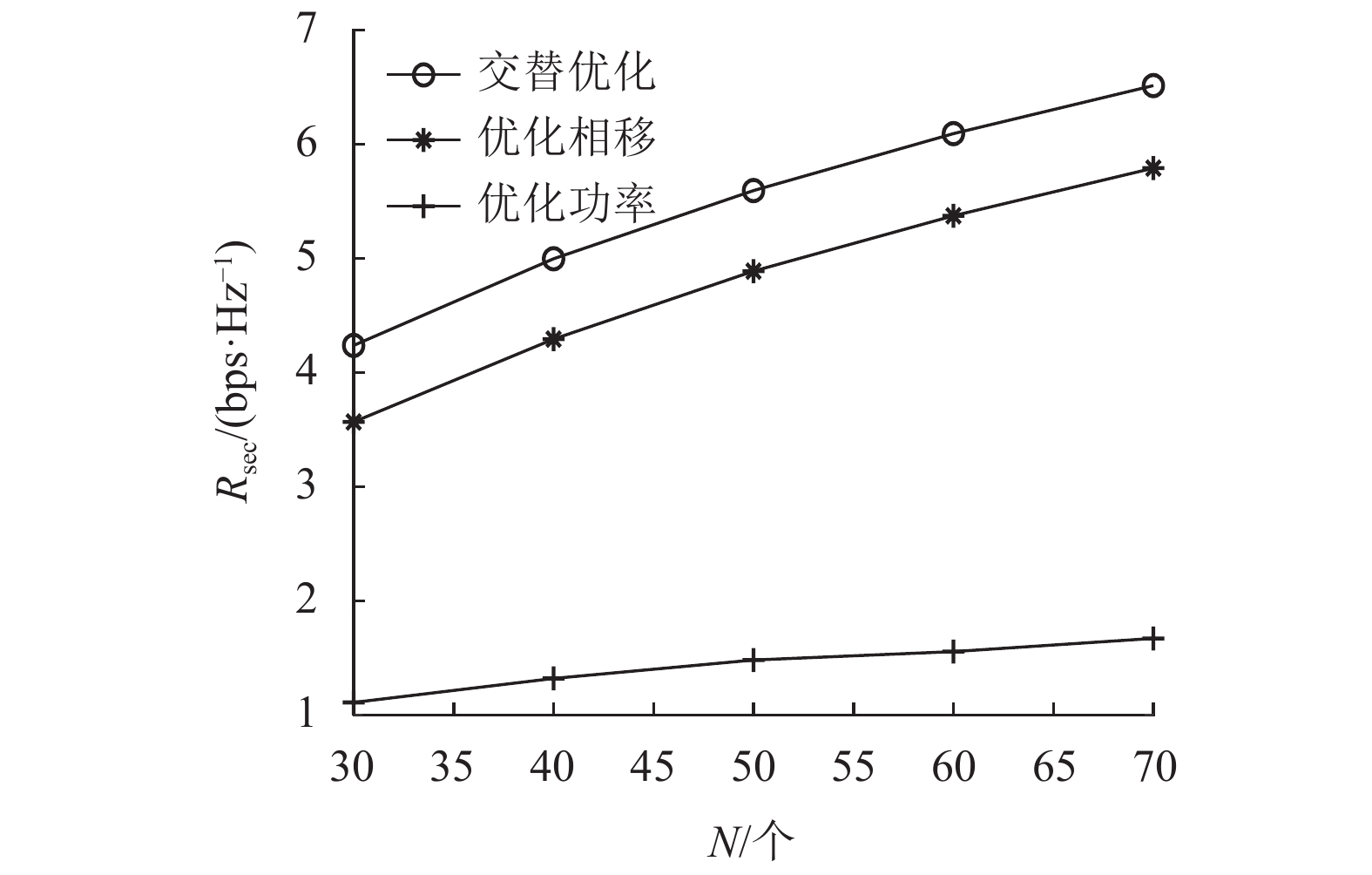
图3显示的是在
|
图 3 不同方案下系统总保密率与RIS中反射元件数量N的关系 Figure 3 Secrecy sum rates versus the number of reflecting elements at the RIS N under different schemes |
本文考虑RIS辅助上行NOMA安全通信系统,通过联合优化用户发射功率和RIS反射相移,使K个用户的总保密率最大化。主要的挑战是所考虑的问题的目标函数是非凹的和RIS的单位模约束。为了解决这些问题,本文将部分目标函数进行一阶泰勒展开,并且转化为SDR的形式进行求解。仿真结果表明,相对于2种基准方案,本文提出的方案能够显著提升RIS辅助无线通信系统的安全性。
| [1] |
SAAD W, BENNI M, CHEN M. A vision of 6G wireless systems: applications, trends, technologies, and open research problems[J].
IEEE Network, 2020, 34(3): 134-142.
DOI: 10.1109/MNET.001.1900287. |
| [2] |
WU Q, ZHANG R. Intelligent reflecting surface enhanced wireless network via joint active and passive beamforming[J].
IEEE Transactions on Wireless Communications, 2019, 18(11): 5394-5409.
DOI: 10.1109/TWC.2019.2936025. |
| [3] |
YAN W, YUAN X, HE Z Q, et al. Passive beamforming and information transfer design for reconfigurable intelligent surfaces aided multiuser MIMO systems[J].
IEEE Journal on Selected Areas in Communications, 2020, 38(8): 1793-1808.
DOI: 10.1109/JSAC.2020.3000811. |
| [4] |
WU Q, ZHANG R. Towards smart and reconfigurable environment: intelligent reflecting surface aided wireless network[J].
IEEE Communications Magazine, 2019, 58(1): 106-112.
|
| [5] |
MU X, LIU Y, GUO L, et al. Exploiting intelligent reflecting surfaces in NOMA networks: joint beamforming optimization[J].
IEEE Transactions on Wireless Communications, 2020, 19(10): 6884-6898.
DOI: 10.1109/TWC.2020.3006915. |
| [6] |
LYU L, CHEN J, NI Q, et al. Cognitive non-orthogonal multiple access with cooperative relaying: anew wireless frontier for 5G spectrum sharing[J].
IEEE Communications Magazine, 2018, 56(4): 188-195.
DOI: 10.1109/MCOM.2018.1700687. |
| [7] |
LYU L, JIANG H, DING Z, et al. Secrecy-enhancing design for cooperative downlink and uplink NOMA with an untrusted relay[J].
IEEE Transactions on Communications, 2020, 68(3): 1698-1715.
DOI: 10.1109/TCOMM.2019.2960345. |
| [8] |
FANG F, XU Y, PHAM Q V, et al. Energy-efficient design of IRS-NOMA networks[J].
IEEE Transactions on Vehicular Technology, 2020, 69(11): 14088-14092.
DOI: 10.1109/TVT.2020.3024005. |
| [9] |
ZUO J, LIU Y, QIN Z, et al. The application of intelligent reflecting surface in downlink NOMA systems[C]// 2020 IEEE International Conference on Communications Workshops (ICC Workshops). Dublin: IEEE, 2020.
|
| [10] |
ZUO J, LIU Y, BASAR E, et al. Intelligent reflecting surface enhanced millimeter-wave NOMA systems[J].
IEEE Communications Letters, 2020, 24(11): 2632-2636.
DOI: 10.1109/LCOMM.2020.3009158. |
| [11] |
CUI M, ZHANG G, ZHANG R. Secure wireless communication via intelligent reflecting surface[J].
IEEE Wireless Communication Letters, 2019, 8(5): 1410-1414.
DOI: 10.1109/LWC.2019.2919685. |
| [12] |
KHISTI A, WORNELL G W. Secure transmission with multiple antennas I: the MISOME wiretap channel[J].
IEEE Transactions on Information Theory, 2010, 56(7): 3088-3104.
DOI: 10.1109/TIT.2010.2048445. |
| [13] |
MUKHERJEE A, FAKOORIAN S A, HUANG J, et al. Principles of physical layer security in multiuser wireless networks: a survey[J].
IEEE Communications Surveys & Tutorials, 2014, 16(3): 1550-1573.
|
| [14] |
LIU L, ZHANG R, CHUA K C. Secrecy wireless information and power transfer with MISO beamforming[J].
IEEE Transactions on Signal Processing, 2013, 62(7): 1850-1863.
|
| [15] |
GUAN X, WU Q, ZHANG R. Intelligent reflecting surface assisted secrecy communication: is artificial noise helpful or not?[J].
IEEE Wireless Communications Letters, 2020, 9(6): 778-782.
DOI: 10.1109/LWC.2020.2969629. |
| [16] |
XU D, YU X, SUN Y, et al. Resource allocation for secure IRS-assisted multiuser MISO systems[C]// 2019 IEEE Globecom Workshops (GC Wkshps). Hawaii: IEEE, 2019: 1-6.
|
| [17] |
ZHANG Z, LYU L, WU Q, et al. Robust and secure communications in intelligent reflecting surface assisted NOMA networks[J].
IEEE Communications Letters, 2021, 25(3): 739-743.
DOI: 10.1109/LCOMM.2020.3039811. |
| [18] |
DONG L, WANG H. Secure MIMO transmission via intelligent reflecting surface[J].
IEEE Wireless Communications Letters, 2020, 9(6): 787-790.
DOI: 10.1109/LWC.2020.2969664. |
| [19] |
YANG G, XU X Y, LIANG Y C. Intelligent reflecting surface assisted non-orthogonal multiple access[EB/OL]. (201-12-30)[2021-05-07]. https://arxiv.org/abs/1907.03133v2.
|
| [20] |
ZENG M, YADAV A, DOBRE O, et al. Energy-efficient joint user-RB association and power allocation for uplink hybrid NOMA-OMA[J].
IEEE Internet of Things Journal, 2019, 6(3): 5119-5131.
DOI: 10.1109/JIOT.2019.2896946. |
| [21] |
LYU L, DING Z, NI Q, et al. Secure MISO-NOMA transmission with artificial noise[J].
IEEE Transactions on Vehicular Technology, 2018, 67(7): 6700-6705.
DOI: 10.1109/TVT.2018.2811733. |
| [22] |
ZHAN C, ZENG Y. Completion time minimization for multi-UAV enabled data collection[J].
IEEE Transactions on Wireless Communications, 2019, 18(10): 4859-4872.
DOI: 10.1109/TWC.2019.2930190. |
| [23] |
BOYD S, VANDENBERGHE L. Convex optimization[M]. UK: Cambridge University Press, 2009.
|
 2022, Vol. 39
2022, Vol. 39

