以慕课(Massive Open Online Courses, MOOC)、微课、智慧学习空间等线上线下混合的教学模式是高校进行教学模式改革的热点，特别最近两年，由于全球化疫情的影响，在线教育更加成为研究的焦点。从课堂教育到在线教育的转变，最大的不同在于学生学习行为的变化，在没有老师监督的情况下，学生的学习态度可能会变得消极。不少研究指出学习行为与成绩具有高度相关性^[1-2]，保持积极的学习状态和良好的学习行为，是接受在线教育的学习者进行有效学习的重要因素。比起课堂教育，在线教育的优势在于可以快捷方便地采集学生的学习行为，有利于研究者建立分析模型探索不同行为对最终成绩的影响，从而制定合适的学习策略来保证学生具有良好的学习行为。对于一个分析模型而言，模型的可解释性有利于揭示数据间的依赖关系，使得模型可信度更高，因而备受关注。

由于互联网教育的广泛发展，近年来研究学生在线学习行为与学习成绩的关系成为了数据挖掘领域一个新的研究热点^[3-4]。Morris等^[5]收集3门本科通识教育课程中共354名学生对应的8种学习行为，使用SPSS(Statistical Product and Service Solutions)中多元回归模型进行分析，得到其中3种(查看的讨论帖子数量、查看的内容页面数量和查看讨论的秒数)学习行为具有统计学显著性。马飞等^[6]使用基于离差平方和的聚集层次聚类算法(Agglomerative Hierarchical Clustering, AHC)和K-means非层次聚类算法对学习行为模式进行聚类分析，将学习者分为积极学习者、消极学习者和惰性学习者。牟智佳^[7]使用K-means聚类分析法进行学习群体特征分析，将学习者分为积极学习者、活动参与者和活动围观者，并提出随着时间推移，积极学习者会逐渐转变成为活动参与者或围观者。沈欣忆等^[8]采用抽样和逐步回归对学习者在线学习行为建模分析，证明学生在线学习行为具有预测学生学习绩效的可能，而且模型系数能在一定程度上反应变量对学习绩效的影响。Wu^[9]使用决策树模型，对学习行为进行分析建模并应用在教学决策系统中。陈德鑫等^[10]指出，深度学习在教育大数据领域可应用于学习追踪、预测、教学辅助及行为分析。孙霞等^[11]使用基于卷积神经网络以及长短期记忆网络组成的混合预测模型对在线学习者的辍学行为进行预测。胡航等^[12]使用weka(Waikato Environment for Knowledge Analysis)软件对深度神经网络与机器学习模型进行对比，而且通过不同场景学习行为日志数据进行学习预测，神经网络模型表现出更高的准确率，但解释性较差。在目前的推理领域和因果分析中，贝叶斯网络的应用非常广泛。如杨婷等^[13]基于信息增益对朴素贝叶斯分类属性进行加权改进，并将其应用于电信用户流失的研究中；蔡瑞初等^[14]将贝叶斯网络应用于基因组关联分析中，探究基因变异间的因果关系；Moe^[15]指出，贝叶斯网络模型的使用对环境风险评估的发展有较大作用；方媛等^[16]基于贝叶斯网络建立多目标决策模型，对公众参与公私合营项目进行决策分析，在考虑投资者和社会公众的利益关系下对项目进行决策规划，进而保证项目的顺利推进。

对于传统的逻辑回归模型而言，影响因素之间的相互作用会对分析结果产生影响，甚至产生严重的多重线性干扰从而降低其模型的准确性，并且目前广泛使用的深度学习模型无法很好地表现出可解释性。另外，贝叶斯网络在MOOC上的应用目前仅局限于朴素贝叶斯分类^[7,17]，而未考虑使用贝叶斯网络研究变量与结果之间的影响程度。考虑到以上因素，本研究使用K2算法进行网络结构学习，通过贝叶斯估计法计算其结构参数，并在构建网络模型的基础上使用Junction Tree算法进行推理，通过概率分析研究不同学习行为对在线学习成绩的影响程度。

1 构建贝叶斯网络模型 1.1 贝叶斯网络

贝叶斯网络是概率模型图，在推理和不确定知识表达中被广泛应用，可表示为 $ {\boldsymbol{G}}= \langle S,P \rangle $ ，S表示网络的拓扑结构，为有向无环图，P表示不同结点的概率分布。结点代表不同的变量，有向边代表了结点之间的相互关系，通过条件概率表来反映这种相互关系的强弱。贝叶斯网络推理模型流程图如图1所示，离散的数据预处理后，由互信息值决定结点顺序后，通过K2算法根据评分 $p $ 学习网络结构，在生成的贝叶斯网络结构中使用贝叶斯估计方法进行参数学习，再基于联合树推理算法，在已知证据的情况下最终计算得出推理结果。

1.2 结构学习

贝叶斯网络的结构学习是通过分析数据，在基于先验知识的前提下求出结点之间的依赖关系，进而求得拓扑结构。贝叶斯网络结构的学习算法可分为3种：基于依赖统计分析的方法利用统计或者信息论的方法来分析变量之间的关系，根据条件独立性检验找到网络的依赖结构；基于评分搜索的方法结合评分函数和搜索算法搜索出评分最高的网络结构；以及混合学习方法。本研究基于第2种方法，以CH(Cooper-Herskovits)评分函数为评分准则，使用K2算法进行搜索，具体步骤如下。

(1) 互信息值计算。对于离散变量 $ {\boldsymbol{X}} $ 和 $ {\boldsymbol{Y}} $ ，互信息值 $ I\left({\boldsymbol{X}};{\boldsymbol{Y}}\right) $ 表示 $ {\boldsymbol{Y}} $ 中包含多少关于 $ {\boldsymbol{X}} $ 的信息，计算公式如式(1)所示。

$ I\left({\boldsymbol{X}};{\boldsymbol{Y}}\right)=\sum\nolimits _{y\in {\boldsymbol{Y}}}\sum\nolimits _{x\in {\boldsymbol{X}}}p(x,y)\mathrm{l}\mathrm{g}\left(\frac{p(x,y)}{p\left(x\right)p\left(y\right)}\right) $

(1)

根据式(1)，计算得到各结点与成绩之间的互信息值。

(2) 确定结点排序。根据互信息值定义，按互信息值从小到大对所求结点进行排序。

(3) 构建网络结构。在结构学习中，网络结构 $ {\boldsymbol{G}} $ 和参数 $ {\theta }_{G} $ 为随机变量，假设数据集D是关于 $ n $ 个变量 $ \{{X}_{1},{X}_{2},\cdots ,{X}_{n}\} $ 的样本， $ {\boldsymbol{G}} $ 的可能取值为所有以 $ \{{X}_{1},{X}_{2},\cdots ,{X}_{n}\} $ 为节点的有向无环图。 $ {\theta }_{G} $ 是与 $ {\boldsymbol{G}} $ 所对应的参数值。从一个空白网络开始，根据结点排序遍历结点，位于待求结点前且后验概率最大的结点成为待求结点的父结点，以此类推直到网络构建完成。假设参数 $ {\theta }_{G} $ 的先验概率分布服从狄利克雷分布，那么所用的CH评分函数的形式为^[18]

$\begin{split} &{\rm{log}}P({\boldsymbol{D}},{\boldsymbol{G}}) = \sum\nolimits_{i = 1}^n {\sum\nolimits_{j = 1}^{{q_i}} {\left[ {{\rm{log}}\left( {\frac{{\varGamma \left( {{\alpha _{ij}}} \right)}}{{\varGamma \left( {{\alpha _{ij}} + {N_{ij}}} \right)}}} \right) + } \right.} } \\ &\left. {\sum\nolimits_{k = 1}^{{r_i}} {\rm{l}} {\rm{og}}\left( {\frac{{\varGamma \left( {{\alpha _{ijk}} + {N_{ijk}}} \right)}}{{\varGamma \left( {{\alpha _{ijk}}} \right)}}} \right)} \right] + {\rm{log}}(P({\boldsymbol{G}})) \end{split}$

(2)

式(2)中： $ \mathrm{l}\mathrm{o}\mathrm{g}P({\boldsymbol{D}},{\boldsymbol{G}}) $ 即CH评分， ${\boldsymbol{D}}$ 和 ${\boldsymbol{G}}$ 分别为给定的数据集和贝叶斯网络拓扑结构， $ n $ 为结点数， $ {r}_{i} $ 表示结点 $ {X}_{i} $ 的状态数， $ \varGamma \left({\alpha }_{ij}\right) $ 为伽马函数，其中 $ {\alpha }_{ij}= $ $ {\sum} _{k}{\alpha }_{ijk} $ ， $ {\alpha }_{ijk} $ 为超系数， $ {q}_{i} $ 表示结点 $ {X}_{i} $ 的父结点的所有取值组合。 $ {N}_{ijk} $ 表示当结点值为 $ k $ 时，其父结点状态值为 $ j $ 所对应的样本数。

1.3 参数学习

贝叶斯网络的参数学习是根据已有结构通过样本学习变量相对于其父结点集合的条件概率分布。常见的参数学习方法是最大似然估计法和贝叶斯方法，本研究采用贝叶斯方法来对参数进行学习。假设贝叶斯网络参数 $ \theta $ 的先验分布 $ P\left(\theta \right|{\boldsymbol{G}}) $ 服从狄利克雷分布，即

$ P\left({\theta }_{ij}|{\boldsymbol{G}}\right)={\rm{Dir}}\left({\alpha }_{ij1},{\alpha }_{ij2},\cdots, {\alpha }_{ij{r}_{i}}\right)=\frac{\varGamma \left({\alpha }_{ij}\right)}{\prod\limits _{k}\varGamma \left({\alpha }_{ijk}\right)}\prod\limits _{k}{\theta }_{ijk}^{{\alpha }_{ijk}} $

(3)

由于参数 $ \theta $ 的后验概率也服从狄利克雷分布，即

$\begin{split} & P\left({\theta }_{ij}|{\boldsymbol{G}},{\boldsymbol{D}}\right)=\frac{P\left({\theta }_{ij}|{\boldsymbol{G}}\right)P\left({\boldsymbol{D}}|{\boldsymbol{G}},{\theta }_{ij}\right)}{P\left({\boldsymbol{D}}\right)}=\\ & \frac{\varGamma \left({\alpha }_{ij}+{N}_{ij}\right)}{\prod\limits _{k}\varGamma \left({\alpha }_{ijk}+{N}_{ijk}\right)}\prod\limits_{k}{\theta }_{ijk}^{{\alpha }_{ijk}+{N}_{ijk}} =\\ & {\rm{Dir}}\left({\alpha }_{ij1}+{N}_{ij1},{\alpha }_{ij2}+{N}_{ij2},\cdots, {\alpha }_{ij{r}_{i}}++{N}_{ij{r}_{i}}\right) \end{split}$

(4)

则参数 $ \theta $ 的最大后验概率估计为

$ {\widehat{\theta }}_{ijk}=\frac{{\alpha }_{ijk}+{N}_{ijk}}{\prod\limits _{k}\left({\alpha }_{ijk}+{N}_{ijk}\right)}=\frac{{\alpha }_{ijk}+{N}_{ijk}}{{\alpha }_{ij}+{N}_{ij}}$

(5)

$ \left( \forall i\in \left[1:{n}\right].\forall j\in \left[1:{q}_{i}\right].\forall k\in \left[1:{r}_{i}\right] \right)$

1.4 实验及有效性验证

本研究使用的数据集xAPI-Edu-Data来自UCI公开数据集，数据集由480条学生记录和16个特征组成，包括305名男性和175名女性。特征主要分为3大类：(1) 人口特征，如性别、民族、出生地。(2) 学术背景特征，如教育阶段、年级、班级、课程等。(3) 行为特征，如课堂举手、浏览资源、浏览公告、讨论次数、家长回答调查、家长对学校满意度以及学生缺席天数。根据成绩对数据分成3类，分别对应成绩低中高的学生。由于原始数据较为繁杂，故需要对数据进行清洗和离散化，只选取部分学习行为特征及其他重要特征。各结点变量定义及取值如表1所示。

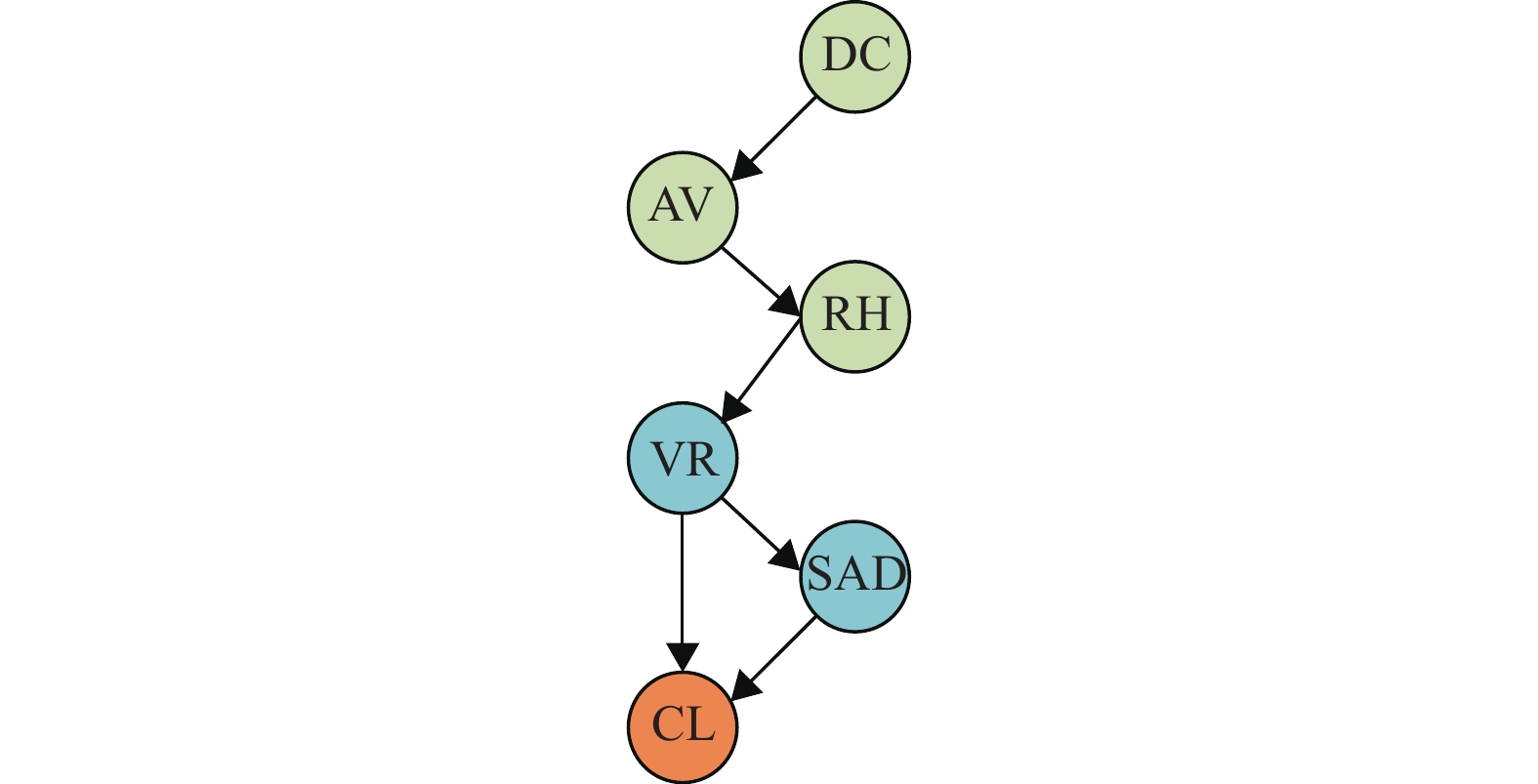
对原始数据进行处理后，首先计算互信息值，通过互信息值对结点进行排序，如表2所示，再通过MATLAB中的FULLBNT工具箱来对结构进行学习，设定最大父结点个数为2，贝叶斯网络结构学习结果如图2所示。

贝叶斯网络的拓扑结构可以直观地观察变量之间的关系。首先变量TP没有出现在贝叶斯网络中，说明该变量与其他变量不存在依赖关系，根据图2的有向边，可得到变量VR与SAD对CL产生直接影响，而DC、AV、RH变量则对CL产生间接影响。

通过MATLAB学习参数，得到贝叶斯网络参数。以SAD结点为例，如表3所示，表中数据表示了缺席天数在浏览课件次数下的后验概率。

为验证贝叶斯模型的有效性，将贝叶斯网络学习后的参数与其实际值进行比较，并且使用SPSS统计软件通过多项logistic回归预测条件概率并与贝叶斯网络参数进行比较。结果如表4所示。贝叶斯网络学习值的最大绝对误差为0.0016，最大相对误差为0.0667，平均绝对误差为0.0007，平均相对误差为0.0069。习得的贝叶斯网络参数表现出较好的精确度，说明该网络有效。与多项Logistic回归相比，贝叶斯网络表现出更小的误差，可验证其有效性。

1.5 准确率对比

为进一步评价贝叶斯网络的预测正确率，将其与目前流行的机器学习及神经网络模型进行比较，进行对比实验的模型分别是决策树(Decision Tree, DT)、随机森林(Random Forest, RF)、朴素贝叶斯(Naïve Bayes Model, NBM)、梯度上升决策树(Gradient Boosting Decision Tree, GBDT)、卷积神经网络(Convolutional Neural Networks, CNN)、长短期记忆网络(Long Short-Term Memory, LSTM)以及混合深度学习模型CNN_LSTM^[11]。

机器学习模型(决策树、随机森林等)由sklearn工具包实现，神经网络模型具体实现细节如表5所示，其中3个对比模型的dropout、batch_size、epochs分别为0.3、64、300，均由Keras实现。

模型预测准确率比较如表6所示，为保证结果的准确性，表中数据均通过分别运行各模型10次后取平均值得出。结果表明，本文的BN模型预测分类准确率最高，组合型的CNN_LSTM模型比单一的深度学习模型(如CNN、LSTM)准确率要更高，但BN模型比CNN_LSTM略胜一筹，也比常用的机器学习预测算法更优，进一步证明其有效性。朴素贝叶斯NBM的正确率与本文的贝叶斯网络正确率最为接近，但由于朴素贝叶斯基于各变量间相互独立的假设，在现实场景中难以满足，而贝叶斯网络能兼顾变量之间的依赖关系，故该模型能表现出更好的适用性。

2 学习行为影响因素分析

本节通过联合树算法，对上述学习到的贝叶斯网络结构以及参数进行推理，从而分析各学习行为因素对学生成绩的影响。

2.1 联合树推理基本原理

联合树推理首先需要构建联合树，然后利用已构建的联合树和参数进行推理。联合树构建算法可表示如下。

1) 生成Moral图

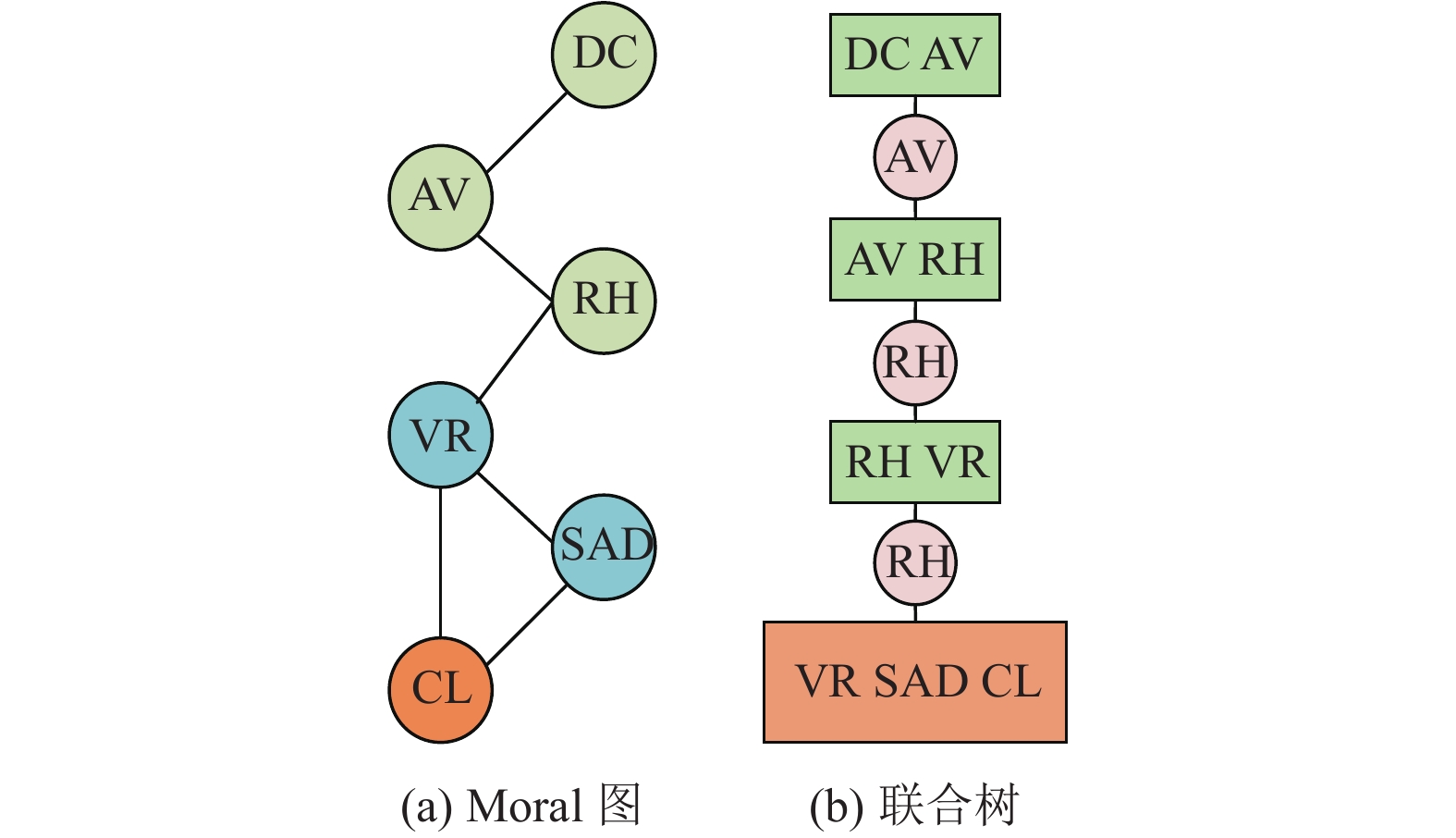
对图中的每一个结点X，用无向边将其对应的父结点连接在一起，然后将图中所有的有向边改成无向边。新添加的边被称为Moral边。根据此步骤，不需要额外边，因此Moral图就是它的无向图，如图3(a)所示。

2) Moral图的三角化

通过添加边来使Moral图中不存在超过3个点的环，从而得到三角化图。由步骤1得到的Moral图不存在超过3个点的环，因此三角化图也是Moral图本身。

3) 找出所有子团

步骤2中生成的三角图中的极大完全子图就是子团。找出三角图中所有的子团。子团有[DC AV]、[AV RH]、[RH VR]和[VR SAD CL]共4个。

4) 建立联合树

团与团之间的交集作为连接两个团结点的分隔结点，分隔结点和团结点组合起来形成联合树。生成的联合树如图3(b)所示。

联合树构建后，会先经历一个概率表的转移，即初始化过程，使树趋于一致。在推理阶段，在设定某些结点的取值作为证据后，结点的概率分布改变，一致状态被破坏，通过消息传播使其重新达到一致状态。联合树推理过程可分为以下3个步骤。

(1) 初始化：通过分布函数 $ {\phi }_{C} $ 将贝叶斯网络的条件概率表转换到联合树的每个结点中，而且每个结点中所有变量的取值都映射到0~1之间。分布函数 $ {\phi }_{C} $ 需要满足式(6)。

$ P\left(U\right)=\frac{\prod\limits _{i}{\phi }_{{C}_{i}}}{\prod\limits _{j}{\phi }_{{C}_{j}}} $

(6)

式中： $ P\left(U\right) $ 是贝叶斯网络所表示的联合概率分布， $ {\phi }_{{C}_{i}} $ 和 $ {\phi }_{{C}_{j}} $ 分别表示联合树中团结点和分隔结点的能量函数。

(2) 消息传播：随机选择一个结点作为根结点，将消息传播过程分为2个阶段。证据收集：消息自底向上传播，传递n−1次；证据扩散：消息自顶向下传播，传递n−1次。一共需要2(n−1)次消息传播。

(3) 计算推理结果：当再次一致时，可以通过能量函数计算任意变量的概率分布，此时团结点的能量函数就是包含其所有变量的联合分布函数。

2.2 影响因素推理分析

使用基于MATLAB的FULLBNT工具箱的联合树推理引擎实现上述流程，分析学习行为对成绩的影响。表7~11的内容均为固定某一变量的值为证据，计算出在该证据的情况下成绩的条件概率。

(1) 举手次数(RH)对成绩的影响：由表7可以看出，不同的举手次数对成绩有较大影响，举手次数小于30次时成绩有48.89%的概率低于69分，而当举手次数大于70次时成绩低于69分的概率不超过7%。这说明在课堂上举手次数越多，学生的课堂参与度越高，学生成绩差的可能性越小。

(2) 浏览在线课件次数(VR)对成绩的影响：从表8可知，浏览在线课件次数小于30次时对成绩的影响程度比举手次数(RH)要更大，有接近70%的概率成绩低于69分。当浏览课件次数位于30~70次时，成绩较大概率分布在70~89分(57.21%)，大于70次时，高于70分的概率超过90%。说明浏览在线课件次数对成绩具有较大的影响，而且在贝叶斯网络中二者存在有向边直接相连，具有直接依赖关系，二者结合证明浏览在线课件的次数对成绩的贡献度较高。

(3) 浏览学校公告次数(AV)对成绩的影响：由表9可知，在浏览学校公告次数小于30次时，低成绩和中等成绩的概率接近。但当浏览公告次数变高时，低成绩的概率迅速降低，证明浏览公告次数的多少可以体现出学习者对待学习是否积极。

(4) 课堂讨论次数(DC)对成绩的影响：由表10可知，课堂讨论次数对成绩的影响不大，但总体上看，课堂讨论次数越少，成绩低的可能性越高。

(5) 学生缺席天数(SAD)对成绩的影响：由表11可知，当缺席天数小于7时，成绩低于69分的概率仅为3.741%，位于中等成绩和高分成绩的分布相差不大，而当缺席天数大于7时，有接近60%的可能性成绩低于69分。缺席天数与课堂参与程度有较大关联，缺席天数的增加意味着学生的课堂参与度低，从而导致其成绩的下降。

贝叶斯网络通过概率表现出学生学习行为对成绩的影响程度，通过网络结构表示出各因素之间的关系，有利于找出影响学生成绩的直接因素。

2.3 可解释性分析

基于概率计算的贝叶斯网络推理具有良好的可解释性，其可解释性具体表现在模型学得的特征重要性及特征最优组合。在贝叶斯网络中，特征重要性表现在特征对结果的影响程度，如图2以及表7~11所示，对成绩有较大影响的特征在贝叶斯网络结构中与成绩直接相连，如学生缺席天数和课堂讨论次数，而影响程度越小的特征节点则与成绩节点距离越远，甚至与成绩之间不存在路径，如课程类型。

除此之外，基于贝叶斯网络的联合树推理还可以生成特征最优组合，特征最优组合可以表示出当结果为某一值时特征的最优取值情况，即实现从结果到原因的诊断推理。如表12所示，当成绩低于69分时，特征最优组合中缺席天数大于7，课堂讨论、浏览公告、浏览课件及举手次数均小于30次，与成绩高于70分时的特征取值截然不同，这说明不同的特征对模型的决策行为具有不同的作用。成绩位于70~89分和90~100分的特征最优组合相同，可能是由于对于当前使用的学习行为特征而言，二者对应的学习行为类似，在下一步研究中，添加特征数量可有效改善这一结果。

3 结论

(1) 研究的6个因素中，有5个因素对学生在线学习成绩产生影响，其中直接影响因素有学生浏览在线课件次数以及学生缺席天数，间接影响有举手次数、浏览学校公告次数和课堂讨论次数。在制定在线教育学习策略时，可以考虑当上述变量超过设置预警值时，对学生进行预警通知，降低其在线学习挂科率。

(2) 与多项logistic模型相比，贝叶斯网络学习的结果误差值更小，学习精度更高，说明本研究模型更加有效。与传统机器学习模型和深度模型相比，贝叶斯网络也表现出不俗的正确率，而且基于概率计算的推理可解释性比深度学习模型要更强。

(3) 基于贝叶斯网络的推理功能，可以通过条件概率清晰表示不同学习行为特征对成绩的影响程度，相比于深度神经网络预测模型来说具备较高的可解释性。

(4) 本研究受数据集的影响，特征变量的选择并不多，未来将会考虑采集更多特征的数据集进行研究。在下一步研究中，会对校内的教务系统数据以及在线教育平台蕴瑜课堂的数据进行分析，从而对学生的学习情况做出更全面的分析，通过辅助教学机制对在线课程进行调整以及对学生进行必要干预，进一步提高在线教育的有效性和针对性。