电子商务逐步向生鲜农产品领域延伸,尤其是近年来方兴未艾的农户对家庭农产品直销模式(Farm to Family,F2F),可有效缩减生鲜农产品流通环节,打造透明供应链,越来越受到生鲜农产品经营者与消费者的青睐。天猫等电商平台近年来也不断涌现产地直发的果蔬、肉蛋农产品旗舰店。F2F模式是指农产品通过电商平台实现从农场直达家庭的新型模式,它可通过互联网对传统线下生鲜农产品供应链进行流程再造,从而有效缩短供应链[1]。在F2F模式下,生鲜农产品供应链系统通常由生鲜农产品生产商(农户)、第三方物流服务提供商(Third Party Logistics service provider)、电商平台组成。第三方物流服务提供商的专业物流服务水平很大程度上保证了生鲜农产品的新鲜程度,从而满足消费者对鲜活产品新鲜度的需求。电商平台客流量大、服务标准化及低成本等特点为生鲜农产品生产商提供了新的销售机会。电商平台提供的展位布置、店铺装修、付款服务、促销、订单管理等服务影响着消费者对产品的诉求,从而影响其购买意愿。
对于供应链的保鲜水平和服务水平,学者主要采用供应链决策与协调机制来对其进行提升。王磊等[2]构建了受生鲜农产品新鲜度和价格影响的消费者时变效用函数,建立了由零售商和供应商组成的两级生鲜农产品供应链利润模型。唐润等[3]构建了生鲜食品新鲜度函数和基于时变效用的市场需求函数,研究了由供应商和零售商组成的生鲜食品双渠道供应链,并通过契约参数的合理设计实现传统渠道和网上直销渠道的协调。Yan等[4]考虑了由生产商与零售商组成的鲜活农产品二级供应链,假设新鲜度会影响产品价格,并给出了消费者的效用函数,针对分散决策导致的利润损失问题,设计了收益共享和批发价折扣契约来协调供应链。冯颖[5]研究了由供应商、TPL和零售商组成的生鲜农产品三级供应链,其中市场需求受零售价格与新鲜度的影响,并设计了物流服务成本分担契约和物流服务数量折扣契约来协调供应链。马雪丽等[6]将农产品的数量和质量损耗均视为TPL保鲜努力的内生变量,考虑保鲜努力与数量/质量弹性的农产品三级供应链决策问题,针对分散决策下供应链各成员决策导致的产品销售量和销售价格扭曲问题,设计了成本分担和收益共享契约来协调供应链。Song等[7]研究了由电商、第三方物流服务商、社区便利店组成的三级生鲜农产品(Fresh Agricultural Product, FAP)供应链,并设计了成本分摊−收益共享联合契约来激励第三方物流服务商提升产品新鲜度。Ma等[8]建立了由第三方物流服务提供商、供应商与零售商组成的鲜活农产品三级供应链的决策模型,其中生鲜产品的市场需求是零售价格、产品新鲜度和随机变量的乘法函数形式,针对分散决策导致的订货量、价格扭曲及利润减少问题,设计了一个成本与收益共享联合契约来协调供应链 。Song等[9]研究了由制造商、TPL、零售商组成的生鲜电商三级供应链,其中生鲜产品的市场需求是零售价格、产品新鲜度、安全追溯系统以及随机变量的线性函数,针对分散决策效率低的问题,设计了一个成本共担−收益共享契约与回扣−收益分享契约来协调供应链。
部分文献在建立生鲜供应链决策与协调模型时,将服务水平纳入到决策变量中。服务水平是影响消费者购物体验的重要因素,近年来受到了越来越多学者的关注。Yulia等[10]讨论了电子零售商和物流服务提供商在电子商务配送最后几公里上寻求服务创新的途径。白世贞等[11]研究市场需求受价格、新鲜水平及促销努力水平影响的两级生鲜供应链的协调问题。Ilkyeong 等[12]研究了生产商的保鲜努力水平和零售商的投资服务水平影响市场需求的二级供应链协调问题,并设计了一个收入共享加上投资成本分摊和增量数量折扣合同来协调供应链。侯玉梅等[13]研究了需求受服务水平影响的生鲜农产品三级供应链协调性问题,设计了基于收益共享和成本共担的契约来激励分销商提高服务水平。Nie等[14]建立了由供应商和零售商构成的双渠道生鲜产品供应链,研究表明供应商和零售商分别通过提高线上服务水平和线下服务水平来提高竞争力。现有文献中关注电商平台服务水平的研究相对较少,Wang等[15]研究了考虑绿色农产品制造商公平的电商直销二级供应链的决策与协调问题,其中市场需求受市场价格、产品绿色度、电商平台服务水平影响,并设计了成本分摊联合佣金契约来协调供应链。本研究将讨论服务水平作为电商平台决策变量的供应链决策与协调机制。
综上所述,有关生鲜电商供应链的研究主要涉及以下因素:网上销售渠道、产品新鲜度、服务水平、协调机制、供应链层级。本研究将结合这些因素,并将服务水平作为电商平台的决策变量,分析生鲜产品生产商、TPL、电商平台关于零售价格、保鲜水平、服务水平的决策过程与供应链协调机制。
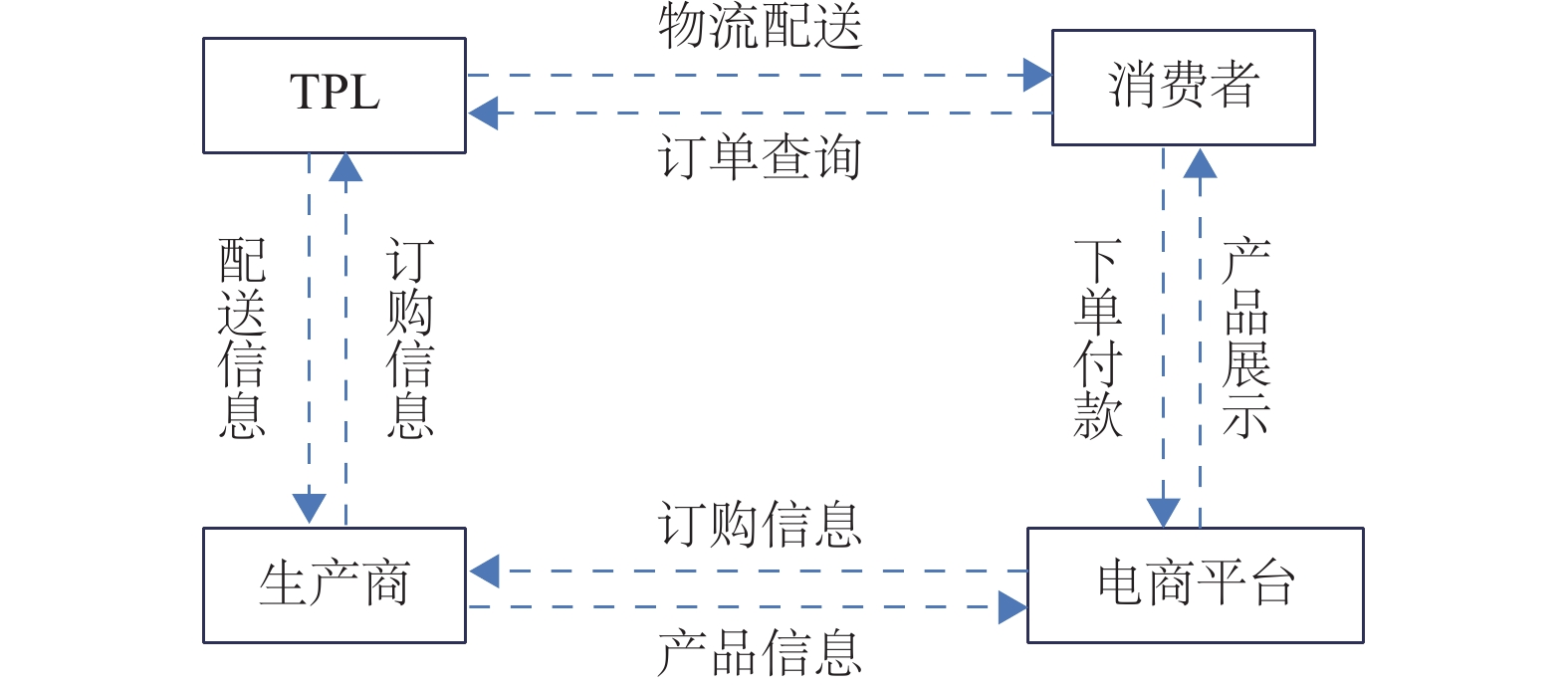
1 问题描述 1.1 模型结构本研究考虑了由一个生鲜产品生产商(以下简称生产商)、第三方物流服务商(TPL)和电商平台组成的三级生鲜电商直销供应链(如图1所示)。生产商通过在电商平台发布产品信息并直销给消费者,订单生成后,产品通过TPL运送到消费者手中。这种F2F直销模式在淘宝与京东等大型电商平台十分常见,飞利浦与大帝照明通过淘宝直销节能灯泡;多乐士、都芳、嘉宝莉在京东上直销环保涂料[15]。电商平台针对不同类型的生产商以及不同的服务收取不同的佣金,这些服务体现在展位布局、店铺装修、支付服务、促销、订单管理等方面。实际运营中电商平台根据产品品类来收取佣金。
|
图 1 生鲜电商三级直销供应链 Figure 1 Three level direct selling supply chain of fresh E-commerce |
假设1 生鲜农产品的新鲜度F受保鲜水平的影响,借鉴文献[9],假设
| $ F(\theta ){\text{ = }}{\theta _{\text{0}}}\theta\;\;\;\; \left( {{\text{0}} \leqslant {\theta _{\text{0}}} \leqslant {\text{1}}} \right) $ |
式中:
假设2 生鲜产品市场需求受产品价格、服务水平、新鲜度的影响且订货量等于市场需求量。参考文献[9, 15],生鲜产品的需求函数为
| $ Q = a - bp + \eta \mu + \beta {\theta _0}\theta $ |
式中:
假设3 借鉴文献[9,15-16],生鲜产品的保鲜成本是保鲜水平的二次函数,即
| $ C(\theta) {\text{ = }}\frac{h}{2}{\theta ^2} $ |
式中:
| $ C(\mu )\text=\frac{k}{2}{\mu }^{2} $ |
式中:
假设4 假设供应链系统各参数值都为正数,且市场需求量与节点企业的利润为正,即
| $ {p}_{{\rm{t}}}>{c}_{{\rm{t}}},\;p>{p}_{{\rm{e}}}+{p}_{{\rm{t}}}+{c}_{{\rm{m}}},\;a-b({c}_{{\rm{t}}}+{c}_{{\rm{m}}}+{p}_{{\rm{e}}})>0 $ |
式中:
集中化的供应链将生产商、TPL、电商平台视为一体,只存在唯一的决策者来作出最佳决策以使供应链利润最大。此时,整个供应链的利润为
| $ {\varPi }^{{\rm{c}}}=(p-{c}_{{\rm{t}}}-{c}_{\mathrm{m}})(a-bp+\eta \mu +\beta {\theta }_{0}\theta )-\frac{k}{2}{\mu }^{2}-\frac{h}{2}{\theta }^{2} $ |
式中:
上式分别对
| $ \frac{\partial {\varPi }^{{\rm{c}}}}{\partial p}=a+\eta \mu +\beta {\theta }_{0}\theta +b({c}_{{\rm{t}}}+{c}_{\mathrm{m}})-{2}bp{=0} $ |
| $\frac{\partial { {\varPi } }^{{\rm{c}}}}{\partial \theta }=\beta {\theta }_{0}(p-{c}_{{\rm{t}}}-{c}_{\mathrm{m}})-h\theta {=0} $ |
| $ \frac{\partial { {\varPi } }^{{\rm{c}}}}{\partial \mu }=\eta (p-{c}_{{\rm{t}}}-{c}_{\mathrm{m}})-k\mu {=0}$ |
联立方程求解可得到集中决策模型下最优的产品价格、保鲜水平、服务水平分别为
| $ {p}_{{\rm{c}}}\text=\frac{ahk\text+(bhk-h{\eta }^{\text{2}}-k{\theta }_{0}{}^{2}{\beta }^{\text{2}})({c}_{{\rm{t}}}+{c}_{{\rm{m}}})}{2bhk-h{\eta }^{\text{2}}-k{\beta }^{\text{2}}{\theta }_{0}{}^{2}} $ |
| $ {\theta }_{{\rm{c}}}=\frac{\beta {\theta }_{0}k(a-b({c}_{{\rm{t}}}+{c}_{{\rm{m}}}))}{2bhk-h{\eta }^{\text{2}}-k{\beta }^{\text{2}}{\theta }_{0}{}^{2}}$ |
| $ {\mu _{\rm{c}}} = \frac{{h\eta (a - b({c_{\rm{t}}} + {c_{\rm{m}}}))}}{{2bhk - h{\eta ^{\text{2}}} - k{\beta ^{\text{2}}}{\theta _0}^2}}$ |
市场价格等变量为正值,假设参数满足条件
| $ {\boldsymbol {H}}({\varPi }^{{\rm{c}}})=\left| {\begin{array}{*{20}{c}} { - 2b}&{\beta {\theta _0}}&\eta \\ {\beta {\theta _0}}&{ - h}&0\\ \eta &0&{ - k} \end{array}} \right|=-2bhk\text+h{\eta }^{2}+k{\beta }^{2}{\theta }_{0}{}^{2}<0 $ |
式中:一阶主子式
| $ {Q_{\rm{c}}} = \frac{{bhk(a - b({c_{\rm{t}}} + {c_{\rm{m}}}))}}{{2bhk - h{\eta ^{\text{2}}} - k{\beta ^{\text{2}}}{\theta _0}^2}} $ |
| $ {{\varPi } ^{\rm{c}}} = \frac{{hk{{(a - b({c_{\rm{t}}} + {c_{\rm{m}}}))}^2}}}{{2(2bhk - h{\eta ^{\text{2}}} - k{\beta ^{\text{2}}}{\theta _0}^2)}}$ |
分散决策下,生产商、TPL、电商平台根据供应链传递的信息以及自身的成本结构非合作地做出决策,以追求利润最大化,三个供应链成员的决策相互影响。模型的Stackelberg博弈顺序为:首先,电商平台先发制人确定最优的服务水平;然后,TPL确定最优运输单价和保鲜水平;最后,生产商确定最优的产品价格。下面采用逆向归纳法分析。
生产商最优决策为
| $ {\varPi _{\rm{m}}} = (p - {p_{\rm{e}}} - {c_{\rm{m}}} - {p_{\rm{t}}})(a - bp + \eta \mu + \beta {\theta _0}\theta ) $ |
式中:
令
| $ p({p}_{{\rm{t}}}\text{,}\theta \text{,}\mu )\text=\frac{a\text+\eta \mu +\beta {\theta }_{0}\theta \text+b({p}_{{\rm{e}}}+{c}_{{\rm{m}}}\text+{p}_{{\rm{t}}})}{2b} $ | (1) |
从而有
| $ Q({p}_{{\rm{t}}}\text{,}\theta \text{,}\mu )\text=\frac{a\text+\eta \mu +\beta {\theta }_{0}\theta -b({p}_{{\rm{e}}}+{c}_{{\rm{m}}}\text+{p}_{{\rm{t}}})}{2b} $ | (2) |
TPT最优决策(令
| $ {\varPi _{\rm{t}}} = ({p_{\rm{t}}} - {c_{\rm{t}}})(a - bp + \eta \mu + \beta {\theta _0}\theta ) - \frac{h}{2}{\theta ^2} $ | (3) |
式中:
将式(1)代入式(3),并将
| $ {p_{\rm{t}}}(\mu ){\text{ = }}\frac{{{\text{2}}h(a + \eta \mu - bA)}}{{4bh - {\beta ^{\text{2}}}{\theta _0}^2}} + {c_{\rm{t}}} $ | (4) |
| $ \theta (\mu ) = \frac{{\beta {\theta _0}(a + \eta \mu -bA)}}{{4bh - {\beta ^{\text{2}}}{\theta _0}^2}} $ | (5) |
将式(4)~(5)代入式(2)有
| $ Q(\mu ){\text{ = }}\frac{{hb(a + \eta \mu -bA)}}{{4bh - {\beta ^{\text{2}}}{\theta _0}^2}} $ | (6) |
| $ {\boldsymbol {H}}({\varPi }_{{\rm{t}}})=\left| {\begin{array}{*{20}{c}} { - b}&{\beta {\theta _0}/2}\\ {\beta {\theta _0}/2}&{ - h} \end{array}} \right|\text=bh-{\beta }^{\text{2}}{\theta }_{0}{}^{2}/\text{4}>\text{0} $ |
一阶主子式
电商平台最优决策为
| $ {\varPi _{\rm{e}}} = {p_{\rm{e}}}(a - bp + \eta \mu + \beta {\theta _0}\theta ) - \frac{k}{2}{\mu ^2} $ | (7) |
式中:
将式(6)代入式(7),并将
| $ \mu = \frac{{{p_{\rm{e}}}bh\eta }}{{k(4bh - {\beta ^{\text{2}}}{\theta _0}^2)}} $ |
因为
| $ \begin{array}{*{20}{c}} {\mu _{{\rm{dc}}}} = \dfrac{{{p_{\rm{e}}}bh\eta }}{{k\left( {4bh - {{\beta _{\,}^2}}\theta _0^2} \right)}}\\ {\theta _{{\rm{dc}}}} = \dfrac{{\beta {\theta _0}(a{{ - }}bA)}}{{4bh - {\beta _{\,}^2}\theta _0^2}} {\text{ + }} \dfrac{{\beta {\theta _0}{p_{\rm{e}}}bh{\eta ^{\text{2}}}}}{{k{{(4bh - {\beta _{\,}^2}\theta _0^2)}{^2}}}} \\ {p_{\rm{t}}} = \dfrac{{{\text{2}}h(a - bA)}}{{4bh - {\beta _{\,}^2}\theta _0^2}} + \dfrac{{{\text{2}}{p_{{\rm{e}}} }b{h^{\text{2}}}{\eta ^{\text{2}}}}}{{k{{(4bh - {\beta _{\,}^2}\theta _0^2)}{^2}}}}{\text{ + }}{c_{\rm{t}}} \end{array} $ |
| $ {p_{{\rm{dc}}}} = \frac{{3h(a{\rm{ - }}bA)}}{{4bh - {\beta ^{\rm{2}}}}} + \frac{{{\rm{3}}{p_{\rm{e}}}b{h^{\rm{2}}}{\eta ^{\rm{2}}}}}{{k{{(4bh - {\beta ^{\rm{2}}})}{^2}}}}{\rm{ + }}A$ |
| $ {Q_{{{\rm{dc}}} }} = \frac{{hb(a - bA)}}{{4bh - {\beta _{\,}^2}\theta _0^2}} + \frac{{{p_{\rm{e}}}{b^{\text{2}}}{h^{\text{2}}}{\eta ^{\text{2}}}}}{{k{{(4bh - {\beta _{\,}^2}\theta _0^2)}{^2}}}} $ |
市场需求量及生产商、TPL、电商平台利润分别为
| $ \begin{array}{*{20}{c}} \varPi _{\rm{m}}^{{\rm{dc}}} = b{h^{\text{2}}}{\Bigg(\dfrac{{k(a - bA)(4bh - {\beta _{\,}^2}\theta _0^2){\text{ + }}{p_{\rm{e}}}bh{\eta ^{\text{2}}}}}{{k{{(4bh - {\beta _{\,}^2}\theta _0^2)}{^2}}}}\Bigg)^2} \\ \varPi _{\rm{t}}^{{\rm{dc}}} = \dfrac{h}{2}(4bh - {\beta _{\,}^2}\theta _0^2){\Bigg(\dfrac{{k(a{{ - }}bA)(4bh - {\beta _{\,}^2}\theta _0^2){\text{ + }}{p_{\rm{e}}}bh{\eta ^{\text{2}}}}}{{k{{(4bh - {\beta _{\,}^2}\theta _0^2)}{^2}}}}\Bigg)^2} \end{array} $ |
| $ \varPi _{\rm{e}}^{{\rm{dc}}} = \frac{{2k{p_{\rm{e}}}bh(a{{ - }}bA)(4bh - {\beta _{\,}^2}\theta _0^2){\text{ + }}{p_{\rm{e}}}^2{b^2}{h^2}{\eta ^{\text{2}}}}}{{2k{{(4bh - {\beta _{\,}^2}\theta _0^2)}{^2}}}} $ |
| $ {\varPi ^{{{\rm{dc}}} }}{\text{ = }}\varPi _{\rm{m}}^{{\rm{dc}}}{\text{ + }}\varPi _{\rm{t}}^{{\rm{dc}}}{\text{ + }}\varPi _{\rm{e}}^{{\rm{dc}}} $ |
命题1
证明
| $\begin{array}{*{20}{c}} {\mu }_{{\rm{dc}}}-{\mu }_{{\rm{c}}}\text=\\ \dfrac{{p}_{{\rm{e}}}bh\eta (2bhk-h{\eta }^{\text{2}}-k{\beta }^{\text{2}}{\theta }_{0}{}^{2})-k(4bh-{\beta }^{\text{2}}{\theta }_{0}{}^{2})h\eta (a-b({c}_{{\rm{t}}}+{c}_{{\rm{m}}}))}{k(4bh-{\beta }^{\text{2}}{\theta }_{0}{}^{2})(2bhk-h{\eta }^{\text{2}}-k{\beta }^{\text{2}}{\theta }_{0}{}^{2})} \lt \end{array} $ |
| $ \frac{{p}_{{\rm{e}}}b(2bh-{\beta }^{\text{2}}{\theta }_{0}{}^{2})-(a-b({c}_{{\rm{t}}}+{c}_{{\rm{m}}}))(4bh-{\beta }^{\text{2}}{\theta }_{0}{}^{2})}{k(4bh-{\beta }^{\text{2}}{\theta }_{0}{}^{2})(2bhk-h{\eta }^{\text{2}}-k{\beta }^{\text{2}}{\theta }_{0}{}^{2})} \lt 0 $ |
同理可证
已知
上述研究可以看出分散决策下的服务水平、保鲜水平均低于集中决策,而当TPL提高保鲜水平和电商平台提高服务水平时,会增加各自的成本。当生产商分摊部分收益给TPL与电商平台时,会弥补部分成本。根据Saha[17]的研究,当供应链成员严格遵守分散决策的报价时,返利契约可以在一定程度上优化两层供应链的利润。因此下面设计一个返利收入共享联合(Consolidated Rebate and Revenue Sharing,CR&RS)契约来协调供应链利润。该契约的思想如下:首先电商平台确定服务水平
| $ \begin{split} \varPi _{\rm{m}}^{{\rm{rc}}} = &((1{{ - }}{\varphi _{\text{1}}}{{ - }}{\varphi _{\text{2}}}){p_{{\rm{dc}}}} - {p_{\rm{e}}} - {c_{\rm{m}}} - {p_{\rm{t}}})(a - b(p - {\phi _{\text{1}}} - {\phi _{\text{2}}}) + \\ & \eta {\mu _{\rm{c}}} + \beta {\theta _0}{\theta _{\rm{c}}}) \end{split} $ |
| $ \begin{split} \varPi _{\rm{t}}^{{\rm{rc}}} = & ({p_{\rm{t}}} - {c_{\rm{t}}} - {\phi _{\text{1}}} + {\varphi _{\text{1}}}{p_{{\rm{dc}}}})(a - b(p - {\phi _{\text{1}}} - {\phi _{\text{2}}}) + \eta {\mu _{\rm{c}}} + \\ & \beta {\theta _0}{\theta _{\rm{c}}}) - \frac{h}{2}{\theta _{\rm{c}}}^2 \end{split} $ |
| $\, \varPi _{\rm{e}}^{{\rm{rc}}} = ({p_{\rm{e}}} - {\phi _{\text{2}}} + {\varphi _2}{p_{{\rm{dc}}}})(a - b(p - {\phi _{\text{1}}} - {\phi _{\text{2}}}) + \eta {\mu _{\rm{c}}} + \beta {\theta _0}{\theta _{\rm{c}}}) - \frac{k}{2}{\mu _{\rm{c}}}^2 $ |
命题2 生鲜电商三级供应链协调以及供应链各成员实现帕累托改善的条件为
| $ {\phi _{\text{1}}}{\text{ + }}{\phi _{\text{2}}}{\text{ = }}{p_{{\rm{dc}}}} - {p_{\rm{c}}}$ |
| $ \begin{array}{*{20}{c}} {{\varphi _1} + {\varphi _2} < \dfrac{{k{M^2}}}{{3hk(a - bA)M + 3{p_{\rm{e}}}b{h^2}{\eta ^2} + kA{M^2}}}} \times \\ {\Bigg( {\dfrac{{b{h^2}}}{{{Q_{\rm{c}}}}}{{\left( {\dfrac{{k(a - bA)M + {p_{\rm{e}}}bh{\eta ^2}}}{{kM}}} \right)}^2} + A + \dfrac{{2hk(a - bA)M + 2{p_{\rm{e}}}b{h^2}{\eta ^2}}}{{k{M^2}}}} \Bigg)} \end{array}$ |
| $ \begin{split} {\varphi _1} >& \dfrac{{k{M^2}}}{{3hk(a - bA)M + 3{p_{\rm{e}}}b{h^2}{\eta ^2} + kA{M^2}}}\times \\& \Bigg( {\dfrac{{hM}}{{2{Q_{\rm{c}}}}}{{\left( {\dfrac{{k(a - bA)M + {p_{\rm{e}}}bh{\eta ^2}}}{{k{M^2}}}} \right)}^2} + \dfrac{{h\theta _{\rm{c}}^2}}{{2{Q_{\rm{c}}}}} - } \Bigg.\\& \Bigg. {\dfrac{{2hk(a - bA)M + 2{p_{\rm{e}}}b{h^2}{\eta ^2}}}{{k{M^2}}} + {\phi _1}} \Bigg) \end{split}$ |
| $ \begin{split} {\varphi }_{\text{2}}>&\frac{k{M}^{\text{2}}}{\text{3}hk(a-bA)M+3{p}_{{\rm{e}}}b{h}^{2}{\eta }^{\text{2}}+kA{M}^{2}} \times\\ &\left(\frac{\text{2}k{p}_{{\rm{e}}}bh(a-bA)M+{p}_{\mathrm{e}}{}^{\text{2}}{b}^{\text{2}}{h}^{\text{2}}{\eta }^{\text{2}}}{\text{2}k{Q}_{{\rm{c}}}{M}^{\text{2}}}+\frac{k{\mu }_{{\rm{c}}}{}^{\text{2}}}{\text{2}{Q}_{\mathrm{c}}}-{p}_{{\rm{e}}}\text{+}{\phi }_{\text{2}}\right) \end{split} $ |
式中:
证明 当供应链各成员的报价与分散决策模型一致时,如果电商平台与TPL共同拟定返利值
命题2意味着当参数满足一定要求时,CR&RS契约可以协调供应链,并能实现供应链各成员的帕累托改进。根据本契约,电商平台和TPL承担服务和保鲜所引起的成本,并共同提供返利,实际运营中谁承担更多的返利取决于双方的谈判能力。
3 数值分析为了进一步验证上述模型的有效性,以及各系数对供应链利润的影响,本节提供数值案例。从上文可知参数满足
| 表 1 3种模式结果对比 Table 1 Comparison of the three modes |
下面分析系数与相关参数变化对供应链各方利润的影响。
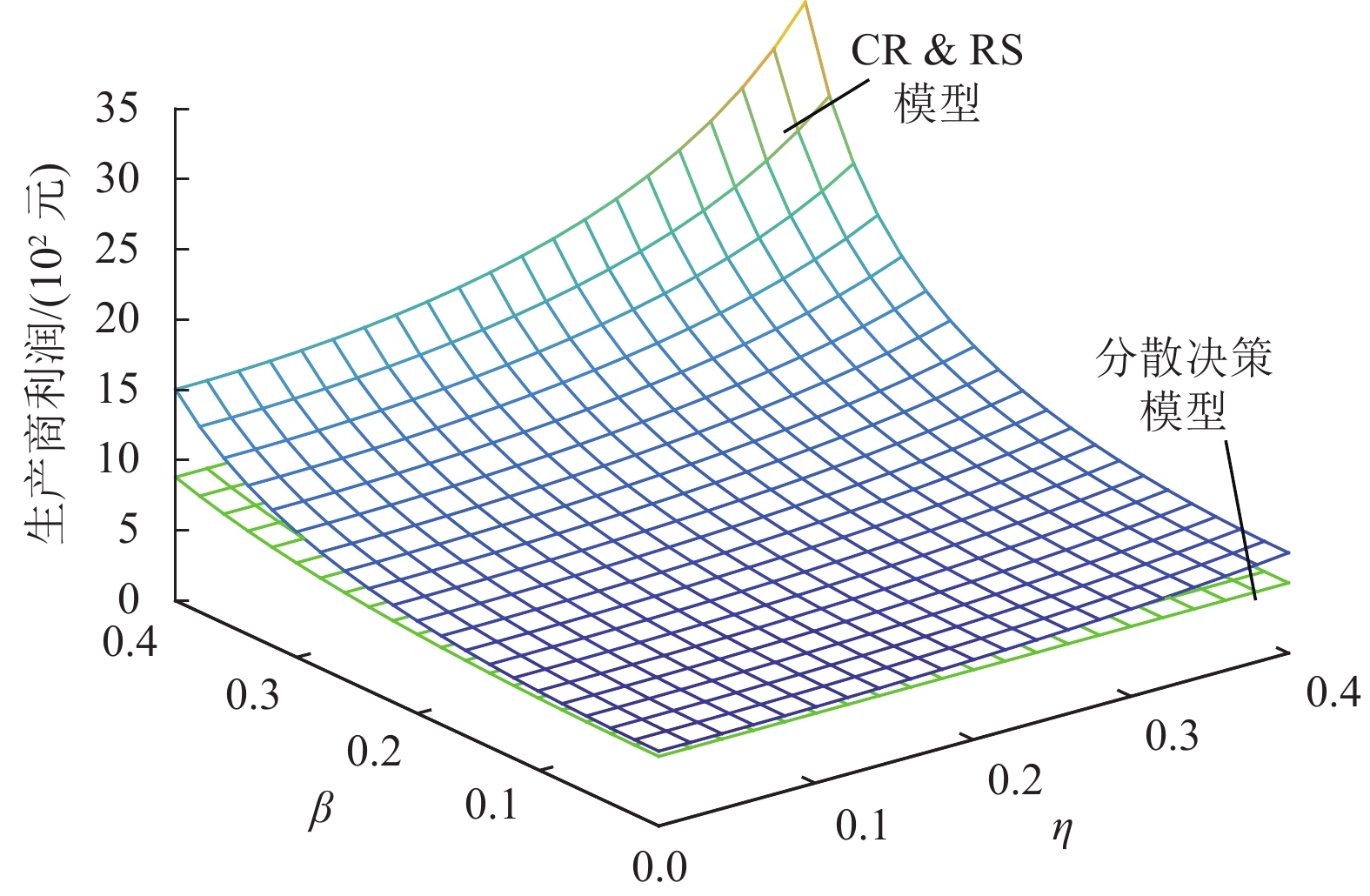
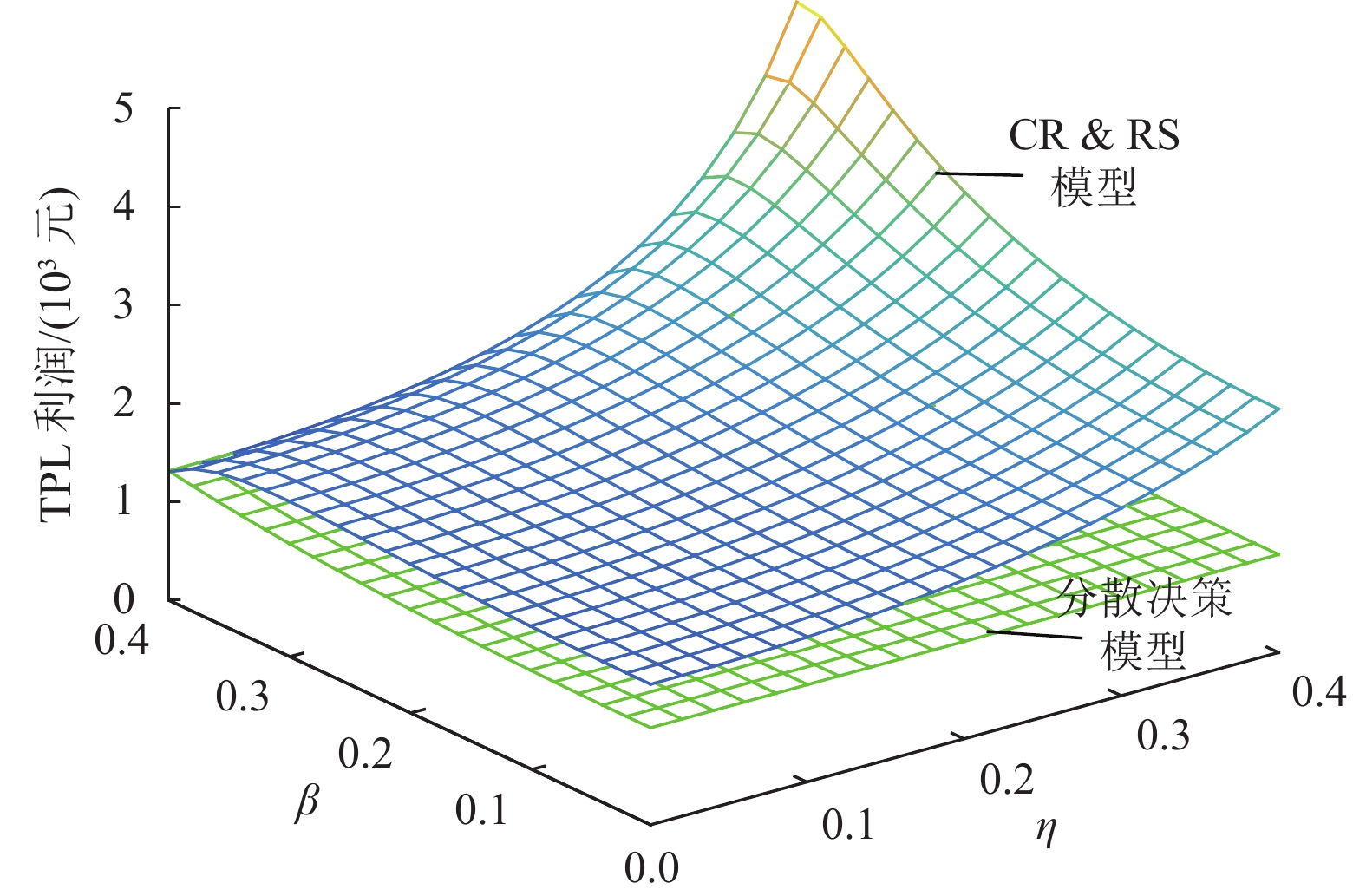
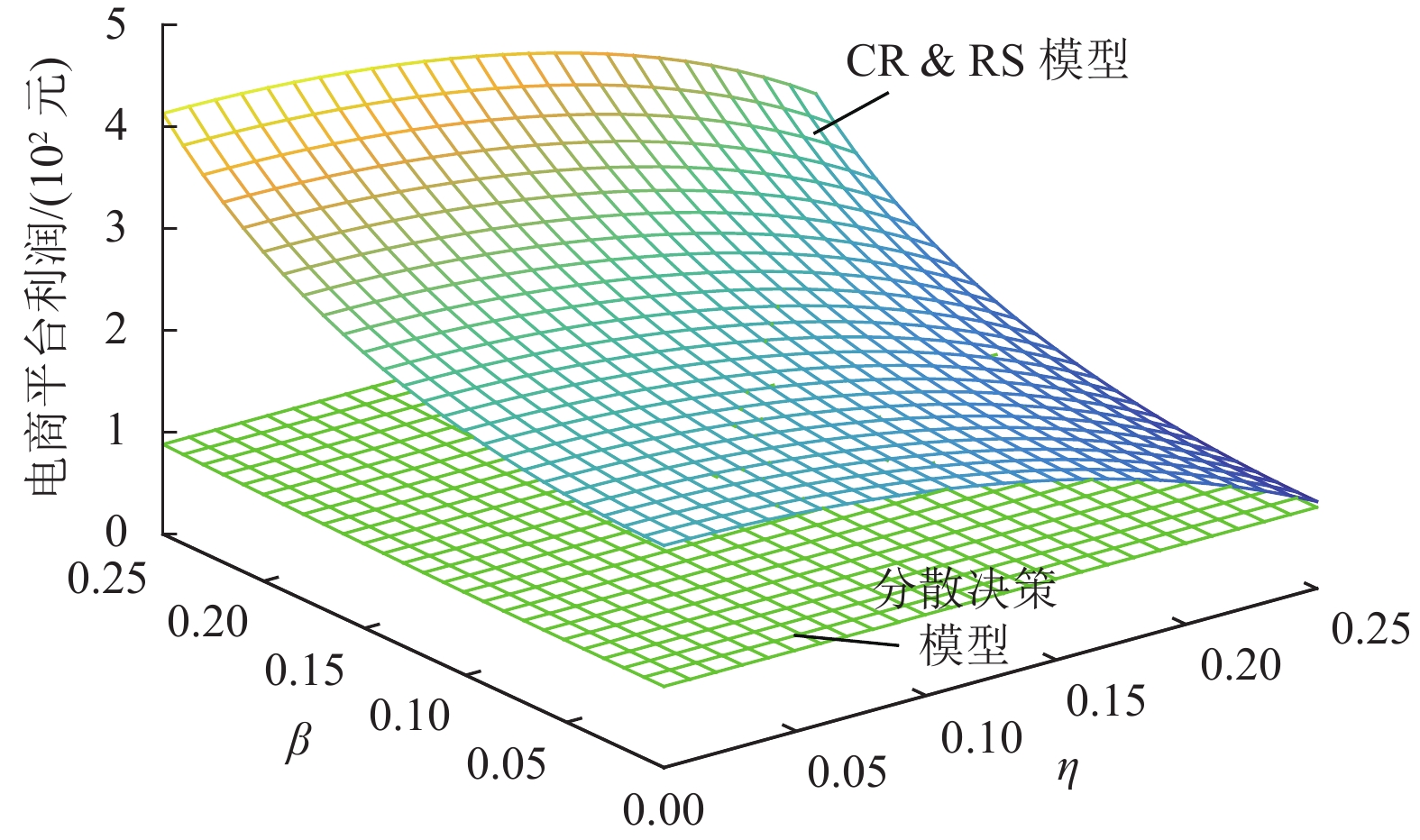
从图2~图4可以看出,分散决策模型下生产商、TPL、电商平台的利润随着系数
|
图 2 |
|
图 3 |
|
图 4 |
从图5~图7可以看出,分散决策模型下生产商、TPL、电商平台的利润随着系数
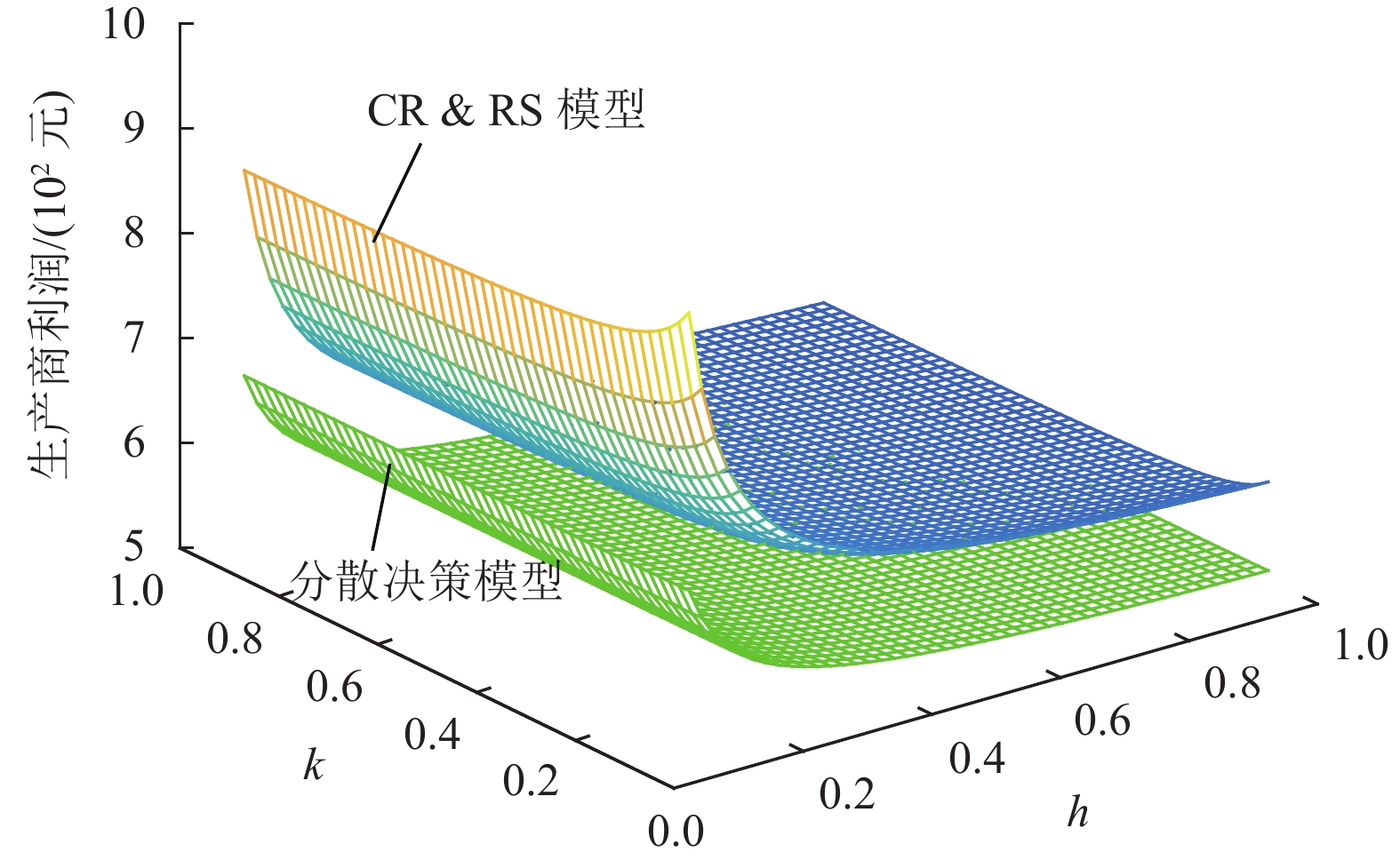
|
图 5 |
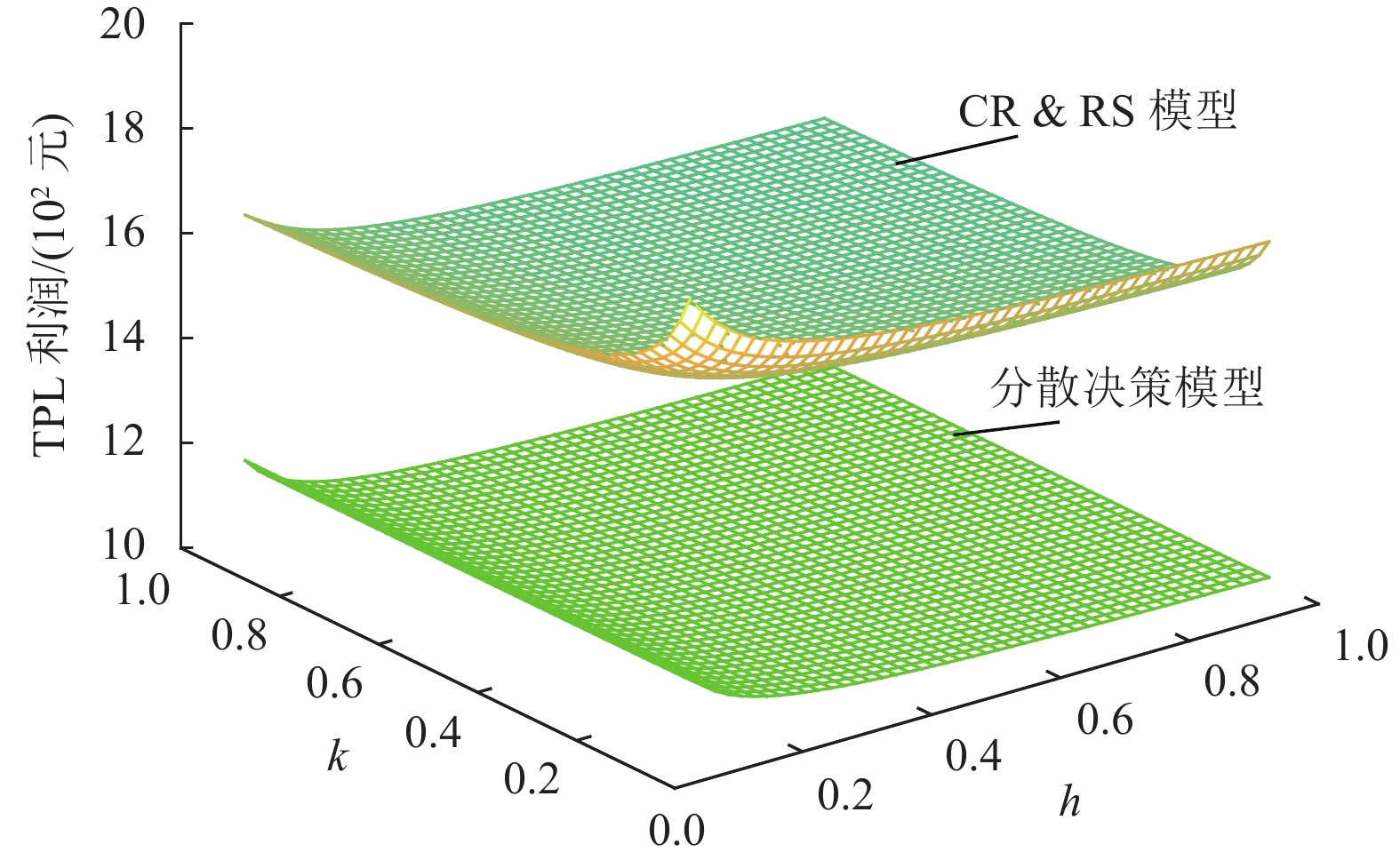
|
图 6 |
从图8~图10可以看出,两种模型都存在生产商与TPL的利润随着系数b、e的增大而减小,电商平台利润随

|
图 7 |
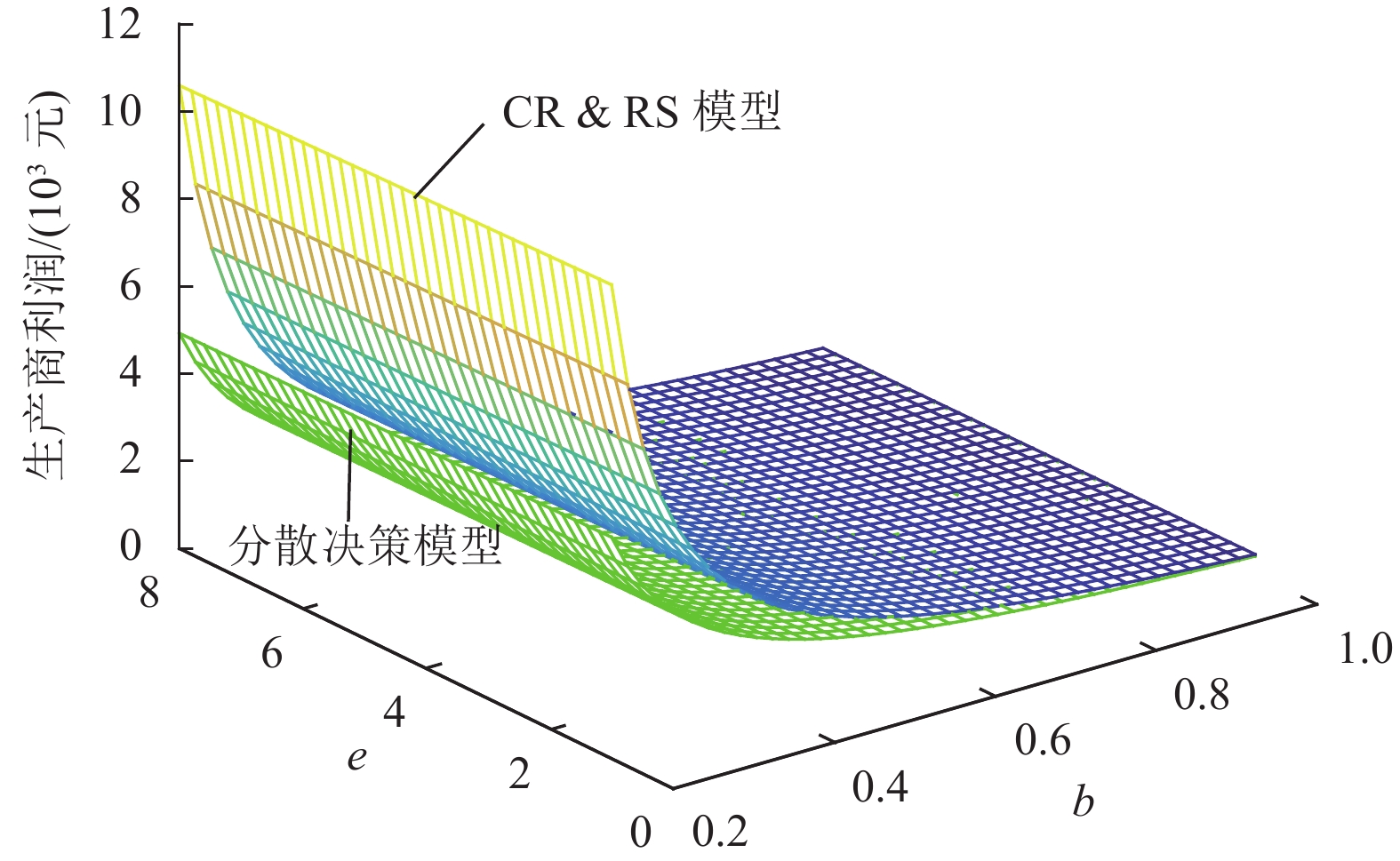
|
图 8 |
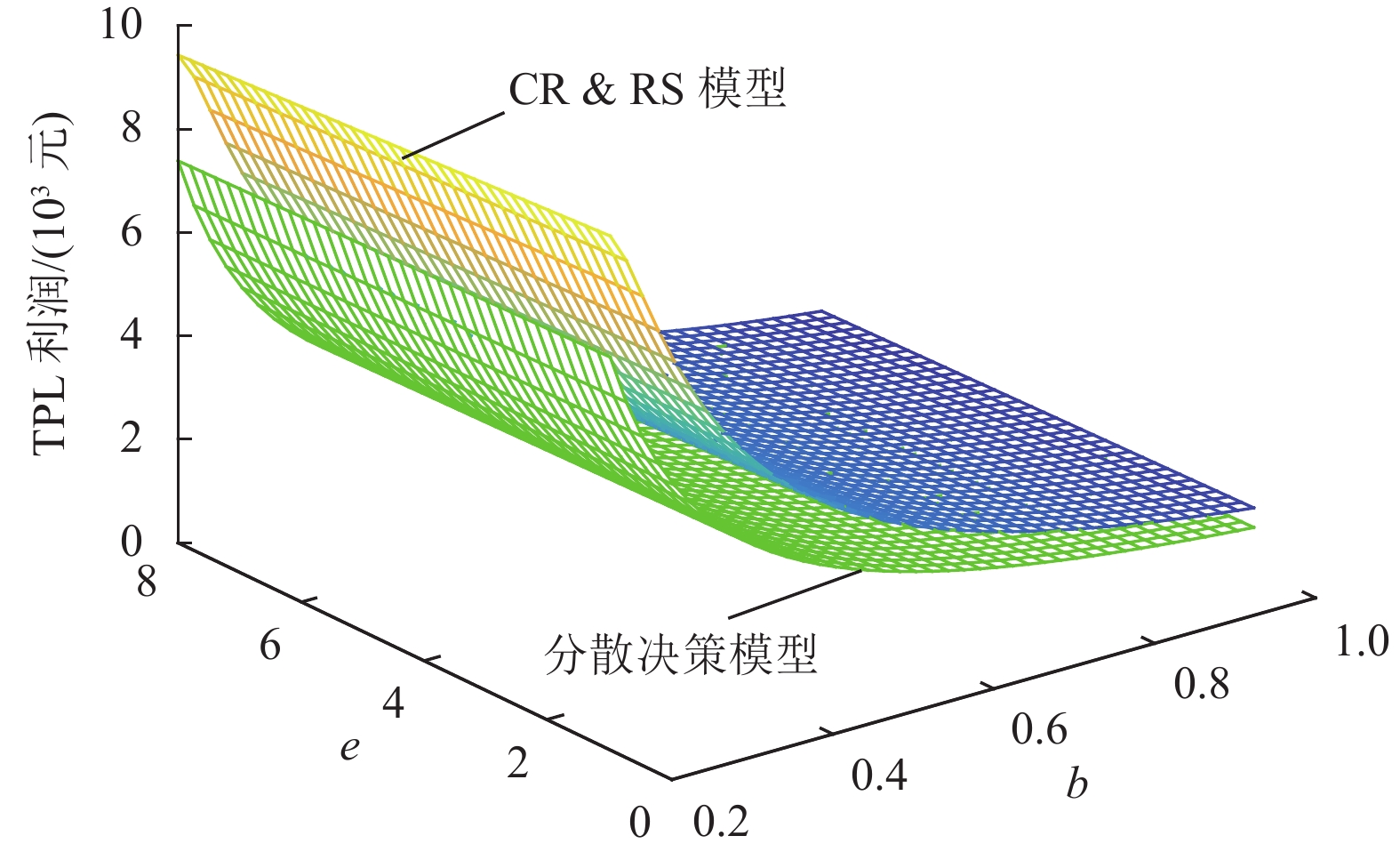
|
图 9 |

|
图 10 |
本文考虑了由生产商、TPL、电商平台组成的生鲜电商三级直销供应链、农产品的市场需求受价格、产品的新鲜度以及网上服务水平多重因素的影响,分别研究了分散与集中决策模型下供应链各方的决策行为和决策绩效。研究结论如下:(1) 分散决策模型下的产品新鲜度、服务水平、产品销量以及供应链利润均低于集中决策模型。(2) 针对分散模型下决策扭曲问题,设计了一个返利收入共享联合契约来协调供应链利润,表明当参数满足一定条件时,该契约能实现供应链协调且实现供应链各成员的帕累托改善。(3) 敏感系数会影响各成员的利润,并影响契约的顺利实施。比如在一定参数范围内,当消费者对价格弹性系数
本文的研究局限于确定性需求的情形,但在现实中,市场需求显示出很大的随机性,且供应链各方关于市场需求、产品新鲜度、服务水平等信息通常不对称。因此,后续可开展市场随机需求下的生鲜电商三级供应链协调问题的研究。
| [1] |
邵腾伟, 吕秀梅. 基于F2F的生鲜农产品C2B众筹预售定价[J].
中国管理科学, 2016, 24(11): 147-152.
SHAO T W, LYU X M. Price on fresh agricultural products by C2B based on F2F[J]. Chinese Journal of Management Science, 2016, 24(11): 147-152. |
| [2] |
王磊, 但斌. 考虑零售商保鲜和消费者效用的生鲜农产品供应链协调[J].
运筹与管理, 2015, 24(5): 44-51.
WANG L, DAN B. Coordination of fresh agricultural supply chain considering retailer's freshness-keeping and consumer utility[J]. Operations Research & Management Science, 2015, 24(5): 44-51. DOI: 10.12005/orms.2015.0157. |
| [3] |
唐润, 彭洋洋. 考虑时间和温度因素的生鲜食品双渠道供应链协调[J].
中国管理科学, 2015, 24(5): 44-51.
TANG R, PENG Y Y. Dual channel coordination of fresh food supply chain considering time and temperature factors[J]. Chinese Journal of Management Science, 2015, 24(5): 44-51. |
| [4] |
YAN B, CHEN X X, CAI C Y, et al. Supply chain coordination of fresh agricultural products based on consumer behavior[J]. Computers and Operations Research, 2010, 123: 1-38.
|
| [5] |
冯颖, 余云龙, 张炎治, 等. TPL服务商参与决策的生鲜农产品三级供应链协调机制[J].
管理工程学报, 2015, 29(4): 213-221.
FENG Y, YU Y L, ZHANG Y Z, et al. Coordination in a three-echelon supply chain of fresh agri-products with TPLSP's participation in decision-making[J]. Journal of Industrial Engineering & Engineering Management, 2015, 29(4): 213-221. |
| [6] |
马雪丽, 王淑云, 金辉, 等. 考虑保鲜努力与数量/质量弹性的农产品三级供应链协调优化[J].
中国管理科学, 2018, 26(2): 175-185.
MA X L, WANG S Y, JIN H, et al. Coordination and optimization of three-echelon agricultural product supply chain considering freshness-keeping effort and quantity/quality elasticity[J]. Chinese Journal of Management Science, 2018, 26(2): 175-185. |
| [7] |
SONG Z L, HE S W. Contract coordination of new fresh produce three-layer supply chain[J].
Industrial Management & Data Systems, 2019, 119(1): 148-169.
|
| [8] |
MA X L, WANG S Y, SARDAR M N, et al. Coordinating a three-echelon fresh agricultural products supply chain considering freshness-keeping effort with asymmetric information[J].
Applied Mathematical Modelling, 2019, 67: 337-356.
DOI: 10.1016/j.apm.2018.10.028. |
| [9] |
SONG Z L, HE S W, XU G S. Decision and coordination of fresh produce three-layer e-commerce supply chain: a new framework[J].
IEEE Access, 2019(7): 30465-30486.
|
| [10] |
YULIA V, POJA S, DANIEL H, et al. Service innovation in e-commerce last mile delivery: mapping the e-customer journey[J].
Journal of Business Research, 2019, 101: 461-468.
DOI: 10.1016/j.jbusres.2019.01.016. |
| [11] |
白世贞, 谢爽. 基于混合契约的生鲜电商供应链协调策略[J].
控制与决策, 2018, 33(11): 2104-2112.
BAI S Z, XIE S. E-commerce of fresh agricultural products supply chain coordination based on compound contract[J]. Storage & Process, 2018, 33(11): 2104-2112. |
| [12] |
ILKYEONG M, YOON J J, SUBRATA S. Investment and coordination decisions in a supply chain of fresh agricultural products[J].
Operational Research, 2018(6): 1-15.
|
| [13] |
侯玉梅, 林梦楠. 需求受服务努力影响的生鲜农产品三级供应链协调性研究[J].
燕山大学学报(哲学社会科学版), 2014, 15(4): 118-124.
HOU Y M, LIN M N. Research on coordination of three-level supply chain of fresh agricultural products affected by service effort[J]. Journal of Yanshan University (Philosophy and Social Sciences Edition), 2014, 15(4): 118-124. |
| [14] |
NIE Q X. The coordination decision of dual-channel fresh food supply chain[J].
International Journal of Intelligent Information Systems, 2019, 8(1): 6-11.
DOI: 10.11648/j.ijiis.20190801.12. |
| [15] |
WANG Y Y, FAN R J, SHEN L. Decisions and coordination of green e-commerce supply chain considering green manufacturer's fairness concerns[J].
International Journal of Production Research, 2020, 58(24): 7471-7489.
DOI: 10.1080/00207543.2020.1765040. |
| [16] |
TALEIZADEH A A, SANE-ZERANG E, CHOI T M. The effect of marketing effort on dual-channel closed-loop supply chain systems[J].
IEEE Journals & Magazine, 2018, 48(2): 265-272.
|
| [17] |
SAHA S. Supply chain coordination through rebate induced contracts[J].
Transportation Research Part E, 2013, 50: 120-137.
|
 2022, Vol. 39
2022, Vol. 39
