共享单车作为一种新型交通方式,不仅解决了“最后一公里”的出行需求,更是呼应了当今社会节能减排、低碳出行的发展要求。然而,共享单车行业也存在一系列问题[1],例如,运营商虽然已将大量共享单车投放到停靠点,但在高峰时期仍然频繁存在“借不到,还不进”现象;与此同时,大量共享单车早晨聚集地铁站及写字楼周边,晚间又向居民区流动,这些现象也被称为“共享单车潮汐效应”[2]。“潮汐现象”是共享单车系统中普遍存在的规律,此现象不仅加剧了城市通行压力,也在一定程度上影响市容市貌。上述问题的产生,实际上是由城市交通需求和车辆运行载体供求的矛盾造成的,一方面,高峰时间段内的潮汐现象驱使各个停靠点的共享单车需求量差别巨大;另一方面,在一定时间段内用户出行趋势相同,短时间内对车辆的需求量波动大,导致停靠点的供需时空失衡。因此,为了实现共享单车可持续发展[3-4],对潮汐现象严重的共享单车停靠点进行“削峰填谷”,给用户进行停靠点的优化选择显得尤为重要。
国内外已有研究主要通过提高停靠点的规划水平缓解共享单车潮汐现象,例如,He等[5]应用短期需求预测模型捕捉共享单车出行数据的时空特征,并在停靠点层面预测需求量,提出了一种基于熵与理想解相似的偏好排序方法(TOPSIS)。Lin等[6]探讨了共享单车系统战略规划,建立数学模型确定停靠点的数量和位置、停靠点之间的路网结构以及起终点的骑行路线,为停靠点规划提供数据支撑。孙文霞等[7]为处理好共享单车与其他出行方式的兼容问题,通过综合分析停靠点及其所在线路相关路网信息,调整汽车公交线路,利用停靠点优化配置提高交通路网利用率。靳爽等[8]基于共享单车停靠点、公交路网的综合调整优化方法,在有限个可供选择的停靠点基础上,建立一种双层规划模型。Erdogan等[9]基于静态自行车再平衡问题,考虑到调度成本最低、各停靠点出入流量平衡,提出一种共享单车系统静态再平衡算法。刘嘉文等[10]为解决共享单车停靠点位置及车辆匹配问题,基于联合覆盖选址思想,提出一种共享单车停靠点选址和初始车辆的多维度优化模型。
上述研究成果对本文的切入点有很大启发,虽然共享单车的出现,极大地方便了人们的出行,但用户在结束行程时“便捷性”选择停放区域,导致城市街道共享单车停靠点淤积占道问题。因此,提升共享单车停靠点规划水平,缓解停靠点的潮汐现象不仅可以从调度[11]着手,还可以从用户停靠点优化选择[12]切入。基于此,本文以城市共享单车停靠点为研究对象,通过给用户提供停靠点优化选择,从源头上实现潮汐点位的“削峰填谷”。本文提出的停靠点优化选择共包括两个维度,第一个维度是对共享单车数据进行挖掘,确定GeoHash编码后的有限个停靠点空间分布,结合热力图对停靠点区域进行网格划分,量化表达共享单车停靠点的使用情况,并使用透视表统计每个编码区域在不同时间的入流量和出流量,进而计算出停靠点潮汐现象较突出的区域。第二个维度是根据第一个维度的结果,利用KNN算法选取20个距离最近的待选停靠点,根据停靠点的潮汐程度,完成候选停靠点的聚类分析,并在考虑停靠点的连通性后,对候选停靠点进行二次划分,筛除非连通性的停靠点,实现对用户停靠点的优化选择,最大限度地实现共享单车的合理利用。
1 算法应用 1.1 GeoHash编码GeoHash编码[13]根据精度不同将区域分解成多个子块,在一定经纬度范围内的子块会拥有相同编码,而且在合适的精度下,GeoHash编码足以解决对点位经纬度的收集和检索问题。GeoHash编码的方法是用二分法分别将需编码的p点经纬度所属区间[a,b]缩小,区间[a,b]不断被分成左右两部分的区间,若
|
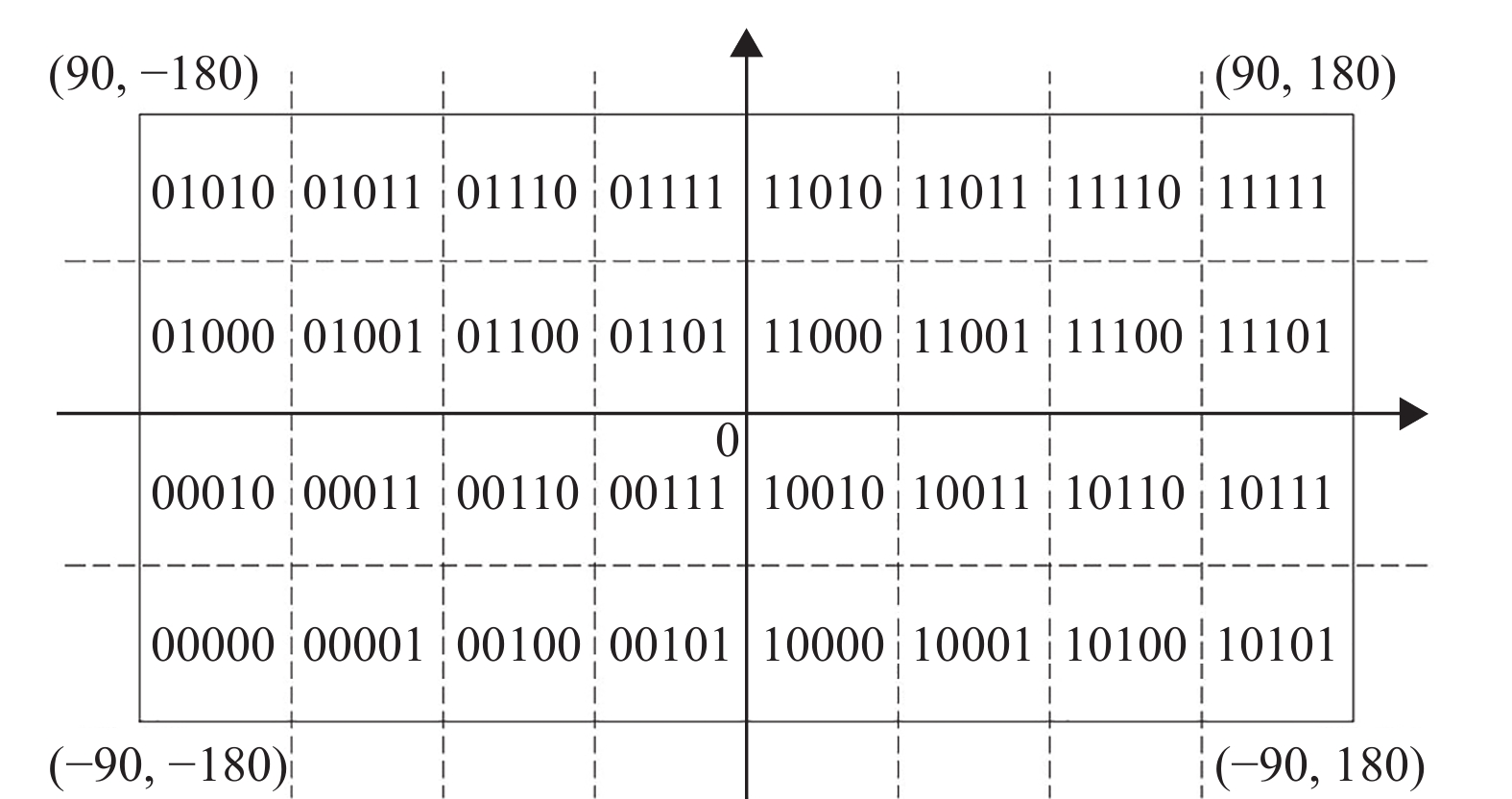
图 1 经纬度的二进制编码 Figure 1 The binary coding of longitude and latitude |
|
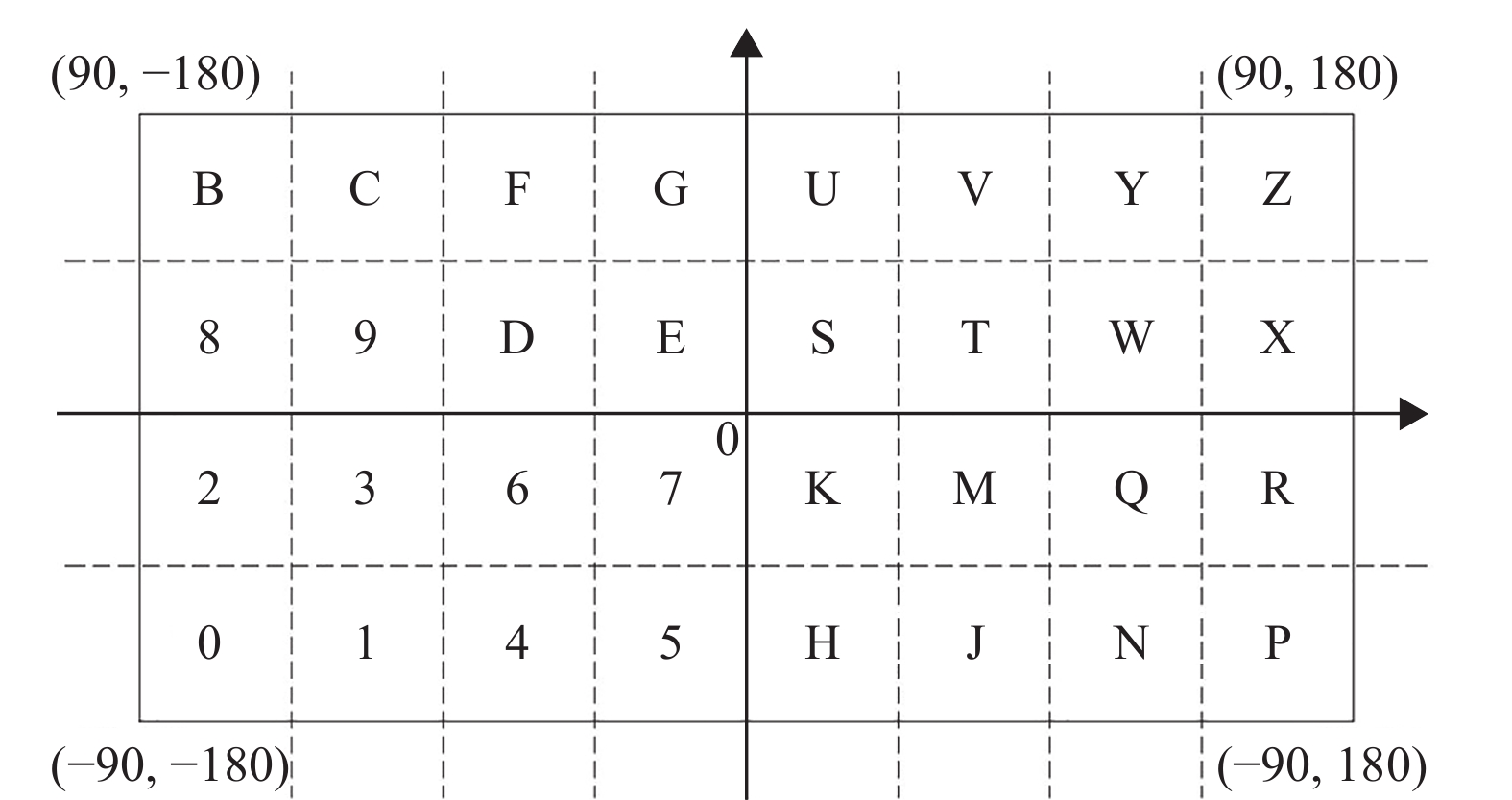
图 2 经纬度的Base32编码 Figure 2 The Base32 encoding of longitude and latitude |
结合研究对象,对共享单车订单数据中经纬度为(118.111688°,24.527919°)的数据进行编码。本次GeoHash编码精度为6,先对经度118.111688°进行逼近编码。地球经度区间分为[−180°,180°],即可将其二分为[−180°,0°)和[0°,180°],可知118.111688°属于右区间[0°,180°],给予标记为1。再将[0°,180°]分为[0°,90°)和[90°,180°],可判断118.111688°为右区间[90°,180°],给予标记为1。如此循环迭代,可以将118.111688°所属的[a,b]区间缩小,使其位置范围愈来愈逼近118.111688°。具体的迭代流程如表1所示,得到经度118.111688°的二进制编码为11010 01111 11110。同理,纬度24.527919°的二进制编码为10100 01011 10001。然后,将经纬度交替进行排序,得到二进制编码为11100 11000 00111 01111 11101 01001。最后,对照表2的Base32编号表,将以5个位(bit)为一组的二进制编码转化成相应的可见字符,得到经纬度(118.111688°,24.527919°)的GeoHash编码为wsk531。
| 表 1 经度118.111688°的GeoHash编码计算 Table 1 GeoHash coding calculation for longitude 118.111688° |
| 表 2 Base32字符编号 Table 2 Base32 character encoding |
根据GeoHash算法编码得到共享单车停靠点编码区域的使用情况,对此进一步采用KNN分类识别算法[15-16]实现停靠点优化选择,即选择非潮汐区域,使用情况无大幅度波动且靠近目的地的停靠点。然而识别结果可能与上述要求不符,因此,选取区域编码后的有限个共享单车初始停靠点,根据欧氏距离最小原则,将聚类结果划分纳入候选停靠点。
假设给定一个共享单车停靠点数据集X={x1, x2,···, xN},xi(i=1,2,···,N)为二维变量、一个测试点
| $ d({x_i},{x_j}) =\sqrt {\mathop \sum \nolimits_{i = 1}^n {({x_i} - {x_j})^2}} $ | (1) |
式中:d(xi,xj)表示测试集与训练集之间的距离,(xi,xj)为数据点(i,j)的坐标值。分别计算待测点
| $ \left\{ \begin{array}{l} {\rm{Sim}}(q,{C_i}) = {\displaystyle\sum\nolimits_{j = 1}^k {\delta ({T_j},{C_i})} \times {\rm{Sim}}(q,{T_j})} \hfill \\ \delta ({T_j},{C_i}) = 1,\,\,{T_j} \in {C_i} \hfill \\ \delta ({T_j},{C_i}) = 0,\,\,{T_j} \notin {C_i} \hfill \\ \end{array} \right. $ | (2) |
式中:Tj表示待测样本
| $ C(q) = {\arg _{C_i}}{\rm{max}}({\rm{Sim}}(q,\,{C_i})) $ | (3) |
采用GeoHash编码和KNN算法进行共享单车停靠点的优化选择,具体步骤如下。
步骤1:根据研究区域进行经纬度编码,得到二进制序列。
步骤2:对二进制编码按照奇偶位合并,进一步整合Base32编码结果。
步骤3:使用透视表统计每个编码区域在不同时间的出入流量。
步骤4:根据编码区域内共享单车停靠点数据,输入数据对象xi,分类中心数量K。
步骤5:选取K个共享单车候选停靠点。
步骤6:分别计算测试集到候选停靠点的距离,将共享单车匹配到最近的候选停靠点。
步骤7:进一步筛除潮汐现象严重的、需过街的停靠点,得到最终结果。
2 共享单车数据与预处理本文的数据时间是2020年12月21日至2020年12月25日(周一至周五),数据范围是厦门市湖里区与思明区,研究样本是工作日早高峰(06:00~09:00)的58万余条哈喽单车订单数据,此外,还包括共享单车停车点位(电子围栏)数据和共享单车轨迹数据。将起点位置(即轨迹数据经纬度)可视化和厦门市矢量边界比对后,可确认共享单车数据皆在位置范围内,基本可以全面反映共享单车的真实使用情况。
2.1 共享单车订单数据订单数据字段包括BICYCLE_ID(车辆编码)、LATITUDE(纬度)、LONGITUDE(经度)、LOCK_STATUS(锁车状态)、UPDATE_TIME(锁车状态更新时间)5个字段。为了隐私保护,车辆编码数据结构只取了前10位。锁车状态中“0”代表开锁状态,“1”代表锁车状态。具体订单数据结构如表3所示。
| 表 3 共享单车的订单数据结构 Table 3 The data structure of shared bikes’ order |
停靠点数据包括FENCE_ID(电子围栏唯一编号)、FENCE_LOC(电子围栏唯一坐标)两个字段。其中,FENCE_ID表示停车区域中每一个电子围栏的顺序编号,而FENCE_LOC表示电子围栏所在位置的坐标串。电子围栏数据结构如表4所示。
| 表 4 停靠点数据结构 Table 4 The data structure of shared bikes’ parking points |
轨迹数据包括BICYCLE_ID(车辆编码)、LOCATING_TIME(定位时间)、LATITUDE(纬度)、LONGITUDE(经度)、SOURCE(数据来源)5个字段,轨迹数据结构如表5所示。其中,车辆编码是指对应此条轨迹数据的车辆名称,轨迹数据与订单数据中的经纬度皆是指提取共享单车数据时的地理坐标位置。
| 表 5 轨迹数据结构 Table 5 The data structure of shared bikes’ tracks |
对共享单车数据进行预处理,可免除噪声数据对结果精确度的影响。数据的预处理主要从以下几个方面进行。
(1) 数据清洗与整理。本文选择的是厦门市思明区与湖里区的共享单车数据,首先,以两区经纬度范围(北纬24.445°至24.512°,东经118.146°至118.082°)为边界,将不在这个经纬度范围的订单数据剔除,其次,将重复的数据和空白的字段清理。
(2) 处理停车点位信息。计算每个停车点的面积和中心经纬度,并用GeoHash库对停车点位经纬度进行编码。
(3) 出入流量分析。将共享单车的订单数据和停车数据相匹配,使用透视表统计每个区域在不同时间的入流量和出流量,进而计算出停靠点潮汐现象较突出的区域。
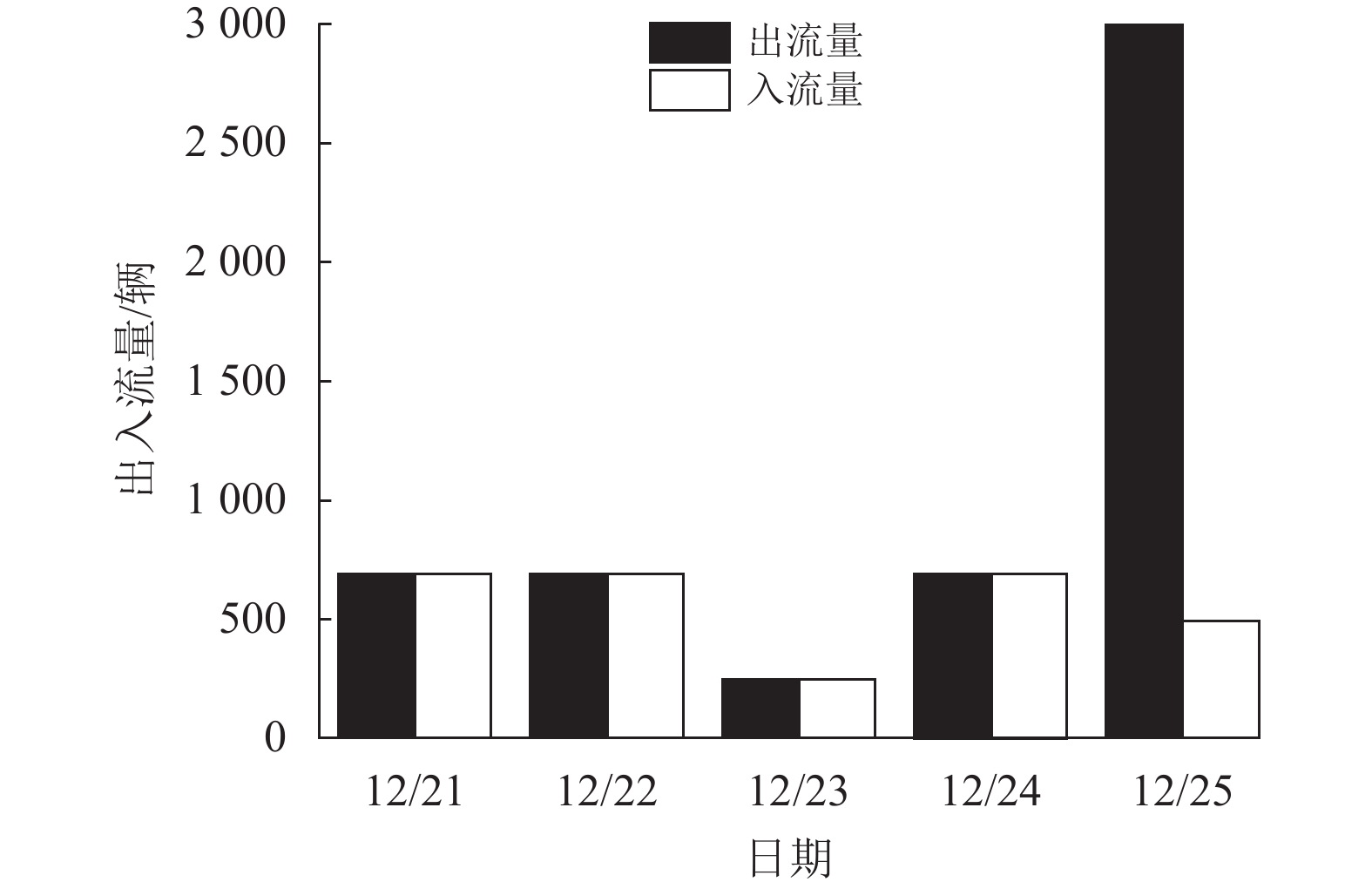
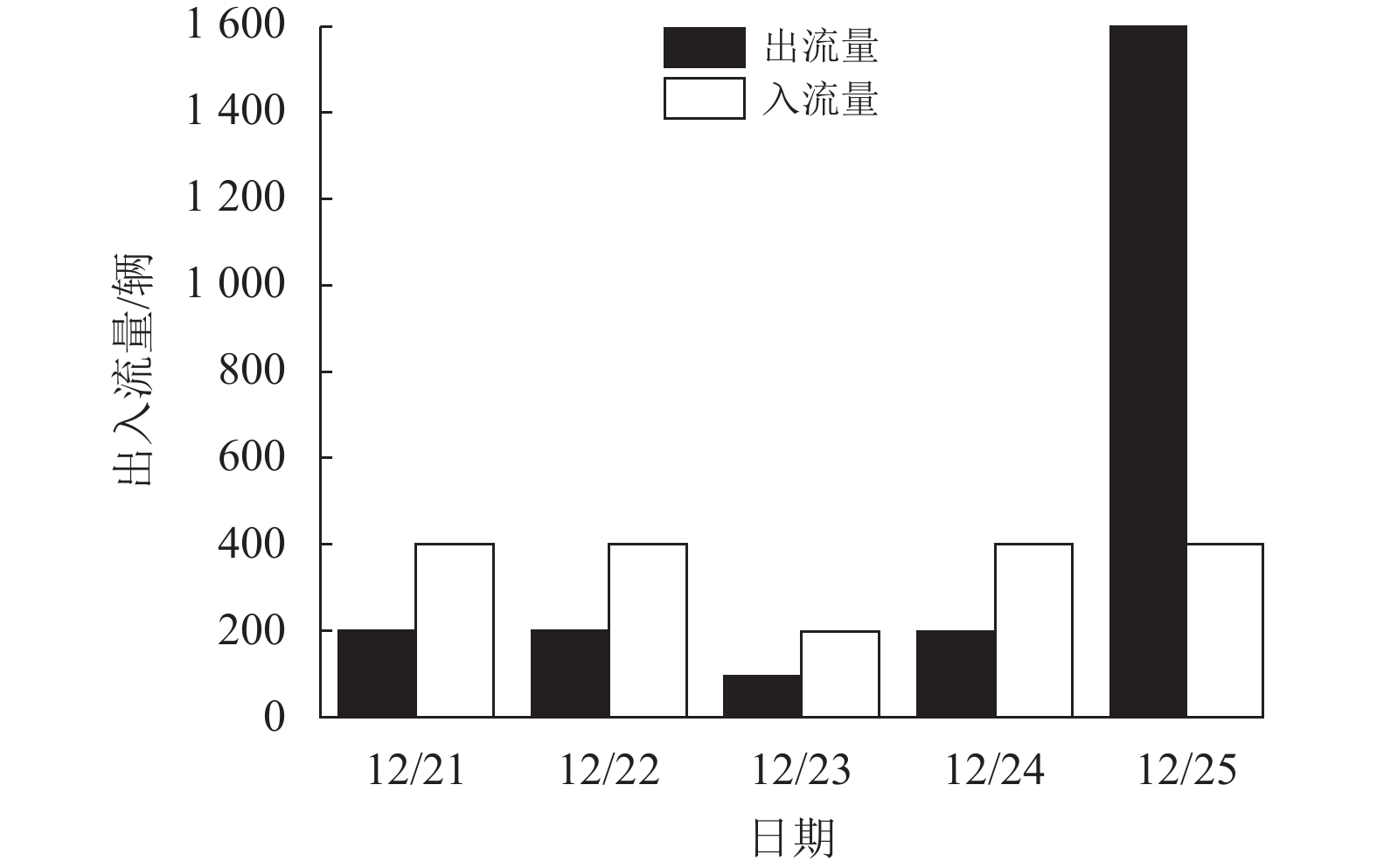
3 数据结果分析与停靠点优化选择 3.1 路段的出入量分析用GeoHash编码检索观日路路段编码为wsk531和wsk532的区域,分别检索到12319个和7267个记录。根据订单信息里的锁车数据,来判断该共享单车在该区域是锁车状态还是开锁状态。锁车状态的单车属于该区域的入流量,开锁状态的单车为出流量。两个区域均在12月21日~12月25日的8时左右出现峰值,根据观日路wsk531的区域工作日早高峰出入流量图(见图3),以及wsk532的区域工作日早高峰出入流量图(见图4),可以得出:(1) 在编码为wsk531的区域,周一、周二和周四的车辆出入量最高峰值为700辆,周三为250辆;在编码为wsk532的区域,周一、周二和周四车辆出入量最高峰值为400辆,周三为200辆。为此,周一、周二和周四的车辆出入量是周三的两倍左右。(2) 在编码为wsk531的区域,周一至周四早高峰的共享单车出入流量相对稳定;而在编码为wsk532的区域,周一至周四早高峰的共享单车入流量与出流量相差明显,入流量是出流量的两倍,存在车辆堆积现象。(3) 编码为wsk531的区域,周五早高峰的共享单车出流量接近3000辆,远高出峰值为500辆的入流量;在编码为wsk532的区域,周五早高峰的共享单车出流量接近1600辆,而入流量峰值只有400辆。基于上述分析可知,造成共享单车停靠点潮汐现象的原因,主要包括使用时间段、日出行时间、共享单车调度、停靠点选择等。
|
图 3 wsk531区域的工作日早高峰出入流量图 Figure 3 The morning peak flow of wsk531 |
|
图 4 wsk532区域的工作日早高峰出入流量图 Figure 4 The morning peak flow of wsk532 |
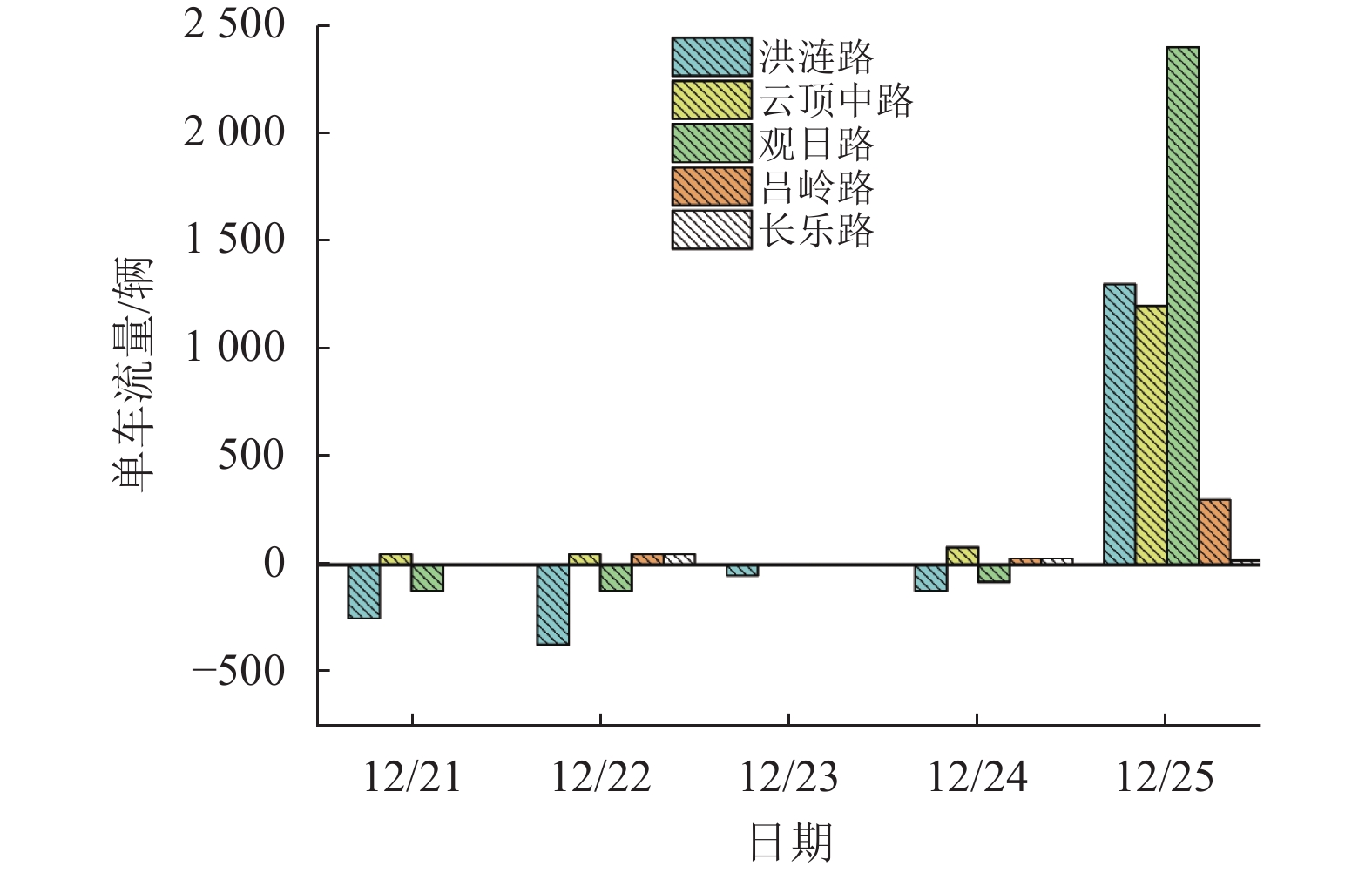
选取洪涟路、云顶中路、观日路、吕岭路和观日路这5条路段的附近区域,对其进行潮汐程度计算,即用出流量减去入流量,当留存量大于区域停靠点平均留存量时,可知该停靠点潮汐现象明显,得到如图5所示的各路段区域潮汐现象:(1) 在21日~24日的早高峰时间段,洪涟路、云顶中路、观日路路段附近区域出现了明显的潮汐现象,而吕岭路和长乐路附近区域的曲线接近于零,其无潮汐现象。(2) 洪涟路和观日路附近区域的车辆流量总数小于零,即入流量大于出流量,说明共享单车投入过多出现堆积现象。云顶中路附近区域的车辆流量总数大于零,说明共享单车供不应求,需要从别的地方调度车辆或者进行引导用户在此路段停靠。(3) 周五当天,5个路段附近区域的车辆流量总数都是大于零,且观日路>洪涟路>云顶中路>吕岭路>长乐路。这就要求在节假日期间,适当增大共享单车的供应数量,或者从区域车流量总数小于零的地方调度车辆。
|
图 5 各路段区域的潮汐状态 Figure 5 The tidal state of shared bikes’ parking points of five road sections |
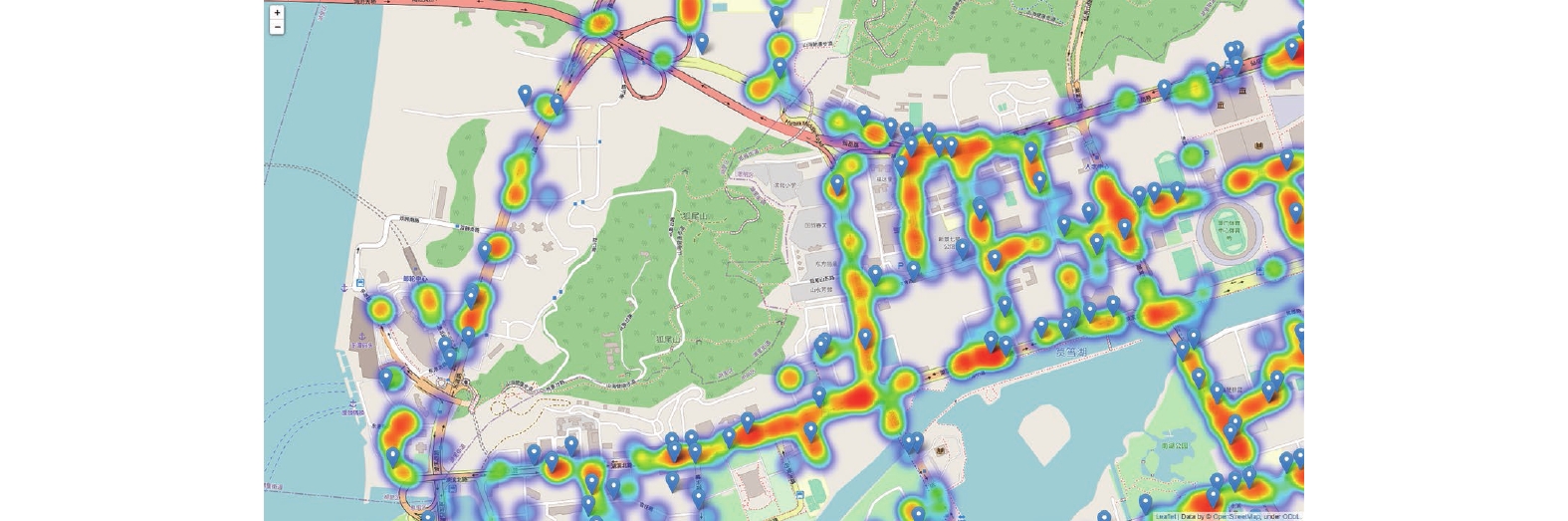
通过整理共享单车订单中同一时间点锁车状态为“1”的单车数据,可以计算出该区域的停车量,得到各个区域的共享单车停车热力图,从而能够把共享单车的停车围栏数据导入热力图中,对其进行对比分析,如图6的某区域停车热度图所示,把图中红黄色区域定义为共享单车停放的区域,蓝色区域定义为规定的停车围栏,可见许多停车点位上没有停放共享单车,例如,湖滨路上的某一路段,左右两侧车辆过多,停车点位不足,导致有很多车辆未停在规定位置。另外,对于潮汐现象严重的区域,可以通过为用户推荐附近没有潮汐现象的停车点位,来缓解共享单车的拥堵现象。有些停靠点虽说距离很近,但可能是在街道的另一边,又或者是在立交桥下,所以,应当考虑街道信息对停靠点优化选择的影响。
|
图 6 某区域的停车热度图 Figure 6 The parking heatmap of an area |
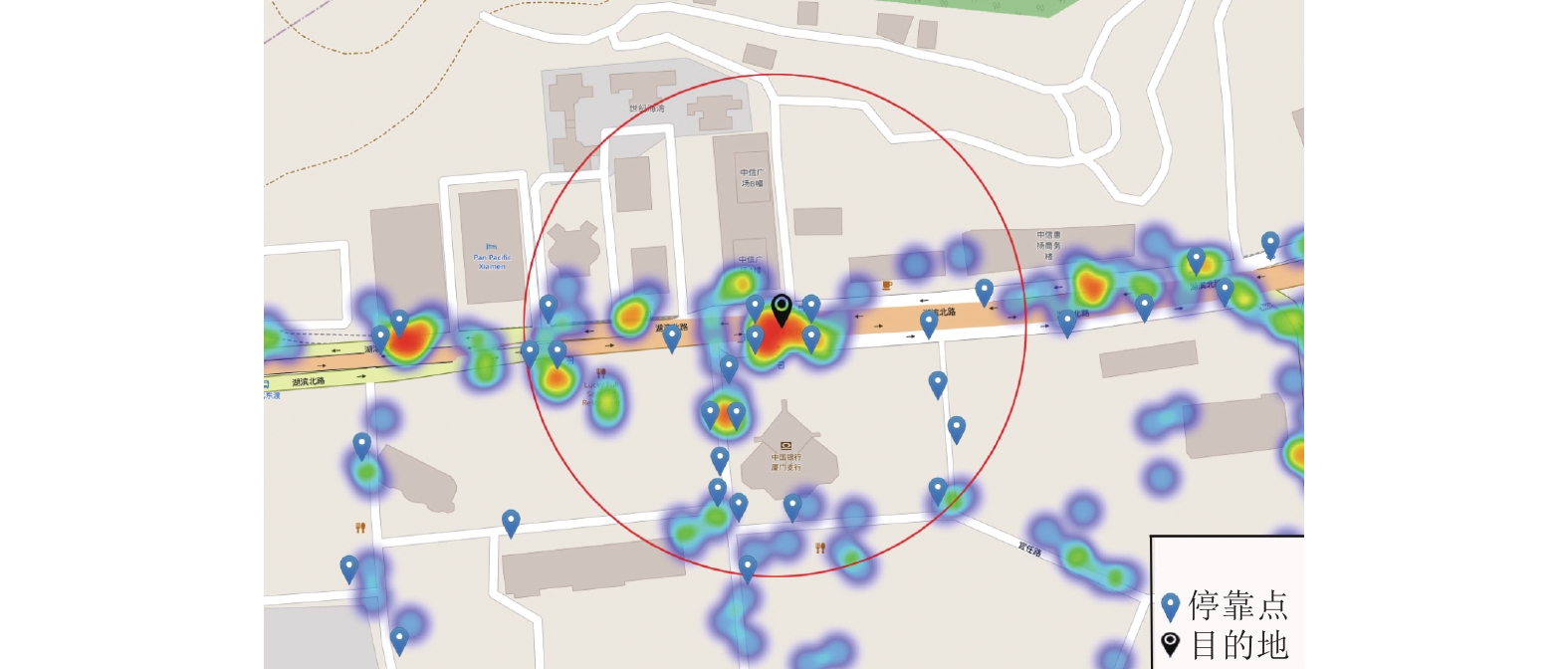
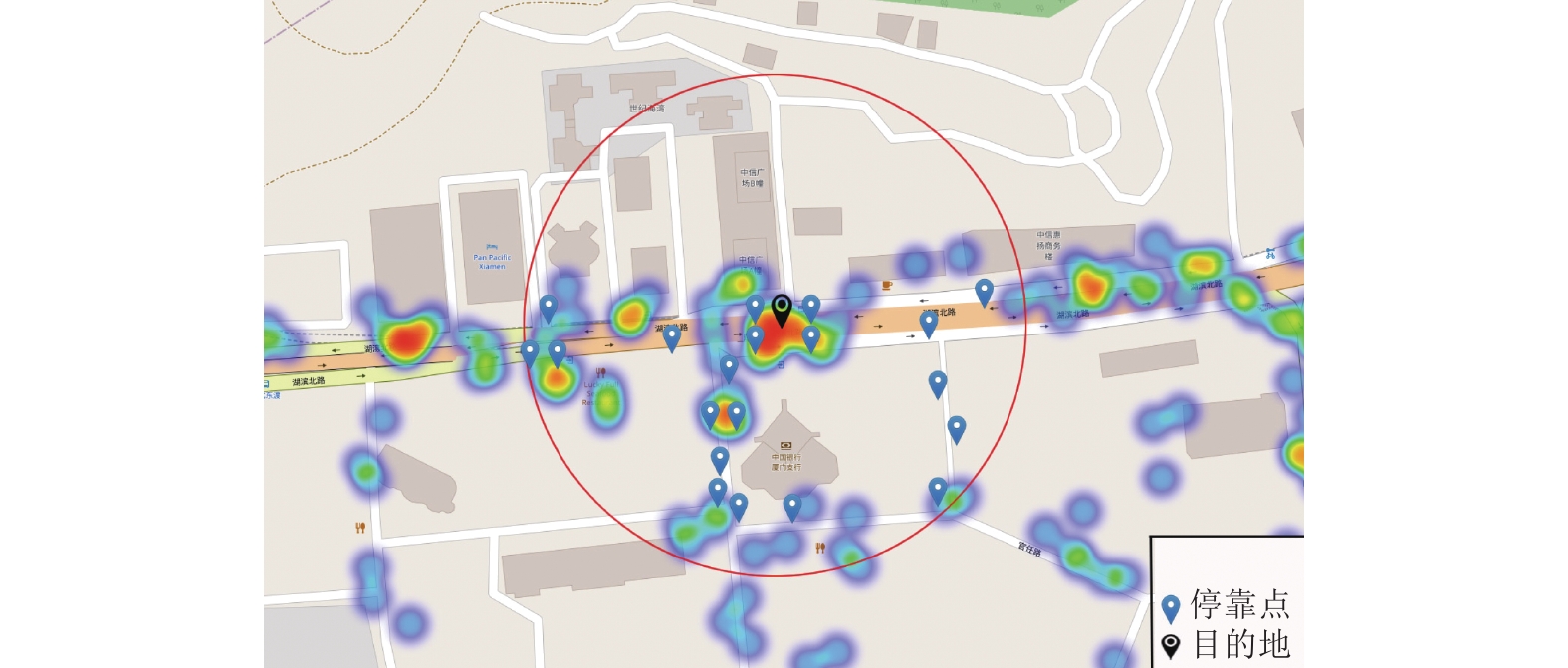
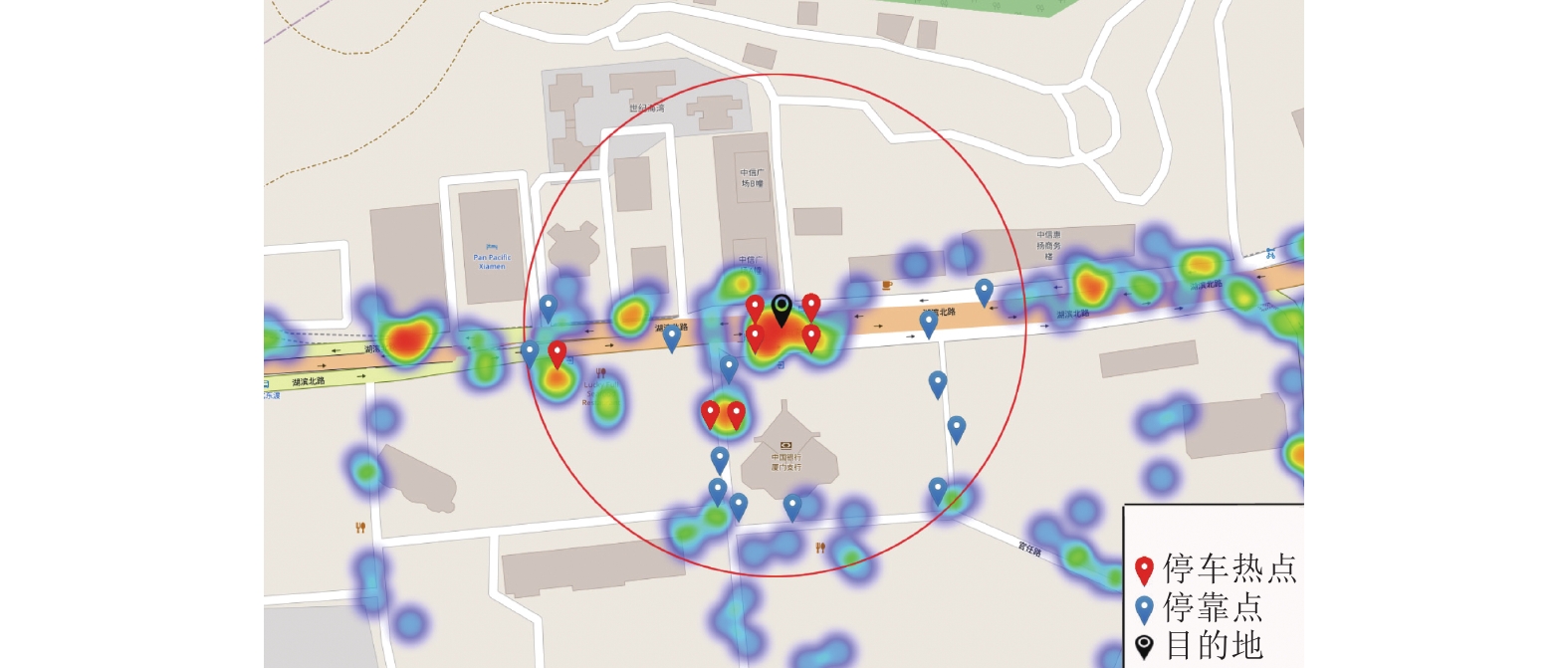
整合数据结果分析,得到共享单车的停靠点热度图,其潮汐程度相差明显,如图7所示。因此,需要对用户停靠点进行优化选择,假设图8中的黑色图标表示用户要到达的目的地,蓝色图标为共享单车停靠点,可见目的地周边提供了较多停靠点,但其中仍存在着一些距离相对较远的停靠点,为此,在用户到达目的地之前,结合其所处的时间段与位置信息,通过GeoHash编码快速检索出停靠点的地理编码;根据路段潮汐统计,可以得出每个街道的具体潮汐情况;其次,按照密度计算(即留存量大于停靠点平均留存量)得到潮汐情况最为严重的停靠点区域;利用KNN算法计算出20个最近的待选停靠点,筛除潮汐现象严重的、需过街的停靠点。图8中用红圈表示的20个待选停靠点,需要根据该时刻的停车热度信息进一步筛选,从而剔除掉有潮汐状况的停靠点,即剔除图9中的红色地标停靠点。
|
图 7 停靠点热度图 Figure 7 The heatmap of shared bikes’ parking points |
|
图 8 20个最近邻停靠点热度图 Figure 8 The heatmap of the 20 nearest neighbor shared bikes’ parking points |
|
图 9 筛选出的潮汐状态严重的停靠点 Figure 9 The selected parking points with serious tidal state |
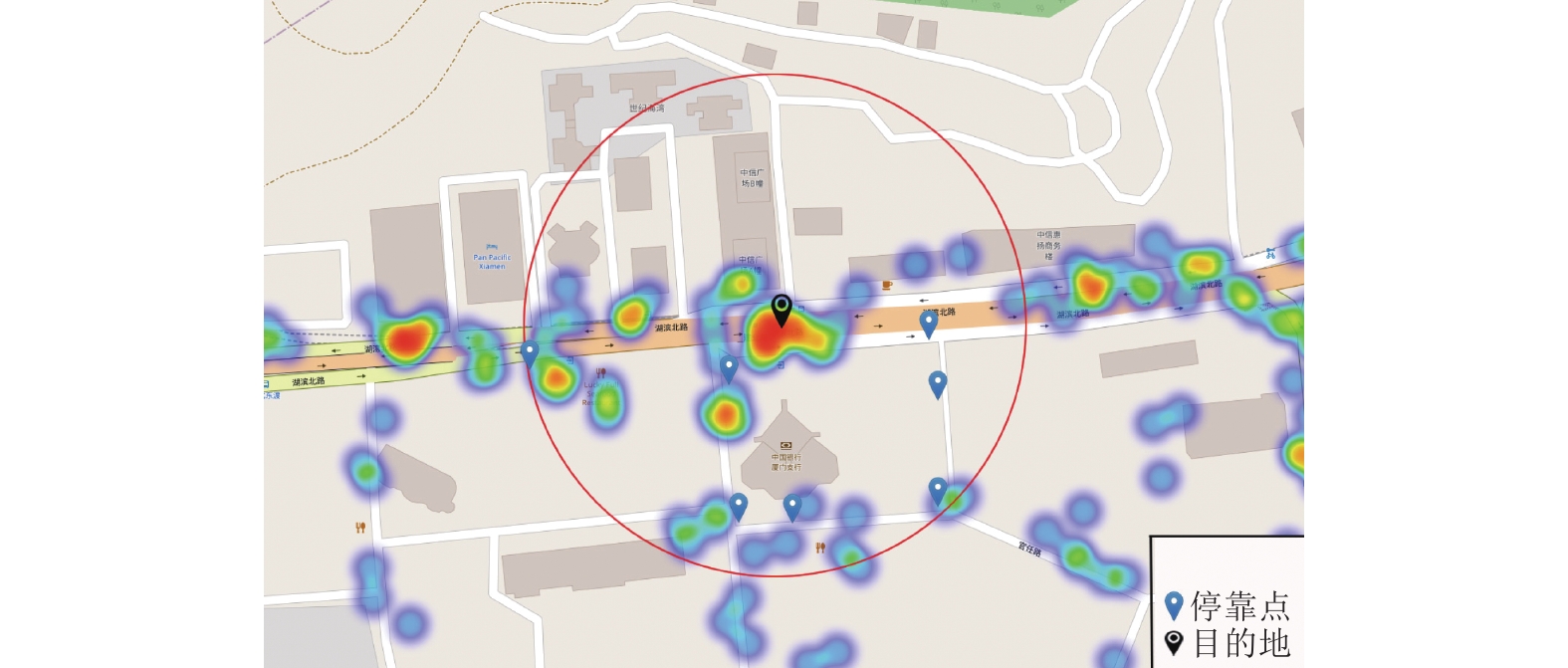
即使筛除图9中含有潮汐状况的停靠点,仍然会存在着许多与目的地不具连通性的区域,因此,根据停靠点的连通性,对待选停靠点再一次进行筛选(例如,剔除需过街、过天桥停靠点),从而把不具连通性的停靠点筛除,得到最终推荐给用户的停靠点,如图10所示。
|
图 10 最终推荐的停靠点示意图 Figure 10 The final recommended parking points |
本文提出一种融合GeoHash和KNN算法,实现共享单车停靠点优化选择的方法,得到以下研究结论:
(1) 共享单车停靠点潮汐现象产生的原因主要包括使用时间段、日出行时间、共享单车调度方法、停靠点选择等,前两者会影响到早高峰通勤时间、节假日出行游玩时间的停靠点优化选择;后两者会影响到共享单车停靠点的调度分配策略。
(2) GeoHash分区编码能够有效地识别共享单车停靠状态不合理的问题,进而确定共享单车的候选停靠点及其数量,还能够结合出行者的目的地以及共享单车停靠点的供给,完成共享单车的时空供需平衡分析,提高共享单车的利用率。
(3) KNN分类识别算法能够有效地识别出潮汐现象严重的共享单车停靠点,进一步确定推荐给用户的候选停靠点及其数量,结合停靠点的连通性以及共享单车停靠点的供给,还可以完成共享单车的最佳停靠点分析,减少用户的停车决策时间。
(4) 在利用大规模共享单车订单数据,确定共享单车停靠点的基础上,使用GeoHash算法对停靠点进行分区编码,并使用KNN算法筛选出具有非潮汐现象的停靠点,能够达到停靠点优化选择的目的,为缓解共享单车停靠点潮汐问题提供有益借鉴。
| [1] |
岳宇君, 胡汉辉. 城市共享单车治理问题的多理论视角解析[J].
当代经济管理, 2019, 41(7): 68-72.
YUE Y J, HU H H. An analysis of the governance of sharing bicycles in cities from the perspective of multiple theories[J]. Contemporary Economy & Management, 2019, 41(7): 68-72. |
| [2] |
孙卓, 李一鸣. 考虑多仓库的共享单车重新配置问题研究[J]. 运筹与管理, 2021, 30(1): 121-129.
SUN Z, LI Y M. Solving a static bike repositioning problem with multiple depots[J]. Operations Research and Management Science, 2021, 30(1): 121-129. |
| [3] |
刘永贤, 牛占文. 共享单车造成的城市治理问题研究[J].
城市发展研究, 2021, 28(5): 135-140.
LIU Y X, NIU Z W. Research on urban governance problems caused by shared bikes[J]. Urban Development Studies, 2021, 28(5): 135-140. DOI: 10.3969/j.issn.1006-3862.2021.05.024. |
| [4] |
SHUI C S, SZETO W Y. A review of bicycle-sharing service planning problems[J].
Transportation Research Part C:Emerging Technologies, 2020, 117(C): 102648.
|
| [5] |
HE M J, MA X Y, JIN Y C. Station importance evaluation in dynamic bike-sharing rebalancing optimization using an entropy-based TOPSIS approach[J].
IEEE Access, 2021, 9: 38119-38131.
DOI: 10.1109/ACCESS.2021.3063881. |
| [6] |
LIN J R, YANG T H. Strategic design of public bicycle sharing systems with service level constraints[J].
Transportation Research Part E:Logistics and Transportation Review, 2011, 4(47): 284-294.
|
| [7] |
孙文霞, 赵晓娟, 马晓静. 基于复杂网络理论的互联网租赁自行车−公交系统站的优化配置[J].
公路交通科技, 2018, 35(10): 111-116.
SUN W X, ZHAO X J, MA X J. Optimal configuration of station of internet rental bicycle-transit system based on complex network theory[J]. Highway and Transportation Research and Development, 2018, 35(10): 111-116. |
| [8] |
靳爽, 庞明宝. 考虑共享单车的城市轨道交通社区接驳规划与公交调度综合优化[J].
公路交通科技, 2020, 37(2): 123-129.
JIN S, PANG M B. Integrated optimization of community connection planning and bus dispatching for urban rail transit considering shared bicycle[J]. Highway and Transportation Research and Development, 2020, 37(2): 123-129. |
| [9] |
ERDOGAN G, BATTARRA M, CALVO R W. An exact algorithm for the static rebalancing problem arising in bicycle sharing systems[J].
European Journal of Operational Research, 2015, 245(3): 667-679.
DOI: 10.1016/j.ejor.2015.03.043. |
| [10] |
刘嘉文, 代颖, 杨斐, 等. 共享单车停放点联合覆盖选址及车辆配置模型[J].
工业工程与管理, 2020, 25(1): 127-135.
LIU J W, DAI Y, YANG F, et al. A cooperative covering model for location of bike sharing stations and its fleet deployment[J]. Industrial Engineering and Management, 2020, 25(1): 127-135. |
| [11] |
AHMED A, KADRE, IMDE K, et al. Lower and upper bounds for scheduling multiple balancing vehicles in bicycle-sharing systems[J].
Soft Computing, 2019, 23(14): 5945-5966.
DOI: 10.1007/s00500-018-3258-y. |
| [12] |
靳爽, 庞明宝. 基于K-means的城市轨道交通社区接驳共享单车停靠点规划[J].
科学技术与工程, 2019, 19(30): 343-347.
JIN S, PANG M B. Planning of shared bicycle stop for urban rail transit community connection based on K-means[J]. Science Technology and Engineering, 2019, 19(30): 343-347. DOI: 10.3969/j.issn.1671-1815.2019.30.051. |
| [13] |
HUANG K, LI G Q, WANG J. Rapid retrieval strategy for massive remote sensing metadata based on GeoHash coding[J].
Remote Sensing Letters, 2018, 9(11): 1070-1078.
DOI: 10.1080/2150704X.2018.1508907. |
| [14] |
金安, 程承旗, 宋树华, 等. 基于GeoHash的面数据区域查[J].
地理与地理信息科学, 2013, 29(5): 31-35.
JIN A, CHENG C Q, SONG S H, et al. Regional query of area data based on GeoHash[J]. Geography and Geo-information Science, 2013, 29(5): 31-35. |
| [15] |
MA C C, DU X H, CAO L F. Improved KNN algorithm for fine-grained classification of encrypted network flow[J].
Electronics, 2020, 9(2): 324.
DOI: 10.3390/electronics9020324. |
| [16] |
NGUYEN G B, LE H H, TRAN H H. Improvement of K-nearest neighbors (KNN) algorithm for network intrusion detection using Shannon-Entropy[J].
Journal of Communications, 2021, 16(8): 347-354.
|
 2022, Vol. 39
2022, Vol. 39

