当今世界能源短缺和环境问题日益严重,有效利用清洁能源如太阳能[1]、地热能[2]和回收余热[3]是缓解能源问题的有效途径,有机朗肯循环(ORC)是最具潜力的低品位热能转换技术之一。工质是ORC的血液,承担能量传递和转换的重要作用,其选择对ORC系统性能有着巨大影响。
纯工质筛选研究相对较成熟,王羽鹏等[4]提出了基于计算机辅助分子设计(Computer-aided Molecular Design)的纯工质设计与ORC系统协同优化,获得了不同热源条件下的设计最优工质。邱观福等[5]提出了考虑环境变工况的ORC设计与运行优化方法,分析环境温度变化情况,选取典型温度作为设计工况,获得ORC最优换热设备设计结构和最佳运行方案。涂俊平等[6]研究了R245fa在水平光滑管内的轴向均匀沸腾传热特性。相比纯工质,混合工质在相变阶段存在温度滑移现象,能更好地与冷热源匹配,提高ORC性能。Braimakis等[7]基于PR方程[8]研究了丁烷、环戊烷、己烷、戊烷、丙烷两两混合物,指出最佳热源温度与临界温度有很强的相关关系,影响混合物循环性能因素有温度滑移和冷却水温升。Zhao等[9]基于REFPROP研究了R245fa 分别与R227ea、R236fa、R236ea、R245ca组成的混合物,以输出功为目标分析蒸发温度、热源进口温度、混合工质温度滑移的影响,结果显示存在与最大输出功相对应的最佳蒸发温度,蒸发温度、热源进口温度对混合物的组成有显著影响。Wu等[10]基于REFPORP研究了混合工质R227ea/R245fa、Butane/R245fa、RC318/R245fa,发现温度滑移接近冷却水的温升时,系统热力学性能最好。郑晓生等[11]研究了R1234ze(E)/R245fa非共沸工质的有机朗肯循环实验性能,与纯工质相比混合工质ORC具有更低的温度水平和更大的过热度,蒸发器内的换热温差更大和冷凝器的换热温差更小。
如上所述,学者们对混合工质筛选做了较多有价值的工作,大多数通过REFPROP获取混合工质物性。然而对于REFPROP中不包含或缺乏实验数据支撑的混合工质,物性预测精度较低。Perturbed-Chain Statistical Associating Fluid Theory(PC-SAFT)[12]是基于微扰理论的半理论半经验方程,能够准确地预测混合工质物性。本文提出基于PC-SAFT计算混合工质物性并进行ORC系统优化的思路,首先基于纯工质库构建备选混合工质组合,然后通过三级启发式规则筛选剔除不合适工质,降低备选工质数量,最后把筛选后的工质编码化,基于遗传算法实现混合工质筛选与ORC系统的同步优化。
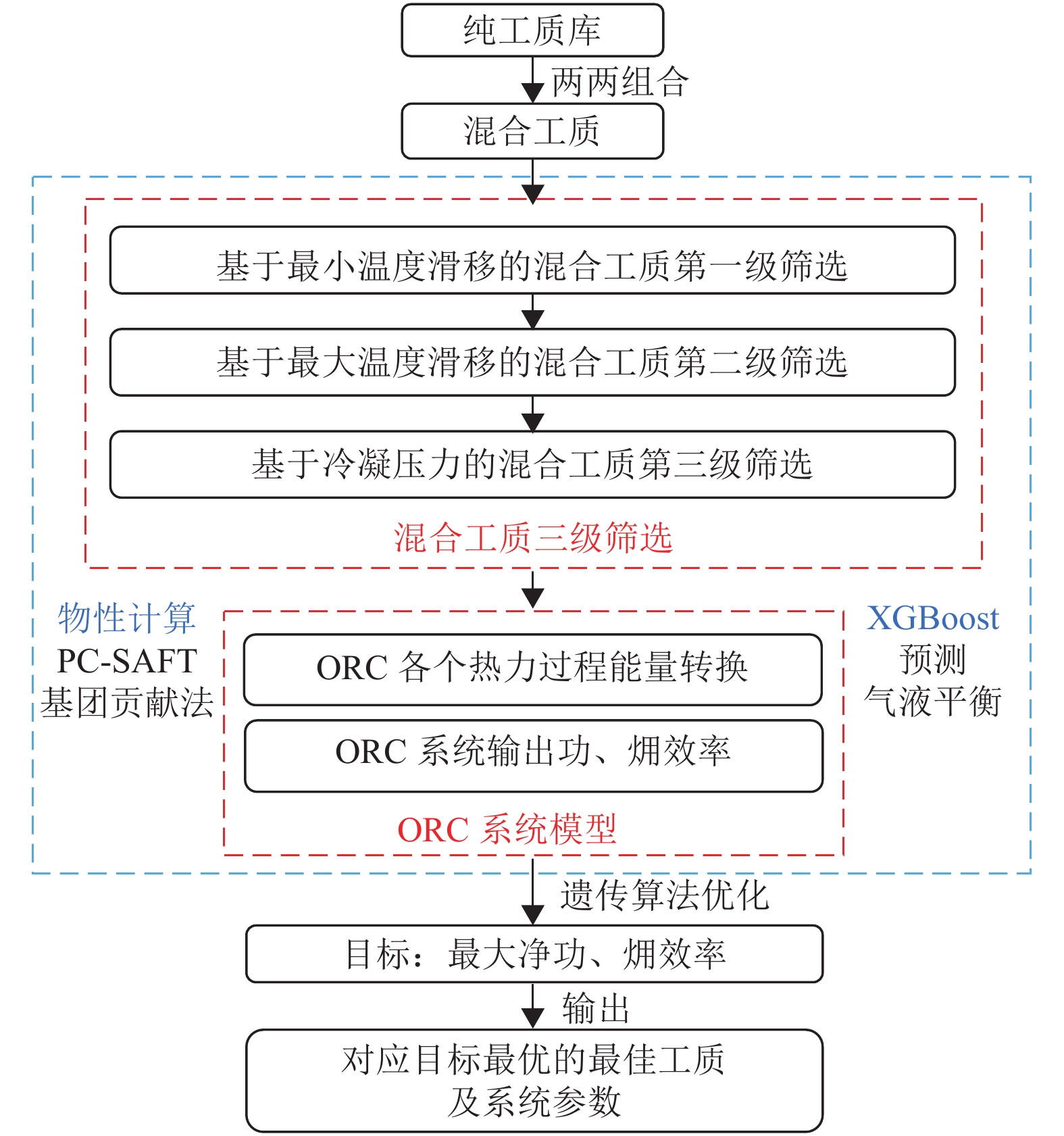
1 问题描述基于分步优化思路,先由纯工质组成混合工质,并基于启发式筛选规则初筛备选工质,然后应用遗传算法实现混合工质筛选与有机朗肯循环系统操作参数同步优化,混合工质物性通过PC-SAFT计算,筛选和优化流程如图1所示。
|
图 1 基于PC-SAFT的混合工质筛选与ORC系统同步优化流程 Figure 1 Flowsheet of working fluid mixture screening and ORC system optimization |
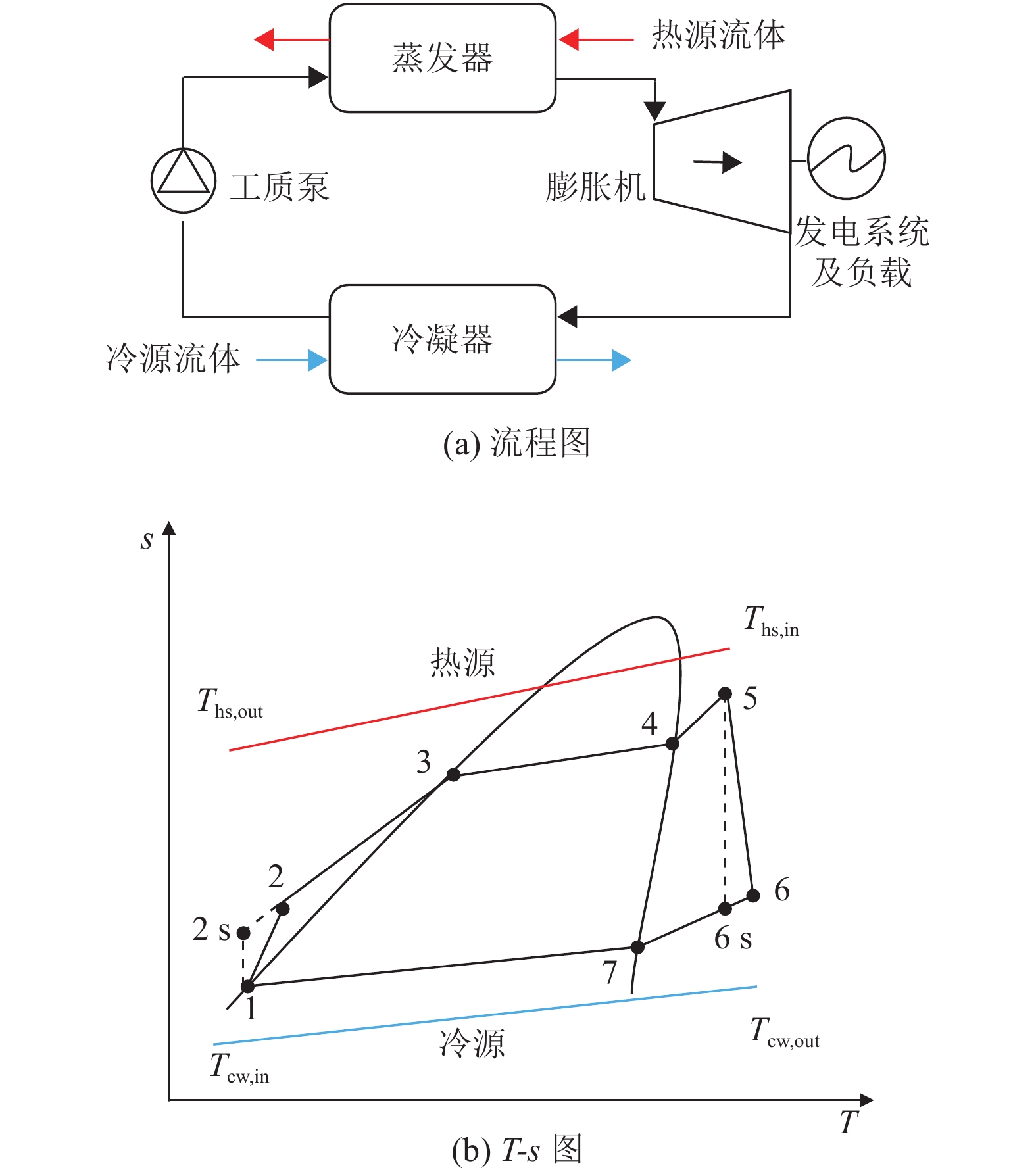
非共沸工质ORC工艺流程和T-s图如图2所示。简单ORC由加压、蒸发、膨胀、冷凝4个基本热力过程组成,工质在泵中被压缩至高压过冷态(1-2),然后在蒸发器中从热源吸热,等压蒸发成过热蒸汽(2-5),随后过热蒸汽在膨胀机中膨胀对外做功(5-6),最后膨胀机出口的乏汽在冷凝器冷凝至初始状态(6-1),完成循环。与纯工质不同,非共沸工质相变过程斜率不为0,存在温度滑移,可以更好匹配冷热源。
工质泵的耗功计算如式(1)所示。
| $ {W}_{\mathrm{p}\mathrm{u}\mathrm{m}\mathrm{p}}={m}_{\mathrm{w}\mathrm{f}}\left({h}_{2}-{h}_{1}\right)=\dfrac{{m}_{\mathrm{w}\mathrm{f}}\left({h}_{2\mathrm{s}}-{h}_{1}\right)}{{\eta }_{\mathrm{p}\mathrm{u}\mathrm{m}\mathrm{p}}} $ | (1) |
式中:mwf为工质质量流量;ηpump为工质泵等熵效率;h为相应点的比焓。
工质在蒸发器中吸热量计算如式(2)所示。
| ${Q}_{\mathrm{e}\mathrm{v}\mathrm{a}\mathrm{p}}={m}_{\mathrm{w}\mathrm{f}}\left({h}_{5}-{h}_{2}\right)={m}_{\mathrm{h}\mathrm{s}}{c}_{{p},\mathrm{h}\mathrm{s}}\left({T}_{\mathrm{h}\mathrm{s},\mathrm{i}\mathrm{n}}-{T}_{\mathrm{h}\mathrm{s},\mathrm{o}\mathrm{u}\mathrm{t}}\right)$ | (2) |
式中:mhs为热源质量流量;cp,hs为热源定压比热容;Ths,in,Ths,out为热源进出口温度。
过热蒸汽在膨胀机中绝热膨胀,对外做功量由式(3)计算。
| ${W}_{\mathrm{t}}={m}_{\mathrm{w}\mathrm{f}}\left({h}_{5}-{h}_{6}\right)={m}_{\mathrm{w}\mathrm{f}}\left({h}_{5}-{h}_{6\mathrm{s}}\right){\eta }_{\mathrm{t}} $ | (3) |
式中:
乏汽进入冷凝器冷凝,冷凝放热量如式(4)所示。
| ${Q}_{\mathrm{c}\mathrm{o}\mathrm{n}}={m}_{\mathrm{w}\mathrm{f}}\left({h}_{6}-{h}_{1}\right)={m}_{\mathrm{c}\mathrm{w}}{c}_{{p},\mathrm{c}\mathrm{w}}\left({T}_{\mathrm{c}\mathrm{w},\mathrm{i}\mathrm{n}}-{T}_{\mathrm{c}\mathrm{w},\mathrm{o}\mathrm{u}\mathrm{t}}\right) $ | (4) |
式中:mcw为冷源质量流量;cp,cw为冷源定压比热容;Tcw,in,Tcw,out为冷源进出口温度。
|
图 2 ORC系统图 Figure 2 ORC diagram |
ORC系统评价指标净功如式(5)所示,㶲效率由式(6~7)计算。
| $ {W}_{\mathrm{n}\mathrm{e}\mathrm{t}}={W}_{\mathrm{t}}-{W}_{\mathrm{p}\mathrm{u}\mathrm{m}\mathrm{p}} $ | (5) |
| $ {\eta }_{{\rm{ex}}}=\frac{{W}_{\mathrm{n}\mathrm{e}\mathrm{t}}}{{m}_{\mathrm{h}\mathrm{s}}{c}_{\mathrm{p},\mathrm{h}\mathrm{s}}\left({T}_{\mathrm{h}\mathrm{s},\mathrm{i}\mathrm{n}}-{T}_{\mathrm{h}\mathrm{s},\mathrm{o}\mathrm{u}\mathrm{t}}\right)\left(1-{T}_{0}/{T}_{\mathrm{h}\mathrm{s},\mathrm{a}}\right)} $ | (6) |
| $ {T}_{\mathrm{h}\mathrm{s},\mathrm{a}}=\frac{{T}_{\mathrm{h}\mathrm{s},\mathrm{i}\mathrm{n}}-{T}_{\mathrm{h}\mathrm{s},\mathrm{o}\mathrm{u}\mathrm{t}}}{2}$ | (7) |
式中:Ths,a为热源平均温度;T0为参考温度,取298.15 K。
2.2 物性计算模型 2.2.1 热物性计算ORC各点比焓值由理想气体焓和余焓组成,见式(8),理想气体焓由Joback和Reid[13]提出的基团贡献法计算,余焓由PC-SAFT计算。
| $ \begin{split} h\left(\xi ,T,P\right)= & \left({h}^{\mathrm{r}\mathrm{e}\mathrm{s}}+{h}^{\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{l}}\right)/{M}_{\mathrm{m}\mathrm{i}\mathrm{x}}=\\ & \Bigg({h}^{\mathrm{r}\mathrm{e}\mathrm{s}}+\displaystyle\sum\limits _{i}^{2}{\xi }_{i}{\displaystyle\int }_{{T}_{0}}^{T}{c}_{{p}}^{i\mathrm{g}}{\rm{d}}T\Bigg)\Bigg/{M}_{\mathrm{m}\mathrm{i}\mathrm{x}} \end{split} $ | (8) |
式中:hideal、hres分别为理想气体焓、余焓;Mmix为混合工质的摩尔质量;ξi为混合工质i组元的摩尔分数;
ORC各点焓值计算需要各点对应的总组分、温度、压力,本文设T4、T1已知,蒸发压力Pevap、冷凝压力Pcon、T3、T7由气液平衡(VLE)计算。
| $ {P}_{\mathrm{e}\mathrm{v}\mathrm{a}\mathrm{p}}={\rm{VLE}}\left(\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{s},\xi ,{T}_{4},{P}_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}}\right) $ | (9) |
| $ {P}_{\mathrm{c}\mathrm{o}\mathrm{n}}={\rm{VLE}}\left(\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{s},\xi ,{T}_{1},{P}_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}}\right) $ | (10) |
| ${T}_{3}={\rm{VLE}}\left(\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{s},\xi ,{P}_{\mathrm{e}\mathrm{v}\mathrm{a}\mathrm{p}},{T}_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}}\right) $ | (11) |
| $ {T}_{7}={\rm{VLE}}\left(\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{s},\xi ,{P}_{\mathrm{c}\mathrm{o}\mathrm{n}},{T}_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}}\right)$ | (12) |
式中:args为PC-SAFT分子参数;Pinit,Tinit分别为压力初值、温度初值。
为了保证膨胀不在两相区发生,设置一定的过热度ΔTs。
| $ {T}_{5}={T}_{4}+{\mathrm{\Delta }T}_{\mathrm{s}} $ | (13) |
PC-SAFT是由Gross和Sadowski[12]提出的计算流体热物理性质的物理模型。在PC-SAFT中,分子假想成一条由片段组成的链,由对应的纯组分参数模拟流体。本文考虑的纯组分参数为片段数m、片段直径σ、片段能量参数ε/kB。PC-SAFT是纯组分和混合物的剩余亥姆霍兹能模型,本文考虑硬链参考项和色散作用对剩余亥姆霍兹能的贡献如式(14)所示,详细计算见文献[12]。
| $ {a}^{\mathrm{r}\mathrm{e}\mathrm{s}}={a}^{\mathrm{h}\mathrm{c}}+{a}^{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}} $ | (14) |
式中:上标hc表示硬链参考项,上标disp表示色散作用项。
压缩因子Z和余焓hres由热力关系推导,见式(15)和式(16)。
| $ Z=1+\eta {\left(\frac{\partial {a}^{\mathrm{r}\mathrm{e}\mathrm{s}}}{\partial \eta }\right)}_{T,{\xi }_{i}}$ | (15) |
| $ {h}^{\mathrm{r}\mathrm{e}\mathrm{s}}=-T{\left(\frac{\partial {a}^{\mathrm{r}\mathrm{e}\mathrm{s}}}{\partial T}\right)}_{\rho ,{\xi }_{i}}+\left(Z-1\right) $ | (16) |
式中:η为分子数密度。
气液平衡计算需要计算组分k的逸度系数φk,逸度系数通过化学残余势计算。
| $ \mathrm{ln}{\varphi }_{k}=\frac{{\mu }_{k}^{\mathrm{r}\mathrm{e}\mathrm{s}}\left(T,v\right)}{{k}_{\mathrm{B}}T}-\mathrm{ln}Z $ | (17) |
残余化学势根据式(18)计算。
| $ \begin{split} \frac{{\mu }_{k}^{\mathrm{r}\mathrm{e}\mathrm{s}}\left(T,v\right)}{{k}_{\mathrm{B}}T}= & {a}^{\mathrm{r}\mathrm{e}\mathrm{s}}+\left(Z-1\right)+{\left(\frac{\partial {a}^{\mathrm{r}\mathrm{e}\mathrm{s}}}{\partial {\xi }_{i}}\right)}_{T,v,{\xi }_{i\ne k}}-\\ & \sum _{j=1}^{N}\left[{\xi }_{i}\left({\left(\frac{\partial {a}^{\mathrm{r}\mathrm{e}\mathrm{s}}}{\partial {\xi }_{i}}\right)}_{T,v,{\xi }_{i\ne j}}\right)\right] \end{split} $ | (18) |
式中:kB为玻尔兹曼常数,1.380649 × 10−23 J/K。
PC-SAFT采用Lorenz-Berthelot混合规则,为了精确关联二元混合物系统,引入二元交互作用系数kij校正混合规则,见式(19)和(20)。二元交互作用系数通常用液体密度和气液平衡实验数据拟合,由于实验数据的缺乏,本文使用Stavrou等[14]提出的QSPR方法估算二元交互作用系数,如式(21)所示。
| $ {\sigma }_{ij}=\frac{{\sigma }_{i}+{\sigma }_{j}}{2} $ | (19) |
| ${\varepsilon }_{ij}=\sqrt{{\varepsilon }_{i}{\varepsilon }_{j}}\left(1-{k}_{ij}\right) $ | (20) |
| $ {k}_{ij}^{\mathrm{Q}\mathrm{S}\mathrm{P}\mathrm{R}}=\sum _{L=1}^{N}{c}_{L}{D}_{L}$ | (21) |
式中:σ为温度无关的片段直径;ε为势阱;下标i、j表示组元;N为描述符的数量;cL为相对应的回归参数;DL为描述符。本文仅考虑非极性非缔合作用,详细计算见文献[14]。
2.3 气液平衡初值预测模型气液平衡是物性计算的起点和重点,一个较好的初值能加快求解速度,提高求解精度。本文采用机器学习极端梯度提升(eXreme Gradient Boosting, XGBoost)集成模型[15],构建露点压力、泡点压力、泡点温度、露点温度的预测模型,作为气液平衡求解的初值。
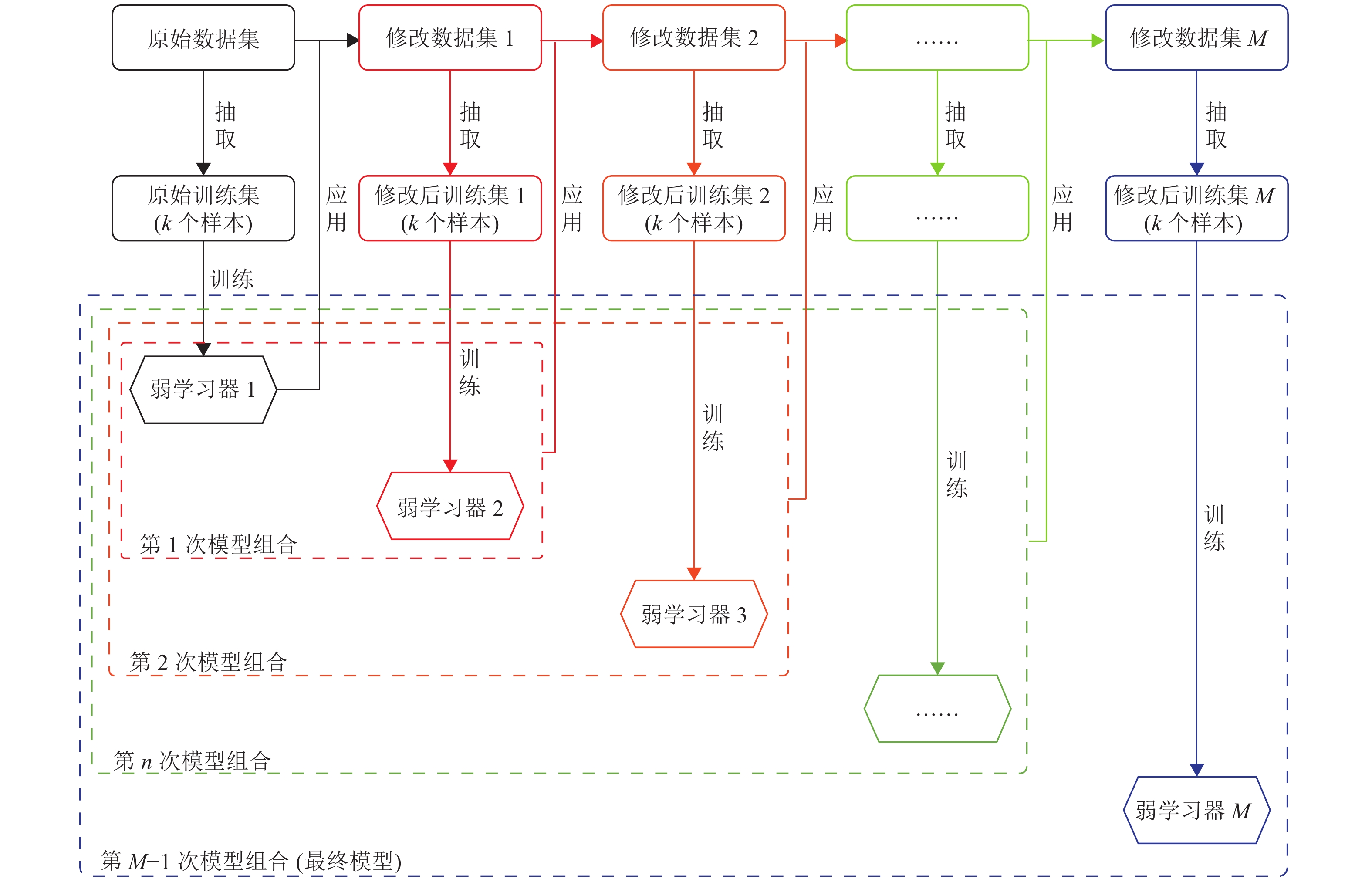
2.3.1 XGBoost集成模型集成学习是指将多个弱学习模型组合,以达到更好的效果。决策树模型是组成XGBoost的弱学习模型,根据最具有区分性的输入变量,把样本或数据集分割为两个或两个以上的子集合,模拟出分区间的阶梯函数,它能够很好地表达非线性关系,适合用来解决分类和回归问题。XGBoost基本原理如图3所示,把M个弱学习器模型组合在一起,每组合出一个模型,就会根据该模型的训练偏差调整训练数据集。后一个弱学习器不断学习前一个组合模型偏差,层层串联一起得到一个强模型。
|
图 3 XGBoost基本原理图 Figure 3 Theory of XGBoost |
训练数据来自54种混合工质的基于PC-SAFT的气液平衡计算(已剔除异常数据)。根据过程不同分为两组:(1) 蒸发过程取
| 表 1 XGBoost模型的输入与输出及训练平均误差 Table 1 Input and output and training average error of XGBoost |
构建包含常见的26种工质的纯工质库,见表2。纯工质两两组合,一共有
| 表 2 纯工质库 Table 2 Database of pure working fluids |
Li等[16]建议混合工质温度滑移在5~15 K较为合适。混合工质最大温度滑移一般出现在组分摩尔比0.5/0.5附近。同组分下泡点温度越高,温度滑移越小,冷凝的温度滑移大于蒸发的温度滑移,选择接近最低冷凝温度的300 K作为泡点温度指标。第一级筛选剔除组分摩尔比0.5/0.5下泡点温度300 K时温度滑移小于5 K的工质组合,排除近共沸工质。为了避免出现过大的温度滑移,第二级筛选剔除组分摩尔比0.1/0.9 (前者为易挥发工质)下泡点温度300 K时温度滑移大于20 K的工质组合。第三级筛选防止冷凝器出现负压,剔除泡点温度300 K时组分摩尔比0.1/0.9 (前者为易挥发工质)下泡点压力小于0.1 MPa的工质组合。以上3条筛选限制都是弱限制,会保留略超过限制的工质组合。在经过三级筛选后混合工质的组合数从325组下降到44组,见表3,有效地缩小了求解范围。
| 表 3 三级筛选结果 Table 3 Result of three-level screening |
混合工质作为优化变量参与ORC系统优化,这是混合整数非线性规划问题,采用遗传算法求解此类问题是一种行之有效的方法[17]。本文采用geatpy[18]差分遗传算法求解混合工质与ORC系统同步优化。在差分遗传算法中,称当代种群的一个父代个体为目标个体。在每一代进化过程中,目标个体变异生成变异个体,然后重组二者维度信息,生成一个被称为试验矢量的子代个体。如果试验个体的评价指标优于目标个体,则取代之作为下一代[19]。ORC系统边界条件如表4所示,热源假定为高温高压工业余热水。把三级筛选后的44种混合工质按1到44整数编号,遗传算法优化变量为混合工质编号、
| 表 4 ORC系统条件 Table 4 General specifications of the ORC case |
以净功、㶲效率最大化为目标的遗传算法优化最后一代前3个体分别如表5、6所示。无论以净功还是㶲效率为目标,冷凝温度
| 表 5 净功前3的混合物及系统操作参数 Table 5 Top 3 mixtures and conditions with the corresponding net power output |
|
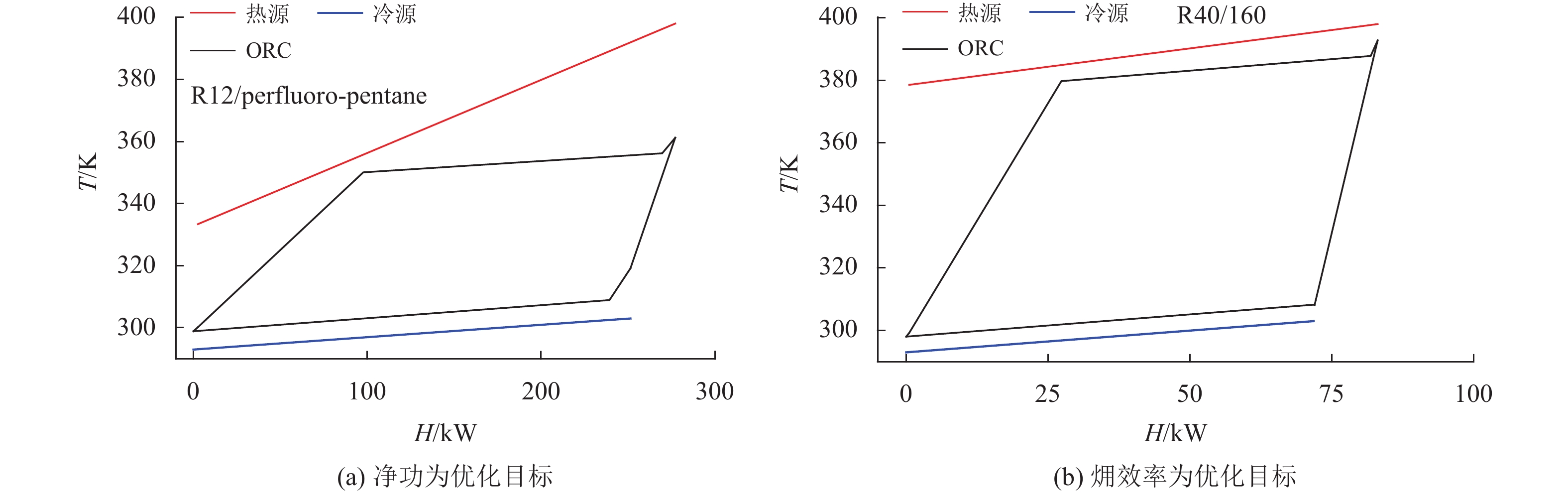
图 4 净功(a)、㶲效率(b)为优化目标的ORC的T-H图 Figure 4 Temperature-enthalpy diagram of the ORC for the optimal net power output(a) and exergy efficiency(b) |
| 表 6 㶲效率前3的混合物及系统操作参数 Table 6 Top 3 mixtures and conditions with the corresponding exergy efficiency |
设置不同的热源进口温度水平,对工质组合与ORC运行参数进行优化,以净功为目标的优化结果如表7所示。随着热源进口温度增大,T4上升,净功随之增大,而T1恰好满足夹点限制的最低温度298 K。工质流量和蒸发焓呈相反的趋势,这是因为相变蒸发吸热量占整个蒸发吸热量的大部分,在温度水平差不多情况下,吸收相同的热量,蒸发焓越小的工质,需要的质量越多。R12/戊烷蒸发焓明显比其他两种工质小,所以流量大得多。以㶲效率为目标的优化结果如表8所示,373,398 K最优工质都是R40/R160。除了423 K,T4都几乎达到恰好满足夹点限制的最高温度,㶲效率增加不明显,甚至降低。丁烯的临界温度为419.29 K,而R40更低,这限制T4达到更高的可能,随之工质与热源的匹配较差,所以㶲效率较低。T1都接近298 K,流量与蒸发焓的趋势与以净功为目标时相同。
| 表 7 不同热源进口温度下以净功为目标优化结果对比 Table 7 Comparison of optimization results with net power output as objective under different heat source inlet temperatures |
| 表 8 不同热源进口温度下以㶲效率为目标优化结果对比 Table 8 Comparison of optimization results with exergy efficiency as objective under different heat source inlet temperatures |
(1) 基于PC-SAFT计算混合工质物性,并对数量庞大的混合工质组合进行筛选,从325组筛选出44种较为合理的混合工质,有效地降低了搜索空间的范围,大大减少计算量。
(2) 基于遗传算法,把混合工质编号,实现混合工质与ORC系统同步优化。以净功、㶲效率为优化目标得到的最后混合工质分别为R12/perfluoro-pentane ,R40/R160。
(3) 不同热源进口温度水平下,不同目标时工质组合与ORC运行参数优化结果对比。以净功为目标时,随着热源进口温度上升,净功增大。以㶲效率为目标时,由于临界温度限制,423 K下㶲效率更低。无论以净功还是㶲效率为目标,冷凝泡点温度都应取最低。流量与蒸发焓变化趋势相反,蒸发焓越小的工质需要流量越大。
| [1] |
宋建忠, 张小松, 李舒宏, 等. 太阳能有机朗肯循环系统的实验特性[J].
化工学报, 2014(12): 4958-4964.
SONG J Z, ZHANG X S, LI S H, et al. Experimental characteristics of solar organic Rankine cycle system[J]. CIESC Journal, 2014(12): 4958-4964. |
| [2] |
刘继芬, 王景甫, 马重芳, 等. 中低温地热发电循环参数的优化[J].
化工学报, 2011, 62(S1): 190-196.
LIU J F, WANG J F, MA C F, et al. Optimization of cycle parameters in low-medium temperature geothermal power generation[J]. CIESC Journal, 2011, 62(S1): 190-196. |
| [3] |
杨凯, 张红光, 宋松松, 等. 变工况下车用柴油机排气余热有机朗肯循环回收系统[J].
化工学报, 2015, 66(3): 1097-1103.
YANG K, ZHANG H G, SONG S S, et al. Waste heat organic Rankine cycle of vehicle diesel engine under variable working conditions[J]. CIESC Journal, 2015, 66(3): 1097-1103. DOI: 10.11949/j.issn.0438-1157.20141119. |
| [4] |
王羽鹏, 罗向龙, 梁俊伟, 等. 有机朗肯循环系统工质设计与系统参数的同步优化[J].
广东工业大学学报, 2020, 37(1): 69-80.
WANG Y P, LUO X L, LIANG J W, et al. A simultaneous optimization of working fluid design and system parameters in organic Rankine cycle[J]. Journal of Guangdong University of Technology, 2020, 37(1): 69-80. DOI: 10.12052/gdutxb.190009. |
| [5] |
邱观福, 罗向龙, 陈健勇, 等. 考虑环境温度变工况的分液冷凝有机朗肯循环系统优化设计[J].
广东工业大学学报, 2019, 36(6): 99-104.
QIU G F, LUO X L, CHEN J Y, et al. An off-design optimization of liquid separation condenser-based organic Rankine cycle under different ambient temperature[J]. Journal of Guangdong University of Technology, 2019, 36(6): 99-104. DOI: 10.12052/gdutxb.190004. |
| [6] |
涂俊平, 黄计康, 罗向龙, 等. 水平光滑管内R245fa轴向均匀沸腾传热特性实验研究[J].
广东工业大学学报, 2020, 37(6): 71-77.
TU J P, HUANG J K, LUO X L, et al. An experimental study of axial uniform boiling heat transfer characteristics of R245fa in horizontal smooth tube[J]. Journal of Guangdong University of Technology, 2020, 37(6): 71-77. DOI: 10.12052/gdutxb.200014. |
| [7] |
BRAIMAKIS K, PREIßINGER M, BRÜGGEMANN D, et al. Low grade waste heat recovery with subcritical and supercritical organic rankine cycle based on natural refrigerants and their binary mixtures[J].
Energy, 2015, 88: 80-92.
DOI: 10.1016/j.energy.2015.03.092. |
| [8] |
PENG D, ROBINSON D B. A new two-constant equation of state[J].
Industrial & Engineering Chemistry Fundamentals, 1976, 15(1): 59-64.
|
| [9] |
ZHAO L, BAO J. Thermodynamic analysis of organic Rankine cycle using zeotropic mixtures[J].
Applied Energy, 2014, 130: 748-756.
DOI: 10.1016/j.apenergy.2014.03.067. |
| [10] |
WU Y, ZHU Y, YU L. Thermal and economic performance analysis of zeotropic mixtures for organic Rankine cycles[J].
Applied Thermal Engineering, 2016, 96: 57-63.
DOI: 10.1016/j.applthermaleng.2015.11.083. |
| [11] |
郑晓生, 罗俊伟, 卢沛, 等. 采用R1234ze(E)/R245fa的非共沸混合工质有机朗肯循环系统实验研究[J].
广东工业大学学报, 2020, 37(3): 114-120.
ZHENG X S, LUO J W, LU P, et al. An experimental study of zeotropic-mixture organic Rankine cycle system utilizing R1234ze (E)/R245fa[J]. Journal of Guangdong University of Technology, 2020, 37(3): 114-120. DOI: 10.12052/gdutxb.190110. |
| [12] |
GROSS J, SADOWSKI G. Perturbed-chain SAFT: an equation of state based on a perturbation theory for chain molecules[J].
Industrial & Engineering Chemistry Research, 2001, 40(4): 1244-1260.
|
| [13] |
JOBACK K G, REID R C. ESTIMATION of pure-component properties from group-contributions[J].
Chemical Engineering Communications, 1987, 57(1-6): 233-243.
DOI: 10.1080/00986448708960487. |
| [14] |
STAVROU M, BARDOW A, GROSS J. Estimation of the binary interaction parameter k of the PC-SAFT Equation of State based on pure component parameters using a QSPR method
[J].
Fluid Phase Equilibria, 2016, 416: 138-149.
DOI: 10.1016/j.fluid.2015.12.016. |
| [15] |
CHEN T, GUESTRIN C. XGBoost: A scalable tree boosting system[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. [s. l.]: ACM, 2016.
|
| [16] |
LI Y, DU M, WU C, et al. Potential of organic Rankine cycle using zeotropic mixtures as working fluids for waste heat recovery[J].
Energy, 2014, 77: 509-519.
DOI: 10.1016/j.energy.2014.09.035. |
| [17] |
王克峰, 姚平经, 袁一, 等. 遗传算法在过程综合混合整数非线性规划中的应用[J].
高校化学工程学报, 1997(4): 65-71.
WANG K F, YAO P J, YUAN Y, et al. Application of genetic algorithm in mixed integer nonlinear programming (MINLP) of process system synthesis[J]. Journal of Chemical Engineering of Chinese Universities, 1997(4): 65-71. |
| [18] |
Geatpy: the genetic and evolutionary algorithm toolbox with high performance in python[EB/OL]. [2020/12/11]. http://www.geatpy.com/.
|
| [19] |
吴亮红, 王耀南. 动态差分进化算法及其应用[M]. 北京: 科学出版社, 2014.
|
 2022, Vol. 39
2022, Vol. 39

