随着柔性梁在航空、航天和风力机等领域的广泛应用,研究者越来越重视其高精度的动力特性分析。如直升机螺旋桨[1]、风力发电机叶片[2]等,这类梁结构具有明显的非线性变形特点,工作时存在不同的回转速度。精确控制柔性旋转梁,需准确分析柔性梁的时域和频域特性。工程中为提高分析效率,通常采用简化梁模型,主要有线性有限元法、模态坐标近似法和柔性多体系统法,但这些方法存在模型精度较低、动力刚化模拟不明显、转动模态仿真不准确等问题。直接采用有限元模型,虽然能精确描述梁结构,但由于自由度显著增加,难以将其用于后续的多场耦合分析。现在计算大转动、非线性大变形梁的动力学问题的主流方法有GEBF(Geometrically Exact Beam Formula)和ANCF(Absolute Node Coordinate Formula)[3]。前者在机翼气弹耦合分析领域得到广泛应用,但存在梁截面姿态插值问题,且广义坐标包含角度和位移,给频域分析的线性化处理带来较大困难。绝对节点坐标法由于质量矩阵为常数矩阵,且直接基于连续介质理论,能方便描述梁的几何非线性特征,并支持高效的时域求解。此外,在构建频域线性化动力学方程时,仅需对刚度矩阵线性化,因此适用于柔性旋转梁模型的时域和频域分析建模。目前,国内外已有专家开展了广泛研究。
Ahmed[4]介绍了绝对节点坐标公式的计算机实现过程,为后续的数值仿真奠定了基础。Zhang等 [5-6]使用不同插值函数的ANCF对平面梁进行了动力特性分析,研究了弯曲和拉伸振动之间的模态耦合现象,但缺少弯扭耦合的相关研究。郑彤等[7]对三维大变形柔性梁系统的动力学建模和仿真进行了研究。建立三维大变形柔性梁系统的动力学模型,解决了ADAMS在计算大变形物体动力学时的局限性问题,但并未涉及动力特性分析。赵春璋等[8-12]建立动力学模型,研究了平面柔性梁大范围转动的变形、仿真精度的影响以及不同梁的理论适用范围,但未对频域响应进行相关的研究。姚震等[13-14]对ANCF的精确性和灵敏度展开了研究,认为不同材料和截面特征对系统末端的运动规律有一定影响,同样未涉及动力特性分析方面的工作。
综上,目前研究主要集中于平面梁的动力学仿真和弯曲梁小变形情况下固有频率的计算,对基于连续介质理论和非线性变形假设的三维柔性旋转梁动力刚化及其动力特性的研究相对较少。
为此,本文基于绝对节点坐标法,结合连续介质理论和几何非线性假设,建立三维柔性梁的动力学模型。通过非线性梁自由单摆仿真实验,验证本文算法的精确性;然后对三维梁的动力学方程进行线性化,构建柔性旋转梁的频域振动方程,计算不同转速下梁的动力刚化现象,并研究柔性旋转梁在不同转速下的模态振型变化。为后续风力机或飞机叶片等的气弹阻尼分析提供指导。
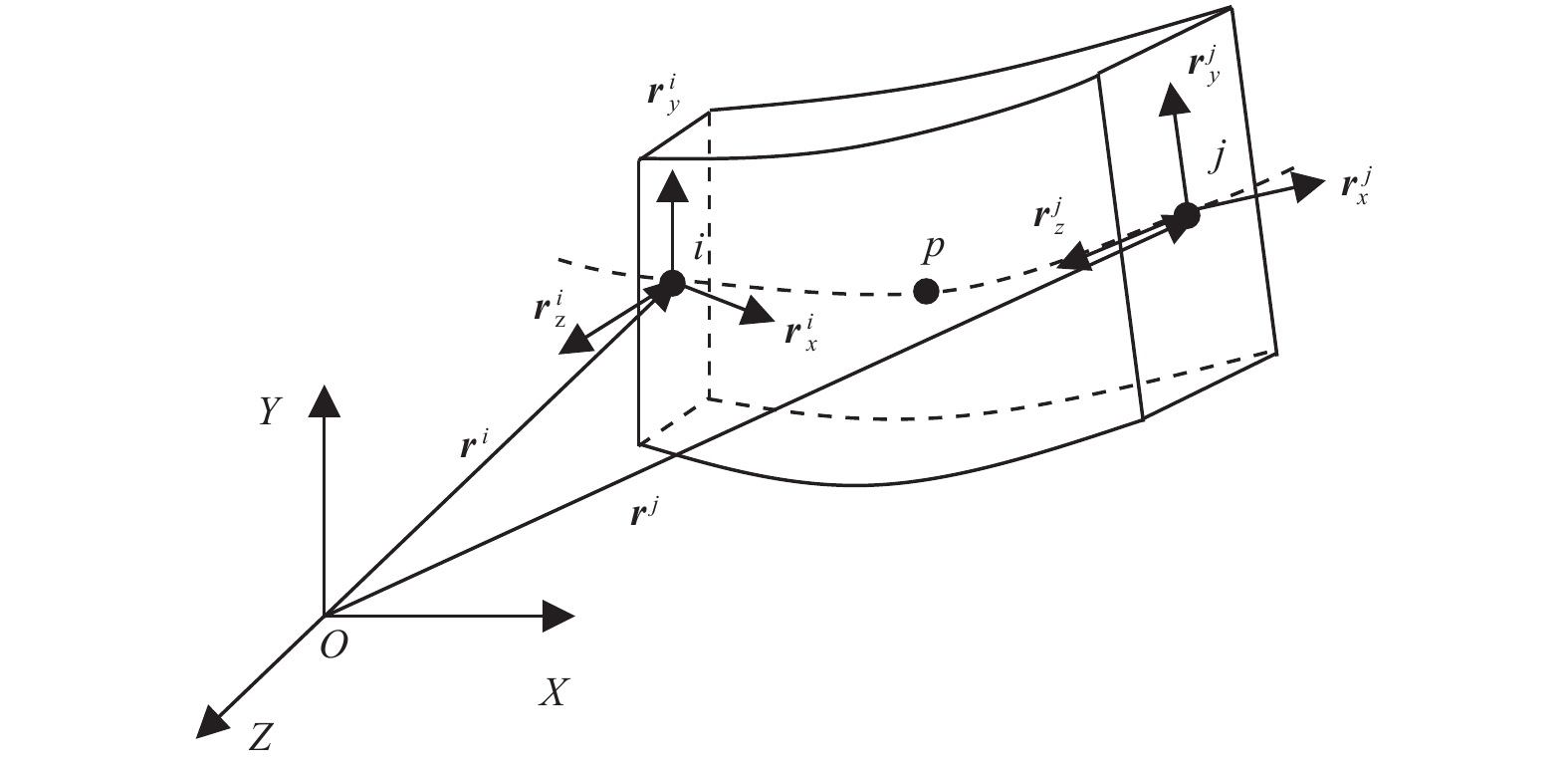
1 绝对节点坐标柔性梁建模 1.1 梁单元位置插值图1为三维二节点梁单元。其中,
| $ {{{\boldsymbol{r}}}}^{p}=\left[\begin{array}{c}{r}_{1}\\ {r}_{2}\\ {r}_{3}\end{array}\right]=\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]={{\boldsymbol{S}}}(x,y,z){{\boldsymbol{e}}}\left(t\right) $ | (1) |
|
图 1 三维变形梁单元 Figure 1 Three dimensional deformed beam element |
本文采用三次插值多项式来描述单元中任意一点的绝对位置。
| $ \left\{\begin{array}{l}{r}_{1}={a}_{0}+{a}_{1}x+{a}_{2}y+{a}_{3}{\textit{z}}+{a}_{4}xy+{a}_{5}x{\textit{z}}+{a}_{6}{x}^{2}+{a}_{7}{x}^{3}\\ {r}_{2}={b}_{0}+{b}_{1}x+{b}_{2}y+{b}_{3}{\textit{z}}+{b}_{4}xy+{b}_{5}x{\textit{z}}+{b}_{6}{x}^{2}+{b}_{7}{x}^{3}\\ {r}_{3}={c}_{0}+{c}_{1}x+{c}_{2}y+{c}_{3}{\textit{z}}+{c}_{4}xy+{c}_{5}x{\textit{z}}+{c}_{6}{x}^{2}+{c}_{7}{x}^{3}\end{array}\right. $ |
式中:
| $ {{\boldsymbol{e}}}\left(t\right)={\left[\begin{array}{cc}{\boldsymbol{e}}_{i}& {\boldsymbol{e}}_{j}\end{array}\right]}^{\mathrm{T}} = {\left[\begin{array}{cccccccc}{\boldsymbol{r}}^{i}& {\boldsymbol{r}}_{x}^{i}& {\boldsymbol{r}}_{y}^{i}& {\boldsymbol{r}}_{z}^{i}& {\boldsymbol{r}}^{j}& {\boldsymbol{r}}_{x}^{j}& {\boldsymbol{r}}_{y}^{j}& {\boldsymbol{r}}_{z}^{j}\end{array}\right]}^{\mathrm{T}} $ | (2) |
式中:
将单元坐标式(2)与三次插值多项式联立,求解待定系数,可得到单元形函数[15]。
| $ \boldsymbol{S}\left(x,y,z\right)= \left[\begin{array}{cccccccc}{\boldsymbol{S}}_{1}\boldsymbol{I}& {\boldsymbol{S}}_{2}\boldsymbol{I}& {\boldsymbol{S}}_{3}\boldsymbol{I}& {\boldsymbol{S}}_{4}\boldsymbol{I}& {\boldsymbol{S}}_{5}\boldsymbol{I}& {\boldsymbol{S}}_{6}\boldsymbol{I}& {\boldsymbol{S}}_{7}\boldsymbol{I}& {\boldsymbol{S}}_{8}\boldsymbol{I}\end{array}\right] $ | (3) |
式中:
| $ \left\{\begin{array}{ll}{\boldsymbol{S}}_{1}=1-3{\xi }^{2}+2{\xi }^{3};& \boldsymbol{S}_{2}=l\left(\xi -2{\xi }^{2}+{\xi }^{3}\right);\\ \boldsymbol{S}_{3}=l\left(\eta -\xi \eta \right);& \boldsymbol{S}_{4}=l\left(\zeta -\xi \zeta \right);\\ \boldsymbol{S}_{5}=3{\xi }^{2}-2{\xi }^{3};& \boldsymbol{S}_{6}=l\left({\xi }^{3}-{\xi }^{2}\right);\\ \boldsymbol{S}_{7}=l\left(\xi \eta \right);& \boldsymbol{S}_{8}=l\left(\xi \zeta \right)\end{array}\right. $ |
式中:
对式(1)进行时间求导可得到任意一点的绝对速度
| $ \dot{\boldsymbol{r}}=\boldsymbol{S}\dot{\boldsymbol{e}} $ | (4) |
梁单元的动能可表示为
| $ {E}_{\mathrm{k}}=\frac{1}{2}\rho \iiint {\dot{\boldsymbol{r}}}^{\mathrm{T}}\dot{\boldsymbol{r}}\mathrm{d}V=\\ \frac{1}{2}{\dot{\boldsymbol{e}}}^{\mathrm{T}}\left(\rho \iiint {\boldsymbol{S}}^{\mathrm{T}}\boldsymbol{S}\mathrm{d}V\right)\dot{\boldsymbol{e}}=\frac{1}{2}{\dot{\boldsymbol{e}}}^{\mathrm{T}}\boldsymbol{M}\dot{\boldsymbol{e}} $ | (5) |
式中:
| $ \boldsymbol{M}=\rho {\int }_{0}^{l}\left(\iint {\boldsymbol{S}}^{\mathrm{T}}\boldsymbol{S}\mathrm{d}A\right)\mathrm{d}x $ | (6) |
式中:
利用连续介质理论和非线性格林应变张量假设,计算梁单元的位移应变关系。梁单元的变形梯度
| $ \boldsymbol{H}=\left[\begin{array}{ccc}\dfrac{{{\partial}} {r}_{1}}{ \partial x}& \dfrac{\partial {r}_{1}}{ \partial y}& \dfrac{\partial {r}_{1}}{ \partial z}\\ \dfrac{\partial {r}_{2}}{ \partial x}& \dfrac{\partial {r}_{2}}{ \partial y}& \dfrac{\partial {r}_{2}}{ \partial z}\\ \dfrac{\partial {r}_{3}}{ \partial x}& \dfrac{\partial {r}_{3}}{ \partial y}& \dfrac{\partial {r}_{3}}{ \partial z}\end{array}\right] $ | (7) |
非线性格林应变张量为
| $ {{\boldsymbol{G}}}=\frac{1}{2}({\boldsymbol{H}}^{\mathrm{T}}\boldsymbol{H}-\boldsymbol{I}) $ | (8) |
将式(1)和式(7)代入式(8)得到
| $ \boldsymbol{G}=\dfrac{1}{2}\left(\left[\begin{array}{lll}{\boldsymbol{e}}^{\mathrm{T}}{\boldsymbol{S}}_{x}\boldsymbol{e}& {\boldsymbol{e}}^{\mathrm{T}}{\boldsymbol{S}}_{xy}\boldsymbol{e}& {\boldsymbol{e}}^{\mathrm{T}}{\boldsymbol{S}}_{{\textit{z}}x}\boldsymbol{e}\\ {\boldsymbol{e}}^{\mathrm{T}}{\boldsymbol{S}}_{xy}\boldsymbol{e}& {\boldsymbol{e}}^{\mathrm{T}}{\boldsymbol{S}}_{y}\boldsymbol{e}& {\boldsymbol{e}}^{\mathrm{T}}{\boldsymbol{S}}_{y{\textit{z}}}\boldsymbol{e}\\ {\boldsymbol{e}}^{\mathrm{T}}{\boldsymbol{S}}_{{\textit{z}}x}\boldsymbol{e}& {\boldsymbol{e}}^{\mathrm{T}}{\boldsymbol{S}}_{y{\textit{z}}}\boldsymbol{e}& {\boldsymbol{e}}^{\mathrm{T}}{\boldsymbol{S}}_{{\textit{z}}}\boldsymbol{e}\end{array}\right]-\boldsymbol{I}\right) $ | (9) |
式中:
| $ \left\{\begin{array}{c}{\boldsymbol{S}}_{x}={\left(\dfrac{\partial {\boldsymbol{S}}_{1}}{ \partial x}\right)}^{\mathrm{T}} \dfrac{\partial {\boldsymbol{S}}_{1}}{ \partial x}+{\left(\dfrac{\partial {\boldsymbol{S}}_{2}}{ \partial x}\right)}^{\mathrm{T}} \dfrac{\partial {\boldsymbol{S}}_{2}}{ \partial x}+{\left(\dfrac{\partial {\boldsymbol{S}}_{3}}{ \partial x}\right)}^{\mathrm{T}} \dfrac{\partial {\boldsymbol{S}}_{3}}{ \partial x}\\ {\boldsymbol{S}}_{y}={\left(\dfrac{\partial {\boldsymbol{S}}_{1}}{ \partial y}\right)}^{\mathrm{T}} \dfrac{\partial {\boldsymbol{S}}_{1}}{ \partial y}+{\left(\dfrac{\partial {\boldsymbol{S}}_{2}}{ \partial y}\right)}^{\mathrm{T}} \dfrac{\partial {\boldsymbol{S}}_{2}}{ \partial y}+{\left(\dfrac{\partial {\boldsymbol{S}}_{3}}{ \partial y}\right)}^{{{\rm{T}}}} \dfrac{\partial {\boldsymbol{S}}_{3}}{ \partial y}\\ {\boldsymbol{S}}_{{\textit{z}}}={\left(\dfrac{\partial {\boldsymbol{S}}_{1}}{ \partial {\textit{z}}}\right)}^{\mathrm{T}} \dfrac{\partial {\boldsymbol{S}}_{1}}{ \partial {\textit{z}}}+{\left(\dfrac{\partial {\boldsymbol{S}}_{2}}{ \partial {\textit{z}}}\right)}^{\mathrm{T}} \dfrac{\partial {\boldsymbol{S}}_{2}}{ \partial {\textit{z}}}+{\left(\dfrac{\partial {\boldsymbol{S}}_{3}}{ \partial {\textit{z}}}\right)}^{\mathrm{T}} \dfrac{\partial {\boldsymbol{S}}_{3}}{ \partial {\textit{z}}}\\ {\boldsymbol{S}}_{xy}={\left(\dfrac{\partial {\boldsymbol{S}}_{1}}{ \partial x}\right)}^{\mathrm{T}} \dfrac{\partial {\boldsymbol{S}}_{1}}{ \partial y}+{\left(\dfrac{\partial {\boldsymbol{S}}_{2}}{ \partial x}\right)}^{\mathrm{T}} \dfrac{\partial {\boldsymbol{S}}_{2}}{ \partial y}+{\left(\dfrac{\partial {\boldsymbol{S}}_{3}}{ \partial x}\right)}^{\mathrm{T}} \dfrac{\partial {\boldsymbol{S}}_{3}}{ \partial y}\\ {\boldsymbol{S}}_{y{\textit{z}}}={\left(\dfrac{\partial {\boldsymbol{S}}_{1}}{ \partial y}\right)}^{\mathrm{T}} \dfrac{\partial {\boldsymbol{S}}_{1}}{ \partial {\textit{z}}}+{\left(\dfrac{\partial {\boldsymbol{S}}_{2}}{ \partial y}\right)}^{\mathrm{T}} \dfrac{\partial {\boldsymbol{S}}_{2}}{ \partial {\textit{z}}}+{\left(\dfrac{\partial {\boldsymbol{S}}_{3}}{ \partial y}\right)}^{\mathrm{T}} \dfrac{\partial {\boldsymbol{S}}_{3}}{ \partial {\textit{z}}}\\ {\boldsymbol{S}}_{{\textit{z}}x}={\left(\dfrac{\partial {\boldsymbol{S}}_{1}}{ \partial {\textit{z}}}\right)}^{\mathrm{T}} \dfrac{\partial {\boldsymbol{S}}_{1}}{ \partial x}+{\left(\dfrac{\partial {\boldsymbol{S}}_{2}}{ \partial {\textit{z}}}\right)}^{\mathrm{T}} \dfrac{\partial {\boldsymbol{S}}_{2}}{ \partial x}+{\left(\dfrac{\partial {\boldsymbol{S}}_{3}}{ \partial {\textit{z}}}\right)}^{\mathrm{T}} \dfrac{\partial {\boldsymbol{S}}_{3}}{ \partial x}\end{array}\right. $ |
将对称的非线性格林应变张量表示为列矢量形式。
| $ \boldsymbol{\varepsilon }={\left[\begin{array}{cccccc}{\boldsymbol{G}}_{11}& {\boldsymbol{G}}_{22}& {\boldsymbol{G}}_{33}& {2\boldsymbol{G}}_{12}& {2\boldsymbol{G}}_{13}& {2\boldsymbol{G}}_{23}\end{array}\right]}^{\mathrm{T}} $ | (10) |
在线弹性本构关系下,应力
| $ \boldsymbol{\sigma }=\boldsymbol{D}\boldsymbol{\varepsilon } $ | (11) |
式中:
根据虚功原理弹性力所作虚功为
| $ {\text{δ}} {V}_{{\rm{w}}}={\int }_{V}{\left(\boldsymbol{D}\boldsymbol{\varepsilon }\right)}^{\mathrm{T}}{\text{δ}} \boldsymbol{\varepsilon }\mathrm{d}{V}={\boldsymbol{e}}^{\mathrm{T}}\boldsymbol{K}{\text{δ}} \boldsymbol{e} $ | (12) |
式中:
| $ \boldsymbol{K}={\boldsymbol{K}}_{\mathrm{l}}+{\boldsymbol{K}}_{\mathrm{n}} $ | (13) |
式中:
| $ {\boldsymbol{K}}_{\mathrm{l}}=-\frac{\left(3\lambda +2\mu \right)}{2}\iiint ({\boldsymbol{S}}_{x}+{\boldsymbol{S}}_{y}+{\boldsymbol{S}}_{z})\mathrm{d}V $ | (14) |
| $ \left\{\begin{array}{l}{\boldsymbol{K}}_{\mathrm{n},1}=\dfrac{1}{2}(\lambda +2\mu )\displaystyle\iiint (({\boldsymbol{e}}^{\mathrm{T}}{\boldsymbol{S}}_{x}\boldsymbol{e}){\boldsymbol{S}}_{x}+\\ \qquad \;\;({\boldsymbol{e}}^{\mathrm{T}}{\boldsymbol{S}}_{y}\boldsymbol{e}){\boldsymbol{S}}_{y}+({\boldsymbol{e}}^{\mathrm{T}}{\boldsymbol{S}}_{{\textit{z}}}\boldsymbol{e}){\boldsymbol{S}}_{{\textit{z}}})\mathrm{d}V\\ {\boldsymbol{K}}_{\mathrm{n},2}=\dfrac{1}{2}\lambda \displaystyle\iiint (({\boldsymbol{e}}^{\mathrm{T}}{\boldsymbol{S}}_{x}\boldsymbol{e}){(\boldsymbol{S}}_{y}+{\boldsymbol{S}}_{{\textit{z}}})+\\ \qquad \;\;({\boldsymbol{e}}^{\mathrm{T}}{\boldsymbol{S}}_{y}\boldsymbol{e})({\boldsymbol{S}}_{x}+{\boldsymbol{S}}_{{\textit{z}}})+({\boldsymbol{e}}^{\mathrm{T}}{\boldsymbol{S}}_{{\textit{z}}}\boldsymbol{e}){(\boldsymbol{S}}_{x}+{\boldsymbol{S}}_{y}\left)\right)\mathrm{d}V\\ {{\boldsymbol{K}}_{\mathrm{n},3}=\mu \displaystyle\iiint (({\boldsymbol{e}}^{\mathrm{T}}{\boldsymbol{S}}_{xy}\boldsymbol{e})}({\boldsymbol{S}_{xy}}+{\boldsymbol{S}}_{xy}^{\mathrm{T}})+\\ \qquad \;\;({\boldsymbol{e}}^{\mathrm{T}}{\boldsymbol{S}}_{y{\textit{z}}}\boldsymbol{e}){(\boldsymbol{S}}_{y{\textit{z}}}+{\boldsymbol{S}}_{y{\textit{z}}}^{\mathrm{T}})+({\boldsymbol{e}}^{\mathrm{T}}{\boldsymbol{S}}_{{\textit{z}}x}\boldsymbol{e}){(\boldsymbol{S}}_{{\textit{z}}x}+{\boldsymbol{S}}_{{\textit{z}}x}^{\mathrm{T}}))\mathrm{d}V\end{array}\right. $ |
| $ \begin{aligned}[b] &{\lambda }=\frac{v}{1+v} \cdot \frac{E}{1-2v} \\ &\mu =\frac{E}{2(1+v)} \end{aligned} $ | (15) |
式(15)中:
根据虚功原理以及式(1),得到外力虚功为
| $ {\text{δ}} {W}_{\mathrm{e}\mathrm{l}\mathrm{e}}={\boldsymbol{F}}^{\mathrm{T}}{\text{δ}} \boldsymbol{r}={\boldsymbol{F}}^{\mathrm{T}}\boldsymbol{S}{\text{δ}} \boldsymbol{e}={\boldsymbol{Q}}_{\mathrm{e}\mathrm{l}\mathrm{e}}^{\mathrm{T}}{\text{δ}} \boldsymbol{e} $ | (16) |
式中:
| $ {\boldsymbol{Q}}_{\mathrm{e}\mathrm{l}\mathrm{e}}^{\mathrm{T}}={\boldsymbol{F}}^{\mathrm{T}}\boldsymbol{S} $ | (17) |
单摆仿真时,需要在单摆被约束的根部施加一转动副约束,使单摆绕着被约束点旋转,此外该转动副亦可施加于梁与梁之间,形成两梁之间的相对转动;多个梁单元时,单元与单元之间不会发生相对移动、扭转和旋转,单元与单元需固结在一起。故本文特介绍2种约束,一种为绕z轴旋转的自由单摆的转动副约束,一种为梁单元之间的固定铰约束。
转动副约束定义如图2(a)所示,点
| $ {\boldsymbol{r}}^{ip}={\boldsymbol{r}}^{jp} $ | (18) |
| $ {\boldsymbol{r}}_{{\textit{z}}}^{ip}={\boldsymbol{r}}_{{\textit{z}}}^{jp} $ | (19) |
固定铰约束如图2(b)所示,点
| $ {\boldsymbol{r}}^{ip}={\boldsymbol{r}}^{jp} \text{;} {\boldsymbol{r}}_{\alpha }^{ip}={\boldsymbol{r}}_{\alpha }^{jp},\;\alpha =x,y,z $ | (20) |
式中:
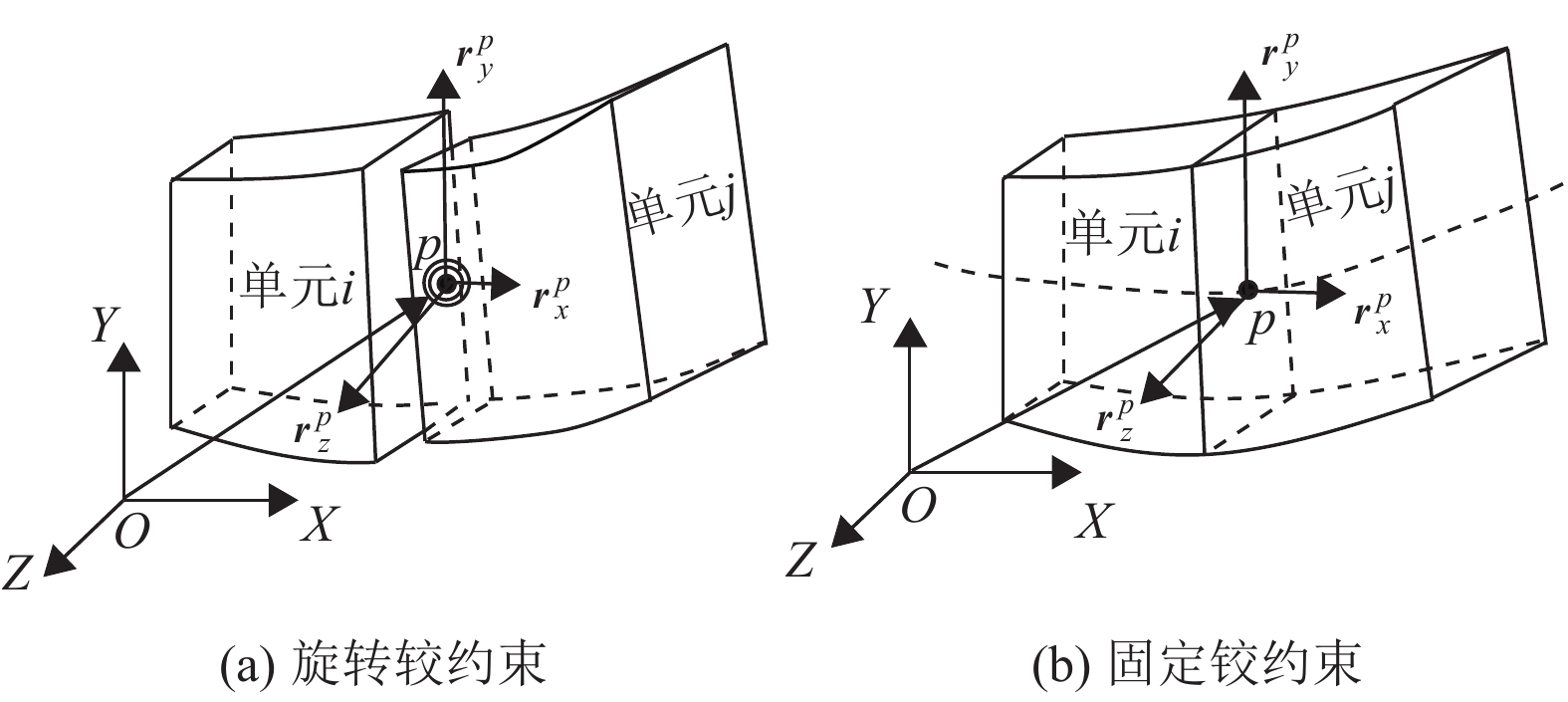
|
图 2 系统约束 Figure 2 System constraints |
由单元质量矩阵、单元刚度矩阵、单元广义力矩阵和组装布尔矩阵
| $ \left\{\begin{array}{l}{\boldsymbol{M}}_{\mathrm{t}\mathrm{m}}={\boldsymbol{B}}^{\mathrm{T}}\boldsymbol{M}\boldsymbol{B}\\ {\boldsymbol{K}}_{\mathrm{t}\mathrm{m}}={\boldsymbol{B}}^{\mathrm{T}}\boldsymbol{K}\boldsymbol{B}\\ {\boldsymbol{Q}}_{\mathrm{t}\mathrm{m}}={\boldsymbol{B}}^{\mathrm{T}}{\boldsymbol{Q}}_{\mathrm{e}\mathrm{l}\mathrm{e}}\end{array}\right. $ | (21) |
考虑梁铰约束,将约束式(18)~(20)与式(21)联立。约束组装矩阵由
| $ \begin{array}{c}{\boldsymbol{M}}_{\mathrm{c}}\left({\boldsymbol{B}}_{\mathrm{c}}\ddot{\boldsymbol{e}}\right)+{\boldsymbol{K}}_{\mathrm{c}}\left({\boldsymbol{B}}_{\mathrm{c}}\boldsymbol{e}\right)={\boldsymbol{Q}}_{\mathrm{c}}\end{array} $ | (22) |
式中:
| $ \left\{\begin{array}{l}{\boldsymbol{M}}_{\mathrm{c}}={{{\boldsymbol{B}}_{\rm{c}}^{\rm{T}}}\boldsymbol{M}}_{\mathrm{t}\mathrm{m}}{\boldsymbol{B}}_{\mathrm{c}}\\ {\boldsymbol{K}}_{\mathrm{c}}={{{\boldsymbol{B}}_{\rm{c}}^{\rm{T}}}\mathit{K}}_{\mathrm{t}\mathrm{m}}{\boldsymbol{B}}_{\mathrm{c}}\\ {\boldsymbol{Q}}_{\mathrm{c}}={{\boldsymbol{B}}_{\mathrm{c}}\boldsymbol{Q}}_{\mathrm{t}\mathrm{m}}\end{array}\right. $ |
用绝对节点坐标方法建模时,节点坐标相对绝对坐标进行定义。当梁绕定轴转动时,为方便描述刚性大范围定轴转动和梁本身的变形运动,引入浮点坐标系,建立旋转梁动力学模型。
在三维空间坐标中,三维柔性梁绕着Z轴旋转,将其投影于旋转平面如图3所示。
图3中
| $ \left[\begin{array}{c}{r}_{1}\\ {r}_{2}\\ {r}_{3}\end{array}\right]=\left[\begin{array}{ccc}\mathrm{c}\mathrm{o}\mathrm{s}\;\theta & -\mathrm{s}\mathrm{i}\mathrm{n}\;\theta & 0\\ \mathrm{s}\mathrm{i}\mathrm{n}\;\theta &\;\;\; \mathrm{c}\mathrm{o}\mathrm{s}\;\theta & 0\\ 0& \;\;\;0& 1\end{array}\right]\left[\begin{array}{c}{\eta }_{1}\\ {\eta }_{2}\\ {\eta }_{3}\end{array}\right]+R\left[\begin{array}{c}\mathrm{c}\mathrm{o}\mathrm{s}\;\theta \\ \mathrm{s}\mathrm{i}\mathrm{n}\;\theta \\ 0\end{array}\right] $ | (23) |
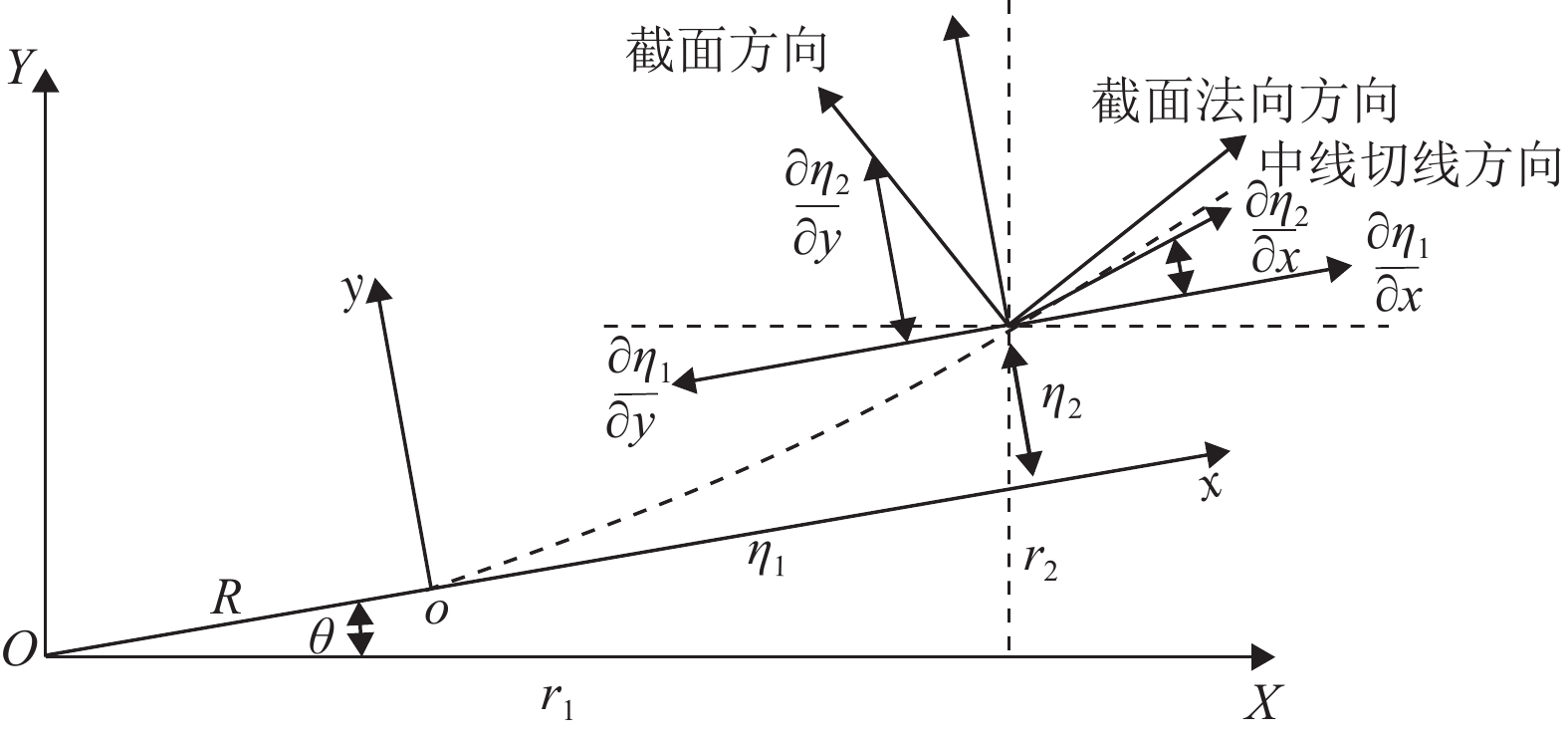
|
图 3 浮动坐标与绝对坐标示意图 Figure 3 Schematic diagram of floating coordinates and absolute coordinate system |
根据单元节点坐标
| $ \boldsymbol{e}\left(t\right)={\boldsymbol{U}}_{\mathrm{C}\mathrm{T}}{\tilde {\boldsymbol{e}}}_{\mathrm{e}\mathrm{l}\mathrm{e}}+{\boldsymbol{e}}_{\mathrm{e}\mathrm{l}\mathrm{e},R} $ | (24) |
式中:
| $ \begin{aligned}[b] &\qquad\qquad\qquad {\boldsymbol{e}}_{\mathrm{e}\mathrm{l}\mathrm{e},R}=R{\boldsymbol{U}}_{\mathrm{C}\mathrm{T}}\boldsymbol{V}\\ &\boldsymbol{V}={\left[\begin{array}{cccccccc}1& 0& 0& \cdots & 1& 0& 0& \cdots \end{array}\right]}^{\mathrm{T}} \end{aligned} $ | (25) |
| $ {\boldsymbol{U}}_{\mathrm{C}\mathrm{T}}=\left[\begin{array}{cc}{\boldsymbol{N}}_{\mathrm{C}\mathrm{T}}& 0\\ 0& {\boldsymbol{N}}_{\mathrm{C}\mathrm{T}}\end{array}\right] $ | (26) |
式(25)~(26)中:
| $ {\boldsymbol{N}}_{\mathrm{C}\mathrm{T}}=\left[\begin{array}{cccc}{\boldsymbol{P}}_{0}& 0& 0& 0\\ 0& {\boldsymbol{P}}_{0}& 0& 0\\ 0& 0& {\boldsymbol{P}}_{0}& 0\\ 0& 0& 0& {\boldsymbol{P}}_{0}\end{array}\right] $ | (27) |
| $ {\boldsymbol{P}}_{0}=\left[\begin{array}{ccc}\mathrm{c}\mathrm{o}\mathrm{s}\;\theta & -\mathrm{s}\mathrm{i}\mathrm{n}\;\theta & 0\\ \mathrm{s}\mathrm{i}\mathrm{n}\;\theta & \mathrm{c}\mathrm{o}\mathrm{s}\;\theta & 0\\ 0& 0& 1\end{array}\right] $ | (28) |
将式(24)代入式(22)中,旋转梁动力学方程为
| $ {\boldsymbol{M}}_{\mathrm{c}}{\ddot{\tilde {\boldsymbol{e}}}}_{\mathrm{c}}+2\dot{\theta }{\boldsymbol{M}}_{1\mathrm{c}}{\dot{\tilde {\boldsymbol{e}}}}_{\mathrm{c}}-{\dot{\theta }}^{2}{\boldsymbol{M}}_{2\mathrm{c}}{\tilde {\boldsymbol{e}}}_{\mathrm{c}} - R{\dot{\theta }}^{2}{\boldsymbol{M}}_{2\mathrm{c}}\boldsymbol{V}+{\boldsymbol{K}}_{\mathrm{c}}\left(\tilde {\boldsymbol{e}}\right){\tilde {\boldsymbol{e}}}_{\mathrm{c}}={\boldsymbol{Q}}_{\mathrm{c}} $ | (29) |
式中:
| $ {\boldsymbol{M}}_{1\mathrm{c}}=\rho {{\boldsymbol{B}}_{\rm{c}}^{\rm{T}}}\left({\int }_{0}^{l}\left(\iint {\boldsymbol{S}}_{\theta }\mathrm{d}A\right)\mathrm{d}x\right){\boldsymbol{B}}_{\mathrm{c}} $ | (30) |
| $ {\boldsymbol{S}}_{\theta }={\left({\boldsymbol{U}}_{\mathrm{C}\mathrm{T}}\right)}^{\mathrm{T}}{\boldsymbol{S}}^{\mathrm{T}}\boldsymbol{S}{{\boldsymbol{U}}_{{\mathrm{C}\mathrm{T}},{\theta}}} \qquad \qquad\;\;$ | (31) |
| $\;{{\boldsymbol{M}}}_{2{\rm{c}}}=\rho {{\boldsymbol{B}}_{\rm{c}}^{\rm{T}}}\left({\int }_{0}^{l}\left(\iint {\boldsymbol{S}}_{\theta \theta }\mathrm{d}A\right)\mathrm{d}x\right){\boldsymbol{B}}_{\mathrm{c}} $ | (32) |
| $ {\boldsymbol{S}}_{\theta \theta }={\left({\boldsymbol{U}}_{\mathrm{C}\mathrm{T}}\right)}^{\mathrm{T}}{\boldsymbol{S}}^{\mathrm{T}}\boldsymbol{S}{{\boldsymbol{U}}_{\mathrm{C}\mathrm{T},\theta \theta }} \qquad \qquad $ | (33) |
为了分析柔性旋转梁的频率特性及其模态变化,采用摄动理论对旋转动力学方程式(29)分别进行
| $ {\boldsymbol{M}}_{\mathrm{c}}{\text{δ}} {\ddot{\tilde {\boldsymbol{e}}}}_{\mathrm{c}}+2\dot{\theta }{\boldsymbol{M}}_{1\mathrm{c}}{\text{δ}} {\dot{\tilde {\boldsymbol{e}}}}_{\mathrm{c}}+ ({\mathit{K}}_{\mathrm{T}1\mathrm{c}}({\tilde {\boldsymbol{e}}}_{\mathrm{e}\mathrm{p}})-{\dot{\theta }}^{2}{\boldsymbol{M}}_{2\mathrm{c}}){\text{δ}} {\tilde {\boldsymbol{e}}}_{\mathrm{c}}=0 $ | (34) |
式中:
| $ {\boldsymbol{K}}_{\mathrm{T}1}\left({\tilde {\boldsymbol{e}}}_{\mathrm{e}\mathrm{p}}\right)=\frac{\partial ({\boldsymbol{K}}_{\mathrm{t}\mathrm{m}}({\tilde {\boldsymbol{e}}}_{\mathrm{e}\mathrm{p}}))}{\partial {\tilde {\boldsymbol{e}}}_{\mathrm{e}\mathrm{p}}}{\tilde {\boldsymbol{e}}}_{\mathrm{e}\mathrm{p}}+{\boldsymbol{K}}_{\mathrm{t}\mathrm{m}}({\tilde {\boldsymbol{e}}}_{\mathrm{e}\mathrm{p}}) $ | (35) |
将
| $ -{\dot{\theta }}^{2}{\boldsymbol{M}}_{2\mathrm{c}}{\tilde {\boldsymbol{e}}}_{\mathrm{e}\mathrm{p}}+{\boldsymbol{K}}_{\mathrm{c}}({\tilde {\boldsymbol{e}}}_{\mathrm{e}\mathrm{p}}){\tilde {\boldsymbol{e}}}_{\mathrm{e}\mathrm{p}}-R{\dot{\theta }}^{2}{\boldsymbol{M}}_{2\mathrm{c}}\boldsymbol{C}=0 $ | (36) |
将
| $ \left(\mathrm{j}\omega \left[\begin{array}{cc}{\boldsymbol{K}}_{\mathrm{T}}& 0\\ 0& {\boldsymbol{M}}_{\mathrm{c}}\end{array}\right]+\left[\begin{array}{cc}0& -{\boldsymbol{K}}_{\mathrm{T}}\\ {\boldsymbol{K}}_{\mathrm{T}}& 2\dot{\theta }{\boldsymbol{M}}_{1\mathrm{c}}\end{array}\right]\right)\boldsymbol{Z}=0 $ | (37) |
式中:
| $ {\boldsymbol{K}}_{\mathrm{T}}={\boldsymbol{K}}_{\mathrm{T}1\mathrm{c}}\left({\tilde{\boldsymbol{e}}}_{\mathrm{e}\mathrm{p}}\right)-{\dot{\theta }}^{2}{\boldsymbol{M}}_{2\mathrm{c}} $ | (38) |
以自由单摆仅受重力作用下的动力学仿真为例,验证本文方法所建梁模型的精确性。此时外力
| $ \boldsymbol{F}=\left[\begin{array}{ccc}0& -\rho {g}& 0\end{array}\right] $ | (39) |
根据形函数
| $ {\boldsymbol{Q}}_{\mathrm{e}\mathrm{l}\mathrm{e}}^{\mathrm{T}}={\int }_{{V}}\left[\begin{array}{ccc}0& -\rho {g}& 0\end{array}\right]\boldsymbol{S}\mathrm{d}V $ | (40) |
式(39)~(40)中:
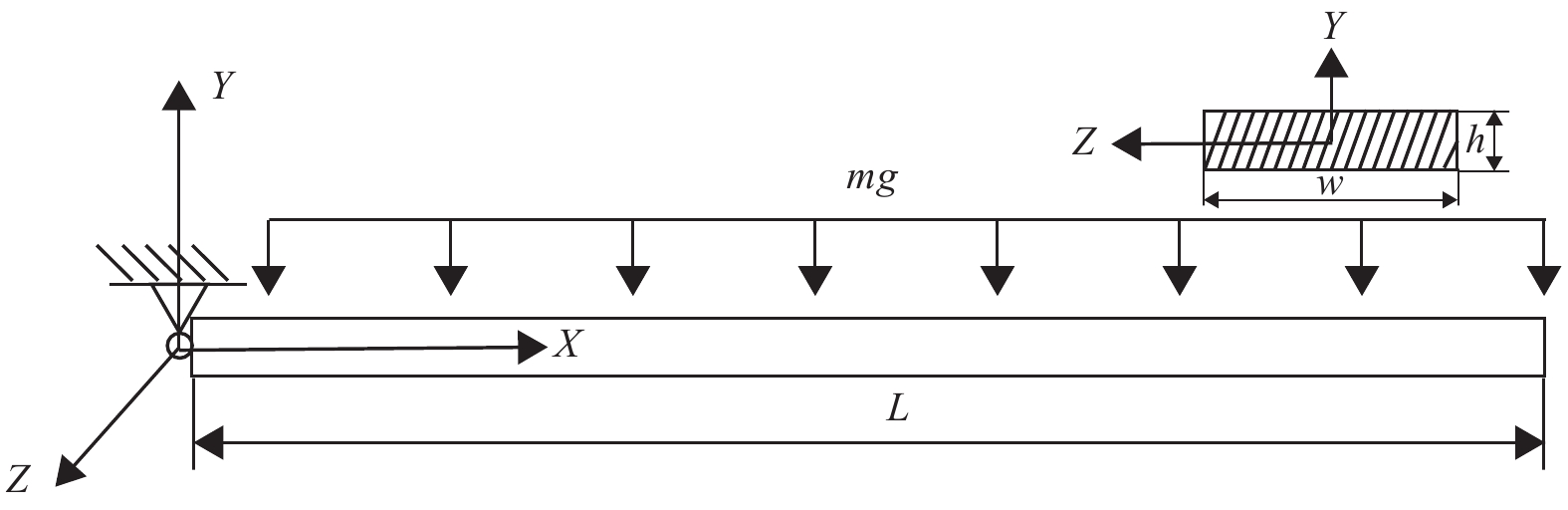
自由单摆如图4所示,柔性梁截面高为
本文根据文献[12]中的算例进行了仿真实验1:弹性模量
|
图 4 自由柔性单摆 Figure 4 Free flexible pendulum |

|
图 5 仿真实验1柔性单摆不同时间下的位置及形状 Figure 5 Position and shape of flexible pendulum at different time |
| 表 1 本文的仿真结果与文献[12]实验结果的对比(t=0.3 s) Table 1 Comparison between simulation results and literature[12] in this paper (t=0.3 s) |
本文也对文献[18]中的算例进行了仿真实验2,其弹性模量

|
图 6 仿真实验2柔性单摆不同时间下的仿真结果 Figure 6 Simulation results of flexible pendulum at different time |
| 表 2 本文仿真结果与文献[18]实验结果的对比(t=0.4 s) Table 2 Comparison between simulation results and literature[18] in this paper (t=0.4 s) |
为了验证旋转梁动力特性仿真精度,本文计算不同转速下的无量纲固有频率,并与文献[19]的计算结果进行对比。
| $ {\omega }_{0}=\sqrt{\frac{E\varGamma }{m{L}^{3}}} $ | (41) |
| $ \varOmega =\gamma {\omega }_{0} $ | (42) |
式(41)~(42)中:
不同转速下无量纲固有频率前三阶计算结果如表3所示,两者结果基本一致,验证了旋转梁动力特性仿真精度。
| 表 3 不同转速下无量纲频率前三阶的结果对比 Table 3 Comparison of the results of the first three orders of dimensionless frequencies at different speeds |
梁模型的空间位置如图4所示,设置弹性模量
如图7~9所示,z方向模态振型从静止时的第3阶振型,变为了图8中转速为10 r/min的第2、6阶振型以及图9中转速为100 r/min的第2、4、6阶振型。随着转速的增加,前6阶中垂直于旋转平面(z方向)的振型所对应的频率会逐渐转换为低阶频率。

|
图 7 静止时前六阶振型 Figure 7 The first six modes at rest |

|
图 8 10 r/min前六阶振型 Figure 8 The first six modes at 10 r/min |

|
图 9 100 r/min时前六阶振型 Figure 9 The first six modes at 100 r/min |
图10中,转速为140 r/min,y方向出现了3阶的振型,z方向出现了2阶振型,第6阶为扭转振型;图11中,转速为300 r/min,y方向出现了2阶的振型,z方向出现了2阶,第4阶为扭转振型,第6阶为拉伸振型。从此可见,随着转速的增加,扭转和拉伸模态振型所对应的频率会逐渐转换为低阶频率。

|
图 10 140 r/min时前六阶振型 Figure 10 The first six modes at 140 r/min |

|
图 11 300 r/min时前六阶振型 Figure 11 The first six modes at 300 r/min |
本文在绝对节点坐标法基础上,运用连续介质理论推导了三维柔性梁的动力学方程,并对不同文献中的单摆案例进行了仿真,验证了本文方法的有效性。然后对动力学方程进行了线性化处理,计算了不同转速下柔性旋转梁的无量纲固有频率,并分析了非线性柔性旋转梁在不同转速下的模态振型变化特性。通过三维柔性梁动力学建模与动力特性的研究可得到以下结论。(1) 本文所建非线性梁模型能精确分析三维柔性梁的时域动力学响应;(2) 带浮动坐标的绝对节点坐标建模方法,能有效分析柔性旋转柔性梁的频域振动特性;(3) 三维柔性旋转梁随着转速的增加出现动力刚化现象,且垂直旋转平面的模态振型以及扭转和拉伸模态振型所对应的频率会转化为低阶频率。
| [1] |
王红州, 蔡恒欲, 任桐欣, 等. 直升机旋翼动力学优化浅析[J].
兵器装备工程学报, 2018, 39(1): 25-28.
WANG H Z, CAI H Y, REN T X, et al. Analysis of helicopter rotor dynamic optimization[J]. Journal of Ordnance Equipment Engineering, 2018, 39(1): 25-28. DOI: 10.11809/bqzbgcxb2018.01.006. |
| [2] |
黄俊东, 夏鸿建, 李德源, 等. 大型风力机柔性叶片非线性气弹模态分析[J].
机械工程学报, 2020, 56(14): 180-187.
HUANG J D, XIA H J, LI D Y, et al. Nonlinear aeroelastic modal analysis of large wind turbine flexible blades[J]. Journal of Mechanical Engineering, 2020, 56(14): 180-187. DOI: 10.3901/JME.2020.14.180. |
| [3] |
REN H. A simple absolute nodal coordinate formulation for thin beams with large deformations and large rotations[J]. Journal of Computational and Nonlinear Dynamics, 2015, 10(6): 061005.
|
| [4] |
AHMED A S. Computer implementation of the absolute nodal coordinate formulation for flexible multibody dynamics[J].
Nonlinear Dynamics, 1998, 16(3): 293-306.
DOI: 10.1023/A:1008072517368. |
| [5] |
ZHANG X S, ZHAGN D G, CHEN S J, et al. Modal characteristics of a rotating flexible beam with a concentrated mass based on the absolute nodal coordinate formulation[J].
Nonlinear Dynamics, 2017, 88(1): 61-77.
DOI: 10.1007/s11071-016-3230-2. |
| [6] |
CHEN Y Z, ZHANG D G, LI L. Dynamic analysis of rotating curved beams by using absolute nodal coordinate formulation based on radial point interpolation method[J].
Journal of Sound and Vibration, 2019, 441: 63-83.
DOI: 10.1016/j.jsv.2018.10.011. |
| [7] |
郑彤, 章定国, 洪嘉振. 三维大变形梁系统的动力学建模与仿真[J].
机械工程学报, 2016, 52(19): 81-87.
ZHENG T, ZHANG D G, HONG J Z. Dynamic modeling and simulation for three dimensional flexible beam systems with large deformations[J]. Journal of Mechanical Engineering, 2016, 52(19): 81-87. DOI: 10.3901/JME.2016.19.081. |
| [8] |
赵春璋, 余海东, 王皓, 等. 基于绝对节点坐标法的变截面梁动力学建模与运动变形分析[J].
机械工程学报, 2014, 50(17): 38-45.
ZHAO C Z, YU H D, WANG H, et al. Dynamic modeling and kinematic behavior of variable crosssection beam based on the absolute nodal coordinate formulation[J]. Journal of Mechanical Engineering, 2014, 50(17): 38-45. DOI: 10.3901/JME.2014.17.038. |
| [9] |
章孝顺, 章定国, 陈思佳, 等. 基于绝对节点坐标法的大变形柔性梁几种动力学模型研究[J].
物理学报, 2016, 65(9): 148-157.
ZHANG X S, ZHANG D G, CHEN S J, et al. Several dynamic models of a large deformation flexiblebeam based on the absolute nodal coordinate formulation[J]. Acta Physical Sinica, 2016, 65(9): 148-157. |
| [10] |
陈渊钊, 章定国, 黎亮. 平面细长梁基于无网格径向基点插值的绝对节点坐标法[J].
振动工程学报, 2018, 31(2): 245-254.
CHEN Y Z, ZHANG D G, LI L. An absolute nodal coordinate formulation based on radial point interpolation method for planar slender beams[J]. Journal of Vibration Engineering, 2018, 31(2): 245-254. |
| [11] |
马超. 绝对节点坐标列式单元动力学建模方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2017.
|
| [12] |
李永亮. 基于绝对节点坐标法的柔性梁动力学建模与分析[D]. 西安: 西安电子科技大学, 2014.
|
| [13] |
姚震, 余海东, 王皓. 基于绝对节点坐标法的柔性梁结构动态特性参数灵敏度分析[J].
机械设计与研究, 2018, 34(3): 30-34.
YAO Z, YU H D, WANG H. Sensitivity analysis of dynamic parameters of flexible beams based on absolute nodal coordinate formulation[J]. Machine Design & Research, 2018, 34(3): 30-34. |
| [14] |
李全乐, 赵春花. 基于绝对节点坐标法的高次插值梁单元建模[J].
上海工程技术大学学报, 2018, 32(4): 329-333.
LI Q L, ZHAO C H. Higher-order interpolation beam element models based on absolute node coordinate formulation[J]. Journal of Shanghai University of Engineering Science, 2018, 32(4): 329-333. DOI: 10.3969/j.issn.1009-444X.2018.04.008. |
| [15] |
田强. 基于绝对节点坐标方法的柔性多体系统动力学研究与应用[D]. 武汉: 华中科技大学, 2009.
|
| [16] |
黎明安. Matlab/Simulink动力学系统建模与仿真[M] . 北京: 国防工业出版社, 2012.
|
| [17] |
MAQUEDA L G, BAUCHAU O A, SHABANA A A. Effect of the centrifugal forces on the finite element eigenvalue solution of a rotating blade: a comparative study[J].
Multibody System Dynamics, 2008, 19(3): 281-302.
DOI: 10.1007/s11044-007-9070-6. |
| [18] |
REFAATY Y, AHMED A S. Three dimensional absolute nodal coordinate formulation for beam elements: implementation and Applications[J]. Journal of Mechanical Design, 2001, 123(4): 614-621.
|
| [19] |
MARCELLO B, AHMED A S. Study of the centrifugal stiffening effect using the finite element absolute nodal coordinate formulation[J].
Multibody System Dynamics, 2002, 7(4): 357-387.
DOI: 10.1023/A:1015567829908. |
 2022, Vol. 39
2022, Vol. 39

