营销效果的量化评估是营销过程中的重要环节之一。准确的量化评估能为后续营销方案优化、营销费用分配等方面提供重要参考依据，有助于提升企业的运营效率。其以市场营销为背景，以人工智能等为技术吸引了多个学科的学者进行研究，是具有重要研究价值的多学科交叉问题^[1-2]。营销效果评估由于其应用驱动性质，具有复杂多样性，需根据问题特性设计，本文主要从人工智能算法设计的角度进行研究。

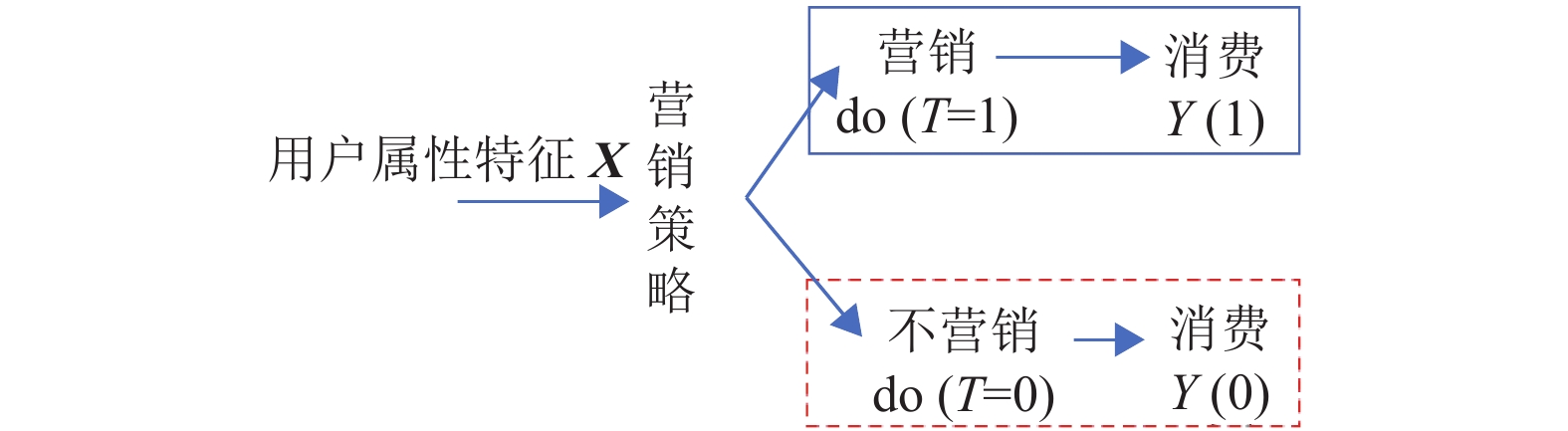
图1是一个典型的营销效果评估过程图。在一个营销系统里，系统先依据用户的属性特征X确定营销对象(如广告曝光、产品推送对象)，再对营销后的消费提升进行定量评估。现实场景中，若营销系统对用户进行了营销(图1中蓝色分支)，则用户在未营销时的情况是未知的(图1中红色分支)，即无法同时观测到用户的两种状态值，这也是营销效果评估的难点。针对这一难点，解决的思路是从未营销的对照组用户中选择与营销组用户属性特征相似的对照样本，用于推断营销组用户在假设未被营销时的“反事实”^[3]状态值。因此，营销效果的量化评估问题本质上是基于“反事实”进行因果效应估计^[4]。

上述因果效应估计问题的解决方法主要包括3类：基于随机干预实验的方法、基于辅助变量的方法和基于因果效应的方法^[5]。其中，基于随机干预实验的方法是解决这类问题的基准方法，其使用随机分组的方式，随机地将研究对象分配至营销组或对照组，可以剔除其他因素的影响，如好友、价格等影响^[6]。典型的随机干预方法有A/B测试^[7-8]，其易于理解，但有时随机实验代价巨大，甚至造成负面的用户体验^[7,9]。不同于随机干预实验，后两类方法则从观察数据出发对因果效应进行估计。其中，基于辅助变量的方法一般需结合场景先验知识对潜在的混杂因子进行建模^[10]，如基于深度学习和工具变量实现建模的DeepIV^[11]，基于变分贝叶斯和隐变量的CEVAE^[12]。在缺乏足够的先验知识场景下，基于因果效应的方法则更为适用，典型思想包括倾向得分逆概率加权(Inverse Probability Weighted Estimator，IPWE)^[4,13]、混杂因子平衡(Confounder Balancing)的方法^[14-15]及基于深度学习和其他方面的扩展^[16-18]。基于因果效应的方法，本质上都需要根据用户的属性特征判断用户进入营销组或对照组的倾向性。

然而，现有的因果效应评估方法主要是基于群体的平均因果效应评估^[16-17,19]，对于实际应用中需要细化评估用户个体的因果效应需求难以进行有效支撑。将现有基于群体的平均因果效应评估方法推广到细粒度用户个体的因果效应评估时，面临着用户属性特征建模难的问题。核心的原因是现有方法多是针对低维样本特征、小观察样本的场景设计^[19](即观察的对照样本量较小)，难以适用于实际营销场景中复杂的用户属性特征、海量的对照组样本。具体包括以下3方面：(1) 实际营销场景中，用户一般包括许多的时序特征，如用户在过去某段时间内的消费序列等，其可能比静态属性特征更能刻画用户。现有的因果效应评估方法虽然已留意到特征表示学习^[20-21]，但用户时序特征的描述问题还有待解决。(2) 实际营销场景中，用户属性特征往往高维且呈现非线性关系。传统的基于线性回归的方法较难有效地学习样本权重，容易存在过拟合问题^[16-17]，虽然部分研究考虑了非线性用户特征的加权问题，但多是针对分组等特定场景而设计。(3) 实际营销场景中，存在大量的对照组样本，若直接使用样本权重估计的方法，因需要学习的样本权重维度高，容易导致结果不稳定、算法不收敛^[14]等问题。

针对实际营销中，用户存在时序非时序属性特征混合、海量对照组样本的现状，本文结合深度学习的建模方法和因果推断的思想，提出了以用户为单位的细粒度混杂平衡的营销效果评估方法。主要贡献包括：(1) 引入深度学习中的长短记忆神经网络对用户的时序特征进行建模，并使用稀疏多层神经网络从用户的时序和非时序属性特征中学习样本统一表示；(2) 引入K近邻方法确定营销组用户的对照组样本，即为每个营销组样本挑选最为相近的对照组用户，避免了样本引入的干扰，从而实现了以用户为单位的细粒度营销效果评估。

1 问题定义

本文以合作公司的线上会员营销为研究背景，研究目标是定量评估营销的效果，包括用户成为会员后一定时期内在平台内的消费提升程度。典型的营销场景包括在线游戏特权卡营销、电商的会员卡营销等。

在本文中，符号定义如下：

$ \boldsymbol{X} $ 表示用户属性特征。实际营销中，用户属性 $ {\boldsymbol{X}}_{i} $ 包括2类：(1) 时序属性 $ {\boldsymbol{X}}_{i}^{{\rm{S}}} $ ，如随时间变化的消费序列、在网时长序列等；(2) 静态属性 $ {\boldsymbol{X}}_{i}^{{\rm{C}}} $ ，如一段时间内不会变化的用户性别、年龄等，这两类特征共同构成了营销效果评估的混杂因子。 $ T $ 表示营销行为,共包括两种营销状态，即被营销和不被营销， $ {T}_{i}\in \left\{\mathrm{0,1}\right\} $ ， $ {T}_{i}=1 $ 和 $ {T}_{i}=0 $ 分别表示用户属于营销组和属于对照组。 $ Y $ 表示用户消费， $ {Y}_{i}\left(1\right) $ 和 $ {Y}_{i}\left(0\right) $ 分别表示用户 $ i $ 在同一时间内被营销和不被营销状态下的消费。三元组 $ ({\boldsymbol{X}}_{i},{T}_{i},{Y}_{i}) $ 表示一个观察样本。

在上述定义下，营销效果评估实际为估计干预样本的平均因果效应 $({\rm{ATT, \;Average \; Causal \; Treatment }}$ ${\rm{on \; the \; Treated}})$ ，如式(1)所示。

$ \mathrm{A}\mathrm{T}\mathrm{T}=\frac{1}{|{{T}}_{i}=1|}\sum\limits _{{T}_{i}=1}\left({Y}_{i}\left(1\right)-{Y}_{i}\left(0\right)\right) $

(1)

即通过对比营销组用户在营销情况下的消费 $ {Y}_{i}\left(1\right) $ 较假设未营销情况下的消费 $ {Y}_{i}\left(0\right) $ 平均提升的程度来评估营销效果。其中，式(1)中的 $ |{{T}}_{i}=1| $ 为营销组的样本数。

解决该问题的核心困难是，在实际场景中，只能获取到营销组( $ {T}_{i}=1 $ )用户 $ {U}_{i} $ 在营销状态下的消费 $ {Y}_{i}\left(1\right) $ ，而无法获得假设 $ {U}_{i} $ 不被营销状态下的消费 $ {Y}_{i}\left(0\right) $ ，这本质上是一个反事实的推断问题。若不借用外部信息，该问题无解。而实际情况中，可以以用户的属性特征信息 $ {\boldsymbol{X}}_{i} $ 为桥梁，进行反事实推断。因此，式(1)可以建模为式(2)的条件干预样本平均因果效应 $({\rm{CATT,\;Conditional \; Average \; Causal \; Treatment \; Effect }}$ ${\rm{ on \; the \; Treated)}}。$

$ \mathrm{C}\mathrm{A}\mathrm{T}\mathrm{T}=\frac{1}{|{{T}}_{{i}}=1|}\sum\limits _{{T}_{i}=1}\left({Y}_{i}\left(1\right)-{Y}_{i}\left(0\right)|{\boldsymbol{X}}_{i}\right) $

(2)

综上，营销效果的量化评估问题可形式化定义为：给定一批观察样本 $ ({\boldsymbol{X}}_{i},{T}_{i},{Y}_{i}) $ ， $ i\in [1,n] $ ，其中，用户属性特征 $ {\boldsymbol{X}}_{i} $ 包括时序用户属性 $ {\boldsymbol{X}}_{i}^{{\rm{S}}} $ 和静态用户属性 $ {\boldsymbol{X}}_{i}^{{\rm{C}}} $ ， $ {T}_{i}\in \left\{\mathrm{0,1}\right\} $ 表示用户是否被营销， $ {Y}_{i}\left(0\right) $ 和 $ {Y}_{i}\left(1\right) $ 表示用户不同营销状态下的消费。则营销效果的量化评估可表示为式(2)所示的条件干预样本平均因果效应问题。

2 细粒度混杂平衡营销效果评估

本节提出了基于用户细粒度混杂平衡的营销效果评估方法，主要包括2个方面：细粒度混杂平衡目标设计、混杂权重函数学习。

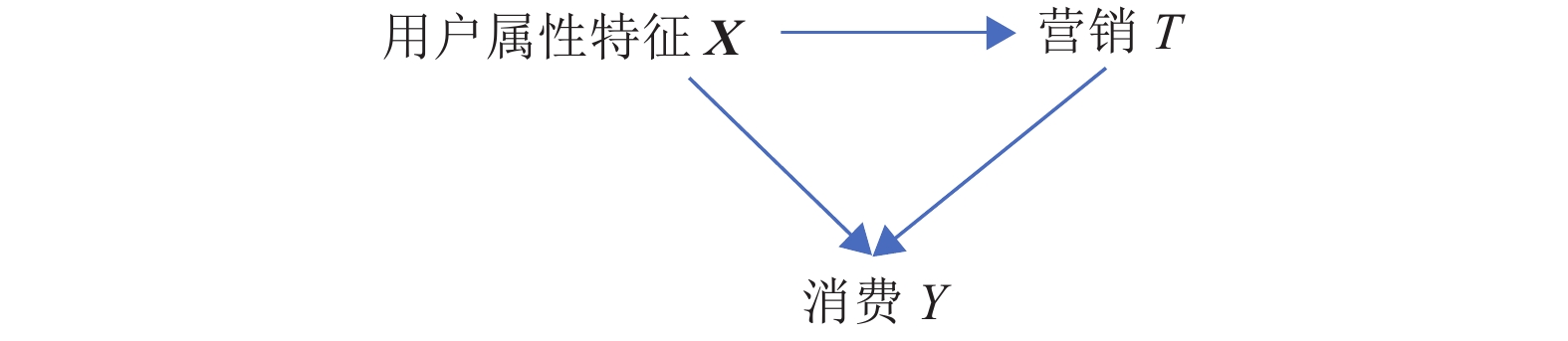
2.1 细粒度混杂平衡目标设计

对营销数据进行因果机制建模是解决式(2)中条件干预样本平均因果效应评估的核心。从图1所示的营销过程图可知，用户属性特征 $ \boldsymbol{X} $ 是用户是否被营销( $ T $ )和用户营销后消费( $ Y $ )的共同原因，即 $ \boldsymbol{X} $ 为混杂因子。因此基于以上信息，可确定营销过程中用户属性、营销情况和营销后消费之间的因果图如图2所示。

在实际中，一般很难直接采用图2的因果图建模，因为用户属性特征 $ \boldsymbol{X} $ 可能包括了大量无关冗余信息。为了消除混杂效应，目前主流的思路是使用倾向值评分匹配和混杂平衡等方法解决。直观思路是从对照组用户中为每一个营销组用户(即 $ {T}_{i}=1 $ 的用户)筛选出满足条件 $ {T}_{j}=0 $ ， $ {\boldsymbol{X}}_{j}={\boldsymbol{X}}_{i} $ 的用户作为参照对象。则式(2)可转化为式(3)进行评估。

$ \mathrm{C}\mathrm{A}\mathrm{T}\mathrm{T}=\frac{1}{|{{T}}_{{i}}=1|}\sum\limits _{{T}_{i}=1,{{T}_{j}=0,\boldsymbol{X}}_{j}={\boldsymbol{X}}_{i}}\left({Y}_{i}\left(1\right)-{Y}_{j}\left(0\right)|{\boldsymbol{X}}_{i}\right) $

(3)

然而，实际场景中一般很难找到与 $ {\boldsymbol{X}}_{i} $ 属性特征完全相同的样本，即很难找到满足条件 $ {T}_{j}=0, \boldsymbol{X}_{j}= $ ${\boldsymbol{X}}_{i} $ 的对照组样本。因此，解决混杂因子的核心问题转化为如何基于观察样本的属性特征对样本进行加权，进而使得营销组和对照组之间的混杂变量分布平衡，并将营销效果评估转化为式(4)所示。

$ \mathrm{C}\mathrm{A}\mathrm{T}\mathrm{T}=\frac{1}{|{{T}}_{{i}}=1|}\sum\limits _{{T}_{i}=1}\left({Y}_{i}\left(1\right)-\sum\nolimits _{{T}_{j}=0}W\left({\boldsymbol{X}}_{j}\right){Y}_{j}\left(0\right)|{\boldsymbol{X}}_{i}\right) $

$ {\rm{s.t.}} \left\{\begin{array}{c}d\left({\boldsymbol{X}}_{i},{\boldsymbol{X}}^{\prime}\right)=0\\ {\boldsymbol{X}}^{\prime}= \displaystyle \sum\limits _{{T}_{j}=0}W\left({\boldsymbol{X}}_{j}\right){\boldsymbol{X}}_{j}\end{array}\right. \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$

(4)

式中： $ {Y}_{i}\left(1\right) $ 为营销组样本的消费， $ \displaystyle \sum\nolimits _{{T}_{j}=0}W\left({\boldsymbol{X}}_{j}\right){Y}_{j}\left(0\right) $ 是以对照组样本为基础进行线性加权得到的伪对照样本的消费。实现式(4)评估的关键是如何对用户属性特征( $ \boldsymbol{X} $ )进行有效建模并获取权重函数 $ W\left(\boldsymbol{X}\right) $ 。通过样本加权的方式对营销组( $ T=1 $ )和对照组( $ T=0 $ )间的混杂变量分布进行平衡。其中 $ W\left(\boldsymbol{X}\right) $ 为用户属性特征( $ \boldsymbol{X} $ )的函数,优化目标是使得混杂因子在营销组和对照组之间的分布平衡，可以通过优化式(5)进行目标求解。

$ \mathrm{arg} \, {{{\rm{min}}}} _W\sum\limits _{{T}_{i}=1}d\left({\boldsymbol{X}}_{i},\sum\limits _{{T}_{j}=0,{\boldsymbol{X}}_{j}\in {\rm{KNN}}\left({\boldsymbol{X}}_{i}\right)}W\left({\boldsymbol{X}}_{j}\right){\boldsymbol{X}}_{j}\right) $

(5)

式中： $ {d}(\mathrm{ },\mathrm{ }) $ 为距离度量函数， $ \mathrm{K}\mathrm{N}\mathrm{N}\left({\boldsymbol{X}}_{i}\right) $ 为 $ {\boldsymbol{X}}_{i} $ 的K近邻样本集合(K-Nearest Neighbor)。该目标函数以 $ {\boldsymbol{X}}_{i} $ 在对照组中挑选出的K近邻样本为基础，学习属性特征的权重函数，再以线性加权的方式逼近对照组的分布。

相比于传统方法，该目标函数结合了倾向值倒数加权和混杂变量平衡的思想。而且通过引入K近邻对照样本，实现了细粒度匹配，避免了干扰样本的引入，一定程度保证了大样本数据学习的稳定性。

2.2 混杂权重函数学习

求解式(5)中 $ W\left(\boldsymbol{X}\right) $ 的目标函数时需先解决以下2个问题：(1) 如何对用户属性特征( $ \boldsymbol{X} $ )设计合理的距离度量函数以确定 $ \mathrm{K}\mathrm{N}\mathrm{N}\left({\boldsymbol{X}}_{i}\right) $ ；(2) 如何基于用户属性特征( $ \boldsymbol{X} $ )构建合适的权重函数 $ W\left(\boldsymbol{X}\right) $ 表示方法。

在设计距离度量函数方面，针对时序特征和非时序属性特征混合的场景，先单独按属性类型计算K近邻，最后再取交集确定 $ \mathrm{K}\mathrm{N}\mathrm{N}\left({\boldsymbol{X}}_{i}\right) $ 。具体地，针对时序特征和静态属性特征数据，分别采取动态时间归整(Dynamic Time Warping，DTW)和欧氏距离进行度量。令 $ \mathrm{K}\mathrm{N}{\mathrm{N}}_{\mathrm{S}}\left({\boldsymbol{X}}_{i}\right) $ 表示时序特征数据的K近邻， $ \mathrm{K}\mathrm{N}{\mathrm{N}}_{\mathrm{C}} \left({\boldsymbol{X}}_{i}\right) $ 表示静态属性特征数据的K近邻，则 $ \mathrm{K}\mathrm{N}\mathrm{N} \left({\boldsymbol{X}}_{i}\right)= $ $ \mathrm{K}\mathrm{N}{\mathrm{N}}_{\mathrm{S}}\left({\boldsymbol{X}}_{i}\right)\cap \mathrm{K}\mathrm{N}{\mathrm{N}}_{\mathrm{C}}\left({\boldsymbol{X}}_{i}\right) $ 。通过取交集的方式确定K近邻，有效避免了DTW序列距离和属性距离之间不同测度距离的融合问题。需说明的是，在K近邻确定过程中，只需要考虑为每个营销组用户选择合适的对照对象，而不必考虑对照组用户是否被选择。

在构建权重函数表示方面，确定 $ \mathrm{K}\mathrm{N}\mathrm{N}\left({\boldsymbol{X}}_{i}\right) $ 后，利用深度学习表达方面的优势。首先，对时序数据使用标准的长短记忆神经网络(Long-Short Term Memory, LSTM)^[22]进行建模；然后，对时序数据和非时序数据使用稀疏多层神经感知网络进行统一学习，以获得样本的相对重要性评分；最后，对所有K近邻的样本重要性评分进行归一化，得到最终样本权重。这种设计方式，解决了传统的逻辑回归分析不能应用于时序特征和非时序特征混合场景的不足性，借鉴了倾向性得分思想，实现了普适场景下的统一权重学习。

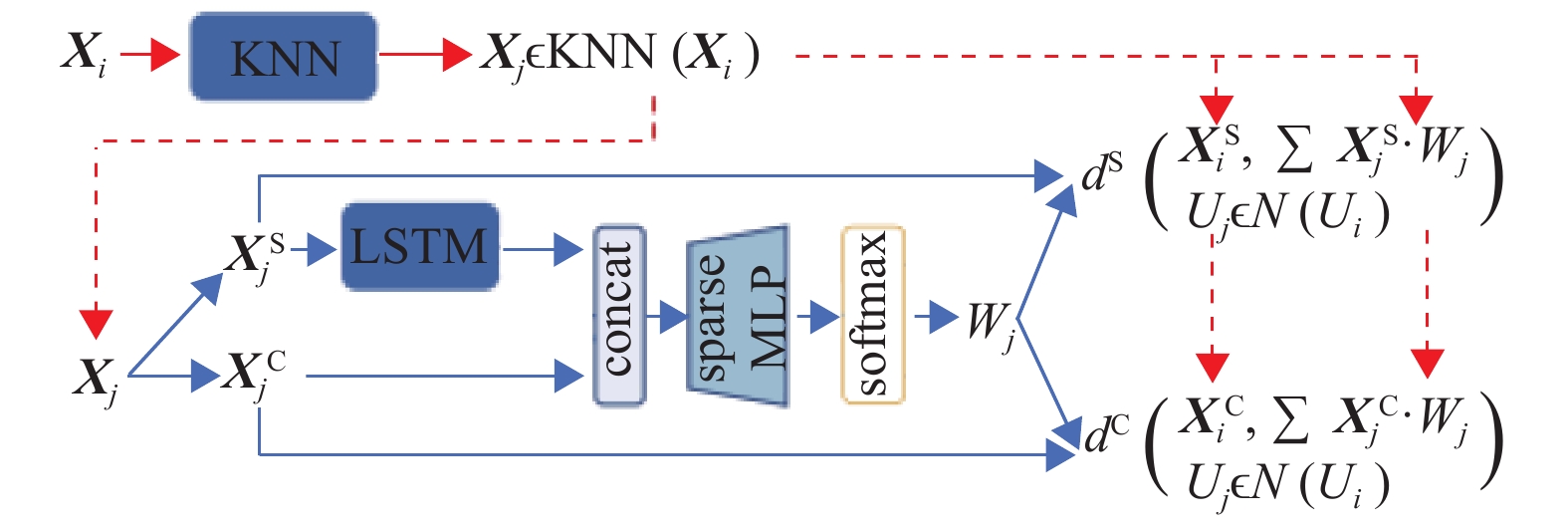
具体流程如图3所示，主要包含以下3个步骤：

(1) 为每个营销组用户 $ {\boldsymbol{X}}_{i} $ 确定 $ \mathrm{K}\mathrm{N}\mathrm{N}\left({\boldsymbol{X}}_{i}\right) $ ，即挑选 ${K} $ 个与 $ {\boldsymbol{X}}_{i} $ 距离最近的对照组样本。挑选出的这部分样本集将用于后续的权重网络训练和因果效应评估(如图3红色虚线部分)。

(2) 针对 $ < {\boldsymbol{X}}_{i},\mathrm{K}\mathrm{N}\mathrm{N}\left({\boldsymbol{X}}_{i}\right) > $ ，目标损失函数的计算如下：首先，针对对照组 $ {\boldsymbol{X}}_{j} $ 的时序特征 $ {\boldsymbol{X}}_{j}^{{\rm{S}}} $ ，使用LSTM进行表示学习，并取最后一个隐状态作为时序特征的表示；然后，将上述时序特征与静态属性特征 $ {\boldsymbol{X}}_{j}^{{\rm{C}}} $ 进行拼接；最后，为选择有用特征，保证模型稳定性，使用稀疏多层神经网络对拼接后的特征进行压缩，将压缩后的特征通过softmax层计算并输出权重。

(3) 上一步骤计算得到的权重，最后通过时序特征及属性特征上的分布对齐作为标准进行评估。上述步骤中时序特征 $ {\boldsymbol{X}}_{j}^{{\rm{S}}} $ 经过LSTM后成功变换到了向量空间，使得后续可以同时采取时序特征和静态特征进行权重计算。但是，最终的评估是在原始的时序特征及静态特征空间，这种设计方式保证了最后的样本权重评估不会被权重学习影响，使算法的稳定性有了保证。

令 $ {\mathrm{\phi }}_{{l}} $ 和 $ {\mathrm{\phi }}_{{m}} $ 分别表示上述LSTM和稀疏多层神经网络，则式(5)可总结为式(6)。

$ \begin{split} & \mathrm{arg} \, \underset{{\phi }_{m},{\phi }_{l}}{{{\rm{min}}}} \, {d}^{{\rm{S}}}\left({\boldsymbol{X}}_{i},\sum\limits _{{\boldsymbol{X}}_{j}\in {\rm{KNN}}({\boldsymbol{X}}_{i})}{\boldsymbol{X}}_{j}^{{\rm{S}}} \cdot {\phi }_{m}({\phi }_{l}({\boldsymbol{X}}_{j}^{{\rm{S}}});{\boldsymbol{X}}_{j}^{{\rm{C}}})\right)+ \\ &{d}^{{\rm{C}}}\left({\boldsymbol{X}}_{i},\sum\limits _{{\boldsymbol{X}}_{j}\in {\rm{KNN}}\left({\boldsymbol{X}}_{i}\right)}{\boldsymbol{X}}_{j}^{{\rm{C}}} \cdot {\phi }_{m}({\phi }_{l}({\boldsymbol{X}}_{j}^{{\rm{S}}});{\boldsymbol{X}}_{j}^{{\rm{C}}})\right) \end{split}$

(6)

式中： $ {{d}}^{\mathrm{S}} $ 和 $ {d}^{\mathrm{C}} $ 分别为时序数据和静态属性数据的距离度量函数，此处分别使用DTW和欧氏距离进行度量。

训练过程中，LSTM和稀疏多层神经网络通过式(6)中目标函数的误差反向传播方式进行学习。同时，考虑到式(6)中两个目标函数有不同取值范围，先对两个目标函数单独训练，再以单独训练后的相对损失作为归一化因子归一，最后采取联合微调的方法学习权重网络 $ W\left(\boldsymbol{X}\right) $ 。需要说明的是在K近邻和最后的目标函数训练部分，考虑到两类属性特征的量纲区别，采取了分别计算的方式；但在计算样本权重的时候，为了综合考虑两类属性特征，在两类特征拼接的基础上采用多层神经网络权重调整的方式来实现两类属性的量纲统一。考虑到计算速度，提前使用DTW计算所有样本对之间的距离函数^[23]。

2.3 模型总结

根据前面算法流程的描述，本文提出的FGCB(Fine Grained Confounder Balancing)算法伪代码可总结为算法1所示。

算法1　FGCB算法

输入：观察样本 $ ({\boldsymbol{X}}_{i},{T}_{i},{Y}_{i}) $ ， $ i\in [1,n] $ ，参数K

输出：因果效应CATT

(1) 对每个营销组( $ T= 1 $ )用户 $ {\boldsymbol{X}}_{i} $ ，从对照组( $ T= $ $ 0 $ )中筛选K近邻集合 $ \mathrm{K}\mathrm{N}\mathrm{N}\left({\boldsymbol{X}}_{i}\right) $ 作为对照样本。

(2) 基于 $ \left\langle{{\boldsymbol{X}}_{i}，\mathrm{K}\mathrm{N}\mathrm{N}\left({\boldsymbol{X}}_{i}\right)}\right\rangle $ ，以式(5)为目标，训练样本权重网络 $ W $ 。

(3) 基于训练后的权重网络 $ W $ 、 $ \left\langle{{\boldsymbol{X}}_{i}，{\rm{KNN}}\left({\boldsymbol{X}}_{i}\right)}\right\rangle $ 及其对应的 $ Y $ ，使用式(4)估计CATT。

需注意的是，本算法通过拟合用户权重网络来实现营销组和对照组在属性特征空间( $ \boldsymbol{X} $ )上的分布对齐(算法1的步骤(1)~(2))，然后基于对齐后得到的样本权重计算消费空间 $ Y $ 上的因果效应(算法1的步骤(3))。因此，本算法不区别传统意义上的训练过程及测试过程。

3 实验及分析 3.1 实验设置

实验场景：以合作的某公司线上会员营销和用户实际的消费数据为例，使用文中算法定量评估会员营销对消费的提升程度，最后与实际的A/B测试数据对比，证明评估算法的有效性。考虑到商业秘密，此处不列出公司具体的名称，并对消费数据进行了脱敏处理。在对数据进行了基本的统计分析后，从总体用户中随机抽样1 000个营销组用户，10000个对照组用户。其中，营销组用户定义为在此次营销活动期内被营销过的用户，对照组用户定义为至统计期在此次营销活动中从未被营销过的用户。并选取了以下用户特征用于评估：(1) 用户的时序特征选取了每个用户被营销前60天(以天为单位)的序列数据，包括：日消费额序列、日在网时长序列、日获取积分序列、特别关注的关键行为日参与次数序列；(2) 用户的属性特征包括：性别、地域、年龄、收入水平、教育程度、累计消费金额、累计在网时长、累计营销次数、VIP等级、在网时长偏好等。此外，为了方便后续的处理，对用户属性特征 $ \boldsymbol{X} $ 的每个属性特征进行 $ {N}\left(\mathrm{0,1}\right) $ 标准化处理，消费额则做缩放处理至 $ \left[\mathrm{0,100}\right] $ 元。

性能指标：为评估FGCB算法的性能，基于估计的CATT，本文使用偏差(Bias)和均方根误差(RMSE)进行性能评估，定义如下

$ \mathrm{B}\mathrm{i}\mathrm{a}\mathrm{s}=\left|\frac{1}{K}{\sum }_{k=0}^{K}\left({\rm{CAT}}{{\rm{T}}}_{k}-{\rm{CATT}}\right)\right| $

(7)

$ \mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\frac{1}{K}{\sum }_{k=0}^{K}{\left({\rm{CAT}}{{\rm{T}}}_{k}-{\rm{CATT}}\right)}^{2}} $

(8)

式中： $ \mathrm{C}\mathrm{A}\mathrm{T}{\mathrm{T}}_{{k}} $ 为使用本文算法评估的第 $ k $ 次结果， $ \mathrm{C}\mathrm{A}\mathrm{T}\mathrm{T} $ 为实际值。由于真实场景中，真实数据是未知的，此处CATT值使用真实的A/B测试结果估计。

基准算法：选取了比较经典和比较新的一些研究工作作为对比。其中，由于基准方法均未对时序数据做特殊设计，输入时将时序数据展开为特征向量的形式。基准算法的实验结果均基于原论文的开源实现，AIPW基于R包的官方实现(具体请见：https://www.rdocumentation.org/packages/RCAL/versions/1.0/topics/ate.aipw)，GANITE和SITE基于原论文公布的代码和建议的参数设置(分别见：https://github.com/jsyoon0823/GANITE和 https://github.com/Osier -Yi/SITE)。具体介绍如下：

AIPW^[4]：经典的基于倾向性得分的因果效应评估方法，倾向性得分使用标准逻辑回归进行估计。

GANITE^[17]：一种基于对抗产生式网络进行反事实分布推断的因果效应评估方法。

DCB^[18]：一种对混杂变量区别对待的平衡因子的因果效应评估方法。因未找到官方源码，该方法的实验结果为本文作者对该方法的重现。

SITE^[21]：一种基于深度表示学习的因果效应评估方法。

FGCB(FGCB-C, FGCB-S, FGCB-G)：本文中提出的FGCB方法及其变体。其中，FGCB为标准模型，FGCB-C只包括用户静态属性特征，FGCB-S只包括用户时序特征，FGCB-G使用全对照组，而不使用K近邻。FGCB方法的主要参数是近邻数K，实验中默认值为5。其余参数设置如下：隐藏层数量设置为输入层维度的2倍，稀疏多层神经网设置为3层全连接网络结合Dropout方式实现。其他参数采用3-折交叉验证的方式进行调整。实现均基于Pytorch1.71版本。

3.2 结果及分析

与基准算法的对比分析：结果如表1所示，本文提出的FGCB在RMSE和Bias两项指标的结果都最好，其中RMSE明显优于其他基准方法。与FGCB结果最为接近的是SITE算法，可能的原因是FGCB和SITE都基于细粒度特征表示进行因果效应评估。上述实验结果有效验证了本文提出的局部样本匹配思想和基于细粒度特征建模的有效性。

剔除实验分析：表2为FGCB及其变种算法的实验结果。通过分别剔除序列信息(即只用属性信息的FGCB-C)和剔除属性信息(即只用序列信息的FGCB-S)模型，可以发现剔除信息后的2种模型结果都有所变差，说明用户的时序信息和静态属性信息都对因果效应的评估具有明显作用。表2的数据结果也验证了使用时序数据建模是FGCB算法结果较优的关键。此外，对比FGCB-G和FGCB的结果可以发现，K近邻局部匹配的思想虽然对Bias的降低不明显，但有助于降低RMSE这一项指标。

近邻参数敏感性分析：FGCB算法中，K近邻的参数K是重要参数之一。为了测试算法对于参数K的敏感性，将K取值 $ [\mathrm{1,5},\mathrm{10,20,30},\mathrm{全}\mathrm{局}] $ 所对应的算法性能结果列出如图4所示。随着K取值的增加，Bias先下降然后稳定在某一水平，说明在一定范围内增加近邻数量K可以减少模型偏差；随着K取值的增加，RMSE先下降后上升，K=5时效果较好，K=10时稳定性略有提高。图4结果说明，针对营销组样本筛选对照样本时，只需选择少量样本即可提升算法的稳定性和准确性。此外，增加近邻域后效果开始下降，也侧面说明了邻域方法的有效性。

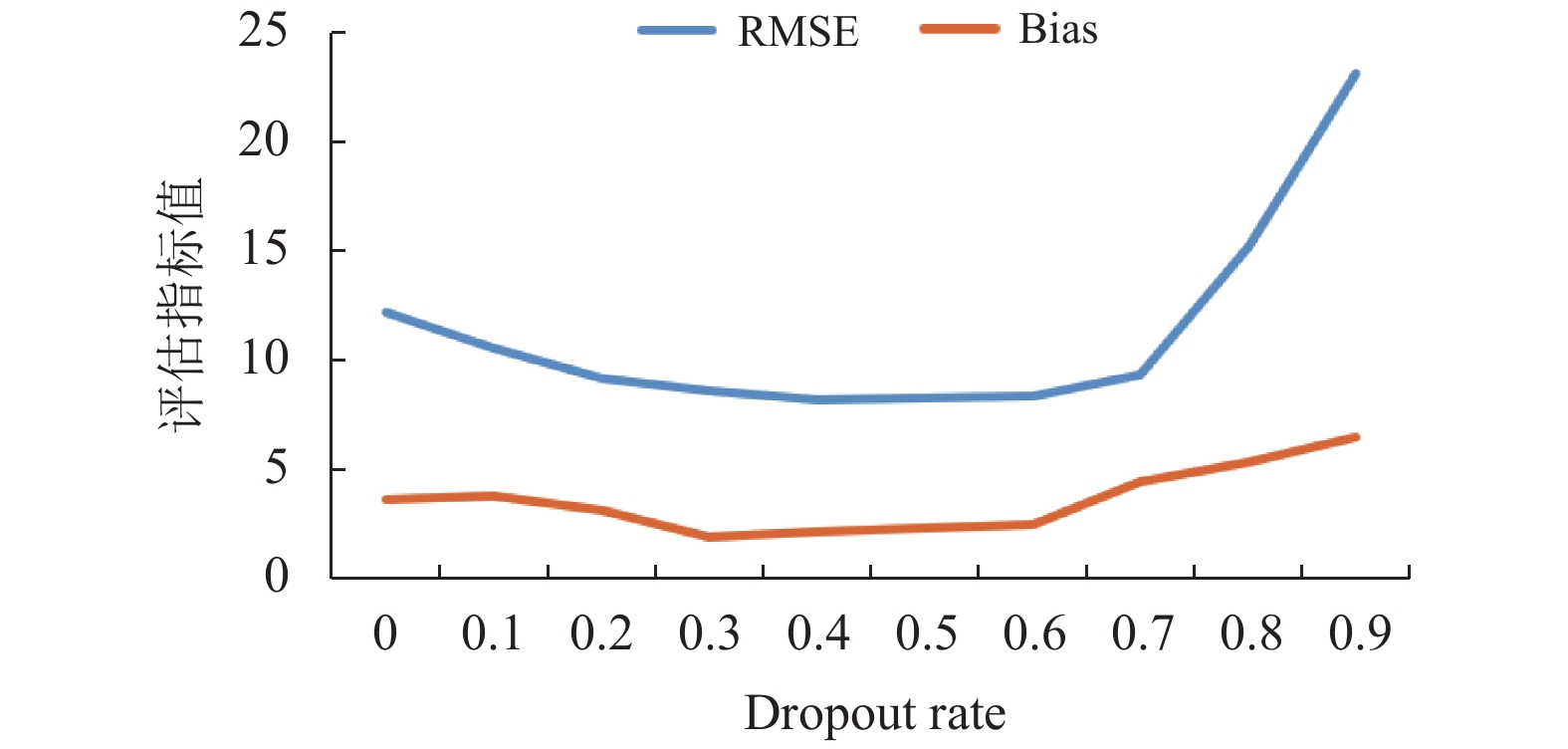
稀疏参数敏感性分析：FGCB算法中，稀疏多层神经网络采取3层全连接网络结合Dropout方式实现，其中剔除率(dropout rate)是稀疏性的重要参数之一。dropout rate对算法性能的影响结果如图5所示。其中，横坐标刻度点为dropout rate值。dropout rate为0.5的时候，模型效果好于全连接网络(dropout rate为0)，说明稀疏策略有效。此外，发现模型性能在最优参数附近对于dropout值不敏感，说明模型在实际应用中的性能得到保证。

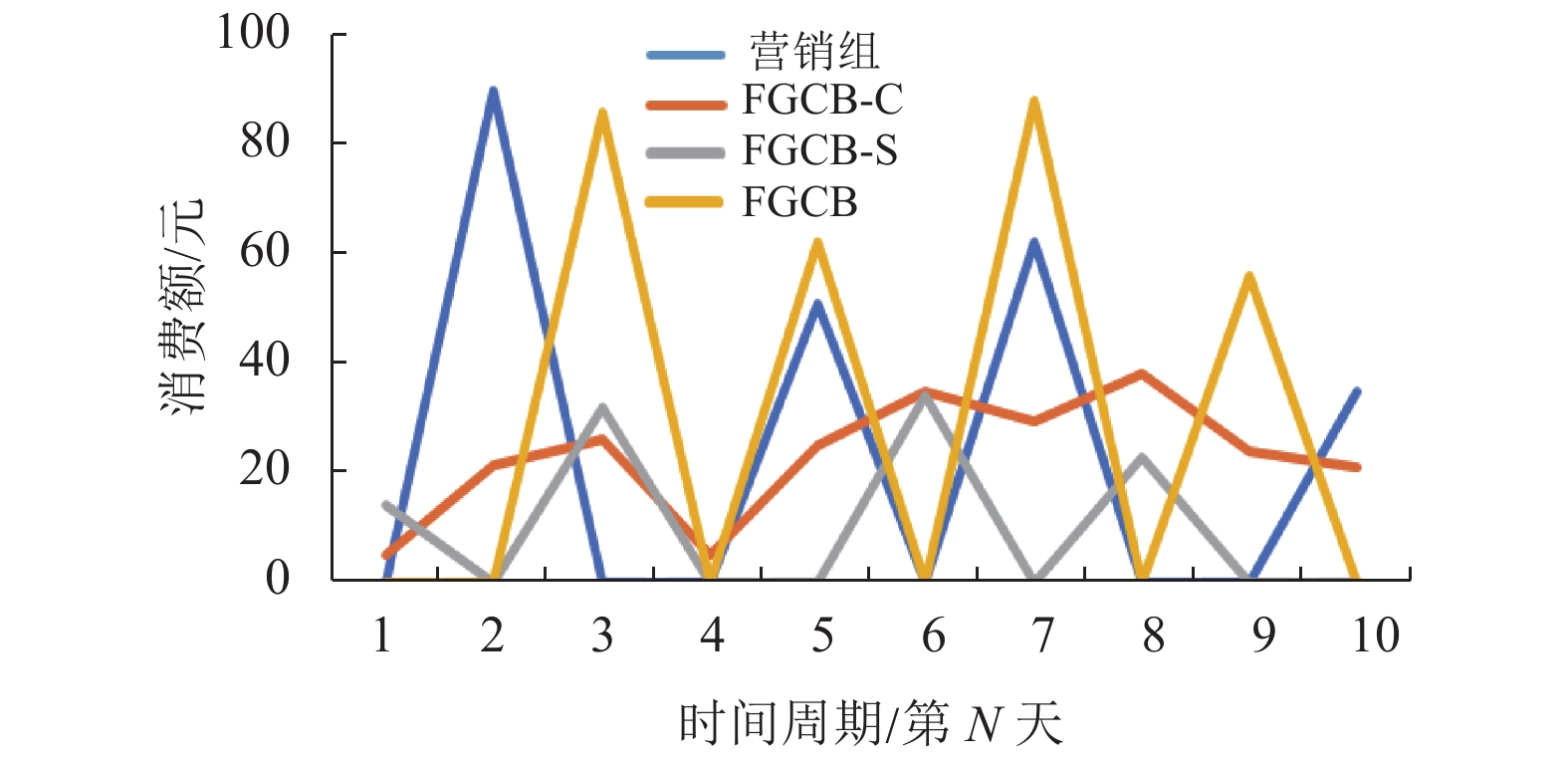
典型案例分析：为了更直观地认识FGCB算法的有效性，选取了几个典型的用户，对FGCB算法及几种变体的结果进行分析。图6为某个营销组用户及其权重最大的近邻用户的消费序列。需说明的是，由于FGCB-G方法在多次实验中结果不稳定，难选择到合适的代表案例，本图未给出FGCB-G的结果。如图6所示，FGCB方法获得的最大权重样本，与营销组样本的周期性和全局性最相似，FGCB-S只使用时序数据，其在筛选对照组样本时，保持了较好的样本周期性特征，而仅使用用户静态属性的FGCB-C则未能很好地刻画周期属性。但是，通过FGCB-S和FGCB的对比分析，发现若忽略了用户静态属性，可能会引入整体的偏差。

4 结束语

本文使用因果效应评估方法对营销效果的量化评估问题进行了建模，针对用户时序非时序特征混合等问题特性提出了细粒度混杂平衡模型，结合了倾向性得分和混杂平衡方法的思想，设计了K近邻选择、时序特征和静态属性分别建模等细粒度策略，实现了稳定的营销效果评估。未来研究包括时序特征对齐和静态特征对齐的优化融合方法、将对抗学习思想引入到样本相似性度量中以进一步提升算法的可靠性等。