2. 广州大学 管理学院,广东 广州 510006;
3. 广州农商银行,广东 广州 510663
2. School of Management, Guangzhou University, Guangzhou 510006, China;
3. Guangzhou Rural Commercial Bank, Guangzhou 510663, China
近年来,我国经济不断由创新驱动发展,正从高速增长向高质量发展转型,科技型中小企业由于在技术创新、获取知识产权与科技成果转化方面存在先天优势,在国民经济中起着越来越重要的作用。科技型中小企业是围绕高校或科研院所,在科学技术新领域取得自主知识产权并实现科技成果向高新技术产品及服务转化的机构[1]。随着我国知识产权规模增大与社会价值总量提升,科技型中小企业在寻求产业政策支持、知识产权资产融资变现、科技成果转化以及扩大企业盈利规模方面的需求日趋明显[2]。从企业融资视角,科技型中小企业虽然科技成果多、知识产权丰富,但受规模小、抵押物不足等条件限制,一般很难达到投贷联动、银行抵押融资及融资租赁的条件[3-4]。在直接融资方式上,由于科技型中小企业发行债券与上市发行股票的门槛较高,科技型中小企业难以争取到发行债券与上市的机会。在间接融资方式上,政策虽鼓励知识产权质押贷款,但商业银行出于风险、成本与不良率控制的要求,一般都要严格履行可接受质押知识产权遴选、贷前尽职调查、出质知识产权条件核实、执行质押贷款担保措施、出质知识产权价值与质押率评估、质押贷款期限确立、贷款合同管理执行、质押登记以及贷后管理等审慎流程[5]。在风险投资与互联网众筹方式上[6],由于知识产权变现周期较长,企业筹资前期的产品及项目一般还尚未成型,难以满足风险投资者的可行性报告与投资建议书等严格的要求。互联网众筹方式则要求项目前期公示与开放,而在此过程中,无形知识产权极容易受到原创复制与侵权,因此很难成为科技型中小企业融资首选。因为科技型中小企业的创新成果转化与产品服务投入效率是企业经营发展的生命线,所以当前融资方式在短期内还不能满足国内大量科技型中小企业对企业盈余以及融资时效、周期、成本的要求。而融资门槛的增加,也限制了科技型中小企业盈利与发展的规模。
知识产权资产证券化集产业政策支持、资产融资与销售、企业盈利于一身,同时又具备企业经营“无形”与“轻量”的特征以及金融工具的收益性、安全性与流动性,是科技型中小企业科技成果转化与企业盈利的重要措施。由于知识产权资产证券化的过程涉及权益价值评估、资产包装销售、向证券市场发行等步骤,且知识产权具有“无形”与“轻量”的特征,加上知识更新迭代与市场需求变化等因素,科技型中小企业在经营中会不断调整无形资产预期收益率。同时,知识产权资产证券化过程中的证券价格极易受外部政策、证券期限、收益率等因素影响,资产价值与收益难以度量,知识产权资产证券化后企业难以开展资产证券化盈余评估。尽管产业政策鼓励开展知识产权资产证券化,但目前科技型中小企业开展业务的门槛仍比较高,开展业务后企业对其业务盈余情况的判断难度也比较大。因此如何利用好知识产权资产证券化以促进资产变现与企业盈利,如何实现企业内外要素良性循环与协同发展,如何在知识产权资产证券化后开展企业盈余判断,已成为新的研究方向。
近年来,学者们也在科技型中小企业融资、知识产权权益评估、知识产权资产证券化与标的资产选择、证券价格影响要素和价格函数确立,以及科技型中小企业盈利与会计盈余等多方面开展研究。在科技型中小企业融资方面,学者们通过可视化与数形分析方法揭示了科技型中小企业融资与科技金融协同演进的规律,研究了科技金融发展与科技型中小企业融资的系统性与关联性。根据金融发展周期理论,结合科技型中小企业成长周期特征及不同时期的融资需求,研究科技型中小企业不同发展阶段的不同融资策略[7]。基于共生理论,从优化共生单元和共生环境的角度提出促进科技型中小企业与金融机构的共生路径[8]。在知识产权评估与资产证券化方面,王炎坤等[9]明确科技成果是科技创造者贡献与能力的认定,而知识产权是权利所有人权益的体现,知识产权通过专有权反映与保护权利所有人的利益。刘伍堂等[10]构建知识产权价值评估指标体系,指出收益额预测、贡献率、收益期限、折现率是知识产权价值评估的影响因素。任丽明等[11]建立了知识产权转让定价模型,将时间、技术、市场、国家政策等因素考虑在知识产权的估价范围内。王磊[12]提出知识产权价值“重置成本法、市场价值法、收益法”的三类评估方法。企业盈余研究方面,通过实证研究和协同学模型,得出中小型科技企业科技成果产业化、金融支持和政府财税支持三者之间呈现出相互螺旋式上升的趋势,提出了科技型中小企业提升盈利的模式。邵永同等[13]研究了知识产权资产证券化过程中资产组合的选择问题,同时提出权重设置的方法。张会洁[14]对盈余管理的动机、手段和方法的相关文献进行了全面梳理。张钰[15]从会计研究的角度说明资产证券化给企业盈余提供了空间与机会,提出了完善资产证券化与盈余管理的措施。陈祥有[16]研究了企业在上市前与上市后盈余的特征,发现企业上市前正向盈余管理程度越大,其上市后经营业绩下降幅度就越大。
上述文献对科技型中小企业融资、知识产权权益评估、资产证券化流程及企业盈余进行全面分析,为业务实践提供了有力指导。但梳理相关文献发现,现有的基于知识产权资产证券化与企业盈利的研究普遍是对产业政策、开展资产证券化业务背景与优势以及存在风险进行探讨,鲜有文献对知识产权资产证券化业务流程进行建模,以及研究函数模型与非线性曲线特征。我国科技型中小企业的知识产权规模大,无形资产多,开展资产证券化后,企业如何从财务会计角度判断自身盈利情况的研究还处于空白,在企业预期收益率变化时盈余变化判断的理论与具有实践指导意义的文献材料尤为缺乏。
本文以科技型中小企业开展资产证券化及业务盈余为研究对象,从理论与实践两方面为科技型中小企业开展知识产权资产证券化提供建议:一是梳理知识产权资产证券化业务流程与证券价格决定要素,将资产负债、收益率、净现值延伸至知识产权资产证券化业务与企业盈余的研究中,明确知识产权资产证券化对科技型中小企业融资与盈利的作用。二是引入金融预期与财务理论以及现金流分析方法,建立资产证券价格函数与业务盈余函数模型,定义函数非线性曲线斜率与弧度,构建知识产权资产证券价格函数曲线的分析方法。三是开展科技型中小企业知识产权资产证券化盈余研究,确定资产证券化后企业的盈余判断条件与盈余判断方法。
1 科技型中小企业知识产权资产证券化的业务模式研究 1.1 知识产权资产证券化流程知识产权资产证券化是科技型中小企业将其拥有的自主创新知识产权或衍生债权资产作为担保,资产经组合、包装、信用评级与信用增强等步骤,发行为市场上可流通证券,借此为企业融资的过程[17]。
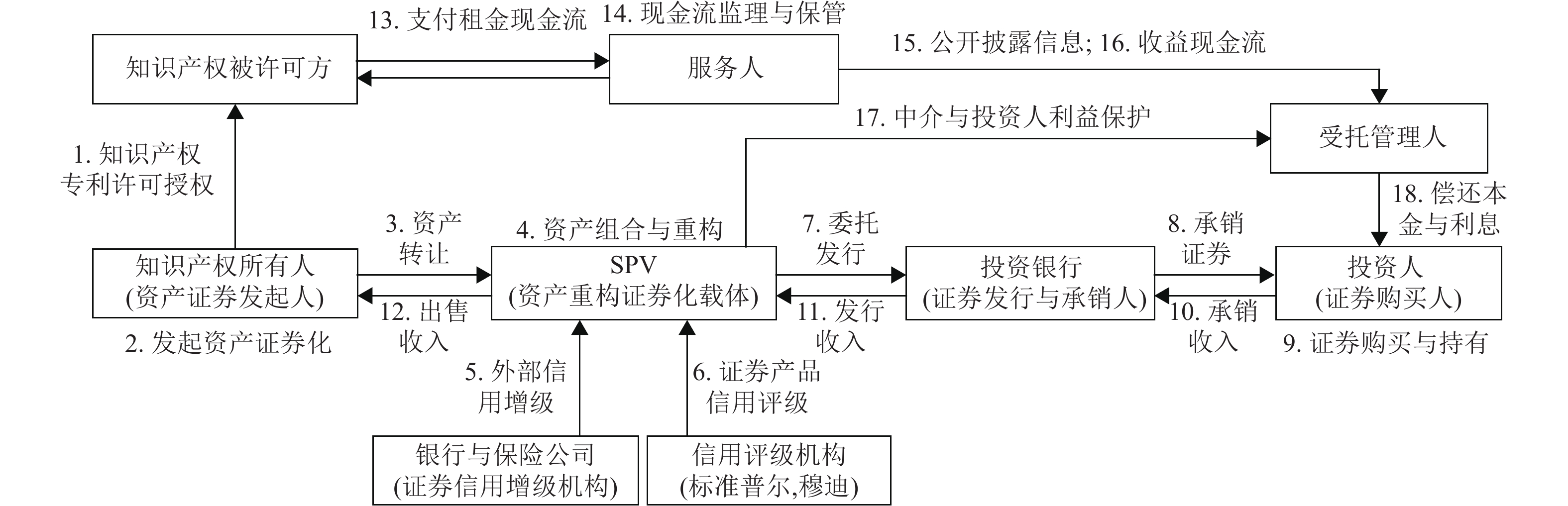
第1步(见图1:1~4):科技型中小企业作为知识产权所有者及业务发起人,将知识产权未来一定期限许可使用收益权销售及转让给资产证券专设机构(Special Purpase Vehicle,SPV),SPV重构组合资产生成收益凭证。第2步(见图1:5):银行或保险公司对收益凭证进行标准化与信用增级,以增加投资者信任。第3步(见图1:6):具备专业与公信力的信用评级机构对收益凭证定义评级,使投资者根据风险偏好投资不同等级的证券。第4步(见图1:7~12):SPV委托投资银行(Investment Bank)作为融资顾问和证券承销商向投资者发行证券,投行将发行收入偿还SPV,SPV将发行收入向科技型中小企业支付知识产权未来许可使用收益权的购买价款。第5步(见图1:13~18):SPV与受托管理人建立受托关系,服务人做现金流监理与保管方,服务人定期收取受益并存入受托管理人(一般为受托银行)账户,服务人向知识产权被许可方收取许可使用费,并将款项存入SPV指定的收款账户,由受托管理人负责管理,受托管理人定期向投资者支付本息[1]。具体流程如图1所示。
|
图 1 知识产权资产证券化过程图 Figure 1 Process diagram of intellectual property asset securitization |
上述业务模式中,科技型中小企业开展知识产权资产证券化的核心在于2个流程:一是第1步,科技型中小企业在知识产权权益价值做了精准评估的基础上,实现知识产权收益权转让;二是第4步,SPV根据知识产权的权益价值评估与资产证券的定义价格,将销售发行所得收入支付给科技型中小企业,科技型中小企业实现融资、资产变现及企业盈利。因此,知识产权资产价值评估与证券价格定义作为资产证券化起点,以及后续证券成功交易与企业盈余的决定因素,成为能否促成交易与实现企业盈余的关键。知识产权作为无形资产,其资产证券化过程易受行业政策、知识更新、市场需求的影响,且知识产权转让授权、资产打包、证券承销与证券化周期的不确定性,也给证券价格定义以及盈余判断带来困难[1]。
1.2 资产证券化与企业盈利关系从公司财务会计角度分析,科技型中小企业实现盈余,是企业持续稳定获取现金与融资,并运用资产来保持与扩大公司经营的过程,公司财务状况与业务盈余情况可用资产负债表与损益表来衡量。其中资产表示企业所有能带来资金流入的有形与无形实物,负债表示企业未来流出的或有资金,所有者权益表示企业资产剔除负债后享有的剩余权益,而公司业务盈余可以用收入减去成本来度量。
较制造业中小企业劳动密集与重资产经营不同,科技型中小企业普遍以高等院校、高新技术、信息技术为研发背景,公司实物资产规模低,有些公司甚至无可变现的实物资产,公司拥有的资产体现为知识成果和脑力劳动,因此在经营上,科技型中小企业更多体现出“轻资产,重无形”的特征[18]。传统科技型中小企业的盈利方式是公司首先通过筹资、融资、贷款等方式取得资金及对应负债,再通过创新与研发产生科技成果,申请注册专利,最后公司再将科技成果转化为生产力、创新产品及服务,同时实现销售而取得收入。但与大中型或制造型企业不同,科技型中小企业实现收益必须依靠产学研结合与科技成果转化,而从科研成果及无形资产到生产销售,再到获取盈利还需要较长的孵化周期,公司追加投入盈利资金并扩大企业规模的效率较低。
知识产权资产证券化是企业将知识产权未来应收账款收益权提前出售,将无形资产提前变现并使用无形资产融资取得资金[19]。新会计准则第 37 号第5条规定:企业发行金融工具,应当按照该金融工具的实质,以及金融资产、金融负债和权益工具的定义,在初始确认时将该金融工具或其组成部分确认为金融资产、金融负债或权益工具。不同于企业知识产权质押贷款以及债券融资与股权融资,知识产权资产证券化不属于负债,而属于资产融资、资产销售以及资产变现过程,知识产权资产证券化可给科技型中小企业带来资金、收入与盈利,因此企业开展资产证券化,将知识产权收益权打包转给具备实施与科技成果转化能力的机构,实现资产提前变现,从而快速投入新的业务生产。知识产权资产证券化促进了企业科技成果快速转化与企业无形资产变现,加快企业盈利。知识产权资产证券化具有改善企业财务状况、提升盈余的综合性作用。
2 资产证券化的盈余模型分析开展知识产权资产证券化后的企业盈余研究,参考新会计准则的规定,如果知识产权资产证券化定义为权益工具与资产销售,那么知识产权资产证券化业务应进行出表处理,此时证券化的资产从资产负债表中剔除,同时证券化收入则计入资产销售收入,而交易成本计入损益。由于盈余表示企业收入款项对于支出款项的预算超过额,并且知识产权资产证券化属于表外业务,为评估企业当期财务与盈余状况,需结合会计权责发生制原则,即应计制及财务损益表“所得=收入−费用”的衡量方法,用企业所有资产和有价证券等现金流入现值与未来各类或有负债、损益等现值流出的差值来判断。其中科技型中小企业现金流入可通过知识产权资产证券化取得资金,也可通过科技成果转化产生,而各类现金流支出可包括企业未来或有负债资金流出和需要向企业所有者支付的所有者权益,以及正常运营费用支出等。根据现金流与净现值的差值来判断,如果现金流净现值差值为正,企业盈利,差值为负,企业亏损。
2.1 知识产权资产证券价格函数目前知识产权资产价值评估主要有3类方法[9]:一是重置成本法,以评估有相同用途与功能的同类资产为参考,以需要重建成本或重新购买相同资产的价值为度量。二是市场价值法,以同期市场统计数据为依据,选取若干与被评估知识产权资产相似的资产交易价格为参考,结合实际市场供求关系进行评估。三是预期收益法,定义资产投资人收益率,将投资人愿意支付价格不超过资产预期产生的回报作为评估依据。
对于重置成本法,由于知识产权作为脑力劳动成果,重新创造成本与创造价值在普遍情况下不能完全对等。对于市场价值法,由于知识产权属于无形资产,评估方法的精准性与主观性、选取参照资产的合理性都可能影响价值评估。因此重置成本法与市场价值法在知识产权定价评估方面还存在不足。预期收益法在评估资产价值方面较为科学与精准,一般在建模与理论研究时采用。因此本文采用预期收益法并结合资产预期收益现金流开展分析。
收益率作为投资收益判断的基本理论参数,被广泛应用在企业资产与证券投资回报的衡量中,资本与项目的收益率高于投资人要求收益率时,资本与项目投入可行。因此借鉴预期收益法,以资产证券价格与收益率的关系作为衡量方法。在指定收益率条件下,对于科技型中小企业持有资产来说,资产证券价格越高,知识产权资产证券化时销售收益越高,对投资人越有利。对负债来说,负债收益率越高外部资金投入收益越多。
科技型中小企业开展知识产权资产证券化后,设资产证券价格函数和负债函数为
| $ {P_A}({R_A}(t),{i_A}(t),n) = \sum\limits_{t = 1}^n {{R_A}(t)} \left( {1 + {i_A}(t)} \right)^{-t} $ | (1) |
式中:
| $ \begin{split} & \mathop {\lim }\limits_{m \to \infty } {P_A}({R_A}(t),{i^{(m)}_A}(t),n) =\\& \mathop {\lim }\limits_{m \to \infty } \sum\limits_{t = 1}^n {{R_A}(t)} {\left( {1 + \frac{{{i^{(m)}_A}(t)}}{m}} \right)^{-mt}} = \sum\limits_{t = 1}^n {{R_A}(t)} {{\text{e}}^{-{\delta _{{A}}}t}} \end{split} $ | (2) |
从函数表达式可以看出,对于企业拥有的无形资产A,如果剔除证券投资人违约等外部行为的影响,资产证券价格函数可由企业对资产证券的收益率
在企业负债端,对于企业负债L,如果证券投资人预期收益率为
| $ {P_L}( {{R_L}(t),{i^{(m)}_L}(t),k} ) = \sum\limits_{t = 1}^k {{R_L}(t)} {( {1 + {i^{(m)}_L}(t)} )^{-t}} = \sum\limits_{t = 1}^k {{R_L}(t)} {{\text{e}}^{-{\delta _L}t}} $ | (3) |
在实际经营中,科技型中小企业一般拥有多个无形知识产权资产对应的多项收入款项,也存在多个负债项目及多个支出款项,假设科技型中小企业全部通过知识产权资产证券化获取资产,定义未来有X项流出资金。为实现企业盈余,科技型中小企业需安排Y项知识产权资产组合开展资产证券化,以实现资金到位,并匹配未来到期负债。因为
因此,以知识产权资产证券价格函数为基础,为进行科技型中小企业资产证券化后的盈余判断,将科技型中小企业的盈余函数定义为
| $ \begin{split} & S({R_L}(t),{R_A}(t),{i^{(m)}_L}(t),{i^{(m)}_A}(t),n,k) =\\& {\rm{P}}{{\rm{V}}_A}({{{R}}_{{A}}}(t),{i^{(m)}_A}(t),n) - {\rm{P}}{{\rm{V}}_L}({R_L}(t),{i^{(m)}_L}(t),k) \end{split} $ | (4) |
为开展盈余函数曲线分析,将资产A复利m次年随时间t变化的收益率
| $ \begin{split} & S(R(t),{i^{(m)}}(t),n,k) = {\rm{P}}{{\rm{V}}_A}(R(t),{i^{(m)}}(t),n) -\\& {\rm{P}}{{\rm{V}}_L}(R(t),{i^{(m)}}(t),k) \end{split} $ | (5) |
如果
上述研究确立了资产证券价格与收益率的关系,在实际中,企业时常对证券价格预期收益率进行调整。由于知识产权资产证券价格函数会随着收益率变化而波动,因此能否找到收益率变化时资产证券价格函数与负债函数的变化规律,建立盈余的判断方法,将有很好的实践指导意义。
2.3.1 定义函数曲线斜率与弧度由于资产证券价格函数与负债函数表达一致,将两者统一设置为P,收益率统一设置为i(m),m为复利年次。先单独对知识产权资产证券价格函数进行推导以建立曲线分析方法。根据导函数的物理意义,一阶导数反映了函数切线斜率的变化速度,二阶导数反映了函数的凹凸性。为研究函数曲线的特征,首先取证券价格函数P对收益率
| $ \begin{split} & {P}^{\prime }({i}^{(m)})\text=\frac{{\rm{\partial}} }{{\rm{\partial}} {i}^{(m)}}{\displaystyle \sum _{t=1}^{n}R(t)}{\left(1+\dfrac{{i}^{(m)}}{m}\right)}^{-mt}= \\& - \frac{1}{\left(1+\dfrac{{i}^{(m)}}{m}\right)}{\displaystyle \sum _{t=1}^{n}tR(t)}{\left(1+\dfrac{{i}^{(m)}}{m}\right)}^{-mt} \end{split}$ | (6) |
| $ {C_{\rm{S}}} = -\frac{{P'({i^{(m)}})}}{{P({i^{(m)}})}} $ | (7) |
式(7)中:
继续变换等式推导,并用
| $ {C}_{{\rm{S}}}\text{=−}\frac{{P}^{\prime }({i}^{(m)})}{P({i}^{(m)})}\text{=−}\frac{1}{P({i}^{(m)})}\cdot\frac{{\rm{d}}P}{{\rm{d}}{i}^{(m)}}\approx \text−\frac{1}{P({i}^{(m)})}\cdot\frac{\Delta P}{\Delta {i}^{(m)}} $ | (8) |
对式(7)变换,得
| $ \Delta P=\frac{\Delta P}{P({i}^{(m)})}\approx \text−\frac{{P}^{\prime }({i}^{(m)})}{P({i}^{(m)})}\Delta {i}^{(m)}\text{=−}{C}_{{\rm{S}}}\Delta {i}^{(m)} $ | (9) |
式中:
进一步研究可知,如果用斜率
因此为减少企业开展资产证券化对应收益的误差,继续寻找更精准的证券价格函数。取知识产权资产证券价格函数对收益率的二阶偏导数。
| $ P''({i^{(m)}}){\text{ = }}\frac{{{\partial ^2}P(R(t),{i^{(m)}},n)}}{{\partial {i^{(m)}}^2}} = \sum\limits_{t = 1}^n {t\left(t + \frac{1}{m}\right)R(t)} {\left( {1 + \frac{{{i^{(m)}}}}{m}} \right)^{-mt - 2}} $ | (10) |
参照
| $ {C_{\rm{R}}} = \frac{{P''({i^{(m)}})}}{{P({i^{(m)}})}} = \frac{1}{{P({i^{(m)}})}}\sum\limits_{t = 1}^n {t\left(t + \frac{1}{m}\right)R(t)} {\left( {1 + \frac{{{i^{(m)}}}}{m}} \right)^{-mt - 2}} $ | (11) |
式中:因为
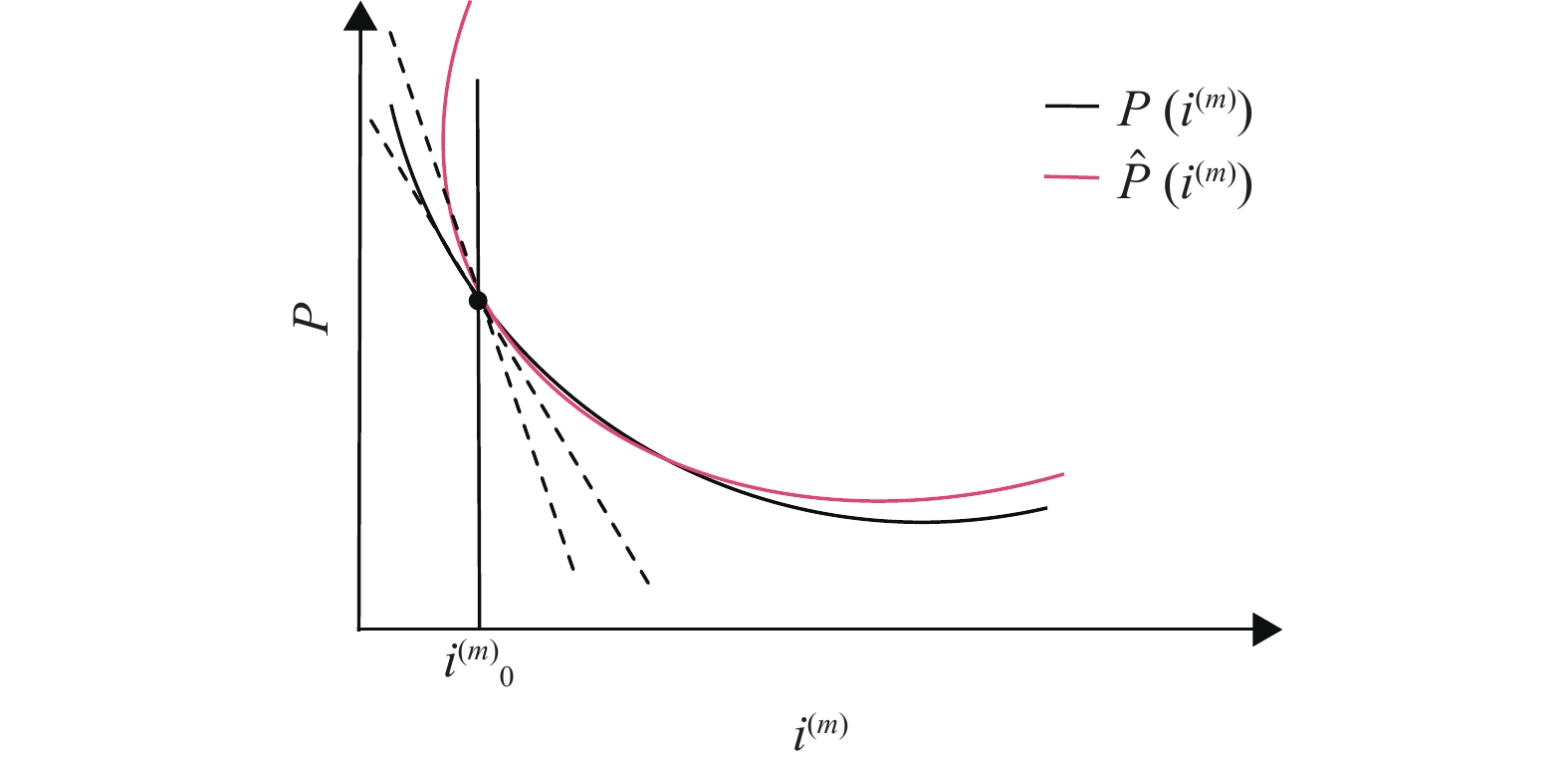
用式(9)计算
|
图 2 知识产权资产证券价格收益率曲线 Figure 2 Yield curve of intellectual property asset securities |
为了更精准地度量指定收益率周围科技型中小企业知识产权资产证券化价格的变化情况,也就是企业资产销售收益情况,进一步对函数表达式进行研究。
指定资产证券化企业预计收益率
| $ P({i}^{(m)})\text=P({i}_{0})\text+{P}^{\prime }({i}_{0})({i}^{(m)}\text−{i}_{0})\text+\frac{1}{2}{P}^{″}({i}_{0})({i}^{(m)}\text−{i}_{0}{)}^{2}\text+o({i}^{(m)}\text−{i}_{0}) $ | (12) |
忽略
| $ \Delta P=\frac{\Delta {i}^{(m)}}{p({i}^{(m)})}\approx \text−{C}_{{\rm{S}}}\Delta {i}^{(m)}\text+\frac{1}{2}{C}_{{\rm{R}}}(\Delta {i}^{(m)}{)}^{2} $ | (13) |
因此在企业某一指定的收益率点
由于知识产权资产价格函数与企业负债函数表达方式一致,企业开展知识产权资产证券化要实现盈利,盈余函数
第一,科技型中小企业开展知识产权资产证券化时,企业所有知识产权资产证券现值应与企业未来应有负债支出的现值相等,以此作为后续企业盈利判断的基础。
第二,企业知识产权资产收益率与外部负债收益率发生变化时,知识产权资产证券价格函数曲线与负债函数曲线应以相同的变化速率与幅度发生变化,知识产权资产证券价格函数曲线斜率
第三,知识产权证券价格函数连续且单调递减,当收益率发生变化时,如资产证券价格函数非线性曲线弧度
上述命题的函数表达为
| $ {\rm{{\rm{P}}}}{{\rm{V}}}_{A}={\rm{P}}{{\rm{V}}}_{L},{C}_{{\rm{S}}\left(A\right)}={C}_{{\rm{S}}\left(L\right)},{C}_{{\rm{R}}\left(A\right)} > {C}_{{\rm{R}}\left(L\right)} $ |
下面给予函数推导并开展命题验证。
第1步,为实现企业盈余,假设科技型中小企业盈余函数为
第2步,为体现曲线斜率变量
| $ \begin{split} & S({R_L}(0),{R_A}(0),{i^{(m)}_L}(0),{i^{(m)}_A}(0),n,k) =\\& {\rm{P}}{{\rm{V}}_A}({R_A}(0),{i^{(m)}_A}(0),n) - {\rm{P}}{{\rm{V}}_L}({R_L}(0),{i^{(m)}_L}(0),k) = 0 \end{split}$ | (14) |
| $ \begin{split} \quad \quad\;{S}^{\prime }({i}^{(m)})= &\frac{\partial S(R(t),{i}^{(m)},n)}{\partial {i}^{(m)}{}}=\frac{\partial {\rm{P}}{{\rm{V}}}_{A}}{\partial x{i}^{(m)}}-\frac{\partial {\rm{P}}{{\rm{V}}}_{L}}{\partial {i}^{(m)}}= \\ &- {C}_{{\rm{S}}\left(A\right)}\cdot {\rm{P}}{{\rm{V}}}_{A}+{C}_{{\rm{S}}\left(L\right)}\cdot {\rm{P}}{{\rm{V}}}_{L}=0 \end{split} $ | (15) |
| $ \begin{split} \quad \quad\;{S}''({i}^{(m)})= &\frac{{\partial }^{2}S(R(t),{i}^{(m)},n)}{\partial {i}^{(m)}{}^{2}}=\frac{{\partial }^{2}{\rm{P}}{{\rm{V}}}_{A}}{\partial {i}^{(m)}{}^{2}}-\frac{{\partial }^{2}{\rm{P}}{{\rm{V}}}_{L}}{\partial {i}^{(m)}{}^{2}}=\\ &{C}_{{\rm{R}}\left(A\right)}\cdot {\rm{P}}{{\rm{V}}}_{A}-{C}_{{\rm{R}}\left(L\right)}\cdot{\rm{}}P{{\rm{}}V}_{L} > 0 \end{split} $ | (16) |
即
| $ S({i^{(m)}}) = 0,\;S'({i^{(m)}}) = 0,\;S''({i^{(m)}}) > 0$ | (17) |
| $\left\{ \begin{array}{l} {\rm{P}}{{\rm{V}}_A}({R_A}(0),{i^{(m)}_A}(0),n) = {\rm{P}}{{\rm{V}}_L}({R_L}(0),{i^{(m)}_L}(0),k) \\ {C}_{{\rm{S}}\left(A\right)}\cdot {\rm{P}}{{\rm{V}}}_{A}= {C}_{{\rm{S}}\left(L\right)}\cdot {\rm{P}}{{\rm{V}}}_{L}\\ {C}_{{\rm{R}}\left(A\right)}\cdot {\rm{P}}{{\rm{V}}}_{A}-{C}_{{\rm{R}}\left(L\right)}{R}_{L}\cdot {\rm{P}}{{\rm{V}}}_{L} > 0 \end{array} \right.$ | (18) |
在假设其他变量不变的情况下,将盈余函数对应收益率变量进行二阶泰勒级数展开,同时忽略高阶无穷小量影响。
| $ S({i^{(m)}} + \Delta {i^{(m)}}) \approx S({i^{(m)}}) + \Delta {i^{(m)}}S'({i^{(m)}}) + \frac{{{{\left( {\Delta {i^{(m)}}} \right)}^2}S''({i^{(m)}})}}{2} > 0 $ | (19) |
那么如果满足组合表达式
因此,如果科技型中小企业开展知识产权资产证券化并定义了收益率预期值、PVA和PVL,可通过计算曲线斜率与相应弧度来判断企业盈余情况。在其他变量不变且收益率不发生随机波动的条件下,只要满足“企业未来资产现金收入与未来负债支出现金现值初始相等,曲线斜率相等,资产证券价格函数的曲线弧度大于负债函数曲线弧度”对应的
另外,可以看出在上述推导及定义函数曲线斜率与弧度的过程中,均在某一收益率值周围度量收益率变化时的资产价格变化或计算盈利函数值。随着期限与时间的变化,实际收益率与资产价格一定发生偏移。因此,在实际研究中对企业开展知识产权资产证券化后的盈余判断需要不断重新测算以确保正确。
3 结语当前,伴随科技型中小企业自主创新能力的提升与维权意识的增强,国内知识产权规模不断扩大,科技型中小企业目前正积极寻求知识产权质押与资产证券化融资以持续扩大企业经营,知识产权资产证券化也越来越受到产业与学术界关注。但是科技型中小企业的轻资产经营特性导致了无形知识产权资产证券化与实物资产证券化不同的特征,特别是知识产权资产的无形性和知识特性,更易受盗版侵权、宏观政策、市场需求偏移等因素的影响,其资产证券化后对应的企业盈余也将受到收益率变化的影响。因此,本文以科技型中小企业开展知识产权资产证券化后的企业盈余判断为研究对象,研究知识产权资产证券价格函数的构成和影响要素,并创新地从函数非线性曲线斜率与弧度入手,研究收益率变化时资产证券价格函数变化的规律,以此总结出基于函数的非线性曲线分析方法,同时构建了科技型中小企业基于收益率的盈余函数,确立企业盈余的判断方法。
首先,梳理科技型中小企业知识产权资产证券化流程,并在前人对科技型中小企业融资、知识产权、企业盈利等理论研究的基础上,确定科技型中小企业开展资产证券化的核心在于无形知识产权权益价值评估,明确知识产权资产证券化具有改善企业财务状况、提升盈余的综合性作用。
其次,结合各类知识产权价值定量评估方法与现金流量法,确定科技型中小企业开展无形知识产权资产证券化后的盈余,可以通过企业未来无形知识资产现金流入现值与未来负债流出资金现值的差值来定义,并基于预期收益法及金融预期理论建立资产证券价格函数表达式与企业盈余函数模型,明确收益现金流贴现值、收益率及证券期限与证券价格、企业盈余之间的关系。建立函数非线性曲线研究方法,通过分析函数的物理特征和计算多阶导函数,证明了知识产权资产证券价格函数单调递减并呈非线性下凹特征,验证了资产证券价格函数曲线弯曲程度越大,知识产权资产证券价格函数收益率越低的特性。
最后,以知识产权资产证券价格函数的研究为基础,提出假设并论证科技型中小企业开展无形资产证券化后实现盈利的判断条件。企业资产证券化后实现盈余,要满足未来资产现金收入与未来负债支出现金现值初始相等、曲线斜率相等、资产证券价格函数曲线弧度应大于负债函数曲线弧度的条件。
综上所述,本文从理论上验证了有关知识产权资产证券化盈余的命题。同时,在梳理科技型中小企业知识产权资产证券化业务流程的基础上,通过资产负债会计分析明确了科技型中小企业无形知识产权资产证券化属于资产融资方式,资产证券化可使科技型中小企业完成无形知识产权的销售。因此,知识产权资产证券化促进了企业科技成果快速转化与企业无形资产变现,加快了企业盈利,具有改善企业财务状况提升盈余的综合性作用。无形知识产权资产证券化后实现盈余的判断方法为高校和科技型中小企业知识产权资产证券化提供了建议。
| [1] |
黄孝武, 任亚奇, 余杰. 宏观经济不确定性与上市公司盈余管理——来自上市公司的经验分析[J].
统计与决策, 2021, 37(1): 174-177.
|
| [2] |
陈思豆, 黄卓铨, 杨兴雨. 考虑限制性卖空的多期模糊投资组合优化模型[J].
广东工业大学学报, 2021, 38(2): 39-47.
CHEN S D, HUANG Z Q, YANG X Y. A multi-period fuzzy portfolio optimization model considering restricted short selling[J]. Journal of Guangdong University of Technology, 2021, 38(2): 39-47. DOI: 10.12052/gdutxb.200100. |
| [3] |
曲江, 刘洪伟, 朱慧, 等. 知识产权资产证券化的价格敏感度[J].
科技管理研究, 2020, 40(16): 200-205.
QU J, LIU H W, ZHU H, et al. Price sensitivity of intellectual property asset securities[J]. Science and Technology Management Research, 2020, 40(16): 200-205. DOI: 10.3969/j.issn.1000-7695.2020.16.026. |
| [4] |
史亚雅, 杨德明. 数字经济时代商业模式创新与盈余管理[J].
科研管理, 2021, 42(4): 170-179.
SHI Y Y, YANG D M. Business model innovation and earnings management in the era of digital economy[J]. Science Research Management, 2021, 42(4): 170-179. |
| [5] |
王晓芳, 王曦, 杨涛. 知识产权证券化基础资产选择及其转让过程中的风险防范[J].
现代商业, 2020, 15(26): 122-123.
|
| [6] |
陈晓, 戴翠玉. A股亏损公司的盈余管理行为与手段研究[J].
中国会计评论, 2004, 2(2): 299-310.
CHEN X, DAI C Y. An empirical analysis on the earnings management of the A-share loss firms[J]. China Accounting Review, 2004, 2(2): 299-310. |
| [7] |
李巧莎. 基于金融成长周期理论的科技型中小企业融资问题研究[J].
科技管理研究, 2013, 33(2): 243-245.
LI Q S. Study on financial problems of technological small and medium-sized enterprises based on financial growth cycle theory[J]. Science and Technology Management Research, 2013, 33(2): 243-245. |
| [8] |
杨兴雨, 刘伟龙, 井明月, 等. 基于模糊收益率的分散化投资组合调整策略[J].
广东工业大学学报, 2020, 37(5): 13-21.
YANG X Y, LIU W L, JING M Y, et al. A diversified portfolio selection strategy based on fuzzy return rate[J]. Journal of Guangdong University of Technology, 2020, 37(5): 13-21. DOI: 10.12052/gdutxb.200071. |
| [9] |
王炎坤, 刘桂芳. 科技成果管理与知识产权制度的关系[J].
科技管理研究, 2002, 22(6): 74-75.
DOI: 10.3969/j.issn.1000-7695.2002.06.024. |
| [10] |
刘伍堂, 王晓冉, 肖霖之, 等. 科技成果知识产权评估指标体系及评估方法[J].
中国资产评估, 2019, 24(6): 30-39.
LIU W T, WANG X R, XIAO L Z, et al. Evaluation index system and evaluation method of intellectual property of scientific and technological achievements[J]. Appraisal Journal of China, 2019, 24(6): 30-39. DOI: 10.3969/j.issn.1007-0265.2019.06.006. |
| [11] |
任丽明, 阴霞, 张振宇, 等. 知识产权转让定价研究——基于双向拍卖模型的分析[J].
价格理论与实践, 2019, 39(7): 128-131.
REN L M, YIN X, ZHANG Z Y, et al. Intellectual property transfer pricing research—based on the analysis of the two-way auction model[J]. Price:Theory & Practice, 2019, 39(7): 128-131. |
| [12] |
王磊. 浅谈知识产权价值评估在市场经济中的运用[J].
中国发明与专利, 2019, 16(8): 82-85.
WANG L. A brief introduction on the application of intellectual property value assessment in market economy[J]. China Invention & Patent, 2019, 16(8): 82-85. DOI: 10.3969/j.issn.1672-6081.2019.08.015. |
| [13] |
邵永同, 王常柏. 科技型中小企业知识产权证券化中的资产组合构建[J].
科技管理研究, 2014, 34(3): 157-160.
SHAO Y T, WANG C B. A study on portfolio construction in intellectual property securitization of high-tech small and medium-sized enterprises[J]. Science and Technology Management Research, 2014, 34(3): 157-160. DOI: 10.3969/j.issn.1000-7695.2014.03.032. |
| [14] |
张会洁. 盈余管理文献综述[J].
农村经济与科技, 2019, 30(20): 106-107.
DOI: 10.3969/j.issn.1007-7103.2019.20.065. |
| [15] |
张钰. 企业资产证券化中的盈余管理[J].
合作经济与科技, 2012(18): 78-79.
DOI: 10.3969/j.issn.1672-190X.2012.18.044. |
| [16] |
陈祥有. A股发行公司IPO前盈余管理与IPO后经营业绩的实证研究[J].
财经理论与实践, 2010, 31(1): 62-65.
CHEN X Y. Empirical research on the relationship between pre-IPO earnings management and post-IPO performance for China firms[J]. The Theory and Practice of Finance and Economics, 2010, 31(1): 62-65. DOI: 10.3969/j.issn.1003-7217.2010.01.013. |
| [17] |
钱艳英. 限制卖空条件下证券组合投资的优化决策[J].
广东工业大学学报, 2002, 29(3): 87-90.
QIAN Y Y. Optimal decision portfolio investment under the condition of nonshort sale[J]. Journal of Guangdong University of Technology, 2002, 29(3): 87-90. DOI: 10.3969/j.issn.1007-7162.2002.03.020. |
| [18] |
胡威. 资产证券化的运行机理及其经济效应[J].
浙江金融, 2012, 31(1): 62-66.
DOI: 10.3969/j.issn.1005-0167.2012.01.014. |
| [19] |
叶琳, 鲍新中. 知识产权证券化风险及其评价研究[J].
财务管理研究, 2020, 69(9): 24-29.
|
 2022, Vol. 39
2022, Vol. 39

