2. 广东顺德创新设计研究院,广东 佛山 528000;
3. 广州柏创机电设备有限公司,广东 广州 511450
2. Guangdong Shunde Innovative Design Institute, Foshan 528000, China;
3. Guangzhou Baichuang Electromechanical Equipment Co., Ltd., Guangzhou 511450, China
自动导引小车(Automated Guided Vehicle,AGV)是一种以微处理器为核心,搭配相关控制驱动系统,使其能够沿着预定目标路线执行自动导引循迹的功能小车。AGV以其自动化的运输特性,正成为当代社会生产中的关键设备[1-2]。
随着现代农业机械化的发展,以农业生产为核心,协同种植、育苗、移栽、运送等农业活动的高效、绿色农业运输方式成为现代农业的重要基础[3]。伴随农村产业结构调整,以单次运量少、距离短且频繁的田间农用运输工具需求日益增长[4]。但是,农业机械化的资金投入往往较大,成本回收周期较长[5];农业大棚环境中的道路条件相对较差,可供于通行的道路宽度往往只有40~60 cm[6],因而研究适用于农业大棚环境的绿色、轻型、低成本的运输机械是目前亟需解决的问题。
将AGV应用于农业大棚运输,借助于AGV自动、高效运行的特点,不仅能够大幅提高农产品运输效率、减少劳动力投入,也是在现代农业机械化上的一个重大突破[7-9]。本文针对大棚农业环境,借助磁导航开发一款轻型、经济化的农用运输AGV;通过改进的分段模糊PID控制算法,提高AGV的路径跟踪精度与运动稳定性[10-11]。经Matlab仿真分析,AGV响应速度快、循迹导引效果好。实验表明,所设计的磁导航AGV在不同驱动速度下都能做到相对稳定的循迹运行,是一种实现农业自动化运输的有效方案。
1 磁导航下轻型农用运输AGV的系统结构与要求以应用于农业大棚蔬菜运输AGV为设计对象,最大工作载荷为20 kg,可供AGV运行的道路宽度为0.6 m,道路为固定的、路况较差的硬质土路面与水泥路面。主要工作任务是将采集好的蔬菜从大棚运输到仓库。农业大棚实景环境如图1所示。

|
图 1 农业大棚实景 Figure 1 Agriculture greenhouse |
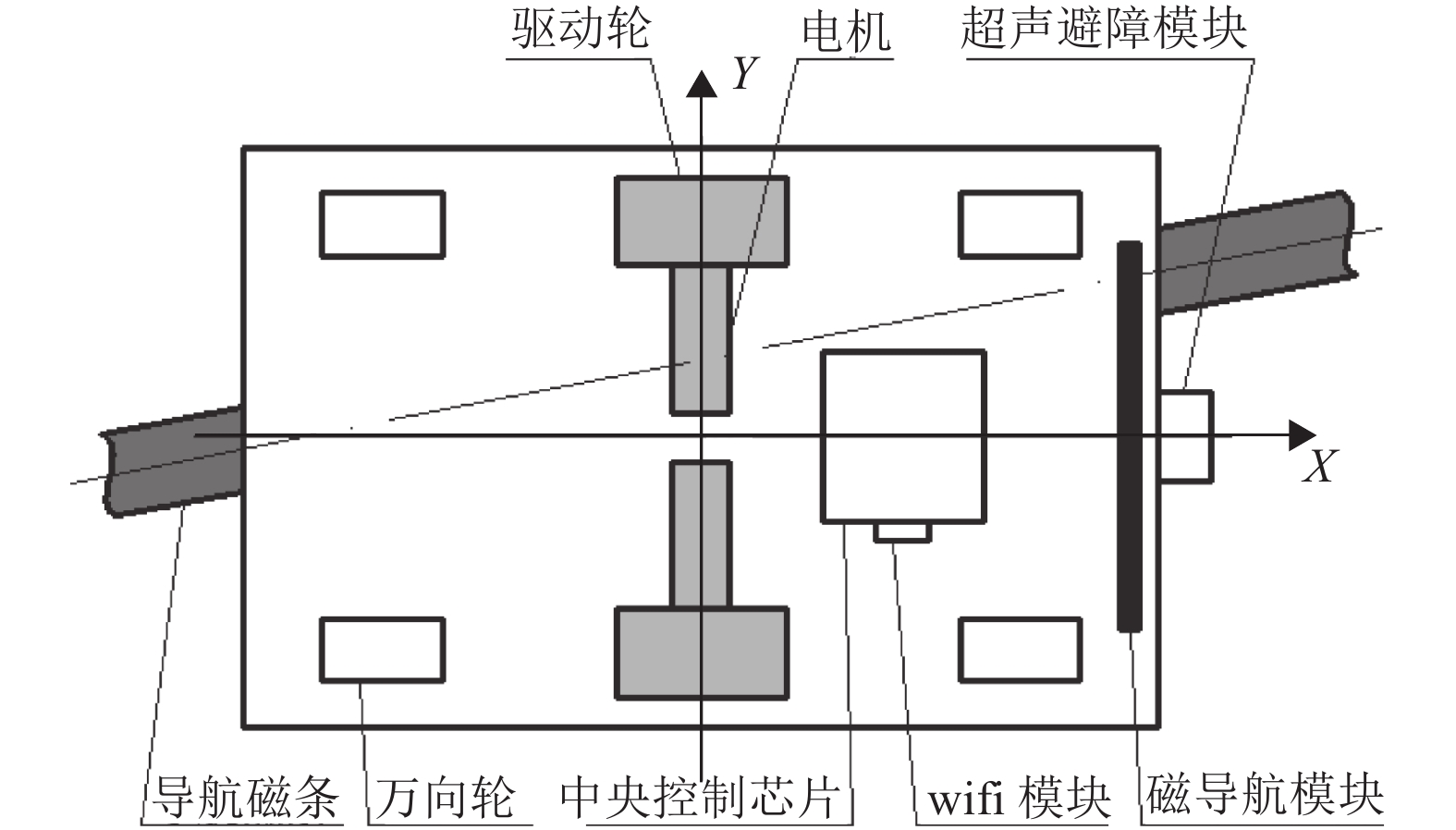
为实现这个工作任务,AGV的组成部分主要包括有由电机和驱动轮组成的驱动系统、保障安全避障运行的超声模块、实现循迹导引的磁导航模块、与上位机通信的wifi模块、控制整个小车的STM32F103VET6中央控制芯片以及搭载这些设备与载货的车体结构等。磁导航下轻型农用运输AGV的系统模型如图2所示。
|
图 2 磁导航轻型农用运输AGV模型 Figure 2 AGV model of magnetic navigation miniature agricultural transportation |
由农用运输AGV的工作条件可知,要求AGV做到在路况相对较差条件下行驶,较小的转弯半径,有足够的有效载荷[12]。于此建立起由两个独立工作的无刷电机和减速器、编码器组成的驱动装置,以实现AGV的运输功能。
AGV的导引方式主要有固定路径导引与自由路径导引[13-14]。考虑到在农业上的经济性与易实现性,以及农业大棚道路的固定性,采用造价便宜的磁导航方式来实现AGV的导引控制[15]。
农用运输AGV的核心目标是在引导装置的导引基础上,AGV能够做到有效运载力的前提,合理、迅速地执行运输任务;并在驱动速度上快速有效响应,在循迹导引上做到在安全范围内行驶,减少位置偏差。因此,对于AGV驱动系统的工作性能,导引装置的功能实现,以及AGV的速度控制、循迹导引具有特定的功能要求。
2 AGV驱动系统运载力核算 2.1 轻型农用运输AGV的驱动结构布局以4个万向轮与两个独立工作的无刷电机驱动轮构成AGV的工作轮,设计AGV的六轮布局模式,车身尺寸长、宽、高分别为0.5、0.4和0.4 m,满足大棚蔬菜运输小车的体型要求,如图2所示。
2.2 驱动电机性能计算及选择应用于农业大棚运输的AGV,其最大工作载荷
| $n = \frac{{60 \cdot v \cdot i}}{{{\text{π}}\cdot d}} = {\rm{371}}.9\;{\rm{ r}}/\min $ | (1) |
电机的驱动力与AGV所工作的农业大棚土路面环境有关,取AGV车轮与路面间的滚动阻力系数
| $ {F_{{\rm{\text{额}}}}} = f \cdot (M + m)g = {\rm{29}}{\rm{.4\;N}} $ | (2) |
| $ {F_{\max }} = {F_{\text{额}}} + (M + m)(a + g\sin \phi ) = {\rm{61}}{\rm{.0\;N}} $ | (3) |
AGV的驱动轮个数k=2,传动效率
| $ {T_{\text{额}}} = \frac{{{F_{\text{额}}} \cdot d}}{{2 \cdot k \cdot \eta \cdot i}} \approx {\rm{0}}{\rm{.21\;N}} \cdot {\rm{m}} $ | (4) |
| ${T_{\max }} = \frac{{{F_{\max }} \cdot d}}{{2 \cdot k \cdot \eta \cdot i}} \approx {\rm{0}}{\rm{.44\;N}} \cdot {\rm{m}}$ | (5) |
则电机的额定功率P额与最大功率Pmax可由式(6)和式(7)求得。
| $ {P_{\text{额}}} = \frac{{{T_{\text{额}}} \cdot n}}{{9550}} \approx {\rm{8}}.{\rm{2\;W}}$ | (6) |
| ${P_{\max }} = \frac{{{T_{\max }} \cdot n}}{{9550}} \approx {\rm{17}}{\rm{.1\;W}}$ | (7) |
考虑一定的设计冗余量,选定众致无刷电机,其技术参数如表1所示。
| 表 1 电机技术参数 Table 1 Technical parameters of motor |
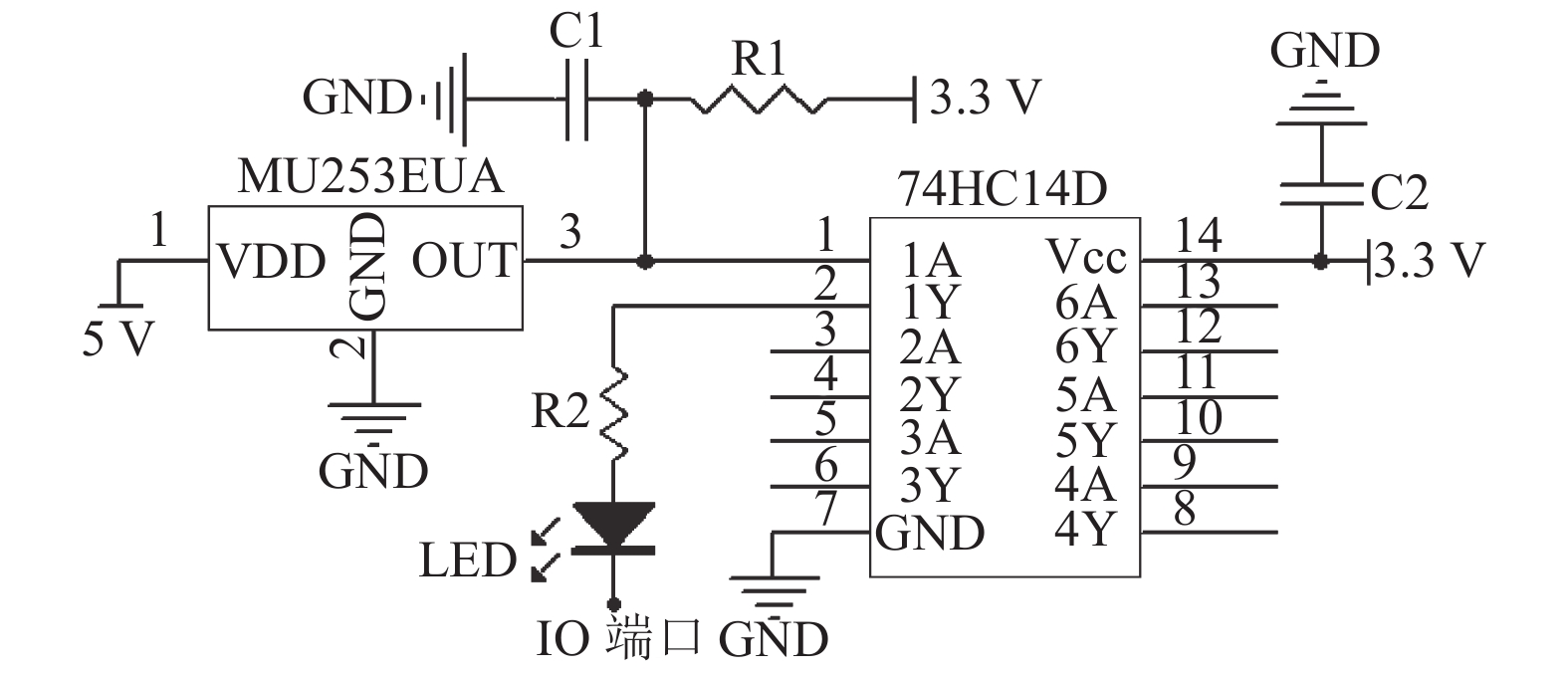
磁导航模块是AGV的“眼睛”,通过磁导航模块的磁性传感器,来检测预铺设好的导航磁条磁场,以此来推断当前AGV与导航磁条的相对位置误差。
所设计的磁性传感器电路原理图如图3所示,通过MH253EUA磁性传感器检测预铺设好的导航磁条磁场,并反馈高、低电平信号到中央控制芯片IO端口。
|
图 3 磁性传感器电路原理图 Figure 3 Circuit diagram of magnetic sensor |
所设计的磁导航模块由11个磁性传感器组成,构成11个检测点位(1~11),点位间距为15 mm。正常工作中,磁导航模块可有效反馈2至3个有效信号。因此,通过分析磁导航模块的反馈信息,即可判断出此时AGV相对于磁条的位置偏差信息。其相应的位置偏差数据解析如表2所示。
| 表 2 磁导航模块偏差数据解析 Table 2 Error data analysis of magnetic navigation module |
设AGV驱动轮的轮距为B,左、右两驱动轮速度分别为V1、V2(设V2>V1)。则小车在行进过程中的额定速度V0[17]为
| ${V_{\rm{0}}} = \frac{{{V_1} + {V_2}}}{2}$ | (8) |
转弯半径R为
| $R = \frac{{B({V_1} + {V_2})}}{{2({V_2} - {V_1})}}$ | (9) |
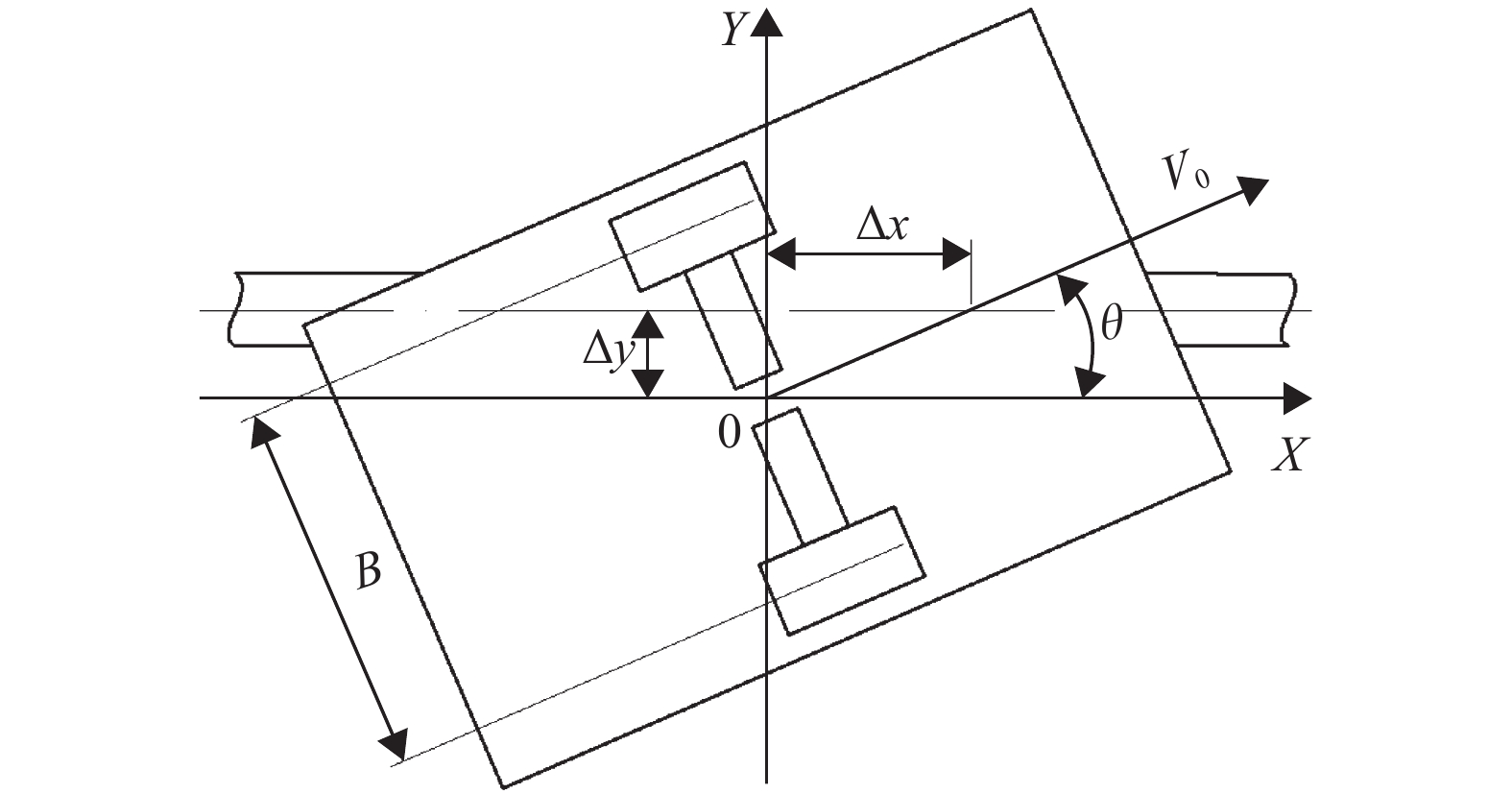
将AGV车体结构简化为两轮驱动模型,则小车在沿着导航磁条运行过程中的运动状态与X方向位置偏差∆x、Y方向位置偏差∆y及角度偏差θ的示意图如图4所示。
|
图 4 磁导引下的AGV运动学模型 Figure 4 AGV kinematics model based on magnetic guidance |
针对图4建立运动学模型,在∆t时间内,小车行驶的过程中出现位置偏差∆x、∆y和角度偏差θ,于是得到偏差方程的数学表达为
| $\left\{ \begin{aligned} & \Delta x = \frac{{{V_1} + {V_2}}}{2} \cdot \Delta t \cdot \cos \theta \\& \Delta y = \frac{{{V_1} + {V_2}}}{2} \cdot \Delta t \cdot \sin \theta \\& \theta = \frac{{{V_1}{\rm{ - }}{V_2}}}{B} \cdot \Delta t \end{aligned}\right.$ | (10) |
对式(10)两边分别进行时间求导,即可得到AGV的空间状态方程[18],为
| $\left[ \begin{array}{c} \dfrac{{\Delta x}}{{{\rm{d}}t}} \\ \dfrac{{\Delta y}}{{{\rm{d}}t}} \\ \dfrac{{\Delta \theta }}{{{\rm{d}}t}} \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{ - \sin \theta }&0 \\ {\sin \theta }&{\cos \theta }&0 \\ 0&0&1 \end{array}} \right]\left[ \begin{array}{c} \dfrac{{{V_1} + {V_2}}}{2} \\ 0 \\ \dfrac{{{V_1}{\rm{ - }}{V_2}}}{B} \end{array} \right]$ | (11) |
方程(11)表明了在全局坐标系下,AGV的运动状态与两驱动轮速度的关系。在实际驱动AGV行进的过程中,小车额定速度设定为V0=0.5 m/s。通过控制两驱动轮的速度差
通过实验采集以AGV驱动系统的脉冲宽度调制(Pulse Width Modulation, PWM)占空比作为系统的输入量、电机的转速作为输出量的响应数据,利用Matlab系统传递函数辨识工具箱模拟仿真驱动系统的传递函数[19],结果如式(12)所示。
| $G(s) = \frac{{0.{\rm{011\;92}}{s^2} - {\rm{13}}{\rm{.83}}s + {\rm{1\;891}}}}{{{s^2} + 77.93s + 437.6}}$ | (12) |
为保证AGV安全、有效地在合理控制范围内运行工作,中央控制芯片的运行控制基本算法是基于误差的PID控制,其数学模型如式(13)所示[20]。
| $u(t) = {K_{\rm{p}}}e(t) + {K_{\rm{i}}}\int_0^t {e(t){\rm{d}}t + {K_{\rm{d}}}} \frac{{{\rm{d}}e(t)}}{{{\rm{d}}t}}$ | (13) |
式中:u(t)为控制量,e(t)为设定值与当前时刻采样值的误差,Kp为比例系数,Ki为积分时间常数,Kd为微分时间常数。
在实际控制算法中,搭配模糊PID控制器,依据当前时刻采样的数据与设定值的误差e及误差的变化率ec,对PID的3个参数(Kp、Ki、Kd)进行在线自调整,该控制系统由两部分组成,即模糊推理部分和常规PID部分,其结构如图5所示[21]。

|
图 5 闭环模糊PID控制系统 Figure 5 Closed loop fuzzy PID control system |
由前述,对于农用运输AGV,可供AGV运行的道路宽度0.6 m,所设计的小车宽为0.4 m,其中左右驱动的轮距B=0.38 m,小车的运行速度为0.5 m/s,负载20 kg,因此,要求AGV的驱动速度有良好动态控制性能,循迹导航稳定运行时位置偏差在±10 mm以内。
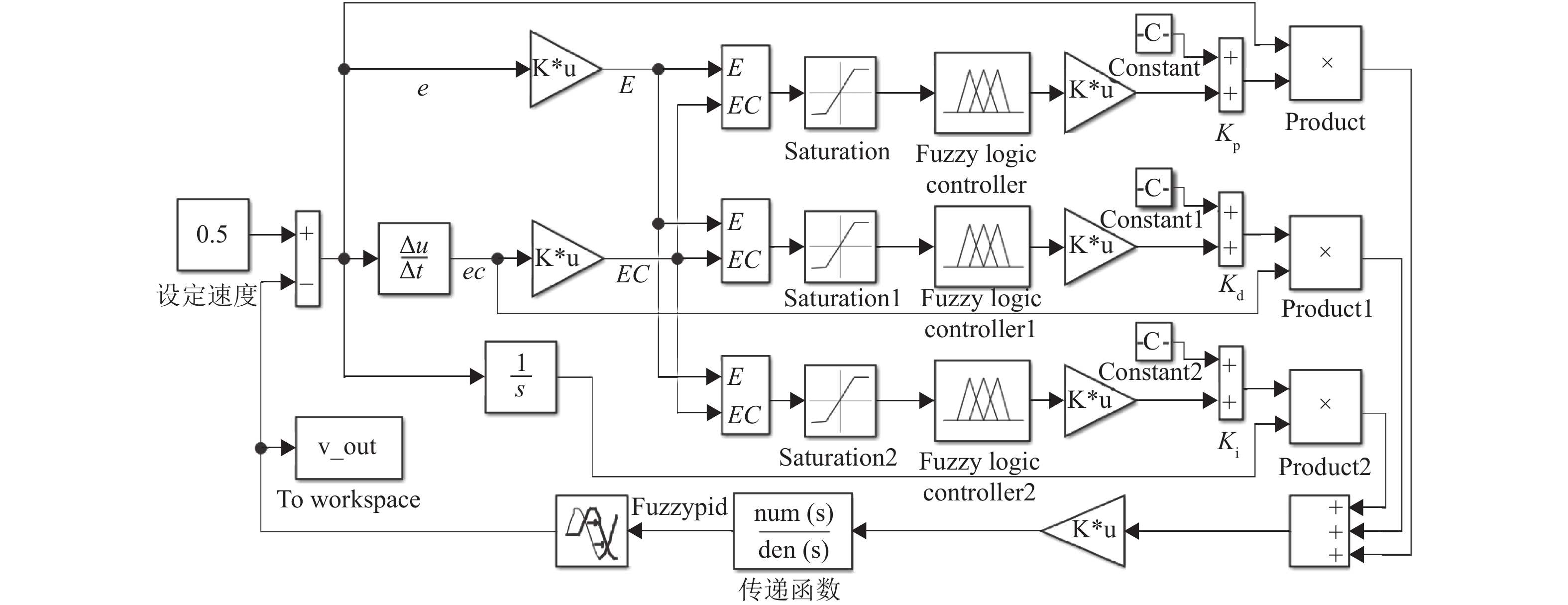
4.1 AGV驱动速度闭环模糊PID仿真与实验利用建立好的AGV驱动系统传递函数公式(12),结合模糊PID控制算法,在Matlab/Simulink工具箱中建立如图6的驱动速度仿真模型。其中,u指代该模块的输入,K指代该模块的增益,E和EC分别表示e和ec乘以增量后的量值。
|
图 6 速度闭环模糊PID仿真模型 Figure 6 Speed closed loop fuzzy PID simulation mode |
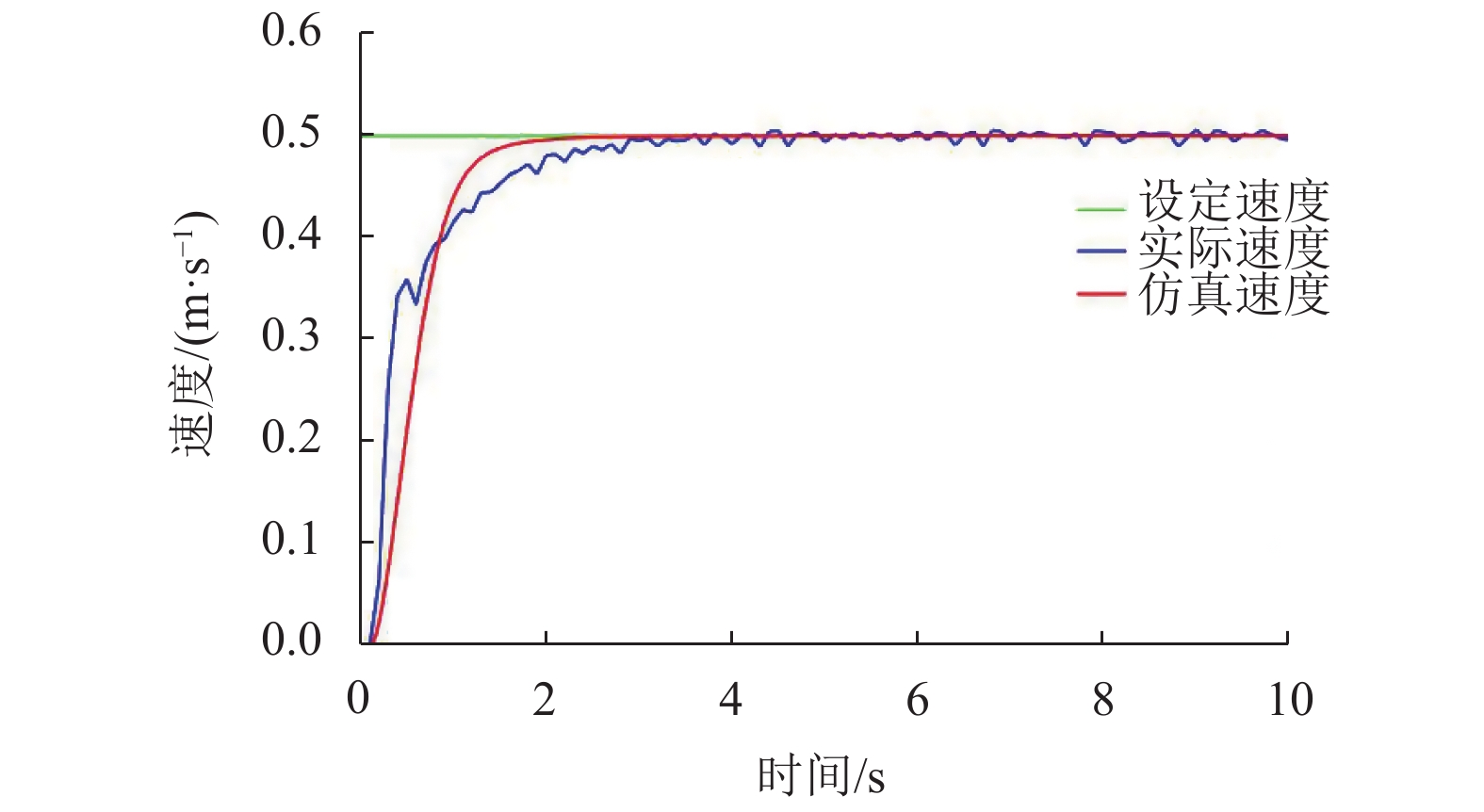
AGV运行测试实验中,采集AGV在设定驱动速度0.5 m/s下的实际车速数据,将仿真数据与实验数据对比,结果如图7所示。
|
图 7 速度控制仿真与实验对比 Figure 7 Comparison of speed control simulation and experiment |
从仿真与实验对比的结果来看,所建立的闭环模糊PID控制器在速度仿真上能够比较有效地反映出当前AGV控制系统的性能。在设定驱动速度为0.5 m/s条件下,AGV能够在4 s内完成速度的控制响应,并最终做到相对稳定运行,速度误差小于5%。可以看出,所设计的闭环PID控制系统能够有效地实现AGV的驱动速度控制,满足了农用运输AGV的驱动速度要求。
4.2 AGV分段模糊PID控制循迹导引仿真循迹导引是指AGV在磁导航模块的作用下,不断检测AGV与导航磁条的相对位置误差,中央控制芯片控制AGV的驱动速度与方向,使得AGV沿着规划的路径行驶。
在AGV循迹导引过程中,常规PID控制算法往往具有时效性差、超调量大、鲁棒性不足等问题,这样就导致在AGV循迹运行过程中位置误差过大且运行不稳定,易触碰到路径两侧的田间植株。笔者设计改进的分段模糊PID控制算法,考虑到导航磁条路径的确定性,针对不同曲率的固定导引路径,采用不同的模糊PID控制器实现模糊PID控制,这样可以实现在较大路径误差输入量时,有效避免控制系统输入响应慢、超调量大等问题,其原理图如图8所示。

|
图 8 分段模糊PID控制原理图 Figure 8 Schematic diagram of piecewise fuzzy PID control |
分段模糊PID控制工作原理:首先在中央控制芯片中独立存放不同道路下的模糊PID控制器1, 2, ···, N,当AGV在铺设好导航磁条的农业大棚道路上运行时,依据反馈的位置偏差变化率信息,判别出小车当前行驶的不同曲率路径;然后中央控制芯片依据不同路径,选择不同的模糊PID控制器,实现不同输入量的输出表达。对比于常规的PID控制算法,可以实现即时地调整PID的3个参数(Kp、Ki、Kd),提高AGV小车在循迹过程中的响应速度,提高运行稳定性。
由方程(11)可知,循迹导引控制实质是控制两驱动轮的速度差

|
图 9 循迹导引仿真模型 Figure 9 Tracking guidance simulation model |
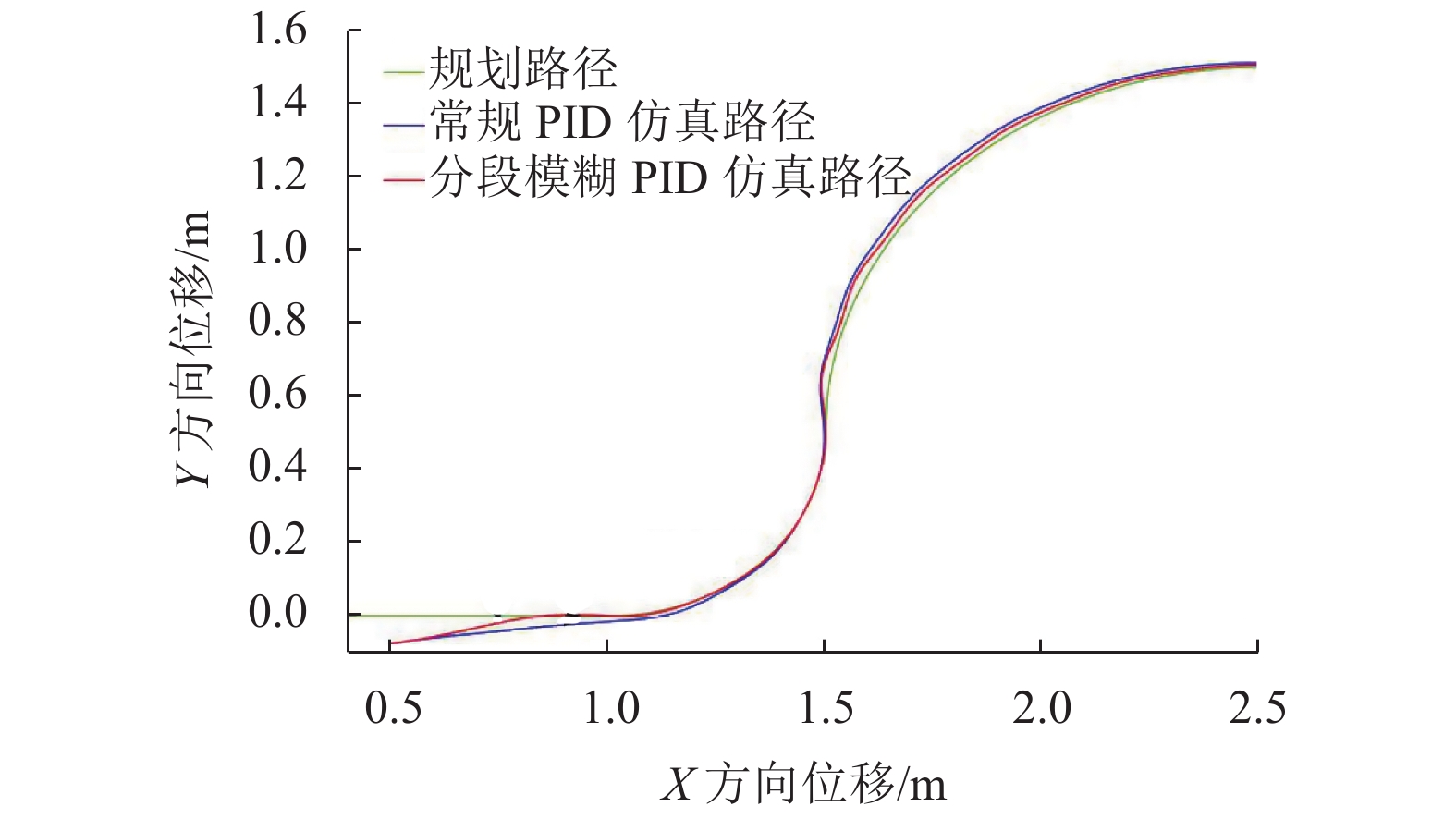
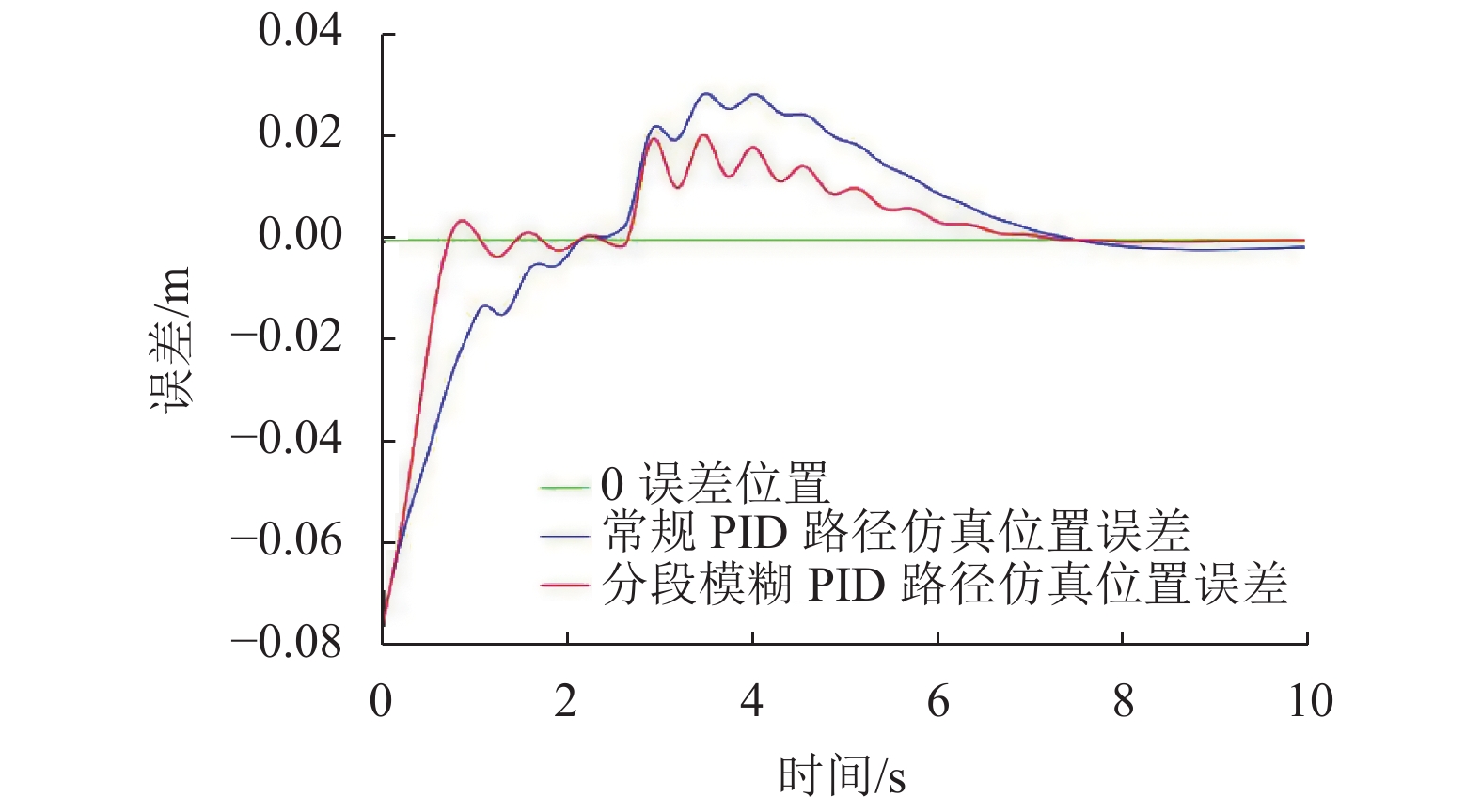
仿真中,设定3条不同曲率的路径,以此来分析循迹导引效果。为有效反映AGV循迹导引控制性能,考虑最大初始误差下AGV的循迹导引情况,设定AGV额定速度V0=0.5 m/s。开始仿真,得到AGV中心点在分段模糊PID算法控制下的仿真路径。同样的,以普通PID控制算法来仿真在相同规划路径、相同初始位置条件下的循迹导引,得到AGV小车中心点在常规PID算法控制下的仿真路径。将分段模糊PID仿真路径、常规PID仿真路径与规划路径导入Matlab中绘图,得到路径对比图10;将分段模糊PID仿真路径中的位置误差与常规PID仿真路径的位置误差导入,得到误差对比图11。
|
图 10 不同控制算法下的仿真路径对比 Figure 10 Comparison of simulation paths under different control algorithms |
|
图 11 不同控制算法下的仿真路径误差对比 Figure 11 Comparison of simulation path errors under different control algorithms |
从图10可以看出,采用分段模糊PID控制算法相比于常规PID控制,能够实现AGV在循迹导引上更为快速的响应跟踪,效果更好,在弯道变化处有较大运行波动,最大运行误差在±20 mm之内;从图11也能看出,所设计的分段模糊PID控制,对比于常规PID有较小的系统超调量,实现了AGV更为快速的稳定运行,误差在±5 mm以内,满足农用运输AGV循迹导引上的位置偏差要求,且具有良好的动态控制性能。
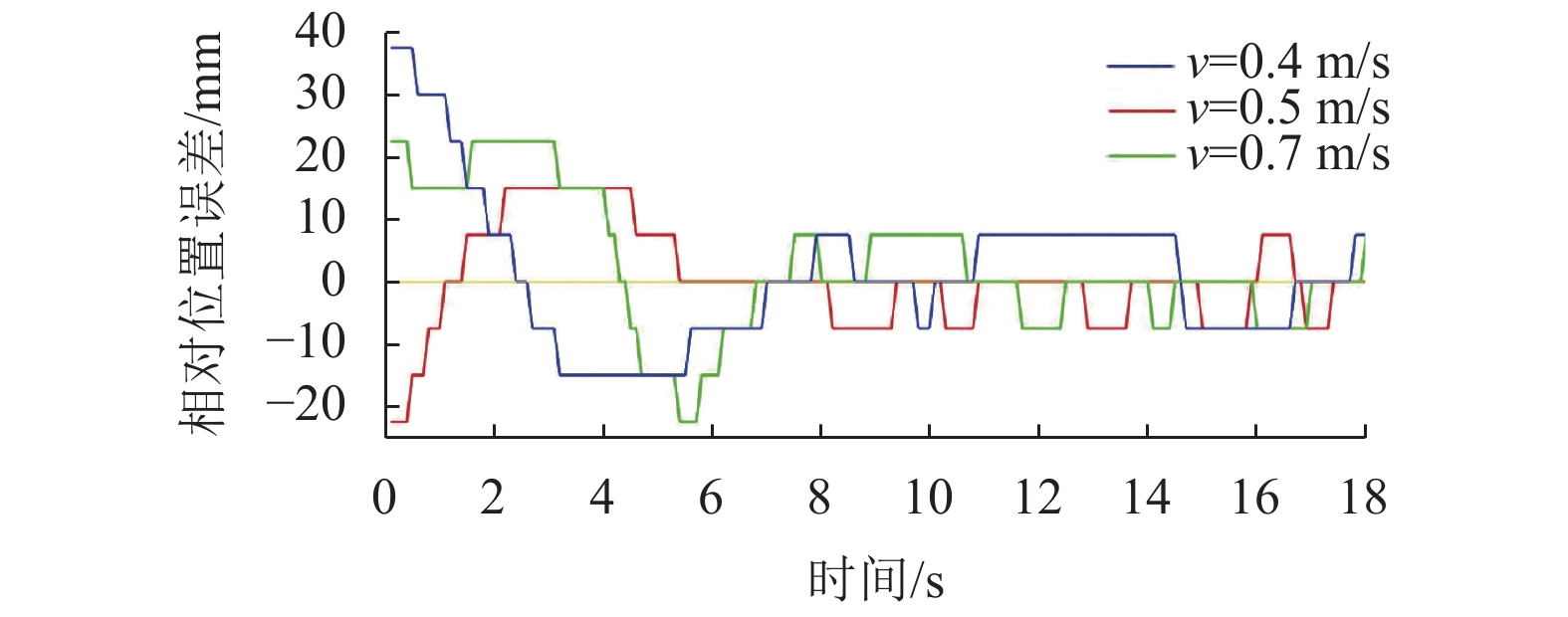
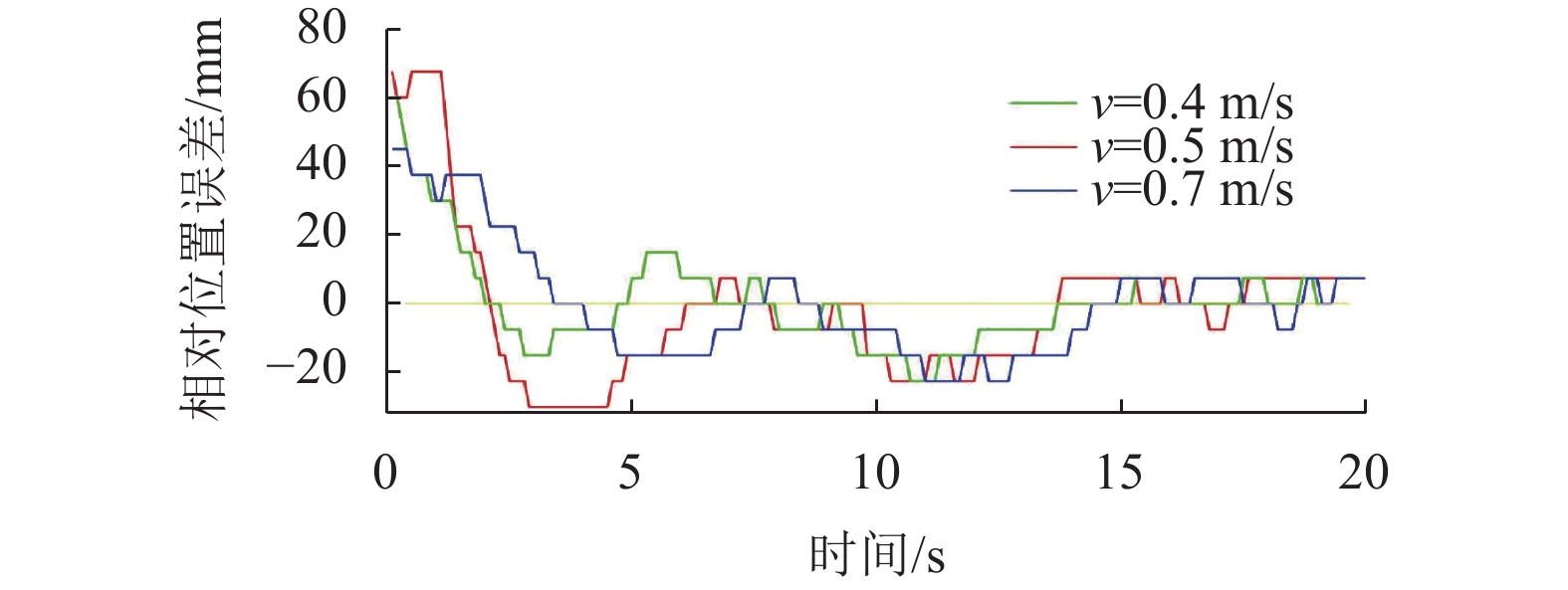
4.3 AGV循迹实验为验证分段模糊PID控制算法在农用运输AGV循迹导引上的实际控制效果,搭建AGV的实验样机,结合现有条件,在户外硬质铺砖路面实验场地铺设直线、S形曲线路径导航磁条进行实验。小车负载20 kg,以指定的不同驱动速度(0.4,0.5和0.7 m/s)、共同的初始位置、不同的初始相对位置误差进行测试,测试实景如图12所示。采集小车在运行过程中与导航磁条的相对位置误差数据,AGV沿着直线路径的循迹导引相对位置误差数据如图13所示。沿着S形曲线路径的循迹导引相对位置误差数据如图14所示。

|
图 12 AGV样机磁导航循迹实验 Figure 12 Magnetic navigation tracking experiment of AGV prototype |
|
图 13 直线循迹导引位置误差 Figure 13 Position error of linear tracking guidance |
|
图 14 曲线循迹导引位置误差 Figure 14 Position error of curve tracking guidance |
从不同驱动速度,AGV沿着直线、S形曲线路径循迹导引相对位置误差数据可以看出,所设计的分段模糊PID控制算法,在AGV运行过程中都能够调节与导航磁条的相对位置误差。稳定运行时,其相对位置误差保持在±7.5 mm以内。但在运行到弯道变化处,运动过程存在一定的不稳定性,位置偏差在±20 mm左右,最终依然能达到稳定运行。证明了该分段模糊PID控制算法的可靠性,满足农用运输AGV循迹导引上的位置偏差要求,也符合仿真中对AGV循迹导引过程的预测。
5 结语本文基于磁导方式采用分段模糊PID控制实现轻型农用AGV的循迹导引与运动控制。通过对AGV驱动模块运载力的核算,达到农用运输AGV的运载能力的要求。驱动速度上,能够在4 s内达到额定的运行速度,且运行稳定。循迹导引上,采用分段模糊PID控制算法,不仅实现了对AGV循迹导引稳定的控制要求,而且改善了常规PID控制算法下在循迹导引过程中响应时间慢、超调量大等问题,证明了该方法有效可行。通过AGV样机,测试AGV在不同驱动速度下直线、S形曲线路径的循迹导引效果,实验结果表明AGV能够在分段模糊PID控制器下沿着规划路径有效地循迹导引运行。综上,所设计的轻型农用AGV在运输功能与运行控制上满足了基本要求,为农用运输AGV在实际的产品设计与闭环控制实现上提供参考。
| [1] |
YU S Y, YE C L, LIU H J, et al. Development of an omnidirectional automated guided vehicle with MY3 wheels[J].
Perspectives in Science, 2016, 7: 364-368.
DOI: 10.1016/j.pisc.2015.11.056. |
| [2] |
张辰贝西, 黄志球. 自动导航车(AGV)发展综述[J].
中国制造业信息化, 2010, 39(1): 53-59.
ZHANG C B X, HUANG Z Q. Evolution summarization of automated guided vehicles (AGV)[J]. Machine Design and Manufacturing Engineering, 2010, 39(1): 53-59. DOI: 10.3969/j.issn.1672-1616.2010.01.014. |
| [3] |
刘明实, 胡祎骁, 罗心皓. 基于农业运输的综合问题分析[J].
经贸实践, 2018(17): 38.
LIU M S, HU Y X, LUO X H. Analysis of comprehensive problems based on agricultural transportation[J]. Economic & Trade, 2018(17): 38. |
| [4] |
孙晓. 轻型电动农用运输机械发展现状和趋势[J].
江苏农机化, 2012(4): 26-27.
SUN X. Development status and trend of light electric agricultural transport machinery[J]. Jiangsu Agricultural Mechanization, 2012(4): 26-27. |
| [5] |
邓文博, 万红珍. 科技创新、农业机械化对广东农业经济增长的影响[J].
五邑大学学报(社会科学版), 2020, 22(4): 67-71.
DENG W B, WAN H Z. The impact of science and technology innovation and agricultural mechanization on agricultural economic growth in Guangdong province[J]. Journal of Wuyi University (Social Sciences Edition), 2020, 22(4): 67-71. DOI: 10.3969/j.issn.1009-1513.2020.04.014. |
| [6] |
陈之群, 曹雪, 胡晓丽, 等. 大棚马铃薯套种茄子3次收获高效栽培技术[J].
中国蔬菜, 2018(5): 101-103.
CHEN Z Q, CAO X, HU X L, et al. High efficient cultivation techniques of potato interplanting with eggplant in greenhouse[J]. China Vegetables, 2018(5): 101-103. |
| [7] |
TAKESHIMA H, HATZENBUEHLER P L, EDEH H O. Effects of agricultural mechanization on economies of scope in crop production in Nigeria[J].
Agricultural Systems, 2020, 177: 102691.
DOI: 10.1016/j.agsy.2019.102691. |
| [8] |
蒲宝山, 陈永快, 王涛, 等. 自动导航车技术发展状况及在农业领域的应用及前景展望[J].
江苏农业科学, 2020, 48(1): 61-65.
PU B S, CHEN Y K, WANG T, et al. Development status of automated guided vehicle technology and its application and prospect in agriculture[J]. Jiangsu Agricultural Sciences, 2020, 48(1): 61-65. |
| [9] |
BELL J, MACDONALD B A, AHN H S, et al. An analysis of automated guided vehicle standards to inform the development of mobile orchard robots[J].
IFAC-PapersOnLine, 2016, 49(16): 475-480.
DOI: 10.1016/j.ifacol.2016.10.086. |
| [10] |
赵晨宇, 陈息坤. 差速转向农业专用AGV小车的设计与模糊控制研究[J].
农机化研究, 2016, 38(11): 123-127.
ZHAO C Y, CHEN X K. Study on fuzzy control of an agricultural dedicated AGV with differential steering[J]. Journal of Agricultural Mechanization Research, 2016, 38(11): 123-127. DOI: 10.3969/j.issn.1003-188X.2016.11.024. |
| [11] |
贺坤. 基于航姿与磁导航传感器融合的四轮转向AGV路径跟踪研究[D]. 镇江: 江苏大学, 2018.
|
| [12] |
罗远杰, 陈息坤, 高艳霞. 现代农业自动化AGV小车的设计与模糊控制研究[J].
工业控制计算机, 2015, 28(12): 68-71.
LUO Y J, CHEN X K, GAO Y X. Study on fuzzy control of AGV used in automation of modern agriculture[J]. Industrial Control Computer, 2015, 28(12): 68-71. DOI: 10.3969/j.issn.1001-182X.2015.12.033. |
| [13] |
KOSTOV M, KOSTOVA V, MARKOSKA R. AGV guidance system simulations with a programmable robotics kit[J].
International Journal of Reasoning-based Intelligent Systems, 2015, 7(1/2): 42-46.
DOI: 10.1504/IJRIS.2015.070911. |
| [14] |
尚婕, 姜文刚, 蔡蓝图. 差速转向的农用自动引导小车控制系统设计[J].
江苏科技大学学报(自然科学版), 2011, 25(5): 453-456.
SHANG J, JIANG W G, CAI L T. Design of control system of agricultural automatic guided vehicle with differential steering[J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 2011, 25(5): 453-456. |
| [15] |
田丽芳. 基于纯滚动转向的采摘机器人轮式AGV系统设计与试验研究[D]. 镇江: 江苏大学, 2016.
|
| [16] |
王锋. 丘陵山地果园动力底盘的坡地通过性研究[D]. 重庆: 西南大学, 2020.
|
| [17] |
肖全. 面向3C自动化生产线的AGV结构设计与控制研究[D]. 广州: 广东工业大学, 2018.
|
| [18] |
鲍金. 基于PID算法的双轮差动式移动机器人定位和导航研究[D]. 沈阳: 东北大学, 2008.
|
| [19] |
叶甲秋. 自动导向小车(AGV)驱动系统辨识与动态特性分析[D]. 南京: 南京航空航天大学, 2010.
|
| [20] |
ZHANG J Y. PID control realization of drying system of the finishing line based on MCGS and PLC[C]//2020 2nd International Conference on Applied Machine Learning and Data Science (ICAMLDS 2020). Chengdu: IOP Publishing, 2020, 1629: 012015.
|
| [21] |
LUO K. Investigation on machinery control system based on fuzzy PID control technology[J].
Applied Mechanics and Materials, 2012, 1999: 130-134.
|
| [22] |
马广志, 吴伟, 党国栋. 基于Simulink的履带机器人路径追踪仿真[J].
机械研究与应用, 2017, 30(6): 77-78.
MA G Z, WU W, DANG G D. Simulation of tracked robot tracking path based on the simulink[J]. Mechanical Research & Application, 2017, 30(6): 77-78. |
 2022, Vol. 39
2022, Vol. 39

