随着网络技术的不断发展,多智能体系统一致性问题深受学者的关注[1-2],并逐渐被应用到实际生活中,如无人机编队、电网能源分配等[3-4]。在实际应用中,多智能体系统难免会遭受到如随机干扰、网络攻击等外部因素的干扰,而这对其一致性有重要影响[4-5]。
一般地,随机干扰对多智能体系统的影响主要反映在系统动态特性或信息传输的信道中。前者可表现为随机噪声和随机出现不确定项等干扰,如文献[6]通过设计新颖的脉冲控制协议,并基于广义伊藤公式与李雅普诺夫稳定性理论得到了系统实现均方一致性的充分条件;文献[7]研究了一类具有随机出现不确定项的非线性多智能体系统的均方一致性问题。后者则一般体现在信息丢包和信道堵塞的建模中[8]。
另一方面,考虑到多智能体系统应用中环境的复杂性及其通信网络的开放性,由网络攻击所引起的网络安全问题也不容忽视。由文献[9-11]可知,攻击会导致多智能体一致性性能达不到理想的要求,并可能进一步导致智能体间的通信瘫痪。一般地,网络攻击主要分为两大类:拒绝服务性攻击和欺骗攻击[12]。在文献[13]中,作者指出在一般情况下,拒绝服务性攻击的目标可以是传感器、控制器或智能体间的传输数据,从而导致信号在传输过程中发生数据丢包或延时的问题。相比之下,欺骗攻击则可能会绕过系统的检测技术并进入系统内部,进而操控控制指令或篡改传输数据,致使系统性能下降甚至变得不稳定[14]。
欺骗攻击可进一步分为虚假数据注入攻击和替代欺骗攻击等类型。虚假数据注入攻击主要是向控制器加入错误数据来破坏系统数据的完整性和准确性,如文献[15]将虚假数据引起的偏差加入到系统中来得到攻击下的系统动力学方程;文献[16]考虑了在传感器的数据传输通道中注入虚假数据情况下非线性多智能体系统一致性问题;文献[17]引入了伯努利变量来描述控制信号是否会受到虚假数据欺骗攻击。替代欺骗攻击则是指控制器受到攻击后会使控制信号被替代为相应的攻击信号,已有的关于欺骗攻击下的多智能体系统一致性的研究主要集中在传感器到控制器信道上的加性攻击,很少考虑替代攻击,文献[3]考虑替代攻击下利普希兹型非线性系统的一致性问题。值得注意的是,目前文献仅仅考虑虚假数据注入攻击或替代攻击[17-19],而同时考虑两者对一致性问题的影响则还未得到相应的研究。如何设计两种攻击下控制器的模型以及如何进一步得到系统实现一致性的条件是一个待解决的问题。
基于上述分析,本文主要研究了一类领导跟随随机多智能体系统在受到两种不同脉冲欺骗攻击情况下实现均方拟一致性问题。利用李雅普诺夫稳定性理论,本文给出了系统实现均方拟一致性的充分条件及相应的误差上界。
本文主要创新点如下:建立了同时受到两种脉冲欺骗攻击和随机噪声干扰下系统的模型;引入服从伯努利分布的随机变量来解决攻击类型的描述及其攻击成功与否的问题。
1 问题描述与预备知识 1.1 图论在多智能体系统中,智能体之间可以相互传递数据,而图论则是能够较好地描述上述关系的工具。一般地,一个图可表示为
考虑一类含有
| $ \begin{split} {\rm{d}}{{\boldsymbol{x}}_i}(t) = &[{\boldsymbol{A}}{{\boldsymbol{x}}_i}(t) + p(t){\boldsymbol{f}}(t,{{\boldsymbol{x}}_i}(t)) + {{\hat {\boldsymbol{u}}}_i}(t)]{\rm{d}}t + \\& \bar {\boldsymbol{\sigma}} (t,{{\boldsymbol{x}}_i}(t)){\rm{d}}{\boldsymbol{\omega}} (t),{\rm{ }}t{\rm{ }} \geqslant {t_0},{\rm{ }}i \in {\cal{N}} \end{split} $ | (1) |
式中:
| $\left\{ \begin{aligned} & \Pr (p(t) = 1) = \bar p \\& \Pr (p(t) = 0) = 1 - \bar p \end{aligned} \right.$ | (2) |
式中:
另一方面,领导者智能体的状态量假设为
| $ \begin{split} {\rm{d}}{{\boldsymbol{x}}_0}(t) = &[{\boldsymbol{A}}{{\boldsymbol{x}}_0}(t) + p(t){\boldsymbol{f}}(t,{{\boldsymbol{x}}_0}(t))]{\rm{d}}t + \\& { \bar {\boldsymbol{\sigma}} (t,{{\boldsymbol{x}}_0}(t)){\rm{d}}{\boldsymbol{\omega }}(t),\;\;\;\;\;\;t \geqslant {t_0}} \end{split} $ | (3) |
考虑控制协议同时遭受两种脉冲欺骗攻击即虚假数据注入脉冲攻击和替代脉冲攻击的影响。此外,引入两个伯努利随机变量来分别描述两种欺骗攻击成功与否。具体脉冲控制协议设计如式(4)所示。
| $ \begin{split} {{\hat {\boldsymbol{u}}}_i}(t) = &\sum\limits_{k = 1}^\infty {[(1 - {\alpha _i}(t)){\eta _k}(\sum\limits_{j \in {N_i}} {{a_{ij}}({{\boldsymbol{x}}_i}(t) - {{\boldsymbol{x}}_j}(t))} } + \\& {c_i}({{\boldsymbol{x}}_i}(t) - {{\boldsymbol{x}}_0}(t))) + {\alpha _i}(t){d_k}{{\boldsymbol{\xi}} _i}(t) + \\& {\beta _i}(t){\psi _k}({{\boldsymbol{x}}_i}(t) - {{\boldsymbol{x}}_0}(t))]\delta (t - {t_k}),{\rm{ }}i \in {\cal{N}} \end{split} $ | (4) |
式中:
| $\left\{ \begin{aligned} & \Pr ({\alpha _i}(t) = 1) = \bar \alpha ,{\rm{ }}\Pr ({\alpha _i}(t) = 0) = 1 - \bar \alpha \\& \Pr ({\beta _i}(t) = 1) = \bar \beta ,\;{\rm{ }}\Pr ({\beta _i}(t) = 0) = 1 - \bar \beta \end{aligned} \right.$ | (5) |
式中:
此外,假设由式(1)和(3)所组成的领导跟随随机多智能体系统状态初值为
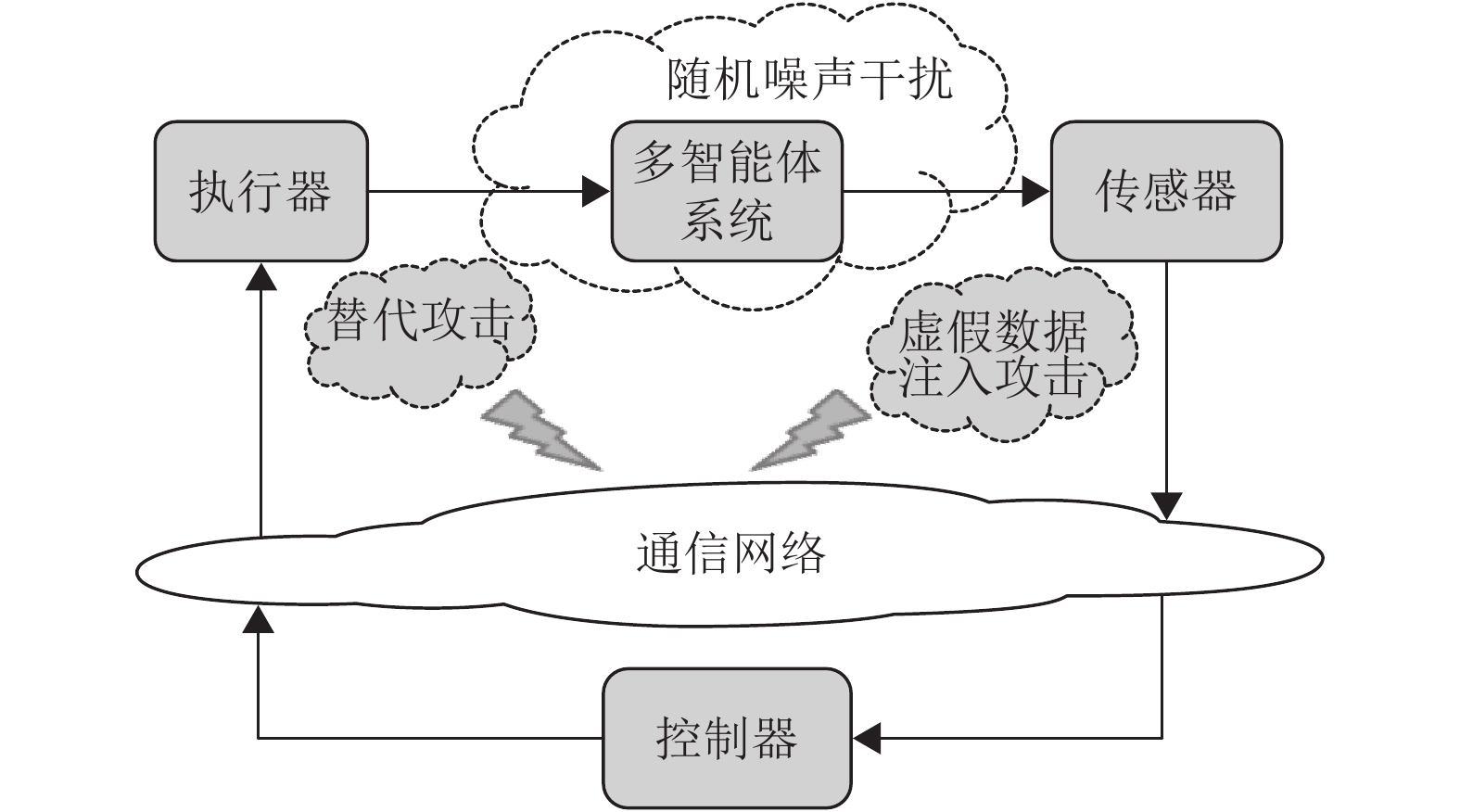
备注1 如图1所示,两种不同欺骗攻击发生在传感器到控制器或控制器到执行器的信道上,且是相互独立的。当替代攻击成功发生时,控制信号将会被篡改为欺骗攻击信号;当虚假数据注入攻击成功发生时,虚假数据则会附加到控制信号中。
|
图 1 两种不同欺骗攻击的攻击原理图 Figure 1 Configuration of two different deception attacks |
将控制协议(4)代入系统(1)中,可得到遭受两种欺骗攻击下跟随者的状态方程如下。
| $ \left\{\begin{aligned} {\rm{d}}{{\boldsymbol{x}}}_{i}(t)=&[{\boldsymbol{A}}{{\boldsymbol{x}}}_{i}(t)+p(t){\boldsymbol{f}}(t,{{\boldsymbol{x}}}_{i}(t))]{\rm{d}}t+\\& \bar{{\boldsymbol{\sigma}} }(t,{{\boldsymbol{x}}}_{i}(t)){\rm{d}}{\boldsymbol{\omega}} (t),\;\;t\geqslant{t}_{0},\;t\ne {t}_{k},\\ \Delta {{\boldsymbol{x}}}_{i}(t)=&{{\boldsymbol{x}}}_{i}({t}_{k}^+)-{{\boldsymbol{x}}}_{i}({t}_{k}^-)=\\& {\beta }_{i}({t}_{k}){\psi }_{k}({{\boldsymbol{x}}}_{i}({t}_{k}^-)-{{\boldsymbol{x}}}_{0}({t}_{k}^-))+{\alpha }_{i}({t}_{k}){d}_{k}{{\boldsymbol{\xi}} }_{i}({t}_{k})+\\& (1-{\alpha }_{i}({t}_{k})){\eta }_{k}\Bigg({\displaystyle \sum _{j\in {N}_{i}}{a}_{ij}({{\boldsymbol{x}}}_{i}({t}_{k}^-)-{{\boldsymbol{x}}}_{j}({t}_{k}^-))}+\Bigg.\\& \Bigg. {c}_{i}({{\boldsymbol{x}}}_{i}({t}_{k}^-)-{{\boldsymbol{x}}}_{0}({t}_{k}^-))\Bigg),\;\;t={t}_{k} \end{aligned}\right. $ | (6) |
式中:
为实现式(1)与式(3)所组成的领导跟随随机多智能体系统在两种欺骗攻击情况下的均方拟一致性,构建如下误差系统。
| $ \left\{\begin{aligned} {\rm{d}}{{\boldsymbol{e}}}_{i}(t)=&[{\boldsymbol{A}}{{\boldsymbol{e}}}_{i}(t)+p(t)\bar{{\boldsymbol{f}}}(t,{{\boldsymbol{e}}}_{i}(t))]{\rm{d}}t+\\& \hat{{\boldsymbol{\sigma}} }(t,{{\boldsymbol{e}}}_{i}(t)){\rm{d}}{\boldsymbol{\omega}} (t),\;\;t\geqslant{t}_{0},\;t\ne {t}_{k},\\ \Delta {{\boldsymbol{e}}}_{i}(t)=&{{\boldsymbol{e}}}_{i}({t}_{k}^+)-{{\boldsymbol{e}}}_{i}({t}_{k}^-) =\\& {\beta }_{i}({t}_{k}){\psi }_{k}{{\boldsymbol{e}}}_{i}({t}_{k}^-)+{\alpha }_{i}({t}_{k}){d}_{k}{{\boldsymbol{\xi}} }_{i}({t}_{k})+\\& (1-{\alpha }_{i}({t}_{k})){\eta }_{k}\Bigg({\displaystyle \sum _{j\in {N}_{i}}{a}_{ij}({{\boldsymbol{e}}}_{i}({t}_{k}^-)-{{\boldsymbol{e}}}_{j}({t}_{k}^-))}+\Bigg. {c}_{i}{{\boldsymbol{e}}}_{i}({t}_{k}^-)\Bigg),\\& t={t}_{k} \end{aligned}\right. $ | (7) |
式中:
备注2 两种欺骗攻击是相互独立的,也就是说它们的攻击时刻可以是不一样的,但均属于脉冲序列
此外,令
| $ \left\{\begin{aligned} & {\rm{d}}{\boldsymbol{e}}(t)=[({{\boldsymbol{I}}}_{N}\otimes {\boldsymbol{A}}){\boldsymbol{e}}(t)+\;p(t)\bar{{\boldsymbol{F}}}(t,{\boldsymbol{e}}(t))]{\rm{d}}t+\\&\qquad \tilde{{\boldsymbol{\sigma}} }(t,{\boldsymbol{e}}(t)){\rm{d}}{\boldsymbol{\omega}} (t),t\;\geqslant\;{t}_{0},\;\;t\ne {t}_{k}\\ & \Delta {\boldsymbol{e}}(t)=[({\eta }_{k}{\boldsymbol{H}}-{\eta }_{k}{\boldsymbol{G}}({t}_{k}){\boldsymbol{H}}+{\psi }_{k}{\boldsymbol{\varLambda}} ({t}_{k}))\otimes {{\boldsymbol{I}}}_{n}]{\boldsymbol{e}}({t}_{k}^-)+\\&\qquad {d}_{k}({\boldsymbol{G}}({t}_{k})\otimes {{\boldsymbol{I}}}_{n}){\boldsymbol{\xi}} ({t}_{k}),t={t}_{k} \end{aligned}\right.$ | (8) |
式中:
备注3 当
以下是本文用到的引理、假设及定义。
引理1 令向量
| $ {{\boldsymbol{\zeta}} }^{\rm{T}}{\boldsymbol{\varUpsilon}} +{{\boldsymbol{\varUpsilon}} }^{\rm{T}}{\boldsymbol{\zeta}} \;\leqslant\;\varepsilon {{\boldsymbol{\zeta}} }^{\rm{T}}{\boldsymbol{\zeta}} +{\varepsilon }^{-1}{{\boldsymbol{\varUpsilon}} }^{\rm{T}}{\boldsymbol{\varUpsilon}} .$ |
假设1 非线性函数
| $ \Vert {\boldsymbol{f}}(t,v)-{\boldsymbol{f}}(t,w)\Vert \;\leqslant\;\Vert \tilde{{\boldsymbol{J}}}(v-w)\Vert ,\;\forall v,w\in {\mathbb{R}}^{n}$ |
| $ \Vert \bar{{\boldsymbol{\sigma}} }(t,q)-\bar{{\boldsymbol{\sigma}} }(t,u)\Vert \;\leqslant\;\Vert {\boldsymbol{\varPhi}} (q-u)\Vert ,\;\forall q,u\in {\mathbb{R}}^{n}$ |
式中:
假设2 替代攻击信号
| $ {\Vert {\boldsymbol{\xi}} ({t}_{k})\Vert }^{2}\le\xi $ |
式中:
定义1 对于任意给定的系统初值
| $ \bar{{\cal{B}}}=\left\{{\boldsymbol{e}}(t)|\underset{t\to +\infty }{\mathrm{lim}}{\rm{E}}\left[{\Vert {\boldsymbol{e}}(t)\Vert }^{2}\right]\;\leqslant\;\bar{\varPi }\right\}$ |
则称由式(1)和式(3)组成的领导跟随随机多智能体系统实现均方拟一致性,且具有均方误差极限的上界
定义2 对函数
| $ \begin{split} {\cal{L}}V(t,y) =& {V_t}(t,y) + {V_y}(t,y)f(t,y) + \\&\frac{1}{2}{\rm{tr}}[{{\boldsymbol{h}}^{\rm{T}}}(t,y){V_{yy}}(t,y){\boldsymbol{h}}(t,y)] \end{split} $ |
式中:
| ${V_t}(t,y) = \frac{{\partial V(t,y)}}{{\partial t}},{V_{yy}}(t,y) = {\left( {\frac{{{\partial ^2}V(t,y)}}{{\partial {y_i}\partial {y_j}}}} \right)_{n \times n}},$ |
| ${V_y}(t,y) = \left( {\frac{{\partial V(t,y)}}{{\partial {y_1}}},\frac{{\partial V(t,y)}}{{\partial {y_2}}}, \cdots ,\frac{{\partial V(t,y)}}{{\partial {y_n}}}} \right)$ |
定理1 在假设1~2成立的情况下,若存在
| $\varsigma = \kappa (\kappa + d\varepsilon \bar \alpha ) \in \left( {0,1} \right)$ | (9) |
| $ 0\leqslant{\tau }_{\mathrm{sup}}<-\frac{\ln\varsigma }{{\lambda }_{\mathrm{max}}({\boldsymbol{\varXi}} )}$ | (10) |
式中:
| $\bar \varPi = \frac{{d\bar \alpha \xi ({\varepsilon ^{ - 1}}\kappa + d)}}{{{{{{{{{{\rm{e}}}}}}^{ - {\lambda _{\max }}(\varXi ){\tau _{\sup }}}} - \varsigma}} }}$ |
证明 考虑以下李雅普诺夫函数
| $V(t,{\boldsymbol{e}}(t)) = {{\boldsymbol{e}}^{\rm{T}}}(t){\boldsymbol{e}}(t)$ | (11) |
由伊藤公式可知,当
| ${\rm{d}}V(t,{\boldsymbol{e}}(t)) = {\cal{L}}V(t,{\boldsymbol{e}}(t)){\rm{d}}t + 2{{\boldsymbol{e}}^{\rm{T}}}(t)\tilde {\boldsymbol{\sigma}} (t,{\boldsymbol{e}}(t)){\rm{d}}{\boldsymbol{\omega}} (t)$ | (12) |
| $ \begin{split} {\cal{L}}V(t,{\boldsymbol{e}}(t)) =& 2{{\boldsymbol{e}}^{\rm{T}}}(t)[({{\boldsymbol{I}}_N} \otimes {\boldsymbol{A}}){\boldsymbol{e}}(t) + \\& p(t)\bar {\boldsymbol{F}}(t,{\boldsymbol{e}}(t))] + {\rm{tr}}[{{\tilde {\boldsymbol{\sigma}} }^{\rm{T}}}(t,{\boldsymbol{e}}(t))\tilde {\boldsymbol{\sigma}} (t,{\boldsymbol{e}}(t))] \end{split} $ | (13) |
由假设1可得
| $ \begin{split} & 2{{\boldsymbol{e}}}^{\rm{T}}(t)p(t)\bar{{\boldsymbol{F}}}(t,{\boldsymbol{e}}(t))\;\leqslant\;2\overline{p}\Vert \tilde{{\boldsymbol{J}}}\Vert {{\boldsymbol{e}}}^{\rm{T}}(t){\boldsymbol{e}}(t)+\\&\qquad 2(p(t)-\overline{p})\Vert \tilde{{\boldsymbol{J}}}\Vert {{\boldsymbol{e}}}^{\rm{T}}(t){\boldsymbol{e}}(t) \end{split}$ | (14) |
| $ {\rm{tr}}[{\tilde{{\boldsymbol{\sigma}} }}^{\rm{T}}(t,{\boldsymbol{e}}(t))\tilde{{\boldsymbol{\sigma}} }(t,{\boldsymbol{e}}(t))]\leqslant {{\boldsymbol{e}}}^{\rm{T}}(t)({{\boldsymbol{I}}}_{N}\otimes ({{\boldsymbol{\varPhi}} }^{\rm{T}}{\boldsymbol{\varPhi}} )){\boldsymbol{e}}(t)$ | (15) |
当
| $ \begin{split} & {\rm{{\rm E}[}}V(t + \iota ,{\boldsymbol{e}}(t + \iota ))] - {\rm{{\rm E}[}}V(t,{\boldsymbol{e}}(t))] = \\&\qquad \mathop \int \nolimits_t^{t + \iota }{\rm{{\rm E}[}}{\cal{L}}V(v,{\boldsymbol{e}}(v))]{\rm{d}}v \end{split} $ |
由此可知,有
当
| $ {D}^+{\rm{E}}[V(t,{\boldsymbol{e}}(t))]\;\leqslant\;{\lambda }_{\mathrm{max}}(\varXi ){\rm{E}}[V(t,{\boldsymbol{e}}(t))]$ | (16) |
式中,
| $ {\rm{E}}[V(t,{\boldsymbol{e}}(t))]\;\leqslant{\rm{ E}}[V({t}_{k-1},{\boldsymbol{e}}({t}_{k-1}))]{{\boldsymbol{{\rm{e}}}}}^{{\lambda }_{\mathrm{max}}(\varXi )(t-{t}_{k-1})}$ | (17) |
当
| $ \begin{split} {\boldsymbol{e}}({t_k}) = &[({{\boldsymbol{I}}_N} + {\eta _k}{\boldsymbol{H}} - {\eta _k}{\boldsymbol{G}}({t_k}){\boldsymbol{H}} + \\& {\psi _k}{\boldsymbol{\varLambda}} ({t_k})) \otimes {{\boldsymbol{I}}_n}]{\boldsymbol{e}}(t_k^ - ){\rm{ }} + {\rm{ }} {d_k}({\boldsymbol{G}}({t_k}) \otimes {{\boldsymbol{I}}_n}){\boldsymbol{\xi}} ({t_k}) \end{split} $ | (18) |
根据式(11)与式(18)可知
| $ \begin{split} & {\rm{{\rm E}[}}V(t_k^ + ,{\boldsymbol{e}}(t_k^ + ))] = {\rm{{\rm E}}}[{{\boldsymbol{e}}^{\rm{T}}}({t_k}){\boldsymbol{e}}({t_k})]{\rm{ = }} \\& {\rm{ {\rm E}[(}}{{\boldsymbol{e}}^{\rm{T}}}(t_k^ - ){{\boldsymbol{M}}^{\rm{T}}}({t_k}) + {{\boldsymbol{\xi}} ^{\rm{T}}}({t_k}){{\boldsymbol{W}}^{\rm{T}}}({t_k})) \times \\& {\rm{ }}({\boldsymbol{M}}({t_k}){\boldsymbol{e}}(t_k^ - ) + {\boldsymbol{W}}({t_k}){\boldsymbol{\xi}} ({t_k})){\rm{] = }} \\& {\rm{ {\rm E}[}}{{\boldsymbol{e}}^{\rm{T}}}(t_k^ - ){{\boldsymbol{M}}^{\rm{T}}}({t_k}){\boldsymbol{M}}({t_k}){\boldsymbol{e}}(t_k^ - ) + {\rm{ }} \\& {\rm{ }}{{\boldsymbol{e}}^{\rm{T}}}(t_k^ - ){{\boldsymbol{M}}^{\rm{T}}}({t_k}){\boldsymbol{W}}({t_k}){\boldsymbol{\xi}} ({t_k}){\rm{ + }} \\& {\rm{ }}{{\boldsymbol{\xi}} ^{\rm{T}}}({t_k}){{\boldsymbol{W}}^{\rm{T}}}({t_k}){\boldsymbol{M}}({t_k}){\boldsymbol{e}}(t_k^ - ) + \\& {\rm{ }}{{\boldsymbol{\xi}} ^{\rm{T}}}({t_k}){{\boldsymbol{W}}^{\rm{T}}}({t_k}){\boldsymbol{W}}({t_k}){\boldsymbol{\xi}} ({t_k}){\rm{] }} \end{split}$ | (19) |
式中
对于式(19)中的第一项,有
| $ \begin{split} & {\rm{{\rm E}[}}{{\boldsymbol{e}}^{\rm{T}}}(t_k^ - ){{\boldsymbol{M}}^{\rm{T}}}({t_k}){\boldsymbol{M}}({t_k}){\boldsymbol{e}}(t_k^ - )]{\rm{ = }} \\& {\rm{ {\rm E}[}}{{\boldsymbol{e}}^{\rm{T}}}(t_k^ - )(({{\boldsymbol{I}}_N} + {\eta _k}{\boldsymbol{H}} - {\eta _k}{\boldsymbol{HG}}({t_k}) + \\ & {\psi }_{k}{\boldsymbol{\varLambda}} ({t}_{k}))\otimes {{\boldsymbol{I}}}_{n})({{\boldsymbol{I}}}_{N}+{\eta }_{k}{\boldsymbol{H}}-{\eta }_{k}{\boldsymbol{G}}({t}_{k}){\boldsymbol{H}}+\\& {\psi }_{k}{\boldsymbol{\varLambda}} ({t}_{k}))\otimes {{\boldsymbol{I}}}_{n}){\boldsymbol{e}}({t}_{k}^-)]\leqslant\\& {(1 + \eta \theta (1 - \bar \alpha ) + \psi \bar \beta )^2}{\rm{{\rm E}}}[V(t_k^ - ,{\boldsymbol{e}}(t_k^ - ))]\leqslant\\& {\kappa ^2}{\rm{{\rm E}}}[V(t_k^ - ,{\boldsymbol{e}}(t_k^ - ))] \end{split} $ | (20) |
式中:
对式(19)中的第二项和第三项,结合引理1,
| $\begin{split} & {\rm{{\rm E}[}}{{\boldsymbol{e}}^{\rm{T}}}(t_k^ - ){{\boldsymbol{M}}^{\rm{T}}}({t_k}){\boldsymbol{W}}({t_k}){\boldsymbol{\xi}} ({t_k}){\rm{ + }} \\& {{\boldsymbol{\xi}} ^{\rm{T}}}({t_k}){{\boldsymbol{W}}^{\rm{T}}}({t_k}){\boldsymbol{M}}({t_k}){\boldsymbol{e}}(t_k^ - )] = \\& {\rm{E}}[{{\boldsymbol{e}}}^{\rm{T}}({t}_{k}^-)(({{\boldsymbol{I}}}_{N}+{\eta }_{k}{\boldsymbol{H}}-{\eta }_{k}{\boldsymbol{HG}}({t}_{k})+\\& {\psi }_{k}{\boldsymbol{\varLambda}} ({t}_{k}))\otimes {{\boldsymbol{I}}}_{n})({d}_{k}{\boldsymbol{G}}({t}_{k})\otimes {{\boldsymbol{I}}}_{n}){\boldsymbol{\xi}} ({t}_{k})+\\& {{\boldsymbol{\xi}} }^{\rm{T}}({t}_{k})({d}_{k}{\boldsymbol{G}}({t}_{k})\otimes {{\boldsymbol{I}}}_{n})(({{\boldsymbol{I}}}_{N}+{\eta }_{k}{\boldsymbol{H}}-\\& {\eta }_{k}{\boldsymbol{G}}({t}_{k}){\boldsymbol{H}}+{\psi }_{k}{\boldsymbol{\varLambda}} ({t}_{k}))\otimes {{\boldsymbol{I}}}_{n}){\boldsymbol{e}}({t}_{k}^-)]\leqslant\\& {d}_{k}\bar{\alpha }{\rm{E}}[{{\boldsymbol{e}}}^{\rm{T}}({t}_{k}^-)(({{\boldsymbol{I}}}_{N}+{\eta }_{k}{\boldsymbol{H}}-{\eta }_{k}{\boldsymbol{HG}}({t}_{k})+\\& {\psi }_{k}{\boldsymbol{\varLambda}} ({t}_{k}))\otimes {{\boldsymbol{I}}}_{n}){\boldsymbol{\xi}} ({t}_{k})+{{\boldsymbol{\xi}} }^{\rm{T}}({t}_{k})(({{\boldsymbol{I}}}_{N}+\\& {\eta }_{k}{\boldsymbol{H}}-{\eta }_{k}{\boldsymbol{G}}({t}_{k}){\boldsymbol{H}}+\\& {\psi }_{k}{\boldsymbol{\varLambda}} ({t}_{k}))\otimes {{\boldsymbol{I}}}_{n}){\boldsymbol{e}}({t}_{k}^-)]\leqslant\\& {d}_{k}\overline{\alpha }\kappa {\rm{E}}[{{\boldsymbol{e}}}^{\rm{T}}({t}_{k}^-){\boldsymbol{\xi}} ({t}_{k})+{{\boldsymbol{\xi}} }^{\rm{T}}({t}_{k}){\boldsymbol{e}}({t}_{k}^-)]\leqslant\\& {d}_{k}\overline{\alpha }\kappa {\rm{E}}[\varepsilon {{\boldsymbol{e}}}^{\rm{T}}({t}_{k}^-){\boldsymbol{e}}({t}_{k}^-)+{\varepsilon }^{-1}{{\boldsymbol{\xi}} }^{\rm{T}}({t}_{k}){\boldsymbol{\xi}} ({t}_{k})]\leqslant\\& d\varepsilon \overline{\alpha }\kappa {\rm{E}}[V({t}_{k}^-,{\boldsymbol{e}}({t}_{k}^-))] + d\overline{\alpha }\kappa {\varepsilon }^{-1}\xi \end{split}$ | (21) |
式中:
对式(19)中的最后一项,有
| $\begin{split} & {\rm{E}}[{{\boldsymbol{\xi}} }^{\rm{T}}({t}_{k}){{\boldsymbol{W}}}^{\rm{T}}({t}_{k}){\boldsymbol{W}}({t}_{k}){\boldsymbol{\xi}} ({t}_{k})]= \\& {\rm{E}}[{{\boldsymbol{\xi}} }^{\rm{T}}({t}_{k})({d}_{k}{\boldsymbol{G}}({t}_{k})\otimes {{\boldsymbol{I}}}_{n}) \times \\& ({d}_{k}{\boldsymbol{G}}({t}_{k})\otimes {{\boldsymbol{I}}}_{n}){\boldsymbol{\xi}} ({t}_{k})]\leqslant\\& {d}_{k}^{2}\overline{\alpha }{\rm{E}}[{{\boldsymbol{\xi}} }^{\rm{T}}({t}_{k}){\boldsymbol{\xi}} ({t}_{k})]\leqslant\;d^{2}\overline{\alpha }\xi \end{split}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ | (22) |
将式(20)~(22)代入式(19)中,有
| $ \begin{split} & {\rm{E[}}V({t}_{k}^+,{\boldsymbol{e}}({t}_{k}^+))]\leqslant\\&{\kappa }^{2}{\rm{E}}[V({t}_{k}^-,{\boldsymbol{e}}({t}_{k}^-))]+d\varepsilon \bar{\alpha }\kappa {\rm{E}}[V({t}_{k}^-,{\boldsymbol{e}}({t}_{k}^-))]+\\& {{d}}\bar{\alpha }\kappa {\varepsilon }^{-1}{{\xi}} +{d}^{2}\bar{\alpha }\xi \;\leqslant\\& \varsigma {\rm{E}}[V({t}_{k}^-,{\boldsymbol{e}}({t}_{k}^-))]+\overline{m} \end{split} $ | (23) |
式中:
对
| $\;\;\;\;\;\; {\rm{E[}}V(t,{\boldsymbol{e}}(t))]\leqslant\varsigma {{\rm{e}}}^{{\lambda }_{\mathrm{max}}(\varXi )(t-{t}_{0})}{\rm{E}}[V({t}_{0},{\boldsymbol{e}}({t}_{0}))]$ |
由此可知,当
| $ \;\;\;\begin{split} & {\rm{E[}}V({t}_{1},{\boldsymbol{e}}({t}_{1}))]\leqslant\varsigma {\rm{E}}[V({t}_{1}^-,{\boldsymbol{e}}({t}_{1}^-))]+\overline{m}\leqslant\\& \varsigma {{\rm{e}}}^{{\lambda }_{\mathrm{max}}(\varXi )({t}_{1}-{t}_{0})}{\rm{E}}[V({t}_{0},{\boldsymbol{e}}({t}_{0}))]+\overline{m} \end{split}$ |
对
| $ {\rm{E[}}V(t,{\boldsymbol{e}}(t))]\;\leqslant{\varsigma }^{2}{{\rm{e}}}^{{\lambda }_{\mathrm{max}}(\varXi )(t-{t}_{0})}{\rm{E}}[V({t}_{0},{\boldsymbol{e}}({t}_{0}))]+ \varsigma {{\rm{e}}}^{{\lambda }_{\mathrm{max}}(\varXi )(t-{t}_{1})}\overline{m}$ |
由此可知,当
| $\;\;\;\;\;\;\;\;\;\;\begin{split} & {\rm{E[}}V({t}_{2},{\boldsymbol{e}}({t}_{2}))]\leqslant\\& {\varsigma }^{2}{{\rm{e}}}^{{\lambda }_{\mathrm{max}}(\varXi )(t-{t}_{0})}{\rm{E}}[V({t}_{0},{\boldsymbol{e}}({t}_{0}))]+\varsigma \overline{m}{{\rm{e}}}^{{\lambda }_{\mathrm{max}}(\varXi )(t-{t}_{1})}+\overline{m} \end{split}$ |
通过迭代法,当
| $ \begin{split} & {\rm{E[}}V(t,{\boldsymbol{e}}(t))]\leqslant\\& {\varsigma }^{k}{{\rm{e}}}^{{\lambda }_{\mathrm{max}}(\varXi )(t-{t}_{0})}{\rm{E}}[V({t}_{0},{\boldsymbol{e}}({t}_{0}))]+\\& {\varsigma }^{k-1}\bar{m}{{\rm{e}}}^{{\lambda }_{\mathrm{max}}(\varXi )(t-{t}_{1})}+{\varsigma }^{k-2} \bar{m}{{\rm{e}}}^{{\lambda }_{\mathrm{max}}(\varXi )(t-{t}_{2})}+\cdots +\\& \overline{m}{{\rm{e}}}^{{\lambda }_{\mathrm{max}}(\varXi )(t-{t}_{k})}\leqslant\\& {\varsigma }^{k}{{\rm{e}}}^{{\lambda }_{\mathrm{max}}(\varXi )(t-{t}_{0})}{\rm{E}}[V({t}_{0},{\boldsymbol{e}}({t}_{0}))]+\\& \frac{\overline{m}{{\rm{e}}}^{{\lambda }_{\mathrm{max}}(\varXi ){\tau }_{\mathrm{sup}}}(1-{({{\rm{e}}}^{{\lambda }_{\mathrm{max}}(\varXi ){\tau }_{\mathrm{sup}}+\ln\varsigma })}^{\bar{k}})}{1-\varsigma {{\rm{e}}}^{{\lambda }_{\mathrm{max}}(\varXi ){\tau }_{\mathrm{sup}}}} \end{split}$ | (24) |
式中:
令
| $ \begin{split} & {\rm{E[}}V(t,{\boldsymbol{e}}(t))]\leqslant\frac{1}{\varsigma }{{\rm{e}}}^{\rho (t-{t}_{0})}{\rm{E}}[V({t}_{0},{\boldsymbol{e}}({t}_{0}))]-\\& \frac{\overline{m}{{\rm{e}}}^{-\ln\varsigma }{{\rm{e}}}^{\rho (t-{t}_{0})}}{1-\varsigma {{\rm{e}}}^{{\lambda }_{\mathrm{max}}(\varXi ){\tau }_{\mathrm{sup}}}}+\frac{\overline{m}}{{{\rm{e}}}^{-{\lambda }_{\mathrm{max}}(\varXi ){\tau }_{\mathrm{sup}}}-\varsigma } \end{split} $ | (25) |
因此,当
| $ \underset{t\to \infty }{\mathrm{lim}}{\rm{E}}\left[{\Vert {\boldsymbol{e}}(t)\Vert }^{2}\right]\;\leqslant\;\frac{\overline{m}}{{{\rm{e}}}^{-{\lambda }_{\mathrm{max}}(\varXi ){\tau }_{\mathrm{sup}}}-\varsigma }$ |
根据式(25)与定义1,取
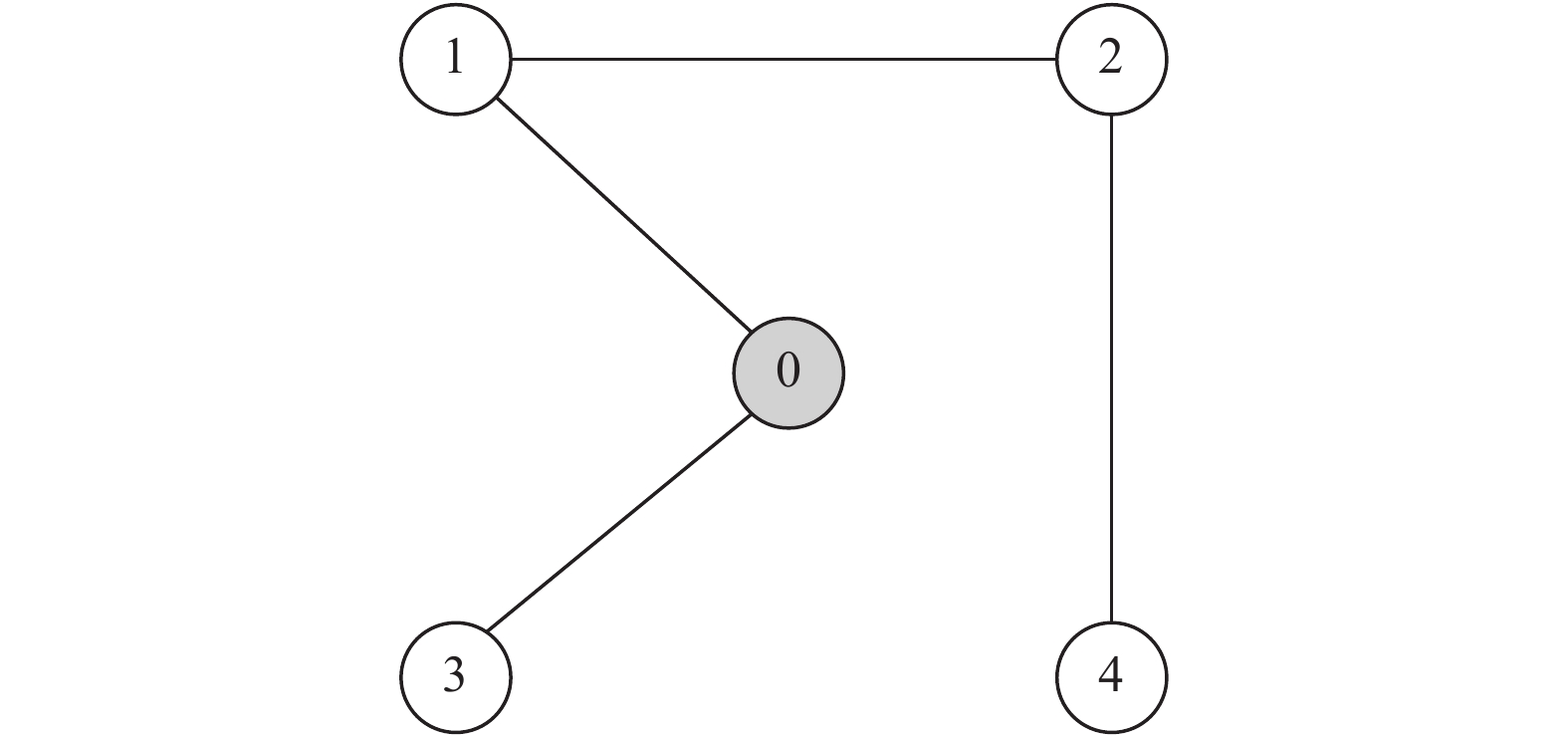
为验证本文结果的有效性,本节考虑由5个3维智能体所组成的蔡氏循环电路组合,其中包含1个领导者和4个跟随者。系统通信拓扑如图2所示。
|
图 2 循环电路组回路拓扑图 Figure 2 Topological diagram of each sub loop in the cycle circuit combination |
由图2可知,矩阵
| $\hat {\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} 1&{ - 1}&0&0 \\ { - 1}&2&0&{ - 1} \\ 0&0&0&0 \\ 0&{ - 1}&0&1 \end{array}} \right],\quad {\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} 1&{}&{}&{} \\ {}&0&{}&{} \\ {}&{}&1&{} \\ {}&{}&{}&0 \end{array}} \right],$ |
| ${\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} 2&{ - 1}&0&0 \\ { - 1}&2&0&{ - 1} \\ 0&0&1&0 \\ 0&{ - 1}&0&1 \end{array}} \right]$ |
设跟随者动力学方程(1)和领导者动力学方程(3)中状态为
| $ {\boldsymbol{A}}=\left[\begin{array}{ccc}-2.2\left(1-0.14\right)& 2.2& 0\\ 1& -1& 1\\ 0& -0.8& 0\end{array}\right]$ |
非线性函数选择
考虑式(4)所设计的控制协议,其中控制增益选择为
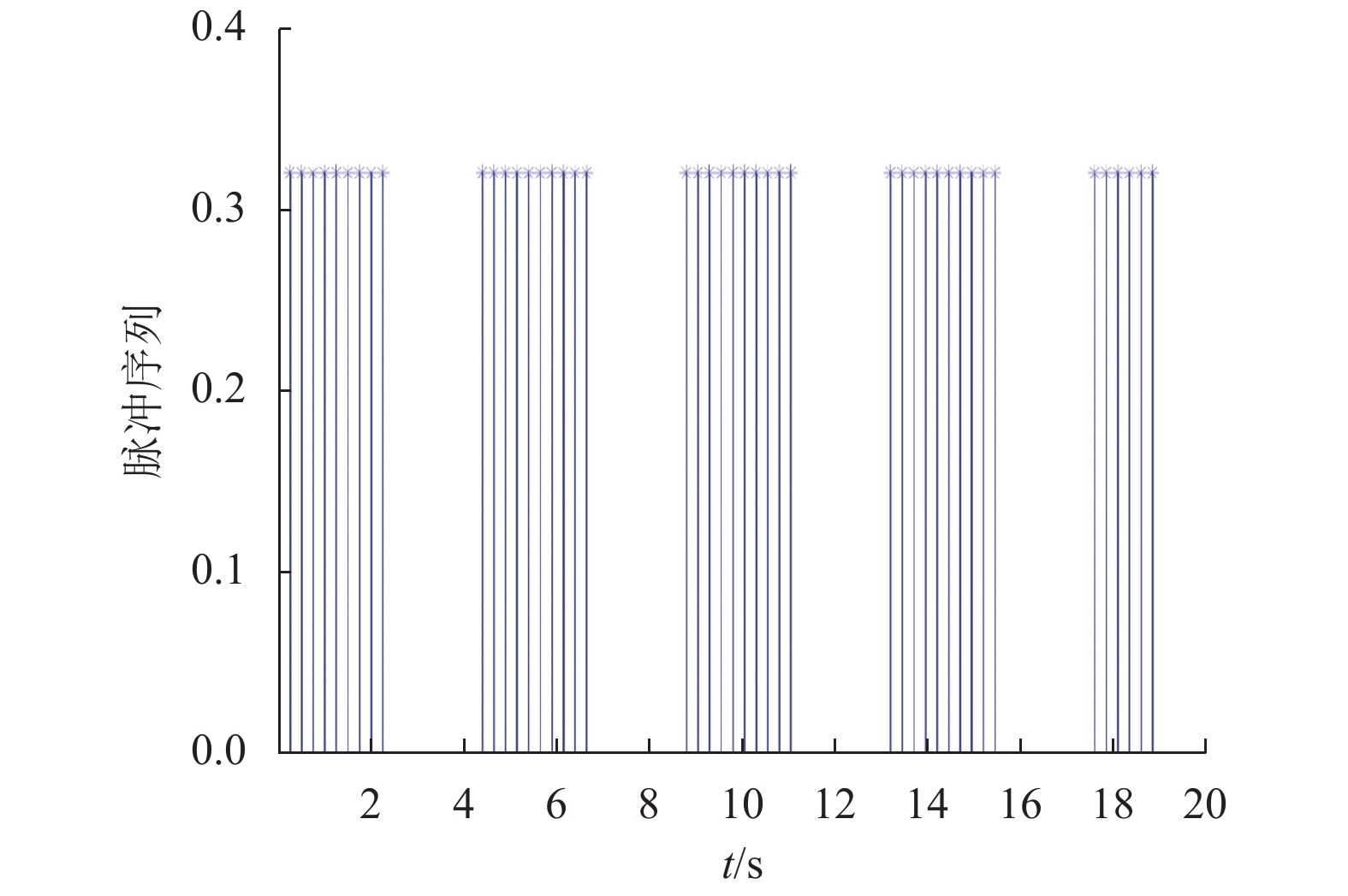
系统(1)采用的脉冲序列如图3所示,设最大控制脉冲间隔
|
图 3 系统(1)脉冲控制信号 Figure 3 The impulse control signal of system (1) |
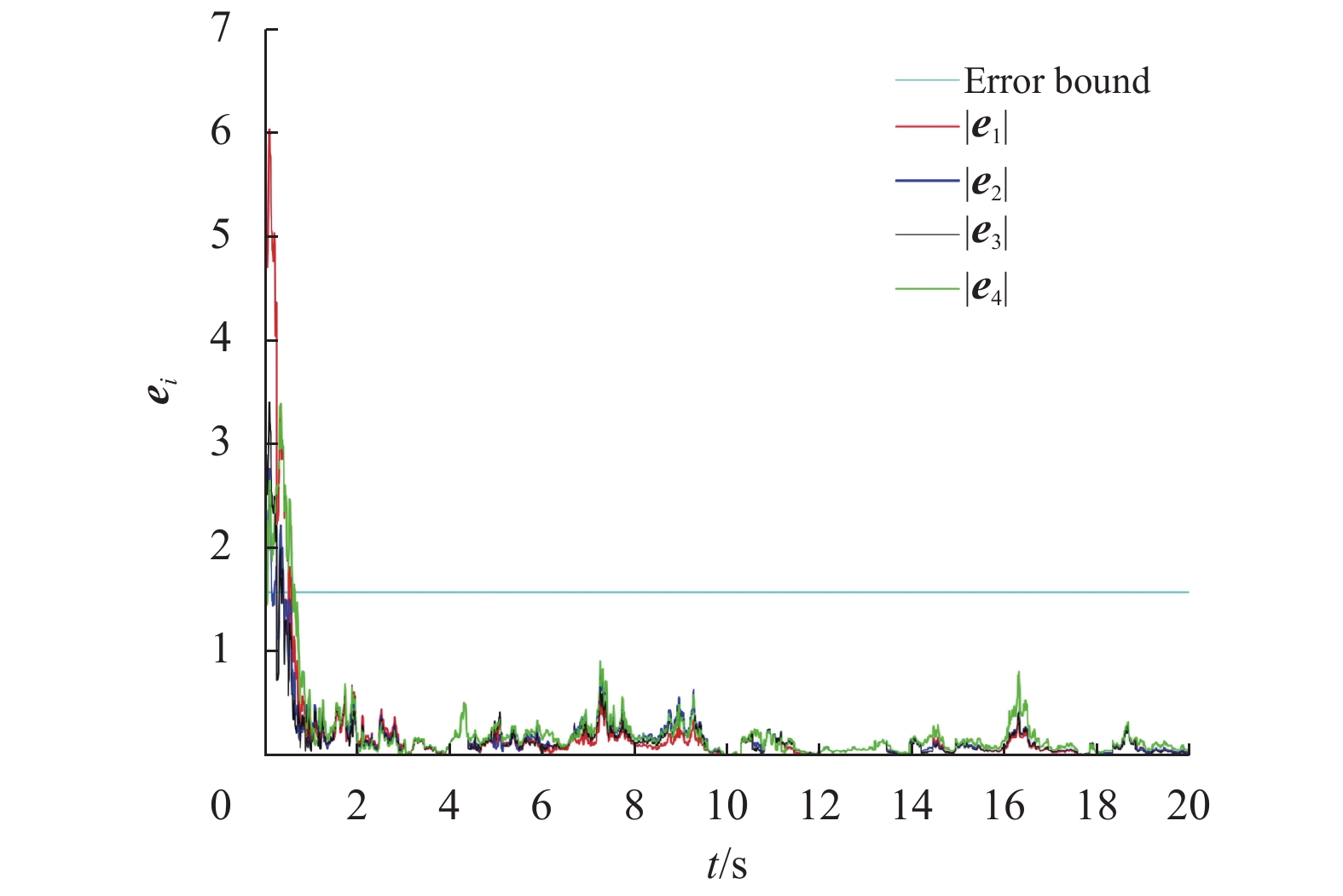
|
图 4 受到两种欺骗攻击时系统的误差轨迹图 Figure 4 The errors' trajectories of the system with two different deception attacks |
|
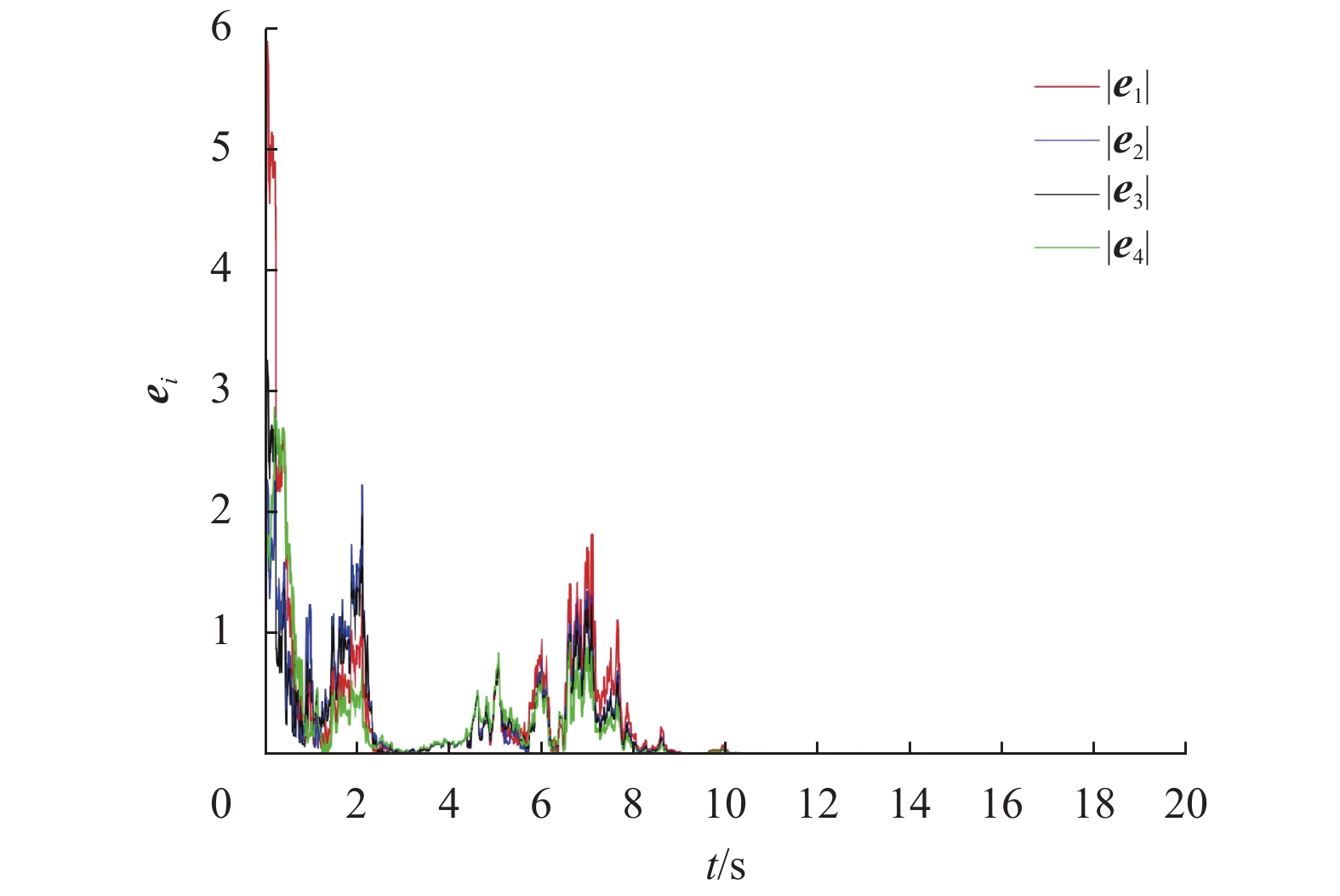
图 5 无欺骗攻击时系统的误差轨迹图 Figure 5 The errors' trajectories of the system without deception attacks |
假设系统初始时刻为
| $ \begin{split} & \left[ {{{\boldsymbol{x}}_0}\left( {{t_0}} \right),{{\boldsymbol{x}}_1}\left( {{t_0}} \right),{{\boldsymbol{x}}_2}\left( {{t_0}} \right),{{\boldsymbol{x}}_3}\left( {{t_0}} \right),{{\boldsymbol{x}}_4}\left( {{t_0}} \right)} \right] = \\& \quad \quad \,\left[ {\begin{array}{*{20}{c}} 1&{ - 0.5}&{ - 0.5}&{ - 1.5}&{2.5} \\ 1&2&{ - 1}&{ - 2}&1 \\ { - 2}&{ - 2.5}&{2.5}&2&{ - 1} \end{array}} \right] \end{split} $ |
此外,令
基于脉冲控制方法,本文研究了一类领导跟随随机多智能体系统在遭受替代攻击和虚假数据注入攻击下的均方拟一致性问题。不同于已有文献,本文同时考虑了两种不同脉冲欺骗攻击对系统均方拟一致性的影响,其中攻击模型采用两个服从伯努利分布的随机变量来描述不同攻击的成功与否,更适用于模拟现实应用中的情形。基于李雅普诺夫稳定性理论和相关随机过程知识,本文给出了两种不同脉冲欺骗攻击下系统实现均方拟一致性的充分条件,同时也给出了误差极限的上界。最后,通过数值仿真例子验证了研究结果的有效性。
| [1] |
周琪, 陈广登, 鲁仁全, 等. 基于干扰观测器的输入饱和多智能体系统事件触发控制[J].
中国科学: 信息科学, 2019, 49(11): 1502-1516.
ZHOU Q, CHEN G D, LU R Q, et al. Disturbance observer-based event triggered control for input saturated multi-agent systems[J]. Chinese Science: Information Science, 2019, 49(11): 1502-1516. |
| [2] |
张弘烨, 彭世国. 基于模型简化法的含有随机时延的多智能体系统一致性研究[J].
广东工业大学学报, 2019, 36(2): 86-90, 96.
ZHANG H Y, PENG S G. A research on the consensus problem of multi-agent systems with random time delays based on model reduction[J]. Journal of Guangdong University of Technology, 2019, 36(2): 86-90, 96. DOI: 10.12052/gdutxb.180084. |
| [3] |
HE W, MO Z, Han Q L, et al. Secure impulsive synchronization in Lipschitz-type multi-agent systems subject to deception attacks[J].
IEEE/CAA Journal of Automatica Sinica, 2020, 7(5): 1326-1334.
|
| [4] |
ZHOU Q, XU S, CHEN B, et al. Stability analysis of delayed genetic regulatory networks with stochastic disturbances[J].
Physics Letters A, 2009, 373(41): 3715-3723.
DOI: 10.1016/j.physleta.2009.08.036. |
| [5] |
HU M, GUO L, HU A, et al. Leader-following consensus of linear multi-agent systems with randomly occurring nonlinearities and uncertainties and stochastic disturbances[J].
Neurocomputing, 2015, 149: 884-890.
DOI: 10.1016/j.neucom.2014.07.047. |
| [6] |
ZHANG Z H, PENG S G, CHEN T. Leader-following mean square consensus of stochastic multi-agent systems with ROUs and RONs under periodically variable impulse time windows[J].
Neurocomputing, 2020, 412: 276-286.
DOI: 10.1016/j.neucom.2020.05.041. |
| [7] |
WANG F, ZHANG Y, ZHANG L, et al. Finite-time consensus of stochastic nonlinear multi-agent systems[J].
International Journal of Fuzzy Systems, 2020, 22(1): 77-88.
DOI: 10.1007/s40815-019-00769-w. |
| [8] |
GONG X, PAN Y J, LI J N, et al. Leader-following consensus for multi-agent systems with stochastic packet dropout[C]//2013 10th IEEE International Conference on Control and Automation (ICCA). Hangzhou: IEEE, 2013: 1160-1165.
|
| [9] |
YE D, YANG X. Distributed event-triggered consensus for nonlinear multi-agent systems subject to cyber attacks[J].
Information Sciences, 2019, 473: 178-189.
DOI: 10.1016/j.ins.2018.09.030. |
| [10] |
ZUO Z, CAO X, WANG Y. Security control of multi-agent systems under false data injection attacks[J].
Neurocomputing, 2020, 404: 240-246.
DOI: 10.1016/j.neucom.2020.04.109. |
| [11] |
FENG J, XIE J, WANG J, et al. Secure synchronization of stochastic complex networks subject to deception attack with nonidentical nodes and internal disturbance[J].
Information Sciences, 2021, 547: 514-525.
DOI: 10.1016/j.ins.2020.08.085. |
| [12] |
HE W, QIAN F, HAN Q L, et al. Almost sure stability of nonlinear systems under random and impulsive sequential attacks[J].
IEEE Transactions on Automatic Control, 2020, 65(9): 3879-3886.
DOI: 10.1109/TAC.2020.2972220. |
| [13] |
ZHAO L, YANG G H. Cooperative adaptive fault-tolerant control for multi-agent systems with deception attacks[J].
Journal of the Franklin Institute, 2020, 357(6): 3419-3433.
DOI: 10.1016/j.jfranklin.2019.12.032. |
| [14] |
LI X M, ZHOU Q, LI P, et al. Event-triggered consensus control for multi-agent systems against false data-injection attacks[J].
IEEE Transactions on Cybernetics, 2019, 50(5): 1856-1866.
|
| [15] |
HE W, GAO X, ZHONG W, et al. Secure impulsive synchronization control of multi-agent systems under deception attacks[J].
Information Sciences, 2018, 459: 354-368.
DOI: 10.1016/j.ins.2018.04.020. |
| [16] |
DING D, WANG Z, HO D W C, et al. Observer-based event-triggering consensus control for multiagent systems with lossy sensors and cyber-attacks[J].
IEEE Transactions on Cybernetics, 2016, 47(8): 1936-1947.
|
| [17] |
MA L, WANG Z, YUAN Y. Consensus control for nonlinear multi-agent systems subject to deception attacks[C]//2016 22nd International Conference on Automation and Computing (ICAC). Colchester: IEEE, 2016: 21-26.
|
| [18] |
伍益明. 恶意攻击下的多智能体系统安全一致性问题研究[D]. 杭州: 浙江工业大学, 2016.
|
| [19] |
常盛. 考虑虚假数据攻击的电力信息物理系统检测方法研究[D]. 秦皇岛: 燕山大学, 2020.
|
 2022, Vol. 39
2022, Vol. 39

