2. 中国科学院 云计算产业技术创新与育成中心,广东 东莞 523808
2. Cloud Computing Center, Chinese Academy of Sciences, Dongguan 523808, China
资源描述框架(Resource Description Framework,RDF)[1]是W3C提出的一种标准元数据模型,用于以机器可读的方式描述Web资源。RDF数据通常被定义为三元组〈s,p,o〉的形式,其中,s(subject)表示主题,p(predicate)表示谓词,o(object)表示宾语,谓词表示主题与宾语之间的语义关系。RDF数据集通常以图的形式表示,图中的顶点表示主题与宾语,而谓词被映射到连接两个顶点的有向边,它表示顶点之间的语义关系。SPARQL是为RDF开发的查询语言,可实现在大规模RDF数据图中迅速地查找符合条件的结果,其查询中的核心问题就是子图模式匹配[2-3]。换言之,针对RDF图数据的模式匹配过程是对大规模RDF数据图进行搜索并找到同构于查询图的数据子图的遍历过程。因此,该问题也可以称为子图匹配问题。子图匹配是图挖掘中一个重要的分支,它作为实现图数据上高效查询的基本操作,也被广泛应用于社会安全、社交网络和生物化学等各个领域的实际问题中[4-5]。随着大数据时代的到来,RDF数据规模逐渐增大,语义关系在RDF数据模型中的描述也更加复杂,随之查询过程更加复杂,查询效率较低。因此,大规模图数据[6-8]的子图匹配问题成为学术界和工业界面临的挑战。
大规模图数据上的子图匹配问题已被证明是一个NP问题,Ullmann提出Ullmann算法[9]查找同构子图时采用深度优先搜索方法将其依次找出。Cordella等[10]提出VF2算法,在Ullmann算法的基础上加入了剪枝操作和搜索匹配,提高了算法运行效率。GraphQ算法[11]数据邻接状态和深度信息进行剪枝操作减少时间开销。GADDI算法[12]在过滤备选节点时采用了构建邻接辨别子结构距离的方法,利用回溯法得到候选子图并完成子图匹配。张硕等[13]提出COPESl算法,采用图集压缩组织方法将多个图结构化地组织起来,同时给出一个基于图挖掘的索引特征生成方法。TurboISO算法[14]为了减小候选节点范围,将查询图构建成NEC-Tree结构形式,并通过深度优先搜索方法进行匹配。对于小规模的单图或图集来说,这些方法比较适用,但无法满足大规模数据图的子图匹配的精确性和高效率的需求。
根据RDF数据图的子图匹配定义,有2种方法来解决匹配问题[15-16]。一种是利用子图同构的精确RDF图匹配算法,其思想是将图G及其标签绑定中所有可能的子图与模式图Q进行比较并获取所有候选子图,然后检查支配关系并返回最佳匹配结果。但是该方法在响应时间上效率不高,可能会产生大量不必要的中间结果,需要对Q与G进行大量子图同构检验,其算法复杂度很高。另一种方法采用近似匹配策略,以减少耗时的穷举搜索,该方法适当降低子图同构和其他传统图相似度量的刚性结构和标签匹配约束。然而,现有的图匹配算法忽略了RDF图的许多特性。例如,这些算法在RDF图中只考虑顶点和边的相似性,而不考虑顶点和边之间的结构。更重要的是,这些算法忽略了资源之间的语义关系,而这些语义关系对于实际应用中的子图匹配问题来说至关重要。
针对以上问题,本文提出基于路径适配的大规模RDF数据子图匹配算法。该算法选择的路径不是以匹配顶点为基本单元,而是基于路径索引搜索子图。首先将模式图分解为一组从根顶点开始到目的顶点结束的路径集;然后将这些路径与数据图进行匹配;并重建与查询路径最匹配的候选路径以生成最终匹配结果。实验测试了在不同数据集上的路径索引构建时间以及F-measure值,与Spath算法、Sapper算法和SQM算法相比,算法查询准确率更高,且具有更高的查询效率。
1 基本概念RDF数据图G=(VG, EG, LG),其中,VG是一组有限的顶点,EG
查询图Q=(VQ, EQ, LQ),其中,VQ是查询图中顶点的集合,EQ是查询图中边的集合,LQ是查询图中顶点对应的标签集合。
定义3 RDF图路径[16]。
在RDF图的上下文中,不同的路径表示顶点之间不同的语义关系。对于一个RDF图,它的根顶点是一个入度为零的顶点,而目标顶点是一个出度为零的顶点。假设G=(V, E, L)是一个RDF图。G中的路径p被定义为不同顶点的有限序列p=v1,v2,···,vn,其中,vi∈V和(vi,vi+1)∈E且i∈[1, n−1]。因为RDF图的结构中不但有顶点,而且边也有标签,所以RDF图的路径表达式可以描述为“顶点−边”交替的序列。
定义4 子图匹配。
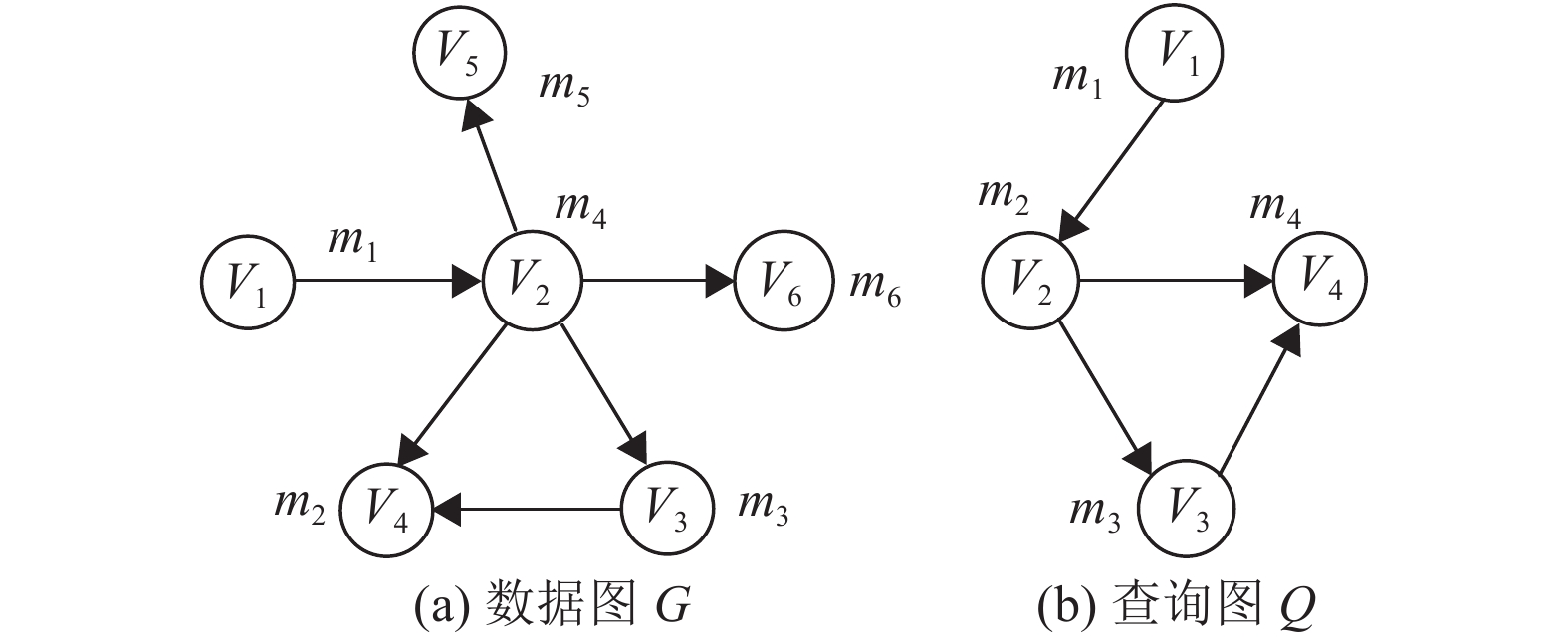
给定一个RDF数据图G和查询图Q,子图匹配查询由元素(顶点和边)匹配、结构匹配等部分组成,其答案是一组子图M,这样子图m∈M类似于查询图。如图1所示,图1(a)表示数据图G,图1(b)表示查询图Q,对于查询图Q,数据图G的子图匹配结果为(m1, m4, m3, m2)。
|
图 1 子图匹配示例 Figure 1 Example of subgraph matching |
子图查询用于识别查询子图在RDF数据图中的出现次数。查询图Q=(VQ, EQ, LQ)是一个RDF图,其中每个顶点v∈VQ用标签LQ标记。查询图指定了数据图G的子图必须满足的结构和语义要求,即:子图查询以查询图Q作为输入,检索包含或类似于查询图的数据图G,并返回检索到的图或由检索到的图组成的新图。
2 基于路径适配的子图匹配算法 2.1 路径适配虽然树和图可以保存更多的结构信息,但它们潜在的庞大规模和昂贵的剪枝成本,甚至超过了搜索空间剪枝的优势,因此路径作为合适的索引模式比树和图更有优势。为了将数据路径与输入查询路径进行比较,并确定哪个数据路径与查询路径最相似,需为路径定义一个距离度量,类似于使用编辑操作定义字符串,通过定义路径编辑距离,即通过编辑操作更改路径,直到存在与查询路径相等的路径。
定义5 编辑操作。
给定一个RDF路径,基本的路径编辑操作包括:替换RDF实体或文字、替换RDF属性、删除一个RDF实例或文字、删除一个RDF属性、插入一个RDF实例或文字、插入一个RDF属性。
定义6 编辑路径。
给定一个RDF路径p和一个编辑序列T=(ω1,ω2,ω3,···,ωn)的编辑操作,编辑路径T(p)=ωn(···ω2(ω1(p))···)。每个基本路径编辑操作ωi被分配一个特定的代价c(ωi)。代价c(ωi)根据编辑操作的类型和所涉及的RDF元素性质而变化。例如,修改顶点标签与顶点插入关系不大,因为后者增加了路径之间的语义距离。显然,如何确定路径中元素组件的相似性和定义编辑操作的代价是关键问题。
将p转化为T(p)的总代价为c(T)=
定义7 路径编辑距离。
给定两条路径p和p',定义p和p'之间的路径编辑距离为:dist(p, p')=
RDF图中的每个元素都依赖于图的结构。相应地,由图中的一些基本元素组成的子结构(如路径或子图)存在的匹配度必须依赖于元素的相对匹配度。例如,路径存在的匹配度与路径中每个元素(顶点和边)的相对匹配度相关。
定义8 假设G=(V,E,L)是一个RDF图,
其中,tm是一个特定于应用的聚合函数,选择最小值作为目标函数,即总体匹配度值
RDF图的不同路径表示RDF图中顶点之间的不同关系。RDF图的路径可以由更多RDF三元组组成,作为“顶点−边”交替序列。因此,可以通过聚合组成匹配路径的三元组集合的匹配度来计算匹配路径的绝对匹配度。
2.3 子图匹配算法根据上述定义,数据路径与输入查询路径之间的路径编辑距离越小,两者越相似,可以通过计算路径上对齐来计算图的相似度。查询图Q在数据图G上的匹配结果就是构成G的连通分量的Q的所有路径的匹配集。为了提高在大规模RDF数据图中的子图匹配准确性和效率,提出基于路径适配的子图匹配算法,算法主要分为3个阶段:
(1) 数据预处理:建立图索引结构。采用上下文感知的路径索引,以获取关于图路径的详细信息,实现对候选匹配项的高效检索。为了提取到达给定顶点V的所有路径的集合,使用广度优先搜索从根开始探索G。为了提高基于路径的查询处理效率,使用反向路径(目标顶点到根顶点)表达式以跳过代价昂贵的图遍历,并将存储的所有根到当前顶点的对应路径表达式构建B+树索引。路径索引包含了RDF图中从当前顶点到所有根的路径表达式,此外,通过相应聚合函数,预先计算并存储每个路径的匹配度。
(2) 查询处理:查询处理由路径分解、寻找候选路径和拼接候选路径3个子阶段组成,图2给出了在RDF数据图G上查询图Q的基本过程。具体步骤如下:① 路径分解。将查询图划分为一组路径Q={q1,q2,···,qk},为便于重构答案子图,采用k-partition交集图保存图查询的结构信息。在k-partition交集图中,一个顶点对应于一个查询路径,而一条边(qi,qj)表示路径qi和qj路径至少共享一个公共顶点,即路径qi可以和qj连接,且它们之间至少有一个交点。② 寻找候选路径。对于每个查询路径q∈Q,使用路径之间的编辑距离dist(q, p)查询路径和候选路径过滤后的匹配集。③ 拼接候选路径。使用图探索算法重构候选路径以获得完整的结果匹配,通过在k-partition交集图中执行消息传递,得到的是包含在G中的一组近似子图。然后,根据路径编辑距离对实际匹配的答案进行排序。

|
图 2 查询处理阶段图 Figure 2 Query processing phase diagram |
(3) 图匹配处理:通过选择最相关的路径并将之与每个集合的路径编辑距离最低的路径连接起来,生成完整的查询匹配。连接条件是路径p和p'之间的连接谓词的数量等于路径q和q'之间的谓词的数量,其中q和q'分别是对应于包含p和p'的集合的路径。
通过以上描述,可以得到基于路径适配的子图匹配算法过程如下:
输入:数据图G,k-partition交集图,所需答案的数量k
输出:查询图Q的前k个近似答案集
将ApproximateAnswersSet的初始值为空集;
当|ApproximateAnswersSet|始终小于k且CandidateSet值不为空时,则ans输出结果为空集;
将k-partition交集图中maxCardinality赋值到q;
将CandidateSet.get(q)赋值到cn;
将cn.dequeueTop()赋值到p;
将集合q赋值到V;
将集合q加入到ans中,结果赋值到ans;
对(Graph, q, p, ans, CandidateSet, k-partitionIntersection V)进行广度优先搜索;
输出ApproximateAnswersSet.put(ans);
返回ApproximateAnswersSet;
循环(p, ans, CandidateSer, k-partitionIntersectionGraph, q, V)的广度优先搜索的执行操作如下;
当(q, q')∈k-partitionIntersectionGraph时,
若q′
cn=CandidateSet.get(q);
p=cn.dequeueTop();
若|L(p)∩L(p')|==|L(q)∩L(q')|那么
ans=ans∪{p'};
π[q']=q;
将(p', ans, CandidateSet, k-partitionIntersection Graph, q', V)进行广度优先搜索;
V=V∪{q'};
在匹配过程中,从一条路径的匹配开始,逐步增加连接路径的匹配。一旦获得了候选集,图搜索算法将通过连接候选集中最相近的路径的方法来执行。首先将结果集ApproximateAnswersSet初始化为一个空集,如果连接过程中没有结果加入,则答案集ans输出空集。如果不能生成k个答案,并且集合候选集CandidateSet不为空,通过选择并组合每个集合候选集的编辑距离按递增顺序排列的路径,得到前k个答案。然后将答案集进行初始化,并选择k-partition交集图中与现有路径重叠顶点(连接谓词)最多的路径q。选择路径q对应的集合cn,并从cn中取出顶层路径p。将路径q添加到访问的匹配路径集合V中,在答案集ans中加入p。通过广度优先搜索遍历获得完整的答案,如函数BFS-visit中所示。最后,将完整答案包含在近似答案集中。通过使用该策略,如果不能找到查询图Q的k个近似答案,则该过程停止。
2.4 算法复杂性在数据预处理中,需要通过遍历RDF图G来构建路径索引结构。对于每个顶点V,采用一种优化的方法实现,即从根顶点进行广度优先搜索遍历来收集路径信息。假设根顶点在G中的平均次数为d,可以直观地说明数据预处理阶段的时间复杂度为O(|V|×d),|V|为RDF图G中的顶点数,d为最大顶点度。
路径分解的核心过程本质上是广度优先搜索处理。广度优先搜索中每个顶点最多只排队一次,复杂度是O(|VQ|)。每条边最多被检查一次,复杂度是O(|EQ|)。因此,子步骤的总运行时间为O(|VQ|+|EQ|),|VQ|和|EQ|分别为查询图Q的顶点数和边数。
寻找候选路径步骤的复杂度为|P|×O(D),其中|P|为集合P中查询路径的数量,D为索引检索到的路径数量,在最坏情况下,与数据的大小成正比。也就是说,必须执行D个插入到候选集,最多执行|P|次。
在查询匹配步骤中,它最多迭代k次,k是返回答案的数量。在每次迭代中,都有一次调用函数BFS-visit,该函数探索k-partition交集图。在最坏的情况下,它的代价是O(h×D),因为它检查h乘以G中的每条数据路径,其中h是k-partition交集图的深度。因此该子步骤的复杂度为O(k×h×D),通过k次调用函数BFS-visit来探索k-partition交集图,即O(h×D)。
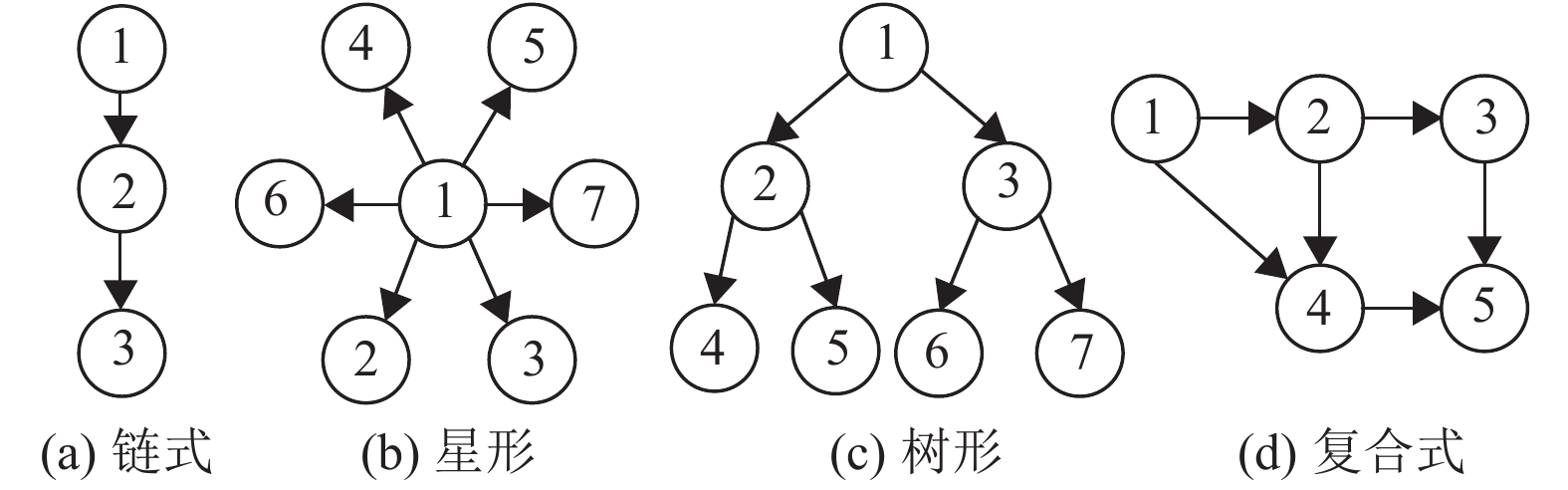
3 实验结果与分析本文实验配置采用Windows10 64位系统,Intel Core(TM) i7-10710U CPU,16 GB内存,实验采用的RDF数据集是来自IMDB的真实子集[16],利用RDF数据构造数据图,其中每个三元组都对应一条连接2个顶点的边,将每个顶点增加一个顶点标签。通过从数据图中随机选择子图,实验中使用的查询图模式有4种,如图3所示。图3(a)为2条路径的链式查询模式。图3(b)是一个简单的、高选择性的星形查询模式,从中心顶点开始,可以分解为6条路径。图3(c)是一个树形查询模式,从根顶点到叶子顶点可以分解为6条路径。图3(d)是组成从根顶点到目标顶点的查询路径的复合式查询模式。
|
图 3 数据集模式图 Figure 3 Data set model diagram |
针对不同RDF子集进行实验测试,得到整个数据预处理阶段基于路径的图索引构建时间和索引路径的数量如表1所示。由表1可知,构建索引的时间和路径数将会随着改变RDF数据图大小而变化,索引时间的增加幅度小于图大小的增加幅度。例如,系统用1563 ms从60 K的3倍数量创建的数据图构建147265条索引路径,尽管60 K图比10 K图大6倍,但索引时间平均增加了2倍。
| 表 1 索引构建对比 Table 1 Index building comparison |
为了验证该子图匹配算法的有效性与合理性。对于每个查询,对有效性的评价基准分别进行测试:(1) 查准率(P)表示返回的相关解与系统找到的所有解的比值;(2) 查全率(R)表示返回的相关解决方案(以RS为单位)占所有解决方案的比值;(3) F-measure(F-M)结合了Precision和Recall的结果,反映了算法的实际效果,即F-M=(2PR)/(R+P)。
通过将RDF图路径适配算法与Spath算法、Sapper算法和SQM算法在数据集上的有效性进行对比,且对比3种算法的R值、P值和F-M值,结果如表2所示。
| 表 2 路径适配算法与其他算法比较 Table 2 The path adaptation algorithm compared with other algorithms |
通过表2测试数据可知,本文算法在查准率R值、查全率P值和F-measure值这3个数据方面都优于其他3种算法,且能够更好地利用结构信息的F-measure值。同时,所有算法的查全率R都会降低结果的质量,因为,随着路径长度的增加,寻找候选路径的搜索空间也会增加,这会导致返回更多的中间匹配项。
4 结语为了提高在大规模图数据上查询图的查询效率,本文提出了一种基于路径适配的大规模RDF数据图上的子图匹配算法,即基于路径的解决方案。该方案将查询图分解为一组可能重叠的路径,找到单个路径的匹配项,并根据特定的上下文条件选取具有良好选择性的可能匹配项子集作为候选项。候选路径进一步连接在一起,以帮助恢复查询图,以最终完成图查询处理。最后将该方法与3种代表性图匹配算法在数据集上进行了比较。实验结果表明,该方法在路径索引构建、有效性方面优于其他方法。
| [1] |
关皓元, 朱斌, 李冠宇, 等. 基于资源描述框架图切分与顶点选择性的高效子图匹配算法[J].
计算机应用, 2019, 39(2): 360-369.
GUAN H Y, ZHU B, LI G Y, et al. Efficient subgraph matching method based on resource description framework graph segmentation and vertex selectivity[J]. Journal of Computer Applications, 2019, 39(2): 360-369. DOI: 10.11772/j.issn.1001-9081.2018061262. |
| [2] |
YU J, LIU X M, LIU Y B, et al. Multiple pattern graph correlations for efficient graph pattern matching[C]//2017 IEEE/ACS 14th International Conference on Computer Systems and Applications. Hammamet: IEEE, 2017: 469-474.
|
| [3] |
关皓元, 朱斌, 李冠宇, 等. 基于RDF图结构切分的高效子图匹配方法[J].
计算机应用, 2018, 38(7): 1898-1904.
GUAN H Y, ZHU B, LI G Y, et al. Efficient subgraph matching method based on structure segmentation of RDF graph[J]. Journal of Computer Applications, 2018, 38(7): 1898-1904. |
| [4] |
MA Z M, CAPRETZ M A M, YAN L. Storing massive resource description framework(RDF) data: a survey[J].
Knowledge Engineering Review, 2016, 31(4): 391-413.
DOI: 10.1017/S0269888916000217. |
| [5] |
罗国辉, 林穗, 姜文超. 一种基于二进制编码处理的数字保序匹配算法[J].
广东工业大学学报, 2017, 34(5): 56-59.
LUO G H, LIN S, JIANG W C. A digital order-preserving-matching algorithm based on binary coding processing[J]. Journal of Guangdong University of Technology, 2017, 34(5): 56-59. DOI: 10.12052/gdutxb.160157. |
| [6] |
于静, 刘燕兵, 张宇, 等. 大规模图数据匹配技术综述[J].
计算机研究与发展, 2015, 52(2): 391-409.
YU J, LIU Y B, ZHANG Y, et al. Survey on large-scale graph pattern matching[J]. Journal of Computer Research and Development, 2015, 52(2): 391-409. DOI: 10.7544/issn1000-1239.2015.20140188. |
| [7] |
许文, 宋文爱, 富丽贞, 等. 面向大规模图数据的分布式子图匹配算法[J].
计算机科学, 2019, 46(4): 28-35.
XU W, SONG W A, FU L Z, et al. Distributed subgraph matching algorithm for large scale graph data[J]. Computer Science, 2019, 46(4): 28-35. DOI: 10.11896/j.issn.1002-137X.2019.04.005. |
| [8] |
李龙洋, 董一鸿, 施炜杰, 等. SQM: 基于Spark的大规模单图上的子图匹配算法[J].
计算机应用, 2019, 39(1): 46-50.
LI L Y, DONG Y H, SHI W J, et al. SQM: subgraph matching algorithm for single large-scale graphs under Spark[J]. Journal of Computer Applications, 2019, 39(1): 46-50. DOI: 10.11772/j.issn.1001-9081.2018071594. |
| [9] |
ULLMANN J R. An algorithm for subgraph isomorphism[J].
Journal of the ACM, 1976, 23(1): 31-42.
DOI: 10.1145/321921.321925. |
| [10] |
CORDELLA L P, FOGGIA P. A (sub)graph isomorpism algorithm for matching large graphs[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(10): 1367-1372.
DOI: 10.1109/TPAMI.2004.75. |
| [11] |
HE H, SINGH A K. Graphs-at-a-time: query language and access methods for graph data bases[C]//Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data. New York: ACM, 2008: 405-418.
|
| [12] |
ZHANG S, LI S, YANG J. GADDI: distance index based subgraph matching in biological networks[C]//Proceedings of the 12th International Conference on Extending Database Technology: Advances in Database Technology. New York: ACM, 2009: 192-203.
|
| [13] |
张硕, 李建中, 高宏, 等. 一种多到一子图同构检测方法[J].
软件学报, 2010, 21(3): 401-414.
ZHANG S, LI J Z, GAO H, et al. Approach for efficient subgraph isomorphism testing for multiple graphs[J]. Journal of Software, 2010, 21(3): 401-414. DOI: 10.3724/SP.J.1001.2010.03478. |
| [14] |
HAN W S, LEE J, LEE J H. TurboISO: towards ultrafast and roubst subgraph isomorphism search in large graph databases[C]//Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data. New York: ACM, 2013: 337-348.
|
| [15] |
孙云浩, 李逢雨, 李冠宇, 等. 面向RDF图的多模式匹配方法[J].
计算机工程与应用, 2020, 56(13): 84-92.
SUN Y H, LI F Y, LI G Y, et al. Multi-pattern matching method for RDF graph[J]. Computer Engineer and Applications, 2020, 56(13): 84-92. DOI: 10.3778/j.issn.1002-8331.1905-0266. |
| [16] |
LI G F, YAN L, MA Z M. An approach for approximate subgraph matching in fuzzy RDF graph[J].
Fuzzy Sets and Systems, 2019, 376: 106-126.
DOI: 10.1016/j.fss.2019.02.021. |
 2022, Vol. 39
2022, Vol. 39

