随着无线通信与人工智能技术的快速发展，智能互联汽车得到迅速推广与普及。先进的车载传感系统与高级的车载娱乐服务使智能汽车产生越来越多有价值的数据(如交通信息、车载娱乐数据)。这些数据常被收集并共享于其他智能汽车或智能交通设施，从而构建更为先进的智能交通系统，为智慧城市的建设打下坚实基础^[1-2]。然而，现有的数据共享中心化管理方式容易遭受单点失效、数据篡改等安全威胁，系统可靠性难以保障。尽管P2P(Peer-to-Peer)共享网络一定程度上克服了单点失效的问题，但由于安全防护和访问权限问题，其在车联网场景下并不实用。

近年来，区块链技术因其去中心化、不可篡改、安全可靠等优点被广泛应用于构建安全可靠的车联网数据共享系统^[3]。文献[2]提出了基于PoW(Proof of Work)和PoS(Proof of Stake)共识的去中心化可信数据管理系统，以实现对车辆数据可信度的评估与管理。在文献[4]中，区块链技术被用于解决数据交易中缺乏透明性、可追溯性和非授权数据修改等问题，作者设计了一种基于区块链的车联网数据交易通用框架，该框架能实现车联网数据安全交易。但上述方法因其共识计算量过大、系统搭建成本过高等问题，并不适用于搭建安全高效的区块链赋能的车联网数据共享系统。现有研究已经把高效的DPoS(Delegated Proof of Stake)共识机制引入到车联网中^[5-6]。委托权益证明DPoS共识机制是PoS共识机制的一种衍生机制，其基本思路是先从持有股份的节点中选出部分代表性节点作为矿工，再由这些矿工依次充当矿工领导者对交易信息进行打包，并由矿工领导者与验证者(即剩余的矿工)共同参与区块验证，进而产生新的区块^[7]。该机制不仅能有效解决PoW共识机制计算资源浪费和PoS共识机制的股份集中化问题，还可以快速地处理交易数据，并具有较高的系统吞吐量，因此该机制能很好地匹配车联网场景服务高并发的需求，具有广泛的应用前景。

然而，传统的基于DPoS共识算法的区块链赋能车联网系统中区块验证者数量有限(常为21个)，容易出现验证者串通合谋、产生错误区块验证结果的情况，从而危害区块链系统的安全性^[8]。为了解决验证者串通合谋的威胁，保证区块验证的安全性，当前矿工领导者产生的区块数据可由轻节点充当验证者进行共同验证和审查^[9]。文献[10]表明智能手机等边缘设备可以充当验证者参与区块验证。虽然更多的随机轻节点参与区块验证能提升区块验证的安全性，但因为区块验证过程需要消耗算力、带宽等资源，所以需要设计有效的激励机制鼓励轻节点参与到区块链赋能车联网的区块验证中。文献[9]利用契约理论激励轻节点参与区块验证以防止验证节点的内部共谋，但该机制无法及时响应轻节点的频繁变更情况。文献[11]提出斯坦伯格博弈来权衡区块验证中的安全要求、验证时延和成本，但该博弈模型建立在所有矿工已知完备环境信息的假设上，并不适用于轻节点频繁更换、环境信息未知的车联网场景。

针对上述研究工作的问题，本文在文献[11]的基础上，把智能汽车和DPoS共识算法的矿工间交互过程建模成斯坦伯格博弈模型，并由区块链用户(即智能汽车)作为博弈主方提供交易费以促进矿工快速、安全地完成区块的打包、验证。验证者作为博弈从方随机招募一定数量的轻节点提供验证服务并赚取交易费。此外，车辆的高移动性会导致车联网环境动态多变^[12]，传统的方案并不适用于此类场景，存在效果差、可扩展性弱等问题^[13]，因此，本文提出基于多智能体强化学习的方案以有效地解决动态多变环境中的区块验证决策问题。并可在环境信息不完备的情况下收敛到接近最优策略，从而最大化区块链用户与验证者的收益，实现高效、安全、可靠的区块验证。

本文的主要贡献如下：(1) 将轻节点引入到基于DPoS共识算法的区块链赋能车联网的数据共享区块验证过程中，保证了区块验证的效率的同时，也提升了区块链用户的满意度。(2) 将智能汽车和验证者之间的交互过程建模成斯坦伯格博弈模型，并通过多智能体近端策略优化算法(Multi-Agent Proximal Policy Optimization ，MAPPO)求解上述博弈过程的纳什均衡解。(3) 与传统Deep Q Network (DQN)方案进行性能对比，并对MAPPO的收敛性能进行了模拟和评估。

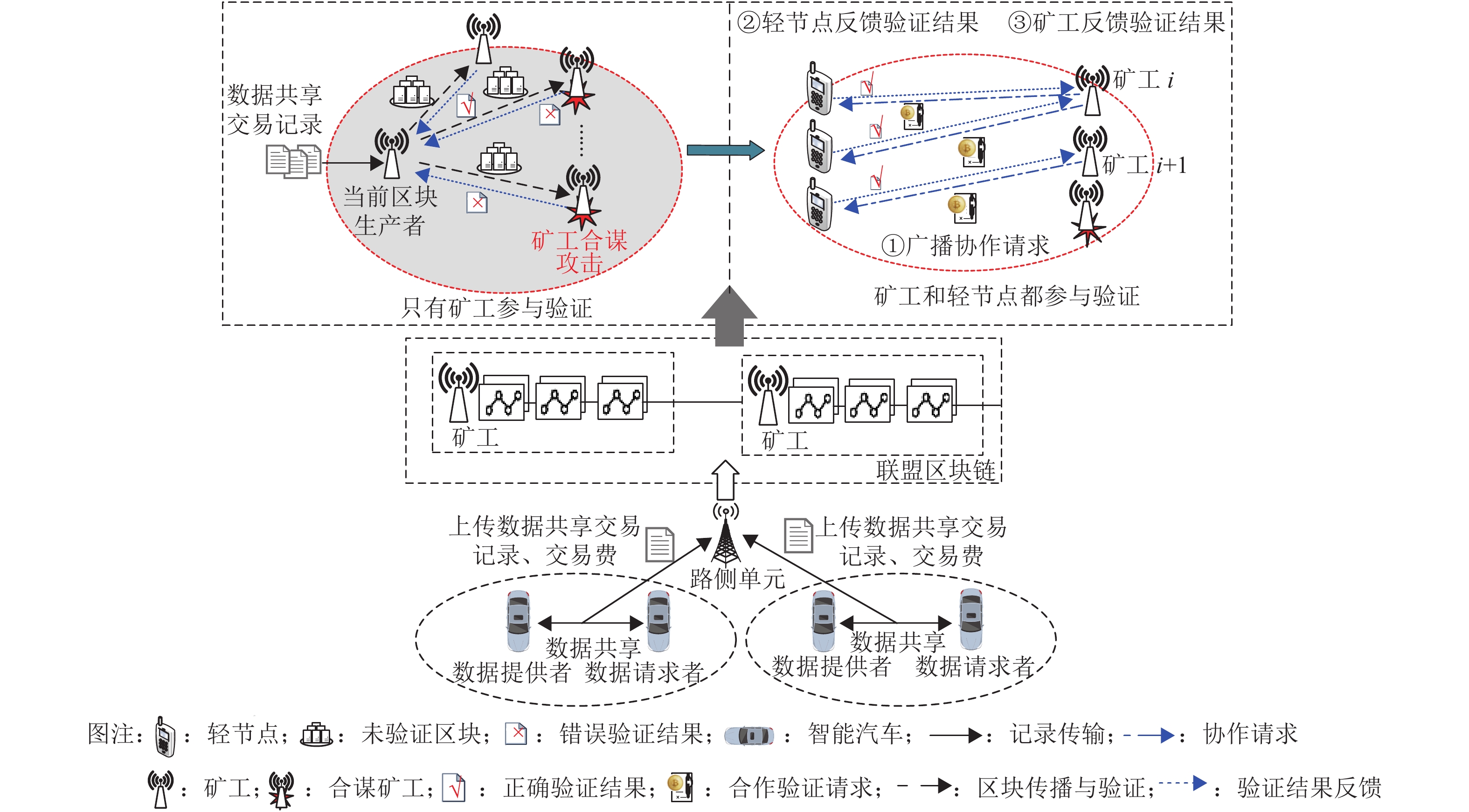
1 基于多智能体强化学习的区块安全验证方案 1.1 系统模型

如图1所示，本文考虑的基于DPoS共识算法的区块链网络主要包含以下实体：(1) 区块链用户(智能汽车)；(2) 矿工；(3) 轻节点。其中矿工和轻节点在区块验证阶段均为验证者角色^[14]。车辆间进行数据共享交易，并定期将生成的交易记录广播到网络中的矿工节点。在DPoS共识算法中，矿工轮流充当区块生产者，每个矿工在一个时间窗口内只能充当一次区块生产者，其余矿工将充当区块验证者角色。具体而言，当前的区块生产者将时间窗口内的合格交易记录放入一个区块中，并将该区块广播给其他矿工进行验证。与PoW等传统方案相比，DPoS中的矿工不需要相互竞争来获得挖矿奖励，矿工群体在完成区块打包和验证任务后，可分得一定奖励(用户交易费总和)。为了防止矿工之间验证合谋，矿工将新区块随机传播给合作的轻节点进行验证，从而保证区块的安全性与可靠性^[15]。

与文献[16-17]类似，基于DPoS的区块链中的每个矿工都根据自己的合作轻节点来分配特定的验证任务。因此，每个矿工都可以根据各自的验证贡献，即合作验证者(轻节点)的数量，从区块链用户那里分享到交易费用 $ f $ ，而矿工和验证者之间也会存在通信成本。轻节点完成区块验证任务后会获得服务奖励，并将验证结果反馈给矿工。

1.2 问题描述

本文考虑一个基于DPoS共识算法的区块链网络，其中包含一组矿工，表示为 $\cal{I}=\{1,\cdots ,i,\cdots ,I\}$ ^[11]。 $\cal{N}=\{{n}_{1},\cdots ,{n}_{i},\cdots ,{n}_{I}\}$ 则表示由所有矿工的策略构成的策略组合，矿工的策略是合作验证者的数量。矿工 $ i $ 的利润函数 ${U}_{m}^{i} $ 包括区块验证贡献获得的预期收入、区块验证的通信成本和合作验证者的招募成本，表示为^[11]

$ {U}_{m}^{i}={w}_{i}f{{n}_{i}}/\Bigg({\sum _{j\in \cal{I}}{n}_{j}}\Bigg)-{c}_{i}{n}_{i} $

(1)

式中： $ {w}_{i} $ 为通过验证获得的预期收入的权重因子， $f{{n}_{i}}/\Bigg({\displaystyle\sum _{j\in \cal{I}}{n}_{j}}\Bigg)$ 为矿工 $ i $ 根据其验证贡献(区块验证所招募的验证者个数为 $ {n}_{i} $ )获得的交易费。因为矿工与其招募的验证者之间常以无线方式进行通信，所以会产生一定的通信成本(如占用带宽资源)^[18]。因此，本文采用 $ {c}_{i}{n}_{i} $ 表示通信成本，其中 $ {c}_{i} > 0 $ 为给定系数，其中包含平均通信成本和合作验证者的招募成本^[11]。

区块链用户的效用函数U_s由预期满意度和激励成本(交易费) f 组成并表示为^[11]

$ {U}_{s}=F\left[{n}_{1},{n}_{2},\cdots ,{n}_{i};{\rho }_{1}\left({n}_{1}\right),{\rho }_{2}\left({n}_{2}\right),\cdots ,{\rho }_{i}\left({n}_{i}\right)\right]-f $

(2)

式中： $ {\rho }_{i}\left({n}_{i}\right) $ 是矿工 $ i\in \cal{I} $ 的区块传播时间， $ F\left[{n}_{1},{n}_{2},\cdots , $ $ {n}_{i};{\rho }_{1}\left({n}_{1}\right),{\rho }_{2}\left({n}_{2}\right),\cdots ,{\rho }_{i}\left({n}_{i}\right)\right] $ 是验证者集合中招募的验证者比例的满意度函数。与文献[11, 19]类似，本文考虑 $F[{n}_{1},{n}_{2},\cdots ,{n}_{i};{\rho }_{1}({n}_{1}),{\rho }_{2}({n}_{2}),\cdots ,{\rho }_{i}({n}_{i})]$ 是变量 $ {\{n}_{1},{n}_{2}, \cdots , $ $ {n}_{i}\} $ 的严格凹函数，其中 $ F\left[\mathrm{0,0},\cdots ,0;{\rho }_{1}\left(0\right),{\rho }_{2}\left(0\right),\cdots , $ $ {\rho }_{i}\left(0\right)\right]=0 $ 。这个满意度函数在每个 $ {n}_{i} $ ( $ i\in \cal{I} $ )上也是单调递增的^[11]。

由于矿工招募的轻节点验证者数目不同，矿工可能有不同的区块传播时间。在区块传播过程中，区块达成共识所需的时间由招募的验证者之间的传输时延 $ {\rho }_{p}^{i} $ 和区块验证时间 $ {\rho }_{v}^{i} $ 共同决定。对于大小为 $ b $ 的区块，达成共识的平均时间表示为 ${\rho }_{i}\left({n}_{i}\right)={\rho }_{p}^{i}+{\rho }_{v}^{i}= $ $ {b{n}_{i}}/({\delta {z}_{1}})+{z}_{2}{n}_{i}b$ ^{[11, 20]}。式中 $ {z}_{1} > 0 $ 和 $ {z}_{2} > 0 $ 为系统给定的系数。 $ \delta $ 为矿工和验证者之间通信链接的有效平均信道链路容量。与文献[11, 20]类似， $ {n}_{i}/{z}_{1} $ 为网络规模参数， $ {z}_{2}{n}_{i} $ 为由网络规模和验证者的平均验证速度共同决定的参数。区块链用户的效用受到区块传播延迟和提供的交易费这两方面的满意度的影响。验证者越多，区块链网络就越安全^[21]。然而，矿工可能需要通过多跳中继与远处的验证者进行通信，这也会导致更长的区块传播时间^[11]。因此，本文定义了一个安全延迟度量 $ {\mu }_{i} $ 来平衡网络规模和矿工 $ i $ 的区块传播时间关系， $ {\mu }_{i} $ 的表达式为^[11]

$ {\mu }_{i}=\frac{{y}_{1}{z}_{1}\delta {T}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{b{y}_{2}\left(1+{z}_{1}{z}_{2}\delta \right)}\cdot {n}_{i}^{q-1} $

(3)

式中： $ {y}_{1} > 0 $ 和 $ {y}_{2} > 0 $ 为系统给定的系数， $ {T}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 为区块链用户对区块传播的最大容忍时延， $ q\geqslant 2 $ 为网络规模的给定因子。为了便于表示，不失一般性地，本文考虑 $ q=2 $ ^{[11, 21]}，因此式(2)可表示为

$ {U}_{s}=F\left({\mu }_{1},{\mu }_{2},\cdots ,{\mu }_{i}\right)-f $

(4)

同样为了便于描述^{[11, 19]}，可知

$ {U}_{s}=\theta \mathrm{log}\Bigg(1+\frac{{y}_{1}{z}_{1}\delta {T}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{b{y}_{2}\left(1+{z}_{1}{z}_{2}\delta \right)}\sum _{i\in \cal{I}}{n}_{i}\Bigg)-f $

(5)

易证 $\dfrac{{\partial }^{2}{U}_{s}}{\partial {f}^{2}} < 0$ ，因此式(5)是一个凹函数，满足上文做出的假设^[11]。

区块链用户和矿工之间的交互可以表述为一个斯坦伯格博弈，其中区块链用户是主方，矿工是从方^{[11, 22]}。在第1阶段，区块链用户设定支付给矿工们的交易费，矿工们根据交易费大小在第2阶段中以最优比例招募验证者。理性的矿工不会以负利润参与挖矿，因此假设区块链用户提供的交易费大于最小值 $ {f}_{\mathrm{m}\mathrm{i}\mathrm{n}} $ 。主、从双方的目标函数为^[11]

主方：

$ \left\{\begin{aligned} & \underset{f}{\mathrm{max}}\;{U}_{s}\left(f\right) \\& {\rm{s.t}}.\;\; {U}_{s}\left(f\right)\geqslant 0 ,\; {f}_{\mathrm{m}\mathrm{a}\mathrm{x}}\geqslant f > {f}_{\mathrm{m}\mathrm{i}\mathrm{n}} \end{aligned}\right. $

(6)

从方：

$ \left\{\begin{aligned} & \mathop {\max }\limits_{{n_i}} \;{U}_{m}^{i}\left({n}_{i}\right) \\& {\rm{ s.t.}}\;\; {U}_{m}^{i}\left({n}_{i}\right)\geqslant 0 ,\; {n}_{\mathrm{m}\mathrm{a}\mathrm{x}}\geqslant {n}_{i}\geqslant 0 \end{aligned} \right. $

(7)

2 多智能体强化学习设计

在本节中，首先介绍多智能体近端策略优化算法，然后利用该算法来解决上述斯坦伯格博弈问题。将多用户参与的斯坦博格博弈转化为局部可观测的马尔可夫决策过程，包括状态空间、观测空间、动作空间、奖励空间和状态转移概率。然后让多智能体在与环境的交互中进行策略迭代与策略提升，找到该博弈的均衡。

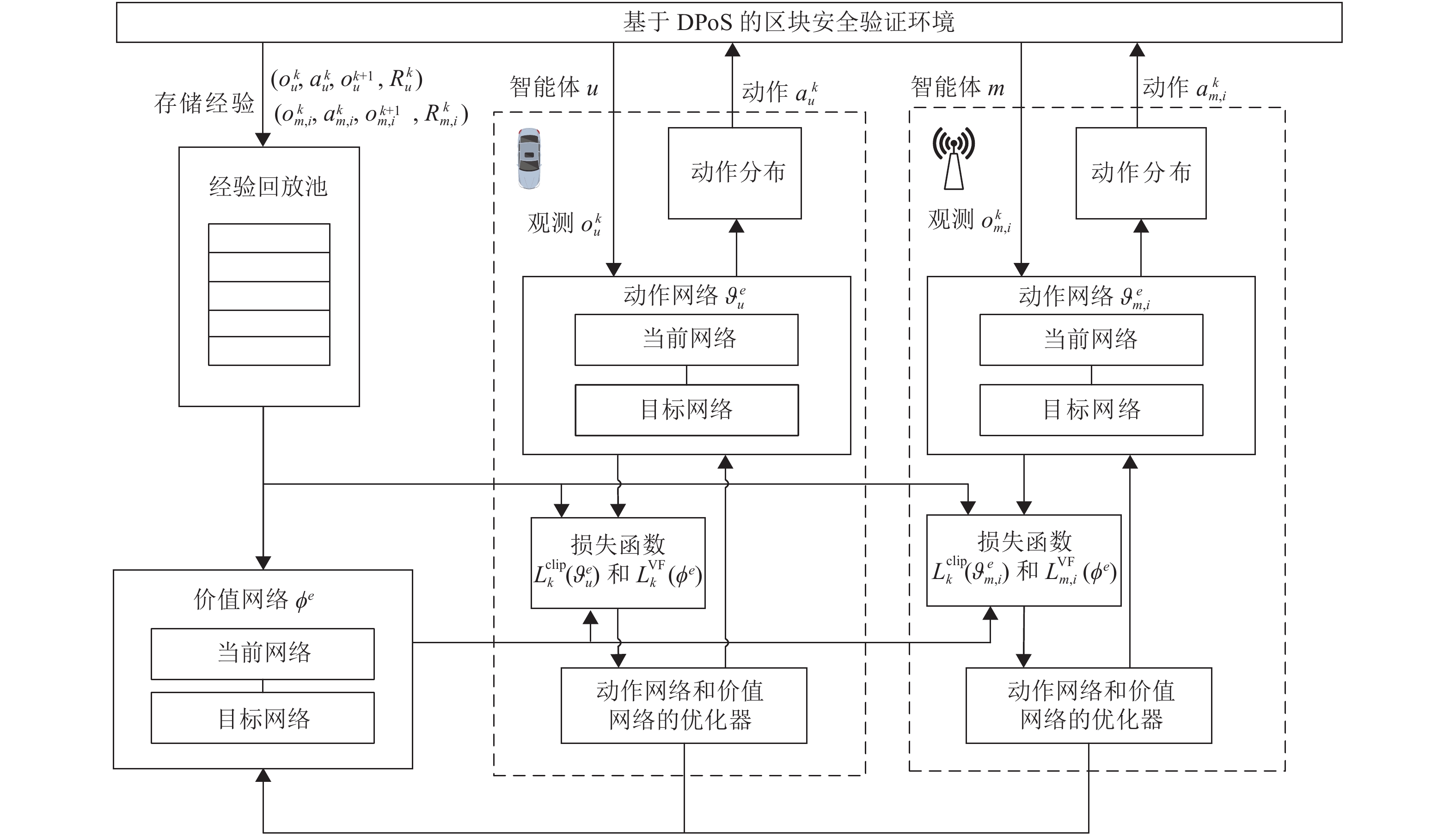
2.1 多智能体系统与局部可观马尔可夫决策过程

多智能体系统是环境和环境中的多个智能体组成的集合，其目标是将大而复杂的系统建设成小而彼此互相通信协调的易于管理的系统^[23]。在智能体学习过程中，智能体首先会观测当前环境的状态，然后根据自身的观察和策略做出动作，并在环境中获得奖励，最后通过最大化累计奖励的方式来更新自身的策略。具体如图2所示。

在本文中， $ {n}^{k}\in {A}_{m} $ 和 $ {f}^{k}\in {A}_{u} $ 分别表示矿工招募的轻节点验证者数量和区块链用户设定的交易费用，其中 $ {A}_{m} $ 和 $ {A}_{u} $ 分别是矿工和区块链用户的动作空间。在每个时间段，矿工和区块链用户依次采取行动。

在时间段 $ k $ ，区块链用户首先根据从方博弈中观察到的状态 $ {s}_{u}^{k}:={\left[{n}_{i}^{k-1}\right]}_{i\in \cal{I}} $ 来设置区块验证的交易费用 $ {f}^{k} $ ，其中 $ {n}_{i}^{k-1} $ 表示在时间段 $ (k-1) $ 矿工 $ i $ 招募的验证者数量。区块链用户的奖励函数可表示为

${U}_{s}=\theta \mathrm{log}\Bigg(1+\frac{{y}_{1}{z}_{1}\delta {T}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{b{y}_{2}\left(1+{z}_{1}{z}_{2}\delta \right)}\sum _{i\in \cal{I}}{n}_{i}^{k-1}\Bigg)-f $

(8)

类似的，每个矿工在观察到区块链用户在时间段 $ k $ 设置的交易费用 $ {f}^{k} $ 后，根据状态 $ {s}_{m}^{k}:={f}^{k} $ 决定其招募的验证者数量 $ {n}^{k} $ 。在斯坦伯格博弈模型中，区块链用户作为主方，矿工作为从方。

定义当前决策轮次 $ k(k=1,\mathrm{ }2,\mathrm{ }\cdots ,K) $ 的全局状态信息为 $ {S}^{k} $ ，其由矿工招募的验证者数量 $ {n}_{i}^{k}(i\in \cal{I}) $ 和用户交易费 $ {f}^{k} $ 组成， $ {S}^{k} $ 表示为

$ \begin{split} &\;\\& {S}^{k}:=\{{n}_{i}^{k},{f}^{k}\} \end{split} $

(9)

智能体根据对环境的部分观测来采取动作。定义区块链用户在当前决策轮次 $ k $ 的观测是之前 $ L $ 轮验证者的数量，并表示为 $ {o}_{u}^{k}:=\left\{{n}_{i}^{k-L},{n}_{i}^{k-L+1}, \cdots ,{n}_{i}^{k-1}\right\}, i\in \cal{I} $ 。区块链用户的策略是 $ \pi ({a}_{u}^{k}|{o}_{u}^{k}) $ ，据此做出的动作为 $ {a}_{u}^{k}:=\left\{{f}^{k}\right\} $ ，获得的奖励是 $ R\left({S}^{k},{a}_{u}^{k}\right)={U}_{s} $ 。定义矿工在当前决策轮次 $ k $ 的观测是之前 $ L $ 轮区块链用户交易费，表示为 $ {o}_{m}^{k}={o}_{m,1}^{k}={o}_{m,2}^{k}=\mathrm{ }\cdots ={o}_{m,i}^{k}= $ $ \{{f}^{k-L},{f}^{k-L+1},\cdots ,{f}^{k-1}\}, $ $ i\in \cal{I} $ 。矿工 $ i $ 的策略是 $ \pi ({a}_{m,i}^{k}|{o}_{m}^{k}) $ ，据此做出的动作是 $ {a}_{m,i}^{k}:=\left\{{n}_{i}^{k}\right\},i\in \cal{I} $ ，矿工 $ i $ 获得的奖励是 $ R({S}^{k},{a}_{m,i}^{k})={U}_{m}^{i} $ 。

2.2 策略迭代

考虑到智能体需要同时与环境和环境中其他的智能体进行交互，智能体在做决策时，其他智能体也在采取动作，因此很难得到一个稳定的最优的策略^[24]。与此同时，多智能体环境在非平稳状态下容易导致马尔可夫性失效，因此直接在多智能体环境中应用单智能体强化学习很难保证收敛性^[25]。MAPPO是PPO(Proximal Policy Optimization)算法应用于多智能体环境的变种，MAPPO同样采用actor-critic架构，不同之处在于critic学习的是一个中心化值函数^[26]，可以保证更好的收敛性能和样本复杂性。

给定策略 $ \pi $ 在状态 $ S $ 下的状态价值函数为 $ {V}_\pi\left(S\right) $ ，表示从状态 $ S $ 出发遵从策略 $ \pi $ 获得的期望回报

$ {V}_\pi\left(S\right):={\mathbb{E}}_\pi\left[\sum _{k=0}^{K}{\gamma }^{k}R({S}^{k},{a}^{k})|{S}^{0}=S\right] $

(10)

式中： $ {\mathbb{E}}_\pi(\cdot ) $ 表示智能体遵循策略 $ \pi $ 的随机变量的期望值。 $ \gamma \in \left[\mathrm{0,1}\right] $ 是奖励的折扣因子。MAPPO中critic和actor误差的计算应分开进行，且分别使用独立的网络( $ \vartheta \mathrm{和}\phi $ )来实现策略以及状态估值^[26]。在状态价值函数 $ {V}_\pi\left(S\right) $ 已知的基础上，通过广义优势评估(Generalized Advantage Estimation，GAE)^[27]来计算方差减小的优势函数 $ A(S,a) $ ，而当前决策轮次k的优势函数表示为

$ A({S}^{k},{a}^{k})=\sum _{l=k}^{K-1}{(\gamma\lambda) }^{l-k}(R({S}^{l},{a}^{l})+{\gamma }V({S}^{(l+1)})-V({S}^{l})) $

(11)

式中：λ为GAE截断系数。根据文献[28]，MAPPO中智能体的代理目标函数定义为

$ {L}_{k}^{\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{p}}({\vartheta }^{e})={\mathbb{E}}_{k}[\mathrm{m}\mathrm{i}\mathrm{n}({r}_{k}^{e}({\vartheta }^{e})A({S}^{k},{a}^{k}),g(\epsilon ,A({S}^{k},{a}^{k})))] $

(12)

式中：

$ {r}^{e}({\vartheta }^{e})=\frac{\pi_{{\vartheta }^{e}}({a}^{k}|{o}^{k})}{\pi_{{\vartheta }^{e\text{'}}}({a}^{k}|{o}^{k})} $

(13)

$ g\left(\epsilon ,A\right)=\left\{\begin{aligned} & \left(1+\epsilon \right)A,A\geqslant 0\\& \left(1-\epsilon \right)A,A < 0 \end{aligned}\right. $

(14)

$ {\vartheta }^{e\text{'}} $ 为用来采样的策略参数，裁剪率 $ \epsilon $ 为超参数，r^e为概率比。

给定轨迹 $ D $ ，智能体的策略通过式(15)进行更新^[26]，更新后得到 ${\vartheta }_{{\rm{new}}}^{e} $ 。

$ {\vartheta }_{\rm{new}}^{e}=\mathrm{arg}\;\underset{\vartheta }{\mathrm{max}}\frac{1}{\left|D\right|}\sum _{D}{\mathbb{E}}_{k}[{L}_{k}^{\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{p}}({\vartheta }^{e})] $

(15)

实际上， $ {\vartheta }^{e} $ 可通过随机梯度上升迭代更新。

$ {\vartheta }^{e}\leftarrow {\vartheta }^{e}+\alpha \nabla {L}_{k}^{\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{p}}\left({\vartheta }^{e}\right) $

(16)

式中： $ \alpha $ 为策略的学习率。

全局critic是通过均方误差回归来更新^[26]，更新后得到 ${\mathrm{\phi }}_{\rm{new}}^{e} $

$ \begin{split} & {{\mathrm{\phi }}_{\rm{new}}^{e}={\rm{arg}}\;\mathop {\min }\limits_{\phi} {L}_{k}^{VF}\left(\phi \right)}=\\& {\rm{arg}}\;\mathop {\min }\limits_{\phi} \frac{1}{\left|D\right|}\sum _{D}\mathbb{E}[(V({S}^{k})-{V}_{\rm{target}}^{k})^{2}] \end{split} $

(17)

因此， $ \phi $ 可以通过随机梯度下降来更新。

$ {\phi }^{e}\leftarrow {\phi }^{e}-\beta \nabla {L}_{k}^{VF}\left(\phi \right) $

(18)

式中： $ \beta $ 为critic的学习率。

具体伪代码如算法1所示。

算法1 策略迭代伪代码

1. 初始化 $ {\vartheta }_{u} $ , $ {\vartheta }_{m,i} $ ( $ i\in \cal{I} $ ), $ \phi $ , $ \mathrm{\gamma } $ , $ \mathrm{\epsilon } $ , $ S $

2. for episode e $ \in 1,\mathrm{ }2,\mathrm{ }\cdots ,E $ do

3. 重置经验回放池 $ {D}_{u},{D}_{m,i}(i\in \cal{I}) $

4. for Round $ k\in 1,\mathrm{ }2,\mathrm{ }\cdots ,K $ do

5. 将用户观测 $ {o}_{u}^{k} $ 输入到策略网络 $ {\vartheta }_{u}^{e} $ ，得到当前动作 $ {a}_{u}^{k} $ 。将矿工们的观测 $ {o}_{m,i}^{k} $ ( $ i\in \cal{I} $ )输入到对应的策略网络 $ {\vartheta }_{m,i}^{e} $ ( $ i\in \cal{I} $ )，分别得到对应动作 $ {a}_{m,i}^{k} $ ( $ i\in \cal{I} $ )。

6. 环境更新 $ {S}^{k}\to {S}^{k+1} $ ，计算奖励 $ {R}_{u}^{k} $ , $ {R}_{m,i}^{k} $ 。

7. end for

8. 收集所有智能体的轨迹： $ {\tau }^{d}={\{{o}_{d}^{k},{a}_{d}^{k},{R}_{d}^{k}\}}_{k=1}^{K} $ ，其中 $ d\in \{u,m\} $ 。

9. 根据式(10)计算 $ {\left\{{V}_{d}^{k}\right\}}_{k=1}^{K} $ 。

10. 根据式(11)计算优势函数 $ {\left\{{A}_{d}^{k}\right\}}_{k=1}^{K} $ 。

11. 存储数据 ${\{{o}_{u}^{k},{a}_{u}^{k},{V}_{u}^{k},{A}_{u}^{k}\}}_{k=1}^{K}$ 到 $ {D}_{u} $ ，存储数据 $\{{o}_{m,i}^{k}, {a}_{m,i}^{k}, $ $ {V}_{m,i}^{k},{A}_{m,i}^{k}\}_{k=1}^{K}$ 到 $ {D}_{m,i}(i\in \cal{I}) $ 。

12. for $ h\in 1,\mathrm{ }2,\mathrm{ }\cdots ,H $ do

13. 随机从经验回放池 $ {D}_{u},{D}_{m,i}(i\in \cal{I}) $ 抽取经验 $ {D}_{h} $ 。

14. 根据式(16)对每个智能体分别更新策略 $ {\vartheta }_{u}^{e} $ ， $ {\vartheta }_{m,i}^{e} $ ( $ i\in \cal{I} $ )。

15. 根据式(18)更新全局critic参数 $ {\phi }^{e} $ 。

16. end for

17. $ {\vartheta }_{u}^{e+1}\leftarrow {\vartheta }_{u}^{e} $ , $ {\vartheta }_{m,i}^{e+1}\leftarrow {\vartheta }_{m,i}^{e} $ , $ {\phi }^{e+1}\leftarrow {\phi }^{e} $ 。

18. end for

3 分析与实验评估

本节采用仿真的方式评估多智能体强化学习算法在上述博弈模型中的相关性能。

3.1 仿真设计

本文仿真实验环境是基于gym构建的，具体参数配置见表1。仿真实验运行在配置Intel Xeon CPU@1.6 GHz×12、TITAN X GPU、64 G 内存、Ubuntu 18.0.1系统、Pytorch 1.2、Python 3.6的台式机上。

在实验过程中，对于所提MAPPO算法，本文采用Adam优化器，学习率( $ \alpha =\beta $ )设置为3×10⁻⁴。策略和值网络均采用两层全连接网络，其中每层有64个神经元，采用ReLU激活函数。设置折扣因子 $ \gamma $ 为0.99，裁剪率 $\epsilon 为0.2$ ，GAE截断系数 $\lambda 为0.95$ ，过去经验轮数 $L为4$ ，批大小为32。本文采用传统深度强化学习Deep Q Network (DQN)算法作为仿真实验的对比算法，所有智能体的策略网络均采用两层全连接网络，其中每层有64个神经元，采用ReLU激活函数，学习率(α=β)设置为3.5×10⁻⁴，折扣因子 $\gamma $ 为0.99，探索率为0.01。同时对上述2种算法进行训练，训练轮数E为100，决策轮次长度K为16。

3.2 实验分析

首先分析所提算法的收敛性能，并进一步研究不同矿工数量对区块链用户和矿工的策略的影响。

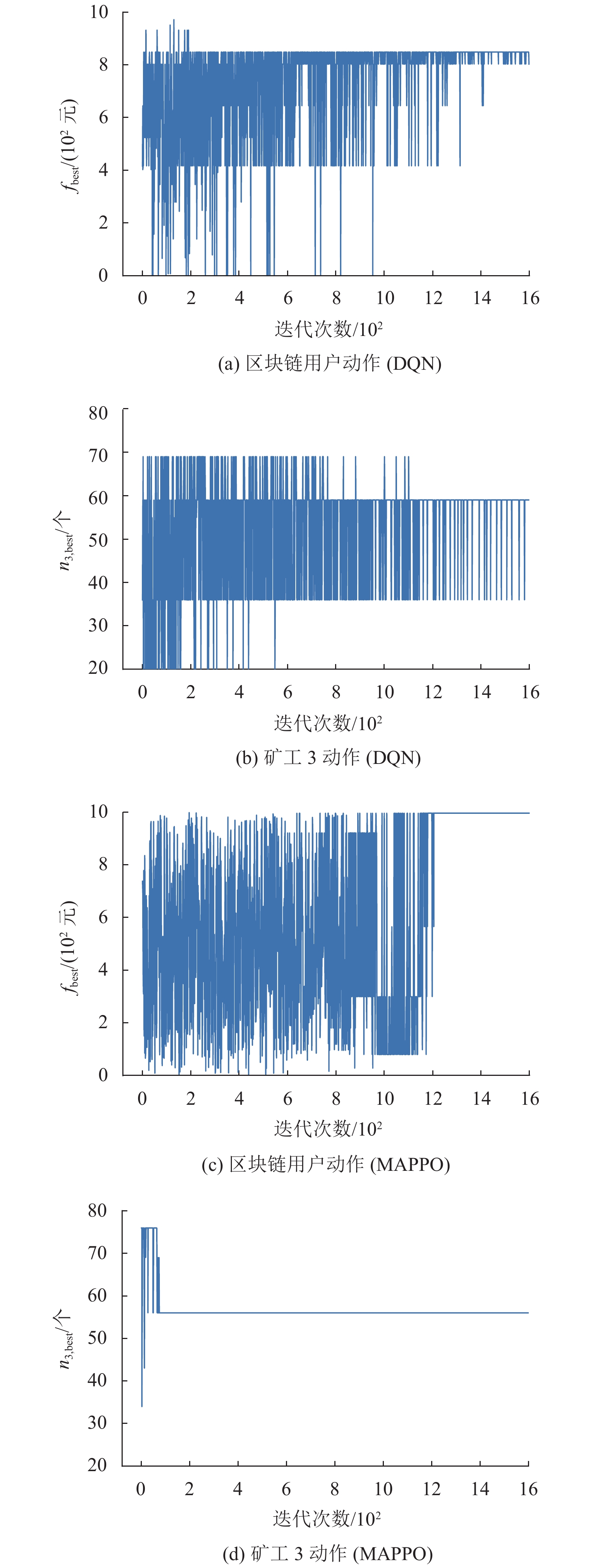
在仿真中，选取并观察其中1个区块链用户和3个矿工的实验性能，分别通过MAPPO算法和DQN算法来学习区块链用户和矿工的安全验证策略。图3为DQN算法和MAPPO算法的收敛性能对比，其中f_best 为最优交易费，n_3,best为矿工3最优验证者数量。MAPPO算法在迭代约1 200次后，算法已基本收敛，这是因为在中心化值函数的指导下，智能体更容易学习到兼顾其他智能体的策略，能同时增加区块链用户的效用和矿工的个人利润。与MAPPO算法相比，DQN算法的性能表现较差，这是因为直接将单智能算法应用到多智能体环境中会导致其无法收敛。

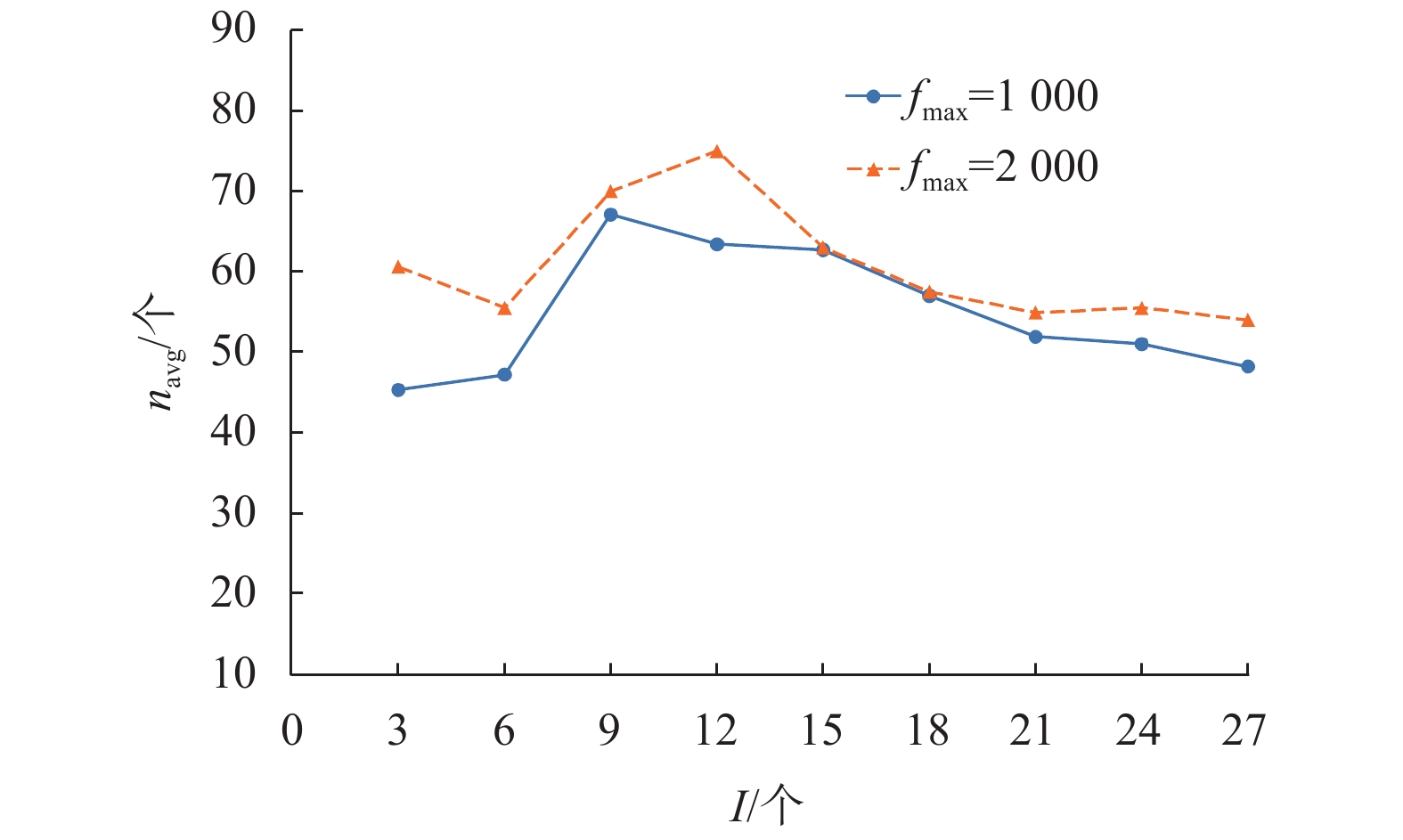
随后，评估不同矿工数量I对平均招募验证者数量n_avg的影响，并将结果记录在图4中。如图4所示，随着矿工数量的增加，验证者的数量先增加后减少。这是因为矿工的收益由其招募的验证者数量决定，随着矿工数量的增加，矿工们为了获得更大的收益，倾向于招募更多的验证者来提供更大的贡献。但随着矿工数量的进一步增加，通信和招募成本增加的速度大于收益增加的速度，矿工们的收益减少。图4同时也显示了用户交易费对平均招募验证者数量的影响。随着用户交易费用的增加，矿工们倾向于招募更多的验证者，这是因为用户交易费用的增加提高了矿工们的期望收益值。

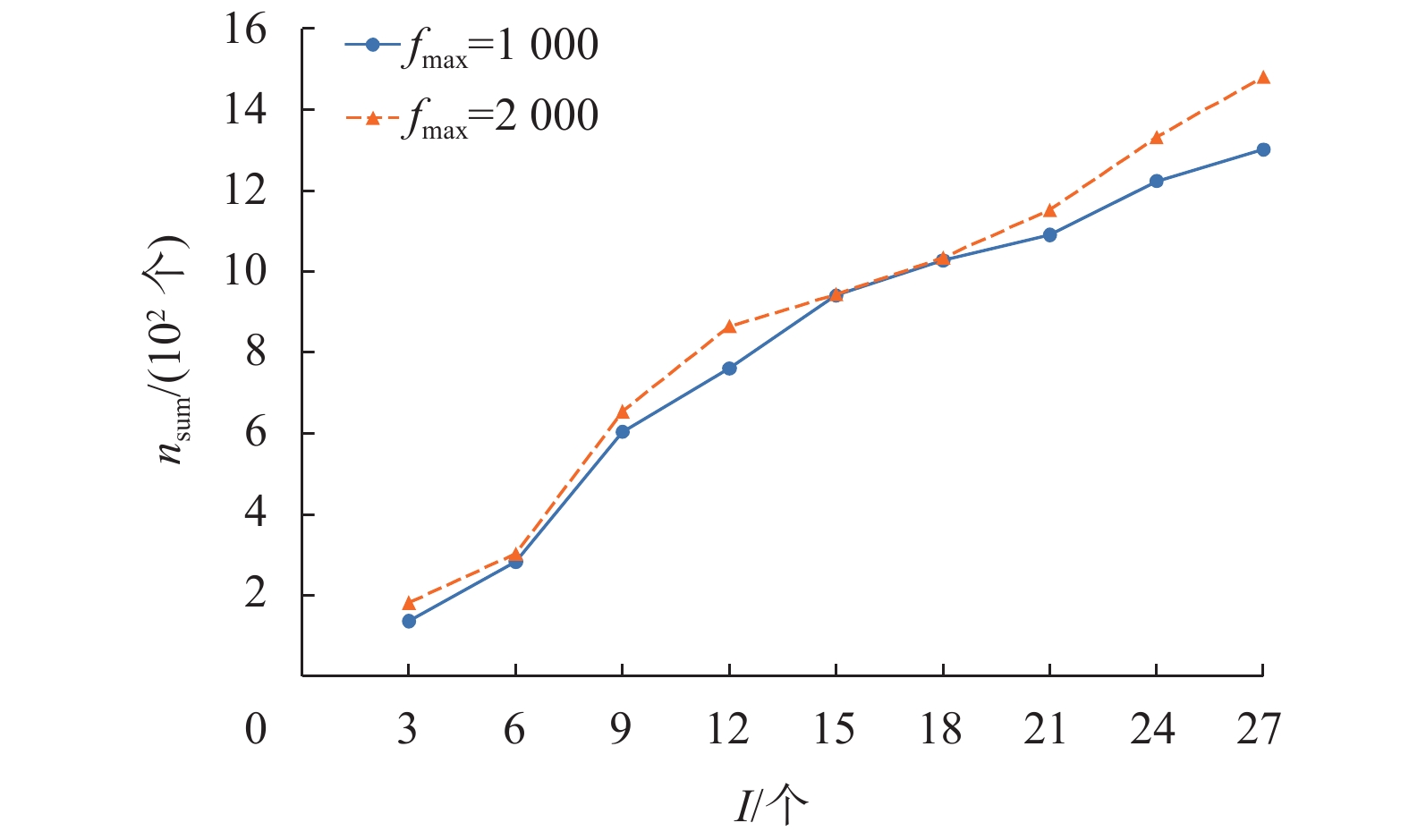
尽管平均招募验证者的个数随着矿工数量的进一步增加而下降，但总的验证者数量n_sum却是在逐渐增加(如图5所示)。这是因为矿工之间的竞争在一定程度上影响了期望回报和招募验证者数量之间的关系，使矿工们依旧有获得回报的动机，这也在一定程度上提高了区块验证的安全性。

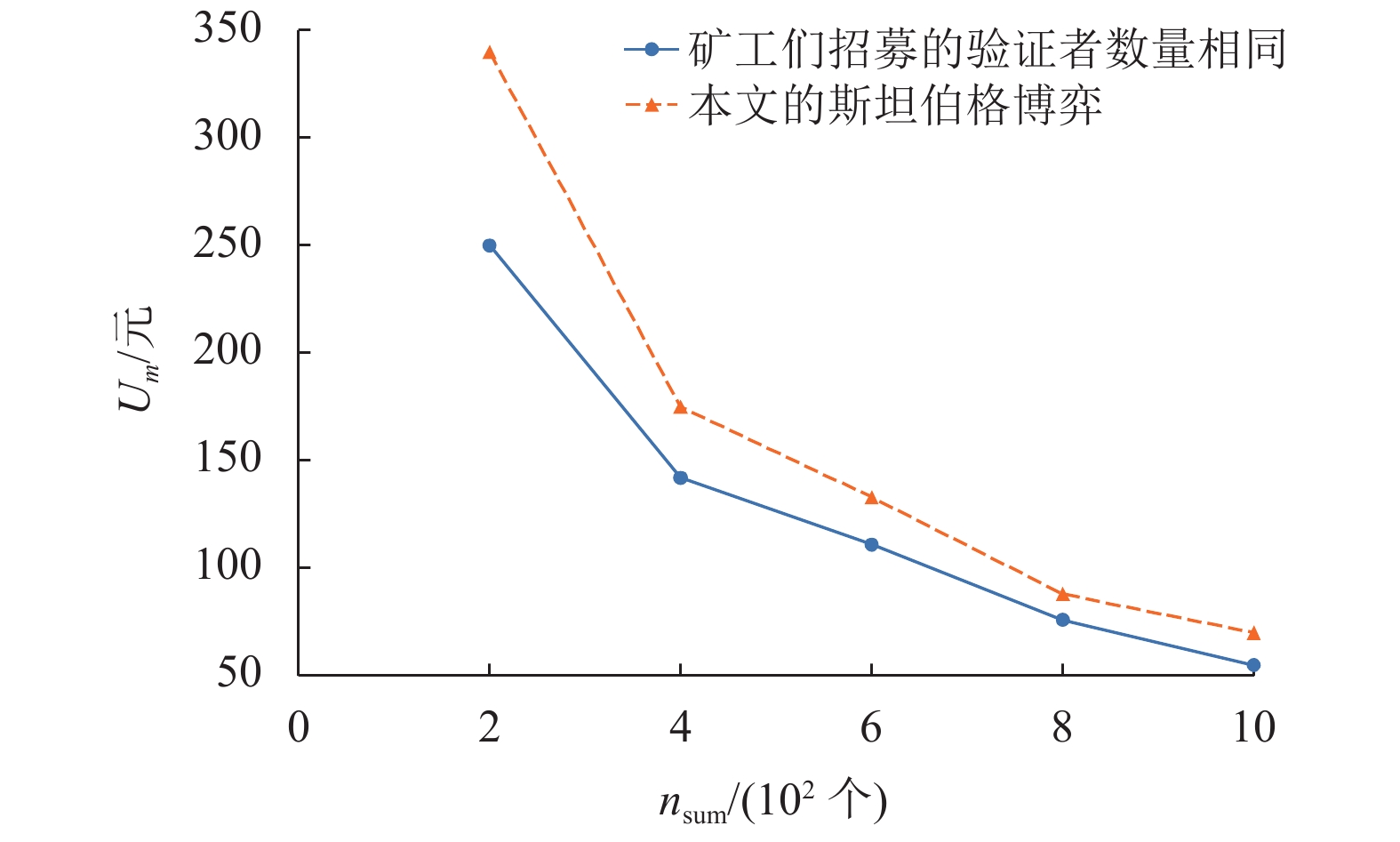
图6显示了总的验证者数量n_sum和矿工收益U_m之间的关系。由于验证者之间存在竞争，当总的验证者数量增加时，矿工的收益减少。此外，本文博弈模型中的矿工利润比每个矿工招募相同数量的轻节点验证者的方案中的矿工利润高，这是因为每个矿工都可以计算最佳招募验证者数量来获得收益最大化。

4 结束语

本文针对基于DPoS共识算法的区块链赋能车联网数据共享的区块验证过程中的共谋问题，把轻节点引入区块验证中，并且将智能汽车和矿工之间的交互建成斯坦伯格博弈模型。通过多智能体近端策略优化算法求解斯塔伯格博弈的纳什均衡解。实验结果表明所提方案可以有效搜索到接近最优的策略，从而保证区块验证的安全性与可靠性。